Validation of a Model for Estimating the Strength of a Vortex Created from the Bound Circulation of a Vortex Generator
Abstract
1. Introduction
2. Methods
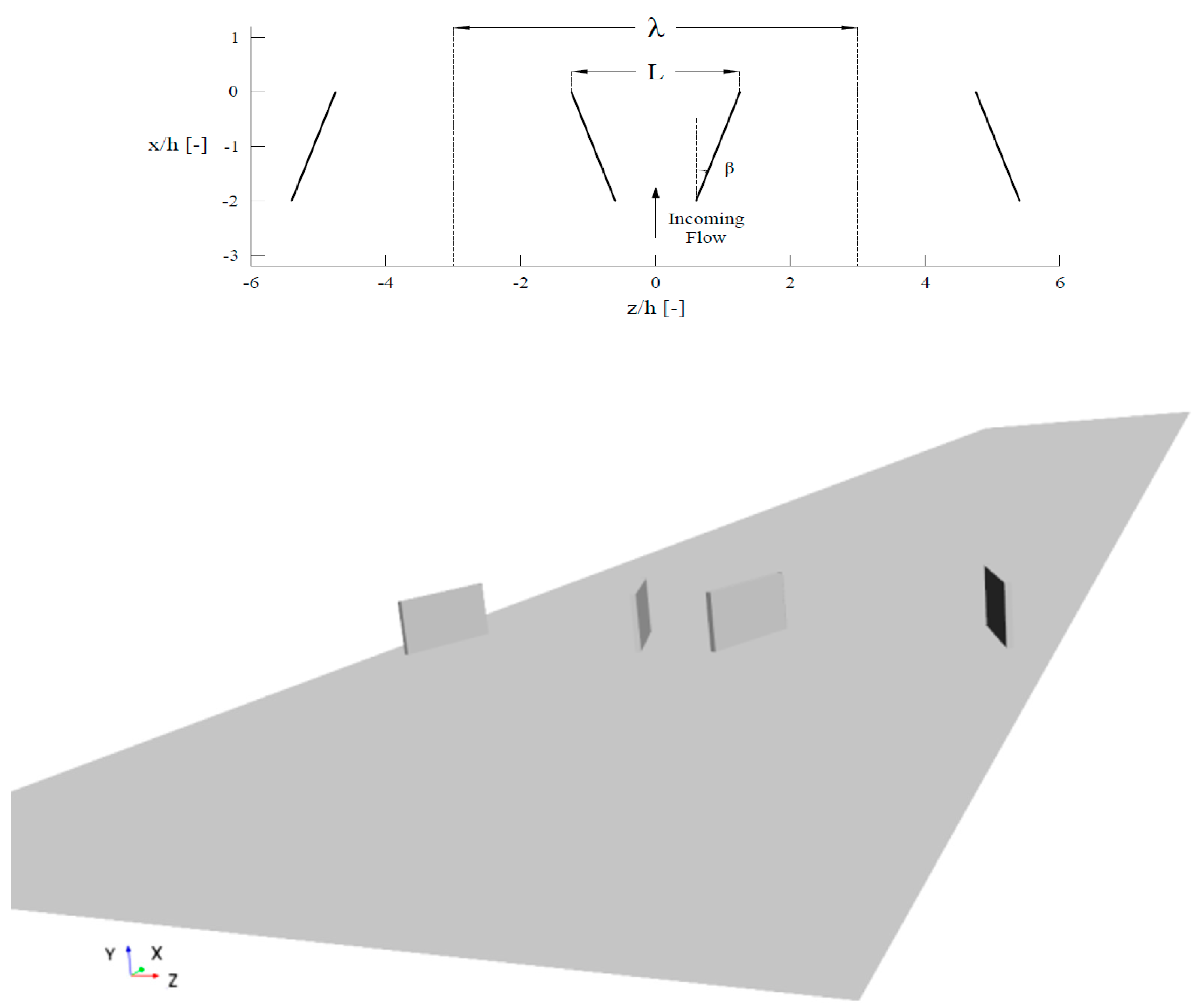
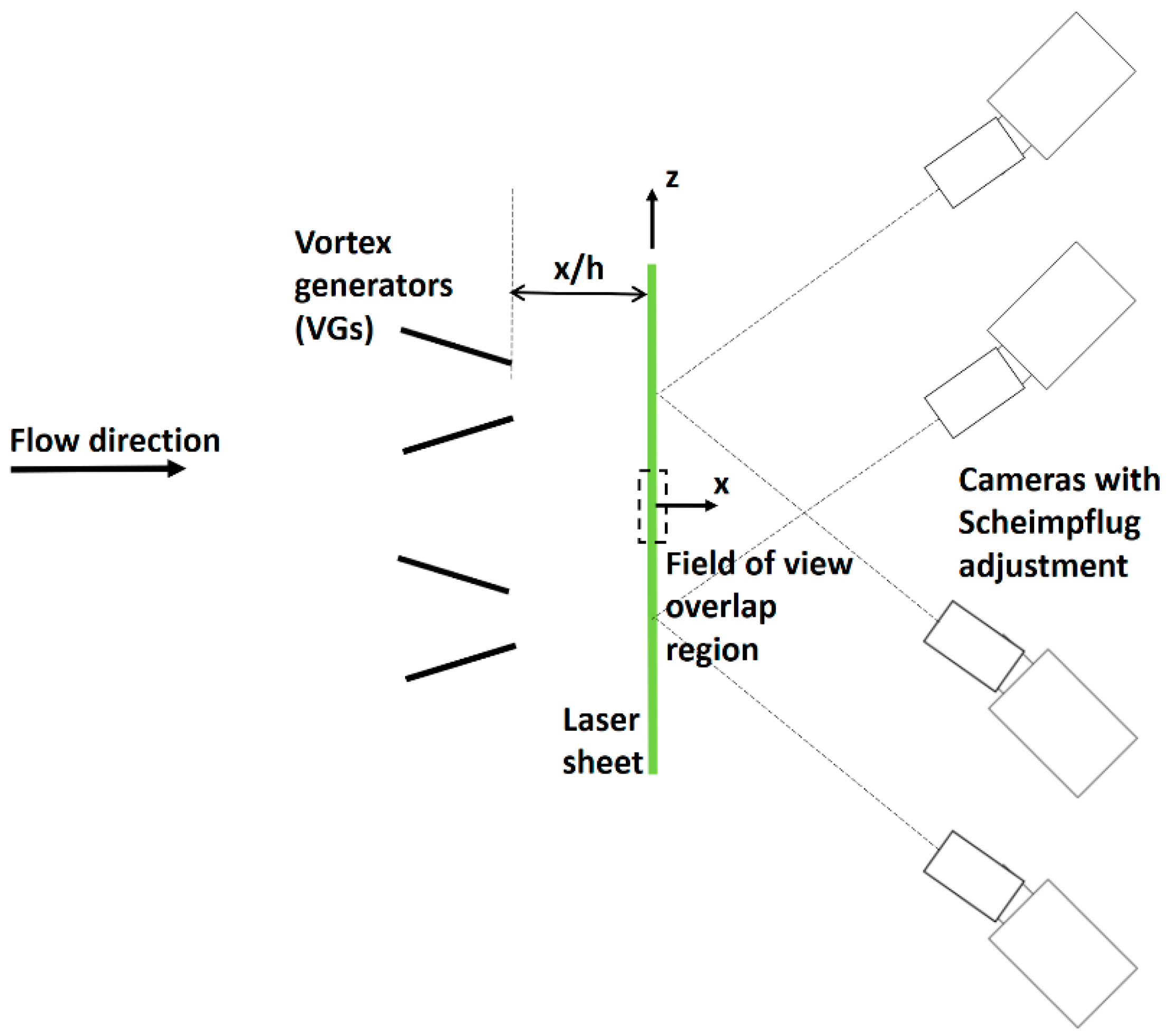
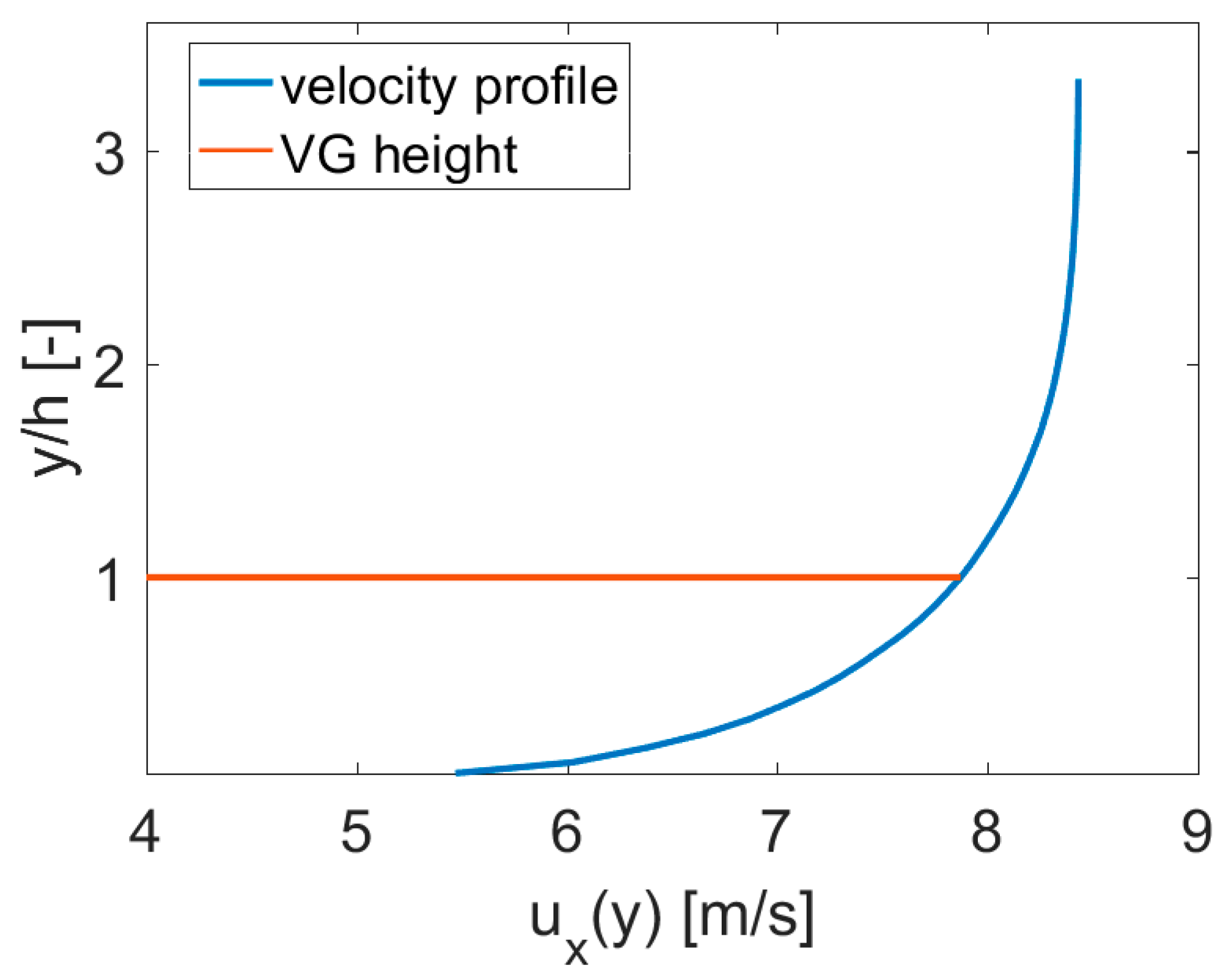
2.1. Experimental Setup
2.2. Numerical Model
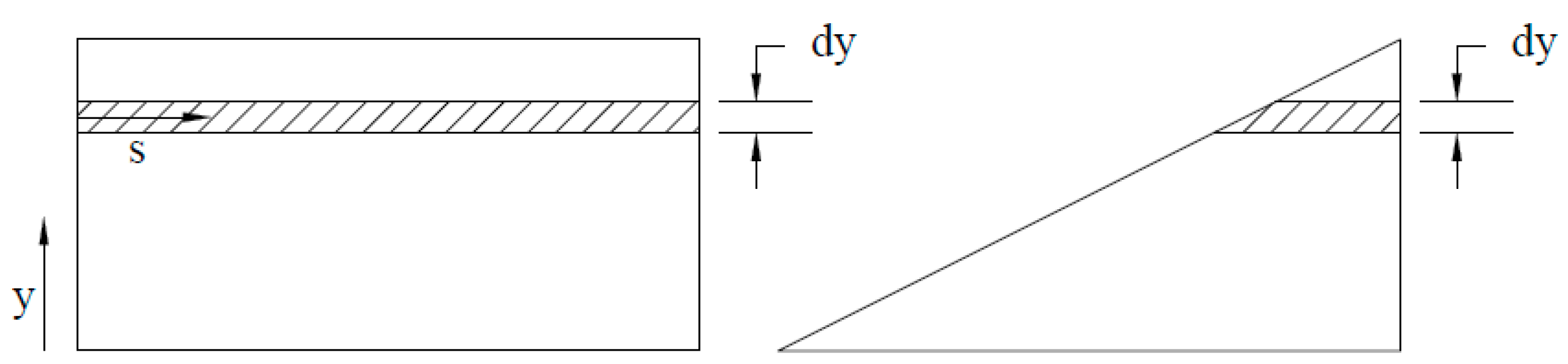
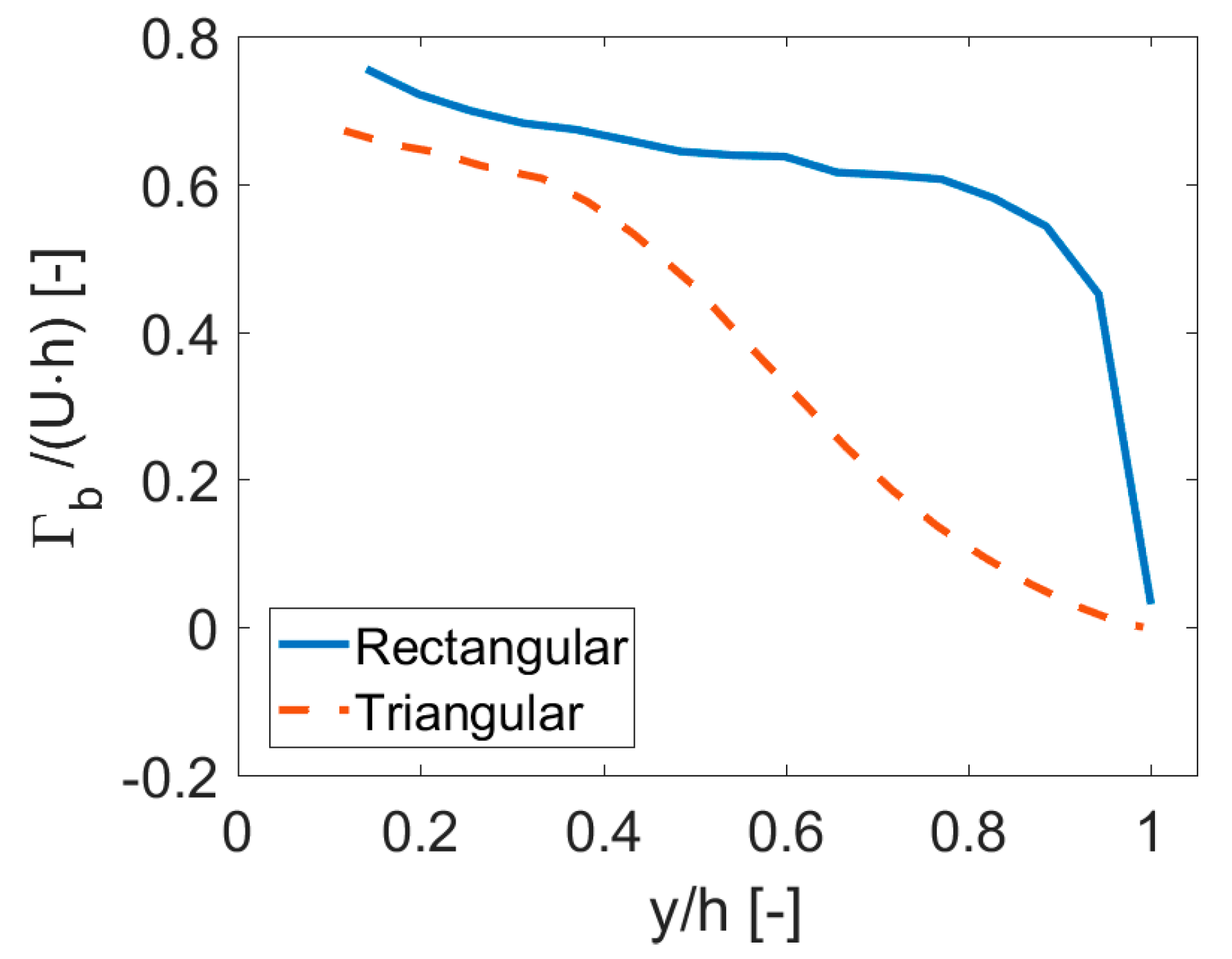
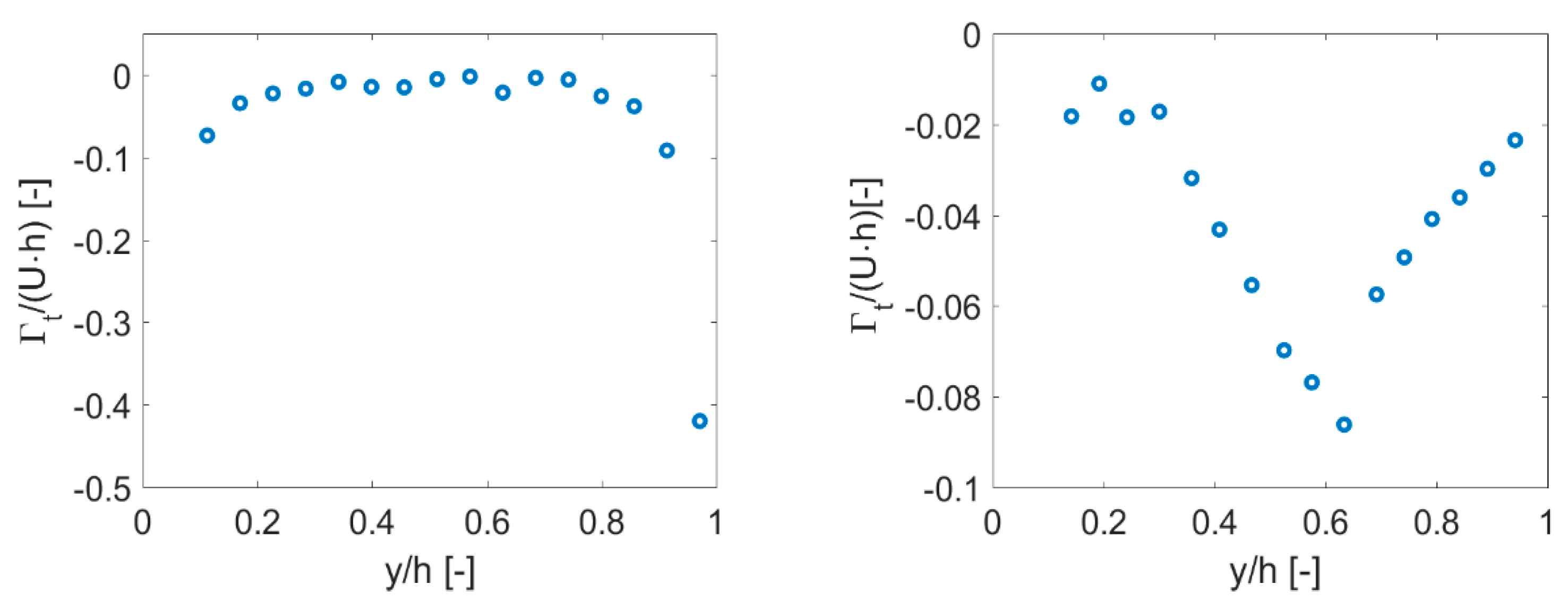
3. Estimating the Bound and Trailed Circulation from CFD
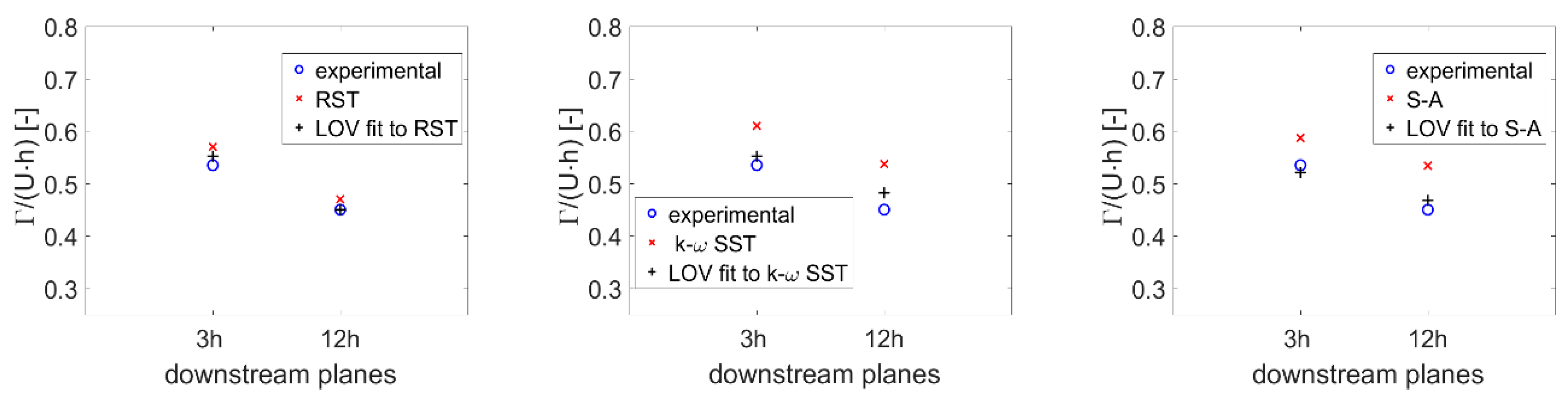
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| VG | Vortex Generator |
| RANS | Reynolds-Averaged Navier–Stokes |
| LOV | Lamb-Oseen Vortex |
| PIV | Particle Image Velocimetry |
| RST | Reynolds Stress Transport Turbulence Model |
| S-A | Spalart–Allmaras Transport Turbulence Model |
References
- Taylor, H.D. The Elimination of Diffuser Separation by Vortex Generators; Research Department Report No. R-4012-3; United Aircraft Corporation: East Hartford, CT, USA, 1947. [Google Scholar]
- Taylor, H.D. Design Criteria for and Applications of the Vortex Generator Mixing Principle; Research Department Report No. M-15038-1; United Aircraft Corporation: East Hartford, CT, USA, 1948. [Google Scholar]
- Taylor, H.D. Summary Report on Vortex Generators; Research Department Report No. R-05280-9; United Aircraft Corporation: East Hartford, CT, USA, 1950. [Google Scholar]
- Wang, H.; Zhang, B.; Qiu, Q.; Xu, X. Flow control on the NREL S809 wind turbine airfoil usingvortexgenerators. Energy 2017, 118, 1210–1221. [Google Scholar] [CrossRef]
- Xia, H.H.; Tang, G.H.; Shi, Y.; Tao, W.Q. Simulation of heat transfer enhancement by longitudinalvortexgeneratorsin dimple heat exchangers. Energy 2014, 74, 27–36. [Google Scholar] [CrossRef]
- Luo, L.; Du, W.; Wang, S.; Wang, L.; Zhang, X. Multi-objective optimization of a solar receiver considering both the dimple/protrusion depth and delta-wingletvortexgenerators. Energy 2017, 137, 1–19. [Google Scholar] [CrossRef]
- Ma, T.; Pandit, J.; Ekkad, S.V.; Huxtable, S.T.; Wang, Q. Simulation of thermoelectric-hydraulic performance of a thermoelectric powergeneratorwith longitudinal vortexgenerators. Energy 2015, 84, 695–703. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Rikhtegar, F.; Sabaghan, A.; Roohi, E. Heat transfer and entropy generation in a microchannel with longitudinal vortex generators using nanofluids. Energy 2016, 101, 190–201. [Google Scholar] [CrossRef]
- Velte, C.M.; Hansen, M.O.L.; Okulov, V.L. Helical structure of longitudinal vortices embedded in turbulent wall-bounded flow. J. Fluid Mech. 2009, 619, 167–177. [Google Scholar] [CrossRef]
- Pearcey, H.H. Shock Induced Separation and Its Prevention by Design and Boundary Layer Control. In Boundary Layer and Flow Control; Lachmann, G.V., Ed.; Pergamon Press: Oxford, UK, 1961; Volume 2, pp. 1166–1344. [Google Scholar]
- Jones, J.P. The Calculation of Paths of Vortices from a System of Vortex Generators, and a Comparison with Experiments; Aeronautical Research Council, Technical Report C.P. No. 361; Aeronautical Research Council: London, UK, 1957. [Google Scholar]
- Smith, F.T. Theoretical prediction and design for vortex generators in turbulent boundary layers. J. Fluid Mech. 1994, 270, 91–131. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Hansen, M.O.L.; Westergaard, C. Phenomenological Model of vortex generators. In IEA, Aerodynamics of Wind Turbines, 9th Symposium; IEA: Paris, France, 1995; pp. 1–7. [Google Scholar]
- Chaviaropoulos, P.K.; Politis, E.S.; Nikolaou, I.G. Phenomenological modeling of vortex generators. In Proceedings of the EWEC 2003, Madrid, Spain, 16–19 June 2003. [Google Scholar]
- Velte, C.M.; Hansen, M.O.L.; Okulov, V. Multiple vortex structures in the wake of a rectangular winglet in ground effect. Exp. Therm. Fluid Sci. 2016, 72, 31–39. [Google Scholar] [CrossRef]
- Charalampous, A.; Foucaut, J.M.; Cuvier, C.; Velte, C.M.; Hansen, M.O.L. Verification of numerical modeling of VG flow by comparing to PIV data. In Proceedings of the Wind Energy Science Conference 2017, Kgs. Lyngby, Denmark, 26–29 June 2017. [Google Scholar]
- Bender, E.E.; Anderson, B.H.; Yagle, P.J. Vortex generator modeling for Navier Stokes codes. In Proceedings of the 1999 3rd ASME, FEDSM’99-6929, San Francisco, CA, USA, 18–23 July 1999. [Google Scholar]
- Manolesos, M.; Sørensen, N.N.; Troldborg, N.; Florentie, L.; Papadakis, G.; Voutsinas, S. Computing the flow past Vortex Generators: Comparison between RANS Simulations and Experiments. The Science of Making Torque from Wind (TORQUE 2016). IOP Publ. J. Phys. Conf. Ser. 2016, 753, 022014. [Google Scholar] [CrossRef]
- Velte, C.M.; Braud, C.; Coudert, S.; Foucaut, J.-M. Vortex generator induced flow in a high re boundary layer. J. Phys. Conf. Ser. (Online) 2014, 555, 012102. [Google Scholar] [CrossRef]
- Foucaut, J.M.; Coudert, S.; Braud, C.; Velte, C. Influence of light sheet separation on SPIV measurement in a large field spanwise plane. Measurement Sci. Technol. 2014, 25, 035304. [Google Scholar] [CrossRef]
- STAR CCM + Users Manual. Available online: http://www.cd-adapco.com/products/star-ccm/documentation (accessed on 2 June 2019).
- Fernández-Gámiz, U.; Velte, C.M.; Réthoré, P.E.; Sørensen, N.N.; Egusquiza, E. Testing of self-similarity and helical symmetry in vortex generator flow simulations. Wind Energy 2016, 19, 1043–1052. [Google Scholar] [CrossRef]
- Velte, C.M.; Hansen, M.O.L.; Cavar, D. Flow analysis of vortex generators on wing sections by stereoscopic particle image velocimetry measurements. Environ. Res. Lett. 2008, 3, 015006. [Google Scholar] [CrossRef]
- Rahimi, H.; Schepers, J.G.; Shen, W.Z.; Ramos Garcia, N.; Scneider, M.S.; Micallef, D.; Simao Ferreira, C.J.; Jost, E.; Klein, L.; Herráez, I. Evaluation of different methods for determining the angle of attack on wind turbine blades with CFD results under axial inflow conditions. Renew. Energy 2018, 125, 866–876. [Google Scholar] [CrossRef]
- Martínez-Filgueira, P.; Fernandez-Gamiz, U.; Zulueta, E.; Errasti, I.; Fernandez-Gauna, B. Parametric study of low-profile vortex generators. Int. J. Hydrogen Energy 2017, 42, 17700–17712. [Google Scholar] [CrossRef]
- Launder, B.; Reece, G.; Rodi, W. Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Gibson, M.; Rodi, W. A Reynolds-stress closure model of turbulence applied to the calculation of a highly curved mixing layer. J. Fluid Mech. 1981, 103, 161–182. [Google Scholar] [CrossRef]
- Poole, D.J.; Bevan, R.L.T.; Allen, C.B.; Rendall, T.C.S. An Aerodynamic Model for Vane-Type Vortex Generators. In Proceedings of the 8th AIAA Flow Control Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Wendt, J. Parametric study of vortices shed from airfoil vortex generators. AIAA J. 2004, 42, 2185–2195. [Google Scholar] [CrossRef]






| Polyhedral Mesh | Rectangular | Triangular |
|---|---|---|
| Base size [m] | 0.05 | 0.05 |
| Relative size close to VGs [%] | 9 | |
| Relative size in the wake region [%] | 11 | - |
| Prism layer mesh | ReD | TrD |
| Number of prism layers | 20 | 20 |
| Prism layer stretching | 1.5 | 1.5 |
| Prism layer thickness [% of the base size] | 5 | 5 |
| Total amount of cells | 11.3 × 106 | 8.2 × 106 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hansen, M.O.L.; Charalampous, A.; Foucaut, J.-M.; Cuvier, C.; Velte, C.M. Validation of a Model for Estimating the Strength of a Vortex Created from the Bound Circulation of a Vortex Generator. Energies 2019, 12, 2781. https://doi.org/10.3390/en12142781
Hansen MOL, Charalampous A, Foucaut J-M, Cuvier C, Velte CM. Validation of a Model for Estimating the Strength of a Vortex Created from the Bound Circulation of a Vortex Generator. Energies. 2019; 12(14):2781. https://doi.org/10.3390/en12142781
Chicago/Turabian StyleHansen, Martin O. L., Antonis Charalampous, Jean-Marc Foucaut, Christophe Cuvier, and Clara M. Velte. 2019. "Validation of a Model for Estimating the Strength of a Vortex Created from the Bound Circulation of a Vortex Generator" Energies 12, no. 14: 2781. https://doi.org/10.3390/en12142781
APA StyleHansen, M. O. L., Charalampous, A., Foucaut, J.-M., Cuvier, C., & Velte, C. M. (2019). Validation of a Model for Estimating the Strength of a Vortex Created from the Bound Circulation of a Vortex Generator. Energies, 12(14), 2781. https://doi.org/10.3390/en12142781






