Reliability-Based Serviceability Limit State Design of a Jacket Substructure for an Offshore Wind Turbine
Abstract
:1. Introduction
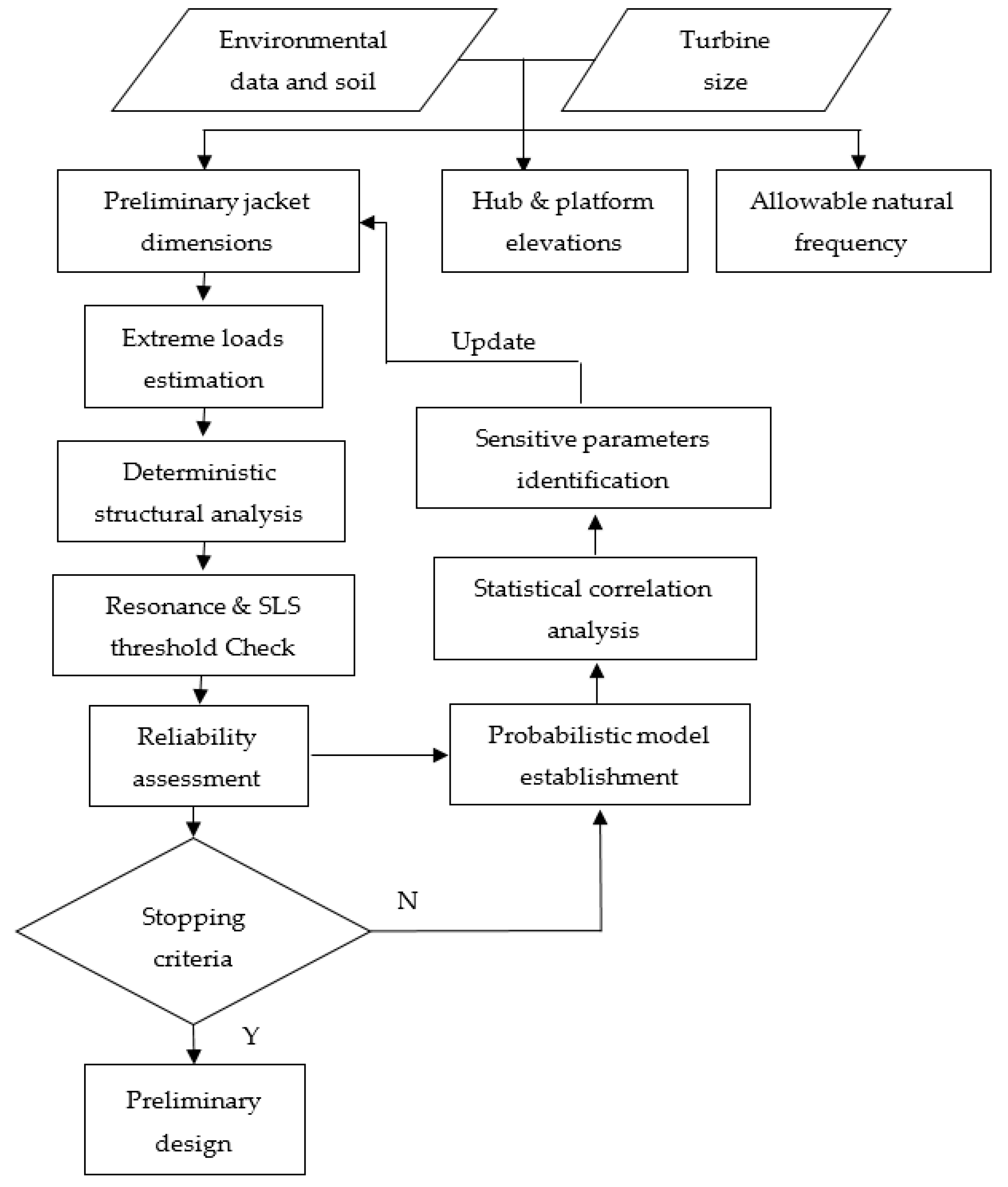
2. Proposed Reliability Analysis and Design Framework
2.1. Correaltion-Based Important Parameter Identification and Reliability Analysis
2.2. The Design Framework
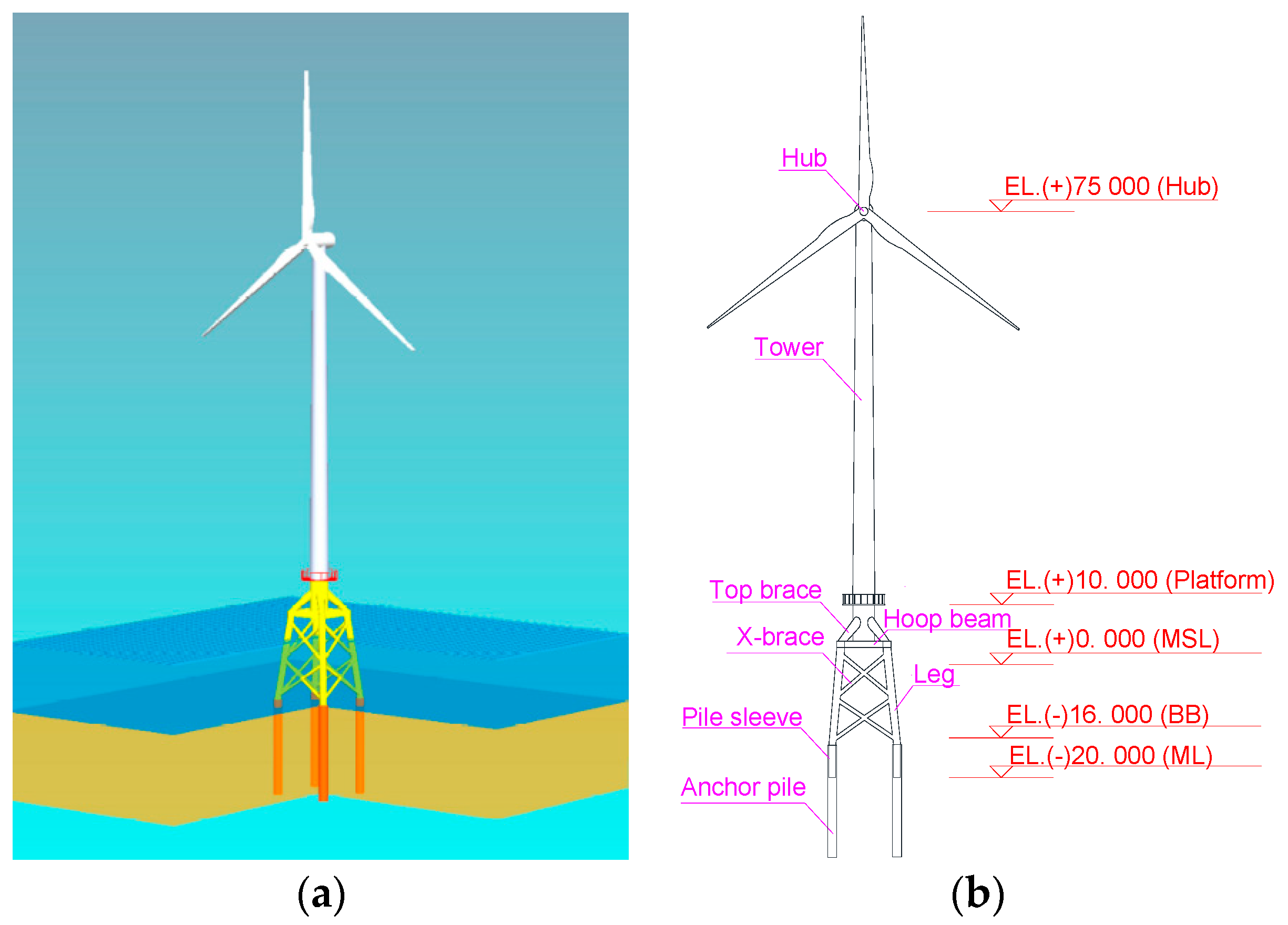
3. The Computational Models of the Support Structures
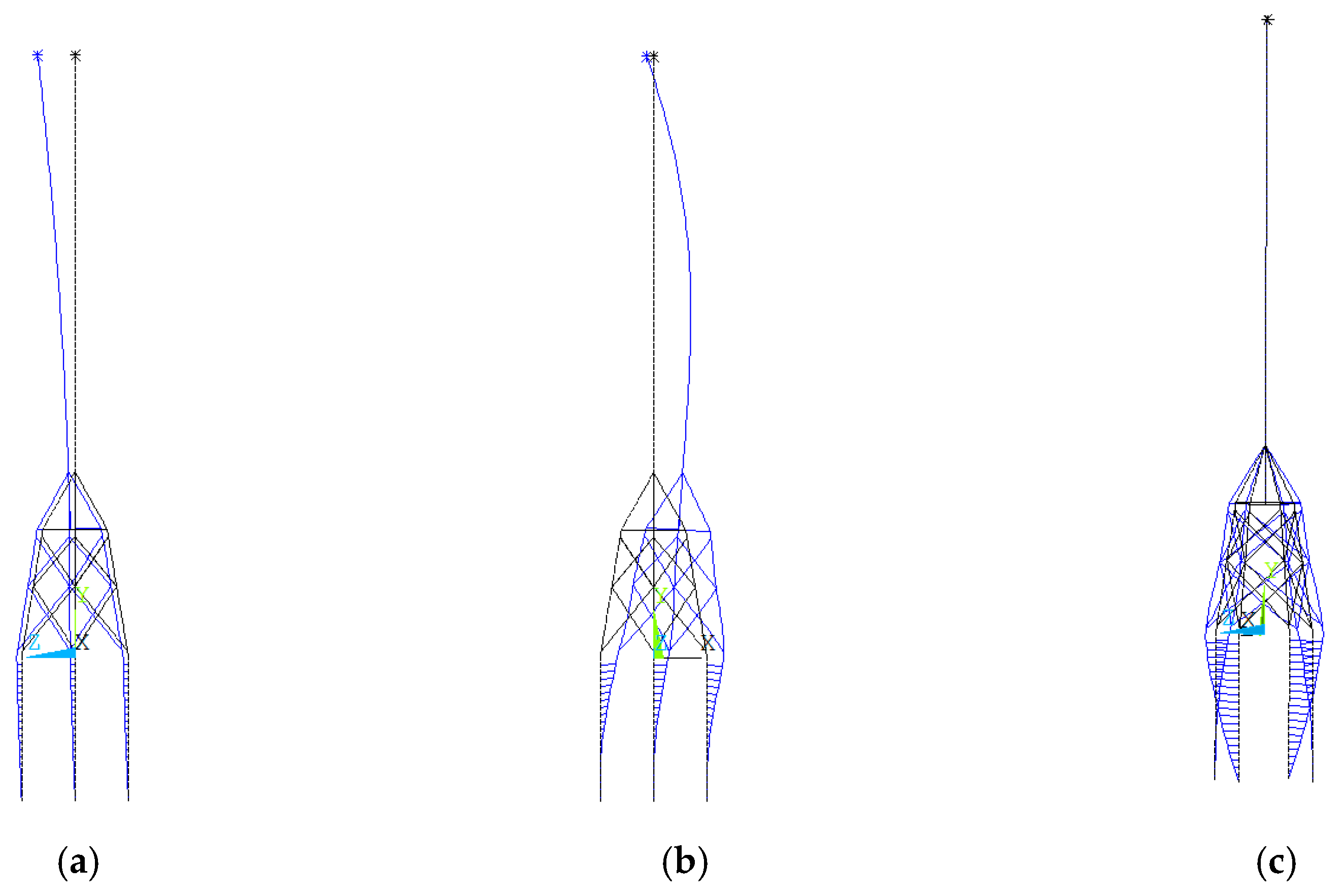
3.1. Jacket Substructure Geometries
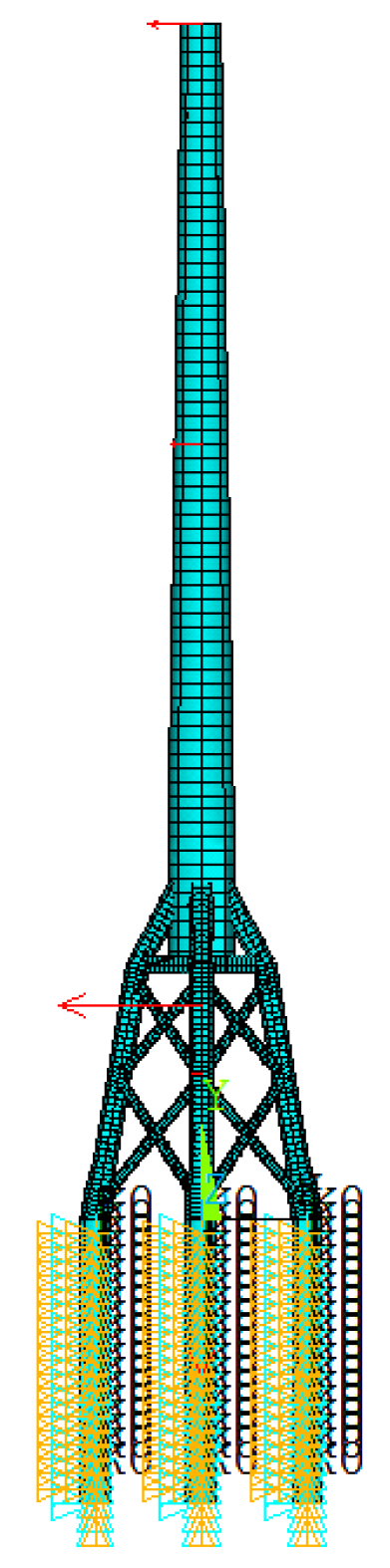
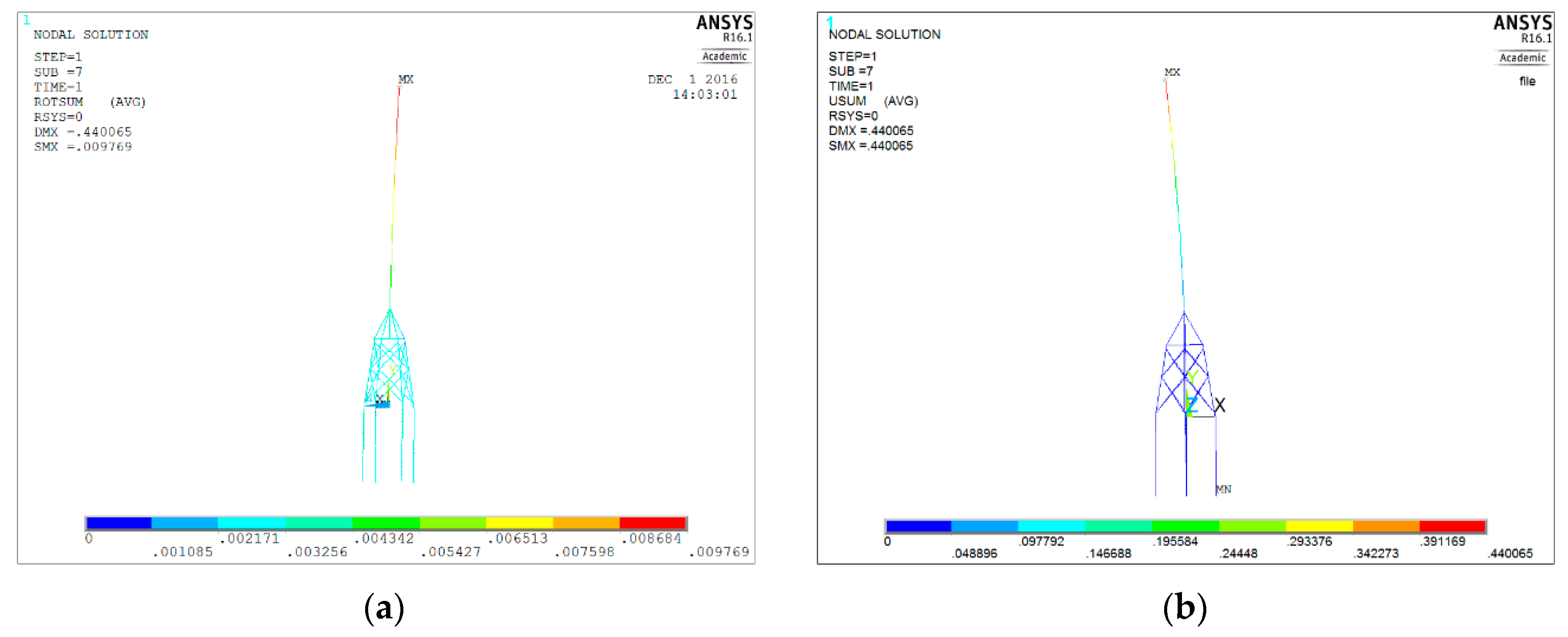
3.2. Modeling for Finite Element Analysis
3.3. Load Models
4. Heuristic Design of Jacket Substructure
5. Probabilistic Analysis
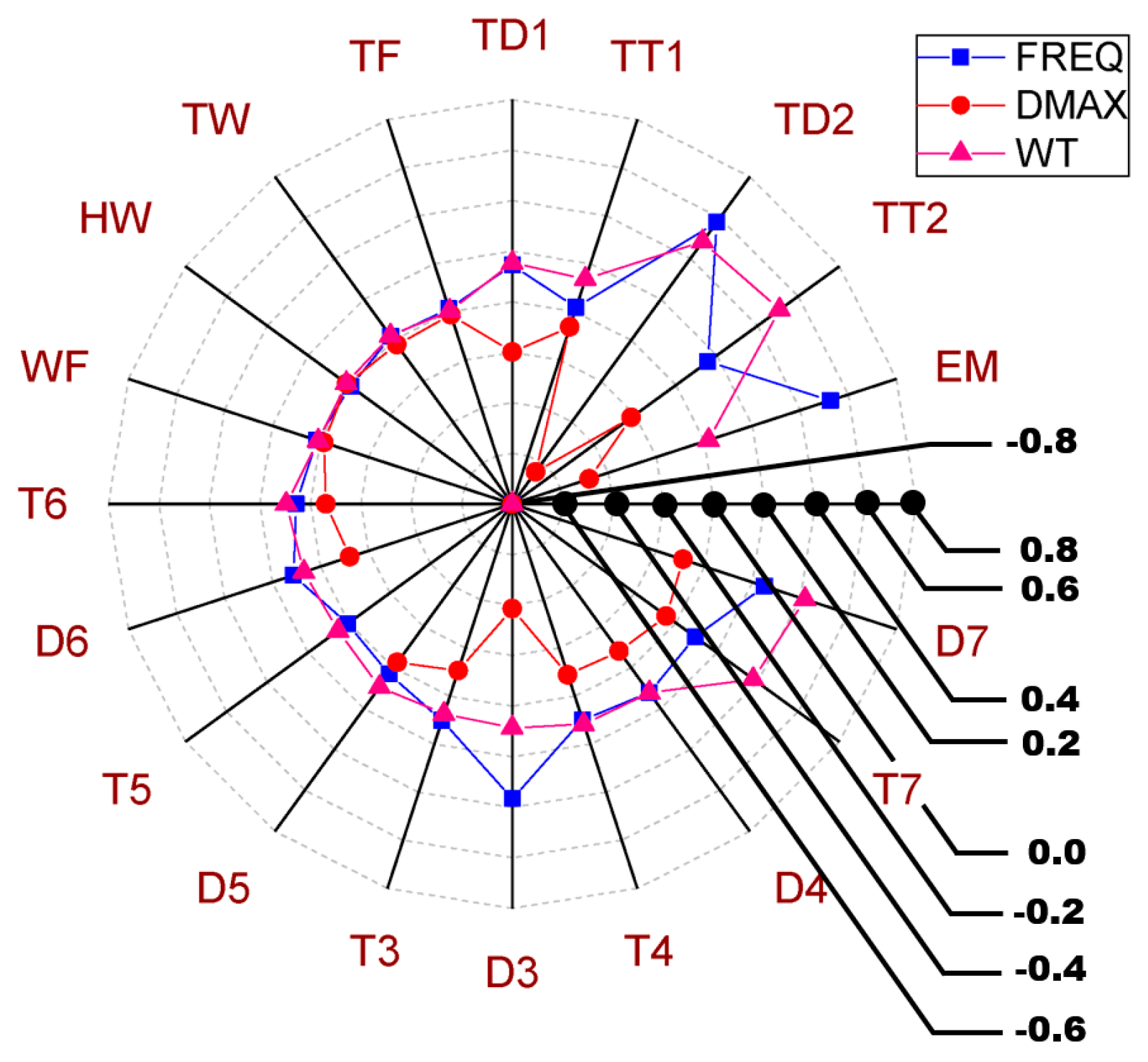
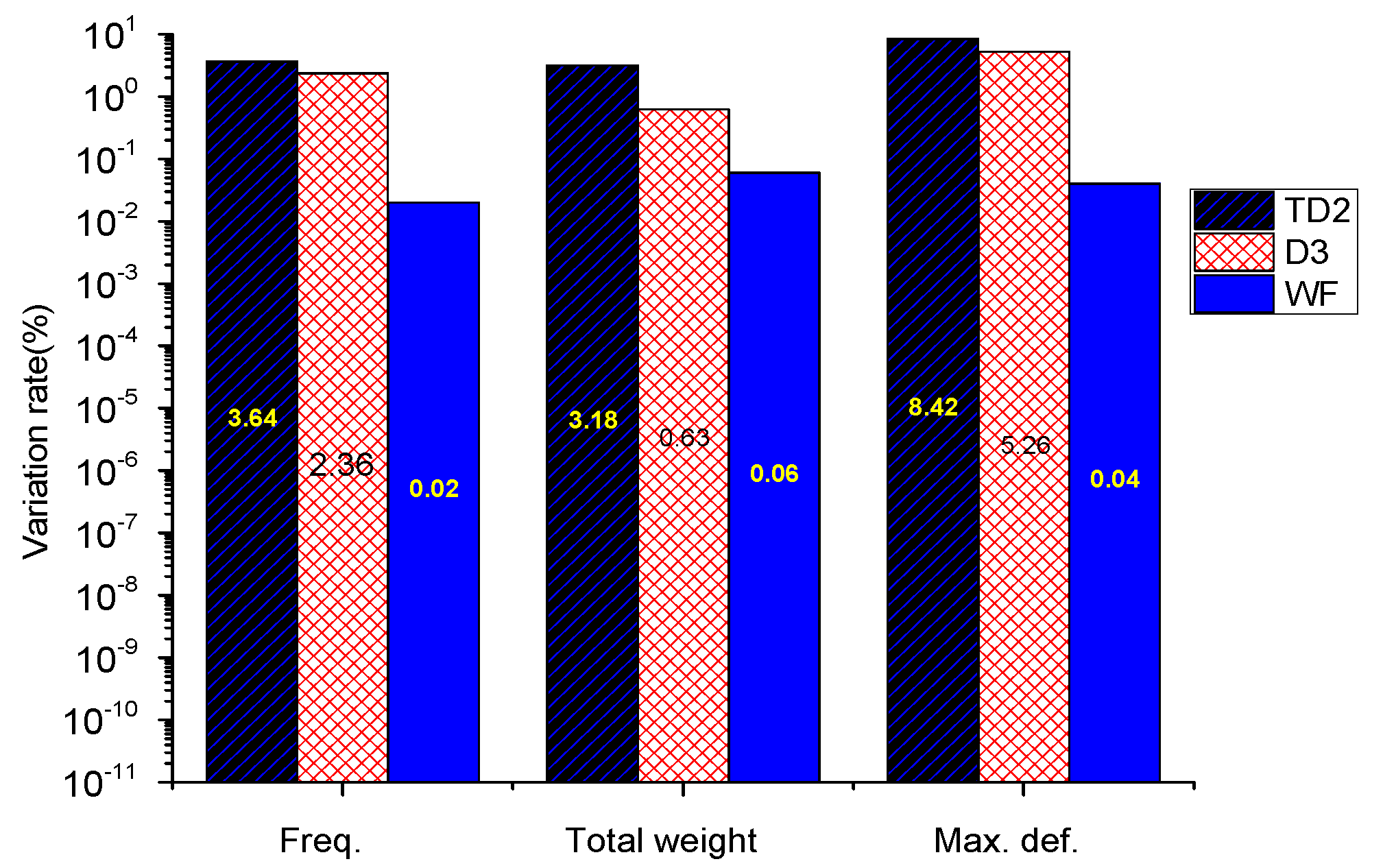
5.1. Important Engineering Demand Parameters Identification
5.2. Reliability Analysis for Target Jacket
5.3. The Comparison between the Deterministic and Probabilistic Analyses Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Annual Market Update. 2018 Global Wind Report. Available online: https://gwec.net/policy-research/reports/ (accessed on 3 July 2019).
- Hensel, J.; Sharma, M.S.R.; Baxter, C.D.P.; Hu, S.-L.J. Development of a technology type factor for jacket structures for offshore wind turbines in Rhode Island. J. Renew. Sustain. Energy 2012, 4, 8–23. [Google Scholar] [CrossRef]
- Offshore Wind Energy Market—Global Industry Analysis, Size, Share, Growth, Trends, and Forecast 2014—2022. Available online: https://www.transparencymarketresearch.com/offshore-wind-energy-market.html (accessed on 3 May 2019).
- Support Structures for Wind Turbines DNV GL AS; Det Norske Veritas: Høvik, Norway, 2016.
- API RP 2A-WSD. Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms—Working Stress Design; American Petroleum Institute (API): Washington, DC, USA, 2014. [Google Scholar]
- Heptonstall, P.; Gross, R.; Greenacre, P.; Cockerill, T. The cost of offshore wind: Understanding the past and projecting the future. Energy Policy 2012, 41, 815–821. [Google Scholar] [CrossRef]
- Blanco, M.I. The economics of wind energy. Renew. Sustain. Energy Rev. 2011, 13, 1372–1382. [Google Scholar] [CrossRef]
- Barbato, M.; Ciampoli, M.; Petrini, F. Effects of modeling parameter uncertainty on the structural response of offshore wind turbines. In Proceedings of the 12th International Conference on Engineering, Science, Construction, and Operations in Challenging Environments 2010 (Earth and Space 2010), Houston, TX, USA, 7–10 March 2004. [Google Scholar]
- Mardfekri, M.; Gardoni, P. Probabilistic demand models and fragility estimates for offshore wind turbine support structures. Eng. Struct. 2013, 52, 478–487. [Google Scholar] [CrossRef]
- Liu, F.S.; Chen, J.F.; Qin, H.D. Frequency response estimation of floating structures by representation of retardation functions with complex exponentials. Mar. Struct. 2017, 54, 144–166. [Google Scholar] [CrossRef]
- El-Din, M.N.; Kim, J. Sensitivity analysis of pile-founded fixed steel jacket platforms subjected to seismic loads. Ocean Eng. 2014, 85, 1–11. [Google Scholar] [CrossRef]
- Yang, H.; Zhu, Y.; Lu, Q.; Zhang, J. Dynamic reliability-based design optimization of the tripod sub-structure of offshore wind turbines. Renew. Energy 2015, 78, 16–25. [Google Scholar] [CrossRef]
- Liu, F.S.; Gao, S.J.; Han, H.W.; Tian, Z.; Liu, P. Interference reduction of high-energy noise for modal parameter identification of offshore wind turbines based on iterative signal extraction. Ocean Eng. 2019, 183, 372–383. [Google Scholar]
- Vahdatirad, M.J.; Bayat, M.; Andersen, L.V.; Ibsen, L.B. Probabilistic finite element stiffness of a laterally loaded monopile based on an improved asymptotic sampling method. J. Civ. Eng. Manag. 2015, 21, 503–513. [Google Scholar] [CrossRef]
- Márquez-Domínguez, S.; Sørensen, J.D. Fatigue Reliability and Calibration of Fatigue Design Factors for Offshore Wind Turbine. Energies 2012, 5, 1816–1834. [Google Scholar] [CrossRef]
- Ziegler, L.; Voormeeren, S.; Schafhirt, S.; Muskulus, M. Design clustering of offshore wind turbines using probabilistic fatigue load estimation. Renew. Energy 2016, 91, 425–433. [Google Scholar] [CrossRef]
- Liu, F.S.; Li, X.G.; Tian, Z.; Zhang, J.H.; Wang, B. Transient Response Estimation of an Offshore Wind Turbine Support System. Energies 2019, 12, 891. [Google Scholar] [CrossRef]
- Dar, F.H.; Meakin, J.R.; Aspden, R.M. Statistical methods in finite element analysis. J. Biomech. 2002, 35, 1155–1161. [Google Scholar] [CrossRef]
- Bjerager, P.; Krenk, S. Parametric sensitivity in first order reliability theory. J. Eng. Mech. ASCE 1989, 115, 1577–1582. [Google Scholar] [CrossRef]
- Der Kiureghian, A.; Dakessian, T. Multiple design points in first and second-order reliability. Struct. Saf. 1998, 20, 37–49. [Google Scholar] [CrossRef]
- Robert, C.P. Monte Carlo Methods; Wiley Online Library: Hoboken, NY, USA, 2004. [Google Scholar]
- Bucher, C.G.; Bourgund, U. A fast and efficient response surface approach for structural reliability problems. Struct. Saf. 1990, 7, 57–66. [Google Scholar] [CrossRef]
- Nowak, A.S.; Collins, K.R. Reliability of Structures; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Valdebenito, M.A.; Pradlwarter, H.J.; Schuëller, G.I. The role of the design point for calculating failure probabilities in view of dimensionality and structural nonlinearities. Struct. Saf. 2012, 32, 101–111. [Google Scholar] [CrossRef]
- Guangdong Electric Power Design Institute. Engineering Geotechnical Investigation Report of Zhuhai Guishan Island Offshore Wind Farm; 44-F4611K-G01; Guangdong Electric Power Design Institute: Guangzhou, China, 2012. (In Chinese) [Google Scholar]
- International Electrotechnical Commision. Wind Turbines—Part 3: Design Requirements for Offshore Wind Turbines; No. IEC61400-3; International Electrotechnical Commision: Geneva, Switzerland, 2009. [Google Scholar]
- Kim, Y.; Kwon, O.J. Effect of Platform Motion on Aerodynamic Performance and Aeroelastic Behavior of Floating Offshore Wind Turbine Blades. Energies 2019, 12, 2519. [Google Scholar] [CrossRef]
- Karimirad, M. Offshore Energy Structures for Wind Power, Wave Energy and Hybrid Marine Platforms; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Hess, P.E.; Bruchman, D.; Assakkaf, I.A.; Ayyub, B.M. Uncertainties in material and geometric strength and load variables. Nav. Eng. J. 2002, 114, 139–165, 209. [Google Scholar] [CrossRef]
- ASTM. A500-93, Standard Specification for Cold-Formed Welded and Seamless Carbon Steel Structural Tubing in Rounds and Shapes; ASTM: West Conshohocken, PA, USA, 2003. [Google Scholar]
- Code JPM. Joint Committee on Structural Safety. Available online: www.jcss.ethz.ch (accessed on 22 October 2016).
- DNV-OS-J101. Design of Offshore Wind Turbine Structures; Det Norske Veritas: Høvik, Norway, 2014. [Google Scholar]
- Wang, F.; Chen, Q.; Yu, G.C. Research on large scale wind driven generator group tower rigidity. Energy Technol. 2005, 20, 38–39. (In Chinese) [Google Scholar]
- Gulvanessian, H.; Calgaro, J.-A.; Holický, M. Designer’s Guide to EN 1990: Eurocode: Basis of Structural Design; Thomas Telford: London, UK, 2002. [Google Scholar]
- ISO I. 2394. General Principles on Reliability for Structures; ISO: Zurich, Switzerland, 2015.
| Random Input Parameters | Symbol | Mean | c.o.v. | Distribution Type | References |
|---|---|---|---|---|---|
| Elastic modulus (GPa) | TM | 210 | 7.6% | Gaussian | [19] |
| Yield strength (MPa) | YS | 355 | 6.8% | Lognormal | |
| Outer diameter of central column (mm) | D1 | 4740 | 10% | Gaussian | [20,21] |
| Thickness of central column (mm) | T1 | 60 | 10% | Gaussian | |
| Outer diameter of top brace bottom (mm) | D2 | 1400 | 10% | Gaussian | |
| Thickness of top brace bottom (mm) | T2 | 60 | 10% | Gaussian | |
| Outer diameter of top brace top (mm) | D3 | 2000 | 10% | Gaussian | |
| Thickness of top brace top(mm) | T3 | 60 | 10% | Gaussian | |
| Outer diameter of leg (mm) | D4 | 1600 | 10% | Gaussian | |
| Thickness of leg (mm) | T4 | 30 | 10% | Gaussian | |
| Outer diameter of X-brace in top (mm) | D5 | 760 | 10% | Gaussian | |
| Thickness of X-brace in top (mm) | T5 | 28 | 10% | Gaussian | |
| Outer diameter of X-brace in bottom (mm) | D6 | 760 | 10% | Gaussian | |
| Thickness of X-brace in bottom(mm) | T6 | 28 | 10% | Gaussian | |
| Outer diameter of anchorage pile (mm) | D7 | 2100 | 10% | Gaussian | |
| Thickness of anchorage pile (mm) | T7 | 50 | 10% | Gaussian | |
| Outer diameter of pile sleeve (mm) | D8 | 1600 | 10% | Gaussian | |
| Thickness of pile sleeve (mm) | T8 | 40 | 10% | Gaussian | |
| Web height of the hoop beam (mm) | HW | 1200 | 10% | Gaussian | |
| Web thickness of the hoop beam (mm) | TW | 25 | 10% | Gaussian | |
| Flange width of the hoop beam (mm) | WF | 500 | 10% | Gaussian | |
| Flange thickness of the hoop beam (mm) | TF | 30 | 10% | Gaussian | |
| Outer diameter of tower top (mm) | TD1 | 2800 | 10% | Gaussian | |
| Thickness of tower top (mm) | TT1 | 60 | 10% | Gaussian | |
| Outer diameter of tower bottom (mm) | TD2 | 4700 | 10% | Gaussian | |
| Thickness of tower bottom (mm) | TT2 | 30 | 10% | Gaussian |
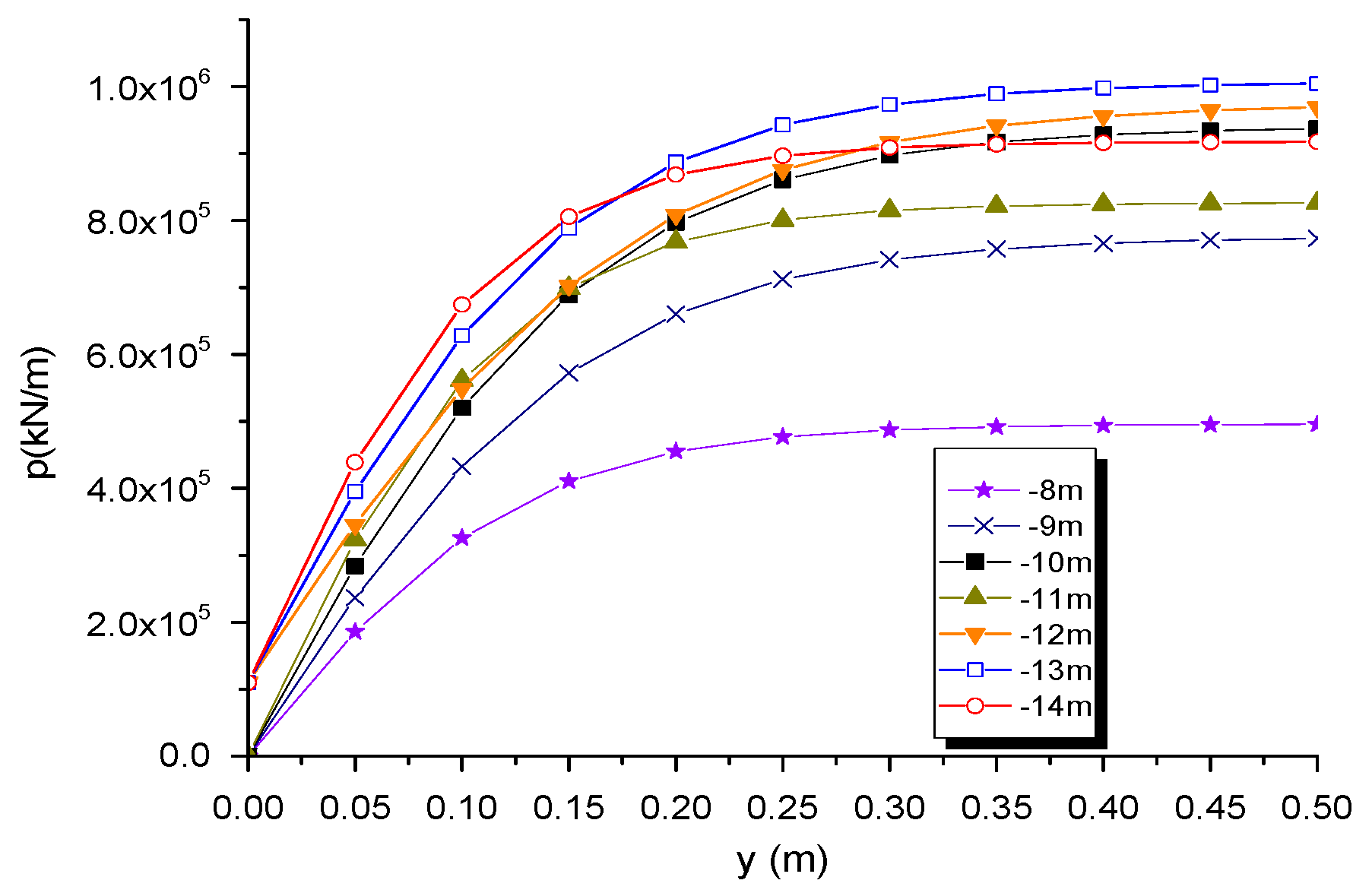
| Soil Layer | Soil Type | Soil Depth | Effective Gravity (kN/m3) | Design Shear Strength (kPa) | E50 | ks | |
|---|---|---|---|---|---|---|---|
| Top of the Soil Layer (m) | Bottom of the Soil Layer (m) | ||||||
| 1 | Very soft—hard silty clay | 0.0 | 7.4 | 4 | 0.02 | ||
| 3.8 | 7.4 | 9 | 0.02 | ||||
| 3.8 | 7.8 | 14 | 0.02 | ||||
| 7.3 | 7.8 | 22 | 0.02 | ||||
| 2 | Medium dense silt | 7.3 | 8.2 | φ = 20° | 5430 | ||
| 8.1 | 8.2 | 5430 | |||||
| 3 | Medium dense silt—fine silt | 8.1 | 8.8 | φ = 25° | 5430 | ||
| 13.3 | 8.8 | 5430 | |||||
| 4 | Medium dense silt | 13.3 | 9.0 | φ = 20° | 5430 | ||
| 14.8 | 9.0 | 5430 | |||||
| 5 | Hard silty clay | 14.8 | 9.0 | 30 | 0.01 | ||
| 17.7 | 9.0 | 0.01 | |||||
| 6 | Dense silt | 17.7 | 9.2 | φ = 25° | 5430 | ||
| 19.7 | 9.2 | 5430 | |||||
| 7 | Dense silt | 19.7 | 9.2 | φ = 30° | 10860 | ||
| 26.7 | 9.2 | 10860 | |||||
| 8 | Dense—very dense silt | 26.7 | 9.2 | φ = 25° | 5430 | ||
| 29.2 | 9.2 | 5430 | |||||
| 9 | Hard—very hard silty clay | 29.2 | 9.3 | 100 | 0.005 | ||
| 33.2 | 9.3 | 100 | 0.005 | ||||
| Young’s Modulus (Steel) (GPa) | Yield Strength (Steel) (MPa) | Poisson’s Ratio (Steel) |
|---|---|---|
| 210 | 355 | 0.3 |
| Components | Size (Diameter) | Size (Thickness) | Unit |
|---|---|---|---|
| Anchor pile | 2000 | 50 | mm |
| Pile sleeve | 1600 | 40 | mm |
| Leg | 1600 | 30 | mm |
| X- brace | 760 | 28 | mm |
| Top brace | 1400 to 2000 | 60 | mm |
| Central column | 4740 | 60 | mm |
| Tower | 2800 to 4740 | 30 to 50 | mm |
| Nacelle and rotor | 163.3 | ton |
| Rank | Maximum Deflection | First Natural Frequency | Total Weight |
|---|---|---|---|
| 1 | TD2 | TD2 | TT2 |
| 2 | EM | EM | TD2 |
| 3 | D3 | D3 | D7 |
| 4 | TT2 | D7 | T7 |
| 5 | TD1 | TT2 | TD1 |
| 15 | TW | TT1 | TW |
| 16 | WF | WF | HW |
| 17 | TF | TF | WF |
| 18 | T5 | T5 | TF |
| 19 | HW | HW | EM |
| Case | Factors of Ex(ε) | Threshold | Failure Probability Pf | Reliability Index |
|---|---|---|---|---|
| 1 | 1 | H/200 | 5.34 × 10−1 | −0.09 |
| H/175 | 2.11 × 10−1 | 0.80 | ||
| H/150 | 4.57 × 10−2 | 1.69 | ||
| H/125 | 6.25 × 10−3 | 2.50 | ||
| H/100 | 3.20 × 10−4 | 3.41 | ||
| 2 | 1.05 | H/200 | 4.10 × 10−1 | 0.23 |
| H/175 | 1.44 × 10−1 | 1.06 | ||
| H/150 | 2.76 × 10−2 | 1.92 | ||
| H/125 | 2.46 × 10−3 | 2.81 | ||
| H/100 | 0 | >3.5 | ||
| 3 | 1.1 | H/200 | 3.06 × 10−1 | 0.51 |
| H/175 | 9.07 × 10−2 | 1.34 | ||
| H/150 | 1.26 × 10−2 | 2.24 | ||
| H/125 | 8.01 × 10−4 | 3.16 | ||
| H/100 | 2.32 × 10−4 | 3.50 | ||
| 4 | 1.15 | H/200 | 2.09 × 10−1 | 0.81 |
| H/175 | 5.78 × 10−2 | 1.57 | ||
| H/150 | 8.45 × 10−3 | 2.39 | ||
| H/125 | 5.09 × 10−4 | 3.29 | ||
| H/100 | 0 | >3.5 | ||
| 5 | 1.2 | H/200 | 1.47 × 10−1 | 1.05 |
| H/175 | 3.33 × 10−2 | 1.83 | ||
| H/150 | 4.64 × 10−3 | 2.60 | ||
| H/125 | 5.30 × 10−4 | 3.27 | ||
| H/100 | 0 | >3.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Kang, W.-H.; Sun, K.; Liu, F. Reliability-Based Serviceability Limit State Design of a Jacket Substructure for an Offshore Wind Turbine. Energies 2019, 12, 2751. https://doi.org/10.3390/en12142751
Zhang J, Kang W-H, Sun K, Liu F. Reliability-Based Serviceability Limit State Design of a Jacket Substructure for an Offshore Wind Turbine. Energies. 2019; 12(14):2751. https://doi.org/10.3390/en12142751
Chicago/Turabian StyleZhang, Jianhua, Won-Hee Kang, Ke Sun, and Fushun Liu. 2019. "Reliability-Based Serviceability Limit State Design of a Jacket Substructure for an Offshore Wind Turbine" Energies 12, no. 14: 2751. https://doi.org/10.3390/en12142751
APA StyleZhang, J., Kang, W.-H., Sun, K., & Liu, F. (2019). Reliability-Based Serviceability Limit State Design of a Jacket Substructure for an Offshore Wind Turbine. Energies, 12(14), 2751. https://doi.org/10.3390/en12142751







