Analysis of the Current Electric Battery Models for Electric Vehicle Simulation
Abstract
1. Introduction
2. Equivalent Circuit Models
2.1. Simple Models
2.1.1. Ideal Battery Model
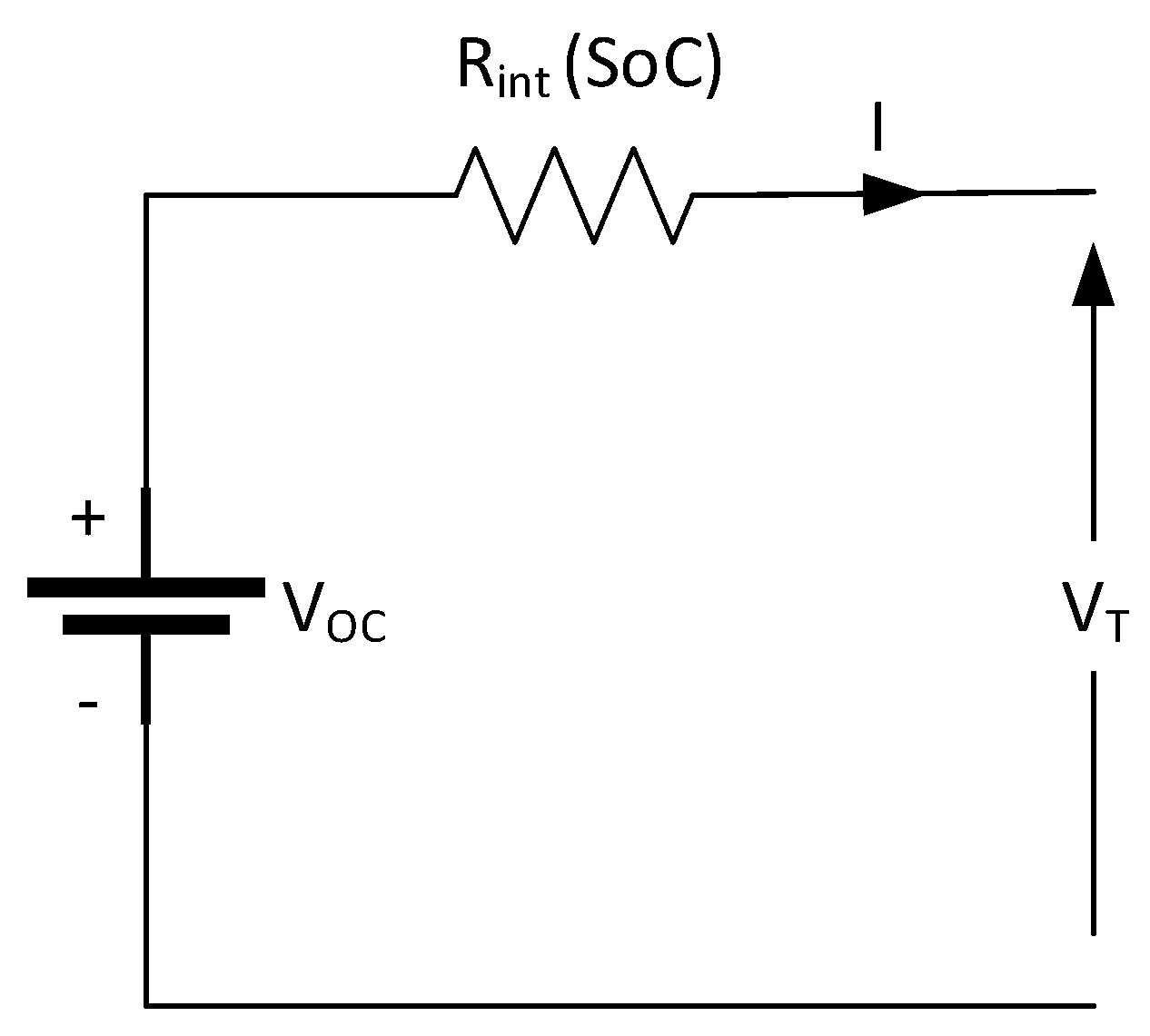
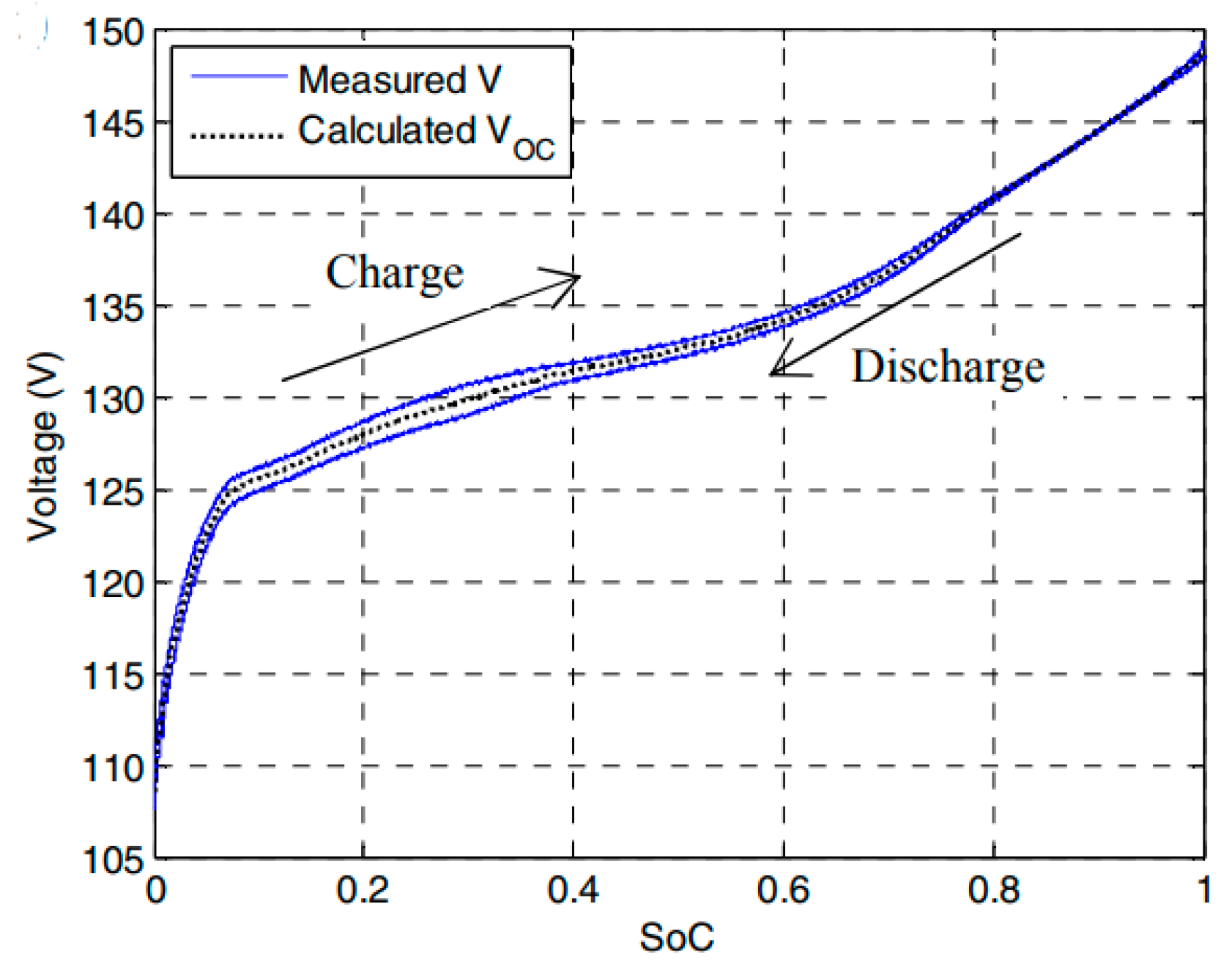
2.1.2. Simple or Linear Battery Model
2.1.3. Enhanced Simple Battery Model
2.1.4. Voltage Sources-Based Model
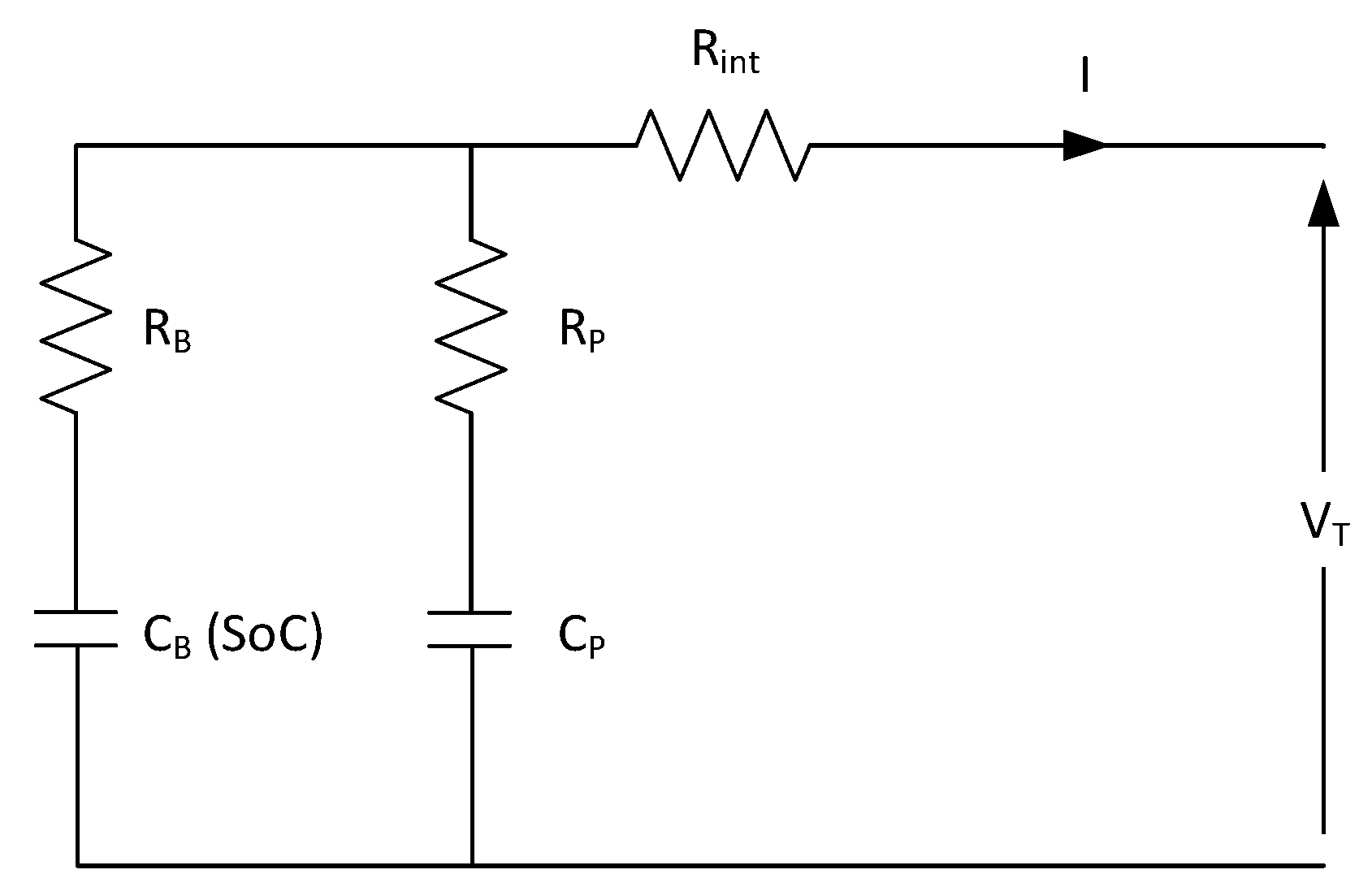
2.1.5. Resistor-Capacitor (RC) or Dynamic Model
2.2. Thevenin-Based Battery Models
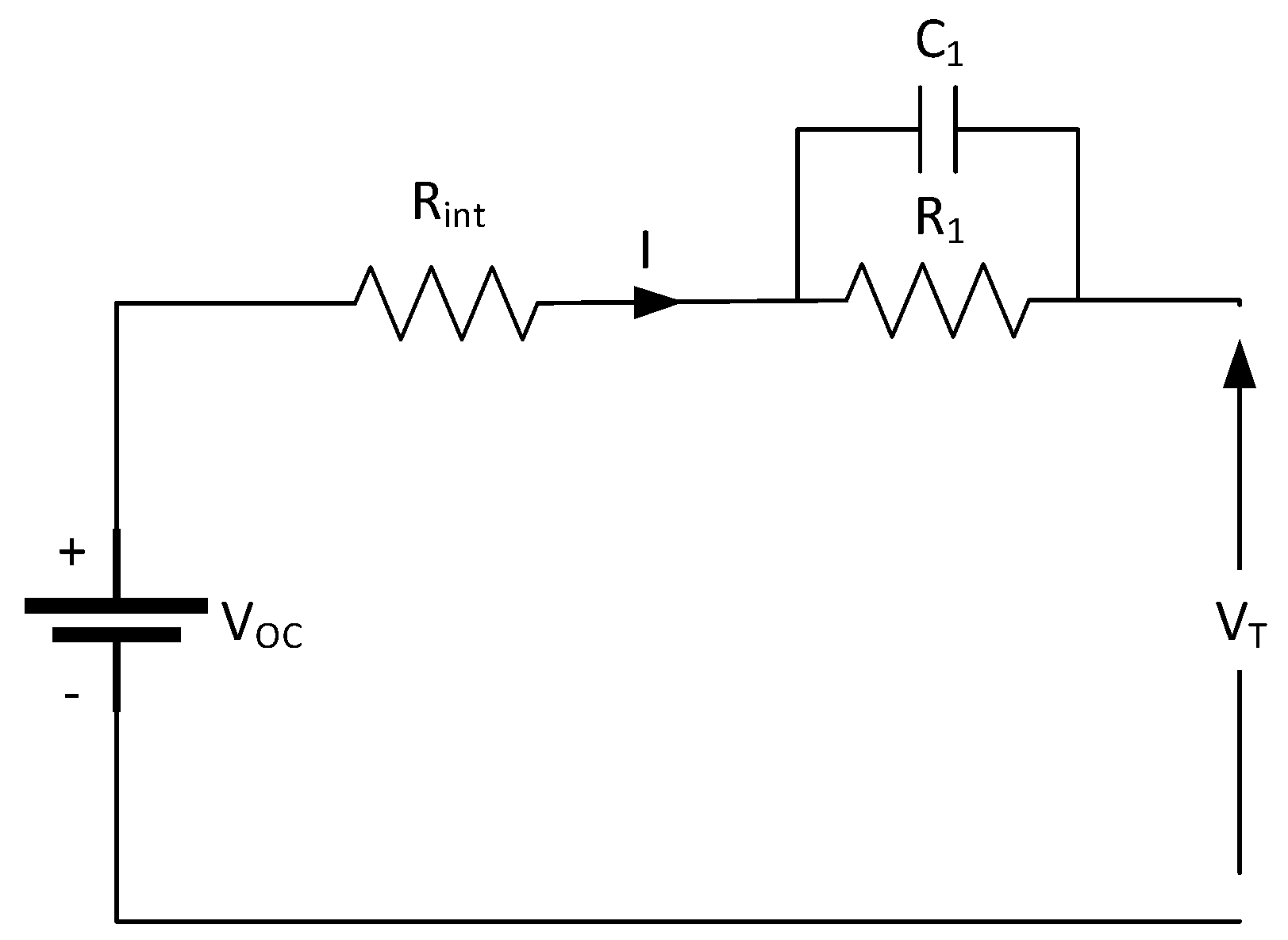
2.2.1. (First-Order) Thevenin Model
2.2.2. Second-Order Thevenin Model
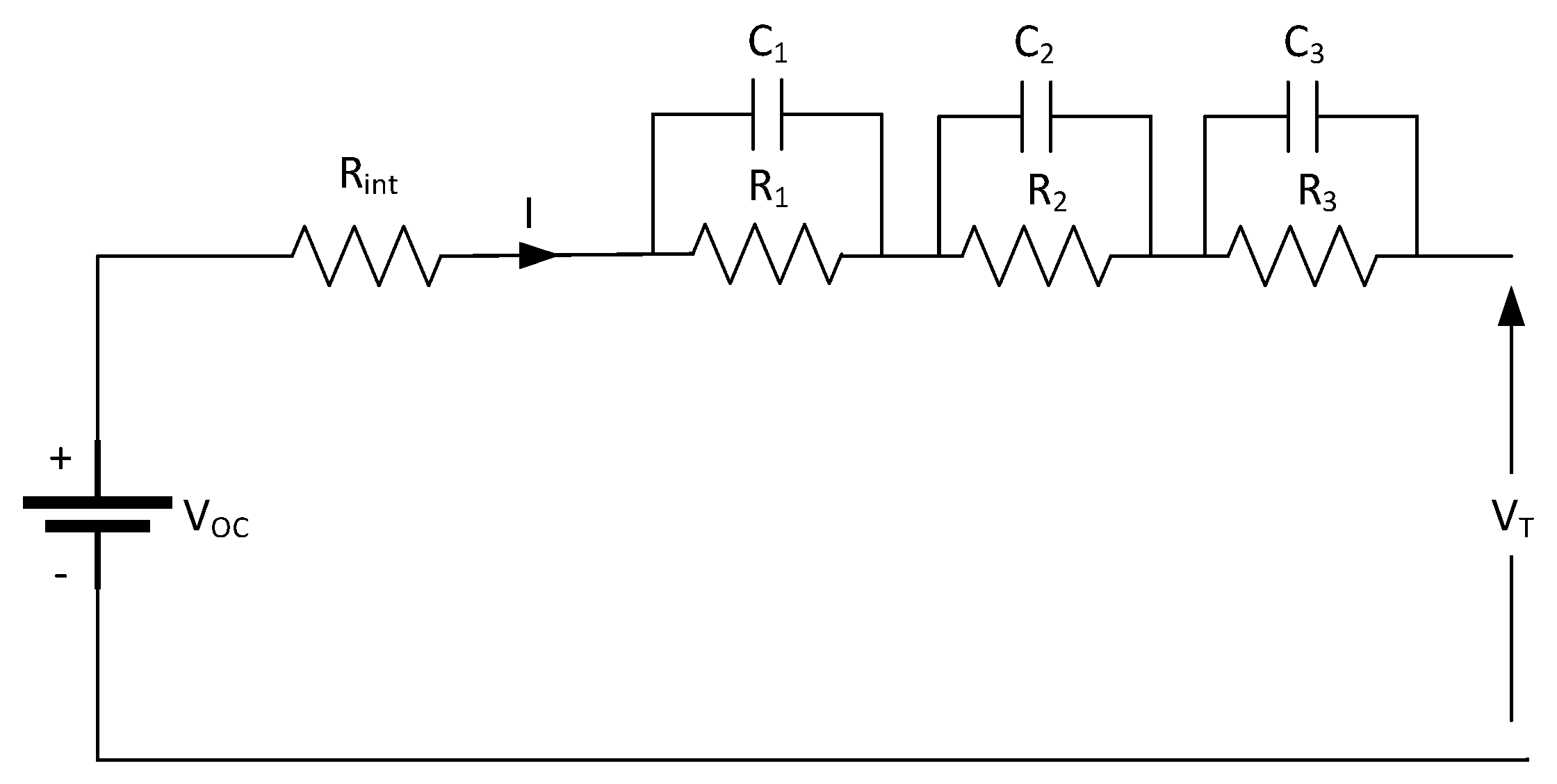
2.2.3. Third-Order Thevenin Model
2.3. PNGV Models
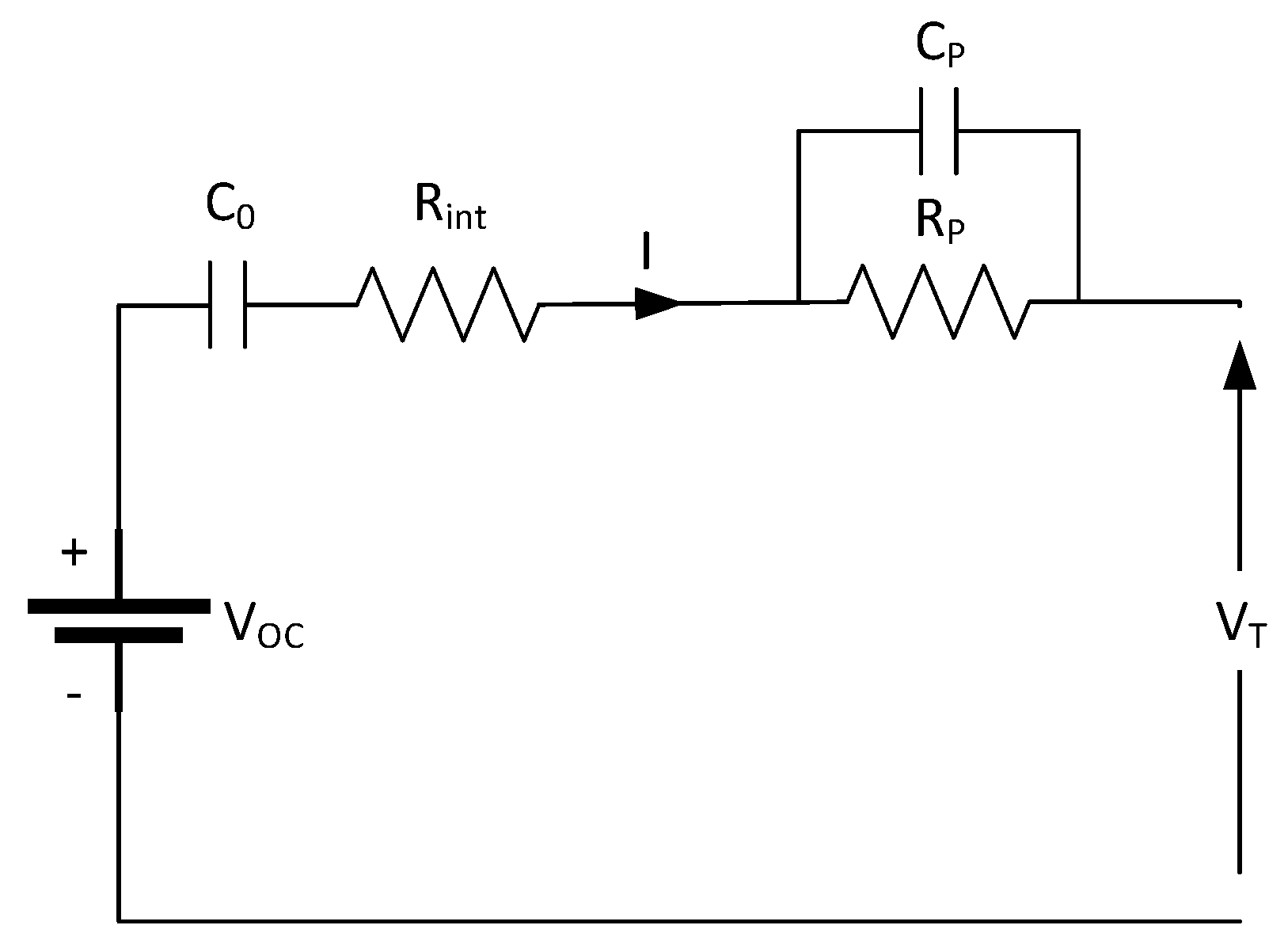
2.3.1. (First-Order) PNGV Model
2.3.2. Second-Order PNGV Model
2.4. Noshin’s Battery Models
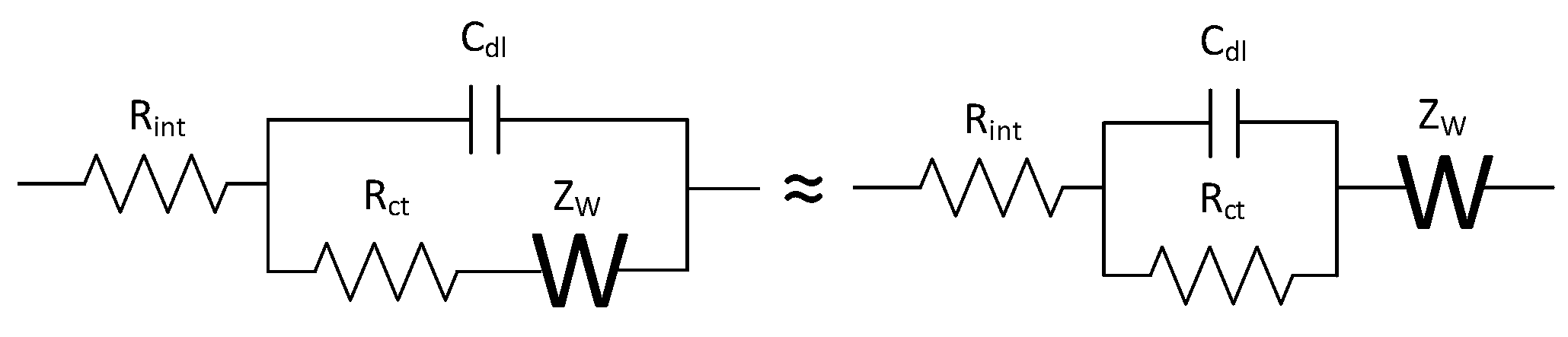
3. Impedance Models
4. Runtime Models
4.1. Simple Runtime Models
4.2. Runtime-Combined Models
5. V-I Performance
6. Conclusions
- Accuracy: An accurate model, and with consideration of enough general aspects is required. These general aspects can be:
- Electrical model: Knowing the I-V behavior of a battery is essential for any study associated with its operation.
- Thermal model: Since a battery resistance varies inversely with temperature, it is common to have accuracy errors in performance simulation and runtime estimation when temperature is neglected.
- Runtime model: Necessary for those studies considering battery runtime, capacity increasing, or effects derived.
- Computational simplicity: A simpler model is preferred easing real-time operation as simulation speed is increased.
- Configuration simplicity: A simple model to be configured is preferred, with the lowest parameters to be identified and defined.
- Interpretability: An interpretable model would ease the identification of the origin if any issue would appear in the battery.
Author Contributions
Funding
Conflicts of Interest
References
- Zamora, I.; San Martín, J.I.; García, J.; Asensio, F.J.; Oñederra, O.; San Martín, J.J.; Aperribay, V. PEM fuel cells in applications of urban public transport. Renew. Energy Power Qual. J. 2011, 1, 599–604. [Google Scholar] [CrossRef]
- Yan, J.; Li, C.; Xu, G.; Xu, Y. A novel on-line self-learning state-of-charge estimation of battery management system for hybrid electric vehicle. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium (IVS), Xi’an China, 3–5 June 2009; pp. 1161–1166. [Google Scholar]
- Shen, J.; Dusmez, S.; Khaligh, A. An advanced electro-thermal cycle-lifetime estimation model for LiFePO4 batteries. In Proceedings of the 2013 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 16–19 June 2013; pp. 1–6. [Google Scholar]
- Eddahech, A.; Briat, O.; Vinassa, J. Real-Time SOC and SOH Estimation for EV Li-Ion Cell Using Online Parameters Identification. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition, Raleigh, NC, USA, 15–20 September 2012. [Google Scholar]
- Hentunen, A.; Lehmuspelto, T.; Suomela, J. Electrical battery model for dynamic simulations of hybrid electric vehicles. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 6–9 September 2011; pp. 1–6. [Google Scholar]
- Lombardi, L.; Tribioli, L.; Cozzolino, R.; Bella, G. Comparative environmental assessment of conventional, electric, hybrid, and fuel cell powertrains based on LCA. Int. J. Life Cycle Assess. 2017, 22, 1989–2006. [Google Scholar] [CrossRef]
- Thomas, C.E. Fuel cell and battery electric vehicles compared. Int. J. Hydrogy Energy 2009, 34, 6005–6020. [Google Scholar] [CrossRef]
- Hu, X.; Zou, C.; Zhang, C.; Li, Y. Technological Developments in Batteries: A Survey of Principal Roles, Types, and Management Needs. IEEE Power Energy Mag. 2017, 15, 20–31. [Google Scholar] [CrossRef]
- Wang, Y.; Ying, H.; Huang, S. Comparison of lithium-ion battery cathode materials and the internal stress development. In Proceedings of the ASME 2011 International Mechanical Engineering Congress & Exposition IMECE2011, Denver, CO, USA, 11–17 November 2011. [Google Scholar]
- An, Z.; Jia, L.; Ding, Y.; Dang, C.; Li, X. A Review on Lithium-ion Power Battery Thermal Management Technologies and Thermal Safety. J. Therm. Sci 2017, 26, 391–412. [Google Scholar] [CrossRef]
- Cheng, K.W.E.; Divakar, B.P.; Wu, H.; Ding, K.; Ho, H.F. Battery-Management System (BMS) and SOC Development for Electrical Vehicles. IEEE Trans. Veh. Technol. 2011, 60, 76–88. [Google Scholar] [CrossRef]
- Chaturvedi, N.A.; Klein, R.; Christensen, J.; Ahmed, J.; Kojic, A. Algorithms for Advanced Battery-Management Systems. CSM 2010, 30, 49–68. [Google Scholar]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and I-V performance. TEC 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Hageman, S.C. Simple PSpice models let you simulate common battery types. Electron. Des. News 1993, 38, 117. [Google Scholar]
- Gold, S. A PSPICE macromodel for lithium-ion batteries. In Proceedings of the Twelfth Annual Battery Conference on Applications and Advances (BCAA), Long Beach, CA, USA, 14–17 January 1997; pp. 215–222. [Google Scholar]
- Jongerden, M.R.; Haverkort, B.R. Which battery model to use? IET Softw. 2009, 3, 445–457. [Google Scholar] [CrossRef]
- Rahmoun, A.; Biechl, H. Parameters identification of equivalent circuit diagrams for li-ion batteries. In Proceedings of the 11th International Symposium PÄRNU “Topical Problems in the Field of Electrical and Power Engineering” and “Doctoral School of Energy and Geotechnology”, Pärnu, Estonia, 16–21 January 2012. [Google Scholar]
- Zhang, R.; Xia, B.; Li, B.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W.; Wang, M. Study on the Characteristics of a High Capacity Nickel Manganese Cobalt Oxide (NMC) Lithium-Ion Battery—An Experimental Investigation. Energies 2018, 11, 2275. [Google Scholar] [CrossRef]
- Nikolian, A.; Firouz, Y.; Gopalakrishnan, R.; Timmermans, J.; Omar, N.; van den Bossche, P.; van Mierlo, J. Lithium Ion Batteries—Development of Advanced Electrical Equivalent Circuit Models for Nickel Manganese Cobalt Lithium-Ion. Energies 2016, 9, 360. [Google Scholar] [CrossRef]
- Ceraolo, M. New dynamical models of lead-acid batteries. IEEE Trans. Power Syst. 2000, 15, 1184–1190. [Google Scholar] [CrossRef]
- Puleston, P.F.; Valenciaga, F.; Battaiotto, P.E.; Mantz, R.J. Passivity/sliding mode control of a stand-alone hybrid generation system. IEE Proc. Control Theory Appl. 2000, 147, 680–686. [Google Scholar]
- Zhu, T.; Min, H.; Yu, Y.; Zhao, Z.; Xu, T.; Chen, Y.; Li, X.; Zhang, C. An Optimized Energy Management Strategy for Preheating Vehicle-Mounted Li-ion Batteries at Subzero Temperatures. Energies 2017, 10, 243. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.; Dekkiche, A. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the 2007 IEEE Vehicle Power and Propulsion Conference (VPPC), Arlington, TX, USA, 9–12 September 2007; pp. 284–289. [Google Scholar]
- Baboselac, I.; Hederić, Z.; Bensić, T. MatLab simulation model for dynamic mode of the Lithium-Ion batteries to power the EV. Teh. Glas. 2017, 11, 7–13. [Google Scholar]
- Pang, S.; Farrell, J.; Du, J.; Barth, M. Battery state-of-charge estimation. In Proceedings of the 2001 American Control Conference. (Cat. No. 01CH37148), Arlington, VA, USA, 25–27 June 2001; Volume 2, p. 1649. [Google Scholar]
- Cun, J.P.; Fiorina, J.N.; Fraisse, M.; Mabboux, H. The experience of a UPS company in advanced battery monitoring. In Proceedings of the Intelec’96-International Telecommunications Energy Conference, Boston, MA, USA, 6–10 October 1996; pp. 646–653. [Google Scholar]
- Chan, H.L. A new battery model for use with battery energy storage systems and electric vehicles power systems. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No.00CH37077), Singapore, 23–27 January 2000; p. 475. [Google Scholar]
- Berrueta, A.; Irigaray, V.; Sanchis, P.; Ursua, A. Lithium-ion battery model and experimental validation. In Proceedings of the 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–8. [Google Scholar]
- Kim, Y.H.; Ha, H.D. Design of interface circuits with electrical battery models. IEEE Trans. Ind. Electron. 1997, 44, 81–86. [Google Scholar] [CrossRef]
- Marcos, J.; Lago, A.; Penalver, C.M.; Doval, J.; Nogueira, A.; Castro, C.; Chamadoira, J. An approach to real behaviour modeling for traction lead-acid batteries. In Proceedings of the 2011 IEEE 32nd Annual Power Electronics Specialists Conference (IEEE Cat. No.01CH37230), Vancouver, BC, Canada, 17–21 June 2001; p. 624. [Google Scholar]
- Sen, C.; Kar, N.C. Battery pack modeling for the analysis of battery management system of a hybrid electric vehicle. In Proceedings of the Battery pack modeling for the analysis of battery management system of a hybrid electric vehicle, Dearborn, MI, USA, 7–10 September 2009; pp. 207–212. [Google Scholar]
- Ali, M.; Kamran, M.; Kumar, P.; Himanshu; Nengroo, S.; Khan, M.; Hussain, A.; Kim, H. An Online Data-Driven Model Identification and Adaptive State of Charge Estimation Approach for Lithium-ion-Batteries Using the Lagrange Multiplier Method. Energies 2018, 11, 2940. [Google Scholar] [CrossRef]
- Kim, D.; Koo, K.; Jeong, J.; Goh, T.; Kim, S. Second-Order Discrete-Time Sliding Mode Observer for State of Charge Determination Based on a Dynamic Resistance Li-Ion Battery Model. Energies 2013, 6, 5538–5551. [Google Scholar] [CrossRef]
- Kim, I.S. Nonlinear State of Charge Estimator for Hybrid Electric Vehicle Battery. IEEE Trans. Power Electron. 2008, 23, 2027–2034. [Google Scholar]
- Ting, T.O.; Man, K.L.; Lim, E.G.; Leach, M. Tuning of Kalman Filter Parameters via Genetic Algorithm for State-of-Charge Estimation in Battery Management System. Sci. World J. 2014, 2014, 176052. [Google Scholar] [CrossRef] [PubMed]
- Zhan, C.; Wu, X.G.; Kromlidis, S.; Ramachandaramurthy, V.K.; Barnes, M.; Jenkins, N.; Ruddell, A.J. Two electrical models of the lead–acid battery used in a dynamic voltage restorer. IEE Proc. Gener. Transm. Distrib. 2003, 150, 175. [Google Scholar] [CrossRef]
- Yuan, S.; Wu, H.; Ma, X.; Yin, C. Stability Analysis for Li-Ion Battery Model Parameters and State of Charge Estimation by Measurement Uncertainty Consideration. Energies 2015, 8, 7729–7751. [Google Scholar] [CrossRef]
- Bruen, T.; Marco, J. Modelling and experimental evaluation of parallel connected lithium ion cells for an electric vehicle battery system. J. Power Sources 2016, 310, 91–101. [Google Scholar] [CrossRef]
- Jonghoon, K.; Cho, B.H. State-of-Charge Estimation and State-of-Health Prediction of a Li-Ion Degraded Battery Based on an EKF Combined With a Per-Unit System. IEEE Trans. Veh. Technol. 2011, 60, 4249–4260. [Google Scholar]
- Hegazy, O.; Barrero, R.; Van Mierlo, J.; Lataire, P.; Omar, N.; Coosemans, T. An Advanced Power Electronics Interface for Electric Vehicles Applications. IEEE Trans. Power Electron. 2013, 28, 5508–5521. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Guo, H.; Ding, Y. Modeling for Lithium-Ion Battery used in Electric Vehicles. Procedia Eng. 2011, 15, 2869–2874. [Google Scholar] [CrossRef]
- Han, H.; Xu, H.; Yuan, Z.; Zhao, Y. Modeling for lithium-ion battery used in electric vehicles. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014. [Google Scholar]
- Fotouhi, A.; Propp, K.; Auger, D.J. Electric vehicle battery model identification and state of charge estimation in real world driving cycles. In Proceedings of the 2015 7th Computer Science and Electronic Engineering Conference, Colchester, UK, 24–25 September 2015; p. 243. [Google Scholar]
- Rahimi-Eichi, H.; Chow, M.Y. Adaptive parameter identification and State-of-Charge estimation of lithium-ion batteries. In Proceedings of the IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 4012–4017. [Google Scholar]
- Erdinc, O.; Vural, B.; Uzunoglu, M. A dynamic lithium-ion battery model considering the effects of temperature and capacity fading. In Proceedings of the 2009 International Conference on Clean Electrical Power, Capri, Italy, 9–11 June 2009; pp. 383–386. [Google Scholar]
- Guo, X.; Kang, L.; Yao, Y.; Huang, Z.; Li, W. Joint Estimation of the Electric Vehicle Power Battery State of Charge Based on the Least Squares Method and the Kalman Filter Algorithm. Energies 2016, 9, 100. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The Co-estimation of State of Charge, State of Health, and State of Function for Lithium-Ion Batteries in Electric Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 92–103. [Google Scholar] [CrossRef]
- Mesbahi, T.; Rizoug, N.; Bartholomeus, P.; Sadoun, R.; Khenfri, F.; Le Moigne, P. Dynamic Model of Li-Ion Batteries Incorporating Electrothermal and Ageing Aspects for Electric Vehicle Applications. IEEE Trans. Ind. Electron. 2018, 65, 1298–1305. [Google Scholar] [CrossRef]
- Chaoui, H.; El Mejdoubi, A.; Gualous, H. Online Parameter Identification of Lithium-Ion Batteries With Surface Temperature Variations. IEEE Trans. Veh. Technol. 2017, 66, 2000–2009. [Google Scholar] [CrossRef]
- Cheng, X.; Yao, L.; Xing, Y.; Pecht, M. Novel Parametric Circuit Modeling for Li-Ion Batteries. Energies 2016, 9, 539. [Google Scholar] [CrossRef]
- Guenther, C.; Barillas, J.K.; Stumpp, S.; Danzer, M.A. A dynamic battery model for simulation of battery-to-grid applications. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–7. [Google Scholar]
- Dong, B.; Tian, Y.; Zhou, C. One Estimating Method of the State of Charge of Power Battery for Electronic Vehicle. In Proceedings of the 2014 Sixth International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 10–11 January 2014; pp. 439–442. [Google Scholar]
- Liu, X.; Li, W.; Zhou, A. PNGV Equivalent Circuit Model and SOC Estimation Algorithm for Lithium Battery Pack Adopted in AGV Vehicle. Access 2018, 6, 23639–23647. [Google Scholar] [CrossRef]
- Ozkurt, C.; Camci, F.; Atamuradov, V.; Odorry, C. Integration of sampling based battery state of health estimation method in electric vehicles. Appl. Energy 2016, 175, 356–367. [Google Scholar] [CrossRef]
- Uddin, K.; Picarelli, A.; Lyness, C.; Taylor, N.; Marco, J. An Acausal Li-Ion Battery Pack Model for Automotive Applications. Energies 2014, 7, 5675–5700. [Google Scholar] [CrossRef]
- U.S. Department Secretary of Energy FreedomCAR Battery Test Manual for IDAHO. Available online: https://avt.inl.gov/sites/default/files/pdf/battery/freedomcar_manual_04_15_03.pdf (accessed on 5 May 2019).
- Omar, N.; Widanage, D.; Abdel Monem, M.; Firouz, Y.; Hegazy, O.; Van den Bossche, P.; Coosemans, T.; Van Mierlo, J. Optimization of an advanced battery model parameter minimization tool and development of a novel electrical model for lithium-ion batteries. Int. Trans. Electr. Energy Syst. 2014, 24, 1747–1767. [Google Scholar] [CrossRef]
- Omar, N.; Daowd, M.; Bossche, P.v.d.; Hegazy, O.; Smekens, J.; Coosemans, T.; Mierlo, J.v. Rechargeable Energy Storage Systems for Plug-in Hybrid Electric Vehicles—Assessment of Electrical Characteristics. Energies 2012, 5, 2952–2988. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modelling: From Lithium-ion toward Lithium-Sulphur. Renew. Sustain. Energy Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, Z.; Lai, Y.; Liu, J.; Li, J.; Liu, Y. Electrochemical Impedance Spectroscopy Study of a Lithium/Sulfur Battery: Modeling and Analysis of Capacity Fading. J. Electrochem. Soc. 2013, 160, A558. [Google Scholar] [CrossRef]
- Alavi, S.M.M.; Birkl, C.R.; Howey, D.A. Time-domain fitting of battery electrochemical impedance models. J. Power Sources 2015, 288, 345–352. [Google Scholar] [CrossRef]
- Troxler, Y.; Wu, B.; Marinescu, M.; Yufit, V.; Patel, Y.; Marquis, A.J.; Brandon, N.P.; Offer, G.J. The effect of thermal gradients on the performance of lithium-ion batteries. J. Power Sources 2014, 247, 1018–1025. [Google Scholar] [CrossRef]
- Dai, H.; Jiang, B.; Wei, X. Impedance Characterization and Modeling of Lithium-Ion Batteries Considering the Internal Temperature Gradient. Energies 2018, 11, 220. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Liaw, B.Y.; Zhang, J. Graphical analysis of electrochemical impedance spectroscopy data in Bode and Nyquist representations. J. Power Sources 2016, 309, 82–98. [Google Scholar] [CrossRef]
- Kollmeyer, P.; Hackl, A.; Emadi, A. Li-ion battery model performance for automotive drive cycles with current pulse and EIS parameterization. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 22–24 June 2017; pp. 486–492. [Google Scholar]
- Plett, G. Battery Management Systems, Volume I: Battery Modeling; Artech House: Norwood, UK, 2015. [Google Scholar]
- Jespersen, J.L.; Tønnesen, A.E.; Nørregaard, K.; Overgaard, L.; Elefsen, F. Capacity Measurements of Li-Ion Batteries using AC Impedance Spectroscopy. World Electr. Veh. J. 2009, 3, 127–133. [Google Scholar] [CrossRef]
- Birkl, C.R.; Howey, D.A. Model identification and parameter estimation for LiFePO4 batteries. In Proceedings of the IET Hybrid and Electric Vehicles Conference 2013 (HEVC 2013), London, UK, 6–7 November 2013. [Google Scholar]
- Schmalstieg, J.; Sauer, D.U. Full Cell Parameterization of a High-Power Lithium-Ion Battery for a Physico-Chemical Model: Part II. Thermal Parameters and Validation. J. Electrochem. Soc. 2018, 165, A3819. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Cao, J. A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model. J. Power Sources 2013, 233, 277–284. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Vinassa, J. Performance comparison of four lithium–ion battery technologies under calendar aging. Energy 2015, 84, 542–550. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Uddin, K.; Chouchelamane, G.H.; Widanage, W.D.; Marco, J. A Comparison between Electrochemical Impedance Spectroscopy and Incremental Capacity-Differential Voltage as Li-ion Diagnostic Techniques to Identify and Quantify the Effects of Degradation Modes within Battery Management Systems. J. Power Sources 2017, 360, 301–318. [Google Scholar] [CrossRef]
- Barai, A.; Chouchelamane, G.H.; Guo, Y.; McGordon, A.; Jennings, P. A study on the impact of lithium-ion cell relaxation on electrochemical impedance spectroscopy. J. Power Sources 2015, 280, 74–80. [Google Scholar] [CrossRef]
- Heubner, C.; Schneider, M.; Michaelis, A. Investigation of charge transfer kinetics of Li-Intercalation in LiFePO4. J. Power Sources 2015, 288, 115–120. [Google Scholar] [CrossRef]
- Olofsson, Y.; Groot, J.; Katrašnik, T.; Tavcčar, G. Impedance spectroscopy characterisation of automotive NMC/graphite Li-ion cells aged with realistic PHEV load profile. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014; pp. 1–6. [Google Scholar]
- Osaka, T.; Momma, T.; Mukoyama, D.; Nara, H. Proposal of novel equivalent circuit for electrochemical impedance analysis of commercially available lithium ion battery. J. Power Sources 2012, 205, 483–486. [Google Scholar] [CrossRef]
- Li, S.E.; Wang, B.; Peng, H.; Hu, X. An electrochemistry-based impedance model for lithium-ion batteries. J. Power Sources 2014, 258, 9–18. [Google Scholar] [CrossRef]
- Zhang, H.; Chow, M.H. Comprehensive dynamic battery modeling for PHEV applications. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25-29 July 2010; pp. 1–6. [Google Scholar]
- Kroeze, R.C.; Krein, P.T. Electrical battery model for use in dynamic electric vehicle simulations. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 1336–1342. [Google Scholar]
- Cao, Y.; Kroeze, R.C.; Krein, P.T. Multi-timescale Parametric Electrical Battery Model for Use in Dynamic Electric Vehicle Simulations. IEEE Trans. Transp. Electr. 2016, 2, 432–442. [Google Scholar] [CrossRef]
- Huria, T.; Ceraolo, M.; Gazzarri, J.; Jackey, R. High fidelity electrical model with thermal dependence for characterization and simulation of high power lithium battery cells. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–8. [Google Scholar]
- Blanco, C.; Sánchez, L.; Gonzalez, M.; Anton, J.C.; Gacia, V.; Viera, J.C. An Equivalent Circuit Model With Variable Effective Capacity for LiFePO4 Batteries. IEEE Trans. Veh. Technol. 2014, 63, 3592–3599. [Google Scholar] [CrossRef]
- Mathew, M.; Kong, Q.H.; McGrory, J.; Fowler, M. Simulation of lithium ion battery replacement in a battery pack for application in electric vehicles. J. Power Sources 2017, 349, 94–104. [Google Scholar] [CrossRef]
- Gao, L.; Liu, S.; Dougal, R.A. Dynamic lithium-ion battery model for system simulation. IEEE Trans. Compon. Packag. Technol. 2002, 25, 495–505. [Google Scholar]
- Verbrugge, M.; Koch, B. Generalized Recursive Algorithm for Adaptive Multiparameter Regression. J. Electrochem. Soc. 2006, 153, A187. [Google Scholar] [CrossRef]
- Nikolian, A.; Jaguemont, J.; de Hoog, J.; Goutam, S.; Omar, N.; Van Den Bossche, P.; Van Mierlo, J. Complete cell-level lithium-ion electrical ECM model for different chemistries (NMC, LFP, LTO) and temperatures (−5 °C to 45 °C)—Optimized modelling techniques. Int. J. Electr. Power Energy Syst. 2018, 98, 133–146. [Google Scholar] [CrossRef]
- Mesbahi, T.; Khenfri, F.; Rizoug, N.; Chaaban, K.; Bartholomeüs, P.; Le Moigne, P. Dynamical modeling of Li-ion batteries for electric vehicle applications based on hybrid Particle Swarm-Nelder-Mead (PSO-NM) optimization algorithm. Electr. Power Syst. Res. 2016, 131, 195–204. [Google Scholar] [CrossRef]
- de Hoog, J.; Jaguemont, J.; Abdel-Monem, M.; Van Den Bossche, P.; Van Mierlo, J.; Omar, N. Combining an Electrothermal and Impedance Aging Model to Investigate Thermal Degradation Caused by Fast Charging. Energies 2018, 11, 804. [Google Scholar] [CrossRef]
- Sidhu, A.; Izadian, A.; Anwar, S. Adaptive Nonlinear Model-Based Fault Diagnosis of Li-Ion Batteries. IEEE Trans. Ind. Electron. 2015, 62, 1002–1011. [Google Scholar] [CrossRef]
- Yuksel, T.; Litster, S.; Viswanathan, V.; Michalek, J.J. Plug-in hybrid electric vehicle LiFePO4 battery life implications of thermal management, driving conditions, and regional climate. J. Power Sources 2017, 338, 49–64. [Google Scholar] [CrossRef]
- Omar, N.; Monem, M.A.; Firouz, Y.; Salminen, J.; Smekens, J.; Hegazy, O.; Gaulous, H.; Mulder, G.; Van den Bossche, P.; Coosemans, T.; et al. Lithium iron phosphate based battery—Assessment of the aging parameters and development of cycle life model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar] [CrossRef]
- Lam, L.; Bauer, P.; Kelder, E. A practical circuit-based model for Li-ion battery cells in electric vehicle applications. In Proceedings of the 2011 IEEE 33rd International Telecommunications Energy Conference (INTELEC), Amsterdam, Netherlands, 9–13 October 2011; pp. 1–9. [Google Scholar]
- Thompson, A.W. Economic implications of lithium ion battery degradation for Vehicle-to-Grid (V2X) services. J. Power Sources 2018, 396, 691–709. [Google Scholar] [CrossRef]














| Model Nature | Model | Data | Physical Interpretability | Analogy | Accuracy | Complexity | Suited Application | ||
|---|---|---|---|---|---|---|---|---|---|
| Electro-chemical | Pure Electro-Chemical | P | H | White box | VH | H | Battery design | ||
| ECM/Reduced order Electro-Chemical | SE | M | Grey box | H | M | ||||
| Electrical | Analytical | Peukert’s model | E | L | Black box | M | M | Prediction | |
| Rakhmatov and Vrudhula | SE | M | M | M | |||||
| Sheperd other iterations | SE | M | M | M | |||||
| State-Space | E | L | M | M | |||||
| ECM | Simples | Simple Rint | E | M | Grey box | L | L | Real time control, SoC estimation, … | |
| Enhanced Rint | SE | M | L | L | |||||
| RC | SE | M | L | L | |||||
| Thevenin | 1st order | SE | M | L–H | L–H | ||||
| 2nd order | SE | M | |||||||
| 3rd order | SE | M | |||||||
| nth order | SE | M | |||||||
| PNGV | 1st order | SE | M | L–H | L–H | ||||
| 2nd order | SE | M | |||||||
| nth order | SE | M | |||||||
| Noshin | SE | M | M | M | |||||
| Neural nets | E | L | H | H | |||||
| Impedance | Frequency domain | SE | L–M | Grey box | M | M | Characterization and real time operation | ||
| Thermal | Analytical Thermal | P–SE | H | White box | H | H | Real time | ||
| ECM Thermal | SE | M | Grey box | M | M | ||||
| Mechanical/Fatigue | Fatigue/Mechanical | P–SE | H | Grey box | H | Design | |||
| Abstract model | Artificial Intelligence | E | L | Black box | M | M | Offline analysis | ||
| Combined models | Electro-Thermal | SE | M | Grey box | M | Real time | |||
| Thermo-electrochemical | P | H | L–H | H | |||||
| Thermo-Mechanical | SE | H | H | ||||||
| Predicting Capability | Thevenin Based/PNGV Models (ECM) | Impedance Based Models | Runtime-Combined Based Models |
|---|---|---|---|
| DC | No | No | Yes |
| AC | Limited | Yes | No |
| Transient | Yes | Limited | Limited |
| Battery Runtime | No | No | Yes |
| Test | 50% SoC, 1C | Pulse Test | DDP Test | Capacity Test 1C | Capacity Test 5C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DoD [%] | 0–5 | 5–90 | 90–100 | 0–5 | 5–90 | 90–100 | 0–5 | 5–90 | 90–100 | 0–5 | 5–90 | 90–100 | |
| Rint | 0.2 | 4.5 | 7 | 14 | 5 | 15 | 20 | 3 | 5 | 18 | 8 | 9 | 19.2 |
| RC | 0.3 | 8 | 2 | 55 | 5 | 5 | 46 | 7 | 2 | 58 | 6 | 5 | 50 |
| Thevenin | 0.2 | 3.5 | 5 | 17 | 4 | 4 | 15 | 2 | 1 | 20 | 2 | 7 | 19 |
| PNGV | 0.2 | 2 | 1.5 | 25 | 4 | 3.5 | 19 | 2 | 1.5 | 29 | 6 | 12 | 18 |
| 2nd order PNGV | 0.1 | 2 | 2 | 19 | 2.5 | 2 | 14 | 2 | 2 | 25 | 4 | 14 | 35 |
| 3rd order PNGV | 0.2 | 1.5 | 2 | 17 | 3 | 1 | 13 | 2 | 2 | 23 | 3 | 12 | 28 |
| Noshin | 0.2 | 2 | 1.5 | 13.5 | 2.5 | 3 | 14 | 2 | 1 | 16.5 | 2 | 2 | 12.5 |
| Model | Objective | Considerations | Battery Type | Year | Ref | |||
|---|---|---|---|---|---|---|---|---|
| Effects | Parameters | |||||||
| ECM | Simple | Ideal | Model | VOC | Li-Ion | 1997 | [15] | |
| Linear | Energy management | SoC, T | VOC, Rint | LFP (Li-Ion) | 2017 | [22] | ||
| HEV Simulation | SoC | Li-Ion | 2007 | [23] | ||||
| 2017 | [24] | |||||||
| SoC estimation | Lead-Acid | 2001 | [25] | |||||
| Model | Ccap, Rint | LFP (Li-Ion) | 2013 | [82] | ||||
| RC | SoC estimation | Pol, Prop, SoC | CB, RB, Rint, RP, CP | Li-Ion | 2013 | [33] | ||
| 2014 | [35] | |||||||
| LIPO (Li-Ion) | 2008 | [34] | ||||||
| Thev | 1 Order | SoC estimation | Pol, SoC | VOC, Rint, RP, CP | LCO (Li-Ion) | 2018 | [32] | |
| Stability analysis and SoC estimation | Li-Ion | 2015 | [37] | |||||
| Batteries parallelization | 2016 | [38] | ||||||
| SoC and SoH model | Pol, SoC, SoH, T | 2011 | [39] | |||||
| Power Electronic | Pol, SoC, | 2013 | [40] | |||||
| EP-Thevenein model | LFP (Li-Ion) | 2011 | [41] | |||||
| Life model | Pol, SoC, T | LFP (Li-Ion) | 2017 | [83] | ||||
| System design | Li-Ion | 2002 | [84] | |||||
| Parameter regression | Pol, SoC, T, Hyst | Pb-acid, NiMH, Li-ion | 2006 | [85] | ||||
| 2 order | Model | T, CF | VOC, Rint, 2RC | Li-Ion | 2009 | [45] | ||
| SoC estimation | Pol, SoC | 2016 | [46] | |||||
| SoC, SoH, and SoF estimation | SoC, SoH, SoF | 2018 | [47] | |||||
| Model | Pol, SoC, SoH, T | NMC (Li-Ion) | 2018 | [48] | ||||
| Characterization | [18] | |||||||
| Model | Pol, SoC, T | NMC, LFP, LTO (Li-Ion) | 2018 | [86] | ||||
| NMC (Li Ion) | 2016 | [87] | ||||||
| 2018 | [88] | |||||||
| Fault diagnosis | Pol, SoC | Li-Ion | 2013 | [89] | ||||
| Life model | Pol, SoC, T, SoH | 2017 | [90] | |||||
| 3 order | Model | SoC,Pol | VOC, Rint, 3RC | Li-Ion | 2016 | [50] | ||
| Model for V2G | SoC, Pol, T, Hyst | 2012 | [51] | |||||
| PNGV | 1 order | SoH estimation | Pol, ID, SoC, | LFP (Li-Ion) | 2018 | [53] | ||
| Pol, ID, SoH, SoC, T | VOC, Rint, C0, RC | 2016 | [54] | |||||
| Model | Pol, ID, Hyst, SoC, T | LFP and NMC (Li-Ion) | 2014 | [55] | ||||
| 2 order | Life model | Pol, SoC, T | VOC, Rint, C0,2RC | LFP (Li-Ion) | 2014 | [91] | ||
| Noshin | Model | Pol, SoC, SoH, T | VOC, Rint, RP, CP | Li-Ion | 2012 | [58] | ||
| Freq | 2 order | Kinetics Study | Pol | VOC, Rint, 2ZArc | LFP (Li-Ion) | 2015 | [74] | |
| Characterization | Pol, SoC, T | NMC (Li-Ion) | 2014 | [75] | ||||
| Model | Pol, SoC | VOC, L, Rint, 2ZArc | Li-Ion | 2014 | [77] | |||
| 3 order | Model | Pol | VOC, L, Rint, 3ZArc | Li-Ion | 2012 | [76] | ||
| RT | Thev | 2 order | Model | Pol, SoC, T, cycles | VOC, Rint, 2RC, Ccap | Li-Ion, Ni-MH | 2006 | [13] |
| Model for EV | LFP (Li-Ion) | 2011 | [92] | |||||
| 3 order | Model for EV | Pol, SoC, T, cycles | VOC, Rint, 3RC, Ccap | Li-Ion | 2011 | [5] | ||
| Li-Ion, Ni-MH | 2008 | [79] | ||||||
| SoC, Pol, T | Li-Ion, Lead acid, Ni-MH | 2016 | [80] | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saldaña, G.; San Martín, J.I.; Zamora, I.; Asensio, F.J.; Oñederra, O. Analysis of the Current Electric Battery Models for Electric Vehicle Simulation. Energies 2019, 12, 2750. https://doi.org/10.3390/en12142750
Saldaña G, San Martín JI, Zamora I, Asensio FJ, Oñederra O. Analysis of the Current Electric Battery Models for Electric Vehicle Simulation. Energies. 2019; 12(14):2750. https://doi.org/10.3390/en12142750
Chicago/Turabian StyleSaldaña, Gaizka, José Ignacio San Martín, Inmaculada Zamora, Francisco Javier Asensio, and Oier Oñederra. 2019. "Analysis of the Current Electric Battery Models for Electric Vehicle Simulation" Energies 12, no. 14: 2750. https://doi.org/10.3390/en12142750
APA StyleSaldaña, G., San Martín, J. I., Zamora, I., Asensio, F. J., & Oñederra, O. (2019). Analysis of the Current Electric Battery Models for Electric Vehicle Simulation. Energies, 12(14), 2750. https://doi.org/10.3390/en12142750






