Steady Flow of a Cement Slurry
Abstract
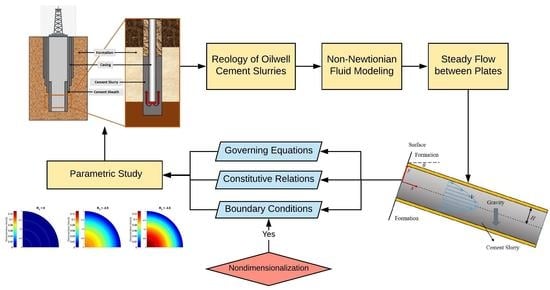
1. Introduction
2. Governing Equations
2.1. Conservation of Mass
2.2. Conservation of Linear Momentum
2.3. Conservation of Angular Momentum
2.4. Convection–Diffusion Equation
3. Constitutive Relations
3.1. Stress Tensor
3.2. Particle Fluxes
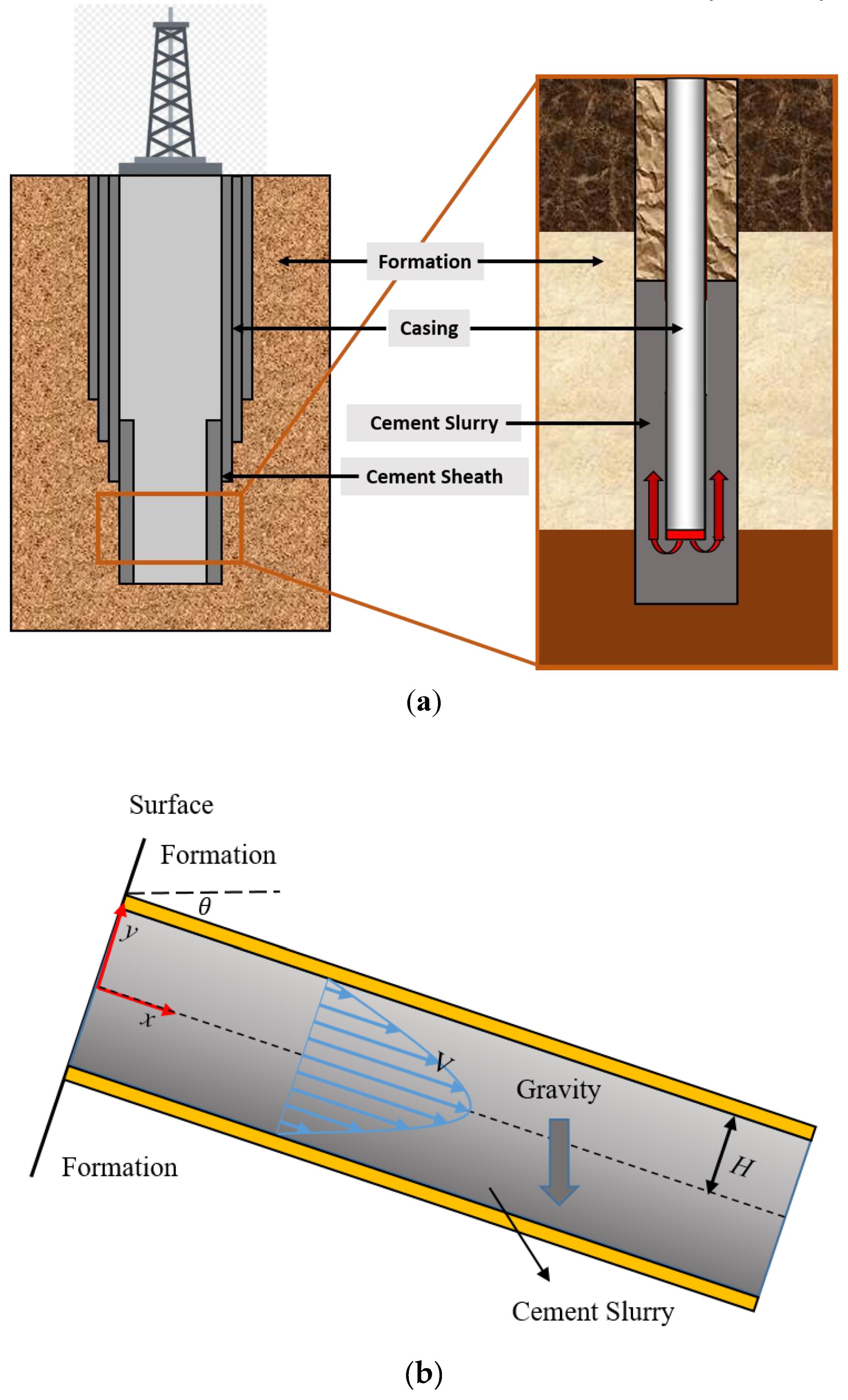
4. Flow between Two Plates
5. Numerical Results and Discussion
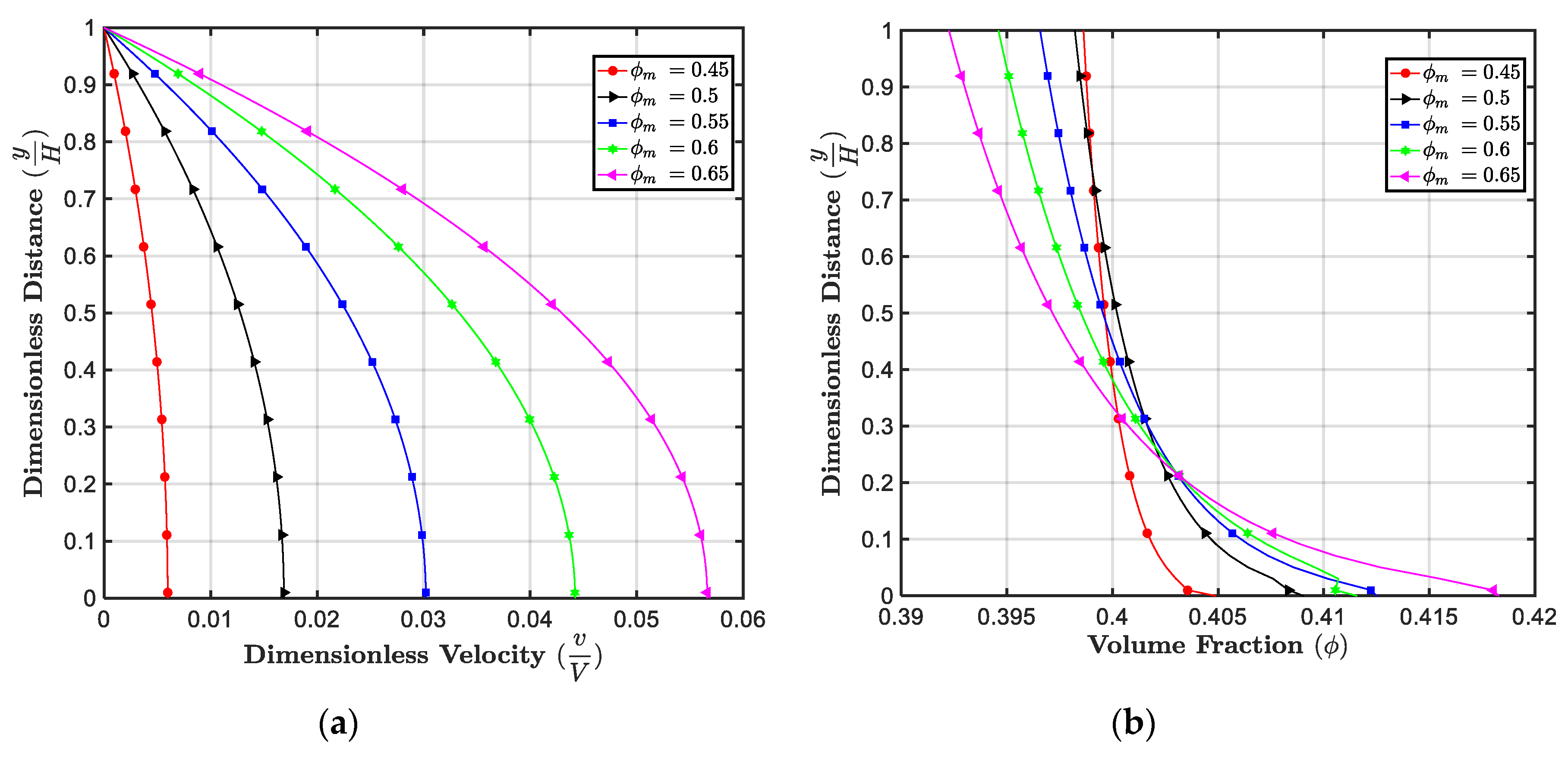
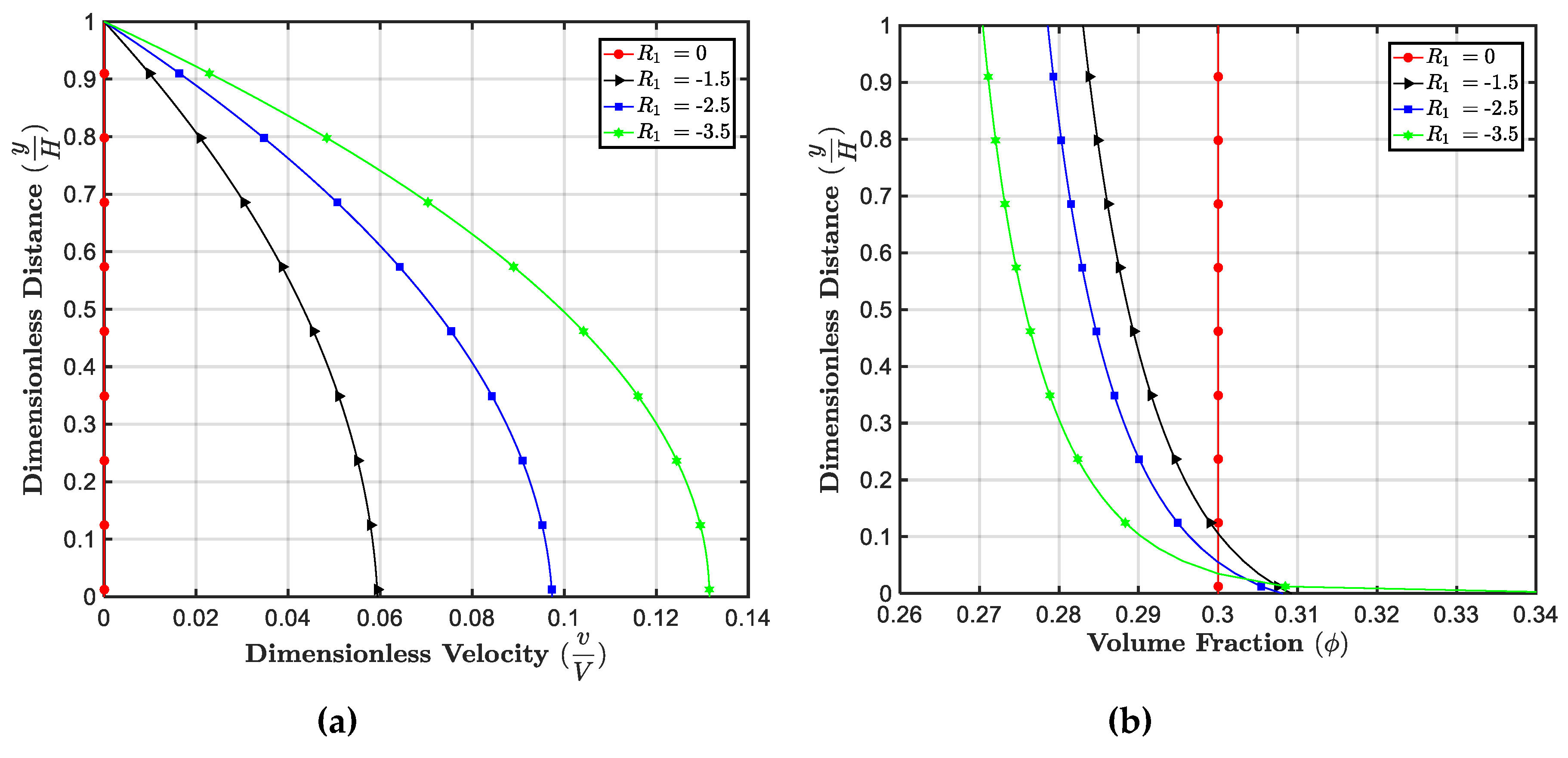
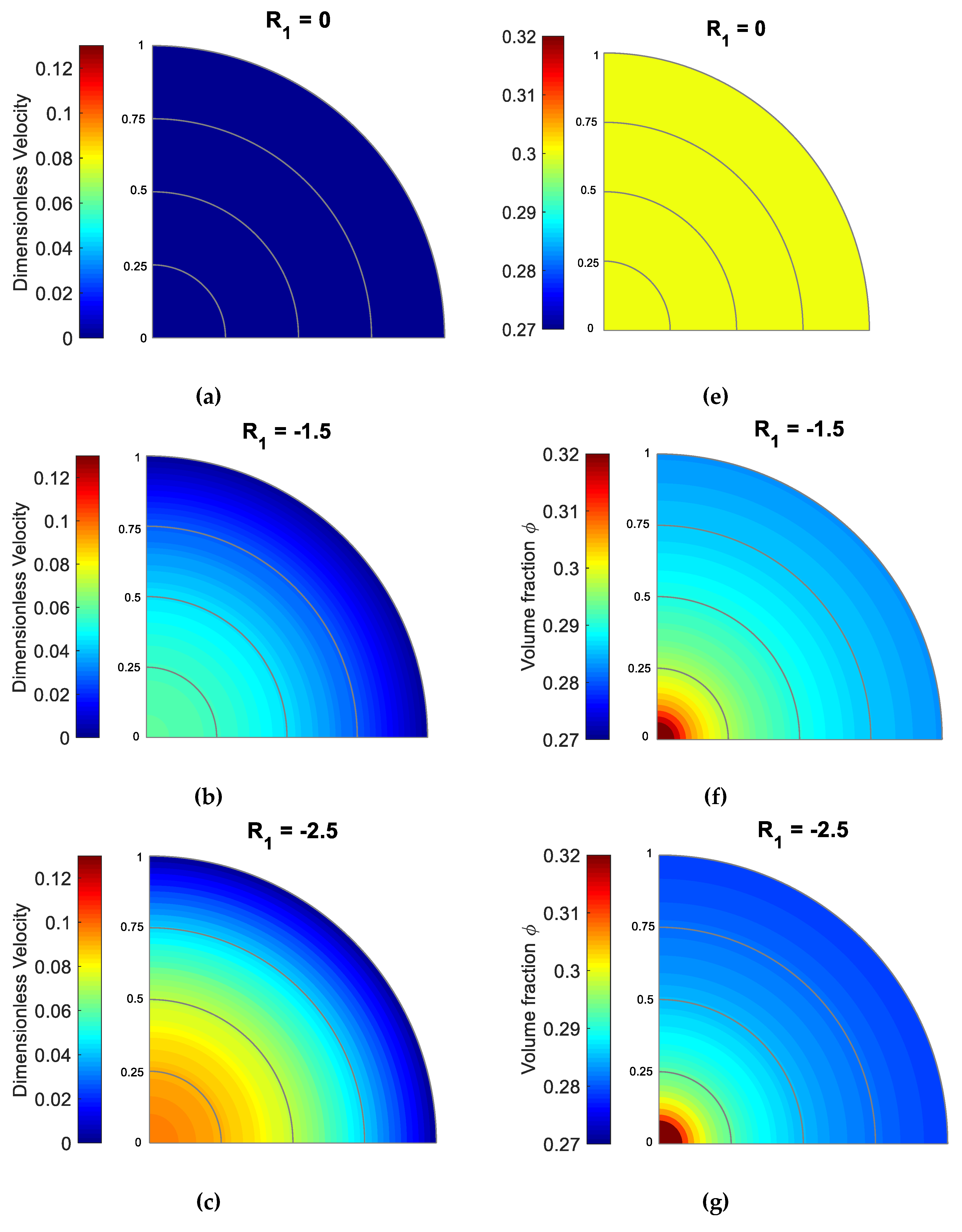
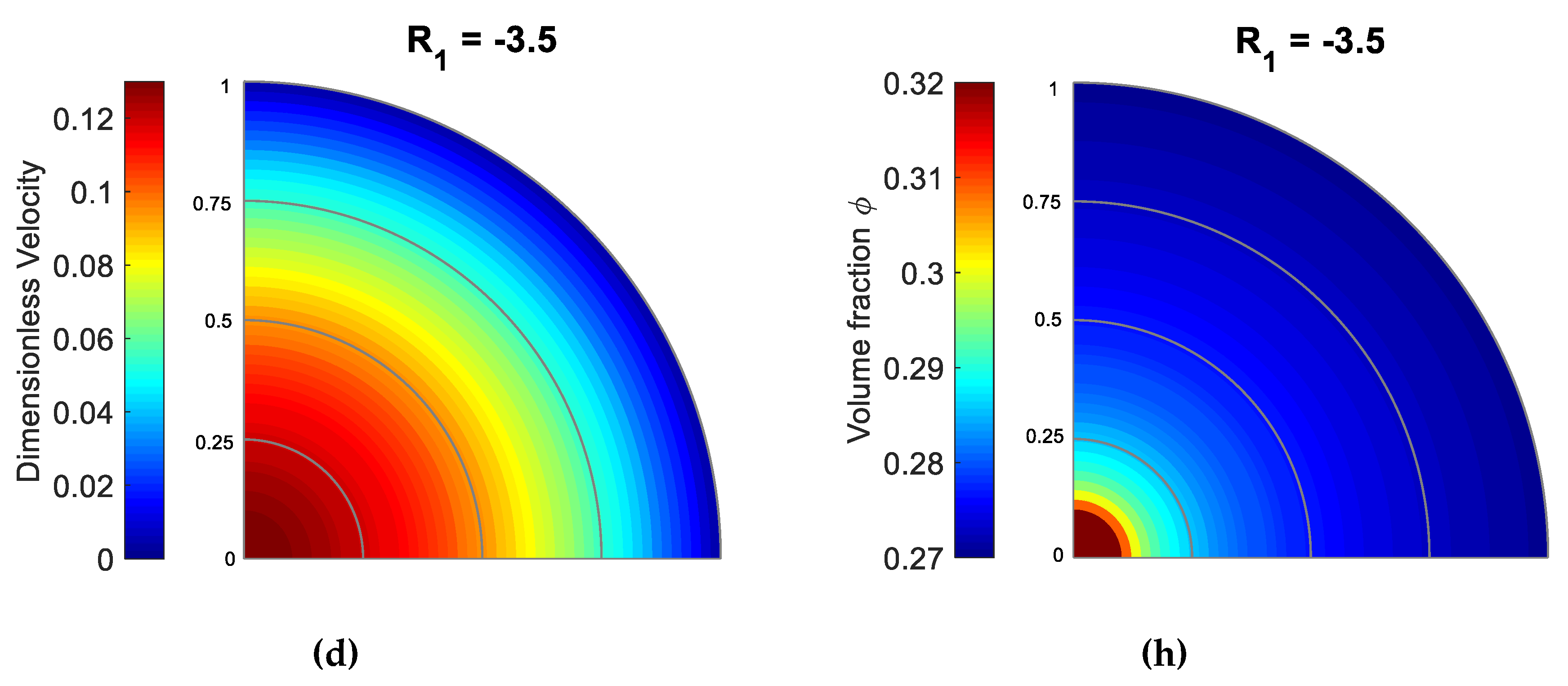
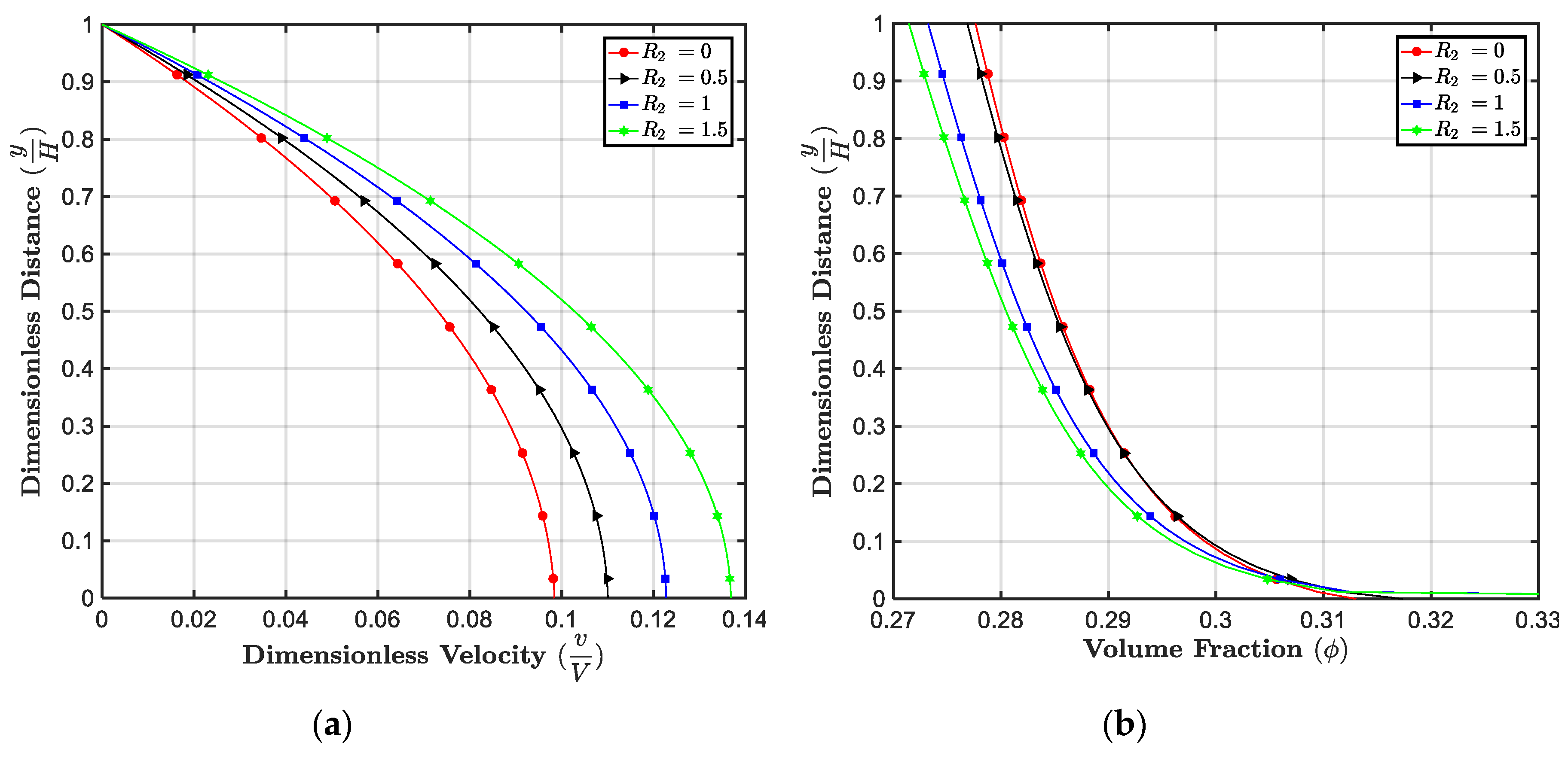
5.1. Effect of
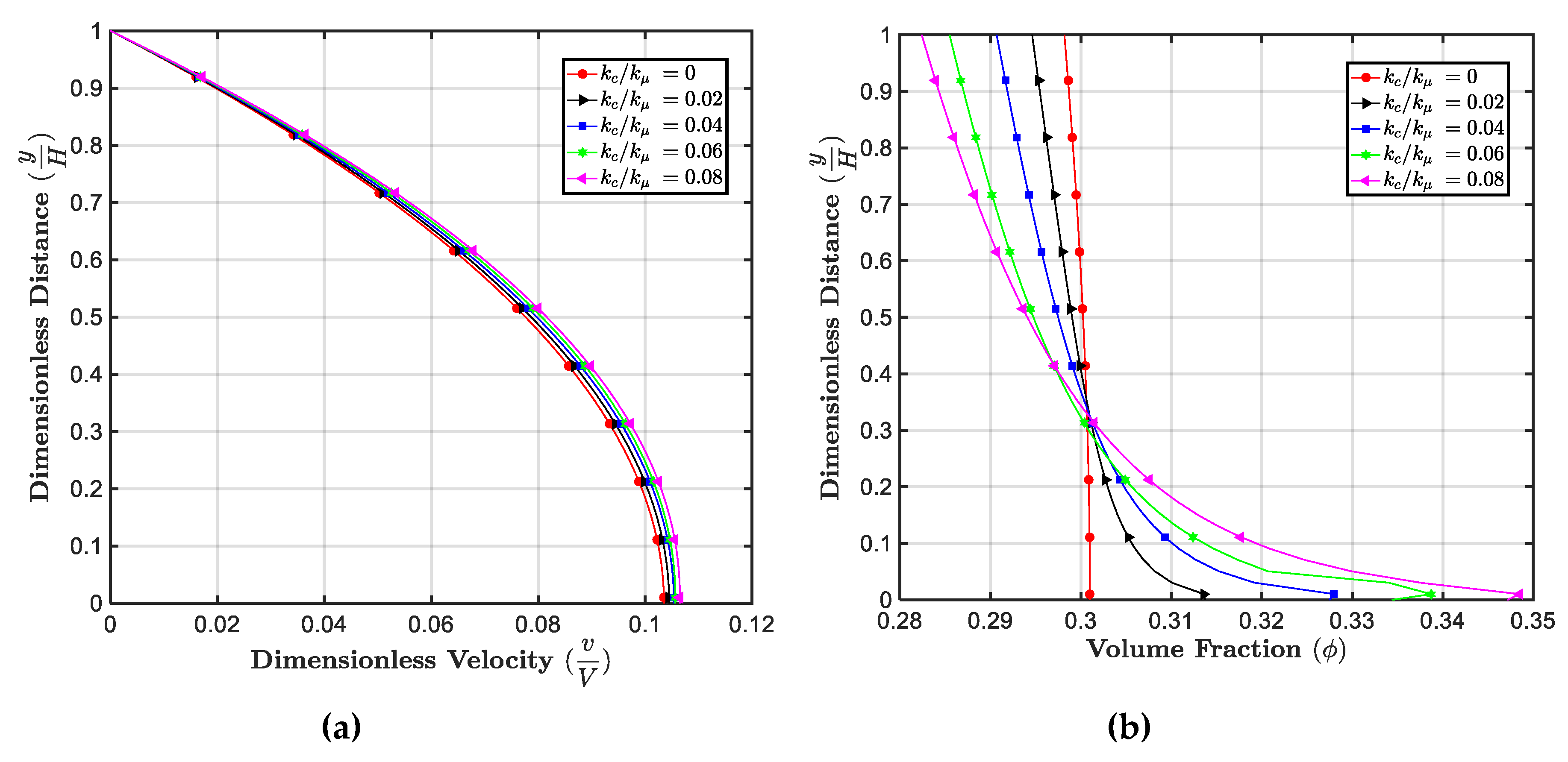
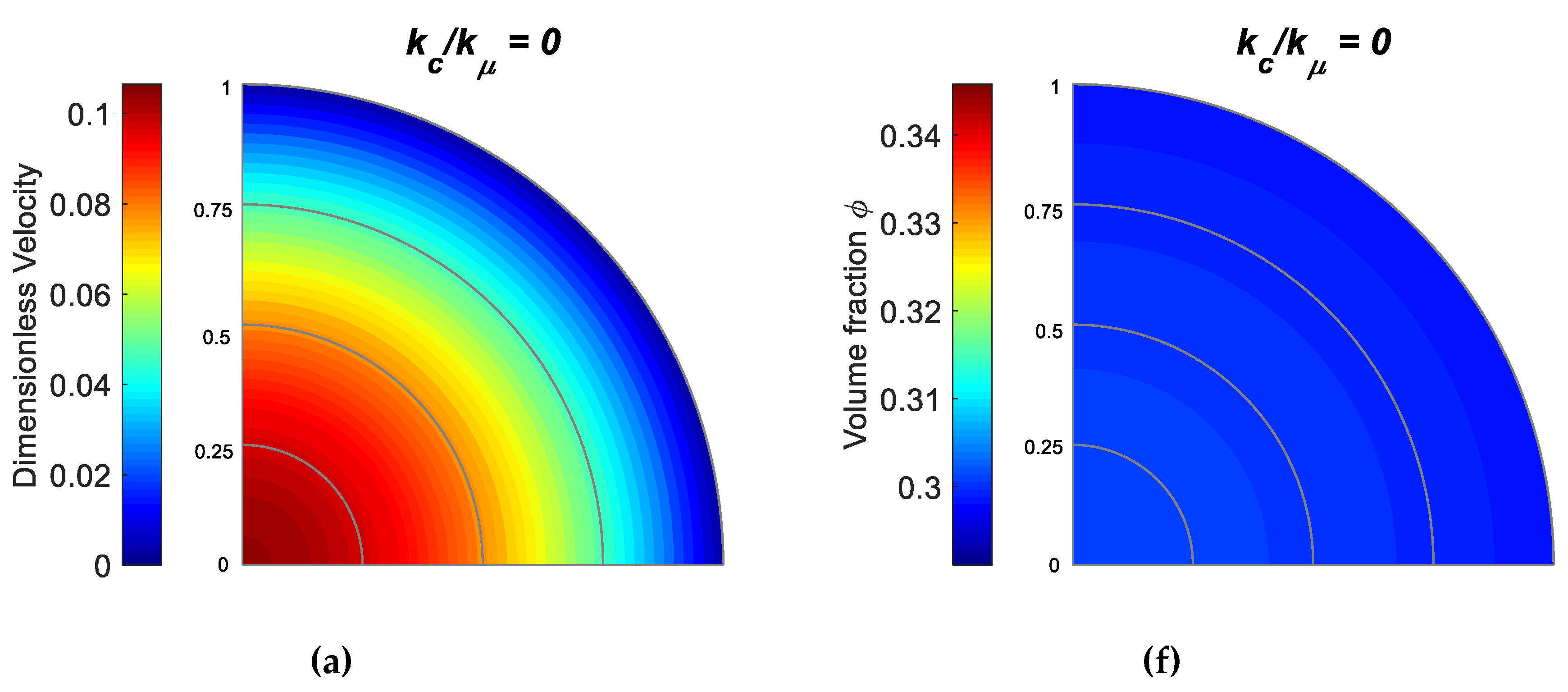
5.2. Effect of
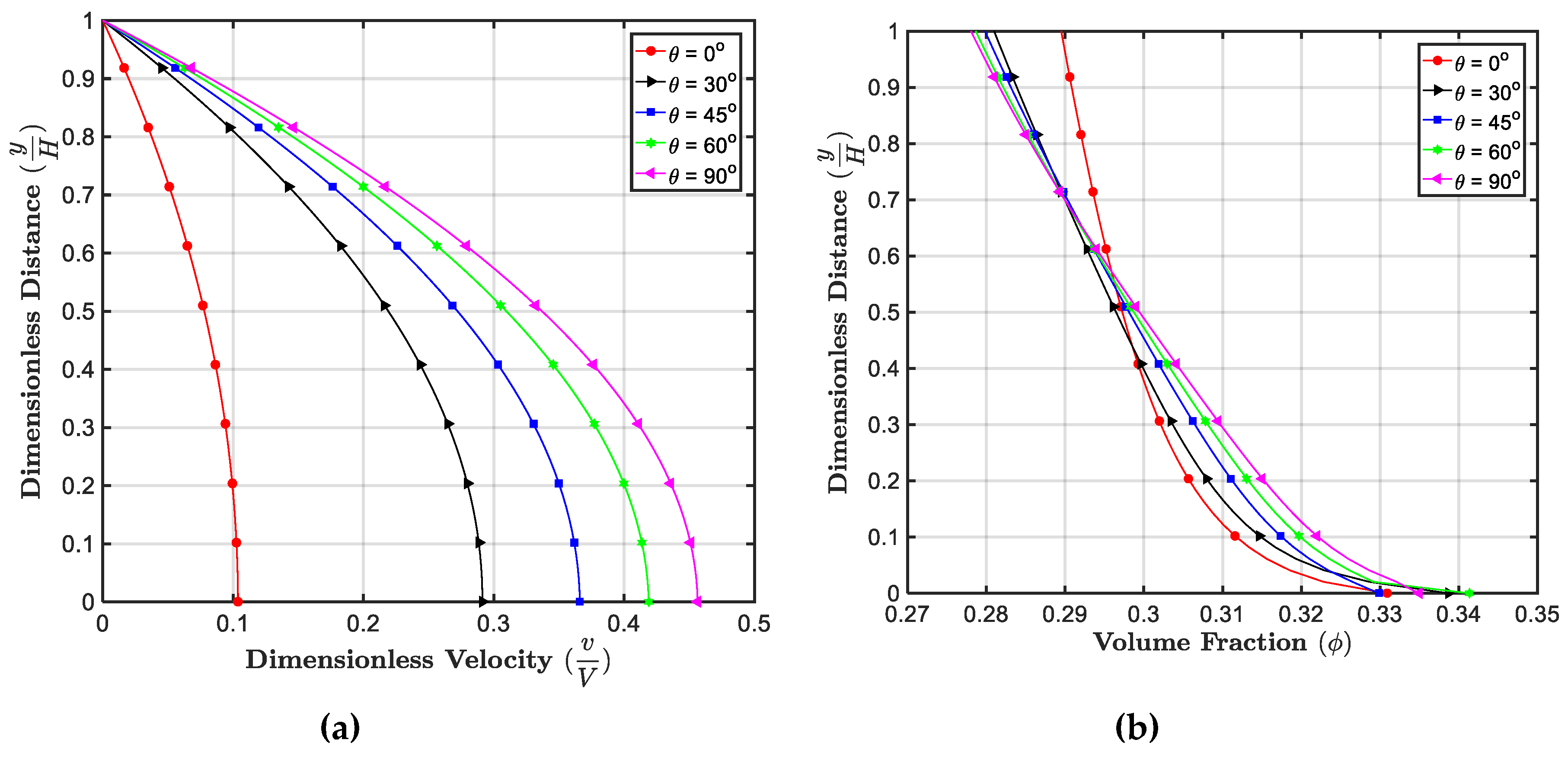
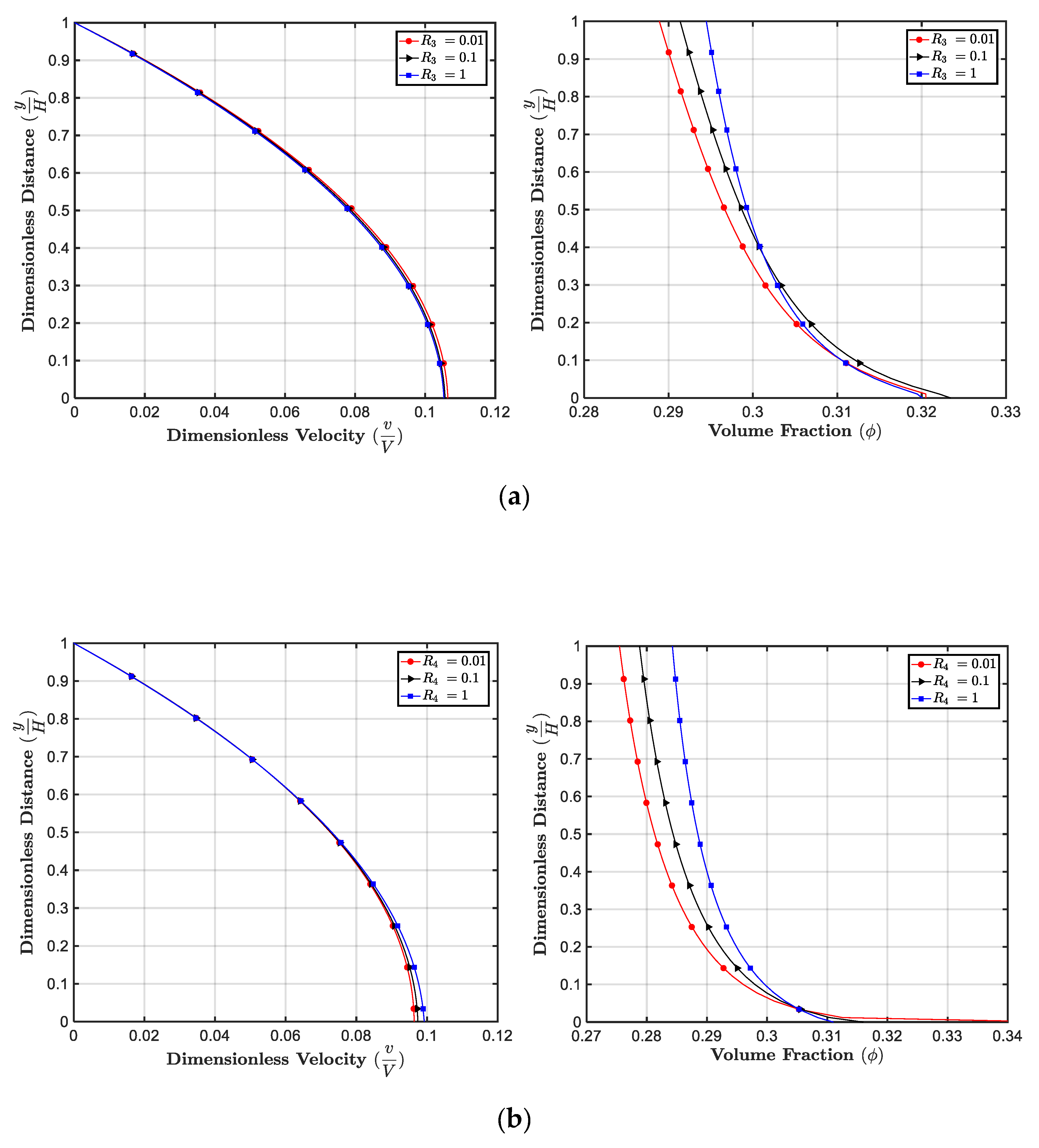
5.3. Effect of
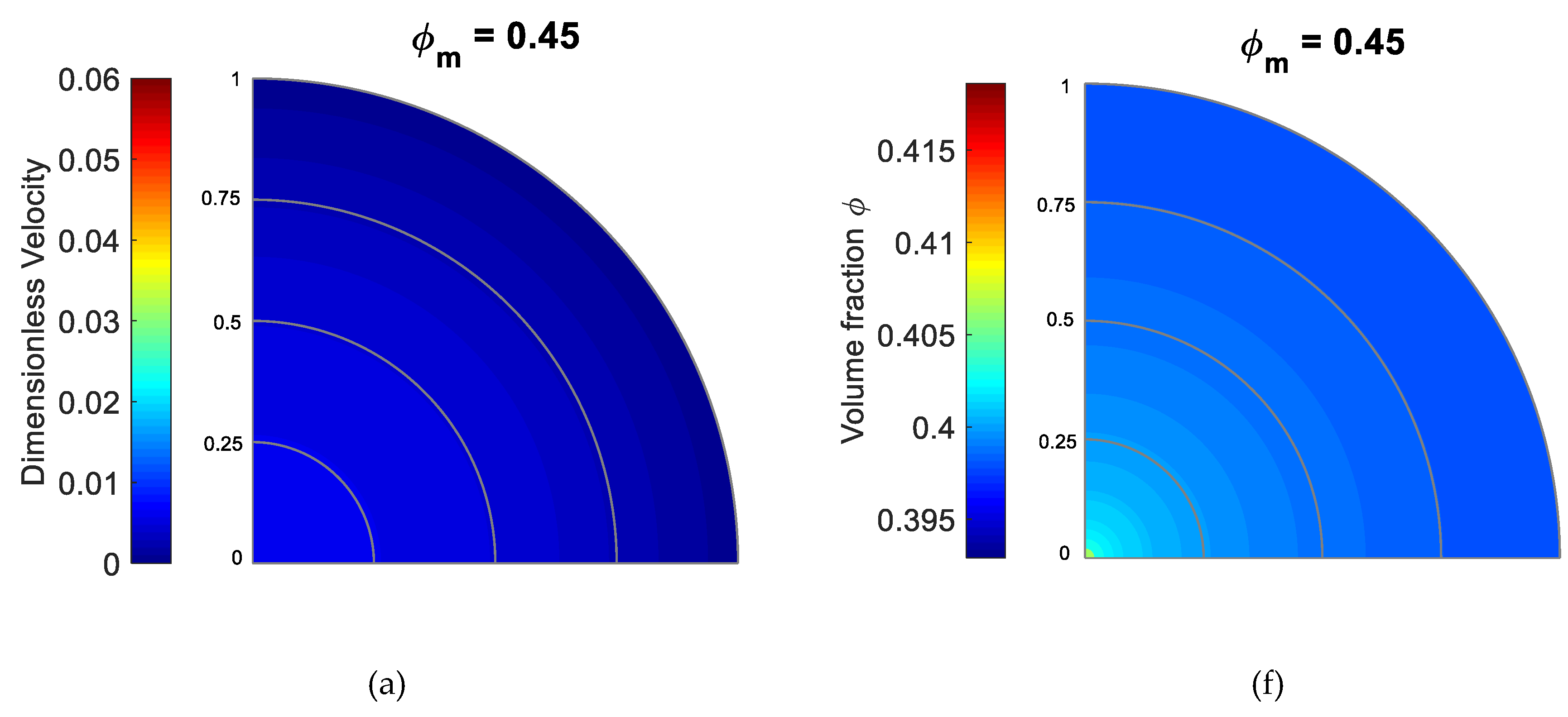
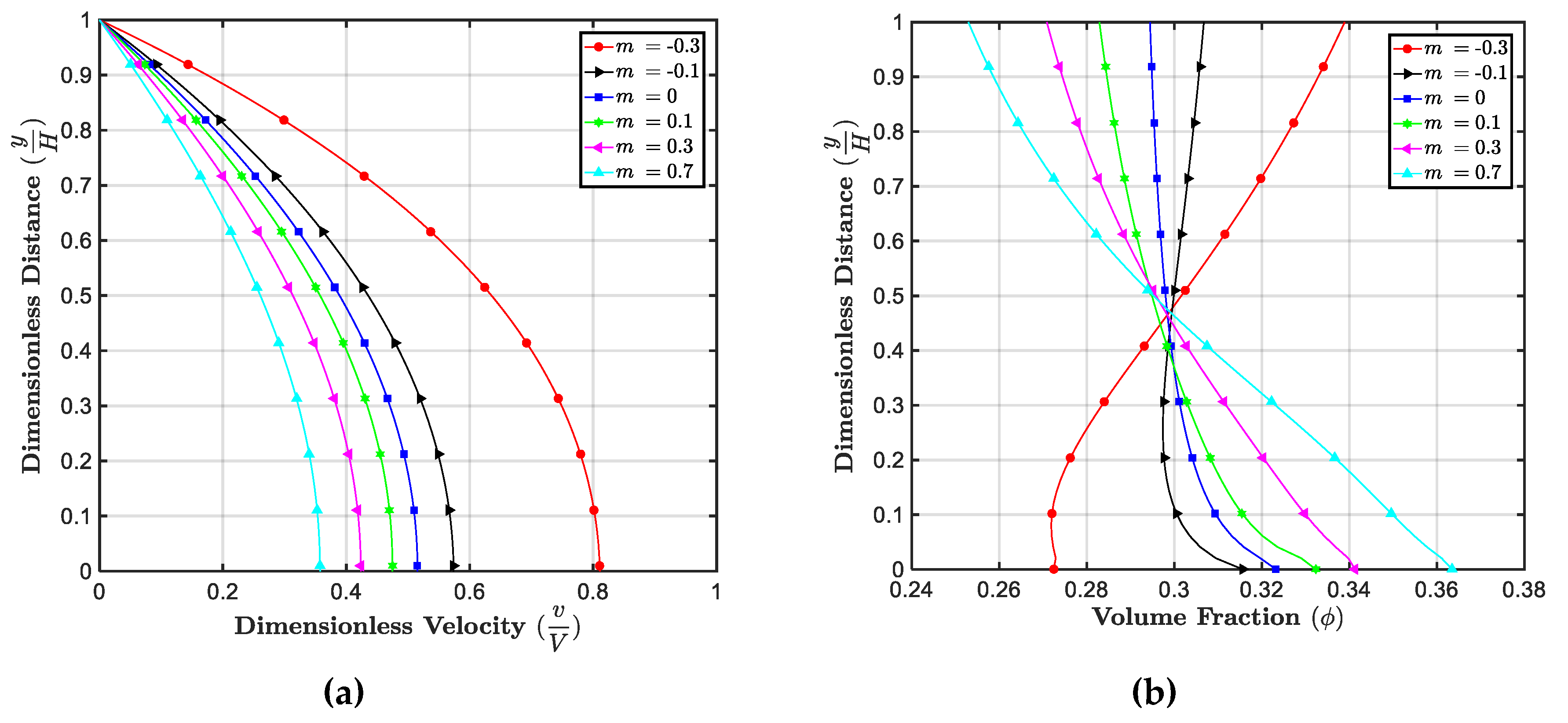
5.4. Effect of m
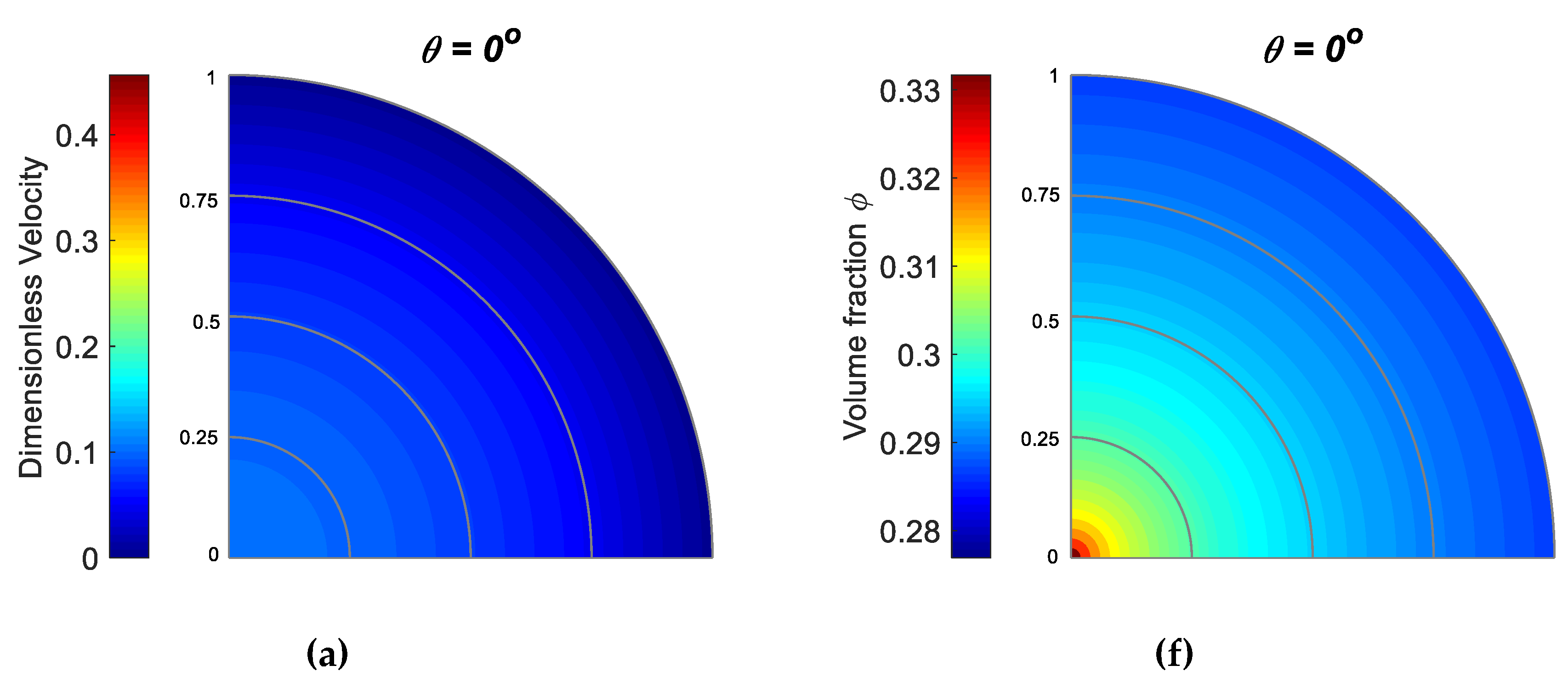
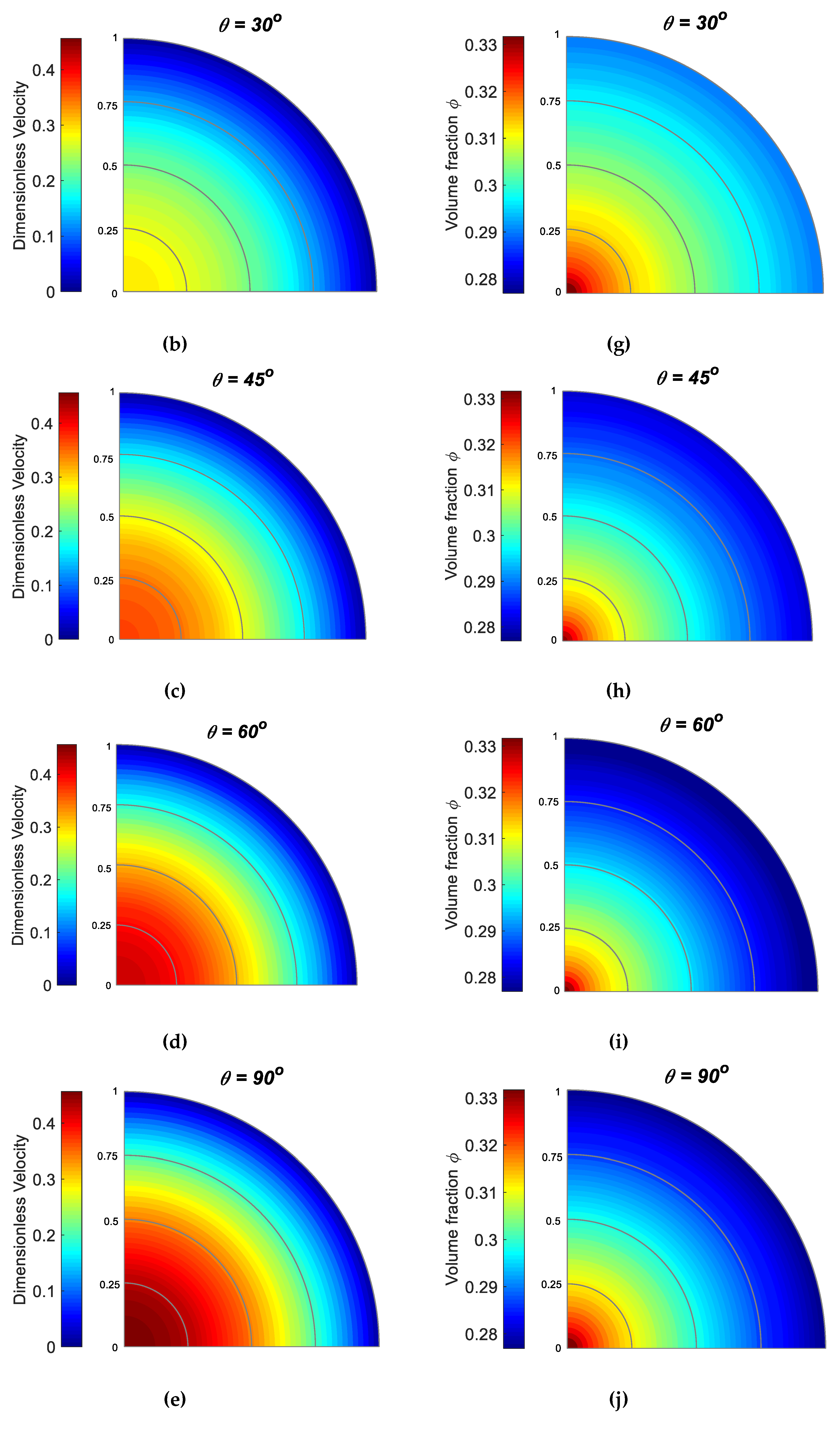
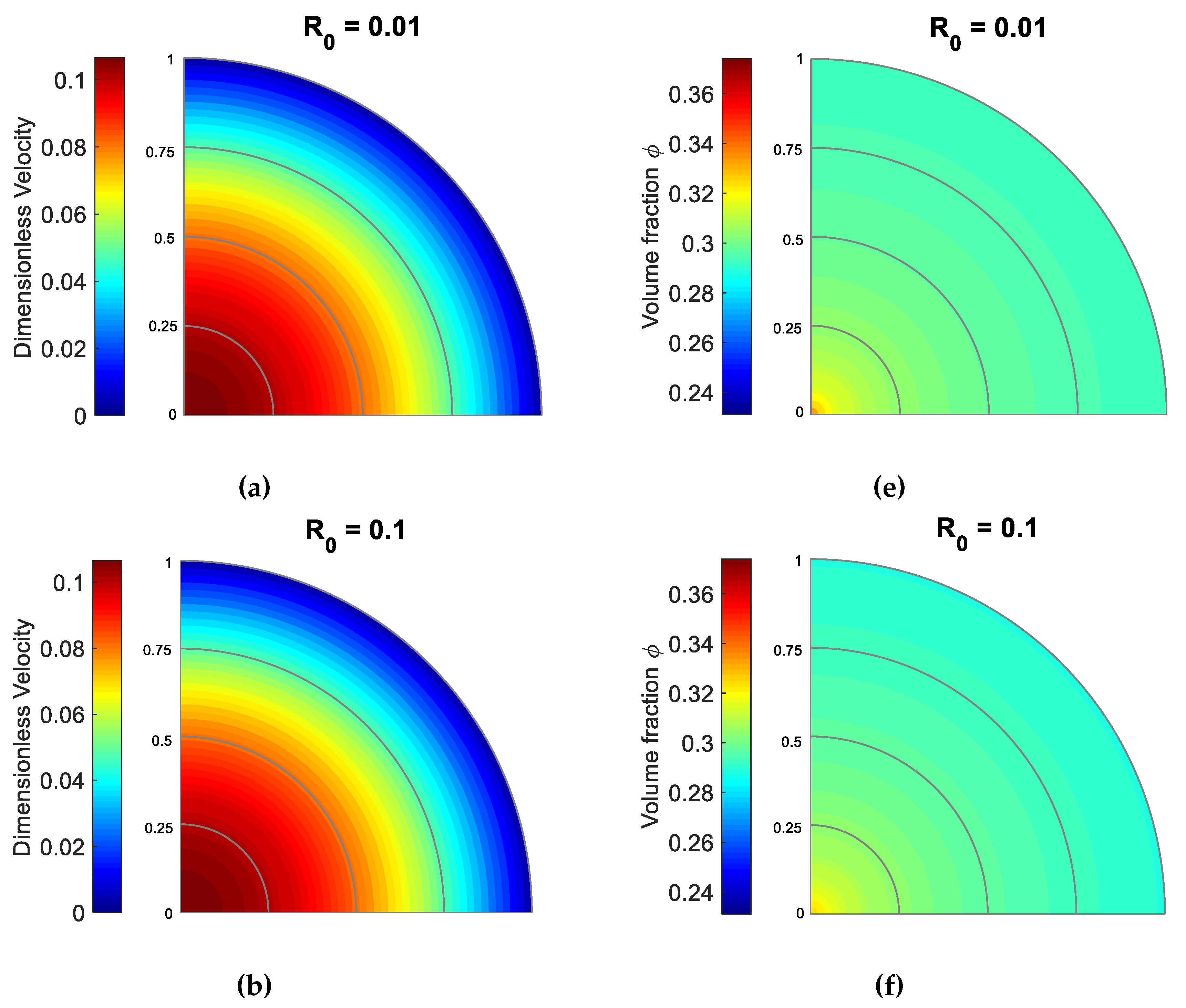
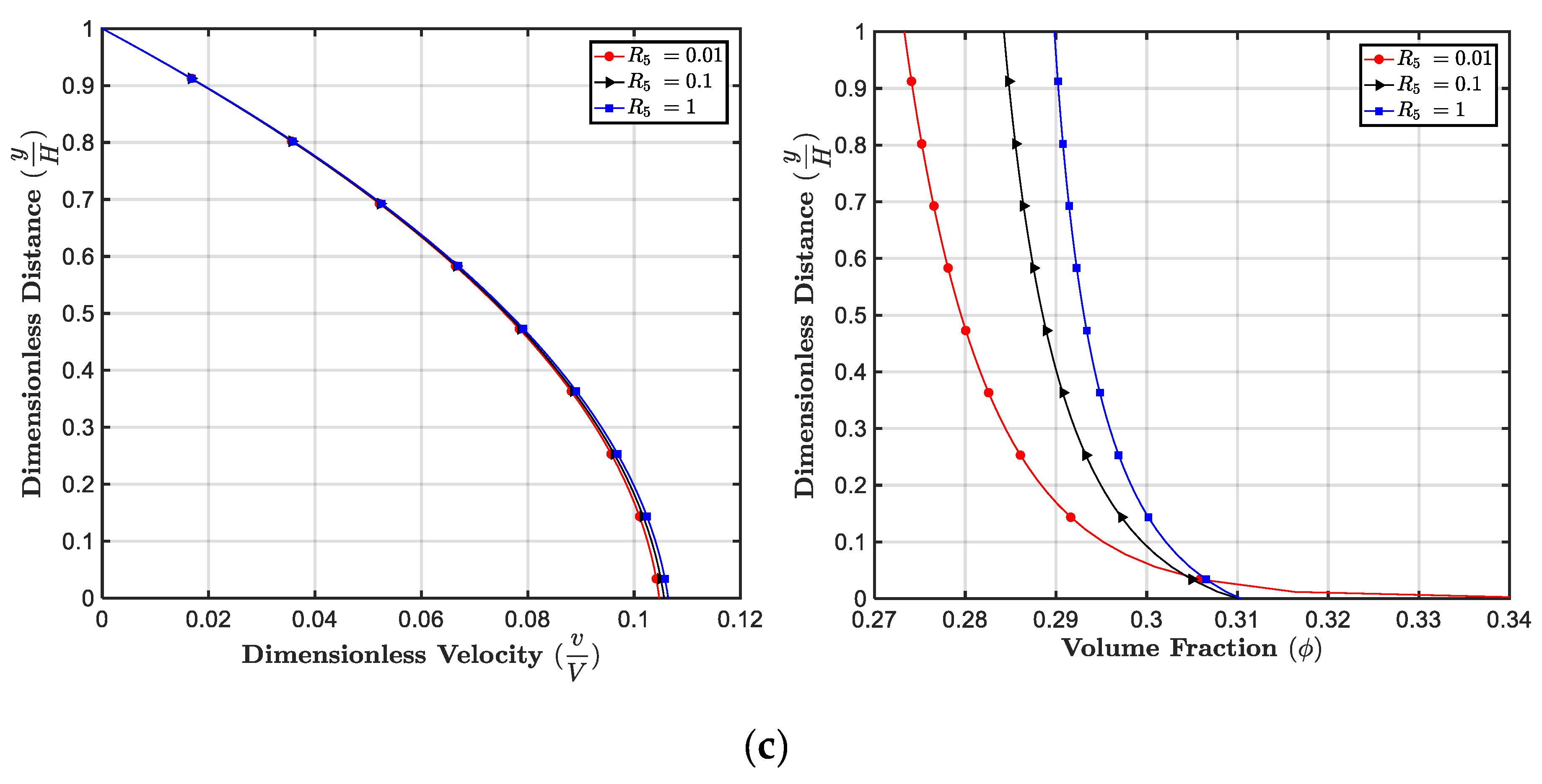
5.5. Effect of
5.6. Effect of
5.7. Effect of
5.8. Effects of , , and
6. Conclusions
Author Contributions
Funding
Acknowledgments
Disclaimer
Conflicts of Interest
Nomenclature
| Symbol | Explanation |
| Density | |
| Acceleration due to gravity | |
| Characteristic length | |
| Reference velocity | |
| Particle radius | |
| Inclination angle | |
| Time | |
| Diffusion coefficient | |
| Cement diffusivity parameter | |
| Shear-rate-dependent diffusion coefficient | |
| Volume fraction-dependent diffusion coefficient | |
| Constant in volume fraction-dependent diffusion coefficient | |
| Cement diffusivity fitting coefficients | |
| Heaviside function | |
| , | Empirical coefficients for transport flux |
| Local shear rate | |
| Volume fraction of particles | |
| Capillary pore in cement | |
| Viscosity | |
| Coefficient of viscosity | |
| Effective viscosity | |
| Concentration-dependent viscosity | |
| Experimental (fitting) parameter for viscosity | |
| Maximum solid concentration | |
| Average value for the volume fraction | |
| Pressure | |
| Modified pressure | |
| Normal stress coefficients | |
| , | Material parameters |
| Dimensionless numbers | |
| Velocity vector | |
| Body force vector | |
| Particle transport flux | |
| Flux contribution due to particles collision | |
| Flux contribution due to variation in viscosity | |
| Brownian diffusive flux | |
| Cauchy stress tensor | |
| Yield stress tensor | |
| Viscous stress tensor | |
| Identity tensor | |
| Gradient of the velocity vector | |
| n-th order Rivlin–Ericksen tensor | |
| Gradient symbol | |
| Divergence operator |
References
- Mindess, S.; Young, J.F. Concrete; Prentice Hall: Englewood, NJ, USA, 1981. [Google Scholar]
- Taylor, H.F. Cement Chemistry; Thomas Telford: London, UK, 1997. [Google Scholar]
- Hanehara, S.; Yamada, K. Interaction between cement and chemical admixture from the point of cement hydration, absorption behaviour of admixture, and paste rheology. Cem. Concr. Res. 1999, 29, 1159–1165. [Google Scholar] [CrossRef]
- Vlachou, P.-V.; Piau, J.-M. Physicochemical study of the hydration process of an oil well cement slurry before setting. Cem. Concr. Res. 1999, 29, 27–36. [Google Scholar] [CrossRef]
- Barbic, L.; Tinta, V.; Lozar, B.; Marinkovic, V. Effect of Storage Time on the Rheological Behavior of Oil Well Cement Slurries. J. Am. Ceram. Soc. 1991, 74, 945–949. [Google Scholar] [CrossRef]
- Worrell, E.; Kermeli, K.; Galitsky, C. Energy Efficiency Improvement and Cost Saving Opportunities for Cement Making an ENERGY STAR® Guide for Energy and Plant Managers; EPA: Washington, DC, USA, 2013.
- Chatziaras, N.; Psomopoulos, C.S.; Themelis, N.J. Use of waste derived fuels in cement industry: A review. Manag. Environ. Qual. Int. J. 2016, 27, 178–193. [Google Scholar] [CrossRef]
- Benhelal, E.; Zahedi, G.; Shamsaei, E.; Bahadori, A. Global strategies and potentials to curb CO2 emissions in cement industry. J. Clean. Prod. 2013, 51, 142–161. [Google Scholar] [CrossRef]
- Bentz, D.P. Three-Dimensional Computer Simulation of Portland Cement Hydration and Microstructure Development. J. Am. Ceram. Soc. 1997, 80, 3–21. [Google Scholar] [CrossRef]
- Haecker, C.; Bentz, D.; Feng, X.; Stutzman, P. Prediction of cement physical properties by virtual testing. Cem. Int. 2003, 1, 86–92. [Google Scholar]
- Bullard, J.W.; Ferraris, C.; Garboczi, E.J.; Martys, N.; Stutzman, P. Virtual cement. Chapt 2004, 10, 1311–1331. [Google Scholar]
- Thomas, J.J.; Biernacki, J.J.; Bullard, J.W.; Bishnoi, S.; Dolado, J.S.; Scherer, G.W.; Luttge, A. Modeling and simulation of cement hydration kinetics and microstructure development. Cem. Concr. Res. 2011, 41, 1257–1278. [Google Scholar] [CrossRef]
- Watts, B.; Tao, C.; Ferraro, C.; Masters, F. Proficiency analysis of VCCTL results for heat of hydration and mortar cube strength. Constr. Build. Mater. 2018, 161, 606–617. [Google Scholar] [CrossRef]
- Tao, C.; Watts, B.; Ferraro, C.C.; Masters, F.J. A Multivariate Computational Framework to Characterize and Rate Virtual Portland Cements. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 266–278. [Google Scholar] [CrossRef]
- Banfill, P.F.G.; Kitching, D.R. 14 Use of a Controlled Stress Rheometer to Study the Yield Stress of Oilwell Cement Slurries. In Rheology of Fresh Cement and Concrete: Proceedings of an International Conference, Liverpool, 1990; CRC Press: Boca Raton, FL, USA, 1990; p. 125. [Google Scholar]
- Bonett, A.; Pafitis, D. Getting to the root of gas migration. Oilfield Rev. 1996, 8, 36–49. [Google Scholar]
- Guan, S.; Rice, J.A.; Li, C.; Li, Y.; Wang, G. Structural displacement measurements using DC coupled radar with active transponder. Struct. Control Health Monit. 2017, 24, e1909. [Google Scholar] [CrossRef]
- Prohaska, M.; Ogbe, D.O.; Economides, M.J. Determining wellbore pressures in cement slurry columns. In Proceedings of the SPE Western Regional Meeting, Anchorage, AK, USA, 26–28 May 1993. [Google Scholar]
- Chenevert, M.E.; Jin, L. Model for predicting wellbore pressures in cement columns. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–11 October 1989. [Google Scholar]
- Stiles, D.A. Successful Cementing in Areas Prone to Shallow Saltwater Flows in Deep-Water Gulf of Mexico. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 1997. [Google Scholar]
- Brandt, W.; Dang, A.S.; Magne, E.; Crowley, D.; Houston, K.; Rennie, A.; Hodder, M.; Stringer, R.; Juiniti, R.; Ohara, S.; et al. Deepening the search for offshore hydrocarbons. Oilfield Rev. 1998, 10, 2–21. [Google Scholar]
- Wallevik, J.E. Thixotropic investigation on cement paste: Experimental and numerical approach. J. Non-Newton. Fluid Mech. 2005, 132, 86–99. [Google Scholar] [CrossRef]
- Foroushan, H.K.; Ozbayoglu, E.M.; Miska, S.Z.; Yu, M.; Gomes, P.J. On the Instability of the Cement/Fluid Interface and Fluid Mixing (includes associated erratum). SPE Drill. Complet. 2018, 33, 63–76. [Google Scholar] [CrossRef]
- Skadsem, H.J.; Kragset, S.; Lund, B.; Ytrehus, J.D.; Taghipour, A. Annular displacement in a highly inclined irregular wellbore: Experimental and three-dimensional numerical simulations. J. Pet. Sci. Eng. 2019, 172, 998–1013. [Google Scholar] [CrossRef]
- Liu, L.; Fang, Z.; Qi, C.; Zhang, B.; Guo, L.; Song, K.I.-I.L. Numerical study on the pipe flow characteristics of the cemented paste backfill slurry considering hydration effects. Powder Technol. 2019, 343, 454–464. [Google Scholar] [CrossRef]
- Murphy, E.; Lomboy, G.; Wang, K.; Sundararajan, S.; Subramaniam, S. The rheology of slurries of athermal cohesive micro-particles immersed in fluid: A computational and experimental comparison. Chem. Eng. Sci. 2019, 193, 411–420. [Google Scholar] [CrossRef]
- Slattery, J.C. Advanced Transport Phenomena; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Probstein, R.F. Physicochemical Hydrodynamics: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Struble, L.; Sun, G.-K. Viscosity of Portland cement paste as a function of concentration. Adv. Cem. Based Mater. 1995, 2, 62–69. [Google Scholar] [CrossRef]
- Banfill, P.F. The rheology of fresh cement and concrete-a review. In Proceedings of the 11th international cement chemistry congress, Durban, South Africa, 11–16 May 2003; Volume 1, pp. 50–62. [Google Scholar]
- Gandelman, R.; Miranda, C.; Teixeira, K.; Martins, A.L.; Waldmann, A. On the rheological parameters governing oilwell cement slurry stability. Annu. Trans. Nord. Rheol. Soc. 2004, 12, 85–91. [Google Scholar]
- Tattersall, G.H.; Banfill, P.F. The Rheology of Fresh Concrete; Pitman Advanced Publishing Program: London, UK, 1983. [Google Scholar]
- Moon, J.; Wang, S. Acoustic method for determining the static gel strength of slurries. In Proceedings of the SPE Rocky Mountain Regional Meeting, Gillette, WY, USA, 15–18 May 1999. [Google Scholar]
- Bellotto, M. Cement paste prior to setting: A rheological approach. Cem. Concr. Res. 2013, 52, 161–168. [Google Scholar] [CrossRef]
- Barnes, H.A. Thixotropy—A review. J. Non-Newton. Fluid Mech. 1997, 70, 1–33. [Google Scholar] [CrossRef]
- Mewis, J.; Wagner, N.J. Colloidal Suspension Rheology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Barnes, H.A. The yield stress—A review or ‘παντα ρει’—Everything flows? J. Non-Newton. Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- Carreau, P.J.; de Kee, D.C.R.; Chhabra, R.P. Rheology of Polymeric Systems: Principles and Applications; Hanser: New York, NY, USA, 1997. [Google Scholar]
- Carreau, P.J.; de Kee, D. Review of some useful rheological equations. Can. J. Chem. Eng. 1979, 57, 3–15. [Google Scholar] [CrossRef]
- Justnes, H.; Vikan, H. Viscosity of cement slurries as a function of solids content. Ann. Trans. Nord. Rheol. Soc. 2005, 13, 75–82. [Google Scholar]
- Asaga, K.; Roy, D.M. Rheological properties of cement mixes: IV. Effects of superplasticizers on viscosity and yield stress. Cem. Concr. Res. 1980, 10, 287–295. [Google Scholar] [CrossRef]
- Vand, V. Viscosity of solutions and suspensions. I. Theory. J. Phys. Chem. 1948, 52, 277–299. [Google Scholar] [CrossRef]
- Roscoe, R. The viscosity of suspensions of rigid spheres. Br. J. Appl. Phys. 1952, 3, 267. [Google Scholar] [CrossRef]
- Bonen, D.; Shah, S.P. Fresh and hardened properties of self-consolidating concrete. Prog. Struct. Eng. Mater. 2005, 7, 14–26. [Google Scholar] [CrossRef]
- Chougnet, A.; Palermo, T.; Audibert, A.; Moan, M. Rheological behaviour of cement and silica suspensions: Particle aggregation modelling. Cem. Concr. Res. 2008, 38, 1297–1301. [Google Scholar] [CrossRef]
- Tregger, N.A.; Pakula, M.E.; Shah, S.P. Influence of clays on the rheology of cement pastes. Cem. Concr. Res. 2010, 40, 384–391. [Google Scholar] [CrossRef]
- Bentz, D.P.; Ferraris, C.F.; Galler, M.A.; Hansen, A.S.; Guynn, J.M. Influence of particle size distributions on yield stress and viscosity of cement–fly ash pastes. Cem. Concr. Res. 2012, 42, 404–409. [Google Scholar] [CrossRef]
- Ouyang, J.; Tan, Y. Rheology of fresh cement asphalt emulsion pastes. Constr. Build. Mater. 2015, 80, 236–243. [Google Scholar] [CrossRef]
- O’Neill, R.; McCarthy, H.O.; Montufar, E.B.; Ginebra, M.P.; Wilson, D.I.; Lennon, A.; Dunne, N. Critical review: Injectability of calcium phosphate pastes and cements. Acta Biomater. 2017, 50, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Massoudi, M. Constitutive modelling of flowing granular materials: A continuum approach. In Granular Materials: Fundamentals and Applications; The Royal Society of Chemistry: Cambridge, UK, 2004; Volume 63. [Google Scholar]
- Massoudi, M.; Mehrabadi, M.M. A continuum model for granular materials: Considering dilatancy and the Mohr-Coulomb criterion. Acta Mech. 2001, 152, 121–138. [Google Scholar] [CrossRef]
- Rivlin, R.S. Further remarks on the stress-deformation relations for isotropic materials. J. Ration. Mech. Anal. 1955, 4, 681–702. [Google Scholar] [CrossRef]
- Truesdell, C.; Noll, W. The Non-linear Field Theories of Mechanics; Springer: Berlin, Germany, 1992. [Google Scholar]
- Man, C.-S.; Sun, Q.-X. On the significance of normal stress effects in the flow of glaciers. J. Glaciol. 1987, 33, 268–273. [Google Scholar] [CrossRef]
- Man, C.-S. Nonsteady channel flow of ice as a modified second-order fluid with power-law viscosity. Arch. Ration. Mech. Anal. 1992, 119, 35–57. [Google Scholar] [CrossRef]
- Dunn, J.E.; Fosdick, R.L. Thermodynamics, stability, and boundedness of fluids of complexity 2 and fluids of second grade. Arch. Ration. Mech. Anal. 1974, 56, 191–252. [Google Scholar] [CrossRef]
- Massoudi, M.; Vaidya, A. On some generalizations of the second grade fluid model. Nonlinear Anal. Real World Appl. 2008, 9, 1169–1183. [Google Scholar] [CrossRef]
- Phillips, R.J.; Armstrong, R.C.; Brown, R.A.; Graham, A.L.; Abbott, J.R. A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A Fluid Dyn. 1992, 4, 30–40. [Google Scholar] [CrossRef]
- Li, Y.; Wu, W.-T.; Liu, X.; Massoudi, M. The effects of particle concentration and various fluxes on the flow of a fluid-solid suspension. Appl. Math. Comput. 2019, 358, 151–160. [Google Scholar] [CrossRef]
- Bridges, C.; Rajagopal, K.R. Pulsatile flow of a chemically-reacting nonlinear fluid. Comput. Math. Appl. 2006, 52, 1131–1144. [Google Scholar] [CrossRef]
- Garboczi, E.J.; Bentz, D.P. Computer simulation of the diffusivity of cement-based materials. J. Mater. Sci. 1992, 27, 2083–2092. [Google Scholar] [CrossRef]
- Snyder, K.A.; Bentz, D.P. Suspended hydration and loss of freezable water in cement pastes exposed to 90% relative humidity. Cem. Concr. Res. 2004, 34, 2045–2056. [Google Scholar] [CrossRef]
- Wu, W.-T.; Aubry, N.; Antaki, J.; McKoy, M.; Massoudi, M. Heat transfer in a drilling fluid with geothermal applications. Energies 2017, 10, 1349. [Google Scholar] [CrossRef]
- Gupta, G.; Massoudi, M. Flow of a generalized second grade fluid between heated plates. Acta Mech. 1993, 99, 21–33. [Google Scholar] [CrossRef]
- Massoudi, M. Boundary conditions in mixture theory and in CFD applications of higher order models. Comput. Math. Appl. 2007, 53, 156–167. [Google Scholar] [CrossRef]
- Dunn, J.E.; Rajagopal, K.R. Fluids of differential type: Critical review and thermodynamic analysis. Int. J. Eng. Sci. 1995, 33, 689–729. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Kaloni, P.N. Some remarks on boundary conditions for flows of fluids of the differential type. Contin. Mech. Appl. 1989, 48, 935–942. [Google Scholar]
- Wu, W.-T.; Massoudi, M. Heat transfer and dissipation effects in the flow of a drilling fluid. Fluids 2016, 1, 4. [Google Scholar] [CrossRef]
- Lootens, D.; Hébraud, P.; Lécolier, E.; van Damme, H. Gelation, Shear-Thinning and Shear-Thickening in Cement Slurries. Oil Gas Sci. Technol. 2004, 59, 31–40. [Google Scholar] [CrossRef]
- Miao, L.; Massoudi, M. Heat transfer analysis and flow of a slag-type fluid: Effects of variable thermal conductivity and viscosity. Int. J. Non-Linear Mech. 2015, 76, 8–19. [Google Scholar] [CrossRef]
- Gudhe, R.; Yalamanchili, R.C.; Massoudi, M. The flow of granular materials in a pipe: Numerical solutions. ASME Appl. Mech. Div.-Publ.-AMD 1993, 160, 41. [Google Scholar]
- Massoudi, M. A note on the meaning of mixture viscosity using the classical continuum theories of mixtures. Int. J. Eng. Sci. 2008, 46, 677–689. [Google Scholar] [CrossRef]
- Massoudi, M. A Mixture Theory formulation for hydraulic or pneumatic transport of solid particles. Int. J. Eng. Sci. 2010, 48, 1440–1461. [Google Scholar] [CrossRef]




| Parameters | Range of Values |
|---|---|
| 0.45, 0.5, 0.55, 0.6, 0.65 | |
| 0, 0.02, 0.04, 0.06, 0.08 | |
| 0°, 30°, 45°, 60°, 90° | |
| −0.3, −0.1, 0, 0.1, 0.3, 0.7 | |
| 0.01, 0.1, 1, 10 | |
| 0, −1.5, −2.5, −3.5 | |
| 0, 0.5, 1, 1.5 | |
| 0.01, 0.1, 1 | |
| 0.01, 0.1, 1 | |
| 0.01, 0.1, 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, C.; Kutchko, B.G.; Rosenbaum, E.; Wu, W.-T.; Massoudi, M. Steady Flow of a Cement Slurry. Energies 2019, 12, 2604. https://doi.org/10.3390/en12132604
Tao C, Kutchko BG, Rosenbaum E, Wu W-T, Massoudi M. Steady Flow of a Cement Slurry. Energies. 2019; 12(13):2604. https://doi.org/10.3390/en12132604
Chicago/Turabian StyleTao, Chengcheng, Barbara G. Kutchko, Eilis Rosenbaum, Wei-Tao Wu, and Mehrdad Massoudi. 2019. "Steady Flow of a Cement Slurry" Energies 12, no. 13: 2604. https://doi.org/10.3390/en12132604
APA StyleTao, C., Kutchko, B. G., Rosenbaum, E., Wu, W.-T., & Massoudi, M. (2019). Steady Flow of a Cement Slurry. Energies, 12(13), 2604. https://doi.org/10.3390/en12132604