Parametrization of a Modified Friedman Kinetic Method to Assess Vine Wood Pyrolysis Using Thermogravimetric Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Vine Wood Sample Preparation
2.2. Proximate and Thermogravimetric Analysis
2.3. Thermogravimetric Data Processing: Deconvolution
2.4. Isoconversional Method
2.5. Reaction Model Determination
3. Results and Discussion
3.1. TG and DTG Analysis
3.2. Figure Deconvolution
3.3. Isoconversional Method
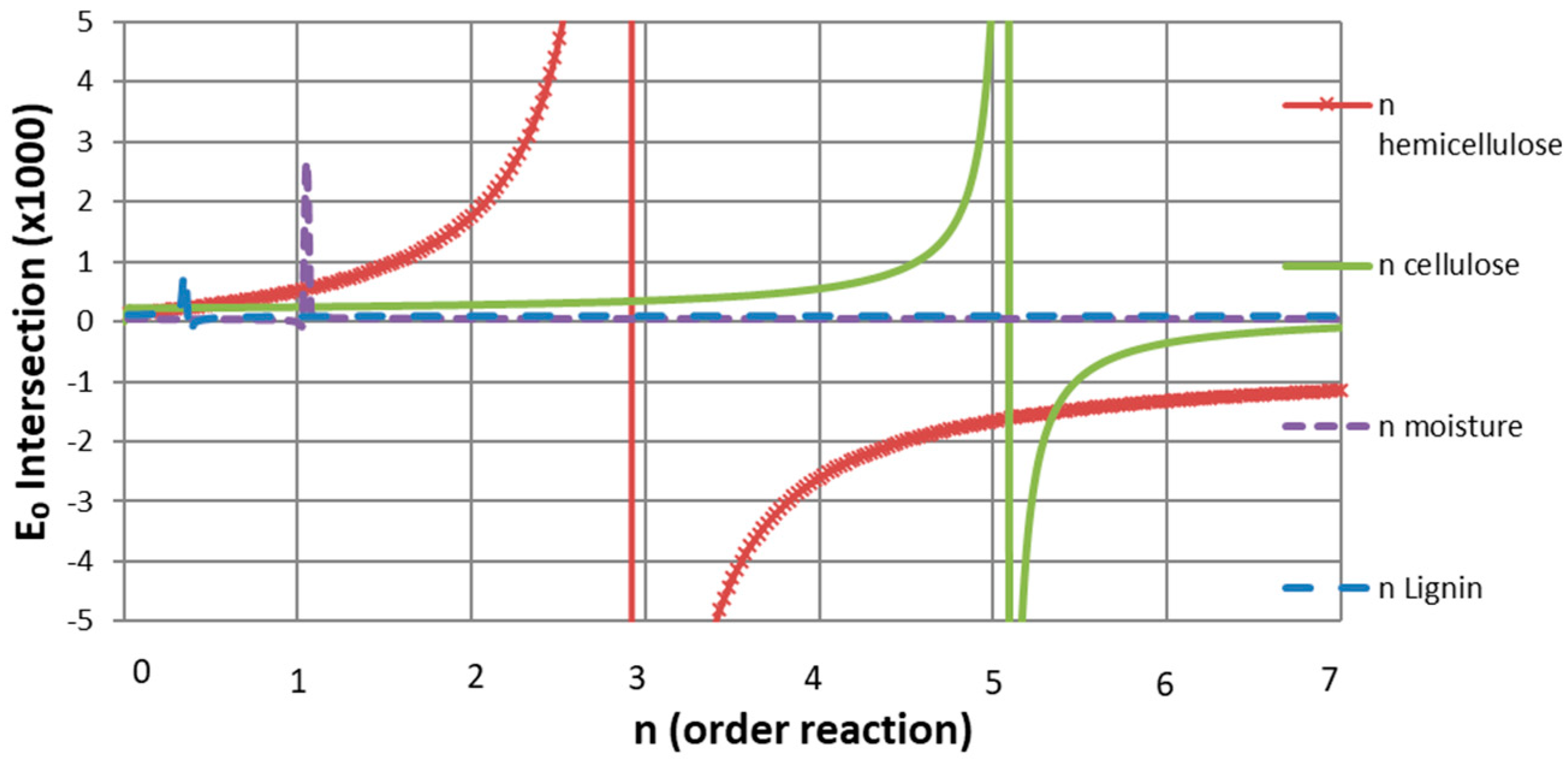
3.4. Reaction Model Determination
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- UNFCCC, Global Warming of 1.5 °C Special Report. 2018. Available online: https://www.ipcc.ch/sr15/ (accessed on 29 December 2018).
- UNFCCC, 2016 Earth Information Day. 2016. Available online: http://unfccc.int/science/workstreams/items/9949.php (accessed on 29 December 2018).
- Diblasi, C. Modeling chemical and physical processes of wood and biomass pyrolysis. Prog. Energy Combust. Sci. 2008, 34, 47–90. [Google Scholar] [CrossRef]
- Rentizelas, A.A.; Li, J. Techno-economic and carbon emissions analysis of biomass torrefaction downstream in international bioenergy supply chains for co-firing. Energy 2016, 114, 129–142. [Google Scholar] [CrossRef]
- Leng, L.; Huang, H. An overview of the effect of pyrolysis process parameters on biochar stability. Bioresour. Technol. 2018, 270, 627–642. [Google Scholar] [CrossRef] [PubMed]
- Collard, F.-X.; Blin, J. A review on pyrolysis of biomass constituents: Mechanisms and composition of the products obtained from the conversion of cellulose, hemicelluloses and lignin. Renew. Sustain. Energy Rev. 2014, 38, 594–608. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, M.; Jiang, E.; Wang, D.; Zhang, K.; Ren, Y.; Jiang, Y. Pyrolysis of Torrefied Biomass. Trends Biotechnol. 2018, 36, 1287–1298. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.; Zhu, M.; Fan, X.; Song, J.; Peng, P.; Li, K.; Jia, W.; Song, H. Influence of pyrolysis temperature and feedstock on carbon fractions of biochar produced from pyrolysis of rice straw, pine wood, pig manure and sewage sludge. Chemosphere 2019, 218, 624–631. [Google Scholar] [CrossRef] [PubMed]
- López, R.; Fernández, C.; Gómez, X.; Martínez, O.; Sánchez, M.E. Thermogravimetric analysis of lignocellulosic and microalgae biomasses and their blends during combustion. J. Therm. Anal. Calorim. 2013, 114, 295–305. [Google Scholar] [CrossRef]
- Criado, J.M.; Sánchez-Jiménez, P.E.; Perez-Maqueda, L.A. Critical study of the isoconversional methods of kinetic analysis. J. Therm. Anal. Calorim. 2008, 92, 199–203. [Google Scholar] [CrossRef]
- Kalogiannis, K.G.; Matsakas, L.; Lappas, A.A.; Rova, U.; Christakopoulos, P. Aromatics from Beechwood Organosolv Lignin through Thermal and Catalytic Pyrolysis. Energies 2019, 12, 1606. [Google Scholar] [CrossRef]
- Yeo, J.Y.; Chin, B.L.F.; Tan, J.K.; Loh, Y.S. Comparative studies on the pyrolysis of cellulose, hemicellulose, and lignin based on combined kinetics. J. Energy Inst. 2017. [Google Scholar] [CrossRef]
- Song, E.; Kim, D.; Jeong, C.-J.; Kim, D.-Y. A Kinetic Study on Combustible Coastal Debris Pyrolysis via Thermogravimetric Analysis. Energies 2019, 12, 836. [Google Scholar] [CrossRef]
- Font, R.; Garrido, M. Friedman and n-reaction order methods applied to pine needles and polyurethane thermal decompositions. Thermochim. Acta 2018, 660, 124–133. [Google Scholar] [CrossRef]
- Braga, R.M.; Melo, D.M.A.; Aquino, F.M.; Freitas, J.C.O.; Melo, M.A.F.; Barros, J.M.F.; Fontes, B.M.S. Characterization and comparative study of pyrolysis kinetics of the rice husk and the elephant grass. J. Therm. Anal. Calorim. 2014, 115, 1915–1920. [Google Scholar] [CrossRef]
- Sanchez, M.; Otero, M.; Gómez, X.; Moran, A. Thermogravimetric kinetic analysis of the combustion of biowastes. Renew. Energy 2009, 34, 1622–1627. [Google Scholar] [CrossRef]
- White, J.E.; Catallo, W.J.; Legendre, B.L. Biomass pyrolysis kinetics: A comparative critical review with relevant agricultural residue case studies. J. Anal. Appl. Pyrolysis 2011, 91, 1–33. [Google Scholar] [CrossRef]
- Jiang, G.; Nowakowski, D.J.; Bridgwater, A.V. A systematic study of the kinetics of lignin pyrolysis. Thermochim. Acta 2010, 498, 61–66. [Google Scholar] [CrossRef]
- Osman, A.I.; Abdelkader, A.; Johnston, C.R.; Morgan, K.; Rooney, D.W. Thermal Investigation and Kinetic Modeling of Lignocellulosic Biomass Combustion for Energy Production and Other Applications. Ind. Eng. Chem. Res. 2017, 56, 12119–12130. [Google Scholar] [CrossRef]
- Várhegyi, G.; Antal, M.J.; Jakab, E.; Szabó, P. Kinetic modeling of biomass pyrolysis. 10 years of a US-Hungarian cooperation. J. Anal. Appl. Pyrolysis 1997, 42, 73–87. [Google Scholar] [CrossRef]
- Szabó, P.; Várhegyi, G.; Till, F.; Faix, O. Thermogravimetric/mass spectrometric characterization of two energy crops, Arundo donax and Miscanthus sinensis. J. Anal. Appl. Pyrolysis 1996, 36, 179–190. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, L.; Han, Z.; Xie, B.; Wu, S. The effects of leaching methods on the combustion characteristics of rice straw. Biomass-Bioenergy 2013, 49, 22–27. [Google Scholar] [CrossRef]
- Kong, Z.; Liaw, S.B.; Gao, X.; Yu, Y.; Wu, H. Leaching characteristics of inherent inorganic nutrients in biochars from the slow and fast pyrolysis of mallee biomass. Fuel 2014, 128, 433–441. [Google Scholar] [CrossRef]
- Haykiri-Acma, H. The role of particle size in the non-isothermal pyrolysis of hazelnut shell. J. Anal. Appl. Pyrolysis 2006, 75, 211–216. [Google Scholar] [CrossRef]
- Cai, J.; Wu, W.; Liu, R. An overview of distributed activation energy model and its application in the pyrolysis of lignocellulosic biomass. Renew. Sustain. Energy Rev. 2014, 36, 236–246. [Google Scholar] [CrossRef]
- Liu, S.; Yu, J.; Bikane, K.; Chen, T.; Ma, C.; Wang, B.; Sun, L. Rubber pyrolysis: Kinetic modeling and vulcanization effects. Energy 2018, 155, 215–225. [Google Scholar] [CrossRef]
- Hu, M.; Chen, Z.; Wang, S.; Guo, D.; Ma, C.; Zhou, Y.; Chen, J.; Laghari, M.; Fazal, S.; Xiao, B.; et al. Thermogravimetric kinetics of lignocellulosic biomass slow pyrolysis using distributed activation energy model, Fraser–Suzuki deconvolution, and iso-conversional method. Energy Convers. Manag. 2016, 118, 1–11. [Google Scholar] [CrossRef]
- Díaz, I.; Rodríguez, M.; Arnaiz, C.; Miguel, G.S.; Domínguez, M. Biomass pyrolysis kinetics through thermogravimetric analysis. Comput. Aided Chem. Eng. 2013, 32, 1–6. [Google Scholar] [CrossRef]
- Perejón, A.; Sánchez-Jiménez, P.E.; Criado, J.M.; Pérez-Maqueda, L.A. Kinetic analysis of complex solid-state reactions. A new deconvolution procedure. J. Phys. Chem. B 2011, 115, 1780–1791. [Google Scholar] [CrossRef] [PubMed]
- Moine, E.C.; Groune, K.; El Hamidi, A.; Khachani, M.; Halim, M.; Arsalane, S. Multistep process kinetics of the non-isothermal pyrolysis of Moroccan Rif oil shale. Energy 2016, 115, 931–941. [Google Scholar] [CrossRef]
- Cheng, Z.; Wu, W.; Ji, P.; Zhou, X.; Liu, R.; Cai, J. Applicability of Fraser-Suzuki function in kinetic analysis of DAEM processes and lignocellulosic biomass pyrolysis processes. J. Therm. Anal. Calorim. 2015, 119, 1429–1438. [Google Scholar] [CrossRef]
- Svoboda, R.; Málek, J. Applicability of Fraser–Suzuki function in kinetic analysis of complex crystallization processes. J. Therm. Anal. Calorim. 2013, 111, 1045–1056. [Google Scholar] [CrossRef]
- Mishra, R.K.; Mohanty, K. Pyrolysis kinetics and thermal behavior of waste sawdust biomass using thermogravimetric analysis. Bioresour. Technol. 2018, 251, 63–74. [Google Scholar] [CrossRef]
- Qiao, Y.; Zhang, L.; Binner, E.; Xu, M.; Li, C.-Z. An investigation of the causes of the difference in coal particle ignition temperature between combustion in air and in O2/CO2. Fuel 2010, 89, 3381–3387. [Google Scholar] [CrossRef]
- Tian, L.; Shen, B.; Xu, H.; Li, F.; Wang, Y.; Singh, S. Thermal behavior of waste tea pyrolysis by TG-FTIR analysis. Energy 2016, 103, 533–542. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Vargas-Moreno, J.; Callejon-Ferre, A.J.; Pérez-Alonso, J.; Marti, B.V. A review of the mathematical models for predicting the heating value of biomass materials. Renew. Sustain. Energy Rev. 2012, 16, 3065–3083. [Google Scholar] [CrossRef]
- Stefanidis, S.D.; Kalogiannis, K.G.; Iliopoulou, E.F.; Michailof, C.M.; Pilavachi, P.A.; Lappas, A.A. A study of lignocellulosic biomass pyrolysis via the pyrolysis of cellulose, hemicellulose and lignin. J. Anal. Appl. Pyrolysis 2014, 105, 143–150. [Google Scholar] [CrossRef]
- Chen, C.; Miao, W.; Zhou, C.; Wu, H. Thermogravimetric pyrolysis kinetics of bamboo waste via Asymmetric Double Sigmoidal (Asym2sig) function deconvolution. Bioresour. Technol. 2017, 225, 48–57. [Google Scholar] [CrossRef]
- Mamleev, V.; Bourbigot, S.; Yvon, J. Kinetic analysis of the thermal decomposition of cellulose: The main step of mass loss. J. Anal. Appl. Pyrolysis 2007, 80, 151–165. [Google Scholar] [CrossRef]
- Fiori, L.; Valbusa, M.; Lorenzi, D.; Fambri, L. Modeling of the devolatilization kinetics during pyrolysis of grape residues. Bioresour. Technol. 2012, 103, 389–397. [Google Scholar] [CrossRef]
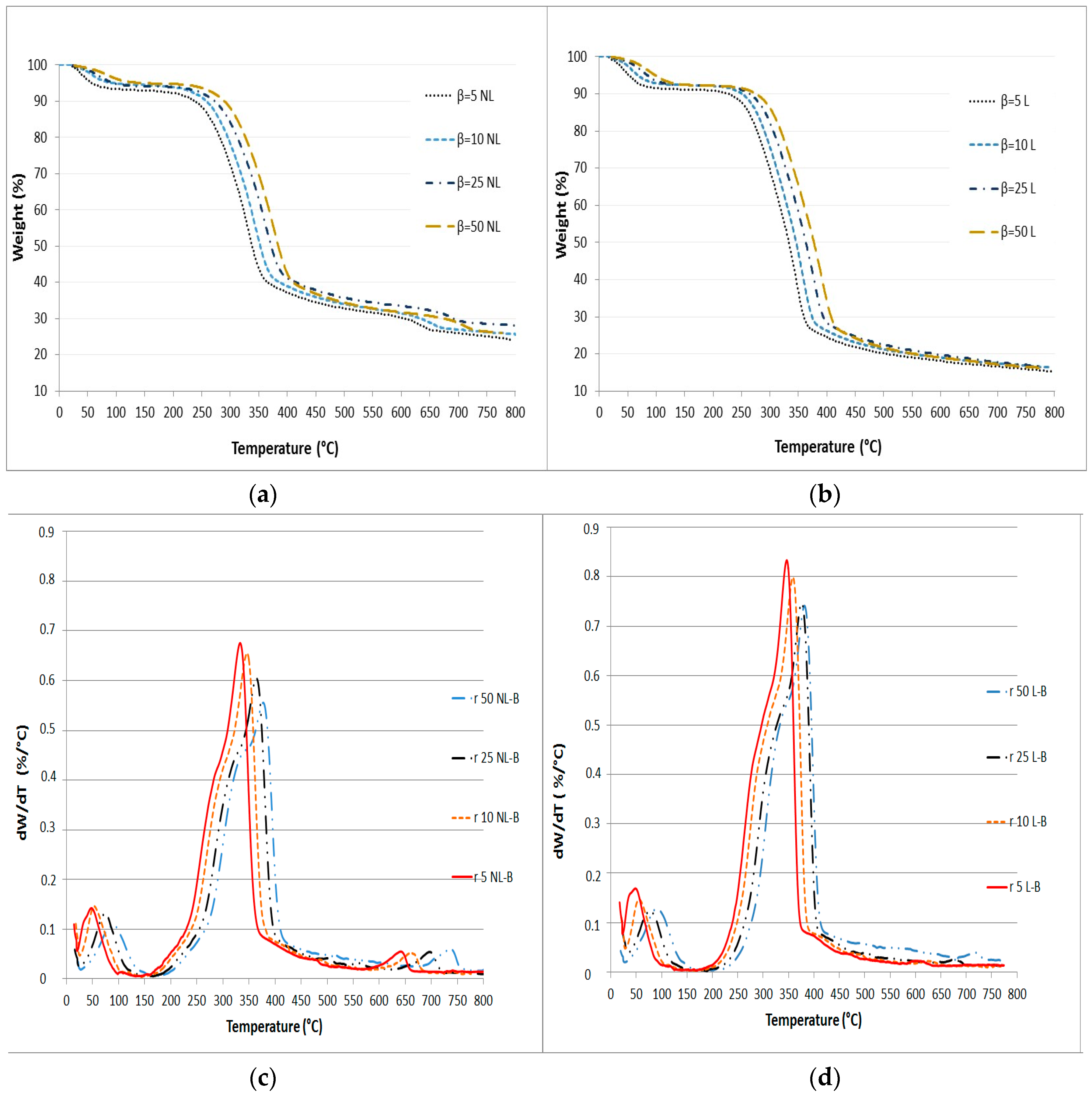

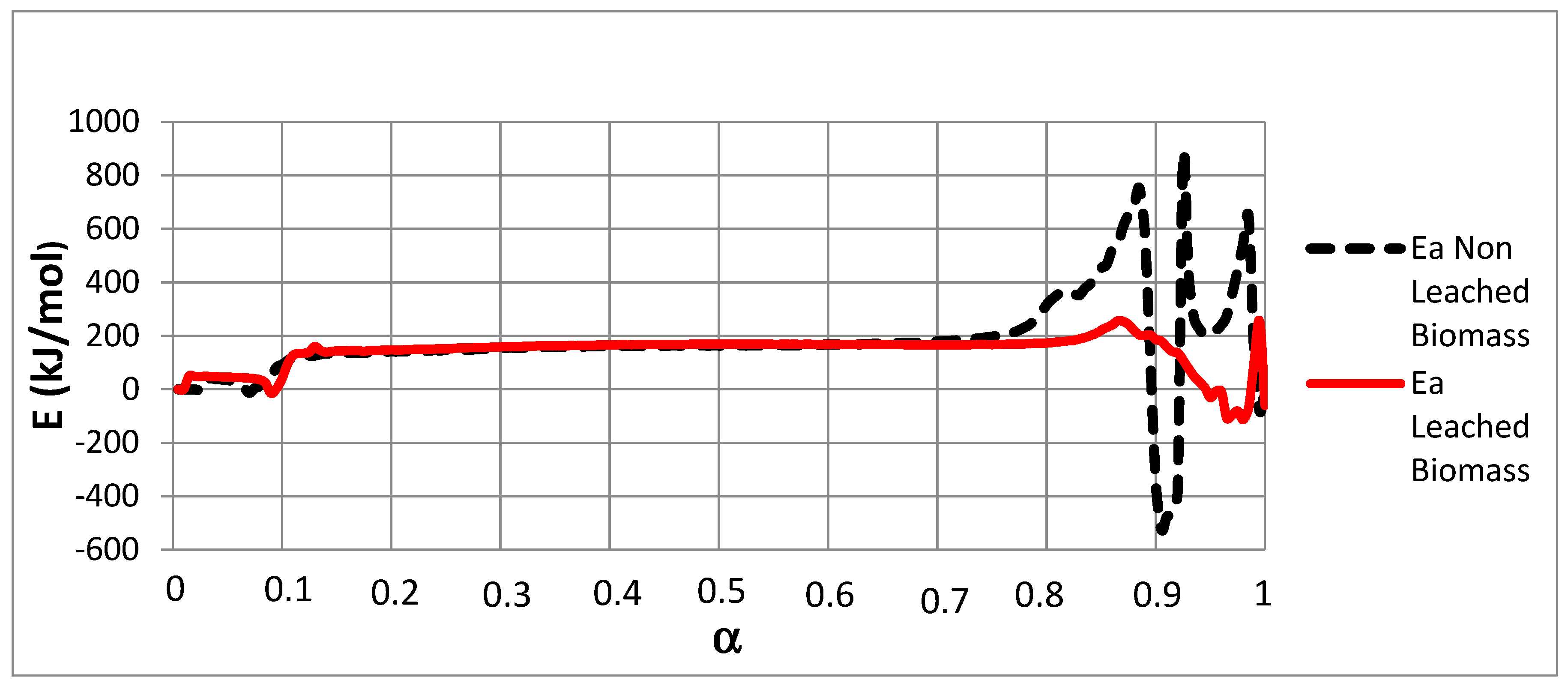
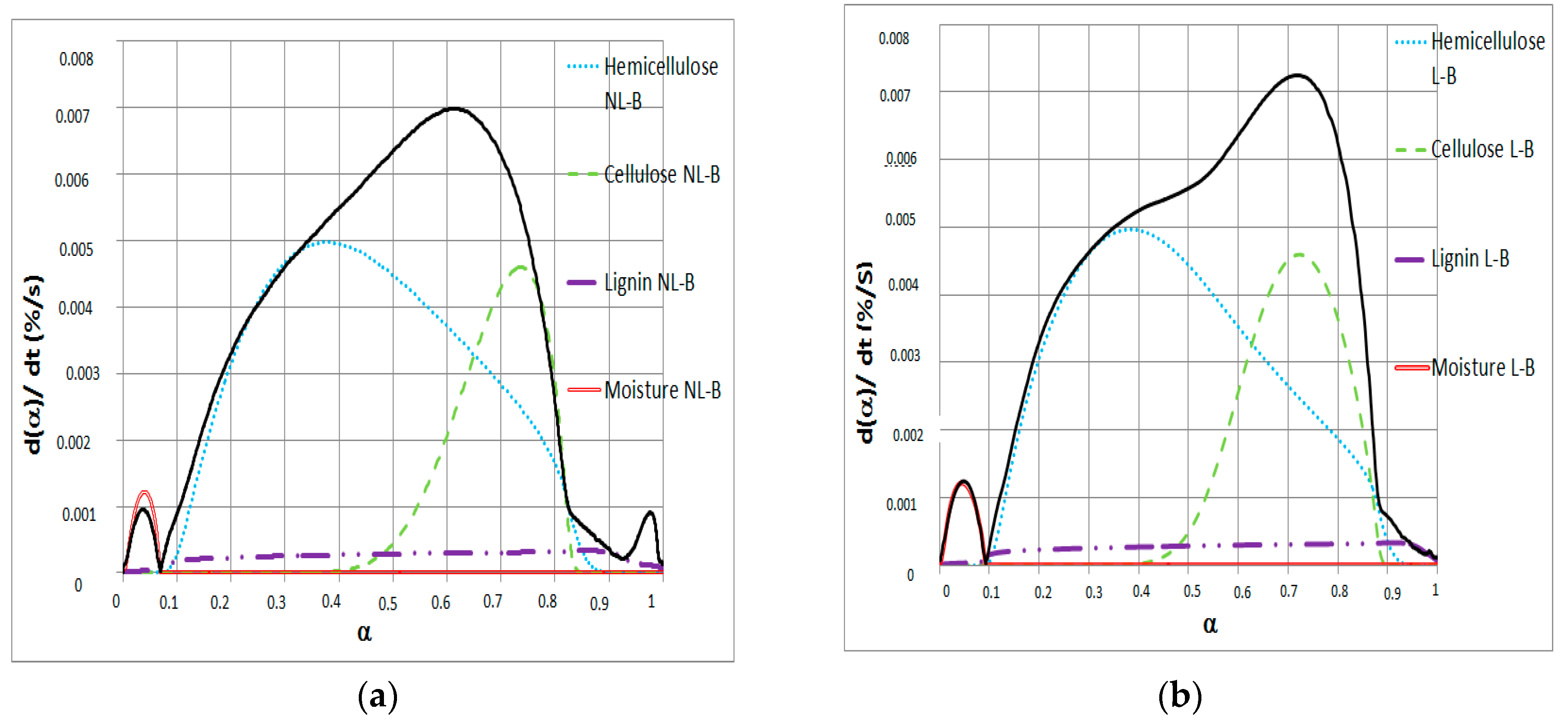

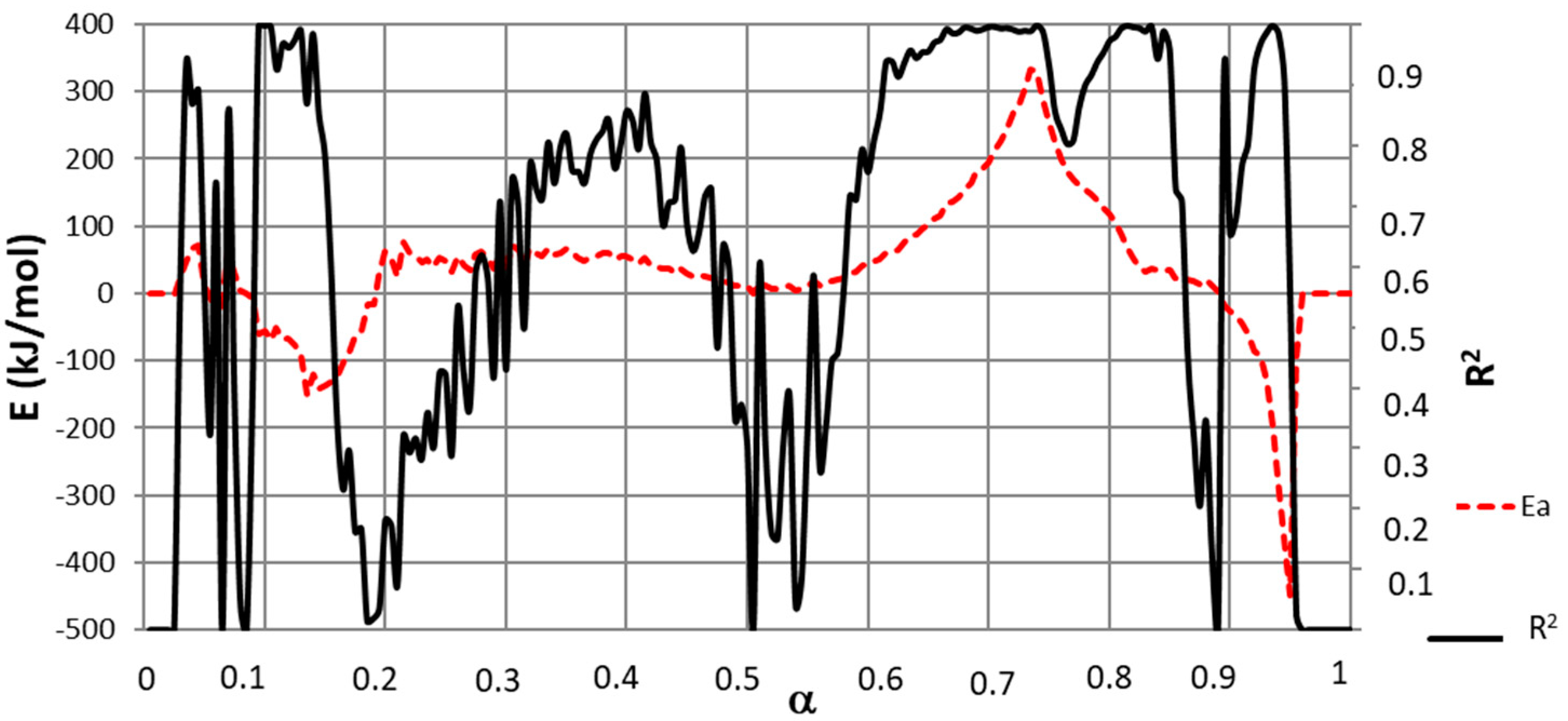
| Particle Size (mm) | X < 1 | 1 < X < 2 | 2 < X < 4 | 4 < X < 8 | 8 < X < 10 | X > 10 |
|---|---|---|---|---|---|---|
| NL-B | 13.4% | 7.4% | 10.8% | 19.7% | 13.5% | 35.2% |
| L-B | 0% | 8.6% | 12.4% | 22.7% | 15.6% | 40.7% |
| Parameter (%) | Moisture | Volatile * | Ash * | Fixed Carbon ** | HHV (MJ/kg) |
|---|---|---|---|---|---|
| NL-B | 9.00 | 70.80 | 13.55 | 15.65 | 16.51 |
| L-B | 3.47 | 82.77 | 1.47 | 15.76 | 18.87 |
| Parameter | 50 °C/min | 25 °C/min | 10 °C/min | 5 °C/min | |||||
|---|---|---|---|---|---|---|---|---|---|
| L-B | NL-B | L-B | NL-B | L-B | NL-B | L-B | NL-B | ||
| Moisture | h | 0.111 | 0.103 | 0.116 | 0.118 | 0.117 | 0.113 | 0.161 | 0.144 |
| s | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | |
| p | 89.315 | 89.315 | 74.969 | 74.969 | 48.113 | 48.113 | 40.050 | 40.050 | |
| w | 62.815 | 62.911 | 62.000 | 62.000 | 62.898 | 62.898 | 62.815 | 62.815 | |
| Hemicellulose | h | 0.486 | 0.380 | 0.459 | 0.351 | 0.462 | 0.383 | 0.450 | 0.383 |
| s | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| p | 342.318 | 337.844 | 326.503 | 326.184 | 313.099 | 313.099 | 307.318 | 307.318 | |
| w | 75.251 | 75.181 | 75.711 | 75.496 | 75.111 | 75.091 | 75.251 | 75.091 | |
| Cellulose | h | 0.491 | 0.320 | 0.491 | 0.405 | 0.495 | 0.390 | 0.491 | 0.390 |
| s | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| p | 383.249 | 379.693 | 375.693 | 372.208 | 355.125 | 355.125 | 343.249 | 343.249 | |
| w | 34.399 | 34.604 | 34.584 | 35.558 | 34.510 | 34.573 | 34.399 | 34.573 | |
| Lignin | h | 0.067 | 0.079 | 0.067 | 0.079 | 0.072 | 0.082 | 0.067 | 0.082 |
| s | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| p | 329.587 | 329.587 | 295.000 | 295.000 | 264.204 | 264.204 | 260.000 | 260.000 | |
| w | 265.835 | 293.415 | 212.920 | 243.415 | 164.061 | 210.767 | 180.835 | 210.767 | |
| (%) | Leached Biomass | Non-Leached Biomass |
|---|---|---|
| Moisture | 7.87 ± 0.57 | 7.60 ± 0.44 |
| Cellulose | 14.01 ± 1.09 | 11.18 ± 1.72 |
| Hemicellulose | 36.43 ± 0.55 | 30.41 ± 0.39 |
| Lignin | 20.14 ± 3.03 | 23.24 ± 1.78 |
| Minor components of Ash | 0.62 ± 1.00 | 1.92 ± 0.47 |
| Total Reaction | 79.07 ± 6.24 | 74.36 ± 4.80 |
| Weight Residual | 20.93 ± 6.24 | 25.64 ± 4.80 |
| Classic Friedman Method | Friedman Method to Deconvoluted Data | Delay Friedman Method with α = 0.05 | |||
|---|---|---|---|---|---|
| Pseudo-component | E (kJ/mol) | Range of α selected | E (kJ/mol) | E (kJ/mol) | Range of α selected (L-B) |
| Moisture | 36.1–49.7 | 0.025–0.065 | 46.8–51.9 | 49.2–57.7 | 0.035–0.065 |
| Hemicellulose | 125.4–146.5 | 0.123–0.240 | 182.8–223.6 | (−55.1) to (−67.6) | 0.123–0.240 |
| Cellulose | 168.3–212.1 | 0.670–0.770 | 187.4–231.2 | 338.0–356.4 | 0.735–0.795 |
| Lignin | unstable | 0.850–0.910 | 71.7–85.4 | 33.3–48.3 | 0.860–0.890 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suárez, S.; Rosas, J.G.; Sánchez, M.E.; López, R.; Gómez, N.; Cara-Jiménez, J. Parametrization of a Modified Friedman Kinetic Method to Assess Vine Wood Pyrolysis Using Thermogravimetric Analysis. Energies 2019, 12, 2599. https://doi.org/10.3390/en12132599
Suárez S, Rosas JG, Sánchez ME, López R, Gómez N, Cara-Jiménez J. Parametrization of a Modified Friedman Kinetic Method to Assess Vine Wood Pyrolysis Using Thermogravimetric Analysis. Energies. 2019; 12(13):2599. https://doi.org/10.3390/en12132599
Chicago/Turabian StyleSuárez, Sergio, Jose Guillermo Rosas, Marta Elena Sánchez, Roberto López, Natalia Gómez, and Jorge Cara-Jiménez. 2019. "Parametrization of a Modified Friedman Kinetic Method to Assess Vine Wood Pyrolysis Using Thermogravimetric Analysis" Energies 12, no. 13: 2599. https://doi.org/10.3390/en12132599
APA StyleSuárez, S., Rosas, J. G., Sánchez, M. E., López, R., Gómez, N., & Cara-Jiménez, J. (2019). Parametrization of a Modified Friedman Kinetic Method to Assess Vine Wood Pyrolysis Using Thermogravimetric Analysis. Energies, 12(13), 2599. https://doi.org/10.3390/en12132599







