Adaptive Integral Backstepping Controller for PMSM with AWPSO Parameters Optimization
Abstract
1. Introduction
2. Design of the AIBC with Differential Term for PMSM
2.1. Design of Adaptive Backstepping Controller with Differential Term
2.2. Design of the AIBC
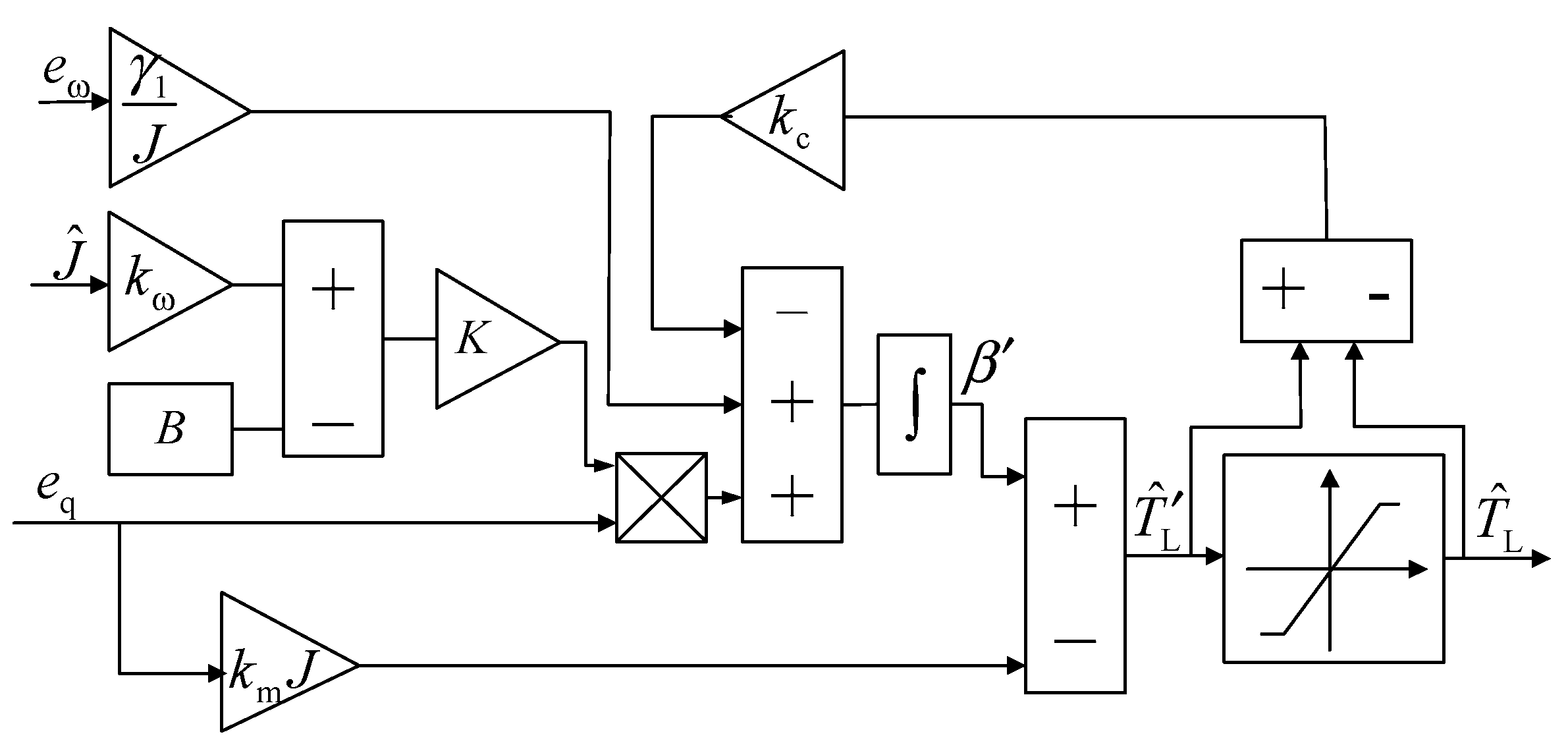
2.3. Design of the Anti-Saturation Torque Observer
2.4. Design of the Integration Algorithm
2.4.1. Design of the AIBC with Differential Term
2.4.2. System Stability Analysis
3. Design of AWPSO for Parameters Optimization of the AIBC with Differential Term
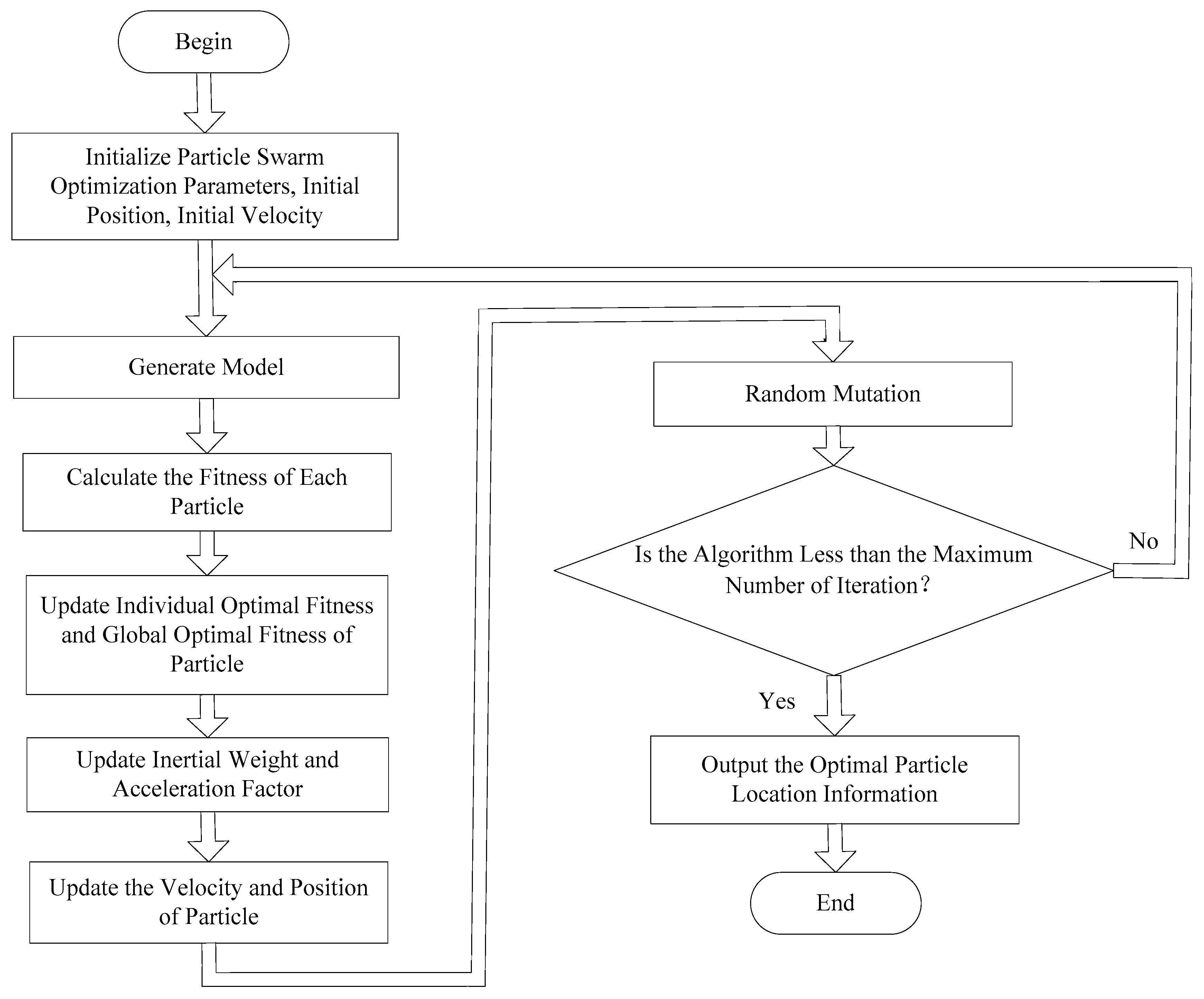
3.1. Principle of AWPSO Algorithm
3.2. Single-Objective AWPSO Algorithm for Solving Multi-Objective Optimization Problem
3.3. AWPSO Algorithm for Parameters Optimization of the AIBC for PMSM
3.3.1. Selection of Fitness Function
3.3.2. AWPSO Parameters Setting
4. Results and Discussion
4.1. Simulation Results
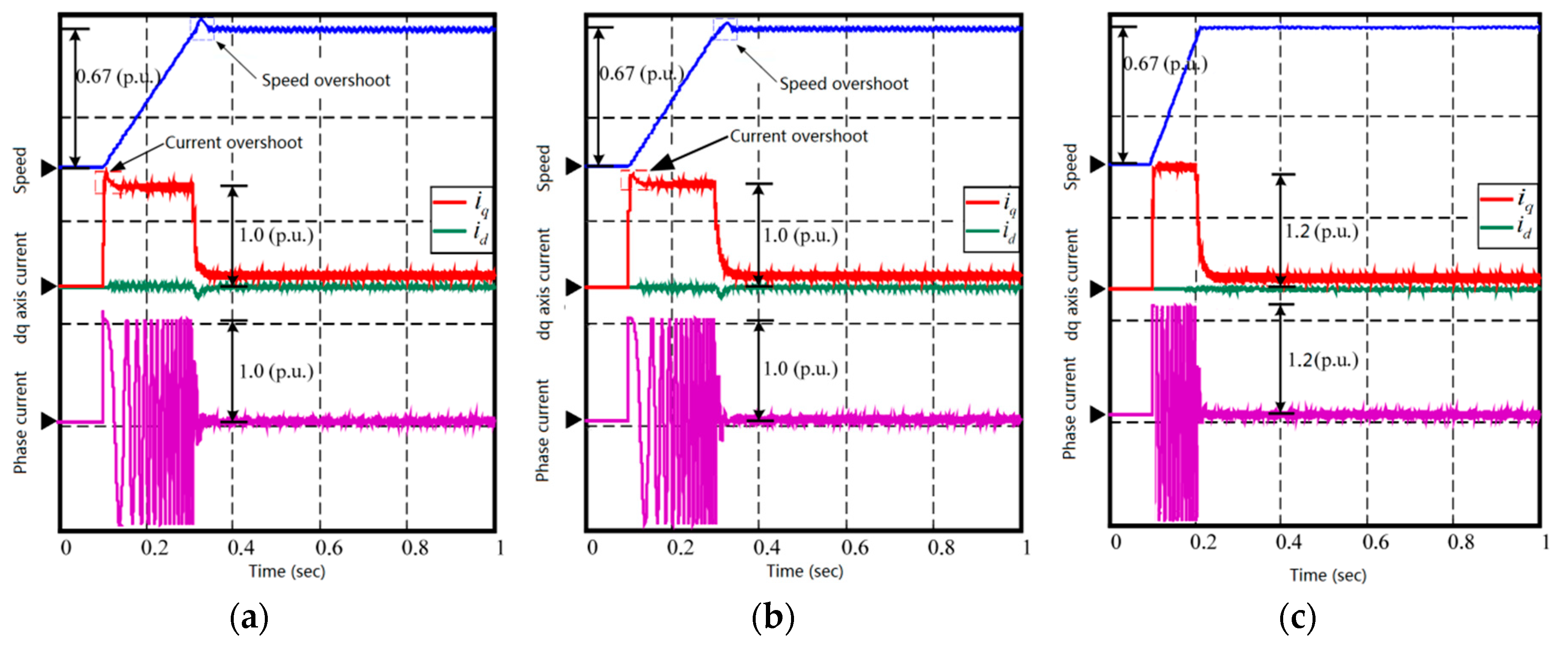
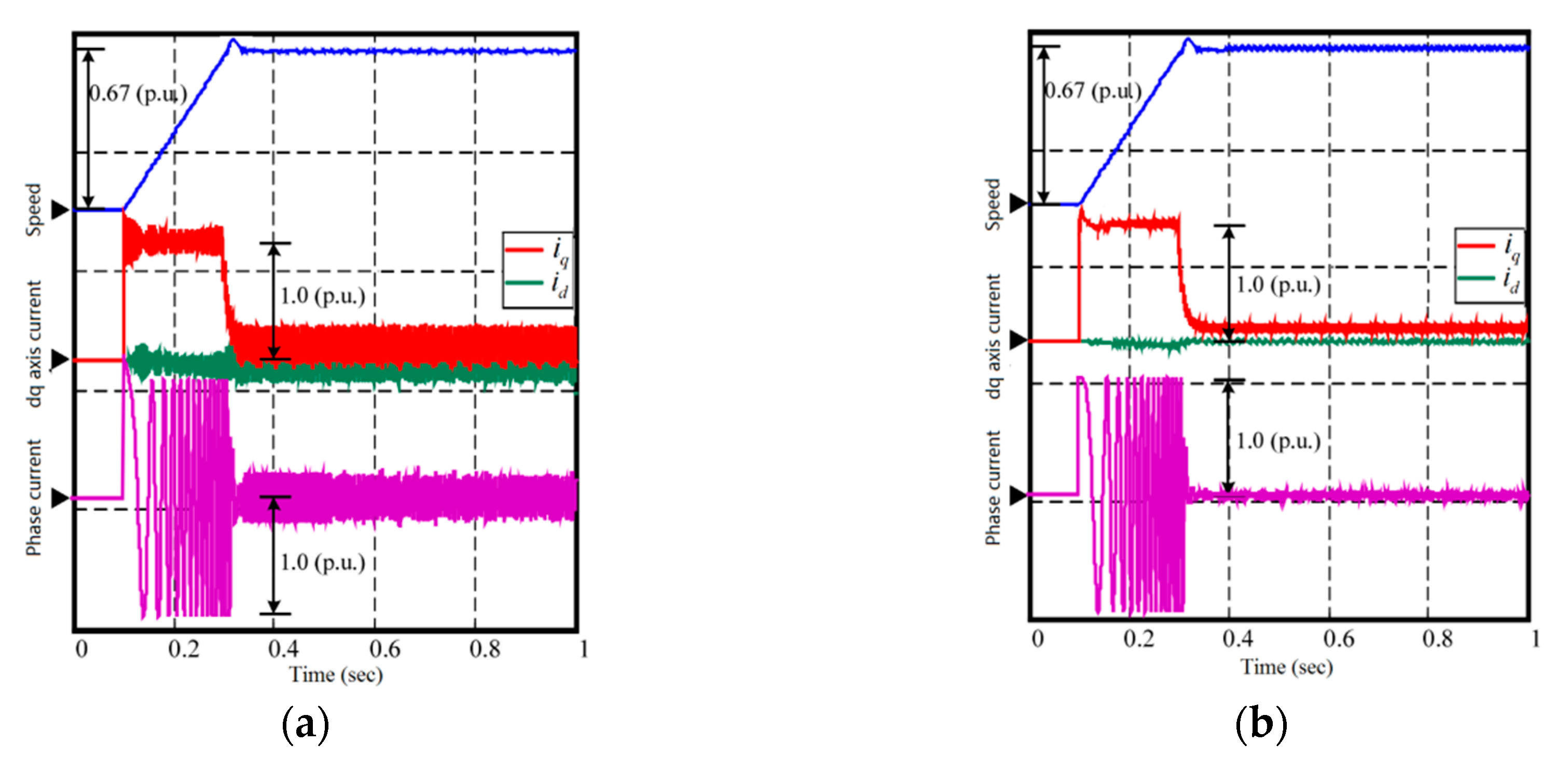
4.1.1. Comparison during Startup
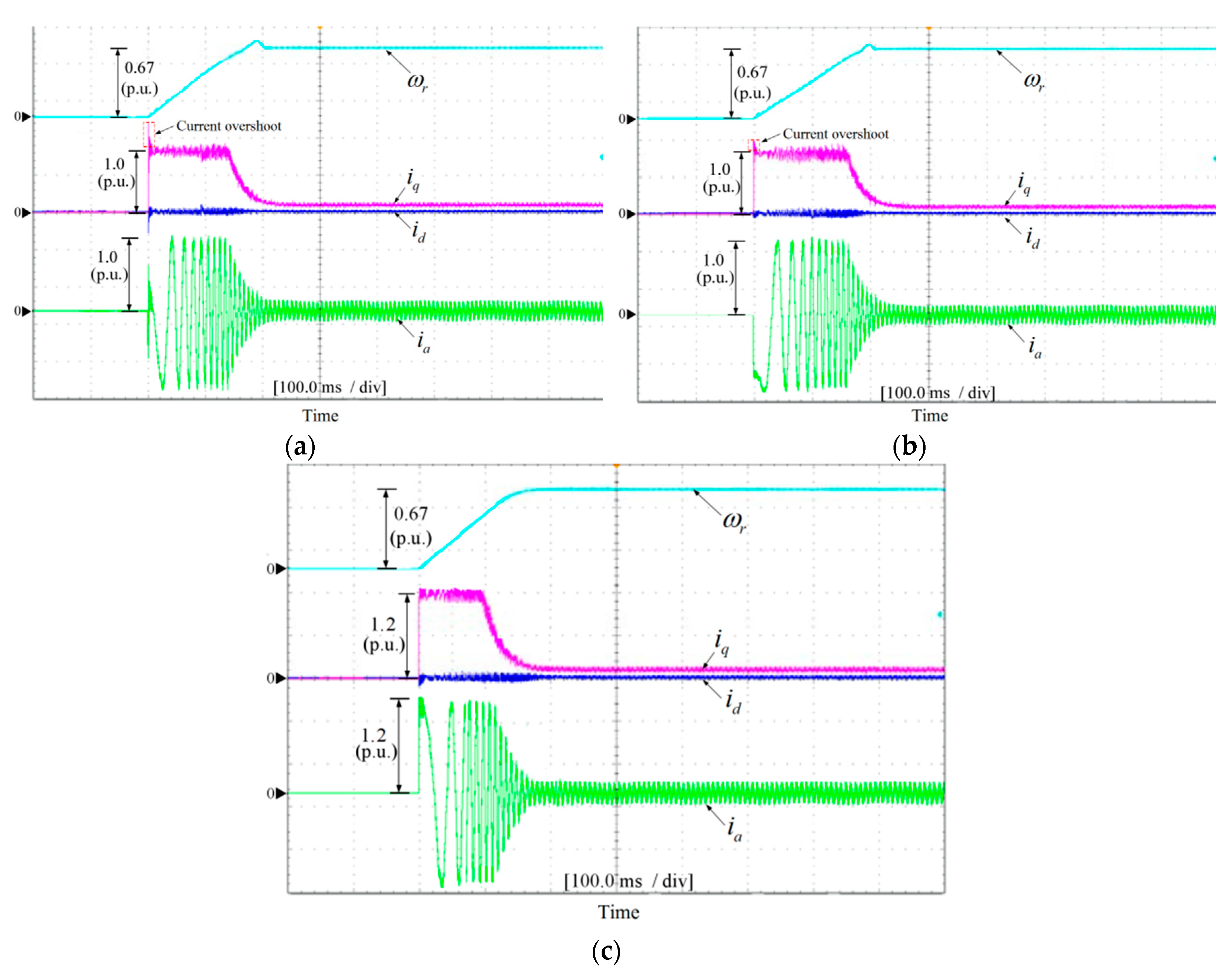
4.1.2. Comparison with Mismatched Resistance
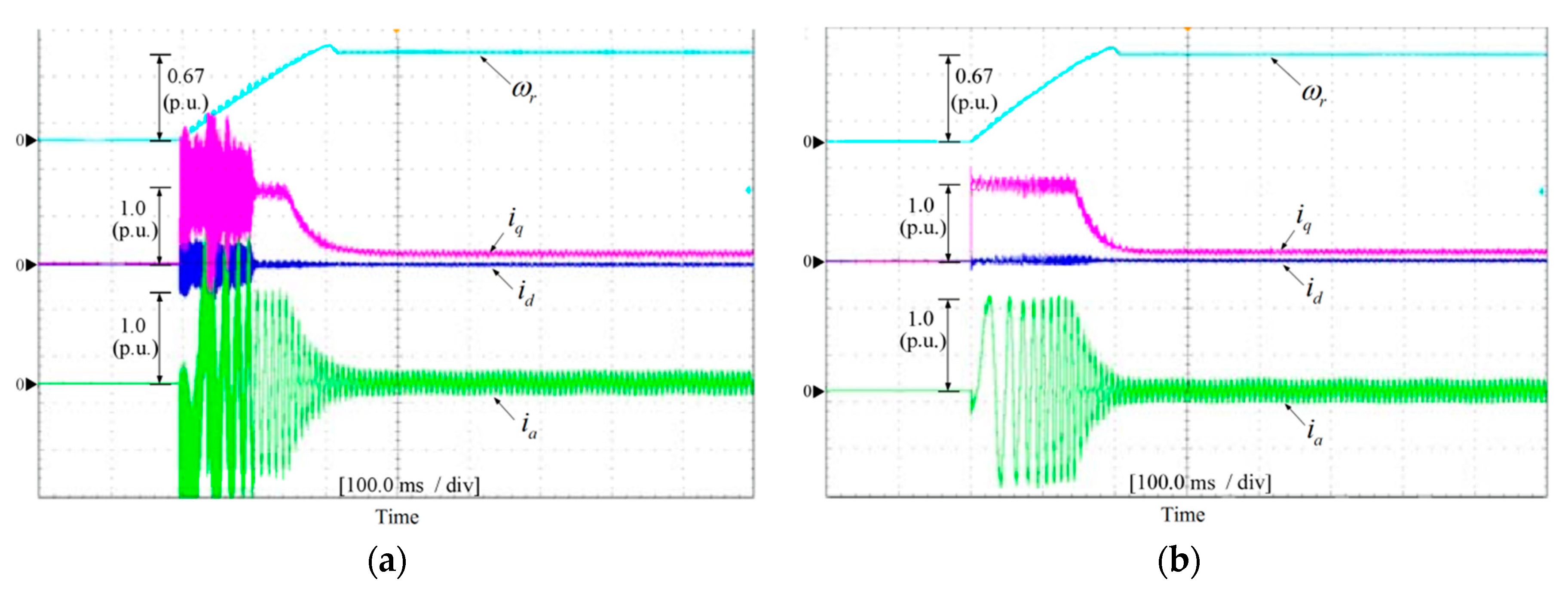
4.1.3. Comparison with Mismatched Inductance
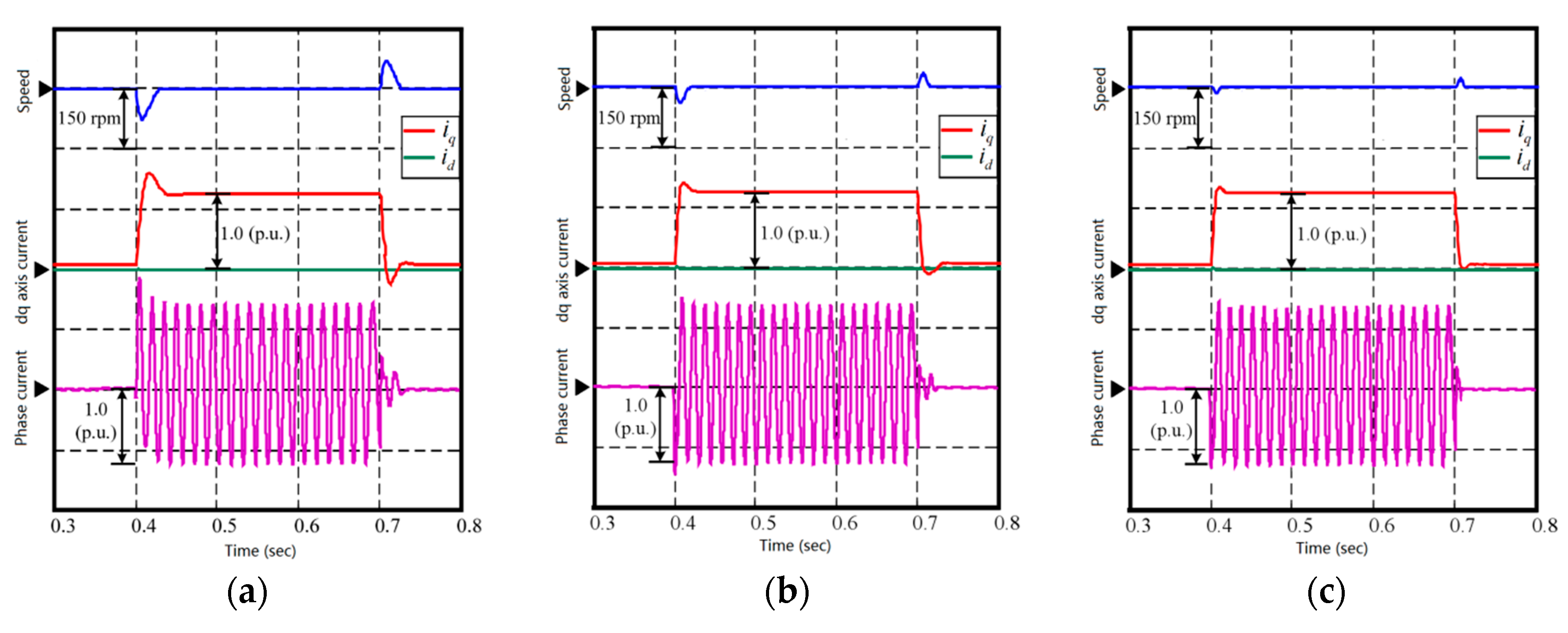
4.1.4. Comparison under Load Sudden Change Condition
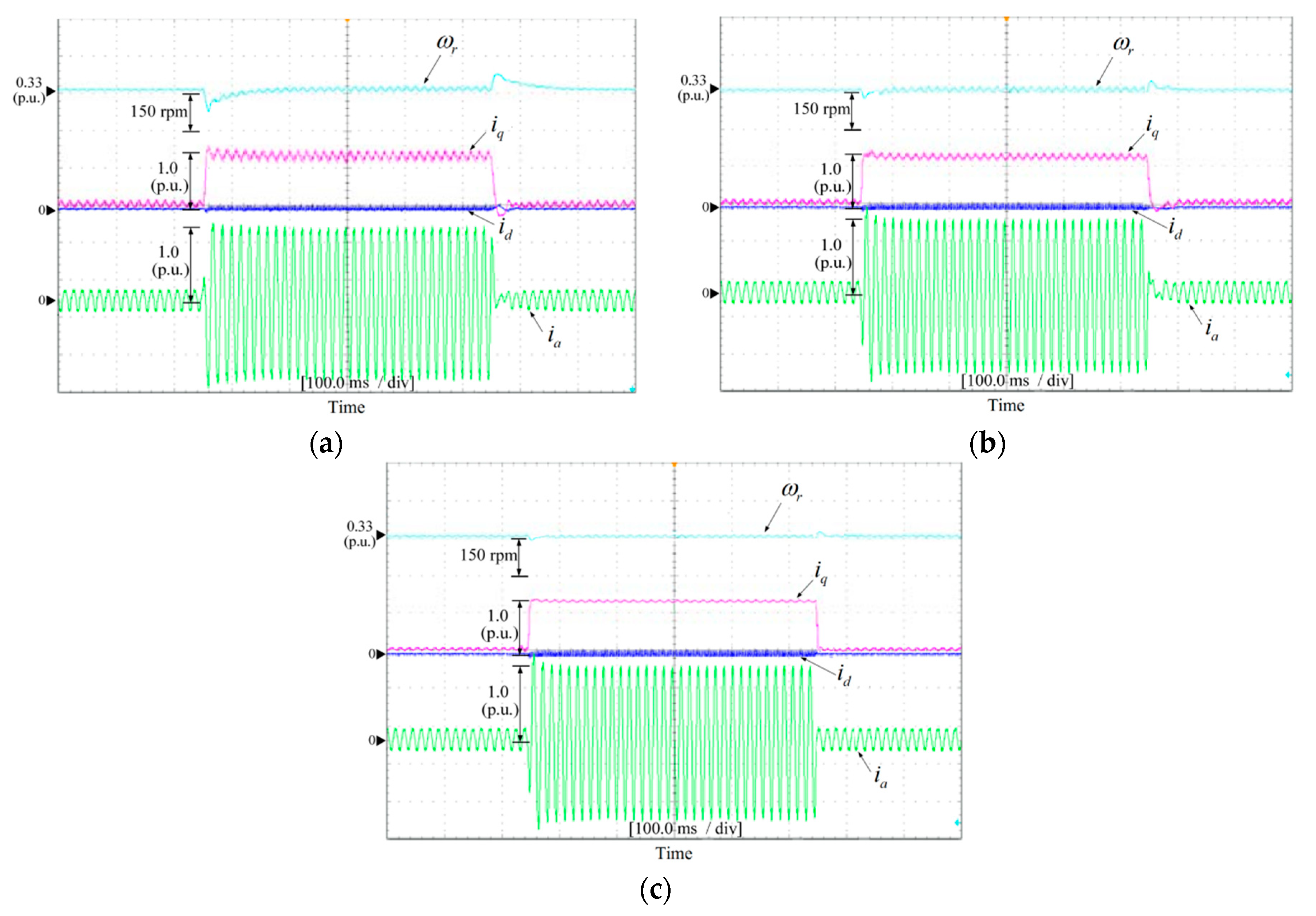
4.2. Experimental Results
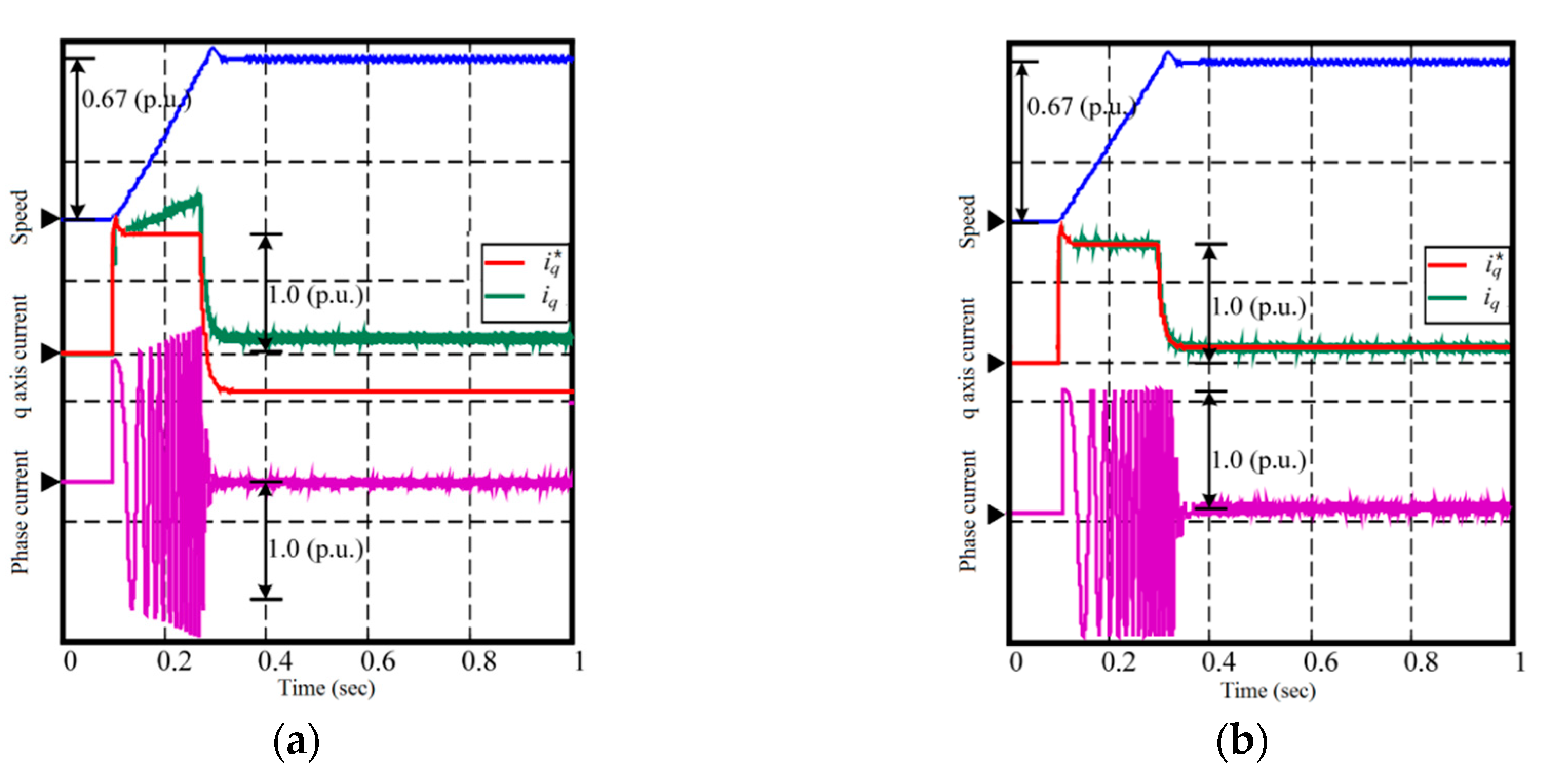
4.2.1. Comparison during Startup
4.2.2. Comparison with Mismatched Resistance
4.2.3. Comparison with Mismatched Inductance
4.2.4. Comparison under Load Sudden Change Condition
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Onsal, M.; Cumhur, B.; Demir, Y.; Yolacan, E. Rotor Design Optimization of a New Flux-Assisted Consequent Pole Spoke-Type Permanent Magnet Torque Motor for Low-Speed Applications. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Yolacan, E.; Guven, M.K.; Aydin, M. A Novel Torque Quality Improvement of an Asymmetric Windings Permanent-Magnet Synchronous Motor. IEEE Trans. Magn. 2017, 53, 1–6. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Cheng, M.; Chau, K.T. Field-Oriented Control and Direct Torque Control for Paralleled VSIs Fed PMSM Drives With Variable Switching Frequencies. IEEE Trans. Power Electron. 2016, 31, 2417–2428. [Google Scholar] [CrossRef]
- Liang, D.; Li, J.; Qu, R.; Kong, W. Adaptive Second-Order Sliding-Mode Observer for PMSM Sensorless Control Considering VSI Nonlinearity. IEEE Trans. Power Electron. 2018, 33, 8994–9004. [Google Scholar] [CrossRef]
- Rachid, E.; Ahmed, J.D.; Muyeen, S.M. Experimental Validation of a Novel PI Speed Controller for AC Motor Drives With Improved Transient Performances. IEEE Trans. Control Syst. Tech. 2018, 26, 1414–1421. [Google Scholar]
- Tursini, M.; Parasiliti, F.; Zhang, D. Real-time gain tuning of PI controllers for high-performance PMSM drives. IEEE Trans. Ind. Appl. 2002, 38, 1018–1026. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Deng, Y. Torque Ripple Minimization of PMSM Based on Robust ILC Via Adaptive Sliding Mode Control. IEEE Trans. Power Electron. 2018, 33, 3655–3671. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, L.; Zhao, K.; Sun, L. Nonlinear Speed Control for PMSM System Using Sliding-Mode Control and Disturbance Compensation Techniques. IEEE Trans. Power Electron. 2013, 28, 1358–1365. [Google Scholar] [CrossRef]
- Liu, X.; Yu, H.; Yu, J.; Zhao, L. Combined Speed and Current Terminal Sliding Mode Control With Nonlinear Disturbance Observer for PMSM Drive. IEEE Access. 2018, 6, 29594–29601. [Google Scholar] [CrossRef]
- Víctor, R.; Domingo, B.; Antoni, A. Fixed Switching Period Discrete-Time Sliding Mode Current Control of a PMSM. IEEE Trans. Ind. Electron. 2018, 65, 2039–2048. [Google Scholar]
- Tomasz, T.; Lech, M.G. Constrained State Feedback Speed Control of PMSM Based on Model Predictive Approach. IEEE Trans. Ind. Electron. 2016, 63, 3867–3875. [Google Scholar]
- Farhad, A. Optimal Feedback Linearization Control of Interior PM Synchronous Motors Subject to Time-Varying Operation Conditions Minimizing Power Loss. IEEE Trans. Ind. Electron. 2018, 65, 5414–5421. [Google Scholar]
- Choi, Y.S.; Choi, H.H.; Jung, J.W.; Kong, W. Feedback Linearization Direct Torque Control With Reduced Torque and Flux Ripples for IPMSM Drives. IEEE Trans. Power Electron. 2016, 31, 3728–3737. [Google Scholar] [CrossRef]
- Li, J.; Ren, H.; Zhong, Y.; Kong, W. Robust Speed Control of Induction Motor Drives Using First-Order Auto-Disturbance Rejection Controllers. IEEE Trans. Ind. Appl. 2015, 51, 712–720. [Google Scholar] [CrossRef]
- Zuo, Y.; Zhu, X.; Quan, L.; Zhang, C. Active Disturbance Rejection Controller for Speed Control of Electrical Drives Using Phase-Locking Loop Observer. IEEE Trans. Ind. Electron. 2018, 66, 1748–1759. [Google Scholar] [CrossRef]
- Yin, Z.; Du, C.; Liu, J.; Sun, X. Research on Autodisturbance-Rejection Control of Induction Motors Based on an Ant Colony Optimization Algorithm. IEEE Trans. Ind. Electron. 2018, 65, 3077–3094. [Google Scholar] [CrossRef]
- Wang, G.; Liu, R.; Zhao, N.; Ding, D. Enhanced Linear ADRC Strategy for HF Pulse Voltage Signal Injection-Based Sensorless IPMSM Drives. IEEE Trans. Power Electron. 2019, 34, 514–525. [Google Scholar] [CrossRef]
- Marcin, M. The Adaptive Backstepping Control of Permanent Magnet Synchronous Motor Supplied by Current Source Inverter. IEEE Trans. Ind. Inform. 2013, 9, 1047–1055. [Google Scholar]
- Jesús, L.F.; Carlos, G.R.; Hebertt, S.R.; Oscar, D. Robust Backstepping Tracking Controller for Low-Speed PMSM Positioning System: Design, Analysis, and Implementation. IEEE Trans. Ind. Inform. 2015, 11, 1130–1141. [Google Scholar]
- Liu, S.; Guo, X.; Zhang, L. Robust Adaptive Backstepping Sliding Mode Control for Six-Phase Permanent Magnet Synchronous Motor Using Recurrent Wavelet Fuzzy Neural Network. IEEE Access. 2017, 5, 14502–14515. [Google Scholar]
- Zhang, Y.; Wen, C.; Yeng, C. Discrete-time robust backstepping adaptive control for nonlinear time-varying systems. IEEE Trans. Autom. Control 2000, 45, 1749–1755. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Z. Disturbance-Observer-Based Robust Backstepping Attitude Stabilization of Spacecraft Under Input Saturation and Measurement Uncertainty. IEEE Trans. Ind. Electron. 2017, 64, 7994–8002. [Google Scholar] [CrossRef]
- Kokotovic, P.V. The joy of feedback: Nonlinear and adaptive. IEEE Control Syst. Mag. 1992, 12, 7–17. [Google Scholar]
- Shieh, H.J.; Shyu, K.K. Nonlinear sliding-mode torque control with adaptive backstepping approach for induction motor drive. IEEE Trans. Ind. Electron. 1999, 46, 380–389. [Google Scholar] [CrossRef]
- Ba, D.; Yeom, H.; Kim, J.; Bae, J. Gain-Adaptive Robust Backstepping Position Control of a BLDC Motor System. IEEE/ASME Trans. Mechatron. 2018, 23, 2470–2481. [Google Scholar]
- Hsu, C.F.; Lin, C.M.; Lee, T.T. Wavelet Adaptive Backstepping Control for a Class of Nonlinear Systems. IEEE Trans. Neural Netw. 2006, 17, 1175–1183. [Google Scholar]
- Yu, X.; Lin, Y. Adaptive Backstepping Quantized Control for a Class of Nonlinear Systems. IEEE Trans. Autom. Control 2017, 62, 981–985. [Google Scholar] [CrossRef]
- Cai, J.; Wen, C.; Su, H.; Liu, Z. Adaptive Backstepping Control for a Class of Nonlinear Systems With Non-Triangular Structural Uncertainties. IEEE Trans. Autom. Control 2017, 62, 5220–5226. [Google Scholar] [CrossRef]
- Sun, L.; Huo, W.; Jiao, Z. Adaptive Backstepping Control of Spacecraft Rendezvous and Proximity Operations With Input Saturation and Full-State Constraint. IEEE Trans. Ind. Electron. 2017, 64, 480–492. [Google Scholar] [CrossRef]
- Lin, F.J.; Chang, C.K.; Huang, P.K. FPGA-Based Adaptive Backstepping Sliding-Mode Control for Linear Induction Motor Drive. IEEE Trans. Power Electron. 2007, 22, 1222–1231. [Google Scholar] [CrossRef]
- Rahman, M.A.; Vilathgamuwa, D.M.; Uddin, M.N.; Tseng, K.J. Nonlinear control of interior permanent-magnet synchronous motor. IEEE Trans. Ind. Appl. 2003, 39, 408–416. [Google Scholar] [CrossRef]
- Chen, M.; Lu, S.; Tseng, K.J. Application of Adaptive Variable Speed Back-Stepping Sliding Mode Controller for PMLSM Position Control. J. Mar. Sci. Technol. 2014, 22, 392–403. [Google Scholar]
- Kim, S.K.; Lee, K.G.; Lee, K.B. Singularity-Free Adaptive Speed Tracking Control for Uncertain Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2016, 31, 1692–1701. [Google Scholar] [CrossRef]
- Sarikhani, A.; Nejadpak, A.; Mohammed, O.A. Coupled Field-Circuit Estimation of Operational Inductance in PM Synchronous Machines by a Real-Time Physics-Based Inductance Observer. IEEE Trans. Magn. 2013, 49, 2283–2286. [Google Scholar] [CrossRef]
- Ni, R.; Wang, G.; Gui, X.; Xu, D. Investigation of d and q-Axis Inductances Influenced by Slot-Pole Combinations Based on Axial Flux Permanent-Magnet Machines. IEEE Trans. Ind. Electron. 2014, 61, 4539–4551. [Google Scholar] [CrossRef]
- Lin, C.M.; Li, H.Y. Intelligent Control Using the Wavelet Fuzzy CMAC Backstepping Control System for Two-Axis Linear Piezoelectric Ceramic Motor Drive Systems. IEEE Trans. Fuzzy Syst. 2014, 22, 791–802. [Google Scholar] [CrossRef]
- Chaoui, H.; Sicard, P. Adaptive Fuzzy Logic Control of Permanent Magnet Synchronous Machines With Nonlinear Friction. IEEE Trans. Ind. Electron. 2012, 59, 1123–1133. [Google Scholar] [CrossRef]
- Kung, Y.S.; Tsai, M.H. FPGA-Based Speed Control IC for PMSM Drive With Adaptive Fuzzy Control. IEEE Trans. Power Electron. 2007, 22, 2476–2486. [Google Scholar] [CrossRef]
- Barkat, S.; Tlemcani, A.; Nouri, H. Noninteracting Adaptive Control of PMSM Using Interval Type-2 Fuzzy Logic Systems. IEEE Trans. Fuzzy Syst. 2011, 19, 925–936. [Google Scholar] [CrossRef]
- Li, S.; Gu, H. Fuzzy Adaptive Internal Model Control Schemes for PMSM Speed-Regulation System. IEEE Trans. Ind. Inform. 2012, 8, 767–779. [Google Scholar] [CrossRef]
- Mahfouf, M.; Chen, M.Y.; Linkens, D.A. Adaptive Weighted Particle Swarm Optimization for Multi-objective Optimal Design of Alloy Steelss. In Proceedings of the 8th International Conference Parallel Problem Solving from Nature, Birmingham, UK, 18–22 September 2004; Volume 19, pp. 762–771. [Google Scholar]
- Parikshit, Y.; Rajesh, K.; Panda, S.K.; Chang, C.S. An Intelligent Tuned Harmony Search Algorithm for Optimisation. Inform. Sci. 2012, 196, 47–72. [Google Scholar]
- Li, J. Distributed cooperative tracking of multi-agent systems with actuator faults. Trans. Inst. Meas. Control. 2015, 37, 1041–1048. [Google Scholar] [CrossRef]
- Li, J.; Li, C.; Yang, X.; Chen, W. Event-triggered containment control of multi-agent systems with high-order dynamics and input delay. Electronics 2018, 7, 343. [Google Scholar] [CrossRef]
- Du, Z.; Zhang, Q.; Liu, L. New delay-dependentrobust stability of discrete singular systems with time-varying delay. Asian Journal of Control. 2011, 13, 136–147. [Google Scholar] [CrossRef]
- Wei, C.; Hao, L.; Yang, T.; Liu, J. Trajectory Optimization of Electrostatic Spray Painting Robots on Curved Surface. Coatings 2017, 7, 155. [Google Scholar] [CrossRef]


| Index Name | Rise Time (s) | Overshoot | Adjustment Time (s) | Steady-State Error | Fitness Value |
|---|---|---|---|---|---|
| J(ISE) | 0.0050 | 56.99% | 0.093 | 0 | 0.004494 |
| J(ITSE) | 0.0080 | 49.87% | 0.080 | 0 | 5.062 × 10−5 |
| J(ISTSE) | 0.0080 | 49.87% | 0.075 | 0 | 1.034 × 10−6 |
| J(IAE) | 0.0050 | 56.99% | 0.093 | 0 | 0.01263 |
| J(ITAE) | 0.0080 | 49.87% | 0.075 | 0 | 0.0002593 |
| J(ISTAE) | 0.0080 | 49.87% | 0.075 | 0 | 1.043 × 10−5 |
| Index Name | Rise Time (s) | Overshoot | Adjustment Time (s) | Steady-State Error | Fitness Value | |
|---|---|---|---|---|---|---|
| J(ISE) | 5 | 0.018 | 21.50% | 0.075 | 0.0079 | 0.01112 |
| 10 | 0.025 | 11.59% | 0.095 | 0.0128 | 0.01297 | |
| 15 | 0.028 | 8.36% | 0.102 | 0.0150 | 0.01380 | |
| 20 | 0.031 | 6.68% | 0.106 | 0.0164 | 0.01430 | |
| 25 | 0.032 | 5.63% | 0.108 | 0.0174 | 0.01465 | |
| 30 | 0.034 | 4.91% | 0.108 | 0.0180 | 0.01490 | |
| J(ITAE) | 5 | 0.032 | 7.34% | 0.078 | 0 | 8.364 × 10−4 |
| 10 | 0.039 | 3.95% | 0.084 | 0 | 8.568 × 10−3 | |
| 15 | 0.063 | 0.10% | 0.087 | 0 | 8.712 × 10−4 | |
| 20 | 0.064 | 0.05% | 0.090 | 0 | 8.870 × 10−4 | |
| 25 | 0.065 | 0.03% | 0.091 | 0 | 8.952 × 10−4 | |
| 30 | 0.065 | 0.02% | 0.092 | 0 | 8.999 × 10−4 |
| 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | ||
|---|---|---|---|---|---|---|---|
| 0.5 | 4.1724 × 10−15 | 0.0299 | 0.1364 | 2.4725 | 11.3792 | 39.7254 | |
| 0.6 | 0.0014 | 1.1725 | 3.9610 | 15.9247 | 45.0983 | 93.8858 | |
| 0.7 | 4.7375 | 18.9028 | 43.1931 | 42.0810 | 139.1420 | 287.7320 | |
| 0.8 | 17.8470 | 65.0720 | 133.3842 | 273.5391 | 355.6194 | 390.6332 | |
| 0.9 | 204.7088 | 423.5116 | 390.8902 | 57.5242 | 605.0966 | 713.4533 | |
| 1.0 | 435.5268 | 435.008 | 675.5462 | 623.2719 | 779.8188 | 875.4876 | |
| 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | ||
|---|---|---|---|---|---|---|---|
| e | 1.9514 × 10−15 | 1.4264 × 10−4 | 1.0015 | 2.8079 | 16.5784 | 19.3834 | |
| 0.6 | 0.1044 | 0.5208 | 14.6278 | 36.9077 | 25.1636 | 123.8342 | |
| 0.7 | 2.5700 | 11.8048 | 60.2017 | 100.0196 | 129.8733 | 198.0033 | |
| 0.8 | 36.1247 | 89.3460 | 151.7832 | 255.4492 | 347.9845 | 359.5684 | |
| 0.9 | 193.7990 | 301.1870 | 375.8477 | 401.8551 | 636.9981 | 681.3515 | |
| 1.0 | 444.6508 | 537.6002 | 611.0245 | 704.7756 | 804.6009 | 840.5120 | |
| Parameters | Units | Values |
|---|---|---|
| Rated power | w | 750 |
| Rated voltage | V | 220 |
| Rated current | A | 4.0 |
| Rated speed | rpm | 3000 |
| Rated torque | N·m | 2.39 |
| Stator resistance | Ω | 2.8 |
| Stator inductance | mH | 3.9 |
| Number of poles | 4 | |
| Rotor magnetic flux linkage | Wb | 0.1 |
| Control Method | Comparison during Startup | Comparison with Mismatched Resistance | Comparison with Mismatched Inductance | Comparison under Load Sudden Change Condition |
|---|---|---|---|---|
| TBC | Rise time: 200 ms; Speed overshoot: 20 rpm; Current overshoot: 15% of rated current | 50% current static error | Obvious current oscillation | Speed fluctuation: 68 rpm |
| AIBC_FP | Rise time: 200 ms; Speed overshoot: 10 rpm; Current overshoot: 10% of rated current | No current static error | No current oscillation | Speed fluctuation: 37 rpm |
| AIBC_AWPSO | Rise time: 100 ms; Speed overshoot: 0 rpm; Current overshoot: 0% of rated current | Speed fluctuation: 15 rpm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Tan, F.; Wu, J.; Ge, H.; Wei, H.; Zhang, Y. Adaptive Integral Backstepping Controller for PMSM with AWPSO Parameters Optimization. Energies 2019, 12, 2596. https://doi.org/10.3390/en12132596
Wang W, Tan F, Wu J, Ge H, Wei H, Zhang Y. Adaptive Integral Backstepping Controller for PMSM with AWPSO Parameters Optimization. Energies. 2019; 12(13):2596. https://doi.org/10.3390/en12132596
Chicago/Turabian StyleWang, Weiran, Fei Tan, Jiaxin Wu, Huilin Ge, Haifeng Wei, and Yi Zhang. 2019. "Adaptive Integral Backstepping Controller for PMSM with AWPSO Parameters Optimization" Energies 12, no. 13: 2596. https://doi.org/10.3390/en12132596
APA StyleWang, W., Tan, F., Wu, J., Ge, H., Wei, H., & Zhang, Y. (2019). Adaptive Integral Backstepping Controller for PMSM with AWPSO Parameters Optimization. Energies, 12(13), 2596. https://doi.org/10.3390/en12132596




