Energy Efficient Foot Trajectory of Trot Motion for Hydraulic Quadruped Robot ^†

Abstract

Quadruped robots can be used to transport loads or conduct rescue missions on tough terrain. In addition to flexibility and adaptability to complex terrain, the hydraulic driven quadruped robots also have the important characteristic of energy consumption. This paper studies the trot gait motions of the quadruped robot SCalf. The energy model including the mechanical power and heat rate is established, which can be used to obtained the energy consumption of the robot. Compared with a cubic spline interpolation reference trajectory, a foot trajectory based on Fourier series is studied to reduce the joints energy consumption, and the parameters of the foot trajectory are acquired by the Pattern Search method. The effectiveness of the energy efficient trajectory is verified by simulations and verified on the robot prototype.

1. Introduction

At present, most common mobile robots are wheeled or tracked, which are more suitable for flat surface. However, these robots still have some difficulties and limitations to pass through tough terrain. Compared with wheeled or tracked robots, legged robots can perform better in tough terrain. After years of development, there has been huge improvements in stability and mobility of the legged robot. However, in the view of energy, the performances of the legged robots are far less than wheeled or tracked robots. Many researchers have turned their attentions to the energy efficiency and energy consumption of legged robots.

Boston Dynamics developed the first generation of the Bigdog robot in 2004 and made a great improvement in the 2008 version [1]. Bigdog has about 50 sensors, including inertial, joint and power system sensors. Joint sensors were integrated on the hydraulic cylinders to measure motions and forces of the actuators. The virtual model was used to control the joint torques of the robot. Semini et al. from IIT (Italian Institute of Technology) built their hydraulic actuated quadruped robot HyQ in 2010 [2]. HyQ used $HoerbigerLB6$ as its joint actuator. Different from the Bigdog, the joint sensors of the HyQ were not integrated. It used the relative encoder $AvagoAEDA3300BE1$ and absolute encoder $austriamicrosystemsAS5045$ to measure the joint positions. The force acting on the cylinder rod was measured by $Burster8417$ force sensor, the force range is 0–5 kN and its accuracy is ±0.5% of the full scale. With this prototype, Boaventura [3] started to study active compliance and realize the force control of the HyQ.

Quadruped robots are widely used in the fields in transporting on rough terrains. The Bigdog and LS3 [4] were used to carry loads in jungle and hill environments. Keisuke et al. [5] designed a quadruped walking robot TITAN-IX, which was used in mine detection and removal. Other quadruped robots were designed with visual system or even an robot arm like HyQ2Max [6], Spot [7] and SpotMini [8]. These robots could identify the environment and realize the functions like climbing stairs or opening doors, which could be used in reconnaissance and rescue missions.

When modelling the quadruped robots, nonlinearity must be taken into consideration. Konstantinos et al. [9] designed an active compliance controller for quadruped robots. Stribeck velocity was added to the modelling of the ground force. For hydraulic actuated quadruped robots, nonlinearity often exists in the modelling of the hydraulic friction. Focchi et al. [10] used a Stribeck friction model to obtain the hydraulic frictions for a hydraulically actuated robot leg.

Compared to other kinds of robots or human beings, the energy analyses of legged robots are different. Researchers started to pay attention to the energy problems on legged robots. Gregorio et al. [11] built an one-legged robot named ARL Monopod; comparisons showed that the Monopod with its 125 W average power was more energy efficient than previously built robots. Li et al. [12] studied the legged robots’ dynamics and optimal control during the flight phase and constructed an optimal path. Wang et al. [13] used an energy-efficient support vector machine to study the energy consumption of the biped walking robots. Bhounsule et al. [14] proposed the concept of the leg ratio and studied the cost of transport with different leg ratio and gait parameters. Roy et al. [15] established the energy model of an electrical six-legged robot and studied the energy consumption during crab walking. Bodrov et al. [16] extended the loss analysis to the actuator motors and proposed a novel strategy to control a hexpod robot. However, the dynamics and energy models of the quadruped robots are different from other kinds of legged robots, which makes them unsuitable for quadruped applications.

Quadruped robots are more stable than monopod or biped robots, and have simple structure compared with the hexpod or robots with more than six legs [17]. Silva et al. [18] studied the best set of gait and locomotion variables during walking of the quadruped locomotion systems. Ikeda et al. [19] analysed the energy flow of a quadruped robot with a flexible trunk joint. Seok et al. [20,21] built an electric actuated quadruped robot Cheetah and established the energy flow of it. Based on the energy flow, several design principles were proposed and implementations of the principles were done to reduce the energy consumption of the robot. The COT (Cost of Transport) of the Cheetah robot is eliminated to 0.51, which is on the same level as other biological runners of similar mass. Kim et al. [22] built a hydraulic actuated quadruped robot with redundancy. In order to decrease the hydraulic flow consumption, a foot rotation angle generation algorithm was proposed, and the energy consumption of the robot was reduced at the same time. Mastalli et al. [23] and Neunert et al. [24] studied the trajectory optimization problem for rough terrain locomotion and contacts conditions. Du et al. [25] formulated two indexes to quantitatively describe the performances of quadruped robots and studied a gait pattern based on the Bezier curve. Wang et al. [26] established the energy model of a quadruped robot and studied the energy consumptions under different gait parameters. The friction rate was not considered and the foot force was simply regarded as half of the total weight. Sanz-Merodio [27] studied the energy efficiency of the hexapod robot SILO6 under different leg configurations. Montes [28] studied the energy consumption and energy efficiency of a hexapod robot. The SCARA configuration legs were used, which could bear high payloads with low energy expenditure, and the slope of the power consumption was low to 0.1606 W/kg. However, the above-mentioned works only studied the energy consumption of electric robots or lacked of a complete energy model for hydraulic actuated robots. To optimize the motion of the robot from the energy perspective, a compact energy model needed to be established to study the energy consumptions of hydraulic actuated quadruped robots.

This work focuses on the motions of the quadruped robot in sagittal plane. The main purpose of this work is to design a energy efficient foot trajectory for the hydraulic driven quadruped robot SCalf. Firstly, the kinematics and dynamics models of the robot leg are built. Then, the foot forces are obtained by using the minimization of norm of foot force method. The energy model of the robot is established by combining the mechanical power and heat rate. Then, an energy efficient foot trajectory based on Fourier series is proposed, and the coefficients of the foot trajectory are obtained through the Pattern Search method. The energy consumption of the proposed trajectory is compared with a reference foot trajectory which is based on the cubic spline interpolation. Computer simulations and physical experiments will be conducted to verify the proposed energy efficient trajectory.

2. Robot Modeling

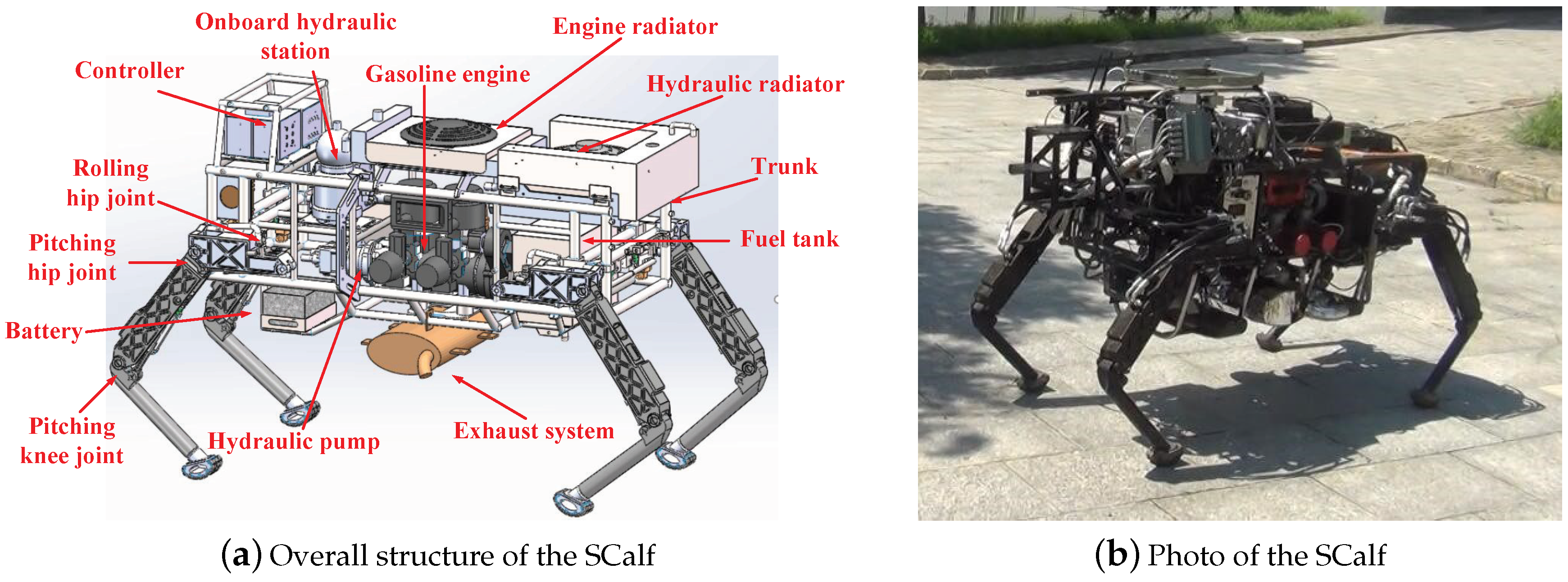
The SCalf robot was built by the Center for Robotics of Shandong University in 2017, and some improvements were made in 2018. The SCalf is a hydraulic driven quadruped robot, which consists of a trunk and four legs as shown in Figure 1. The robot is powered by hydraulic system driven by a gasoline engine. A variable displacement piston pump is connected to the gasoline engine to provide hydraulic flow for the whole robot system. The legs configuration of the robot use backward/forward configuration to improve the gradeability and load capacity [29]. The control system, hydraulic system and battery are placed inside the trunk. Each leg of the robot has three degree of freedoms (DOFs), which are defined as pitching knee joint, pitching hip joint and rolling hip joint. The joints of the robot are all actuated by hydraulic cylinders. With the 3DOF structure, the endpoint of the foot can move in a three-dimensional workspace with the hip joint as its origin, and the robot can realize omnidirectional movement in space. To make the robot easy to control, the trunk of the SCalf is built using a symmetric structure. The SCalf is used to transport loads on rough terrains and has a load capacity of 200 kg. The robot can be controlled by a remoter or follow with a navigator by using the visual system.

The hydraulic cylinder and sensors used on the SCalf are shown in Figure 2. The stroke of the hydraulic cylinder is 98 mm. The selection of the position sensor depends on the piston stroke of the actuator. The $REC38L$ series position sensor of $VISHAY$ is chosen, the span and accuracy of the position sensor are 100 mm and 0.1 mm, respectively. The force sensor is the $M3626AP$ series from $SRI$. The output voltage of the force sensor is −5 mV to 5 mV, and the range of the force sensor is 0 to 14,000 N.

2.1. General Method

With the development of legged robots, the studies of energy consumption are getting further. Most motions of the legged robots are realized by the motions of leg joints with specific trajectories. This work explains the method to design an energy efficient foot trajectory for legged robots. In order to find the energy efficient trajectory, the following research routine can be used in Figure 3.

The main contents of the study can be divided into following parts.

1. Robotic modelling. The first thing is to establish the model of the robot including the kinematic and dynamics model. Kinematic model is used to obtain the relationship between the foot endpoints and joint positions, while dynamics model can acquire the joint torques $\tau$. When the robot is in the stance phase, joint torques will be increased and the foot force algorithm is used to calculate the joint torques.

2. Establishment of the energy model. In order to obtain the energy consumption of the robot, the energy model has to be established. From the introduction section, many researchers only considered the mechanical power in their work. However, in a real robot system, heat rate can be really big and can’t be neglected. The frictional characteristic and modelling of different actuators varies greatly and need to be analyzed according to the actuator type.

3. Design of the energy efficient trajectory. To minimize the energy consumption, the energy efficient trajectory will be designed and the parameters of the trajectory need to be optimized. Here, the energy consumption is used as the objective function as shown in Equation (1). The energy consumption E is written as the integral of the joint power and represented by the joint position $\theta$, where P and H are the mechanical power and heat rate of the joint respectively. The constraints of the objective function are defined by the mechanical limitations of the joint positions. With the objective function, optimization algorithms can be used to decide the parameters of the energy efficient trajectory:

$$minE\left(\theta \right)={\int }_0^T[P\left(\theta \right)+H\left(\theta \right)]dt.$$

(1)

In order to study the energy consumption of legged robots, the SCalf robot is used as an example in this work. To simplify the calculation of the energy consumption, the following preconditions are made:

(a) The robot moves forward in a straight path on flat surface. The robot uses trot gait to move with the duty cycle as 50%. As the robot doesn’t have lateral movement, only the pitching knee and pitching hip joints are taken into consideration. When looking from front of the robot, the legs are perpendicular to the ground, as the joint positions of the rolling hip joints are set as zero.

(b) When walking on a flat surface, the variation of the trunk height is small, and the height of robot trunk can be regarded as constant. Therefore, the acceleration along the z-axis is considered as zero.

(c) The center of mass (COM) of the trunk body is assumed to be at the geometric center of the body.

(d) The right-front (RF) leg and left-hind (LH) leg are in the stance phase.

2.2. Kinematics of the SCalf Robot

The four legs of the robot have the same mechanical parameters and structure. Here, the RF leg of the robot is used to establish corresponding models, the model of the RF leg is shown in Figure 4. According to the precondition (a), the robot only moves in the sagittal plane, the kinematics are discussed in planar view in in Figure 4b.

In Figure 4, the RF leg can be divided into the hip, thigh and shank parts. The origin of the coordinate frame {$O_h$} is fixed at the rolling hip joint. x-direction is pointing horizontally to the front of the robot. z-direction is vertical to the ground and points upwards. y-direction is confirmed by the right-hand rule. $l_0$ and $l_3$ are the mechanical parameters of the hip joint, where $l_0$ = 45 mm and $l_3$ = 57 mm. $l_1$ and $m_1$ are the length and mass of the thigh part, and $l_2$ and $m_2$ are the length and mass of the shank part. ${\theta }_1$ and ${\theta }_2$ are the joint positions of the pitching hip and pitching knee joints. ${\tau }_1$ and ${\tau }_2$ are the joint torques of the two joints. The COMs of the thigh and shank part are defined by $l_{m1}$, $l_{m2}$, ${\epsilon }_1$ and ${\epsilon }_2$. When these parts rotate around their own joint shafts, the moments of inertia are $I_1$ and $I_2$ respectively. The values of the above structure parameters are shown in

Table 1. Parameters of the thigh and shank parts.

Parameter (i = 1,2)	Thigh	Shank
Mass($m_i$/Kg)	4.10	2.24
Length($l_i$/mm)	450.99	404.87
COM position($l_{mi}$/mm)	210.43	227.20
COM angle(${\epsilon }_i$/rad)	0.037	−0.083
Moment of inertia($I_i$/Kg·m${}^2$)	0.178	0.057

.

The location of the foot endpoint in {$O_h$} can be expressed as follows. The legs are perpendicular to the ground (precondition a), the foot endpoint position in y axis equals $-l_3$:

$$\left\{\begin{array}{c}x=-l_{1}sin{\theta }_1-l_{2}sin({\theta }_1+{\theta }_2),\hfill \\ z=-l_0-l_{1}cos{\theta }_1-l_{2}cos({\theta }_1+{\theta }_2).\hfill \end{array}\right.$$

(2)

By solving Equation (2), the joint positions can be obtained as

$$\left\{\begin{array}{c}{\theta }_1=-\varphi -arctan(\frac{x}{-l_0-z}),\hfill \\ {\theta }_2=\pi -arccos(\frac{l_1^2+l_2^2-{\xi }^2}{2l_1{l}_2}),\hfill \end{array}\right.$$

(3)

where

$$\left\{\begin{array}{c}\xi =\sqrt{{(-l_0-z)}^2+x^2},\hfill \\ \varphi =arccos(\frac{l_1^2+{\xi }^2-l_2^2}{2l_1\xi }).\hfill \end{array}\right.$$

(4)

For the LH leg, the joint positions are obtained as the following equation:

$$\left\{\begin{array}{c}{\theta }_1=\varphi -arctan(\frac{x}{-l_0-z}),\hfill \\ {\theta }_2=arccos(\frac{l_1^2+l_2^2-{\xi }^2}{2l_1{l}_2})-\pi .\hfill \end{array}\right.$$

(5)

The Jacobian matrix of the single leg model can also be calculated by Equation (2):

$$J=\left[\begin{array}{cc}-l_{1}cos{\theta }_1-l_{2}cos({\theta }_1+{\theta }_2)& -l_{2}cos({\theta }_1+{\theta }_2),\\ l_{1}sin{\theta }_1+l_{2}sin({\theta }_1+{\theta }_2)& l_{2}sin({\theta }_1+{\theta }_2).\end{array}\right]$$

(6)

According to the foot trajectory and Equation (3), the joint positions can be obtained. The angular velocities $\dot{{\theta }_i}$ and angular accelerations $\ddot{{\theta }_i}$ of the joints can be calculated through the differential of the joint positions ${\theta }_i$ and angular velocities $\dot{{\theta }_i}$ respectively, where $i=1,2$.

2.3. Dynamics of the SCalf Robot

The dynamics equation of the robot is used to calculate the joint torque vector $\mathit{\tau }$. Here, the Lagrangian method is used to acquire the dynamics model of the single leg. The Lagrangian method can establish the dynamic model in the view of energy. It can avoid complex calculations of the interaction forces between the joints, and can describe the relationship between the external forces and motions in a generalized coordinate [30].

The dynamic model of the single leg with n-DOF can be written as follows:

$$\frac{d}{dt}\frac{\partial L}{\partial \dot{\mathit{\theta }}}-\frac{\partial L}{\partial \mathit{\theta }}=\mathit{Q},$$

(7)

where

$$L=E_k-E_p.$$

(8)

In the above equations, L is the Lagrangian function, $\mathit{\theta }={[{\theta }_1^T,\dots ,{\theta }_n^T]}^T\in {\mathit{R}}^{n\times 1}$ is the joint position vector, $\dot{\mathit{\theta }}={[{\dot{\theta }}_1^T,\dots ,{\dot{\theta }}_n^T]}^T\in {\mathit{R}}^{n\times 1}$ is the joint angular velocity vector, and $\mathit{Q}=[Q_1,\dots Q_n]\in {\mathit{R}}^{n\times 1}$ is the generalized force vector in the generalized coordinate [31]. $E_k$ and $E_p$ are the kinetic and potential energy of the single leg system, respectively.

The generalized force vector is defined in Equation (9), where ${\mathit{F}}_G={[F_x,F_y,F_z]}^T\in {\mathit{R}}^{3\times 1}$ is the ground reaction force vector, ${\mathit{J}}^T\in {\mathit{R}}^{n\times n}$ is the transposed matrix of the single leg Jacobian matrix, and $\mathit{\tau }=[{\tau }_1^T,\dots ,{\tau }_n^T]\in {\mathit{R}}^{n\times 1}$ is the joint torque vector

$$\mathit{Q}=\mathit{\tau }-{\mathit{J}}^T{\mathit{F}}_G.$$

(9)

During the swing phase, there are no contacts between foot and ground, therefore the ground reaction force ${\mathit{F}}_{\mathit{G}}$ equals 0. During the stance phase, the ground reaction force vector becomes undetermined. A foot force distribution method will be introduced in the next section.

According to Equations (7)–(9), the dynamic equation can be written as Equation (10):

$$\mathit{\tau }-{\mathit{J}}^T{\mathit{F}}_{\mathit{G}}=\mathit{M}(\mathit{\theta })\ddot{\mathit{\theta }}+\mathit{C}(\mathit{\theta },\dot{\mathit{\theta }})\dot{\mathit{\theta }}+\mathit{G}(\mathit{\theta }).$$

(10)

In Equation (10), $\mathit{C}(\mathit{\theta },\dot{\mathit{\theta }})\in {\mathit{R}}^{n\times n}$ is the Coriolis and centrifugal forces matrix, $\mathit{M}(\mathit{\theta })\in {\mathit{R}}^{n\times n}$ is the inertia matrix, and $\mathit{G}(\mathit{\theta })\in {\mathit{R}}^{n\times 1}$ is the gravitational loading vector.

For the movement in the sagittal plane, only 2 DOFs need to be considered, hence n = 2. According to the parameters in Figure 4, the kinetic energy $E_k$ and potential energy $E_p$ can be calculated. In the following equations, ${\theta }_{\epsilon 1}={\theta }_1+{\epsilon }_1$, ${\theta }_{\epsilon 2}={\theta }_2+{\epsilon }_2$, and ${\theta }_{\epsilon 12}={\theta }_1+{\theta }_2+{\epsilon }_2$.

The kinetic energy of the single leg system, thigh and shank parts are shown as follows:

$$E_k=E_{k1}+E_{k2},$$

(11)

$$E_{k1}=\frac{1}{2}{m}_1{v}_{c1}^2+\frac{1}{2}{I}_1{\dot{{\theta }_1}}^2,$$

(12)

$$E_{k2}=\frac{1}{2}{m}_2{v}_{c2}^2+\frac{1}{2}{I}_2{(\dot{{\theta }_1}+\dot{{\theta }_2})}^2,$$

(13)

where $v_{c1}$ and $v_{c2}$ are the COM velocities of each parts, which are calculated as follows:

$$v_{c1}^2={\dot{{\theta }_1}}^2{l}_{m1}^2,$$

(14)

$$v_{c2}^2={\dot{{\theta }_1}}^2{l}_1^2+{(\dot{{\theta }_1}+\dot{{\theta }_2})}^2{l}_{m2}^2+2\dot{{\theta }_1}(\dot{{\theta }_1}+\dot{{\theta }_2})l_1{l}_{m2}cos{\theta }_{\epsilon 2}.$$

(15)

The potential energy of the single leg system, thigh and shank parts can be obtained by the following equations:

$$E_p=E_{p1}+E_{p2},$$

(16)

$$E_{p1}=-m_{1}g(l_0+l_{m1}cos{\theta }_{\epsilon 1}),$$

(17)

$$E_{p2}=-m_{2}g(l_0+l_{1}cos{\theta }_1+l_{m2}cos{\theta }_{\epsilon 12}).$$

(18)

In Equation (10), $\mathit{M}(\mathit{\theta })$ is a 2 × 2 matrix and written as follows:

$$\mathit{M}(\mathit{\theta })=\left[\begin{array}{cc}{M}_{11}(\theta )& M_{12}(\theta )\\ M_{21}(\theta )& M_{22}(\theta )\end{array}\right],$$

(19)

where

$$M_{11}(\theta )=I_1+I_2+m_1{l}_{m1}^2+m_2(l_1^2+l_{m2}^2+2l_1{l}_{m2}cos{\theta }_{\epsilon 2}),$$

(20)

$$\begin{array}{c}\hfill M_{12}(\theta )=M_{21}(\theta )=m_2{l}_{m2}^2+m_2{l}_1{l}_{m2}cos{\theta }_{\epsilon 2}+I_2,\end{array}$$

(21)

$$M_{22}(\theta )=m_2{l}_{m2}^2+I_2.$$

(22)

The matrix $\mathit{C}(\mathit{\theta },\dot{\mathit{\theta }})$ is shown in Equation (23):

$$\mathit{C}(\mathit{\theta },\dot{\mathit{\theta }})=\left[\begin{array}{cc}{C}_{11}(\theta ,\dot{\theta })& C_{21}(\theta ,\dot{\theta })\\ C_{12}(\theta ,\dot{\theta })& C_{22}(\theta ,\dot{\theta })\end{array}\right],$$

(23)

where

$$C_{11}(\theta ,\dot{\theta })=-\dot{{\theta }_2}{m}_2{l}_1{l}_{m2}sin{\theta }_{\epsilon 2},$$

(24)

$$C_{12}(\theta ,\dot{\theta })=-(\dot{{\theta }_1}+\dot{{\theta }_2})m_2{l}_1{l}_{m2}sin{\theta }_{\epsilon 2},$$

(25)

$$C_{21}(\theta ,\dot{\theta })=\dot{{\theta }_1}{m}_2{l}_1{l}_{m2}sin{\theta }_{\epsilon 2},$$

(26)

$$C_{22}(\theta ,\dot{\theta })=0.$$

(27)

The gravitational loading vector $\mathit{G}(\mathit{\theta })$ is shown in the following equation. g is the gravity acceleration:

$$\mathit{G}(\mathit{\theta })=\left[\begin{array}{c}{m}_{1}g{l}_{m1}sin{\theta }_{\epsilon 1}+m_{2}g(l_{1}sin{\theta }_1+l_{m2}sin{\theta }_{\epsilon 12})\\ m_{2}g{l}_{m2}cos{\theta }_{\epsilon 12}\end{array}\right].$$

(28)

3. The Foot Force Distribution

When analysing the foot force distribution, the slippages between the foot endpoint and ground are neglected [32]. In addition, compared with the trunk mass, the masses of the swing legs are very small. Therefore, the inertia of the swing legs can be negligible. For the motions in the sagittal plane, the ground force of each leg can be simplified into a two component force, one normal and one tangential to the surface (along the x-axis and z-axis). The static force diagram of the robot in the sagittal plane is shown in Figure 5.

For the foot force distribution problem, the method with the minimization of norm of foot force is used. For a heavy robot like the SCalf, the contact forces between feet and ground can cause many negative effects, which may damage the mechanical structure and make the robot hard to control [33]. The minimization of norm of foot force method can minimum the norm solution of the foot force and reduce the compact between ground and robot [34].

A coordinate frame $\left\{O_b\right\}$ is established at the geometric center of the body, the coordinates of the support foot endpoints in $\left\{O_b\right\}$ are $\{x_F,z_F\}$ and $\{x_H,z_H\}$, respectively (the positions in the y-axis are 0). In Figure 5, the ground reaction force ${\mathit{F}}_{\mathit{G}}={[{\mathit{f}}_{\mathit{F}},{\mathit{f}}_{\mathit{H}}]}^T\in {\mathit{R}}^{4\times 1}$, where ${\mathit{f}}_{\mathit{F}}={[f_{F,x},f_{F,z}]}^T\in {\mathit{R}}^{2\times 1}$ and ${\mathit{f}}_{\mathit{H}}={[f_{H,x},f_{H,z}]}^T\in {\mathit{R}}^{2\times 1}$ are the ground reaction forces of the RF and LH legs, respectively, and the subscripts x and z represent for the normal and tangential component of the ground reaction force. The vector $\mathit{W}={[F_x,F_z,T_y]}^T\in {\mathit{R}}^{3\times 1}$ contains the forces and moment acting on the robot’s COM in the sagittal plane. In addition, the inertial effects of the legs are neglected. Under these conditions, the forces and moment balance equations can be written as follows:

$$F_x=f_{F,x}+f_{H,x},$$

(29)

$$F_z=f_{F,z}+f_{H,z},$$

(30)

$$T_y=f_{F,x}{z}_F-f_{F,z}{x}_F+f_{H,x}{z}_H-f_{H,z}{x}_H.$$

(31)

Equations (29)–(31) can be written in a matrix form as follows:

$$\mathit{A}·{\mathit{F}}_{\mathit{G}}=\mathit{W},$$

(32)

where $\mathit{A}\in {\mathit{R}}^{3\times 4}$ is shown here:

$$\mathit{A}=\left[\begin{array}{cccc}1& 0& 1& 0\\ 0& 1& 0& 1\\ z_F& -x_F& z_H& -x_H\end{array}\right].$$

(33)

The values of $F_x$, $F_z$ and $T_y$ are given for the straight motion on the flat surface, $F_x=Ma$, $F_z=Mg$ and $T_y=0$, where M is the trunk mass, and g is the gravitational acceleration. a is the acceleration of the trunk and can be obtained by the foot trajectory during the stance phase.

In the Equation (32), there are four unknowns but only three equations, which is indeterminate. Here, we use the least squared method. It uses the closest solution under Euclidean distance as the approximate solution. The result can be written in matrix form as follows:

$${\mathit{F}}_{\mathit{G}}={\mathit{A}}^T{(\mathit{A}{\mathit{A}}^T)}^{-1}\mathit{W}.$$

(34)

In Equation (34), the matrix ${\mathit{A}}^{+}={\mathit{A}}^T{(\mathit{A}{\mathit{A}}^T)}^{-1}\in {\mathit{R}}^{4\times 3}$ is the pseudoinverse matrix of $\mathit{A}$. As the third component of $\mathit{W}$ ($T_y$) is zero, the parameters in the last column of ${\mathit{A}}^{+}$ can be neglected. The value of ${\mathit{A}}^{+}$ is shown as follows:

$${\mathit{A}}^{+}=\left[\begin{array}{ccc}{\displaystyle \frac{a_{11}^{+}}{2\mathsf{\Sigma }}}& {\displaystyle \frac{a_{12}^{+}}{2\mathsf{\Sigma }}}& \times \\ {\displaystyle \frac{a_{21}^{+}}{2\mathsf{\Sigma }}}& {\displaystyle \frac{a_{22}^{+}}{2\mathsf{\Sigma }}}& \times \\ {\displaystyle \frac{a_{31}^{+}}{2\mathsf{\Sigma }}}& {\displaystyle \frac{a_{32}^{+}}{2\mathsf{\Sigma }}}& \times \\ {\displaystyle \frac{a_{41}^{+}}{2\mathsf{\Sigma }}}& {\displaystyle \frac{a_{42}^{+}}{2\mathsf{\Sigma }}}& \times \end{array}\right],$$

(35)

where

$$a_{11}^{+}={(x_F-x_H)}^2+2z_H^2-2z_H{z}_F,$$

(36)

$$a_{12}^{+}=(x_F+x_H)(z_F-z_H),$$

(37)

$$a_{21}^{+}=(x_F-x_H)(z_F+z_H),$$

(38)

$$a_{22}^{+}={(z_F-z_H)}^2+2x_H^2-2x_H{x}_F,$$

(39)

$$a_{31}^{+}={(x_F-x_H)}^2+2z_F^2-2z_H{z}_F,$$

(40)

$$a_{32}^{+}=(x_F+x_H)(z_H-z_F),$$

(41)

$$a_{41}^{+}=(x_H-x_F)(z_F+z_H),$$

(42)

$$a_{42}^{+}={(z_F-z_H)}^2+2x_F^2-2x_H{x}_F,$$

(43)

$$\mathsf{\Sigma }={(x_F-x_H)}^2+{(z_F-z_H)}^2.$$

(44)

The joint torques ${\mathit{\tau }}_{\mathit{G}}\in {\mathit{R}}^{4\times 1}$ produced by the feet forces can be written as follows:

$${\mathit{\tau }}_{\mathit{G}}={{\mathit{J}}_{\mathit{G}}}^T·{\mathit{F}}_{\mathit{G}},$$

(45)

where

$${\mathit{J}}_{\mathit{G}}=\left[\begin{array}{cc}{\mathit{J}}_{\mathit{F}}& \mathit{0}\\ \mathit{0}& {\mathit{J}}_{\mathit{H}}\end{array}\right].$$

(46)

In Equation (46), ${\mathit{J}}_{\mathit{F}}\in {\mathit{R}}^{2\times 2}$ and ${\mathit{J}}_{\mathit{H}}\in {\mathit{R}}^{2\times 2}$ are the Jacobian of the front and hind legs, respectively.

4. The Energy Model of the SCalf

In this work, the joint energy consumptions are obtained by the integral of the joint powers. For different foot trajectories, the gait parameters including the step height, step length and gait cycle are set as the same. Therefore, the robot can move the same distance in one gait cycle with different foot trajectories. In Equation (47), the energy consumption of a cycle is calculated, where P is the joint power, T is the gait cycle, and E is the joint energy consumption of a cycle:

$$E={\int }_0^{T}Pdt.$$

(47)

The mechanical power and heat rate are both included in the calculation of the joint power:

$$P=|\tau \dot{\theta }|+f_f{\dot{x}}_p.$$

(48)

In Equation (48), the two terms on the right of the equal mark are the mechanical power and heat rate caused by the cylinder frictions, where both the shortening/lengthening processes are included. $\dot{\theta }$ is the joint angular velocity, $\tau$ is the joint torque provided, ${\dot{x}}_p$ and $f_f$ are the velocity and friction of the cylinder respectively, where ${\dot{x}}_p$ is the differential of the corresponding cylinder length.

The frictions of hydraulic cylinders are highly nonlinear. In the most general case, the nonlinear friction force on the piston depends not only on the actuator velocity ${\dot{x}}_p$ but also on the pressure difference $\Delta p$ across the piston, and possibly on the piston position $x_p$ and temperature t [35]:

$$f_f=f_f(x_p,{\dot{x}}_p,\Delta p,\theta ,t).$$

(49)

A more practical model of the friction was proposed by Stribeck [36]. The model divides friction forces into static friction, Coulomb friction and viscous friction. The viscous friction is proportional to the velocity and contributes to stability and damping in hydraulic systems. The Coulomb friction is a constant force only depends on the sign of the piston velocity. The static friction acts mainly at zero velocity. It decays exponentially to zero as soon as the piston starts to move [3]. An empirical friction function is shown here:

$$f_f({\dot{x}}_p)=B{\dot{x}}_p+sign({\dot{x}}_p)\left(F_{c0}+F_{s0}{e}^{-\frac{|{\dot{x}}_p|}{C_s}}\right),$$

(50)

where $F_{s0}$ is the static friction coefficient (N), B is the viscous friction coefficient (Ns/m), $C_s$ is the static decay friction coefficient (m/s), and $F_{c0}$ is the Coulomb friction coefficient (N).

For the asymmetry cylinder used on the SCalf robot, the frictions during extension and shortening are different. To calculate the friction properly, Equation (50) should be extended to the following equation [37]:

$$f_f({\dot{x}}_p)=\left\{\begin{array}{c}{B}^{+}{\dot{x}}_p+\left(F_{c0}^{+}+F_{s0}^{+}{e}^{-\frac{|{\dot{x}}_p|}{C_s^{+}}}\right),{\dot{x}}_p>0,\hfill \\ B^{-}{\dot{x}}_p-\left(F_{c0}^{-}+F_{s0}^{-}{e}^{-\frac{|{\dot{x}}_p|}{C_s^{-}}}\right),{\dot{x}}_p<0.\hfill \end{array}\right.$$

(51)

Using the measured result made by Polzer et al. [38], the parameters in Equation (51) can be obtained as follows. When ${\dot{x}}_p\ge$ 0, B = 220 Ns/m, $F_{c0}$ = 50 N, $F_{s0}$ = 30 N and $C_s$ = 0.015 m/s. When ${\dot{x}}_p<$ 0, B = 180 Ns/m, $F_{c0}$ = 50 N, $F_{s0}$ = 20 N and $C_s$ = 0.007 m/s.

According to the joint positions and the mechanical structure of the single leg, the lengths of hydraulic cylinders and joint positions are mapped as follows, where $c_1$ and $c_2$ are the cylinder lengths, ${\theta }_1$ and ${\theta }_2$ are the joint positions. The structure parameters in the following equation are illustrated in Figure 6 and listed in

Table 2. Mechanical parameters used in Figure 6.

Joint	${\mathit{a}}_{\mathit{i}}$(mm)	${\mathit{b}}_{\mathit{i}}$(mm)	Angles(°)
Pitching hip joint	289.26	56.87	$e_1$ = 5.36	$e_2$ = 54.90
Pitching knee joint	289.26	56.89	$e_3$ = 8.02	$e_4$ = 2.35

:

$$\left\{\begin{array}{c}{c}_1=\sqrt{a_1^2+b_1^2-2a_1{b}_{1}cos(-{\theta }_1+\frac{\pi }{2}-e_1-e_2)},\hfill \\ c_2=\sqrt{a_2^2+b_2^2-2a_2{b}_{2}cos(-{\theta }_2+\pi -e_3+e_4)}.\hfill \end{array}\right.$$

(52)

The cylinder velocities can be obtained by the differential of the cylinder lengths:

$${\dot{x}}_p=\frac{d{c}_i}{dt},i=1,2.$$

(53)

5. The Foot Trajectory Analyses

The motion during one gait cycle can be divided into a stance phase and a swing phase. The two legs in a diagonal position have the same condition in each phase. The foot force and the leg model of one leg in two phases are different, therefore we discuss different foot trajectory for different phases. Here, the foot trajectories based on the single leg model are analysed.

5.1. Stance Phase

During the stance phase, the legs support the trunk to move forward. In order to make the trunk move steadily, the acceleration of the foot trajectory on the x-axis needs to be as small as possible, frequent changes in trunk speed will increase the difficulty of control. In addition, according to Equation (34), when trunk acceleration increases, the first component of the vector $\mathit{W}$ would raise too, which will raise the foot forces and finally increase the joint torques. On the basis of Equations (47) and (48), the joint power and energy consumption will have a significant growth.

Based on the above analyses, a linear trajectory was used to keep the trunk making a uniform motion during the stance phase, the equation in the single leg coordinate system $\left\{O_h\right\}$ is shown below. S is the step length, T is the gait cycle and $z_0$ is the standing height:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_{st}(t)=\frac{S}{2}(1-\frac{4t}{T}),\hfill \\ z_{st}(t)=-z_0.\hfill \end{array}\right.\end{array}$$

(54)

According to Equation (54), the motion conditions of foot endpoint at the beginning and end of the stance phase can be obtained in

Table 3. The initial and terminated conditions of the stance phase.

Items(time)	x-Direction	z-Direction
position(0)	${\displaystyle \frac{S}{2}}$	$-z_0$
position(${\displaystyle \frac{T}{2}}$)	$-{\displaystyle \frac{S}{2}}$	$-z_0$
velocity(0)	$-{\displaystyle \frac{2S}{T}}$	0
velocity(${\displaystyle \frac{T}{2}}$)	$-{\displaystyle \frac{2S}{T}}$	0

, which are used to calculate the trajectory equations during the swing phase. The zero velocity on the z-direction can also eliminate the impulse when the feet touch the ground.

5.2. Swing Phase

During the swing phase, an energy efficient foot trajectory is proposed to decrease the joint energy consumption. To compare the energy consumption of the optimal foot trajectory, a foot trajectory reported by Meng et al. [39] is used as the reference foot trajectory.

5.2.1. Reference Foot Trajectory

To reduce the impact produced by the swing leg movements, the swing legs have to move with no abrupt changes on velocity. In order to make the robot have the ability to adapt to the slightly undulating ground, the endpoints of the swing legs would retreat a little when off the ground and before landing.

In order to meet the requirements, a foot trajectory planning method based on the cubic spline interpolation is used in the x-direction, and, for the foot lifting, the cosine curve is used. H is the step height:

$$\left\{\begin{array}{c}{x}_{sw,ref}(t)=\frac{S}{2}(-\frac{64t^3}{T^3}+\frac{144t^2}{T^2}-\frac{100t}{T}+21),\hfill \\ z_{sw,ref}(t)=H·\frac{1-cos\frac{4\pi t}{T}}{2}.\hfill \end{array}\right.$$

(55)

5.2.2. Energy Efficient Foot Trajectory

In the swing phase, the joint angular velocity is expressed by a Fourier series to describe all the possible motions [40]. In order to simplify the equation and reduce calculation time, only the first two cosine terms and first two sine terms as well as the constant term are considered:

$$\dot{\theta }=a_0+a_{1}sin(\frac{\pi t}{T})+b_{1}cos(\frac{\pi t}{T}),+a_{2}sin(\frac{2\pi t}{T})+b_{2}cos(\frac{2\pi t}{T}).$$

(56)

The joint position and joint acceleration can be obtained by integrating and differentiating Equation (56):

$$\theta =a_{0}t-\frac{a_{1}T}{\pi }cos(\frac{\pi t}{T})+\frac{b_{1}T}{\pi }sin(\frac{\pi t}{T})-\frac{a_{2}T}{2\pi }cos(\frac{2\pi t}{T})+\frac{b_{2}T}{2\pi }sin(\frac{2\pi t}{T})+C,$$

(57)

$$\ddot{\theta }=\frac{a_1\pi }{T}cos(\frac{\pi t}{T})-\frac{b_1\pi }{T}sin(\frac{\pi t}{T})+\frac{2a_2\pi }{T}cos(\frac{2\pi t}{T})-\frac{2b_2\pi }{T}sin(\frac{2\pi t}{T}).$$

(58)

In Equations (56)–(58), $a_0$, $a_1$, $a_2$, $b_1$ and $b_2$ are Fourier coefficients, C is the constant term.

To obtain the parameters’ value of the Fourier series, the four parameters in Table 3 are used. In addition, to ensure the obstacle crossing ability of the proposed foot trajectory, the foot endpoint needs to lift above the ground for some distances. Here, we assume the terrain clearance in the middle of the swing phase ($t=3T/4$) is $H_o$. The value of $H_o$ we use is numerically equal to the step height H.

According to the above analyses with Equations (56) and (57), the following equations can be acquired:

$$\left\{\begin{array}{c}\dot{\theta }(\frac{T}{2})={\dot{\theta }}_{T/2},\hfill \\ \dot{\theta }(T)={\dot{\theta }}_T,\hfill \\ \theta (\frac{T}{2})={\theta }_{T/2},\hfill \\ \theta (T)={\theta }_T,\hfill \\ \theta (\frac{3T}{4})={\theta }_{3T/4}.\hfill \end{array}\right.$$

(59)

In Equation (59), ${\theta }_{T/2}$, ${\theta }_T$ and ${\theta }_{3T/4}$ are the joint positions at t = $T/2$, t = T(t = 0) and t = $3T/4$. ${\dot{\theta }}_{T/2}$ and ${\dot{\theta }}_T$ are the joint angular velocities at t = $T/2$, t = T(t = 0) and can be acquired by the following equation:

$$\dot{\mathit{\theta }}={\mathit{J}}^{-1}\dot{\mathit{v}},$$

(60)

where $\dot{\mathit{v}}={[v_x,v_z]}^T={[-4S/T,0]}^T$, and the inverse matrix of the Jacobian J is presented as follows:

$${\mathit{J}}^{-1}=\frac{1}{-l_1{l}_{2}sin{\theta }_2}·\left[\begin{array}{cc}{l}_{2}sin{\theta }_{12}& l_{2}cos{\theta }_{12}\\ -l_{1}sin{\theta }_1-l_{2}sin{\theta }_{12}& -l_{1}cos{\theta }_1-l_{2}cos{\theta }_{12}\end{array}\right].$$

(61)

By solving Equation (59), the Fourier coefficients $a_0$, $a_1$, $a_2$, $b_1$ and $b_2$ can be represented by the constant C and the initial and terminated conditions of the stance phase in Table 3, which are shown in Appendix A. By changing the parameter C for both the pitching hip joint and pitching knee joint, different trajectories can be generated among the given points.

5.3. Energy Efficient Trajectory Generating Method

In order to reduce energy consumptions, the parameter C in Equation (57) needs to be acquired through an optimization method.

The selection of C is a typical unconstrained multidimensional minimum problem. Here, we choose the Pattern Search method (PS), namely the Hooke–Jeeves method. The method mainly consists of two moving processes, detection movement and mode movement. The detection movement is the movement along the direction of the coordinate axis, while the mode movement is the movement along the straight line between two adjacent detection points. The two moving modes alternate in order to follow the optimal direction of the function values.

Then, the objective function of this optimization problem can be written in Equation (62):

$$E(\theta )={\int }_0^T(|\tau \dot{\theta }|+f_f{\dot{x}}_p)dt.$$

(62)

The variables in this equation can be expressed in terms of joint position. The joint torque $\tau$, the hydraulic friction force $f_f$ and cylinder velocity ${\dot{x}}_p$ can be obtained by Equations (10), (51) and (53), respectively.

By using the PS method, the value of C can be obtained and the equations of foot trajectories are settled. To make sure the foot trajectories can work effectively on the robot, the mechanical position limitation needs to be calculated. The cylinder length ranges of different joints in different legs are all 240 mm to 338 mm. The range of the joint positions can be calculated using Equation (67), as shown in

Table 4. The joint position ranges of different joints.

Leg	Pitching Hip Joint	Pitching Knee Joint
RF/LF leg	−2.032 to 0.047 rad	0.491 to 2.570 rad
LH/RH leg	−0.047 to 2.032 rad	−2.570 to −0.491 rad

.

6. Simulations and Experiments

In this section, some simulations and experiments are conducted to verify the joint energy consumptions of the proposed foot trajectory.

According to the theoretical analyses in this work, the PS method is used in MATLAB (R2016a, Mathwork Co., Natick, MA, USA) to obtain trajectory parameters of different legs. The proposed trajectory is verified in simulation and experiments. The results of the energy efficient trajectory are compared with the reference trajectory. The flow chart of this work is illustrated in Figure 7.

6.1. MATLAB Simulation

In this section, the foot trajectory parameters need to be obtained through the PS method. Here, we set the gait cycle T as 0.5 s. The terrain clearance in the middle of the swing phase ($t=3T/4$) H is set as 0.08 m. To verify the proposed trajectory, the step length S is set as 0.25 m. Therefore, the speed of the robot can be obtained as 1.0 m/s. The duty cycles of the RF and LH foot trajectories are both 50%. The time duration of the stance phase and swing phase are both 0.25 s. The trunk of the robot can be regarded as a cuboid. The distances between the COM of the robot and rolling hip joint in x- and z-directions are 0.68 m and 0.15 m, respectively, which are used to confirm the position of the foot endpoints in the trunk coordinate frame $\left\{O_b\right\}$.

The parameters of the PS method are chosen as follows, acceleration coefficient $\gamma =1.4$, shrinkage coefficient $\beta =0.2$. The initial point and initial step are defined as (0,0) and (0.5,0.5) respectively. In order to improve the speed of the algorithm, the precision is chosen as 0.1.

The optimization processes of RF leg by using the PS method are shown in Figure 8. The variations of constants $C_1$, $C_2$ and the values of the objective function $E(\theta )$ during swing phases (different trajectories have same energy consumptions in stance phase) are illustrated. The optimal parameters of the RF leg are $C_1$ = −33.76, $C_2$ = 15.30, and the iteration number is 108.

The trajectory parameters of the LH leg can also be calculated and shown in

Table 5. The optimal parameters calculated by the Pattern Search method.

Leg	${\mathit{C}}_1$	${\mathit{C}}_2$	Iteration Number
RF leg	−33.76	15.30	108
LH leg	−29.58	−2.28	155

.

According to Table 5 and results in Appendix A, the foot trajectory equations of the joints during the swing phase can be obtained in Equations (63)–(66).

The pitching hip joint of the RF leg,

$${\theta }_{1RF}=83.46t+\frac{71.39T}{\pi }cos(\frac{\pi t}{T})+\frac{92.19T}{\pi }sin(\frac{\pi t}{T})+\frac{29.64T}{2\pi }cos(\frac{2\pi t}{T})+\frac{10.18T}{2\pi }sin(\frac{2\pi t}{T})-33.76.$$

(63)

The pitching knee joint of the RF leg,

$${\theta }_{2RF}=-25.91t-\frac{1.54T}{\pi }cos(\frac{\pi t}{T})-\frac{50.31T}{\pi }sin(\frac{\pi t}{T})-\frac{11.14T}{2\pi }cos(\frac{2\pi t}{T})-\frac{23.74T}{2\pi }sin(\frac{2\pi t}{T})+15.30.$$

(64)

The pitching hip joint of the LH leg,

$${\theta }_{1LH}=85.40t+\frac{94.28T}{\pi }cos(\frac{\pi t}{T})+\frac{73.17T}{\pi }sin(\frac{\pi t}{T})+\frac{30.47T}{2\pi }cos(\frac{2\pi t}{T})-\frac{10.18T}{2\pi }sin(\frac{2\pi t}{T})-29.58.$$

(65)

The pitching knee joint of the LH leg,

$${\theta }_{2LH}=-8.80t-\frac{33.22T}{\pi }cos(\frac{\pi t}{T})+\frac{15.62T}{\pi }sin(\frac{\pi t}{T})-\frac{3.78T}{2\pi }cos(\frac{2\pi t}{T})+\frac{23.74T}{2\pi }sin(\frac{2\pi t}{T})-2.28.$$

(66)

For the MATLAB simulation, the joint torques can be acquired according to the analyses of the foot force distribution. In this section, only the curves of the RF leg are illustrated. However, the energy consumption of the RF and LH legs are both obtained. The sample frequency of the MATLAB is 200 Hz. The joint positions and torques are illustrated in Figure 9 and Figure 10. The curves of the leg powers and foot trajectories can be obtained in Figure 11 and Figure 12.

The mean energy consumptions of 10 cycles in MATLAB are shown in

Table 6. The mean energy consumptions in MATLAB.

Trajectory	Leg	Stance Phase	Swing Phase	Total Energy
Reference	RF leg	56.86 J	28.18 J	85.04 J
	LH leg	55.03 J	27.81 J	82.84 J
Proposed	RF leg	56.98 J	20.78 J	77.76 J
	LH leg	55.24 J	21.42 J	76.66 J

. For the RF leg, the energy consumption during swing phase and whole cycle are decrease by 26.26% and 8.56%. For the LH leg, the decrements are 22.98% and 7.46% respectively. The other two legs have same structure and mechanical parameters as the RF and LH legs, hence the energy consumptions are same. The total consumption is decreased by 8.02% and the average total leg power in one cycle is reduced from 671.52 W to 617.68 W.

6.2. Experiments on the SCalf Robot

The SCalf robot adopts the centralized control system, and all of the motion plannings and servo controls are completed by the cRIO-9039 controller from the National Instruments corporation (Austin, TX, USA). The controller can record the sensor data with a frequency of 80 Hz. The displacement and force sensors mounted on the cylinders can be used to measure the cylinder lengths and joint forces, respectively. In order to obtained the data of the joint positions and torques, transitions need to be made. Here, we still use the RF leg as an example.

For joint calculations, the parameters in Equations (67) and (68) are illustrated in Figure 6. The joint positions can be acquired by the cylinder lengths:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\theta }_1=\frac{\pi }{2}-arccos(\frac{a_1^2+b_1^2-c_1^2}{2a_1{b}_1})-e_1-e_2,\hfill \\ {\theta }_2=\pi -arccos(\frac{a_2^2+b_2^2-c_2^2}{2a_2{b}_2})-e_3+e_4.\hfill \end{array}\right.\end{array}$$

(67)

The torques are equal to the forces multiplied by their force arms, where i = 1, 2:

$${\tau }_i=f_i·a_i\sqrt{1-{(\frac{a_i^2+c_i^2-b_1^2}{2a_i{c}_i})}^2}.$$

(68)

The foot force distribution algorithm is verified in the prototype experiment. The curve of real foot force is compared with the simulation as in Figure 13. During the stance phase, the foot force is increased dramatically and fluctuates around half of the trunk weight (980N).

The reference and proposed trajectories are tested on the SCalf. With the data of sensors, the joint positions and torques can be calculated by the above two equations and are shown in Figure 14 and Figure 15. The curve of the leg powers and foot trajectories can also be acquired in Figure 16 and Figure 17. The mean energy consumptions of five gait cycles in experiments are shown in

Table 7. The mean energy consumptions in physical experiments.

Trajectory	Leg	Stance Phase	Swing Phase	Total Energy
Reference	RF leg	42.50 J	29.46 J	71.96 J
	LH leg	39.46 J	28.57 J	68.03 J
Proposed	RF leg	39.48 J	26.86 J	66.34 J
	LH leg	38.17 J	24.91 J	63.08 J

.

Based on Table 7, the energy consumptions of the RF leg during the swing phase and whole cycle have dropped by 8.82% and 7.82%. For the LH leg, the decrements become 12.80% and 7.27%, respectively. The decrement of the total energy is 7.55%. The average total power in one cycle is decreased from 559.96 W to 517.68 W.

The energy efficient trajectory curve is plotted in Figure 18. Figure 18a shows the discrete snapshots of the foot, and, when putting these snapshots together, the full trajectory is obtained in Figure 18b.

6.3. Discussion

In the precondition (b) of Section II, the height of the robot trunk is regarded as constant and the acceleration along the z-axis is considered as zero. Actual changes of the trunk height above the ground is hard to measure by existed sensors. Therefore, the data in Webots are used. Webots is a robot simulator that provides a complete development environment to model, program and simulate robots [41]. A GPS is mounted on the robot trunk to record the trunk height in Webots. In Figure 19, the height and acceleration of the trunk COM along the z-axis are illustrated. Based on the results, the biggest fluctuation of the height and acceleration are 0.004 m and $1.2\times {10}^{-4}$ m/s${}^2$, respectively, and the precondition (b) is proved to be valid.

Figure 20 shows the comparison of the joint positions of MATLAB (given values) and physical experiment by using the energy efficient trajectory. In order to see the variations clearly, the joint position curves are plotted separately. It is shown that the physical prototype can track the given trajectory effectively. In addition, the joint positions in MATLAB and experiments are within the ranges in Table 4.

By comparing Figure 10 and Figure 15, we can find that the change trends of different torque data are similar. During the stance phase, the legs need to support the weight of the trunk. Therefore, the joint torques in stance phase are much higher than in the swing phase, especially for the pitching knee joints.

The energy consumption results of different foot trajectories in simulations and experiments are illustrated in Table 6 and Table 7. By using the energy efficient foot trajectory, the total joint energy consumptions in simulations and experiments are dropped by 8.02% and 7.55%. The advantages of the proposed trajectory are mainly reflected in the swing phase. During the swing phase, the decrements become to 28.02% and 10.81%. The data in Table 6 and Table 7 are close, which means the models proposed in this work can be proved by the experiment results. However, there are still some differences between the results of the simulation and experiment, especially for the data during the stance phase, which are caused by different foot force distributions.

7. Conclusions

In this work, an energy efficient foot trajectory based on the Fourier series for a hydraulic actuated quadruped robot was proposed. First, the kinematics model, dynamics model and foot force distribution of the robot were analysed. Then, a detailed joint energy model of the hydraulic actuated quadruped robot including mechanical power and heat rate was derived. According to the energy model, a energy efficient trajectory is obtained based on the Fourier series, and the coefficients of the proposed trajectory are obtained by using the Pattern Search method. The energy consumptions of the proposed trajectory were compared with a reference trajectory which is based on the cubic spline interpolation.

An obvious decline of the energy consumption can be seen with the energy efficient trajectory. The total joint energy consumptions in simulation and experiment are dropped by 8.02% and 7.55%. The average power of the physical prototype is decreased from 559.96 W to 517.68 W. In addition, the terrain clearance in the middle of the swing phase makes the proposed trajectory have a certain obstacle crossing ability. Through the results of computer simulation and physical experiment, the effectiveness of the energy efficient trajectory for the hydraulic actuated quadruped robots can be proved.