Impedance Modeling and Stability Analysis of the Converters in a Double-Fed Induction Generator (DFIG)-Based System

Chen, Xunjun; Liu, Zhigang

doi:10.3390/en12132500

Open AccessArticle

Impedance Modeling and Stability Analysis of the Converters in a Double-Fed Induction Generator (DFIG)-Based System

by

Xunjun Chen

and

Zhigang Liu

^*

School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China

^*

Author to whom correspondence should be addressed.

Energies 2019, 12(13), 2500; https://doi.org/10.3390/en12132500

Submission received: 12 June 2019 / Revised: 24 June 2019 / Accepted: 26 June 2019 / Published: 28 June 2019

(This article belongs to the Special Issue Modern Power System Dynamics, Stability and Control)

Download

Browse Figures

Versions Notes

Abstract

:

Harmonic stability of double-fed induction generators (DFIGs) now has become a significant topic because of its harmful impact on power quality issues of the system. Since the double pulse width modulation (PWM) converter is one of the main harmonic sources in DFIGs, it may cause harmonic instability with increasing harmonic contents. Thus, the modeling and stability analyses of PWM converters in DFIGs are essential steps to assess the harmonic stability of DFIGs. Aiming at dual PWM converters, which include the grid side converter (GSC) and the rotor side converter (RSC), this paper divides converters into two parts: circuit modules and control modules. Closed-loop input impedance models of each module are then derived by means of transfer functions. Hence, the stability of the system can be readily predicted through Nyquist diagrams. The contributions of parameters to the system’s harmonic stability are also identified. Finally, time-domain simulations are conducted in a real-time digital simulation (RTDS) system. Simulation results confirm that the established impedance model can effectively reveal the stability of the DFIG-based system and can give critical conditions for the occurrence of harmonic instability.

Keywords:

DFIG; PWM converter; impedance modeling; harmonic instability; RTDS

1. Introduction

When it comes to wind power generation, a double-fed induction generator (DFIG) is a more advanced and ideal technology in wind generation development. Compared with other wind generators, DFIGs have many advantages in performance such as their good stability when they are connected to the grid and their decoupled control of active and reactive power [1,2,3]. These advantages are based on double pulse width modulation (PWM) converters, which are widely used in DFIG systems for their independent control of reactive power at both sides. However, double PWM converters are the main harmonic sources in DFIGs and will inject a large number of harmonics into the grid current, causing voltage fluctuation and distortions in the system [4,5]. With increasing harmonic currents, the system faces great challenges in power quality and stability issues [6].

In recent years, the proportion of DFIGs in wind power systems has vividly increased due to the rapid development of renewable power sources. As a consequence, the converter harmonic stability is becoming an important issue that must be solved. In order to analyze the stability of a DFIG-based system, two effective system-level methods have been proposed for stability analyses: a time-domain eigenvalue analysis based on the state-space model and an impedance-based analysis based on the transfer functions in the frequency domain [7,8,9,10,11,12,13]. The eigenvalue analysis usually involves the derivation of system matrices, which leads to high computational complexity in modeling the system. Different from an eigenvalue analysis approach, an impedance-based analysis can easily assess system stability without prior knowledge of system parameters. This allows the modeling of converters to turn into black-box modeling, and this practice will significantly improve modeling efficiency. What is more, an impedance-based approach can capture converter terminal dynamics at the point of connection (PoC) and then translate them into an impedance representation [14]. So, because of the easy access to converter terminal dynamics and the high modeling efficiency, the impedance-based analysis is applied for rotor side converter (RSC) and grid side converter (GSC) impedance modeling, and the equivalent closed-loop impedance of a DFIG-based system is given in this paper.

The impedance-based analysis is first developed for a dc power system and then expanded to a three-phase ac system [15]. An impedance model based on transfer functions of inverters in a three-phase power system was developed [16,17,18,19]. In [16,17], the parallel grid-connected converter filter system was established by impedance modeling to study the harmonic resonances and dynamics of converters. In [18], the general impedance model of converter terminals at the LCL filter was derived to analyze the harmonic instability of wind farms. Xiao and Gole [19] derived a macro impedance model and analyzed the dynamics of converters at the ac side by using frequency scanning; however, this macro model did not reveal detailed contributions of each parameter to the system’s harmonic stability. The difficulty of modeling RSC and GSC in DFIGs is their different control strategies and the detailed power flow interactions between them [20]. However, previous works and papers lacked focus on the macro modeling of DFIGs, which is useful for system-level analyses. Moreover, detailed converter modeling that includes control systems with the phase lock loop (PLL) is often overlooked; thus, specific parametric influences on harmonic stability cannot be predicted.

In order to fill this gap, this paper attempts to utilize an impedance-based approach in DFIG-based systems and formulate detailed models of RSC and GSC with means of transfer functions. Thus, harmonic stability of a DFIG-based system can be readily assessed. Figure 1 depicts the modeling and analysis procedures in this paper. Impedance modeling procedures of RSC and GSC can be respectively divided into two parts, where detailed small-signal models of main circuits and control systems with PLL are formulated as transfer functions. The closed-loop impedance of the whole DFIG-based system then can be obtained considering the electrical relationship between dc variables and power grid parameters. At last, Nyquist stability criteria are applied to analyze the stability of the system, and a real-time digital simulation (RTDS) is used to verify the theoretical analysis.

The rest of this paper is organized as follows: In Section 2 and Section 3 the small-signal models of RSC and GSC in DFIG are derived by means of transfer functions. In Section 4, equivalent systems of DFIG and closed-loop impedance are obtained, and then RTDS simulations are conducted to verify the impedance model. In the last part, results of the whole impedance modeling and the analysis of stability are summarized.

2. Small-Signal Modeling of the Rotor Side Convertor (RSC) in the Double-Fed Induction Generator (DFIG)

Figure 2 gives the general architecture of the DFIG-based system, where RSC is connected to the power grid via motors, and GSC is directly connected to the power grid [21]. The structure diagram of RSC is given in Figure 3. According to Figure 1, the small-signal models of RSC, including the main circuit and the control system with PLL, will be derived in this section.

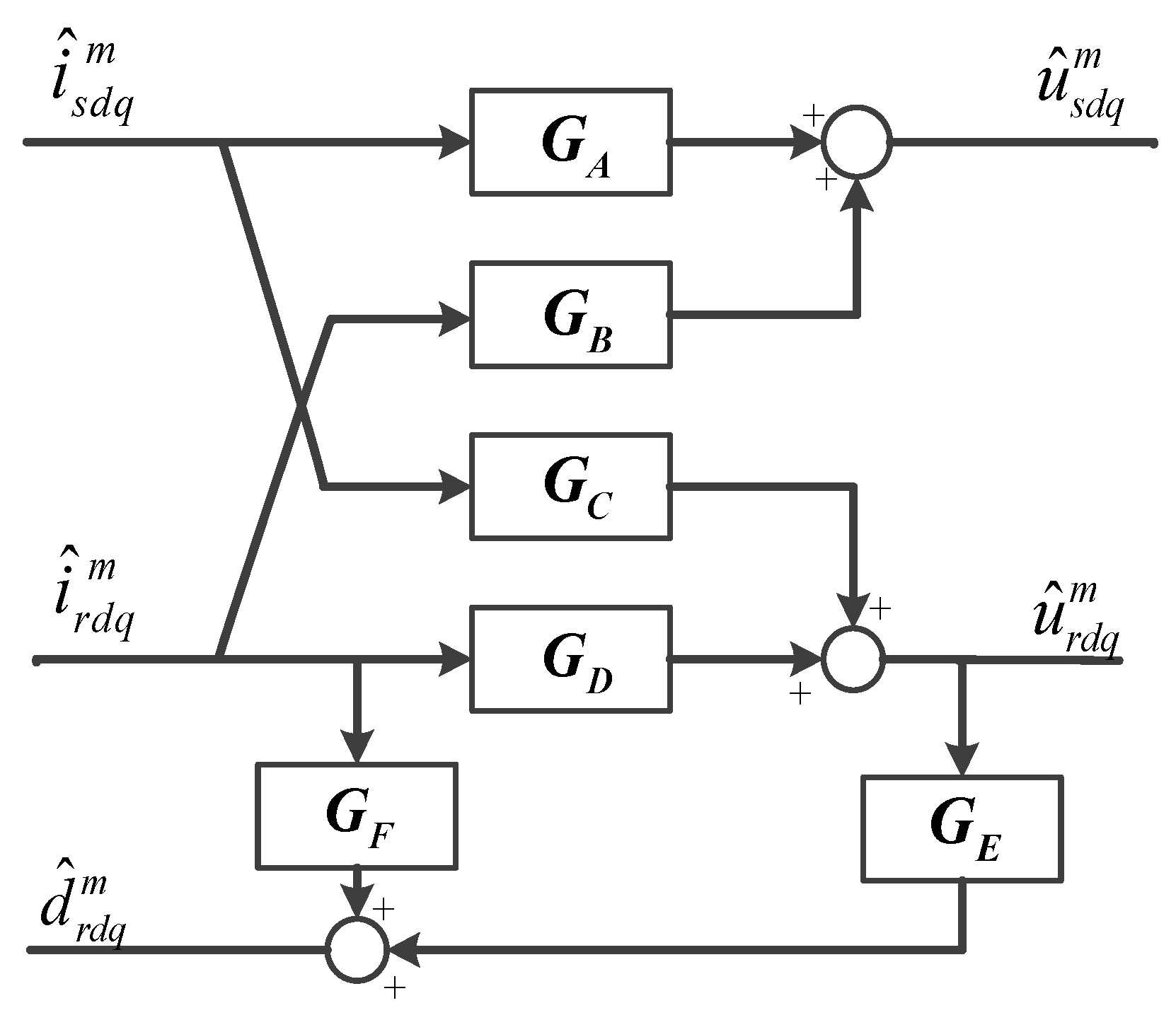
2.1. Small-Signal Modeling of the RSC Circuit

From Figure 3, the electromagnetic equation of the rotor and stator in DFIG in the dq frame can be given by:

{\begin{cases} u_{s d}^{} = - R_{s m} i_{s d} + \frac{d ψ_{s d}}{d t} - ω_{1} ψ_{s q} \\ u_{s q}^{} = - R_{s m} i_{s q} + \frac{d ψ_{s q}}{d t} + ω_{1} ψ_{s d} \\ u_{r d} = R_{r m} i_{r d} + \frac{d ψ_{r d}}{d t} - ω_{s l i p} ψ_{r q} \\ u_{r q} = R_{r m} i_{r q} + \frac{d ψ_{r q}}{d t} + ω_{s l i p} ψ_{r d} \end{cases}

(1)

where

u_{s d}

and

u_{s q}

, respectively, mean the dq axis stator voltages;

u_{r d}

and

u_{r q}

, respectively, mean the dq axis rotor voltages;

R_{s m}

and

R_{r m}

respectively mean the stator resistance and the rotor resistance;

i_{s d, q}

means dq axis stator currents; and

i_{r d, q}

means dq axis rotor currents.

ψ_{s d}

and

ψ_{s q}

are the stator flux vectors in the dq axis.

ψ_{r d}

and

ψ_{s q}

are the rotor flux vectors in the dq axis;

ω_{s l i p} = ω_{1} - ω_{r}

.

In fact, the equation of flux in Equation (1) is given as:

{\begin{cases} ψ_{s d} = - L_{s m} i_{s d} + L_{m} i_{r d} \\ ψ_{s q} = - L_{s m} i_{s q} + L_{m} i_{r q} \\ ψ_{r d} = - L_{m} i_{s d} + L_{r m} i_{r d} \\ ψ_{r q} = - L_{m} i_{s q} + L_{r m} i_{r q} \end{cases}

(2)

where

L_{s m}

is the self-inductance of the stator,

L_{r m}

is the self-inductance of the rotor, and

L_{m}

is the mutual inductance.

Using Equation (2) in Equation (1), the small-signal transfer function from currents and voltages can be obtained. The superscript and subscript

{\hat{x}}^{m}

means small-signal variables in the main circuit, and the subscript

x_{s, r, g}

represents the variables of the stator, rotor, and grid, respectively.

\begin{array}{l} [\begin{array}{l} {\hat{u}}_{s d}^{m} \\ {\hat{u}}_{s q}^{m} \\ {\hat{u}}_{r d}^{m} \\ {\hat{u}}_{r q}^{m} \end{array}] & = [\begin{array}{l} - R_{s m} - s L_{s m} ω_{1} L_{s m} s L_{m} - ω_{1} L_{m} \\ - ω_{1} L_{s m} - R_{s m} - s L_{s m} ω_{1} L_{m} s L_{m} \\ - s L_{m} ω_{s l i p} L_{m} R_{r} + ​ ​ ​ s L_{r m} - ω_{s l i p} L_{r m} \\ - ω_{s l i p} L_{m} - s L_{m} ω_{s l i p} L_{r m} R_{r} + s L_{r m} \end{array}] [\begin{array}{l} {\hat{i}}_{s d}^{m} \\ {\hat{i}}_{s q}^{m} \\ {\hat{i}}_{r d}^{m} \\ {\hat{i}}_{r q}^{m} \end{array}] \\ = [\begin{array}{l} Z_{s s d d} Z_{s s d q} Z_{s r d d} Z_{s r d q} \\ Z_{s s q d} Z_{s s q q} Z_{s r q d} Z_{s r q q} \\ Z_{r s d d} Z_{r s d q} Z_{r r d d} Z_{r r d q} \\ Z_{r s q d} Z_{r s q q} Z_{r r q d} Z_{r r q q} \end{array}] [\begin{array}{l} {\hat{i}}_{s d}^{m} \\ {\hat{i}}_{s q}^{m} \\ {\hat{i}}_{r d}^{m} \\ {\hat{i}}_{r q}^{m} \end{array}] \\ = [\begin{matrix} G_{A} & G_{B} \\ G_{C} & G_{D} \end{matrix}] [\begin{array}{l} {\hat{i}}_{s d}^{m} \\ {\hat{i}}_{s q}^{m} \\ {\hat{i}}_{r d}^{m} \\ {\hat{i}}_{r q}^{m} \end{array}] \end{array}

(3)

The transfer function matrixes from rotor and stator currents to rotor and stator voltages are defined in Equation (4), where

G_{A}

means the module transfer function from stator currents to stator voltages,

G_{B}

means the module transfer function from rotor currents to stator voltages,

G_{C}

means the module transfer function from stator currents to rotor voltages, and

G_{D}

is the module transfer function from rotor currents to rotor voltages.

\begin{array}{l} G_{A} = [\begin{array}{l} Z_{s s d d} Z_{s s d q} \\ Z_{s s q d} Z_{s s q q} \end{array}] \begin{matrix} , & G_{B} = [\begin{array}{l} Z_{s r d d} Z_{s r d q} \\ Z_{s r q d} Z_{s r q q} \end{array}] \end{matrix} \\ G_{C} = [\begin{array}{l} Z_{r s d d} Z_{r s d q} \\ Z_{r s q d} Z_{r s q q} \end{array}] \begin{matrix} , & G_{D} = [\begin{array}{l} Z_{r r d d} Z_{r r d q} \\ Z_{r r q d} Z_{r r q q} \end{array}] \end{matrix} \end{array}

(4)

The structure diagram of RSC is shown in Figure 4. From this diagram, the relationship between the DC voltage and rotor voltages can be given as:

{\begin{cases} u_{c d}^{} = u_{r d} + R_{r} i_{r d} + L_{r} \frac{d i_{r d}}{d t} - ω_{s l i p} L_{r} i_{r q} \\ u_{c q}^{} = u_{r q} + R_{r} i_{r q} + L_{r} \frac{d i_{r q}}{d t} + ω_{s l i p} L_{r} i_{r d} \end{cases}

(5)

Hence, the small-signal model between DC voltage and rotor voltage can be obtained from Equation (5) as:

{\begin{cases} {\hat{d}}_{r d}^{m} U_{d c} = {\hat{u}}_{r d}^{m} + R_{r} {\hat{i}}_{r d}^{m} + s L_{r} {\hat{i}}_{r d}^{m} - ω_{s l i p} L_{r} {\hat{i}}_{r q}^{m} \\ {\hat{d}}_{r q}^{m} U_{d c} = {\hat{u}}_{r q}^{m} + R_{r} {\hat{i}}_{r q}^{m} + s L_{r} {\hat{i}}_{r q}^{m} + ω_{s l i p} L_{r} {\hat{i}}_{r d}^{m} \end{cases}

(6)

Reorganizing Equation (6) in the form of matrixes, the small-signal model of the RSC main circuit can be written as:

A [\begin{array}{l} {\hat{i}}_{r d}^{m} \\ {\hat{i}}_{r q}^{m} \\ {\hat{d}}_{r d}^{m} \\ {\hat{d}}_{r q}^{m} \end{array}] = B [\begin{array}{l} {\hat{u}}_{r d}^{m} \\ {\hat{u}}_{r q}^{m} \end{array}] \begin{matrix} , & C [\begin{array}{l} {\hat{u}}_{r d}^{m} \\ {\hat{u}}_{r q}^{m} \\ {\hat{d}}_{r d}^{m} \\ {\hat{d}}_{r q}^{m} \end{array}] = D [\begin{array}{l} {\hat{i}}_{r d}^{m} \\ {\hat{i}}_{r q}^{m} \end{array}] \end{matrix},

(7)

where

A = [\begin{matrix} R_{r} + s L_{r} & - ω_{s l i p} L_{r} & - U_{d c} & 0 \\ ω_{s l i p} L_{r} & R_{r} + s L_{r} & 0 & - U_{d c} \end{matrix}] \begin{matrix} , & B \end{matrix} = [\begin{matrix} - 1 & 0 \\ 0 & - 1 \end{matrix}]

(8)

C = [\begin{matrix} 1 & 0 & - U_{d c} & 0 \\ 0 & 1 & 0 & - U_{d c} \end{matrix}] \begin{matrix} , & D = \end{matrix} [\begin{matrix} - R_{r} - s L_{r} & ω_{s l i p} L_{r} \\ - ω_{s l i p} L_{r} & - R_{r} - s L_{r} \end{matrix}]

(9)

Hence, using Equations (7), (8) and (9), the small-signal transfer relationship between the rotor side variables and the duty cycle can be written as:

{\begin{cases} G_{E} = [0 0 1 1] A^{- 1} B \\ G_{F} = [0 0 1 1] C^{- 1} D \end{cases},

(10)

where

G_{E}

and

G_{F}

are transfer functions from the rotor voltage to the duty cycle and the rotor current to the duty cycle, respectively. And then, combining the transfer functions in Equations (4) and (10), the diagram of the small-signal transfer model of the RSC circuit is given as shown in Figure 5.

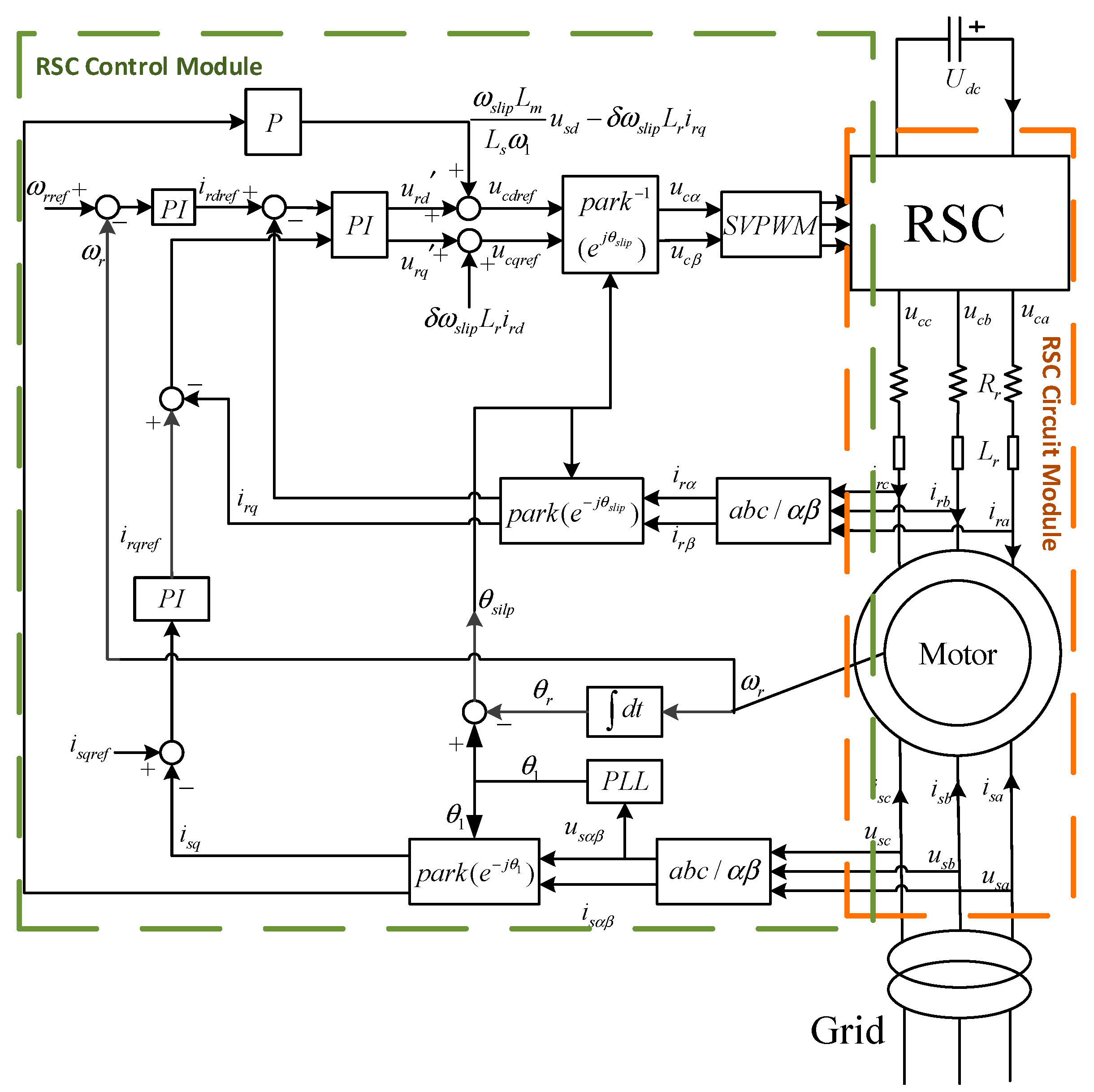
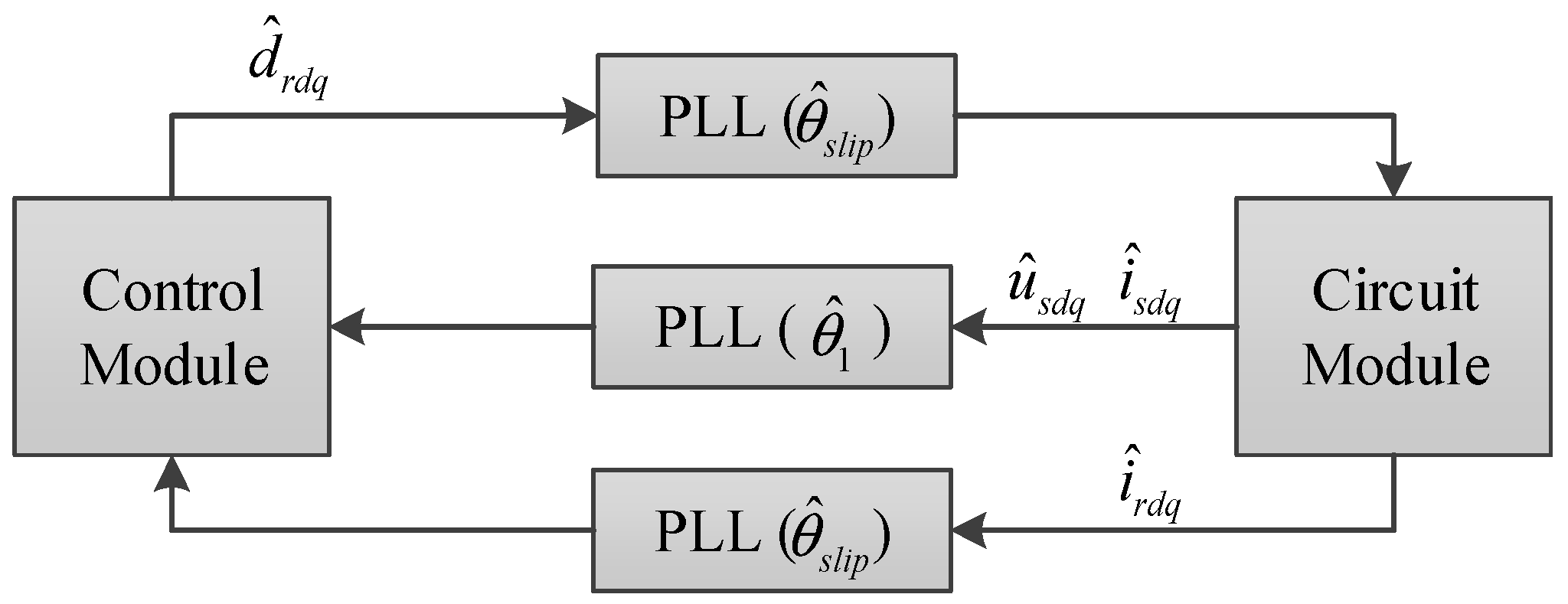
2.2. Small-Signal Modeling of RSC Control with PLL

The RSC control in DFIG is designed for balancing the speed of motors, which fluctuates when the wind speed is changing. According to Figure 1 and Figure 3, the control system of RSC is a dual closed-loop control, which includes the inner current controller and the outer speed controller [22], and then its current control equation and speed control equation can be given as:

{\begin{cases} u_{r d r e f}^{} = (k_{i r P} + \frac{k_{i r I}}{s}) (i_{r d r e f} - i_{r d}) - δ ω_{s l i p} L_{r} i_{r q} + \frac{ω_{s l i p} L_{m}}{L_{s} ω_{1}} u_{s d} \\ u_{r q r e f}^{} = (k_{i r P} + \frac{k_{i r I}}{s}) (i_{r q r e f} - i_{r q}) u_{r q} + δ ω_{s l i p} L_{r} i_{r d} \end{cases};

(11)

{\begin{cases} i_{r d}^{} = (k_{ω r P} + \frac{k_{ω r I}}{s}) (ω_{r r e f} - ω_{r}) \\ i_{r q}^{} = (k_{i s P} + \frac{k_{i s I}}{s}) (i_{s d r e f} - i_{s d}) \end{cases};

(12)

where

u_{r d r e f}

and

u_{r q r e f}

are the reference dq rotor voltages;

i_{r d r e f}

and

i_{r q r e f}

are the reference dq rotor currents;

k_{i r P}

and

k_{i r I}

are, respectively, proportional (P) and integral (I) coefficients of the inner rotor current control;

k_{ω r P}

and

k_{ω r I}

represent P and I coefficients of the outer rotor speed controller, respectively;

k_{i s P}

and

k_{i s I}

are P and I coefficients of the outer stator current controller, respectively; and

δ

is the magnetic flux leakage (MFL) coefficient of DFIG,

δ = 1 - L_{m}^{2} / (L_{s} L_{r m})

.

Hence, using Equations (11) and (12), the small-signal transfer functions of RSC control can be obtained. The superscript and subscript

{\hat{x}}^{c}

means small-signal variables in the control system.

[\begin{array}{l} {\hat{u}}_{r d r e f}^{c} \\ {\hat{u}}_{r q r e f}^{c} \end{array}] = G_{i r P I} [\begin{array}{l} {\hat{i}}_{r d r e f}^{c} - {\hat{i}}_{r d}^{c} \\ {\hat{i}}_{r q r e f}^{c} - {\hat{i}}_{r q}^{c} \end{array}] + G_{I} [\begin{array}{l} {\hat{i}}_{r d}^{c} \\ {\hat{i}}_{r q}^{c} \end{array}] + G_{r s} [\begin{array}{l} {\hat{u}}_{s d}^{c} \\ {\hat{u}}_{s q}^{c} \end{array}];

(13)

[\begin{array}{l} {\hat{i}}_{r d r e f}^{c} \\ {\hat{i}}_{r q r e f}^{c} \end{array}] = G_{ω r P I} {\hat{ω}}_{r} + G_{i s} [\begin{array}{l} {\hat{i}}_{s d}^{c} \\ {\hat{i}}_{s q}^{c} \end{array}];

(14)

where

G_{i r P I} = [\begin{matrix} k_{i r P} + \frac{k_{i r I}}{s} & 0 \\ 0 & k_{i r P} + \frac{k_{i r I}}{s} \end{matrix}] \begin{matrix} , & G_{I} = \end{matrix} [\begin{matrix} 0 & - δ ω_{s l i p} L_{r} \\ δ ω_{s l i p} L_{r} & 0 \end{matrix}] \begin{matrix} , & G_{r s} = [\begin{array}{l} \frac{ω_{s l i p} L_{m}}{L_{s} ω_{1}} 0 \\ 0 0 \end{array}] \end{matrix}

(15)

G_{ω r P I} = [\begin{array}{l} - k_{ω r P} - \frac{k_{ω r I}}{s} \\ 0 \end{array}] \begin{matrix} , & G_{is} = [\begin{array}{l} 0 0 \\ - k_{i s P} - \frac{k_{i s I}}{s} 0 \end{array}] \end{matrix}

(16)

By using Equations (13)–(16), the control diagram of RSC can be obtained as shown in Figure 6. And according to Figure 3, the Park transformation in PLL covers three angular variables in the RSC control module. These variables are the rotor speed angle

θ_{r}

, the system phase angle

θ_{1}

, and the deviation between the previous angles, the slip angle

θ_{s l i p}

.

In order to obtain the model considering PLL small-signal perturbations, the electromagnetic torque equation of DFIG needs to be given.

T_{e} = n_{p} L_{m} (i_{s d} i_{r q} - i_{s q} i_{r d}) .

(17)

Combining Equations (2) and (17), the electromagnetic torque can be written as:

T_{e} = - \frac{n_{p} L_{m} U_{s}}{L_{s} ω_{1}} i_{r d}

(18)

Then, with the mechanical dynamic of wind turbines in Equation (19), the small-signal model of the rotor speed angle can be obtained in Equation (20). Also, with the same method, the small-signal model of the system phase angle through PLL can be obtained in Equation (21).

T_{m e c h} - T_{e} = \frac{J}{n_{p}} \frac{d ω_{r}}{d t};

(19)

{\hat{θ}}_{r} = \frac{n_{p}}{s^{2} J} \frac{n_{p} L_{m} U_{s}}{L_{s} ω_{1}} {\hat{i}}_{r d}^{m};

(20)

{\hat{θ}}_{1} = \frac{k_{r p p l l} + \frac{k_{r i p l l}}{s}}{s + (k_{r p p l l} + \frac{k_{r i p l l}}{s}) E_{r d}} {\hat{u}}_{s q}^{m};

(21)

where

J

is the turbine moment of inertia.

Then according to the mathematical relationship in Figure 3 and the transfer path shown in Figure 7, the small-signal transfer model with PLL from the RSC circuit module to the RSC control module can be written as:

\begin{array}{l} [\begin{matrix} {\hat{i}}_{r d}^{c} \\ {\hat{i}}_{r q}^{c} \end{matrix}] & = [\begin{array}{l} 1 - \frac{n_{p}}{s^{2} J} \frac{n_{p} L_{m} U_{s}}{L_{s} ω_{1}} I_{r q}^{m} 0 \\ \frac{n_{p}}{s^{2} J} \frac{n_{p} L_{m} U_{s}}{L_{s} ω_{1}} I_{r d}^{m} 1 \end{array}] [\begin{array}{l} {\hat{i}}_{r d}^{m} \\ {\hat{i}}_{r q}^{m} \end{array}] + [\begin{array}{l} 0 \frac{I_{r q}^{m} (k_{p p l l} + \frac{k_{i p l l}}{s})}{s + (k_{p p l l} + \frac{k_{i p l l}}{s}) E_{r d}} \\ 0 - \frac{I_{r d}^{m} (k_{p p l l} + \frac{k_{i p l l}}{s})}{s + (k_{p p l l} + \frac{k_{i p l l}}{s}) E_{r d}} \end{array}] [\begin{array}{l} {\hat{u}}_{s d}^{m} \\ {\hat{u}}_{s q}^{m} \end{array}] \\ = G_{P L L i} [\begin{array}{l} {\hat{i}}_{r d}^{m} \\ {\hat{i}}_{r q}^{m} \end{array}] + G_{P L L 1} [\begin{array}{l} {\hat{u}}_{s d}^{m} \\ {\hat{u}}_{s q}^{m} \end{array}] \end{array}

(22)

Similarly, the small-signal transfer model of the duty cycle in RSC from the circuit module to the control module through PLL and that of stator voltages and currents through PLL can also be obtained.

\begin{array}{l} [\begin{matrix} {\hat{d}}_{r d}^{m} \\ {\hat{d}}_{r q}^{m} \end{matrix}] & = [\begin{matrix} {\hat{d}}_{r d}^{c} \\ {\hat{d}}_{r q}^{c} \end{matrix}] + [\begin{array}{l} 0 - \frac{k_{r p p l l} + \frac{k_{r i p l l}}{s}}{s + (k_{r p p l l} + \frac{k_{r i p l l}}{s}) E_{r d}} D_{r q}^{m} \\ 0 \frac{k_{r p p l l} + \frac{k_{r i p l l}}{s}}{s + (k_{r p p l l} + \frac{k_{r i p l l}}{s}) E_{r d}} D_{r d}^{m} \end{array}] [\begin{array}{l} {\hat{u}}_{s d}^{m} \\ {\hat{u}}_{s q}^{m} \end{array}] + [\begin{array}{l} \frac{n_{p}}{s^{2} J} \frac{n_{p} L_{m} U_{s}}{L_{s} ω_{1}} D_{r q}^{m} 0 \\ - \frac{n_{p}}{s^{2} J} \frac{n_{p} L_{m} U_{s}}{L_{s} ω_{1}} D_{r d}^{m} 0 \end{array}] [\begin{array}{l} {\hat{i}}_{r d}^{m} \\ {\hat{i}}_{r q}^{m} \end{array}] \\ = [\begin{matrix} {\hat{d}}_{r d}^{c} \\ {\hat{d}}_{r q}^{c} \end{matrix}] + G_{P L L 3} [\begin{array}{l} {\hat{u}}_{s d}^{m} \\ {\hat{u}}_{s q}^{m} \end{array}] + G_{P L L 2} [\begin{array}{l} {\hat{i}}_{r d}^{m} \\ {\hat{i}}_{r q}^{m} \end{array}] \end{array}

(23)

[\begin{matrix} {\hat{u}}_{s d}^{c} \\ {\hat{u}}_{s q}^{c} \end{matrix}] = [\begin{array}{l} 1 \frac{k_{r p p l l} + \frac{k_{r i p l l}}{s}}{s + (k_{r p p l l} + \frac{k_{r i p l l}}{s}) E_{r d}} E_{r q}^{m} \\ 0 1 - \frac{k_{r p p l l} + \frac{k_{r i p l l}}{s}}{s + (k_{r p p l l} + \frac{k_{r i p l l}}{s}) E_{r d}} E_{r d}^{m} \end{array}] [\begin{array}{l} {\hat{u}}_{s d}^{m} \\ {\hat{u}}_{s q}^{m} \end{array}] = G_{P L L u} [\begin{array}{l} {\hat{u}}_{s d}^{m} \\ {\hat{u}}_{s q}^{m} \end{array}]

(24)

[\begin{matrix} {\hat{i}}_{s d}^{c} \\ {\hat{i}}_{s q}^{c} \end{matrix}] = [\begin{array}{l} {\hat{i}}_{s d}^{m} + I_{s q}^{m} \frac{k_{r p p l l} + \frac{k_{r i p l l}}{s}}{s + (k_{r p p l l} + \frac{k_{r i p l l}}{s}) E_{r d}} {\hat{u}}_{s q}^{m} \\ {\hat{i}}_{s q}^{m} - I_{s d}^{m} \frac{k_{r p p l l} + \frac{k_{r i p l l}}{s}}{s + (k_{r p p l l} + \frac{k_{r i p l l}}{s}) E_{r d}} {\hat{u}}_{s q}^{m} \end{array}] = [\begin{matrix} {\hat{i}}_{s d}^{m} \\ {\hat{i}}_{s q}^{m} \end{matrix}] + G_{P L L 4} [\begin{array}{l} {\hat{u}}_{s d}^{m} \\ {\hat{u}}_{s q}^{m} \end{array}]

(25)

Hence, using Equations (22)–(25), the transfer diagram of RSC control with PLL can be obtained in Figure 8.

3. Small-Signal Modeling of the Grid Side Convertor (GSC) in DFIG

Similar to the modeling procedures of RSC in Section 2, the small-signal model of GSC in Figure 1 can also be divided into two parts: the main circuit module and the control module. However, the model of GSC must take the dc variables into account because the control strategy of GSC contains the outer voltage control loop where dc variables are in the dc link. Figure 9 depicts the structure diagram of GSC including the main circuit and the control system.

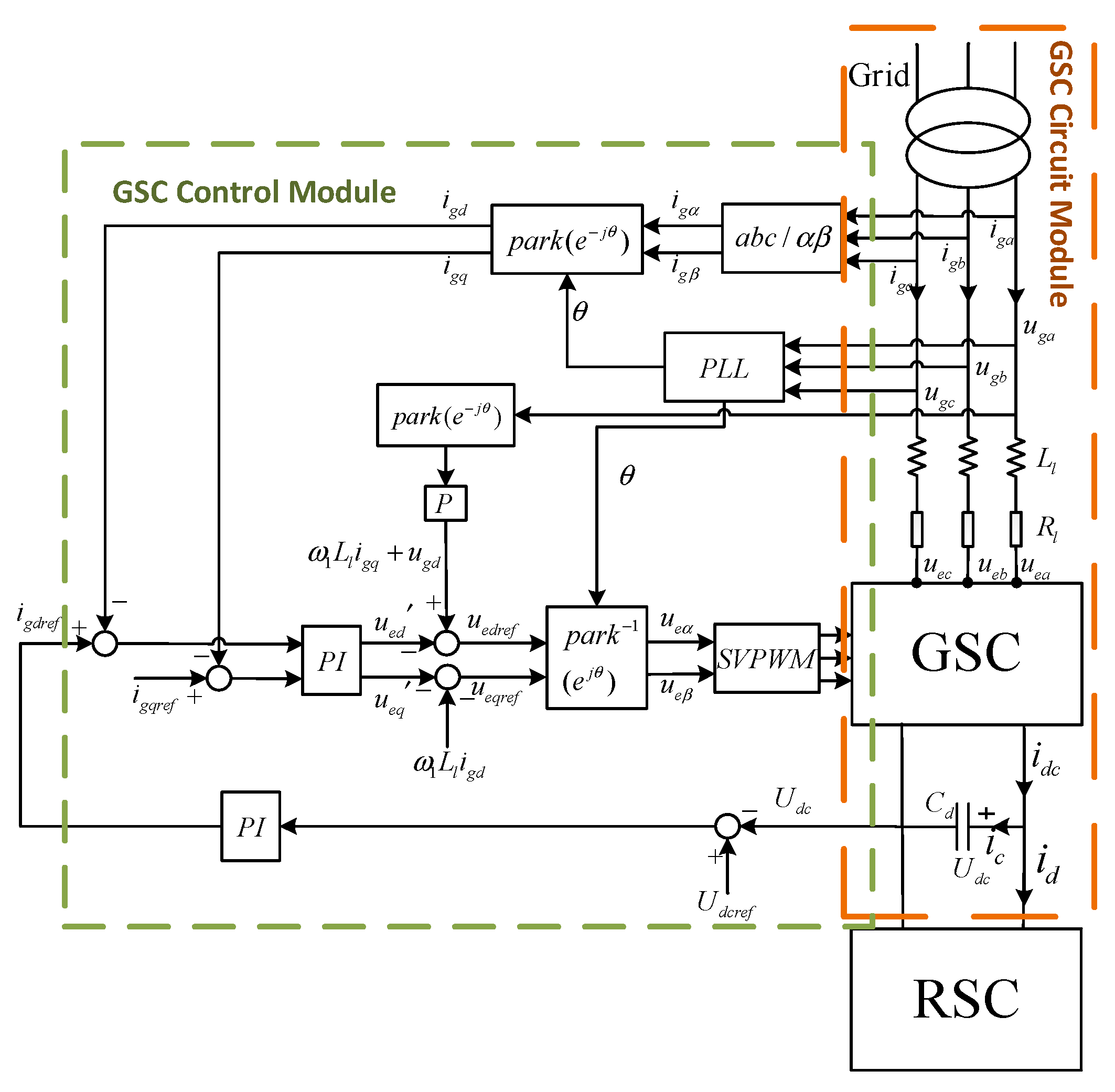
3.1. Small-Signal Modeling of the GSC Circuit

According to Figure 9, the small-signal model of the GSC circuit and the DC interconnection between RSC and GSC can be written as:

{\begin{cases} D_{d} {\hat{u}}_{d c}^{m} + {\hat{d}}_{d}^{m} U_{d c} = {\hat{u}}_{g d}^{m} - R_{l} {\hat{i}}_{g d}^{m} - s L_{l} {\hat{i}}_{g d}^{m} + ω_{1} L_{l} {\hat{i}}_{g q}^{m} \\ D_{q} {\hat{u}}_{d c}^{m} + {\hat{d}}_{q}^{m} U_{d c} = {\hat{u}}_{g q}^{m} - R_{l} {\hat{i}}_{g q}^{m} - s L_{l} {\hat{i}}_{g q}^{m} - ω_{1} L_{l} {\hat{i}}_{g d}^{m} \end{cases}

(26)

s C_{d} {\hat{u}}_{d c}^{m} = \frac{3}{2} ({\hat{d}}_{d}^{m} I_{g d} + {\hat{d}}_{q}^{m} I_{g q} + D_{d} {\hat{i}}_{g d}^{m} + D_{q} {\hat{i}}_{g q}^{m} - {\hat{d}}_{r d}^{m} I_{r d} - {\hat{d}}_{r q}^{m} I_{r q} - D_{r d} {\hat{i}}_{r d}^{m} - D_{r q} {\hat{i}}_{r q}^{m})

(27)

where

D_{d}

and

D_{q}

are stable GSC duty cycles in the dq frame, respectively; and

I_{g d}

and

I_{g q}

are GSC output currents at a steady operation point in the dq frame. By rearranging Equations (26) and (27), the small-signal transfer model can be obtained as:

H {[\begin{matrix} {\hat{i}}_{g d}^{m} & {\hat{i}}_{g q}^{m} & {\hat{u}}_{d c}^{m} & {\hat{u}}_{g d}^{m} & {\hat{u}}_{g q}^{m} & {\hat{d}}_{r d}^{m} & {\hat{d}}_{r q}^{m} & {\hat{i}}_{r d}^{m} & {\hat{i}}_{r q}^{m} \end{matrix}]}^{T} = J [\begin{array}{l} {\hat{d}}_{d}^{m} \\ {\hat{d}}_{q}^{m} \end{array}];

(28)

where

\begin{matrix} H = [\begin{array}{l} R_{l} + s L_{l} & - ω_{1} L_{l} & D_{d} & 1 & 0 & 0 & 0 & 0 & 0 \\ ω_{1} L_{l} & R_{l} + s L_{l} & D_{q} & 0 & - 1 & 0 & 0 & 0 & 0 \\ - \frac{3}{2} D_{d} & - \frac{3}{2} D_{q} & s C_{d} & 0 & 0 & \frac{3}{2} I_{r d} & \frac{3}{2} I_{r q} & \frac{3}{2} D_{r d} & \frac{3}{2} D_{r q} \end{array}] \\ J = [\begin{matrix} - U_{d c} & 0 \\ 0 & - U_{d c} \\ \frac{3}{2} I_{g d} & \frac{3}{2} I_{g q} \end{matrix}] \end{matrix}

(29)

Then, using the same method in Equations (7)–(10), the small-signal transfer functions

G_{H}

and

G_{M}

, which are the transfer matrixes from

{\hat{d}}_{d q}^{m}

to

{\hat{u}}_{d c}^{m}

and from

{\hat{d}}_{d q}^{m}

to

{\hat{i}}_{g d q}^{m}

, respectively, can be obtained in Equation (30). Also, similar small-signal transfer functions of the other variables can be obtained:

G_{J}

, the transfer function from

{\hat{u}}_{g d q}^{m}

to

{\hat{u}}_{d c}^{m}

;

G_{N}

, the transfer function from

{\hat{u}}_{g d q}^{m}

to

{\hat{i}}_{g d q}^{m}

;

G_{K}

, the transfer function from

{\hat{d}}_{r d q}^{m}

to

{\hat{u}}_{d c}^{m}

;

G_{L}

, from

{\hat{d}}_{r d q}^{m}

to

{\hat{i}}_{g d q}^{m}

;

G_{O}

, from

{\hat{i}}_{r d q}^{m}

to

{\hat{u}}_{d c}^{m}

; and

G_{P}

is the transfer function from

{\hat{i}}_{r d q}^{m}

to

{\hat{i}}_{g d q}^{m}

. These transfer functions have mathematical forms similar to Equation (30).

{\begin{cases} G_{H} = [\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] H^{- 1} J \\ G_{M} = [\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] H_{}^{- 1} J \end{cases} .

(30)

Then, a similar small-signal diagram of the GSC circuit, like Figure 5, can be drawn in Figure 10.

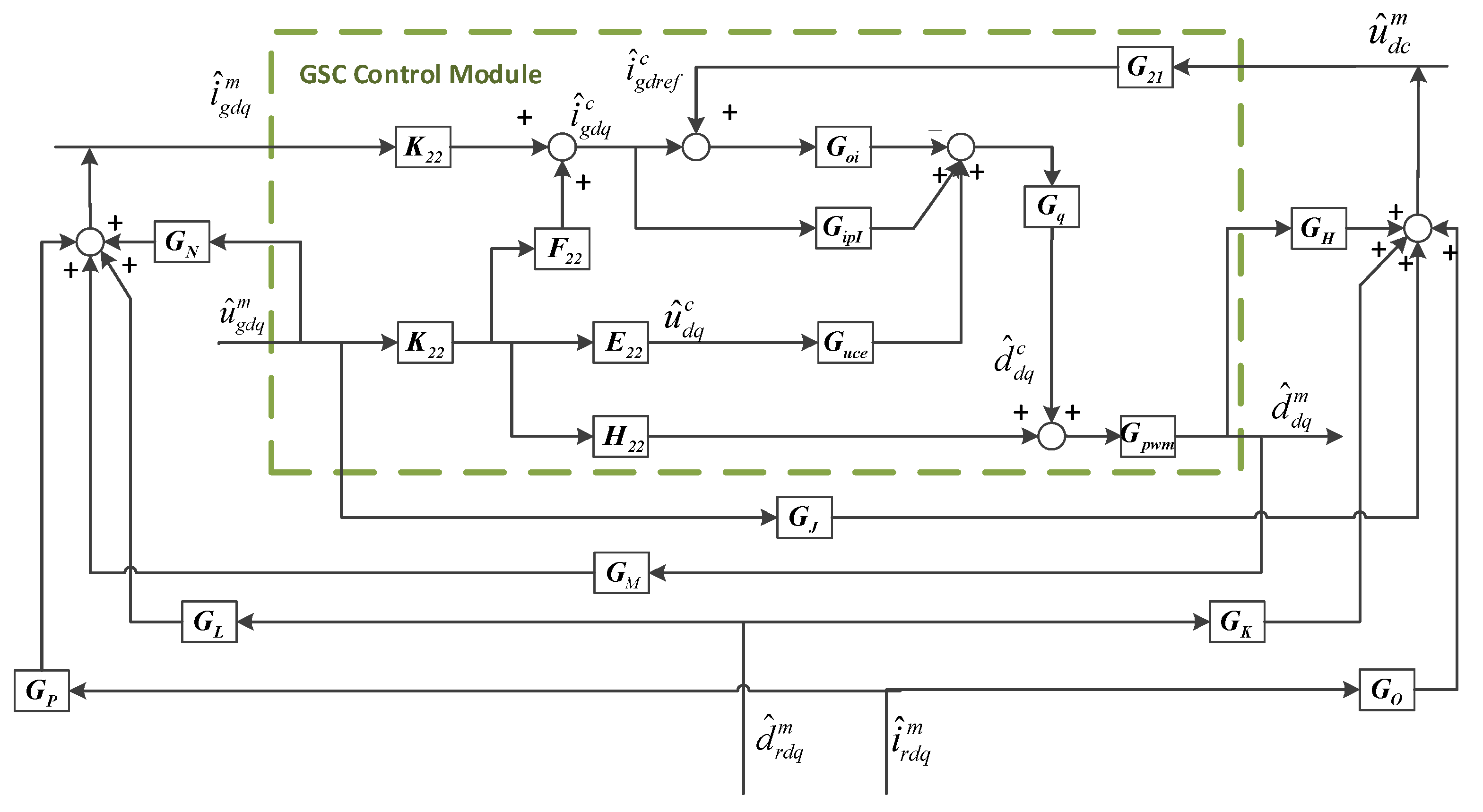
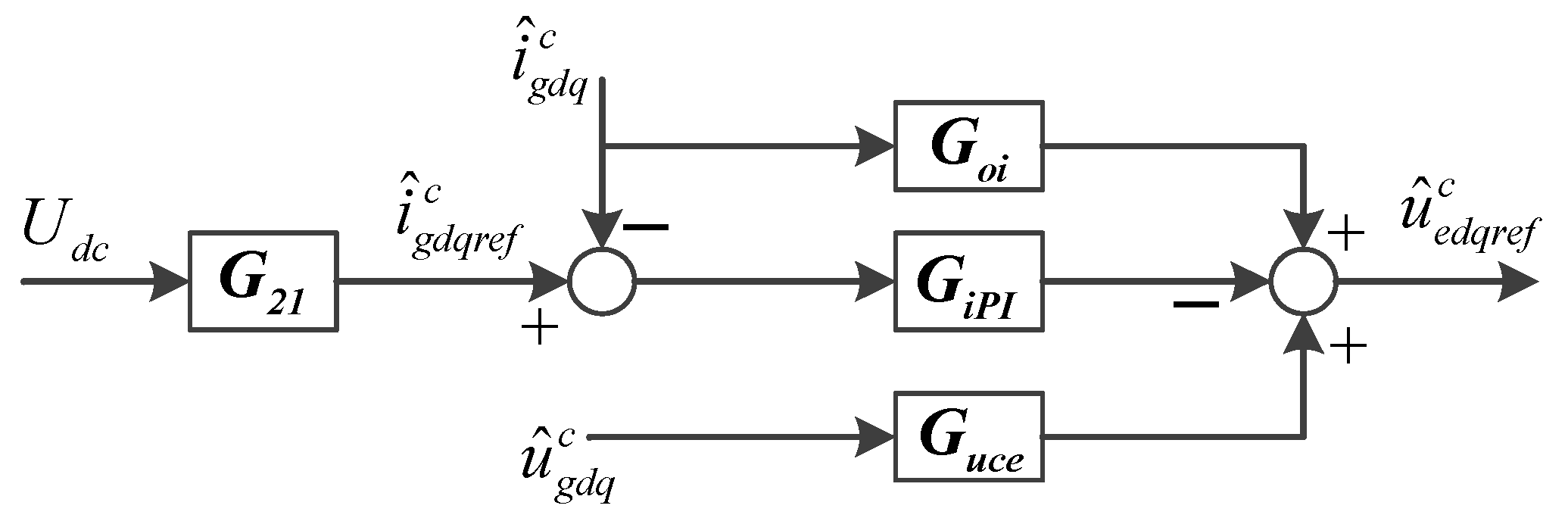
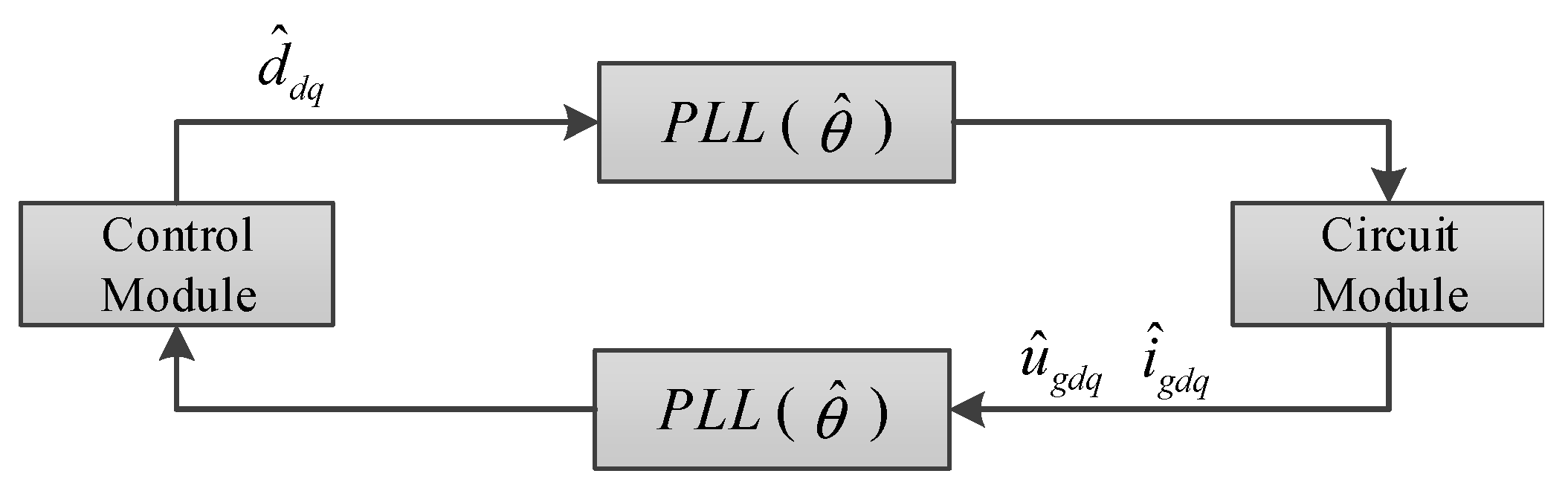
3.2. Small-Signal Modeling of GSC Control with PLL

The control system of GSC is composed of the inner current controller and the outer voltage controller, which can be written as follows [22]. Then, the GSC control small-signal diagram excluding PLL can be obtained by Figure 11.

[\begin{array}{l} {\hat{u}}_{e d r e f}^{c} \\ {\hat{u}}_{e q r e f}^{c} \end{array}] = - G_{i P I} [\begin{array}{l} {\hat{i}}_{g d r e f}^{c} - {\hat{i}}_{g d}^{c} \\ {\hat{i}}_{g q r e f}^{c} - {\hat{i}}_{g q}^{c} \end{array}] + G_{o i} [\begin{array}{l} {\hat{i}}_{g d}^{c} \\ {\hat{i}}_{g q}^{c} \end{array}] + G_{u c e} [\begin{array}{l} {\hat{u}}_{g d}^{c} \\ {\hat{u}}_{g q}^{c} \end{array}];

(31)

[\begin{array}{l} {\hat{i}}_{g d r e f}^{c} \\ {\hat{i}}_{g q r e f}^{c} \end{array}] = [\begin{array}{l} - k_{U_{d c} P} - \frac{k_{U_{d c} I}}{s} \\ 0 \end{array}] U_{d c} = G_{21} U_{d c};

(32)

where

\begin{matrix} G_{i P I} = [\begin{array}{l} k_{i g P} + \frac{k_{i g I}}{s} 0 \\ 0 k_{i g P} + \frac{k_{i g I}}{s} \end{array}] \end{matrix} \begin{matrix} , & G_{oi} = [\begin{array}{l} 0 ω_{1} L_{l} \\ - ω_{1} L_{l} 0 \end{array}] \end{matrix} \begin{matrix} , & G_{uce} = [\begin{array}{l} 1 0 \\ 0 1 \end{array}] \end{matrix}

(33)

The angular relationship between the GSC circuit module and the GSC control module with PLL is displayed in Figure 12. From Figure 9 and Figure 12, a transfer diagram of the GSC control system with PLL can be drawn in Figure 13 by using the small-signal transfer models of the GSC control system described by Equations (34)–(36).

[\begin{array}{l} {\hat{u}}_{g d}^{c} \\ {\hat{u}}_{g q}^{c} \end{array}] = [\begin{matrix} 1 & 0 \\ 0 & 1 - \frac{E_{g d} G_{p i}}{(s + G_{p i} E_{g d})} \end{matrix}] [\begin{array}{l} {\hat{u}}_{g d}^{m} \\ {\hat{u}}_{g q}^{m} \end{array}] = E_{22} [\begin{array}{l} {\hat{u}}_{g d}^{m} \\ {\hat{u}}_{g q}^{m} \end{array}];

(34)

[\begin{array}{l} {\hat{d}}_{d}^{m} \\ {\hat{d}}_{q}^{m} \end{array}] = [\begin{array}{l} {\hat{d}}_{d}^{c} \\ {\hat{d}}_{q}^{c} \end{array}] + [\begin{matrix} 0 & \frac{D_{q} G_{p i}}{(s + G_{p i} E_{g d})} \\ 0 & \frac{- D_{d} G_{p i}}{(s + G_{p i} E_{g d})} \end{matrix}] [\begin{array}{l} {\hat{u}}_{g d}^{m} \\ {\hat{u}}_{g q}^{m} \end{array}] = [\begin{array}{l} {\hat{d}}_{d}^{c} \\ {\hat{d}}_{q}^{c} \end{array}] + H_{22} [\begin{array}{l} {\hat{u}}_{g d}^{m} \\ {\hat{u}}_{g q}^{m} \end{array}];

(35)

[\begin{array}{l} {\hat{i}}_{g d}^{c} \\ {\hat{i}}_{g q}^{c} \end{array}] = [\begin{array}{l} {\hat{i}}_{g d}^{m} \\ {\hat{i}}_{g q}^{m} \end{array}] + [\begin{matrix} 0 & 0 \\ 0 & \frac{- I_{g d} G_{p i}}{(s + G_{p i} E_{g d})} \end{matrix}] [\begin{array}{l} {\hat{u}}_{g d}^{m} \\ {\hat{u}}_{g q}^{m} \end{array}] = [\begin{array}{l} {\hat{i}}_{g d}^{m} \\ {\hat{i}}_{g q}^{m} \end{array}] + F_{22} [\begin{array}{l} {\hat{u}}_{g d}^{m} \\ {\hat{u}}_{g q}^{m} \end{array}];

(36)

where

G_{p i}

is the transfer function of the PI controller in PLL,

G_{p i} = k_{p p l l} + k_{i p l l} / s

.

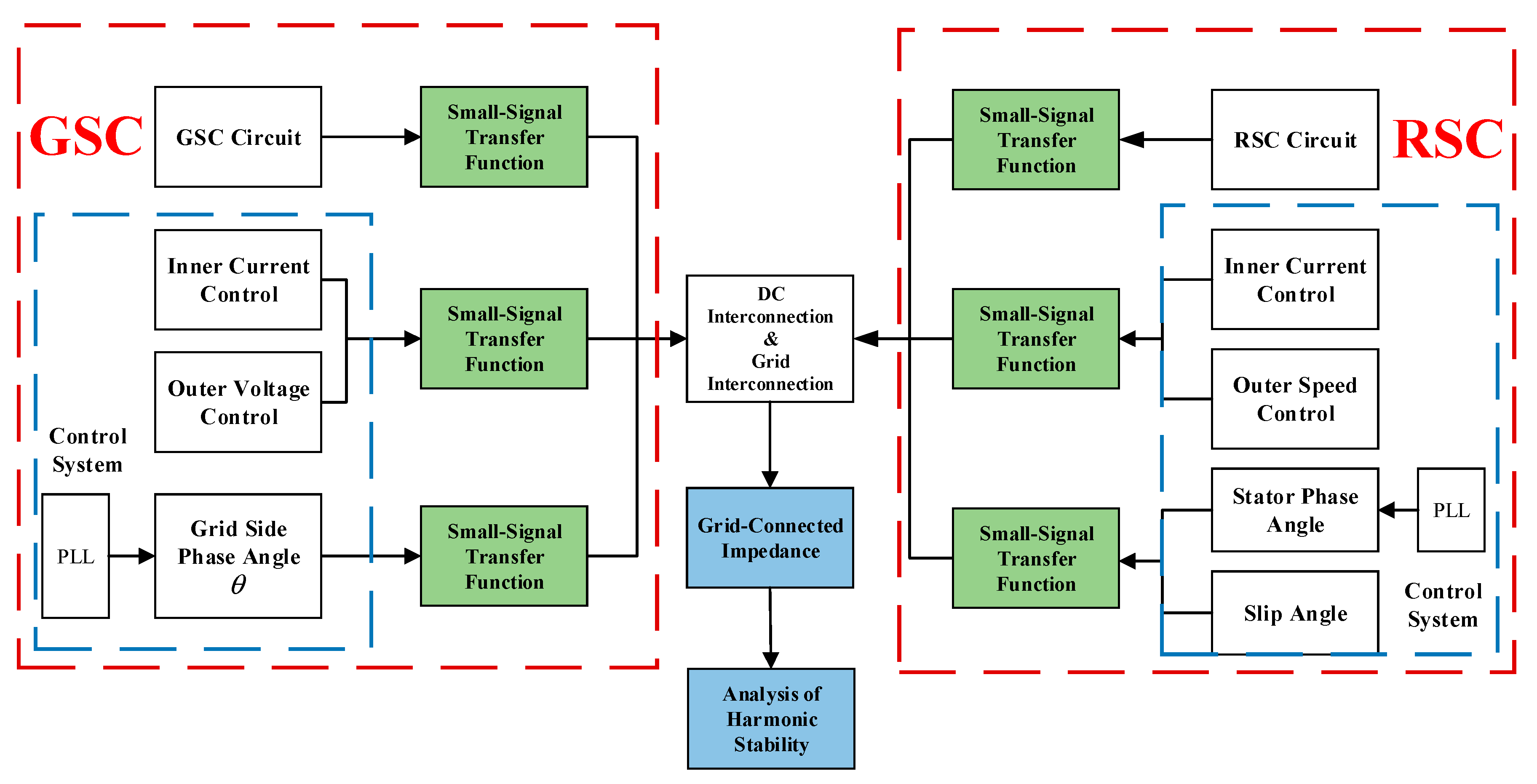
4. Analysis of Harmonic Stability and Real-Time Digital Simulation (RTDS) Verification

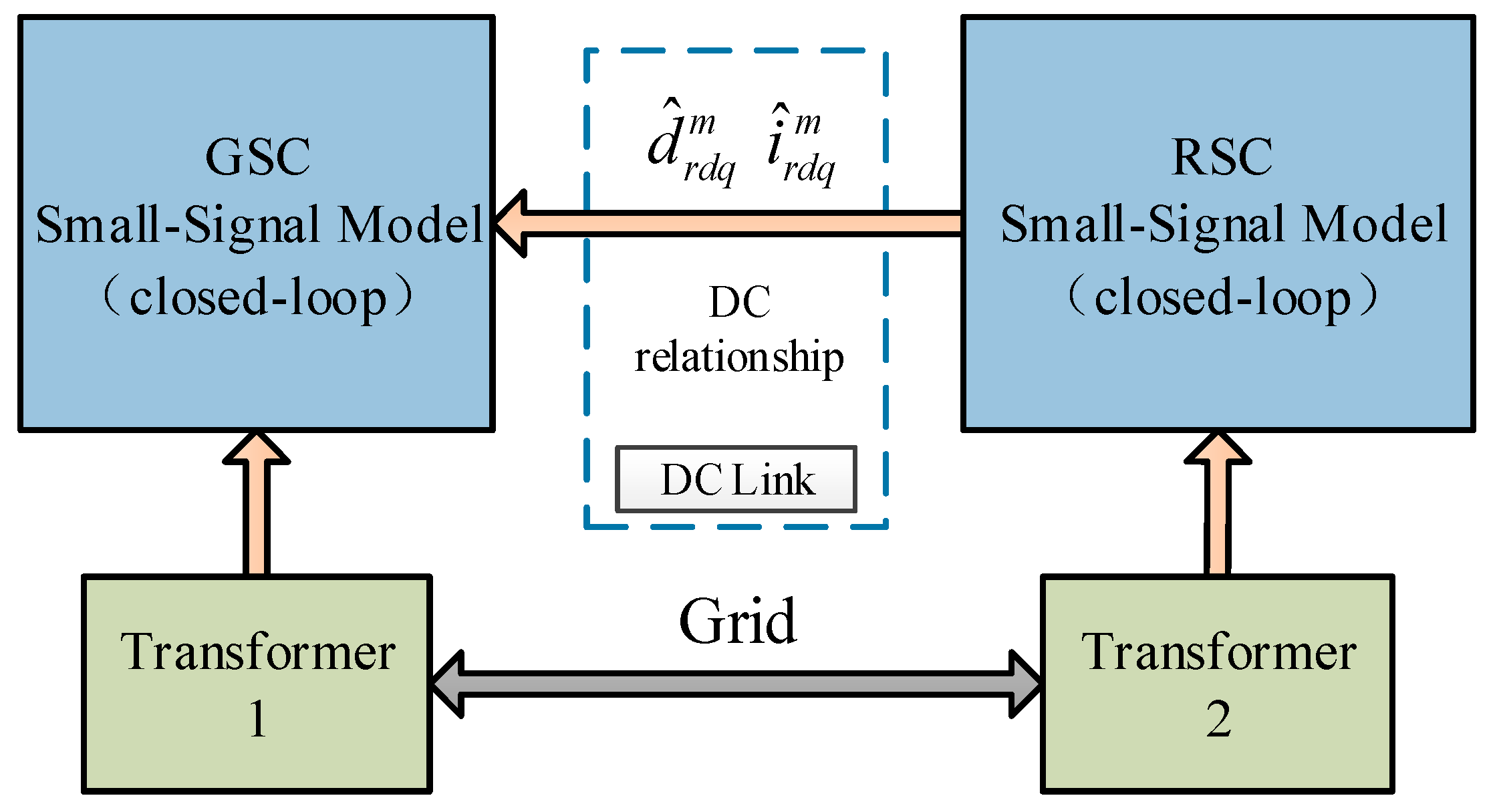
4.1. Impedance Modeling of Equivalent Systems

4.1.1. Input Impedance Modeling of RSC and GSC connected in DFIG

With the small-signal transfer models of circuit modules and control modules derived in Section 2 and Section 3, the whole equivalent architecture of the RSC and GSC in DFIGs can be obtained (the structure diagram is provided in Appendix A). Also, the schematic diagram of the whole closed-loop system can be easily obtained in Figure 14 considering the DC and grid-side AC variables relationship between RSC and GSC.

In Figure 14, the variables in the DC link are described in Equation (37) by using the RSC small-signal model in Section 2. Substituting variables in Figure 10, Figure 11 and Figure 13 with Equation (37), the GSC small-signal models can be written as given in Equation (38).

{\begin{cases} {\hat{d}}_{r d q}^{m} = [(G_{E} G_{D} + G_{F}) {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1} (B_{22} - G_{E} G_{C}) + G_{E} G_{C}] {\hat{i}}_{s d q}^{m} \\ + (G_{E} G_{D} + G_{F}) {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1} A_{22} {\hat{u}}_{s d q}^{m} \\ {\hat{i}}_{r d q}^{m} = {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1} [(B_{22} - G_{E} G_{C}) {\hat{i}}_{s d q}^{m} + A_{22} {\hat{u}}_{s d q}^{m}] \end{cases};

(37)

{\begin{cases} {\hat{i}}_{g d q}^{m} = G_{N} {\hat{u}}_{g d q}^{m} + G_{M} {\hat{d}}_{d q}^{m} + G_{P} {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1} [(B_{22} - G_{E} G_{C}) {\hat{i}}_{s d q}^{m} + A_{22} {\hat{u}}_{s d q}^{m}] \\ + G_{L} {\begin{cases} [(G_{E} G_{D} + G_{F}) {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1} (B_{22} - G_{E} G_{C}) + G_{E} G_{C}] {\hat{i}}_{s d q}^{m} \\ + (G_{E} G_{D} + G_{F}) {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1} A_{22} {\hat{u}}_{s d q}^{m} \end{cases}} \\ {\hat{u}}_{d c}^{m} = G_{J} {\hat{u}}_{g d q}^{m} + G_{H} {\hat{d}}_{d q}^{m} + G_{O} {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1} [(B_{22} - G_{E} G_{C}) {\hat{i}}_{s d q}^{m} + A_{22} {\hat{u}}_{s d q}^{m}] \\ + G_{K} {\begin{cases} [(G_{E} G_{D} + G_{F}) {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1} (B_{22} - G_{E} G_{C}) + G_{E} G_{C}] {\hat{i}}_{s d q}^{m} \\ + (G_{E} G_{D} + G_{F}) {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1} A_{22} {\hat{u}}_{s d q}^{m} \end{cases}} \\ {\hat{d}}_{d q}^{m} = G_{P W M} {\begin{cases} G_{q 2} (G_{i p I} K_{22} + G_{o i} K_{22}) {\hat{i}}_{g d q}^{m} + [\begin{array}{l} G_{q 2} G_{o i} F_{22} K_{22} + G_{q 2} G_{u c e} E_{22} K_{22} \\ + G_{q 2} G_{i p I} F_{22} K_{22} + H_{22} K_{22} \end{array}] {\hat{u}}_{g d q}^{m} \\ - G_{q 2} G_{i p I} G_{21} {\hat{u}}_{d c}^{m} \end{cases}} \end{cases};

(38)

where

G_{PWM}

is the time-delay function, and

G_{q}

and

G_{q 2}

are the normalized functions to normalize the control signal. The detailed transfer matrixes in Equations (37) and (38) are also provided in Appendix A.

Furthermore, assuming that the transformer ratio

k_{12} = 1

in this studied system, the equivalent input impedance of RSC and GSC can be obtained in Equation (39). Also, the detailed transfer matrixes are provided in Appendix B.

\begin{matrix} Z_{g d q} & = \frac{{\hat{u}}_{g d q}^{m}}{{\hat{i}}_{g d q}^{m}} \\ = \frac{[\begin{array}{l} G_{M} {(D_{22} G_{21} G_{H} + I)}^{- 1} \cdot (O_{22} P_{22} + R_{22} P_{22} + G_{P W M} G_{E} G_{C} - D_{22} K_{22} - G_{P W M} G_{q} G_{o i} K_{22}) \\ + I - S_{22} P_{22} - G_{L} U_{22} P_{22} - G_{E} G_{C} \end{array}]}{[\begin{array}{l} G_{M} {(D_{22} G_{21} G_{H} + I)}^{- 1} \cdot (O_{22} - D_{22} G_{21} G_{J} - O_{22} A_{22} - R_{22} A_{22}) \\ + G_{N} + S_{22} A_{22} + G_{L} U_{22} A_{22} \end{array}]} \end{matrix}

(39)

4.1.2. Impedance Modeling of the Grid-Connected System

Figure 15 depicts the equivalent DFIG-based system circuit. The power grid cable uses the Π-section model, and then the impedance of grid in dq frame can be written as:

Z_{u d q} = [\begin{matrix} R_{u} + s L_{u} & - ω_{1} L_{u} \\ ω_{1} L_{u} & R_{u} + s L_{u} \end{matrix}],

(40)

where

R_{u}

is the equivalent grid resistance and

L_{u}

is the equivalent grid inductance.

Hence, the grid-connected impedance can be obtained using Equations (39) and (40) from Figure 15, and the system closed-loop feedback gain can also be written as:

L_{d q} = Z_{u d q} Z_{g d q}^{- 1} = [\begin{matrix} Z_{u d d} & Z_{u d q} \\ Z_{u q d} & Z_{u q q} \end{matrix}] [\begin{matrix} Y_{g d d} & Y_{g d q} \\ Y_{g q d} & Y_{g q q} \end{matrix}] .

(41)

Based on this feedback loop gain, the stability of the system’s equivalent circuit can be assessed through Nyquist diagrams.

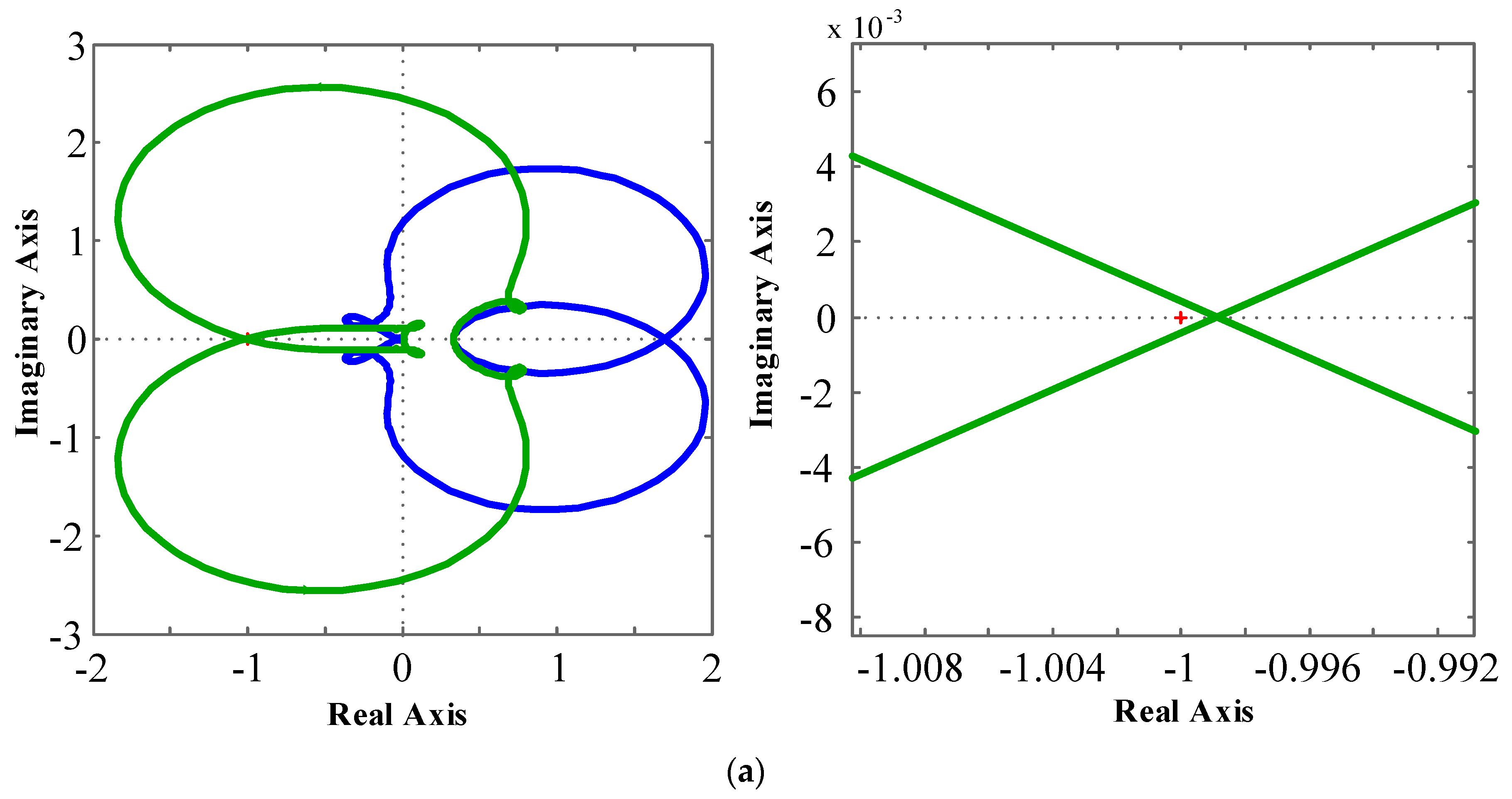
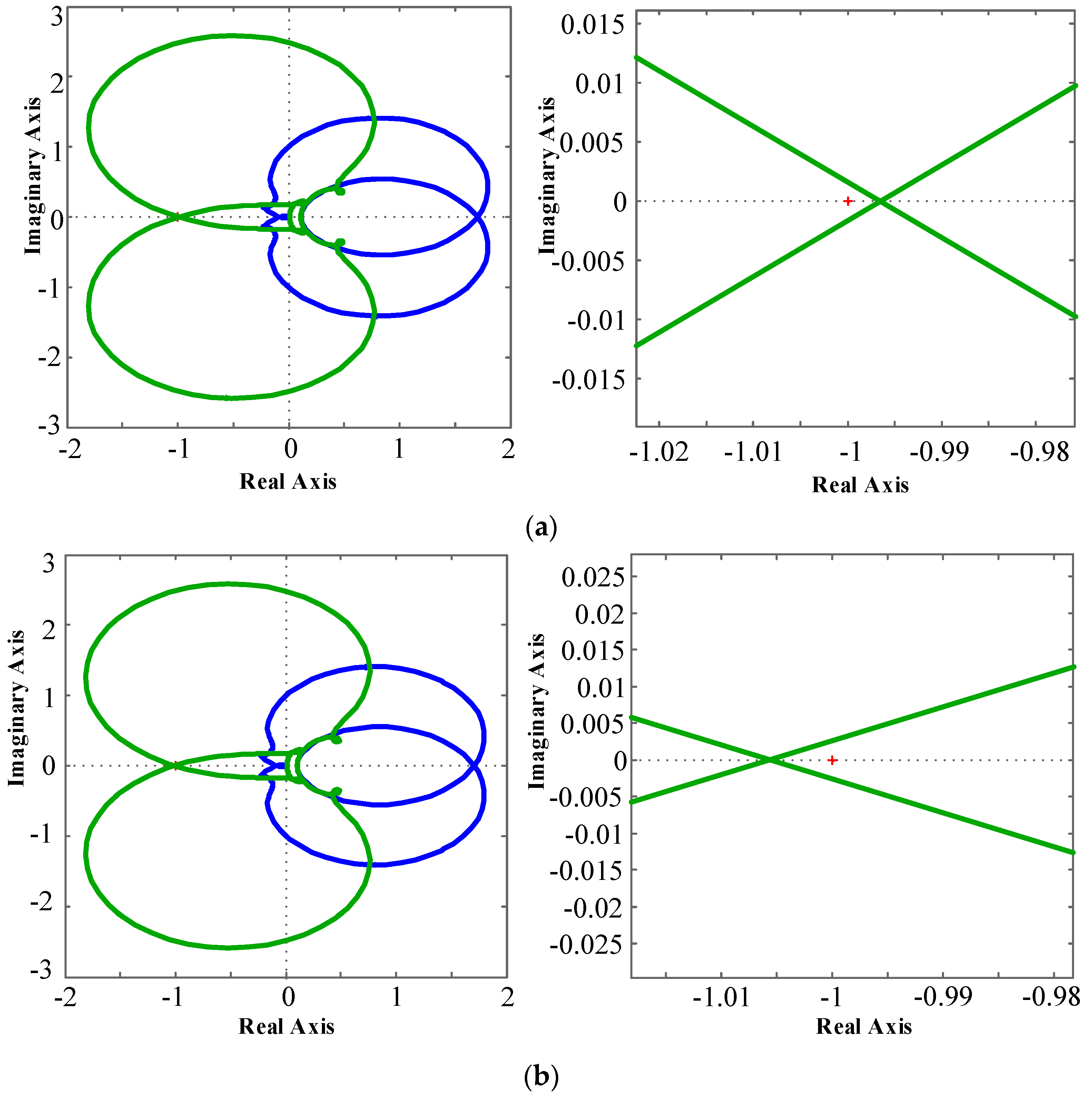
4.2. Impedance-Based Stability Analysis

The system’s electrical parameters are listed in Table 1, which give the condition of the system stable operating point. Table 2 gives the parameters of the control systems for both RSC and GSC, which are also in the stable case. RSC and GSC are also designed with the same parameters considering the simplicity. Both RSC and GSC are working at the stable operating point with the controller parameters listed in Table 2. This provides a theoretical precondition for using the feedback loop in Figure 15 to evaluate the stability of the studied system. Since the impedance model of the studied system is designed as single input single output (SISO) model, the Nyquist stability criterion can be directly applied to analyze the system’s stability [23].

To analyze the stability of the studied system, the Nyquist criterion can be applied to the equivalent system [24]. Stability trends can be observed from the Nyquist diagrams by altering the circuit electrical parameters or controller parameters [25]. Furthermore, according to the Nyquist diagram, the parametric contributions to the system’s harmonic stability can be predicted, and then the critical condition of the stable system can be given.

4.2.1. Circuit parameters stability assessment

Figure 16 depicts Nyquist plots of the feedback loop gain of the equivalent circuit. In this case, it is obvious that when the GSC inductance increases (L_l increases from 3.7 to 3.8 mH), the system soon turns unstable. Furthermore, the other circuit electrical parameters are also adjusted to obtain the respective contributions to the system stability, and these parametric stability assessments are listed in Table 3. The delta (∆) in Table 3 is a mark used to represent that the adjusted parameter has little impact on the stability of the studied system.

In fact, adjusting the inductance of RSC and GSC and the dc capacitance in the dc link will greatly affect the system’s harmonic stability. The cases where harmonic stability will improve when the inductances of RSC and GSC decrease are omitted in Table 3. So, by choosing the optimal parameters of RSC and GSC, the wind farm manufacturer can improve stability of the system and better avoid the occurrence of harmonic instability.

4.2.2. Controller parameters stability assessment

Figure 17 depicts Nyquist diagrams of the feedback loop gain. In this case, the P parameters of the inner current controller in GSC are reduced (

k_{i g P}

decreases from 1 to 0.9). It is clear that the curve encloses (−1, j0) which means the feedback loop gain becomes unstable and there might be harmonic instability in the power grid. Similar conclusions can be found in Table 4 where assessments of other controller parameters are listed.

4.2.3. Mechanical parameters stability assessment

Figure 18 shows Nyquist plots of the feedback loop gain after the moment of inertia was reduced. The diagram indicates that when the mechanical parameters of the wind turbine such as the moment of inertia are changing, the system may become unstable because the inertia relates the wind speed to fluctuation control. Actually, when the inertia increases, the control of the wind speed fluctuation will get worse so the system will easily lean to instability. Under this situation, bad speed control may lead to harmonic frequency oscillation in the power grid.

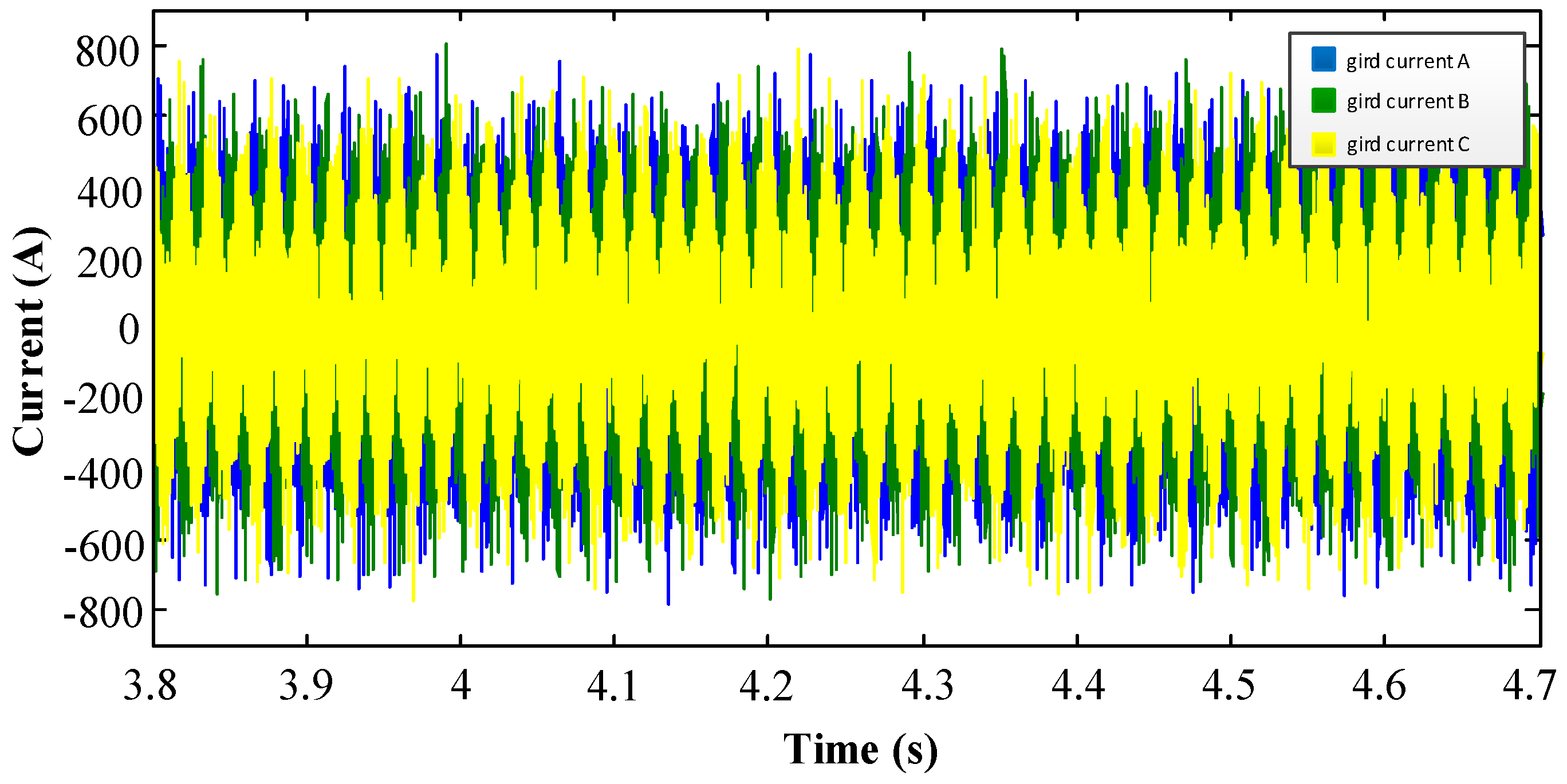
4.3. RTDS Simulation Verification

RTDS is a kind of commercial simulator that is widely used around the world. Compared with other simulation platforms, RTDS has many advantages such as its faster computing speed and real-time interconnection with practical devices [26,27,28,29]. In order to validate a frequency-domain stability analysis of the equivalent model based on the impedance method, a time-domain DFIG-based system is built by the real-time simulator CAD (RSCAD), which is connected to RTDS. The simulated RSC and GSC parameters and grid electrical constants are given in Table 1 and Table 2. Then, parameters are adjusted to evaluate harmonic stability. Moreover, conclusions in Table 3 and Table 4 are validated. In this paper, only the case where GSC inductance is changed will be discussed (considering the paper length).

Figure 19 shows the simulated three-phase grid currents in GSC with the parameters given in Table 1 and Table 2. In this case, GSC inductance is adjusted (

L_{l}

= 3.7 mH). The system is still in a stable status; however, there are many harmonic components in the grid currents. The system’s stability is not that good, and this result coincides with conclusions in Table 3. In contrast, Figure 20 shows the simulated grid currents after GSC inductance increased (

L_{l}

= 3.8 mH). It is obvious that there is harmonic instability in the studied system and the system becomes unstable, which confirms the conclusions in Table 3 and the frequency-domain analysis in Figure 16.

Then, the fast Fourier transform (FFT) analysis of the simulated grid-side output currents in the unstable case is accomplished using the output data of RTDS. Figure 21 shows the detailed harmonic components in the simulated grid currents. It is clear that the main amplified harmonic components are 250.1 (5th harmonic), 349.7 (7th harmonic), 1901 (38th harmonic), 2099.1 (42nd harmonic), 3951.6 (79th harmonic), and 4050.4 Hz (81st harmonic).

In fact, 5th and 7th harmonic components mainly exist in RSC and 38th, 42nd, 79th and 81st harmonic components exist both in RSC and GSC [30]. And when the system parameters are not matched well, the existing harmonics both in RSC and GSC will be continuously amplified and interact with each other through the DC link, thereby generating harmonic instability and jeopardizing the power quality and stability of the entire system. Table 5 lists the values of parameters for the critical stability case. The results shown in Table 5 confirm the theoretical analysis in the frequency domain and, thus, verify the impedance model derived in this paper.

5. Conclusions

This paper is presented and discussed based on impedance modeling and the steps of the harmonic stability analysis of DFIG systems. Both the small-signal models of RSC and GSC are obtained as transfer functions, which include circuits modules and controller modules with PLL perturbations. The equivalent input impedances of RSC and GSC are obtained, and then Nyquist diagrams are applied to analyze stability based on the impedance model. The assessment of contributions to the system stability of each parameter is also accomplished. Finally, the studied system is built in RSCAD with RTDS. The simulated results confirm the frequency-domain analysis, and, thus, the correctness of the small-signal models of RSC and GSC are verified. The RTDS simulation shows that 5th and 7th harmonics in RSC and 38th, 42nd, 79th, and 81st harmonics in both side converters are continuously amplified to cause the harmonic instability. And last, the critical conditions for harmonic instability are given in this paper.

Based on the analysis results and simulations in this paper, it can be concluded that the causes of the system’s harmonic instability include:

The mismatch of the stator circuit parameters in the DFIG motor will gradually amplify the existing harmonics, which will cause the system to be unstable.
The mismatch between the inductance parameters and the capacitance parameters of the dual PWM converter and its controller parameters will also amplify the harmonics and destabilize the system.
The moment of inertia of the system itself will directly affect the magnitude of fluctuations in the wind speed, and thus will also affect the stability of the system’s harmonics.

Author Contributions

The individual contribution of each author are as follows: Conceptualization, X.C. and Z.L.; Formal analysis, X.C.; Methodology, X.C. and Z.L.; Validation, X.C.; Writing—original draft, X.C. and Z.L.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

The architecture of RSC and GSC based on the small-signal transfer functions can be obtained by combining Figure 5, Figure 6 and Figure 8 in Section 2 and Figure 10, Figure 11 and Figure 13 in Section 3. The diagram of RSC and GSC are respectively shown in Figure A1 and Figure A2.

Figure A1. The small-signal transfer diagram of RSC with PLL.

Figure A2. The small-signal transfer diagram of GSC with PLL.

The detailed transfer matrixes in Equations (37) and (38) are given as follows:

A_{22} = G_{P W M} [G_{q} (\begin{array}{l} G_{r s} G_{P L L u} K_{u s} + G_{I} G_{P L L 1} K_{u s} \\ + G_{i r P I} G_{i s} G_{P L L 4} K_{u s} - G_{i r P I} G_{P L L 1} K_{u s} \end{array}) + G_{P L L 3} K_{u s}];

(A1)

B_{22} = G_{P W M} G_{q} G_{i r P I} G_{i s} K_{i s};

(A2)

C_{22} = G_{P W M} [G_{q} (G_{I} G_{P L L i} K_{i r} + G_{i r P I} G_{ω r P I} G_{r} K_{22} - G_{i r P I} G_{P L L i} K_{i r}) + G_{P L L 2} K_{i r}];

(A3)

Appendix B

The detailed transfer matrixes of the equivalent input impedance of converters in Equation (39) are given as follows:

D_{22} = G_{P W M} G_{q 2} G_{i p I}

(A4)

P_{22} = B_{22} - G_{E} G_{C}

(A5)

O_{22} = G_{P W M} (G_{q 2} G_{o i} F_{22} K_{22} + G_{q 2} G_{u c e} E_{22} K_{22} + G_{q 2} G_{i p I} F_{22} K_{22} + H_{22} K_{22})

(A6)

Q_{22} = G_{P W M} G_{q} G_{i p I} G_{21} G_{O} {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1}

(A7)

S_{22} = G_{P} {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1}

(A8)

R_{22} = G_{P W M} G_{q} G_{i p I} G_{21} G_{K} (G_{E} G_{D} + G_{F}) {(G_{E} G_{D} + G_{F} - C_{22})}^{- 1}

(A9)

References

Li, J.; Corzine, K. Harmonic Compensation for Variable Speed DFIG Wind Turbines Using Multiple Reference Frame Theory. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015. [Google Scholar]
Yipeng, S.; Heng, N. Modularized control strategy and performance analysis of DFIG system under unbalanced and harmonic grid voltage. IEEE Trans. Power Electron. 2015, 30, 4831–4842. [Google Scholar]
Swami, N.K.N.; Bhim, S. Doubly fed induction generator for wind energy conversion systems with integrated active filter capabilities. IEEE Trans. Ind. Inform. 2015, 11, 923–933. [Google Scholar] [CrossRef]
Li, J.; Nader, S.; Stephen, W. Modeling of Large Wind Farm Systems for Dynamic and Harmonics Analysis. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008. [Google Scholar]
Fan, L.; Yuvarajan, S.; Kavasseri, R. Harmonic Analysis of a DFIG for a Wind Energy Conversion System. IEEE Trans. Energy Convers. 2010, 25, 181–190. [Google Scholar]
McKenna, R.; Ostman, V.d.; Leye, P.; Fichtner, W. Key Challenges and Prospects for Large Wind Turbines. Renew. Sustain. Energy Rev. 2016, 53, 1212–1221. [Google Scholar] [CrossRef]
Wang, Y.; Wang, X.; Blaabjerg, F.; Chen, Z. Eigenvalue-based Harmonic Stability Analysis Method in Inverter-Fed Power Systems. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015. [Google Scholar]
Wang, X.; Blaabjerg, F.; Liserre, M.; Chen, Z.; He, J.; Li, Y. An Active Damper for Stabilizing Power-Electronics-Based AC Systems. IEEE Trans. Power Electron. 2014, 29, 3318–3329. [Google Scholar] [CrossRef]
Kwon, J.; Wang, X.; Blaabjerg, F.; Bak, C.L. Comparison of LTI and LTP Models for Stability Analysis of Grid Converters. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016. [Google Scholar]
Bakhshizadeh, M.K.; Wang, X.; Blaabjerg, F.; Hjerrild, J.; Kocewiak, L.; Bak, C.L.; Hesselbæk, B. Couplings in Phase Domain Impedance Modeling of Grid-Connected Converters. IEEE Trans. Power Electron. 2016, 31, 6792–6796. [Google Scholar]
Kwon, J.B.; Wang, X.; Blaabjerg, F.; Bak, C.L.; Wood, A.R.; Watson, N.R. Harmonic Instability Analysis of a Single-Phase Grid-Connected Converter Using a Harmonic State-Space Modeling Method. IEEE Trans. Ind. Appl. 2016, 52, 4188–4200. [Google Scholar] [CrossRef]
Wang, Y.; Wang, X.; Blaabjerg, F.; Chen, Z. Harmonic Resonance Assessment of Multiple Paralleled Grid-Connected Inverters System. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017—ECCE Asia), Kaohsiung, Taiwan, China, 3–7 June 2017. [Google Scholar]
Wang, X.; Blaabjerg, F. Harmonic Stability in Power Electronic-Based Power Systems: Concept, Modeling, and Analysis. IEEE Trans. Smart Grid 2019, 10, 2858–2870. [Google Scholar] [CrossRef]
Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
Belkhayat, M. Stability Criteria for AC Power Systems with Regulated Loads. Ph.D. Thesis, School of Electrical and Computer, Engineering, Purdue University, West Lafayette, IN, USA, December 1997. [Google Scholar]
Schweizer, M.; Kolar, J.W. Shifting input filter resonances—An intelligent converter behaviour for maintaining system stability. In Proceedings of the 2010 International Power Electronics Conference (ECCE ASIA), Sapporo, Japan, 21–24 June 2010; pp. 906–913. [Google Scholar]
Wang, X.; Blaabjerg, F.; Chen, Z.; Wu, W. Resonance Analysis in Parallel Voltage-Controlled Distributed Generation Inverters. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 2977–2983. [Google Scholar]
Lu, M.; Wang, X.; Blaabjerg, F.; Loh, P.C. An Analysis Method for Harmonic Resonance and Stability of Multi-Paralleled LCL-Filtered Inverters. In Proceedings of the 2015 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aachen, Germany, 22–25 June 2015. [Google Scholar]
Xiao, J.; Gole, A.M. A frequency scanning method for the identification of harmonic instabilities in HVDC systems. IEEE Trans. Power Del. 1995, 10, 1875–1881. [Google Scholar] [CrossRef]
Le, V.; Li, X.; Li, Y.; Dong, L.T.; Le, C. An Innovative Control Strategy to Improve the Fault Ride-Through Capability of DFIGs Based on Wind Energy Conversion Systems. Energies 2016, 9, 69. [Google Scholar] [CrossRef]
Jabr, H.M.; Lu, D.; Kar, N.C. Design and Implementation of Neuro-Fuzzy Vector Control for Wind-Driven Doubly-Fed Induction Generator. IEEE Trans. Sustain. Energy 2011, 2, 404–413. [Google Scholar] [CrossRef]
Nian, H.; Song, Y.; Zhou, P.; He, Y. Improved Direct Power Control of a Wind Turbine Driven Doubly Fed Induction Generator During Transient Grid Voltage Unbalance. IEEE Trans. Energy Convers. 2011, 26, 976–986. [Google Scholar] [CrossRef]
Wang, X.; Blaabjerg, F.; Wu, W. Modeling and Analysis of Harmonic Stability in an AC Power-Electronics-Based Power System. IEEE Trans. Power Electron. 2014, 29, 6421–6432. [Google Scholar] [CrossRef]
Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Inverse Nyquist Stability Criterion for Grid-Tied Inverters. IEEE Trans. Power Electron. 2017, 32, 1548–1556. [Google Scholar] [CrossRef]
Yoon, C.; Wang, X.; Silva, F.M.F.D.; Bak, C.L.; Blaabjerg, F. Harmonic Stability Assessment for Multi-Paralleled, Grid-Connected Inverters. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition (CICED), Shanghai, China, 5–8 November 2014; pp. 1098–1103. [Google Scholar]
Wang, L.; Gao, H.; Zou, G. Modeling Methodology and Fault Simulation of Distribution Networks Integrated with Inverter-Based DG. Control. Mod. Power Syst. 2017, 2, 31. [Google Scholar] [CrossRef]
Zhu, R.; Chen, Z.; Tang, Y.; Deng, F.; Wu, X. Dual-Loop Control Strategy for DFIG-Based Wind Turbines Under Grid Voltage Disturbances. IEEE Trans. Power Electron. 2016, 31, 2239–2253. [Google Scholar] [CrossRef]
Alaboudy, A.H.K.; Zeineldin, H.H. Flicker Minimization of DFIG Based Wind Turbines with Optimal Reactive Current Management. In Proceedings of the 2011 IEEE PES Conference on Innovative Smart Grid Technologies - Middle East (ISGT Middle East), Jeddah, Saudi Arabia, 17–20 December 2011; pp. 1–5. [Google Scholar]
Ismail, F.S.A.; Hassan, M.A.; Abido, M.A. RTDS Implementation of STATCOM-Based Power System Stabilizers. Can. J. Electr. Comput. Eng. 2014, 37, 48–56. [Google Scholar] [CrossRef]
Liu, J.; Liu, Z. Harmonic Analyzing of the Double PWM Converter in DFIG Based on Mathematical Model. Energies 2017, 10, 2087. [Google Scholar] [CrossRef]

Figure 1. The logic path of modeling and analysis procedures in this paper. Both rotor side convertor (RSC) and grid side convertor (GSC) models can be divided into two parts: the main circuit module and the control module with PLL.

Figure 2. The structure diagram of the double-fed induction generator (DFIG)-based system.

Figure 3. The structure diagram of RSC with the control system. The GSC and dc link are substituted by a dc voltage source. The orange dash line box is the circuit module of RSC, and the green dash line box is the control module of RSC.

Figure 4. The structure diagram of the RSC main circuit.

Figure 5. The small-signal transfer diagram of the RSC circuit in DFIG.

Figure 6. The small-signal transfer diagram of RSC control without PLL in DFIG.

Figure 7. The angular transfer relationship between circuit module and control module on the rotor side.

Figure 8. The small-signal transfer diagram of PLL in the RSC control. This PLL model links the variables from the circuit module to the control module.

Figure 9. The structure diagram of GSC in DFIG. The orange dash line box is the circuit module of GSC, and the green dash line box is the control module of GSC. The dc link is taken into consideration when modeling the GSC circuit.

Figure 10. The small-signal transfer diagram of the GSC circuit.

Figure 11. The small-signal transfer diagram of the GSC control excepting PLL.

Figure 12. The angular transfer relationship between the circuit module and the control module in GSC.

Figure 13. The small-signal transfer diagram of PLL in GSC control, which shows the transfer relationship of variables from the circuit module to the control module.

Figure 14. The schematic diagram of RSC and GSC in DFIG. The RSC and GSC small-signal models are interconnected with their dc variables in a dc link, and these two kinds of converters are all connected with the power grid through transformers. The system is thus a closed-loop system.

Figure 15. The equivalent circuit of the DFIG-based system. (a) The system’s equivalent circuit based on the grid output impedance and converter input impedance; (b) is the transfer diagram of the circuit described in (a), and the feedback loop can be used to evaluate the system’s stability by applying the Nyquist stability criterion.

Figure 16. The Nyquist plots of the feedback loop gain: (a) Nyquist plots in the stable case (

L_{l}

= 3.7 mH), the graphs on the right are the magnified parts in (−1, j0). The curve does not encircle the point (−1, j0), which predicts the system is still stable; (b) Nyquist plots in the unstable case (

L_{l}

= 3.8 mH), the graphs on the right are the magnified parts in (−1, j0). The curves finally enclose the point (−1, j0) and the system becomes unstable.

Figure 16. The Nyquist plots of the feedback loop gain: (a) Nyquist plots in the stable case (

L_{l}

= 3.7 mH), the graphs on the right are the magnified parts in (−1, j0). The curve does not encircle the point (−1, j0), which predicts the system is still stable; (b) Nyquist plots in the unstable case (

L_{l}

= 3.8 mH), the graphs on the right are the magnified parts in (−1, j0). The curves finally enclose the point (−1, j0) and the system becomes unstable.

Figure 17. The Nyquist plots of the feedback loop gain: (a) Nyquist plots in the stable case (

k_{i g P}

= 1), the graphs on the right are the magnified parts in (−1, j0). The point (−1, j0) is not enclosed by the curve, and the system is still stable; (b) Nyquist plots in the unstable case (

k_{i g P}

= 0.9), the graphs on the right are the magnified parts in (−1, j0). The curves enclose (−1, j0) and the system becomes unstable.

Figure 17. The Nyquist plots of the feedback loop gain: (a) Nyquist plots in the stable case (

k_{i g P}

= 1), the graphs on the right are the magnified parts in (−1, j0). The point (−1, j0) is not enclosed by the curve, and the system is still stable; (b) Nyquist plots in the unstable case (

k_{i g P}

= 0.9), the graphs on the right are the magnified parts in (−1, j0). The curves enclose (−1, j0) and the system becomes unstable.

Figure 18. Nyquist plots of the feedback loop gain: (a) Nyquist plots in the stable case (

J

= 0.293 kg∙m²), the graphs on the right are the magnified parts in (−1, j0). The point (−1, j0) is not enclosed by the curve, and the system is thus stable; (b) Nyquist plots in the unstable case (

J

= 0.294 kg∙m²), the graphs on the right are the magnified parts in (−1, j0), which is enclosed by the curve, and the system becomes unstable.

Figure 18. Nyquist plots of the feedback loop gain: (a) Nyquist plots in the stable case (

J

= 0.293 kg∙m²), the graphs on the right are the magnified parts in (−1, j0). The point (−1, j0) is not enclosed by the curve, and the system is thus stable; (b) Nyquist plots in the unstable case (

J

= 0.294 kg∙m²), the graphs on the right are the magnified parts in (−1, j0), which is enclosed by the curve, and the system becomes unstable.

Figure 19. The simulated three-phase grid output currents of GSC in the stable case (

L_{l}

= 3.7 mH).

Figure 19. The simulated three-phase grid output currents of GSC in the stable case (

L_{l}

= 3.7 mH).

Figure 20. The simulated three-phase grid output currents of GSC in the unstable case (

L_{l}

= 3.8 mH): (a) Full view of three phase simulated currents; (b) magnified view of the simulated current of phase b.

Figure 20. The simulated three-phase grid output currents of GSC in the unstable case (

L_{l}

= 3.8 mH): (a) Full view of three phase simulated currents; (b) magnified view of the simulated current of phase b.

Figure 21. The FFT analysis of the simulated grid currents in the unstable.

Table 1. The electrical parameters of the DFIG-based system.

Electrical Parameter		Value	Electrical Parameter		Value
$f_{1}$	Fundamental frequency	50 Hz	$L_{m}$	RS mutual inductance	0.108 H
$R_{u}$	Grid resistance	0.3 Ω	$R_{r}$	RSC resistance	0.15 Ω
$L_{u}$	Grid inductance	0.03 H	$L_{r}$	RSC inductance	1.2 mH
$R_{s m}$	Stator resistance	0.262 Ω	$R_{l}$	GSC resistance	0.15 Ω
$L_{s m}$	Stator self-inductance	0.122 H	$L_{l}$	GSC inductance	1.2 mH
$R_{r m}$	Rotor resistance	0.2 Ω	$C_{d}$	DC shunt capacitance	2.2 mF
$L_{r m}$	Rotor self-inductance	0.119 H	$U_{d r e f}$	DC rated voltage	500 V

Table 2. The controller parameters of RSC and GSC.

Controller Parameters		Value	Controller Parameters		Value
RSC stator current controller	$k_{i s P}$	0.3	GSC outer voltage controller	$k_{u g P}$	0.1
RSC stator current controller	$k_{i s I}$	5	GSC outer voltage controller	$k_{u g I}$	10
RSC outer speed controller	$k_{ω r P}$	0.5	PLL controller	$k_{r p p l l}$	3
RSC outer speed controller	$k_{ω r I}$	10		$k_{r i p l l}$	1400
RSC inner current controller	$k_{i r P}$	13.87		$k_{p p l l}$	3
RSC inner current controller	$k_{i r I}$	68		$k_{i p l l}$	1400
GSC inner current controller	$k_{i g P}$	5	Moment of inertia	$J$	0.1425 kg∙m²
GSC inner current controller	$k_{i g I}$	100

Table 3. Circuit parameter influences and assessments on the system’s stability ¹.

Parameters (Stable Case)	Adjusted Value	Stability Assessment	Parameters (Stable Case)	Adjusted Value	Stability Assessment
$L_{l, r}$ (1.2 mH)	3.7 mH	Stability ↓²	$L_{r m}$ (0.119 H)	0.05 H	∆
$L_{l, r}$ (1.2 mH)	3.8 mH	Unstable	$L_{r m}$ (0.119 H)	0.45 H	∆
$R_{l, r}$ (0.15 Ω)	0.02 Ω	∆ ³	$R_{r m}$ (0.2 Ω)	0.02 Ω	∆
$R_{l, r}$ (0.15 Ω)	0.5 Ω	∆	$R_{r m}$ (0.2 Ω)	0.5 Ω	∆
$L_{s m}$ (0.122 H)	0.315 H	Stability ↓	$L_{m}$ (0.108 H)	0.025 H	∆
$L_{s m}$ (0.122 H)	0.316 H	Unstable	$L_{m}$ (0.108 H)	0.390 H	∆
$R_{s m}$ (0.262 Ω)	0.105 Ω	Stability ↓	$C_{d}$ (2.2 mF)	4.3 mF	Stability ↓
$R_{s m}$ (0.262 Ω)	0.104 Ω	Unstable	$C_{d}$ (2.2 mF)	4.4 mF	Unstable

¹ Comparisons and assessments of stability are based on the stable case whose system parameters are given in Table 1 and Table 2. ² Down-arrows mean that the system stability is degraded. ³ The mark ∆ represents that the adjusted parameters have little effects on the stability of the studied system.

Table 4. Controller parameter ¹ influences and assessments on the system’s stability.

Parameters (Stable Case)	Adjusted Value	Stability Assessment	Parameters (Stable Case)	Adjusted Value	Stability Assessment
$k_{i g P}$ (5)	1	Stability ↓²	$k_{i r I}$ (68)	107	Stability ↓
$k_{i g P}$ (5)	0.9	Unstable	$k_{i r I}$ (68)	108	Unstable
$k_{i g I}$ (100)	145	Stability ↓	$k_{ω r P}$ (0.5)	1.7	Stability ↓
$k_{i g I}$ (100)	146	Unstable	$k_{ω r P}$ (0.5)	1.8	Unstable
$k_{u g P}$ (0.1)	0.9	Stability ↓	$k_{ω r I}$ (10)	3.2	Stability ↓
$k_{u g P}$ (0.1)	1	Unstable	$k_{ω r I}$ (10)	3.1	Unstable
$k_{u g I}$ (10)	36	Stability ↓	$k_{i s P}$ (0.3)	1.1	Stability ↓
$k_{u g I}$ (10)	37	Unstable	$k_{i s P}$ (0.3)	1.2	Unstable
$k_{i r P}$ (13.8)	7.3	Stability ↓	$k_{i s I}$ (5)	1.6	Stability ↓
$k_{i r P}$ (13.8)	7.2	Unstable	$k_{i s I}$ (5)	1.5	Unstable

¹ The controller parameters can be divided into the RSC controller (outer speed PI and inner current PI) and the GSC controller (outer voltage PI and inner current PI). ² Down-arrows mean that the system stability is degraded.

Table 5. The values of parameters for the critical stability case.

Parameter	Simulated Value	Deviation	Parameter	Simulated Value	Deviation
$L_{l}$	3.8 mH	0	$k_{u g I}$	38.5	3.9%
$L_{r}$	3.8 mH	0	$k_{i r P}$	7.2	0
$L_{s m}$	0.315 mH	0.3%	$k_{i r I}$	108	0
$R_{s m}$	0.104 Ω	0	$k_{ω r P}$	1.9	5.3%
$C_{d}$	4.5 mF	2.2%	$k_{ω r I}$	3.3	6.1%
$k_{i g P}$	0.9	0	$k_{i s P}$	1.2	0
$k_{i g I}$	146	0	$k_{i s I}$	1.5	0
$k_{u g P}$	1.06	5.7%	$J$	0.292 kg∙m²	0.7%

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Chen, X.; Liu, Z. Impedance Modeling and Stability Analysis of the Converters in a Double-Fed Induction Generator (DFIG)-Based System. Energies 2019, 12, 2500. https://doi.org/10.3390/en12132500

AMA Style

Chen X, Liu Z. Impedance Modeling and Stability Analysis of the Converters in a Double-Fed Induction Generator (DFIG)-Based System. Energies. 2019; 12(13):2500. https://doi.org/10.3390/en12132500

Chicago/Turabian Style

Chen, Xunjun, and Zhigang Liu. 2019. "Impedance Modeling and Stability Analysis of the Converters in a Double-Fed Induction Generator (DFIG)-Based System" Energies 12, no. 13: 2500. https://doi.org/10.3390/en12132500

APA Style

Chen, X., & Liu, Z. (2019). Impedance Modeling and Stability Analysis of the Converters in a Double-Fed Induction Generator (DFIG)-Based System. Energies, 12(13), 2500. https://doi.org/10.3390/en12132500

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

Impedance Modeling and Stability Analysis of the Converters in a Double-Fed Induction Generator (DFIG)-Based System

Abstract

1. Introduction

2. Small-Signal Modeling of the Rotor Side Convertor (RSC) in the Double-Fed Induction Generator (DFIG)

2.1. Small-Signal Modeling of the RSC Circuit

2.2. Small-Signal Modeling of RSC Control with PLL

3. Small-Signal Modeling of the Grid Side Convertor (GSC) in DFIG

3.1. Small-Signal Modeling of the GSC Circuit

3.2. Small-Signal Modeling of GSC Control with PLL

4. Analysis of Harmonic Stability and Real-Time Digital Simulation (RTDS) Verification

4.1. Impedance Modeling of Equivalent Systems

4.1.1. Input Impedance Modeling of RSC and GSC connected in DFIG

4.1.2. Impedance Modeling of the Grid-Connected System

4.2. Impedance-Based Stability Analysis

4.2.1. Circuit parameters stability assessment

4.2.2. Controller parameters stability assessment

4.2.3. Mechanical parameters stability assessment

4.3. RTDS Simulation Verification

5. Conclusions

Author Contributions

Funding

Conflicts of Interest

Appendix A

Appendix B

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI