Primal-Dual Learning Based Risk-Averse Optimal Integrated Allocation of Hybrid Energy Generation Plants under Uncertainty
Abstract
:1. Introduction
1.1. Motivations
1.2. Literature Review
1.3. Contributions
- We propose a stochastic bi-objective 0-1 mixed nonlinear programming to model the integrated allocation of hybrid energy generation plants under uncertainty. We aim to minimize total expected costs and CO2 emissions to meet energy demand.
- We propose a risk-constrained stochastic optimization model to control the potential risks caused by uncertainty in demand. The coherent risk measure (i.e., conditional value-at-risk (CVaR)), is incorporated to evaluate risks and express risk preferences. We also provide an equivalent model to transform the bi-objective model to a single-objective model, which is important to solving the NP-hard problem.
- We develop a primal-dual based learning algorithm to solve the risk-averse model. By the Lagrange duality, we first present a saddle point problem, then update the primal and dual variables simultaneously. We show that the algorithm does not need to assume that probability distribution is known a priori, and that a desirable gap can be achieved by utilizing historical data.
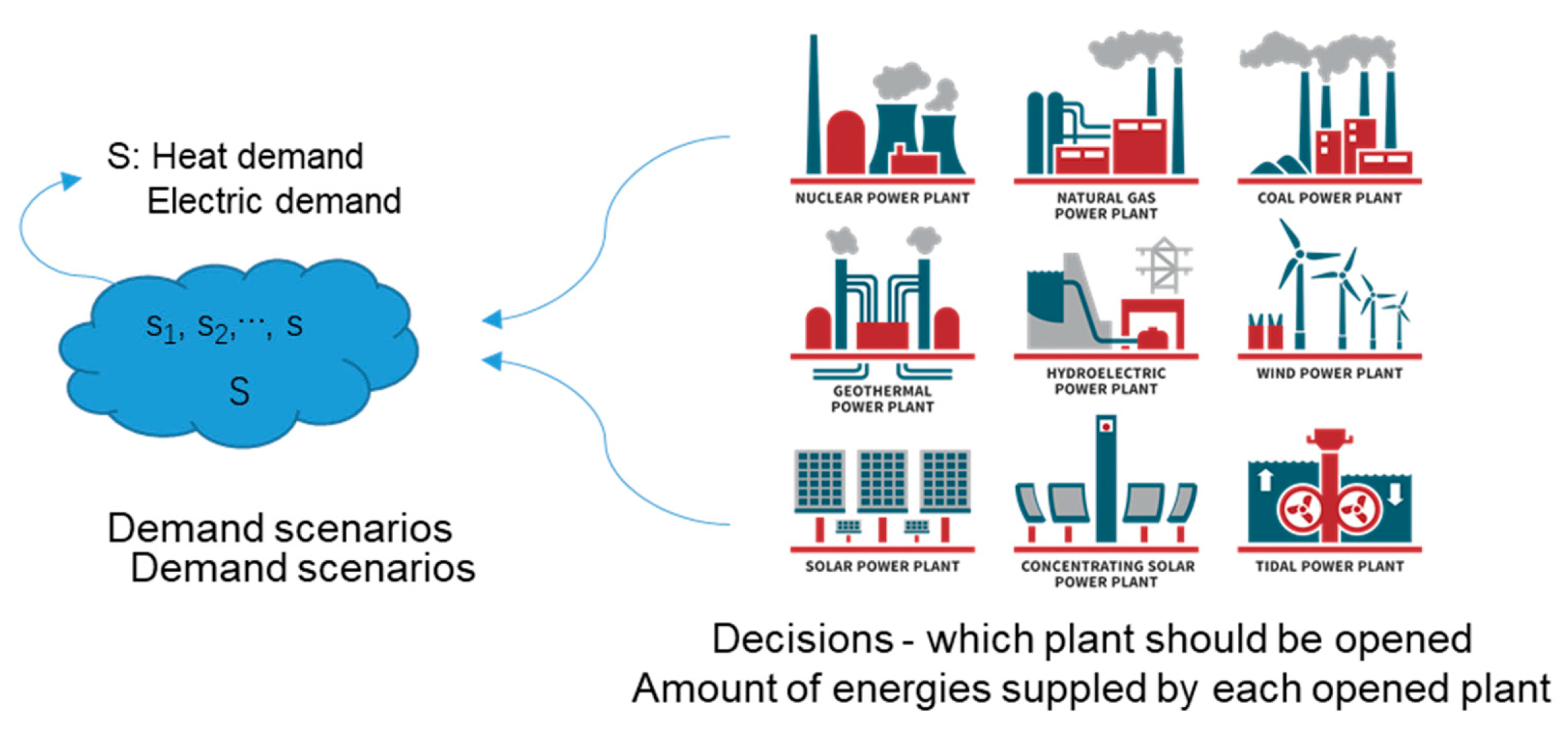
2. Problem Description and Model Formulation
2.1. Problem Description and Classic Model
2.2. Risk-Averse Model
- Monotonicity: If , then ;
- Subadditivity: holds;
- Positive homogeneity: If , then .
- Translation invariance: For , we have .
3. Solution Method
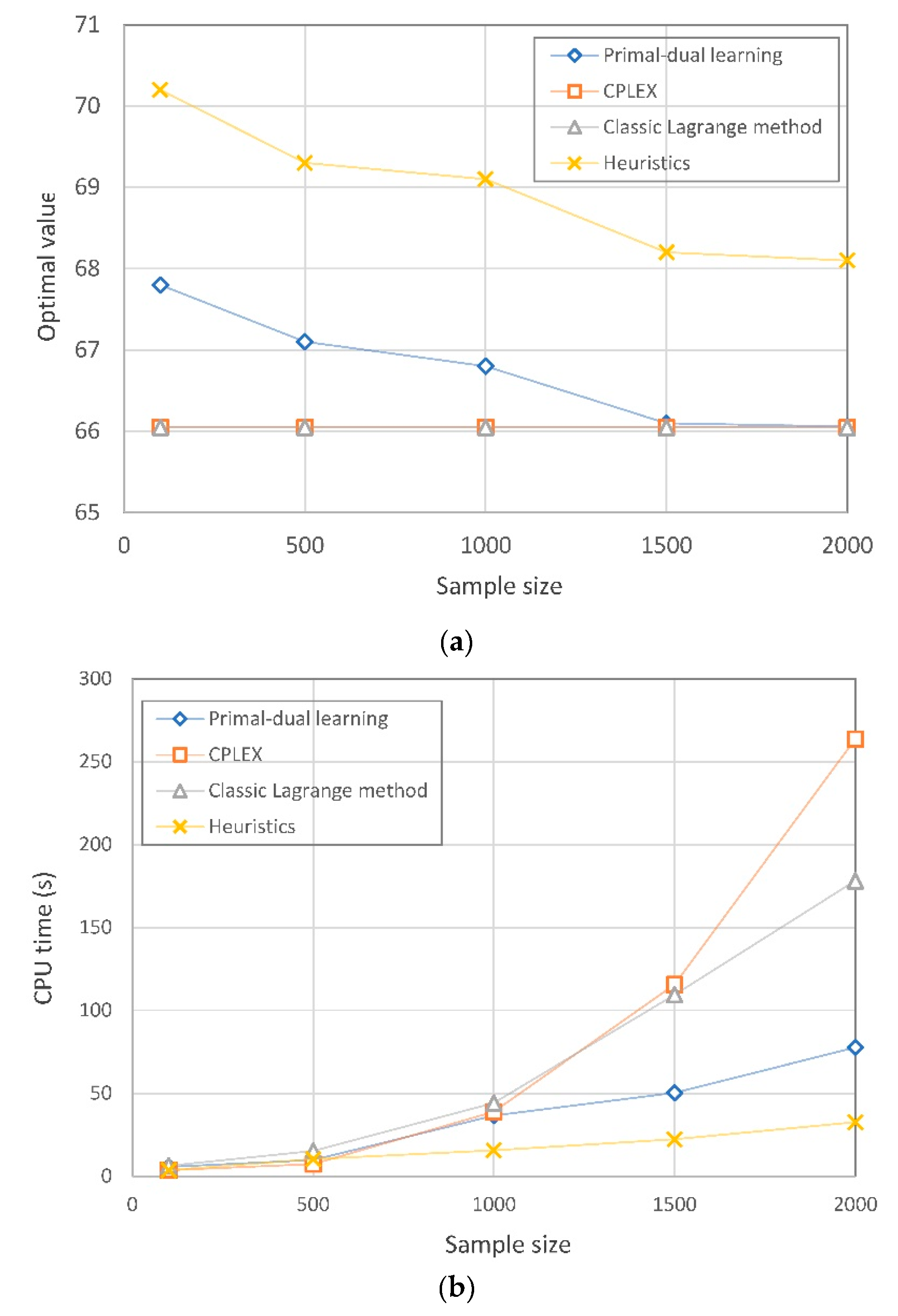
4. Numerical Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alanne, K.; Saari, A. Distributed energy generation and sustainable development. Renew. Sust. Energy Rev. 2006, 10, 539–558. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, K.; Zhang, W.T.; Lee, K.Y. Hierarchical energy management for the multienergy carriers system with different interest bodies. Energies 2018, 11, 2834. [Google Scholar] [CrossRef]
- Lopez-Rey, A.C.-R.S.; Gil-Ortego, R.; Colmenar-Santos, A. Evaluation of supply–demand adaptation of photovoltaic–wind hybrid plants integrated into an urban environment. Energies 2019, 12, 1780. [Google Scholar] [CrossRef]
- Bruno, S.D.G.; La Scala, M.; Meloni, C. A microforecasting module for energy management in residential and tertiary buildings. Energies 2019, 12, 1006. [Google Scholar] [CrossRef]
- Chen, C.; Long, H.L.; Zeng, X.T. Planning a sustainable urban electric power system with considering effects of new energy resources and clean production levels under uncertainty: A case study of tianjin, china. J. Clean. Prod. 2018, 173, 67–81. [Google Scholar] [CrossRef]
- Ebrahimi, S.B. A stochastic multi-objective location-allocation-routing problem for tire supply chain considering sustainability aspects and quantity discounts. J. Clean. Prod. 2018, 198, 704–720. [Google Scholar] [CrossRef]
- Niet, T.; Lyseng, B.; English, J.; Keller, V.; Palmer-Wilson, K.; Moazzen, I.; Robertson, B.; Wild, P.; Rowe, A. Hedging the risk of increased emissions in long term energy planning. Energy Strateg. Rev. 2017, 16, 1–12. [Google Scholar] [CrossRef]
- Chen, Y.Z.; He, L.; Li, J.; Cheng, X.; Lu, H.W. An inexact bi-level simulation-optimization model for conjunctive regional renewable energy planning and air pollution control for electric power generation systems. Appl. Energy 2016, 183, 969–983. [Google Scholar] [CrossRef]
- Xie, Y.L.; Huang, G.H.; Li, W.; Ji, L. Carbon and air pollutants constrained energy planning for clean power generation with a robust optimization model-a case study of jining city, china. Appl. Energy 2014, 136, 150–167. [Google Scholar] [CrossRef]
- Xie, Y.L.; Wang, L.R.; Huang, G.H.; Xia, D.H.; Ji, L. A stochastic inexact robust model for regional energy system management and emission reduction potential analysis-a case study of zibo city, china. Energies 2018, 11, 2108. [Google Scholar] [CrossRef]
- Xie, Y.L.; Xia, D.H.; Ji, L.; Zhou, W.N.; Huang, G.H. An inexact cost-risk balanced model for regional energy structure adjustment management and resources environmental effect analysis—A case study of shandong province, china. Energy 2017, 126, 374–391. [Google Scholar] [CrossRef]
- Ji, L.; Huang, G.H.; Xie, Y.L.; Zhou, Y.; Zhou, J.F. Robust cost-risk tradeoff for day-ahead schedule optimization in residential microgrid system under worst-case conditional value-at risk consideration. Energy 2018, 153, 324–337. [Google Scholar] [CrossRef]
- Lee, S.K.; Mogi, G.; Kim, J.W. Energy technology roadmap for the next 10 years: The case of korea. Energy Policy 2009, 37, 588–596. [Google Scholar] [CrossRef]
- Powell, W.B.; George, A.; Simao, H.; Scott, W.; Lamont, A.; Stewart, J. Smart: A stochastic multiscale model for the analysis of energy resources, technology, and policy. Informs J. Comput. 2012, 24, 665–682. [Google Scholar] [CrossRef]
- Pereira, M.V.F.; Pinto, L.M.V.G. Multi-stage stochastic optimization applied to energy planning. Math Program 1991, 52, 359–375. [Google Scholar] [CrossRef]
- Zhao, J.Y.; Hobbs, B.F.; Pang, J.S. Long-run equilibrium modeling of emissions allowance allocation systems in electric power markets. Oper. Res. 2010, 58, 529–548. [Google Scholar] [CrossRef]
- Simon, C.; Parkinson, N.D. Long-term energy planning with uncertain environmental performance metrics. Appl. Energy 2015, 147, 402–412. [Google Scholar]
- Snyder, L.V. Facility location under uncertainty: A review. IIE Trans. 2006, 38, 537–554. [Google Scholar] [CrossRef]
- Dicorato, M.; Forte, G.; Trovato, M. Environmental-constrained energy planning using energy-efficiency and distributed-generation facilities. Renew. Energy 2008, 33, 1297–1313. [Google Scholar] [CrossRef]
- Muis, Z.A.; Hashim, H.; Manan, Z.A.; Taha, F.M.; Douglas, P.L. Optimal planning of renewable energy-integrated electricity generation schemes with co2 reduction target. Renew. Energy 2010, 35, 2562e2570. [Google Scholar] [CrossRef]
- Modarres, M.; Izadpanahi, E. Aggregate production planning by focusing on energy saving: A robust optimization approach. J. Clean. Prod. 2016, 133, 1074–1085. [Google Scholar] [CrossRef]
- Dellino, G.; Kleijnen, J.P.C.; Meloni, C. Robust optimization in simulation: Taguchi and krige combined. Informs J. Comput. 2012, 24, 471–484. [Google Scholar] [CrossRef]
- Yu, G.D.; Haskell, W.B.; Liu, Y. Resilient facility location against the risk of disruptions. Transport Res. B Methodol. 2017, 104, 82–105. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust optimization - methodology and applications. Math Program 2002, 92, 453–480. [Google Scholar] [CrossRef]
- Yu, G.D.; Li, F.; Yang, Y. Robust supply chain networks design and ambiguous risk preferences. Int. J. Prod. Res. 2017, 55, 1168–1182. [Google Scholar] [CrossRef]
- Shapiro, A. On kusuoka representation of law invariant risk measures. Math. Oper. Res. 2013, 38, 142–152. [Google Scholar] [CrossRef]




| Notations | Meanings |
|---|---|
| Set | |
| I | The set of electrical energy or co-generation technologies, indexed by i |
| J | The set of heat generation technologies, indexed by j |
| S | The set of scenarios, indexed by s |
| N | The set of energy generation technologies and facilities, N = {I,J}, indexed by n |
| Parameters | |
| Total demand of energy in the region under scenario s | |
| Total demand of heating energy in the region under scenario s | |
| Daily operating cost of facility n under scenario s | |
| Fixed cost of building a facility n | |
| Fraction co-generation from facility i used to supply electricity, | |
| Capacity of facility n | |
| CO2 emission rate by facility n | |
| Budget of CO2 emissions | |
| Waste disposed at a landfill plant of electricity facility n | |
| W | Capacity of a landfill plant |
| The probability of scenario s occurring | |
| The risk level and | |
| Decision variables | |
| Binary variable, indicates building or making additions to facility n under scenario s and 0 otherwise | |
| Amount of energy generated from supplier n under scenario s, | |
| Amount of electrical heat energy generated from supplier i under scenario s, | |
| Amount of heat and electrical energy from supplier i as co-generation under scenario s, |
| Primal-dual-based static learning algorithm |
| Input: total iterations T, set counter t = 1, step size γ >0 |
| 1. Set , |
| 2. Draw a sample according to the distribution |
| 3. Compute the gradient ascent of primal variables and gradient descent of dual variable |
| 4. Update |
| 5. Increment t = t + 1 and go to Step 2 |
| Output: |
| Year | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Demand | 381,471 | 386,597 | 399,548 | 412,548 | 415,425 | 412,597 | 425,895 | 435,879 | 445,135 | 445,987 | 452,369 |
| Year | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Coal | 1,925,482 | 1,926,987 | 1,935,698 | 1,939,874 | 1,965,474 | 1,968,957 | 1,978,465 | 1,965,789 | 1,978,459 | 1,985,458 | 1,992,548 |
| Petroleum | 98,552 | 99,658 | 102,450 | 102,548 | 102,658 | 102,365 | 102,987 | 108,974 | 110,220 | 123,051 | 129,540 |
| Natural gas | 635,478 | 659,874 | 669,587 | 675,948 | 701,254 | 709,842 | 713,587 | 719,854 | 723,658 | 739,587 | 752,548 |
| Nuclear | 712,641 | 712,584 | 723,658 | 736,548 | 745,694 | 754,618 | 759,847 | 765,814 | 773,248 | 782,147 | 793,256 |
| Wind turbine | 7125 | 8426 | 8845 | 9014 | 9814 | 9921 | 10,111 | 10,954 | 11,024 | 11,984 | 12,364 |
| Solar thermal | 654 | 785 | 798 | 823 | 865 | 877 | 895 | 921 | 933 | 954 | 966 |
| Year | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Coal | 29.3 | 29.5 | 31.1 | 30.6 | 32.8 | 33.9 | 36.5 | 35.2 | 37.6 | 38.6 | 39.0 |
| Petroleum | 25.1 | 25.3 | 26.8 | 26.4 | 26.9 | 27.9 | 30.7 | 30.2 | 31.6 | 32.3 | 33.2 |
| Natural gas | 32.6 | 33.6 | 34.9 | 35.7 | 37.5 | 38.5 | 38.1 | 39.6 | 40.3 | 40.8 | 40.6 |
| Nuclear | 26.3 | 26.2 | 25.1 | 24.2 | 23.6 | 25.2 | 22.5 | 22.3 | 24.2 | 21.9 | 21.8 |
| Wind turbine | 10.1 | 10.2 | 9.9 | 9.8 | 9.8 | 9.6 | 9.5 | 9.5 | 9.7 | 9.5 | 9.5 |
| Solar thermal | 9.3 | 9.3 | 9.2 | 9.1 | 9.1 | 9.2 | 9.0 | 9.0 | 8.8 | 8.6 | 8.7 |
| Year | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Coal | 5.69 | 5.87 | 5.99 | 6.25 | 6.36 | 6.78 | 7.21 | 7.56 | 7.88 | 8.30 | 8.91 |
| Petroleum | 2.36 | 2.55 | 2.89 | 3.21 | 3.45 | 3.98 | 4.33 | 4.51 | 4.88 | 5.02 | 5.44 |
| Natural gas | 1.38 | 1.65 | 1.98 | 2.22 | 2.56 | 3.68 | 3.44 | 3.59 | 3.89 | 4.22 | 5.23 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Xia, X.; Yu, G. Primal-Dual Learning Based Risk-Averse Optimal Integrated Allocation of Hybrid Energy Generation Plants under Uncertainty. Energies 2019, 12, 2275. https://doi.org/10.3390/en12122275
Zhao X, Xia X, Yu G. Primal-Dual Learning Based Risk-Averse Optimal Integrated Allocation of Hybrid Energy Generation Plants under Uncertainty. Energies. 2019; 12(12):2275. https://doi.org/10.3390/en12122275
Chicago/Turabian StyleZhao, Xiao, Xuhui Xia, and Guodong Yu. 2019. "Primal-Dual Learning Based Risk-Averse Optimal Integrated Allocation of Hybrid Energy Generation Plants under Uncertainty" Energies 12, no. 12: 2275. https://doi.org/10.3390/en12122275
APA StyleZhao, X., Xia, X., & Yu, G. (2019). Primal-Dual Learning Based Risk-Averse Optimal Integrated Allocation of Hybrid Energy Generation Plants under Uncertainty. Energies, 12(12), 2275. https://doi.org/10.3390/en12122275




