On the Energy Efficiency of Millimeter Wave Massive MIMO Based on Hybrid Architecture
Abstract
:1. Introduction
- We formulate and derive the spectral efficiency of mmWave Massive MIMO by using the hybrid precoding.
- The realistic model of the circuit power consumption is derived and used for the formulation and computation of energy efficiency in this article.
- The hybrid precoders and decoders are designed by taking the unit-modulus constraint and all the system constraint into account.
- We propose the PCEM algorithm to optimize the energy efficiency by taking all the constraint into account.
- The comparison is presented between the proposed and reference algorithms and the complexity of the proposed algorithm is computed to highlight the significance of the proposed algorithm.
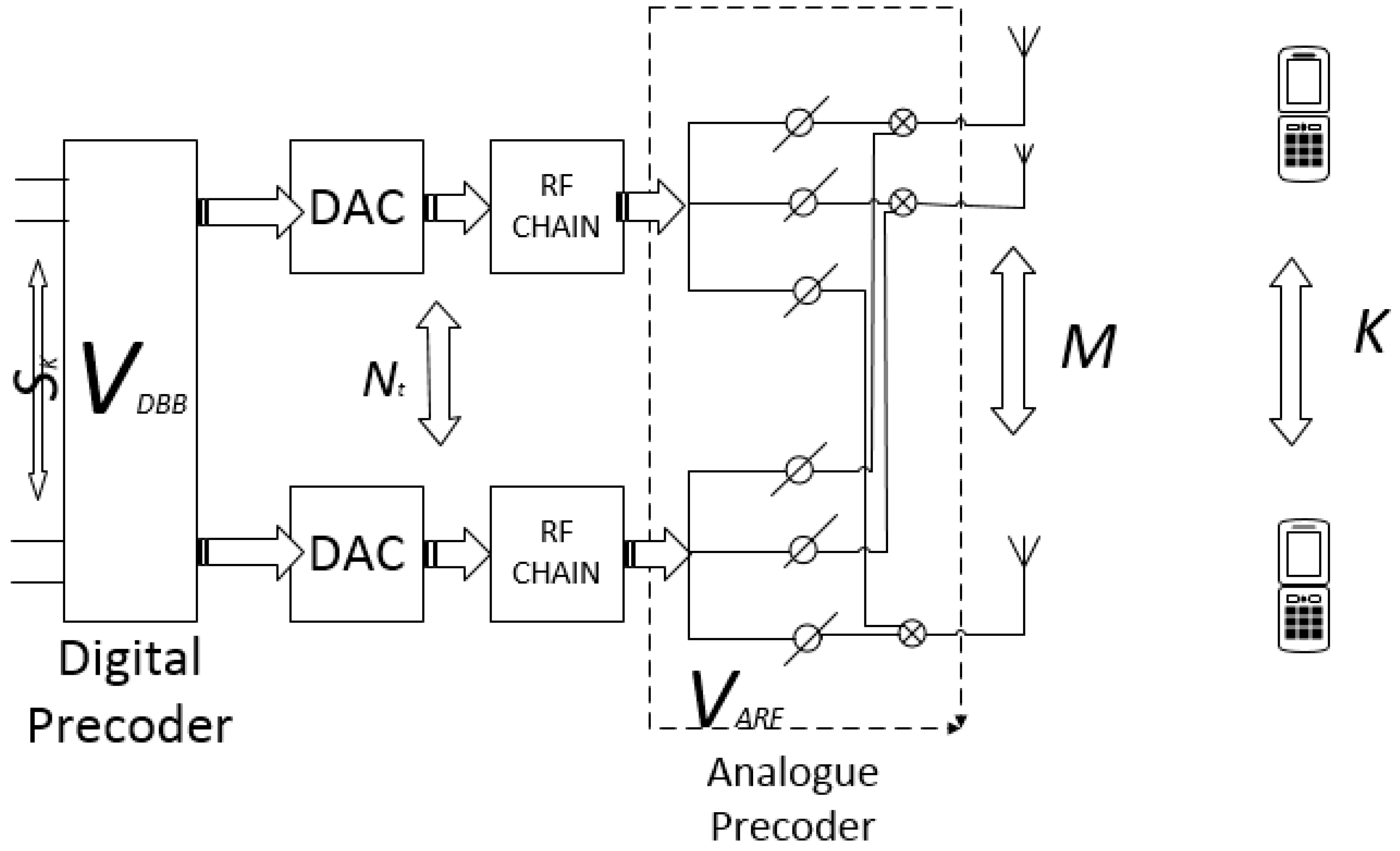
2. System Model
3. Millimeter Wave Channel Modeling
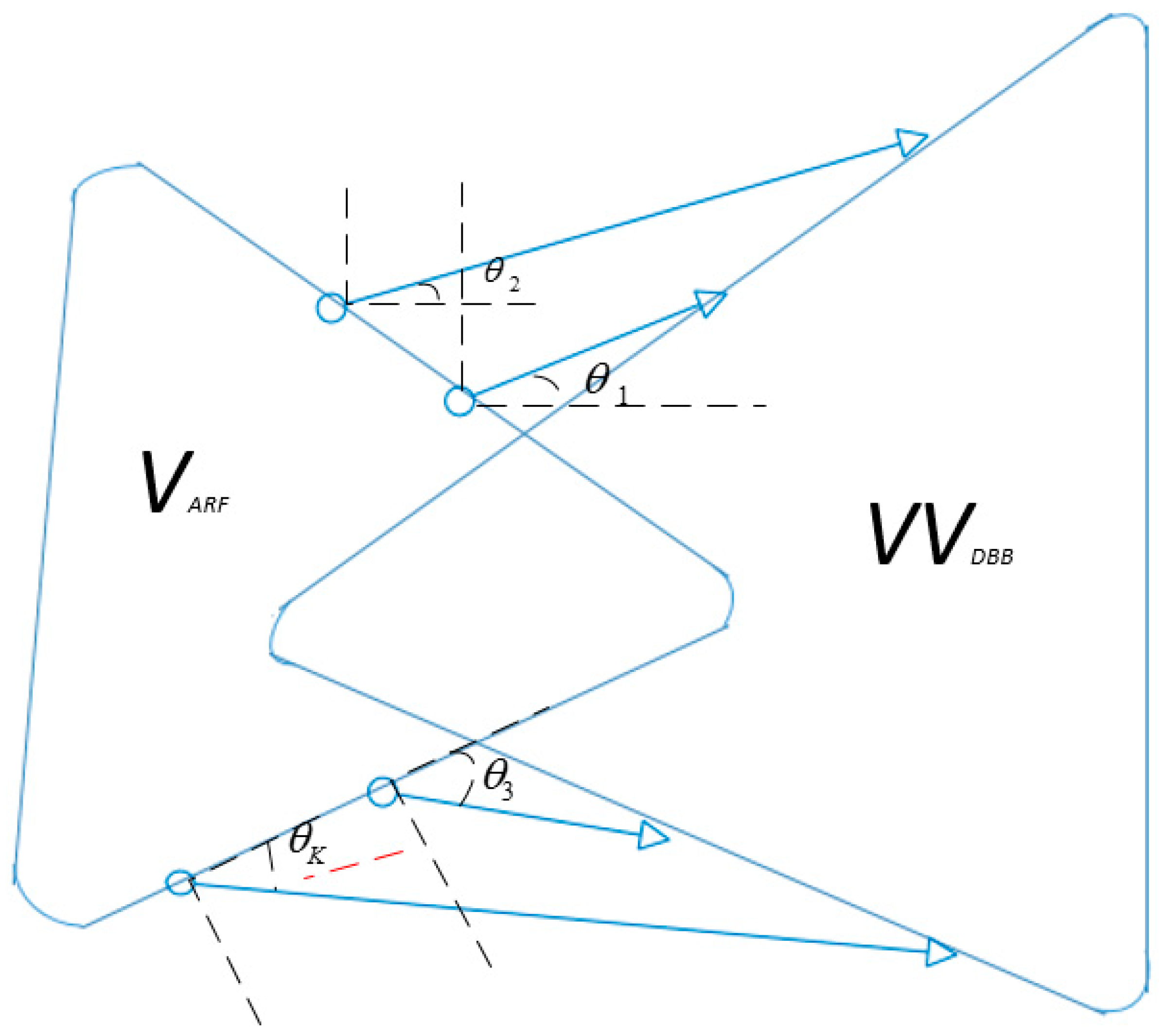
4. Modeling of the Hybrid Precoders and Decoders
- The low complexity algorithm is required to solve the (5) during each transmission time;
- All the non- zero entries of have the constraint of unit modulus, i.e., ;
- It is difficult to find the solution due to the constraint of unit modulus and the product of with ;
- Therefore, we need to simplify Equation (5) to get rid of the products of with .
5. Modeling of the Power Consumption
6. Proposed Algorithm and the Optimization of Energy Efficiency
| Algorithm 1 Power Controlled Energy Maximization (PCEM) Algorithm |
| Require: , , , , and . |
| 1. Build the and with arbitrary angles. |
| 2. Generate for the given number of and by using the (4). |
| 3. Compute SVD and SVD by using the (9). |
| 4. Update the and by using the (8). |
| 5. Use the and to compute the and by using the (10). |
| 6. Use the , H, , and to compute the optimal transmitted power by using the (30). |
| 7. Use the optimal to compute , and by using the (3), (15) and (21) respectively. |
| 8. Use the optimal , , , to compute the optimal . |
| 9. Return , and . |
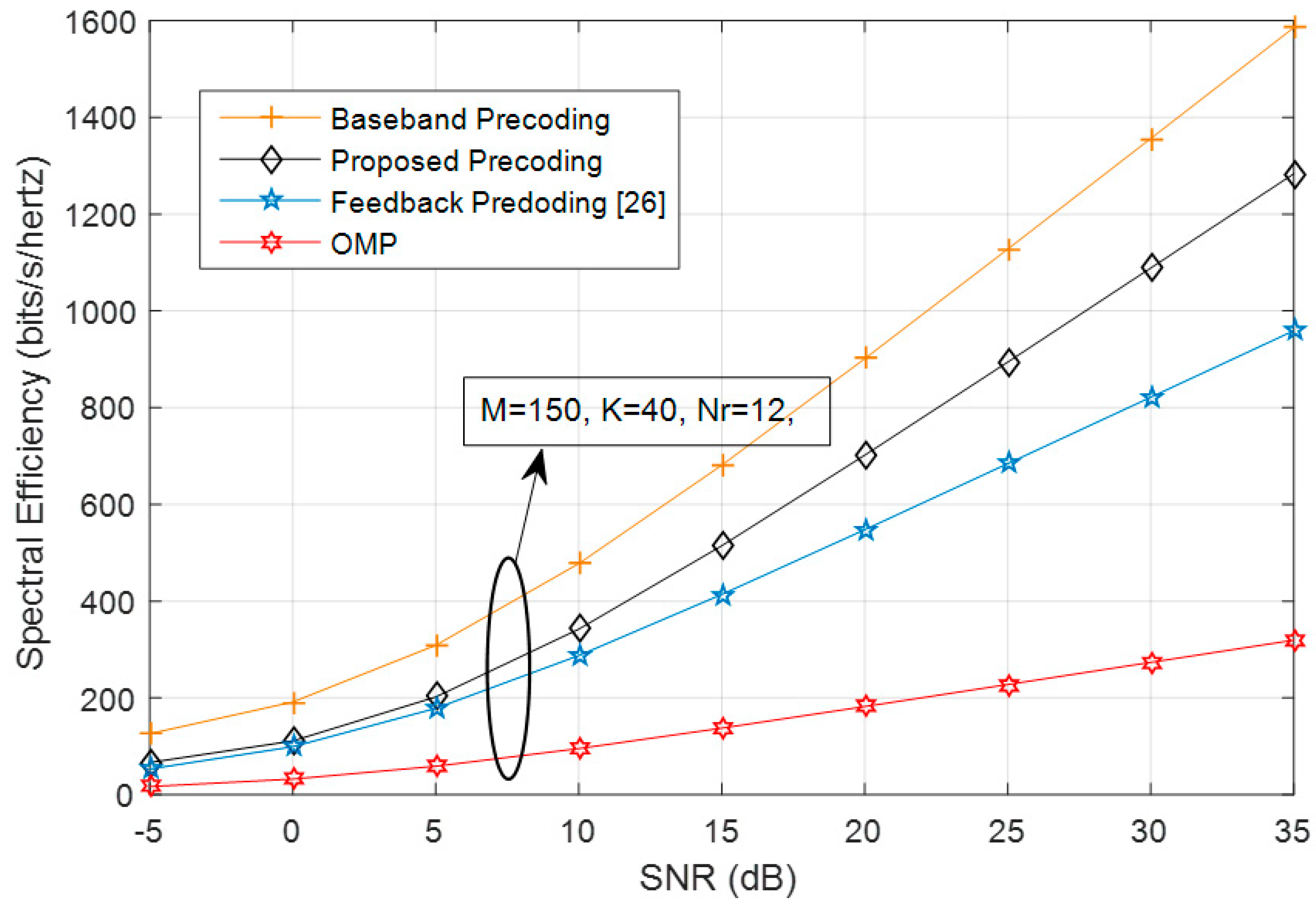
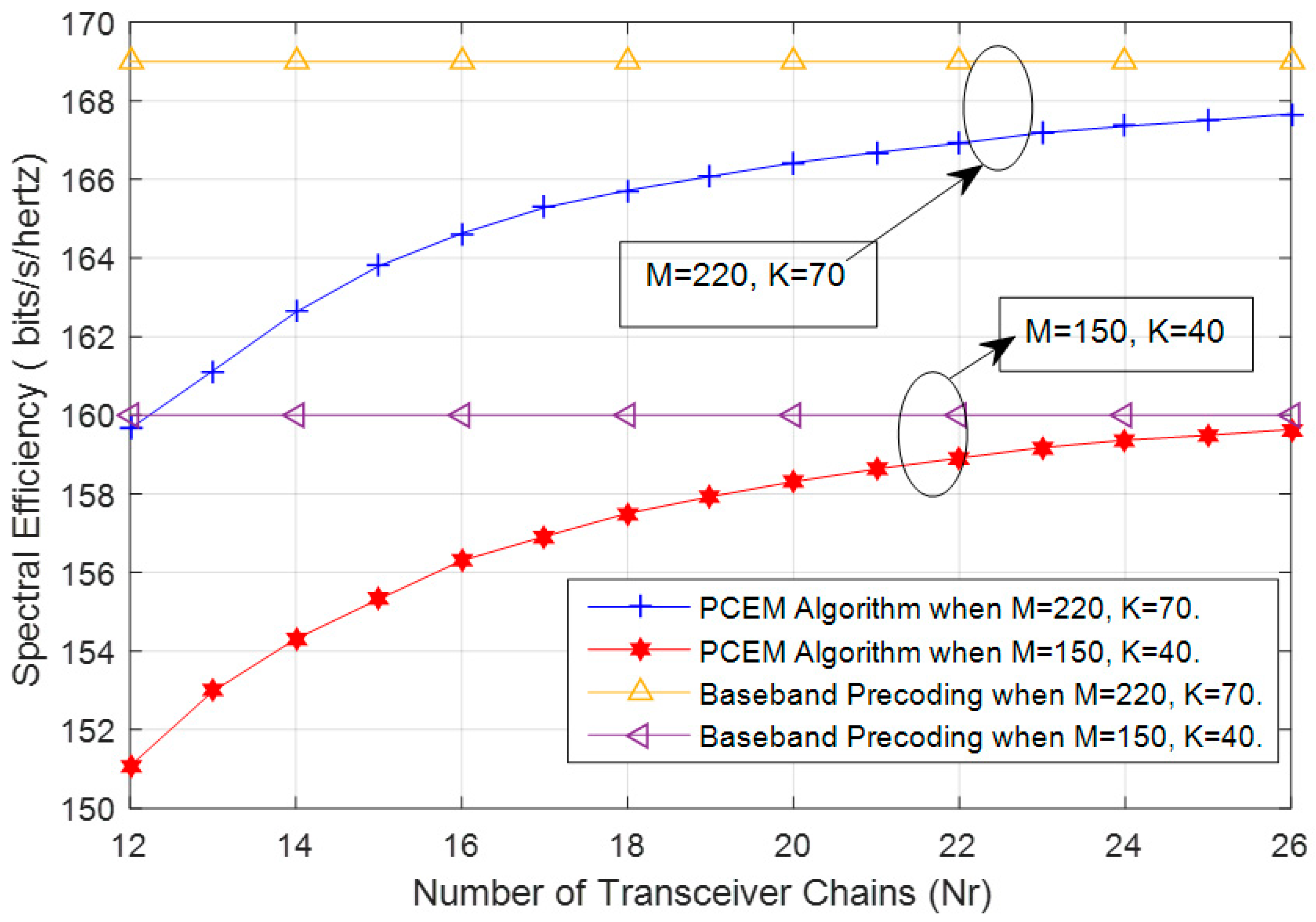
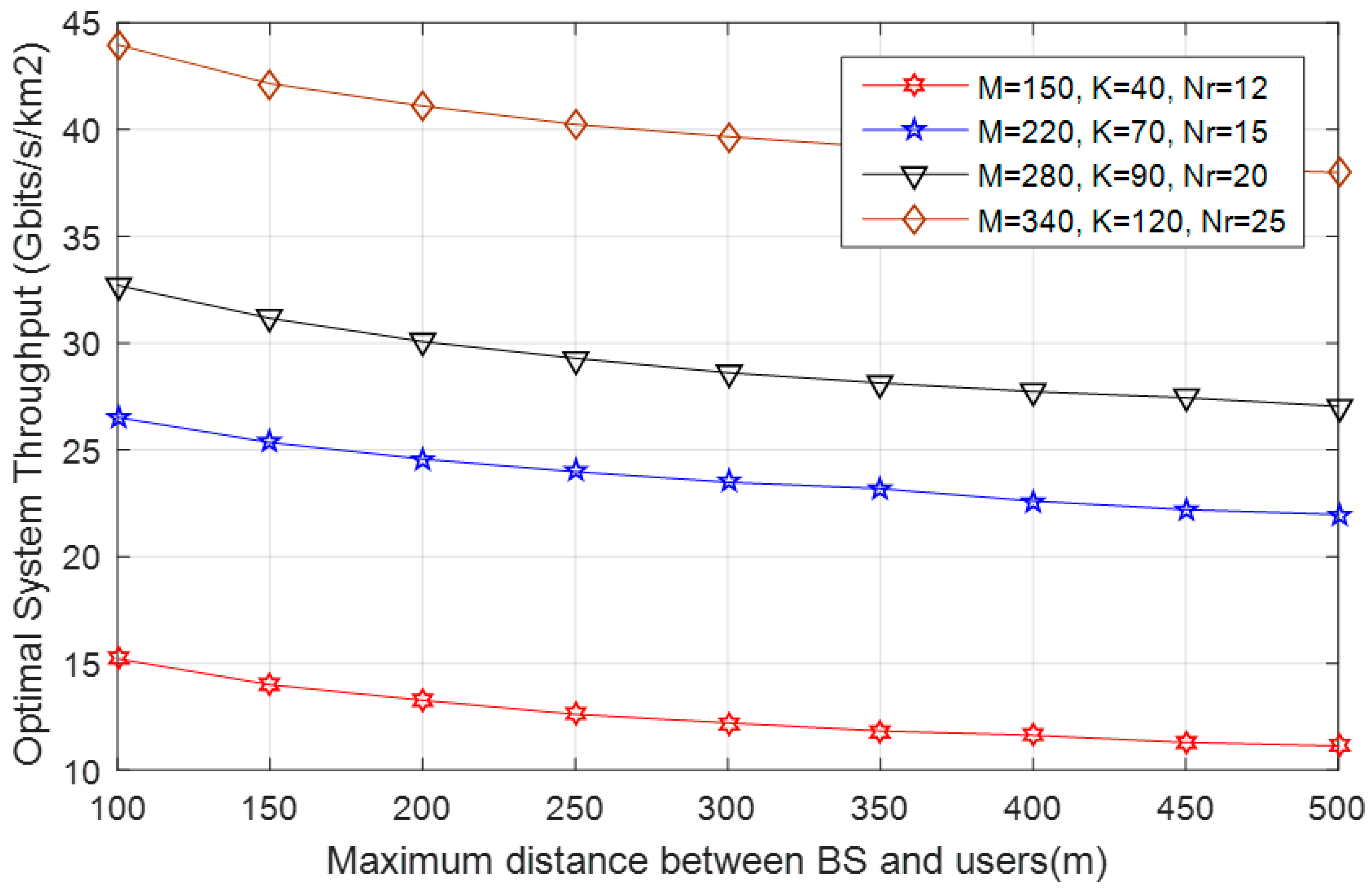
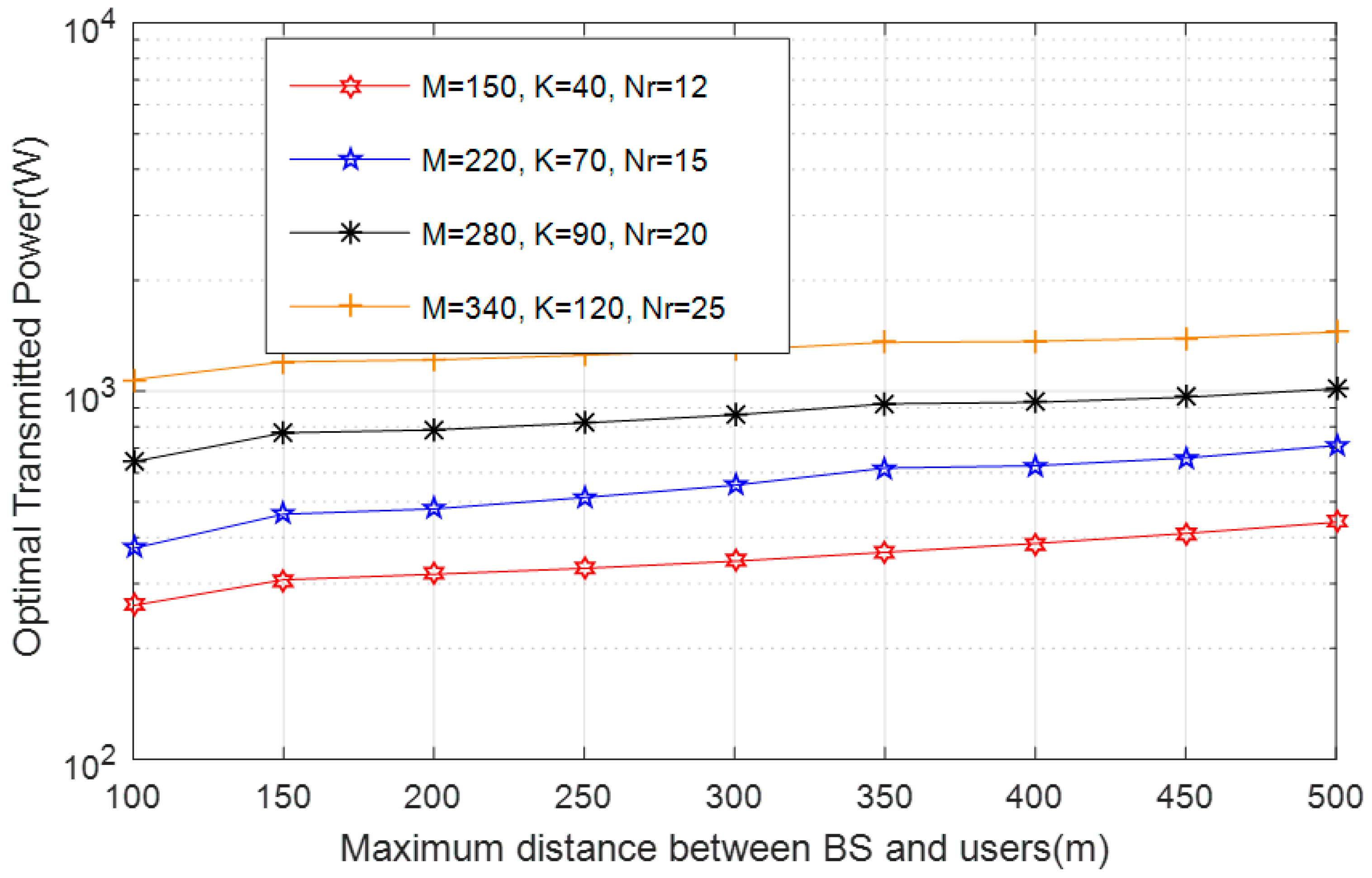
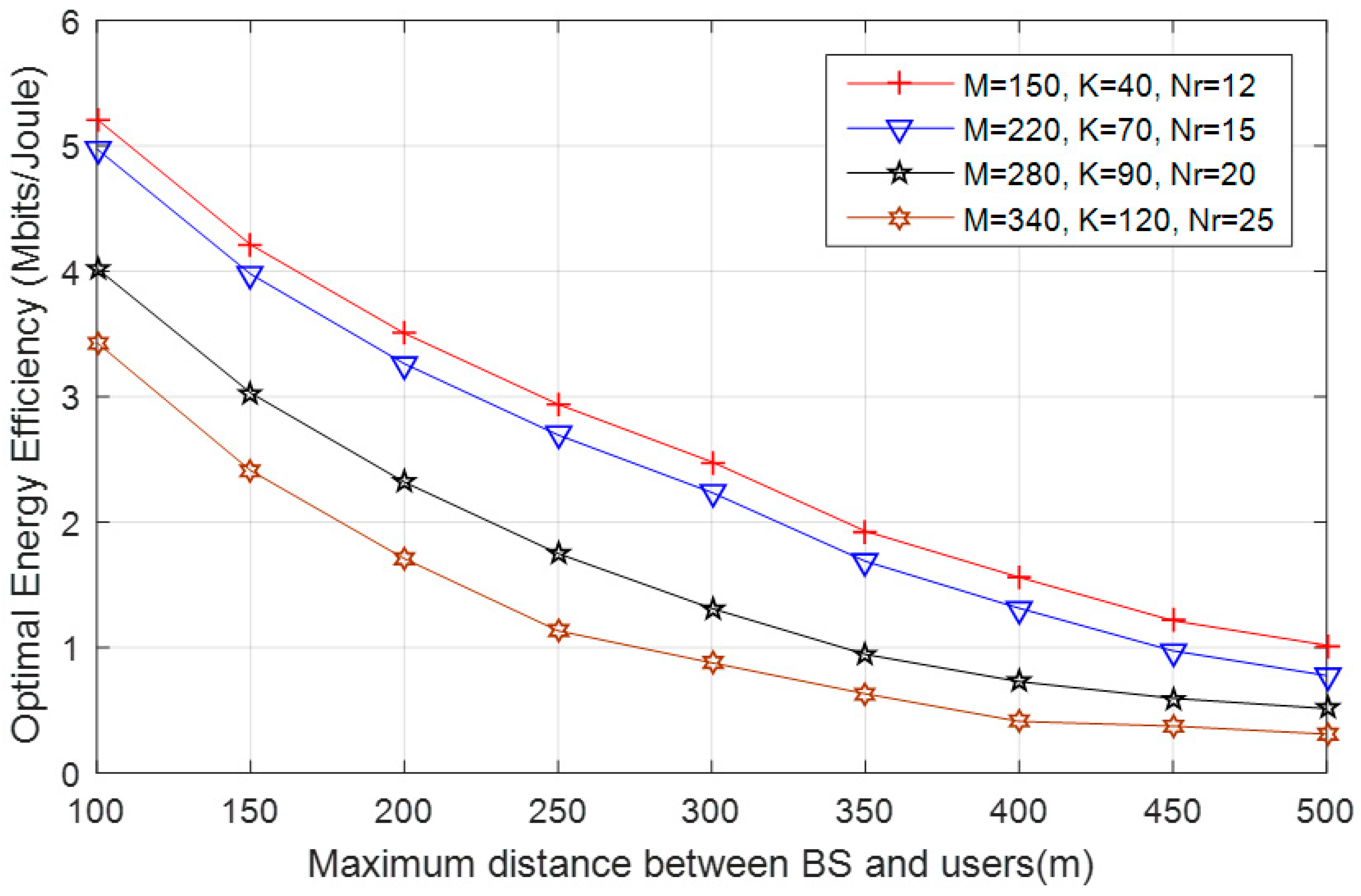
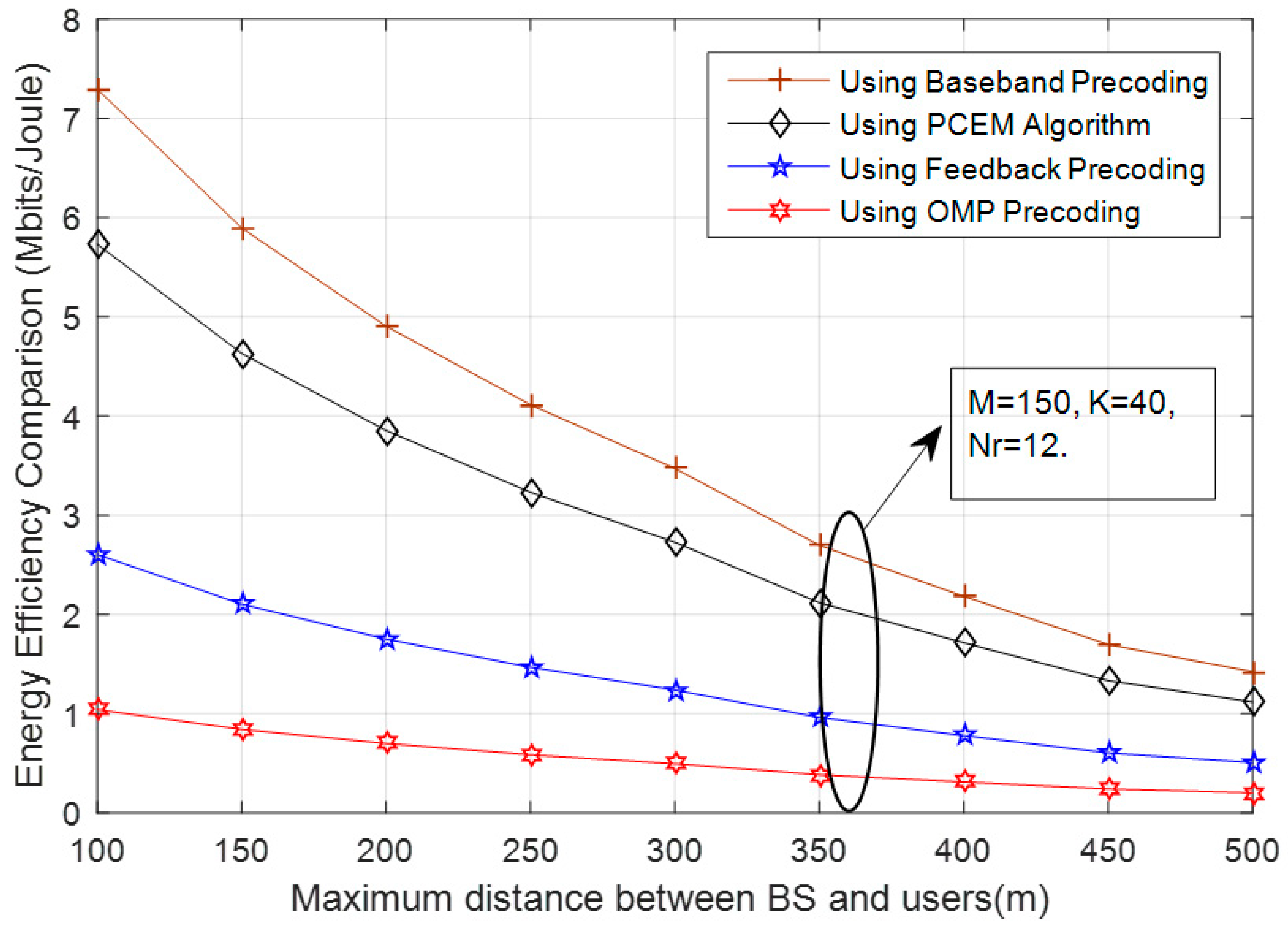
7. Simulation Results
8. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Ramezani, P.; Jamalipour, A. Toward the evolution of wireless powered communication networks for the future Internet of Things. IEEE Netw. 2017, 31, 62–69. [Google Scholar] [CrossRef]
- Vu, T.X.; Chatzinotas, S.; Ottersten, B. Edge-caching wireless networks: Energy-efficient design and optimization. IEEE Trans. Wirel. Commun. 2018, 17, 2827–2839. [Google Scholar] [CrossRef]
- Cisco. Cisco Visual Networking Index: Global Mobile Data Traffic Forecast Update 2016–2021; White Paper; Cisco: San Jose, CA, USA, 2017. [Google Scholar]
- Liang, W.; Ng, S.X.; Hanzo, L. Cooperative overlay spectrum access in cognitive radio networks. IEEE Commun. Surv. Tutor. 2017, 19, 1924–1944. [Google Scholar] [CrossRef]
- Zorba, H.O. Spread spectrum versus non-spread spectrum techniques to combat mobile radio impairments. In Proceedings of the IEEE/AFCEA EUROCOMM 2000. Information Systems for Enhanced Public Safety and Security, Munich, Germany, 9–19 May 2000; pp. 228–232. [Google Scholar]
- Liang, Y.C.; Chen, K.C.; Li, G.Y.; Mahonen, P. Cognitive radio networking and communications: An overview. IEEE Trans. Veh. Technol. 2011, 60, 3386–3407. [Google Scholar] [CrossRef]
- Hidayah, N.; Adnan, M.; Rafiqul, I.M.; Zahirul Alam, A.H.M. Massive MIMO for Fifth Generation (5G): Opportunities and Challenges. In Proceedings of the 2016 International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 26–27 July 2016; pp. 47–52. [Google Scholar]
- Han, S.; Chih-Lin, I.; Xu, Z.; Rowell, C. Large-scale antenna systems with hybrid analog and digital beamforming for millimeter wave 5G. IEEE Commun. Mag. 2015, 53, 186–194. [Google Scholar] [CrossRef]
- Wong, V.W.S.; Schober, R.; Ng, D.W.K.; Wang, L. Key Technologies for 5G Wireless Systems, 1st ed.; Cambridge University Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Wu, Q.; Li, G.Y.; Chen, W.; Ng, D.W.K.; Schober, R. An Overview of Sustainable Green 5G Networks. IEEE Wirel. Commun. 2017, 24, 72–80. [Google Scholar] [CrossRef] [Green Version]
- Guariglia, E. Entropy and fractal antennas. Entropy 2016, 18, 84. [Google Scholar] [CrossRef]
- Ahmad Khan, A.; Uthansakul, P.; Duangmanee, P.; Uthansakul, M. Energy Efficient Design of Massive MIMO by Considering the Effects of Nonlinear Amplifiers. Energies 2018, 11, 1045. [Google Scholar] [CrossRef]
- Uthansakul, P.; Ahmad Khan, A.; Uthansakul, M.; Duangmanee, P. Energy Efficient Design of Massive MIMO Based on Closely Spaced Antennas: Mutual Coupling Effect. Energies 2018, 11, 2029. [Google Scholar] [CrossRef]
- El Ayach, O.; Rajagopal, S.; Abu-Surra, S.; Pi, Z.; Heath, R.W. Spatially sparse precoding in millimeter wave MIMO systems. IEEE Trans. Wirel. Commun. 2014, 13, 1499–1513. [Google Scholar] [CrossRef]
- Payami, S.; Ghoraishi, M.; Dianati, M. Hybrid beamforming for large antenna arrays with phase shifter selection. IEEE Trans. Wireless Commun. 2016, 15, 7258–7271. [Google Scholar] [CrossRef]
- Ni, W.; Dong, X.; Lu, W.S. Near-optimal hybrid processing for massive MIMO systems via matrix decomposition. IEEE Trans. Signal Process. 2015, 65, 3922–3933. [Google Scholar] [CrossRef]
- Alkhateeb, A.; El Ayach, O.; Leus, G.; Heath, R.W. Channel estimation and hybrid precoding for millimeter wave cellular systems. IEEE J. Sel. Topics Signal Process. 2014, 8, 831–846. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Maccartney, G.R.; Samimi, M.K.; Sun, S. Wideband millimeter-wave propagation measurements and channel models for future wireless communication system design. IEEE Trans. Commun. 2015, 63, 3029–3056. [Google Scholar] [CrossRef]
- Heath, R.W.; Gonzalez-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A. An overview of signal processing techniques for millimeter wave MIMO Systems. IEEE J. Spec. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Singh, J.; Ponnuru, S.; Madhow, U. Multi-Gigabit communication: The ADC bottleneck. In Proceedings of the IEEE International Conference on Ultra-Wideband, Vancouver, BC, Canada, 9–11 September 2009; pp. 47–52. [Google Scholar]
- Love, D.J.; Heath, R.W. Equal gain transmission in multiple-input multiple-output wireless systems. IEEE Trans. Commun. 2003, 51, 1102–1110. [Google Scholar] [CrossRef] [Green Version]
- Baykas, T.; Sum, C.S.; Lan, Z.; Wang, J.; Rahman, M.A.; Harada, H.; Kato, S. IEEE 802.15.3c: The first ieee wireless standard for data rates over 1 Gb/s. IEEE Commun. Mag. 2011, 49, 114–121. [Google Scholar] [CrossRef]
- Hur, S.; Kim, T.; Love, D.J.; Krogmeier, J.V.; Thomas, T.A.; Ghosh, A. Millimeter wave beamforming for wireless backhaul and access in small cell networks. IEEE Trans. Commun. 2013, 61, 4391–4403. [Google Scholar] [CrossRef]
- Hajimiri, A.; Hashemi, H.; Natarajan, A.; Guan, X.; Komijani, A. Integrated phased array systems in silicon. Proc. IEEE 2005, 93, 1637–1655. [Google Scholar] [CrossRef]
- Doan, C.H.; Emami, S.; Sobel, D.A.; Niknejad, A.M.; Brodersen, R.W. Design considerations for 60 GHz CMOS radios. IEEE Commun. Mag. 2004, 42, 132–140. [Google Scholar] [CrossRef]
- Alkhateeb, A.; Leus, G.; Heath, R.W. Limited Feedback Hybrid Precoding for Multi-User Millimeter Wave Systems. IEEE Trans. Wirel. Commun. 2015, 14, 6481–6494. [Google Scholar] [CrossRef] [Green Version]
- Alkhateeb, A.; El Ayach, O.; Leus, G.; Heath, R. Hybrid precoding for millimeter wave cellular systems with partial channel knowledge. In Proceedings of the Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 10−15 February 2013; pp. 1–5. [Google Scholar]
- Kim, C.; Kim, T.; Seol, J. Multi-beam transmission diversity with hybrid beamforming for MIMO-OFDM systems. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, USA, 9–13 December 2013; pp. 61–65. [Google Scholar]
- Drineas, P.; Mahoney, M.W. On the Nyström method for approximating a gram matrix for improved Kernel-based learning. J. Mach. Learn. Res. 2005, 6, 2153–2475. [Google Scholar]
- Jain, P.; Netrapalli, P.; Sanghavi, S. Low-rank matrix completion using alternating minimization. In Proceedings of the 45th ACM Symp. Theory Comput. (STOC), Palo Alto, CA, USA, 1–4 June 2013; pp. 665–674. [Google Scholar]
- Yu, X.; Juei-Chin, S.; Zhang, J.; Letaief, K. Alternating Minimization Algorithms for Hybrid Precoding in Millimeter Wave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 485–500. [Google Scholar] [CrossRef] [Green Version]
- Venkateswaran, V.; Pivit, F.; Guan, L. Hybrid RF and digital beamformer for cellular networks: Algorithms, microwave architectures, and measurements. IEEE Trans. Microw. Theory Tech. 2016, 64, 2226–2243. [Google Scholar] [CrossRef]
- Sudarshan, P.; Mehta, N.B.; Molisch, A.F.; Zhang, J. Antenna selection with RF pre-processing: Robustness to RF and selection nonidealities. In Proceedings of the IEEE Radio Wireless Conference, Atlanta, GA, USA, 22 September 2004; pp. 665–674. [Google Scholar]
- Garcia-Rodriguez, A.; Venkateswaran, V.; Rulikowski, P.; Masouros, C. Hybrid analog–digital precoding revisited under realistic RF modeling. IEEE Wireless Commun. Lett. 2016, 5, 528–531. [Google Scholar] [CrossRef]
- Méndez-Rial, R.; Rusu, C.; González-Prelcic, N.; Alkhateeb, A.; Heath, R.W. Hybrid MIMO architectures for millimeter wave communications: Phase shifters or switches? IEEE Access 2016, 4, 247–267. [Google Scholar] [CrossRef]
- Tsinos, C.G.; Maleki, S.; Chatzinotas, S.; Ottersten, B. On the energy-efficiency of hybrid analog-digital transceivers for large antenna array systems. IEEE J. Sel. Areas Commun. 2017, 35, 1980–1995. [Google Scholar] [CrossRef]
- Wei, Z.; Ng, D.W.K.; Yuan, J. NOMA for Hybrid MmWave Communication Systems with Beamwidth Control. IEEE J. Sel. Top. Signal Process. 2019, in press. [Google Scholar] [CrossRef]
- Wu, X.; Liu, D.; Yin, F. Hybrid Beamforming for Multi-User Massive MIMO Systems. IEEE Trans. Commun. 2018, 66, 3879–3891. [Google Scholar] [CrossRef]
- Khan, A.A.; Uthansakul, P.; Uthansakul, M. Energy Efficient Design of Massive MIMO by Incorporating with Mutual Coupling. Int. J. Commun. Antenna Prop. 2017, 7, 198–207. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Transmission Bandwidth () | 20 MHz |
| Coherence Block () | 1800 |
| Fixed power () | 18 W |
| Mixer power () | 19 mW |
| LNA power () | 14 mW |
| Path loss exponent () | 3.8 |
| Shifters power () | 30 mW |
| Total Noise Power () | ‒96 dBm |
| Total Pilot Length () | 2 m |
| Oscillator power () | 5 mW |
| Phase shifters power () | 0.5 dB |
| Combiners power () | 0.6 dB |
| Number of Transceiver chains when fixed (, ) | 8 |
| Coding power () | 0.7 W |
| Decoding power () | 0.2 W |
| Minimum distance between the BS and users () | 32 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uthansakul, P.; Ahmad Khan, A. On the Energy Efficiency of Millimeter Wave Massive MIMO Based on Hybrid Architecture. Energies 2019, 12, 2227. https://doi.org/10.3390/en12112227
Uthansakul P, Ahmad Khan A. On the Energy Efficiency of Millimeter Wave Massive MIMO Based on Hybrid Architecture. Energies. 2019; 12(11):2227. https://doi.org/10.3390/en12112227
Chicago/Turabian StyleUthansakul, Peerapong, and Arfat Ahmad Khan. 2019. "On the Energy Efficiency of Millimeter Wave Massive MIMO Based on Hybrid Architecture" Energies 12, no. 11: 2227. https://doi.org/10.3390/en12112227
APA StyleUthansakul, P., & Ahmad Khan, A. (2019). On the Energy Efficiency of Millimeter Wave Massive MIMO Based on Hybrid Architecture. Energies, 12(11), 2227. https://doi.org/10.3390/en12112227





