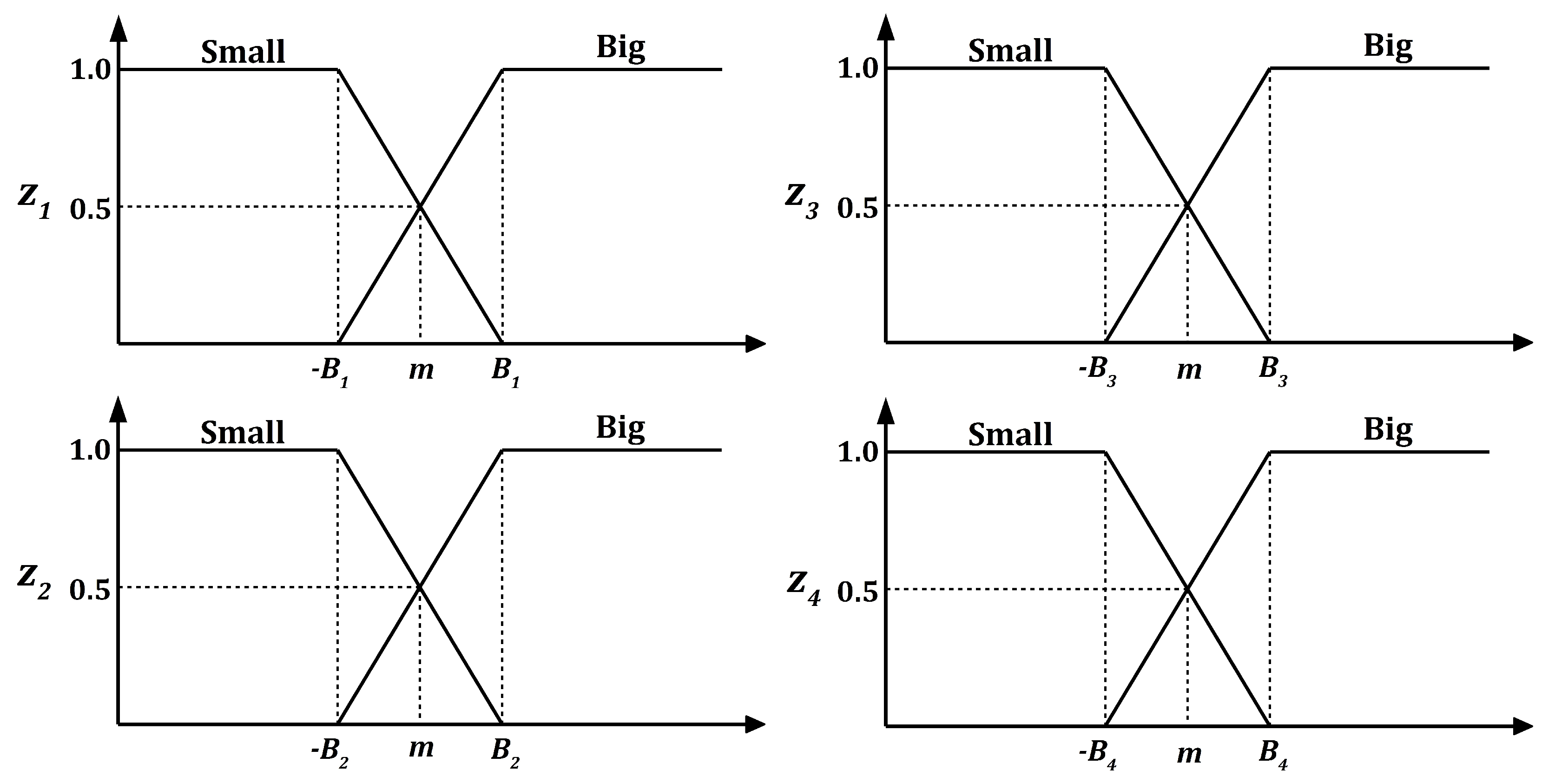
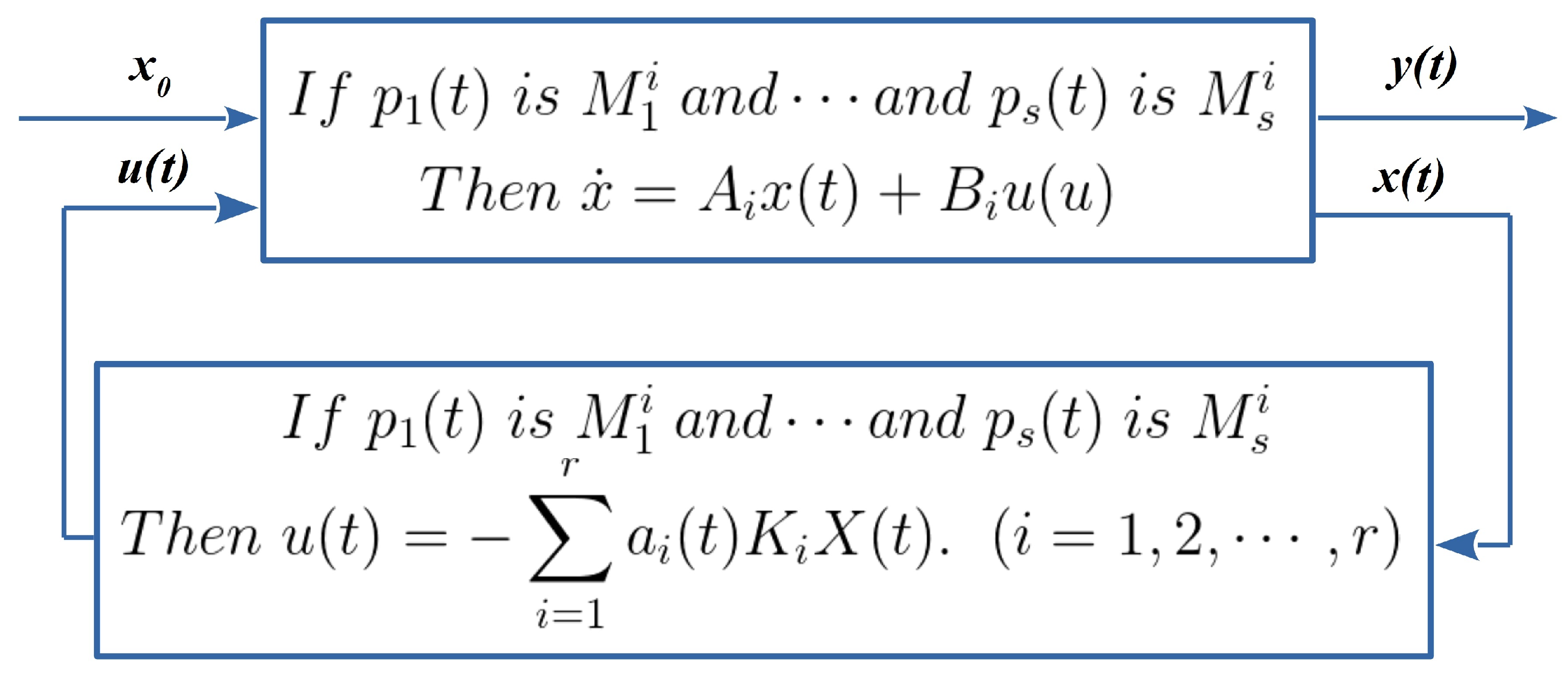1. Introduction
Many years ago, in 1965, fuzzy sets and logic system were introduced by renowned researcher Zadeh. Although fuzzy logic is applied in numerous complex industrial applications, for example steam engines by Mamdani’s, speed control of a DC motor applications and boiler fusion [
1,
2], Kickert’s proposed linguistic rules that describe human operator’s control strategy which is applied to control warm water plant [
3], and Ostergaard’s introduced fuzzy logic control of heat exchange system [
4], fuzzy sets and control theory have ability to replicate operator’s control strategy in to linguistic rules however stability analysis, robustness and optimality features are not existed, contradictory modern and conventional control theories have these features which are very significant in fail-safe critical engineering applications. Therefore, from long time being considerable attentiveness is gaining in terms of stability evaluation and methodical design of fuzzy control systems which are inherently nonlinear.
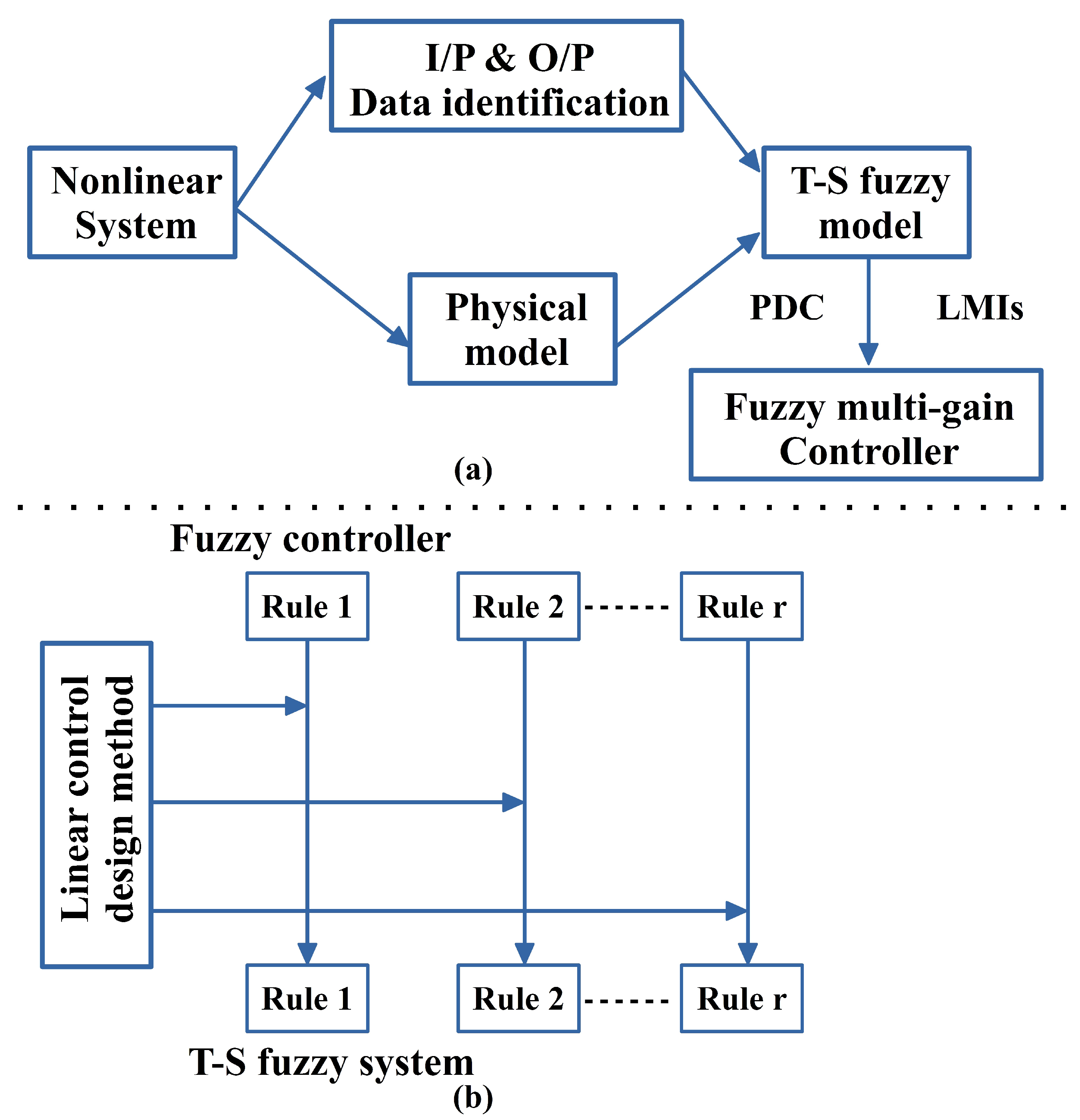
Describing linear systems from nonlinear systems by the “Takagi–Sugeno (T–S) fuzzy model”, initially introduced by Takagi and Sugeno [
5], which works on the local dynamics of the nonlinear system, the linear models described by different state space regions, particularly at an operating region of the nonlinear system. The overall system is obtained by fuzzy blending of these linear models [
2]. The design procedure of the “T–S fuzzy model-based controller” is explained in detail by [
6,
7], the author of [
6] explain the systematic approach to design state feedback fuzzy controllers for T–S fuzzy models and in [
7], the authors implement real-time T–S fuzzy model-based controller for shunt compensator. Based on the T–S fuzzy model, Wang et al. designed a linear controller by using “parallel distributed compensation (PDC)”, the system was described by T–S fuzzy model, in this scheme a linear state feedback controller was designed for each linear model [
2,
8]. Since way back in 1992, Tanaka and Sugeno was proposed sufficient stabilization conditions for T–S fuzzy controllers [
9]. However, form these conditions the existence of positive definite matrix
P is necessitate which satisfies a set of Lyapunov inequalities [
2]. The authors of [
2] proposed an overall fuzzy model by fuzzy blending of all liner model at particular operating region, the controller synthesis is a difficult task for nonlinear system which described by T–S fuzzy model, this problem is turned into simple mathematical equation solver by involving “linear matrix inequalities (LMIs)”. These LMIs can be solved using optimization methods like the interior-point convex optimization method [
2,
10]. The less conservative stabilization and optimum performance sufficient conditions for T–S fuzzy control systems can be transformed into set of LMIs, LMI Toolbox can be used to solve these LMIs [
11]. Finally, Khaber et. al. proposed a T–S fuzzy model for inverted pendulum on a moving cart which is highly nonlinear system, thereafter author proposed state feedback controller for two T–S fuzzy-rule and MATLAB software ware used to wrote the code and solve LMIs [
12]. However, it is crucial to identify the common Lyapunov function that satisfies sufficient stability conditions of all fuzzy models for complex nonlinear systems. Beyond this limitation, a mathematical model of the nonlinear system is a key challenges [
13].
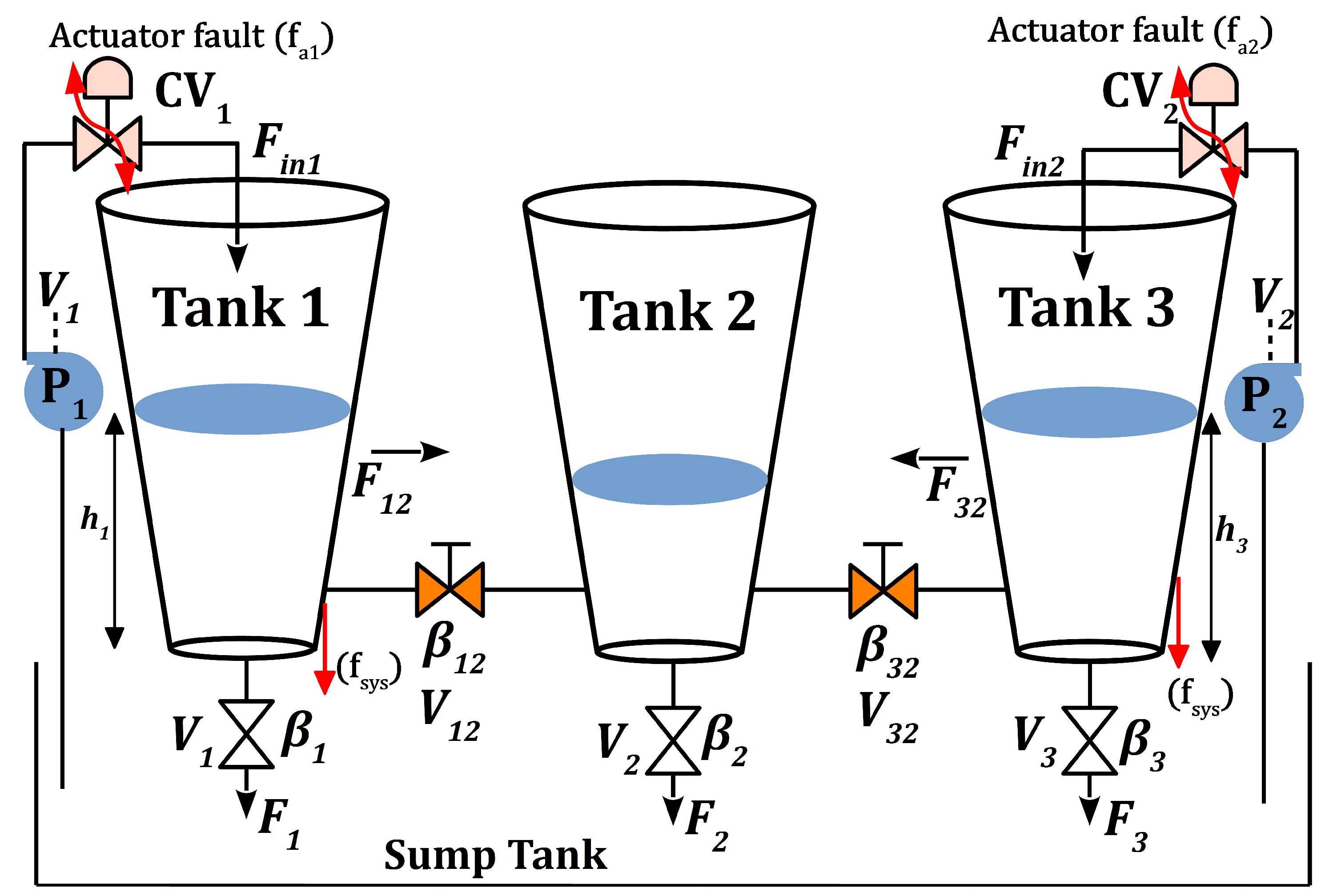
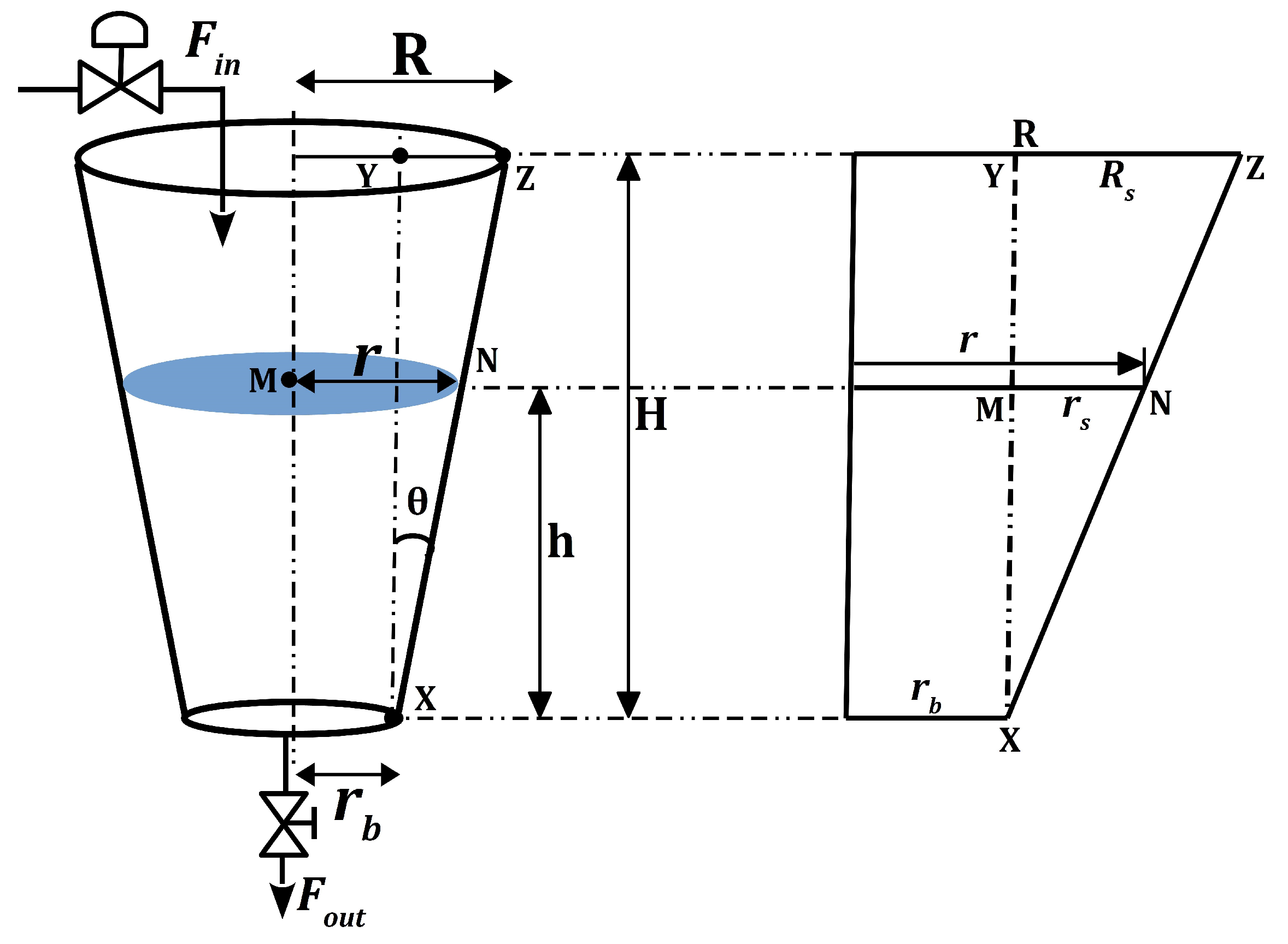
Controlling of process variable like flow rate and liquid level in closed tanks are the very common control problems in the chemical process, food processing, cement industries and petrochemical industries [
14,
15,
16,
17]. Generally, the liquids are pumped and stored in the tanks for processing; again it is pumped to other tanks for other operations. The conical tanks are widely used in liquid treatment industry, concrete industry and hydro metallurgical industries [
18]. In the present decade, researchers focusing on the level control problem and numerous literature exist that covers conventional to state of the art level control of cylindrical and cone-shaped tanks. This literature addressed and validated control schemes by simulation as well as experimental setup and several control techniques have been employed [
18,
19,
20,
21,
22]. The three interacting conical tank level (TICTL) process is a typical two input two output (TITO) process which exhibits nonlinear characteristics and dynamic coupling effect between inputs and outputs. The control of TITO process requires dedicated multiloop or multivariable control system. Commonly, the process industries employ multiloop proportional integral derivative (PID) controller because of its simple structure, robustness and failure tolerance [
23]. The multiloop PID controllers produce better control performance for the system with modest interaction. But it fails to provide desirable control performance for the system with severe interaction effect between inputs and outputs.
The decoupled control scheme and multivariable centralized controller are designed with linear PI/PID controller, which are failed to produce reasonable performance for the nonlinear system. Hence, the adaptive PI/PID control has been designed for nonlinear multi input multi output (MIMO) systems by combining family of linear PI/PID controller with gain scheduling scheme. The adaptive PI/PID controller with gain scheduling scheme is limited up to abrupt changes of the process operating points across the boundaries of the operating regions, and it will fail at points other than these operating points. To overcome this limitation author of [
24] have demonstrated the fuzzy gain scheduler-based PID control for process control application. In recently author of the [
25] has been claimed that fuzzy logic based gain scheduler provides satisfactory control performance for nonlinear system. In article [
26], the author used multimodal-based gain scheduler for controlling the level of liquid in the single conical tank (SISO) process, where the linear PID controllers are found in three operating regions and then weighted scheduler is designed to adjust the Controller parameter based on the operating regions. Reference [
27] has developed a fuzzy logic controller for nonlinear spherical tank level process, in that fuzzy rule base is tuned using a genetic algorithm and it has been claimed that fuzzy logic control is more remarkable than conventional PI control. References [
28,
29,
30] have demonstrated fuzzy gain scheduler-based PID controller for nonlinear MIMO process. After the motivation and literature survey for T–S fuzzy model-based controller and fuzzy logic base controller for nonlinear system, in this article we design a stable fault tolerant controller for the T–S fuzzy model-based control system using LMIs approach. To validate the proposed fault tolerant approach we take TICTL process as a case study. In artificial intelligence (AI) neural network (NN) is also used to fault tolerant control applications, NN will used to estimate the faults and take controlling action accordingly, some application and implementation of NN is presented in [
17,
31]. The author of [
32] design stable T–S fuzzy controller by optimization, and in [
33] author has design linear controller by applying Takagi–Sugeno fuzzy model and adding partial uncertainty in reference trajectory.
The major contributions of the paper are as follows. A novel stable fault tolerant controller is designed based on T–S fuzzy model and controller synthesis is done via LMIs for the three conical tank level control process and considering model uncertainties and two type of faults. The state feedback control law is designed based on T–S fuzzy model and parallel distribution compensation (PDC) method. The quadratic stability theory is used to prove the quadratic stability of the uncertain three conical tank system based on the T–S fuzzy model. We provide an effective method of designing fuzzy multigain controllers according to PDC algorithm and linear matrix inequality (LMI) to ensure the controller satisfies fuzzy controller performance.
The objective of this work is to develop a T–S fuzzy model for the proposed highly nonlinear TICTL process and then to design stable fault tolerant control system to control the liquid level of tank 1, tank 3 irrespective of fault occurs into the system. In this paper, parallel distributed compensation is used to design the linear controller for each linear model. The controller performance are demonstrated using three error indices IAE, ISE and IATE. The state feedback gains are found for all linear T–S fuzzy model in region 3 of TICTL process hence it gives guarantee stability and optimum performance. Also it overcame the interaction effect between loops and improved the servo, regulatory performance of closed loop system.
This work is organized as follows:
Section 2 includes process description of TICTL process, mathematical model of the process along with linerized model with specific region 3.
Section 3 presents the Fault tolerant controller using T–S fuzzy model-based controller for TICTL process subject to two possible faults.
Section 4 presents the simulation results of regulatory and servo response of TICTL process with and without faults, along with error calculation is presented. Finally in
Section 5 the main conclusions of the work and future work are drawn.
4. Simulation Results
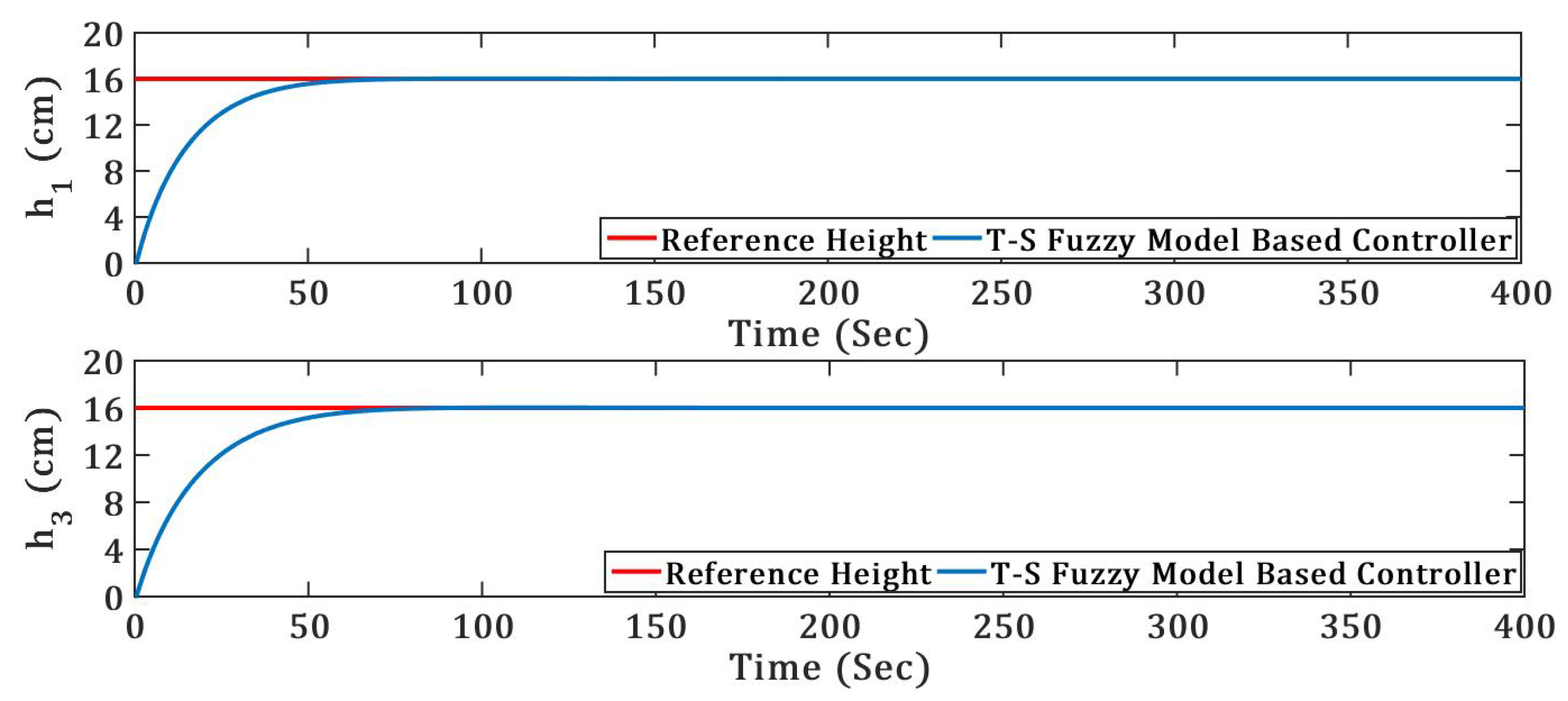
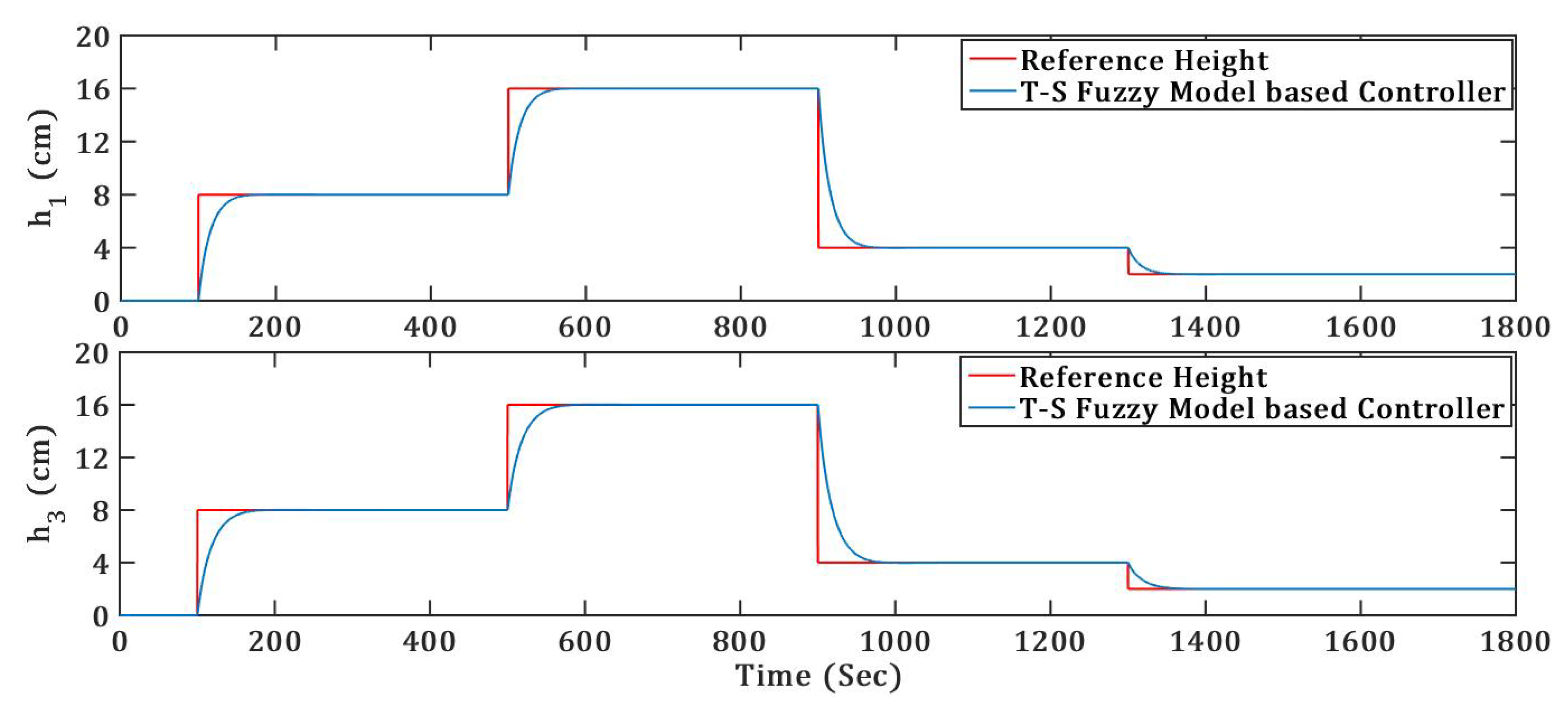
In the proposed research, the TICTL process model was established on the mass balance equation. The open loop data was generated and the operating regions are selected from the input output characteristics. The linear T–S fuzzy state space model was developed for TICTL for operating region 3. Also state feedback linear controller was designed for every linear TICTL process model. To simulate the proposed controller MATLAB platform was used, simulation of regulatory and servo responses of TICTL process was carried out in two phases. One was without fault and the other one was with a system component
and actuator
faults. In the first phase, regulatory and servo response of TICTL process was carried out and presented in
Figure 6 and
Figure 7. The controller parameters of the T–S fuzzy model-based controller is presented in
Table 3. Observing the simulation results of
Figure 6 and
Figure 7 controller is track the reference height efficiently, smoothly and without overshoot.
To validate the proposed controller performance against the faulty condition (like system component and actuator faults), it was tested on a prototype model of TICTL with regulatory and servo responses with two possible faults.
Two fault nature is taken for validation (i) Abrupt nature and (ii) Incipient nature.
Abrupt fault: The fault occurs into the system at time
instance and magnitude is constant with respect to time [
17]. The abrupt fault behavior with respect to time were modeled by a step function given by Equation (
29),
where
is the occurrence time of the fault.
Incipient fault: The fault occurs into the system in between specific time interval and magnitude profile of the fault with respect to time is increasing between time interval [
35]. Incipient fault time profiles are modeled by Equation (
30),
where the scalar
> 0 presents the unidentified fault transformation rate. Small values of
indicate gradually developing faults, also known as incipient faults [
35]. For large values of
, the time profile
approaches a step function, which models abrupt faults.This two nature of system component (leak) and actuator fault was introduced into the TICTL process and tested the proposed controller for regulatory and servo response.
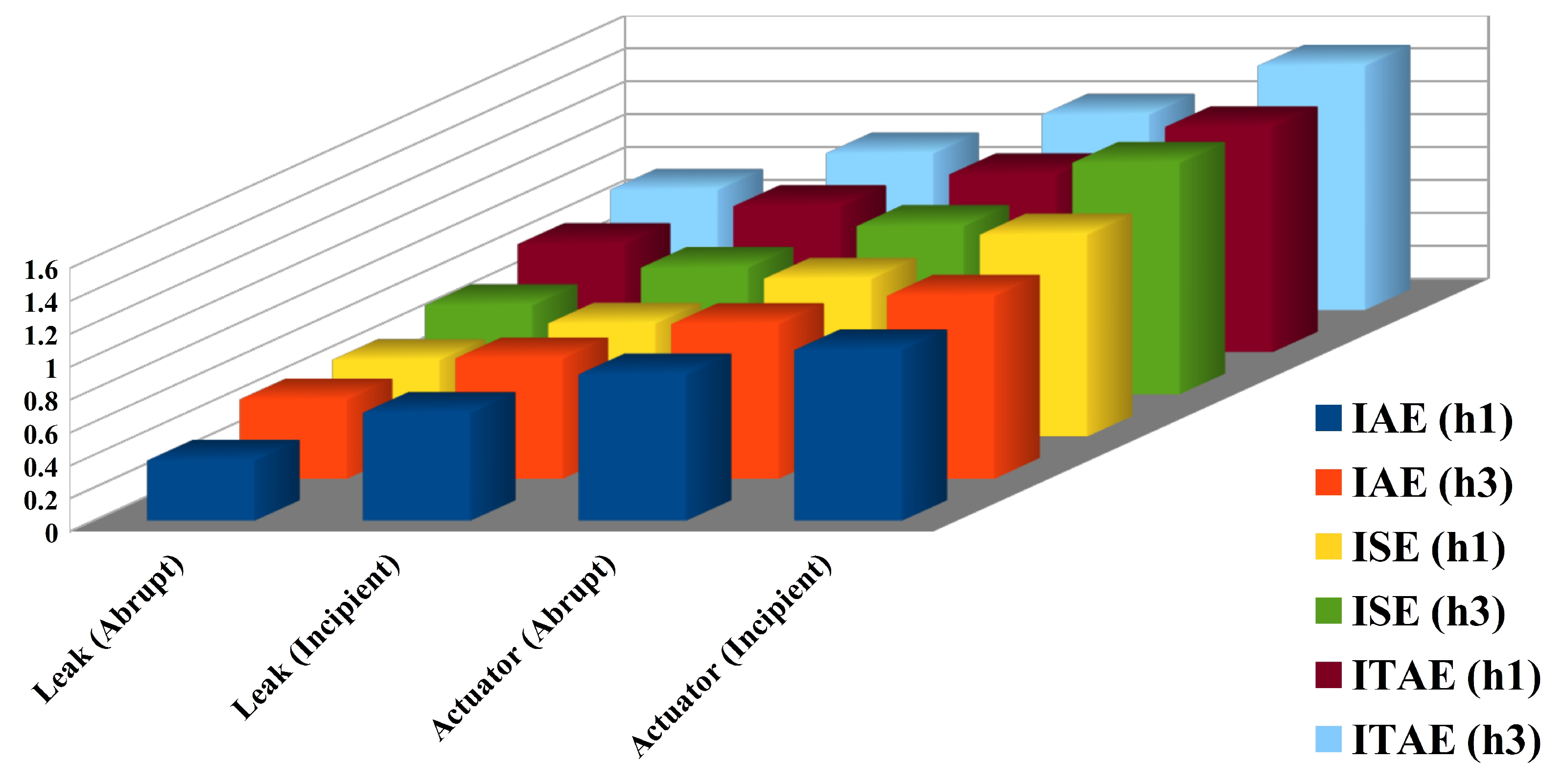
In the second simulation phase regulatory response carried out for TICTL process with two possible fault in abrupt and incipient nature, and found the pre-fault and post-fault response of proposed controller. To check the controller performance, three integral error indices, namely IAE, ISE and IATE, were calculated for each case. The error formula presented as following equations,
where
e is error. First four simulation presented TICTL process regulatory response with possible two nature of faults (system component and actuator faults). As given in the mathematical model, the TICTL process output is
and
. The two output tank height regulatory response is presented in the following subsection. The fault tolerance behavior of the proposed controller was measured with fault recovery time
, this terminology given by,
Fault recovery time: The time required to achieve previous correct state of the system from faulty state, this terminology is known as fault tolerance ability of the controller.
Proposed T–S fuzzy model-based controller established its effectiveness against the system component (leak) and actuator faults which was proven using fault recovery time results and resulting figures.
4.1. Regulatory Response With Faults
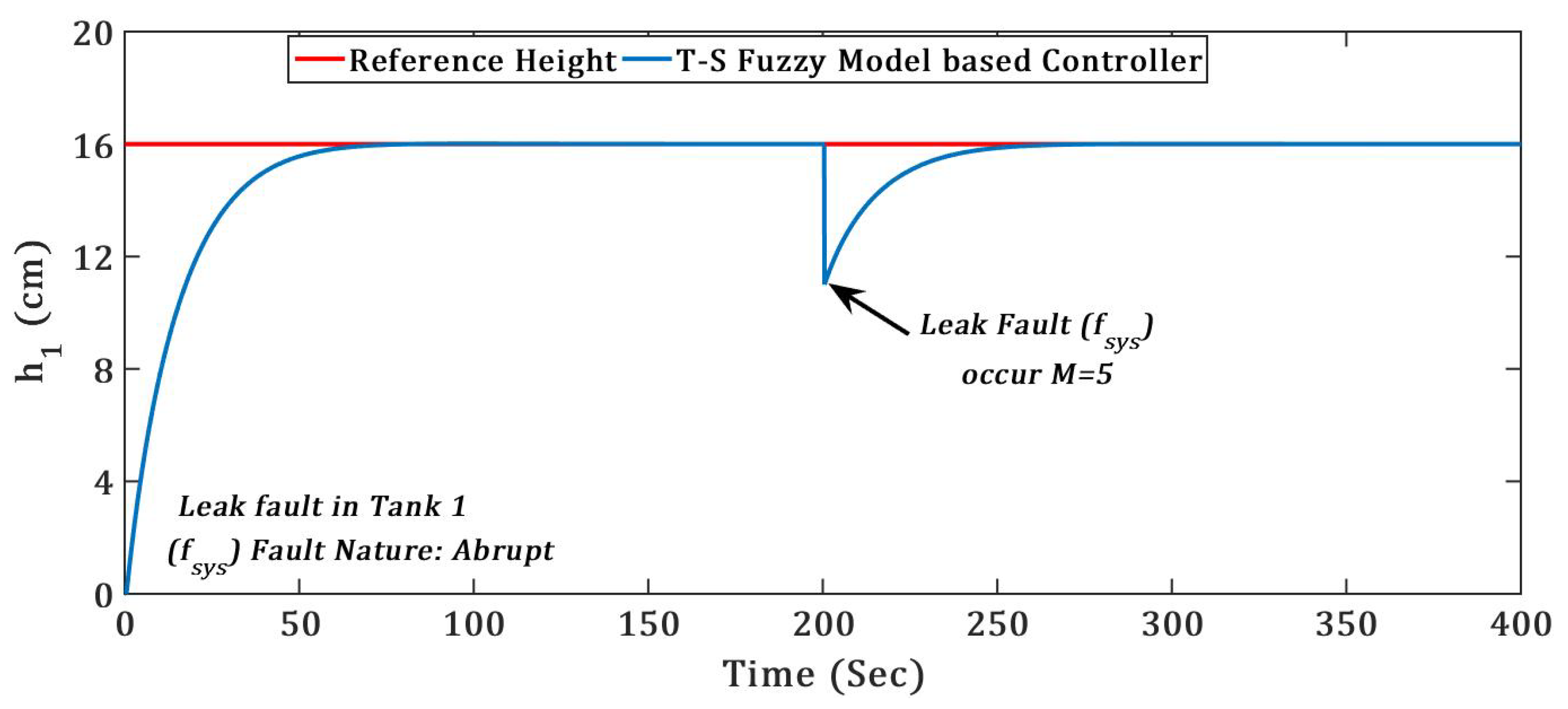
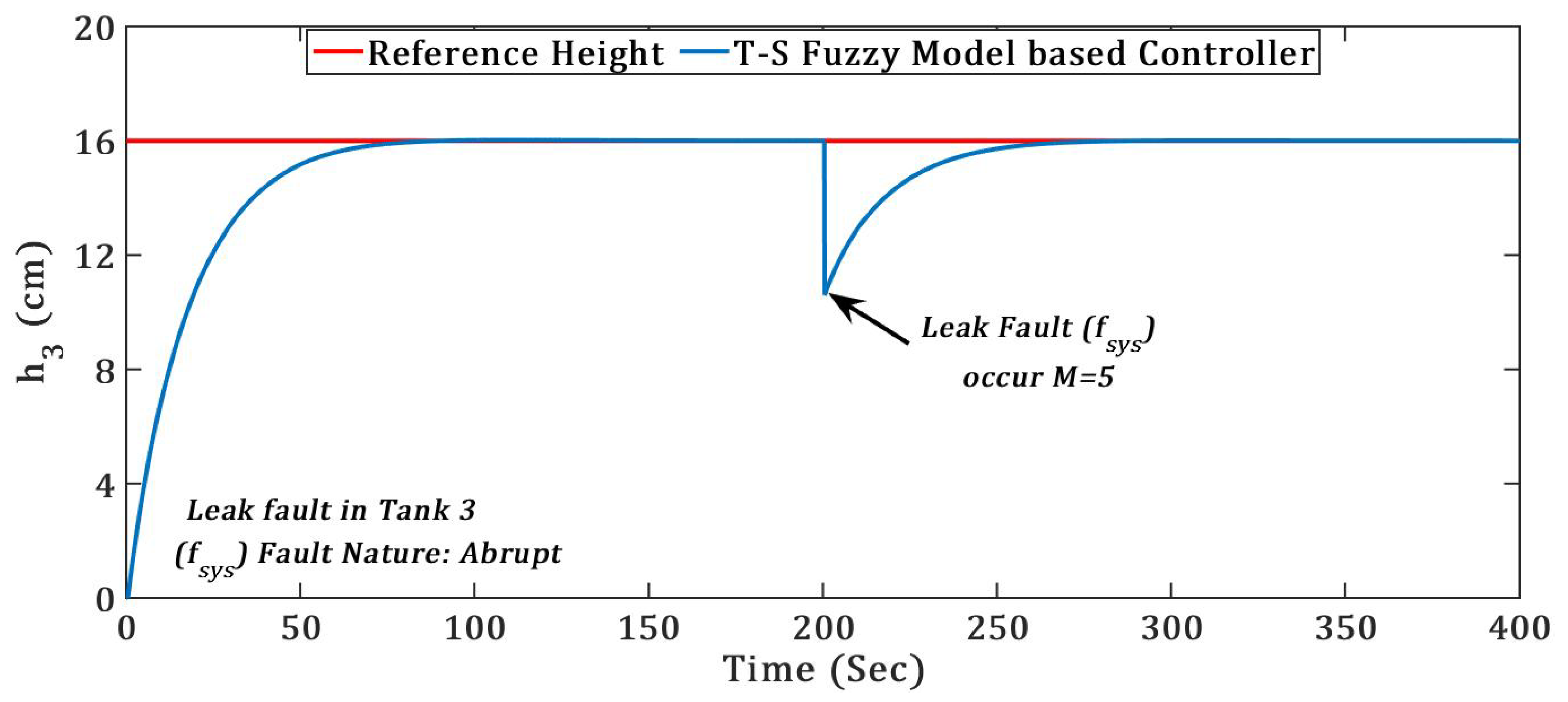
(1) TICTL process regulatory with abrupt nature of System component fault
The system component fault considered into this simulation is tank bottom leak in tank 1 and tank 3. At the occurrence of the leak fault into the system drastically level of tank is reduced and hence it degrades the performance drastically, even system will leads to instability when magnitude is big. The two abrupt system component
(leak) fault occurs in tank 1 and tank 3 at the same time
= 200 s with fault magnitude M = 5, the regulatory responses of both the tank with system component fault is presented in
Figure 8 and
Figure 9.
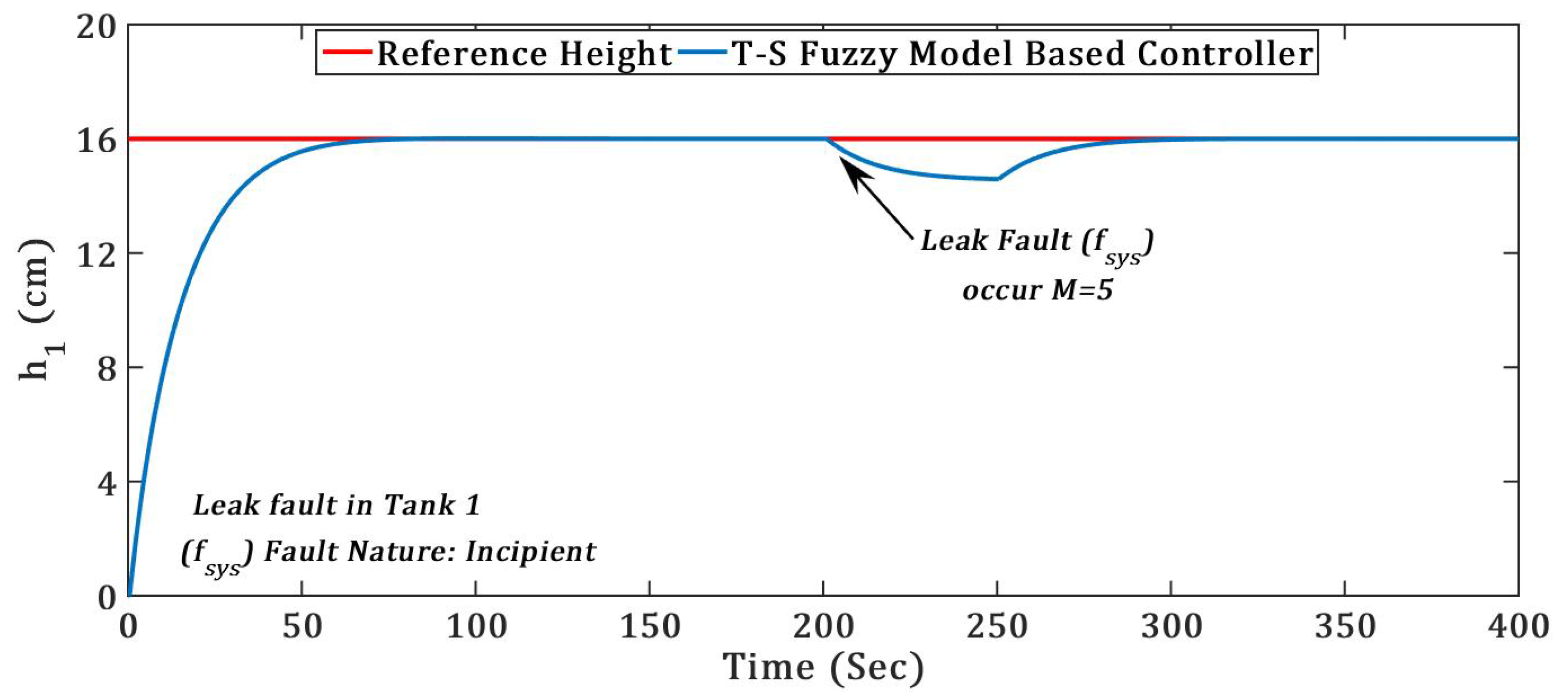
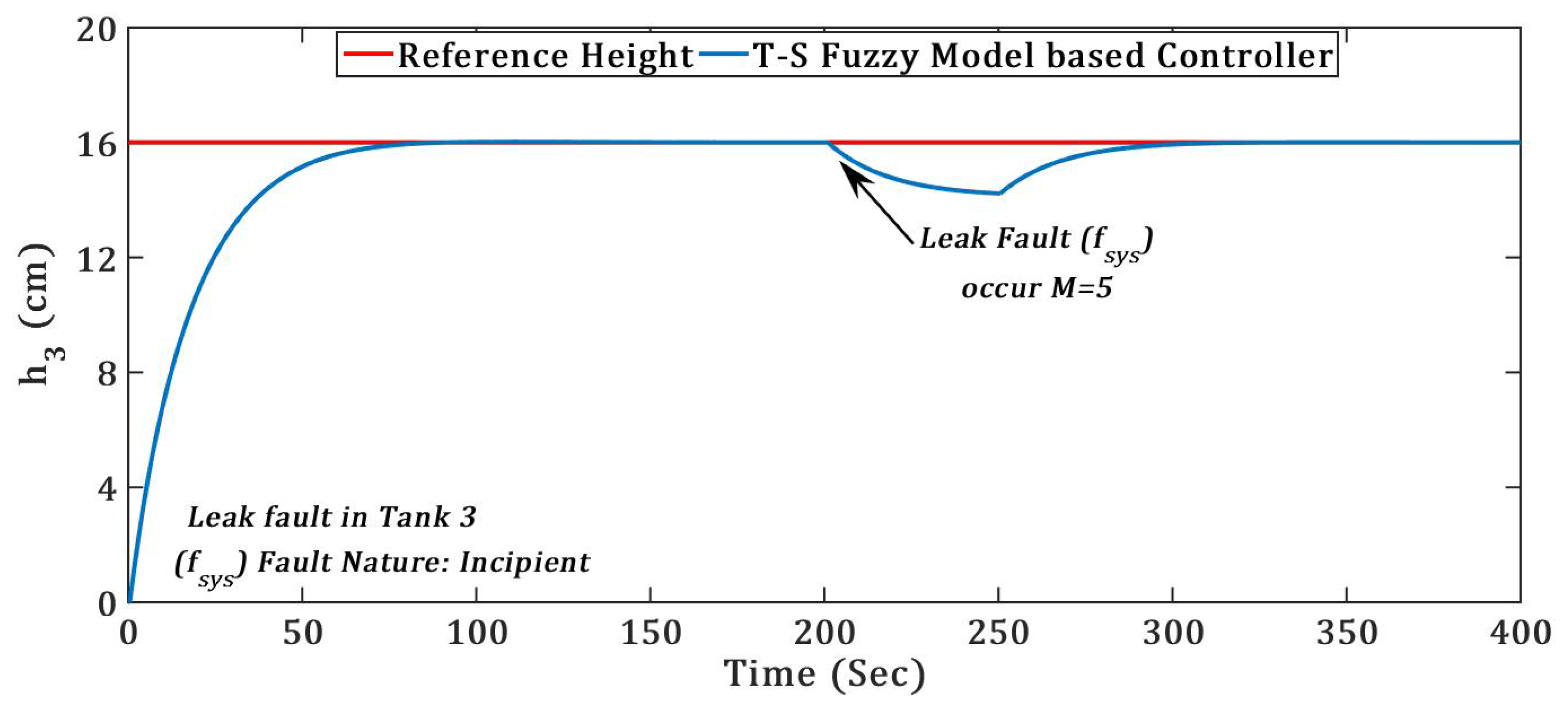
(2) TICTL process regulatory with incipient nature of System component fault
Now,
Figure 10 and
Figure 11 presents the regulatory response of the TICTL process with the two incipient system component
(leak) fault. The two fault occurred in tanks 1 and 3 separately at the same time
= 200 s with fault magnitude M = 5.
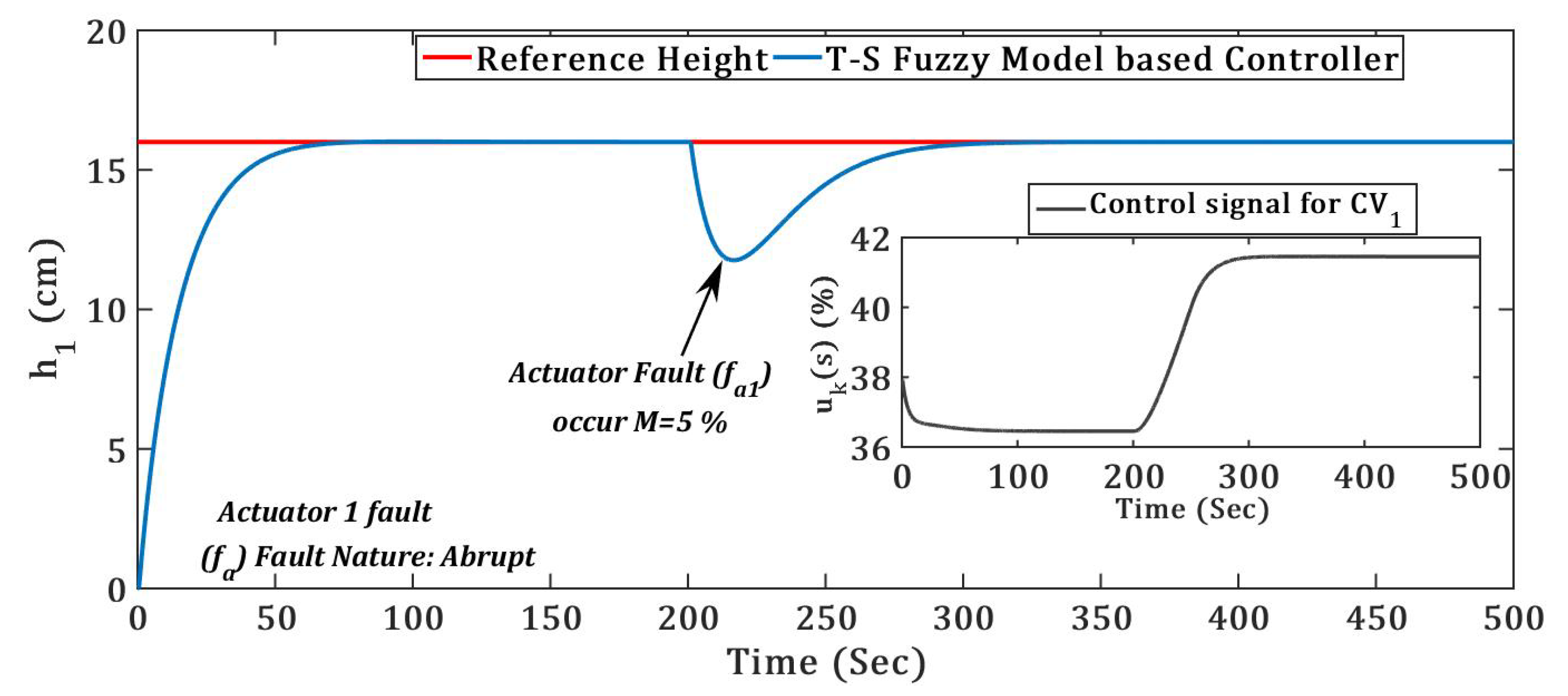
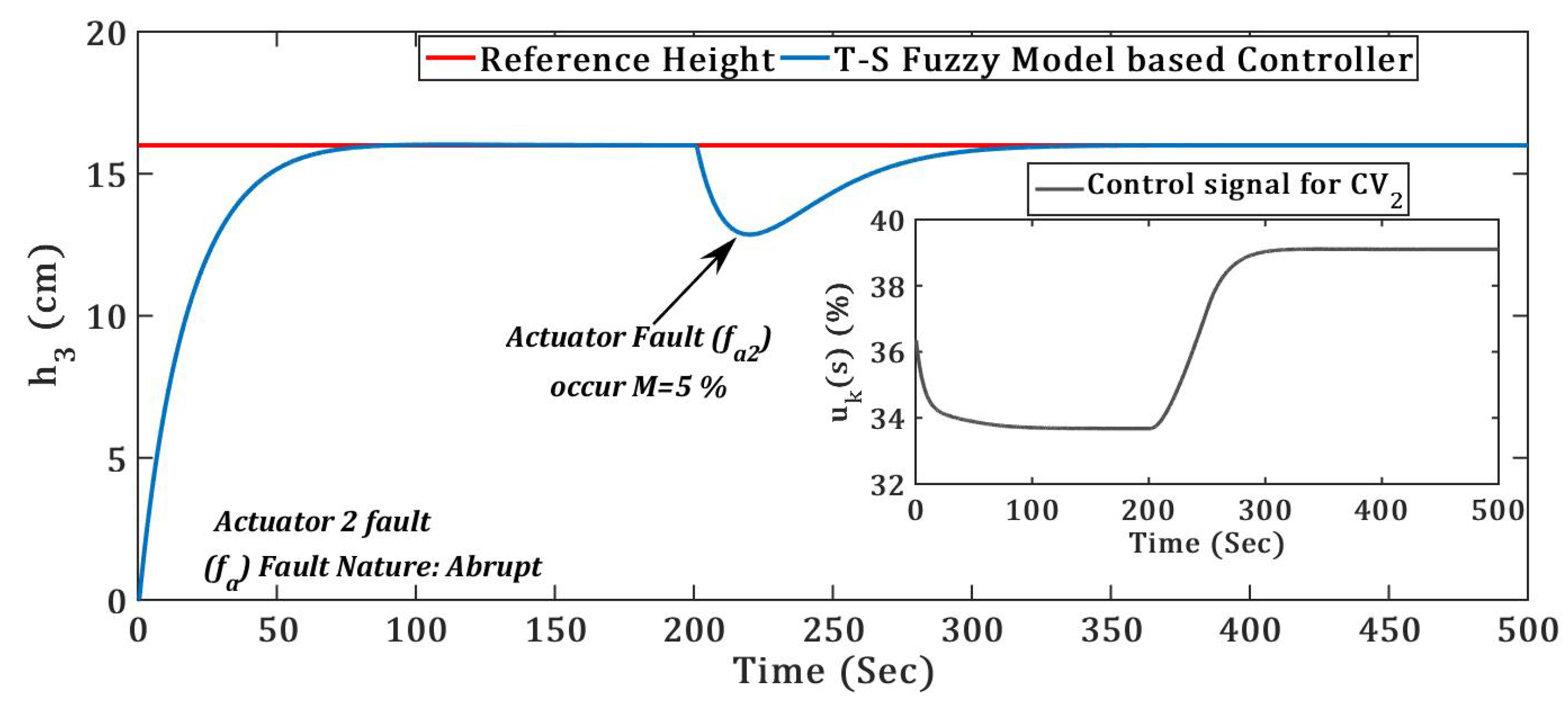
(3) TICTL process regulatory with abrupt nature of actuator fault
An actuator is a major component of any closed loop control system to control the manipulated variable and hence the controlled variable is controlled [
36]. Hence, the actuator fault occurring in the TICTL process conventional controller did not give system stability and optimum response. In
Figure 12 and
Figure 13, we conferred the stability and optimum response even though the abrupt actuator fault occurred in the TICTL process.
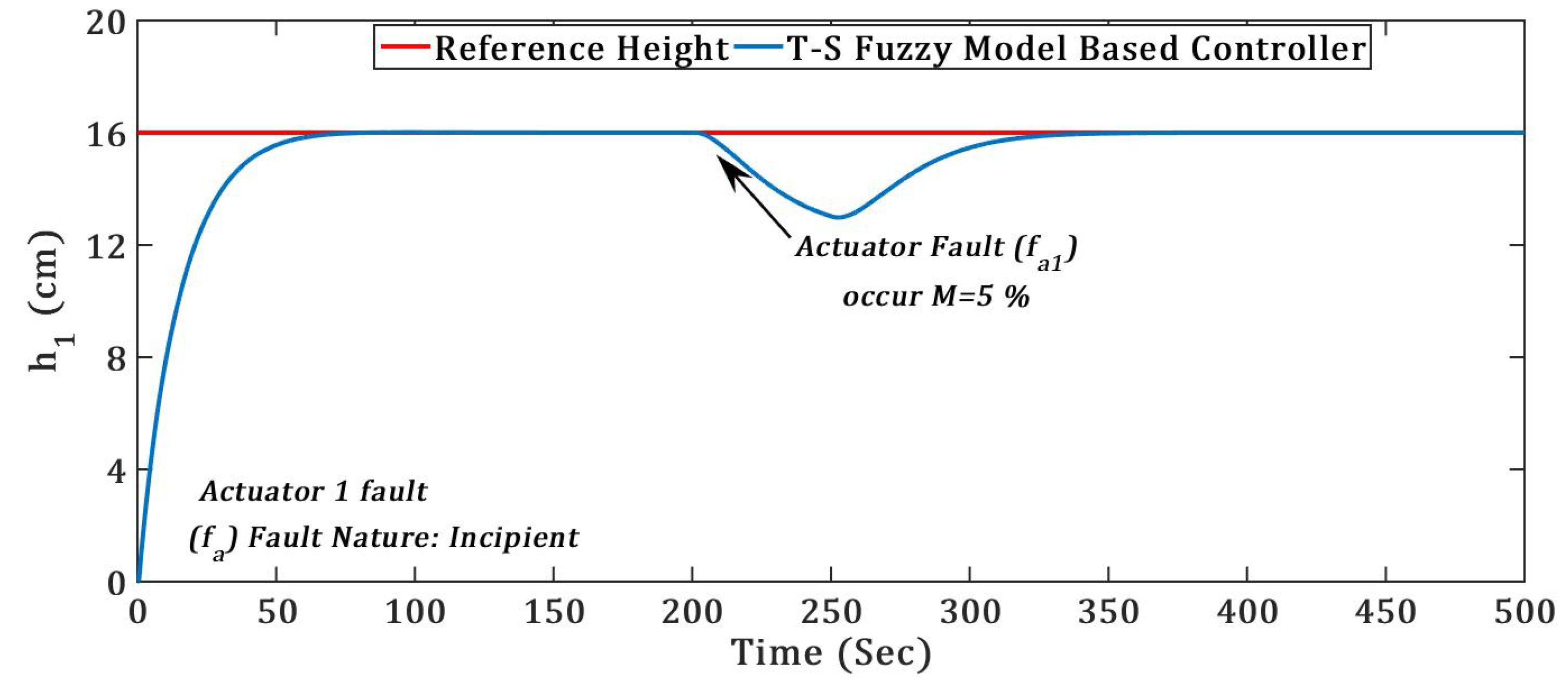
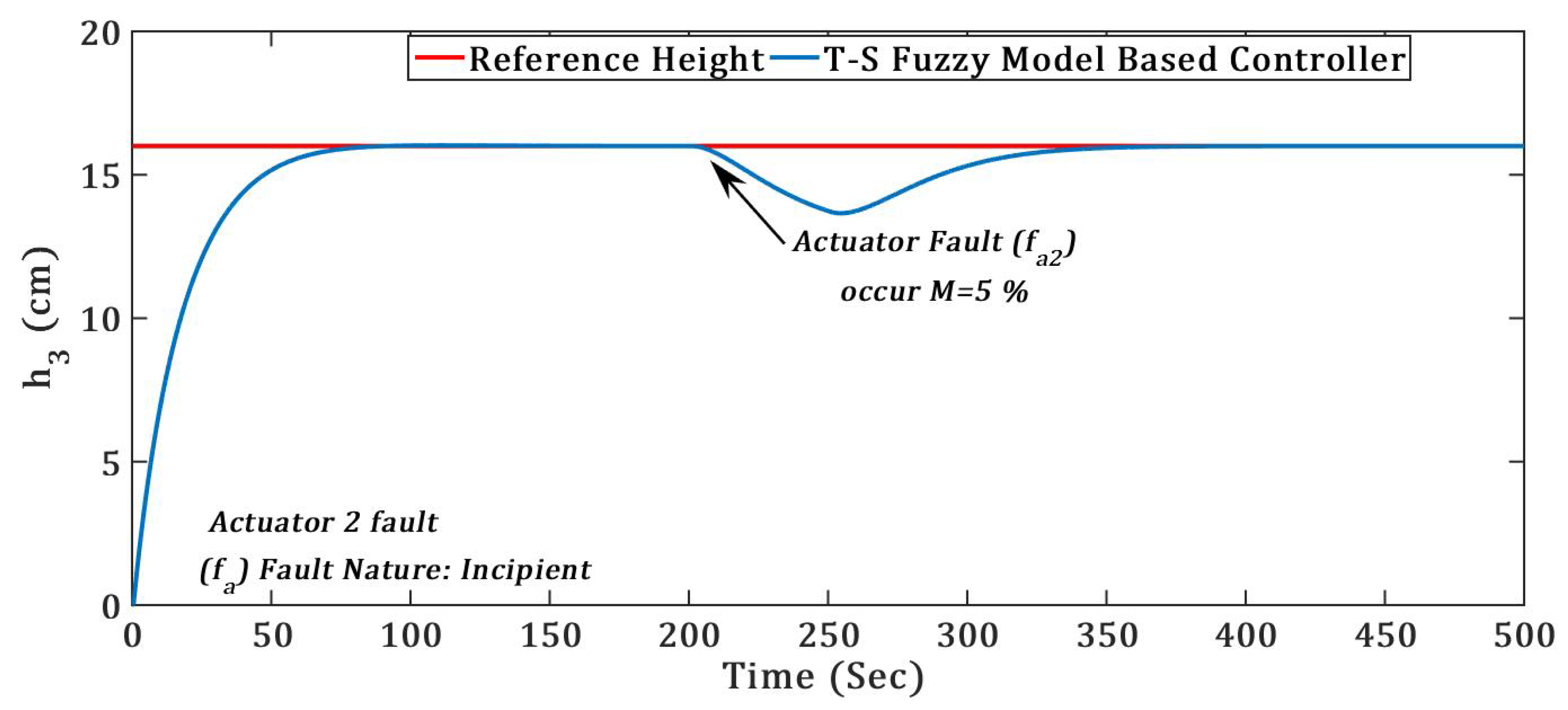
(4) TICTL process regulatory with incipient nature of actuator fault
Figure 14 and
Figure 15 clearly presents the effectiveness of the proposed T–S fuzzy model-based controller against the incipient actuator fault
and
, and fault recovery time (
) for proposed controller is presented in
Table 4. The two separate actuator faults introduced in the TICTL process with same magnitude at time
= 200 s.
Steady state behaviour of the controller is presented in
Table 5, it is given by Fault Recovery Time
in terms of
. Integral error indices for proposed controller presented in
Table 6 for two type and two nature of faults.
Critical Observations for Regulatory Responses of T–S Fuzzy Model-Based Controller
From the minute observations of the simulation results, the actuator fault degraded system performance severally when compared with system component (leak) faults.
From the two different nature of the faults, the incipient nature of faults will degrade performance significantly as compared to abrupt nature of faults.
Fault recovery time for both the abrupt actuator fault and was almost double as compared to both abrupt system component and (leak) faults.
Fault recovery time for both incipient actuator fault and was almost 1.5 times as compared to both incipient system component and (leak) faults.
Simultaneous fault is introduced into the TICTL process with time, controller simulation and validation were not performed for multiple faults occurs at the same time into the system.
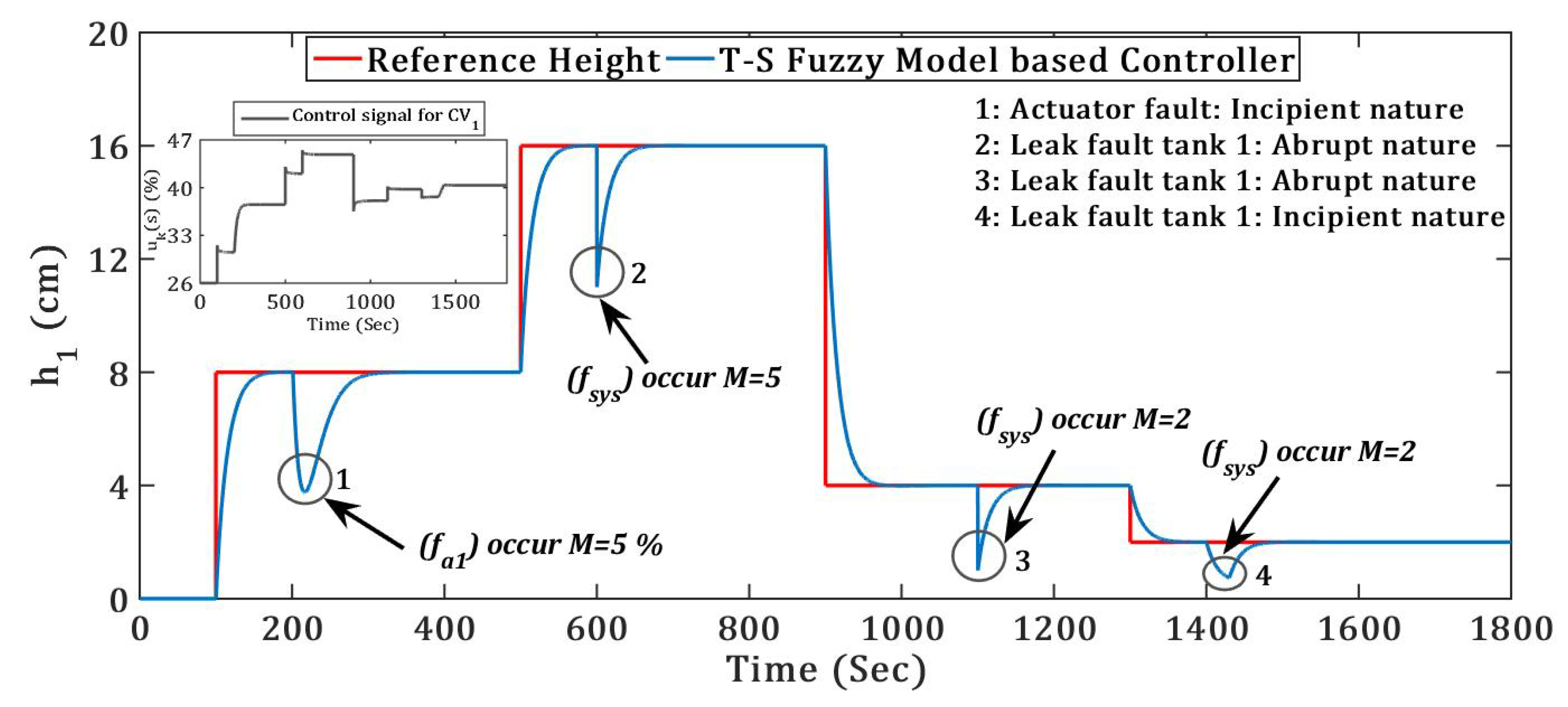
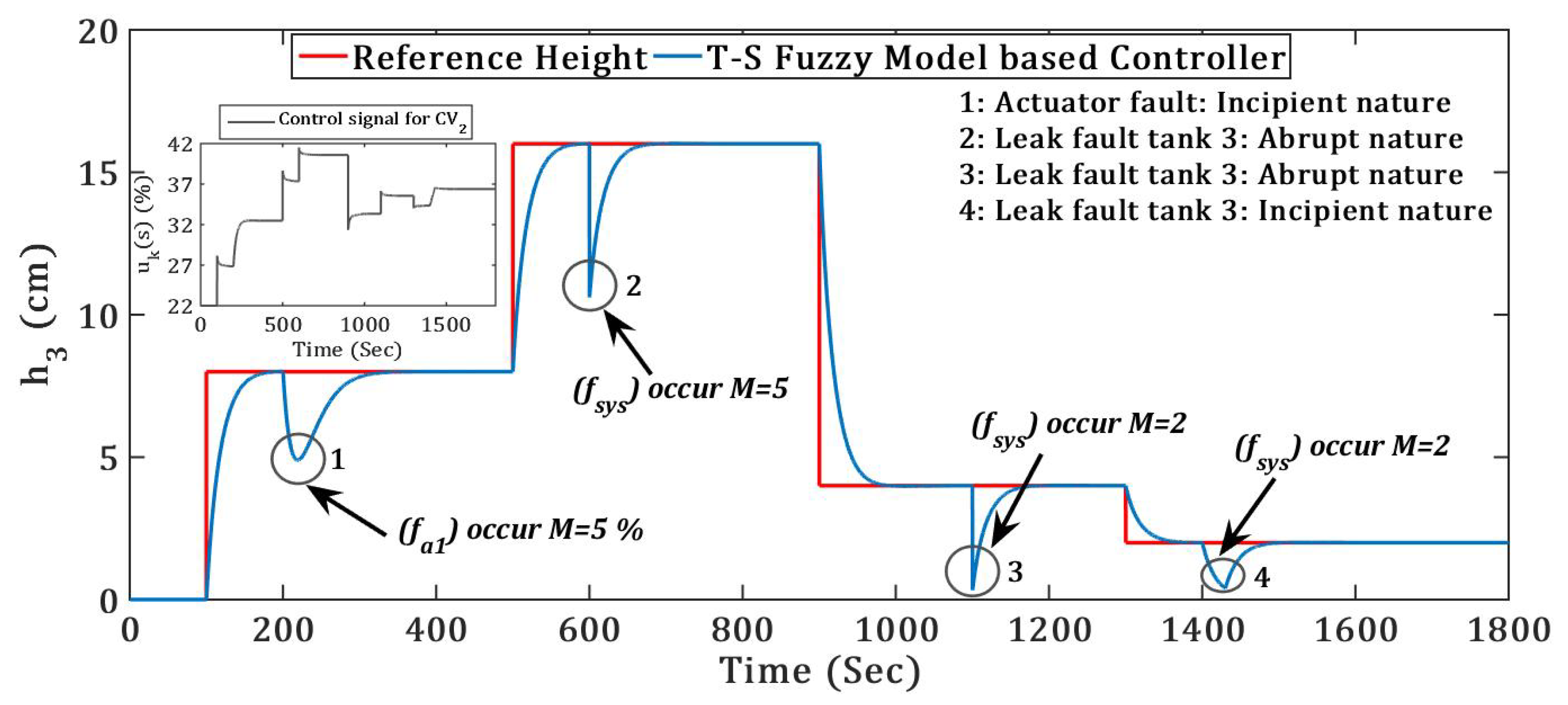
4.2. Servo Responses with Multiple Faults in Different Types
Proposed controller efficacy was tested with servo response subject to multiple faults into the TICTL process. Two different natures of leak and actuator faults introduced into the system plant, the simulation results of the proposed controller was presented for tank 1 height (
) and tank 3 height (
) are presented in
Figure 16 and
Figure 17 respectively. Simulation results clearly show the superiority of the controllers irrespective of multiple faults in terms of stability and optimum performance, which was established using three integral error indices depicted in
Table 7. Four faults were introduced into the system simultaneously with time, fault 1
occurred at
= 200 s, fault 2
occurred at
= 600 s, fault 3
occurred at
= 1100 s, and fault 4
occurred at
= 1400 s.
Critical Observations for Servo Responses of T–S Fuzzy Model-Based Controller
The proposed controller tracked the reference height efficiently as compared to reference height .
Servo response of proposed controller for height gave more to all three integral error indices as compared to servo response of height.
Every integral performance index had certain advantages in control system design. The ITAE criterion tried to minimize time multiplied absolute error of the control system. The time multiplication term penalized the error more at the later stages than at the beginning and hence effectively reduced the settling time (
) and percentage of overshoot (
). At the same time when sudden change of input occurred, the ITAE-based controller design gave lower controller output, hence actuator never saturated and actuator life increased. However the lower controller output was sluggish to the controller response. In
Figure 18, the bar chart presents the comparative integral error for regulatory response of TICTL process subject to system component (leak) and actuator faults with abrupt and incipient nature of faults.
5. Conclusions
The research article presents methodical design procedure which assures stability and excellent control performance of T–S fuzzy model base control systems. It is discovered that the state feedback controller design for nonlinear system presented by T–S fuzzy models at a local operating region of nonlinear system, can be minimized to a LMIs problem that can be solved using MATLAB software program. Also paper presents three conical tank interacting process is proposed and mathematical model was developed using mass balance equation after that T–S fuzzy model is developed for region 3. It is evident that the present controller design has a superior performance (refer simulation results) even though system component and actuator fault occurs in the the system. Therefore, the specified highly nonlinear system such as TICTL process can be controlled by using this strategy in an uncomplicated, easy, and organized way. The proposed control strategy performances are measured in reference of settling time , peak overshoot , ISE, IAE, ITAE. Furthermore, the simulation results of the novel fault tolerant controller design for a TICTL process presented with transient and steady state response, as illustrated in the simulation results. Thus, the authors suggest that the proposed strategy can be useful in real-time industrial applications.
As revealed before, the main research scopes in fuzzy control systems are mainly stabilization, optimality and robustness. Recently, these concepts are getting more fascinating due to fuzzy control working superior to conventional control schemes as described in Zadeh’s papers [
37,
38]. In the real world, for any control system the main concern is system stability, according to Zadeh’s philosophy the scientific term system’s stability are actually fuzzy his one of the paper that in reality most empirical concepts such as stability are actually fuzzy and as demonstration he considers the definition of the Lyapunov stability which is homologous, i.e., a system is either stable or unstable, with no degrees of stability allowed [
2]. He identified to the need for reformulation of many basic abstraction in empirical theories with demonstration [
2] also Dubois present legacy of the fuzzy logic since inception, and discussed three potential understanding of the grades of membership to a fuzzy set [
39].
In the future scope of work, the proposed system is highly nonlinear and modeling uncertainty due to this reason, instead of type 1 fuzzy set (T1FS) interval type 2 fuzzy sets (IT2FS) will be used. The main reason of the using type 2 fuzzy systems for nonlinear and interacting systems is, type 2 fuzzy sets having inherent footprint of uncertainty (FoU) in between upper and lower membership functions which can laminate the model uncertainty as well as giving robustness against the noise [
40]. Furthermore, the relaxed stability condition is proposed for type 2 T–S fuzzy model-based controller based on the grade of membership functions and validate it on a proposed system subject to faults and model uncertainty. Also, operating regions 1 and 2 of TICTL process will be the scope of the work. At the same time experimental validation of the proposed controller is the future scope of this current work. The major challenges to implementing IT2FLS is computational time for converting type 2 to type 1 fuzzy sets in the processing unit [
41]. But the same advanced algorithm is implemented for fast computation of type 2 to type 1 fuzzy set conversion presented in [
42,
43].