Study on A Simple Model to Forecast the Electricity Demand under China’s New Normal Situation
Abstract
1. Introduction
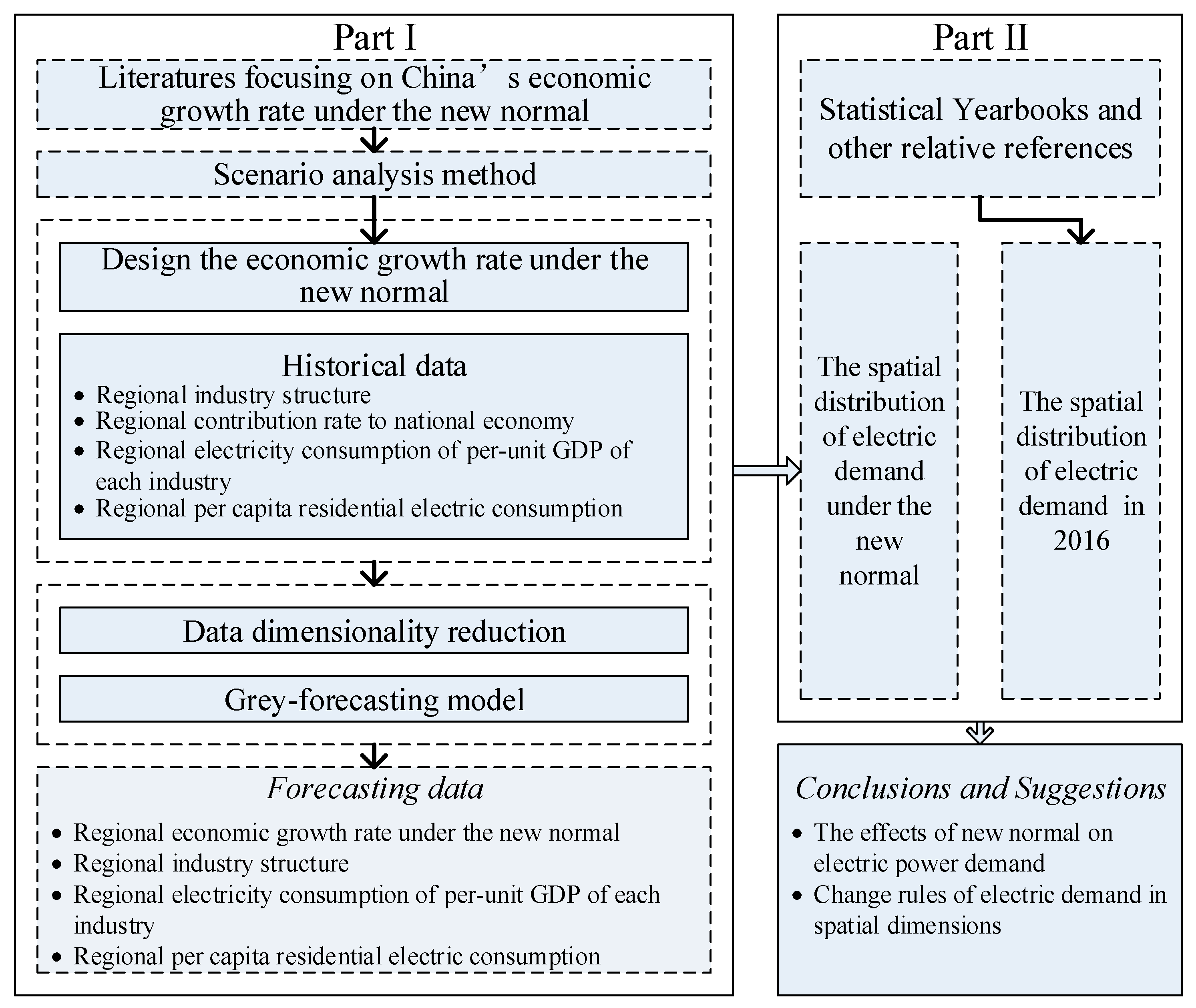
- Disaggregating the national economic growth into all provinces, except Taiwan, Hong Kong, and Macao. Based on the time series data of national and regional GDP (source: http://data.stats.gov.cn/), the regional contribution rate to national economic development is calculated by province. Then, the future regional contribution rate to national economic development is forecasted with the data dimensionality reduction method and the GM(1,1) model. Additionally, literature research and the scenario analysis method are combined to design the national economic growth rate under the new norm.
- Model industrial structure and electricity consumption per unit of GDP for primary industry, secondary industry, and tertiary industry by province. The data dimensionality reduction method and GM(1,1) model are also used to project the industrial structure in different provinces based on the historical data. Electricity consumption per unit of GDP of the three industries in different regions are forecasted with the GM(1,1) model and regression model up until 2025.
- Forecast the regional residential household electricity demand up until 2025. In this part, a multivariate linear regression model, which considers the influences of regional GDP and population, is applied to predict the regional electricity power demand of households. The next section introduces the model framework and underlying theories applied to the study.
2. Methods
2.1. Model Framework
2.2. Method and Theory
2.2.1. Data Dimensionality Reduction Method
2.2.2. The GM(1,1) Model
2.3. Input Data and Calculations
2.3.1. Data Sources
2.3.2. National Economic Growth Rate Design
2.3.3. Forecasting of Each Province’s Contribution Rate to the National Economic Growth
2.3.4. Regional Industrial Structure Design
2.3.5. Per Unit GDP Electric Consumption Design
2.3.6. Household Electricity Consumption Design
3. Results
3.1. National Electric Power Demand
3.2. Spatial Variations of Electricity Demand in Provinces
3.3. Regional Electricity Consumption Structure
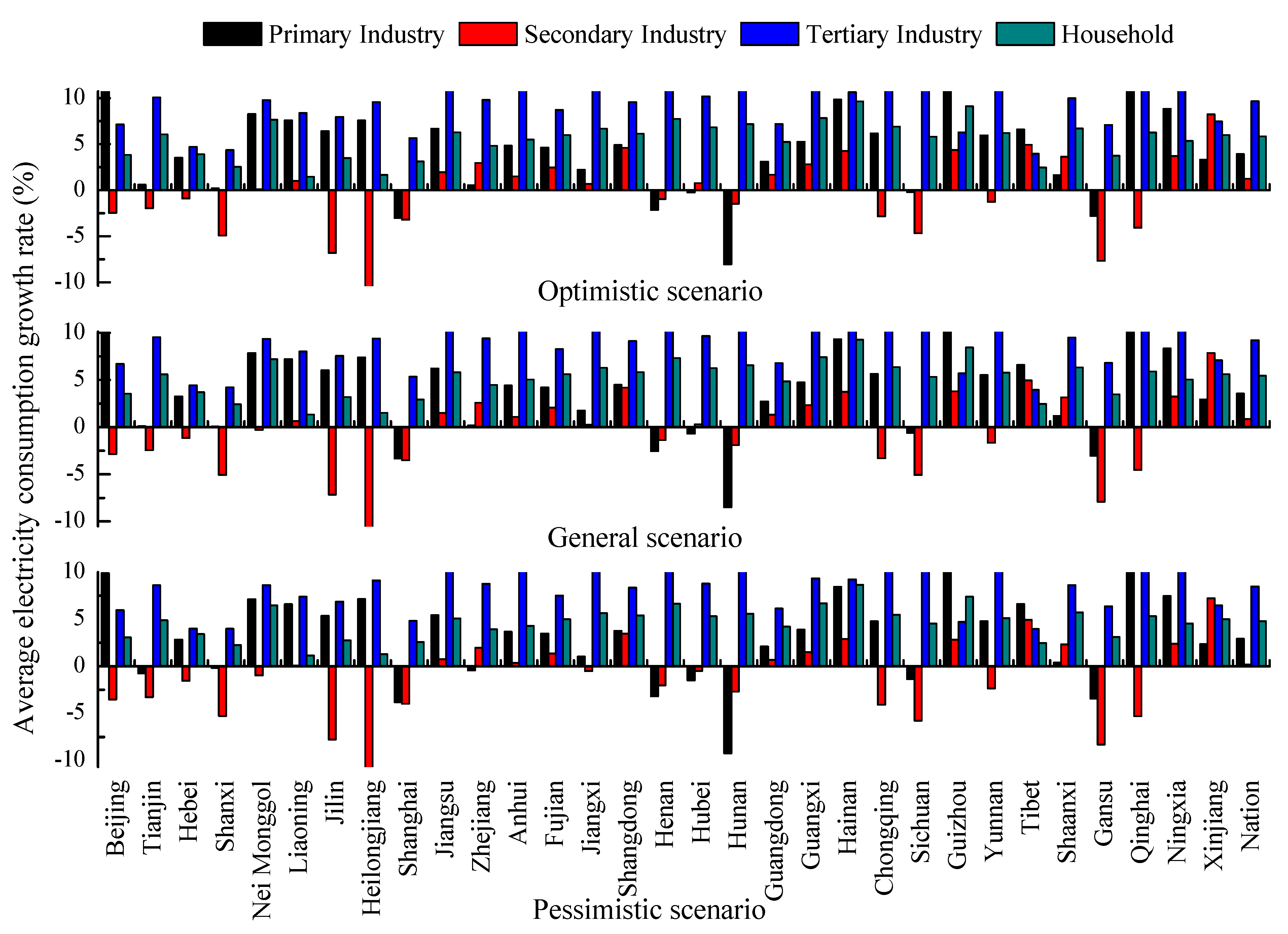
3.4. Average Electricity Consumption Growth Rate
4. Discussion
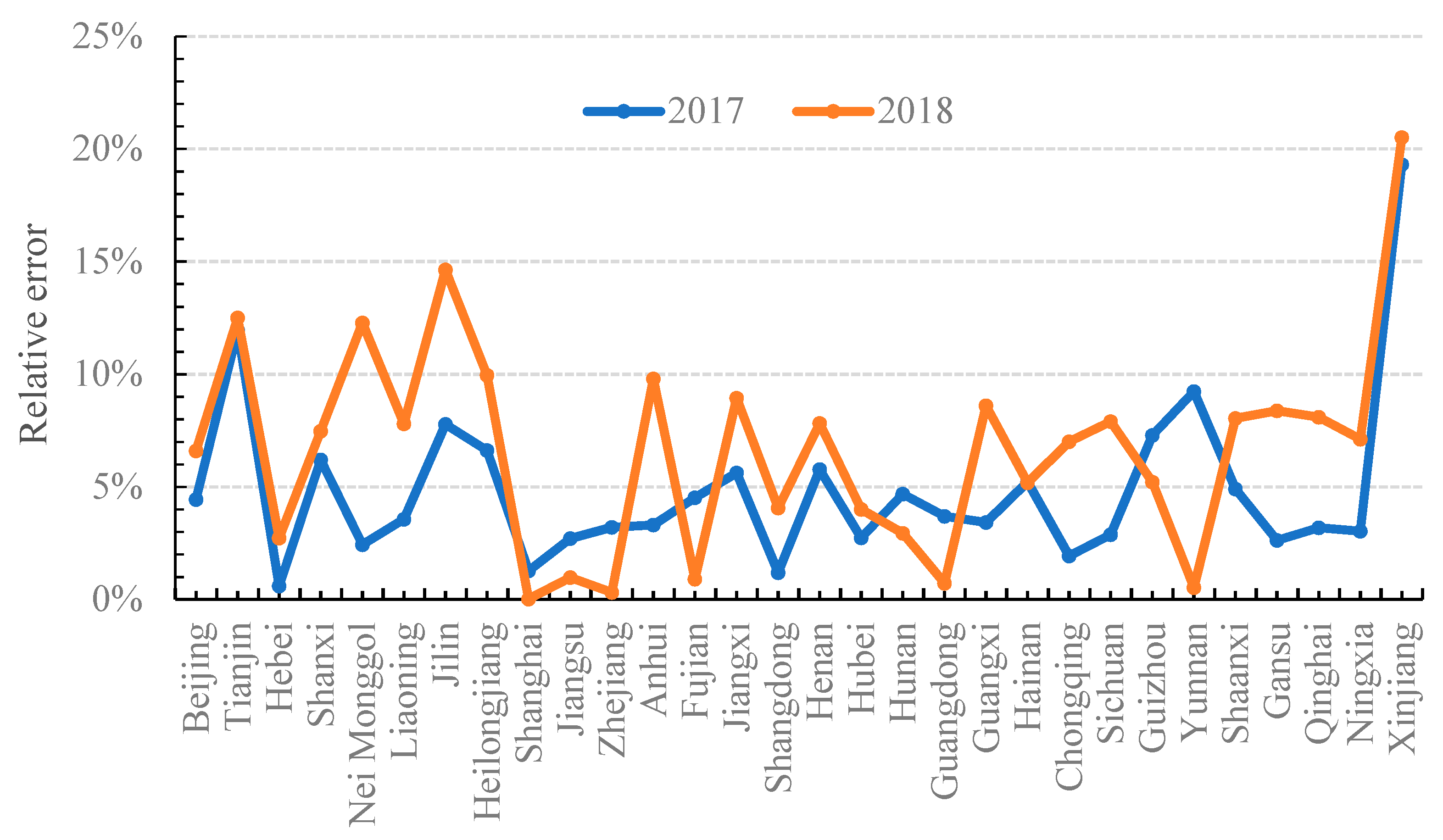
4.1. Comparison to the Actual Electric Consumption in 2017 and 2018
4.2. Comparison to Other Studies
4.3. The Changes in Electricity Demand under the New Economic Normal
5. Conclusions
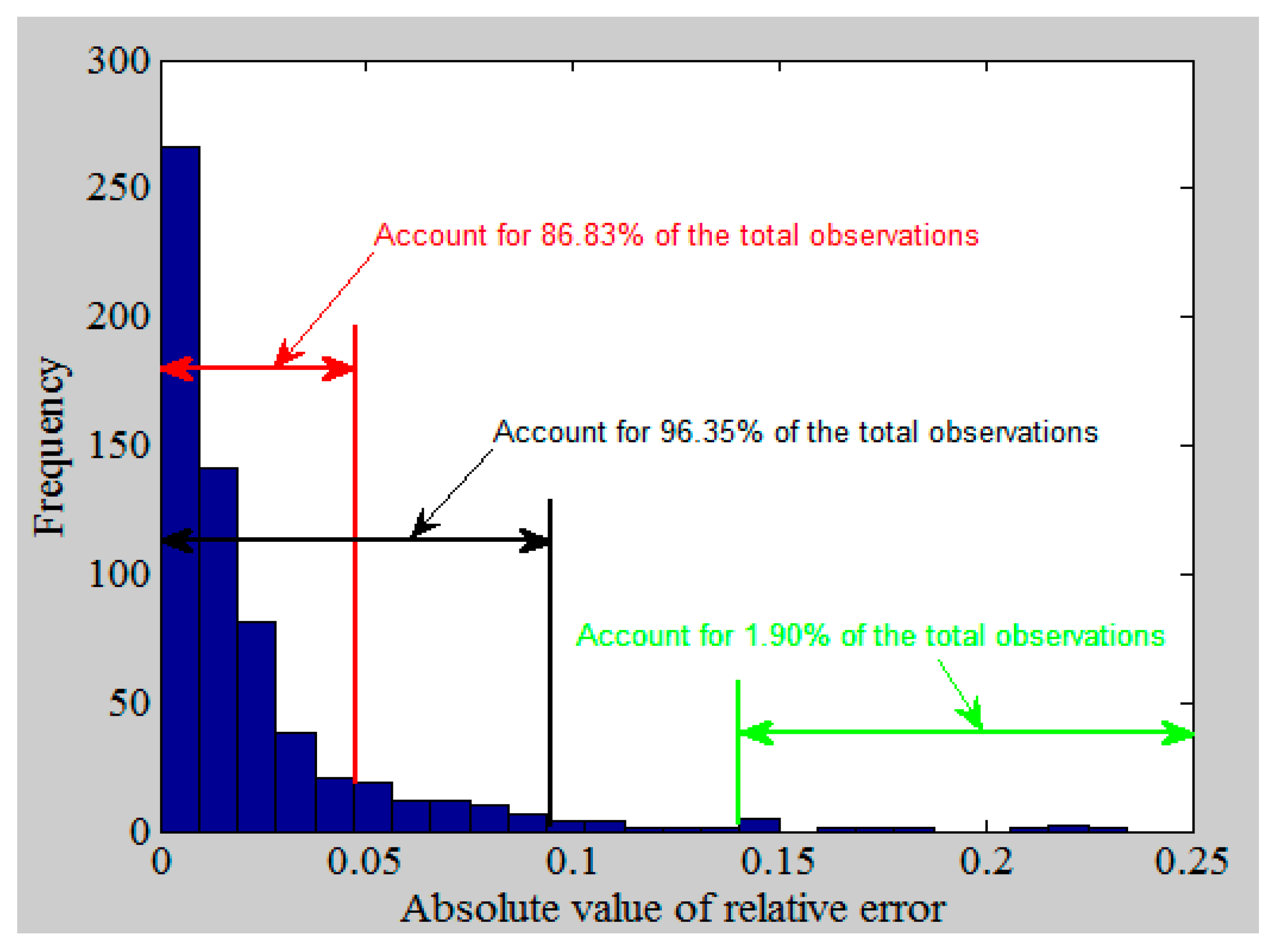
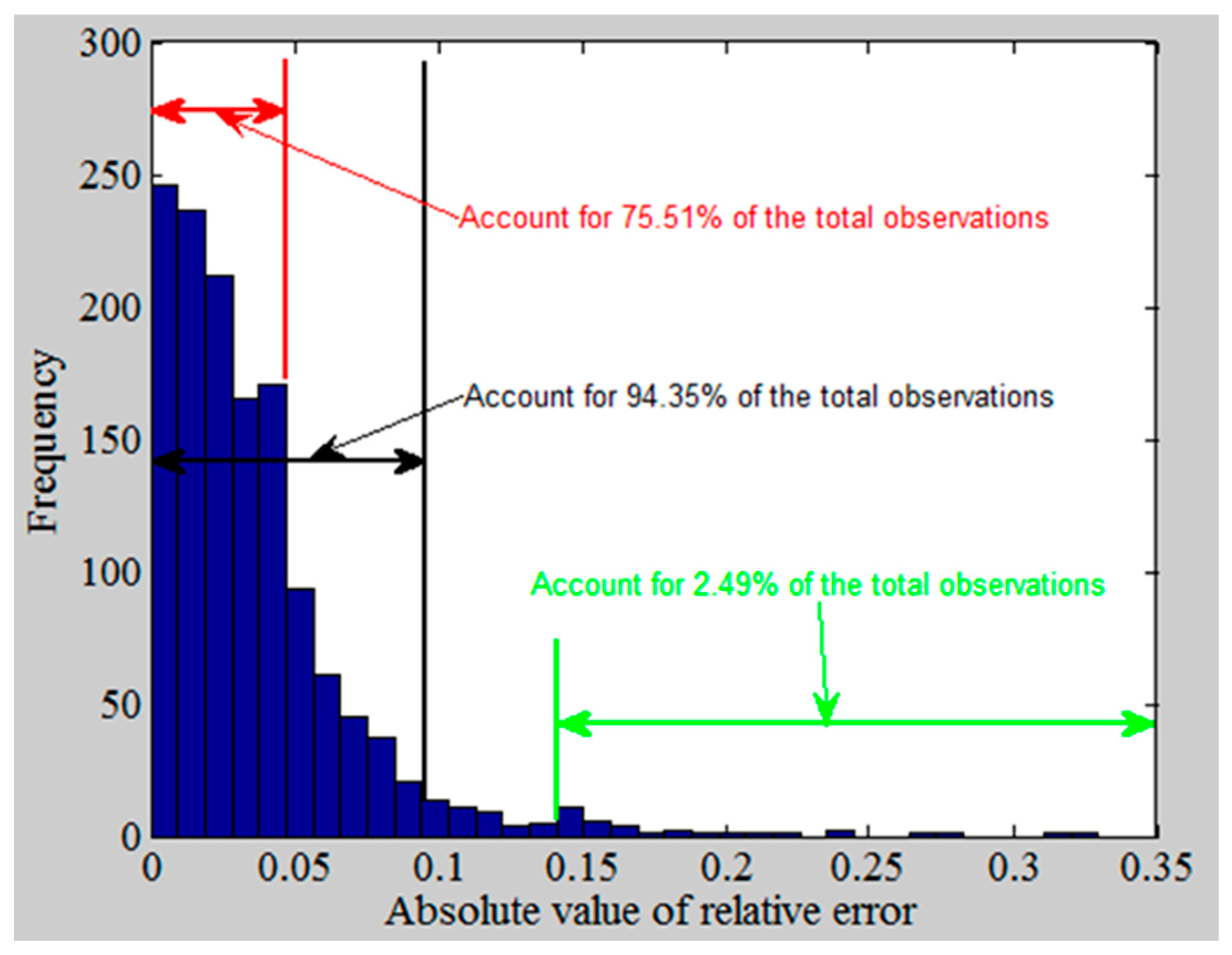
- This model was proven to be highly reliable. Compared with the actual national electric power consumption in 2017 and 2018, the prediction error of the proposed method is 2.90% and 2.60%, respectively. The average prediction error of regional electric consumption in 2017 and 2018 is 4.84% and 6.70%, respectively.
- In the optimistic scenario, general scenario, and pessimistic scenario, the electricity demand in 2025 will be 8458.85 billion kW·h, 8198.41 billion kW·h, and 7772.16 billion kW·h, respectively. Although the total electricity demand will increase, it will not peak between 2017 and 2025. Additionally, electricity consumption in the mid-west provinces will increase, and the eastern provinces will continue to be the country’s load center.
- Under the situation of China’s new normal, the electricity demand is expected to increase slowly in the secondary industry; the average electric demand growth rate between 2017 and 2025 respectively is 1.25%, 0.85%, and 0.17% under the optimistic scenario, general scenario, and pessimistic scenario. However, the electricity consumption growth rate will be much higher in the tertiary industry and household sector, and the predicted growth rates under the three scenarios are 9.65%, 9.22%, and 8.38% for the tertiary industry, and 5.85%, 5.45%, and 4.80% for the household sector, respectively. Besides, the respectively electricity growth rates of the primary industry are 3.94%, 3.56%, and 2.92% under the three scenarios.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Province | Natural Population Growth Rate (‰) | Province | Natural Population Growth Rate (‰) | ||
|---|---|---|---|---|---|
| Beijing | 1961.20 | 4.12 | Hubei | 5723.77 | 5.07 |
| Tianjin | 1293.82 | 1.83 | Hunan | 6568.37 | 6.56 |
| Hebei | 7185.42 | 6.06 | Guangdong | 10430.03 | 7.44 |
| Shanxi | 3571.21 | 4.77 | Guangxi | 4602.66 | 7.87 |
| Nei Monggol | 2470.63 | 3.30 | Hainan | 867.15 | 8.57 |
| Liaoning | 4374.63 | −0.18 | Chongqing | 2884.00 | 4.53 |
| Jilin | 2746.22 | −0.05 | Sichuan | 8041.82 | 3.49 |
| Heilongjiang | 3831.22 | −0.49 | Guizhou | 3476.65 | 6.50 |
| Shanghai | 2301.39 | 4.00 | Yunnan | 4596.60 | 6.61 |
| Jiangsu | 7865.99 | 2.73 | Tibet | 300.21 | 10.68 |
| Zhejiang | 5442.00 | 5.70 | Shaanxi | 3732.74 | 4.41 |
| Anhui | 5950.10 | 7.06 | Gansu | 2557.53 | 6.00 |
| Fujian | 3552.00 | 8.30 | Qinghai | 562.67 | 8.52 |
| Jiangxi | 4456.74 | 7.29 | Ningxia | 630.14 | 8.97 |
| Shandong | 9579.31 | 10.84 | Xinjiang | 2181.33 | 11.08 |
| Henan | 9402.36 | 6.15 |
| Province | Sample Regression Model | Province | Sample Regression Model | Province | Sample Regression Model |
|---|---|---|---|---|---|
| Beijing | Zhejiang | Hainan | |||
| Tianjin | Anhui | Chong-qing | |||
| Hebei | Fujian | Sichuan | |||
| Shanxi | Jiangxi | Guizhou | |||
| Nei Monggol | Shan-dong | Yunnan | |||
| Liaoning | Henan | Shaanxi | |||
| Jilin | Hubei | Gansu | |||
| Heilong-jiang | Hunan | Qinghai | |||
| Shanghai | Guang-dong | Ningxia | |||
| Jiangsu | Guangxi | Xinjiang |
| Province | Beijing | Tianjin | Hebei | Shanxi | Nei Monggol | Liaoning | Jilin | Heilongjiang | Shanghai | ||||||||||||||||||
| PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | |
| 2017* | 0.5 | 19.3 | 80.2 | 1.2 | 40.8 | 58.0 | 10.9 | 47.6 | 41.5 | 5.2 | 41.3 | 53.5 | 10.2 | 39.8 | 50.0 | 9.1 | 39.3 | 51.6 | 9.3 | 45.9 | 44.8 | 18.3 | 26.5 | 55.2 | 0.4 | 29.8 | 69.8 |
| 2017 | 0.9 | 18.7 | 80.3 | 0.9 | 44.0 | 55.1 | 11.4 | 48.8 | 39.7 | 5.9 | 41.9 | 52.2 | 10.9 | 42.1 | 47.0 | 8.9 | 42.9 | 44.2 | 9.7 | 47.7 | 42.5 | 19.0 | 29.1 | 51.9 | 0.5 | 29.6 | 69.9 |
| 2020 | 0.9 | 17.0 | 82.2 | 0.7 | 39.7 | 59.6 | 11.1 | 47.1 | 41.9 | 5.7 | 38.1 | 56.2 | 9.4 | 41.3 | 49.3 | 8.7 | 39.5 | 51.8 | 8.8 | 45.0 | 46.2 | 21.0 | 22.5 | 56.5 | 0.4 | 25.1 | 74.5 |
| 2023 | 0.8 | 15.4 | 83.9 | 0.6 | 35.7 | 63.7 | 10.7 | 45.3 | 44.0 | 5.6 | 36.6 | 57.8 | 9.3 | 36.7 | 54.0 | 8.6 | 36.2 | 55.2 | 7.9 | 42.3 | 48.6 | 22.3 | 18.3 | 59.4 | 0.3 | 21.2 | 78.5 |
| 2025 | 0.8 | 14.4 | 84.9 | 0.5 | 33.2 | 66.3 | 10.5 | 44.2 | 45.3 | 5.5 | 35.3 | 59.2 | 9.3 | 33.8 | 56.9 | 8.5 | 34.1 | 57.4 | 7.4 | 40.6 | 52.0 | 23.0 | 16.4 | 60.6 | 0.2 | 18.9 | 80.9 |
| Province | Jiangsu | Zhejiang | Anhui | Fujian | Jiangxi | Shandong | Henan | Hubei | Hunan | ||||||||||||||||||
| PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | |
| 2017* | 4.7 | 45.0 | 50.3 | 3.9 | 43.4 | 52.7 | 9.5 | 49.0 | 41.5 | 7.6 | 48.8 | 43.6 | 9.4 | 47.9 | 42.7 | 6.7 | 45.3 | 48.0 | 9.6 | 47.7 | 42.7 | 10.3 | 44.5 | 45.2 | 10.7 | 40.9 | 48.4 |
| 2017 | 4.9 | 44.5 | 50.6 | 3.5 | 45.7 | 50.9 | 10.2 | 51.2 | 38.7 | 7.4 | 50.8 | 41.8 | 11.0 | 48.3 | 40.7 | 7.7 | 45.8 | 46.5 | 10.9 | 48.9 | 40.2 | 10.6 | 45.0 | 44.3 | 10.6 | 42.8 | 46.7 |
| 2020 | 4.4 | 41.4 | 54.2 | 3.0 | 43.4 | 53.6 | 9.0 | 49.8 | 41.3 | 6.8 | 50.3 | 42.9 | 11.0 | 44.9 | 44.1 | 7.0 | 42.8 | 50.1 | 9.9 | 46.1 | 44.0 | 9.6 | 42.9 | 47.5 | 9.1 | 40.0 | 50.8 |
| 2023 | 3.9 | 38.5 | 57.6 | 2.6 | 41.1 | 56.3 | 7.9 | 48.3 | 43.8 | 6.2 | 49.7 | 44.1 | 10.9 | 41.6 | 47.4 | 6.5 | 39.9 | 53.6 | 8.9 | 43.4 | 47.7 | 8.7 | 40.7 | 50.6 | 7.9 | 37.4 | 54.8 |
| 2025 | 3.6 | 36.6 | 59.8 | 2.3 | 39.7 | 58.0 | 7.2 | 47.3 | 45.5 | 5.8 | 49.4 | 44.9 | 10.9 | 39.5 | 49.6 | 6.1 | 38.0 | 55.9 | 8.3 | 41.6 | 50.1 | 8.1 | 39.3 | 52.6 | 7.1 | 35.6 | 57.3 |
| Province | Guangdong | Guangxi | Hainan | Chongqing | Sichuan | Guizhou | Yunnan | Tibet | Shaanxi | ||||||||||||||||||
| PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | |
| 2017* | 4.2 | 43.0 | 52.8 | 14.2 | 45.6 | 40.2 | 22.0 | 22.3 | 55.7 | 6.9 | 44.1 | 49.0 | 11.6 | 38.7 | 49.7 | 14.9 | 40.2 | 44.9 | 14.0 | 38.6 | 47.4 | 9.4 | 39.2 | 51.4 | 7.9 | 49.8 | 42.3 |
| 2017 | 4.1 | 44.5 | 51.4 | 14.7 | 46.9 | 38.4 | 20.6 | 24.5 | 54.8 | 6.6 | 44.5 | 49.0 | 10.5 | 42.2 | 47.3 | 14.6 | 41.6 | 43.8 | 15.6 | 38.3 | 46.1 | 7.8 | 39.2 | 53.0 | 8.5 | 49.3 | 42.2 |
| 2020 | 3.7 | 42.6 | 53.7 | 13.1 | 48.1 | 38.7 | 18.4 | 23.4 | 58.2 | 5.7 | 41.5 | 52.8 | 8.8 | 37.1 | 54.1 | 15.4 | 42.8 | 41.7 | 15.7 | 35.8 | 48.6 | 6.2 | 41.4 | 52.4 | 7.9 | 45.9 | 46.2 |
| 2023 | 3.3 | 40.8 | 55.9 | 11.7 | 49.2 | 39.1 | 16.4 | 22.2 | 61.4 | 5.0 | 38.7 | 56.4 | 7.4 | 32.3 | 60.3 | 16.3 | 44.1 | 39.6 | 15.8 | 33.3 | 50.9 | 4.9 | 43.2 | 51.9 | 7.4 | 42.7 | 49.9 |
| 2025 | 3.0 | 39.6 | 57.4 | 10.9 | 49.9 | 39.3 | 15.2 | 21.4 | 63.4 | 4.5 | 36.8 | 58.7 | 6.6 | 29.4 | 64.0 | 16.8 | 44.9 | 38.2 | 15.8 | 31.7 | 53.5 | 4.2 | 44.3 | 51.5 | 7.1 | 40.6 | 52.3 |
| Province | Gansu | Qinghai | Ningxia | Xinjiang | |||||||||||||||||||||||
| PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | ||||||||||||||||
| 2017* | 13.9 | 33.4 | 52.7 | 9.9 | 44.7 | 46.3 | 7.6 | 45.8 | 46.6 | 15.5 | 39.3 | 45.2 | |||||||||||||||
| 2017 | 13.4 | 34.4 | 52.1 | 8.8 | 45.9 | 45.2 | 8.4 | 46.2 | 45.4 | 16.1 | 38.5 | 45.4 | |||||||||||||||
| 2020 | 13.0 | 28.7 | 58.3 | 8.4 | 39.6 | 52.0 | 8.4 | 44.2 | 47.4 | 15.4 | 35.1 | 49.4 | |||||||||||||||
| 2023 | 12.5 | 23.6 | 63.8 | 8.0 | 33.9 | 58.1 | 8.4 | 42.2 | 49.4 | 14.8 | 32.0 | 53.3 | |||||||||||||||
| 2025 | 12.2 | 20.6 | 67.2 | 7.7 | 30.4 | 61.9 | 8.4 | 40.9 | 50.7 | 14.3 | 30.0 | 55.7 | |||||||||||||||
| Province | Beijing | Tianjin | Hebei | Shanxi | Nei Monggol | Liaoning | Jilin | Heilongjiang | ||||||||||||||||
| PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | |
| 2017 | 1400.7 | 495.9 | 252.5 | 688.4 | 789.5 | 161.6 | 345.7 | 1590.6 | 279.1 | 515.8 | 2701.6 | 253.0 | 286.7 | 2719.5 | 146.9 | 143.0 | 1551.1 | 240.9 | 87.8 | 522.1 | 189.7 | 159.3 | 1121.0 | 164.2 |
| 2020 | 1699.6 | 419.4 | 251.3 | 690.9 | 644.5 | 157.3 | 353.0 | 1430.6 | 272.9 | 500.9 | 2483.3 | 250.3 | 304.6 | 2548.8 | 147.0 | 154.0 | 1486.0 | 245.4 | 98.3 | 374.1 | 186.2 | 169.5 | 986.3 | 183.2 |
| 2023 | 2069.9 | 355.5 | 250.1 | 693.2 | 528.7 | 153.1 | 362.7 | 1295.7 | 267.0 | 484.8 | 2284.0 | 247.7 | 324.5 | 2393.4 | 147.0 | 166.5 | 1424.7 | 249.9 | 111.0 | 271.0 | 182.8 | 180.4 | 863.4 | 209.7 |
| 2025 | 2365.1 | 318.6 | 249.3 | 694.5 | 464.6 | 150.4 | 370.5 | 1216.2 | 263.2 | 474.4 | 2159.3 | 246.0 | 339.0 | 2297.7 | 147.1 | 175.6 | 1383.2 | 252.8 | 120.9 | 219.9 | 180.6 | 187.9 | 788.6 | 232.4 |
| Province | Shanghai | Jiangsu | Zhejiang | Anhui | Fujian | Jiangxi | Shandong | Henan | ||||||||||||||||
| PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | |
| 2017 | 557.8 | 953.8 | 238.8 | 110.0 | 1241.9 | 181.1 | 113.8 | 1403.0 | 237.1 | 63.1 | 993.9 | 240.5 | 95.1 | 945.5 | 229.2 | 56.7 | 846.0 | 234.1 | 198.8 | 1305.4 | 157.0 | 206.9 | 1242.2 | 247.9 |
| 2020 | 636.6 | 894.2 | 232.8 | 120.6 | 1146.9 | 190.6 | 114.1 | 1370.4 | 254.0 | 68.2 | 881.6 | 268.5 | 98.5 | 847.7 | 236.9 | 49.5 | 756.1 | 275.8 | 206.3 | 1329.8 | 159.2 | 179.6 | 1062.7 | 266.2 |
| 2023 | 726.9 | 837.1 | 226.9 | 133.6 | 1061.2 | 200.6 | 114.2 | 1339.6 | 272.1 | 73.9 | 783.8 | 299.6 | 102.2 | 762.5 | 244.9 | 43.2 | 676.6 | 325.0 | 214.6 | 1346.6 | 161.5 | 155.3 | 914.3 | 283.3 |
| 2025 | 795.2 | 800.4 | 223.1 | 143.8 | 1008.1 | 207.5 | 114.2 | 1319.0 | 284.8 | 78.0 | 725.1 | 322.4 | 105.0 | 711.2 | 250.3 | 39.4 | 628.6 | 362.6 | 220.8 | 1356.9 | 163.1 | 141.0 | 829.7 | 294.4 |
| Province | Hubei | Hunan | Guangdong | Guangxi | Hainan | Chongqing | Sichuan | Guizhou | ||||||||||||||||
| PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | |
| 2017 | 72.4 | 919.2 | 183.7 | 60.0 | 743.4 | 175.5 | 260.1 | 1071.2 | 252.4 | 100.0 | 1113.3 | 229.2 | 158.9 | 1554.8 | 356.4 | 31.8 | 714.5 | 242.3 | 32.5 | 1039.1 | 200.9 | 30.1 | 2036.1 | 197.0 |
| 2020 | 63.2 | 787.9 | 184.4 | 41.5 | 609.2 | 185.3 | 269.3 | 993.4 | 252.2 | 104.1 | 938.3 | 246.0 | 188.0 | 1474.9 | 363.8 | 35.0 | 556.6 | 279.7 | 31.4 | 835.4 | 209.9 | 31.6 | 1708.2 | 189.8 |
| 2023 | 55.8 | 678.6 | 184.6 | 30.5 | 502.2 | 195.6 | 279.0 | 924.0 | 252.1 | 108.4 | 794.1 | 263.9 | 222.6 | 1398.3 | 371.4 | 38.3 | 436.2 | 322.8 | 30.3 | 676.2 | 219.4 | 33.6 | 1441.9 | 183.3 |
| 2025 | 51.3 | 615.4 | 184.6 | 25.4 | 443.0 | 202.8 | 285.8 | 881.3 | 252.0 | 111.3 | 712.0 | 276.6 | 249.3 | 1349.5 | 376.6 | 40.7 | 372.7 | 355.2 | 29.6 | 589.2 | 225.9 | 35.3 | 1291.4 | 179.1 |
| Province | Yunnan | Shaanxi | Gansu | Qinghai | Ningxia | Xinjiang | Unit | |||||||||||||||||
| PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | PI | SI | TI | kW·h/(104 Yuan) | ||||||
| 2017 | 64.6 | 2057.5 | 231.6 | 239.3 | 942.5 | 259.1 | 509.2 | 3393.0 | 326.6 | 98.9 | 4755.2 | 257.9 | 669.7 | 5876.4 | 280.2 | 838.1 | 5257.0 | 255.6 | ||||||
| 2020 | 62.8 | 1737.6 | 250.8 | 216.0 | 904.9 | 255.3 | 430.6 | 2882.8 | 326.0 | 139.4 | 3867.2 | 272.7 | 690.8 | 5476.1 | 311.1 | 822.8 | 6259.6 | 251.0 | ||||||
| 2023 | 61.3 | 1487.2 | 274.4 | 194.9 | 870.3 | 251.8 | 367.3 | 2459.7 | 325.4 | 207.4 | 3187.8 | 288.8 | 712.4 | 5118.6 | 345.3 | 811.6 | 7470.4 | 247.1 | ||||||
| 2025 | 60.4 | 1349.2 | 292.5 | 182.0 | 846.6 | 249.5 | 331.5 | 2219.1 | 325.1 | 280.8 | 2820.6 | 300.1 | 727.3 | 4902.2 | 370.2 | 807.5 | 8419.2 | 244.9 | ||||||
| Province | Beijing | Tianjin | Hebei | Shanxi | Nei Monggol | Liaoning | Jilin | Heilongjiang | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | |
| 2017 | 195.9 | 195.9 | 195.9 | 96.2 | 96.2 | 96.2 | 381.3 | 381.3 | 381.3 | 149.4 | 149.4 | 149.4 | 143.3 | 143.3 | 143.3 | 202.7 | 202.7 | 202.7 | 114.1 | 114.1 | 114.1 | 167.9 | 167.9 | 167.9 |
| 2020 | 220.2 | 218.4 | 216.6 | 115.9 | 114.4 | 112.9 | 433.4 | 430.9 | 428.3 | 162.5 | 161.9 | 161.3 | 179.6 | 177.4 | 175.3 | 211.6 | 210.9 | 210.2 | 126.3 | 125.3 | 124.4 | 178.0 | 177.1 | 176.3 |
| 2023 | 245.9 | 241.8 | 235.8 | 137.5 | 134.1 | 129.0 | 484.2 | 478.6 | 470.7 | 174.8 | 173.5 | 171.8 | 223.3 | 217.7 | 209.7 | 221.0 | 219.3 | 216.8 | 139.7 | 137.5 | 134.3 | 186.6 | 184.8 | 182.3 |
| 2025 | 264.8 | 258.8 | 249.4 | 153.9 | 148.9 | 140.9 | 518.1 | 510.3 | 498.5 | 182.6 | 181.0 | 178.4 | 258.4 | 249.8 | 236.3 | 227.7 | 225.3 | 221.5 | 150.0 | 146.7 | 141.6 | 191.8 | 189.4 | 185.8 |
| Province | Shanghai | Jiangsu | Zhejiang | Anhui | Fujian | Jiangxi | Shandong | Henan | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | |
| 2017 | 240.7 | 240.7 | 240.7 | 656.2 | 656.2 | 656.2 | 561.6 | 561.6 | 561.6 | 294.7 | 294.7 | 294.7 | 433.4 | 433.4 | 433.4 | 218.1 | 218.1 | 218.1 | 585.1 | 585.1 | 585.1 | 510.8 | 510.8 | 510.8 |
| 2020 | 265.8 | 264.2 | 262.6 | 791.2 | 781.5 | 771.8 | 651.0 | 644.7 | 638.6 | 349.0 | 345.4 | 341.7 | 520.0 | 514.5 | 509.1 | 267.3 | 264.5 | 261.6 | 708.0 | 702.5 | 697.2 | 643.3 | 635.9 | 628.5 |
| 2023 | 290.6 | 287.1 | 281.9 | 946.0 | 922.2 | 887.5 | 747.3 | 732.7 | 711.6 | 406.6 | 396.6 | 382.4 | 616.8 | 603.6 | 584.3 | 323.1 | 316.1 | 305.7 | 841.9 | 828.8 | 809.8 | 801.4 | 782.9 | 755.7 |
| 2025 | 307.8 | 302.8 | 295.1 | 1067.4 | 1031.4 | 975.1 | 819.2 | 797.6 | 764.1 | 452.3 | 436.6 | 412.5 | 690.8 | 670.9 | 639.9 | 366.3 | 355.5 | 338.7 | 941.0 | 921.4 | 890.9 | 928.1 | 899.4 | 854.5 |
| Province | Hubei | Hunan | Guangdong | Guangxi | Hainan | Chongqing | Sichuan | Guizhou | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | |
| 2017 | 348.8 | 348.8 | 348.8 | 392.0 | 392.0 | 392.0 | 978.4 | 978.4 | 978.4 | 264.6 | 264.6 | 264.6 | 55.3 | 55.3 | 55.3 | 182.6 | 182.6 | 182.6 | 391.3 | 391.3 | 391.3 | 286.0 | 286.0 | 286.0 |
| 2020 | 424.0 | 417.4 | 410.9 | 482.4 | 474.5 | 466.7 | 1147.7 | 1135.2 | 1122.8 | 333.1 | 329.1 | 325.2 | 73.1 | 72.4 | 71.6 | 222.6 | 219.4 | 216.2 | 462.2 | 456.2 | 450.3 | 372.5 | 365.9 | 359.4 |
| 2023 | 515.8 | 499.4 | 475.4 | 591.6 | 572.2 | 543.8 | 1332.2 | 1302.7 | 1259.9 | 416.4 | 406.4 | 391.6 | 96.1 | 94.2 | 91.2 | 271.2 | 263.3 | 251.5 | 546.3 | 531.7 | 510.3 | 481.5 | 464.6 | 439.6 |
| 2025 | 592.0 | 566.8 | 527.3 | 681.6 | 651.9 | 605.2 | 1471.4 | 1427.6 | 1359.8 | 484.1 | 468.8 | 444.3 | 115.6 | 112.4 | 107.4 | 311.4 | 299.1 | 279.7 | 614.6 | 592.3 | 557.4 | 573.8 | 547.2 | 505.2 |
| Province | Yunnan | Tibet | Shaanxi | Gansu | Qinghai | Ningxia | Xinjiang | Unit | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | 102 million kW·h | |||
| 2017 | 246.2 | 246.2 | 246.2 | 7.0 | 7.0 | 7.0 | 197.6 | 197.6 | 197.6 | 85.2 | 85.2 | 85.2 | 25.8 | 25.8 | 25.8 | 25.6 | 25.6 | 25.6 | 90.8 | 90.8 | 90.8 | |||
| 2020 | 296.4 | 293.0 | 289.7 | 7.6 | 7.6 | 7.6 | 240.8 | 238.3 | 235.9 | 96.0 | 95.3 | 94.6 | 31.1 | 30.8 | 30.5 | 30.0 | 29.7 | 29.5 | 108.7 | 107.6 | 106.4 | |||
| 2023 | 353.6 | 345.4 | 333.5 | 8.1 | 8.1 | 8.1 | 291.7 | 285.6 | 276.7 | 106.8 | 105.2 | 102.9 | 37.1 | 36.4 | 35.3 | 34.9 | 34.4 | 33.5 | 129.0 | 126.3 | 122.3 | |||
| 2025 | 398.2 | 385.8 | 366.5 | 8.5 | 8.5 | 8.5 | 332.0 | 322.9 | 308.3 | 114.3 | 112.0 | 108.5 | 41.9 | 40.8 | 39.0 | 38.9 | 37.9 | 36.5 | 144.7 | 140.6 | 134.1 | |||
| Province | Beijing | Tianjin | Hebei | Shanxi | Nei Monggol | Liaoning | Jilin | Heilongjiang | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | |
| 2017 | 1.57 | 1.57 | 1.57 | 1.48 | 1.48 | 1.48 | 5.33 | 5.33 | 5.33 | 2.88 | 2.88 | 2.88 | 4.35 | 4.35 | 4.35 | 3.17 | 3.17 | 3.17 | 1.00 | 1.00 | 1.00 | 1.34 | 1.34 | 1.34 |
| 2020 | 1.65 | 1.65 | 1.65 | 1.42 | 1.41 | 1.41 | 4.97 | 4.99 | 5.01 | 2.41 | 2.43 | 2.44 | 4.13 | 4.13 | 4.13 | 3.13 | 3.13 | 3.14 | 0.87 | 0.88 | 0.88 | 1.12 | 1.13 | 1.13 |
| 2025 | 1.76 | 1.76 | 1.76 | 1.32 | 1.31 | 1.29 | 4.28 | 4.34 | 4.43 | 1.74 | 1.78 | 1.84 | 3.72 | 3.72 | 3.71 | 2.93 | 2.95 | 2.98 | 0.75 | 0.75 | 0.75 | 0.88 | 0.90 | 0.93 |
| Province | Shanghai | Jiangsu | Zhejiang | Anhui | Fujian | Jiangxi | Shandong | Henan | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | |
| 2017 | 2.38 | 2.38 | 2.38 | 9.19 | 9.19 | 9.19 | 6.67 | 6.67 | 6.67 | 2.86 | 2.86 | 2.86 | 3.40 | 3.40 | 3.40 | 1.88 | 1.88 | 1.88 | 8.47 | 8.47 | 8.47 | 5.59 | 5.59 | 5.59 |
| 2020 | 2.25 | 2.26 | 2.26 | 9.43 | 9.41 | 9.40 | 6.93 | 6.93 | 6.94 | 2.93 | 2.93 | 2.93 | 3.51 | 3.51 | 3.51 | 1.97 | 1.96 | 1.96 | 9.11 | 9.11 | 9.11 | 5.42 | 5.42 | 5.42 |
| 2025 | 2.00 | 2.02 | 2.05 | 9.68 | 9.64 | 9.57 | 7.18 | 7.20 | 7.24 | 3.05 | 3.04 | 3.03 | 3.63 | 3.62 | 3.62 | 2.18 | 2.17 | 2.16 | 9.83 | 9.83 | 9.83 | 5.24 | 5.24 | 5.24 |
| Province | Hubei | Hunan | Guangdong | Guangxi | Hainan | Chongqing | Sichuan | Guizhou | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | |
| 2017 | 3.23 | 3.23 | 3.23 | 2.70 | 2.70 | 2.70 | 9.52 | 9.52 | 9.52 | 2.30 | 2.30 | 2.30 | 0.49 | 0.49 | 0.49 | 1.56 | 1.56 | 1.56 | 3.50 | 3.50 | 3.50 | 2.29 | 2.29 | 2.29 |
| 2020 | 3.24 | 3.23 | 3.23 | 2.69 | 2.68 | 2.67 | 9.63 | 9.63 | 9.64 | 2.41 | 2.41 | 2.40 | 0.56 | 0.56 | 0.56 | 1.59 | 1.58 | 1.58 | 3.22 | 3.22 | 3.21 | 2.45 | 2.44 | 2.43 |
| 2025 | 3.27 | 3.25 | 3.20 | 2.76 | 2.74 | 2.71 | 9.56 | 9.58 | 9.61 | 2.60 | 2.59 | 2.56 | 0.67 | 0.67 | 0.66 | 1.80 | 1.79 | 1.76 | 3.01 | 3.00 | 2.98 | 2.71 | 2.68 | 2.61 |
| Province | Yunnan | Tibet | Shaanxi | Gansu | Qinghai | Ningxia | Xinjiang | Unit | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | % | |||
| 2017 | 2.59 | 2.59 | 2.59 | 0.06 | 0.06 | 0.06 | 2.19 | 2.19 | 2.19 | 1.75 | 1.75 | 1.75 | 1.02 | 1.02 | 1.02 | 1.55 | 1.55 | 1.55 | 3.69 | 3.69 | 3.69 | |||
| 2020 | 2.45 | 2.45 | 2.45 | 0.06 | 0.06 | 0.06 | 2.33 | 2.32 | 2.32 | 1.40 | 1.41 | 1.41 | 0.87 | 0.87 | 0.86 | 1.61 | 1.60 | 1.60 | 4.24 | 4.25 | 4.26 | |||
| 2025 | 2.32 | 2.31 | 2.31 | 0.06 | 0.06 | 0.07 | 2.52 | 2.51 | 2.49 | 0.99 | 1.00 | 1.02 | 0.69 | 0.68 | 0.68 | 1.68 | 1.67 | 1.66 | 5.20 | 5.21 | 5.25 | |||
| Province | Beijing | Tianjin | Hebei | Shanxi | Nei Monggol | Liaoning | Jilin | Heilongjiang | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | |
| PI | 5.35 | 5.34 | 5.32 | 1.18 | 1.17 | 1.17 | 4.79 | 4.78 | 4.78 | 2.76 | 2.76 | 2.76 | 3.24 | 3.24 | 3.24 | 2.14 | 2.14 | 2.13 | 3.55 | 3.54 | 3.53 | 11.50 | 11.50 | 11.50 |
| SI | 13.66 | 13.64 | 13.59 | 51.70 | 51.65 | 51.55 | 66.22 | 66.17 | 66.08 | 68.06 | 68.05 | 68.02 | 79.92 | 79.93 | 79.94 | 67.85 | 67.74 | 67.55 | 35.42 | 35.36 | 35.22 | 25.33 | 25.33 | 25.32 |
| TI | 63.18 | 63.08 | 62.86 | 33.37 | 33.34 | 33.27 | 14.70 | 14.69 | 14.67 | 16.76 | 16.76 | 16.75 | 8.64 | 8.64 | 8.64 | 20.84 | 20.81 | 20.75 | 37.26 | 37.19 | 37.04 | 37.51 | 37.51 | 37.49 |
| Household | 17.81 | 17.95 | 18.22 | 13.76 | 13.83 | 14.01 | 14.30 | 14.36 | 14.48 | 12.41 | 12.43 | 12.47 | 8.21 | 8.19 | 8.19 | 9.17 | 9.31 | 9.57 | 23.77 | 23.92 | 24.21 | 25.65 | 25.66 | 25.69 |
| Province | Shanghai | Jiangsu | Zhejiang | Anhui | Fujian | Jiangxi | Shandong | Henan | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | |
| PI | 0.40 | 0.40 | 0.40 | 0.90 | 0.90 | 0.90 | 0.33 | 0.33 | 0.33 | 0.94 | 0.94 | 0.94 | 1.00 | 1.00 | 1.00 | 0.79 | 0.79 | 0.79 | 1.92 | 1.92 | 1.92 | 1.83 | 1.83 | 1.83 |
| SI | 37.12 | 37.07 | 36.97 | 64.41 | 64.40 | 64.36 | 65.51 | 65.49 | 65.44 | 57.10 | 57.13 | 57.13 | 57.95 | 57.90 | 57.78 | 46.04 | 45.99 | 45.88 | 73.74 | 73.64 | 73.45 | 54.13 | 54.13 | 54.10 |
| TI | 44.29 | 44.22 | 44.10 | 21.65 | 21.65 | 21.64 | 20.67 | 20.66 | 20.65 | 24.41 | 24.42 | 24.42 | 18.54 | 18.52 | 18.48 | 33.30 | 33.26 | 33.18 | 13.02 | 13.01 | 12.97 | 23.09 | 23.09 | 23.07 |
| Household | 18.20 | 18.31 | 18.54 | 13.04 | 13.05 | 13.11 | 13.49 | 13.51 | 13.58 | 17.55 | 17.51 | 17.51 | 22.52 | 22.58 | 22.74 | 19.87 | 19.96 | 20.15 | 11.31 | 11.43 | 11.66 | 20.95 | 20.95 | 21.00 |
| Province | Hubei | Hunan | Guangdong | Guangxi | Hainan | Chongqing | Sichuan | Guizhou | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | |
| PI | 0.95 | 0.95 | 0.95 | 0.47 | 0.47 | 0.47 | 1.42 | 1.42 | 1.42 | 1.98 | 1.98 | 1.97 | 5.33 | 5.32 | 5.30 | 0.42 | 0.42 | 0.42 | 0.46 | 0.46 | 0.46 | 0.68 | 0.68 | 0.68 |
| SI | 55.40 | 55.47 | 55.55 | 40.55 | 40.64 | 40.77 | 56.83 | 56.84 | 56.83 | 58.20 | 58.13 | 57.97 | 40.71 | 40.62 | 40.45 | 31.40 | 31.42 | 31.42 | 41.12 | 41.14 | 41.14 | 66.46 | 66.53 | 66.59 |
| TI | 22.25 | 22.28 | 22.31 | 29.84 | 29.91 | 30.00 | 23.55 | 23.56 | 23.55 | 17.81 | 17.79 | 17.74 | 33.64 | 33.57 | 33.43 | 47.70 | 47.72 | 47.73 | 34.27 | 34.28 | 34.29 | 7.84 | 7.85 | 7.86 |
| Household | 21.41 | 21.30 | 21.19 | 29.15 | 28.98 | 28.77 | 18.20 | 18.18 | 18.20 | 22.01 | 22.10 | 22.32 | 20.32 | 20.49 | 20.82 | 20.48 | 20.44 | 20.43 | 24.16 | 24.12 | 24.11 | 25.02 | 24.94 | 24.87 |
| Province | Yunnan | Tibet | Shaanxi | Gansu | Qinghai | Ningxia | Xinjiang | Unit | ||||||||||||||||
| OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | OS | GS | PS | % | |||
| PI | 1.29 | 1.29 | 1.29 | 5.83 | 5.83 | 5.83 | 2.22 | 2.22 | 2.22 | 4.87 | 4.87 | 4.87 | 1.88 | 1.88 | 1.88 | 2.64 | 2.64 | 2.64 | 4.03 | 4.03 | 4.03 | |||
| SI | 57.66 | 57.65 | 57.58 | 48.54 | 48.54 | 48.54 | 59.60 | 59.52 | 59.35 | 55.15 | 55.15 | 55.13 | 74.71 | 74.65 | 74.54 | 86.54 | 86.50 | 86.44 | 87.92 | 87.92 | 87.92 | |||
| TI | 20.71 | 20.71 | 20.69 | 29.13 | 29.13 | 29.13 | 22.62 | 22.59 | 22.53 | 26.29 | 26.29 | 26.28 | 16.19 | 16.18 | 16.15 | 8.09 | 8.09 | 8.09 | 4.76 | 4.76 | 4.76 | |||
| Household | 20.33 | 20.35 | 20.44 | 16.50 | 16.50 | 16.50 | 15.55 | 15.67 | 15.90 | 13.70 | 13.70 | 13.73 | 7.22 | 7.29 | 7.43 | 2.73 | 2.76 | 2.84 | 3.29 | 3.29 | 3.29 | |||
| Reference | Region | Method | Electricity Demand | GDP growth rate | Industrial Structure |
|---|---|---|---|---|---|
| This paper | Nation | Proposed method | Please see Table A6. | Please see Table 2. | PI: 7.36% in 2020 and 6.49% in 2025 SI: 40.89% in 2020 and 36.79% in 2025 TI: 51.75% in 2020 and 56.72% in 2025 |
| Jiang Lin et al. [59] | Nation | Linear regression | The electricity demand in 2020 and 2025 is estimated to be 6696 billion kW·h and 8323 billion kW·h, respectively. | National GDP growth rate used in this study is 7.0% from 2016 to 2020 and 5.9% from 2021 to 2025. | Tertiary GDP share is about 51.6% in 2020, and 56.1% in 2025 |
| Zhaoguang Hu et al. [56] | Nation | ANN and simulation | The electricity demand is estimated to be 7407–7734 billion kW·h in2020 and 8446~8789 billion kW·h in 2025. | National GDP growth rate used in this study is 7.9% from 2016 to 2020 and 5.4% from 2021 to 2025. | PI: 6.8% in 2020 and 6.3% in 2025 SI: 44.5% in 2020 and 42.1% in 2025 TI: 48.7% in 2020 and 51.6% in 2025 |
| International Energy Agency (IEA) [60] | Nation | Not mentioned | The electricity demand is estimated to be between 7330 and 8224 billion kW·h in 2025. | The average annual GDP growth rate from 2016 to 2025 is 5.8%. | The service sector rises to 56% by 2025. |
| Xiaoping He et al. [57] | Nation | Co-integration model | High scenario: 8094.7 billion kW·h in 2020 Middle scenario: 7527.3 billion kW·h in 2020 Low scenario: 6994.8 billion kW·h in 2020 | High scenario: 8% from 2016 to 2020 Middle scenario: 7% from 2016 to 2020 Low scenario: 6% from 2016 to 2020 | The proportion of the secondary industry is 50% in 2020. |
| Baoguo Shan [58] | Nation | CGE | High scenario: 7583 billion kW·h in 2020 Middle scenario: 7301 billion kW·h in 2020 Low scenario: 7027 billion kW·h in 2020 | High scenario: 6.8% during 2016 to 2020 Middle scenario: 6.6% during 2016 to 2020 Low scenario: 6.5% during 2016 to 2020 | High scenario: 6.6% (PI), 43.1% (SI), 50.3% (TI) Middle scenario: 6.7% (PI), 40.2% (SI), 53.1% (TI) Low scenario: 6.0% (PI), 37.8% (SI), 56.2% (TI) |
| This paper | Beijing | Proposed method | OS 117.63 billion kW·h in 2020 GS: 116.55 billion kW·h in 2020 | OS: 6.64% GS: 6.14% PS: 5.34% | Please see Table 3. |
| Bin Wang et al. [61] | Beijing | Incremental dynamic analysis (IDA) | The electricity demand for Beijing in 2020 is estimated to be between 112.37 and 116.68 billion kW·h. | Beijing’s annual GDP growth rate is estimated to be 6.5% from 2016 to 2020. | PI: 0.5% in 2020 SI: 16.0% in 2020 TI: 83.5% in 2020 |
| This paper | Tianjin | Proposed method | OS: 100.9 and 111.9 billion kW·h in 2020 and 2025 GS: 99.7 and 107.6 billion kW·h in 2020 and 2025 PS: 98.5 and 100.6 billion kW·h in 2020 and 2025 | OS: 7.54% GS: 6.93% PS: 5.93% | Please see Table 3. |
| Yongxu He [11] | Tianjin | SD | 116.62 billion kW·h in 2020 and 128.59 billion kW·h in 2025 | No more details about the GDP growth rate. | The proportion of the secondary industry is about 40% in 2020 and 38% in 2025. |
| This paper | Jiangsu | Proposed method | OS: 671.25 billion kW·h in 2020 GS: 664.31 billion kW·h in 2020 PS: 657.40 billion kW·h in 2020 | OS: 7.30% GS: 6.76% PS: 5.88% | Please see Table 3. |
| Jing Shi et al. [62] | Jiangsu | Linear regression | 655 billion kW·h in 2020 | Jiangsu’s annual GDP growth rate is estimated to be 7.5% from 2016 to 2020. | No more details about the changes in the industrial structure. |
| This paper | Ningxia | Proposed method | OS: 114.45 billion kW·h in 2020 GS: 113.26 billion kW·h in 2020 GS: 112.07 billion kW·h in 2020 | OS: 7.78% GS: 7.21% PS: 6.28% | Please see Table 3. |
| Xing Tian et al. [63] | Ningxia | Grey Verhulst | 105.08 billion kW·h in 2020 | No more details about the GDP growth rate. | No more details about the changes in the industrial structure. |
References
- Zhai, X.; Ma, Q.; Yang, R. Factors influencing CO2 emissions in China’s power industry: Co-integration analysis. Energy Policy 2013, 57, 89–98. [Google Scholar] [CrossRef]
- Guo, J.; Zhu, L.; Fan, Y. Emission path planning based on dynamic abatement cost curve. European J. Oper. Res. 2016, 255, 996–1013. [Google Scholar] [CrossRef]
- Pérez-García, J.; Moral-Carcedo, J. Analysis and long term forecasting of electricity demand trough a decomposition model: A case study for Spain. Energy 2016, 97, 127–143. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Electricity consumption forecasting in Italy using linear regression models. Energy 2009, 34, 1413–1421. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Linear regression models to forecast electricity consumption in Italy. Energy Sources Part B 2013, 8, 86–93. [Google Scholar] [CrossRef]
- Lin, B. Structural change, efficiency improvement and electric demand forecasting. Econ. Res. J. 2003, 5, 57–65. [Google Scholar]
- De Cabral, J.; Legey, L.F.L.; de Cabral, M.V. Electricity consumption forecasting in Brazil: A spatial econometrics approach. Energy 2017, 126, 124–131. [Google Scholar] [CrossRef]
- García-Ascanio, C.; Maté, C. Electric power demand forecasting using interval time series: A comparison between VAR and iMLP. Energy Policy 2010, 38, 715–725. [Google Scholar] [CrossRef]
- Jaramillo-Morán, M.A.; González-Romera, E.; Carmona-Fernández, D. Monthly electric demand forecasting with neural filters. Int. J. Electr. Power Energy Syst. 2013, 49, 253–263. [Google Scholar] [CrossRef]
- González-Romera, E.; Jaramillo-Morán, M.Á.; Carmona-Fernández, D. Forecasting of the electric energy demand trend and monthly fluctuation with neural networks. Comput. Ind. Eng. 2007, 52, 336–343. [Google Scholar] [CrossRef]
- He, Y.; Jiao, J.; Chen, Q.; Ge, S.; Chang, Y.; Xu, Y. Urban long term electricity demand forecast method based on system dynamic of the new economic normal: The case of Tianjin. Energy 2017, 133, 9–22. [Google Scholar] [CrossRef]
- Ahmad, T.; Chen, H. Utility companies strategy for short-term energy demand forecasting using machine learning based models. Sustain. Cities Soc. 2018, 39, 401–417. [Google Scholar] [CrossRef]
- Le Cam, M.; Daoud, A.; Zmeureanu, R. Forecasting electric demand of supply fan using fata mining techniques. Energy 2016, 101, 541–557. [Google Scholar] [CrossRef]
- Song, Z.; Niu, D.; Dai, S.; Xiao, X.; Wang, Y. Incorporating the influence of China’s industry capacity elimination policies in electricity demand forecasting. Util. Policy 2017, 47, 1–11. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, J.; Shi, Y.; Zhu, K.; Pu, G. Multi-agent based experimental analysis on bidding mechanism in electricity auction markets. Int. J. Electr. Power Energy Syst. 2012, 43, 696–702. [Google Scholar] [CrossRef]
- Karfopoulos, E.; Tena, L.; Torres, A.; Salas, P.; Jorda, J.G.; Dimeas, A.; Hatziargyriou, N. A multi-agent system providing demand response services from residential consumers. Electr. Power Syst. Res. 2015, 120, 163–176. [Google Scholar] [CrossRef]
- Matthew, G., Jr.; Nuttall, W.J.; Mestel, B.; Dooley, L.S. A dynamic simulation of low-carbon policy influences on endogenous electricity demand in an isolated island system. Energy Policy 2017, 109, 121–131. [Google Scholar] [CrossRef]
- Perwez, U.; Sohail, A.; Hassan, S.F.; Zia, U. The long-term forecast of Pakistan’s electricity supply and demand: An application of long range energy alternatives planning. Energy 2015, 93, 2423–2435. [Google Scholar] [CrossRef]
- He, Y.X.; Yang, L.F.; He, H.Y.; Wang, Y.J. Electricity demand price elasticity in China based on computable general equilibrium model analysis. Energy 2011, 36, 1115–1123. [Google Scholar] [CrossRef]
- Mu, T.; Xia, Q.; Kang, C. Input-output table of electricity demand and its application. Energy 2010, 35, 326–331. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, K.; Yang, S.; Shao, Z. On electricity consumption and economic growth in China. Renew. Sustain. Energy Rev. 2017, 76, 353–368. [Google Scholar] [CrossRef]
- Cheng, Y.S.; Wong, W.K.; Woo, C.K. How much have electricity shortages hampered China’s GDP growth? Energy Policy 2013, 55, 369–373. [Google Scholar] [CrossRef]
- Li, B.; Li, T.; Yu, M.; Chen, B. Can equalization of public services narrow the regional disparities in China? A spatial econometrics approach. China Econ. Rev. 2017, 44, 67–78. [Google Scholar] [CrossRef]
- Sun, X.; Li, J.; Qiao, H.; Zhang, B. Energy implications of China’s regional development: New insights from multi-regional input-output analysis. Appl. Energy 2017, 196, 118–131. [Google Scholar] [CrossRef]
- Tung, R.L. Opportunities and Challenges Ahead of China’s “New Normal”. Long Range Plan. 2016, 5, 632–640. [Google Scholar] [CrossRef]
- Suhono, S. Long-term electricity demand forecasting of Sumatera System based on electricity consumption intensity and Indonesia Population Projection 2010–2035. Energy Procedia 2015, 68, 455–462. [Google Scholar] [CrossRef]
- Fecher, R.S.; Senatla, M.; Yamba, F.; Lukesa, B.; Himunzowa, G.; Heaps, C.; Chapman, A.; Mahumane, G.; Tembo, B.; Nyambe, I. Electricity supply and demand scenarios for the Southern African power pool. Energy Policy 2017, 101, 403–414. [Google Scholar] [CrossRef]
- Wu, G.; Wang, W.; Zhang, X. Analysis of Economic Potential Growth Rate of China under the New Normal. J. Financ. Res. 2015, 8, 46–63. [Google Scholar]
- Guo, Y.; Chen, Y. The Estimate of China’s Potential Economic Growth and Its Policy Implication: 1979–2020. Econ. Perspect. 2015, 2, 12–18. [Google Scholar]
- Shao, F.; Gou, W.; Kuang, H. Potential Growth of China: Long-term Tendency and Economic Policies. J. Financ. Res. 2014, 12, 39–54. [Google Scholar]
- Lin, Y. China’s Economic Development in the Era of Global Change. New Financ. 2017, 2, 4–7. [Google Scholar]
- Wang, J. Prospect of Chinese Future Economic Growth and Policy. China Natl. Conditi. Strength 2017, 1, 22–25. [Google Scholar]
- Johansen, S.; Juselius, K. Maximum Likelihood Estimation and Inferences with Applications to the Demand for Electricity. Oxf. Bull. Econ. Stat. 1990, 52, 461–472. [Google Scholar]
- Liu, Z.; Zhu, K.; Yan, J.; Shi, Y. The Analysis of Power Sector Carbon Mitigation Potential in the Industrial Structure Optimization Scene. J. Ind. Eng. Eng. Manag. 2014, 28, 87–92. [Google Scholar]
- Verdejo, H.; Awerkin, A.; Becker, C.; Olguin, G. Statistic linear parametric techniques for residential electric energy demand forecasting. A review and an implementation to Chile. Renew. Sustain. Energy Rev. 2017, 74, 512–521. [Google Scholar] [CrossRef]
- Son, H.; Kim, C. Short-term forecasting of electricity demand for the residential sector using weather and social variables. Resour. Conserv. Recycl. 2017, 123, 200–207. [Google Scholar] [CrossRef]
- Pessanha, J.F.M.; Leon, N. Forecasting long-term electricity demand in the residential sector. Procedia Comput. Sci. 2015, 55, 529–538. [Google Scholar] [CrossRef]
- Domanska, D.; Lukasik, S. Handling high-dimensional data in air pollution forecasting tasks. Ecol. Inform. 2016, 34, 70–91. [Google Scholar] [CrossRef]
- Lu, Z.; Li, J.; Qiao, Y.; Zhao, J.; Yang, C. Multiple data source dimensionality reduction pretreatment used in ultra-short term wind resource forecast. Power Syst. Technol. 2015, 39, 1275–1280. [Google Scholar]
- Bouzgou, H.; Gueymard, C.A. Minimum redundancy—Maximum relevance with extreme learning machines for global solar radiation forecasting: Toward an optimized dimensionality reduction for solar time series. Sol. Energy 2017, 158, 595–609. [Google Scholar] [CrossRef]
- Malvoni, M.; de Giorgi, M.G.; Congedo, P.M. Photovoltaic forecast based on hybrid PCA-LSSVM using dimensionality reducted data. Neurocomputing 2016, 211, 72–83. [Google Scholar] [CrossRef]
- Sermpinis, G.; Stasinakis, C.; Hassanniakalager, A. Reverse adaptive krill herd locally weighted support vector regression for forecasting and trading exchange traded funds. Eur. J. Oper. Res. 2017, 263, 540–558. [Google Scholar] [CrossRef]
- Huang, S.-C. Integrating nonlinear graph based dimensionality reduction schemes with SVMs for credit rating forecasting. Expert Syst. Appl. 2009, 36, 7515–7518. [Google Scholar] [CrossRef]
- Sun, S.; Qiao, H.; Wei, Y.; Wang, S. A new dynamic integrated approach for wind speed forecasting. Appl. Energy 2017, 197, 151–162. [Google Scholar] [CrossRef]
- Zhong, X.; Enke, D. Forecasting daily stock market return using dimensionality reduction. Expert Syst. Appl. 2017, 67, 126–139. [Google Scholar] [CrossRef]
- Li, Y.; Wu, T.; Marshall, N.; Steinerberger, S. Extracting geography from trade data. Phys. A 2017, 473, 205–212. [Google Scholar] [CrossRef]
- Brentari, E.; Levaggi, R.; Zuccolotto, P. Pricing Strategies for Italian Red Wine. Food Qual. Prefer. 2011, 22, 725–732. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 209, 2323–2326. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, H. Principal manifolds and nonlinear dimensionality reduction via local tangent space aligrment. SIAM J. Sci. Comput. 2004, 26, 313–338. [Google Scholar] [CrossRef]
- Scholkopf, B.; Smola, A.J.; Muller, K.R. Nonlinear component analysis as a kernel eigenvalue problem. Neur. Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- National Development and Reform Commission, National Energy Administration. The 13th Five Year Plan of Electricity; 2016. Available online: http://www.ndrc.gov.cn/fzgggz/fzgh/ghwb/gjjgh/201706/t20170605_849994.html (accessed on 11 June 2019).
- National Bureau of Statistics. The Statistics Communiqué on National Economy and Social Development of China 2017. 2018. Available online: http://www.stats.gov.cn/tjsj/tjgb/ndtjgb/ (accessed on 11 June 2019).
- National Bureau of Statistics. Electricity Consumption of the Whole Society in 2018. Available online: http://www.nea.gov.cn/2019-01/18/c_137754978.htm (accessed on 18 January 2019).
- Hu, Z.; Tan, X.; Xu, Z. An Exploration into China’s Economic Development and Electricity Demand by the Year 2050; China Electric Power Press: Beijing, China, 2014; pp. 141–160. [Google Scholar] [CrossRef]
- He, X.; Liu, X.; Lin, Y. China’s electricity demand forecast under urbanization process. Econ. Res. J. 2009, 1, 118–130. [Google Scholar]
- Shan, B.; Sun, X.; Li, J.; Wang, X.; Ma, D. Analysis on the China’s Electricity Demand Growth under the New Economic Norm. Electr. Power 2017, 50, 19–24. [Google Scholar]
- Lin, J.; He, G.; Yuan, A. Economic rebalancing and electricity demand in China. Electr. J. 2016, 29, 48–54. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2017; Organization for Economic Co-operation and Development: Pairs, France, 2017. [Google Scholar]
- Wang, B.; Zhang, X.; Ji, L.; Xue, Y. Driving factors analysis for the power consumption and load forecasting of Beijing City. Electr. Power 2018, 51, 178–184. [Google Scholar] [CrossRef]
- Shi, J.; Zhou, Q.; Tan, J.; Zhu, L. Analysis on the electric power demand of Jiangsu Province under China’s New normal. Electr. Power 2017, 50, 10–15. [Google Scholar] [CrossRef]
- Tian, X.; Yu, L.; Dong, X.; Qi, C. Analysis and prospect of electricity demand in Ningxia under China’s new normal. Electr. Power 2017, 50, 27–32. [Google Scholar]
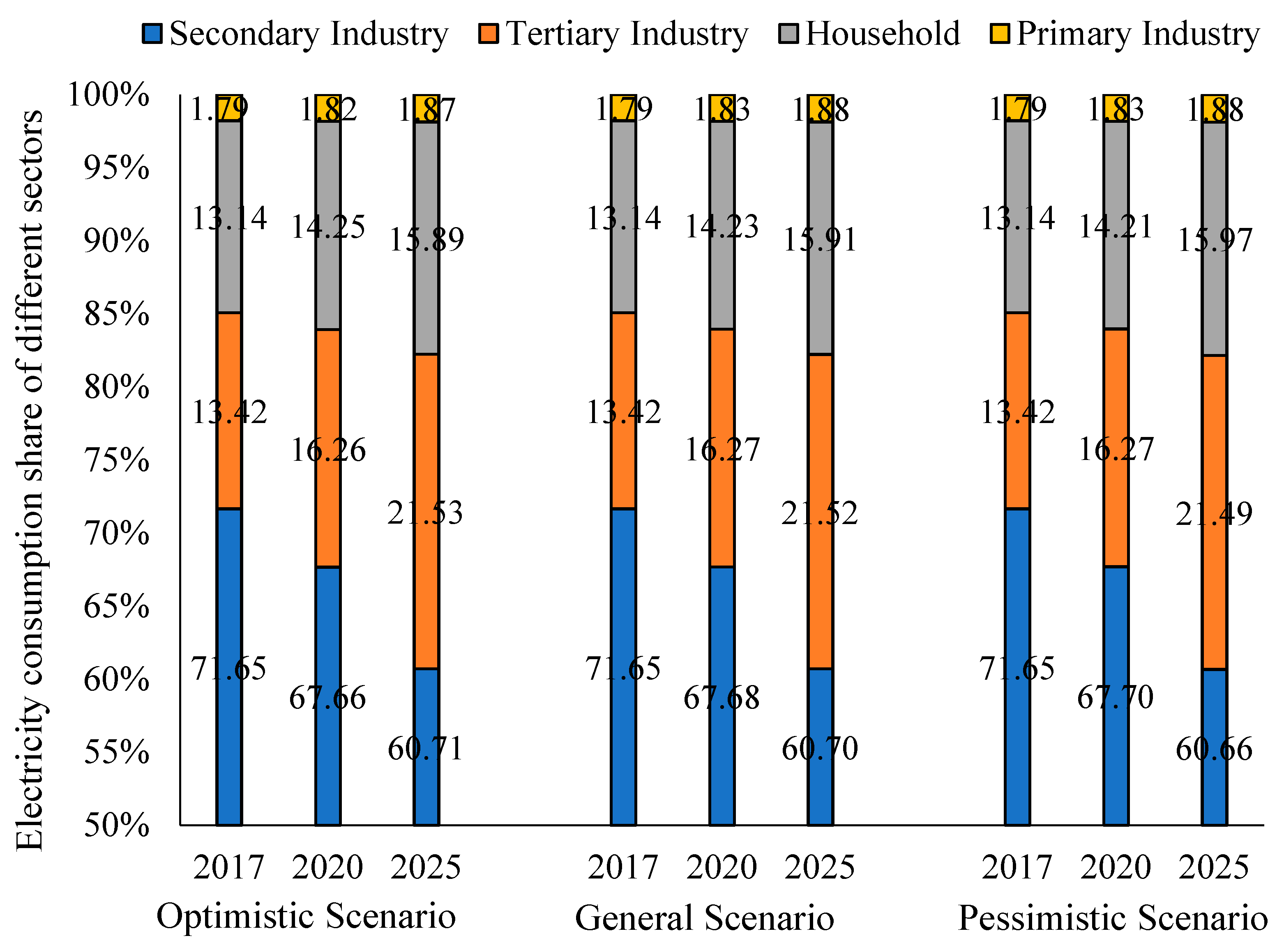
| Parameter | Scenario | 2017–2020 | 2021–2025 | References |
|---|---|---|---|---|
| Economic growth rate | Optimistic scenario | 7% | 6.5% | [28,29,30,31,32] |
| General scenario | 6.5% | 6% | ||
| Pessimistic scenario | 6% | 5% |
| p | Province | 2017 | 2020 | 2023 | 2025 | p | Province | 2017 | 2020 | 2023 | 2025 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Beijing | 3.55 | 3.51 | 3.47 | 3.42 | 17 | Hubei | 4.93 | 5.02 | 5.12 | 5.21 |
| 2 | Tianjin | 3.15 | 3.21 | 3.26 | 3.31 | 18 | Hunan | 4.63 | 4.71 | 4.78 | 4.86 |
| 3 | Hebei | 2.80 | 2.66 | 2.52 | 2.38 | 19 | Guangdong | 9.46 | 9.35 | 9.24 | 9.12 |
| 4 | Shanxi | 0.68 | 0.62 | 0.56 | 0.51 | 20 | Guangxi | 2.78 | 2.85 | 2.91 | 2.98 |
| 5 | Nei Monggol | 2.36 | 2.36 | 2.37 | 2.37 | 21 | Hainan | 0.62 | 0.63 | 0.65 | 0.66 |
| 6 | Liaoning | 2.67 | 2.59 | 2.51 | 2.44 | 22 | Chongqing | 2.69 | 2.76 | 2.82 | 2.88 |
| 7 | Jilin | 1.80 | 1.79 | 1.78 | 1.76 | 23 | Sichuan | 4.52 | 4.57 | 4.62 | 4.68 |
| 8 | Heilongjiang | 0.90 | 0.83 | 0.76 | 0.70 | 24 | Guizhou | 2.13 | 2.21 | 2.29 | 2.37 |
| 9 | Shanghai | 2.80 | 2.71 | 2.62 | 2.53 | 25 | Yunnan | 1.93 | 1.94 | 1.96 | 1.97 |
| 10 | Jiangsu | 11.15 | 11.24 | 11.32 | 11.40 | 26 | Tibet | 0.17 | 0.17 | 0.18 | 0.18 |
| 11 | Zhejiang | 5.41 | 5.33 | 5.25 | 5.18 | 27 | Shaanxi | 2.83 | 2.88 | 2.94 | 2.99 |
| 12 | Anhui | 3.18 | 3.19 | 3.21 | 3.22 | 28 | Gansu | 0.59 | 0.57 | 0.55 | 0.53 |
| 13 | Fujian | 3.79 | 3.79 | 3.80 | 3.80 | 29 | Qinghai | 0.39 | 0. 40 | 0. 41 | 0. 42 |
| 14 | Jiangxi | 2.59 | 2.62 | 2.65 | 2.68 | 30 | Ningxia | 0.47 | 0.48 | 0.49 | 0.50 |
| 15 | Shandong | 8.94 | 8.94 | 8.93 | 8.93 | 31 | Xinjiang | 1.03 | 1.02 | 1.01 | 0.99 |
| 16 | Henan | 5.07 | 5.06 | 5.05 | 5.04 | Unit | % | ||||
| Scenario | Sector | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | 2024 | 2025 |
|---|---|---|---|---|---|---|---|---|---|---|
| OS | Primary industry | 116.22 | 120.31 | 124.82 | 129.96 | 134.81 | 140.06 | 145.74 | 151.77 | 158.30 |
| Secondary industry | 4650.36 | 4686.57 | 4753.93 | 4818.67 | 4871.44 | 4929.81 | 4991.70 | 5060.98 | 5135.27 | |
| Tertiary industry | 871.30 | 956.26 | 1052.86 | 1158.29 | 1268.75 | 1389.06 | 1520.45 | 1664.13 | 1820.95 | |
| Household | 852.85 | 903.53 | 957.50 | 1015.13 | 1072.87 | 1134.37 | 1199.91 | 1268.96 | 1344.33 | |
| Total | 6490.73 | 6666.67 | 6889.11 | 7122.05 | 7347.87 | 7593.30 | 7857.80 | 8145.84 | 8458.85 | |
| GS | Primary industry | 116.22 | 120.31 | 124.31 | 128.91 | 133.16 | 137.78 | 142.78 | 148.06 | 153.79 |
| Secondary industry | 4650.36 | 4686.57 | 4732.96 | 4776.13 | 4806.84 | 4842.61 | 4881.33 | 4926.74 | 4976.44 | |
| Tertiary industry | 871.30 | 956.26 | 1048.19 | 1148.00 | 1251.81 | 1364.32 | 1486.58 | 1619.64 | 1764.15 | |
| Household | 852.85 | 903.53 | 950.71 | 1004.20 | 1057.30 | 1113.60 | 1173.32 | 1235.88 | 1304.03 | |
| Total | 6490.73 | 6666.67 | 6856.17 | 7057.24 | 7249.11 | 7458.31 | 7684.01 | 7930.32 | 8198.41 | |
| PS | Primary industry | 116.22 | 120.31 | 123.80 | 127.85 | 130.99 | 134.42 | 138.15 | 142.08 | 146.36 |
| Secondary industry | 4650.36 | 4686.57 | 4711.98 | 4733.79 | 4721.58 | 4713.99 | 4708.89 | 4709.81 | 4714.31 | |
| Tertiary industry | 871.30 | 956.26 | 1043.51 | 1137.76 | 1229.47 | 1327.84 | 1433.68 | 1547.74 | 1670.39 | |
| Household | 852.85 | 903.53 | 943.95 | 993.37 | 1038.14 | 1085.12 | 1134.51 | 1185.62 | 1241.10 | |
| Total | 6490.73 | 6666.67 | 6823.24 | 6992.77 | 7120.18 | 7261.37 | 7415.23 | 7585.25 | 7772.16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.; Zhu, K.; Liu, Z.; Lieu, J.; Tan, X. Study on A Simple Model to Forecast the Electricity Demand under China’s New Normal Situation. Energies 2019, 12, 2220. https://doi.org/10.3390/en12112220
Lin J, Zhu K, Liu Z, Lieu J, Tan X. Study on A Simple Model to Forecast the Electricity Demand under China’s New Normal Situation. Energies. 2019; 12(11):2220. https://doi.org/10.3390/en12112220
Chicago/Turabian StyleLin, Jinchai, Kaiwei Zhu, Zhen Liu, Jenny Lieu, and Xianchun Tan. 2019. "Study on A Simple Model to Forecast the Electricity Demand under China’s New Normal Situation" Energies 12, no. 11: 2220. https://doi.org/10.3390/en12112220
APA StyleLin, J., Zhu, K., Liu, Z., Lieu, J., & Tan, X. (2019). Study on A Simple Model to Forecast the Electricity Demand under China’s New Normal Situation. Energies, 12(11), 2220. https://doi.org/10.3390/en12112220





