Improving Performance of Far Users in Cognitive Radio: Exploiting NOMA and Wireless Power Transfer
Abstract
1. Introduction
- Reliable transmission of AF relaying scheme required in such CR-NOMA system with a common relay and EH policy was studied. This implementation of two schemes is designed to satisfy the users’ condition in terms of channel quality with respect to the more reliable transmitted information. We intend to analyze the system performance of EH assisted CR-NOMA networks through the Rayleigh fading channels.
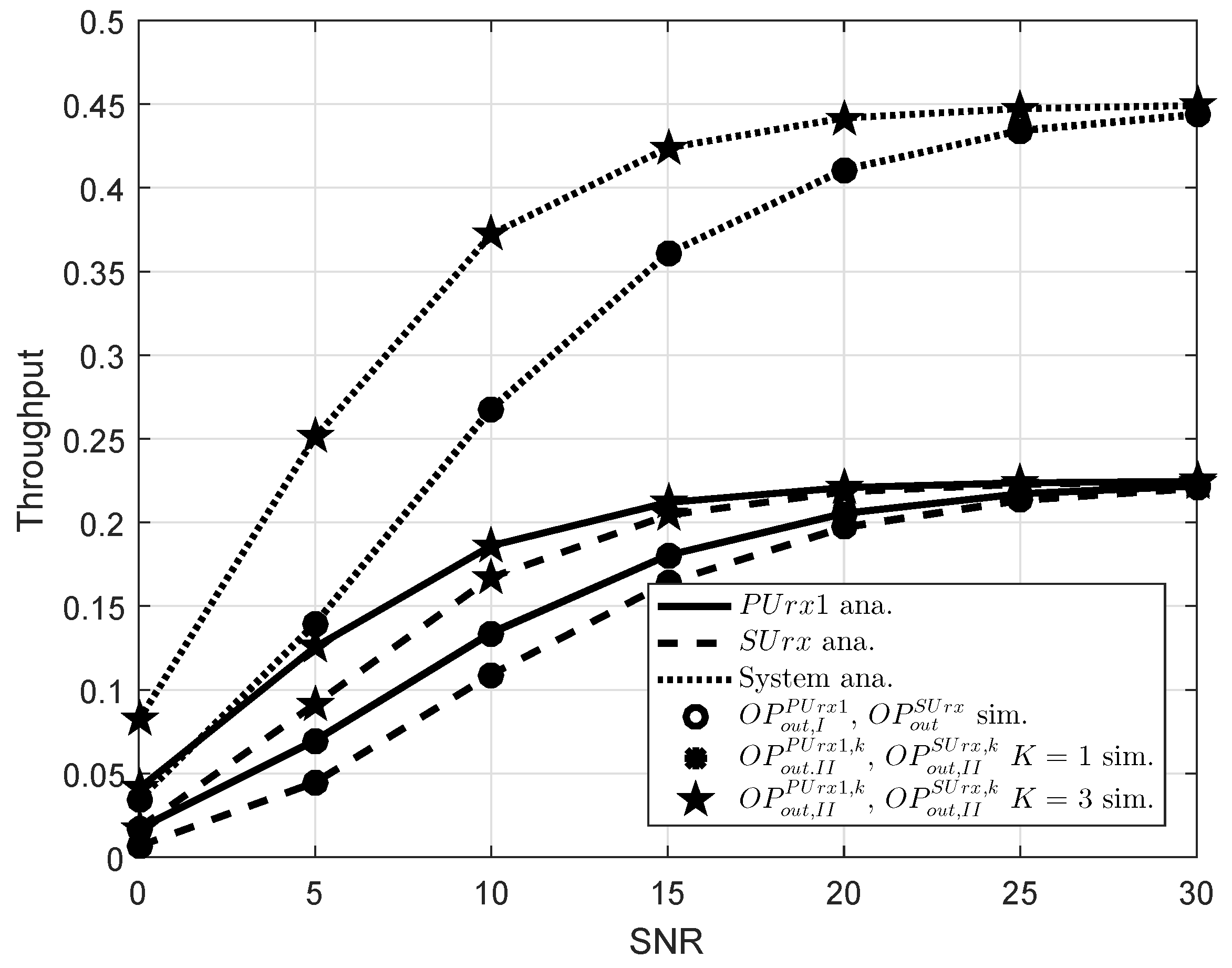
- The exact expressions of outage probability is presented and then throughput is further examined. From the achieved results, we analyze the effects of a number of factors including power allocation factors, transmit SNR, and the number of relays to prove the superiority of such CR NOMA model.
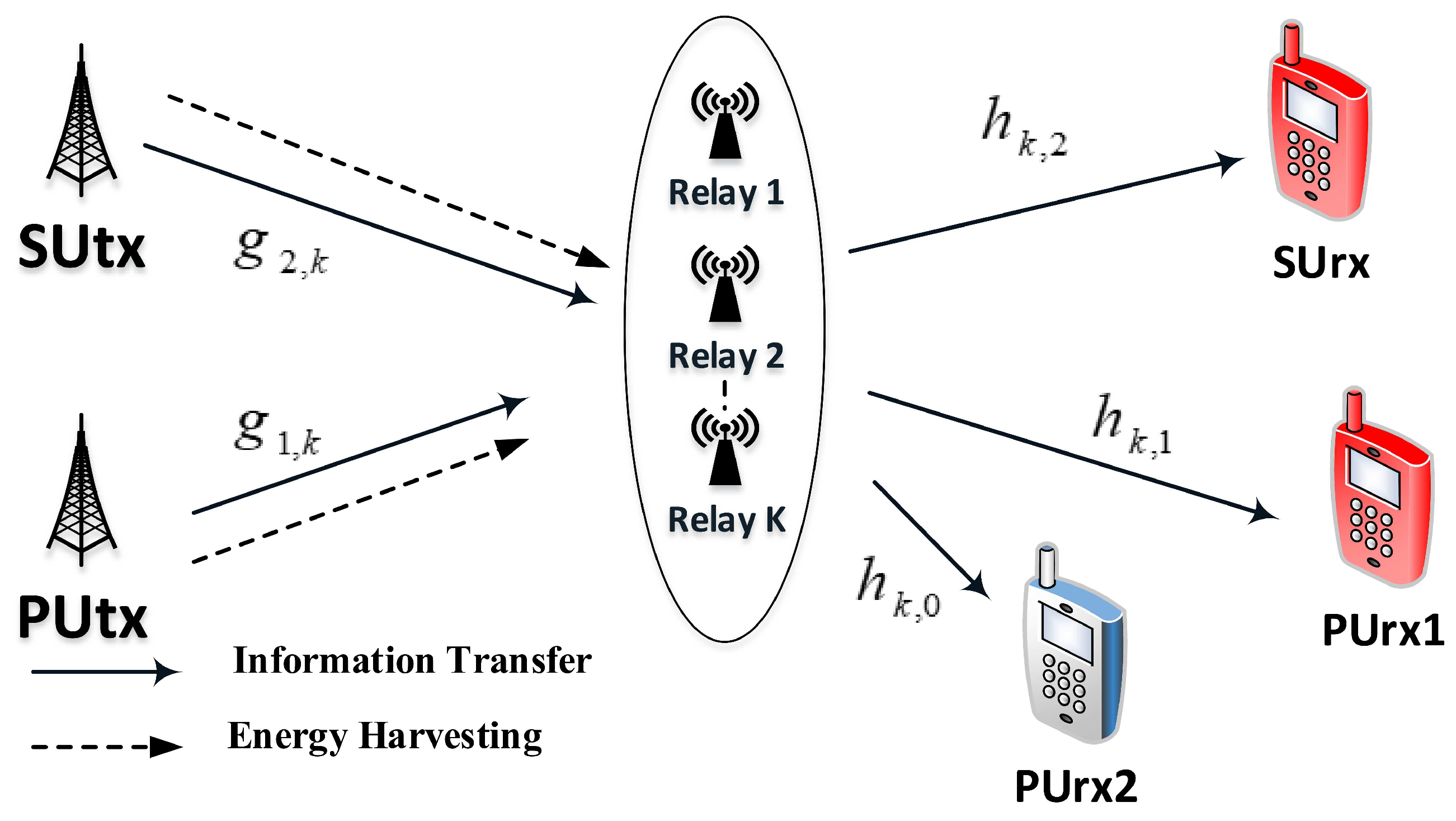
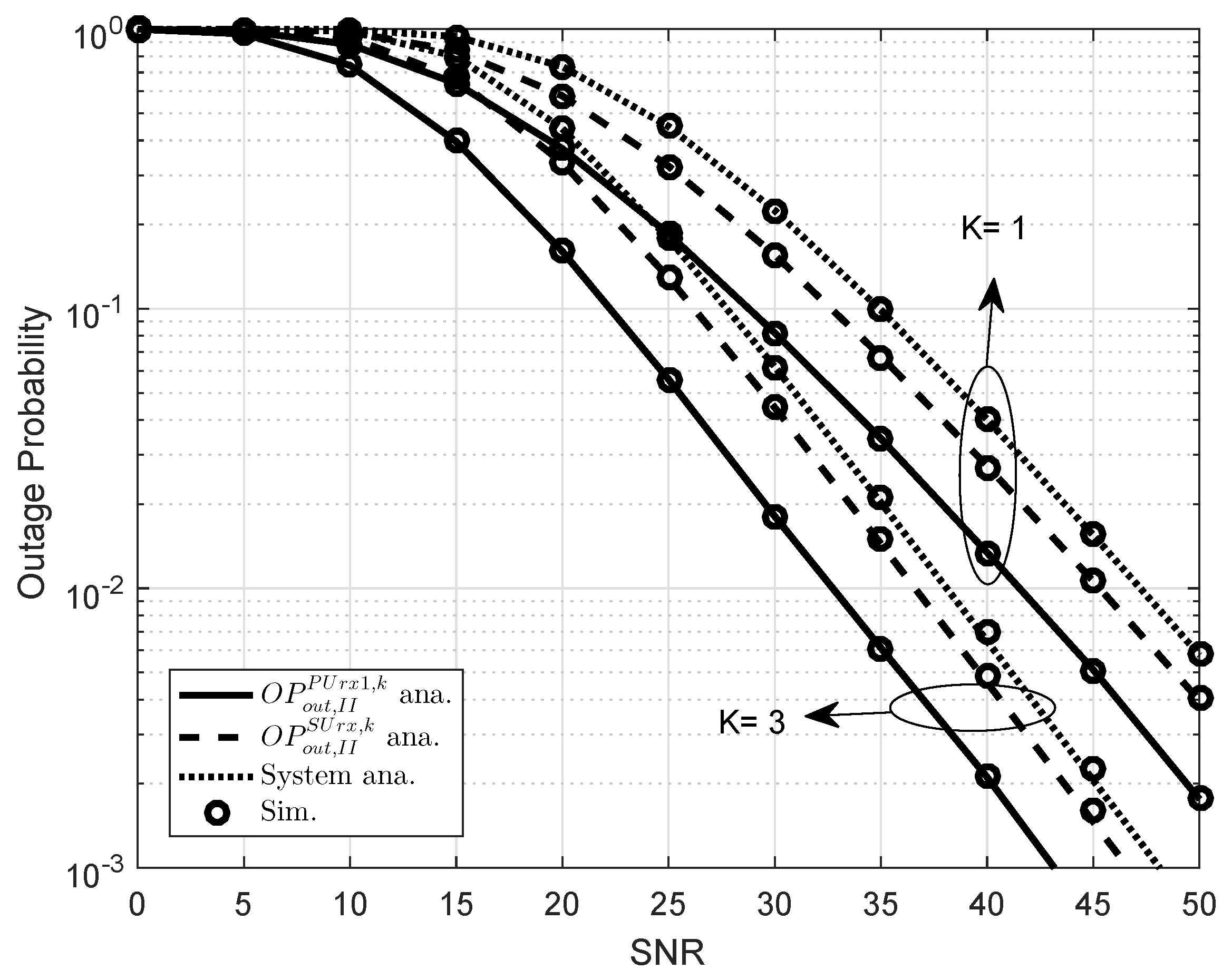
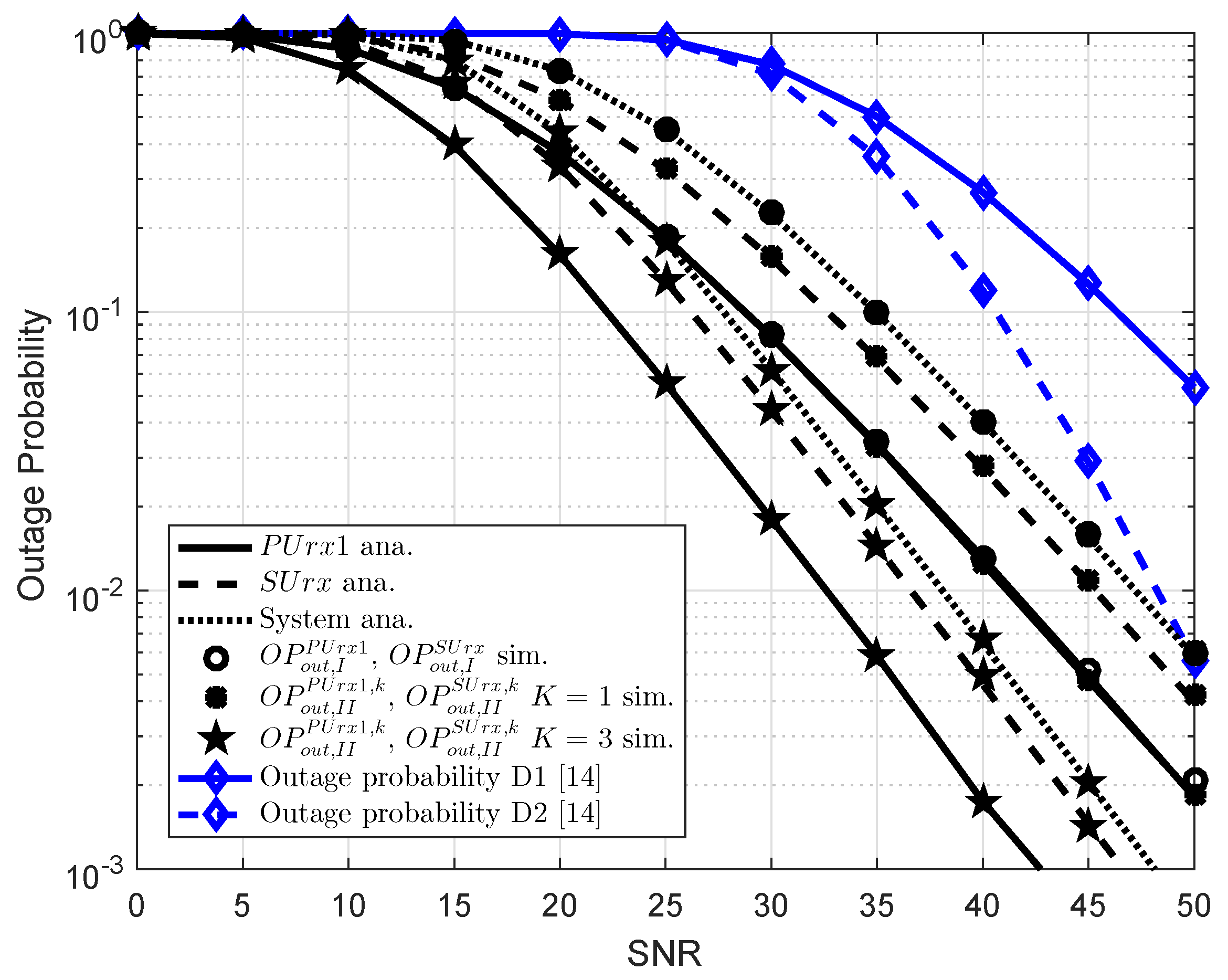
- As extended model, multiple relay selection in Scheme 2 is introduced in EH assisted CR NOMA to increase data rate and reliability of transmission compared to singe relay systems reported in Scheme 1. Moreover, the EH assisted CR-NOMA systems illustrate an improved performance as increasing the number of selected relays.
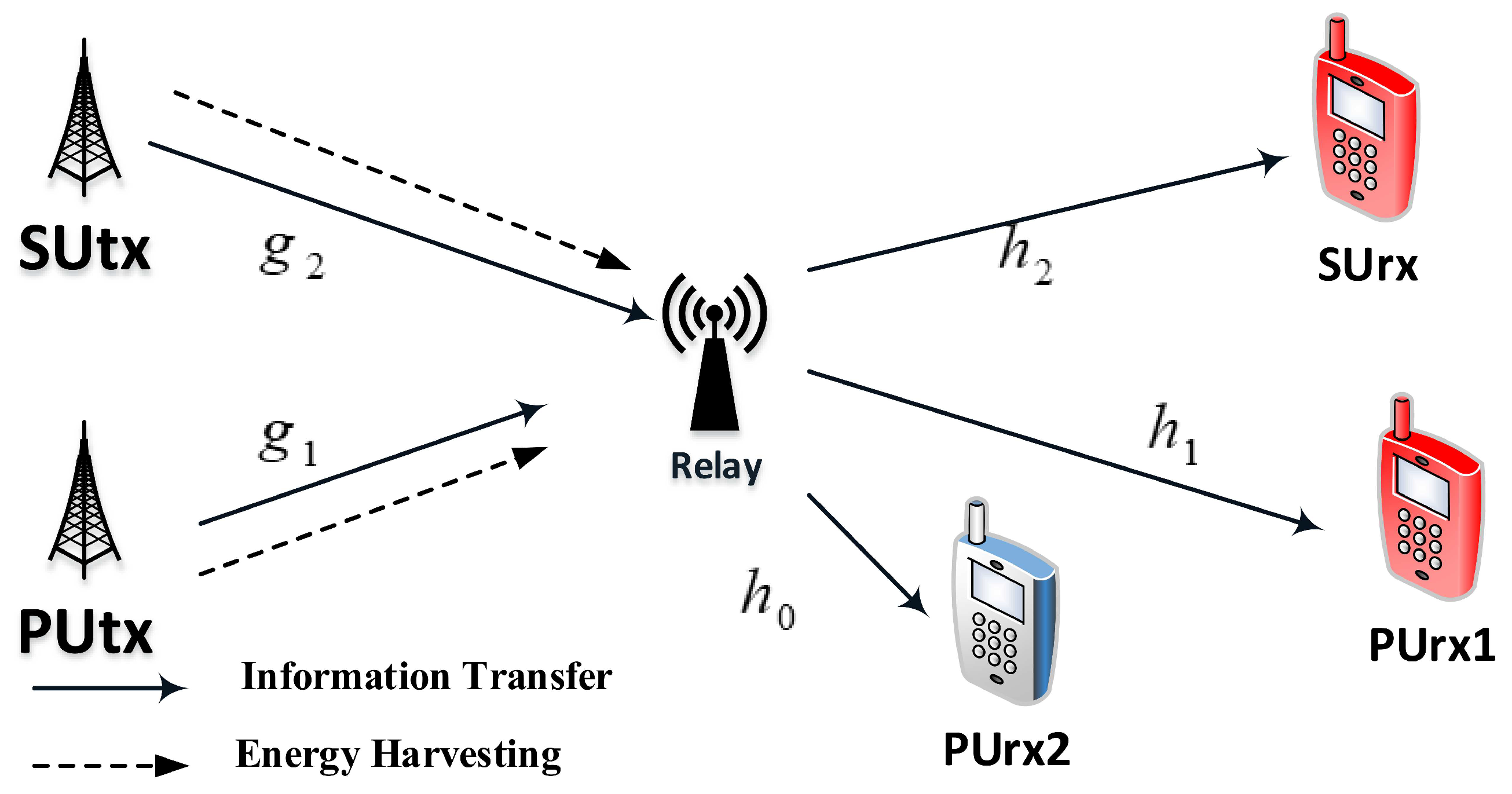
2. System Model
3. Performance Analysis in Scheme 1
3.1. Calculation of SNR
3.2. Outage and Throughput Performance Analysis
- If
- If
- If
- If
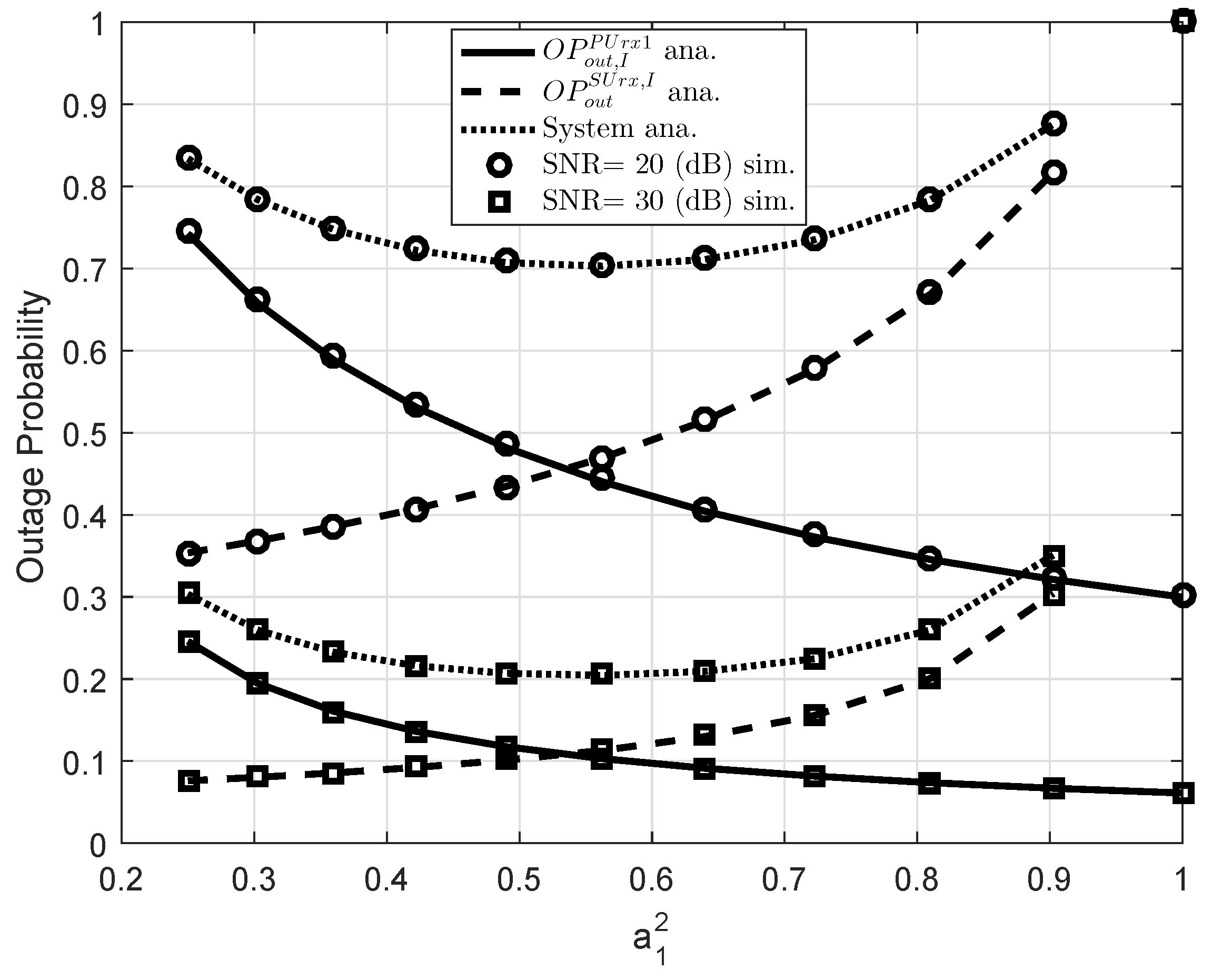
3.3. Consideration on Overall Performance in Terms of Outage Behavior and Throughput
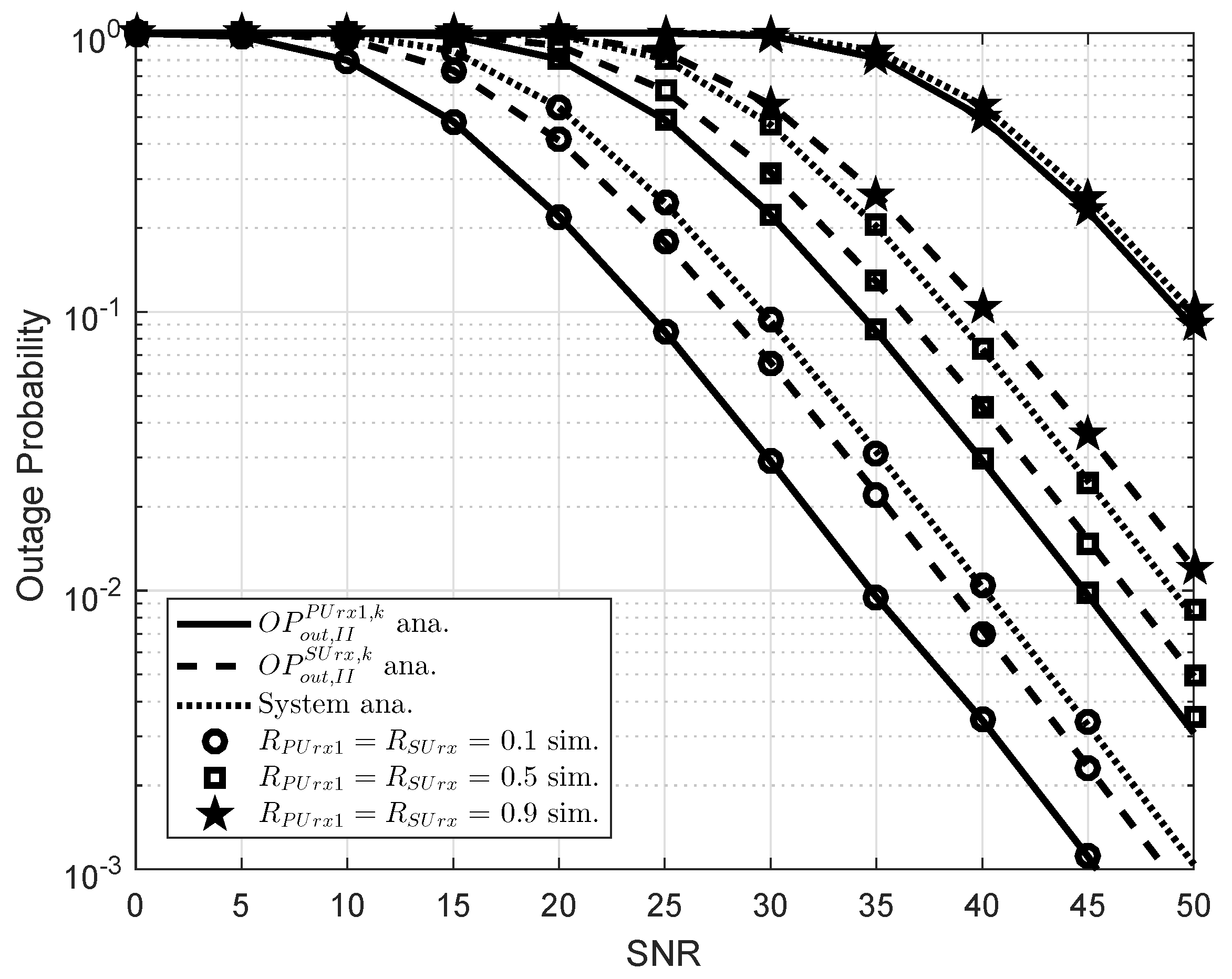
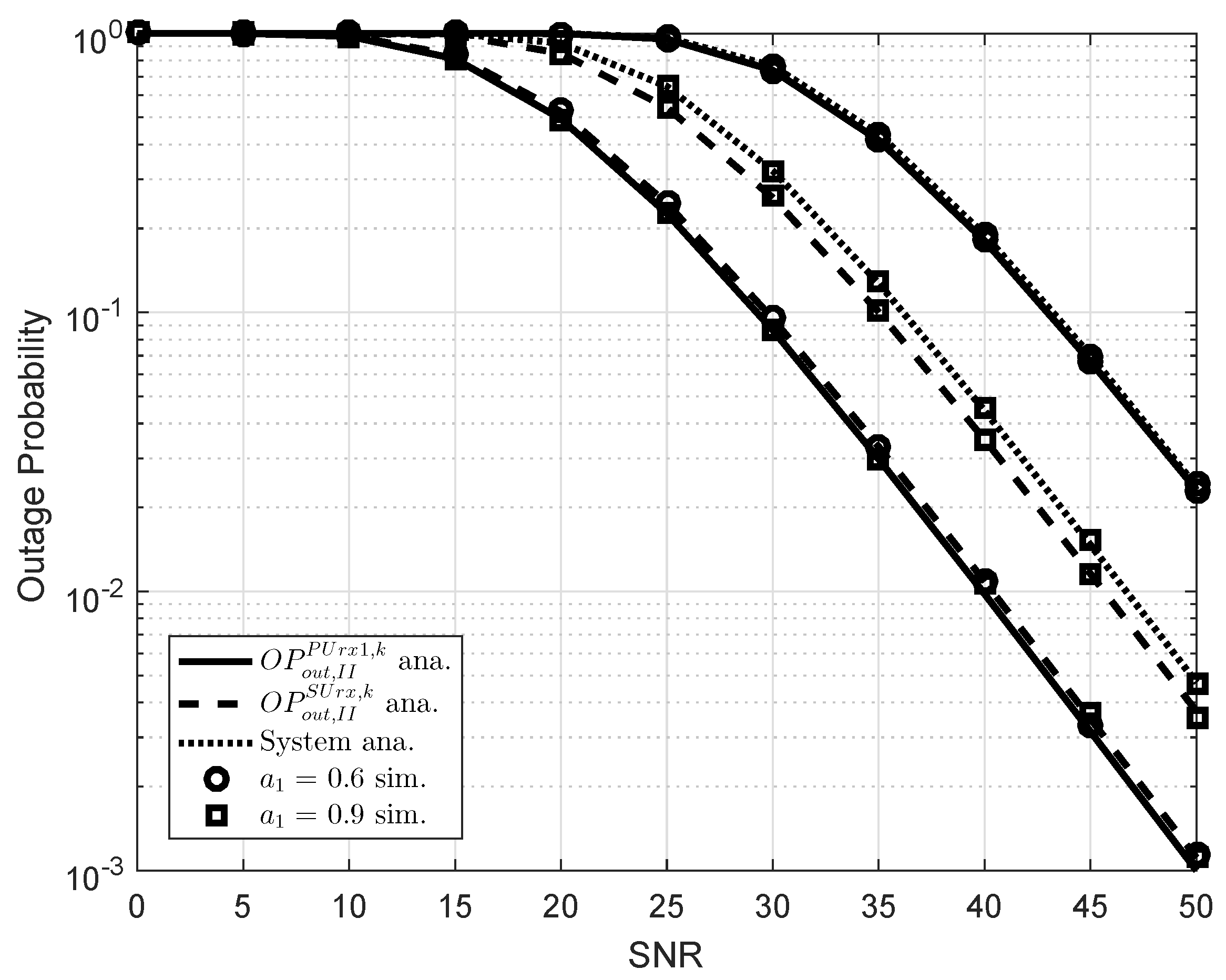
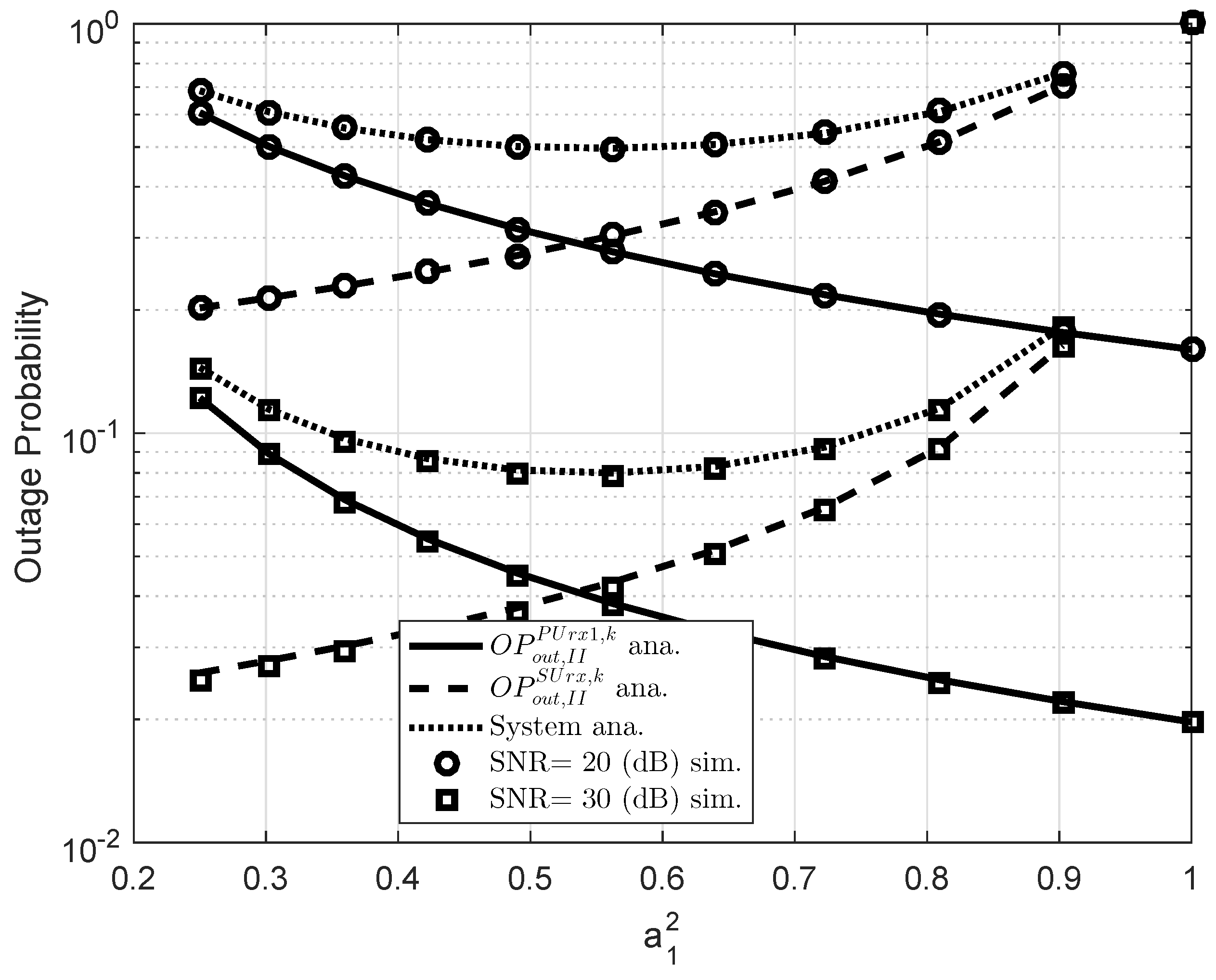
4. Performance Analysis in Scheme 2
- If
- If
- If
- If
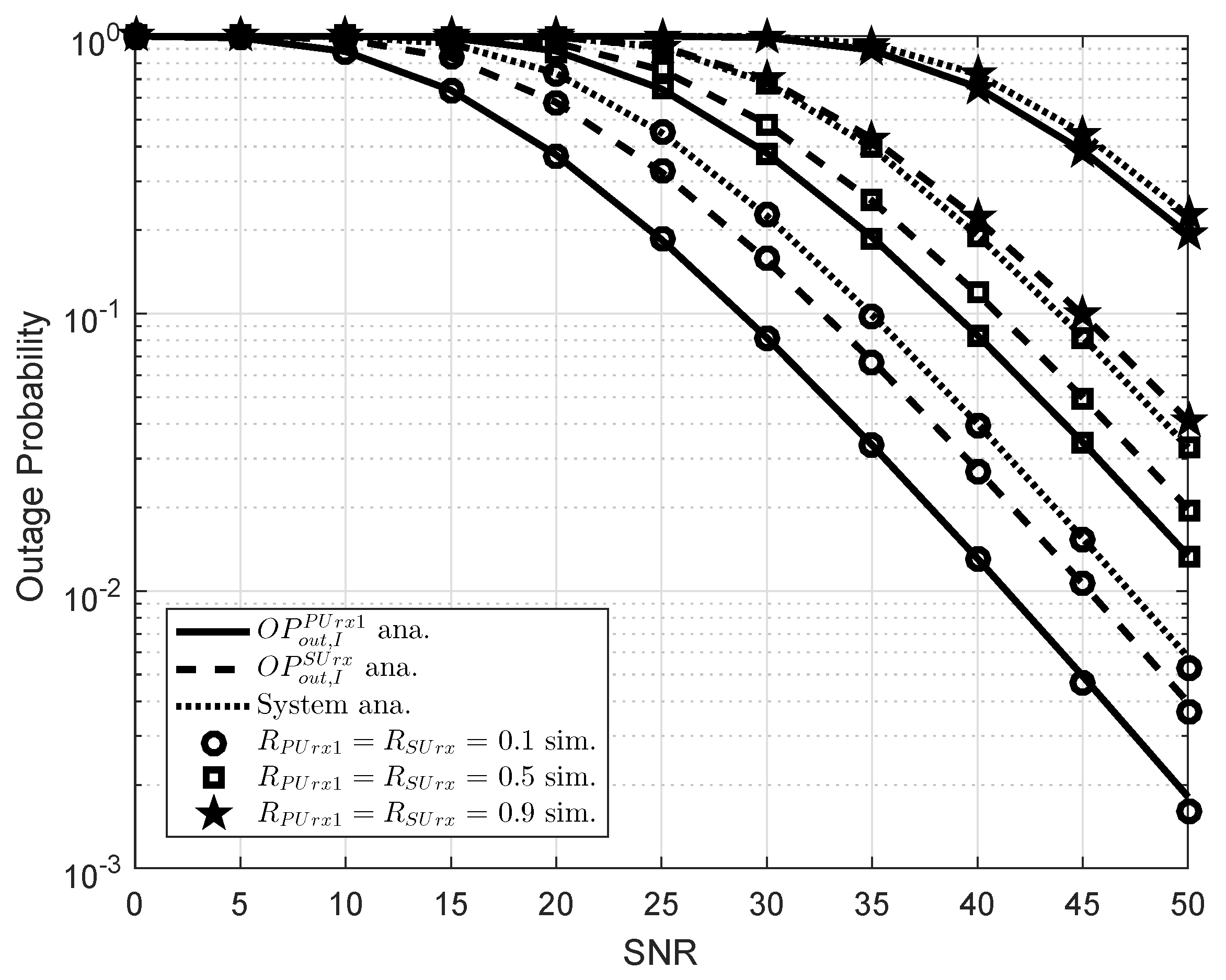
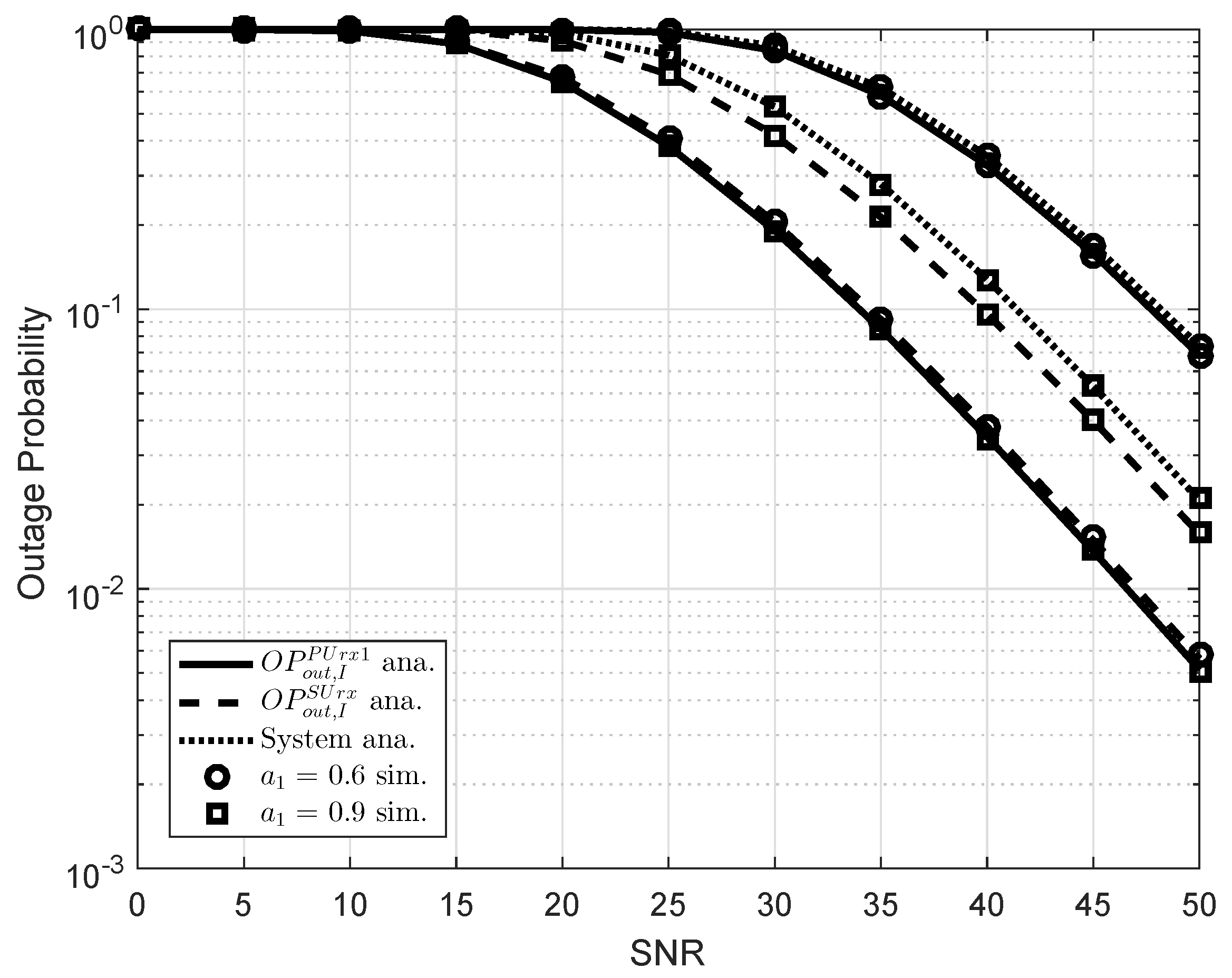
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Proposition 1
Appendix B. Proof of Proposition 3
References
- Lv, L.; Chen, J.; Ni, Q. Cooperative Non-Orthogonal Multiple Access in Cognitive Radio. IEEE Commun. Lett. 2016, 20, 2059–2062. [Google Scholar] [CrossRef]
- Wei, L.; Jing, T.; Fan, X.; Wen, Y.; Huo, Y. The Secrecy Analysis over Physical Layer in NOMA-Enabled Cognitive Radio Networks. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; p. 16. [Google Scholar]
- Wang, D.; Men, S. Secure Energy Efficiency for NOMA Based Cognitive Radio Networks with Nonlinear Energy Harvesting. IEEE Access 2018, 6, 62707–62716. [Google Scholar] [CrossRef]
- Do, D.-T.; Nguyen, H.-S.; Voznak, M.; Nguyen, T.-S. Wireless powered relaying networks under imperfect channel state information: system performance and optimal policy for instantaneous rate. Radioengineering 2017, 26, 869–877. [Google Scholar] [CrossRef]
- Bae, Y.H.; Baek, J.W. Optimal Design of RF Energy-Harvesting Network: Throughput and Delay Perspective. Sensors 2019, 19, 145. [Google Scholar] [CrossRef] [PubMed]
- Gunduz, D.; Devillers, B. Two-hop communication with energy harvesting. In Proceedings of the 2011 4th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), San Juan, Puerto Rico, 13–16 December 2011; pp. 201–204. [Google Scholar]
- Xin, J.; Liu, W.; Zhang, C.; Liu, A. An Energy Conserving and Transmission Radius Adaptive Scheme to Optimize Performance of Energy Harvesting Sensor Networks. Sensors 2018, 18, 2885. [Google Scholar]
- Liu, X.; Jia, Y.; Wen, Z.; Zou, J.; Li, S. Beamforming Design for Full-Duplex SWIPT with Co-Channel Interference in Wireless Sensor Systems. Sensors 2018, 18, 3362. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.N.; Do, D.-T.; Tran, P.T.; Voznak, M. Time Switching for Wireless Communications with Full-Duplex Relaying in Imperfect CSI Condition. KSII Trans. Internet Inf. Syst. 2016, 10, 4223–4239. [Google Scholar]
- Nguyen, T.-L.; Do, D.-T. Exploiting Impacts of Intercell Interference on SWIPT-assisted Non-orthogonal Multiple Access. Wirel. Commun. Mob. Comput. 2018, 2018, 2525492. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Do, D.-T.; Nguyen, X.X.; Nguyen, N.T.; Ha, D.H. Wireless information and power transfer for full duplex relaying networks: performance analysis. In Proceedings of the Recent Advances in Electrical Engineering and Related Sciences (AETA 2015), Ho Chi Minh City, Vietnam, 9–12 December 2015; pp. 53–62. [Google Scholar]
- Tran, T.-N.; Do, D.-T.; Voznak, M. On Outage Probability and Throughput Performance of Cognitive Radio Inspired NOMA Relay System. Adv. Electr. Electron. Eng. 2018, 16, 501–512. [Google Scholar] [CrossRef]
- Men, J.; Ge, J.; Zhang, C. Performance analysis of non-orthogonal multiple access for relaying networks over nakagami-m fading channels. IEEE Trans. Veh. Technol. 2017, 66, 1200–1208. [Google Scholar] [CrossRef]
- Do, D.T.; Le, C.-B. Application of NOMA in Wireless System with Wireless Power Transfer Scheme: Outage and Ergodic Capacity Performance Analysis. Sensors 2018, 18, 3501. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.; Wang, J.; Kang, G.; Liu, Y. Uplink nonorthogonal multiple access in 5G systems. IEEE Commun. Lett. 2016, 20, 458–461. [Google Scholar] [CrossRef]
- Ding, Z.; Fan, P.; Poor, H.V. Impact of User Pairing on 5G Nonorthogonal Multiple Access Downlink Transmissions. IEEE Trans. Vehic. Tech. 2016, 65, 1462–1465. [Google Scholar] [CrossRef]
- Ding, Z.; Schober, R.; Poor, H.V. A General MIMO Framework for NOMA Downlink and Uplink Transmission Based on Signal Alignment. IEEE Trans. Wirel. Commun. 2016, 15, 4438–4454. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, Z.; Elkashlan, M. Non-orthogonal Multiple Access in Large-Scale Underlay Cognitive Radio Networks. IEEE Trans. Vehic. Tech. 2016, 65, 152–157. [Google Scholar] [CrossRef]
- Lv, L.; Ni, Q.; Ding, Z. Application of Non-Orthogonal Multiple Access in Cooperative Spectrum-Sharing Networks over Nakagami-m Fading Channels. IEEE Trans. Vehic. Tech. 2017, 66, 5506–5511. [Google Scholar] [CrossRef]
- Lv, L.; Ni, Q.; Ding, Z. Design of Cooperative Non-Orthogonal Multicast Cognitive Multiple Access for 5G Systems: User Scheduling and Performance Analysis. IEEE Trans. Commun. 2017, 65, 2641–2656. [Google Scholar] [CrossRef]
- Kader, F.; Shin, S.Y. Cooperative Spectrum Sharing with Space Time Block Coding and Non-Orthogonal Multiple Access. In Proceedings of the 8th ICUFN, Vienna, Austria, 5–8 July 2016. [Google Scholar]
- Zhang, Y.; Yang, Q.; Zheng, T. Energy Efficiency Optimization in Cognitive Radio Inspired Non-Orthogonal Multiple Access. In Proceedings of the IEEE 27th PIMRC, Valencia, Spain, 4–8 September 2016. [Google Scholar]
- Liu, X.; Wang, Y.; Liu, S.; Meng, J. Spectrum Resource Optimization for NOMA-Based Cognitive Radio in 5G Communications. IEEE Access 2018, 6, 24904–24911. [Google Scholar] [CrossRef]
- Nandan, N.; Majhi, S.; Wu, H.-C. Secure Beamforming for MIMO-NOMA Based Cognitive Radio Network. IEEE Commun. Lett. 2018. [Google Scholar] [CrossRef]
- Wang, Q.; Ge, J.; Li, Q.; Bu, Q. Joint Relay and Antenna Selection for Cognitive Radio-Inspired Non-orthogonal Multiple Access. In Proceedings of the IEEE International Conference on Communications Workshops (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Im, G.; Lee, J.H. Outage Probability for Cooperative NOMA Systems with Imperfect SIC in Cognitive Radio Networks. IEEE Commun. Lett. 2019, 23, 692–695. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 6th ed.; Academic Press: New York, NY, USA, 2000. [Google Scholar]
- Lee, S.; da Costa, D.B.; Vien, Q.; Duong, T.Q.; de Sousa, R.T. Non-orthogonal multiple access schemes with partial relay selection. IET Commun. 2017, 11, 846–854. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Nguyen, M.-S.; Do, D.-T.; Voznak, M. Improving Performance of Far Users in Cognitive Radio: Exploiting NOMA and Wireless Power Transfer. Energies 2019, 12, 2206. https://doi.org/10.3390/en12112206
Van Nguyen M-S, Do D-T, Voznak M. Improving Performance of Far Users in Cognitive Radio: Exploiting NOMA and Wireless Power Transfer. Energies. 2019; 12(11):2206. https://doi.org/10.3390/en12112206
Chicago/Turabian StyleVan Nguyen, Minh-Sang, Dinh-Thuan Do, and Miroslav Voznak. 2019. "Improving Performance of Far Users in Cognitive Radio: Exploiting NOMA and Wireless Power Transfer" Energies 12, no. 11: 2206. https://doi.org/10.3390/en12112206
APA StyleVan Nguyen, M.-S., Do, D.-T., & Voznak, M. (2019). Improving Performance of Far Users in Cognitive Radio: Exploiting NOMA and Wireless Power Transfer. Energies, 12(11), 2206. https://doi.org/10.3390/en12112206






