Abstract
To support high-level wind energy utilization, wind power prediction has become a more and more attractive topic. To improve prediction accuracy and flexibility, joint point-interval prediction of wind power via a stepwise procedure is studied in this paper. Firstly, time-information-granularity (TIG) is defined for ultra-short-term wind speed prediction. Hidden features of wind speed in TIGs are extracted via principal component analysis (PCA) and classified via adaptive affinity propagation (ADAP) clustering. Then, Gaussian process regression (GPR) with joint point-interval estimation ability is adopted for stepwise prediction of the wind power, including wind speed prediction and wind turbine power curve (WTPC) modeling. Considering the sequential uncertainties of stepwise prediction, theoretical support for an uncertainty enlargement effect is deduced. Uncertainties’ transmission from single-step or receding multi-step wind speed prediction to wind power prediction is explained in detail. After that, normalized indexes for point-interval estimation performance are presented for GPR parameters’ optimization via a hybrid particle swarm optimization-differential evolution (PSO-DE) algorithm. K-fold cross validation (K-CV) is used to test the model stability. Moreover, due to the timeliness of data-driven GPR models, an evolutionary prediction mechanism via sliding time window is proposed to guarantee the required accuracy. Finally, measured data from a wind farm in northern China are acquired for validation. From the simulation results, several conclusions can be drawn: the multi-model structure has insignificant advantages for wind speed prediction via GPR; joint point-interval prediction of wind power is realizable and very reasonable; uncertainty enlargement exists for stepwise prediction of wind power while it is more significant after receding multi-step prediction of wind speed; a reasonable quantification mechanism for uncertainty is revealed and validated.
1. Introduction
Nowadays, large-scale and distributed utilization of wind power has been widely developed. In the long run, wind power generation will play an important role in the future energy structure [1] while constantly improving its own shortcomings such as wind turbine noise impact [2,3,4,5] and wind energy volatility. With the rapid growth of the proportion of grid-connected wind power, whether for a large-grid or for a micro-grid, the volatility of primary wind energy is usually a concern for the safe and economic operation of the power grid. Against this background, wind power prediction is very helpful to enhance our knowledge of the wind energy variation and help increase the controllability of wind power. As a result, it has become very important for the modern wind power industry [6].
Wind power prediction can be realized with different time scales such as ultra-short-term, short- term, medium-term and long-term, etc. Among them, short-term prediction of wind power for a wind farm has been popularly studied [7], serving for day-ahead dispatching, pre-dispatching or on-line dispatching. Especially, due to increasing accuracy [8], numerical weather prediction provides more support for the power prediction of wind farms in a wide area. However, for a wind turbine at a specific-site, the spatial scale is too small and numerical weather prediction information become inaccurate. Considering the requirements such as optimal control of wind turbines, economic power dispatching of wind farms and auxiliary peak/frequency modulation service, etc., the ultra-short-term power prediction of wind turbines has attracted more and more attention. This is the main object of study in this paper.
Due to the fact accurate numerical weather prediction information is not easily accessible for wind turbines, stepwise prediction is very suitable, usually including wind speed prediction and WTPC modeling. It is flexible enough to identify the accuracy of each step. In [6,9], stepwise prediction of wind power using predicted wind speed and WTPC was clearly introduced. Nevertheless, in many publications, wind speed prediction and WTPC modeling are studied separately.
In [10], Hu, et al., used generalized principal component analysis for the classification of wind patterns. Support vector regression was utilized for local modeling and a switching strategy was proposed for global short-term prediction. In [11], a time adaptive filter-based empirical mode decomposition was used to decompose wind speed series into several intrinsic modes and global short-term predictions were realized through assembled calculation of local models via an extreme learning machine approach. In the above studies, short-term point prediction of wind speed was the main concern and attention was paid to the classification of hidden wind speed patterns. Thereafter, the randomness of wind speed is examined to yield interval predictions. In [12], an empirical wavelet transform was employed to extract meaningful information from wind speed series and a hybrid GPR model was built for short-term interval prediction of wind speeds. Using similar schemes, in [13,14], variational mode decomposition was combined with relevance vector machine and low rank multi-kernel ridge regression to realize short-term interval predictions of wind speed. However, ultra-short-term interval prediction of wind speed hasn’t been studied. Besides, the mean square error is always used as the objective for parameter optimization of prediction algorithms. In [15], evaluation indexes for interval prediction performance of wind speed were defined to form a multi-objective framework. However, the point prediction performance wasn’t involved. Then, separate optimization of point or interval prediction performance may worsen that of the other one.
WTPC is a kind of steady-state description of the power generation characteristics of a wind turbine. Different from the designed WTPC given by the original equipment manufacturer (OEM), the actual data distribution of wind speed and power shows a banding shape influenced by many random factors. Using parametric or non-parametric methods, WTPC modeling has been widely studied [16,17]. Especially, uncertainty modeling of WTPC has been paid certain attention. In [18,19], using Gaussian and conditional kernel density estimation, respectively, joint probability distributions of wind speed and power were established, whereas only point estimation of WTPC was discussed. In [20,21], Bai, et al., adopted conditional copula to establish the joint probability distribution of wind speed and power, where only interval estimation of WTPC was discussed. In [22], fuzzy cluster, BP neural network and Monte-Carlo algorithms were compared to obtain probabilistic WTPC models. According to these references, joint point-interval estimation of WTPC has not been clearly claimed. Furthermore, the relationship between point and interval estimation has not been revealed. Meanwhile, how to evaluate and optimize the joint point-interval estimation performance still lacks relevant research.
Affected by stochastic wind energy and complex interference factors, uncertainty prediction of wind power is necessary [23,24]. If a stepwise procedure is executed, how to deal with the sequential uncertainties of wind speed prediction and WTPC modeling is a critical question. In [25], Liu, et al., studied interval prediction of wind power for a wind farm considering the uncertainty of wind speed prediction via ARMA-GARCH and the operation probability of wind turbines. It suggested the necessity of considering sequential uncertainties for wind power prediction. However, it is different from the ultra-short-term prediction of wind power for a wind turbine where both the uncertainties of wind speed prediction and WTPC modeling need to be considered.
Comparing different interval modeling methods, two classes can be obtained. One class is based on conditional probability distribution of output against inputs where regression values in view of conditional expectation and boundaries under certain confidence degree can be obtained. The methods such as conditional kernel density estimation, conditional copula, GPR and relevant vector machine belong to this class, where point and interval estimation can be jointly realized. The other class is based on conditional probability of prediction error against predicted values using normal point regression algorithms. Confidence boundaries of prediction error can be also yielded [26,27]. Under different application scenarios such as single-step or multi-step prediction of wind power, appropriate method should be selected to get reasonable description form of interval prediction.
Considering the feasibility of ultra-short-term wind power prediction via a stepwise procedure, GPR is chosen as the main algorithm for wind speed prediction and WTPC modeling. On this basis, the main contributions of this paper may be listed as follows:
- The concept of TIG is defined to build an input-output matrix for ultra-short-term wind speed prediction. A PCA-clustering scheme is proposed to extract hidden wind patterns in TIGs.
- Joint point-interval prediction of wind power is clearly claimed and studied via GPR. Theoretical support for uncertainty enlargement due to sequential uncertainties during stepwise procedure is deduced.
- Normalized and comprehensive evaluation indexes for joint point-interval estimation performance are defined systematically. Hybrid PSO-DE algorithm and K-CV method are used to obtain better and more stable performance.
- After single-step or receding multi-step wind speed prediction, uncertainty enlargement effects during stepwise wind power prediction is revealed and validated using parametric and non-parametric interval modeling methods.
The rest of the paper is organized as follows: Section 2 presents the establishment of a multi-model structure for wind speed prediction. Section 3 completely proposes the joint point-interval prediction of wind power via stepwise procedure. Section 4 defines normalized and comprehensive evaluation indexes for joint point-interval prediction of wind power while evolutionary updating mechanism is raised. Simulation and analysis are executed in Section 5. Section 6 concludes the paper.
2. Establishment of Multi-Model Structure for Wind Speed Prediction
2.1. Formation of Input-Ouput Matrix
To realize receding wind power prediction of a single wind turbine, a stepwise procedure is adopted in this paper, including receding wind speed prediction and WTPC modeling. We set the sampling period as TV and split the wind speed time series into many segments, where a segment is defined by Vi = [vi1, vi2, …, vij, …, vin] = [vi(k), vi(k + 1), …, vi(k + j), …, vi(k + n − 1)] where Vi+1 = [vi(k + s), vi(k + 1 + s), …, vi(k + j + s), …, vi(k + n − 1 + s)] (1 ≤ s ≤ n). Different values of s mean different ways of sampling the data. Vi is the i-th wind speed segment with n elements sequentially distributed along n time instants. Vi is a TIG in time-domain space. Assume m segments can be obtained, making up the following matrix V.
For V, rows are seen as r repetitions. Columns from 1 to (n − 1) are seen as inputs, shown by Vi,In = [vi1, vi2, …, vij, …, vin−1]. The n-th column is seen as output, shown by Vi,Out = vin (i = 1, 2,…, r; j = 1, 2,…, n). As a result, for receding wind speed prediction, V is the input-output matrix. Relatively, WTPC modeling is independent of receding prediction of wind speed. Only wind speed and power data are needed as the input and output of WTPC modeling.
2.2. Feature Extraction of Hidden Wind Speed Patterns
For a wind turbine at a specific site, the wind conditions may change with the seasons, wind directions and spatial terrains. It is intuitive that prediction accuracy may be raised under the same wind conditions. However, it is not certain for different prediction algorithms. In this subsection, wind speed is used to represent wind conditions and hidden wind speed patterns are extracted.
Using TIGs of wind speed, PCA [28] is an effective post-processing manner to extract features of TIGs and to form feature-information-granules. It is convenient for dimensionality reduction of high-dimensional data via a statistical procedure. Then, noise and unimportant features can be removed to enhance the calculation efficiency. It uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components where the first principal component has the largest possible variance and each succeeding component in turn has the highest variance possible under the constraint that it is orthogonal to the preceding components. Each component vector is a linear combination of input variables and all component vectors form an uncorrelated orthogonal basis set.
Based on Equation (1), we remove the column mean values of V and it becomes a column-wise zero empirical mean. Then, PCA is executed and p new features can be obtained where xil = ω1l∙vi1 + ω2l∙vi2 +…+ ωjl∙vij +…+ ωnl∙vin = ωl∙ViT(ωl = [ω1l, ω2l,…, ωjl,…, ωnl]; l = 1, 2,…, h). As a result, feature matrix can be represented as follows:
If n is chosen to be much bigger than h, the dimensionality reduction effect becomes obvious. This provides good convenience for the subsequent calculation.
2.3. Classification of Extracted Features via Clustering
Extracted features represent the main hidden information in TIGs. To classify them, an adaptive classification strategy via clustering is presented here. Firstly, unsupervised clustering algorithms such as K-medoids clustering, fuzzy C-means (FCM) clustering, Gaussian-mixture-model (GMM) clustering and ADAP clustering, are adopted and compared. Secondly, to evaluate clustering effects, the silhouette coefficient is used considering inter-cluster and intra-cluster effects which has better and more balanced evaluation performance than other evaluation indexes such as Davies-Bouldin index and Dunn-Validity index. The silhouette coefficient range is [−1,1] and it measures how similar an object is to its own cluster compared to other clusters. A high value suggests that the object is well suited to its own cluster and poorly suited to the neighboring clusters.
Silhouette coefficients can be calculated with any distance metric including Euclidean distance and Manhattan distance, etc. Define dintra(ui) as average distance between point ui and all other points within the same cluster. Define dintel(ui) as average distance between point ui and all points in any other cluster. Then, the silhouette coefficient [29] is calculated by:
where the value close to 1 means that the point is appropriately clustered; the value close to −1 means that the point would be more appropriately clustered in its neighbouring cluster; a zero value means that the point is on the border of two clusters. Using the silhouette coefficient, the effects of different clustering algorithms can be evaluated and even optimized by the intelligent evolutionary algorithms such as genetic algorithm (GA), PSO and DE algorithms. Finally, wind speed TIGs can be classified via clustering. Besides, new input TIGs can also be classified into reasonable clusters via the silhouette coefficient. It provides a judgment for model switching under a multi-model structure.
Overall, as shown in Figure 1, the classification scheme of hidden wind speed patterns is wholly proposed to establish multi-model structure for receding wind speed prediction.
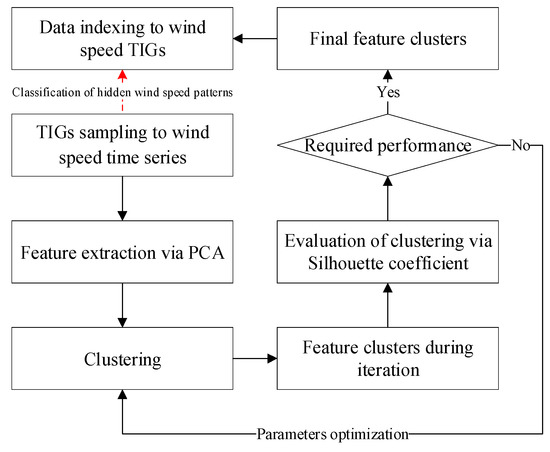
Figure 1.
Diagram of classification of hidden wind speed patterns.
3. Joint Point-Interval Prediction of Wind Power via Stepwise Procedure
3.1. Joint Point-Interval Modeling
Stepwise prediction of wind power includes wind speed prediction and WTPC modeling. Herein, each step is taken as a joint point-interval modeling process. For regression algorithms such as artificial neural network (ANN), support vector machine (SVM), GPR and RVM, the point output is usually the conditional expectation of inputs. To realize joint point-interval modeling, not only conditional expectation but also conditional probability are needed where GPR is capable to fulfill this task.
GPR is a supervised method for regression and probabilistic prediction. Based on measured data, nonparametric kernel-based probabilistic models can be built. Computing empirical confidence intervals is an advantage of GPR. Assume the measured training data set {(ai, bi); i = 1, 2,…, nTrai} where ai∈Rc and bi∈R. Estimation of bi can be represented by [26]:
where ε is noise assumed to be independent normal distribution with variance σ2. f(a) can be seen as a feature space in form f(a) = ϕ(a)Tα where ϕ(a) is basis function and α is coefficients. f(a) is also a Gaussian process defined as follows [30]:
where a and a′ are any two points in Rc; K(•) is the chosen kernel function. From Equation (5), it suggests that each observation in a is normal distribution and joint probability distribution of observations in a is a multivariate normal distribution due to every finite linear combination of these observations are still normal distribution. Meanwhile, estimated output of Equation (4) is also a normal distribution which can be represented by [30]:
Assume testing input data are a*. Then, testing output and training output form the following joint normal distribution [26]:
As a result, regression values of testing inputs, conditional expectation of under (a, , a*), can be calculated by [30]:
where cov(•) is a covariance vector of under (a, , a*). In Equation (8), m* is regression output. Based on the covariance vector, conditional probability distribution of output can also be obtained. Thus, GPR can be directly used for joint point-interval modeling. The whole procedure is shown in Figure 2.
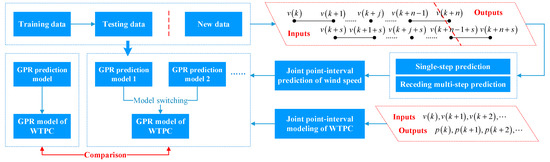
Figure 2.
Diagram of joint point-interval prediction of wind power via stepwise procedure.
3.2. Sequential Uncertainties of Stepwise Procedure Based on Single-Step Prediction of Wind Speed
Using stepwise procedure, wind speed prediction and WTPC modeling are carried out separately via GPR. From Equation (1), we assume the training and testing data are (VIn, VOut) and (VIn*, VOut*) for GPR modeling of wind speed prediction. Then, testing output VOut* is represented by:
where for details of the calculation one can refer to Equation (8). Uncertainties transmission during single-step wind speed prediction is shown in Figure 3a. Point and interval predictions of wind speed at sequential time points composes new inputs to WTPC model.
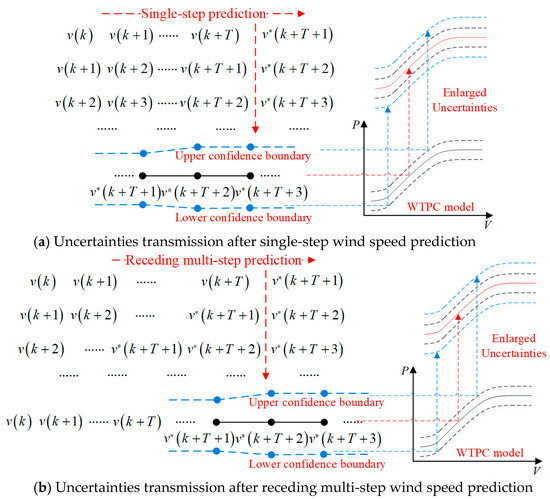
Figure 3.
Diagram of uncertainties transmission during wind power prediction.
For WTPC modeling, input and output are wind speed V and active power PAct. Assume training and testing data are (V, PAct) and (V*, PAct*) for GPR modeling of WTPC. Then, the testing output of PAct* is represented by:
For stepwise prediction based on single-step prediction of wind speed, results of wind speed prediction are input of WTPC model where V = VOut. Due to the fact Equations (9) and (10) are both normal distributions, the final output of PAct* can also be shown as:
where V* = Vout*. From Equation (11), the final output reflects the enlargement effect of sequential uncertainties at each step. As a result, confidence intervals of WTPC output are also enlarged, as shown in Figure 3a. To obtain the required results, the uncertainty of each step can be adjusted separately.
3.3. Sequential Uncertainties of Stepwise Procedure Based on Receding Multi-Step Prediction of Wind Speed
GPR is a single-step prediction method. If multi-step prediction is needed, receding wind speed prediction should be executed, where the predicted value v*(k + T + 1) at current time k + T + 1 is used as input for the prediction at next time k + T + 2. In this case, the uncertainties of point and interval prediction at the current time are also passed to the next time. Then, how to quantify the transferred uncertainties during receding multi-step prediction is a critical problem. Of course, if receding predictions are input to WTPC model, the predicted power also succeeds these uncertainties, shown in Figure 3b.
At each step of receding wind speed prediction, the relationship between input and output is variable. Thus, joint point-interval prediction at different times will yield different results. This suggests that only the statistical results at each prediction step will be meaningful. Instead of obtaining joint point-interval predictions by GPR, confidence intervals of prediction errors are used to describe uncertainties at each prediction step. Herein, KDE and Gaussian methods are compared to calculate confidence intervals of prediction errors at different receding steps. Using KDE, non-parametric probability distribution can be obtained according to prediction error distribution at each step. Using Gaussian method, parametric probability distribution can be obtained where Gaussian distribution is assumed at each step. They are both adopted to validate that their confidence intervals of prediction errors at each step have great similarity.
4. Evolutionary Prediction Mechanism
4.1. Prediction Performance Evaluation
Regarding joint point-interval prediction, how to evaluate or optimize prediction performance and how to guarantee timeliness of models, are still problems to be solved in this section.
For point prediction of wind speed or power, error-based indexes such as mean absolute error (MAE), root mean square error (RMSE) and their deformations, etc., are usually used for evaluation. For interval prediction, indexes such as prediction intervals coverage probability (PICP), coverage error (CE) and prediction intervals average width (PIAW), etc., are usually used [15,31].
In essence, confidence intervals, output by GPR, are again the conditional probability input. Thus, PICP and CE indexes need to be calculated for certain input. Through dividing range of input into bins, they can also be calculated for certain bin. Assume the required confidence against the l-th input bin is α, PICP in this bin is defined as follows:
where Np(l) is number of points falling into confidence intervals with required confidence α against the l-th input bin. κi(α)(l) is an indicative function for the i-th point (if this point falls into the confidence interval, κi(α) = 1; otherwise κi(α) = 0). Then, CE of confidence interval against the l-th input bin is:
For wind speed prediction by GPR, partition of input bins may be roughly realized by clustering. For WTPC modeling by GPR, partition of input bins mainly refers to wind speed range. However, in actual execution, input data are non-uniform and calculation of Equations (12) and (13) is inaccurate and complex. When cj/gj→1 (cj, gj are arbitrary positive integers), the following equation exists:
According to Equation (14), PICP and CE indexes under different input bins have the same limit with that directly calculated in the intervals under the whole input range. It is easy to be executed, defined by:
where MPICP and MCE are the mixed statistics of PICP and MCE, respectively. Np is total number of predicted points. Especially, for a higher confidence degree approaching 1, limits of Equations (12) and (15), Equations (13) and (16) approach closer with each other according to Equation (14). In this paper, MPICP and MCE indexes are adopted in actual execution. Besides, PIAW is defined by:
where Ui(α) and Li(α) are upper and lower intervals for the i-th point.
In order to comprehensively evaluate the performance of joint point-interval prediction, weighted-index (WI) are proposed as follows:
where λ* represents the weight. NRMSE, NMCE and NPIAW are normalization of RMSE, MCE and PIAW, defined as follows:
where mean(*) represents average value. Wset represents pre-setted interval width.
4.2. Optimal Modeling, Corss Validation and Sliding Updation of Prediction Models
Using WI as optimization target, the GPR model may be optimized to obtain a more balanced performance. Herein, a hybrid PSO-DE algorithm is used. Based on the standard PSO and DE algorithms, the steps of the hybrid PSO-DE algorithm [32] are shown in Figure 4. Assume the maximum iterations of PSO and DE algorithms are Ipso and Ide. In the early stage, PSO is executed until the iteration times exceed Ipso/2. Then, new particles with the number of 20% of the initial population size are generated in the neighborhood of obtained optimal position. Following this step, the DE algorithm is executed for the newly generated particles until the iteration times exceed Ide. The optimal solutions obtained by DE is then evaluated by the fitness function of PSO. Nested execution of DE can be repeated during execution of PSO until iteration times of PSO exceed Ipso and then the PSO-DE algorithm terminates. This hybrid algorithm combines the fast global convergence of PSO and the high-precision search ability of DE. Thus, the optimizing efficiency and accuracy can be greatly improved.
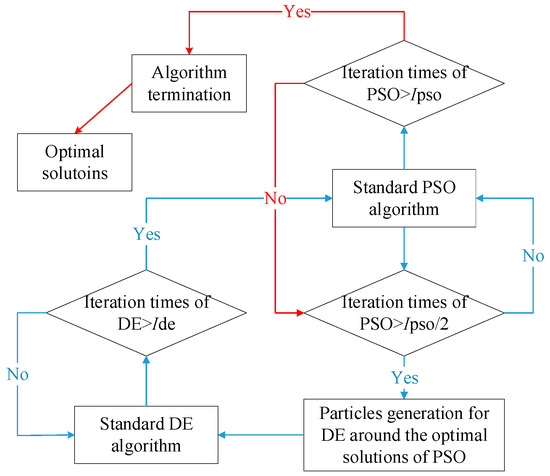
Figure 4.
Diagram of hybrid PSO-DE algorithm.
For training and testing of GPR, K-CV is adopted to verify stability and robustness of GPR models. Average WI value of k times is used to evaluate the modeling performance. The optimal GPR modeling procedure is shown in Figure 5, which can be both used for wind speed prediction and WTPC modeling.
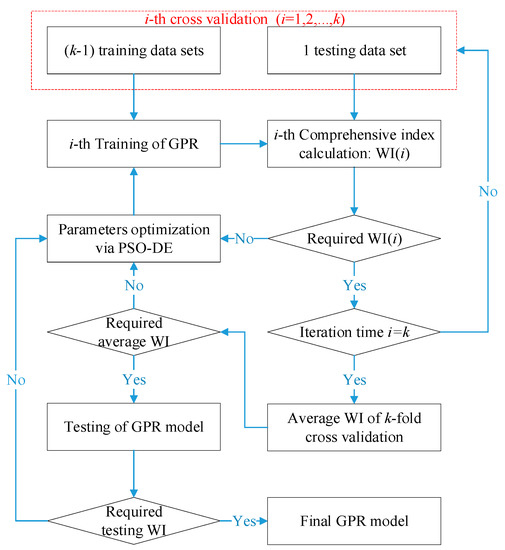
Figure 5.
Diagram of GPR modeling procedure.
Due to the fact the GPR model is built using historical data from a past certain period, its timeliness also depends on these data. Thus, a non-negligible question is the timeliness of the data-based model. It needs to be updated in time. Herein, a sliding-time-window is adopted where the database for modeling is incrementally updated with a certain time window. As a result, GPR models are also regularly updated in time. Trigger mechanism of model updating can be event-driven by monitoring of WI or time-driven by sliding-time-window.
5. Simulations
Based on the data from the supervisory control and data acquisition (SCADA) system of a wind farm located in northern China, wind speed and power data are acquired and preprocessed for prediction. In the wind farm, 1.5 megawatt wind turbines with variable-speed variable-pitch ability are mainly used. The sampling period of the data is 15 min, which is also the time interval of single-step prediction.
5.1. Decision of TIG Length for Wind Speed Prediction
TIG length predetermines the input dimensions of GPR. Herein, single-step prediction of wind speed using different TIG lengths are tested to select an appropriate length. We arbitrarily choose wind speed data with a sampling period of 15 min. Two thousand (2000) data points are randomly selected for training (1600 points) and testing (400 points). Besides, for GPR modeling, type of basis-function is pure quadratic and the type of kernel-function is square exponential, defined as follows:
where σl is the characteristic length scale. σf is the signal standard deviation. Mean square error (MSE) is used for optimization the parameters such as σ, σl and σf. Indexes such as NRMSE, NMACE, NPIAW and WI are used for evaluation where weights are all 1/3, as shown in Table 1.

Table 1.
Testing of TIG length.
Two samples are randomly selected for testing under each TIG length. From Table 1, NMACE varies obviously while the indexes of NRMSE and NPIAW perform relatively stable. When the TIG length is greater than or equal to 6, their WIs become stable at the same bound level. To avoid unnecessary computational burden, 6 is selected as the TIG length in this paper.
5.2. Necessity of Comprehensive Optimization Based on WI
Normally, the parameters of GPR are optimized using MSE of point prediction as the objective. This doesn’t consider interval performance. In extreme cases, excessively optimizing MSE may cause performance deterioration of the interval prediction. Thus, in this subsection, different objectives are tested for wind speed prediction and WTPC modeling using GPR where PSO-DE is adopted.
For wind speed prediction via GPR, testing results are shown in Table 2 and Figure 6. In Figure 6, ‘Estimated 1’, ‘Upper 1’ and ‘Lower 1’ are results using WI as objective. ‘Estimated 2’, ‘Upper 2’ and ‘Lower 2’ are results using MSE as objective. Just using MSE as optimization objective, its point prediction index, NRMSE, is very close with that of WI. However, their interval prediction indexes, NMACE and NPIAW are distinguished from each other greatly. As a result, their WIs are also different. These results reflect a truth that using WI as objective is necessary for parameter optimization of GPR when predicting wind speed. Of course, lower boundaries in Figure 6 are retained to show interval modeling effect of WTPC from a statistical view. In actual, physical boundaries of wind speed should be considered. Usually, zero line is the lower physical boundary of wind speed whereas upper boundary of GPR fulfills its physical meaning.

Table 2.
Testing of wind speed prediction using different objectives.
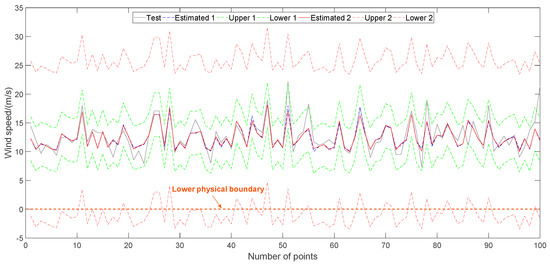
Figure 6.
Comparison of wind speed prediction using different objectives.
For WTPC modeling via GPR, testing results are shown in Table 3, Figure 7 and Figure 8. In Figure 7 and Figure 8, ‘Estimated 1’, ‘Upper 1’ and ‘Lower 1’ are results using WI as objective. ‘Estimated 2’, ‘Upper 2’ and ‘Lower 2’ are results using MSE as objective. It can be found that taking MSE or WI as objective has very little influence on modeling performance. Moreover, the two objectives have very close modeling effects, including both the point and interval indexes. Thus, it is unnecessary to distinguish the usage of MSE and WI for parameter optimization of WTPC modeling via GPR. In Figure 7, wind power exceeding cut-in wind speed 3 m/s is shown. In Figure 8, physical boundaries of wind power should be also paid attention where zero line is the lower physical boundary whereas upper boundary of GPR fulfills its physical meaning.

Table 3.
Testing of WTPC modeling using different objectives.
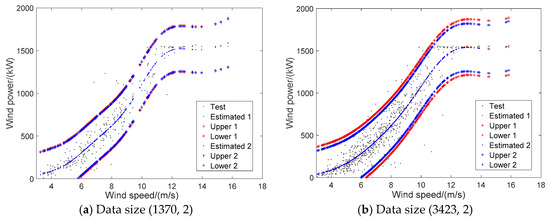
Figure 7.
Comparison of WTPC models using different objectives.
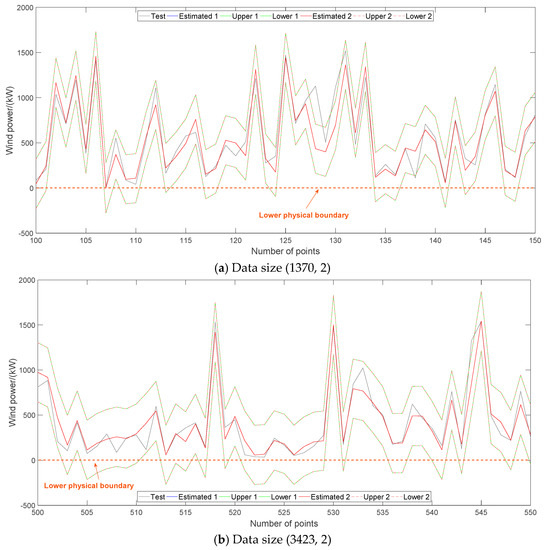
Figure 8.
Comparison of WTPC output using different objectives for data size (3423, 2).
5.3. Establishment and Testing of Multi-Model Structure via PCA-Clustering Scheme
Intuitively, partition of wind speed patterns can raise prediction accuracy of wind speed. However, under the Bayesian framework of GPR, it will be seriously tested in this subsection. To identify the hidden wind speed patterns effectively, PCA-clustering strategy is presented. Herein, the total size of the data sample is (6300, 6) where the input is five dimensional and the output is one dimensional. After feature extraction, three dominant features are used for clustering, where K-medoids, ADAP, FCM and GMM clustering methods are compared. The results are shown in Table 4 using the silhouette coefficient as evaluation index. Concerning consumed time, K-medoids, FCM and GMM performs well, whereas ADAP is very time consuming. When the cluster number equals 2, all methods have similar silhouette coefficients. However, the data uniformities of the clusters are different. For K-medoids, FCM and GMM methods, data points of the two clusters are 641|5659, 597|5703, 1082|5218 and 2066|4234, respectively. In contrast, though ADAP is time consuming, it has a better silhouette coefficient and data uniformity. Thus, the data by ADAP with two clusters is utilized for sequential research, shown in Figure 9. Lines of quartile for each cluster clearly divide the data samples. It provides good foundation for establishment of a multi-model structure.

Table 4.
Comparison of different clustering methods.
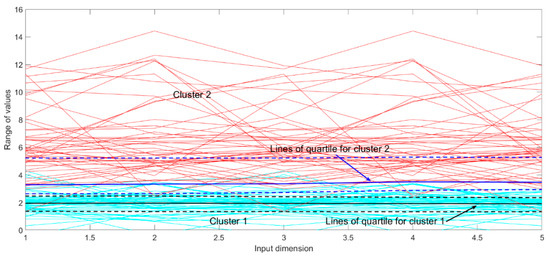
Figure 9.
Display of ADAP clustering results.
Taking WI as objective, a comparison of different data samples is shown in Table 5 and Figure 10, where five-fold cross validation is adopted to show the effectiveness of the GPR models. Analyzing the input data patterns in Figure 9, the variation of the data of cluster-2 is stronger than that of the data of cluster-1. This explains, according to RMSE, NMACE and NPIAW, why he GPR model based on the data of cluster-2 performs worse than that based on the data of cluster-1. Due to the fact NRMSE is normalized by the mean value of output in Equation (19), it also explains that why the NRMSE values of cluster-2 are smaller than those of cluster-1. In contrast, the indexes of the GPR model based on total data samples are a compromise between that based on the data of cluster-1 and cluster-2.

Table 5.
Performance of different data samples by five-fold cross validation.
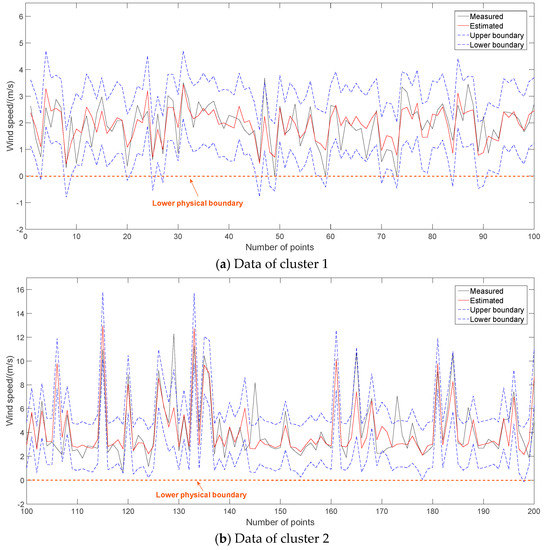
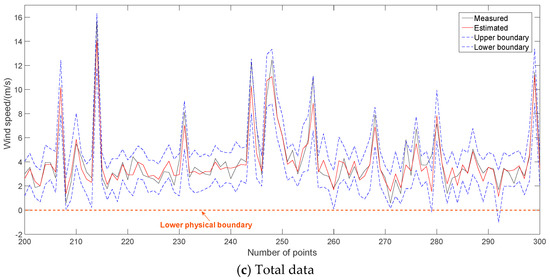
Figure 10.
Prediction output of wind speed via GPR models based on different data types.
The testing results suggest a truth, namely that that partition of wind speed patterns is uncertain to raise wind speed prediction accuracy for GPR modeling under a Bayesian framework. Regression and interval prediction by GPR is based on posterior probability of historical and new input data. It is highly dependent on distribution of the input data. In summary, for wind speed prediction by GPR, a multi-model structure doesn’t offer a significant improvement and its establishment may be unnecessary.
5.4. Wind Power Predcition Based on Single-Step Wind Speed Prediction Considering Sequential Uncertainties
Using the GPR model of single-step wind speed prediction in Figure 10c and the new WTPC model, their sequential uncertainties for wind power prediction is studied in this subsection. Herein, 6377 data pairs of wind speed-power are adopted for WTPC modeling. As shown in Figure 11, NRMSE, NMACE, NPIAW and WI of the final WTPC model via GPR are 0.2567, 0.007074, 0.2804 and 0.1813, respectively.
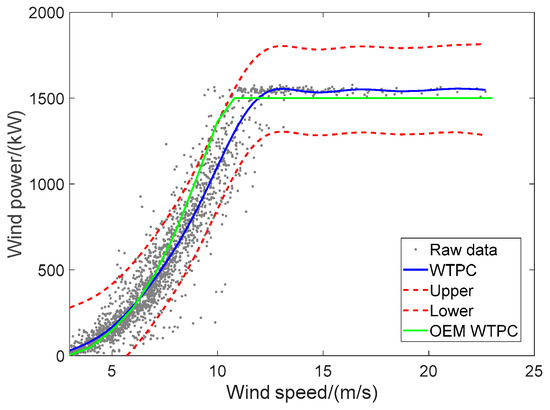
Figure 11.
WTPC model via GPR.
Considering the sequential uncertainties of wind speed prediction and WTPC modeling, the output of a single-step wind power prediction is shown in Figure 12. Calculating the conditional probability distribution of the output error against the estimated power using the KDE and Gaussian methods, their confidence intervals under confidence 0.95 are also shown in Figure 12. Gaussian is a parametric method for estimating confidence interval while KDE is a non-parametric method for that. Evaluation indexes for interval prediction performances, such as NMACE, NPIAW and WI, of them are shown in Table 6. It can be found that the confidence interval of GPR is very similar with that of KDE and Gaussian. In Figure 12, the upper and lower boundaries of these methods are directly shown from a statistical viewpoint to display the modeling effects while physical boundaries of wind power should be considered in actuality.
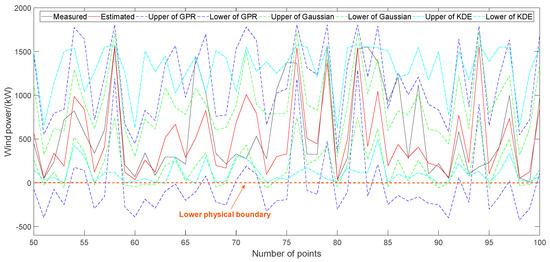
Figure 12.
Single-step wind power prediction considering sequential uncertainties.

Table 6.
Comparison of interval prediction performance via different methods.
In summary, the above simulation results reflects a truth that the sequential uncertainties of wind speed prediction and WTPC modeling is perfectly validated. In the future, if a stepwise procedure is adopted for the wind power prediction of wind turbines, the accuracy of each step can be monitored and improved to guarantee a good final accuracy.
5.5. Wind Power Predcition Based on Multi-Step Wind Speed Prediction Considering Sequential Uncertainties
Different from the single-step prediction, multi-step wind speed prediction is discussed in this subsection. In this case, the uncertainties during multi-step prediction need to be considered. As introduced in Section 3.3, only the statistics of the output error at each step are meaningful. Firstly, uncertainties transmission during ten-step wind speed prediction are shown in Table 7 and Figure 13, where the KDE and Gaussian methods are adopted to calculate the mean value and confidence intervals (with confidence 0.95) of the prediction error. All the statistical values of the KDE and Gaussian methods show the enlargement effects of receding steps during the ten-step wind speed prediction.

Table 7.
Error statistic of receding ten-step wind speed prediction.
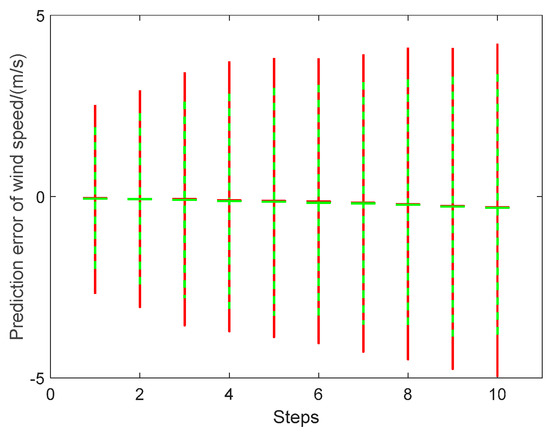
Figure 13.
Error statistic of ten-step wind speed prediction for KDE and Gaussian methods. (Red line: KDE; Green dotted line: Gaussian).
Using the actual wind speed or receding estimated wind speed as input, uncertainties transmission during ten-step wind power prediction are shown in Table 8 and Table 9, Figure 14 and Figure 15. For receding wind power using the actual wind speed as input, the input matrix is formed by one-step iteration. When it is input to the WTPC model, the outputs at different step are massively repetitive. As a result, when using the actual wind speed as input, the statistical values of the wind power error at each step remain relatively stable for both the KDE and Gaussian methods. In contrast, when using the receding estimated wind speed as input, the enlargement effects of receding steps during ten-step wind power prediction are significant. Especially, the upper and lower boundaries under confidence 0.95 show this enlargement effect. Mean values are calculated using positive and negative errors.

Table 8.
Error statistic of ten-step wind power prediction via KDE.

Table 9.
Error statistic of ten-step wind power prediction via Gaussian.
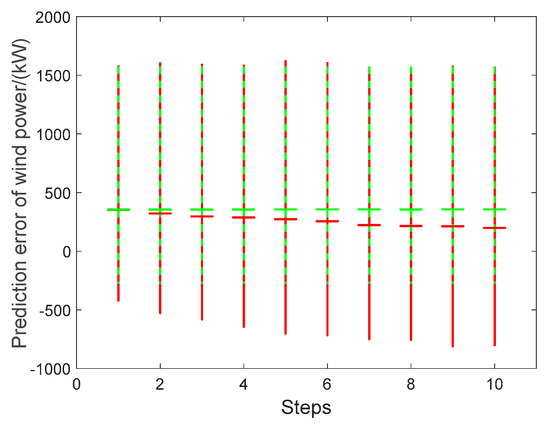
Figure 14.
Error statistic of ten-step wind power prediction using actual and estimated wind speed via KDE method (Red line: Estimated data; Green dotted line: Actual data).
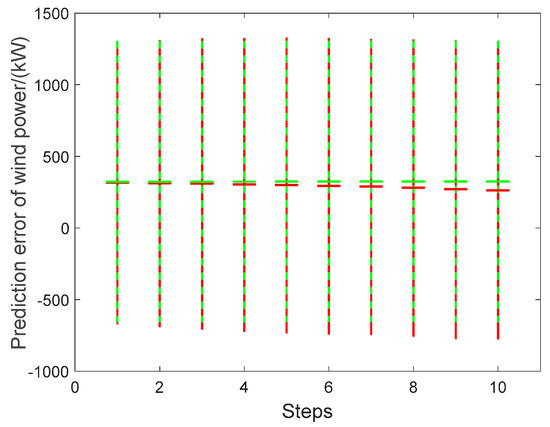
Figure 15.
Error statistic of ten-step wind power prediction using actual and estimated wind speed via Gaussian method (Red line: Estimated data; Green dotted line: Actual data).
In summary, our simulation results clearly show the uncertainties transmission of receding ten-step wind power prediction from receding ten-step wind speed prediction, where the enlargement effects of receding steps also exist. In particular, wind power values of receding ten-step prediction using receding estimated wind speed as input have greater uncertainties than that using actual wind speed as input. Besides, a new uncertainty evaluation mechanism based on output error statistics is revealed here for receding multi-step predictions.
6. Conclusions
Wind speed and power prediction is a feasible and economic way to raise our knowledge of wind source and the controllability of wind power generation. Moreover, ultra-short-term wind power prediction is helpful to the refined operation of wind turbines and wind farms. Nowadays, this becomes more and more important. Considering the uncertainties of random factors, joint point-interval prediction of wind power via a Gaussian process regression (GPR) method is studied in this paper, where a stepwise procedure is adopted considering the sequential uncertainties of wind speed prediction and wind turbine power curve (WTPC) modeling. Testing via GPR, input-output matrix with five-dimensional input and one-dimensional output is determined for ultra-term wind speed prediction. On this basis, a principal component analysis (PCA)-adaptive affinity propagation (ADAP) scheme is validated to partition wind speed patterns with better silhouette coefficients and more uniform data clusters. Then, a multi-model structure for wind speed prediction can be built, but after validation it shows little improvement over single-model prediction via GPR. Subsequently, normalized evaluation indexes for joint point-interval estimation performance are defined. Through testing, a weighted-index (WI) must be used as objective for wind speed prediction by GPR while it is unnecessary for WTPC modeling by GPR, where a particle swarm optimization-differential evolution (PSO-DE) is adopted to guarantee optimization efficiency. Thereafter, the theoretical principle for the sequential uncertainties of wind speed prediction and WTPC modeling is deduced. Using kernel density estimation (KDE) and Gaussian methods to calculate confidence intervals of output error against estimated wind power, they are similar with that of GPR which perfectly validates the effectiveness of the uncertainties transmission principle. Besides, uncertainties transmission by stepwise procedure and uncertainties enlargement by receding steps are also revealed where a new evaluation mechanism based on statistics to output error is revealed using KDE and Gaussian methods. Overall, the above research should prove meaningful for uncertainty prediction of wind power in the ultra-short-term and is very helpful for the future development of wind power generation.
Author Contributions
The individual contributions of the authors are provided as following: conceptualization, Y.H.; methodology, Y.H., Y.Q.; validation, Y.H., Y.Q.; writing—original draft preparation, Y.H.; funding acquisition, J.C. and L.Y.; supervision, Y.H. and L.P.
Funding
This research was funded by ‘the research on Intelligent Control Technology of Wind Turbine (Guodian United Power Technology Company Limited), grant number 17001’, ‘Hebei Provincial Key Research and Development Program, grant number 18214316D’, the Fundamental Research Funds for the Central Universities, grant number 2019MS024′.
Conflicts of Interest
The authors declare no conflict of interest.
References
- International Energy Agency. World Energy Outlook. 2018. Available online: https://www.iea.org/weo/ (accessed on 13 November 2018).
- Luca, F.; Stefano, C.; Gaetano, L. A procedure for deriving wind turbine noise limits by taking into account annoyance. Sci. Total Environ. 2019, 648, 728–736. [Google Scholar] [CrossRef]
- Luca, F.; Paolo, G.; Gaetano, L.; Stefano, C. Analytical assessment of wind turbine noise impact at receiver by means of residual noise determination without the wind farm shutdown. Noise Control Eng. J. 2017, 65, 417–433. [Google Scholar] [CrossRef]
- Michaud, D.S.; Feder, K.; Keith, S.E.; Voicescu, S.A. Exposure to wind turbine noise: Perceptual responses and reported health effects. J. Acoust. Soc. Am. 2016, 139, 1443–1454. [Google Scholar] [CrossRef] [PubMed]
- Hanning, C.D.; Evans, A. Wind turbine noise. Br. Med. J. 2012, 344, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Renani, E.T.; Elias, M.F.M.; Rahim, N.A. Using data-driven approach for wind power prediction: A comparative study. Energy Convers. Manag. 2016, 118, 193–203. [Google Scholar] [CrossRef]
- Giebel, G.; Brownsword, R.; Kariniotakis, G. The State-of-the-Art in Short-Term Prediction of Wind Power: A Literature Overview, 2nd ed.; RisØ National Laboratory: Roskilde, Denmark, 2016. [Google Scholar]
- Yesilbudak, M.; Sagiroglu, S.; Colak, I. A novel implementation of kNN classifier based on multi-tupled metrological input data for wind power prediction. Energy Convers. Manag. 2017, 135, 434–444. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Q.; Srinivasan, D.; Wang, Z. Wind power curve modeling and wind power forecasting with inconsistent data. IEEE Trans. Sustain. Energy 2019, 10, 16–25. [Google Scholar] [CrossRef]
- Hu, Q.; Su, P.; Yu, D.; Liu, J. Pattern-based wind speed prediction based on generalized principle component analysis. IEEE Trans. Sustain. Energy 2014, 5, 866–874. [Google Scholar] [CrossRef]
- Zheng, W.; Peng, X.; Lu, D.; Zhang, D.; Liu, Y.; Lin, Z.; Lin, L. Composite quantile regression extreme learning machine with feature selection for short-term wind speed forecasting: A new approach. Energy Convers. Manag. 2017, 151, 737–752. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J. Short-term wind speed prediction using empirical wavelet transform and Gaussian process regression. Energy 2015, 93, 1456–1466. [Google Scholar] [CrossRef]
- Fan, L.; Wei, Z.; Li, H.; Kowk, W.C.; Sun, G.; Sun, Y. Short-term wind speed interval prediction based on VMD and BA-RVM algorithm. Electr. Power Autom. Equip. 2017, 37, 93–100. [Google Scholar] [CrossRef]
- Naik, J.; Bisoi, R.; Dash, P.K. Prediction interval forecasting of wind speed and wind power using modes decomposition based low rank multi-kernel ridge regression. Renew. Energy 2018, 129, 357–383. [Google Scholar] [CrossRef]
- Shrivastava, N.A.; Lohia, K.; Panigrahi, B.K. A multiobjective framework for wind speed prediction interval forecasts. Renew. Energy 2016, 87, 903–910. [Google Scholar] [CrossRef]
- Chang, T.; Liu, F.; Ko, H.; Cheng, S.; Sun, L.; Kuo, S. Comparative analysis on power curve models of wind turbine generator in estimation capacity factor. Energy 2014, 73, 88–95. [Google Scholar] [CrossRef]
- Lydia, M.; Kumar, S.S.; Selvakumar, A.I.; Kumar, G.E.P. A comprehensive review on wind turbine power curve modeling techniques. Renew. Sustain. Energy Rev. 2014, 30, 452–460. [Google Scholar] [CrossRef]
- Villanueva, D.; Feijóo, A. Normal-based model for true power curves of wind turbines. IEEE Trans. Sustain. Energy 2016, 7, 1005–1011. [Google Scholar] [CrossRef]
- Jeon, J.; Taylor, J.W. Using conditional kernel density estimation for wind power density forecasting. J. Am. Stat. Assoc. 2012, 107, 66–79. [Google Scholar] [CrossRef]
- Bai, G.; Fleck, B.; Zuo, M.J. A stochastic power curve for wind turbines with reduced variability using conditional Copula. Wind Energy 2016, 19, 1519–1534. [Google Scholar] [CrossRef]
- Hu, Y.; Qiao, Y.; Liu, J.; Zhu, H. Adaptive confidence boundary modeling of wind turbine power curve using SCADA data and its application. IEEE Trans. Sustain. Energy 2018, 1–12. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, H.; Liu, Y.; Han, S.; Li, L. Uncertainty estimation for wind energy conversion by probabilistic wind turbine power curve modeling. Appl. Energy 2019, 239, 1356–1370. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, J.; Wang, X. Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energy Rev. 2014, 32, 255–270. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Fan, S.; Zareipour, H.; Troccoli, A.; Hyndman, R.J. Probabilistic energy forecasting: Global energy forecasting competition 2014 and beyond. Int. J. Forecast. 2016, 32, 896–913. [Google Scholar] [CrossRef]
- Liu, H.; Shi, J.; Erdem, E. An integrated wind power forecasting methodology: Interval estimation of wind speed, operation probability of wind turbine, and conditional expected wind power output of a wind farm. Int. J. Green Energy 2012, 151–176. [Google Scholar] [CrossRef]
- Zhang, N.; Kang, C.; Xia, Q.; Liang, J. Modeling conditional forecast error for wind power in generation scheduling. IEEE Trans. Power Syst. 2014, 29, 1316–1324. [Google Scholar] [CrossRef]
- Cui, M.; Krishnan, V.; Hodge, B.M.; Zhang, J. A copula-based conditional probabilistic forecast model for wind power ramps. IEEE Trans. Smart Grid 2018, 1–13. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principle components. J. Educ. Psychol. 1933, 24, 417–441, 498–520. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; ISBN 0-471-24195-4. [Google Scholar]
- Wan, C.; Zhao, X.; Pinson, P.; Zhao, Y.D.; Wong, K.P. Optimal prediction intervals of wind power generation. IEEE Trans. Power Syst. 2014, 29, 1166–1174. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, X.; He, X. New hybrid optimization based on differential evolution and particle swarm optimization. Comput. Eng. Appl. 2012, 48, 46–48. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).