4.1. Overall Results
The model predicts short run decreases in annual electricity sector CO
2e emissions from current levels of 17% from a
$25/ton carbon tax and 22% from a
$50/ton carbon price. The emissions levels for the three modeled scenarios are displayed in
Table 3. There were 5.7 billion total tons of U.S. CO
2e greenhouse gas emissions emitted in 2017 [
55]. The simulated electricity emissions reductions are equivalent to 4.9% and 6.3% reductions in economy-wide greenhouse gas emissions for the
$25 and
$50 case, holding emissions from all other industries constant. The short run electricity emissions reductions from a
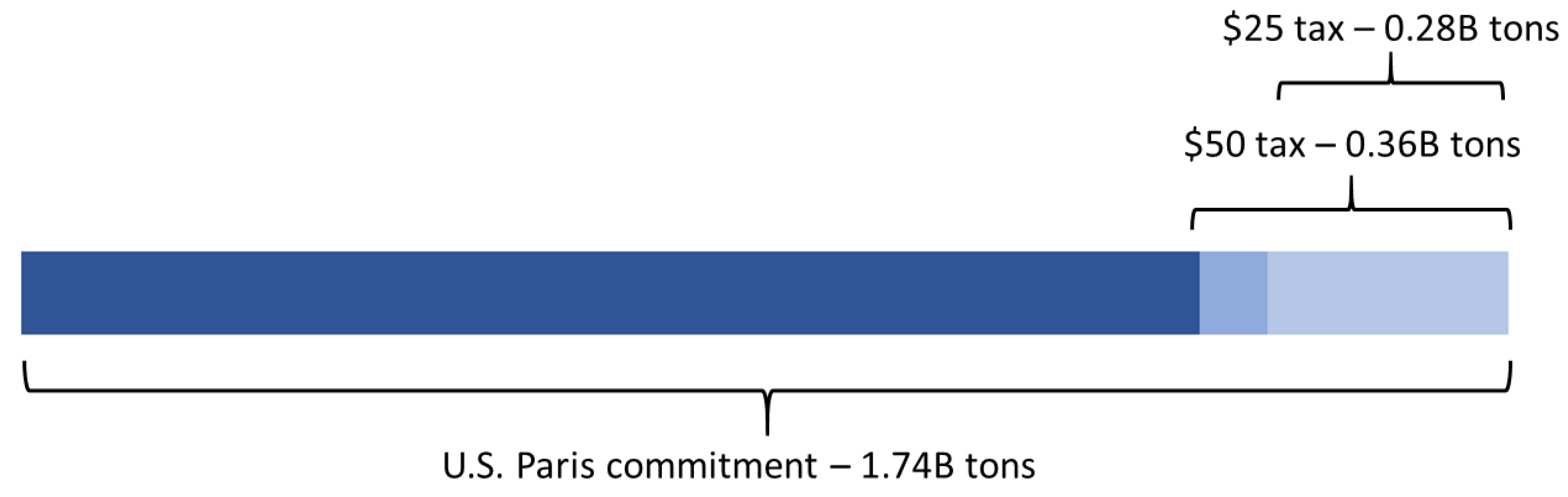
$50/ton tax are equivalent to approximately 21% of the U.S.’s voluntary 2025 greenhouse gas reduction commitment under the Paris Climate Accord [
58]. This calculation is presented visually in
Figure 5. The short run electricity greenhouse gas emissions reductions estimates come from operational changes to the existing capital stock. They do not include additional long run emissions reductions caused by new investments in low-carbon electricity production and retirements of high-carbon electricity production assets caused by the policy.
These results suggest significant short run emissions reductions can be achieved from a U.S. carbon price on the electricity sector. The tax on these emissions generates $33.5 billion in government revenue in the $25 scenario, and $63.0 billion in the $50 scenario.
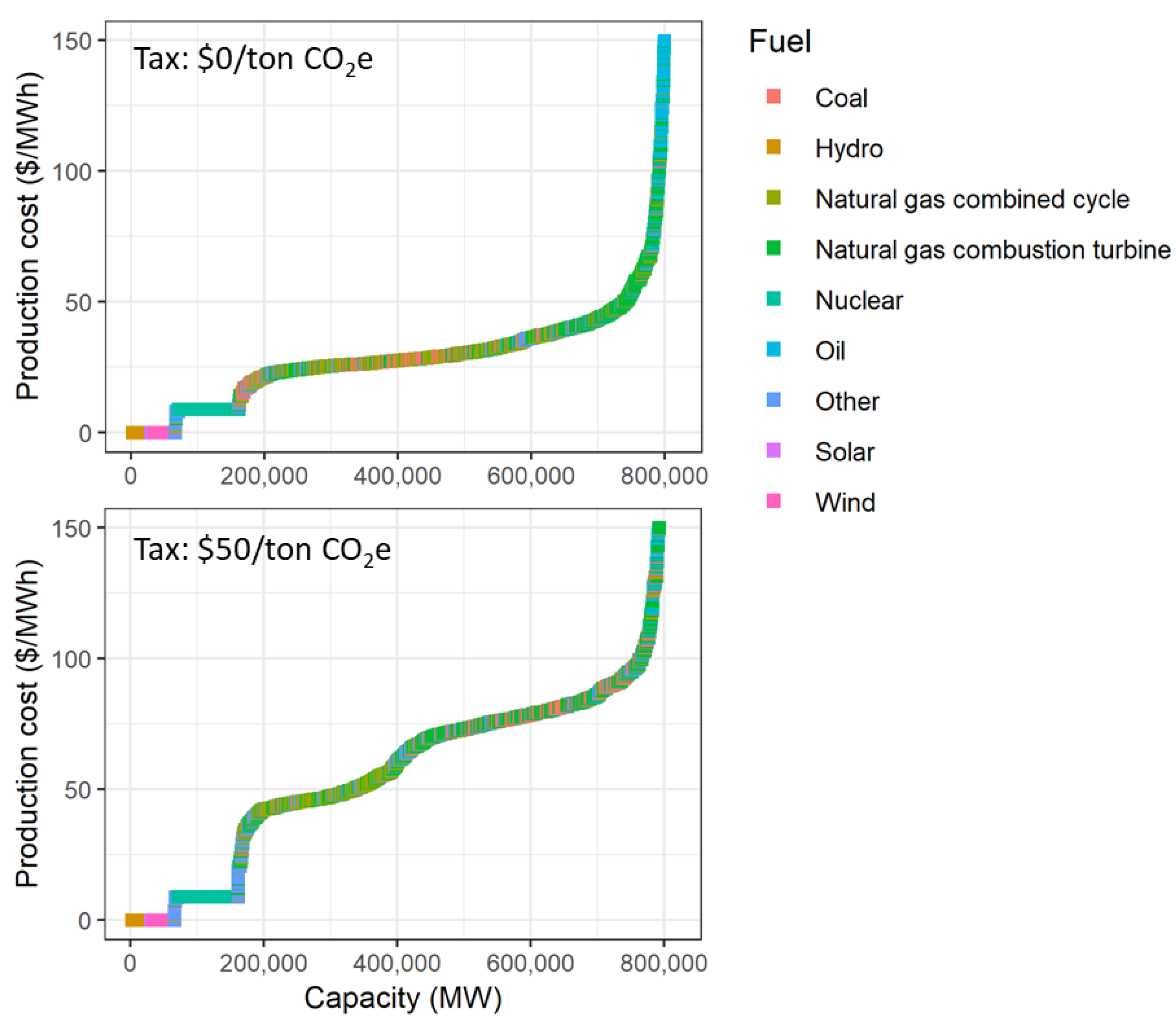
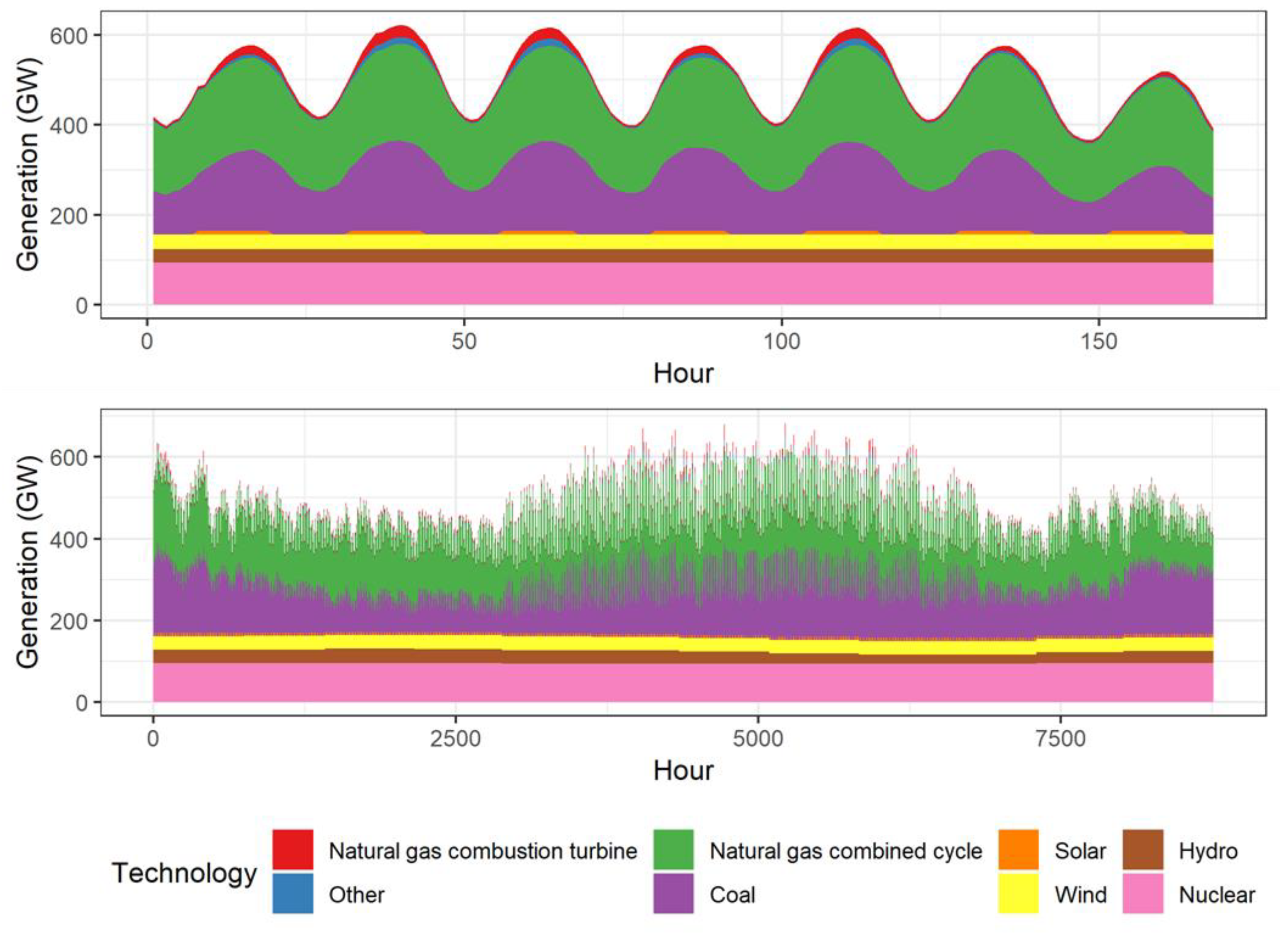
Almost all of the short run emissions reductions come from switching electricity fuel consumption from coal to natural gas. As discussed in
Section 3.4, this is because most marginal electricity production in the U.S. is produced from one of these fuels, and a carbon price will have a relatively large immediate effect on the short run marginal costs of coal and natural gas power plants.
Table 4 displays total generation from coal and natural gas generation in each of the three scenarios. It shows the model estimates a 43% short run reduction in U.S. coal generation from a
$25/ton carbon price, and a 59% reduction from a
$50/ton price. Much of this is offset by increased natural gas generation of 30% and 40% in the two scenarios, respectively.
The results also suggest a carbon price will have significant short run price effects in wholesale electricity markets. The largest price impacts occur in coal-heavy markets including the Central, Mid-Atlantic, and Midwest regions.
Table 5 presents average prices by scenario broken out by market region. The column ‘
$50/ton—Baseline’ displays the change in price after implementing a
$50/ton price. The final column displays emissions elasticity of price, calculated as the percent change in total regional emissions divided by the percent change in average price. This calculation provides insight into the short run cost-effectiveness of emissions reductions. A lower number indicates a larger emissions decrease relative to its increase in price. The Northwest region has the lowest value, showing that a 1% increase in average price is associated with a 0.35% decrease in regional emissions due to the policy. The positive value for California represents the fact that both price and emissions increased as a result of the carbon policy.
The price impacts are qualified by the fact that these are first order effect estimates derived from short run supply side adjustments to the carbon price. In the electricity industry, most customers are insulated from short run price changes through long term contracts and regulator-approved retail electricity prices. These price increases will eventually be offset by downward pressure from reduced demand and new investments in electricity supply, both of which are second-order effects not considered in the model.
Transmission flows adjust so that regions which experience relatively larger increases in marginal production costs after the carbon price import more energy from less-affected regions.
Table 6 presents average transmission flows across regions in the baseline and
$50/ton scenarios. The most striking impact is in the Northwest region. Electricity trade from the Northwest to California dropped to approximately one-third of the baseline level, offset by a trade reversal from California and the Southwest region. Ample transmission capacity between these three regions, along with relatively more cost-competitive natural gas capacity across the Western U.S. after the carbon price, resulted in the Northwest drastically reducing coal generation in the
$50 scenario to one-fifth of its baseline level. These results are qualified by the fact that there are hydroelectric production constraints across the west that are not modeled but determine in part regional trade. Furthermore, there are market structures and contractual relationships across the west and other regions that are not modeled but tend to reinforce status quo levels of regional trade in the short run [
59].
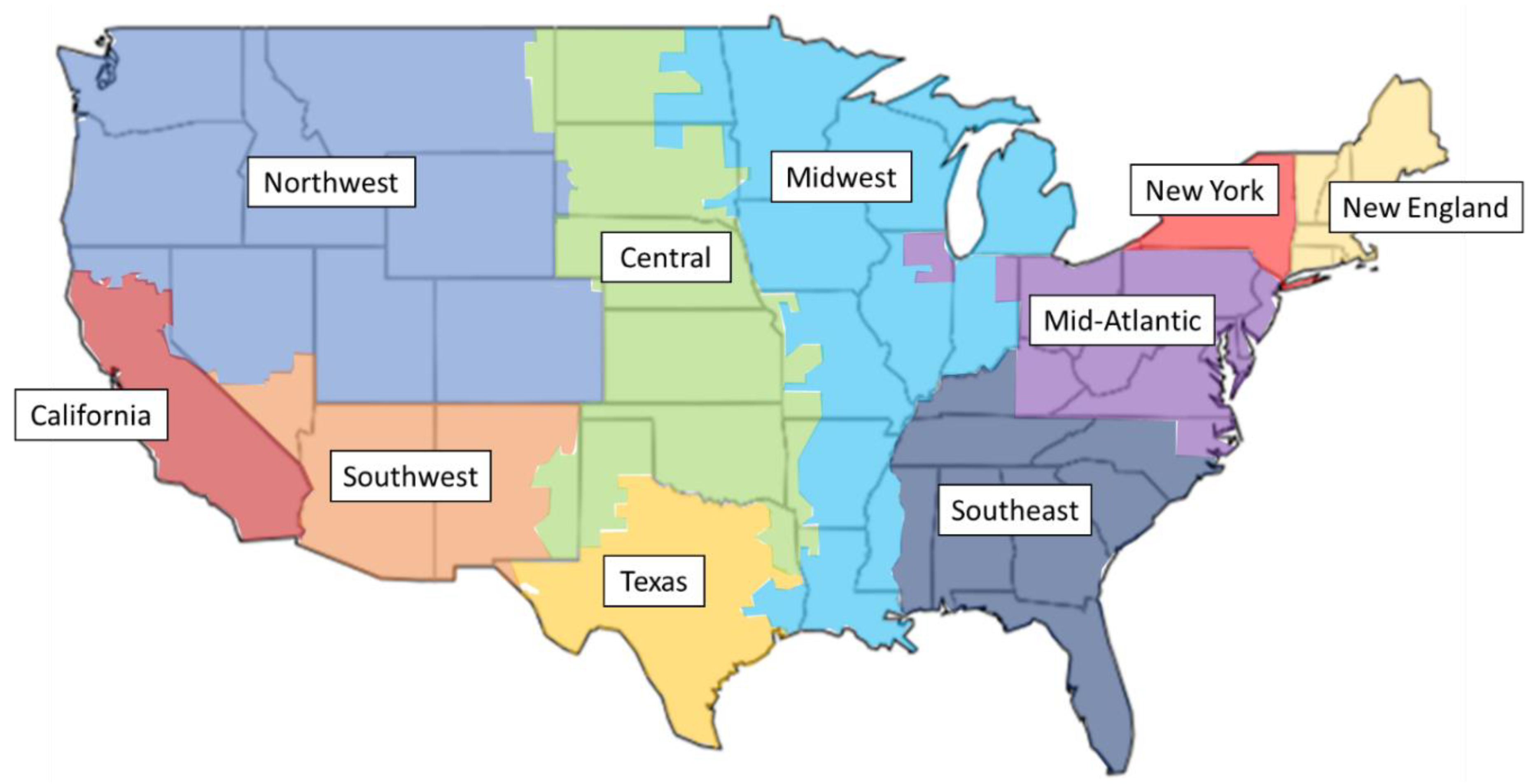
4.2. State-Level Results
Implementing a national carbon price in the U.S. would most likely occur after political negotiation and compromise among state representatives in the U.S. Congress. Understanding state-level impacts is politically important for developing national carbon policy. This section analyzes state impacts on emissions, generation, costs, and tax revenue.
Table 7 at the end of this section displays a comprehensive set of model results for each state. The results in
Table 7 are discussed more fully with multiple references throughout this section.
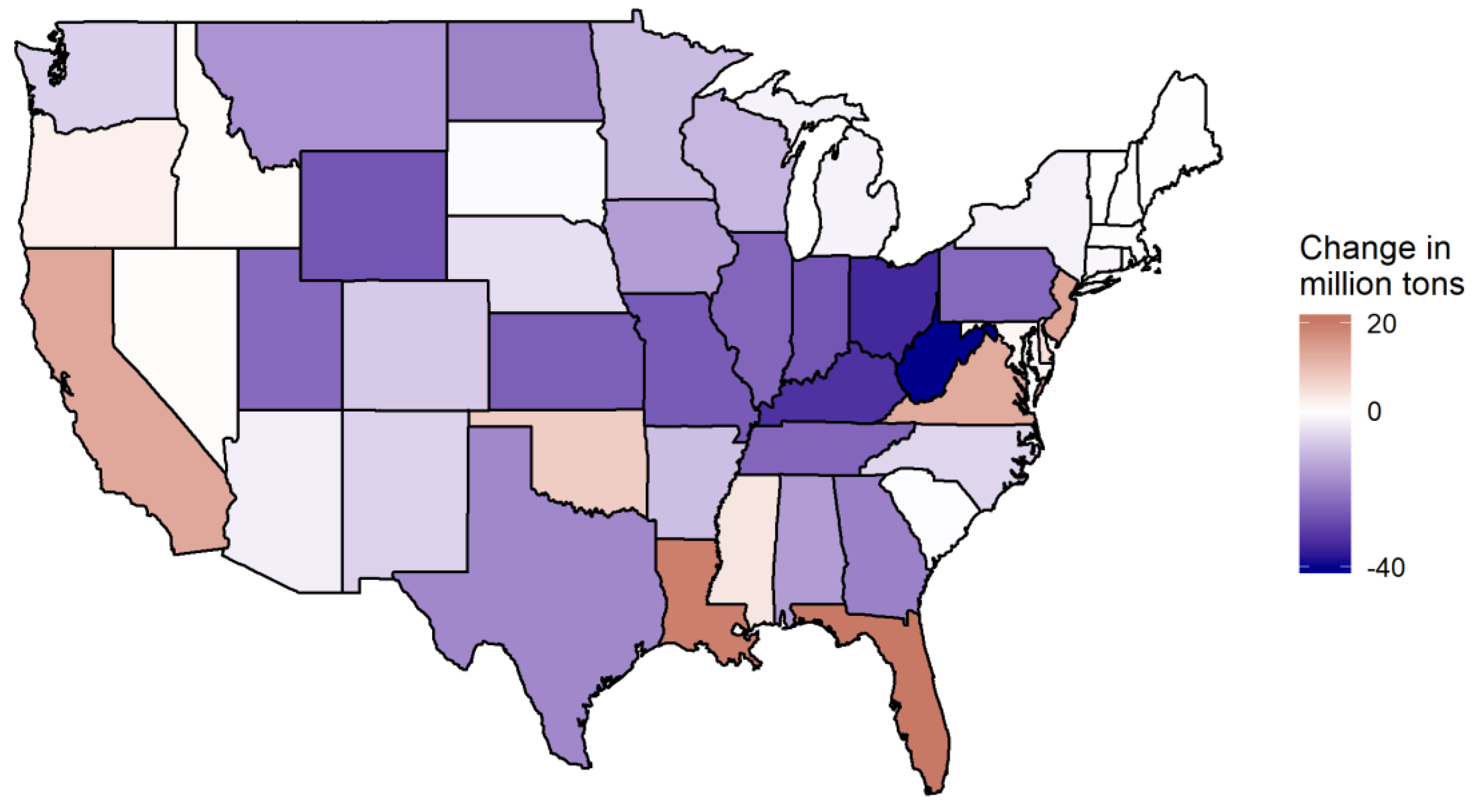
Figure 6 maps changes in CO
2e emissions by state after simulating a
$50/ton price. These correspond to the ‘CO
2e’ columns in
Table 7. Most net emissions reductions at the state level occur in coal-heavy states that are part of large regional markets, including West Virginia, Ohio, and Kentucky. These states reduce coal production and replace it with lower-carbon electricity production from neighboring states. Perhaps surprisingly, the cost-minimizing response to a federal carbon price involves increasing emissions in several states, including California, Florida, and Louisiana. These net emissions increases occur in states that are increasing natural gas production to offset coal reductions in neighboring states. This can be seen more explicitly in
Figure 7., which maps state-level changes in coal and natural gas generation (the ‘Coal’ and ‘Gas’ columns in
Table 7.). For example, West Virginia has a relatively large coal decrease and small natural gas increase. On the other hand, California increases natural gas generation but does not increase coal because the state has almost zero coal generation before the carbon policy. Political goals of individual states may interfere with the cost-minimizing short run policy response estimated by the model. Many states have individual greenhouse gas emissions reductions programs. For example, California’s greenhouse gas policies could prevent an increase in emissions after a carbon price, which would likely lessen the emissions reductions achieved in neighboring states. States which are predicted to have large emissions reductions, like West Virginia and Ohio, have large coal industries, which may be politically organized such that they can mitigate their industry’s decline and achieve lower emissions reductions. A detailed analysis of the political economy for each state would be important to further understanding the prospects of carbon policy.
Examining changes in electricity production costs by state provides additional insights into the effects of carbon policy. Production costs include the fuel, operations, maintenance, and emissions costs needed to produce electricity. They are equal to the area under the electricity supply curve, including the curves previously displayed in
Figure 2. State production costs decrease when coal generation decreases, and increase when natural gas generation increases. These production costs should not be interpreted as net costs to society from the carbon policy. Rather, they provide insights into the magnitude of shifts in generation between fuel types and across states. As described in more detail in
Section 3, the model assumes suppliers minimize costs and sell in a competitive market. As a result, suppliers would not incur production costs if there was not adequate revenue available in the market to cover their costs.
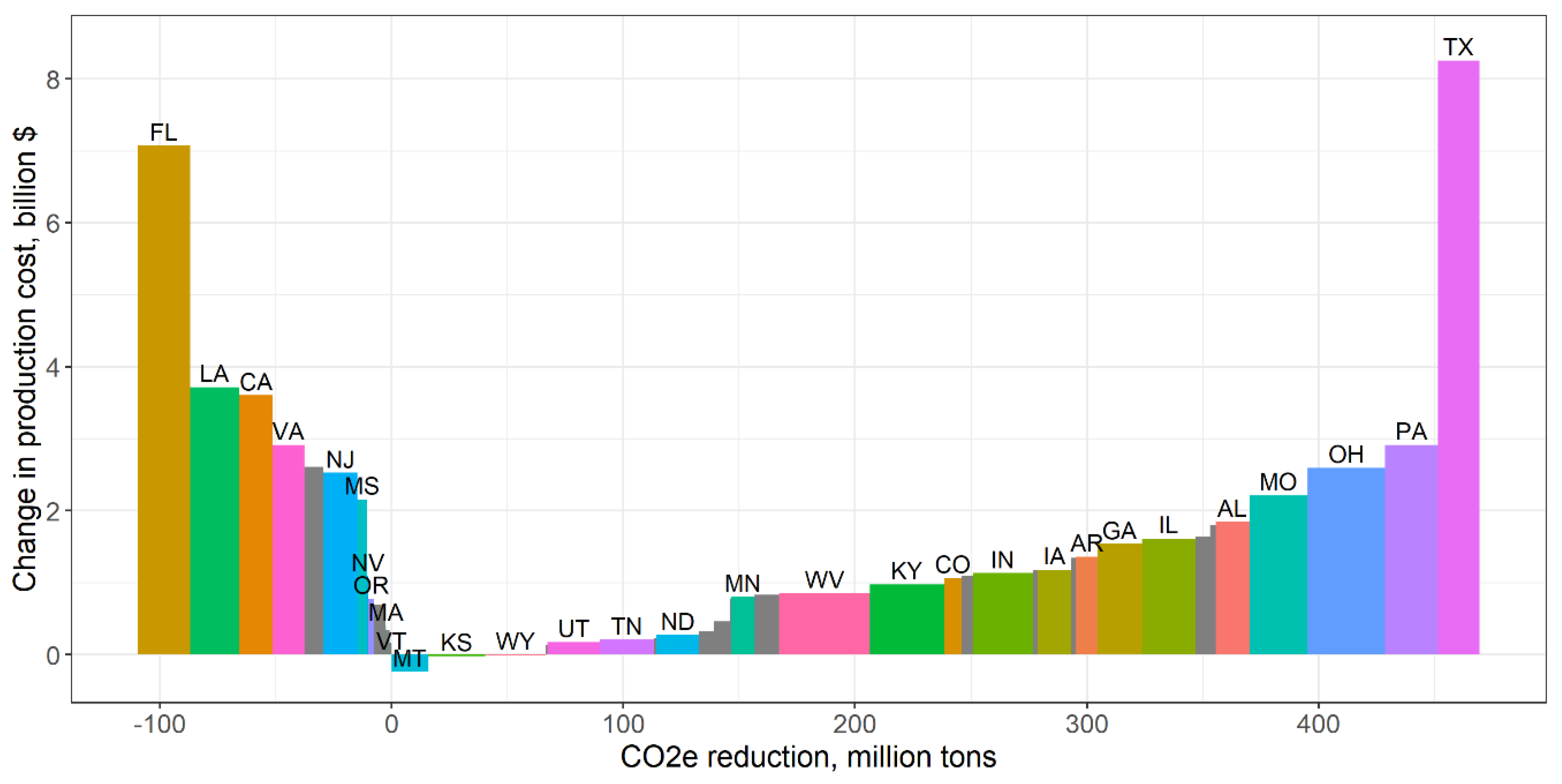
Figure 8 plots the change in production costs by state on the vertical axis as a result of a
$50/ton price. The horizontal axis displays the state’s reduction in CO
2e emissions from a
$50/ton price. The width of each bar is proportional to the magnitude of emissions reduction. States that increase emissions are located to the left of zero on the horizontal axis, while states to the right of zero reduced emissions. State-level production cost changes correspond to the “Cost” columns in
Table 7.
Figure 8 shows a few interesting results. All states to the left of the origin increased emissions after a carbon tax, because they increased natural gas generation after a carbon price to serve demand in neighboring states. Montana experienced a net decrease in electricity production costs after a
$50/ton carbon tax, even though all emitting electricity production became more expensive. This occurred because Montana coal producers decreased production while out-of-state electricity producers increased generation to make up the deficit. Both Florida and Texas had large increases in natural gas generation combined with large in-state electricity consumption, leading to their relatively large production costs increases.
All states that have emitting electricity production generate federal government revenue from the carbon tax. Tax revenue collected by state is displayed in the ‘Tax’ columns in
Table 7. The highest revenue-generating states in the
$50/ton scenario are Texas, Florida, and California at
$7.0,
$4.6, and
$3.3 billion per year, respectively. The revenue raised by a carbon tax could be rebated as an equal lump sum to all U.S. citizens. This policy proposal is motivated by income inequality concerns and the desire to make a carbon tax revenue neutral. The
$63 billion raised from the electricity industry in the
$50/ton scenario would result in approximately
$194 per person per year in rebates.
A flat rebate is contrasted with the fact that per capita tax revenue varies across states. This results in wealth transfers between states. States with high populations and/or low-emitting electricity are likely to pay less in carbon taxes than the per capita rebate their citizens receive. In the
$50/ton scenario, all U.S. citizens receive a
$194 rebate per year. However, residents of California and New York pay only
$82 and
$62 carbon tax per person, respectively, while residents of West Virginia pay
$1077 per person. State population data for 2018 from the U.S. Census Bureau were used in these calculations [
60].
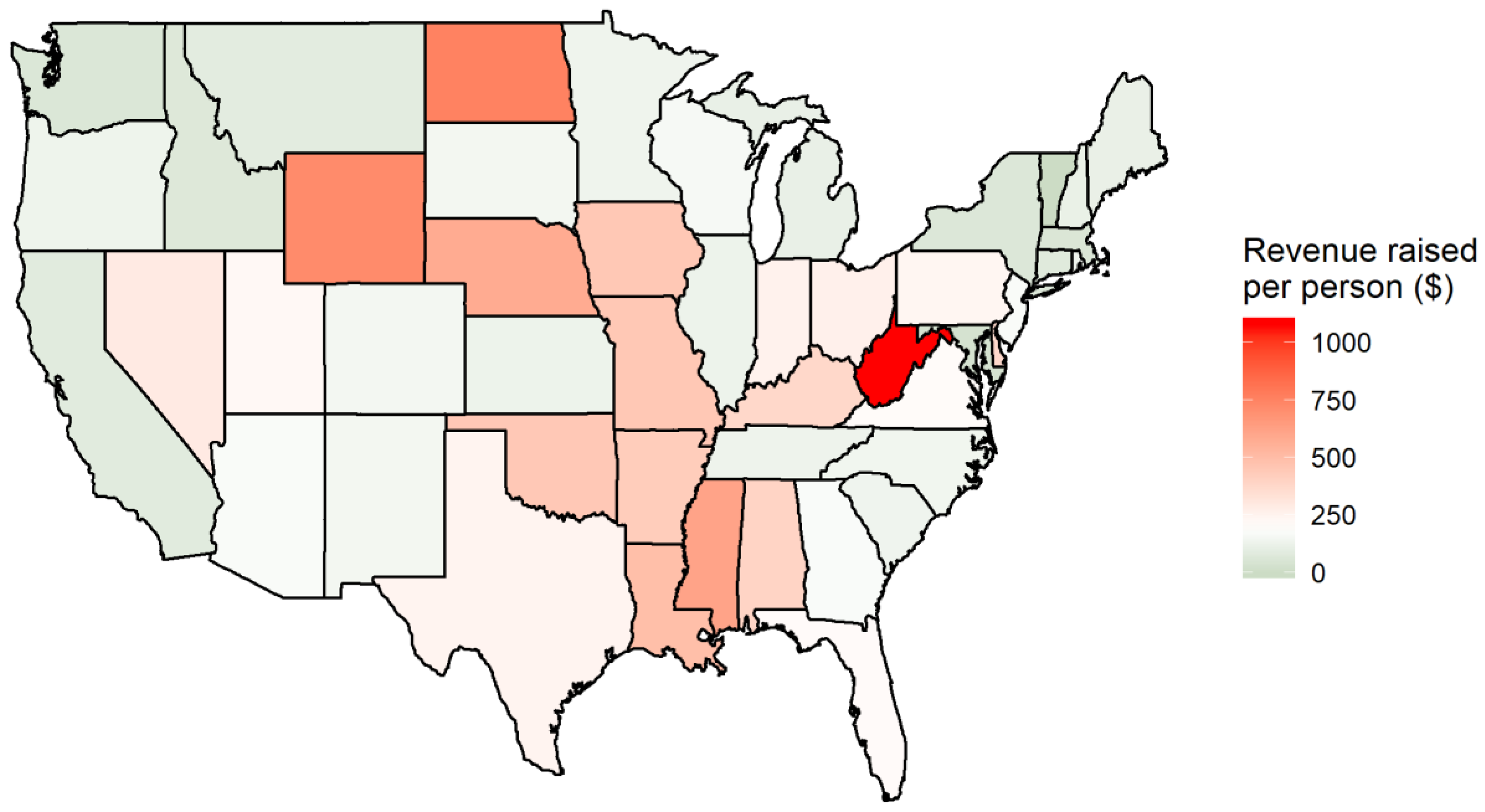
Figure 9 displays taxes per person for the
$50/ton scenario by state, and is color-coded to highlight the wealth transfer across states. On the color scale, the flat rebate of
$194 is set to white. States that pay less than
$194 in per capita carbon tax are on the green portion of the spectrum, while states that pay more than
$194 per capita are on the red portion. In general,
Figure 9 shows that a flat per capita rebate of electricity carbon tax revenue redistributes wealth from states in the middle of the country to states near the east or west coasts, with several exceptions.
One could assume that members of Congress will vote for a carbon tax and rebate policy if their state’s constituents receive a short term net benefit from the rebate. These are the states tinted green in
Figure 9. In this case the policy would receive 54 votes in the Senate (a 56% majority) and 254 votes in the House of Representatives (a 59% majority), not including the legislators from Hawaii and Alaska, and be implemented into law.
The tax revenue results suggest a negative relationship between a state’s wealth and their per capita carbon tax revenue. The correlation coefficient between a state’s 2018 gross state product and the per capita revenue in the $50/ton scenario is −0.27. While correlation does not imply causation, it can be speculated from this empirical observation that states with wealthier citizens are more likely to demand cleaner energy production, or import dirty energy from neighbors, to avoid experiencing the harmful effects of air pollution. As a result, the wealthier states would have a lower carbon tax burden, and receive a relatively higher benefit from a per capita revenue rebate.