1. Introduction
The deregulation process in the energy sector has encouraged a transformation of the Electric Power Systems (EPS). EPS are defined as networks of electrical components deployed to supply, transfer, store and use electric power. Nevertheless, in the last decades, EPS are changing their classical scheme, which has been traditionally characterized by a centralized top-down operated architecture, to a distributed model. This new scheme is strongly characterized by an increasing integration of Renewable Energy Sources (RES) [
1,
2]. In this scenario of transformation, microgrids, which are defined as coordinated aggregations of loads and generation resources in medium and low voltage grids [
3], play a fundamental role [
4,
5]. This is mainly due to their capability of integrating and exploiting RES, together with additional benefits, such as enhancing the entrance of electric vehicles [
6]. Microgrids are generally composed by a certain set of loads, conventional and renewable generation units, and storage units, being these last components operated as independent and controllable units [
7,
8], either connected or disconnected from the grid [
9].
The operation of a microgrid is performed by using Energy Management Systems (EMS) [
10], which are responsible for commanding the local generation, storage and flexible demand resources. EMS dispatches the active energy from RES and control the load consumption in the most optimal way. This management is normally carried out on the basis of an established criterion [
11]. In this context, the problem of Unit Commitment (UC) represents an important tool to study the optimal scheduling of generation resources [
12], contributing not only to improve the stability and reliability of the microgrid, but also reducing the environmental impact and the costs associated to the operation [
13]. The UC consists of finding the most suitable schedule for coordinating the different generation and storage units to achieve a target objective, such as minimizing the cost or maximizing the benefits.
Once the UC is solved, the Economic Dispatch (ED) is responsible for assigning the generation reference to the programmed units, satisfying the power demand together with the physical constraints of the grid [
14]. Sometimes, this problem is tackled considering the possible uncertainty in the power generated of the RES or the demand. Thus, this combined problem aims to deal with the variability of both the RES and the demand [
1,
7].
In general, the uncertainty in the UC problem is represented by the formulation of a set of scenarios, which are made on the basis of the predictions of the demand and the RES generation. In contrast, deterministic approaches are commonly used, where a single scenario is considered [
15,
16]. Given these features, stochastic approaches are crucial to address an optimal management of microgrids [
17], which has motivated several studies in the literature [
18,
19,
20]. These approaches contribute to the robustness of the solution, making them more appropriate to microgrid implementations.
Finally, it is worth pointing out the complexity of the combined UC and ED problem [
21]. The schedule of the dispatchable generation units together with the management of the ESS, with the additional consideration of uncertainties in the demand forecasting generates a non-convex mathematical problem, which combines strong non-linearities and mixed integer formulation. Although some authors have proposed to linearize the objective functions, it introduces inaccuracies into the resulting operation cost. In addition, such linearization should be done at each operation point, which can result in a slow iterative procedure. Therefore, such approach can suffer from convergence and scalability problems for high dimensional scenarios. Similar to linear programming based approaches, metaheuristic algorithms such as evolutionary algorithms allow dealing with non-linearities in an effective way since the search engine is based on genetic operations (selection, crossover, and mutation) among potential solutions. Given these characteristics of the combined UC and ED problem, solving it in the most optimal way constitutes itself a challenge. Furthermore, it is important to note that small deviations in the solution might imply noticeable effects in the operational and maintenance costs of the microgrid, also affecting the level of emissions. For these reasons, the use of meta-heuristic approaches is of particular relevance.
The main contributions of this work are summarized:
A new methodology is introduced to deal with the generation schedule problem of a microgrid where the demand forecasting is affected by uncertainties. This approach ensures the robustness of the algorithm at the expense of affecting the operational and environmental cost of the installation.
The microgrid model includes several operation modes optimizing different aspects of the microgrid such as power cost, emissions, and robust operation with respect to the demand variability. Combined operation modes, where a combination of objective functions are used, are considered.
An evolutionary approach for solving the UC and ED problems in microgrids is presented.
The paper is organized as follows.
Section 2 presents the related work of current approaches that have addressed EMS in microgrids.
Section 3 introduces the stochastic UC and ED problems in a microgrid. In
Section 4, the different components of the microgrid are modeled in detail.
Section 5 presents the operation modes of the considered microgrid. In
Section 6, an evolutionary computational approach is proposed to address the problem.
Section 7 contains the evaluation of the proposed approach through extensive simulations. Finally, in
Section 8 some conclusions and remarks are drawn together with future work lines.
2. Related Work
An extensive review of the objectives, constraints and algorithms used in EMS for microgrids is addressed in [
18], where the authors provided a brief summary of the main strategies used to tackle this problem: linear, non-linear, stochastic, dynamic and non-differential programming. In addition, a classification of the different optimization techniques reported in the literature is presented.
The UC problem is generally classified as Mixed Integer Non-Linear Programming (MINLP) [
19,
22,
23]. An illustrative work is [
22], where the authors proposed a profit-based UC problem with non-linear emissions penalty. This penalty has been transformed through a mixed-integer formulation, while the non-linearities of the fuel cost function are addressed by means of a piece-wise linearization. The proposed algorithm is used to solve several architectures, exhibiting good results. A very similar strategy is used in [
23], where numerical results confirm the robustness of the approach. The authors of [
24] proposed a MILP to determine a fair cost distribution among smart homes with microgrid, obtaining noticeable cost reductions and fair cost distribution among multiple homes under a set of test scenarios.
Despite of the high efficiency of MILP approaches, it is worth pointing out that the computational cost of these approaches increases drastically with the number of integer variables. To address this drawback, several proposals are discussed. In [
25], a multi-step method is used to consider the combinatorial calculations of unit outage events. This method noticeably improves the calculations of the spinning reserve, while reducing the computational burden. The authors of [
26] proposed the resolution of different scales separately, by means of a bottom-up approach, keeping track of the error. This strategy strongly reduces the computational time required to find an optimal solution without sacrificing the quality of the results. Therefore, it improves the capability of MILP approaches to address large-scale modelling of urban energy systems. In addition, in [
27], the authors proposed an improved MILP to increase the efficiency of the approach for its application to big scale grids, where the results in different scales show a dramatic improvement in comparison with other MILP proposed in the literature. It is also relevant to highlight the capability of these approaches to address the energy optimization in city environments [
28]. A relevant work is found in [
29], where the scheduling problem of building energy supply is addressed to minimize the overall cost of the energy consumption. Mixed-Integer Quadratic Problem (MIQP) is also used to address the UC problem. An illustrative work can be found in [
30], where the authors proposed an improved MIQP, which improves its efficiency by means of relaxation and decoupling techniques.
In addition to both MILP and MIQP approaches, a wide variety of optimization algorithms are proposed in the literature [
31,
32] to address this problem (see
Table 1, where the most relevant works are summarized). The studied works present a wide variety of architectures, generally including controllable RES and operating either isolated or connected to the grid.
An illustrative example can be found in [
13], where two optimization algorithms are developed, based on a Genetic Algorithm (GA) and MILP, respectively. Both algorithms are used in a radial low-voltage European microgrid for which the authors formulated a set of objective functions and constraints, attending to the different modes of operation of the microgrid, such as cost-efficiency, grid supporting, reliable isolated operation, eco-friendliness and multi-functional operations. The results demonstrate a better performance of the GA in comparison to MILP. Similarly, in [
31], a more complex problem is formulated by considering start-up and shut-down costs associated to the distributed generators (DGs). This approach is used in a microgrid, being the problem addressed by means of a hybrid optimal algorithm, which consists in decomposing the problem into Integer Programming (IP) to solve the UC problem and Non-Linear Programming (NLP) to solve the ED problem. After that, both GA and interior-point algorithms are used to solve the IP and NLP problems, respectively. An Enhanced Genetic Algorithm (EGA) is proposed in [
33] to address both the UC and ED problems simultaneously. The performance and effectiveness of the developed GA is verified in a set of case-study optimization scenarios, which are applied to a typical test microgrid. The simulation results demonstrate a good performance (in terms of computational time and robustness) of the optimizer under grid-connected operation mode, in contrast with the isolated mode, where the computational resources required increase.
In [
34], the minimization of the energy cost is assumed as the objective function for the optimization problem. The problem is addressed by applying an evolutionary approach based on Memory-Based Genetic Algorithm (MGA). The results are compared with two variants of Particle Swarm Optimization (PSO) algorithms, exhibiting a noticeably superior behavior. Similarly, the authors of [
35] addressed the same problem by improving a GA with the integration of a Simulated Annealing (SA) algorithm to accelerate the convergence, demonstrating a clear advantage in convergence time.
In [
36], the optimal size of the storage systems and the RE micro-sources is studied by means of a fuzzy multi-objective optimization model. The approach is based on a chaos optimization algorithm, which is introduced into a Binary particles Swarm Optimization (BPSO) algorithm, to propose a Chaotic BPSO (CBPSO). Furthermore, some authors proposed the use of Monte Carlo simulations as a tool to generate scenarios. In [
37], the non-parametric neural network based prediction intervals (PIs) are implemented for forecast uncertainty quantification of wind power. A GA is then used to solve the Stochastic Unit Commitment (SUC) problem, being the Monte Carlo simulations used to create the scenarios. The simulation results demonstrate a better performance of the CBPSO in comparison with the original BPSO. Similarly, in [
32], the uncertainty of demand and wind sources is considered, being modeled by means of absolute percentage error. Demand and wind power scenarios are generated using Monte Carlo simulations. To optimize the UC problem, the priority list method (PL algorithm) [
38] is applied.
As steps forward with respect to the previous works, this paper proposes:
Two main modes of operation are considered: cost effective operation mode, in which the main aim is to minimize the operation and maintenance cost of the overall system; and eco-mode operation mode, in which the objective is to reduce the polluted emissions of the dispatchable units.
The general model improves the scheduling problem of microgrids by considering different levels of reliability according to the uncertainty of the forecast demand. Thus, the spinning reserve of dispatchable generation units guarantees that the variability of the demand is covered.
3. Problem Description
New types of generation technologies have emerged and have been gradually integrated into the existing power systems in the last decades [
39], moving their classical architecture to distributed schemes. These technologies have associated lower emissions and lower operation costs than conventional generators. Examples of this type of technologies are micro-turbines, photo-voltaics and fuel cells, among others. Despite the positive features aforementioned, the application of these distributed architectures have many associated problems that must be deeply studied [
40]. This challenge can be partially addressed by microgrids, which are entities that coordinate the Distributed Energy Resources (DER) in a consistently more decentralized way, thereby reducing the control burden on the grid and permitting them to provide their full benefits [
41].
Under this new paradigm, a microgrid contains multiple generators that have a wide range of operation modes. Thus, several strategies can be applied to meet the required power demand, which varies from hour to hour over the day [
12]. This problem is formally defined as the Unit Commitment (UC) and Economic Dispatch (ED) problems. The general objective of both is to minimize the total operating cost, while satisfying all of the constraints so that a given security level can be met [
14,
42,
43]. The UC problem studies which generators must be in operation at certain time instant, while the ED studies, once the generators connected to the grid are known, the power that must be supplied by each of them.
These approaches attend to cover not only to economical factors, but it also considers environmental and technical limitations.
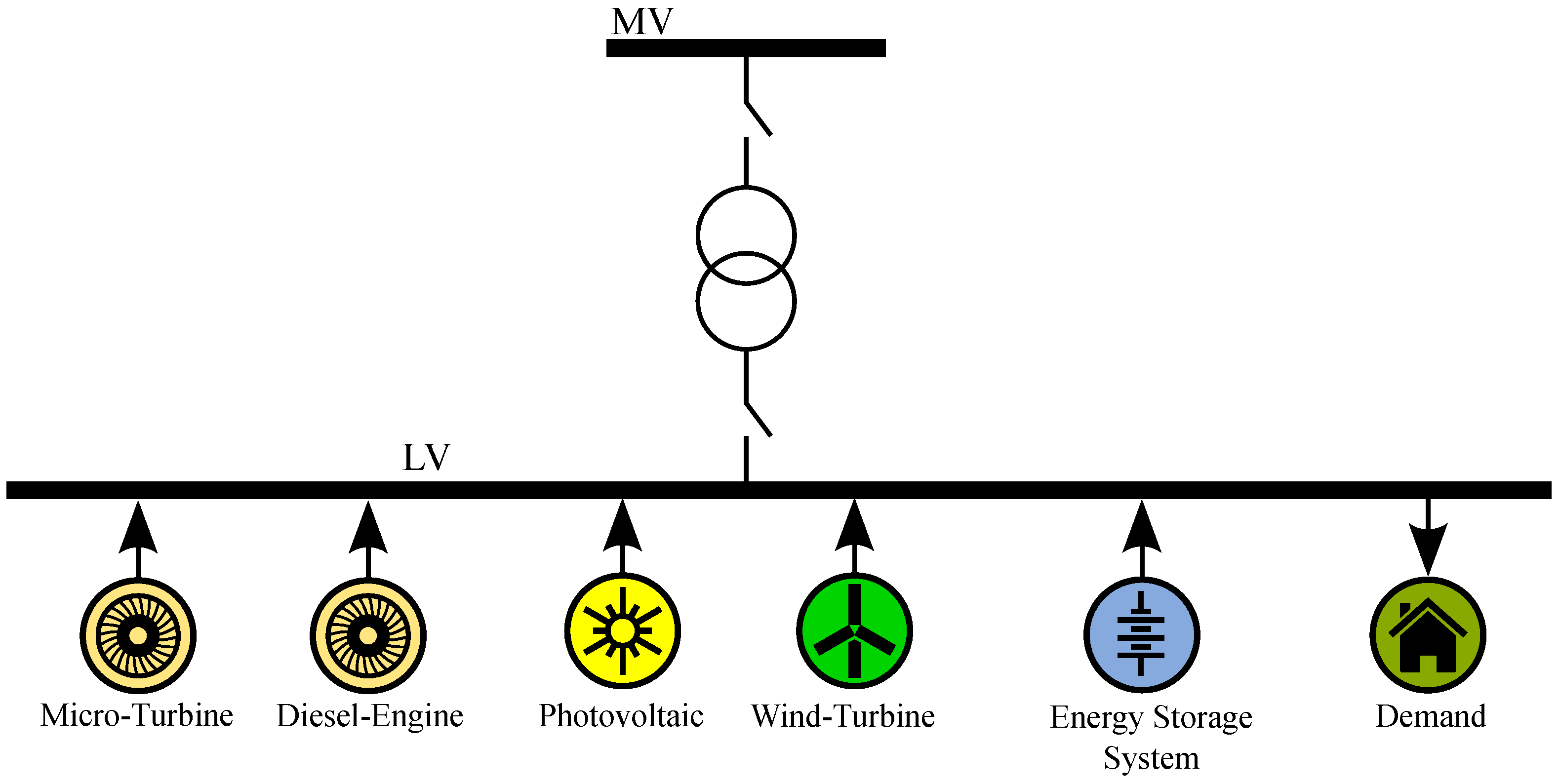
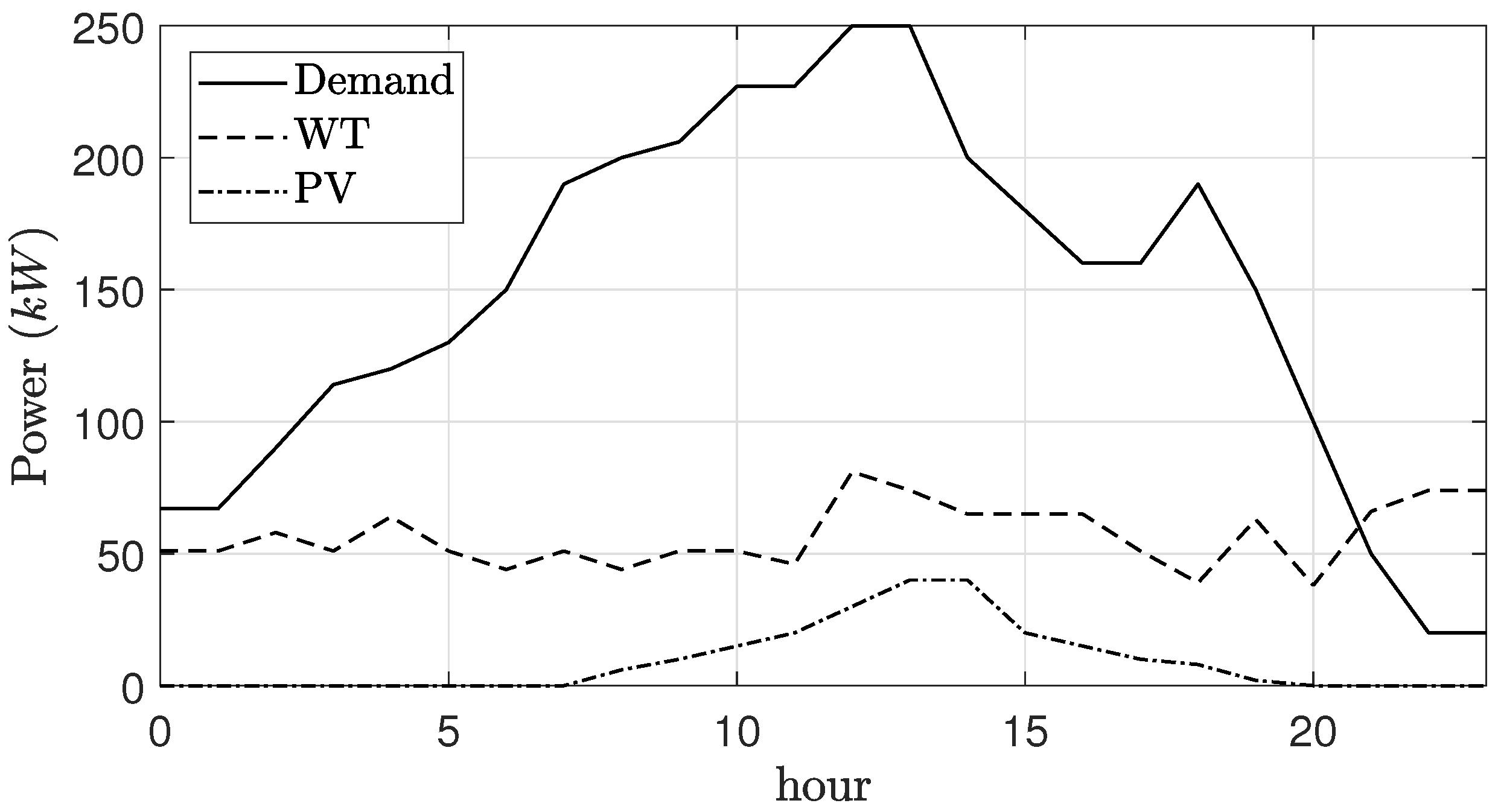
In particular in this paper, we consider the study of the microgrid depicted in
Figure 1. This grid contains four generators, being two of them dispatchable generating units. Recall that a dispatchable generating unit refers to sources of electricity that can be used on demand at the request of operators, that is, can be turned on and off, or can adjust their power output according to the needs. Thus, the microgrid under study is composed by a diesel engine (DE) and a microturbine (MT) as dispatchable units, and a wind turbine (WT) and a photo-voltaic plant (PV) as non-controllable RES. Finally, an Energy Storage System (ESS) is also considered. The model of these components, together with the customer demands, is studied in the subsequent sections. Thus, the problem studied is to determine the power supplied by the different generators as well as the power supplied or demanded by the ESS at every time instant, minimizing certain cost function. This cost function attends to economical, technical, and environmental factors. It is relevant to note that this is a generic microgrid, being the proposed method equally valid to any other microgrid scheme.
4. System Modeling
The upcoming sections deal with the model taken into consideration for the generation schedule problem. All models presented in this section have been used widely, however, in practice, their accuracy can vary substantially. Nevertheless, since the paper presents a robust solution to the UC and ED problems, when uncertainties in the demand forecasting are considered, greater uncertainties can be established in order to take into account other model inaccuracies.
4.1. Demand Forecasting
One important issue that has a significant impact on the solution of the problem is the accuracy of the considered data. The energy demanded in the microgrid implies the effective utilization of the energy resources to ensure reliability level in the energy supply. Nevertheless, the demand in a microgrid is usually estimated based on the habits of the customers and data records. This demand forecasting can fall into inaccuracy when no information about the grid is known or new entities connect to the network.
In this paper, we consider an estimated curve of demand that is affected by a final error. This error is considered to follow a normal distribution at every time instant t, , whose average, , is considered zero and the standard deviation, , varies according to the level of reliability required to the problem resolution. In that way, if we consider a high value of , the uncertainty in the demand forecasting will be greater and a more robust solution must be contributed to guarantee the electrical supply under normal operation.
Let
and
be the estimation and the real power demanded from the microgrid at time
t, respectively, and let
be the estimation error of the demand forecasting at time
t. Thus, it is clear that
with
.
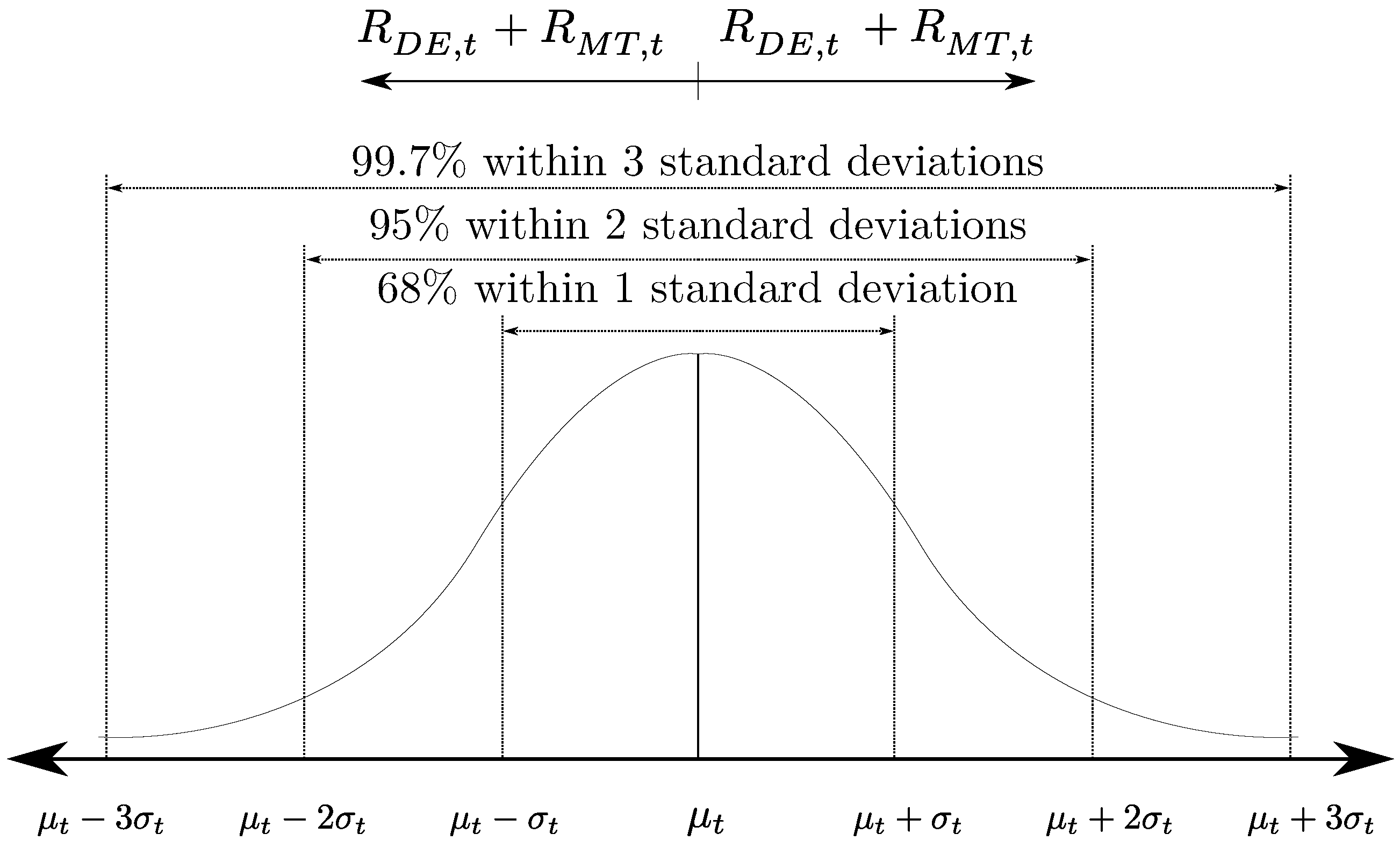
It is worth pointing out that, for the normal distribution
, the values less than one standard deviation,
, away from the mean,
, account for 68.27% of the set, while two and three standard deviation away from the mean account for 95.45% and 99.73% of the set, respectively [
44]. Thus, if the solution of the problem guarantees the supply of a power demanded
, then a reliable solution is achieved with a high confidence interval. To obtain a good estimation of the demand forecasting uncertainties, an ARMA (Auto Regressive Moving Average) model was trained with two years of estimation data.
4.2. Photo-Voltaic Generator
A PV generator consists of a set of PV panels connected among them that provide power to one or more solar inverters. These inverters transform the DC power received into AC power that is finally consumed in the grid. The power produced by a PV plant depends on many factors, such as the solar irradiation, the ambient and solar cell temperatures, and the modules degradation. Furthermore, the power generated by these kind of systems is directly related with the operational point of the solar modules. This operational point is fixed by the power inverter by using a Maximum Power Point Tracking (MPPT). In that way, the system will always operate supplying the maximum amount of power available in the resources.
In this paper, we consider the simplified model presented in [
45] that is shown next:
where
is the output power of the PV plant at time
t,
is the solar irradiance at
t and
,
and
are the the maximum power, the irradiance and the temperature under Standard Test Conditions (STC), respectively. Those values correspond to a cell temperature of 25
C and an irradiance of 1000 W/m
with an air mass 1.5. Finally,
n denotes the number of PV panels,
k is the power temperature coefficient (
C) and
is the temperature of the module at time
t, which can be calculated as
, where
is the ambient temperature (
C) and
is a constant module provided by the manufacturer.
4.3. Wind Turbine
There exist many publications dealing with the modeling and simulation of wind turbines [
46,
47]. Most of these models have a great level of detail and are used below to perform stability analysis (see, for instance, [
48]). For our study, we consider the sequel simplified model of the generator:
where
and
represent the rated power (
) and wind speed (
), respectively, and
,
and
v are the cut-in, cut-out and actual wind speed, respectively. For a more detailed information about the model, reader is referred to [
49].
4.4. Diesel Engine
Nowadays, diesel engines are the most common type of microgrid generator technology in use. The operation cost of a power system can be expressed as a function of its real power output and it is usually modeled as a quadratic polynomial with the shape:
where
is the total fuel cost (€/h) at time
t,
is the power output at time
t and
(
e/h),
(
e/kW h) and
(
e/kW
h) are parameters specified by the manufacturer [
50], and are strongly conditioned by the type of engine, generator and fuel. Additionally, let
and
be the minimum and maximum power that the DE can supply at every time instant. Then,
4.5. Microturbine
The MT model is similar to the DE model. Nevertheless, in this case, the operation cost curve parameters are adopted to model the performance and efficiency of a MT unit [
51]. Thus, the operation cost can be expressed as:
where
is the total gas cost (€/h) at time
t,
is the power output at time
t and
(€/h),
(€/Kw h) and
(€/Kw
h) are parameters specified by the manufacturer [
50,
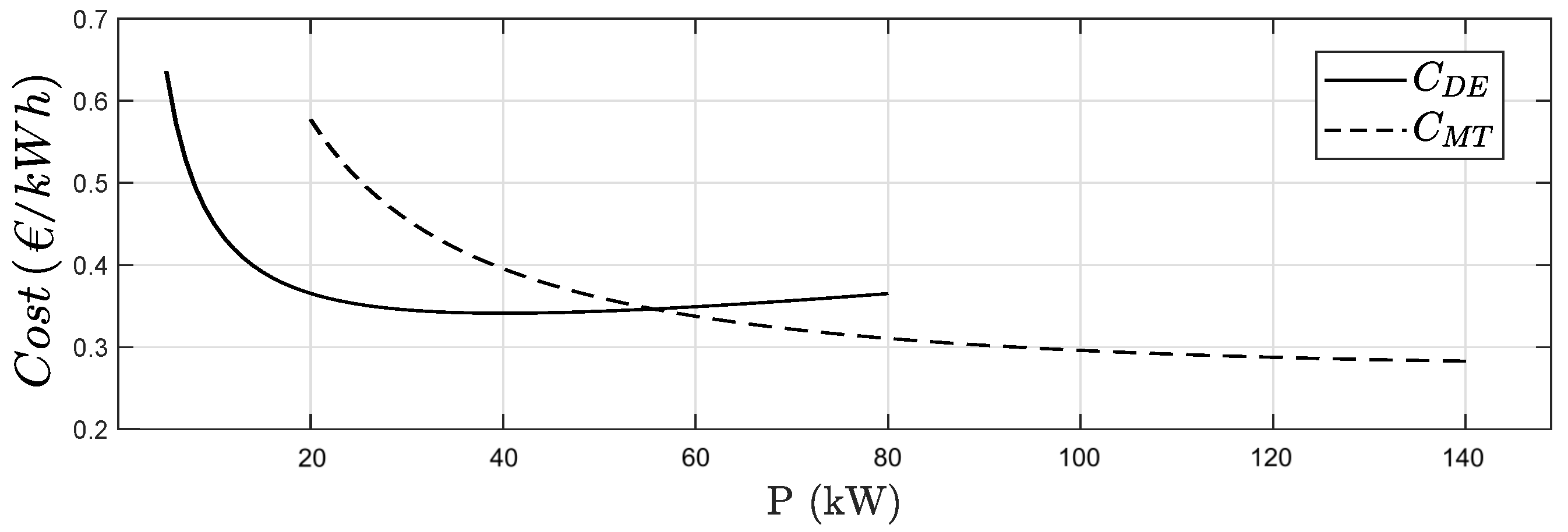
51], and depend on the type of turbine, generator and gas. The operation cost curves of the DE and MT in function of the power given will be presented in subsequent sections. Analogously with the DE, the power generated by the MT is physically limited:
where
and
are the minimum and maximum power that the DE can supply at every time instant.
4.6. Spinning Reserve
The term spinning reserve is widely used in the literature [
52,
53]. Nevertheless, this service can be defined in different ways leading to confusion. We define this concept as it is done in [
54]: the spinning reserve is the unused capacity that can be activated on decision of the system operator and is provided by devices, which are synchronized to the network and able to change the active power.
Note that this capacity is only found in the dispatchable units, as they are the only units that can be used on demand. Thus, we denote
and
the spinning reserve of the DE and the MT at time instant
t, respectively. These parameters are mathematically defined next:
4.7. Energy Storage System
Batteries are electrochemical devices that store energy from other AC or DC sources for later use [
51]. The battery allows the microgrid to cover demand peaks and to store excesses of generation due to its quick response. We consider a set of batteries that conforms an ESS. An ESS is particularized by three parameters:
The capacity is the amount of electric charge that the ESS can deliver at the rated voltage.
The maximum charge rate is a measure of the rate at which a battery can be charged.
The maximum discharge rate is a measure of the rate at which a battery can be discharged.
Let
be the power demanded or supplied by the ESS at time
t. Note that the value of
can be both positive or negative. If
, the ESS is supplying power to the microgrid, while, when
, the ESS is charging and acting as a consumer. Attending to the charging/discharging rate, both parameters are bounded due to physical limitations:
Let
be the State of Charge of the ESS at every time
t. According to the energy stored in the battery, the
will take different values. Two constraints must be taken into consideration when dealing with the state of charge of the ESS. The
must lay in a band bounded by the capacity of the battery and the minimum admissible state of charge. That is:
where
and
are the lower and upper boundaries for the
. Additionally, it is important to point out that the battery is a dynamical system, that is, the state of charge of the ESS depends on the previous power flows through its terminals. Thus,
where
and
are, respectively, the charging and discharging efficiency and
is the time between samples. Recall that, when
and ESS is discharging, the
decreases. Conversely, when
and ESS is charging, the
increases its value.
4.8. Power Balance
In contrast with other approaches to the same problem, similar to Nemati et al. [
13], we consider an isolated microgrid, i.e., it lacks connection to the distribution network. This fact implies that the power demanded by the customers must be locally supplied by the distributed energy resources presented in the microgrid. Thus, the power balance must be fulfilled at every time interval
t, that is
It is important to point out that, when considering uncertainties in the demand forecasting, the estimation error must be taken into account in the problem in order to guarantee the reliability of the solution provided. This reliability is met with the well-sizing of the spinning reserve. Thus, the following constraint must be added to the problem:
where
is the standard deviation of the estimation error and
is a scalar parameter that, once fixed, establishes the reliability degree of the solution adopted. A deeper study of this issue is presented in
Section 5.3.
4.9. Other Operation Costs
In addition to all the costs aforementioned, the operation of the microgrid introduces extra costs associated to maintenance, start-up and emissions costs.
Maintenance cost: The operating and maintenance cost of each dispatchable generating unit is assumed to be proportional to the power production [
51,
55]:
where
(€/kW h) and
(€/kW h) are the maintenance costs of DE and MT, respectively.
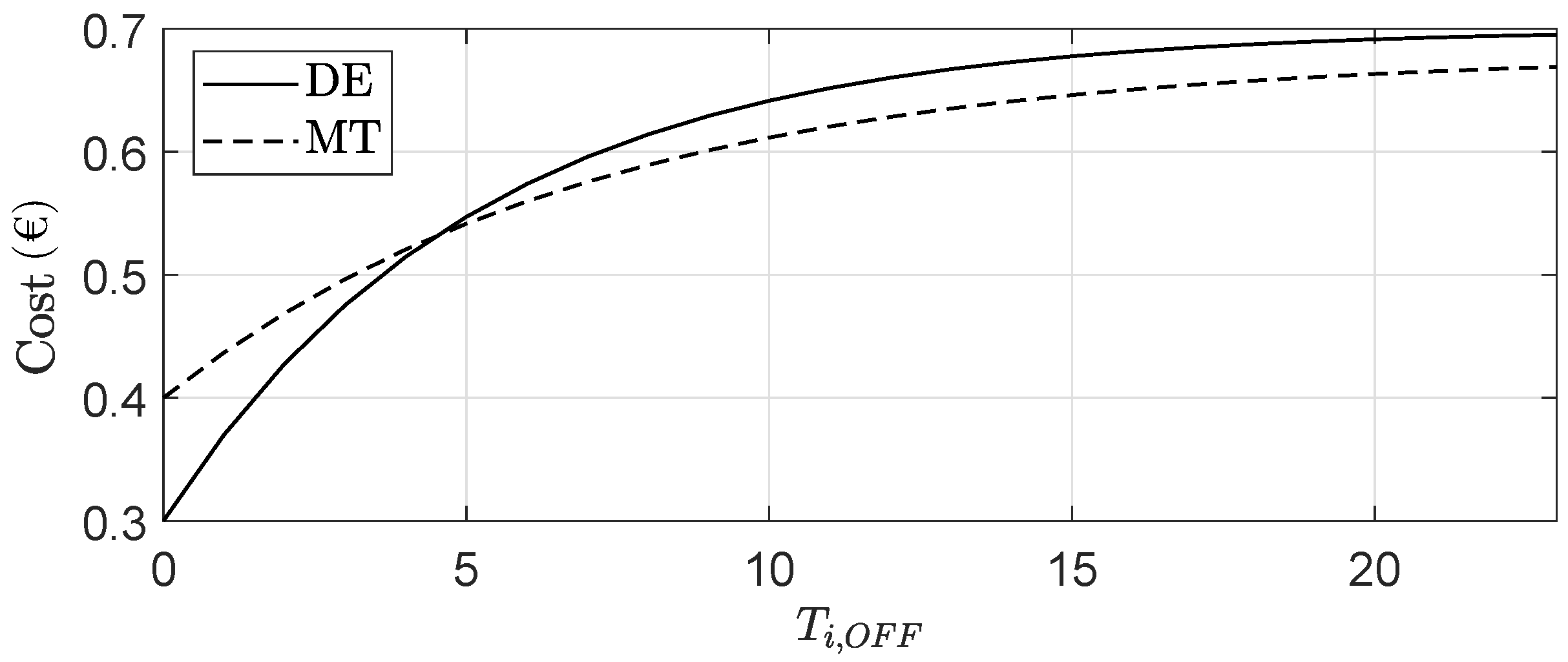
Start-up cost: The generator start-up cost depends on the time at which the unit has been off prior to start up [
56]. Thus, the start-up cost at any given time can be estimated as [
57]:
where
and
(€) are the hot start-up costs,
and
(€) are the cold start-up costs,
and
(€) are the unit cooling time constant and
and
represent the time that each unit has been off (for a more detailed explanation about this expression, the reader is referred to [
57]).
Emission costs: The cost of environmental externalities (production of pollutants CO
, SO
or NO
) is assumed to be a linear function of energy generation [
13]:
where
is the number of emission types,
is externality costs of emission type
k (€/kg), and
and
are the emission factors of the dispatchable generating units and the emission type
k (kg/kW h).
5. Microgrid Operation Modes
As introduced in the previous sections, there exist a high number of limitations and cost parameters to take into consideration when scheduling the power generation in a microgrid. In this section, several operation modes are presented. In each of them, a certain operation criterion is followed to optimize a particular cost function.
5.1. Cost-Effective Operation Mode
This operation mode is focused on the reduction of the overall cost of the microgrid. Thus, the cost function considers the sequel parameters:
cost of operation and maintenance of the dispatchable units (DE and MT);
start-up costs of the dispatchable units (DE and MT); and
fuel and gas costs of the DE and MT, respectively.
The cost function is mathematically defined as follows:
5.2. Eco-Mode Operation
In this operation mode, the main aim is to guarantee the electric supply in the microgrid, ensuring a minimization of the detrimental emissions that are the main cause of climate change. Climate change is expected to have unprecedented implications on where people can settle, grow food, build cities, and rely on functioning ecosystems for the services they provide. In many places, temperature changes and sea-level rise are already putting ecosystems under stress and affecting human well-being. This fact has induced many countries to set up policies to fight against climate change. At European level, a comprehensive package of policy measures to reduce greenhouse gas emissions has been initiated through the European Climate Change Program (ECCP).
Thus, based on the models defined in previous sections, the eco-cost function can be written as:
where it is important to note that the rest of elements does not imply any cost.
5.3. Robust Operation Mode
As mentioned in
Section 4, this paper considers uncertainties in the demand forecasting. This issue becomes a problem when trying to operate the microgrid in isolated mode, i.e., disconnected from the main grid. Thus, it is reasonable to consider a complementary mode of operation that guarantees the reliability of the studied microgrid.
The consideration of these uncertainties in the problem is what is nowadays known as Stochastic Unit Commitment (SUC) problem. This problem requires a more robust solution, which is able to deal with the uncertainties presented in the proposed formulation. In this paper, we consider that the estimation error of the demand forecasting follows a normal distribution with mean zero and standard deviation at time
t,
, as exposed in
Section 4.1. The solution proposed consists in designing the spinning reserves of the dispatchable units in such a way that the reserve power can meet the demand estimation error for several levels of reliability according to the value of
introduced in Equation (14) (
Figure 2 shows the reliability level for values of
,
and
).
This mode of operation is complementary to the ones described above since it includes additional constraints to the problem, not changing the cost functions in Equations (21) and (22). In this mode, more expensive solutions are expected to be obtained, given the severe constraints related to robustness that they must fulfill.
6. Evolutionary Computational Approach
Genetic algorithms (GAs) are meta-heuristic algorithms that have been widely used for solving complex engineering problems [
58,
59]. GAs are based on the Darwinian theory of biological evolution. The basic idea is to have a set of potential solutions, called the population, which evolves over a number of generations by using genetic operators such as selection, crossover, and mutation [
60]. The potential solutions encode in a chromosome-like structure the designing variables. This structure is called an individual and each designing variable represents a gene. In this work, the designing variables are the power supplied/consumed by MT, DE, and ESS since they are the elements of the considered microgrid that have higher impact on the operational cost of the microgrid (see
Figure 1). RES, such as PV and WT, will always contribute to the demanded power as long as the solar and wind conditions are favorable, since their maintenance and operational costs can be neglected with respect to the DE and MT generators. Furthermore, since the power balance at each time instant should be fulfilled, whether the ESS supply or consume power at each time interval
t, is determined by the power balance between the demand and the generation of the rest of elements of the microgrid.
6.1. Genetic Algorithm Implementation
There are many possible implementations of single-objective GAs [
61]. In the proposed approach, a mupluslambda variant is used [
62]. Algorithm 1 shows the implemented approach. The algorithm begins with a random initial population
, which is evaluated. It is important that the individuals that form the initial population are valid. This aspect is relevant in problems with multiple constrains as the one described in this paper (see
Section 4). Then, offspring
is created by using crossover and mutation operations.
and
refer to the crossover and mutation probabilities, respectively. Both
and
are hyper-parameters of the algorithm that should be selected carefully to guarantee a good converge of the GA. Next, the offspring is evaluated, and the new population
is selected from the offspring generated and the previous population
. This approach guarantees a good level of elitism since parents and offspring compete each other to be selected for the next generation [
62]. After completion, the algorithm returns the best individual obtained throughout the generations.
| Algorithm 1: GA mupluslambda. |
| 1 Create initial population |
| 2 Evaluate |
| 3 |
| 4 while do |
![Energies 12 02143 i001 Energies 12 02143 i001]() |
| 10 end |
6.1.1. Individual Representation
Each individual represents a list containing the power supplied by both MT and DE for a period of 24 h, using intervals of 1 h. Therefore, the size of each individual is 48 genes. It is worth recalling that the power supplied or consumed by the ESS can be derived from the power balance, and the renewable sources will always contribute to the demanded power as long as the climate conditions are suitable.
Figure 3 shows the encoding used to represents the individuals of the GA.
6.1.2. Fitness Function
The fitness function used depends on the operation mode of the microgrid. Three operation modes have been defined in
Section 5 that use a single-objective fitness function, such as cost-effective, eco-mode, and robust operation modes.
In the case of cost-effective mode, the objective function is defined as:
In the case of eco-mode, the objective function used is:
In the case of robust mode, the fitness function used is:
It is important to highlight that, in the three fitness functions in Equations (23)–(25), the death penalty is used to penalize invalid solutions. Therefore, these invalid solutions do not participate in the genetic operations since they are not chosen by the selection scheme.
6.1.3. Genetic Operators
Tournament selection mechanism is used since it provides suitable results [
61]. In each tournament, a number of individuals are randomly selected, which compete each other to be chosen as a parent; the best one is then selected as one of the parents to be used in crossover and mutation operations [
61]. A tournament size of three has been demonstrated to be suitable for the majority of problems. Regarding the crossover operation, two schemes have been evaluated: two-point and Simulated Binary Crossover (SBX) [
63] methods. The two-point crossover consists of swapping the genetic information of two parents using two points as the indexes of the genetic exchange. SBX is a method to simulate one point crossover for continuous variables. An eta hyper-parameter is used to determine the similarity among selected parents and children. A high eta value will produce children resembling their parents, while a small eta value will produce much more different solutions. The mutation scheme used is a tailored Gaussian mutation algorithm, where each variable can change according to a Gaussian distribution with mean
and standard deviation
. The variability of a given gene after mutation depends on the value of
.
8. Conclusions and Further Work
The present study was carried out for developing a GA to address the problem of finding the most suitable solution for the UC and ED problems in a microgrid. Based on the results, several conclusions can be formulated.
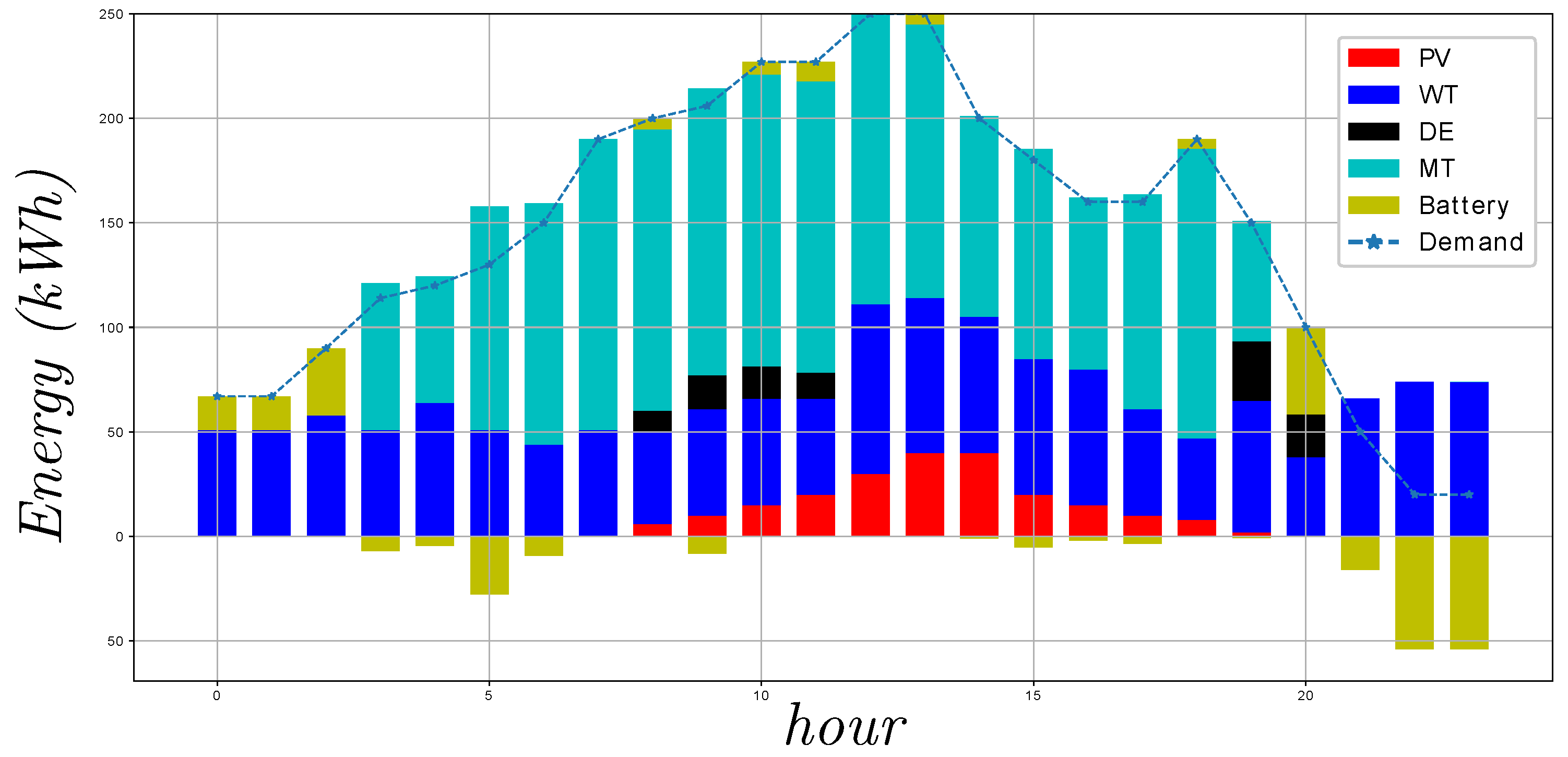
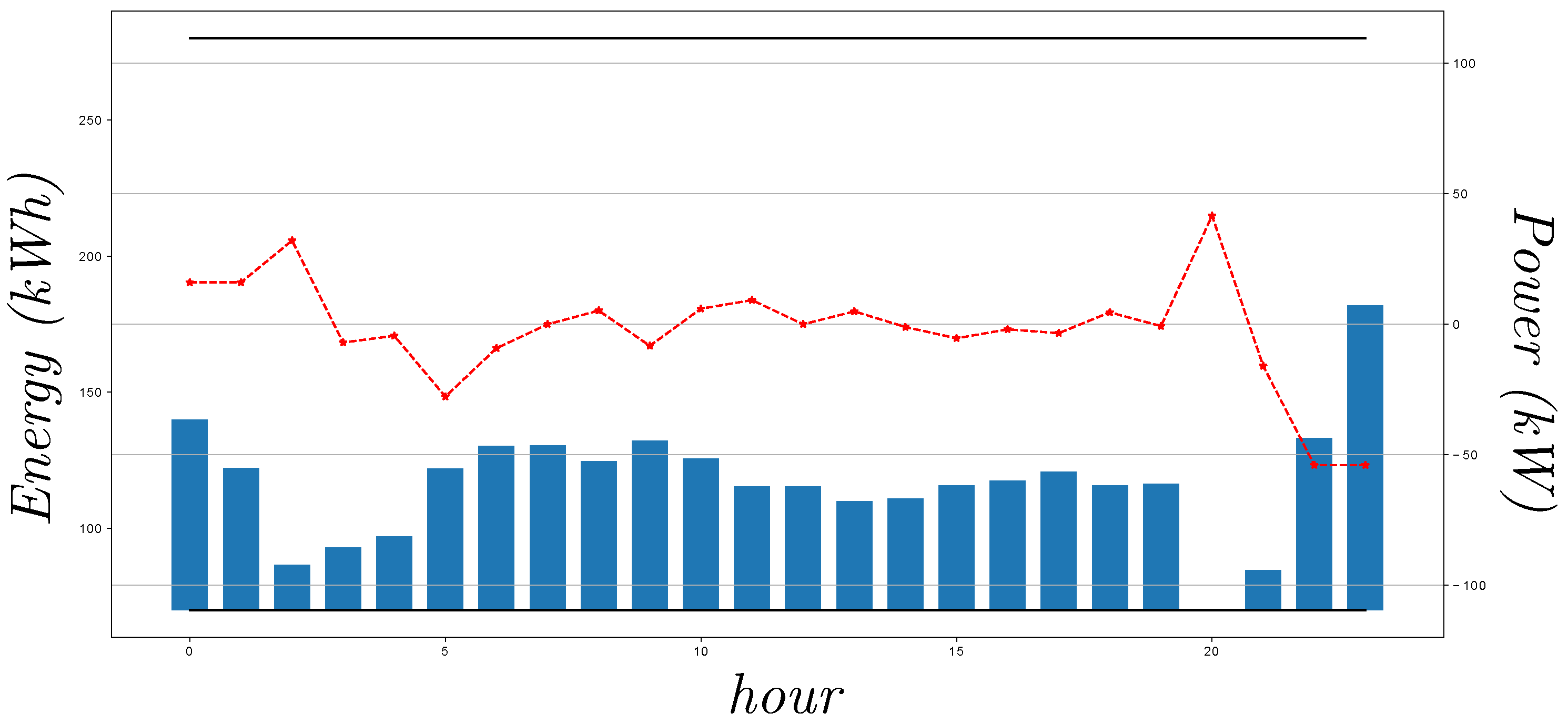
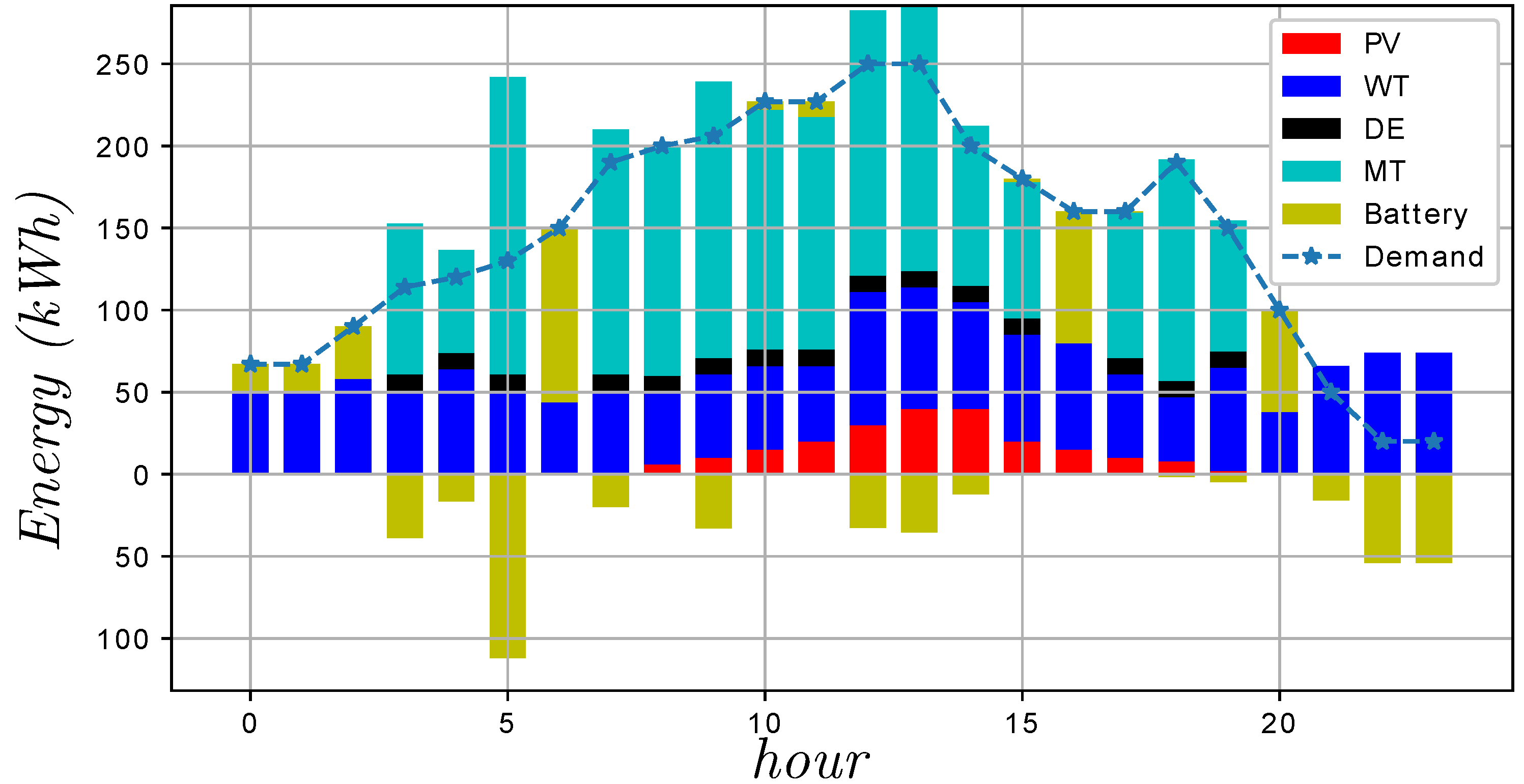
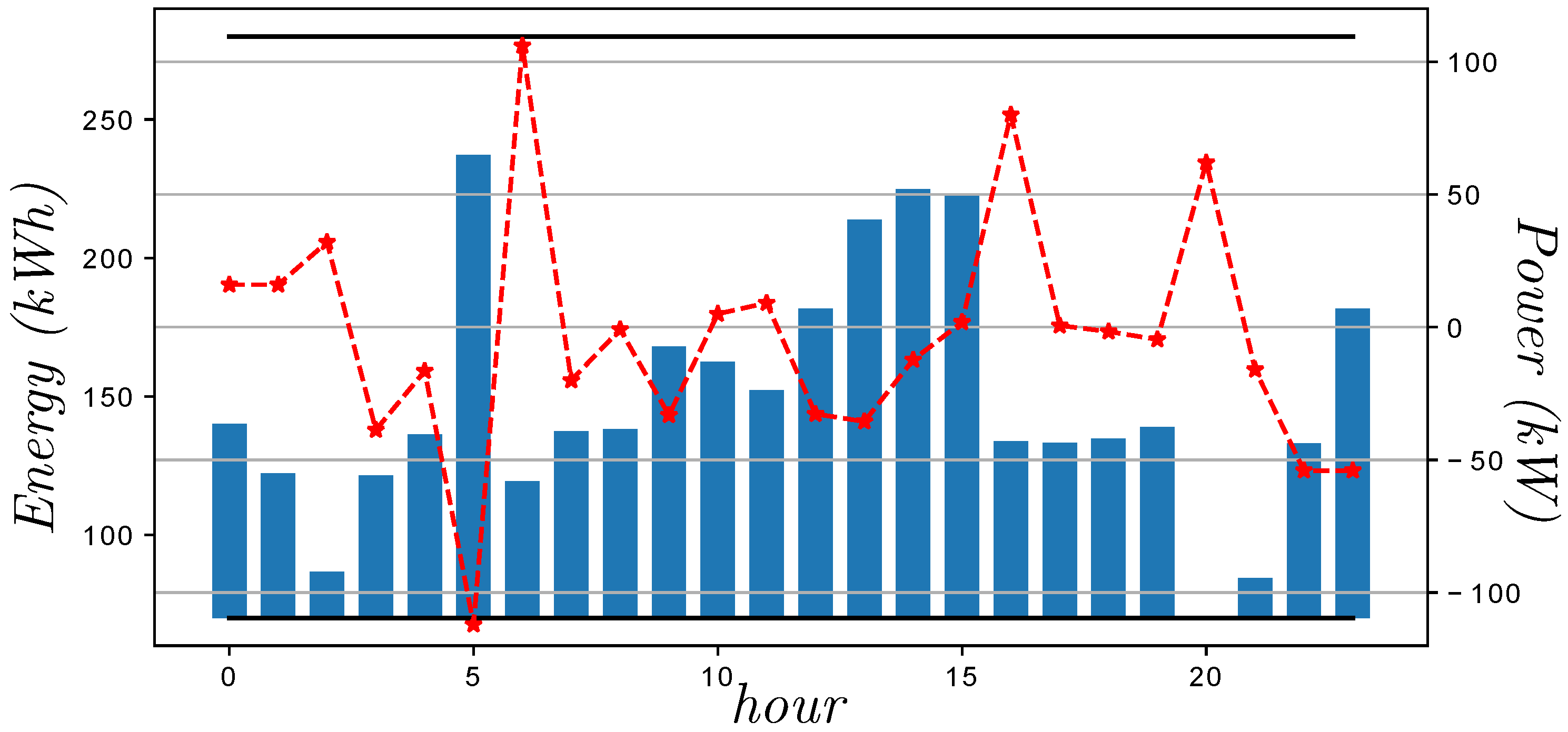
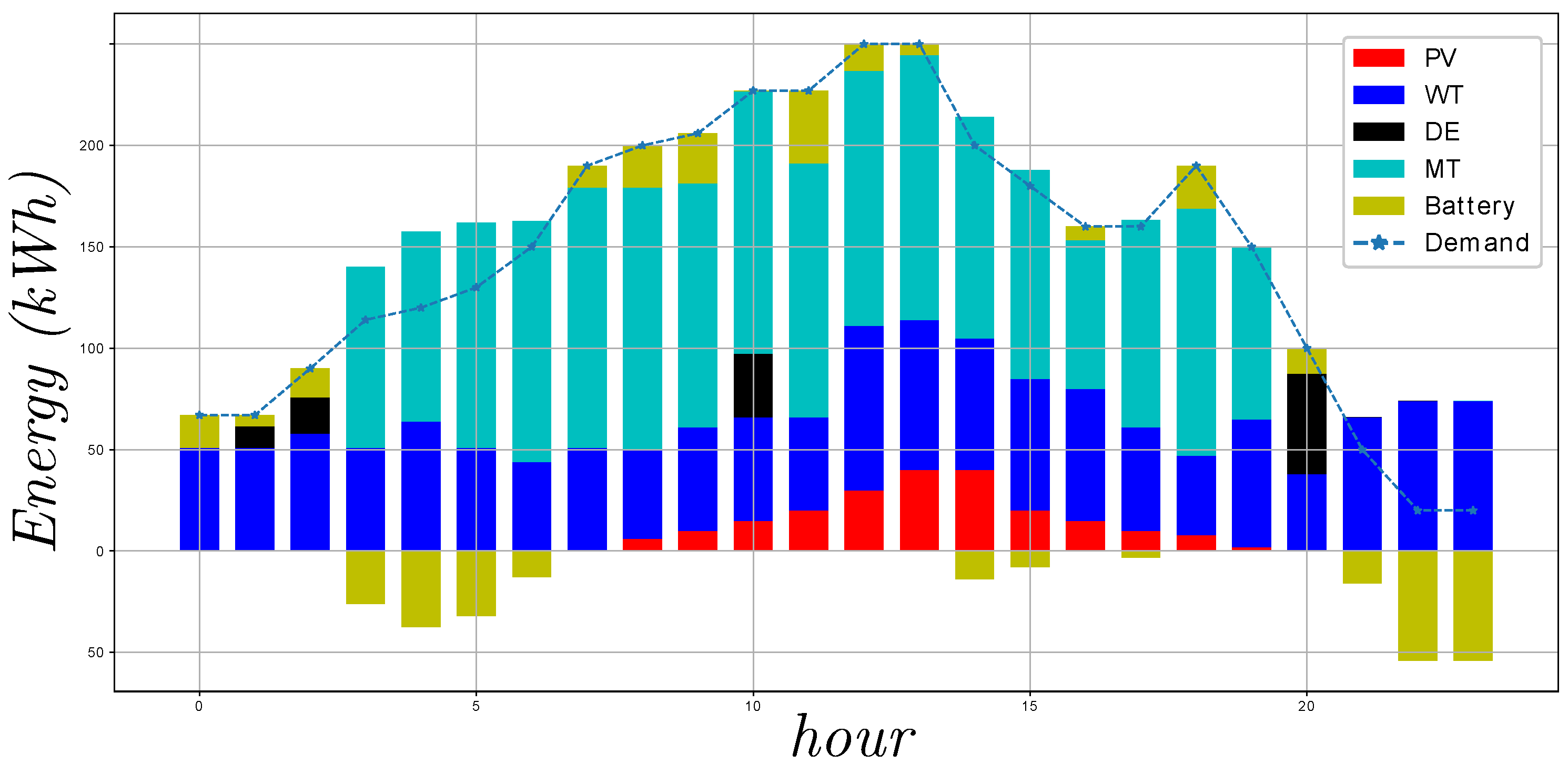
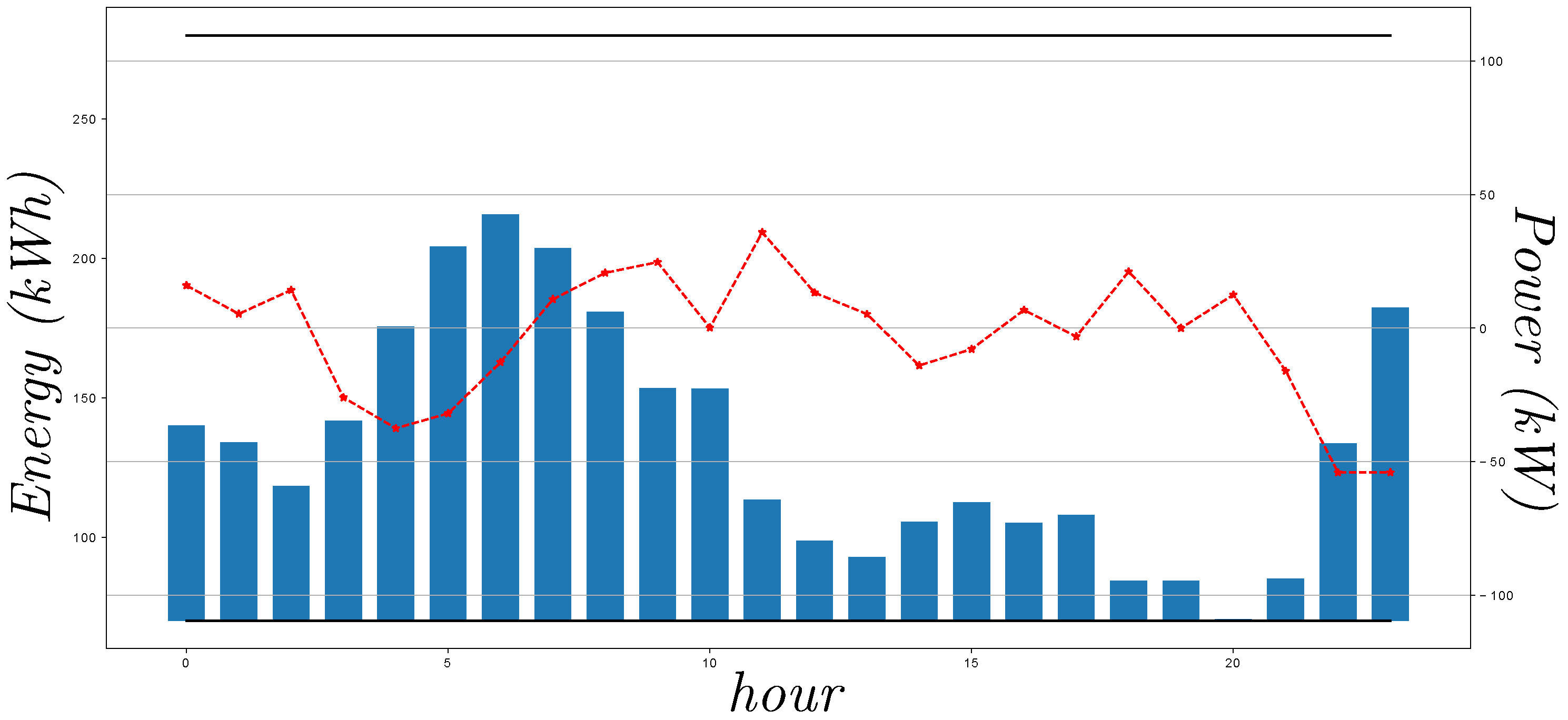
First, a detailed model of a microgrid was introduced to propose three case-studies (operation modes), which were addressed to validate the benefits of the GA to solve the combined problem of UC and ED. When the cost-effective operation mode was considered, the solution prioritized the use of DE instead of MT for low values of demanded power. However, when MT must be employed, it generated high amounts of power to have an appropriate power/cost ratio. With respect to the eco-mode operation mode, the microgrid minimized the use of DE due to its high levels of emissions, which are proportional to the power generated. In addition, the management of the battery system in both cases worked to reach the corresponding objectives, being an element of relevant importance to achieve this aim.
Regarding the limitations of the present work, the computational time required by the GA makes it low efficient to addressing the problem in real-time. In addition, despite the goodness of the obtained results, the absence of guarantee of finding global solutions must always be taken into account, as the algorithm might converge at local minimum. For this reason, an appropriate tuning of the GA parameters is necessary when modifying the problem scenario. In future works, the results of the proposed evolutionary approach will be compared with other metaheuristic algorithms such as Particle Swarm Optimization (PSO) and Evolutionary Strategies (ES), among other techniques.
Considering the benefits of the proposed approach, several improvements are proposed as a further work. First, to increase the reliability of the results, a more sophisticated model of the ESS that considers the effects of battery degradation must be considered. In this same line of improvement, the implementation of an electricity price short-term forecasting is also proposed to develop a prize-based UC. Finally, the study of this optimization problem in a multi-objective mode is considered as further work. A multi-objective approach would provide a better understanding of the problem.