A Modified Partial Power structure for Quasi Z-Source Converter to Improve Voltage Gain and Power Rating
Abstract
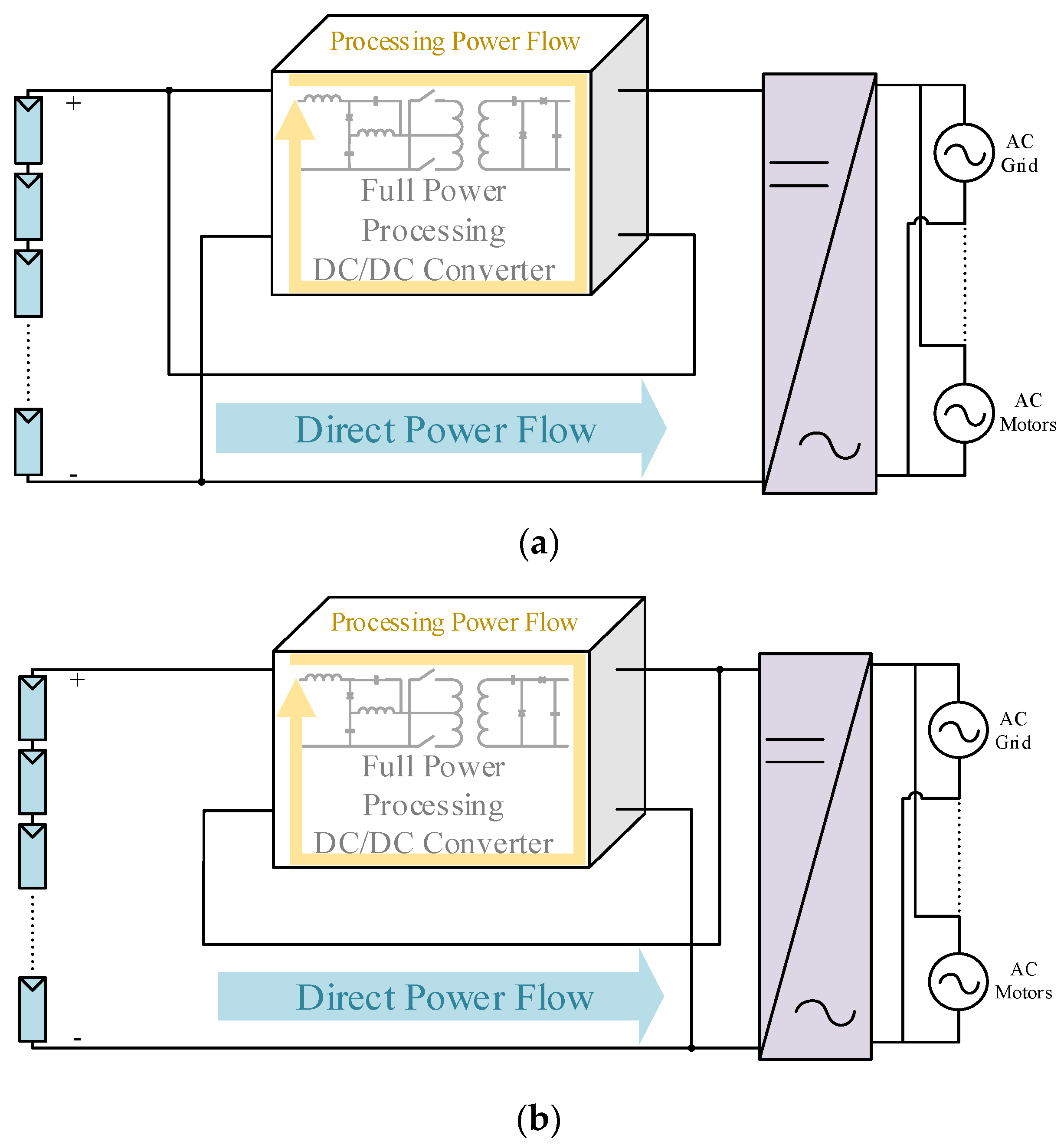
:1. Introduction
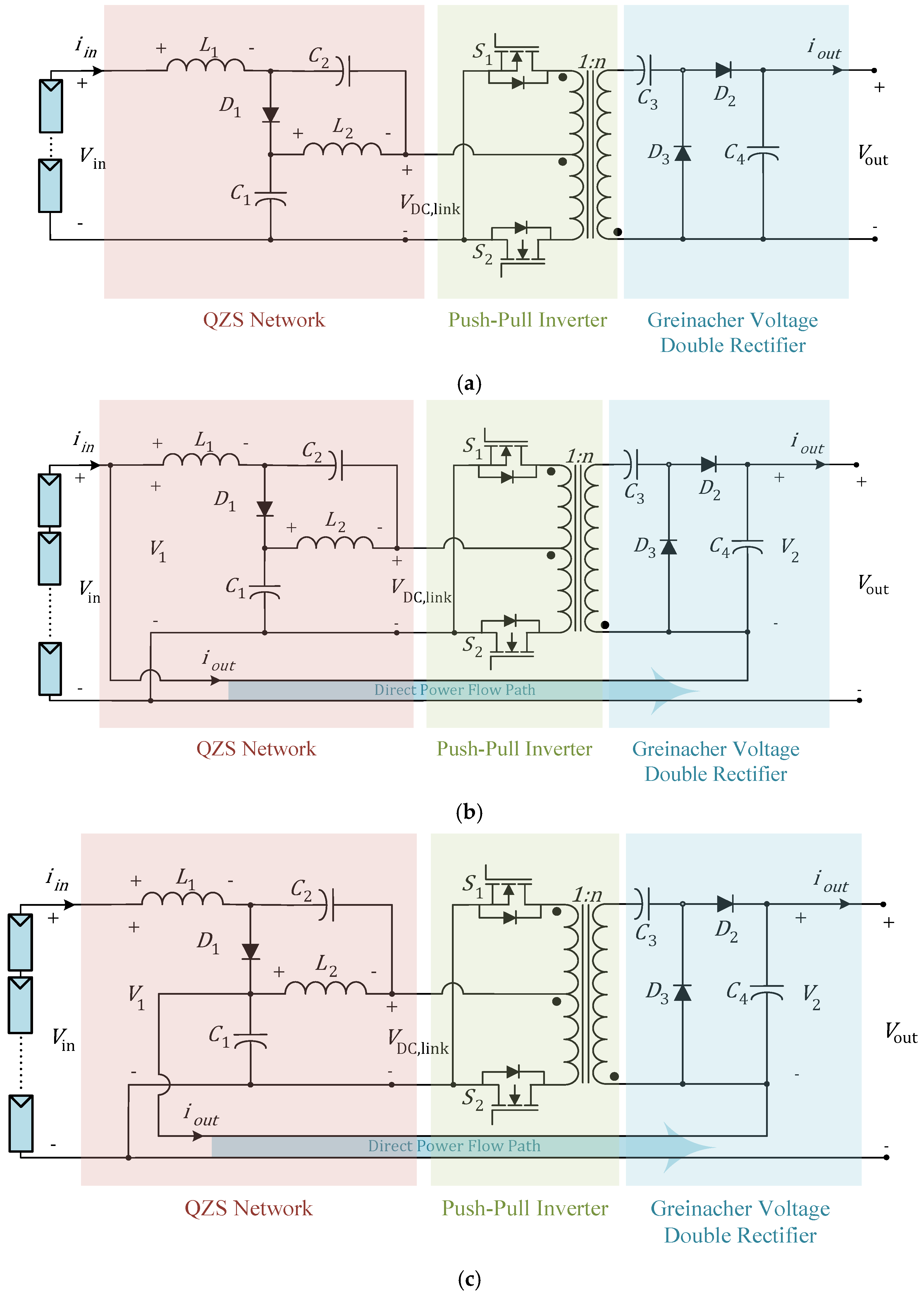
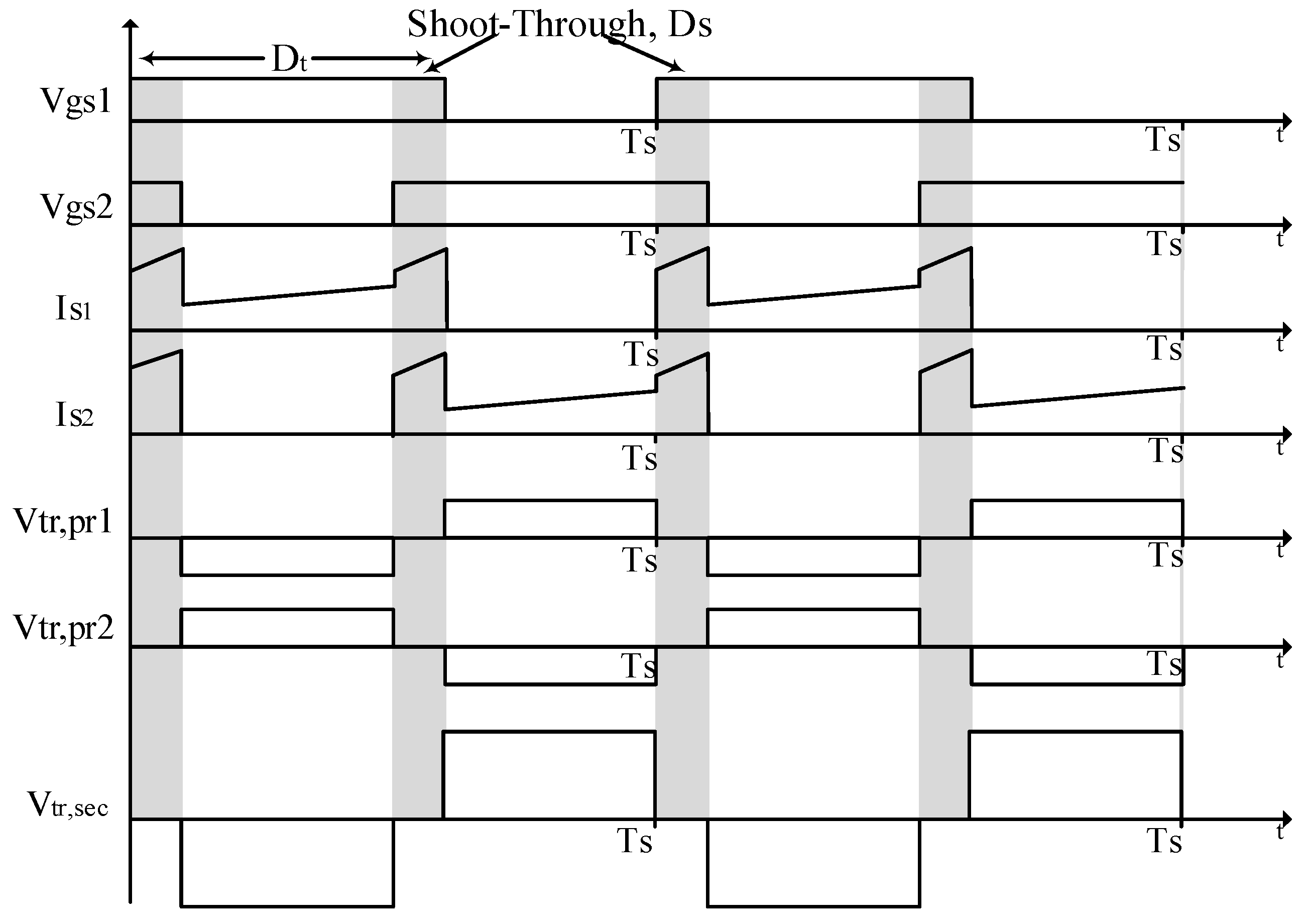
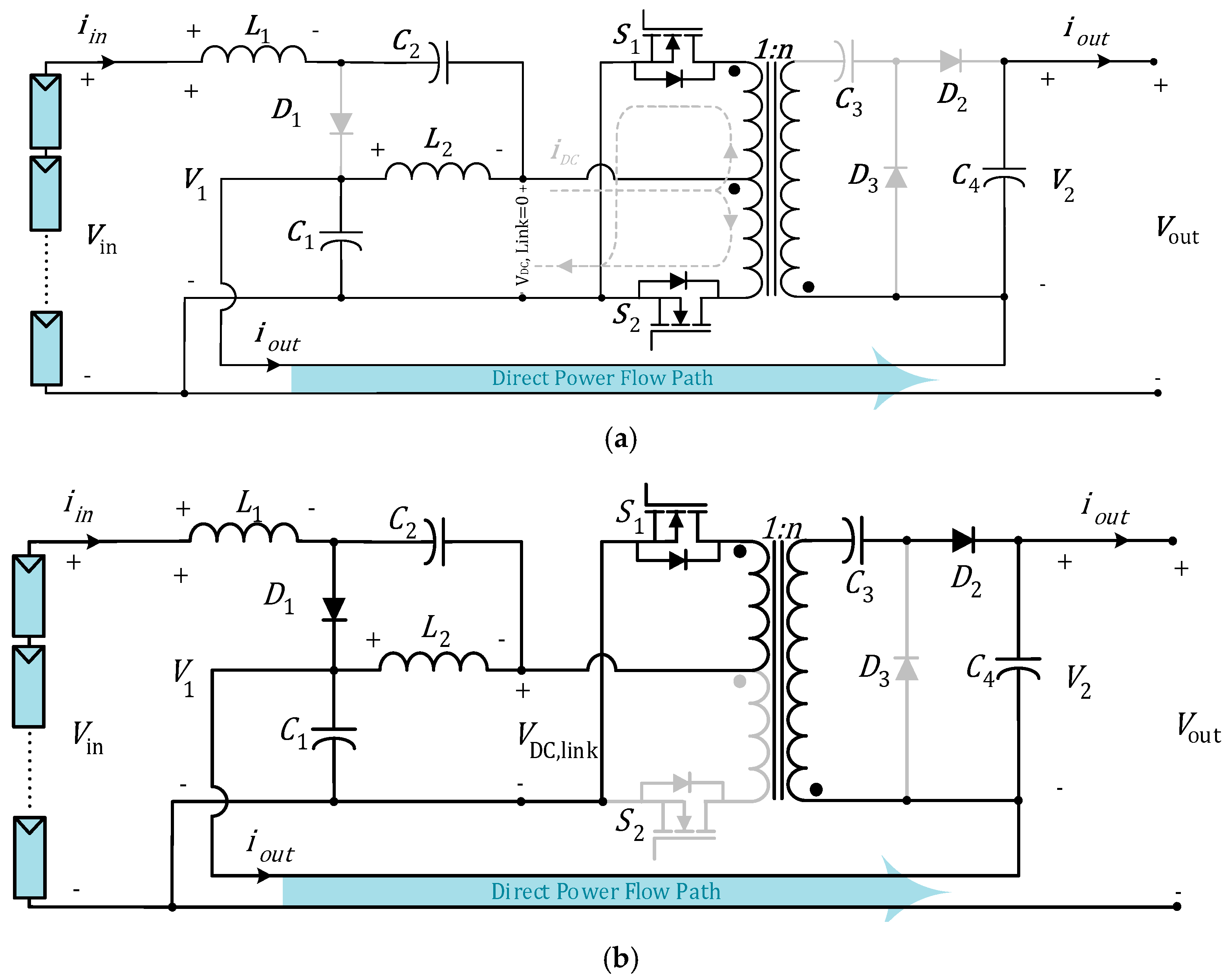
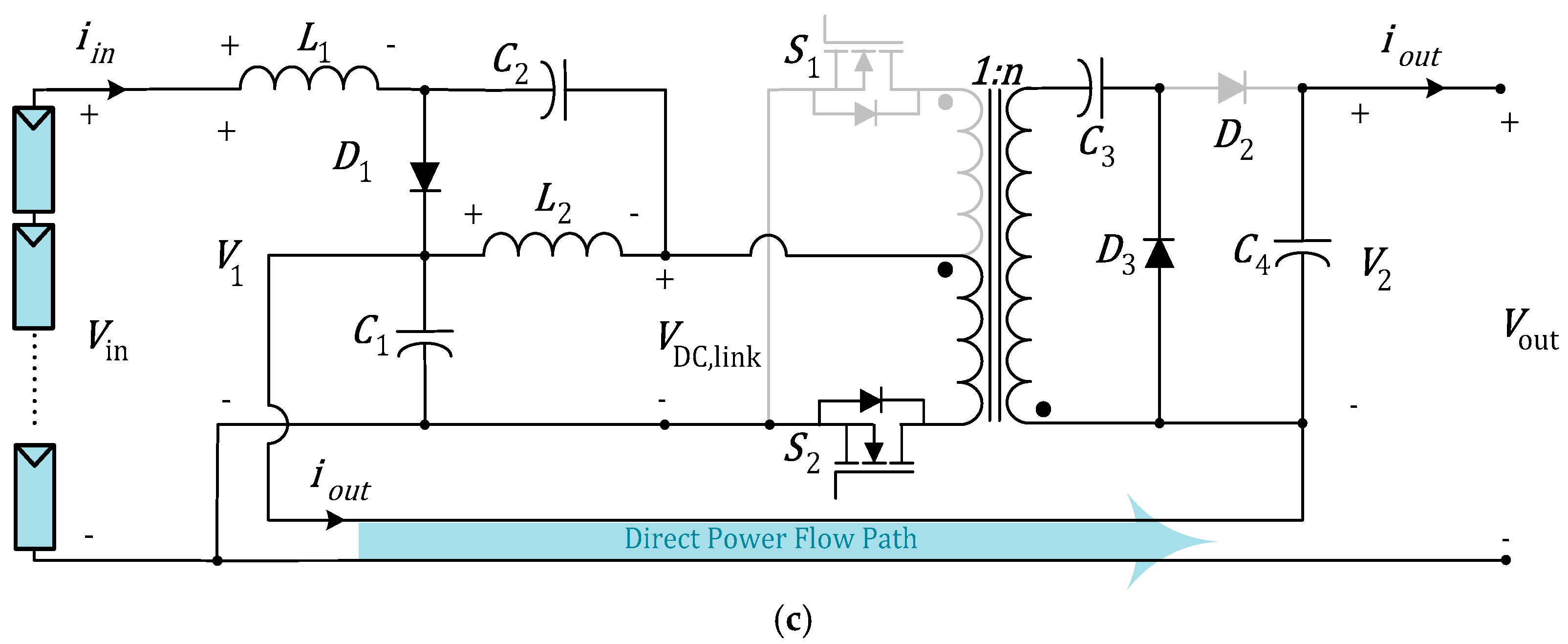
2. Operation Principles and Topology Analysis of the Proposed Converter
3. Comparison and Evaluation of Topologies
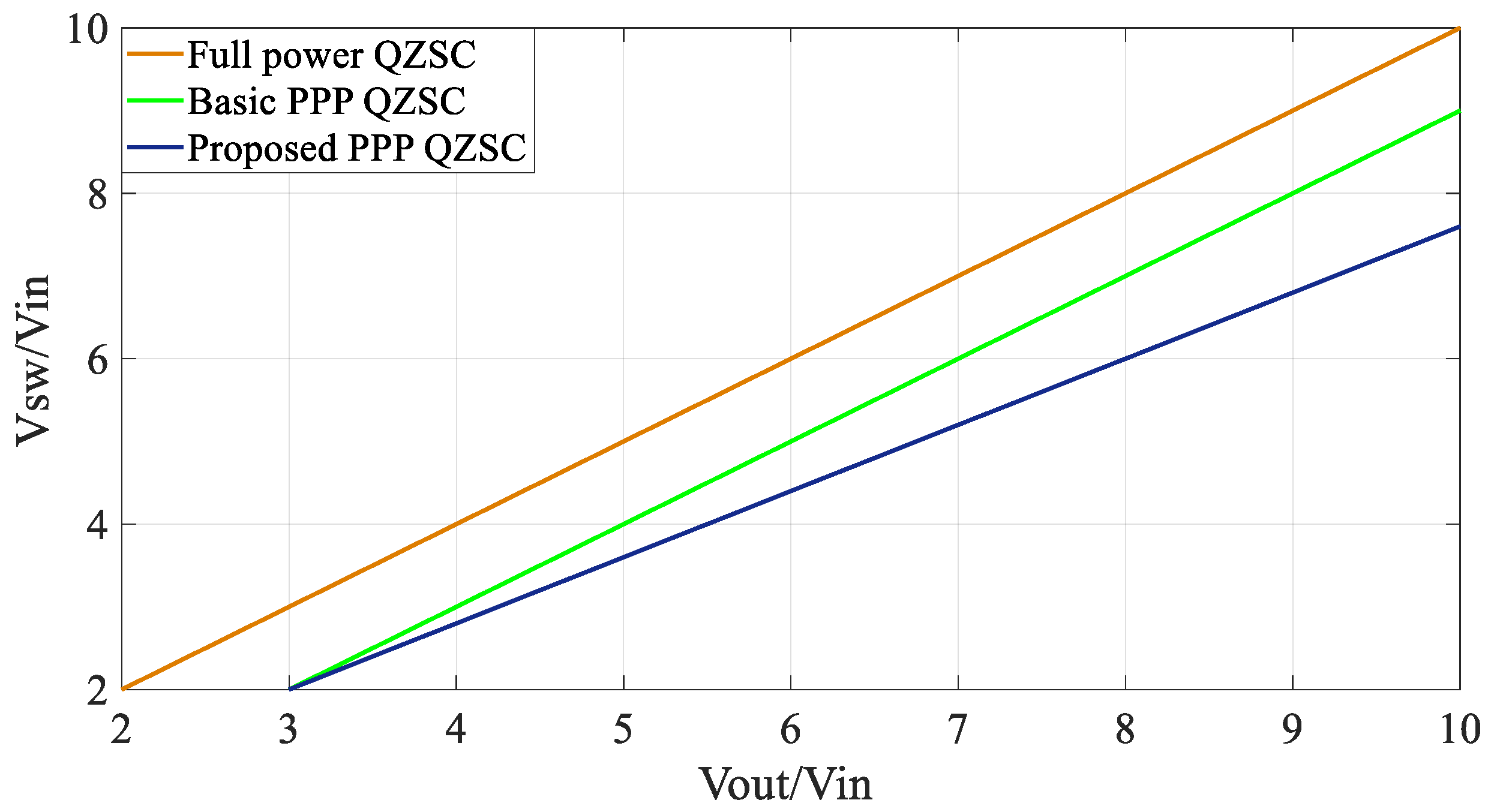
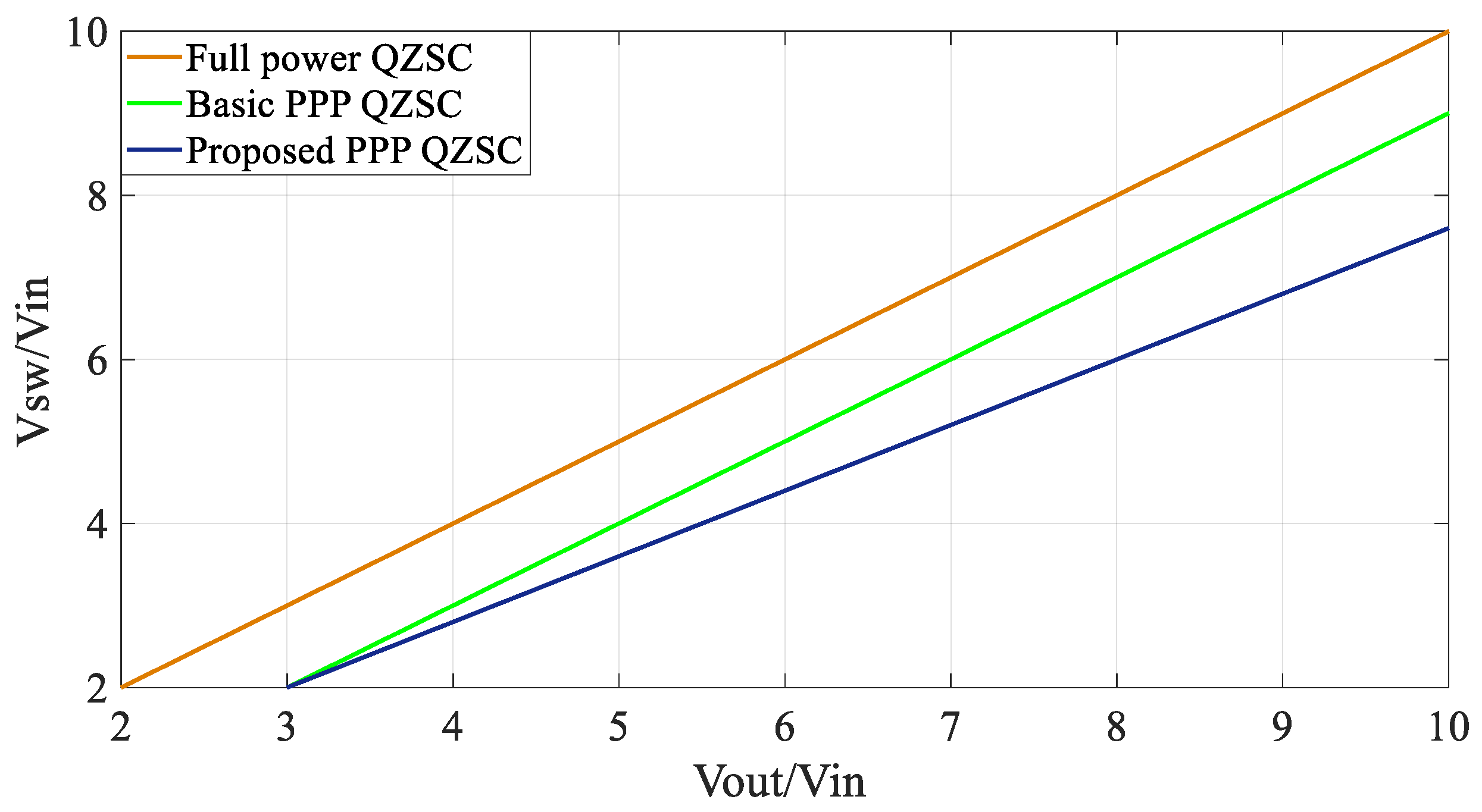
3.1. Voltage and Current Stress Analysis
3.2. Element Design
3.3. Comparison
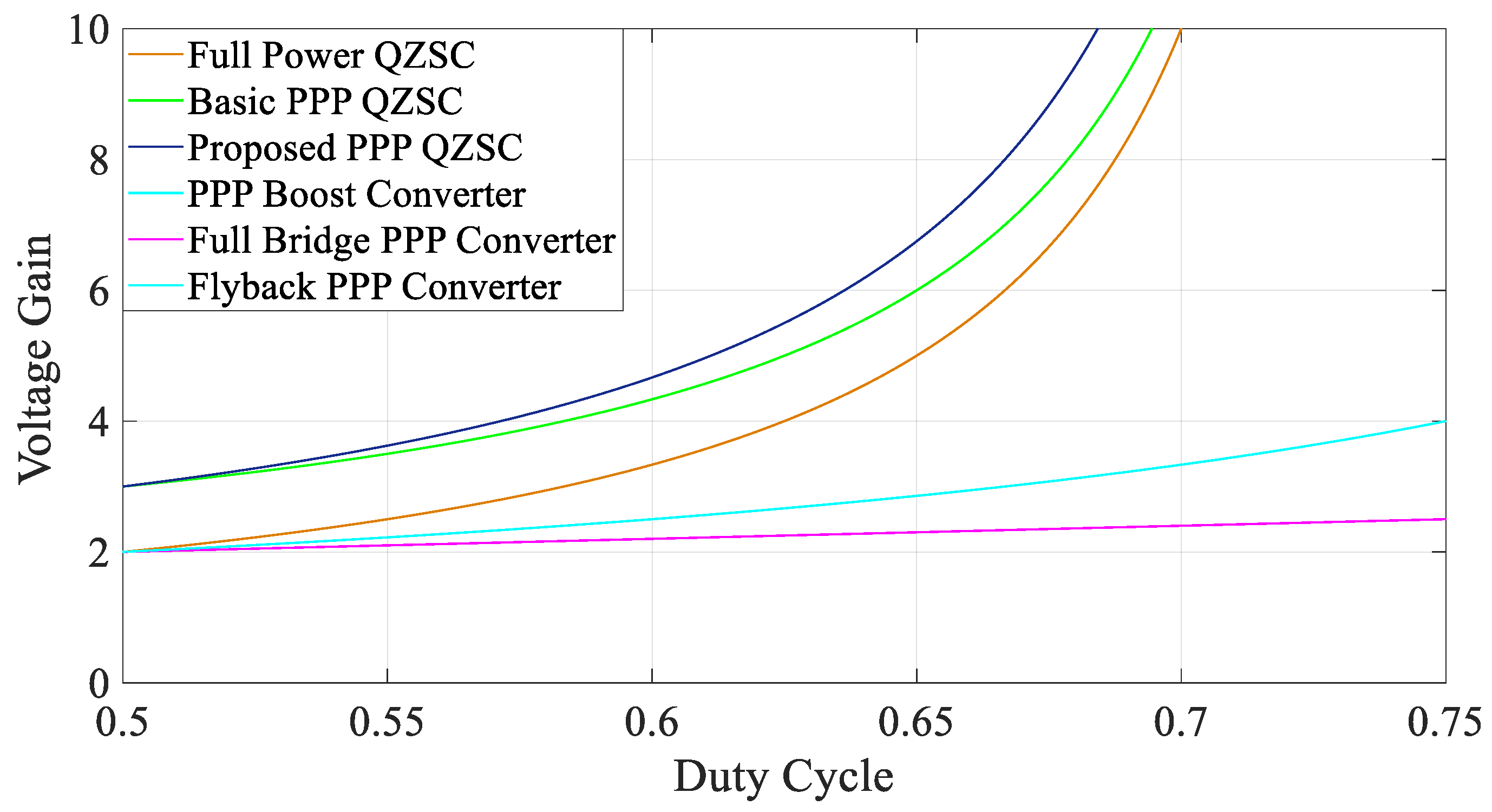
3.4. Voltage Gain Comparison
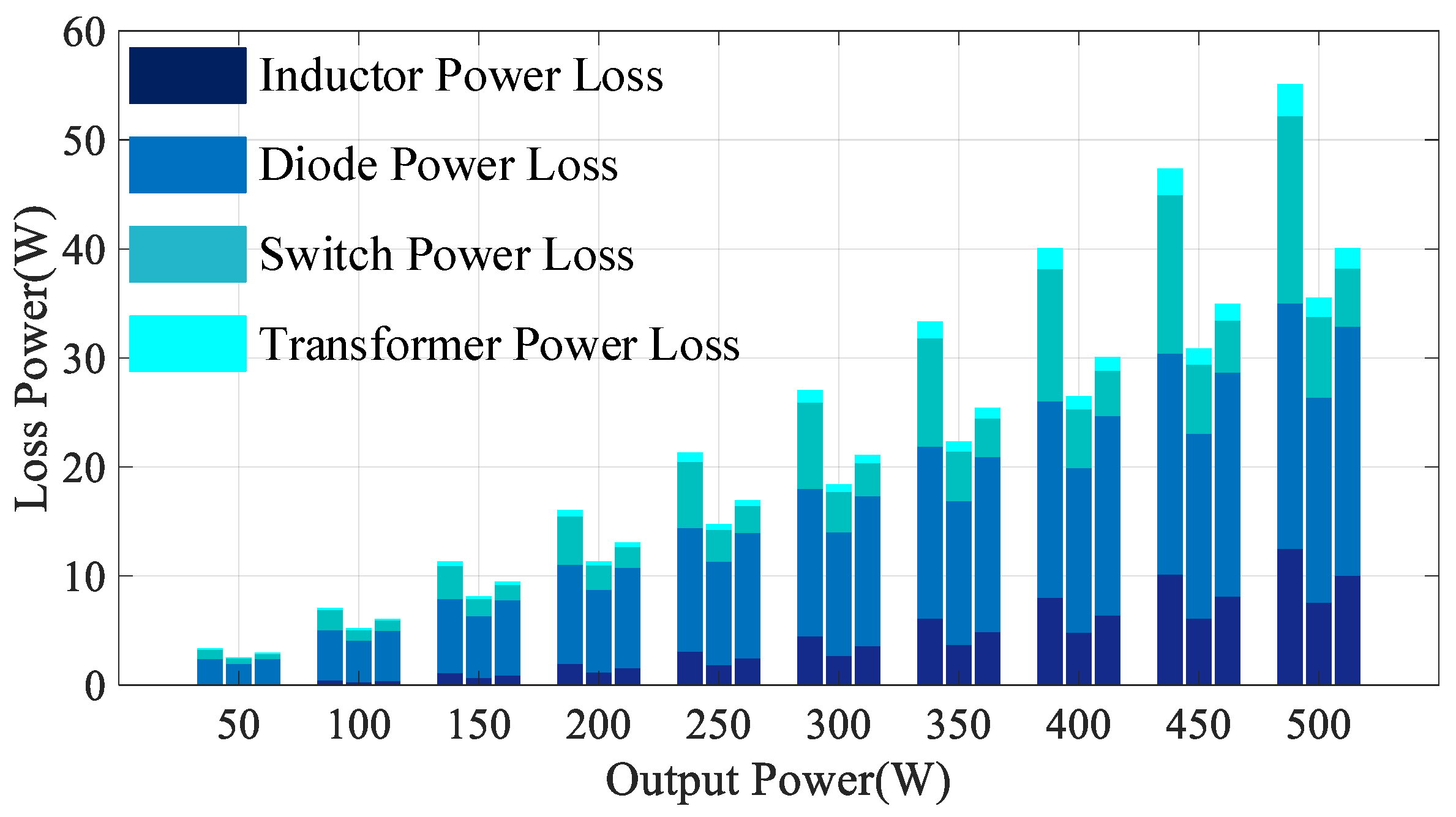
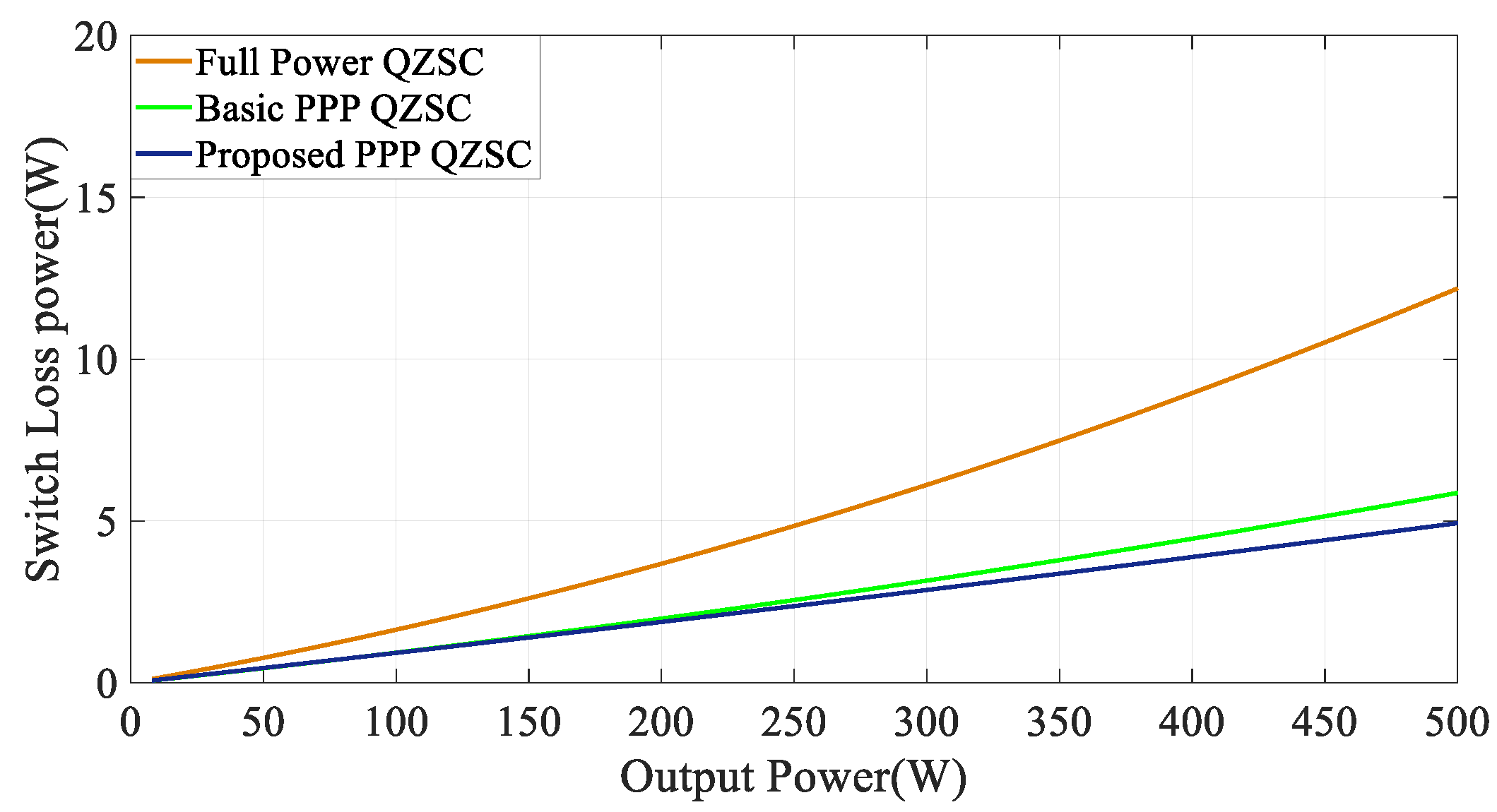
3.5. Losses Comparison
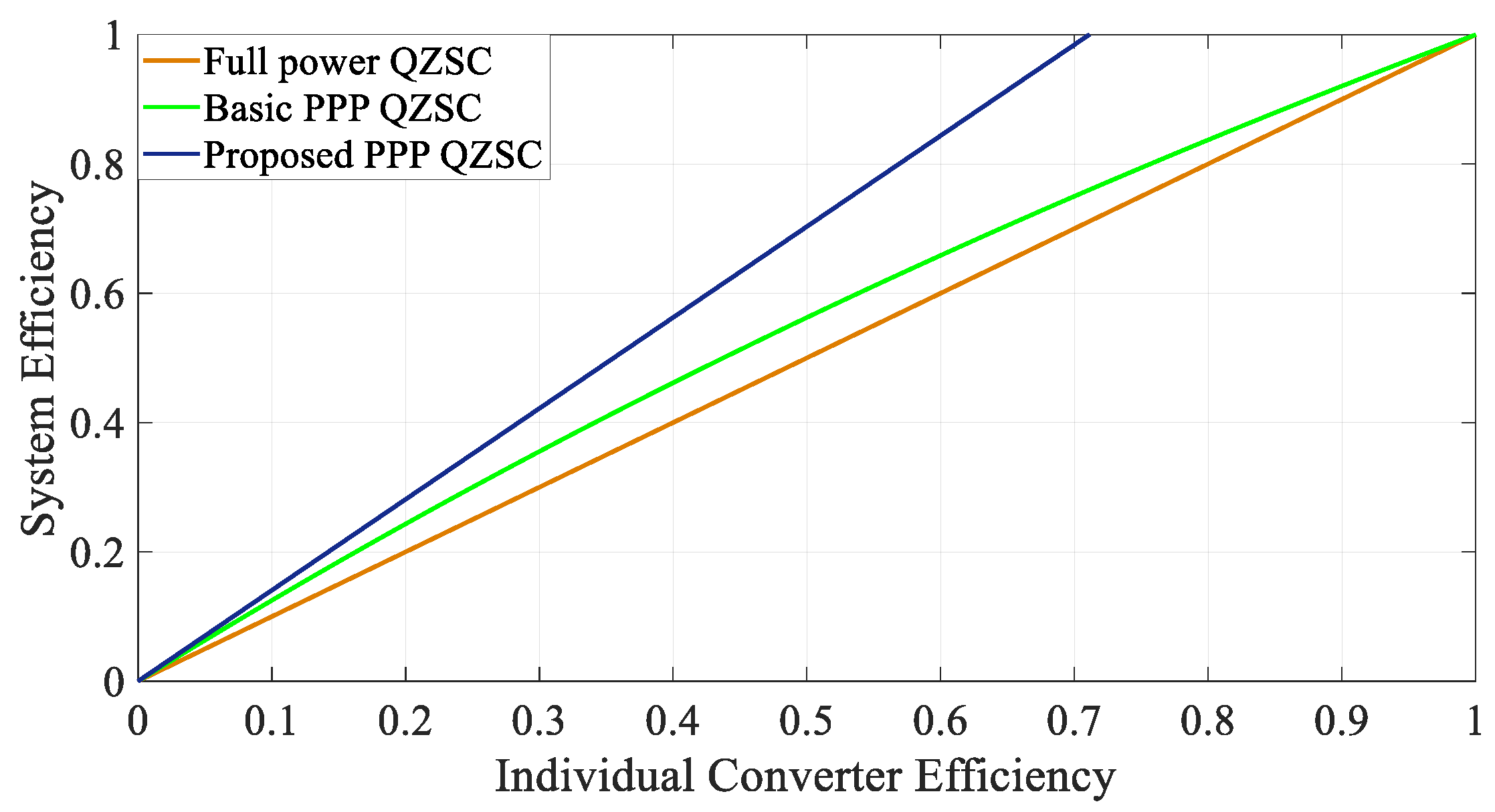
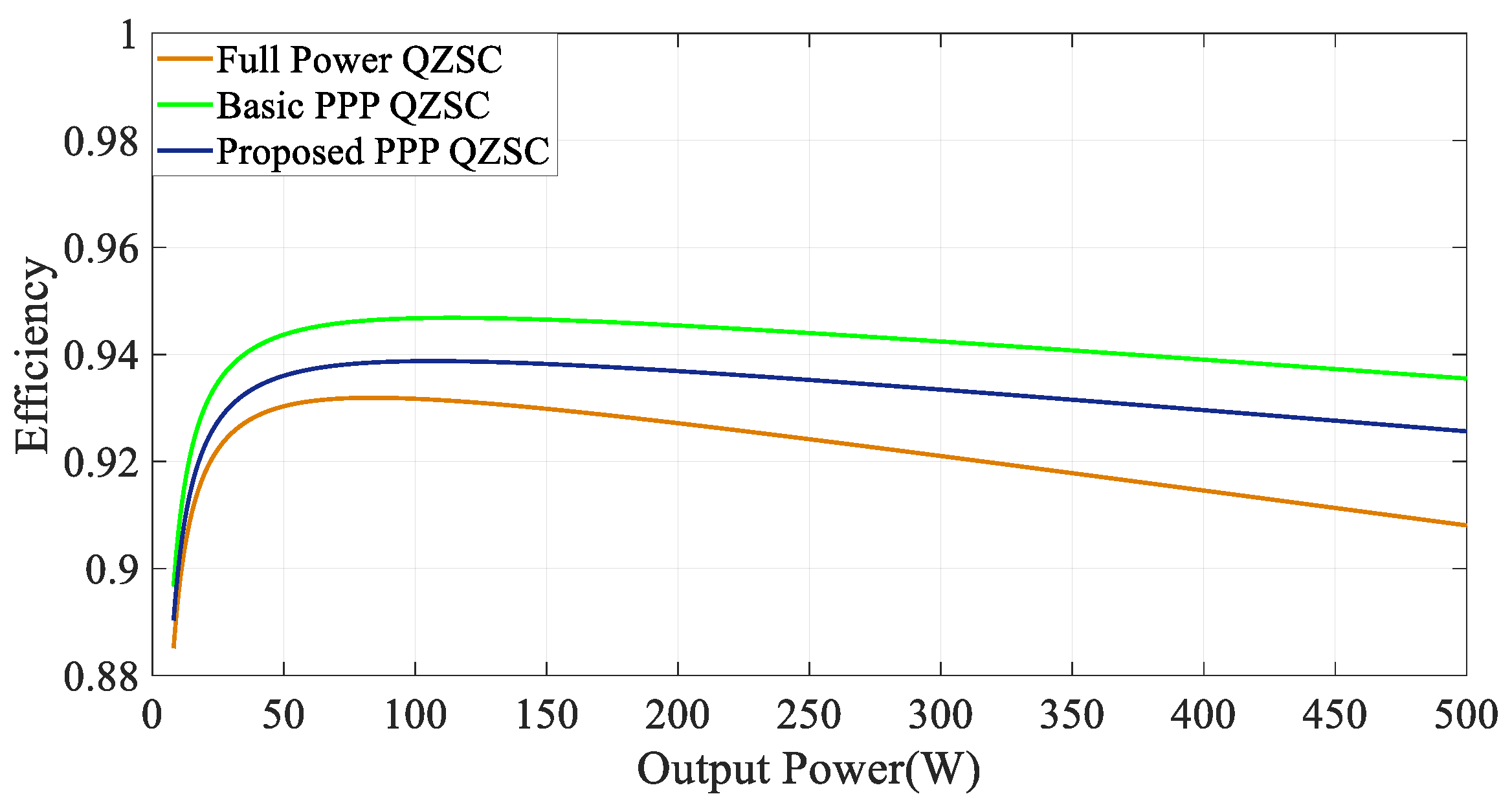
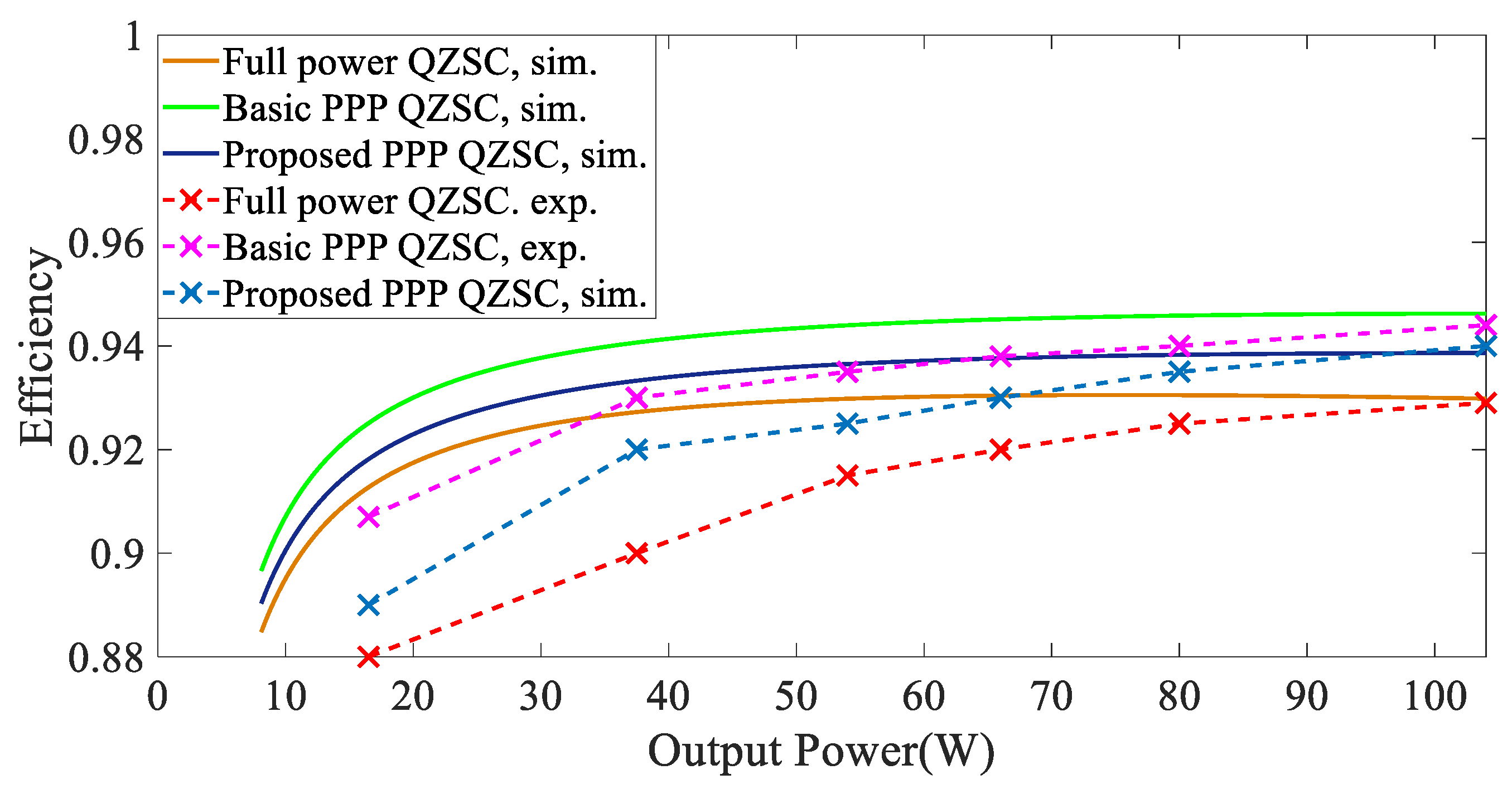
3.6. Efficiency Comparison
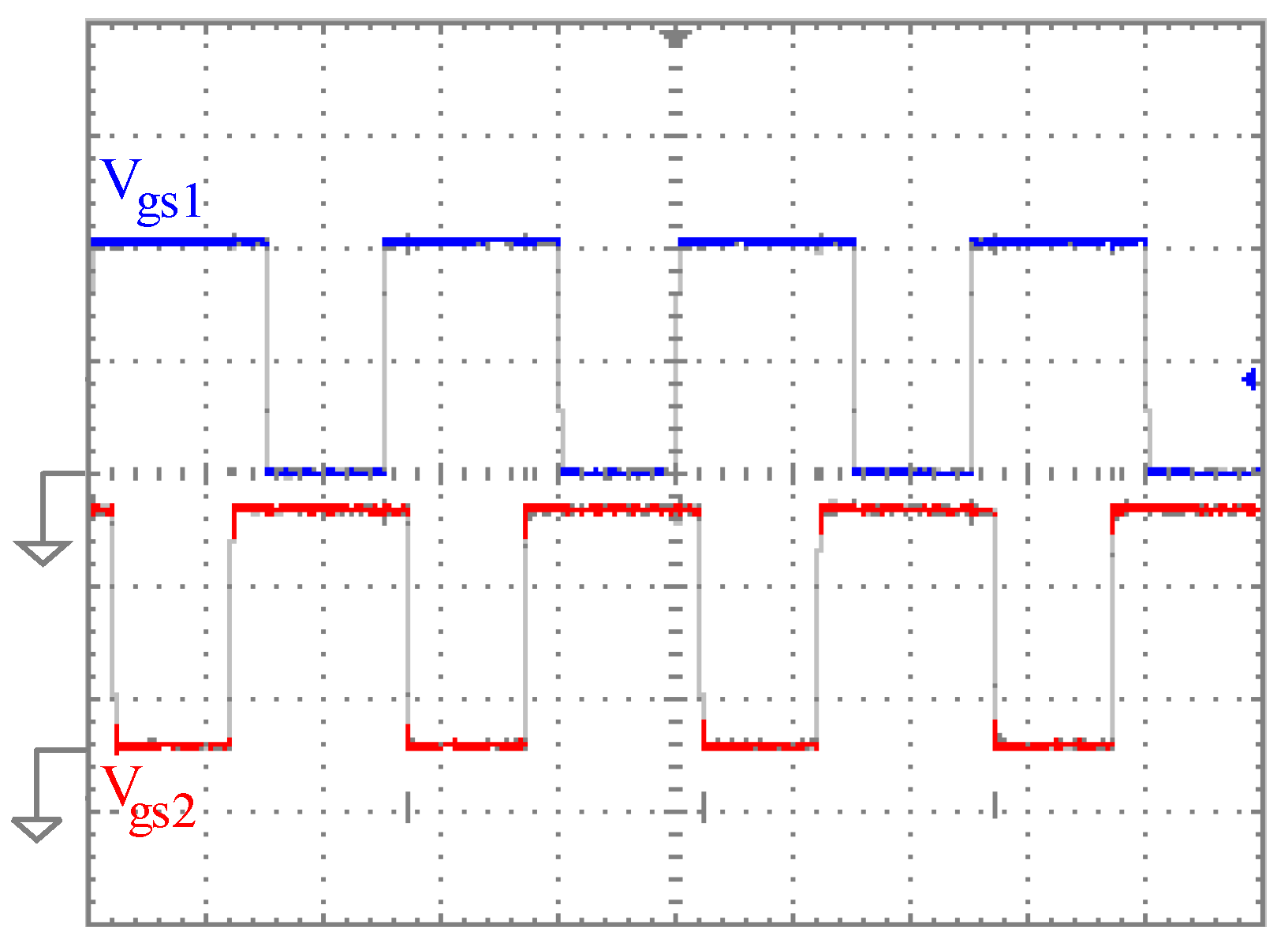
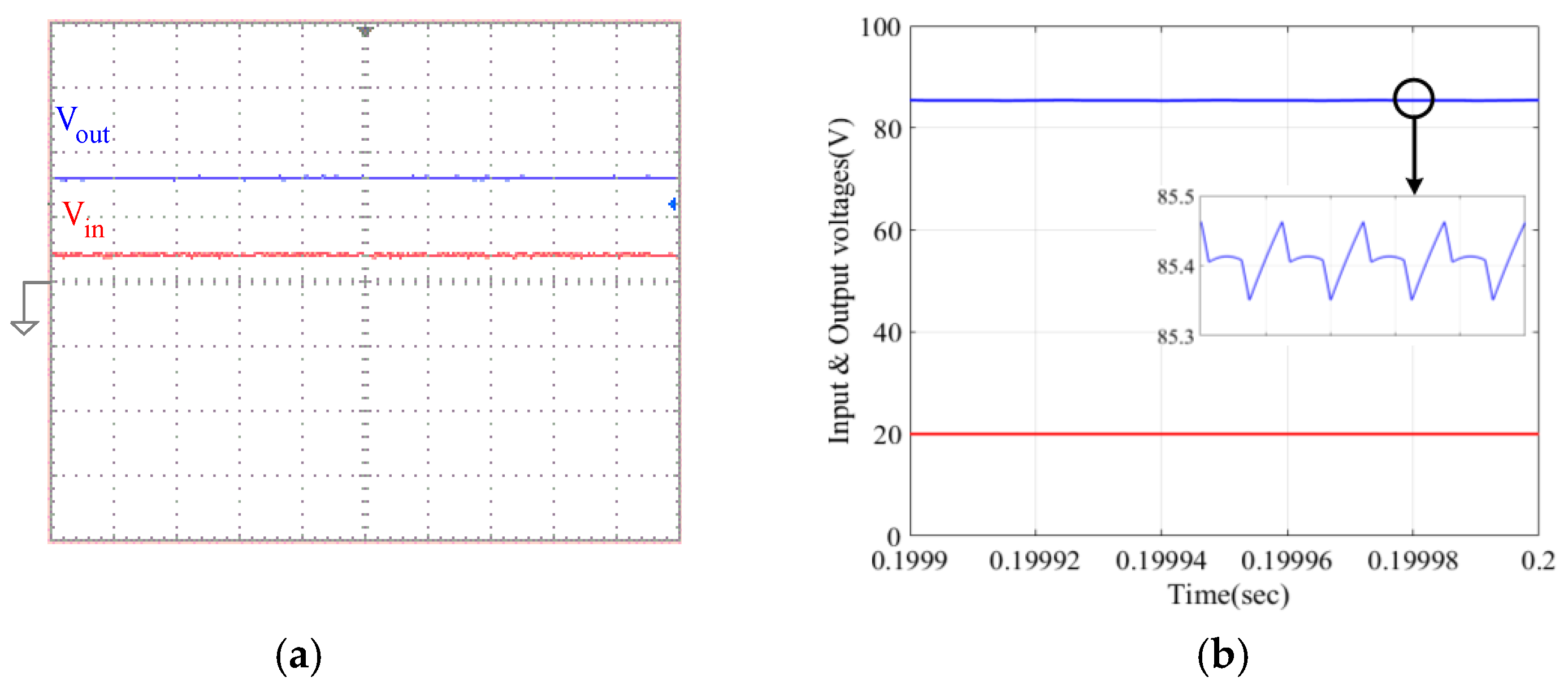
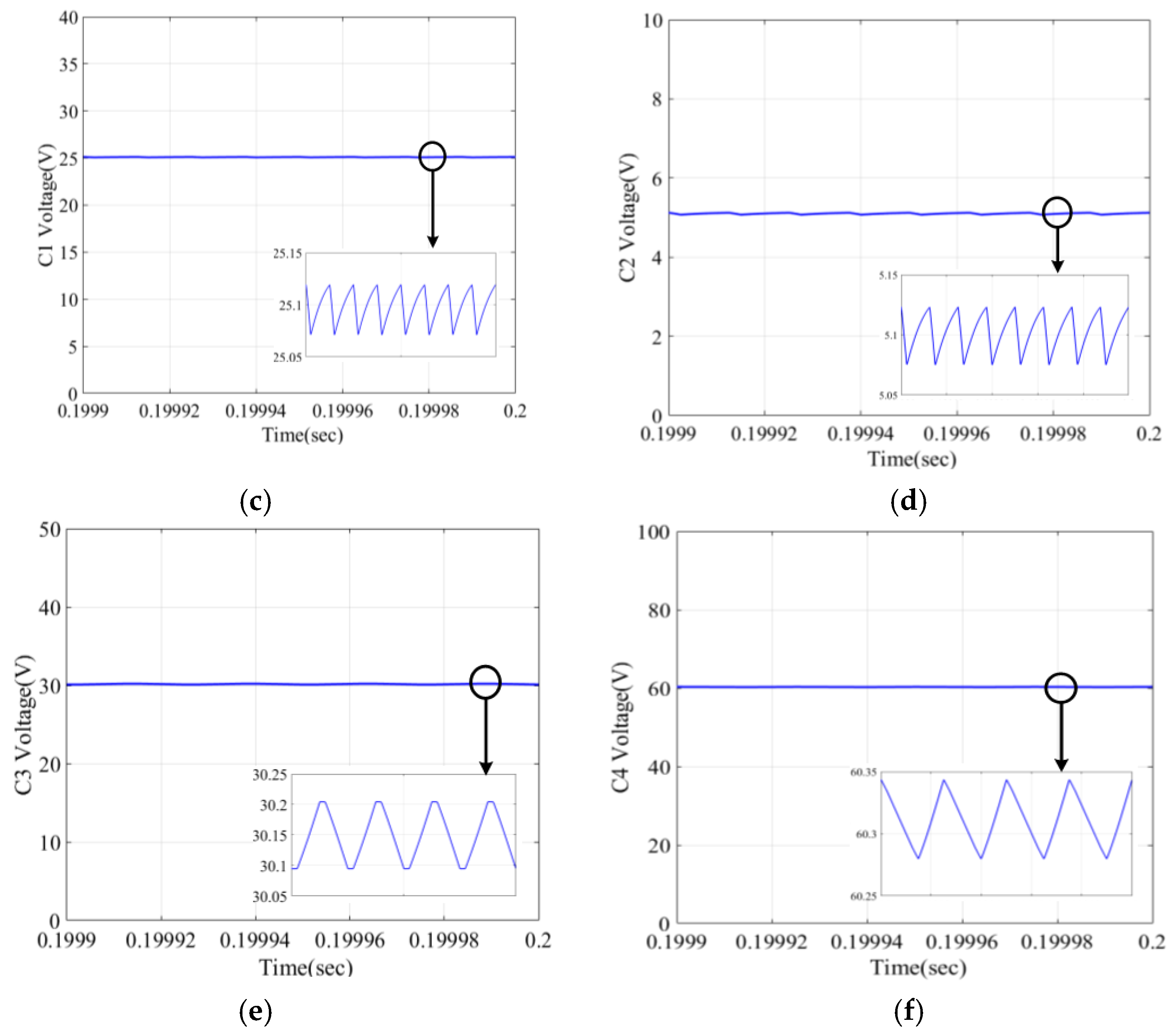
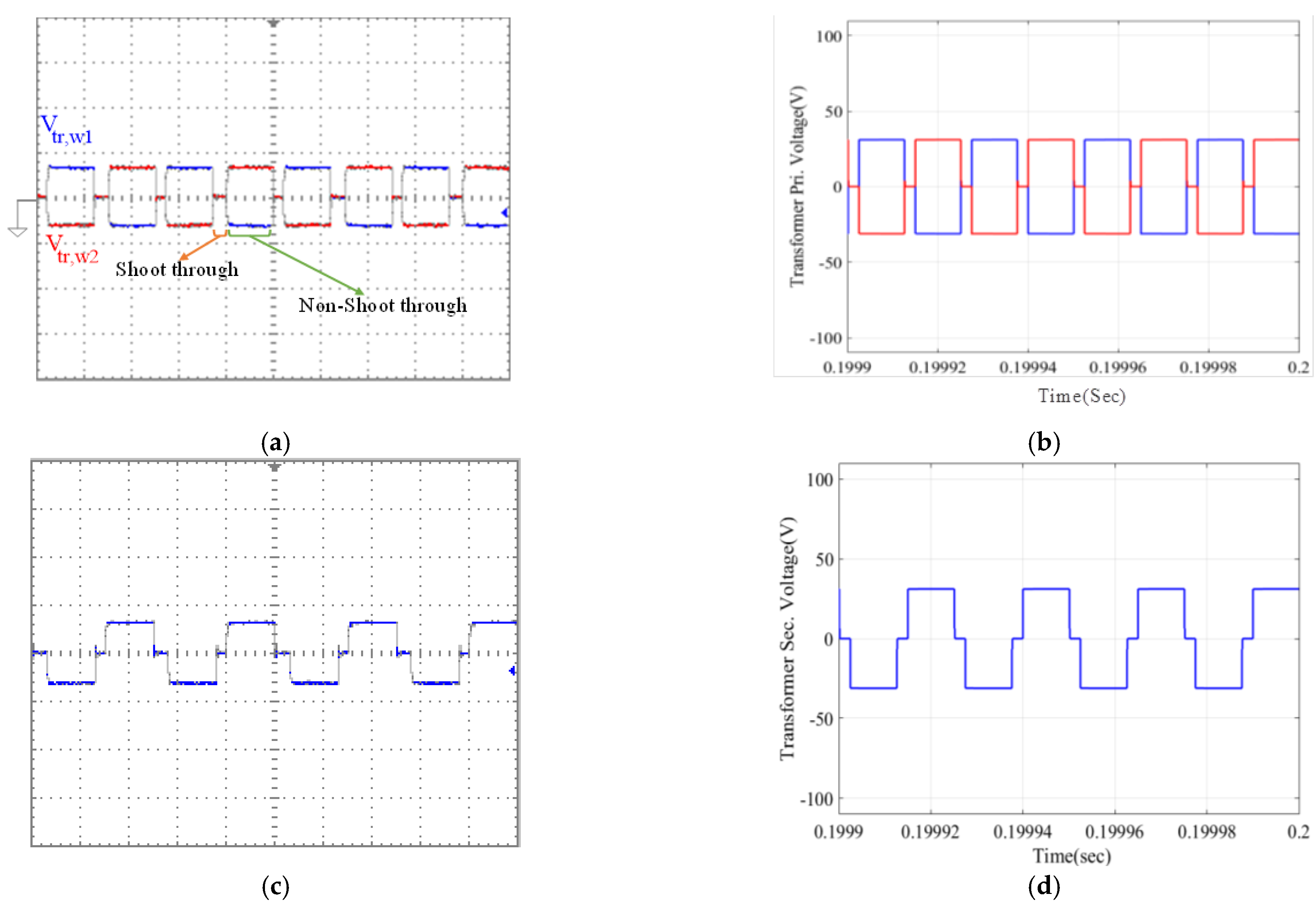
4. Simulation and Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, J.; Yeates, K.; Han, Y. Analysis of high efficiency DC/DC converter processing partial input/output power. In Proceedings of the 2013 IEEE 14th Workshop on Control and Modeling for Power Electronics (COMPEL), Salt Lake City, UT, USA, 23–26 June 2013; pp. 1–8. [Google Scholar]
- Button, R.M. An advanced photovoltaic array regulator module. In Proceedings of the IECEC 96. 31st Intersociety Energy Conversion Engineering Conference, Washington, DC, USA, 11–16 August 1996; Volume 1, pp. 519–524. [Google Scholar]
- Agamy, M.; Harfman-Todorovic, M.; Elasser, A.; Essakiappan, S. A transformer-less partial power boost converter for PV applications using a three-level switching cell. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 2934–2939. [Google Scholar]
- Badawy, M.O.; Sozer, Y. A partial power processing of battery/ultra-Capacitor hybrid energy storage system for electric vehicles. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 3162–3168. [Google Scholar]
- Kasper, M.; Bortis, D.; Friedli, T.; Kolar, J.W. Classification and comparative evaluation of PV panel integrated DC-DC converter concepts. In Proceedings of the 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. LS1e.4-1–LS1e.4-8. [Google Scholar]
- Zapata, J.W.; Meynard, T.A.; Kouro, S. Partial power DC-DC converter for large-scale photovoltaic systems. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016; pp. 1–6. [Google Scholar]
- Ahmad, M.W.; Anand, S. Power decoupling in solar PV system using partial power processing converter. In Proceedings of the 2016 10th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Bydgoszcz, Poland, 29 June–1 July 2016; pp. 196–201. [Google Scholar]
- Chen, L.; Wu, H.; Xu, P.; Hu, H.; Wan, C. A high step-down non-isolated bus converter with partial power conversion based on synchronous LLC resonant converter. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 1950–1955. [Google Scholar]
- Zhao, J.; Han, Y. A GaN-based partial power converter with MHz reconfigurable switched-capacitor and RF SEPIC. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–7. [Google Scholar]
- Zapata, J.W.; Renaudineau, H.; Kouro, S.; Perez, M.A.; Meynard, T.A. Partial power DC-DC converter for photovoltaic microinverters. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 6740–6745. [Google Scholar]
- Agamy, M.S.; Harfman-Todorovic, M.; Elasser, A.; Chi, S.; Steigerwald, R.L.; Sabate, J.A.; McCann, A.J.; Zhang, L.; Mueller, F.J. An Efficient Partial Power Processing DC/DC Converter for Distributed PV Architectures. IEEE Trans. Power Electron. 2014, 29, 674–686. [Google Scholar] [CrossRef]
- Suntio, T.; Kuperman, A. Comments on an Efficient Partial Power Processing DC/DC Converter for Distributed PV Architectures. IEEE Trans. Power Electron. 2015, 30, 2372. [Google Scholar] [CrossRef]
- Chen, M.; Gao, F.; Yang, T. A central capacitor partial power processing DC/DC converter. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 1995–2002. [Google Scholar]
- Chen, M.; Gao, F.; Sha, Z. A zero-voltage-transition auxiliary network for central capacitor partial power processing DC/DC converter. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1170–1176. [Google Scholar]
- Elrayyah, A.; Badawey, M.; Sozer, Y. Feeding partial power into line capacitors for low cost and efficient MPPT of photovoltaic strings. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 392–397. [Google Scholar]
- Zientarski, J.R.R.; Pinheiro, J.R.; da Silva Martins, M.L.; Hey, H.L. Understanding the partial power processing concept: A case-study of buck-boost dc/dc series regulator. In Proceedings of the 2015 IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, Brazil, 29 November–2 December 2015; pp. 1–6. [Google Scholar]
- Karimi, M.; Mahdavi, M.; Torki Harchegani, A. A New Soft Switching qZSC Converter by Using Coupled Inductor. Electr. Power Compon. Syst. 2018, 46, 270–277. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Peng, F.Z.; Blaabjerg, F.; Loh, P.C.; Town, G.E. Impedance-Source Networks for Electric Power Conversion Part I: A Topological Review. IEEE Trans. Power Electron. 2015, 30, 699–716. [Google Scholar] [CrossRef]
- Peng, F.Z. Z-source inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Cao, D.; Peng, F.Z. A Family of Z-source and Quasi-Z-source DC-DC Converters. In Proceedings of the 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 1097–1101. [Google Scholar]
- Chub, A.; Vinnikov, D.; Blaabjerg, F.; Peng, F.Z. A Review of Galvanically Isolated Impedance-Source DC–DC Converters. IEEE Trans. Power Electron. 2016, 31, 2808–2828. [Google Scholar] [CrossRef]
- Ran, Y.; Wang, W.; Liu, K.; Liu, H. A Power Decoupling Solution for Improved Y-Source Single-Phase Grid-Connected Inverter. Electr. Power Compon. Syst. 2018, 1–12. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H. Z-Source Inverter: Topology Improvements Review. IEEE Ind. Electron. Mag. 2016, 10, 6–24. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Peng, F.Z.; Blaabjerg, F.; Loh, P.C.; Town, G.E.; Yang, S. Impedance-Source Networks for Electric Power Conversion Part II: Review of Control and Modulation Techniques. IEEE Trans. Power Electron. 2015, 30, 1887–1906. [Google Scholar] [CrossRef]
- Beer, K.; Piepenbreier, B. Properties and advantages of the quasi-Z-source inverter for DC-AC conversion for electric vehicle applications. In Proceedings of the 2010 Emobility—Electrical Power Train, Leipzig, Germany, 8–9 November 2010; pp. 1–6. [Google Scholar]
- Nabinejad, A.; Rajaei, A.; Mardaneh, M. A Systematic Approach to Extract State Space Averaged Equations and Small Signal Model of Partial Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2019, in press. [Google Scholar] [CrossRef]


| Converter | Voltage Stress | Current Stress | |
| Switches | Full Power QZSC [22] | ||
| Basic PPP QZSC | |||
| Proposed PPP QZSC | |||
| Diode D1 | Full Power QZSC | ||
| Basic PPP QZSC | |||
| Proposed PPP QZSC | |||
| Diode D2 & D3 | Full Power QZSC | ||
| Basic PPP QZSC | |||
| Proposed PPP QZSC | |||
| Converter | Inductor L1 | Inductor L2 | |
| Current Stress | Full Power QZSC | ||
| Basic PPP QZSC | |||
| Proposed PPP QZSC | |||
| Parameters | Symbols | Value/Part no. |
|---|---|---|
| Output Voltage | Vout | 90 V |
| Input Voltage | Vin | 20 V |
| Switching Frequency | fs | 40 kHz |
| Duty Cycle | Dt | 0.6 |
| Transformer turn ratio | n | 1:1:1 |
| Primary and secondary resistance | Rwp, Rws | 0.01 Ω |
| Inductance | L1, L2 | 200 µH |
| Inductor resistance | RL1, RL2 | 0.01 Ω |
| Diode Forward Voltage | Vd | 0.98 V |
| capacitance | C1, C2, C3, C4 | 100 µF |
| Switch on resistance | Ron | 0.18 Ω |
| Switch | S1, S2 | IRF640N |
| Converter | Individual Converter Output Voltage | Individual Converter Efficiency | System Efficiency |
|---|---|---|---|
| Full power QZSC | |||
| Basic PPP QZSC | |||
| Proposed PPP QZSC |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Honarmand, S.; Rajaei, A.; Shahparasti, M.; Luna, A.; Pouresmaeil, E. A Modified Partial Power structure for Quasi Z-Source Converter to Improve Voltage Gain and Power Rating. Energies 2019, 12, 2139. https://doi.org/10.3390/en12112139
Honarmand S, Rajaei A, Shahparasti M, Luna A, Pouresmaeil E. A Modified Partial Power structure for Quasi Z-Source Converter to Improve Voltage Gain and Power Rating. Energies. 2019; 12(11):2139. https://doi.org/10.3390/en12112139
Chicago/Turabian StyleHonarmand, Shahin, Amirhossein Rajaei, Mahdi Shahparasti, Alvaro Luna, and Edris Pouresmaeil. 2019. "A Modified Partial Power structure for Quasi Z-Source Converter to Improve Voltage Gain and Power Rating" Energies 12, no. 11: 2139. https://doi.org/10.3390/en12112139
APA StyleHonarmand, S., Rajaei, A., Shahparasti, M., Luna, A., & Pouresmaeil, E. (2019). A Modified Partial Power structure for Quasi Z-Source Converter to Improve Voltage Gain and Power Rating. Energies, 12(11), 2139. https://doi.org/10.3390/en12112139








