District Heating Load Prediction Algorithm Based on Feature Fusion LSTM Model
Abstract
:1. Introduction
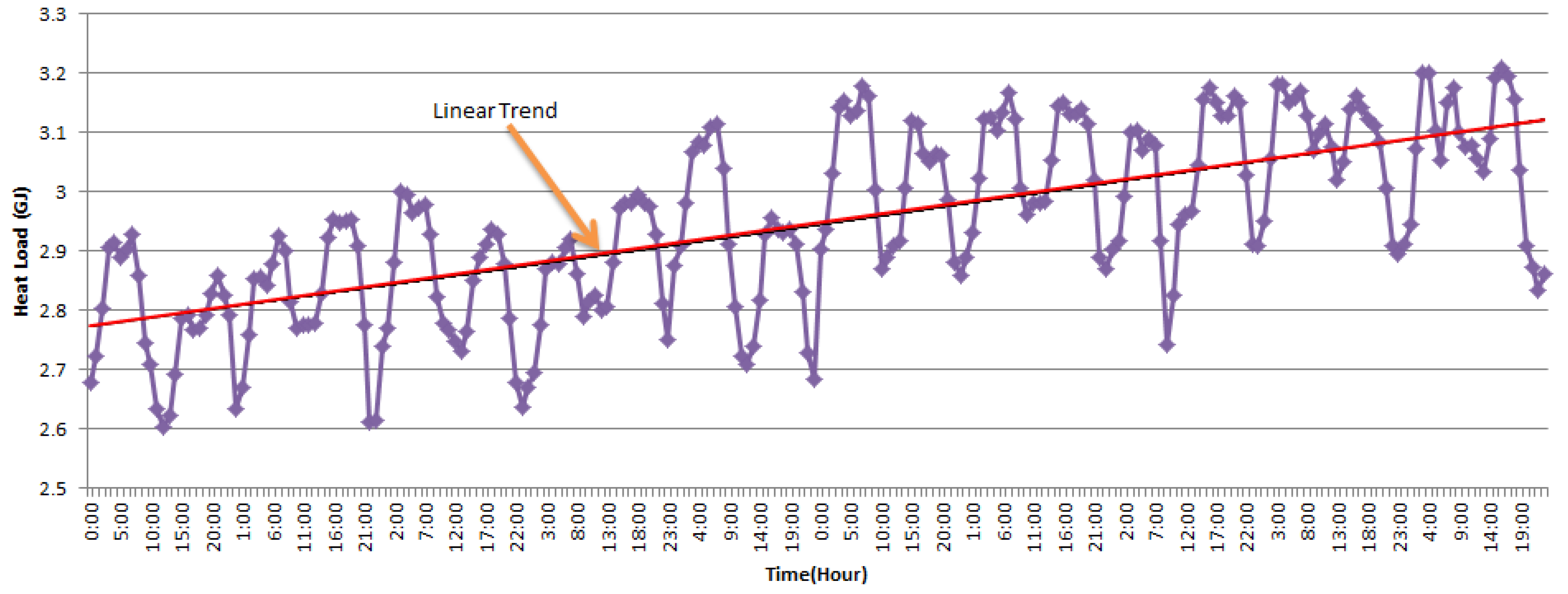
2. Feature Analysis and Selection of Heating Load in SDHS
- (1)
- Internal factors:
- Historical heat load (GJ)
- Secondary supply temperature (supply temp for short) (°C)
- Secondary return temperature (return temp for short) (°C)
- Instantaneous flow rate (flow rate for short) (m3/h)
- (2)
- External factors:
- Outdoor temperature (outdoor temp for short) (°C)
3. Methodology and Analysis
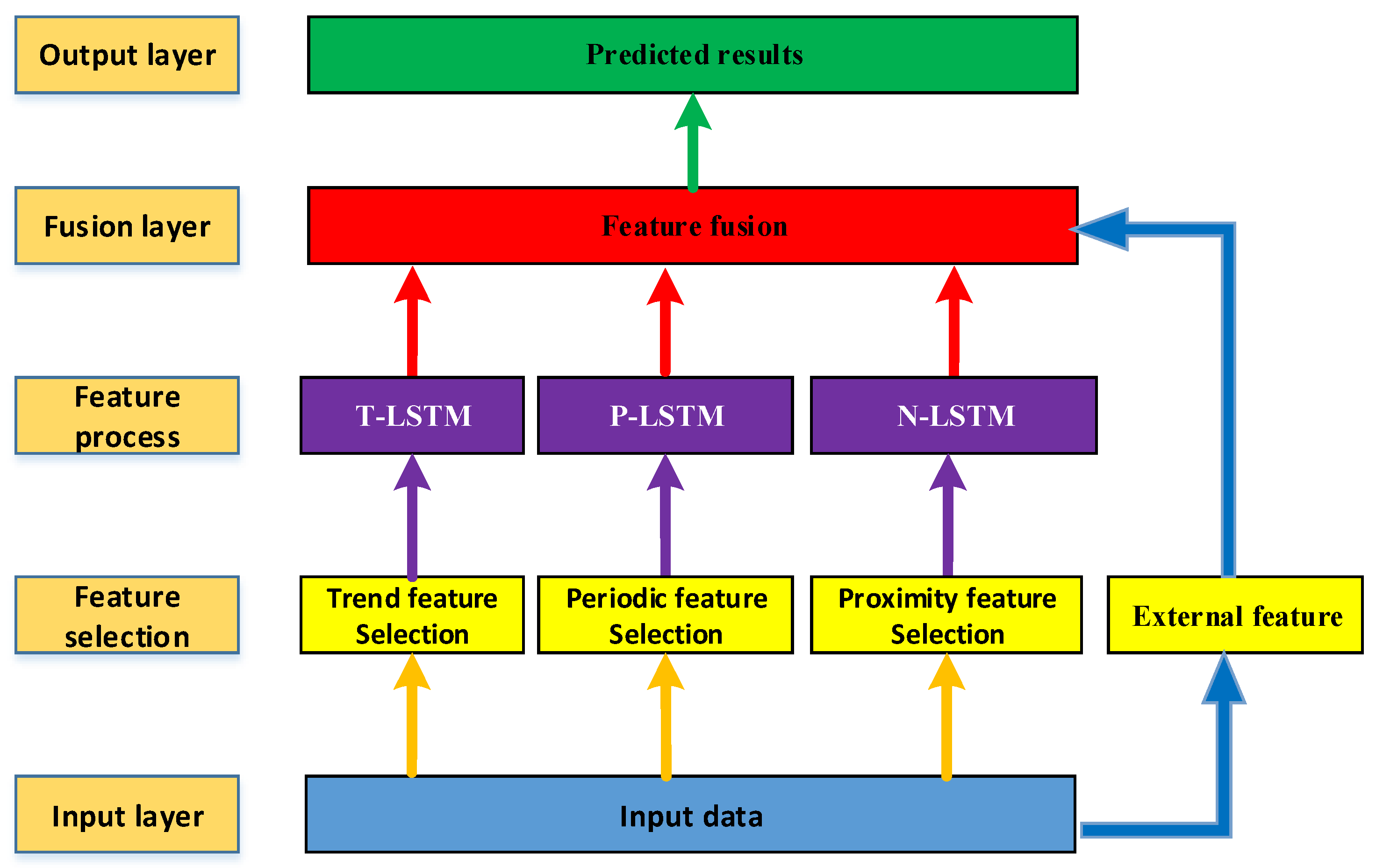
3.1. The Architecture of the Proposed FFLSTM
3.2. The Mathmatical Model of FFLSTM
- represents the input vector composed of the outdoor temperature, heat consumption, secondary supply temperature, secondary return temperature, and instantaneous flow rate in the (h-i)th hour. The hours factor p = (1,2,…,24) represents the interval from the predicted time of the proximity input data, ranging from 1 to 24 h.
- represents the input vectors such as the outdoor temperature, heat consumption, secondary supply temperature, secondary return temperature, and instantaneous flow in the (h-24j)th hour. The days factor q = (1,2,…,7) represents the interval from the predicted time of the periodic input data, ranging from 1 to 7 days.
- represents the input vector of the outdoor temperature, heat consumption, secondary water supply temperature, secondary water return temperature, and instantaneous flow in the (h-24×7k)th hour. The weeks factor r = (1, 2, 3, 4) represents the interval from the predicted time of the trend input data, ranging from 1 to 4 weeks.
3.3. Evaluation Criteria
4. Experiments and Discussion
4.1. System Background and Data Description
4.2. Time Delay Factors Selection and Different Time-Scale Models
4.3. Parameter Selection and Performance Evaluation
4.4. Compared with the Base LSTM Models
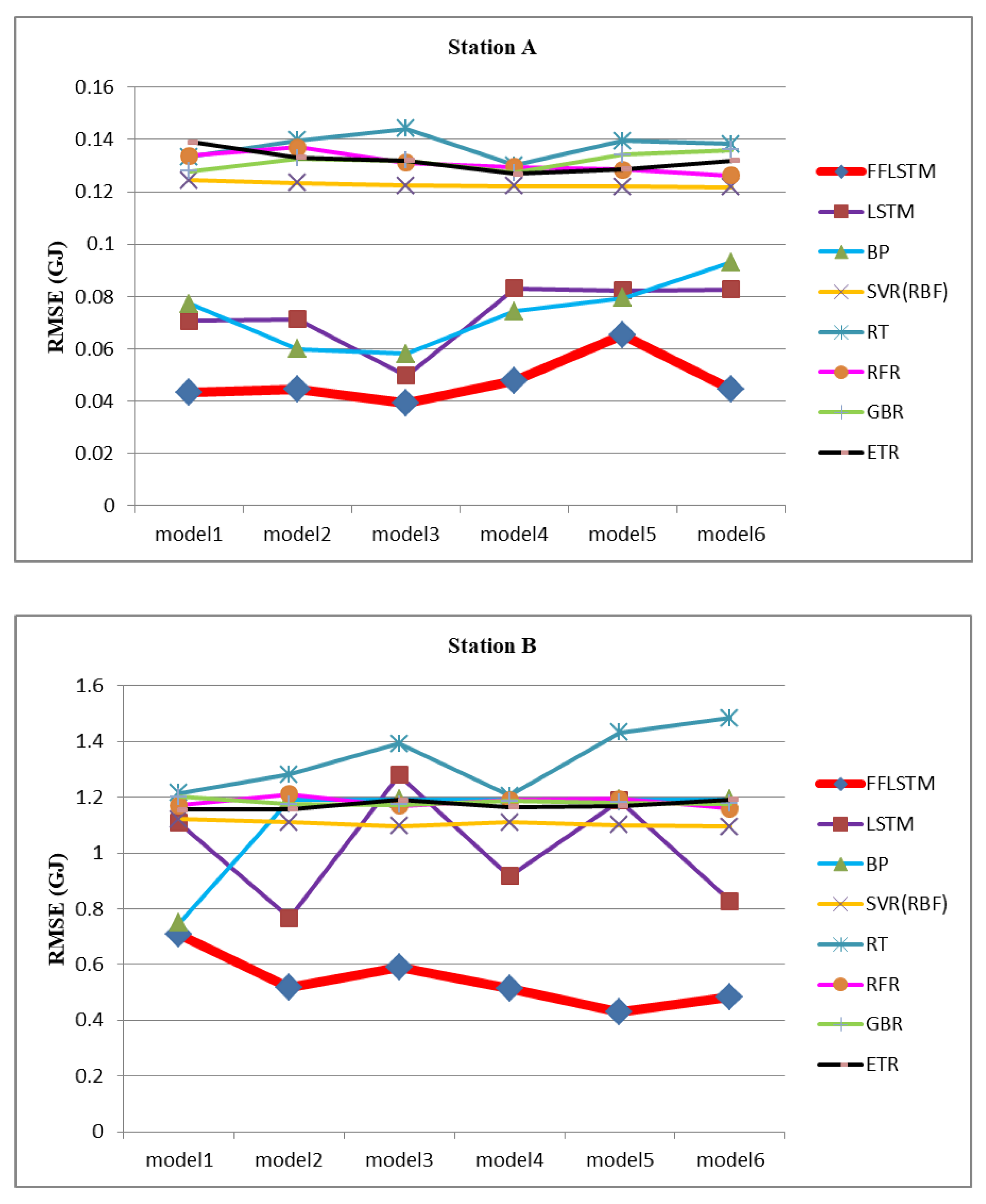
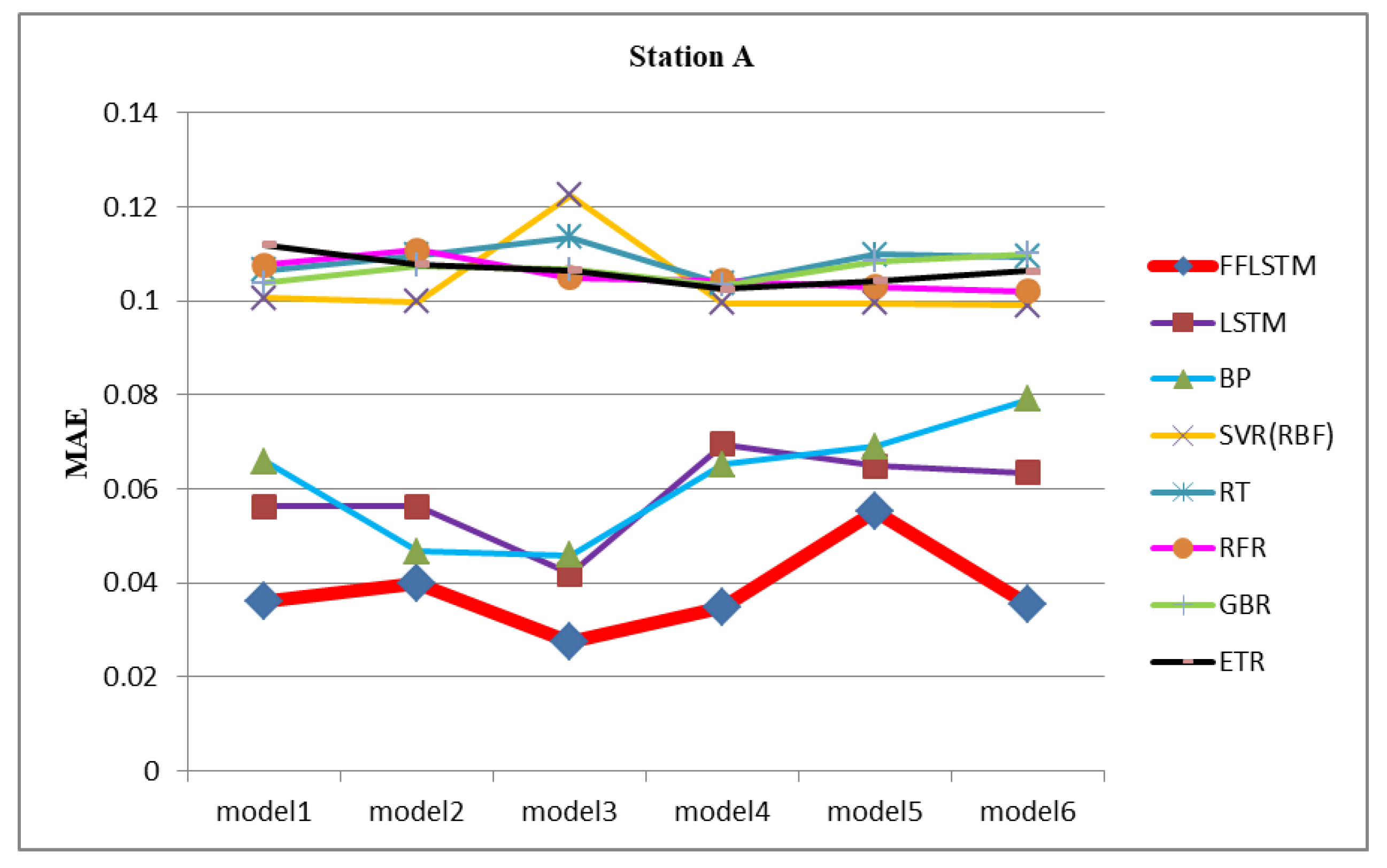
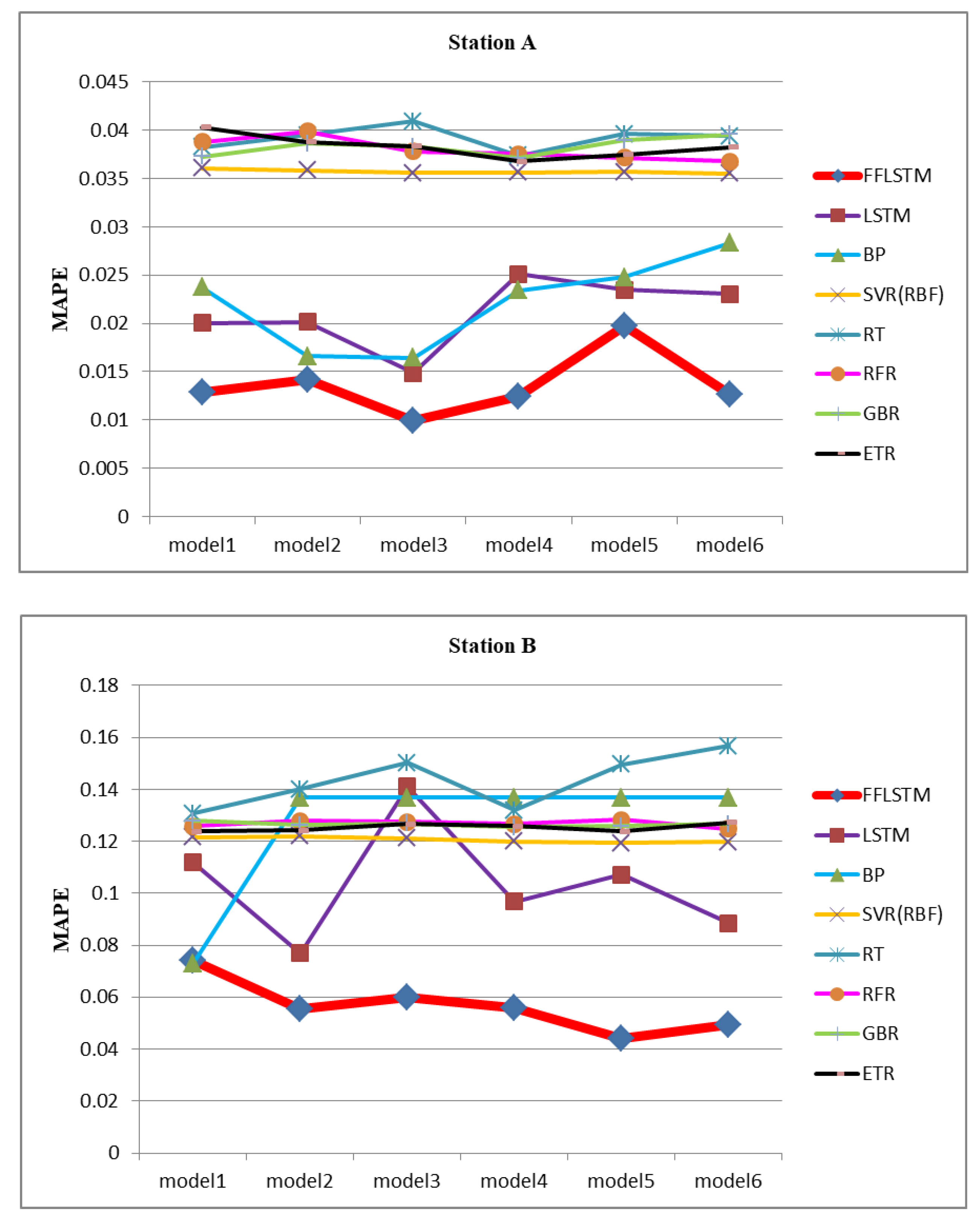
4.5. Compared with Other Algorithms
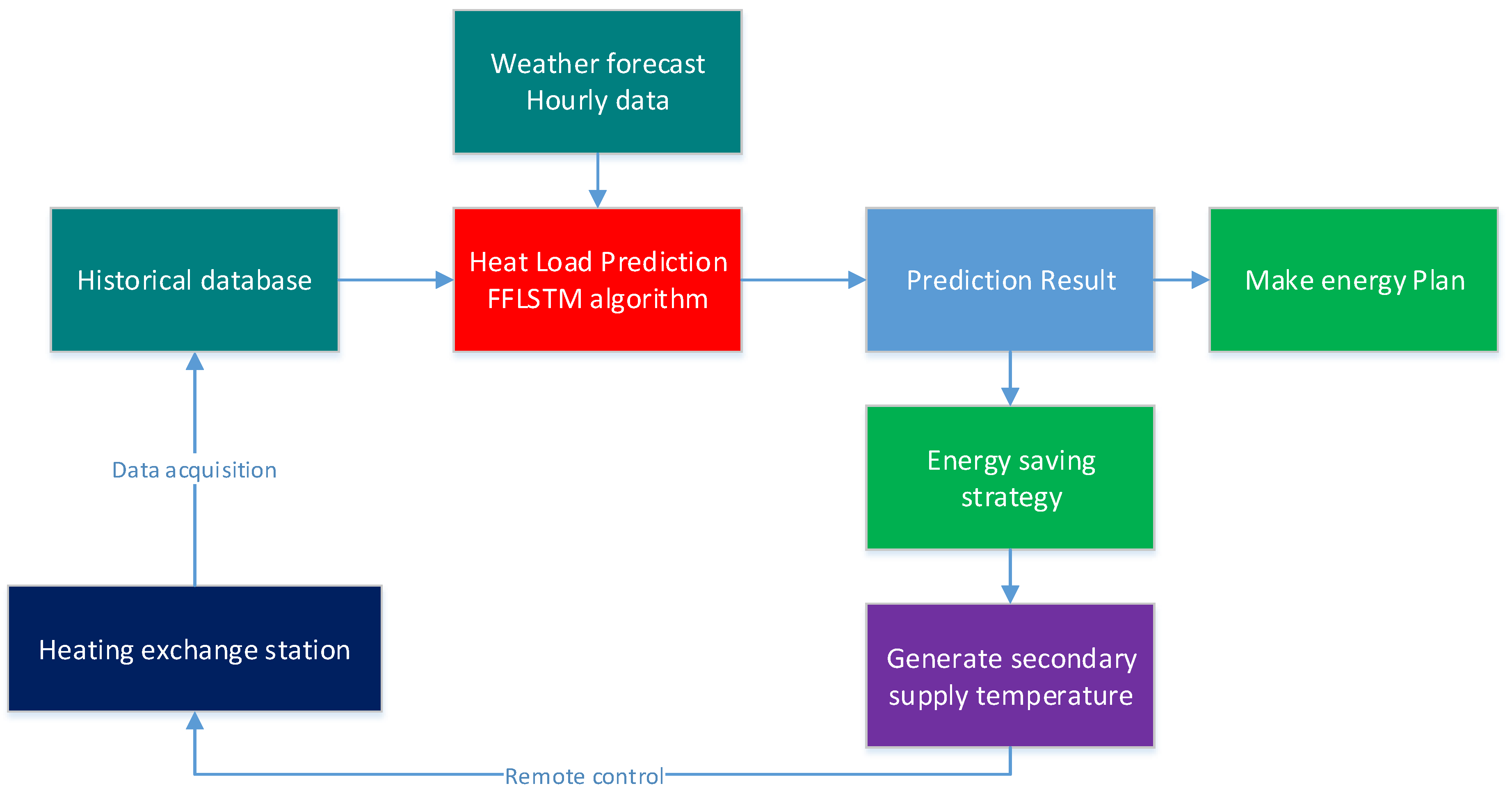
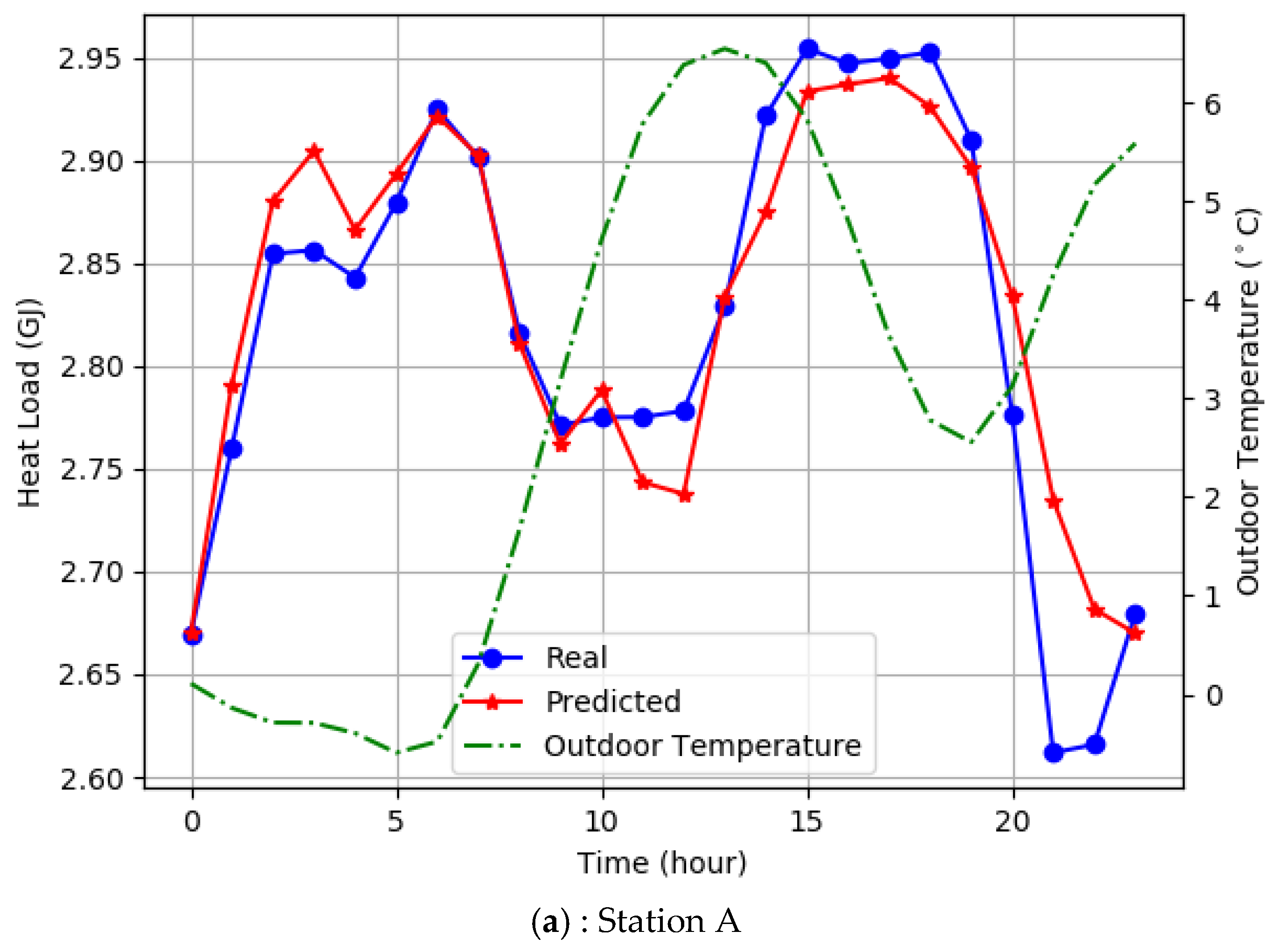
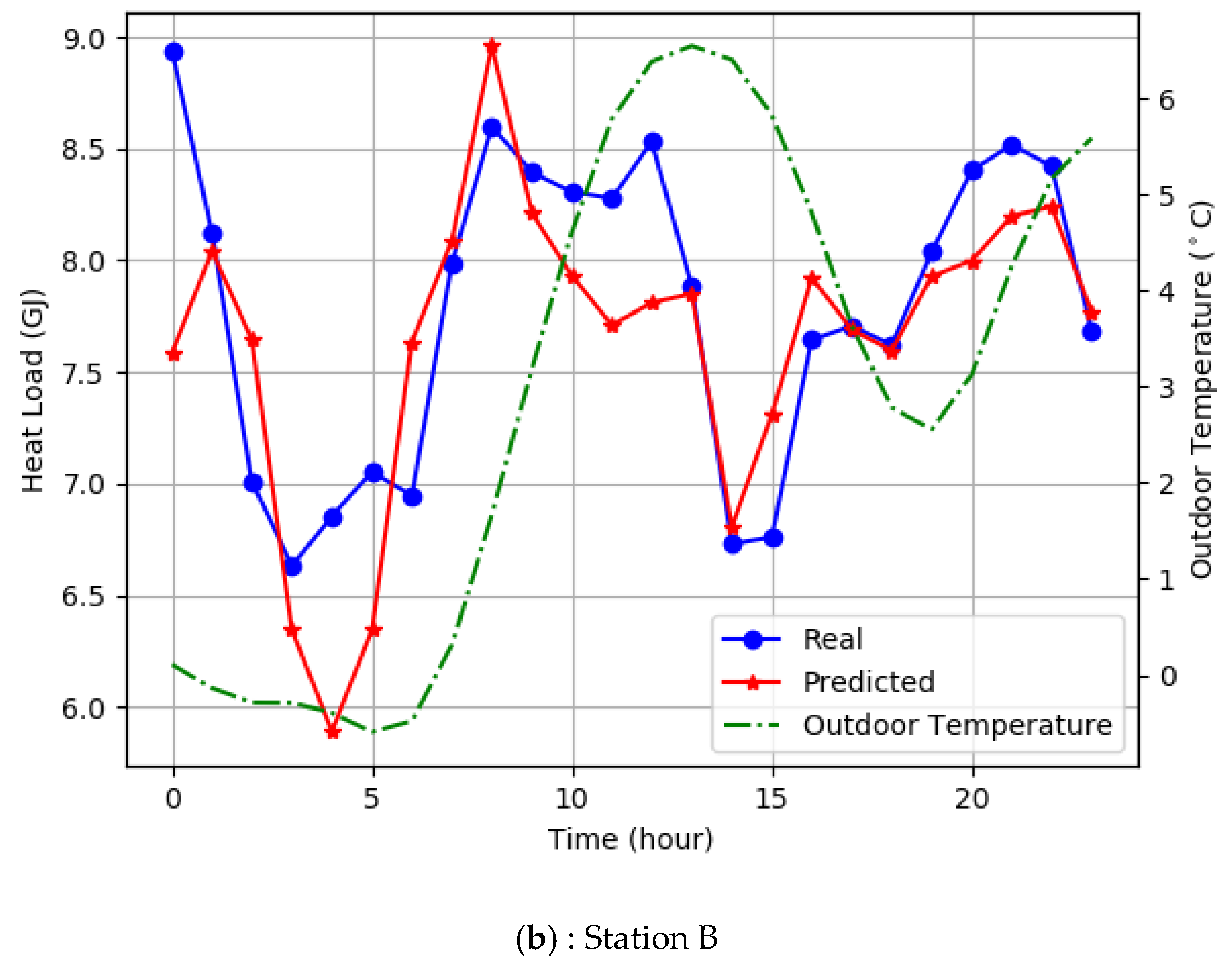
4.6. System Verification and Energy Saving Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ANFIS | adaptive neuro-fuzzy inferences system |
| ANN | artificial neural networks |
| BP | back propagation |
| DHS | district heating system |
| DL | deep learning |
| ELM | extreme learning machines |
| ETR | extra trees regression |
| FFA | firefly algorithm |
| FFLSTM | feature fusion long short-term memory |
| GA | genetic algorithm |
| GA–SVR | genetic algorithm–support vector regression |
| GBR | gradient boosting regression |
| IA | immune algorithm |
| IoT | Internet of Things |
| LSTM | long short-term memory |
| MAE | mean absolute error |
| MAPE | mean absolute percentage error |
| MVA | multivariate autoregressive |
| N-LSTM | proximity LSTM |
| PLS | Partial Least Square |
| P-LSTM | periodic LSTM |
| PM10 | particulate matter 10 |
| PSO | particle swarm optimization |
| RBF | radial kernel function |
| RFR | random forest regression |
| RMSE | root-mean-square error |
| RNN | recurrent neural networks |
| RT | regression tree |
| SCADA | supervisory control and data acquisition |
| SDHS | smart district heating system |
| SVM | support vector machine |
References
- Ebenstein, A.; Fan, M.Y.; Greenstone, M.; He, G.J.; Zhou, M.G. New evidence on the impact of sustained exposure to air pollution on life expectancy from China’s Huai River Policy. Proc. Natl. Acad. Sci. USA 2017, 114, 10384–10389. [Google Scholar] [CrossRef] [PubMed]
- Chou, J.-S.; Bui, D.-K. Modeling heating and cooling loads by artificial intelligence for energy-efficient building design. Energy Build. 2014, 82, 437–446. [Google Scholar] [CrossRef]
- Dotzauer, E. Simple model for prediction of loads in district-heating systems. Appl. Energy 2002, 73, 277–284. [Google Scholar] [CrossRef]
- Karatasou, S.; Santamouris, M.; Geros, V. Modeling and predicting building’s energy use with artificial neural networks: Methods and results. Energy Build. 2006, 38, 949–958. [Google Scholar] [CrossRef]
- Boithias, F.; El Mankibi, M.; Michel, P. Genetic algorithms based optimization of artificial neural network architecture for buildings’ indoor discomfort and energy consumption prediction. Build. Simul. 2012, 5, 95–106. [Google Scholar] [CrossRef]
- Cai, H.; Shen, S.; Lin, Q.; Li, X.; Xiao, H. Predicting the energy consumption of residential buildings for regional electricity supply-side and demand-side management. IEEE Access 2019, 7, 30386–30397. [Google Scholar] [CrossRef]
- Zhang, F.; Deb, C.; Lee, S.E.; Yang, J.; Shah, K.W. Time series forecasting for building energy consumption using weighted Support Vector Regression with differential evolution optimization technique. Energy Build. 2016, 126, 94–103. [Google Scholar] [CrossRef]
- Fan, G.-F.; Peng, L.-L.; Hong, W.-C.; Sun, F. Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2016, 173, 958–970. [Google Scholar] [CrossRef]
- Hong, W.-C. Electric load forecasting by support vector model. Appl. Math. Model. 2009, 33, 2444–2454. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Q.; Yuan, T. Research on short-term and ultra-short-term cooling load prediction models for office buildings. Energy Build. 2017, 154, 254–267. [Google Scholar] [CrossRef]
- Wang, M.; Tian, Q. Dynamic Heat Supply Prediction Using Support Vector Regression Optimized by Particle Swarm Optimization Algorithm. Math. Probl. Eng. 2016, 2016, 3968324. [Google Scholar] [CrossRef]
- Al-Shammari, E.T.; Keivani, A.; Shamshirband, S.; Mostafaeipour, A.; Yee, P.L.; Petkovic, D.; Ch, S. Prediction of heat load in district heating systems by Support Vector Machine with Firefly searching algorithm. Energy 2016, 95, 266–273. [Google Scholar] [CrossRef]
- Lee, A.; Geem, Z.; Suh, K.-D. Determination of Optimal Initial Weights of an Artificial Neural Network by Using the Harmony Search Algorithm: Application to Breakwater Armor Stones. Appl. Sci. 2016, 6, 164. [Google Scholar] [CrossRef]
- Dalipi, F.; Yildirim Yayilgan, S.; Gebremedhin, A. Data-Driven Machine-Learning Model in District Heating System for Heat Load Prediction: A Comparison Study. Appl. Comput. Intell. Soft Comput. 2016, 2016, 3403150. [Google Scholar] [CrossRef]
- Sajjadi, S.; Shamshirband, S.; Alizamir, M.; Yee, P.L.; Mansor, Z.; Manaf, A.A.; Altameem, T.A.; Mostafaeipour, A. Extreme learning machine for prediction of heat load in district heating systems. Energy Build. 2016, 122, 222–227. [Google Scholar] [CrossRef]
- Roy, S.S.; Roy, R.; Balas, V.E. Estimating heating load in buildings using multivariate adaptive regression splines, extreme learning machine, a hybrid model of MARS and ELM. Renew. Sustain. Energy Rev. 2018, 82, 4256–4268. [Google Scholar]
- Kato, K.; Sakawa, M.; Ishimaru, K.; Ushiro, S.; Shibano, T. Heat Load Prediction through Recurrent Neural Network in District Heating and Cooling Systems. In Proceedings of the 2008 IEEE International Conference on Systems, Man And Cybernetics, Singapore, 12–15 October 2008; p. 1400. [Google Scholar]
- Shamshirband, S.; Petković, D.; Enayatifar, R.; Hanan Abdullah, A.; Marković, D.; Lee, M.; Ahmad, R. Heat load prediction in district heating systems with adaptive neuro-fuzzy method. Renew. Sustain. Energy Rev. 2015, 48, 760–767. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Li, C.; Ding, Z.; Zhao, D.; Yi, J.; Zhang, G. Building Energy Consumption Prediction: An Extreme Deep Learning Approach. Energies 2017, 10, 1025. [Google Scholar] [CrossRef]
- Fu, G. Deep belief network based ensemble approach for cooling load forecasting of air-conditioning system. Energy 2018, 148, 269–282. [Google Scholar] [CrossRef]
- Liu, F.; Cai, M.; Wang, L.; Lu, Y. An ensemble model based on adaptive noise reducer and over-fitting prevention LSTM for multivariate time series forecasting. IEEE Access 2019, 7, 26102–26115. [Google Scholar] [CrossRef]
- Han, L.Y.; Peng, Y.X.; Li, Y.H.; Yong, B.B.; Zhou, Q.G.; Shu, L. Enhanced Deep Networks for short-Term and Medium-Term Load Forecasting. IEEE Access 2019, 7, 4045–4055. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal Deep Learning LSTM Model for Electric Load Forecasting using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1626. [Google Scholar] [CrossRef]
- Tian, C.; Ma, J.; Zhang, C.; Zhan, P. A Deep Neural Network Model for Short-Term Load Forecast Based on Long Short-Term Memory Network and Convolutional Neural Network. Energies 2018, 11, 3493. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M. Single and Multi-Sequence Deep Learning Models for Short and Medium Term Electric Load Forecasting. Energies 2019, 12, 149. [Google Scholar] [CrossRef]
- Liang, Y.; Ke, S.; Zhang, J.; Yi, X.; Zheng, Y. GeoMAN: Multi-Level Attention Networks for Geo-Sensory Time Series Prediction; IJCAI: Stockholm, Sweden, 19 July 2018; pp. 3428–3434. [Google Scholar]
- Lopez, E.; Valle, C.; Allende, H.; Gil, E.; Madsen, H. Wind Power Forecasting Based on Echo State Networks and Long Short-Term Memory. Energies 2018, 11, 526. [Google Scholar] [CrossRef]
- Shi, X.; Lei, X.; Huang, Q.; Huang, S.; Ren, K.; Hu, Y. Hourly Day-Ahead Wind Power Prediction Using the Hybrid Model of Variational Model Decomposition and Long Short-Term Memory. Energies 2018, 11, 3227. [Google Scholar] [CrossRef]


| Literature | Algorithm | Influencing Factors |
|---|---|---|
| [3] | ARMA | outdoor temperature, heat load, behavior of the consumers |
| [11] | PSO–SVR | outdoor temperature, supply water temperature, supply water pressure, circular flow, heat load |
| [12] | SVM–FFA | time lagged heat load, outdoor temperature, primary return temperatures |
| [14] | SVR, PLS, RT | forward temperature, return temperature, flow rate, heat load |
| [15] | ELM | outdoor temperature, primary supply temperature, primary return temperature, flow on primary side |
| [18] | ANFIS | outdoor temperature, primary supply temperature, primary return temperature, secondary supply temperature, secondary return temperature, flow on primary side |
| Time intervals | Historical Heat load | Outdoor Temp | Supply Temp | Return Temp | Flow Rate |
|---|---|---|---|---|---|
| p = 1 h | 0.913 | −0.339 | 0.767 | 0.710 | 0.783 |
| p = 2 h | 0.729 | −0.301 | 0.577 | 0.538 | 0.549 |
| p = 3 h | 0.553 | −0.275 | 0.379 | 0.360 | 0.320 |
| p = 4 h | 0.408 | 0.271 | 0.206 | 0.208 | 0.124 |
| p = 5 h | 0.291 | 0.294 | 0.090 | 0.123 | 0.027 |
| q =1 d | 0.765 | −0.224 | 0.768 | 0.717 | 0.693 |
| q = 2 d | 0.626 | −0.219 | 0.579 | 0.396 | 0.524 |
| q = 3 d | 0.151 | −0.157 | 0.045 | −0.086 | 0.140 |
| q = 4 d | −0.128 | −0.117 | −0.189 | −0.283 | 0.069 |
| r = 1 w | −0.529 | 0.257 | −0.545 | −0.578 | 0.390 |
| r = 2 w | 0.395 | −0.126 | 0.726 | 0.691 | 0.377 |
| Model | Proximity Factor (p) | Periodic Factor (q) | Trend Factor (r) |
|---|---|---|---|
| model 1 | 1 h | 1 d | 1 w |
| model 2 | 2 h | 1 d | 1 w |
| model 3 | 3 h | 1 d | 1 w |
| model 4 | 1 h | 2 d | 1 w |
| model 5 | 2 h | 2 d | 1 w |
| model 6 | 3 h | 2 d | 1 w |
| Parameters | Value | Description |
|---|---|---|
| hide_unit | 20 | the number of hidden cells |
| learn_rate | 0.006 | the value of the learning rate |
| time_step | 5 | the value of the time step |
| batch_size | 20 | the value of the batch size |
| iter_count | 200 | the number of iterations |
| Parameters Set | Turning Parameter | Value | Train | Test | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | MAPE | RMSE | MAE | MAPE | |||
| hide_unit = 20 time_step = 5 batch_size = 20 iter_count = 200 | learn_rate | 0.0006 | 0.027 | 0.020 | 0.007 | 0.049 | 0.039 | 0.014 |
| 0.0001 | 0.043 | 0.034 | 0.011 | 0.053 | 0.044 | 0.016 | ||
| 0.003 | 0.021 | 0.014 | 0.005 | 0.048 | 0.039 | 0.014 | ||
| 0.001 | 0.027 | 0.019 | 0.006 | 0.048 | 0.040 | 0.014 | ||
| 0.002 | 0.022 | 0.014 | 0.005 | 0.044 | 0.035 | 0.013 | ||
| learn_rate = 0.002 hide_unit = 20 time_step = 5 iter_count = 200 | batch_size | 5 | 0.187 | 0.013 | 0.004 | 0.045 | 0.036 | 0.013 |
| 10 | 0.025 | 0.019 | 0.006 | 0.052 | 0.041 | 0.015 | ||
| 12 | 0.021 | 0.015 | 0.005 | 0.051 | 0.042 | 0.015 | ||
| 15 | 0.022 | 0.015 | 0.004 | 0.046 | 0.038 | 0.013 | ||
| 20 | 0.022 | 0.014 | 0.005 | 0.044 | 0.035 | 0.013 | ||
| learn_rate = 0.002 hide_unit = 20 batch_size = 20 iter_count = 200 | time_step | 7 | 0.020 | 0.013 | 0.004 | 0.051 | 0.044 | 0.016 |
| 10 | 0.021 | 0.016 | 0.005 | 0.051 | 0.042 | 0.015 | ||
| 12 | 0.021 | 0.015 | 0.005 | 0.038 | 0.029 | 0.011 | ||
| 15 | 0.019 | 0.013 | 0.004 | 0.054 | 0.042 | 0.015 | ||
| 20 | 0.019 | 0.014 | 0.005 | 0.045 | 0.037 | 0.013 | ||
| learn_rate = 0.002 batch_size = 20 time_step = 12 iter_count = 200 | hide_unit | 5 | 0.033 | 0.025 | 0.009 | 0.031 | 0.026 | 0.009 |
| 7 | 0.029 | 0.023 | 0.008 | 0.041 | 0.034 | 0.012 | ||
| 10 | 0.023 | 0.017 | 0.006 | 0.035 | 0.031 | 0.011 | ||
| 12 | 0.022 | 0.017 | 0.006 | 0.046 | 0.034 | 0.012 | ||
| 15 | 0.019 | 0.014 | 0.005 | 0.044 | 0.035 | 0.013 | ||
| Parameters | Value | Description |
|---|---|---|
| hide_unit | 5 | the number of hidden cells |
| learn_rate | 0.002 | the value of the learning rate |
| time_step | 12 | the value of the time step |
| batch_size | 20 | the value of the batch size |
| iter_count | 200 | the number of iterations with early stopping |
| Algorithm | Model | Station A | Station B | ||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | MAPE | RMSE | MAE | MAPE | ||
| FFLSTM | model 1 | 0.043 | 0.035 | 0.012 | 0.624 | 0.491 | 0.064 |
| N-LSTM | 0.050 | 0.039 | 0.014 | 0.707 | 0.575 | 0.074 | |
| P-LSTM | 0.099 | 0.087 | 0.031 | 1.205 | 0.953 | 0.128 | |
| T-LSTM | 0.129 | 0.113 | 0.040 | 1.061 | 0.883 | 0.118 | |
| FFLSTM | model 2 | 0.044 | 0.040 | 0.014 | 0.518 | 0.414 | 0.055 |
| N-LSTM | 0.045 | 0.034 | 0.012 | 0.694 | 0.593 | 0.079 | |
| P-LSTM | 0.104 | 0.089 | 0.031 | 1.468 | 1.086 | 0.149 | |
| T-LSTM | 0.131 | 0.107 | 0.038 | 1.038 | 0.882 | 0.117 | |
| FFLSTM | model 3 | 0.039 | 0.028 | 0.010 | 0.589 | 0.453 | 0.060 |
| N-LSTM | 0.039 | 0.029 | 0.010 | 0.920 | 0.699 | 0.093 | |
| P-LSTM | 0.106 | 0.095 | 0.033 | 1.325 | 0.955 | 0.128 | |
| T-LSTM | 0.136 | 0.105 | 0.037 | 1.223 | 1.010 | 0.131 | |
| FFLSTM | model 4 | 0.048 | 0.035 | 0.012 | 0.512 | 0.422 | 0.056 |
| N-LSTM | 0.048 | 0.035 | 0.013 | 0.834 | 0.597 | 0.081 | |
| P-LSTM | 0.072 | 0.063 | 0.022 | 1.448 | 1.129 | 0.153 | |
| T-LSTM | 0.097 | 0.081 | 0.029 | 1.511 | 1.130 | 0.157 | |
| FFLSTM | model 5 | 0.065 | 0.050 | 0.018 | 0.428 | 0.335 | 0.044 |
| N-LSTM | 0.066 | 0.055 | 0.020 | 0.763 | 0.614 | 0.084 | |
| P-LSTM | 0.088 | 0.076 | 0.027 | 0.964 | 0.760 | 0.102 | |
| T-LSTM | 0.133 | 0.101 | 0.035 | 0.999 | 0.798 | 0.109 | |
| FFLSTM | model 6 | 0.042 | 0.032 | 0.012 | 0.485 | 0.381 | 0.049 |
| N-LSTM | 0.045 | 0.035 | 0.013 | 0.699 | 0.579 | 0.078 | |
| P-LSTM | 0.090 | 0.074 | 0.026 | 1.071 | 0.878 | 0.115 | |
| T-LSTM | 0.097 | 0.078 | 0.028 | 1.232 | 1.014 | 0.136 | |
| Algorithm | Model | Station A | Station B | ||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | MAPE | RMSE | MAE | MAPE | ||
| FFLSTM | model1 | 0.043 | 0.035 | 0.012 | 0.707 | 0.575 | 0.074 |
| LSTM | 0.070 | 0.056 | 0.020 | 1.109 | 0.850 | 0.112 | |
| BP | 0.077 | 0.065 | 0.023 | 0.750 | 0.549 | 0.073 | |
| SVR(RBF) | 0.124 | 0.100 | 0.036 | 1.121 | 0.930 | 0.122 | |
| RT | 0.133 | 0.106 | 0.038 | 1.216 | 0.994 | 0.131 | |
| RFR | 0.133 | 0.107 | 0.038 | 1.172 | 0.957 | 0.126 | |
| GBR | 0.127 | 0.103 | 0.037 | 1.201 | 0.980 | 0.128 | |
| ETR | 0.139 | 0.111 | 0.040 | 1.155 | 0.947 | 0.124 | |
| FFLSTM | model2 | 0.044 | 0.040 | 0.014 | 0.518 | 0.414 | 0.055 |
| LSTM | 0.071 | 0.056 | 0.020 | 0.766 | 0.590 | 0.077 | |
| BP | 0.060 | 0.047 | 0.017 | 1.191 | 0.966 | 0.137 | |
| SVR(RBF) | 0.123 | 0.100 | 0.036 | 1.109 | 0.921 | 0.122 | |
| RT | 0.140 | 0.110 | 0.039 | 1.282 | 1.042 | 0.140 | |
| RFR | 0.137 | 0.111 | 0.040 | 1.210 | 0.983 | 0.128 | |
| GBR | 0.133 | 0.107 | 0.039 | 1.176 | 0.960 | 0.126 | |
| ETR | 0.133 | 0.108 | 0.039 | 1.157 | 0.948 | 0.124 | |
| FFLSTM | model3 | 0.039 | 0.028 | 0.010 | 0.589 | 0.453 | 0.060 |
| LSTM | 0.050 | 0.042 | 0.015 | 1.279 | 1.041 | 0.141 | |
| BP | 0.058 | 0.046 | 0.016 | 1.191 | 0.966 | 0.137 | |
| SVR(RBF) | 0.122 | 0.122 | 0.036 | 1.096 | 0.912 | 0.121 | |
| RT | 0.144 | 0.114 | 0.041 | 1.393 | 1.143 | 0.150 | |
| RFR | 0.131 | 0.105 | 0.038 | 1.170 | 0.964 | 0.127 | |
| GBR | 0.132 | 0.107 | 0.038 | 1.173 | 0.960 | 0.127 | |
| ETR | 0.132 | 0.107 | 0.038 | 1.189 | 0.972 | 0.127 | |
| FFLSTM | model4 | 0.033 | 0.027 | 0.010 | 0.556 | 0.445 | 0.058 |
| LSTM | 0.090 | 0.068 | 0.025 | 1.059 | 0.832 | 0.108 | |
| BP | 0.066 | 0.050 | 0.018 | 1.191 | 0.966 | 0.137 | |
| SVR(RBF) | 0.123 | 0.100 | 0.036 | 1.110 | 0.923 | 0.120 | |
| RT | 0.133 | 0.106 | 0.038 | 1.234 | 1.006 | 0.132 | |
| RFR | 0.122 | 0.098 | 0.035 | 1.210 | 0.982 | 0.128 | |
| GBR | 0.142 | 0.116 | 0.041 | 1.174 | 0.963 | 0.125 | |
| ETR | 0.130 | 0.106 | 0.038 | 1.167 | 0.962 | 0.126 | |
| FFLSTM | model5 | 0.055 | 0.037 | 0.013 | 0.572 | 0.414 | 0.056 |
| LSTM | 0.105 | 0.075 | 0.027 | 1.169 | 0.969 | 0.129 | |
| BP | 0.068 | 0.051 | 0.018 | 1.191 | 0.966 | 0.137 | |
| SVR(RBF) | 0.122 | 0.099 | 0.036 | 1.093 | 0.913 | 0.119 | |
| RT | 0.136 | 0.107 | 0.039 | 1.283 | 1.051 | 0.139 | |
| RFR | 0.131 | 0.105 | 0.038 | 1.169 | 0.962 | 0.126 | |
| GBR | 0.141 | 0.115 | 0.041 | 1.149 | 0.944 | 0.123 | |
| ETR | 0.129 | 0.104 | 0.038 | 1.106 | 0.918 | 0.119 | |
| FFLSTM | model6 | 0.030 | 0.026 | 0.009 | 0.535 | 0.404 | 0.055 |
| LSTM | 0.068 | 0.054 | 0.019 | 1.540 | 1.193 | 0.166 | |
| BP | 0.066 | 0.052 | 0.019 | 1.191 | 0.966 | 0.137 | |
| SVR(RBF) | 0.122 | 0.098 | 0.035 | 1.086 | 0.909 | 0.119 | |
| RT | 0.134 | 0.106 | 0.038 | 1.467 | 1.162 | 0.154 | |
| RFR | 0.128 | 0.103 | 0.037 | 1.173 | 0.961 | 0.127 | |
| GBR | 0.140 | 0.114 | 0.041 | 1.150 | 0.944 | 0.124 | |
| ETR | 0.125 | 0.101 | 0.036 | 1.123 | 0.933 | 0.122 | |
| Algorithm | Station A | Station B |
|---|---|---|
| Accuracy (%) | Accuracy (%) | |
| FFLSTM | 98.87 | 94.03 |
| LSTM | 97.9 | 87.78 |
| BP | 98.15 | 87.37 |
| SVR(RBF) | 96.42 | 87.95 |
| RT | 96.12 | 85.9 |
| RFR | 96.87 | 87.3 |
| GBR | 96.05 | 87.45 |
| ETR | 96.18 | 87.63 |
| Year | Heat Consumption (GJ) | |
|---|---|---|
| Station A | Station B | |
| 2017 | 10,762 | 31,601 |
| 2018 | 9711 | 29,010 |
| Energy saving rate | 9.7% | 8.2% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, G.; Pan, Y.; Lin, T.; Song, J.; Qi, C.; Wang, Z. District Heating Load Prediction Algorithm Based on Feature Fusion LSTM Model. Energies 2019, 12, 2122. https://doi.org/10.3390/en12112122
Xue G, Pan Y, Lin T, Song J, Qi C, Wang Z. District Heating Load Prediction Algorithm Based on Feature Fusion LSTM Model. Energies. 2019; 12(11):2122. https://doi.org/10.3390/en12112122
Chicago/Turabian StyleXue, Guixiang, Yu Pan, Tao Lin, Jiancai Song, Chengying Qi, and Zhipan Wang. 2019. "District Heating Load Prediction Algorithm Based on Feature Fusion LSTM Model" Energies 12, no. 11: 2122. https://doi.org/10.3390/en12112122
APA StyleXue, G., Pan, Y., Lin, T., Song, J., Qi, C., & Wang, Z. (2019). District Heating Load Prediction Algorithm Based on Feature Fusion LSTM Model. Energies, 12(11), 2122. https://doi.org/10.3390/en12112122





