Decentralized Optimal Control of a Microgrid with Solar PV, BESS and Thermostatically Controlled Loads
Abstract
1. Introduction
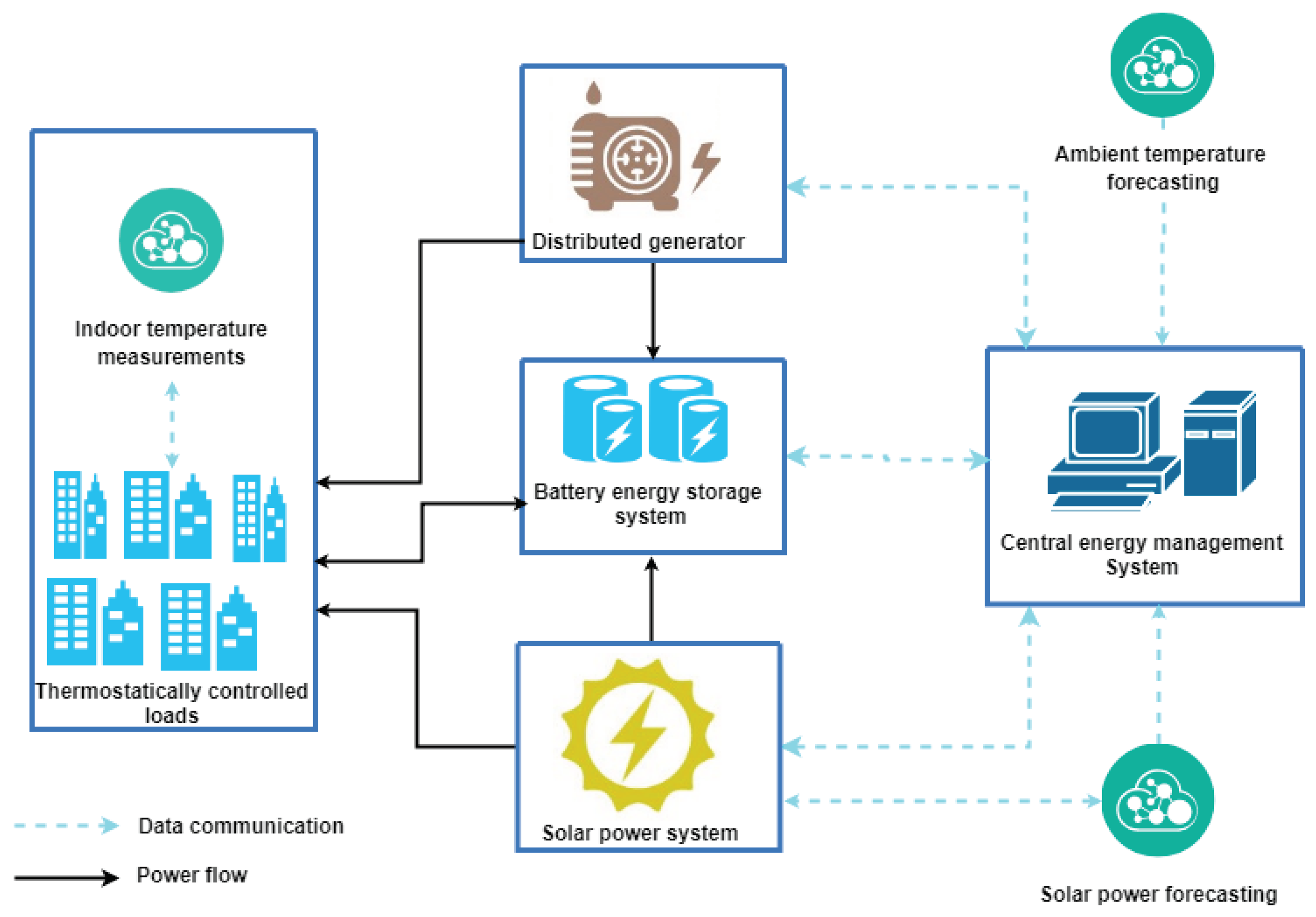
2. Problem Statement
3. System Model
3.1. Distributed Generator
3.2. Battery Energy Storage System
3.3. Solar Power Generation Unit
3.4. Thermostatically Controlled Loads
4. Optimization Problem
- The sum of solar power and the minimum power output of DG are higher than the power demand from TCLs, while the energy stored in the BESS is close to the upper limit, which cannot accommodate the excessive energy.
- The sum of solar power and the minimum power output of DG are much higher than the power demand from TCLs, and the actual power on the microgrid is limited by the maximum charging speed of BESS, which cannot meet the constraint (13).
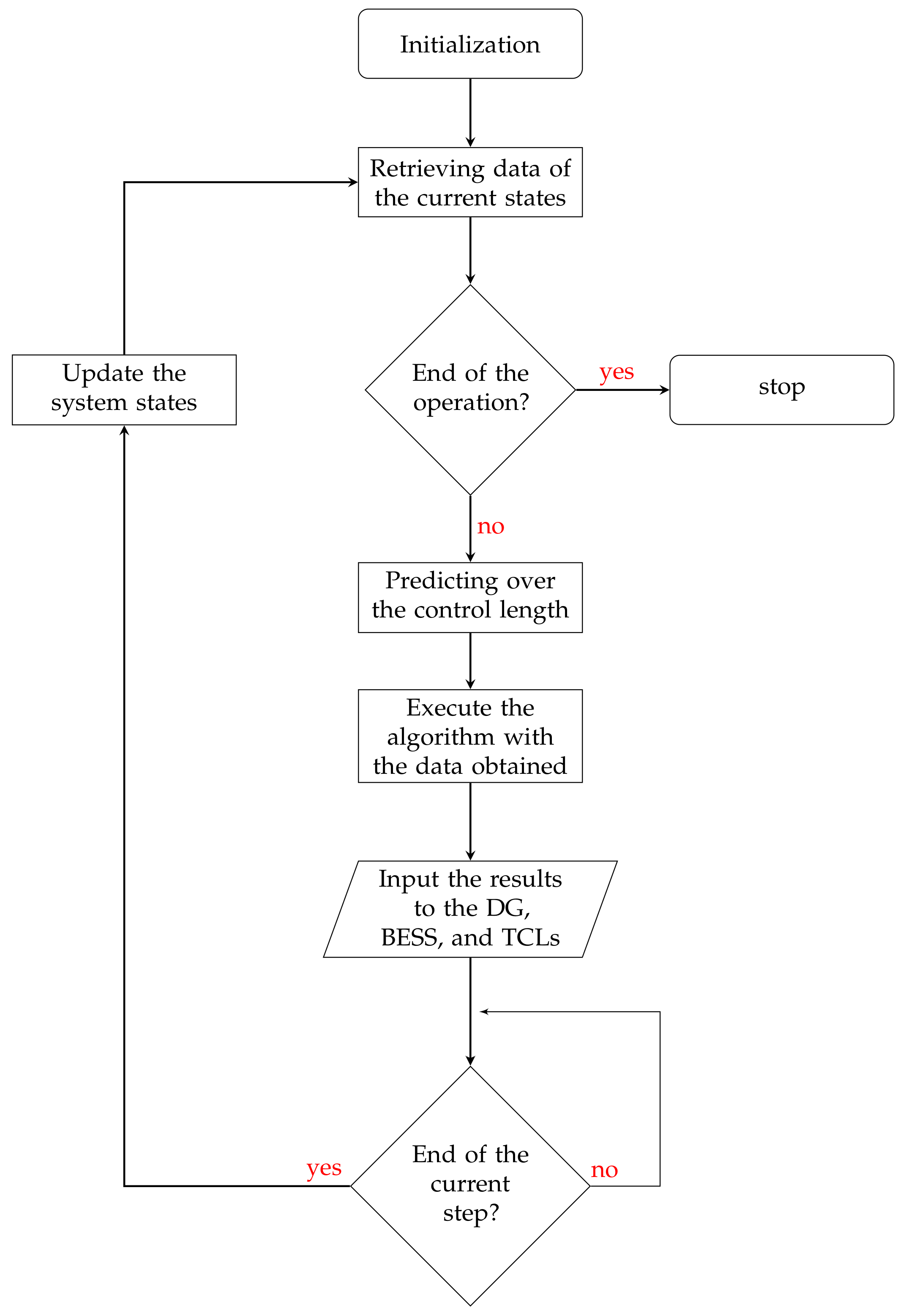
5. Simulation
5.1. Set Up
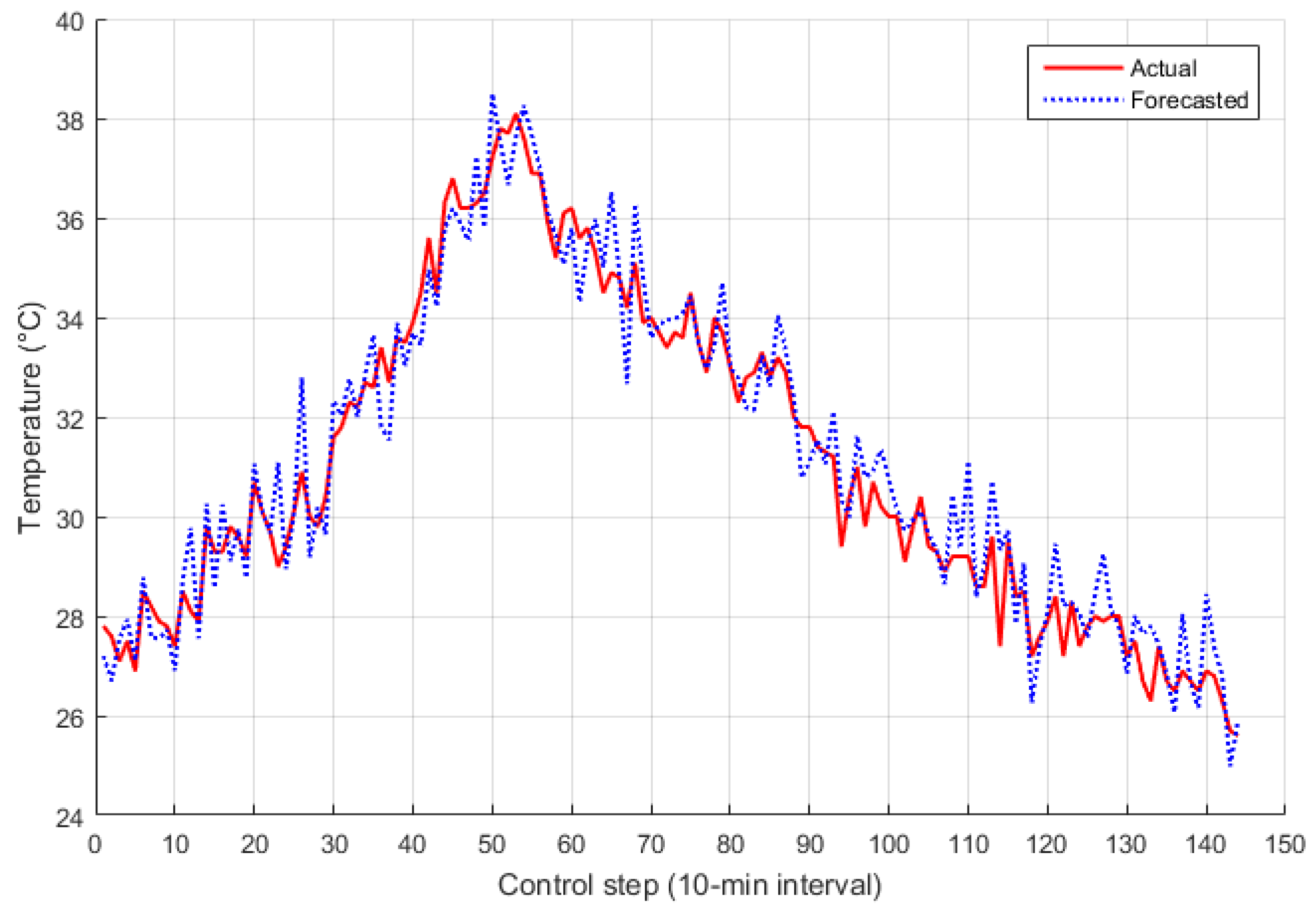
5.2. System Parameters and Database
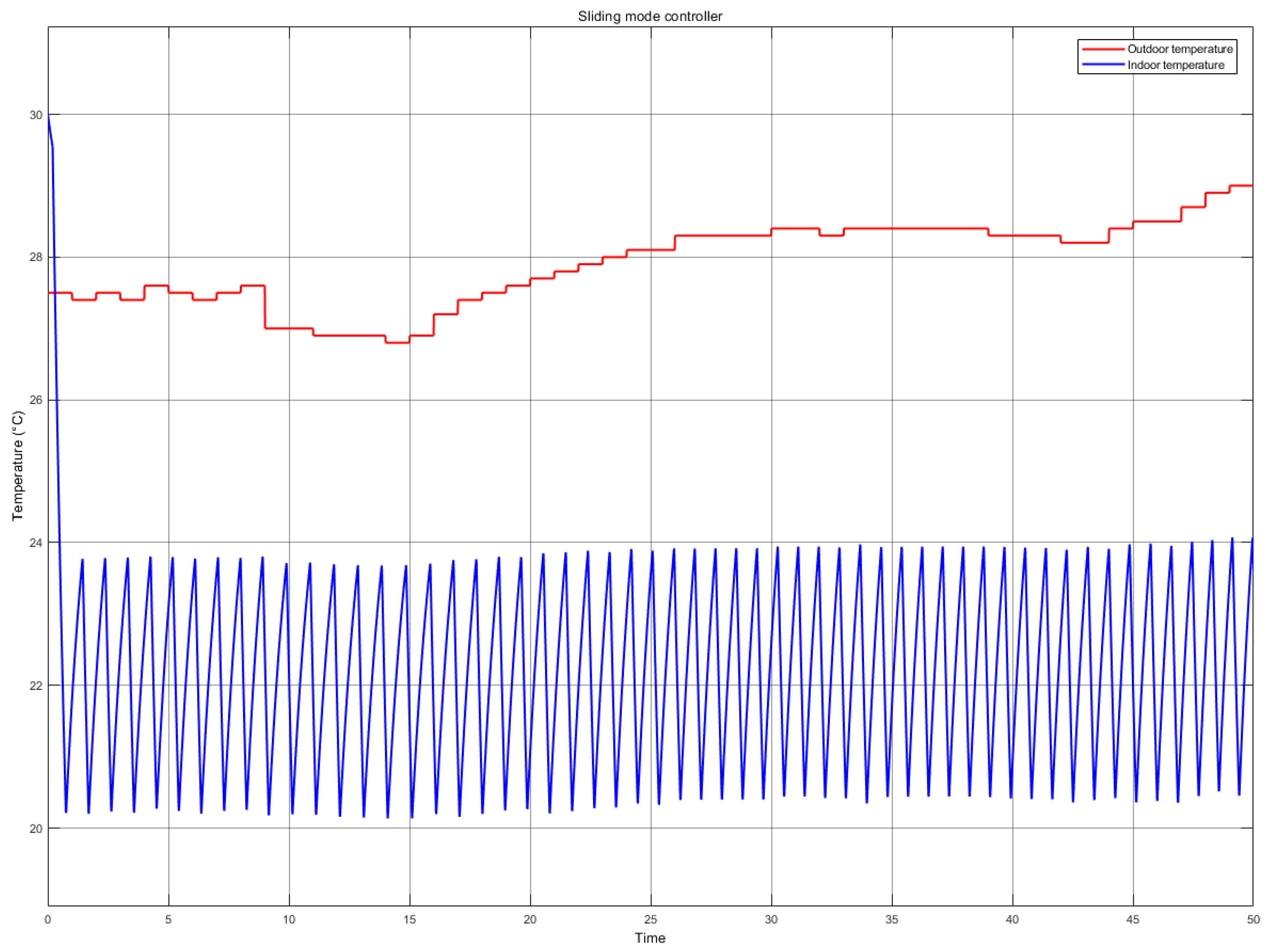
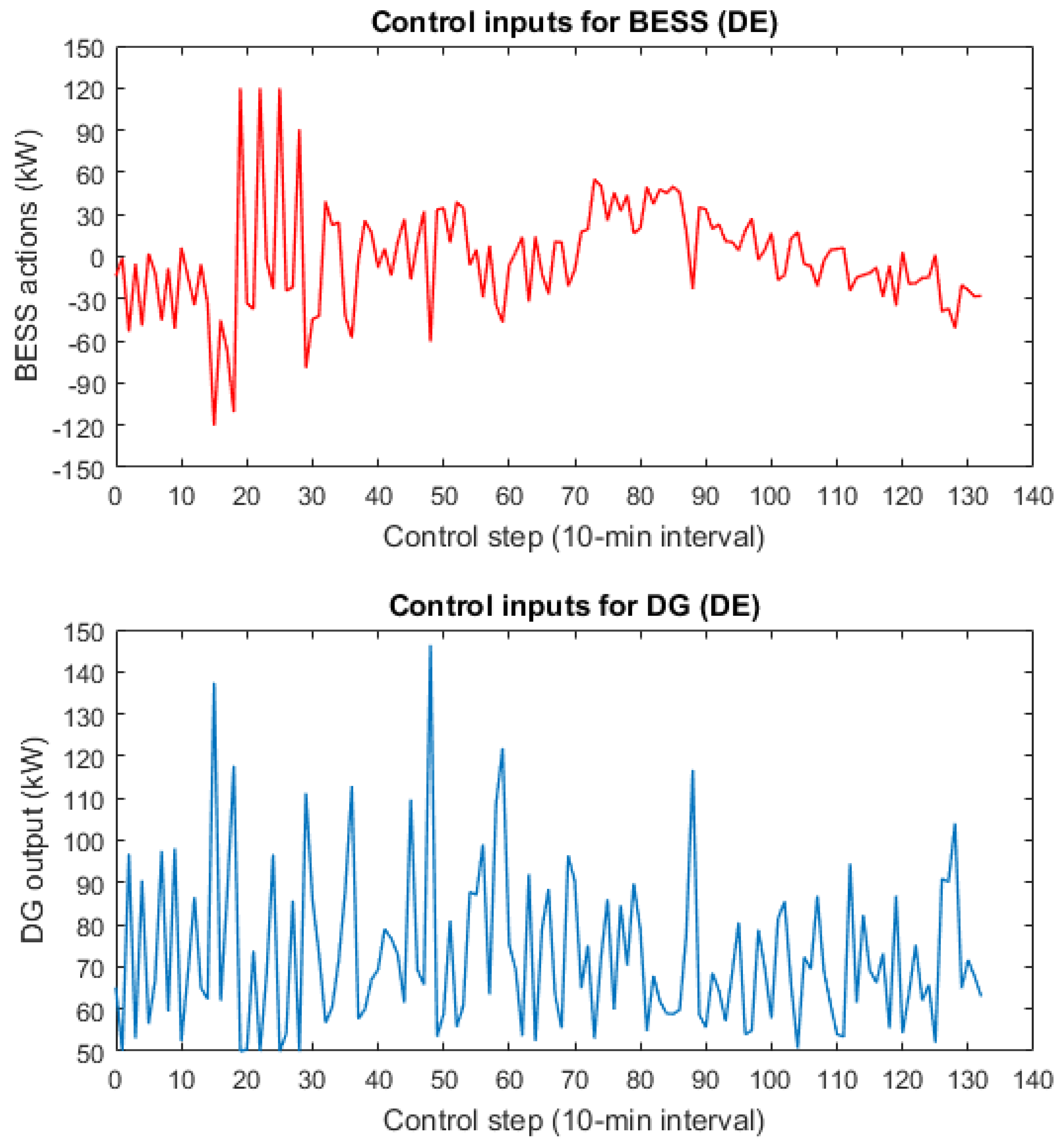
5.3. Simulation Results
5.4. Comparison Study
| Algorithm 1 Differential evolution |
|
5.5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BESS | Battery energy storage system |
| RES | Renewable energy system |
| TCL | Thermostatically controlled load |
| DG | Distributed generator |
| PV | Photo voltaic |
| MPC | Model predictive control |
| DE | Differential evolution |
| Cost coefficients of the generator | |
| d | Charge\discharge loss factor of the battery energy storage system |
| Output power of the generator | |
| Minimum output power of the generator | |
| Maximum output power of the generator | |
| Charge\discharge power the battery energy storage system | |
| Minimum action of the battery energy storage system | |
| Maximum action of the battery energy storage system | |
| Cost coefficients of the battery energy storage system | |
| Energy state of the battery energy storage system | |
| Minimum energy state of the battery | |
| Maximum energy state of the battery | |
| Indoor temperature in the region of thermostatically controlled load i | |
| Outdoor temperature | |
| Coefficients of thermostatically controlled load i | |
| Minimum temperature in the comfortable range | |
| Maximum temperature in the comfortable range | |
| Power rating of thermostatically controlled load i | |
| Switching action of thermostatically controlled load i | |
| Power output of the solar power system | |
| Maximum power output of the solar power system | |
| Maximum tolerance level of the total power on the microgrid | |
| Power curtailed in the microgrid | |
| Cost of power curtailed in the microgrid | |
| Sampling rate | |
| Factor to convert power to energy |
References
- Khalid, M.; Ahmadi, A.; Savkin, A.V.; Agelidis, V.G. Minimizing the energy cost for microgrids integrated with renewable energy resources and conventional generation using controlled battery energy storage. Renew. Energy 2016, 97, 646–655. [Google Scholar] [CrossRef]
- Wang, D.; Qiu, J.; Reedman, L.; Meng, K.; Lai, L.L. Two-stage energy management for networked microgrids with high renewable penetration. Appl. Energy 2018, 226, 39–48. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Li, G.; Zhao, D.; Tian, W. Optimal scheduling of an isolated microgrid with battery storage considering load and renewable generation uncertainties. IEEE Trans. Ind. Electron. 2019, 66, 1565–1575. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Li, G.; Mu, Y.; Zhao, D.; Chen, C.; Shen, B. Optimal scheduling of isolated microgrid with an electric vehicle battery swapping station in multi-stakeholder scenarios: A bi-level programming approach via real-time pricing. Appl. Energy 2018, 232, 54–68. [Google Scholar] [CrossRef]
- Meng, K.; Wang, D.; Dong, Z.Y.; Gao, X.; Zheng, Y.; Wong, K.P. Distributed control of thermostatically controlled loads in distribution network with high penetration of solar PV. CSEE J. Power Energy Syst. 2017, 3, 53–62. [Google Scholar]
- Kundu, S.; Sinitsyn, N.; Backhaus, S.; Hiskens, I. Modeling and control of thermostatically controlled loads. arXiv 2011, arXiv:1101.2157. [Google Scholar]
- Bomela, W.; Zlotnik, A.; Li, J.S. A phase model approach for thermostatically controlled load demand response. Appl. Energy 2018, 228, 667–680. [Google Scholar] [CrossRef]
- Wei, C.; Xu, J.; Liao, S.; Sun, Y.; Jiang, Y.; Zhang, Z. Coordination optimization of multiple thermostatically controlled load groups in distribution network with renewable energy. Appl. Energy 2018, 231, 456–467. [Google Scholar] [CrossRef]
- Luo, F.; Xu, Z.; Meng, K.; Yang Dong, Z. Optimal operation scheduling for microgrid with high penetrations of solar power and thermostatically controlled loads. Sci. Technol. Built Environ. 2016, 22, 666–673. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, C.; Wu, J.; Wang, J.; Cheng, M.; Li, G. Optimal scheduling of aggregated thermostatically controlled loads with renewable generation in the intraday electricity market. Appl. Energy 2017, 188, 456–465. [Google Scholar] [CrossRef]
- Khalid, M.; Savkin, A.V. A model predictive control approach to the problem of wind power smoothing with controlled battery storage. Renew. Energy 2010, 35, 1520–1526. [Google Scholar] [CrossRef]
- Khalid, M.; Aguilera, R.P.; Savkin, A.V.; Agelidis, V.G. A market-oriented wind power dispatch strategy using adaptive price thresholds and battery energy storage. Wind Energy 2018, 21, 242–254. [Google Scholar] [CrossRef]
- Khalid, M.; Aguilera, R.P.; Savkin, A.V.; Agelidis, V.G. On maximizing profit of wind-battery supported power station based on wind power and energy price forecasting. Appl. Energy 2018, 211, 764–773. [Google Scholar] [CrossRef]
- Khalid, M.; AlMuhaini, M.; Aguilera, R.P.; Savkin, A.V. Method for planning a wind–solar–battery hybrid power plant with optimal generation-demand matching. IET Renew. Power Gener. 2018, 12, 1800–1806. [Google Scholar] [CrossRef]
- Khalid, M.; Savkin, A.V. An optimal operation of wind energy storage system for frequency control based on model predictive control. Renew. Energy 2012, 48, 127–132. [Google Scholar] [CrossRef]
- Qiu, J.; Meng, K.; Zheng, Y.; Dong, Z.Y. Optimal scheduling of distributed energy resources as a virtual power plant in a transactive energy framework. IET Gener. Trans. Dis. 2017, 11, 3417–3427. [Google Scholar] [CrossRef]
- Sideratos, G.; Hatziargyriou, N.D. An advanced statistical method for wind power forecasting. IEEE Trans. Power Syst. 2007, 22, 258–265. [Google Scholar] [CrossRef]
- Khalid, M.; Savkin, A.V. A method for short-term wind power prediction with multiple observation points. IEEE Trans. Power Syst. 2012, 27, 579–586. [Google Scholar] [CrossRef]
- Asrari, A.; Wu, T.X.; Ramos, B. A hybrid algorithm for short-term solar power prediction—Sunshine state case study. IEEE Trans. Sustain. Energy 2017, 8, 582–591. [Google Scholar] [CrossRef]
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Weatherzone. Sydney Observations. 2018. Available online: http://www.weatherzone.com.au/nsw/sydney/ (accessed on 20 October 2018).
- Fleetwood, K. An Introduction to Differential Evolution. 2018. Available online: http://www.maths.uq.edu.au/MASCOS/Multi-Agent04/Fleetwood.pdf (accessed on 12 March 2019).
- Ahlers, F.J. Differential Evolution (DE) for Conituous Function Optimization (an Algorithm by Kenneth Price and Rainer Storn). 2018. Available online: http://www1.icsi.berkeley.edu/~storn/code.html (accessed on 12 March 2019).
- Cortés-Antonio, P.; Rangel-González, J.; Villa-Vargas, L.A.; Ramírez-Salinas, M.A.; Molina-Lozano, H.; Batyrshin, I. Design and implementation of differential evolution algorithm on FPGA for double-precision floating-point representation. Acta Polytech. Hung. 2014, 11, 139–153. [Google Scholar]


| DG | a | b | c | ||
| 50 kW | 500 kW | 0.01 | 0.1 | 0 | |
| BESS | |||||
| 120 kw | 0 | 0.008 | 0.008 | 60/kWh | |
| TCL | n | ||||
| 3200 | 23 | 300 | 1.05 |
| BESS Operation Cost ($) | DG Operation Cost ($) | Total | |
|---|---|---|---|
| DE NP:60 | 8541.54 | 986.11 | 9527.65 |
| DE NP:120 | 8389.07 | 1003.39 | 9392.46 |
| DE NP:180 | 8209.49 | 814.89 | 9024.39 |
| Proposed scheme | 8181.21 | 425.76 | 8606.98 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuo, W.; Savkin, A.V.; Meng, K. Decentralized Optimal Control of a Microgrid with Solar PV, BESS and Thermostatically Controlled Loads. Energies 2019, 12, 2111. https://doi.org/10.3390/en12112111
Zhuo W, Savkin AV, Meng K. Decentralized Optimal Control of a Microgrid with Solar PV, BESS and Thermostatically Controlled Loads. Energies. 2019; 12(11):2111. https://doi.org/10.3390/en12112111
Chicago/Turabian StyleZhuo, Wenhao, Andrey V. Savkin, and Ke Meng. 2019. "Decentralized Optimal Control of a Microgrid with Solar PV, BESS and Thermostatically Controlled Loads" Energies 12, no. 11: 2111. https://doi.org/10.3390/en12112111
APA StyleZhuo, W., Savkin, A. V., & Meng, K. (2019). Decentralized Optimal Control of a Microgrid with Solar PV, BESS and Thermostatically Controlled Loads. Energies, 12(11), 2111. https://doi.org/10.3390/en12112111





