1. Introduction and Motivation for the Work
BEMs are key elements of the Energy Performance of Buildings Directive, and they are at the basis of Energy Performance Certificates (EPCs) and assessment. Assessment and certification processes should be user-friendly, cost-effective, and more reliable in order to instill trust in investors in the energy efficiency sector [
1]. Therefore, the next generation of EPCs will need to fulfill these requirements, as well as the next generation of BEMs. Until now, EPCs have been based on two concepts [
2]: standard energy rating and measured energy rating. In the former, the energy consumed by a building is calculated through an energy model (law-driven models, Option D of the International Performance Measurement and Verification Protocol (IPMVP)) [
3], and in the latter, the energy is measured through meters and sensors installed in the building (data-driven models, Option C of the IPMVP).
In a previous paper written by some of the authors [
4], it was explained in detail how this new generation of BEMs should be produced and that the new technique is able to merge the law-driven models [
5] and the data-driven models [
6,
7,
8,
9], resulting in “law-data-driven models”. In summary, the concept uses well-known software such as EnergyPlus [
10] to combine the model based on as-built parameters with the model based on parameters estimated using measurements of the system and, through a calibration process, producing the new technique. This technique has produced very good results and is based on the use of measured temperature from the real building as part of the energy balance of the BEM, following the idea that Sonderegger postulated in 1977:
“Instead of telling the computer how the building is built and asking it for the indoor temperature, one tells the computer the measured indoor temperature and asks it for the building parameters” [
11].
SABINA is a project that is looking for services on the grid based on the “demand response” concept [
12] and the idea of increasing the amount of renewable energy consumed locally by buildings. To reach the EU’s long-term objectives for reducing greenhouse gas emissions, this share should reach more than 30% in 2030, and almost 50% in some scenarios in 2050 [
13]; new management systems are thus required. What is most needed is additional flexibility in the system. SABINA targets the most economic source possible: existing thermal inertia in buildings [
14]. This goal requires models that capture the thermal dynamics of the building, and the Zero Energy Calibration (ZEC) methodology has been chosen to select those kinds of models [
4]. The usefulness of a model depends on the accuracy and reliability of its output, but all models are imperfect abstractions of reality, because there is imprecision and uncertainty associated with any model.
Currently, there is the protocol IPMVP [
3], and two guidelines: FEMP [
15] and ASHRAE [
16], which offer a set of error indices (
,
, and
) to evaluate the quality of the calibrated models considering the monthly and hourly energy consumption (simulated vs. real). Other methodologies use indoor air temperature (simulated vs. real) to calibrate the building models with the same indices [
4,
17,
18,
19,
20]. When doing so, it is not clear if these indices, which were selected for energy evaluation, will have a good performance for temperature. In this paper, a large number of error indices have been analyzed with the aim of selecting the best ones to choose the model that represents the real building indoor air temperature. This new evaluation methodology has been tested and verified in different building models: the “Amigos” [
4], “Humanities” [
21], and “The School of Architecture” [
22] at the Pamplona Campus of the University of Navarre. In this paper, the office building of the School of Architecture has been used, as it is explained in the following sections.
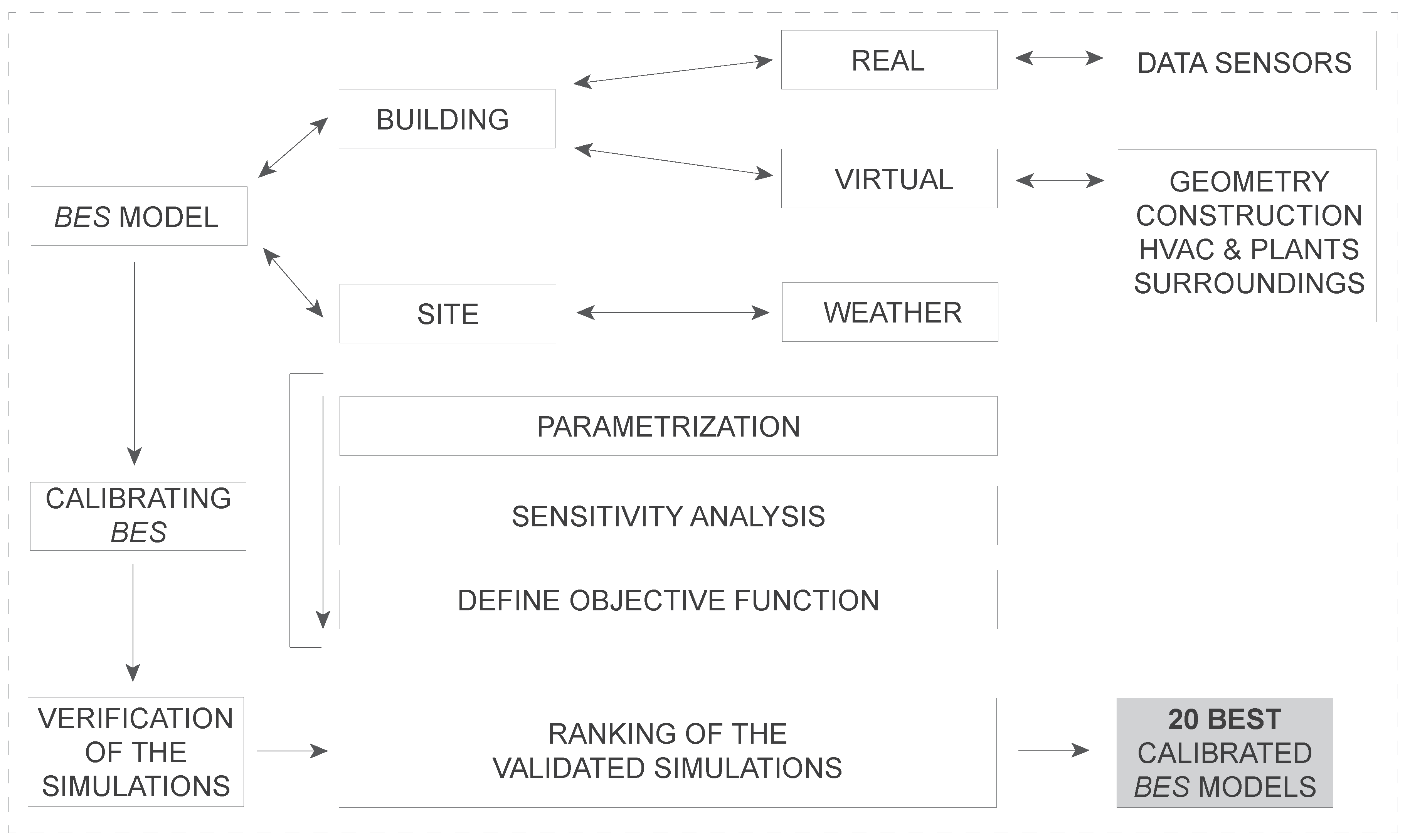
Summary of the ZEC Methodology
The Zero Energy Calibration (ZEC) is a methodology for building envelope calibration. The ZEC principle is based on the idea that when introducing the free oscillation temperature of a building in the model, as a dynamic set-point, the energy consumed by the HVAC equipment in that period should be zero. If this is not the case, the reason should be the wrong configuration of the building parameters, and the algorithm (genetic algorithm) will look for a new vector of envelope parameters that will produce a lower energy consumption (heating plus cooling). The process finishes when the energy (the objective function) cannot be reduced further and the model envelope is calibrated.
In most automatic calibration techniques [
23,
24], the simulation data are used at the end of the process to be compared with the measured data, and the goal is to minimize an error value in what is known as uncertainty analysis. In such cases, the statistical indices (
,
, and
) are the objective functions that will guide the algorithm in the search for the calibrated model [
25,
26,
27].
The main ways of calibration do not allow entering into the calibration process as many measured data as necessary, and thus, the thermal characterization of the model will not be improved. In this methodology (ZEC), there is no restriction in the creation of thermal zones. The major simplification that ZEC offers is that there is no implementation of uncertainty analysis in coordination with the automatic calibration algorithm and the simulation program, which makes it simpler and therefore more accessible to all kinds of professionals with energy simulation skills, but without programing capabilities.
For this reason, the ZEC methodology is simple in execution. The algorithm used to perform the thermal zone energy balance in EnergyPlus is the Conduction Transfer Function (CTF), which offers a very fast and elegant solution to solve the Fourier differential equation and to find the temperature of the thermal zone. However, as explained in the EnergyPlus Engineering Reference,
“conduction transfer function series become progressively more unstable as the time step decreases. This became a problem as investigations into short time step computational methods for the zone/system interactions progressed because, eventually, this instability caused the entire simulation to diverge” [
28]. This divergence is translated into extra energy consumption that affects the objective function used by ZEC, a problem that has been well documented and evaluated by Wetter et al. [
29]. The result of this extra energy consumption is that some models with slightly higher energy consumption have better uncertainty temperature results than the best models selected by the energy of the objective function. From a practical point of view, this means that the best model cannot be chosen directly from the results offered by the algorithm unless an uncertainty temperature analysis is subsequently performed, in the same way as other similar works [
26,
27,
30,
31].
Taking into account the indices’ combination proposed by ASHRAE (
,
, and
) [
16], the authors worked with a new statistical index that was called the
[
4], which was the arithmetic sum of errors
,
, and
. The model with the lowest
was the one considered to have the best performance. As the indices’ combination proposed by ASHRAE (
,
, and
) is based on energy uncertainty analysis and the new proposal is based on temperature uncertainty analysis, this paper intends to confirm if there is any other statistical index or combination of indices that can improve the selection of the best model.
The uncertainty analysis should classify the best models according to the capacity to reduce the error between real temperature inside the building and simulated temperature produced by the building model. From a practical point of view, a good correlation should be found between temperature and energy with respect to the selected temperature error (uncertainty index).
In order to check if a different index can choose a better model, a list of a number of error metrics that been studied in
Section 2, classified into seven groups (bias error indices, uncertainty indices based on absolute deviations, uncertainty indices based on square deviations, goodness-of-fit metrics, efficiency criteria, indices for model discrimination, and proximity measures), according to the application or structure and the statistical methodology description used to select the metrics that identify the best-adjusted calibrated energy model.
Section 3 outlines the cases of study and the description of the building used to check the methodology.
Section 4 presents the performance of the metrics described in
Section 2 over two case studies: a synthetic energy model and a real building model, each under the same conditions. The conclusions that we have reached in this paper and future research considerations are presented in
Section 5.
3. Cases Studies, Building Description, and Models’ Preparation
In order to carry out this methodology, the calibration process was checked under two assumptions. In
Section 4, two cases were developed. In the first case, the real data were produced synthetically from a BEM, as recommended by the
ASHRAE Fundamentals Handbook [
35], with the idea of avoiding the inaccuracy of the temperature meters. In this case, the quality of the parameters resembled quite faithfully the parameters of the model that originated the data. In the second case, the model was calibrated with real data from meters inside the building. On this occasion, the gap between real and simulated data was clearer, as will be seen in the results.
The building selected for generating both case studies explored in this paper was the Architecture School administrative building of the University of Navarra (
Figure 1).
The Architecture School was designed by the architects Rafael Echaide, Carlos Sobrini, and Eugenio Aguinaga and was built between 1974 and 1978. It won the “National Award for Architecture in Brick” in 1980. The building is organized along an interior garden with four zones at different levels that accommodate the needs of the school.
Through a transparent gallery, connected to the main building, people can access the office area, which is the building object of this paper. It is mainly used as an administration building and by postgraduate students of the different master’s programs of the School of Architecture, and it mainly keeps business hours.
It is a freestanding single-story building of almost 760 square meters. It is a porticoed structure of concrete, and the interior and exterior walls were made of red clinker brick fabric, while the building frames were made in situ of aluminum with an air chamber and a light gold color.
The space allocation consists of a succession of offices for personnel that face southeast and northwest, an administration zone facing northwest, an open working space and master classrooms facing southeast, and a corridor in the middle connecting the spaces.
The building energy model has been divided into 25 thermal zones, one for each room (
Figure 2). The HVAC system has been introduced through the option of ideal loads offered by EnergyPlus.
The calibration methodology was carried out by ZEC, described in the previous paragraphs, the process of which is defined in
Figure 3.
The last step in the ZEC methodology after calibration is to obtain the 20 best models of the calibration process for each period.
4. Methodology to Evaluate Energy Models: Analysis of Case Studies
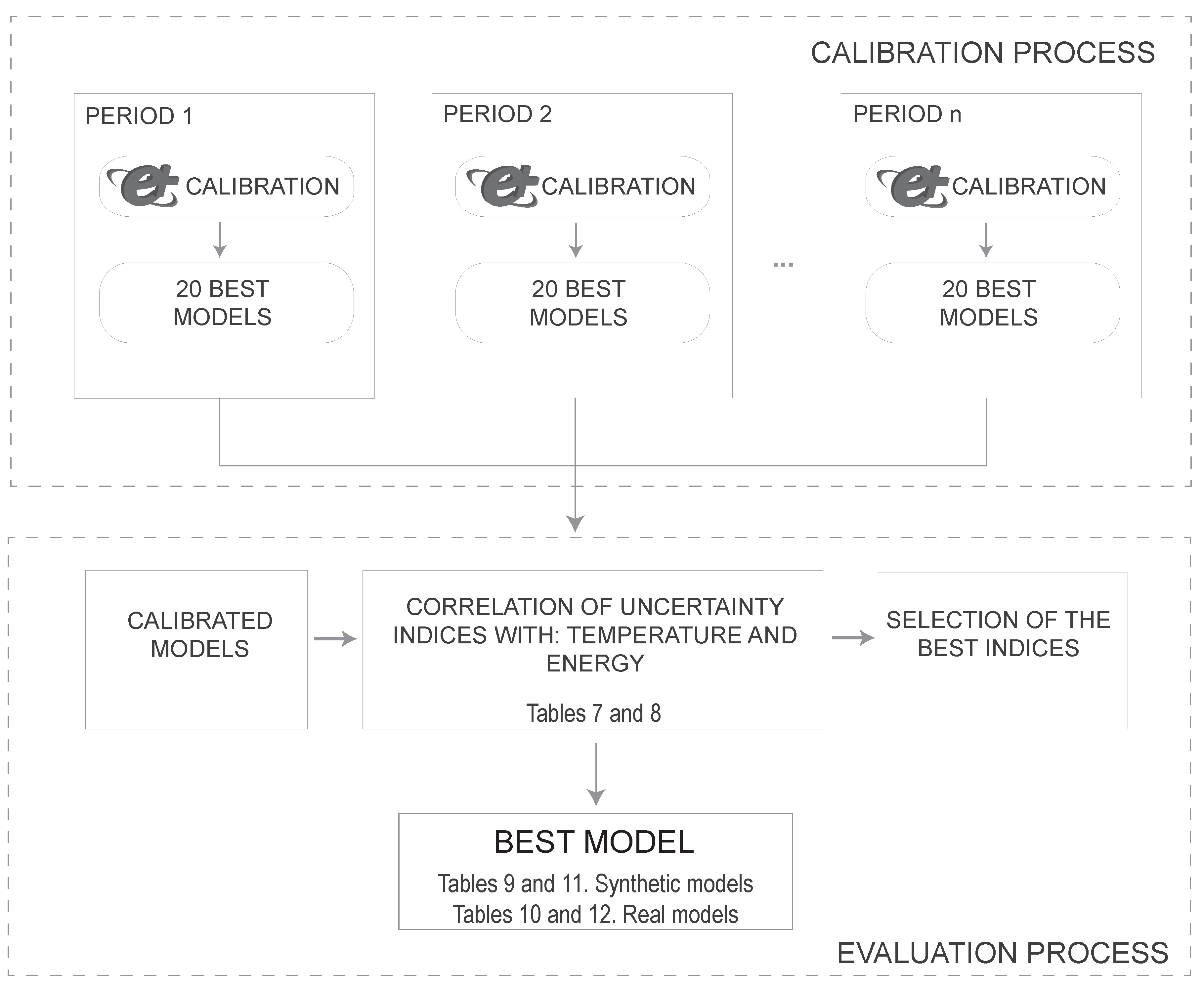
For evaluation of the models, a global checking period is defined to validate the best models of each calibration period. In the ZEC methodology, the evaluation involves performing an uncertainty analysis that compares the simulated temperature during the free oscillation times of the checking period with the measured temperature from the real building. This allows the analysis of all the models on equal terms to generate a ranking of simulations in order to choose the best solution (
Figure 4).
To carry out this research, the model has been calibrated, using the ZEC methodology, in 16 different calibrated periods choosing the 20 best models, with the lower energy of each period, generating a total of 320 models. The models have been identified by , where is the calibration period (from 1–16) and is the model with respect to its position in the energy ranking (from 1–20). These models are evaluated in a common checking period, obtaining the results of their indices of uncertainty and the energy consumed. This study was conducted for both a model with synthetic data and a model with real data.
In the following section, a methodology will be developed to choose the best model among these 320. The methodology proposed a correlation analysis and was performed between the uncertainty indices described in
Section 2 and the energy consumption and measured temperature. The energy consumption was calculated from 320 simulations checked over the same period, corresponding to the BEM described in
Section 3. The uncertainty indices were calculated using the measured temperatures from a synthetic and a real model in 25 thermal zones.
The correlation was calculated over the mean temperature of these 25 zones, and the real and simulated temperatures were weighted for the relative volume of every zone. Thus, the real (
) and simulated (
) mean weighted temperature vectors were defined as:
where
and
are the real and simulated temperatures of the thermal zone
j at time
i and
is the
j-thermal zone volume in cubic meters (35).
For a given model, the best uncertainty indices must have the higher
for small values of
; therefore, the correlation between error indices and
(
) could help to identify them. The highest values of these correlations are reached for narrow
-wide bands, shown in
Table 7 for a synthetic model and in
Table 8 for a real model.
Another relevant point to determine which indices are appropriate for the best-performing model is the correlation between them and energy consumption. The right column of
Table 7 and
Table 8 shows the calculated values.
In both cases, there are groups of indices differentiated by the -value where they reach the maximum correlation:
In the first group, the indices whose maximum correlation is reached at for a synthetic model and for a real model are measures calculated by the absolute value of the distances.
The second group reaches the maximum at and for a synthetic model and real model, respectively, and they are calculated with squared distances.
In the third group, the value of varies from to for a synthetic model and from to for a real model. They are not related to a specific distance measure.
The indices , , and are omitted in the results tables since their method of calculation was subjected to cancellation errors and their performance was poor. Another group of indices, , , , , , and the Pearson Correlation Coefficient (r), were omitted because they had redundant information; that is, they were a direct part of the calculation of other measures with equal or better performance, and their correlations were equal to one in the temperature datasets analyzed here. and had a similar performance to , and the same happens between the indices pairs: and , and , with respect to , and the Pearson correlation coefficient with respect to the Spearman correlation coefficient.
With the results obtained in the previous
Table 7 and
Table 8, we can make the selection of the indices for the evaluation of the models. These indices must meet two objectives: good correlation of the indices with temperature and with energy.
is one of the indices that fulfills these two premises for a synthetic model and a real model.
Once the indices with which to evaluate the models have been chosen, we proceed to compare them with the old methodology () for the proposed cases: synthetic and real.
In
Table 9 (synthetic case) and
Table 10 (real case), we have the twenty best models ranked by
(old methodology). In the first one (synthetic case), thirteen out of twenty of these models are among the best of the energy ranking. The best model of
Table 9 (P13_M10) was the twenty fifth in the energy ranking.
In the second one (real case), three out of twenty of these models were among the best of the energy ranking. The best model of
Table 10 (P10_M2) was the twenty ninth in the energy ranking.
With the new methodology, the results obtained for the synthetic and real case can be evaluated in
Table 11 and
Table 12. In these tables, the twenty best models are ordered by index
. For a synthetic case,
Table 11, we can see how seventeen out of twenty of these models were among the best for the energy ranking. The best model of
Table 11 (P5_M4) was the tenth in the energy ranking and the number one in the rest of the indices. For the real case,
Table 12, ten out of twenty of these models were among the best of the energy ranking. The best model of
Table 10 (P9_M8) was the second in the energy ranking and the number one in the rest of the indices.
Depending on the methodology used to choose the best model, the results obtained are different.
For the case of synthetic models, if we rely on the old methodology, the best selected model is P13_M10 and would be ranked twenty fifth in the energy ranking. With the new methodology, the best model was P5_M4 and it had the tenth position in the energy ranking. Analyzing both models, we can see that the model ranked by (new methodology) had a better performance with respect to the temperature curves, as shown by its , 100% with a = 0.2; while the model chosen with (old methodology) had a for a = 0.2 of 99.7 %.
The same situation would occur if we analyze the real case. The best model selected with (old methodology) was P10_M2 with a position of 29 in the energy ranking, and if we ranked by (new methodology), the best model would P9_M8, being the Number 2 model in the energy ranking. By carefully examining both models, we can conclude that the model classified with the new methodology was better than the one chosen by , as shown by its . The model P9_M8 had a for a = 1 of 90.1 %, while for the model P10_M2, it was 84.7 %.
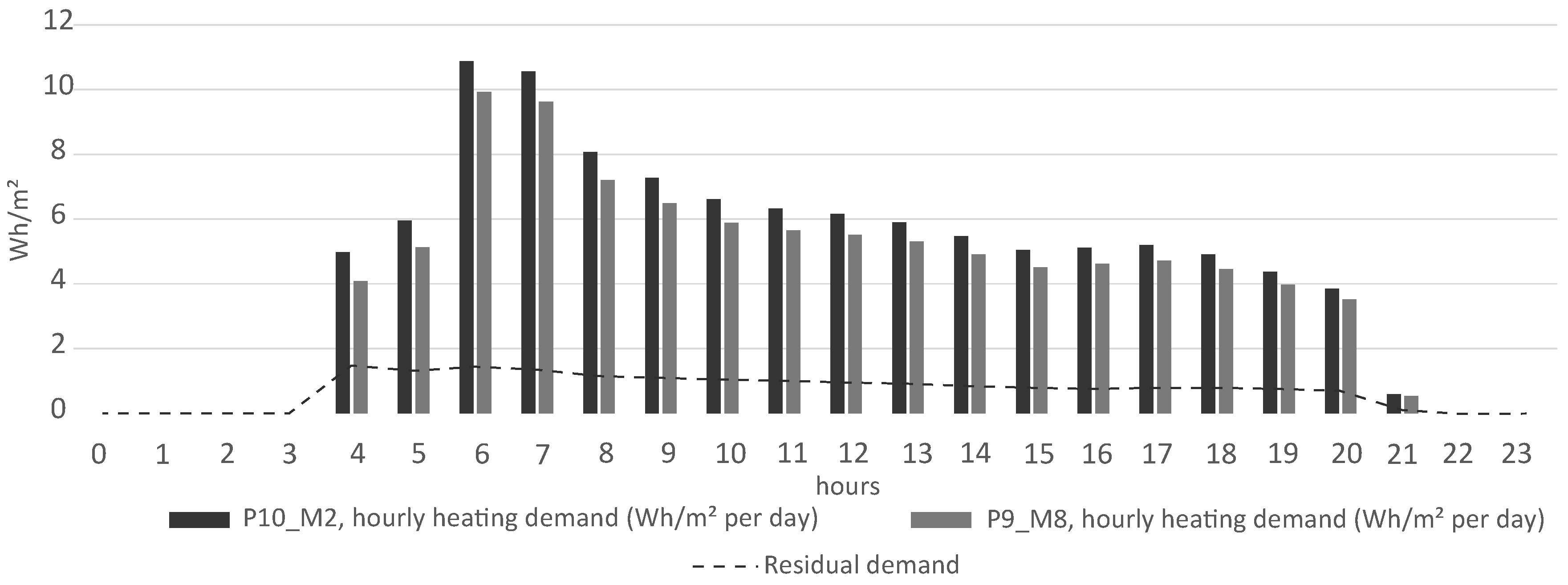
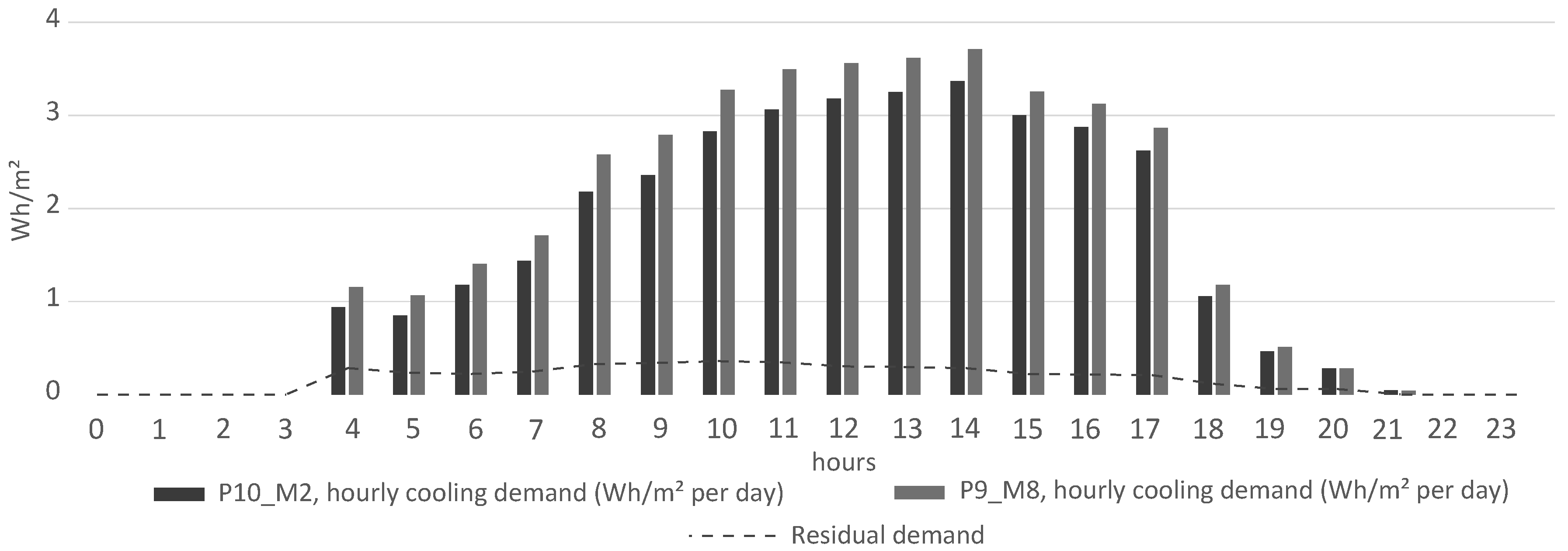
Choosing the best model from a list of calibrated models is crucial in many applications like model predictive control (MPC), where the optimization is based on an hour by hour control of the energy demand of the model in order to reach the goals of the objective function that are related to an increase/decrease of energy consumption during specific time periods. Therefore, having a reliable methodology that gives us this result is paramount. The variation of energy that the two selected models have for the real case, using the old and the new methodology, is significant, as can be seen in
Figure 5 and
Figure 6, where the accumulated energy at hourly time steps has been represented for heating and cooling demand.
5. Conclusions and Future Research
After obtaining the results of the cases described in the previous sections, it is clear that a single index is not enough in order to select the best model. , , , , , , and seem to be the best group of indices to find the best model in both case studies: the synthetic model and the real model. An agreement between all the indices would be desirable in order to choose the best model, as has been demonstrated in this study. In the case of the , this index not only helps to rank the models, but also can be used as a measure to quantify the quality of the model. This value () demonstrates the actual gap between the calibration process carried out with synthetic data or with real data.
The results that were presented within
Section 4 show that the chosen indices based on
(
,
,
,
,
) worked well for time series of temperature data. We estimate that they would still work well in more general scenarios, but some other indices given in this paper could appear to be more appropriate for particular situations. The index
had the best correlation between energy and temperature with respect to uncertainty indices in the real case and good performance in the synthetic case. This index was computed after a log-transformation of the data; then it was one minus the ratio between the
and the difference between the log of the mean and the mean of the log of the observed temperatures. The
index was again based on a ratio of the
and, now, the square of the coefficient of variation of the observed temperatures. Index
was the ratio between the relative
and a kind of
comparing the observed and simulated temperatures to the mean of the observed temperatures. The
index was based again on the square of the cover the mean. The
index was also based on the
, now controlled by the consecutive jumps of temperatures. This is especially interesting since it was the only index that took into account the possible correlation between near measures in time. The
index was a relative absolute error index. It can be seen that most of these indices were based on an appropriate ratio of the
. Finally, the
was rather intuitive, measuring the observations in a suitable band around the simulated values.
The past results obtained with the have been improved with this procedure, as well as the concept of ZEC; calibration by energy was strengthened with this methodology because more models with low energy consumption were among the best models, and there was no uncertainty about the selection of the model in the evaluation process because there was a general agreement between different indices about which one was the best.
A big difference between the synthetic model and real model has been observed, and the new methodology performed better under the real case scenario. This premise has proven to be true, since the methodology presented in this paper is being applied to different buildings and in different calibration periods, showing similar results to those obtained in the previous sections. It is a promising area of research where more calibrated buildings in different environments could be studied. The SABINA project will offer this opportunity.
While in this study, we have used the values of the index to rank the best model offered by the calibration process, in future research, specific values of these indices, in a similar way to that provided by ASHRAE Guideline 14 [
16], could be obtained in order to give an idea of the quality of the model. The next generation of BEMs should be classified as complying with the level of quality fed by these indices, depending on the types of applications that are required.