Modified Modeling and System Stabilization of Shunt Active Power Filter Compensating Loads with μF Capacitance
Abstract
:1. Introduction
2. Problems of Conventional Model of Shunt APF
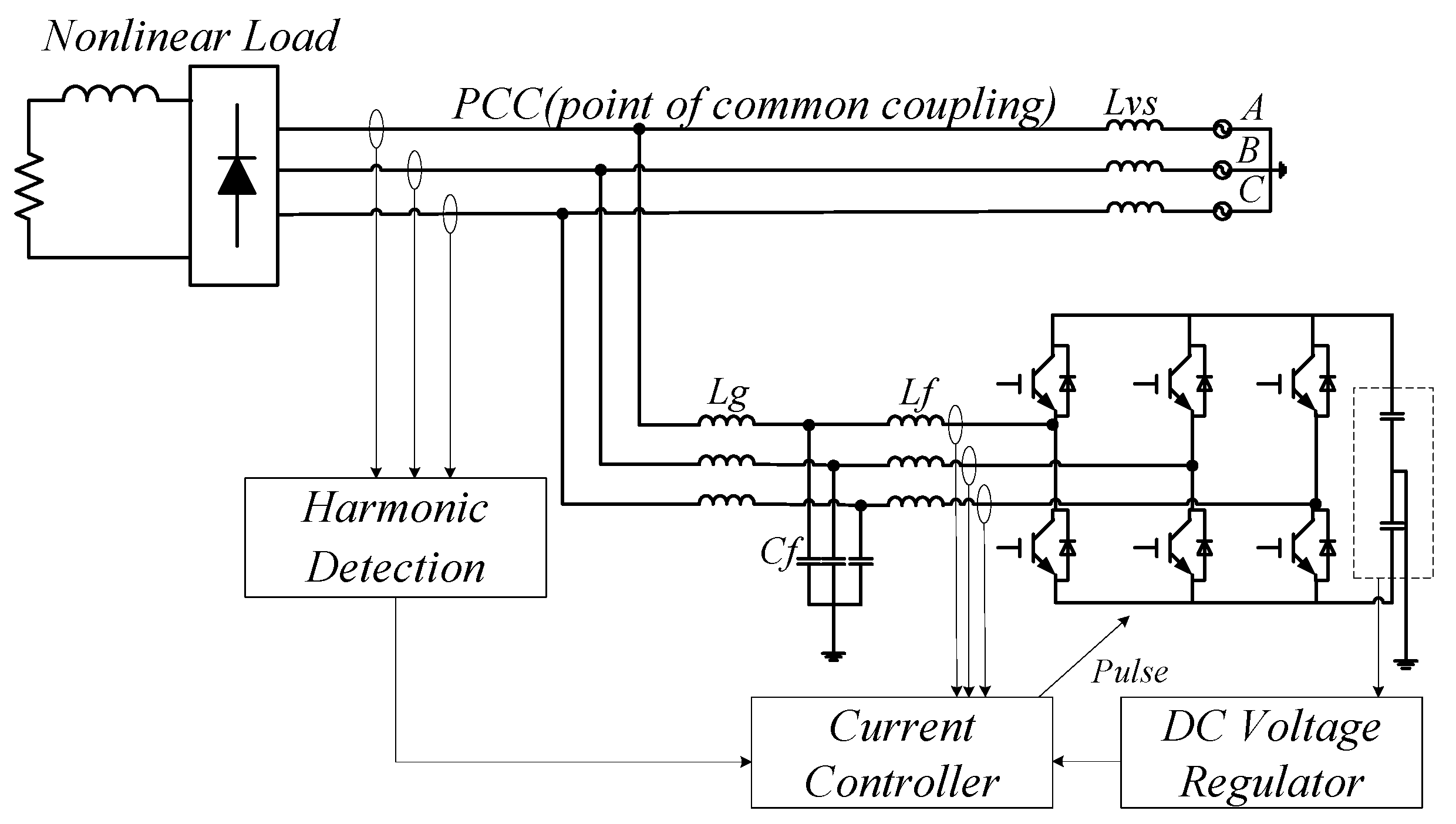
2.1. Review of Shunt Active Power Filter
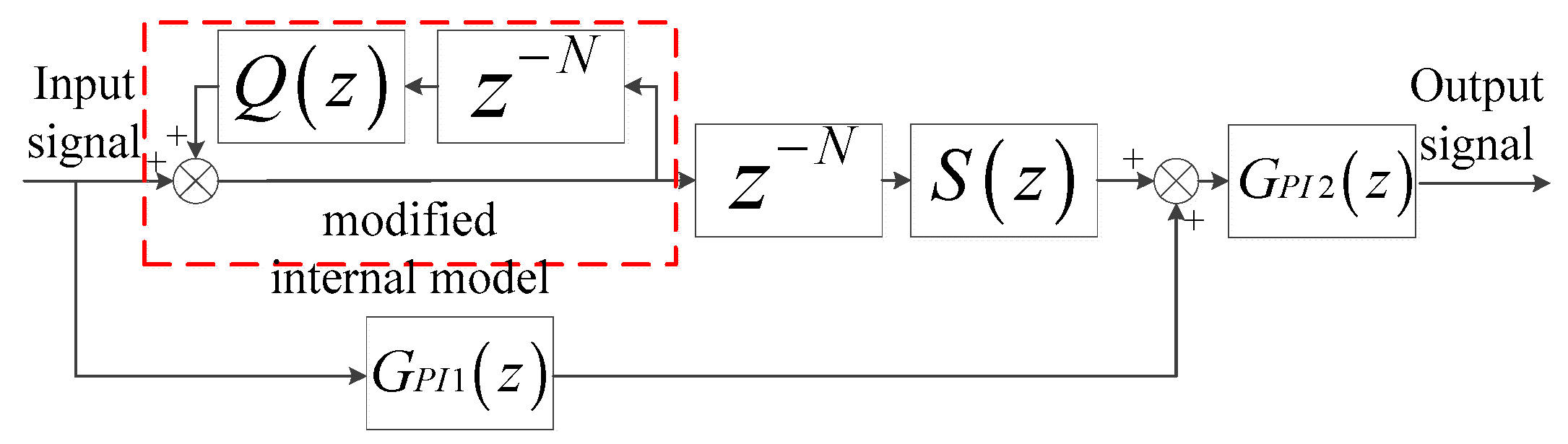
2.2. Review of Hybrid Repetitive Controller
2.3. Conventional Model and Stability Problem of APF
- Transfer function T(z) does not have poles outside the unit circle.
- H(z) = |Q(z) − S(z)P(z)| < 1, z = ejωTs, ω ⸦ [0, π/Ts].
2.4. Flaws of Conventional Model of Shunt APF
3. Modified Model of Shunt APF and its Stability Analysis
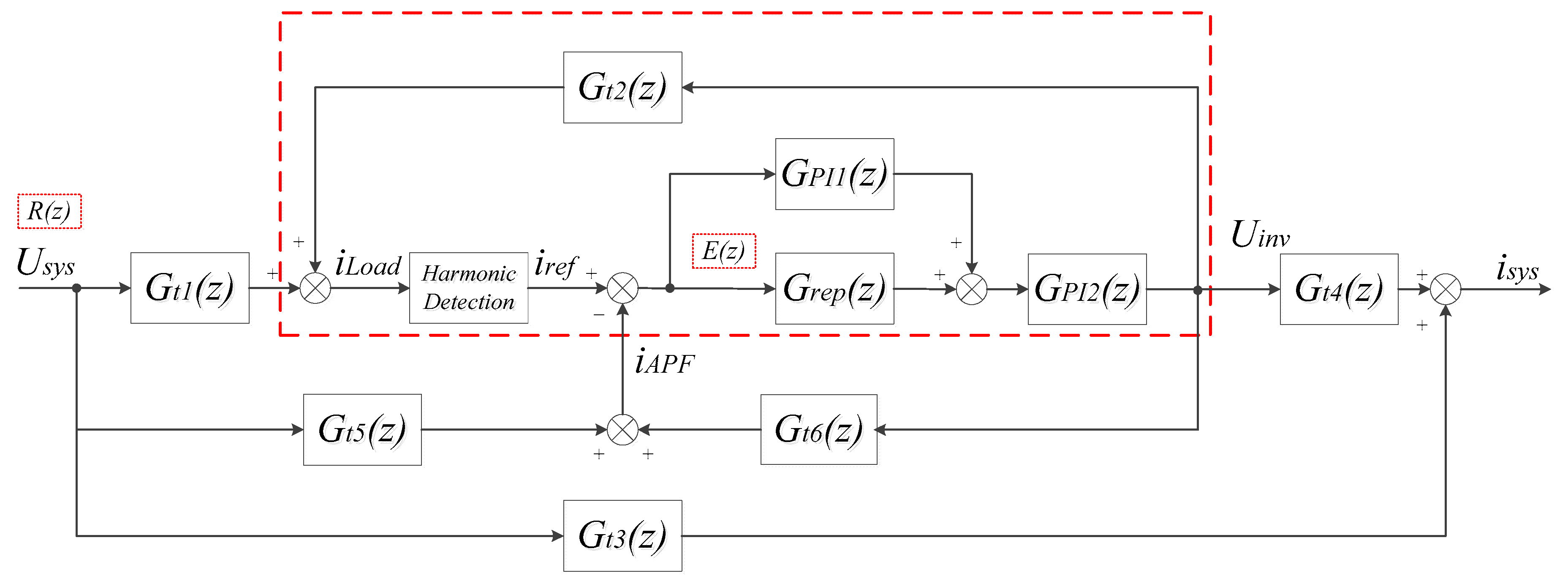
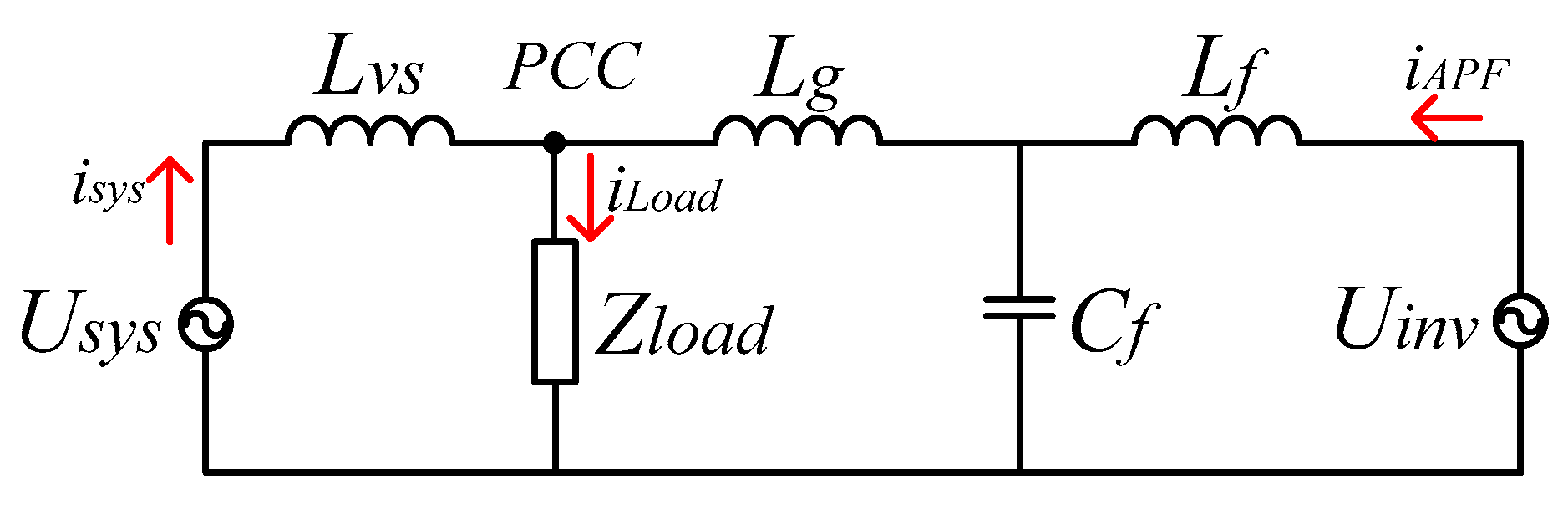
3.1. Modeling Shunt Active Power Filter
3.2. Stability Analysis of Shunt APF System
- Transfer function T(z) does not have poles outside the unit circle.
- H(z) = |Q(z) – S(z)P(z)| <1, z = ejωTs, ω ⸦ [0, π/Ts].
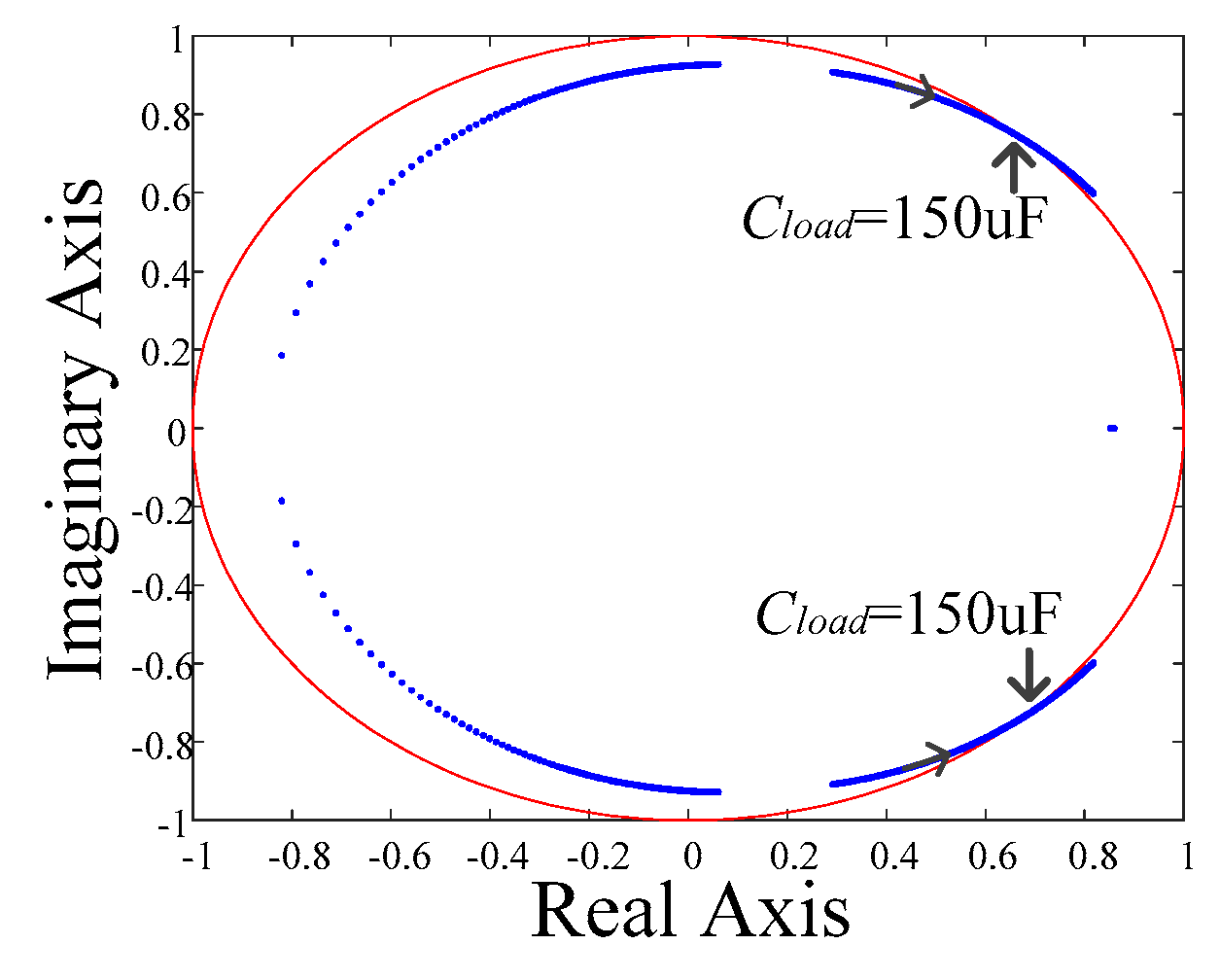
3.3. Mechanism of Resonance Under Capacitance Load
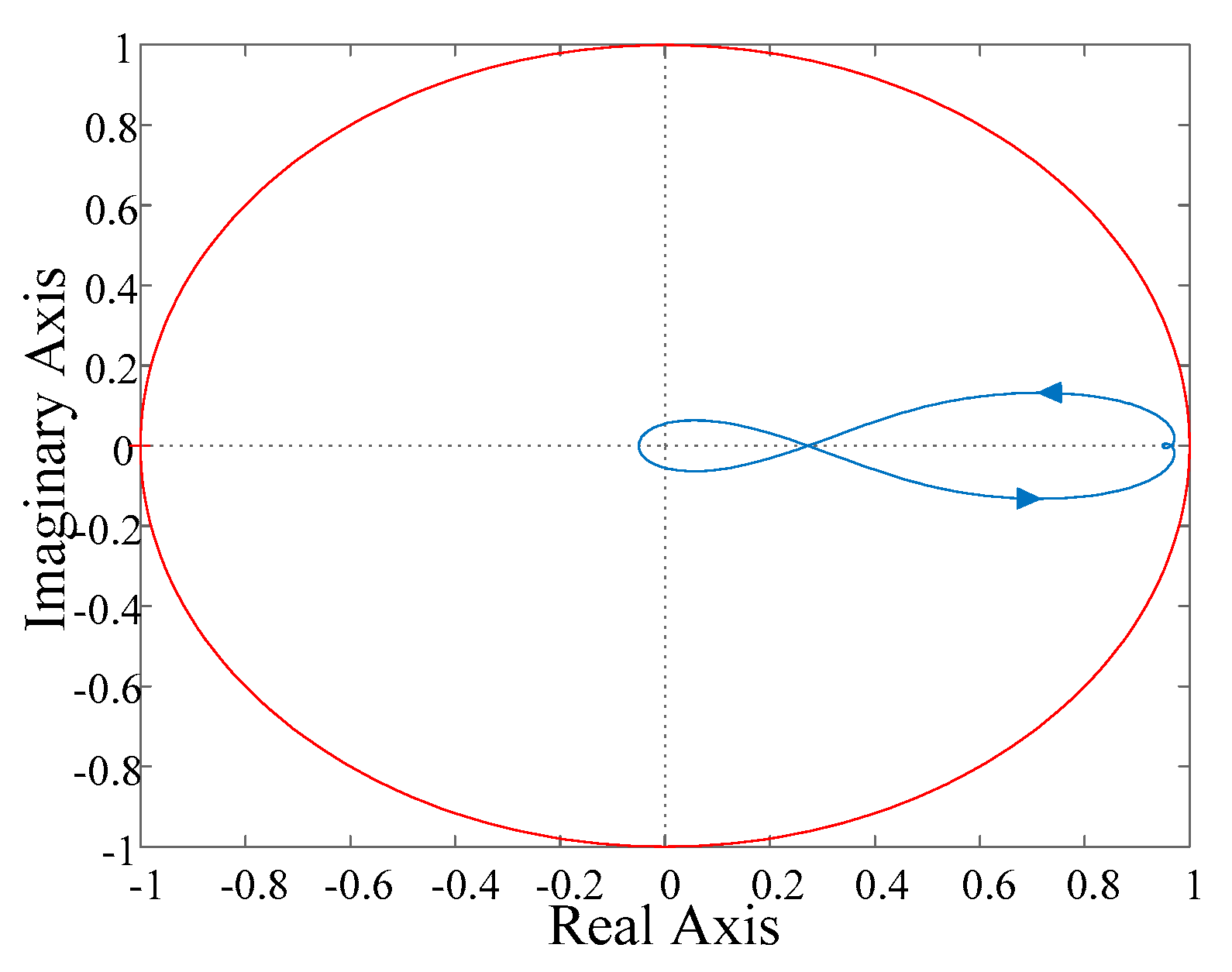
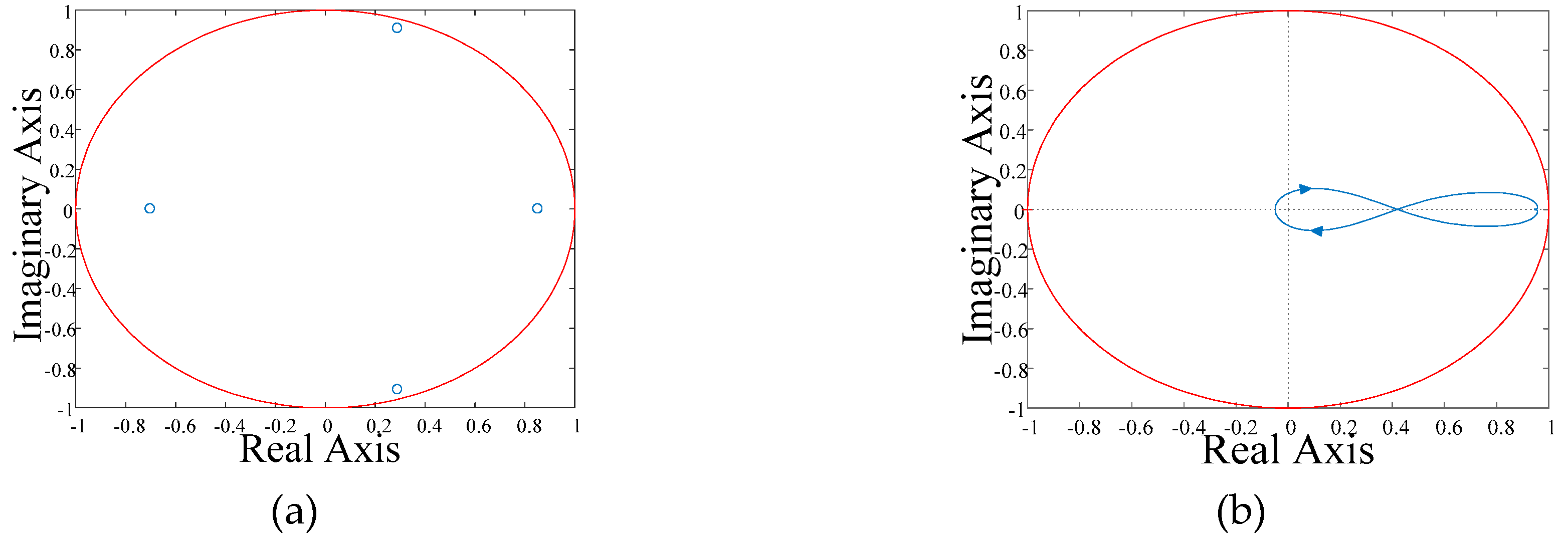
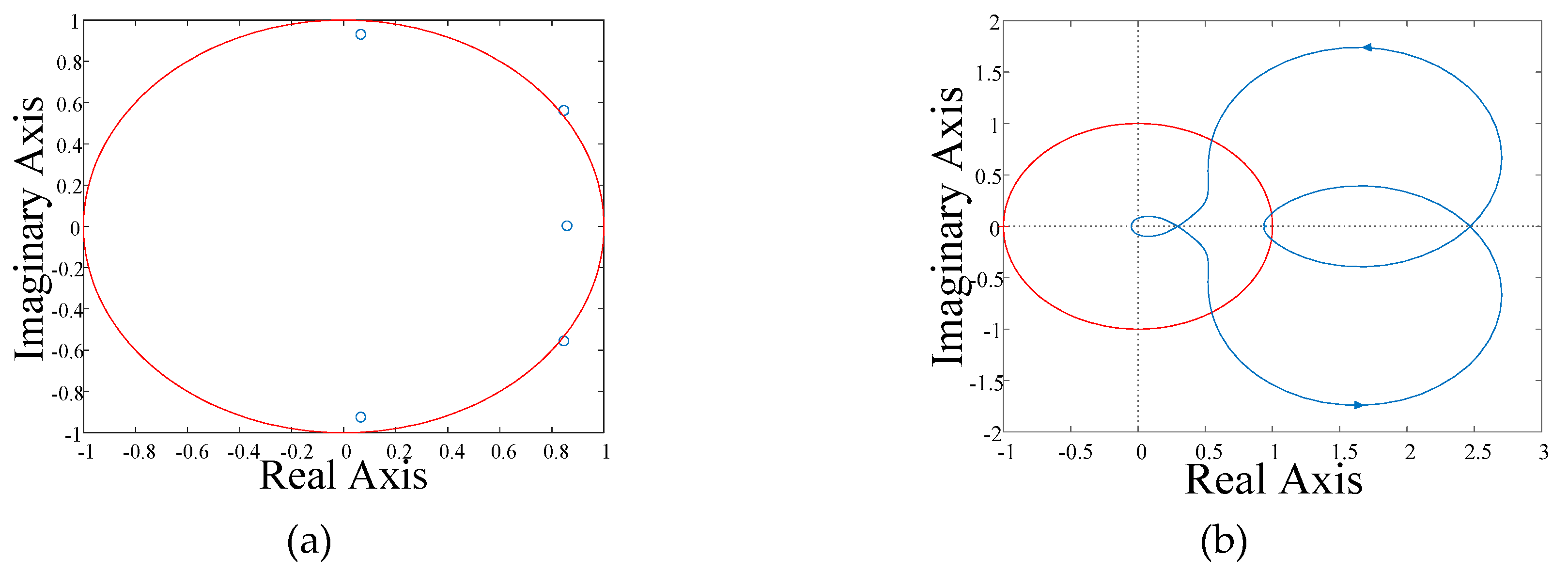
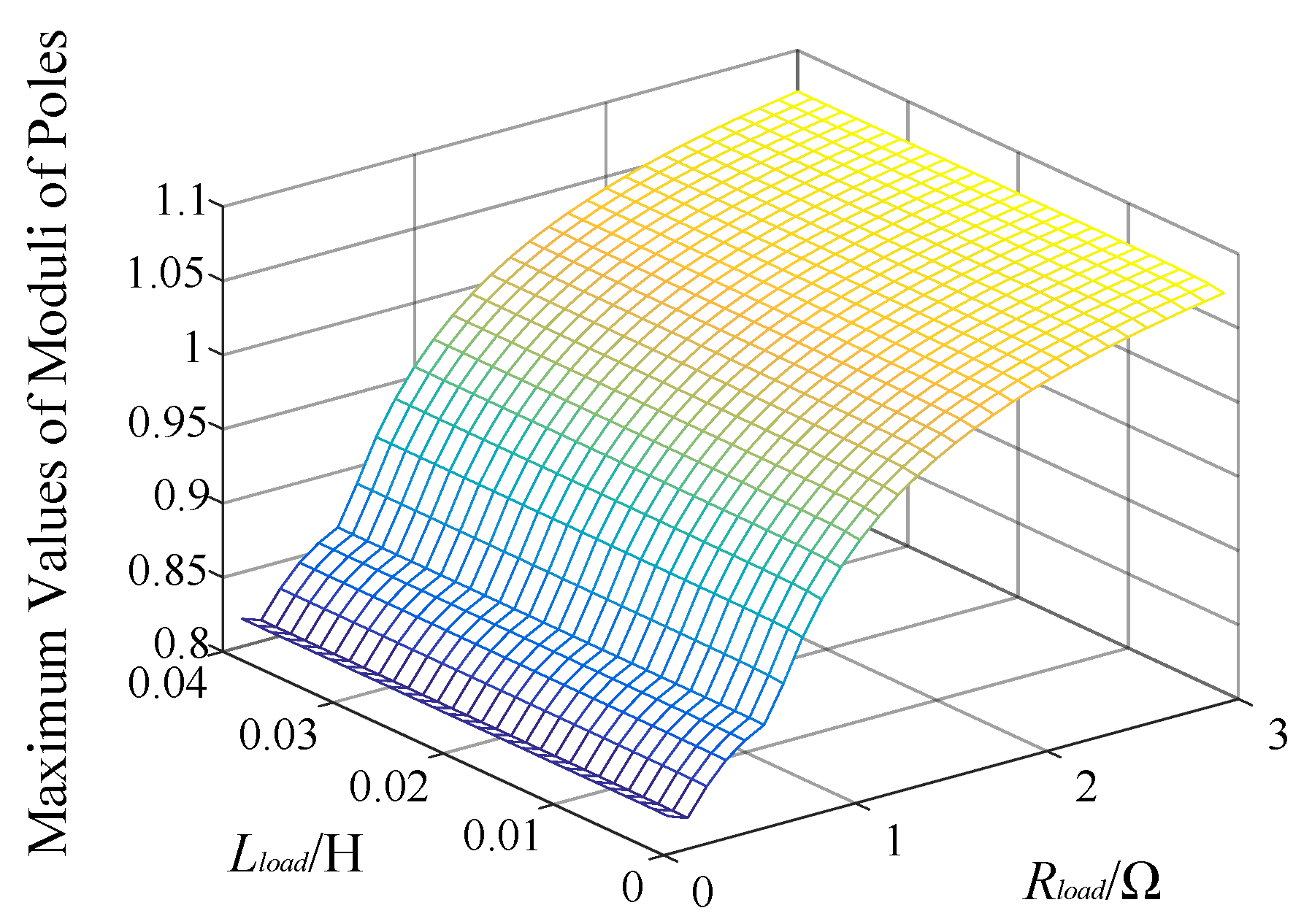
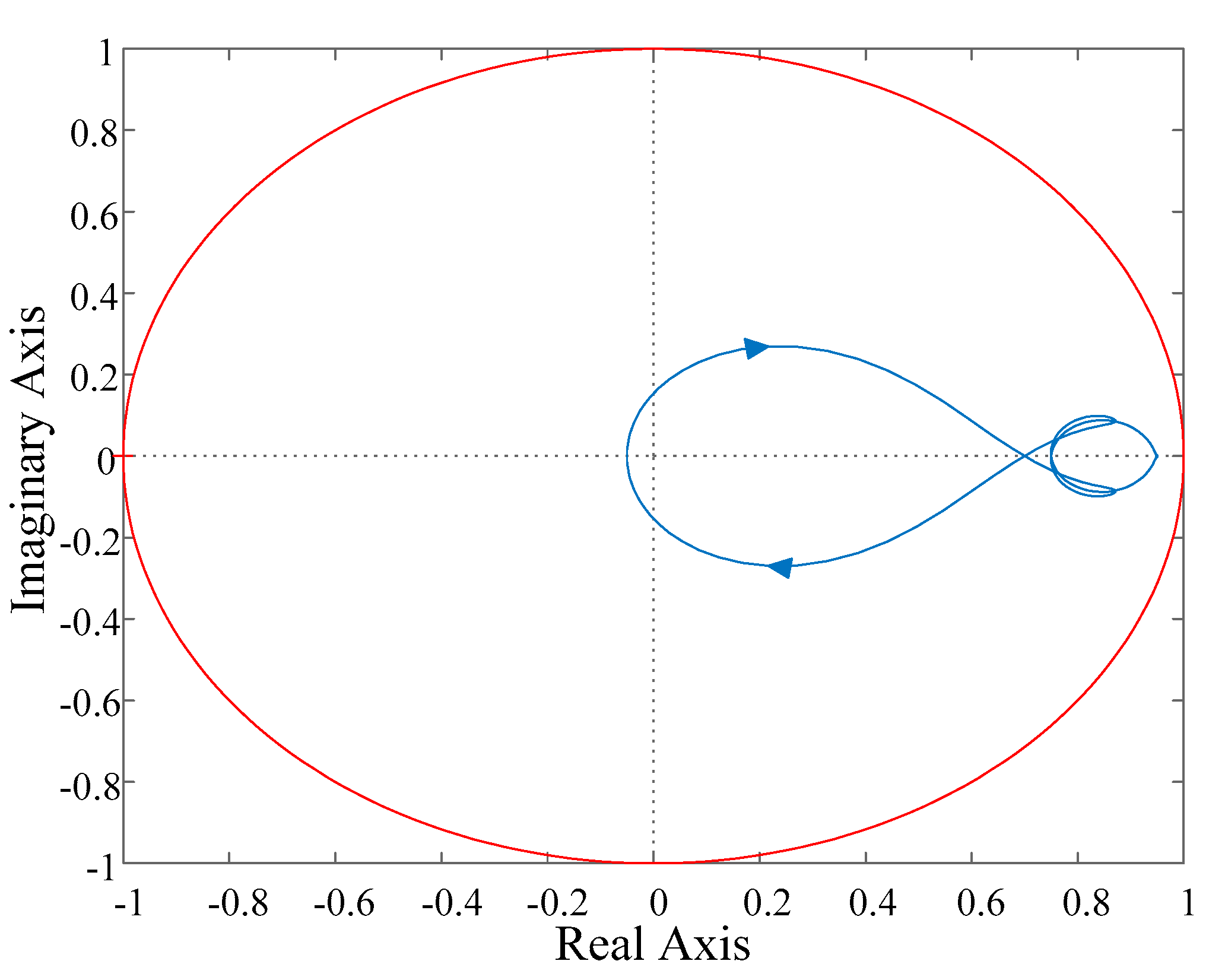
3.4. Stability of External Circuit: T(z)
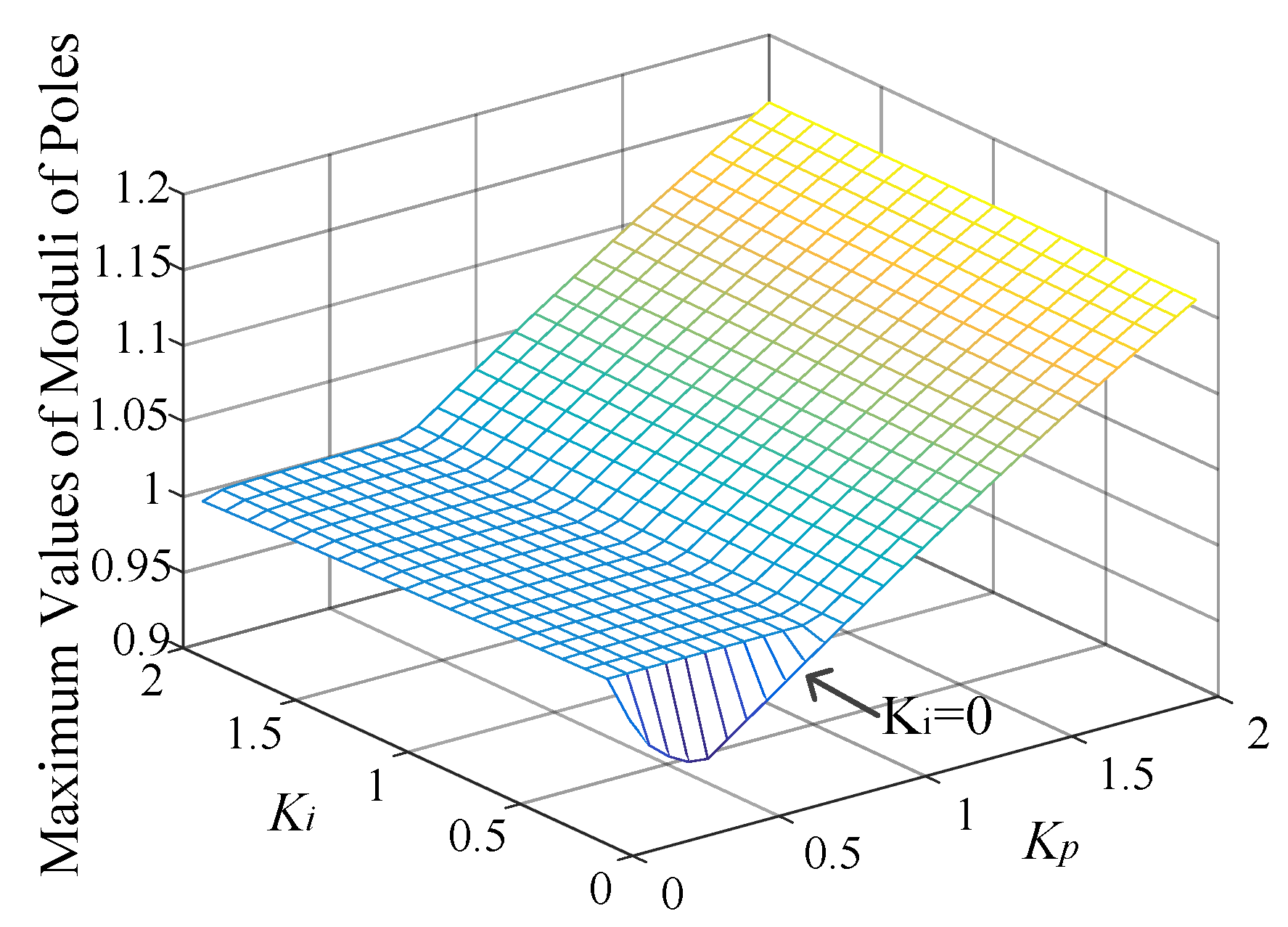
3.5. Stability of Hybrid Controller: H(z)
4. System Stabilization Strategies
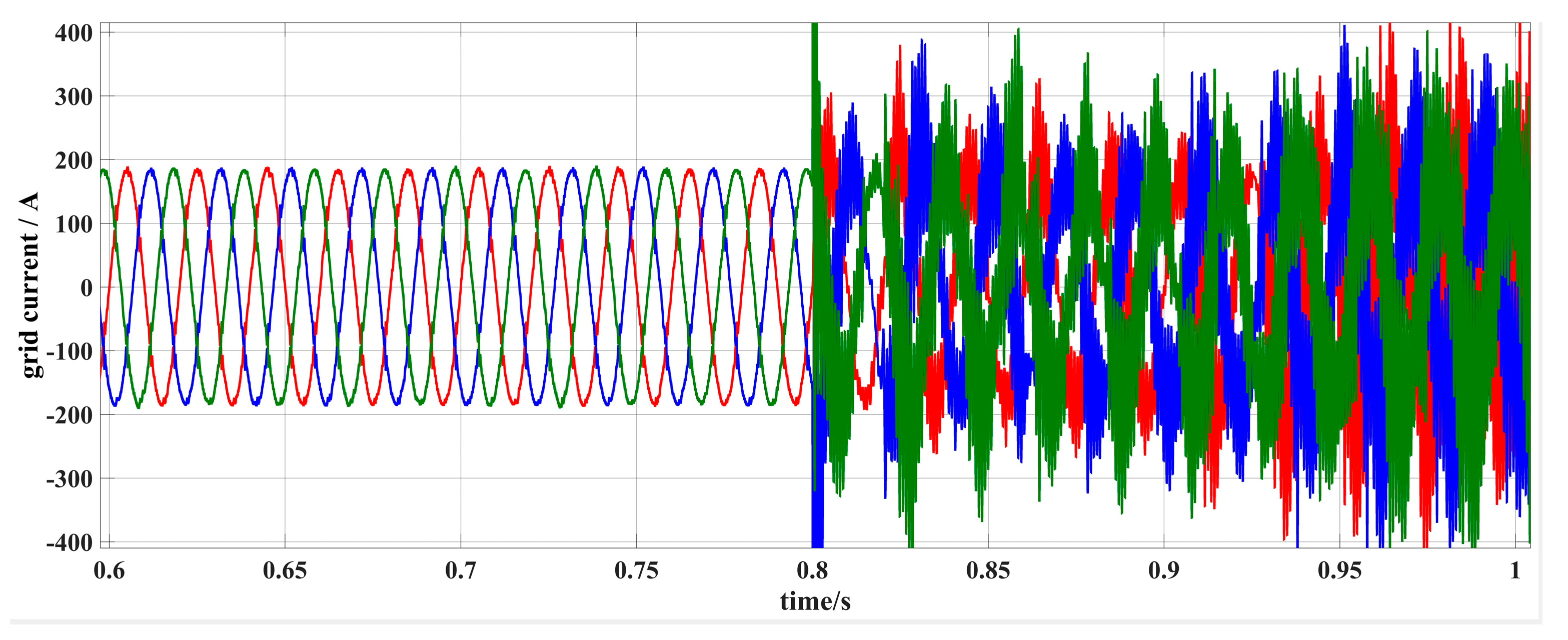
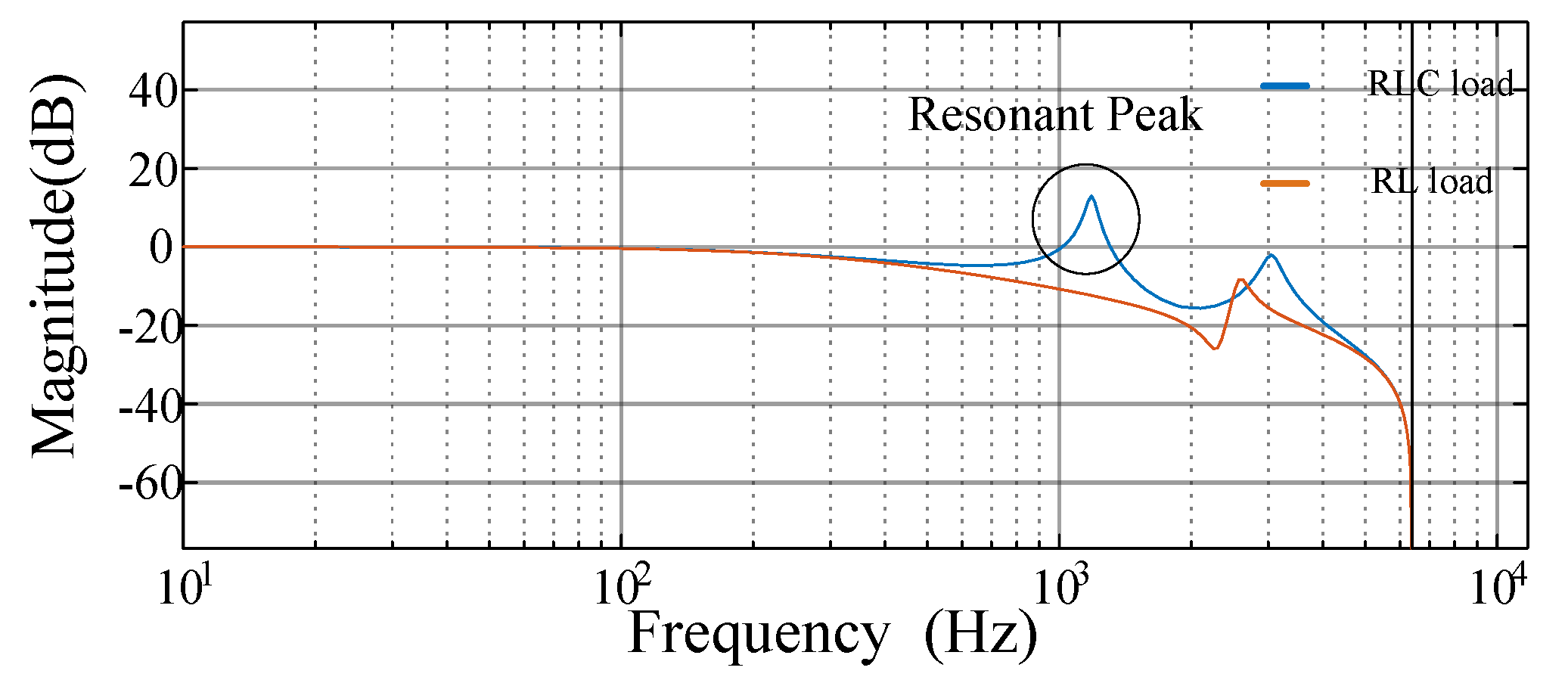
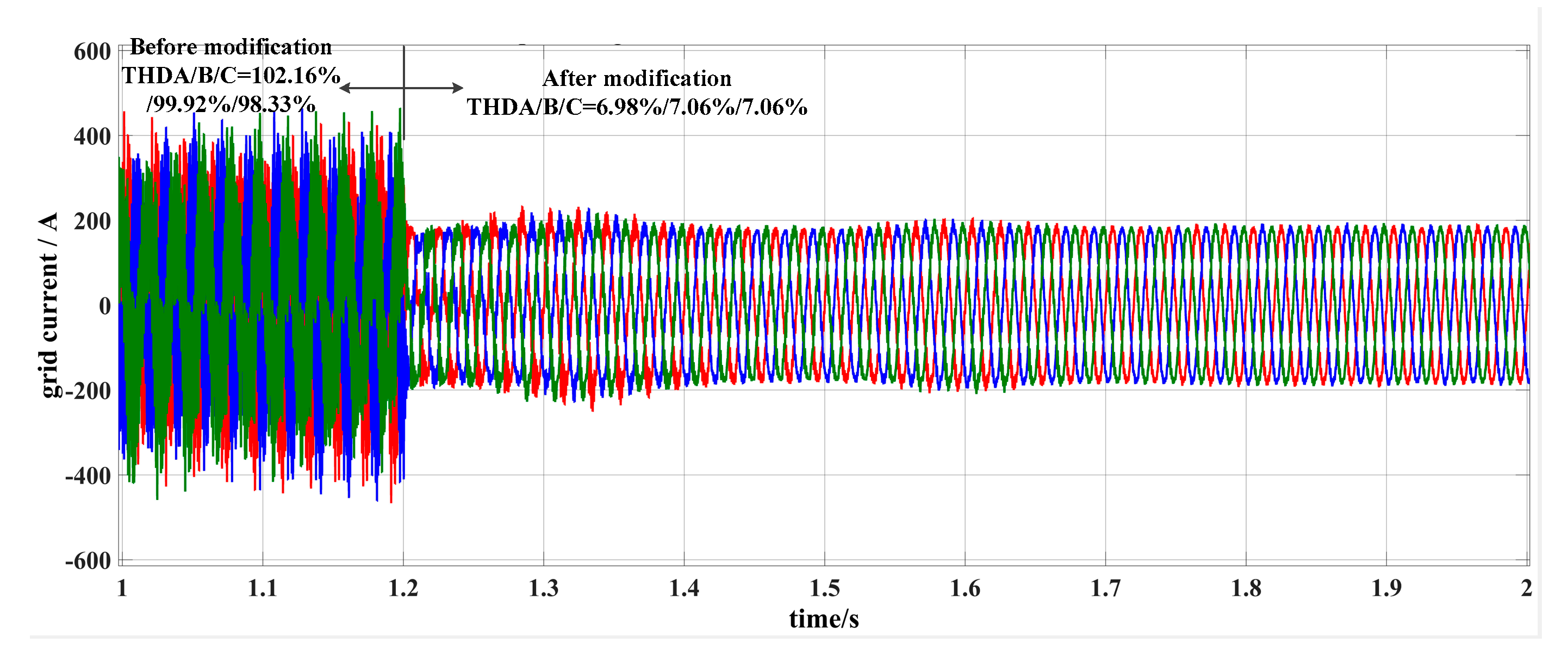
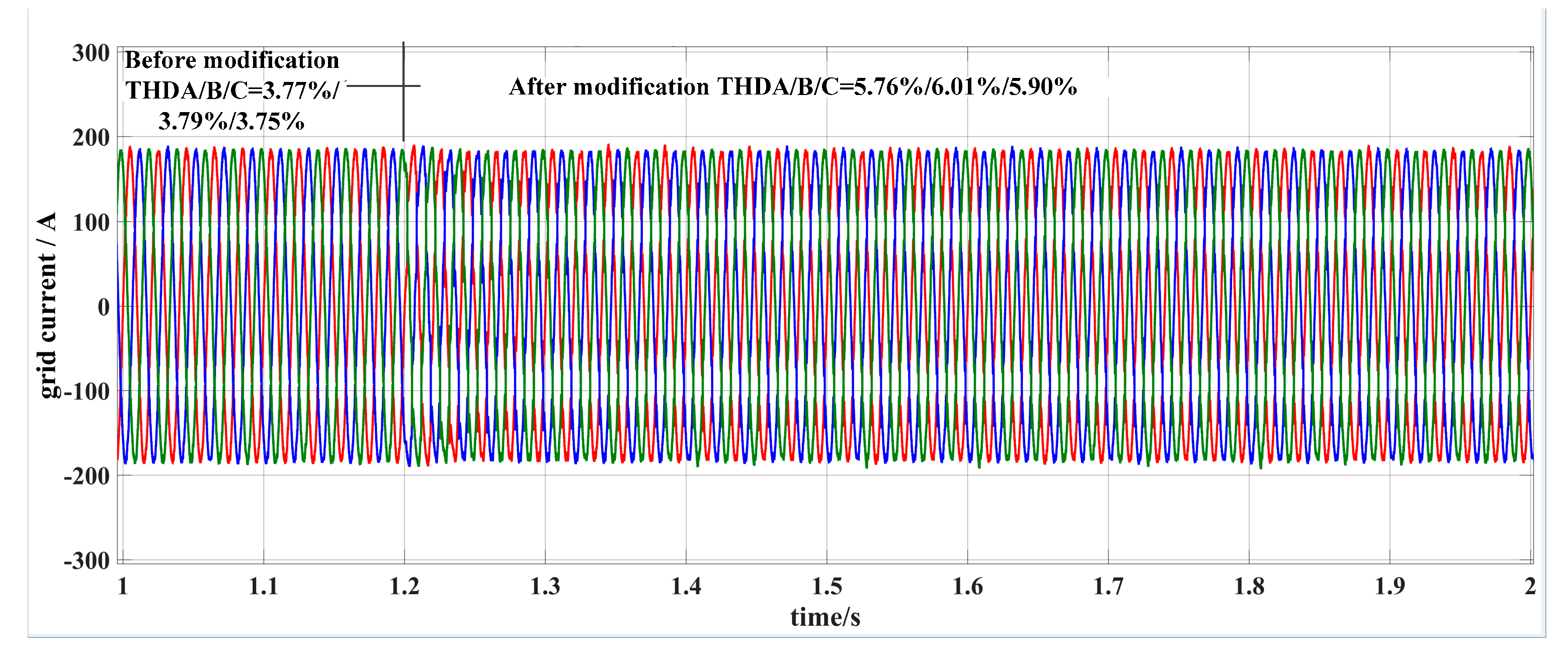
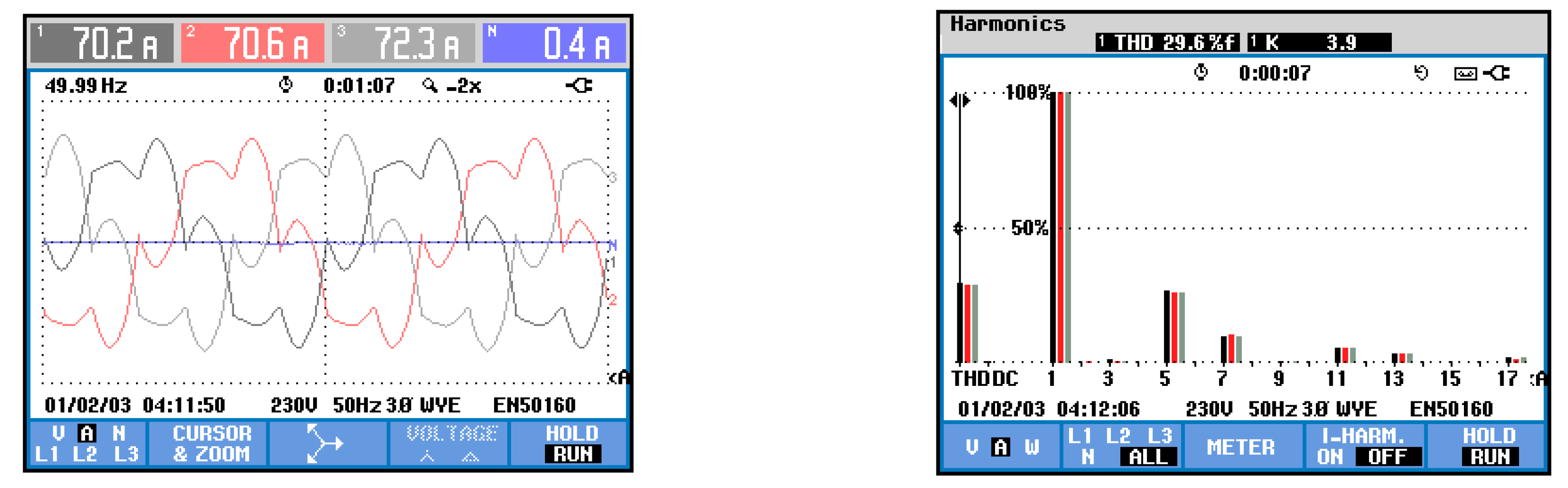
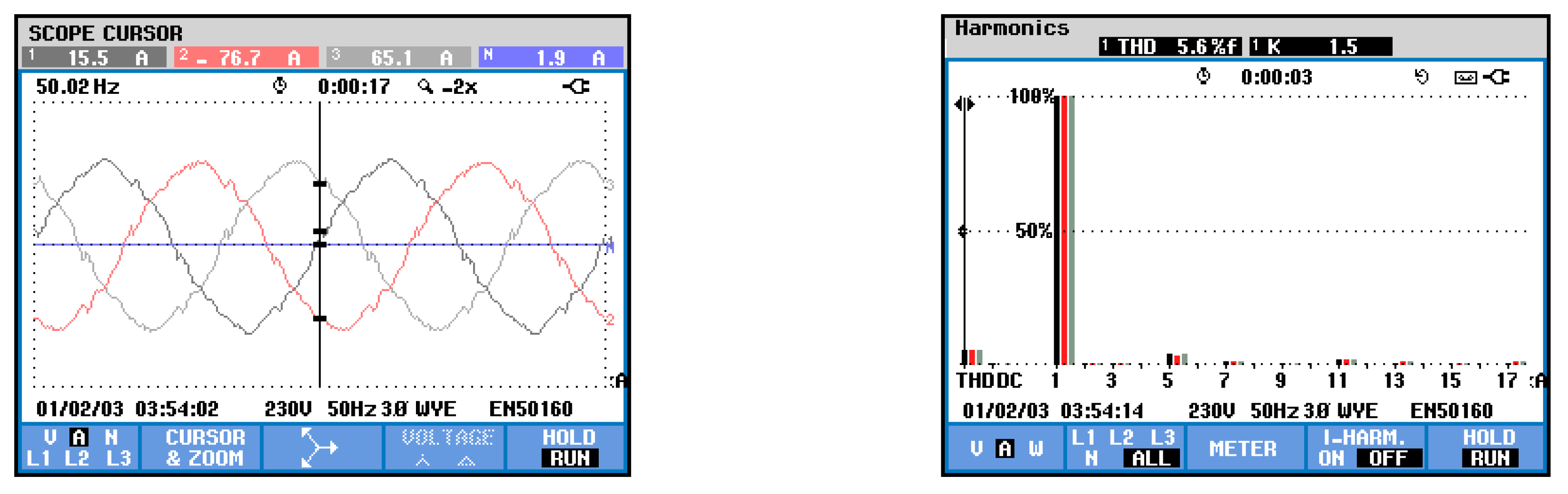
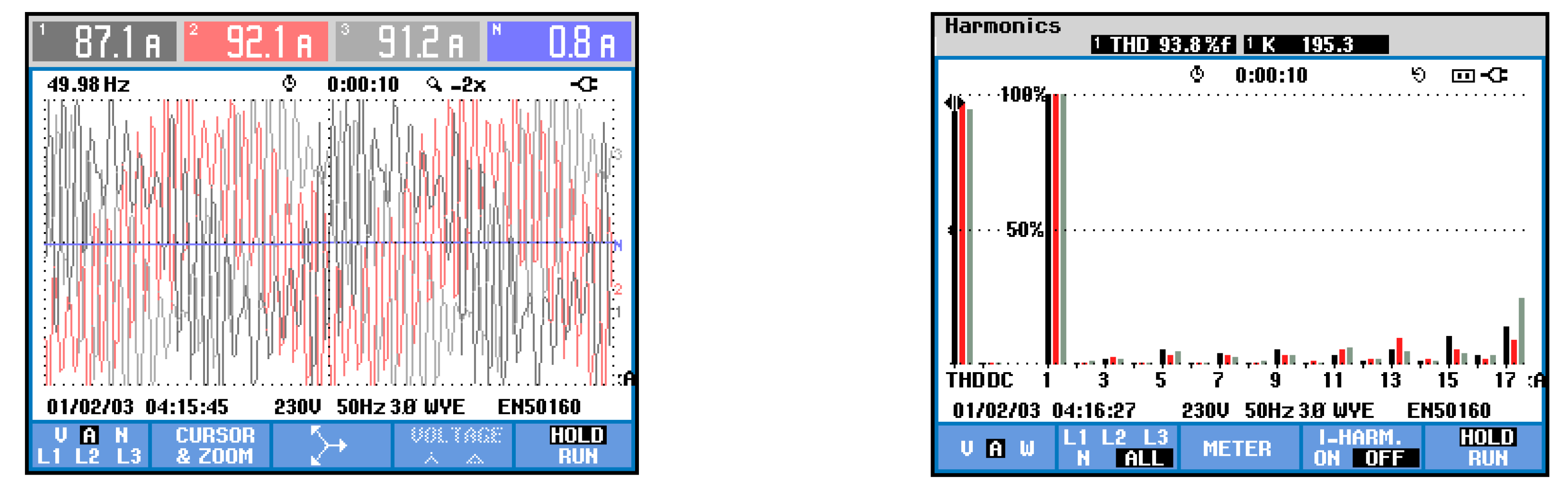
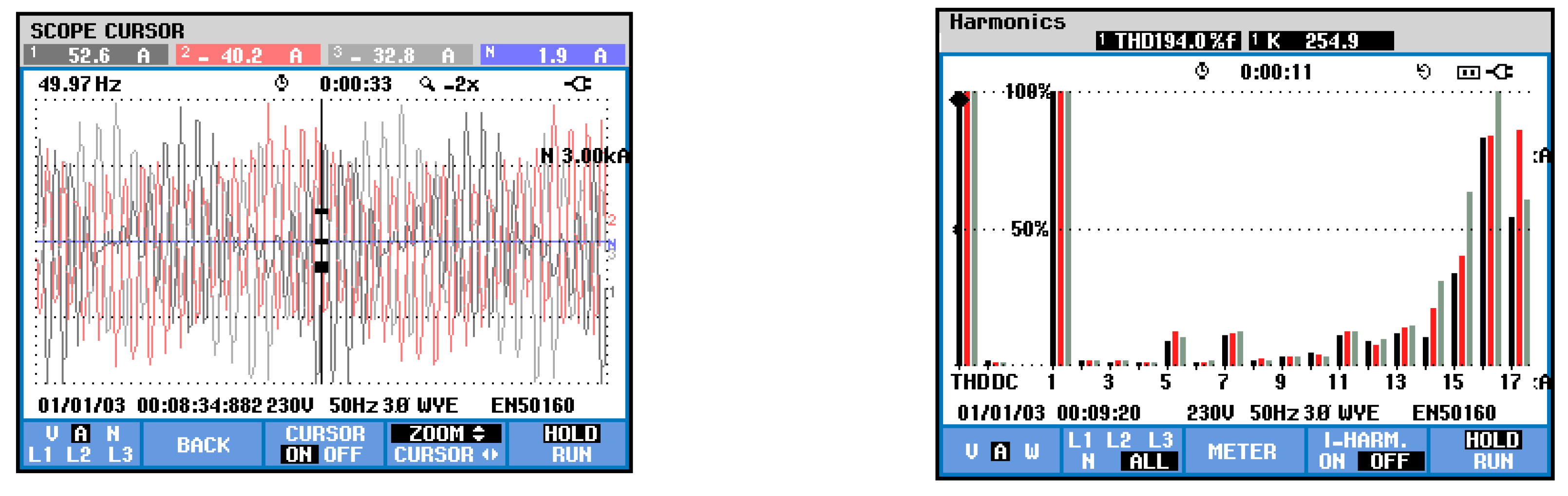
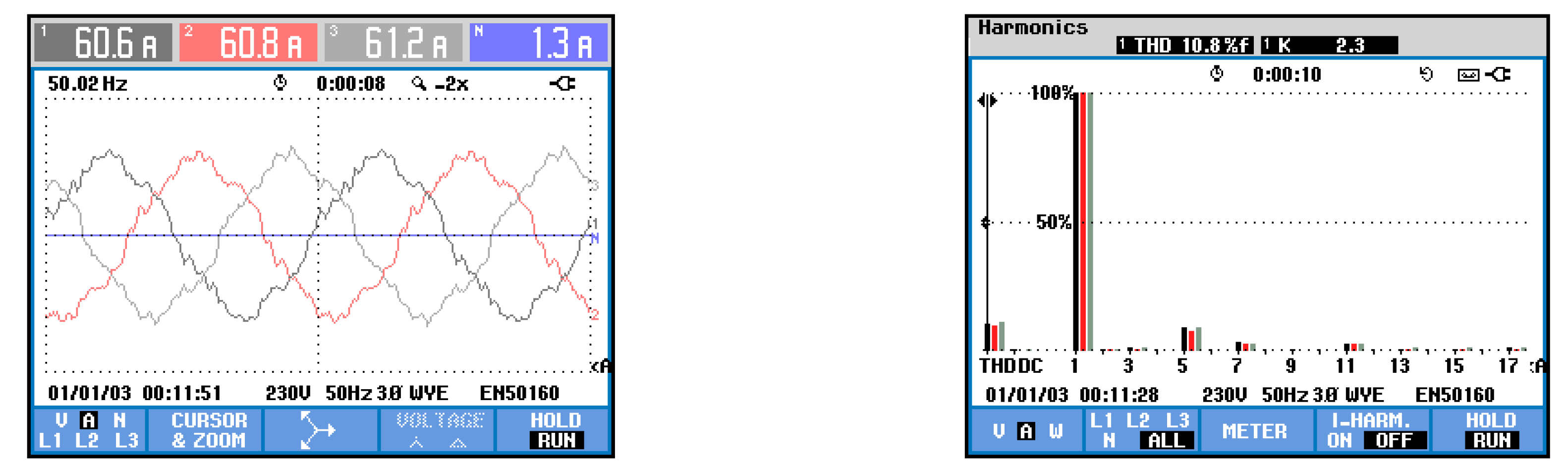
5. Simulation and Experimental Results
5.1. Simulation Results
5.2. Experimental Results
6. Conclusions
- The dynamic characteristics of input signals of active power filter were taken into account.
- The external circuit (power grids and the loads) were modelled.
- The stability problem of the system could be reflected more accurately.
Author Contributions
Funding
Conflicts of Interest
References
- Wang, L.; Lam, C.; Wong, M. Hybrid structure of static var compensator and hybrid active power filter (SVC//HAPF) for medium-voltage heavy loads compensation. IEEE Trans. Ind. Electron. 2018, 65, 4432–4442. [Google Scholar] [CrossRef]
- Sasaki, H.; Machida, T. A new method to eliminate AC harmonic current by magnetic compensation consideration on basic design. IEEE Trans. Power Appar. Syst. 1971, 90, 2009–2019. [Google Scholar] [CrossRef]
- Tareen, W.; Mekhielf, S. Three-phase transformerless shunt active power filter with reduced switch count for harmonic compensation in grid-connected applications. IEEE Trans. Power Electron. 2018, 33, 4868–4881. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Chen, S.; Zhang, Z.; Zhang, Y. A simplified minimum DC-link voltage control strategy for shunt active power filters. Energies 2018, 11, 2407. [Google Scholar] [CrossRef]
- Bosch, S.; Staiger, J.; Steinhart, H. Predictive current control for an active power filter with LCL-filter. IEEE Trans. Ind. Electron. 2018, 65, 4943–4952. [Google Scholar] [CrossRef]
- Wang, L.; Lam, C.; Wong, M. Unbalanced control strategy for a thyristor-controlled LC-coupling hybrid active power filter in three-phase three-wire systems. IEEE Trans. Power Electron. 2017, 32, 1056–1069. [Google Scholar] [CrossRef]
- Li, S.; Liang, X.; Fei, J. Dynamic surface adaptive fuzzy control of three-phase active power filter. IEEE Access. 2016, 4, 9451–9458. [Google Scholar] [CrossRef]
- Fei, J.; Chu, Y.; Hou, S. A backstepping neural global sliding mode control using fuzzy approximator for three-phase active power filter. IEEE Access. 2017, 5, 16021–16032. [Google Scholar] [CrossRef]
- Liu, N.; Fei, J. Adaptive fractional sliding mode control of active power filter based on dual RBF neural networks. IEEE Access. 2017, 5, 27590–27598. [Google Scholar] [CrossRef]
- Hou, S.; Fei, J.; Chu, Y.; Chen, C. Experimental investigation of adaptive fuzzy global sliding mode control of single-phase shunt active power filters. IEEE Access. 2019, 7, 64442–64449. [Google Scholar] [CrossRef]
- Zeng, Z.; Yang, J.; Chen, S.; Huang, J. Fast-transient repetitive control strategy for a three-phase LCL filter-based shunt active power filter. J. Power Electron. 2014, 14, 392–401. [Google Scholar] [CrossRef]
- Fang, Z. Application issues and characteristics of active power filters. IEEE Ind. Appl. Mag. 1998, 4, 21–30. [Google Scholar] [CrossRef]
- Fang, Z. Harmonic sources and filtering approaches. IEEE Ind. Appl. Mag. 2001, 7, 18–25. [Google Scholar]
- Ceaki, O.; Vatu, R.; Golovanov, N.; Porumb, R.; Seritan, G. Analysis of SVC influence on the power quality for grid-connected PV plants. In Proceedings of the 2014 International Symposium on Fundamentals of Electrical Engineering (ISFEE), Bucharest, Romania, 28–29 November 2014. [Google Scholar]
- Ceaki, O.; Vatu, R.; Mancasi, M.; Porumb, R.; Seritan, G. Analysis of electromagnetic disturbances with or without SVC device. In Proceedings of the 2015 50th International Universities Power Engineering Conference (UPEC), Stoke on Trent, UK, 1–4 September 2015. [Google Scholar]
- Francis, B.; Wonham, W. The internal model principle of control theory. Automatica 1976, 12, 457–465. [Google Scholar] [CrossRef]
- Grino, R.; Castello, R.; Fossas, E. Digital control of a single-phase shunt active power filter. In Proceedings of the IEEE 34th Annual Conference on Power Electronics Specialist, Acapulco, Mexico, 15–19 June 2003; pp. 1038–1042. [Google Scholar]
- Zimann, F.; Neto, R.; Neves, F.; Souza, H.E.P.; Batschauer, A.L.; Rech, C. A complex repetitive controller based on the generalized delayed signal cancelation method. IEEE Trans. Ind. Electron. 2019, 66, 2857–2867. [Google Scholar] [CrossRef]
- Fang, J.; Xiao, G.; Yang, X.; Tang, Y. Parameter design of a novel series-parallel-resonant LCL filter for single-phase half-bridge active power filters. IEEE Trans. Power Electron. 2017, 32, 200–217. [Google Scholar] [CrossRef]
- Xie, C.; Zhao, X.; Savaghebi, M.; Meng, L.; Meng, L.; Guerrero, J.M.; Vasquez, G.C. Multirate fractional-order repetitive control of shunt active power filter suitable for microgrid applications. IEEE J. Emerg. Sel. Topics Power Electron. 2017, 5, 809–819. [Google Scholar] [CrossRef]
- Zou, Z.; Zhou, K.; Wang, Z.; Cheng, M. Frequency-adaptive fractional-order repetitive control of shunt active power filters. IEEE Trans. Ind. Electron. 2015, 62, 1659–1668. [Google Scholar] [CrossRef]
- Grino, R.; Cardoner, R.; Castello, R.; Fossas, E. Digital repetitive control of a three-phase four-wire shunt active filter. IEEE Trans. Ind. Electron. 2007, 54, 1495–1503. [Google Scholar] [CrossRef]
- Castello, R.; Grino, R.; Fossas, E. Odd-harmonic digital repetitive control of a single-phase current active filter. IEEE Trans. Power Electron. 2004, 19, 1060–1068. [Google Scholar] [CrossRef]
- Yang, L.; Yang, J. A robust dual-loop current control method with a delay-compensation control link for LCL-type shunt active power filters. IEEE Trans. Power Electron. 2018, 34, 6183–6199. [Google Scholar] [CrossRef]
- Grino, R.; Castello, R. Digital repetitive plug-in controller for odd-harmonic periodic references and disturbances. Automatica 2005, 41, 153–157. [Google Scholar] [CrossRef]
- Jiang, S.; Cao, D.; Peng, F.Z.; Li, Y.; Liu, J. Low-THD, fast-transient, and cost-effective synchronous-frame repetitive controller for three-phase UPS inverters. IEEE Trans. Power Electron. 2012, 27, 2994–3005. [Google Scholar] [CrossRef]
- Cerrada, A.; Ardila, O.; Batlle, V.; Roncero-Sanchez, P.; Garcia-Gonzalez, P. Application of a repetitive controller for a three-phase active power filter. IEEE Trans. Power Electron. 2007, 22, 237–246. [Google Scholar] [CrossRef]
- Sun, J.; Gong, J.; Chen, B.; Zha, X. Analysis and design of repetitive controller based on regeneration spectrum and sensitivity function in active power filter system. IET Power Electron. 2014, 7, 2133–2140. [Google Scholar] [CrossRef]
- Tanaka, T.; Akagi, H. A new method of harmonic power detection based on the instantaneous active power in three-phase circuits. IEEE Trans. Power Del. 1995, 10, 1737–1742. [Google Scholar] [CrossRef]
- Peng, F.; Ott, W.; Adams, D. Harmonic and reactive power compensation based on the generalized instantaneous reactive power theory for three-phase four-wire systems. IEEE Trans. Power Electron. 1998, 13, 1174–1181. [Google Scholar] [CrossRef]
- Soares, V.; Verdelho, P.; Marques, G. An instantaneous active power and reactive current component method for active filters. IEEE Trans. Power Electron. 2000, 15, 660–669. [Google Scholar] [CrossRef]
- Lascu, C.; Asiminoaei, C.; Boldea, I.; Blaabjerg, F. High performance current controller for selective harmonic compensation in active power filters. IEEE Trans. Power Electrons. 2007, 22, 1826–1835. [Google Scholar] [CrossRef]
- Girgis, A.; Chang, W.; Makram, E. A digital recursive measurement scheme for on-line tracking of power system harmonics. IEEE Trans. Power Del. 1991, 6, 1153–1160. [Google Scholar] [CrossRef]
- Li, H.; Zhuo, F.; Wang, Z.; Lei, W.; Wu, L. A novel time-domain current-detection algorithm for shunt active power filters. IEEE Trans. Power Syst. 2005, 20, 644–651. [Google Scholar] [CrossRef]
- Kouchaki, A.; Nymand, M. Analytical design of passive LCL filter for three-phase two-level power factor correction rectifiers. IEEE Trans. Power Electron. 2018, 33, 3012–3022. [Google Scholar] [CrossRef]
- Jayalath, S.; Hanif, M. Generalized LCL-filter design algorithm for grid-connected voltage-source inverter. IEEE Trans. Ind. Electron. 2017, 64, 1905–1915. [Google Scholar] [CrossRef]
- Jiao, Y.; Lee, F. LCL filter design and inductor current ripple analysis for a three-level NPC grid interface converter. IEEE Trans. Power Electron. 2015, 30, 4659–4668. [Google Scholar] [CrossRef]
- Liu, Q.; Peng, L.; Kang, Y.; Tang, S.; Wu, D.; Qi, Y. A novel design and optimization method of an LCL filter for a shunt active power filter. IEEE Trans. Ind. Electron. 2014, 61, 4000–4010. [Google Scholar] [CrossRef]
- Zhang, B.; Zhou, K.; Wang, D. Multirate repetitive control for PWM DC/AC converters. IEEE Trans. Ind. Electron. 2014, 61, 2883–2890. [Google Scholar] [CrossRef]







| Circuit Parameters | Controller Part | |||
|---|---|---|---|---|
| Symbol | Parameter | Physical Meanings | Control Unit | Illustration |
| Usys | 220 V | System phase voltage (RMS) | N = 256 | fs/f0 |
| Lvs | 50 μH | System reactance | Q(z) = 0.95 | Attenuation coefficient |
| Udc | 700 V | DC bus voltage of APF | GPI1(z) = 1 | Proportion unit |
| f0 | 50 Hz | Frequency of distribution network | GPI2(z) = 1 | Proportion unit |
| fs | 12.8 kHz | Sample frequency | S(z) | Corrector |
| Lf | 0.375 mH | Inductance of inverter side of LCL | ||
| Lg | 0.075 mH | Inductance of grid side of LCL | ||
| Cf | 30 μF | Capacitor of LCL | ||
| Rload | 4.4 Ω | Parallel active load | ||
| Lload | 15 mH | Parallel inductance load | ||
| Cload(Y) | 90 μF | Y connecting parallel capacitance load | ||
| Cload(Δ) | 276.5 μF | Δ connecting parallel capacitance load | ||
| 3 ph rectifier load | Represents harmonics | |||
| Rline | 0.05 Ω | Represents line resistance | ||
| Usys | 220 V | System phase voltage (RMS) | ||
| Dynamic characteristics of input signals are ignored |
| External circuits (power grids and loads) are ignored |
| Some stability problems cannot be reflected |
| Before Modification | |
| Control unit | Values |
| GPI2(z) | Kp = 1; Ki = 0.0001 |
| GLP(z) 2nd Butterworth low-pass filter | Cut–off frequency = 500 Hz |
| After Modification | |
| GPI2(z) | Kp = 0.5; Ki = 0.0001 |
| GLP(z) 2nd Butterworth low-pass filter | Cut–off frequency = 1000 Hz |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bing, Y.; Jiang, D.; Liang, Y.; Jiang, C.; He, T.; Yang, L.; Hu, P. Modified Modeling and System Stabilization of Shunt Active Power Filter Compensating Loads with μF Capacitance. Energies 2019, 12, 2084. https://doi.org/10.3390/en12112084
Bing Y, Jiang D, Liang Y, Jiang C, He T, Yang L, Hu P. Modified Modeling and System Stabilization of Shunt Active Power Filter Compensating Loads with μF Capacitance. Energies. 2019; 12(11):2084. https://doi.org/10.3390/en12112084
Chicago/Turabian StyleBing, Yuqi, Daozhuo Jiang, Yiqiao Liang, Chongxi Jiang, Tianxiang He, Lei Yang, and Pengfei Hu. 2019. "Modified Modeling and System Stabilization of Shunt Active Power Filter Compensating Loads with μF Capacitance" Energies 12, no. 11: 2084. https://doi.org/10.3390/en12112084
APA StyleBing, Y., Jiang, D., Liang, Y., Jiang, C., He, T., Yang, L., & Hu, P. (2019). Modified Modeling and System Stabilization of Shunt Active Power Filter Compensating Loads with μF Capacitance. Energies, 12(11), 2084. https://doi.org/10.3390/en12112084





