A New Model to Simulate Local Market Power in a Multi-Area Electricity Market: Application to the European Case †
Abstract
1. Introduction
- The article proposes a model that allows the market equilibrium in a multi-area electricity system under non-perfect competition to be computed efficiently.
- An original methodology is implemented. It makes use of an original clustering algorithm, developed to extract the representative network configurations using hourly prices for each area in the system.
- The proposed model is applied into a real-size European case, which consists of the Central Western European (CWE) and Iberian electricity markets.
2. Methodology
2.1. Market Equilibrium Model
| Parameters: | |
| demand in area a in period p | |
| cost function for agent e in area a in period p | |
| price spread for agent e in area a in period p | |
| conjectured-price response for agent e in area a in period p, depending on agent e’s production in area | |
matrix where a correspondence between areas and interconnections is defined as follows:
| |
| maximum power flow in interconnection l | |
| maximum power produced by agent e in area a | |
| minimum power flow in interconnection l | |
| minimum power produced by agent e in area a | |
| Decision variables: | |
| power for agent e in area a in period p | |
| power flow in interconnection l in period p | |
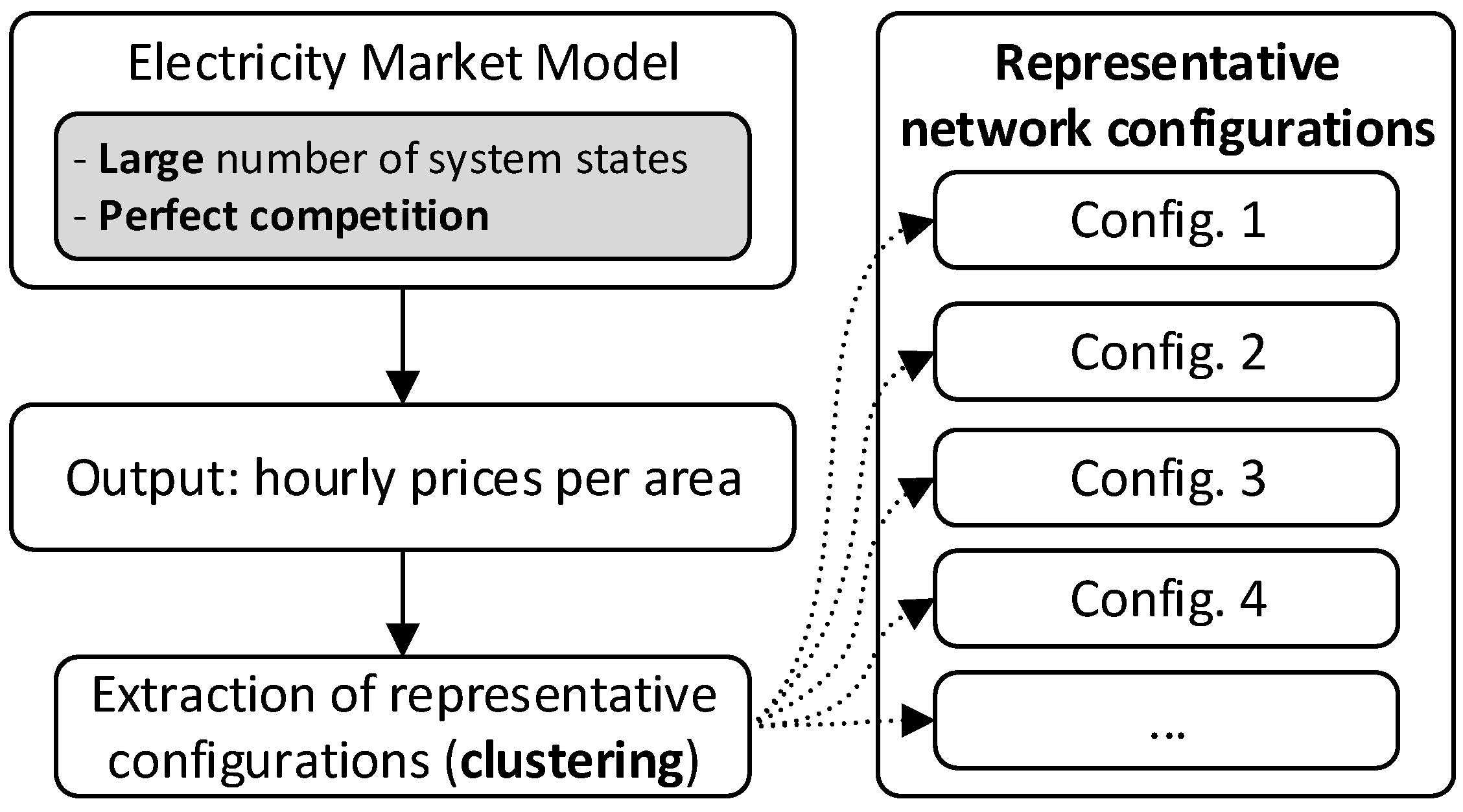
2.2. Network Configuration Reduction
- Step 1
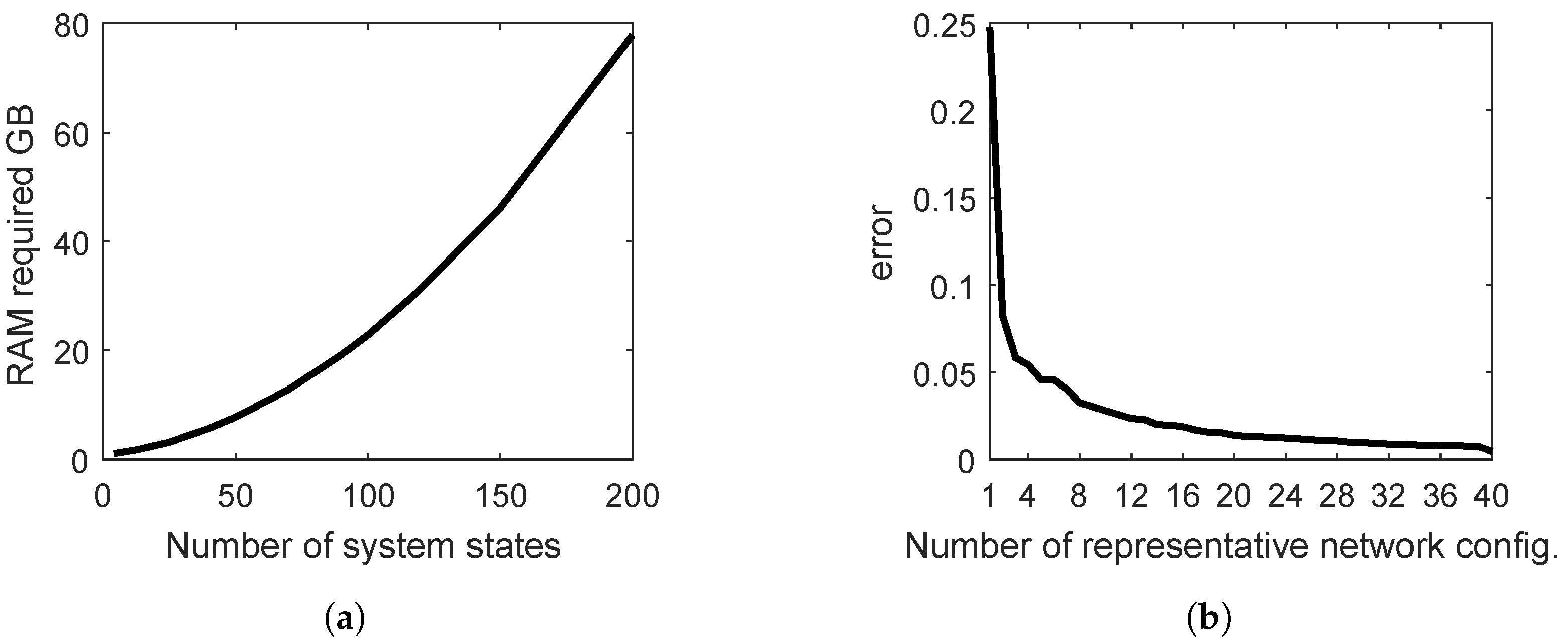
- An electricity market equilibrium model, under perfect competition, is run to compute hourly prices per area. For this execution, a compromised number of system states is used that satisfies both the accuracy of the solution and the computational power necessary to run the model.
- Step 2
- A clustering method is applied to the prices obtained in Step 1 to extract the representative network configurations.
- Step 3
- With the information of the representatives in Step 2, the user can input a spread per agent and configuration for each hour throughout the horizon of the problem. These spreads are defined based on the agents’ expected market behavior.
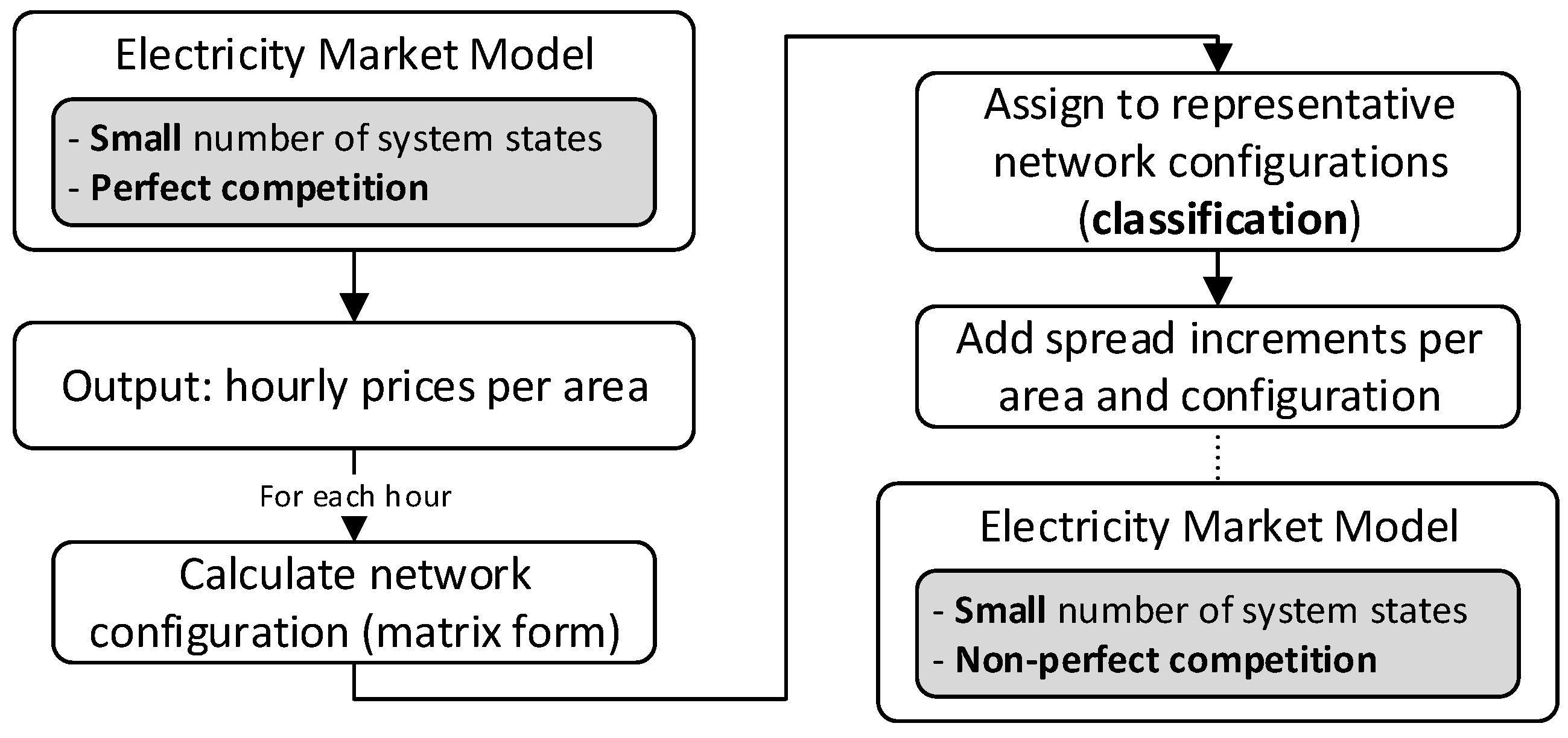
- Step 4
- The model under perfect competition in Step 1 is run again, this time under normal conditions in terms of the number of system states (significantly less than the number used in the initial computation in Step 1), which yield a solution notably quicker. For each hour, the resulting prices’ configuration is classified into one of the main representatives.
- Step 5
- Given the relationships spread-configuration (in Step 3) and configuration-hour (in Step 4), it is now possible to run the model in Step 4 under non-perfect competition.
2.2.1. Clustering Algorithm
| Algorithm 1 Clustering algorithm. |
|
2.2.2. Classification Procedure
3. Case Study and Results
3.1. System Description
3.2. Network Configurations Methodology Implementation
3.3. Model under Non-Perfect Competition
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Creti, A.; Fumagalli, E.; Fumagalli, E. Integration of electricity markets in Europe: Relevant issues for Italy. Energy Policy 2010, 38, 6966–6976. [Google Scholar] [CrossRef]
- Domanico, F. Concentration in the European electricity industry: The internal market as solution? Energy Policy 2007, 35, 5064–5076. [Google Scholar] [CrossRef]
- Turvey, R. Interconnector economics. Energy Policy 2006, 34, 1457–1472. [Google Scholar] [CrossRef]
- Beus, M.; Pavić, I.; Štritof, I.; Capuder, T.; Pandžić, H. Electricity Market Design in Croatia within the European Electricity Market—Recommendations for Further Development. Energies 2018, 11, 346. [Google Scholar] [CrossRef]
- Borenstein, S.; Bushnell, J.; Stoft, S. The competitive effects of transmission capacity in a deregulated electricity industry. RAND J. Econ. 2000, 31, 294. [Google Scholar] [CrossRef]
- Cardell, J.B.; Hitt, C.C.; Hogan, W.W. Market power and strategic interaction in electricity networks. Resour. Energy Econ. 1997, 19, 109–137. [Google Scholar] [CrossRef]
- Hobbs, B.F. Linear complementarity models of Nash-Cournot competition in bilateral and POOLCO power markets. IEEE Trans. Power Syst. 2001, 16, 194–202. [Google Scholar] [CrossRef]
- Neuhoff, K.; Barquín, J.; Boots, M.G.; Ehrenmann, A.; Hobbs, B.F.; Rijkers, F.A.; Vázquez, M. Network-constrained Cournot models of liberalized electricity markets: The devil is in the details. Energy Econ. 2005, 27, 495–525. [Google Scholar] [CrossRef]
- Barquín, J.; Centeno, E.; Reneses, J. Medium-term generation programming in competitive environments: A new optimisation approach for market equilibrium computing. IEE Proc. Gener. Transm. Distrib. 2004, 151, 119. [Google Scholar] [CrossRef]
- Campos, F.A.; Villar, J.; Barquín, J. Solving Cournot equilibriums with variational inequalities algorithms. IET Gener. Transm. Distrib. 2010, 4, 268. [Google Scholar] [CrossRef]
- Gountis, V.P.; Bakirtzis, A.G. Efficient determination of Cournot equilibria in electricity markets. IEEE Trans. Power Syst. 2004, 19, 1837–1844. [Google Scholar] [CrossRef]
- Nguyen, D.; Wong, K.P. Analysis of competitive power market with constant elasticity function. IEE Proc. Gener. Transm. Distrib. 2003, 150, 595. [Google Scholar] [CrossRef]
- Barquín, J.; Vázquez, M. Cournot equilibrium calculation in power networks: An optimization approach with price response computation. IEEE Trans. Power Syst. 2008, 23, 317–326. [Google Scholar] [CrossRef]
- Von Stackelberg, H. Theory of the Market Economy; Oxford University Press: Oxford, UK, 1952. [Google Scholar]
- Quick, D.M.; Carey, J.M. An analysis of market power mitigation strategies in Colorado’s electricity industry. Energy J. 2001, 22, 55–77. [Google Scholar] [CrossRef]
- Baldick, R. Computing the electricity market equilibrium: Uses of market equilibrium models. In Proceedings of the 2006 IEEEPES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 66–73. [Google Scholar] [CrossRef]
- Ventosa, M.; Baíllo, Á.; Ramos, A.; Rivier, M. Electricity market modeling trends. Energy Policy 2005, 33, 897–913. [Google Scholar] [CrossRef]
- Fernández-Menéndez, F.; Vitoriano, B.; Barquín, J. Cross-border electricity trading modelling: A market equilibrium approach. Jornadas Hispano-lusas de Ingeniería Eléctrica 2005, 30, 1–7. [Google Scholar]
- Barquín, J.; Vitoriano, B.; Centeno, E.; Fernández-Menéndez, F. An optimization-based conjectured supply function equilibrium model for network constrained electricity markets. J. Oper. Res. Soc. 2009, 60, 1719–1729. [Google Scholar] [CrossRef]
- Campos, F.A.; Roman, A.; Villar, J.; Díaz, C.A. Two-zone electricity equilibrium computation with Mixed Integer Programming. In Proceedings of the 2014 11th International Conference on the European Energy Market (EEM), Krakow, Poland, 28–30 May 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Díaz, C.A.; Campos, F.A.; Villar, J.; Rodríguez, M.Á. Endogenous computation of conjectured supply functions with network constraints. Electr. Power Syst. Res. 2012, 90, 117–125. [Google Scholar] [CrossRef]
- Díaz, C.A.; Campos, F.A.; Villar, J.; Rodríguez, M.Á. Fundamental conjectured supply function equilibrium: Application to the iberian system. In Proceedings of the 2011 8th International Conference on the European Energy Market (EEM), Zagreb, Croatia, 25–27 May 2011; pp. 232–237. [Google Scholar] [CrossRef]
- Díaz, C.A.; Webster, M.D.; Villar, J.; Campos, F.A. Dynamics of market power in ERCOT system: A Fundamental CSFE With Network Constraints. IEEE Trans. Power Syst. 2016, 31, 861–871. [Google Scholar] [CrossRef]
- Ahmadi-Khatir, A.; Conejo, A.J.; Cherkaoui, R. Multi-area unit scheduling and reserve allocation under wind power uncertainty. IEEE Trans. Power Syst. 2014, 29, 1701–1710. [Google Scholar] [CrossRef]
- Biskas, P.N.; Chatzigiannis, D.I.; Bakirtzis, A.G. European electricity market integration with mixed market designs—Part II: Solution Algorithm and Case Studies. IEEE Trans. Power Syst. 2014, 29, 466–475. [Google Scholar] [CrossRef]
- Kurzidem, M. Analysis of Flow-Based Market Coupling in Oligopolistic Power Markets. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2010. [Google Scholar] [CrossRef]
- Oggioni, G.; Smeers, Y.; Allevi, E.; Schaible, S. A generalized Nash equilibrium model of market coupling in the European power system. Netw. Spat. Econ. 2012, 12, 503–560. [Google Scholar] [CrossRef]
- Savelli, I.; Giannitrapani, A.; Paoletti, S.; Vicino, A. An optimization model for the electricity market clearing problem with uniform purchase price and zonal selling prices. IEEE Trans. Power Syst. 2017, 33, 2864–2873. [Google Scholar] [CrossRef]
- Vlachos, A.G.; Biskas, P.N. Simultaneous clearing of energy and reserves in multi-area markets under mixed pricing rules. IEEE Trans. Power Syst. 2011, 26, 2460–2471. [Google Scholar] [CrossRef]
- Orgaz, A.; Bello, A.; Reneses, J. Multi-area electricity market equilibrium model and its application to the European case. In Proceedings of the 2017 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- García-Alcalde, A.; Ventosa, M.; Rivier, M.; Ramos, A.; Relano, G. Fitting electricity market models: A conjectural variations approach. In Proceedings of the 14th Power Systems Computation Conference 2002, Seville, Spain, 24–28 June 2002. [Google Scholar]
- Song, Y.; Ni, Y.; Wen, F.; Wu, F.F. Conjectural variation based learning model of strategic bidding in spot market. Int. J. Electr. Power Energy Syst. 2004, 26, 797–804. [Google Scholar] [CrossRef]
- Linares, P.; Santos, F.J.; Ventosa, M.; Lapiedra, L. Impacts of the European emissions trading scheme directive and permit assignment methods on the Spanish electricity sector. Energy J. 2006, 27, 79–98. [Google Scholar] [CrossRef]
- Fernández-Menéndez, F. Análisis de Mercados Eléctricos Interconectados con Restricciones de Red. Ph.D. Thesis, Universidad Pontificia Comillas, Instituto de Investigación Tecnológica (IIT), Madrid, Spain, 2015. [Google Scholar]
- Barquín, J.; Centeno, E.; Reneses, J. Stochastic market equilibrium model for generation planning. Probab. Eng. Inform. Sci. 2005, 19, 533–546. [Google Scholar] [CrossRef]
- Centeno, E.; Reneses, J.; Barquin, J. Strategic Analysis of Electricity Markets Under Uncertainty: A Conjectured-Price-Response Approach. IEEE Trans. Power Syst. 2007, 22, 423–432. [Google Scholar] [CrossRef]
- Wogrin, S.; Dueñas, P.; Delgadillo, A.; Reneses, J. A new approach to model load levels in electric power systems with high renewable penetration. IEEE Trans. Power Syst. 2014, 29, 2210–2218. [Google Scholar] [CrossRef]
- Bompard, E.; Zalzar, S.; Huang, T.; Purvins, A.; Masera, M. Baltic Power Systems’ Integration into the EU Market Coupling under Different Desynchronization Schemes: A Comparative Market Analysis. Energies 2018, 11, 1945. [Google Scholar] [CrossRef]
- López de Haro, S.; Sánchez Martín, P.; de La Hoz Ardiz, J.E.; Fernández Caro, J. Estimating conjectural variations for electricity market models. Eur. J. Oper. Res. 2007, 181, 1322–1338. [Google Scholar] [CrossRef]
- Liu, J.D.; Lie, T.T. Empirical dynamic oligopoly behavior analysis in electricity markets. In Proceedings of the 2004 International Conference on Power System Technology, POWERCON, Singapore, 21–24 November 2004; pp. 1768–1773. [Google Scholar] [CrossRef]
- Díaz, C.A.; Villar, J.; Campos, F.A.; Reneses, J. Electricity market equilibrium based on conjectural variations. Electr. Power Syst. Res. 2010, 80, 1572–1579. [Google Scholar] [CrossRef]


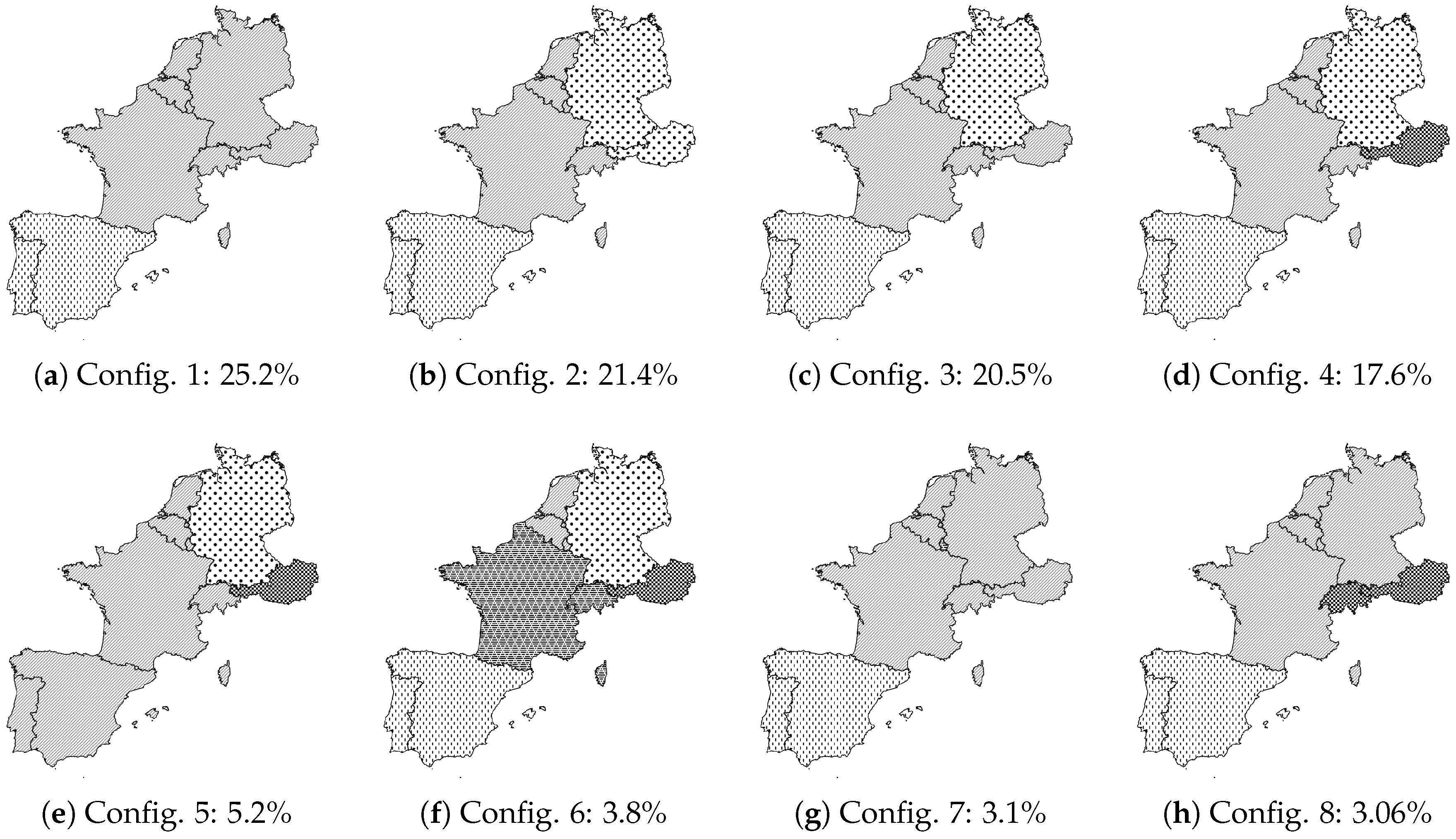
| Network Configuration | Number of Hours | Mean Spread Increment (c€/kWh) |
|---|---|---|
| Config. 1 | 297 | 0 |
| Config. 2 | 0 | - |
| Config. 3 | 58 | 0.23 |
| Config. 4 | 79 | 0.35 |
| Config. 5 | 0 | - |
| Config. 6 | 310 | 1.14 |
| Config. 7 | 0 | - |
| Config. 8 | 0 | - |
| Perfect Competition | Non-Perfect Competition |
|---|---|
| 24.52 | 27.05 |
| Perfect Competition | Non-Perfect Competition |
|---|---|
| 133.40 | 147.57 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orgaz, A.; Bello, A.; Reneses, J. A New Model to Simulate Local Market Power in a Multi-Area Electricity Market: Application to the European Case. Energies 2019, 12, 2068. https://doi.org/10.3390/en12112068
Orgaz A, Bello A, Reneses J. A New Model to Simulate Local Market Power in a Multi-Area Electricity Market: Application to the European Case. Energies. 2019; 12(11):2068. https://doi.org/10.3390/en12112068
Chicago/Turabian StyleOrgaz, Alberto, Antonio Bello, and Javier Reneses. 2019. "A New Model to Simulate Local Market Power in a Multi-Area Electricity Market: Application to the European Case" Energies 12, no. 11: 2068. https://doi.org/10.3390/en12112068
APA StyleOrgaz, A., Bello, A., & Reneses, J. (2019). A New Model to Simulate Local Market Power in a Multi-Area Electricity Market: Application to the European Case. Energies, 12(11), 2068. https://doi.org/10.3390/en12112068






