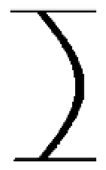Abstract
This paper presents a quantitative visualization study and a theoretical analysis of two-phase flow relevant to polymer electrolyte membrane fuel cells (PEMFCs) in which liquid water management is critical to performance. Experiments were conducted in an air-flow microchannel with a hydrophobic surface and a side pore through which water was injected to mimic the cathode of a PEMFC. Four distinct flow patterns were identified: liquid bridge (plug), slug/plug, film flow, and water droplet flow under small Weber number conditions. Liquid bridges first evolve with quasi-static properties while remaining pinned; after reaching a critical volume, bridges depart from axisymmetry, block the flow channel, and exhibit lateral oscillations. A model that accounts for capillarity at low Bond number is proposed and shown to successfully predict the morphology, critical liquid volume and evolution of the liquid bridge, including deformation and complete blockage under specific conditions. The generality of the model is also illustrated for flow conditions encountered in the manipulation of polymeric materials and formation of liquid bridges between patterned surfaces. The experiments provide a database for validation of theoretical and computational methods.
1. Introduction
Multiphase flows and heat transfer in micro channels are found in an increasing number of applications [1,2,3,4,5,6] and allow innovations not realizable with conventional channels. Examples of microchannel two-phase flows include compact heat exchangers [2], cooling of electronic components [7], chemical separation processes [8] and biomedical systems [9]. The liquid phase in such systems can form a liquid bridge, droplets, slugs, or films [1,2] that result in partial or complete occlusion of the channel, giving rise to complex flow regimes. A number of studies have focused on two-phase flows in micro-channels related to fuel cells [1,10], where water generated as a by-product of electrochemical reactions can often condense. Excess accumulation of water (“flooding”) reduces reactant transport and limits performance [11,12], but can also impact durability and operation under sub-zero temperatures [13,14]. Hydrophobic surfaces that promote water transport are commonly used to alleviate water management problems, and much ongoing research targets novel approaches such as surfaces with varying contact angles [15] and electrode structures that further facilitate water transport [16,17]. Effective deployment of these approaches requires an improved understanding of the underlying liquid water transport flow regimes, which depends on a wide range of parameters including surface tension forces and wettability.
In one of the earliest ex-situ visualization studies of two-phase flows in micro-channels related to fuel cells, Steinbrenner et al. [18,19] reported that slug flow was favored over bridge/plug flow for high air-flow rates and low liquid flow rates, but that stratified flow was dominant at high-liquid flow rates. Channel geometry was however found to significantly impact the flow regimes and the corresponding air/liquid flow ratios. The underlying physics of slug formation was analyzed by Cheah et al. [1], who extended the simplified force balance of Cho et al. [20] to show that slug formation minimizes the interfacial energy of water drops in channels and that droplet dynamics are dominated by a stick-slip motion pattern. Slugs typically form only at low reactant gas flow rates when partial liquid bridges grow sufficiently large.
The combination of low liquid volume fractions, hydrophobicity, small hydraulic diameters, and low flow rates (Reynolds numbers) gives rise to two-phase flows, where surface forces are dominant. The experimental flow maps obtained from quantitative flow visualization show significant differences between hydrophilic [18,21,22] and hydrophobic channels [12]. Fundamental challenges on both theoretical [11,23] and experimental [24] fronts remain in understanding of the flow regimes in such systems, including the impact of geometrical and surface parameters. This study is particularly concerned with bridging phenomena, which can play an important role in micro-channels as well as in PEMFCs.
The so-called liquid bridge is a mass of liquid spanning between two or more solid surfaces and held by capillary forces. Such bridges form when capillary forces are larger than other surface or body forces (pressure, gravity, magnetic, thermal, etc.). Liquid bridges have attracted scientific interest for more than a century as fundamental problems, as well as for their occurrence in nature, including human organs [25] and the wet adhesion of insects on surfaces [26]. The broad range of engineering applications includes porous media [9,27,28,29] and macro-, micro-, and even nano-systems technology [30,31]. The role, of capillary bridges has been analyzed for various processes and treated in a number of monographs, studies and reviews covering stability limits, axisymmetric equilibrium, rupture, and the influence of gravity [32,33,34,35,36,37,38] and the mechanisms associated with the formation, evolution, and collapse of capillary bridges [25].
Computational modeling of two-phase flows in micro-channels includes the volume-of-fluid (VOF) approach [39,40] as well as 2-D [41,42] and 3-D [43,44] simulations and, more recently, the Lattice-Boltzmann method [45] with dynamic interface tracking. Zhu et al. [43,44] incorporated in their solution the pores through which water emerges in the main gas flow micro-channel. This modeling detail was shown to be critical in the physical representation of the formation of a droplet and its subsequent detachment and motion when subjected to air-flow. In particular, for droplet detachment, a significantly higher critical air velocity was predicted compared to the simplified case when water droplets were initially assumed to be resting on the surface. Fundamental aspects of water transport in PEMFC flow channels have been investigated computationally [46] and experimentally [1,12], highlighting some key interactions of dynamics with capillary forces and wetting properties. Some of the particularly challenging issues to resolve are the characterization and modeling of the dynamic contact angle [11,23] and the prescription of complex boundary conditions such as sliding on hydrophobic surfaces [47]. Better understanding of fundamental processes can open the door to novel water management such as the use of passive capillary transport explored by Tobias et al. [48] who designed channel geometries that exploit specific modes of droplet shapes. Although typical Reynolds numbers of fuel-cell operation correspond to laminar flow regimes, the flow can become turbulent under some circumstances. Niu et al. [49] recently investigated this regime was by using direct numerical simulations combined with VOF. Turbulence was found to have a significant impact on the critical droplet size for break-up or coalescence.
A key issue that arises in VOF simulations and other interface tracking methods is the needs for experimental data to inform model improvement and physical representation of the dynamic contact angle and associated hysteresis. Due to the difficulty of performing operando measurements in fuel cells for instance, most quantitative experiments have been conducted in laboratory models of micro-channels. Theodorakakos et al. [41] used a high-aspect-ratio geometry to observe a single droplet placed on the surface of different GDLs and obtained dynamic contact angles for input into VOF simulations. However, the channel dimensions were significantly larger than fuel-cell gas channels. Experiments in micro-channels with smaller hydraulic diameters were reported by Wu and Djilali [12] on the dynamic evolution of water droplets emerging from a single channel and their associated flow regimes, and by Minor et al. [50] who examined the interaction between air flow and a water droplet, and measured the velocity field inside the droplet as well as droplet deformation and contact angle hysteresis. Slug flow and channel blockage were observed in [12] at low Reynolds number, whereas a periodic pattern of droplet emergence, growth, and detachment appeared as Re increased. At higher velocities (Re), the flow transitioned to a wavy water film pattern. The characteristic frequencies of droplet shedding and a flow map of the flow regimes as a function of superficial air and water velocities were also reported with broadly similar characteristics to those of Cheah et al. [1]. There has also been some success in conducting operando experiments using X-ray [51], MRI [52], and neutron beam imaging [53], but these require custom-designed cells and have limited spatial resolution. The flow in fuel-cell channels is closely coupled to the water transport process in the porous electrode that forms one of the channel “walls”, and consequently much work has been directed at studying the evolution of liquid water therein [54,55].
The earliest works on liquid bridges are due to Poisson, Delauney, Plateau and Rayleigh [56,57,58] resulting in the theoretical formulation and experimental validation of static stability boundaries in terms of dimensionless parameters including slenderness , dimensionless volume , and Bond number (, , V, and being respectively liquid height, radius, liquid volume, and surface tension. These static stability limits were subsequently shown to be represented by a single closed piecewise curve on the slenderness/volume plane [59], and each set of dimensionless parameters (, , ) defines a minimum volume where a stable liquid bridge can form, and three unstable modes. Numerous experimental and theoretical studies [60,61,62] have extended these analyses to account for contact angle, geometrical parameters, and surface energy effects as well as the influence of gravity and electrical fields. For example, DaRiva and Martinez [60] showed that the contact angle should not exceed π, or else the liquid bridge will spread over the surface, and Gomez et al. [34] described analytically the effect of small axisymmetric imperfection on the behavior of liquid bridges supported by two circular, coaxial disks.
In relatively simple systems, meniscus properties and the capillary force involved in liquid bridges can be determined analytically from the Laplace-Young equation [63], while in more complex situations involving shear resistance simulation are required. Wikland for instance performed lattice Boltzmann simulation in conjunction with a new method for the treatment of wetting boundary conditions [64] to analyze liquid bridge between two smooth, non-porous, and chemically homogeneous plates related two-phase flow problems in fibre networks.
The increasing body of research devoted to two-phase flows in microchannels underscores their importance in a range of technological applications that cover a wide range of scales and configurations [2,7,8,65]. A number of classifications and two-phase flow maps have been proposed in the literature, but inconsistencies remain in identifying two-phase flow patterns and the transition boundaries between patterns/regimes; some of these inconsistencies may be due to the significant impact of the nature and inhomogeneity of the surfaces that can for instance yield to scatter in the “stick slip” behaviour [1]. Furthermore, data related to the dynamic contact angle, the contact line, and the triple-velocity point are insufficient. Such data are critical for modeling purposes [66]. Finally, many of the studies performed on liquid bridges have focused on equilibrium shape, morphology and stability limits that do not cover conditions encountered in in PEM fuel cells in particular. The current paper addresses some of these gaps through a combined experimental and theoretical analysis that quantifies some of the key parameters required in the modeling process. The focus is on the mechanisms leading to the observed flow regimes, and on the formation and characteristics of capillary bridges in particular.
2. Experimental
2.1. Microchannel Set-Up and Method
Imaging techniques allowing direct observation of liquid water in PEMFCs require custom made cells that differ substantially in size and design to fit the imaging environment and use different materials from graphite and metal typically used in commercial cells in order to allow the required optical, X-ray, MRI or neutron beam access. The materials used in imaging cells include acrylic glass [48]; PDMS [1,12]; PEEK (polyetheretherketone) [52]; and POM (polyoxymethylene) [53]. In this work, the experimental model of the cathode channel was manufactured using PDMS (polydimethylsiloxane). This casting material has been used in a number of previous studies related to PEM fuel cells, as it provides the transparency required for optical access as well as hydrophobic characteristics similar to those of a GDL [1,12,24]. The fabrication procedure is described in detail by Wu and Djilali [12]. The micro-fluidic chip design consisted of two perpendicular micro-channels, as shown in Figure 1. A square pore in a 50-μm-wide and 250-μm-long gas channel was selected for the current study. The square geometry is computationally convenient to reproduce without requiring grid skewing or unacceptable grid aspect ratios and was expected to exhibit all the salient physical mechanisms while maintaining an appropriate value range for key dimensionless parameters.

Figure 1.
Transparent micro-fluidic chip used for visualization experiments.
Figure 2 shows a schematic of the apparatus used to conduct the experiments consisting of the micro-fluidic chip, a microscope, a high-speed camera, a water syringe pump, a flow-meter, and a data acquisition system. The test apparatus was also equipped with a differential pressure transducer not used in this study. The liquid phase was injected through the 50 μm wide pore into the micro-channel where a steady airflow rate was maintained for each measurement. The videos documenting capillary bridge development and the two-phase flow evolution at the T-junction were obtained using a high-speed camera (Phantom MiRo4 from Vision Research Inc., Wayne New Jersey) with an 800 × 600 image size CMOS active pixel sensor, a 12-bit pixel depth, and a maximum full-resolution frame rate of 1000 fps.
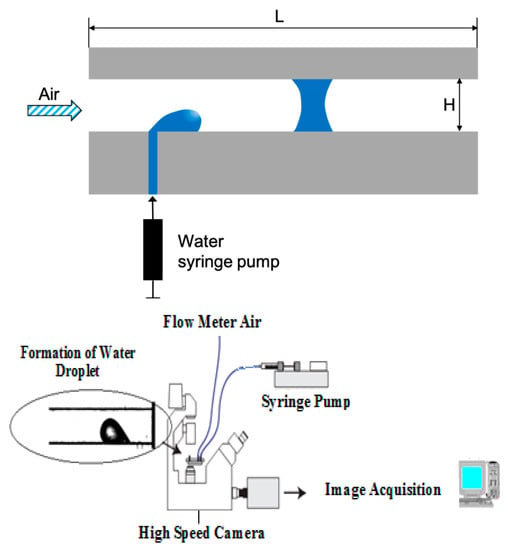
Figure 2.
Experimental setup: schematic of water injection into microchannel and formation of water droplet and capillary bridge (Top); flow control and data acquisition (Bottom).
The images were captured using an inverted fluorescent microscope (Zeiss Axiovert 200 M) and magnified by a 5 × X objective. The interface formed between the two fluids could evolve as drops (film, slug, or plug) depending on flow rates. The injection of liquid water through the pore and into the channel was with a programmable syringe pump; water flow rate ranged from 0 μL/min to 6 μL/min, to correspond to conditions in a typical PEMF fuel-cell operation [12]. The air-flow rate was varied up to from 0 to 37.5 SCCM, with lower, with lower air-flow rate selected to investigate liquid bridge formation. The process of formation of each flow pattern was registered in detail by visual observation, a video recorder, and a digital camera (Phantom). The system was allowed to reach steady state before the air and liquid flow rates were recorded. Water injection was stopped between the two tests until the micro-channel was cleared of residual liquid and dried out by flowing dry air for about 10 min. The next test conditions were then set up.
Table 1 summarizes the experimental conditions. The average gas and liquid superficial velocities were obtained from their respective volumetric flow rates as follows: and , where is the cross-sectional area, is the air volumetric flow rate, and is the liquid volumetric flow rate. In these experiments, the liquid superficial velocity ranged from to , and the gas superficial velocity varied from 0 to . Table 1 summarizes the experimental conditions and physical parameters, and Table 2 gives all the input conditions used in the ex-situ experiments.

Table 1.
Experimental conditions and physical parameters.

Table 2.
Input conditions used in the ex-situ experiments (liquid superficial velocity was kept at = 0.04 m/s).
2.2. Image Processing Technique and in-House MATLAB Scripts
Image processing was performed using a MATLAB script developed to analyze the image of the liquid fraction emerging into the main channel during operation. The method enables hands-free measurements using image acquisition and processing and enables extraction of flow parameters such as contact angle, base diameter (width or chord length), droplet height, radius of curvature, void fraction, coordinates and velocity of the triple point, and the contact patch (area wetted by the droplet).
During these experiments, all videos were converted into individual frames to extract information about image pixel values. Different flow patterns were then identified from the recorded videos. Each frame contained a snapshot of the flow at a specific time. A digital image processing procedure illustrated in Figure 3 was carried out for each individual frame to extract the entire two-phase flow profile. The Canny edge detection algorithm [67] implemented in MATLAB was used to determine the boundaries of the flow regimes representing slug, droplet, plug, or film flow on the solid surface. The output the edge detector was subsequently analyzed with an algorithm that determined contact angles. Since the edge in an image can point in any direction, edge detection was performed in two steps: Canny edge detection was used to provide a smooth edge (Figure 3e), and Sobel edge detection was then used to provide edge orientation. The contact angle was then measured as the angle between the slope of the water droplet at its intersection with the solid surface. All measured quantities (height, base diameter, …) were evaluated with an uncertainty of ±1 pixel.
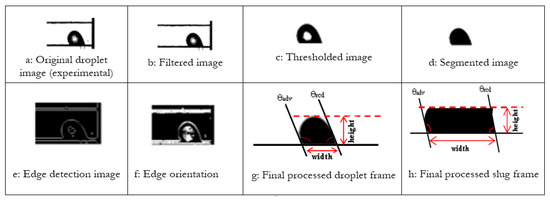
Figure 3.
Sequence showing digital capture and detection of dynamic water droplet and slug movement within the channel to extract desired flow parameters.
3. Liquid Bridge MODEL
The experimental results presented in the next Section cover a range of flow regimes. Of particular interest in this study is the liquid bridge/plug flow regime which has received relatively limited attention for flow conditions corresponding to fuel cells, and where slug/plug flow can partially or completely obstruct air flow through the channel, thereby increasing the possibility of flooding and transients that induce degradation. This section presents a theoretical model of the resulting quasi-static liquid bridge with the objective of predicting the morphology, the critical amount of liquid water needed to form a plug, as well as the time of obstruction of the micro-channel.
3.1. Formulation
The fluid configuration considered is sketched in Figure 4 and Figure 5. An isothermal mass of liquid water of volume Vcrit is held between two parallel plates (collector plates and lower surface) separated by a distance H (height). Under zero-gravity conditions and in the absence of other buoyancy forces [65], the profile of the liquid water bridge assumes an axisymmetric shape, and its capillary surface is ∑ in with a constant mean curvature of 2, which forms a constant contact angle θ. Figure 4 shows the coordinates of this system. The coordinate of the axisymmetric liquid bridge along the symmetry axis is denoted by (the axis of rotation), denotes the vertical axis, S is the arc length along the liquid generator, and θ is the contact angle. The pressure difference between the inner (liquid) and outer (air) phases ΔP = Pinside − Poutside is constant within the liquid bridge; i.e., it is independent of S.
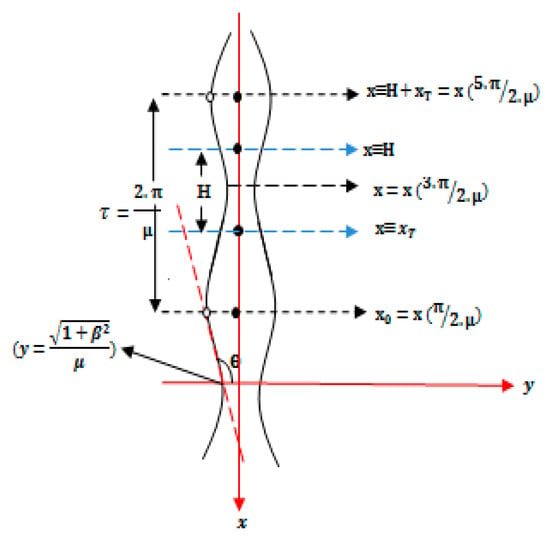
Figure 4.
Schematic of liquid bridge profile parameters and coordinates.
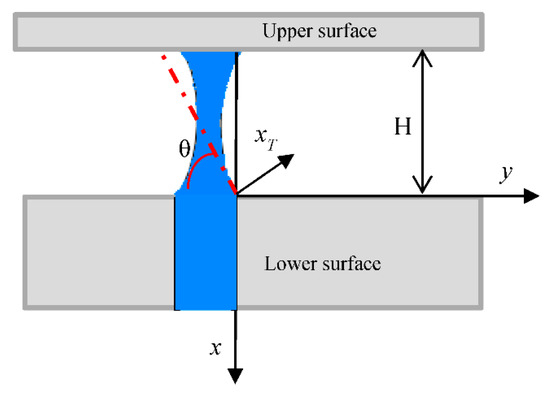
Figure 5.
Schematic of a capillary bridge and geometric parameters.
The liquid bridge density is ρw, the viscosity is μw, and the surface tension associated with the interface is . The density and viscosity of the surrounding air are negligible compared to water and do not affect the dynamics of the liquid bridge. In the absence of gravity effects (the Bond number B ≈ 0 (10−4)), the equilibrium surface is a surface of constant mean curvature, and for the axisymmetric case, the bridge can have a cylindrical, spherical, catenoidal, unduloidal, or nodoidal shape. These properties are uniform and constant under isothermal conditions. When viscous and body forces are negligible, the shape of the liquid bridge should be in equilibrium, with a constant mean curvature everywhere and a profile satisfying the Young-Laplace equation, which relates capillary pressure to the curvature of the interface [68]:
This is a second-order differential equation for the liquid profile . We may assume , where is the mean curvature. Note that a negative curvature in the plane corresponds to a concave bridge and a positive curvature to a convex bridge. Following Kenmotsu [69,70], parametric solutions of Equation (1) can be obtained for any complete surface of revolution with constant mean curvature by considering a periodic smooth curve with period , representing the profile of a Delaunay surface parameterized by the arc length . The one-parameter family of Delaunay surfaces of revolution having constant mean curvature is given by [70]:
or more explicitly:
The morphology of liquid water bridges in the micro-channel requires determination of the two integration constants and a numerical solution of Equation (1) with boundary conditions corresponding to the system geometry and the specification from experiments of the liquid bridge height and of the contact angle .
Appendix B provides the detailed derivation of the expressions for determining which are obtained considering the generalized shape and geometric constraints on the interface.
Once the solution for is determined, the profile of the liquid bridge in 3-D is deduced by rotation around the axis of symmetry and follows the parametric equation (Appendix B):
where
and the critical volume (minimum liquid volume to form equilibrium liquid bridge) is given by (Appendix B):
where and are given by:
with and (see Appendix B).
3.2. Numerical Solution
The liquid bridge profile was determined using MATLAB to solve the second-order differential Equation (1) in conjunction with the two relations for determining the integration constants . The procedure is detailed in Appendix B and requires: (i) selection of initial value for β; (ii) incremental stepping of β to determine the roots of the quadratic relation governing the shape of the interface; (iii) determination of the second unknown constant μ; (iv) calculation of the critical liquid volume Equation (4); (v) iteration of procedure and update of β and μ until critical liquid volume converged with measured value within prescribed tolerance; (vi) determination of bridge shape from Equation (3).
A summary of the parameters used in the prediction and critical values for the volume of water necessary to form the quasi-static bridge before it breaks down is provided in (Appendix B).
4. Results and Discussion
4.1. Flow Patterns
Figure 6 depicts the four flow patterns identified from the experiments: liquid water bridge/plug; slug/plug; liquid film; and droplet flow.
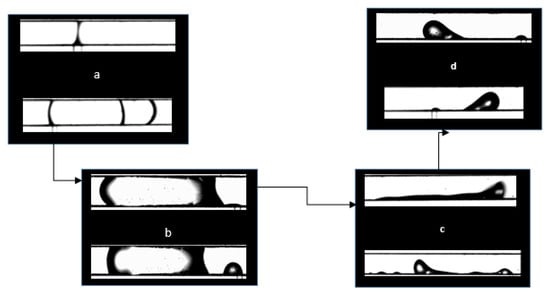
Figure 6.
Representative images of two-phase flow structures: (a) liquid water bridge/plug, (b) slug/plug, (c) film flow, and (d) droplet flow.
4.1.1. Liquid Bridge/Plug: Relatively Dry Air Conditions ()
Concave Liquid Bridge/Plug
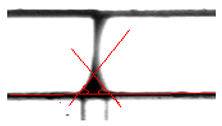
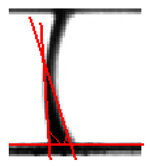
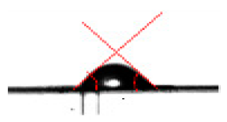
Figure 7 shows the liquid bridge/plug configuration. At the beginning, at t = 0 milliseconds (ms), the water erupted quickly from the pore to the opposite wall of the main air micro-channel. This equilibrium state remained up to . The contact angle and the critical liquid volume Vcrit of the (plug) bridge were measured at their stability limits just before deformation with the bridge retaining quasi-static characteristics. Subsequently growth beyond Vcrit = 405 nl led to the onset of lateral oscillations at , followed by rapid deformation and very fast instability without breakage (). Note that in the last images, at and , the water supply appears insufficient to form another bridge. A sessile water droplet, characterized by a water volume = 34 nL and a contact angle θleft = θright = 57.96°, was finally formed and remained attached to the water bridge, obstructing the air micro-channel completely. This is consistent with plug flow observed to cause complete blockage of the bipolar plate channels in PEM fuel-cell flow [13]. The formation and stability of these liquid bridges is further discussed in Section 4 in conjunction with a mathematical model developed to predict the morphology, time of obstruction of the micro-channel, and the critical amount of liquid water needed to form a plug.
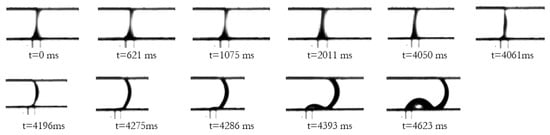
Figure 7.
Water bridge/plug evolution.
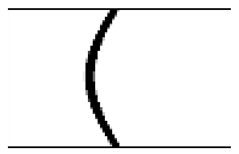
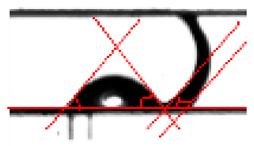
Convex Liquid Bridge/Plug
After the channel was dried out, water was injected at a rate of 6 μL/min () without air flow and at a Weber number of . These conditions led to convex water liquid bridge formation; the water liquid plug entered the bifurcation and quickly split into three plugs, as seen in Figure 8. The convex curvature was not constant along the liquid surface, implying local pressure gradients in the flow pulling it into the main channel. The rapidity of the plug formation indicates wetting forces were dominant compared to the driving pressure. The plug, upon exiting the junction, split into three caps (two on the right and one on the left) and propagated in the main micro-channel. Both right plugs moved three times faster than the left plug and disappeared after 1.48 s, whereas the latter lasted 4.58 s while blocking the whole channel. Note that a steady liquid supply was kept on during this experiment.
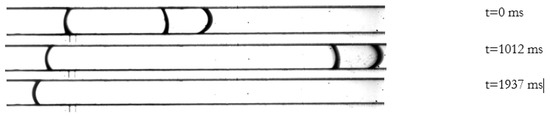
Figure 8.
High-speed images of a convex liquid bridge: liquid is accumulated into the pore, forms a capillary, propagates, and splits into three convex plugs.
4.1.2. Droplet Flow ()
Figure 9 and Figure 10 show typical shapes and evolution of water droplets observed in this work. For the vertically aligned channel in Figure 9, while the first droplet was convected along the surface in the same direction as gravity, a second droplet appeared and grew until reaching a threshold size and detached, and so on.

Figure 9.
Emergence and shape evolution of a droplet (vertical channel).

Figure 10.
Droplet flow patterns for = 10 m/s (horizontal channel).
As long as the droplets remained below the critical size and were subjected to the cross-flow air stream, they deformed along the longitudinal direction, as depicted in Figure 9; with different advancing (θadv) and receding (θrcd) contact angles. This flow pattern was characterized by a small Weber number for water (≈3.12 × 10−5 to 1.12 × 10−3) indicating that interfacial tension overwhelmed inertial forces. The droplet flows illustrated in Figure 10 for the horizontal channel were obtained by increasing the water flow rate by small increments while keeping constant air flow rate ( = 37.5 SCCM; = 10 m/s). In this operating range, droplets were formed and easily removed from the surface. The high flow rates at which this regime was observed are consistent with the observations of Gu et al. [71] in microfluidic systems.
4.1.3. Slug/Plug Flow ()
Slug/plug flow is characterized by a large water formation when droplets expand to the entire height of the channel. Slugs formed at moderate flow rates ( = 0.04 to 0.1 m/s, = 1.6 to 3.7 m/s) in a sequence illustrated in Figure 11, with the emerging droplets growing to cover the channel side to side without initially contacting the upper wall. A gap allowing air flow over the droplet and inducing deformation due to shear is shown up to t = 126 ms. Once a critical value was reached, the droplet started wetting the upper wall with a slug forming between t = 326 and 449 ms and eventually spanning the entire channel.

Figure 11.
Slug formation.
4.1.4. Film Flow
This flow regime appeared mainly at moderate air and water velocities (, with water spreading on the surface both in the spanwise and streamwise directions. The thickness of the water film was not uniform as shown in Figure 12 and exhibited both residual droplets that can act as nucleation sites for subsequent droplet-to-film transition, as well as surface waviness due to hydrodynamic instabilities at the water-air interface. Though it is characterized by low channel blockage and downstream transport driven by shear, film flow can be much more problematic than slug flow in a fuel cell as it typically results in larger coverage of the surface and thus impedes the transport of air/oxygen to the reaction sites [43].
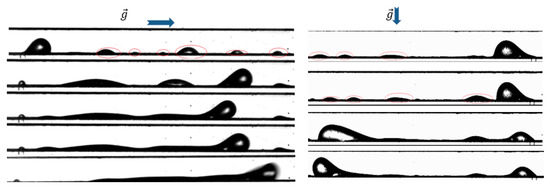
Figure 12.
Visualization of liquid film formation in air flow.
4.2. Droplet and Slug Characteristics
4.2.1. Contact Angles
The contact angle was defined as the angle between the wall of the micro-channel and the line tangent to the droplet (slug or other type) flow emanating from the point where the three separate phases were in contact as illustrated earlier in Figure 3g,h. In the regimes investigated here, the droplet/slug formation and shedding process was quasi periodic. The evolution of the dynamic advancing and receding contact angles during one slug flow formation cycle (75 ms ≤ t ≤ 450 ms) is shown in Figure 13. As the slug began to move, the advancing contact angle approached 105°, and the receding contact angle approached 60° at the detachment point.
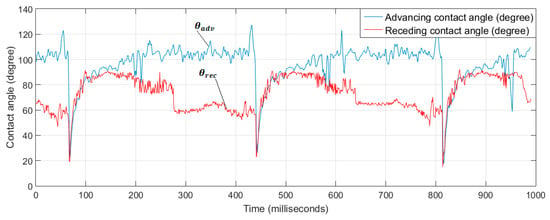
Figure 13.
Slug advancing (blue line) and receding (red) contact angle results from image processing.
Figure 14a shows the evolution of the droplet contact angles for approximately five cycles (0 ≤ t < 500 10−3 s). The dynamic process is closely linked to the growth and detachment of the droplets: as the droplet emerged and grew, the advancing angle increased to 125°, while the receding contact angle remains constant at ~90°. As the droplet grows, blockage increases, and the air flow over the droplet accelerates. The combined effect of pressure and shear applied by the air flow deforms the droplet, the receding angle decreases significantly to 20°; correspondingly, surface tension pinning the droplet decreases and the droplet eventually detaches. Figure 14b provides a detailed illustration of droplet emergence and detachment sequence for a water flow rate of 1 μL/min and an air flow rate of 37.5 SCCM. A key aspect of the process is the highly dynamic nature of the contact line and the significant departure of both advancing and receding angles from the static value. This is a particularly challenging aspect of two-phase flow simulations [11,23]; for instance the recent simulations in [15] exhibit a maximum hysteresis of ~ 5° between advancing and receding values compared to up to over 100° experimentally.
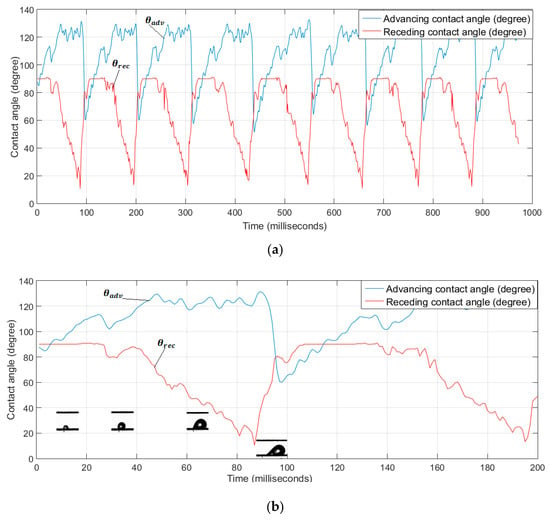
Figure 14.
Dynamic contact angles. (a) Contact angles resulting from image processing; (b) Droplet cycle: Advancing and receding contact angles (obtained for = 1 μL/min, = 37.5 SCCM).
4.2.2. Geometric Characteristics
Base Diameter
The water slug/droplet base diameter was taken as the distance between the extremities of a single water slug. Figure 15 shows water slug lengths (or widths, noted here as slug base diameter in the horizontal plane) measured from several experimental images for each run using image analysis. This plot shows a fast evolution of slug length over time; the numerical value of slug width at detachment was 1100 μm. However, for droplet flow, the droplet base diameter did not exceed 380 μm at detachment, as shown in Figure 16a,b; this value seems to be independent of gravity.
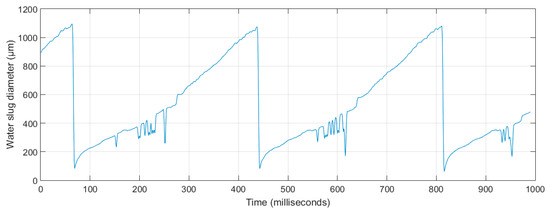
Figure 15.
Dynamic evolution of slug diameter obtained from image processing.
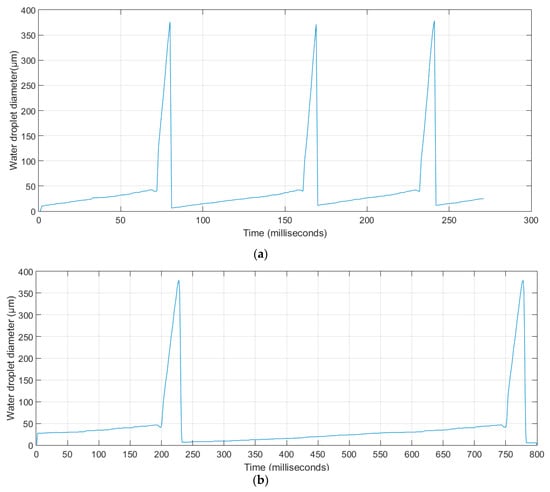
Figure 16.
Dynamic evolution of droplet diameter: (a) flow parallel to gravity; (b) flow perpendicular to gravity.
Height
Figure 17 illustrates the variation of slug height over time, where height is defined as the distance from the lower base (or GDL) to the upper boundary of the slug. For one slug formation cycle (0.075 s ≤ t ≤ 0.450 s), the height increased gradually up to 230 μm, then jumped the remaining 20 μm to reach the upper wall and cover the entire micro-channel height (250 μm).
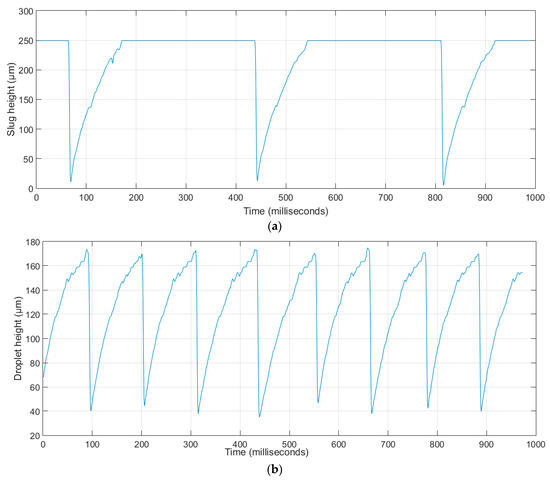
Figure 17.
Height: (a) slug flow; (b) droplet flow.
Figure 17b shows an example of droplet height recorded as a function of time. The same growth was observed for droplet flow that did not reach the upper wall. Note that the droplet height at detachment over eight formation cycles did not exceed 175 μm, which was much greater than the width of the feed channel (50 μm) that could represent the GDL pore size. In fact, the recorded droplet height was between 170 μm and 175 μm, which was within the resolution of the measurements.
4.2.3. Liquid Fraction
The void fraction or liquid fraction is the key physical value for determining numerous other important parameters such as two-phase flow density and viscosity, but it is also a key operational parameter in a fuel cell as it provides a measure of the effectiveness of water management. In this study, an area-averaged liquid fraction was defined as the ratio of the cross section occupied by the water phase to the channel cross section. The results for both slug and droplet flow are shown in Figure 18 and Figure 19, respectively with maxima of 86% in the case of slug flow and 8% for droplet flow. The high value in the case of slug flow is expected to result in significant pressure surges and transients.
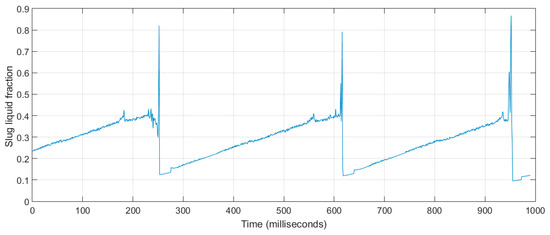
Figure 18.
Liquid fraction distribution in slug flow.
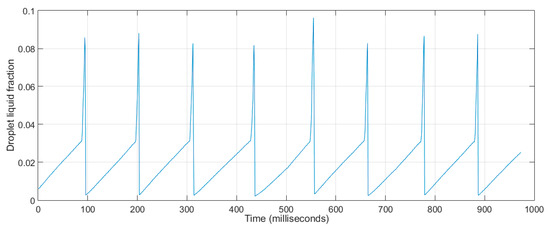
Figure 19.
Liquid fraction distribution in droplet flow.
4.2.4. Triple-Phase Point Contact Velocity
The triple-point velocity (TPV) corresponding to the trailing edge of the contact line where air and water meet with the solid wall was measured. The evolution of the TPV was used for droplet/slug motion as a criterion for detecting the time at which the water droplet/slug detached from the pore. Figure 20 shows a plot of the measured advancing θadv and receding θrcd contact angles simultaneously with the TPV. The position of the triple point remained quasi-fixed over the duration of emergence, formation, and growth, and its velocity (TPV) was equal to zero. The droplet or slug attained maximum height and base diameter (contact width) coincide with the largest advancing contact angle and smallest receding contact angle. As noted earlier this is also the stage where hydrodynamic forces (pressure and shear) are maximum. When these forces exceed the pinning force, the droplet detaches quite abruptly as indicated by the spikes in the TPV evolution in Figure 20 and Figure 21.
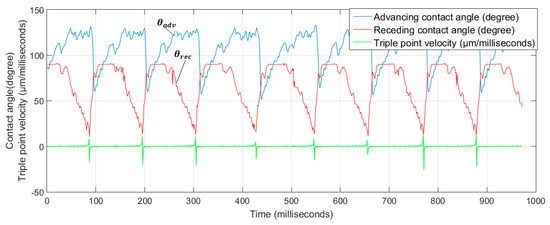
Figure 20.
Advancing (blue line) and receding (red) contact angles and triple-point velocity (black) versus time for nine droplet flow formation cycles for = 0.0067 m/s, = 10 m/s.
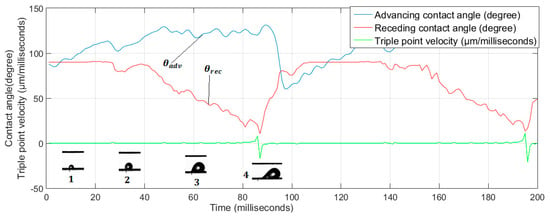
Figure 21.
Water droplet images and corresponding evolution of θadv, θrcd, and TPV: (1) at droplet emergence, (2) droplet growth, (3) onset of droplet deformation, (4) detachment.
The TPV remained zero as long as long as the droplet was pinned and θrcd > 20°. Once both θadv and θrcd reached their extrema, the TPV spiked to a maximum value (20 × 103 µm/s) and then decreased sharply to its minimum (−25 × 103 µm/s). This behavior can be explained by noting that after detachment of the trailing edge: (a) due to capillary forces at the break-away interface, some of the water is sucked back into the pore column and feed into the new emerging droplet; (b) the detaching droplet exhibit high frequency interfacial oscillations observed in the high speed footage. The period in the droplet detachment cycle was 95 ms as opposed to 600 milliseconds for the slug cycles primarily due to the larger volume build up required before detachment of the latter.
Figure 22 shows images of slug detachment in the channel at three instants (69, 440, and 815 milliseconds) and at slug formation at 275 milliseconds. These images show that the slug appeared in the channel around 200 milliseconds after detachment, i.e., at 275, 640, and 970 milliseconds. These timings were selected to provide some insight into the positive and negative signs of the TPV observed here, notably for droplet flow. As shown in Figure 22, the slug triple-point peak is slightly different from that of the droplet triple-point. As noted previously, the plot in Figure 22 exhibits two peaks (one negative, and one positive). Although this phenomenon occurred practically at the same time for droplet flow (see Figure 20 and Figure 21), this was not the case for slug flow; a new slug started to appear 200 milliseconds after detachment of the former one. The triple point velocities were −40 × 103 and 20 × 103 μm/s at detachment and formation respectively. Similarly, for the negative velocity: after film break-up, the remaining liquid shrank to feed the emerging water that would form the future slug.
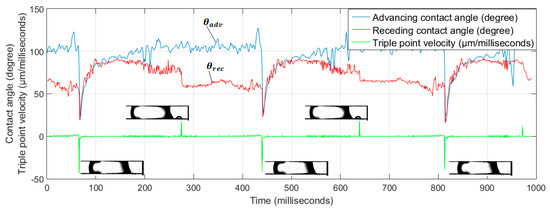
Figure 22.
Time evolution of triple-point velocity, slug formation and detachment, and dynamic contact angles during slug flow.
Table A1 (Appendix A) summarizes the experimental conditions and the major parameters obtained from quantitative image analysis. The results for water flow rates ranged from = 0 μL/min to = 6 μL/min. Note that the recorded mean values for height, base diameter, contact angle, and liquid fraction did not show significant differences for a given flow regime when the gas superficial velocity was increased. However, these parameters were altered by changes in the channel orientation. Also, the height, liquid fraction, and droplet width for flow perpendicular to gravity were smaller than those obtained under the same conditions for flow parallel to gravity (Appendix A). The results for film flow clearly confirm this observation. In parallel flow, the width and height of the film were greater than those for perpendicular flow. These results are somewhat counterintuitive. On the other hand, the shape of the liquid droplets did not change significantly.
4.3. Liquid Bridge Regime: Comparison of Experiments and Model Predictions
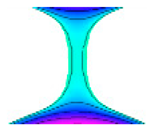
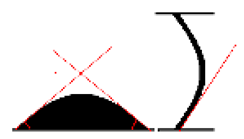
Table 3 compares the experimentally recorded images and the predicted shapes of the liquid bridge under the same conditions. The convex shape (a), which is not presented here for brevity, was also simulated correctly by the proposed model. In general, the model reproduces the morphology of the bridge successfully and predicts the critical liquid volume necessary to form the equilibrium bridge (b: concave shape). Some deformation and slight departure from symmetry was observed experimentally at times t = 4050.084 ms (c) and 4286.055 ms (d), when the bridge assumed an arch shape, although the simulated shape of the bridge corresponding to this case remained symmetric. The last image, at t = 4623.729 ms, shows that the deformation of the concave bridge together with the formation of a sessile droplet were simulated correctly (Table 3f).

Table 3.
Comparison of liquid bridge shapes obtained numerically and experimentally.
The ability of the model in predicting the morphology, the critical liquid volume to form a plug, as well as the time of obstruction makes it useful for assessing and mitigating the potential for flooding/blockage by slug/plug flow in PEM fuel cells, but it should be noted that this analytic model is limited to quasi-equilibrium bridges. The model is not valid when viscous and inertial forces are important or when the bridge exhibits dynamic behaviour [72]. For instance, modeling of the nonlinear process leading to liquid bridge breakup when the critical volume is surpassed requires the solution of the Navier-Stokes equations [73]. Nonetheless there are a range of flow conditions and practical flow problems besides fuel cells for which the present model is useful, and further simulations were conducted corresponding to various cases in the literature to assess its validity. For instance, the experimental behaviour of aqueous solutions of hydroxyethyl cellulose (HEC) in a high-speed forward roll-coating operation under roll flow conditions [74], showed that only the medium- and high-molecular-weight HEC solutions formed filaments in the nip region. Measurements showed that the subsequent formation of a ‘roll-mist’ from break-up of these threads was directly connected to the extensional viscosity of the fluid. Figure 23 compares the present prediction to the experimental results of [74]. The profile corresponded to only a portion of a fundamental unduloid surface (Figure 4) confined between the two coordinates and .
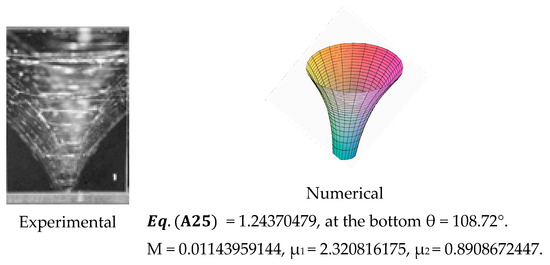
Figure 23.
Comparison between experimental [74] and numerical unduloid surfaces.
Next, we considered the configuration investigated experimentally by Grilli et al. [75]. This consisted of a glass slide supporting a sessile nano-drop as a liquid reservoir, facing a lithium niobate (LN) substrate at distance D. A temperature change in the LN substrate built up an electrical charge through the pyroelectric effect resulting in a strong electrical field acting on the PDMS drop and creating a bridge across the two substrates, as shown in Figure 24. As the process evolved, the liquid was depleted, and the bridge transitioned to a thin column that eventually became unstable. An interesting phenomenon is the formation of “beads” on the string which is reproduced by the model.
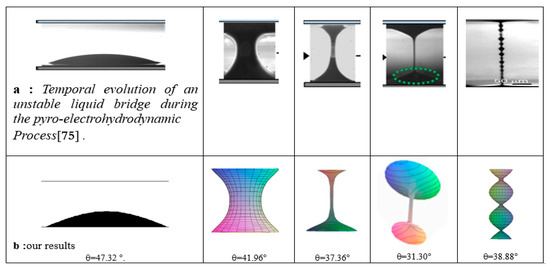
Figure 24.
Comparison of model predictions to experiments reported by Grilli et al., 2011 [75].
The model was finally used to predict the morphological evolution of non-axisymmetric capillary bridges in a slit-pore geometry of variable size [76]. The results are omitted for brevity, but showed the model tracked very satisfactorily the evolution and transition of bridges exhibiting a large increase in mean curvature and a transition from concave to convex interfaces.
5. Concluding Remarks
Fuel cells operate under a wide range of reactant flow rates and liquid water generation rates. Proper water management, which is critical to performance, requires good understanding and quantification of the flow conditions that favour particular two-phase flow regimes. A combined experimental-theoretical analysis was conducted with a focus on the mechanisms leading to the observed flow regimes, and on the formation and characteristics of capillary bridges, in particular.
Quantitative flow visualization experiments were conducted in a 250 × 250 µm2 cross section hydrophobic micro-channel representative of the cathode of a polymer electrolyte membrane fuel cell. Water was injected into the channel through a 50 × 50 µm2 pore, and the flow evolution, for both cases aligned with and perpendicular to gravity, was analyzed in terms of void fraction, dynamic contact angles, liquid volume, and triple-point velocities. Four distinct flow patterns were identified experimentally: liquid bridge (plug), slug/plug, film flow, and water droplet flow under conditions corresponding to small Weber numbers (≈10−5 to 10−3) covering the operating range in PEM fuel cells. The visualization experiments revealed that:
- Slug and water bridge (plug) flow are dominant at lower air-flow rates, whereas film flow is typically present at intermediate air flow and water droplet flow at higher air-flow rates.
- Water droplets are stable for extended periods (τ = 110 ms) without coalescence, and result in small liquid fractions (αwater = 0.085 to 0.12).
- Aside from slightly enhancing the spreading of water droplets and the film regime, gravity did not substantially affect the flow patterns in the range of Weber numbers investigated.
Quantitative image analysis allowed automatic detection of liquid water under both static and dynamic conditions and yielded information about water distribution among the various two-phase flow structures, and liquid water structural information. Liquid bridges were found to form under relatively moderate water-flow rates and very low air-flow rates and result in partial or complete blockage of the micro-channel, their shape, and the contact angle of a bridge take quasi static values during the initial formation and evolution while the bridge remains pinned. After reaching a critical volume, bridges were observed to depart from axisymmetry, block the flow channel, and exhibit lateral oscillations. An important observation and a challenge from the view point of numerical simulations is the significant variation of the dynamic contact angles, throughout the two-phase cycles. These dynamic contact angles depart significantly from the static value and exhibit large hysteresis.
A theoretical model was developed to predict the morphology, the critical liquid volume to form a plug, as well as the time of obstruction in a micro-channel. The model was shown to correctly reproduce the morphology of bridges observed in this experimental work as well as in various studies related to the manipulation of polymeric materials in which complex patterns such as high curvatures, transition from concave to convex interfaces and “beading”.
The semi-analytic model can be applied to assess and mitigate the potential for flooding/blockage by slug/plug flow in PEM fuel cells, and the comprehensive characterization data reported in the study can inform design guidelines for micro-channels in fuel cells and other applications as well as validate and improve computational simulations based on methods such as volume of fluid (VOF) and lattice-Boltzmann.
Author Contributions
Conceptualization, E.-K.S.-I., J.L. and N.D.; experimental methodology N.I.-R., E.-K.S.-I., J.L. and N.D.; mathematical model N.I.-R., E.-K.S.-I., A.K. and J.L.; image processing and analysis, N.I.-R., A.S. and N.D..; writing, review and editing N.I.-R., E.-K.S.-I. and N.D; supervision E.K.S.-I. and N.D.
Funding
The experimental component of this study was supported by funds from the Natural Sciences and Engineering Research Council of Canada (NSERC).
Acknowledgments
The authors would like to acknowledge Roger T.C. Wu, previously with the Institute for Integrated Energy Systems, University of Victoria, for his valuable help with the experimental set-up and S. Kakaç for helpful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Cross sectional area, | |
| Bond number | |
| Ca | Capillary number |
| g | Gravitational acceleration, m/s2 |
| H | Height, m |
| Mean curvature | |
| J | Superficial velocity, m/s |
| L | Length, m |
| P | Pressure, Pa |
| Pc | Capillary pressure, Pa |
| Q | Flow volume rate, for air in SCCM, for water in µl/min |
| S | Arc length along the liquid generator |
| T | Temperature, degree Celsius |
| t | Time, seconds |
| TPV | Triple point velocity, m/s |
| U | Change of variable, Equation (A6) |
| V | Volume, liter |
| Weber number | |
| Flow quality | |
| Abscissa where the liquid/air interface meets the GDL surface | |
| Greek symbols | |
| α | Volume fraction, % |
| β | First unknown constant, eq. |
| θ | Contact angle, degree |
| µ | Second unknown constant, eq. |
| Dynamic viscosity, Pa.s | |
| σ | Surface tension, N/m |
| τ | Period, seconds |
| φ | Explicit solution |
| ρ | Density, Kg/ |
| Subscripts | |
| 1, 2 | First and second roots |
| adv | Advancing |
| g | Gas (air) |
| h | Horizontal |
| l | Liquid (here, it’s water) |
| rec | Receding |
| T | Triple point (water/air/solid) |
| v | Vertical |
Appendix A

Table A1.
Summary of the various parameters obtained by the image processing program.
Table A1.
Summary of the various parameters obtained by the image processing program.
| Flow Pattern | [m/s] | [m/s] | Temp. [°C] | Pressure [Pa] | Interval Time [] | Droplet Height [] | Droplet Base Diameter [] | Liquid Fraction % | Time of Detachment [ms] | Volume at Detachment [nl] | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| For perpendicular flow | ||||||||||||
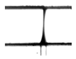 Capillary Bridge concave | 40.0 | 0.00 | 22.88 | 114591 | 1000 | Bridge/plug 250 | Pore diameter | 65 | 65 | |||
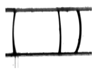 Capillary Bridge convex | 40.0 | 0.00 | 22.80 | 114798 | 1000 | 250 | θleft = 91.68 θright = 79.84 | θleft = 58.20 θright = 121.8 | ||||
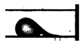 Droplet | 6.7 | 9.82 | 22.88 | 114591 | 1000 | 172 | 300 | 125° | 15° | 0.085 | 96.5 | 1.61 |
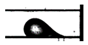 Droplet flow | 13.3 | 9.57 | 23.01 | 114798 | 1000 | 170 | 305 | 125° | 20° | 0.085 | 102.0 | 3.40 |
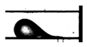 Droplet flow | 20.0 | 9.39 | 23.11 | 115075 | 1000 | 170 | 315 | 125° | 20° | 0.085 | 84.0 | 4.20 |
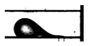 Droplet flow | 27.0 | 9.47 | 23.27 | 114384 | 1000 | 170 | 322 | 125° | 20° | 0.085 | 98.0 | 6.50 |
 Slug flow | 40.0 | 1.60 | 24.03 | 114384 | 1000 | 250 | 1100 | 110° | 20° | 0.900 | 175.0 | 17.50 |
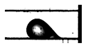 Droplet flow | 40.0 | 10.00 | 23.88 | 114798 | 165 | 175 | 325 | 125° | 20° | 0.085 | 110.0 | 11.00 |
 Film flow | 40.0 | 4.00 | 24.20 | 115074 | 1000 | 179 | 1468 | 120° | 15° | 0.19 | 106.2 | 26.55 |
| For parallel flow | ||||||||||||
 Droplet flow | 40.0 | 10.00 | 23.88 | 114798 | 167 | 210 | 380 | 120° | 10° | 0.120 | 86.0 | 8.60 |
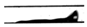 Film flow | 40.0 | 4.00 | 24.03 | 115074 | 1000 | 187 | 1666 | 125° | 20° | 0.30 | 65.0 | 16.25 |
Appendix B. Derivation of Liquid Bridge Model
Appendix B.1. Governing Equations
The profile and an liquid bridge under equilibrium with constant mean curvature, the curvature of the interface and the capillary pressure are related by the Young-Laplace equation [68]:
Referring to Figure 4 in the main body of the paper, and considering any complete surface of revolution with constant mean curvature , a parametric solutions of Equation (A1) can be obtained by considering a periodic smooth curve with period , representing the profile of a Delaunay surface parameterized by the arc length . [69]:
or more explicitly:
The numerical solution of Equation (A1) requires determination of the two integration constants with boundary conditions corresponding to the system geometry.
The function increases monotonically when goes to and satisfies the condition [70]:
Hence, must be chosen appropriately such that
The problem has an explicit solution, . In this case, the derivative is taken at point . The latter can be interpreted as the triple point where both fluids (air and water) meet the solid substrate (or the GDL in the PEM fuel cell). More specifically, this is the contact point of the water bridge with the surface having a contact angle . Note that is determined as the cotangent of the lower surface (the GDL in the case of a PEM fuel cell) to the liquid water surface at , where . For the geometry shown earlier in Figure 4 and Figure 5, the contact angle is related to the shape of the liquid water interface by:
(the prime indicates a derivative with respect to x). Note that the contact angle θ for a liquid capillary bridge is prescribed from experimental conditions. Introducing , then , and
After some basic mathematical manipulations, Equation (A6) can be cast in the form of a quadratic equation in
The solution of Equation (A7) depends on the discriminant , which in the present case must be greater or equal to zero; that is,
This equation has two distinct roots, denoted here as and , which can be found from ). Hence, the first arbitrary constant can be deduced from Equations (A4) and (A8) and must satisfy:
In this case, where , the surface of revolution takes an interesting form, called an unduloid Delaunay surface. The concave shape of the liquid bridge is only part of the Delaunay surface at the coordinates x and x = (see Figure 4).
The next step is to determine the second constant . The abscissa, where the liquid interface/air meets the lower surface, is denoted as , where the subscript T refers to the triple point and can be expressed as (see Figure 5):
with period :
Restricting our attention to the constant height of the liquid bridge H, the position of is determined by
Recall that U and dU = cos , which further leads to = , and consequently Equation (A12) expressed in terms of U yields:
Combining Equations (A12) and (A13) with Equation (A10) yields:
Introducing I(μ,β),
Equation (A14) in terms of then reads:
where is a function of , which is periodic with a period of ; the period (Equation (A11)) is then given as:
or after expansion,
Making use of , Equation (A17) reads as follows:
By combining Equations (A11) and (A19), Equation (A14) can be expressed as:
Equation (A20) leads to a relation between the second arbitrary constant and the total height of the micro-channel:
For a given H (channel height), the constant can be readily deduced. Similarly, the amount of fluid in the liquid bridge (the volume element enclosed by its surface of revolution) can be obtained as . This leads to the following liquid bridge volume:
Recall that , and U this implies that , and the liquid bridge volume is then:
For the geometry shown earlier in Figure 5, it follows that the liquid bridge volume can be expressed as:
By making use of I(μ,β) in the liquid volume equation (Equation (A22)), and after some mathematical manipulations and taking into account the boundary conditions, the liquid bridge volume takes on a relatively simple form that can be expressed as:
Furthermore, is then given by:
Taking Equation (A24) into account:
where and are given as follows:
Equation (A25) can be re-written to reveal that , the equilibrium critical volume, must satisfy the following equation to form an axisymmetric concave shape and an equilibrium liquid bridge:
The profile shape of the liquid bridge in 3-D is deduced by rotation of the curve around the axis of symmetry (the x-axis) and obeys the parametric equation:
where
Making use of the term implies that (where U can be U1 or U2). Then . Therefore, in Equation (A27), using and as integration variables with yields:
Appendix B.2. Numerical Solution
MATLAB was used to solve the nonlinear partial differential Equation (A1) in conjunction with Equations (A21) and (A26). As a test example, simulations were performed for flow conditions corresponding to the following experimental conditions: channel height H = 250 μm and a water flow rate Qwater = 6 μL/min. To determine precisely the first unknown constant , the initial value of was selected within the range 1 ≥ β ≥ 0.53 and stepped in increment of 0.047 to obtain the roots of Equation (A8). The corresponding value of second unknown constant μ was then found from Equation (A21). The critical liquid volume is readily calculated using Equation (A26). The procedure was iterated by updating the value of β until the critical liquid volume converged on the measured value within the desired accuracy, i.e., by ensuring the left hand side of Equation (A26) was equal to 1 within a set tolerance. Once β and μ determined, the predicted shape of the bridge was given by Equation (A27). Depending on the value of β, a number of configurations are predicted as depicted in Figure A1.
An interesting observation is that only one of these configurations will actually satisfy the physics of the problem according to the experimental conditions, namely the liquid volume necessary to develop the equilibrium liquid bridge and the contact angle. Figure A1 shows that the isolines are an important aspect of the water bridge setting. As a matter of fact, only the last figure (for β = 0.909) shows the isolines meeting both sides of the micro-channel and satisfying Equation (A26); this figure characterizes the formation of the bridge. In contrast, the isolines for β ranging from 0.53 to 0.9130 do not extend over the height of the micro-channel.
This study next examined a method that may be used to determine the choice of possible configurations for given values of the experimental conditions. For these configurations, the critical liquid volume and the contact angle must agree with the experimental values. The process is repeated until the critical liquid volume converges to the experimental values.
The procedure for obtaining the critical volume of the liquid bridge in its equilibrium shape before breaking down is conducted according to a trial-and-error scheme. The numerical computations predict the minimum liquid volume (critical volume) necessary to form the equilibrium bridge as = 400.0 nL, which is within 1.2% of the experimental result. A summary of the parameters used in the prediction and critical values for the volume of water necessary to form the quasi-static bridge before it breaks down is provided in Table A2. The values include the two roots, U1 and U2, and the two constants .

Figure A1.
Computed morphology of the concave bridge: effect of the choice of parameter β.

Table A2.
Computed morphology of the concave bridge: effect of the choice of parameter β.
Table A2.
Computed morphology of the concave bridge: effect of the choice of parameter β.
| θ (°) | |λ| | 0.53 | U1 | U2 | μ | (Experimental) | Numerical | |
|---|---|---|---|---|---|---|---|---|
| 65° | 0.466 | Β = 0.909 | 0.6059230857 | 0.99885410 | 0.01143959144 | 405.0084 nl | 400.000 | 1.24 |
References
- Cheah, M.J.; Kevrekidis, I.G.; Benziger, J.B. Water slug to drop and film transitions in gas-flow channels. Langmuir 2013, 29, 15122–15136. [Google Scholar] [CrossRef] [PubMed]
- Chinnov, E.A.; Ron’shin, F.V.; Kabov, O.A. Regimes of two-phase flow in micro- and mini-channels. Thermophys. Aeromech. 2015, 22, 265–284. [Google Scholar] [CrossRef]
- Kakaç, S.; Yenner, Y.; Pramuanjaroenkij, A. Convective Heat Transfer, 3rd ed.; CRC Press, Taylor and Francis: Boca Raton, FL, USA, 2014; ISBN 9781466583443. [Google Scholar]
- Qu, J.; Wu, H.; Cheng, P. Start-up, heat transfer and flow characteristics of silicon-based micro pulsating heat pipes. Int. J. Heat Mass Transf. 2012, 55, 6109–6120. [Google Scholar] [CrossRef]
- Wu, H.Y.; Cheng, P. An experimental study of convective heat transfer in silicon microchannels with different surface conditions. Int. J. Heat Mass Transf. 2003, 46, 2547–2556. [Google Scholar] [CrossRef]
- Ong, C.L.; Thome, J.R. Macro-to-microchannel transition in two-phase flow, Part 1: Two-phase flow patterns and film thickness measurements. Exp. Therm. Fluid Sci. 2011, 35, 37–47. [Google Scholar] [CrossRef]
- Wang, P.; McCluskey, P.; Bar-Cohen, A. Two-Phase Liquid Cooling for Thermal Management of IGBT Power Electronic Module. J. Electron. Packag. 2013, 135, 021001. [Google Scholar] [CrossRef]
- Basauri, A.; Gomez-Pastora, J.; Fallanza, M.; Bringa, E.; Ortiz, I. Predictive model for the design of reactive micro-separations. Sep. Purif. Technol. 2019, 209, 900–907. [Google Scholar] [CrossRef]
- Zheng, Y. Liquid Plug Dynamics in Pulmonary Airways. Ph.D. Thesis, Biomedical Engineering, University of Michigan, Ann Arbor, MI, USA, 2008. [Google Scholar]
- Yang, H.; Zhao, T.S.; Ye, Q. In-situ visualization study of CO2 gas bubble behavior in DMFC anode flow fields. J. Power Sources 2005, 139, 79–90. [Google Scholar] [CrossRef]
- Djilali, N. Computational modelling of PEM fuel cells: Challenges and opportunities. Energy 2007, 32, 269–280. [Google Scholar] [CrossRef]
- Wu, T.C.; Djilali, N. Experimental investigation of water droplet emergence in a model polymer electrolyte membrane fuel cell microchannel. J. Power Sources 2012, 208, 248–256. [Google Scholar] [CrossRef][Green Version]
- Kandlikar, S.; Lu, Z.; Trabold, T.; Owejan, J.; Gagliardo, J.; Allen, J.; Shahbazian-Yassar, R. Visualization of Fuel Cell Water Transport and Performance Characterization under Freezing Conditions; Final Technical Report; U.S. Department of Energy: Washington, DC, USA, 2010.
- Zhan, Z.; Zhao, H.; Sui, P.C.; Jiang, P.; Pan, M.; Djilali, N. Numerical analysis of ice-induced stresses in the membrane electrode assembly of a PEM fuel cell under sub-freezing operating conditions. Int. J. Hydrogen Energy 2018, 43, 4563–4582. [Google Scholar] [CrossRef]
- Shen, J.; Liu, Z.; Liu, F.; Liu, W. Numerical Simulation of Water Transport in a Proton Exchange Membrane Fuel Cell Flow Channel. Energies 2018, 11, 1770. [Google Scholar] [CrossRef]
- Chevalier, S.; Ge, N.; Lee, J.; George, M.G.; Liu, H.; Shrestha, P.; Muirhead, D.; Lavielle, N.; Hatton, B.D.; Bazylak, A. Novel electrospun gas diffusion layers for polymer electrolyte membrane fuel cells: Part II. In operando synchrotron imaging for microscale liquid water transport characterization. J. Power Sources 2017, 352, 281–290. [Google Scholar] [CrossRef]
- Hasanpour, S.; Ahadi, M.; Bahrami, M.; Djilali, N.; Akbari, M. Woven gas diffusion layers for polymer electrolyte membrane fuel cells: Liquid water transport and conductivity trade-offs. J. Power Sources 2018, 403, 192–198. [Google Scholar] [CrossRef]
- Steinbrenner, J.E.; Lee, E.S.; Wang, F.M.; Fang, C.; Hidrovo, C.H.; Goodson, K.E. Flow regime evolution in long, serpentine micro channels with a porous carbon paper wall. In Proceedings of the ASME 2008 International Mechanical Engineering Congress and Exposition, Boston, MA, USA, 31 October–6 November 2008; pp. 773–781. [Google Scholar]
- Steinbrenner, J.E.; Lee, E.S.; Hidrovo, C.H.; Eaton, J.K.; Goodson, K.E. Impact of channel geometry on two-phase flow in fuel cell micro channels. J. Power Sources 2011, 196, 5012–5020. [Google Scholar] [CrossRef]
- Cho, S.C.; Wang, Y.; Chen, K.S. Droplet dynamics in a polymer electrolyte fuel cell gas flow channel: Forces, deformation, and detachment, I: Theoretical and numerical analyses. J. Power Sources 2012, 206, 119–128. [Google Scholar] [CrossRef]
- Coleman, J.W.; Garimella, S. Characterization of two-phase flow patterns in small-diameter round and rectangular tubes. Int. J. Heat Mass Transf. 1999, 42, 2869–2881. [Google Scholar] [CrossRef]
- Serizawa, A.; Feng, Z.; Kawara, Z. Two-phase flow in micro-channels. Exp. Therm. Fluid Sci. 2012, 26, 703–714. [Google Scholar] [CrossRef]
- Jarauta, A.; Ryzhakov, P. Challenges in Computational Modeling of Two-Phase Transport in Polymer Electrolyte Fuel Cells Flow Channels: A Review. Arch. Comput. Methods Eng. 2018, 25, 1027–1057. [Google Scholar] [CrossRef]
- Bazylak, A. Liquid water visualization in PEM fuel cells: A review. Int. J. Hydrogen Energy 2009, 34, 3845–3857. [Google Scholar] [CrossRef]
- George, R.B.; Light, R.W.; Matthay, M.A. Chest Medicine: Essentials of Pulmonary and Critical Care Medicine, 2nd ed.; Williams & Wilkins: Baltimore, MD, USA, 1990; 512p. [Google Scholar]
- Gorb, S.N. The design of the fly adhesive pad: Distal tenent setae are adapted to the delivery of an adhesive secretion. Proc. R. Soc. Lond. B Biol. Sci. 1998, 265, 747–752. [Google Scholar] [CrossRef]
- Melrose, J.C. Model calculations for capillary condensation. AIChE J. 1996, 12, 986–994. [Google Scholar] [CrossRef]
- Zasadzinski, J.N.; Sweeney, J.B.; Davis, H.T.; Scriven, L.E. Finite-element calculation of fluid menisci and thin films in model porous media. J. Colloid Interface Sci. 1987, 119, 108–116. [Google Scholar] [CrossRef]
- Witkowski, L.M.; Walker, J.S. Solutocapillary instabilities in liquid bridges. Phys. Fluids 2002, 14, 2647–2656. [Google Scholar] [CrossRef]
- Fisher, R.A. On the capillary forces in an ideal soil. J. Agric. Sci. 1926, 16, 492–505. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 2nd ed.; Academic Press: London, UK, 1992. [Google Scholar]
- Kralchevsky, P.A.; Nagayama, K. Capillary Bridges and Capillary-Bridge Forces. Stud. Interface Sci. 2001, 10, 469–502. [Google Scholar]
- Klaas, M.; Koch, E.; Schröder, W. Fundamental medical and engineering investigations on protective artificial respiration. In Notes on Numerical Fluid Mechanical and Multidisciplinary Design; Springer: Berlin/Heidelberg, Germany, 2011; Volume 116, pp. 78–80. [Google Scholar]
- Gomez, M.; Parra, I.E.; Perales, J.M. Mechanical imperfections effect on the minimum volume stability limit of liquid bridges. Phys. Fluids 2002, 14, 2029–2042. [Google Scholar] [CrossRef]
- Shevtsova, V.; Gaponenko, Y.A.; Nepomnyashchy, A. Thermocapillary tow regimes and instability caused by a gas stream along the interface. J. Fluid Mech. 2013, 714, 644–670. [Google Scholar] [CrossRef]
- Qian, B.; Kenneth, S.B. The motion, stability and breakup of stretching liquid bridge with a receding contact angle. J. Fluid Mech. 2011, 666, 554–572. [Google Scholar] [CrossRef]
- Kralchevsky, P.A.; Denskov, N.D. Capillary forces and structuring in layers of colloid particles. J. Curr. Opin. Colloid Interface Sci. 2001, 6, 383–401. [Google Scholar] [CrossRef]
- Yang, L.; Tuabc, Y.; Fang, H. Modeling the rupture of a capillary liquid bridge between a sphere and plane. Soft Matter R. Soc. Chem. 2010, 24, 6178–6182. [Google Scholar] [CrossRef]
- Hoang, D.A.; van Steijn, V.; Portela, L.M.; Kreutzer, M.T.; Kleijn, C.R. Benchmark numerical simulations of segmented two-phase flows in microchannels using the Volume of Fluid method. Comput. Fluids 2013, 86, 28–36. [Google Scholar] [CrossRef]
- Li, S.Z.; Chen, R.; Wang, H.; Liao, Q.; Zhu, X.; Wang, Z.B.; He, X.F. Numerical investigation of the moving liquid column coalescing with a droplet in triangular microchannels using CLSVOF method. Sci. Bull. 2015, 60, 1911–1926. [Google Scholar] [CrossRef]
- Theodorakakos, A.; Ous, T.; Gavaises, A.; Nouri, J.M.; Nikolopoulos, N.; Yanagihara, H. Dynamics of water droplets detached from porous surfaces of relevance to PEM fuel cells. J. Colloid Interface Sci. 2006, 300, 673–687. [Google Scholar] [CrossRef]
- Zhu, X.; Sui, P.C.; Djilali, N. Numerical simulation of emergence of a water droplet from a pore into a microchannel gas stream. Microfluid. Nanofluid. 2008, 4, 543–555. [Google Scholar] [CrossRef]
- Zhu, X.; Sui, P.C.; Djilali, N. Three-dimensional numerical simulations of water droplet dynamics in a PEMFC gas channel. J. Power Sources 2008, 181, 101–115. [Google Scholar] [CrossRef]
- Zhu, X.; Liao, Q.; Sui, P.C.; Djilali, N. Numerical investigation of water droplet dynamics in a low-temperature fuel cell microchannel: Effect of channel geometry. J. Power Sources 2010, 195, 801–812. [Google Scholar] [CrossRef]
- Yang, K.; Guo, Z.L. Multiple-relaxation-time lattice Boltzmann model for binary mixtures of nonideal fluids based on the Enskog kinetic theory. Sci. Bull. 2015, 60, 634–647. [Google Scholar] [CrossRef]
- Zhu, X.; Sui, P.C.; Djilali, N. Dynamic behaviour of liquid water emerging from a GDL pore into a PEMFC gas flow channel. J. Power Sources 2007, 172, 287–295. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, X.; Chen, R.; Shangguan, X. Water Transport and Removal in PEMFC Gas Flow Channel with Various Water Droplet Locations and Channel Surface Wettability. Energies 2018, 11, 880. [Google Scholar] [CrossRef]
- Tobias, M.; Nils, P.; Muller, C.; Zengerle, R.; Koltay, P. Passive water removal in fuel cells by capillary droplet actuation. Sens. Actuators A Phys. 2008, 143, 49–57. [Google Scholar]
- Niu, Z.; Wang, R.; Jiao, K.; Du, Q.; Yin, Y. Direct numerical simulation of low Reynolds number turbulent air-water transport in fuel cell flow channel. Sci. Bull. 2017, 62, 31–39. [Google Scholar] [CrossRef]
- Minor, G.; Djilali, N.; Sinton, D.; Oshkai, P. Flow within a water droplet subjected to an air stream in a hydrophobic microchannel. Fluid Dyn. Res. 2009, 41, 045506. [Google Scholar] [CrossRef]
- Lee, S.J.; Lim, S.K.; Park, G.G.; Kim, C.S. X-ray imaging of water distribution in a polymer electrolyte fuel cell. J. Power Sources 2008, 185, 867–870. [Google Scholar] [CrossRef]
- Minard, K.R.; Viswanathan, V.V.; Majors, P.D.; Wang, L.Q.; Rieke, P.C. Magnetic resonance imaging (MRI) of PEM dehydration and gas manifold flooding during continuous fuel cell operation. J. Power Sources 2006, 161, 856–863. [Google Scholar] [CrossRef]
- Feindel, K.; LaRocque, L.A.; Starke, D.; Bergens, S.; Wasylishen, R. In-situ observations of water production and distribution in an operating H2/O2 PEM fuel cell assembly using 1H NMR microscopy. J. Am. Chem. Soc. 2004, 126, 11436–11437. [Google Scholar] [CrossRef]
- Lu, Z.; Daino, M.M.; Rath, C.; Kandlikar, S.G. Water management studies in PEM fuel cells, Part III: Dynamic breakthrough and intermittent drainage characteristics from GDLs with and without MPLs. Int. J. Hydrogen Energy 2010, 35, 4222–4233. [Google Scholar] [CrossRef]
- Tuber, K.; Pocza, D.; Hebling, C. Visualization of water buildup in the cathode of a transparent PEM fuel cell. J. Power Sources 2003, 124, 403–414. [Google Scholar] [CrossRef]
- Poisson, S.D. Nouvelle Théorie de L’action Capillaire; Bachelier Père et Fils: Quai des Augustins, Paris, France, 1830. [Google Scholar]
- Plateau, J. Experimental and Theoretical Researches on the Figures of Equilibrium of a Liquid Mass Withdrawn from the Action of Gravity; Annual Report of the Smithsonian Institution: Washington, DC, USA, 1863; pp. 207–285. [Google Scholar]
- Lord Rayleigh. On the instability of jets. Proc. Lond. Math. Soc. 1879, 10, 4–13. [Google Scholar]
- Slobozhanin, L.A.; Perales, J.M. Stability of liquid bridges between equal disks in an axial gravity field. Phys. Fluids A 1993, 5, 1305–1314. [Google Scholar] [CrossRef]
- Da Riva, I.; Martinez, I. Floating Zone Stability; Exp 1-ES-331, In ESA SP-14; European Space Agency: Paris, France, 1979; pp. 67–73. [Google Scholar]
- Gillette, R.D.; Dyson, D.C. Stability of fluid interfaces of revolution between equal solid circular plates. J. Chem. Eng. 1971, 2, 44–54. [Google Scholar] [CrossRef]
- Meseguer, J.; Espino, J.; Perales, J.M.; Laveron-Simavilla, A. On the breaking of long, axisymmetric liquid bridges between unequal supporting disks at minimum volume stability limit. Eur. J. Mech. B Fluids 2003, 22, 355–368. [Google Scholar] [CrossRef]
- Orr, F.M.; Scriven, L.E.; Rivas, A.P. Pendular rings between solids: Meniscus properties and capillary force. J. Fluid Mech. 1975, 67, 723–742. [Google Scholar] [CrossRef]
- Wiklund, H. Lattice Boltzmann Simulations of Two-Phase Flow in Fibre Network Systems. Ph.D. Thesis, Mid-Sweden University, Sundsvall, Sweden, 2012. [Google Scholar]
- Anderson, R.; Zhang, L.; Ding, Y.; Blanco, M.; Bi, X.; Wilkinson, D.P. A critical review of two-phase flow in gas channels of PEM fuel cells. J. Power Sources 2010, 195, 4531–4553. [Google Scholar] [CrossRef]
- Wörner, M. Numerical modeling of multiphase flows in microfluidics and micro process engineering: A review of methods and applications. Microfluid. Nanofluid. 2012, 12, 841–886. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Rynhart, P.; McKibbin, R.; McLachlan, R.; Jones, J.R. Mathematical modelling of granulation: Static and dynamic liquid bridges. Res. Lett. Inf. Math. Sci. 2002, 3, 199–212. [Google Scholar]
- Kenmotsu, K. Surfaces of revolution with prescribed mean curvature Tohoku. Math. J. 1980, 32, 147–153. [Google Scholar]
- Kenmotsu, K. Surfaces of revolution with periodic mean curvature. Osaka J. Math. 2003, 40, 687–696. [Google Scholar]
- Gu, H.; Duits, M.H.G.; Mugele, F. Droplet formation and merging in two-phase flow microfluidics. Int. J. Mol. Sci. 2011, 12, 2572–2597. [Google Scholar] [CrossRef]
- Herrada, M.A.; López-Herrera, J.M.; Vega, E.J.; Montanero, J.M. Numerical simulation of a liquid bridge in a coaxial gas flow. Phys. Fluids 2011, 23, 012101. [Google Scholar] [CrossRef]
- Vega, E.J.; Montanero, J.M.; Herrada, M.A.; Ferrera, C. Dynamics of an axisymmetric liquid bridge close to the minimum-volume stability limit. Phys. Rev. E 2014, 90, 013015. [Google Scholar] [CrossRef]
- Fernando, R.H.; Xing, L.-L.; Glass, J.E. Erratum to Rheology parameters controlling spray atomization and roll misting behavior of waterborne coatings. Prog. Org. Coat. 2001, 42, 284–288. [Google Scholar] [CrossRef]
- Grilli, S.; Coppola, S.; Vespini, V.; Merola, F.; Finizio, A.; Ferraro, P. 3D lithography by rapid curing of the liquid instabilities at nanoscale. Proc. Natl. Acad. Sci. USA 2011, 108, 15106–15111. [Google Scholar] [CrossRef] [PubMed]
- Broesch, D.; Frechette, J. From concave to convex: Capillary bridges in slit pore geometry. Langmuir 2012, 28, 15548–15554. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).