An Energy Potential Estimation Methodology and Novel Prototype Design for Building-Integrated Wind Turbines
Abstract
1. Introduction
- They can work as standalone devices, so they can provide energy in isolated locations without a connection to the electric grid.
- They work in distributed micro-generation mode, thus minimizing energy losses due to transport and distribution. These devices generate energy at a site that is close to the final user, thus dramatically reducing the need for electric infrastructures.
- Furthermore, it can be combined with photovoltaic energy in hybrid installations to enable the optimal use and management of shared electric accumulators.
2. Data and Methodology
2.1. Data and Location
2.1.1. Anemometers and ERA5
2.1.2. Quantile-Mapping Calibration
2.2. ROSEO-BIWT Design
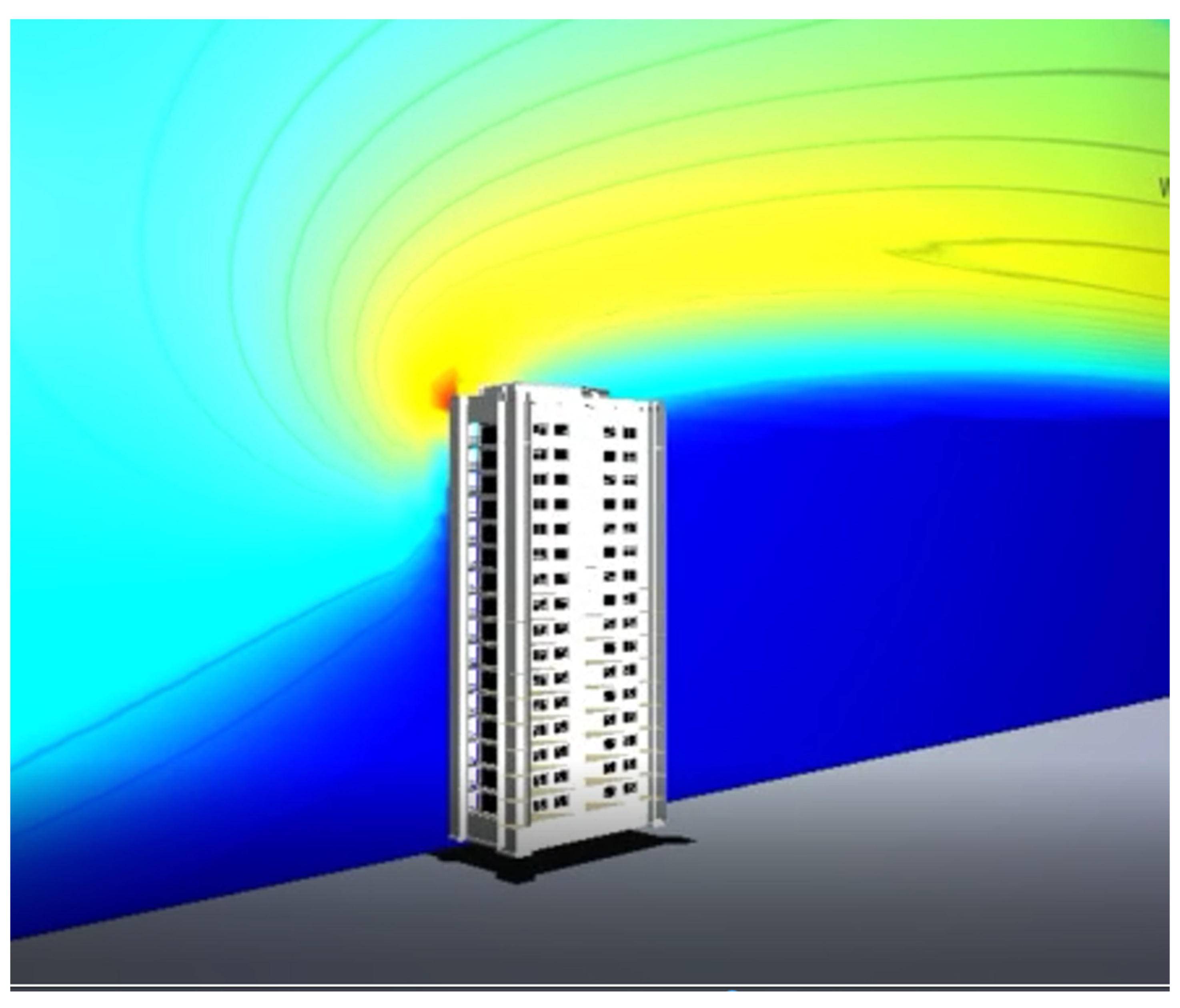
2.2.1. The Location on the Upper Edge of the Building
2.2.2. Savonius Turbine
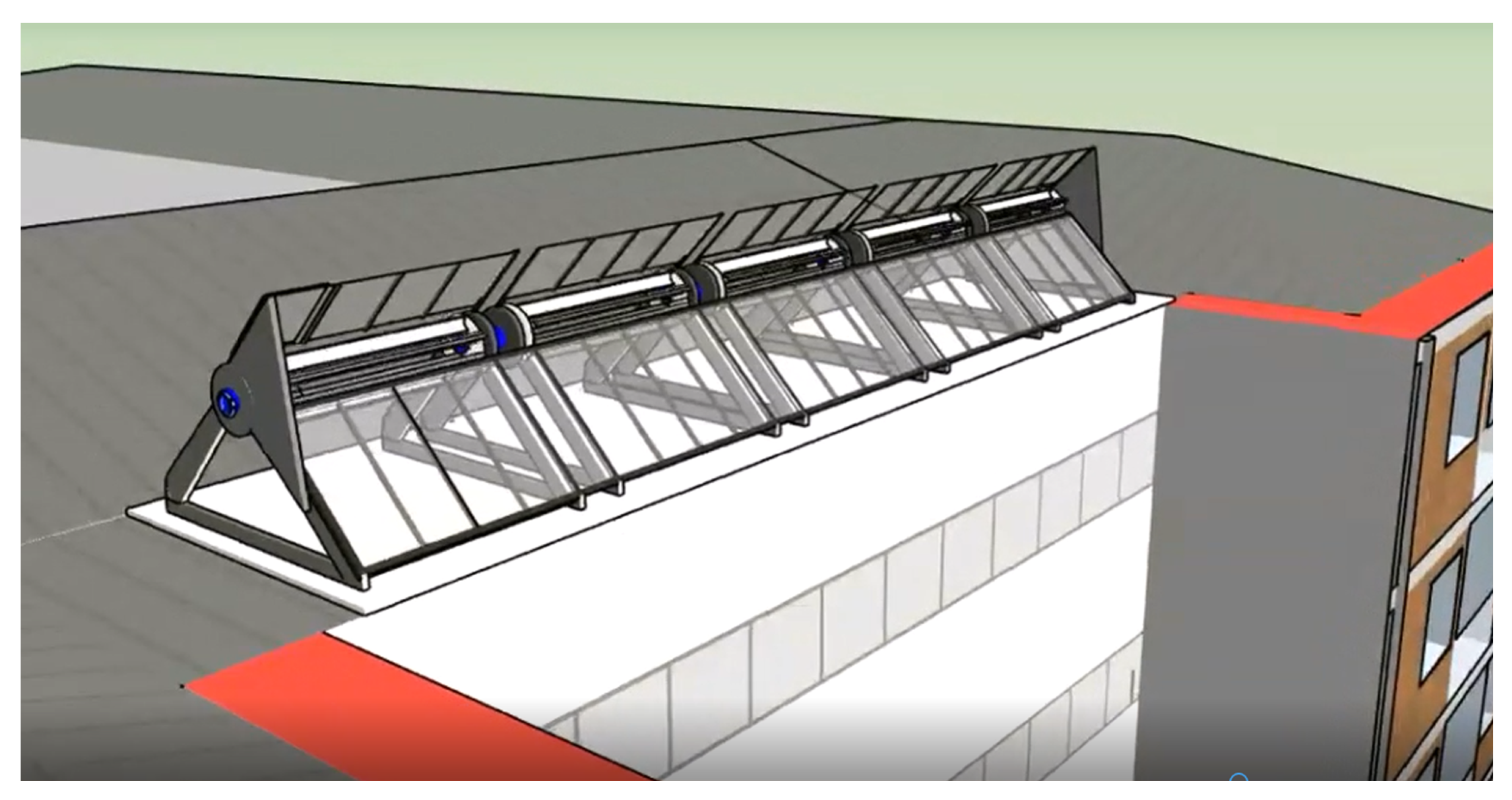
2.2.3. The Final Design
2.3. Experiments in the Wind Tunnel
- First, according to the literature, the augmentation factor of the wind speed on the edge of the buildings is around 1.2. Wind speed augmentation is the result of the union between the usual horizontal component and the vertical component.
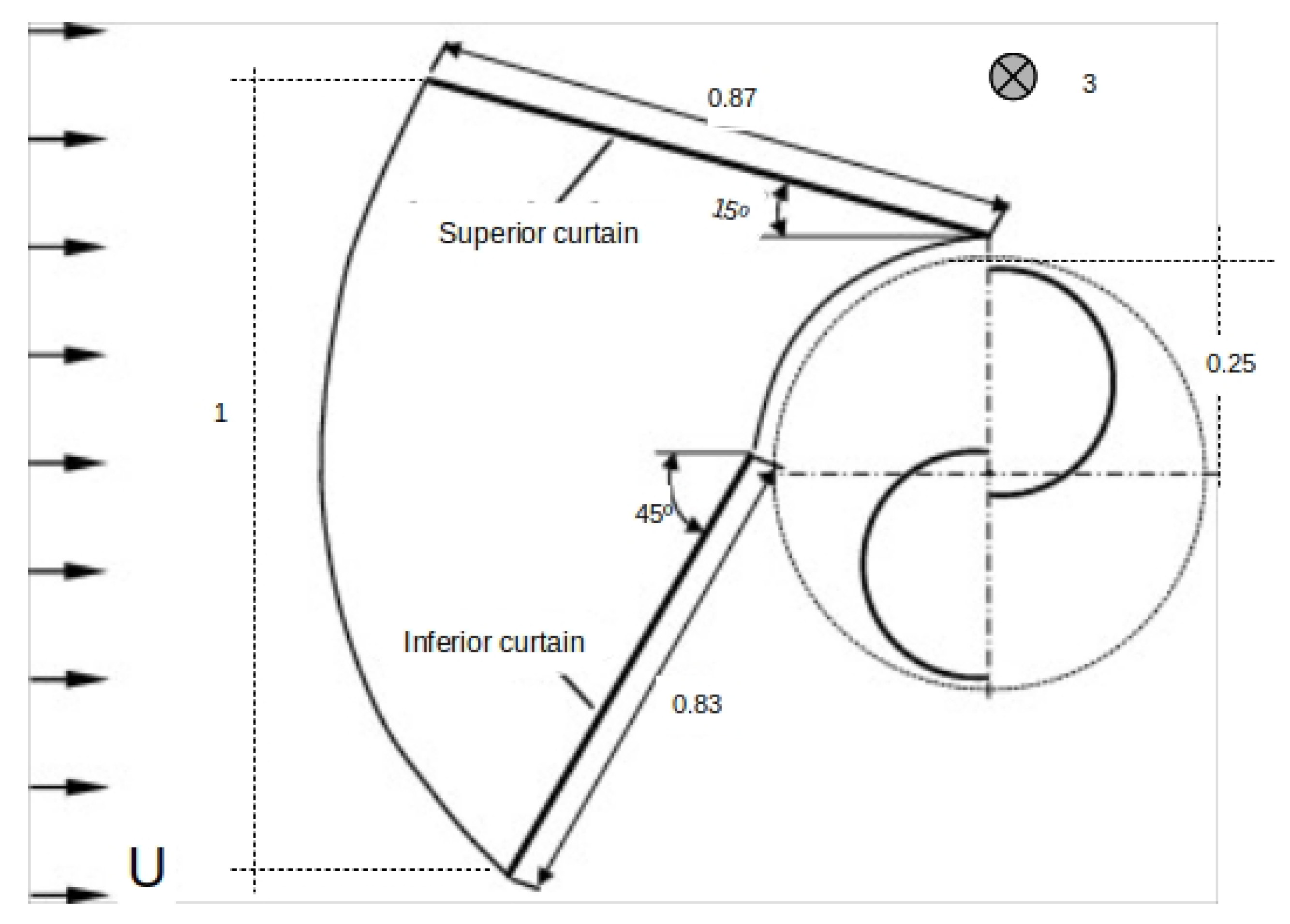
- Then, the previous augmentation factor should be multiplied by the new increment provided by the vanes. These factors will be measured for different wind speeds in the wind tunnel of the university using a small-scale model of a building with curtain-type vanes (see Figure 5) and a rotor or 2 cm diameter.
- A similar experiment will be performed for a real Savonius with one inferior vane and will be critically compared with other studies.
- Finally, the Weibull distribution at the location obtained by the previously described calibration methodology will be applied to the measured power curve that includes . Thus, the amount of hours at rated power due to this augmentation will be an interesting parameter about energy production.
3. Results
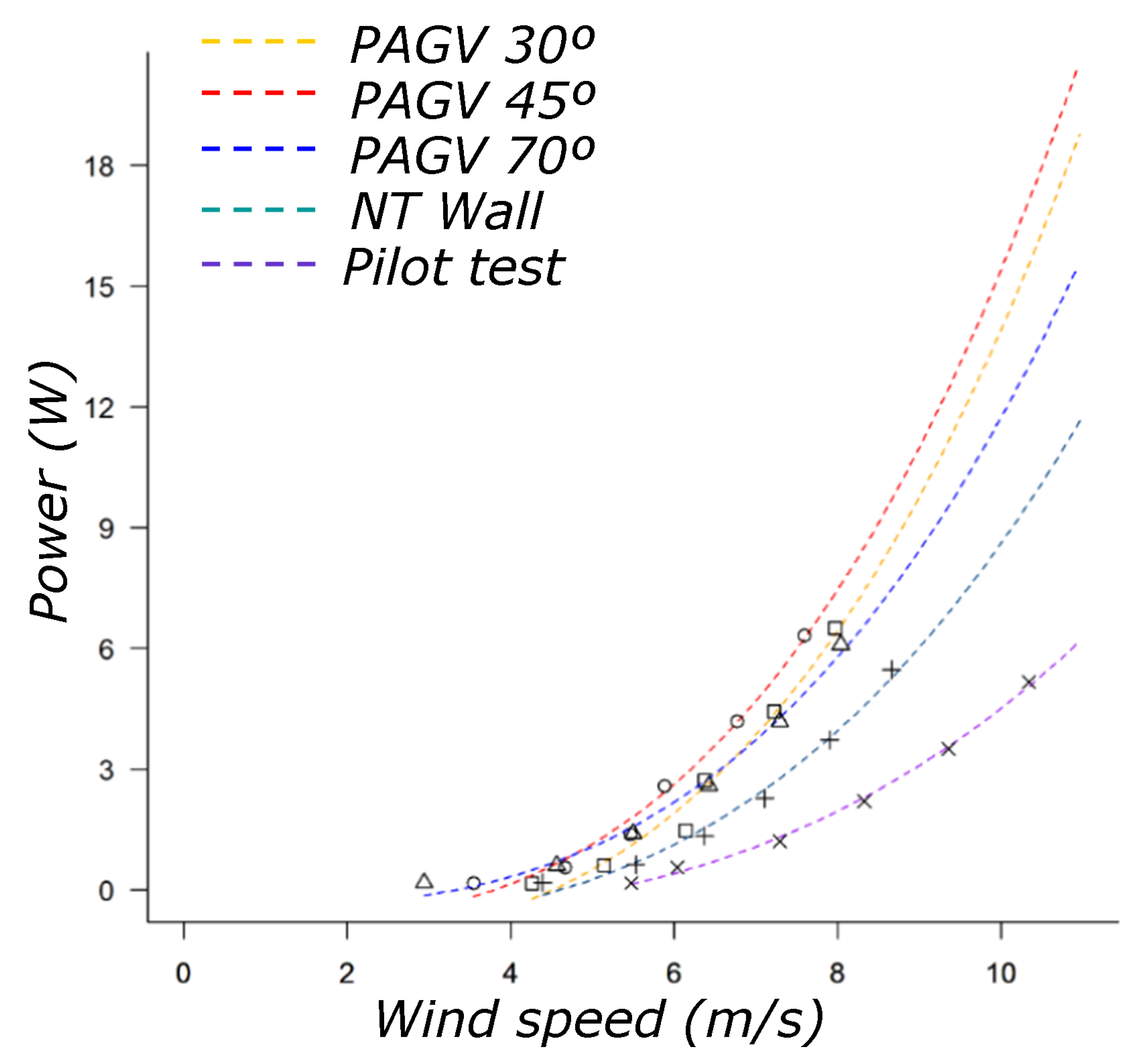
3.1. Effect of the PAGV in the Real Savonius
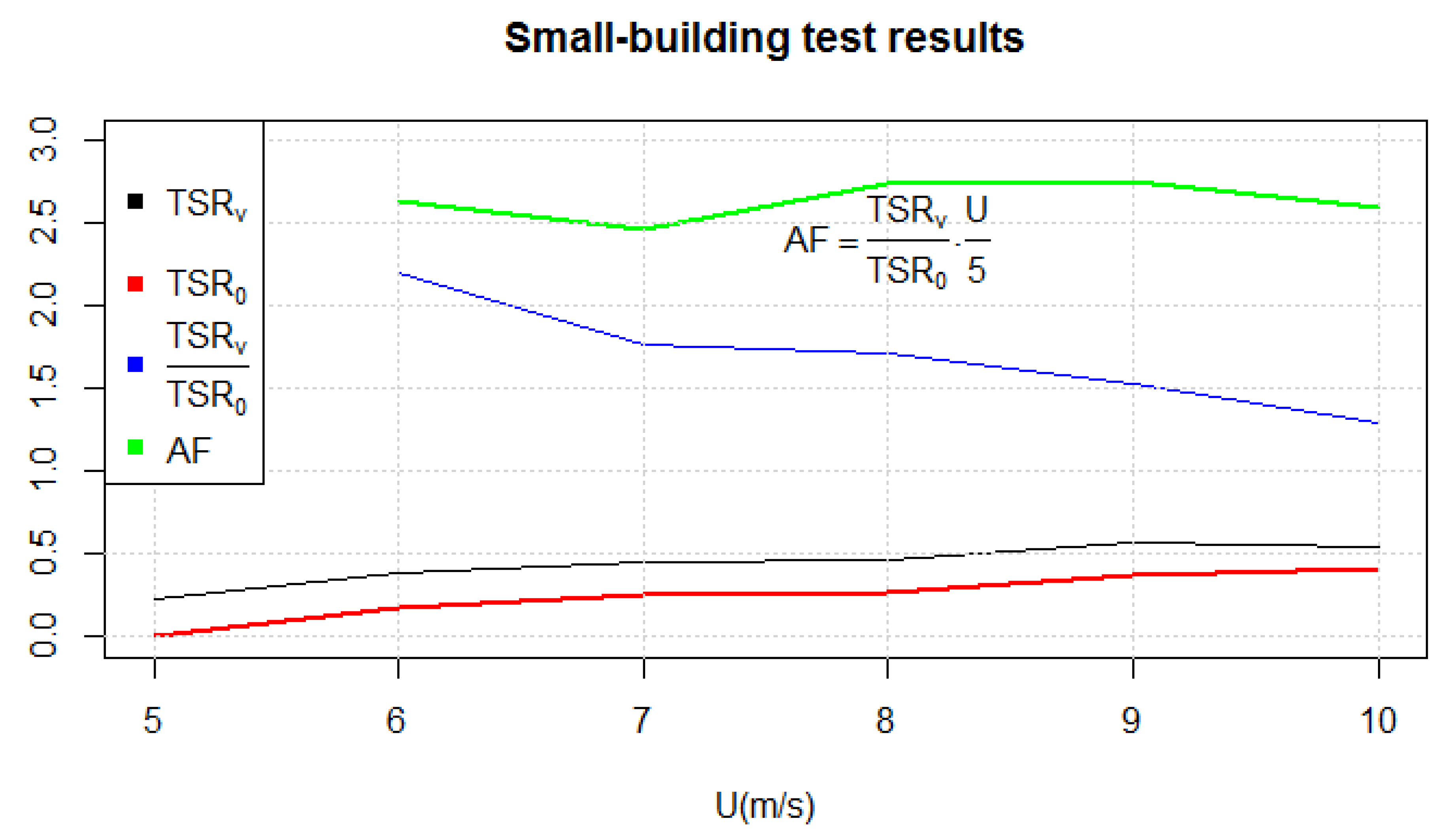
3.2. Augmentation Factor in the Small-Scale Building Model
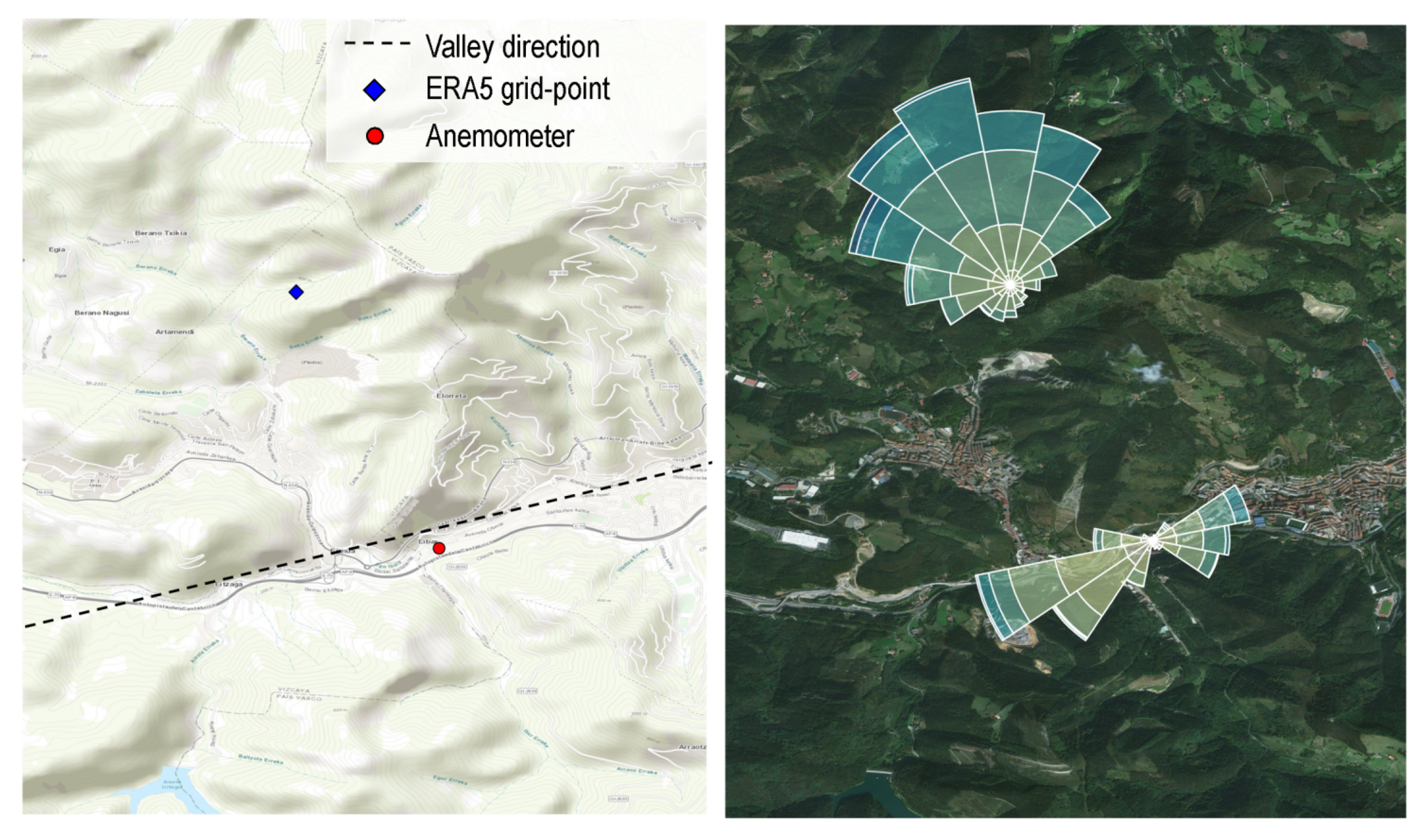
3.3. Wind Rose around the Building
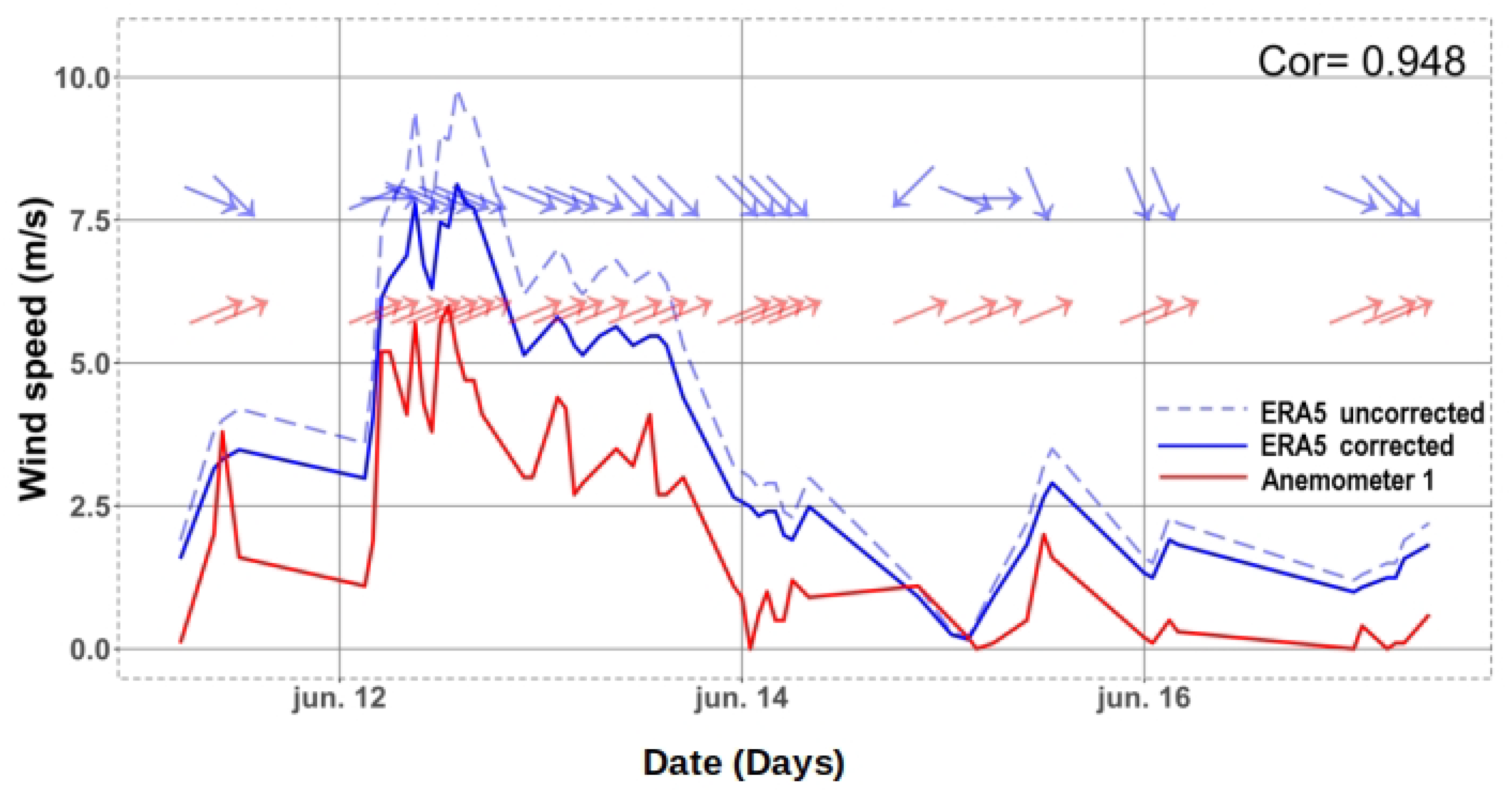
3.4. Comparison between ERA5 and the Anemometer
3.5. Estimation of the Energy Potential
- According to Mertens [38] and the initial experiments with our small-scale building in the wind tunnel, the wind increases its velocity by 20% at the upper edge of a typical building.
- The simplest PAGVs have increased the wind speed by four times, with a corresponding increase in to a value as high as 0.37 [47]. Although higher values can be obtained with wider entrances, the authors will use an of 4 for the estimation, although there is also a 20% augmentation due to the additional architectonic acceleration at the upper edge.
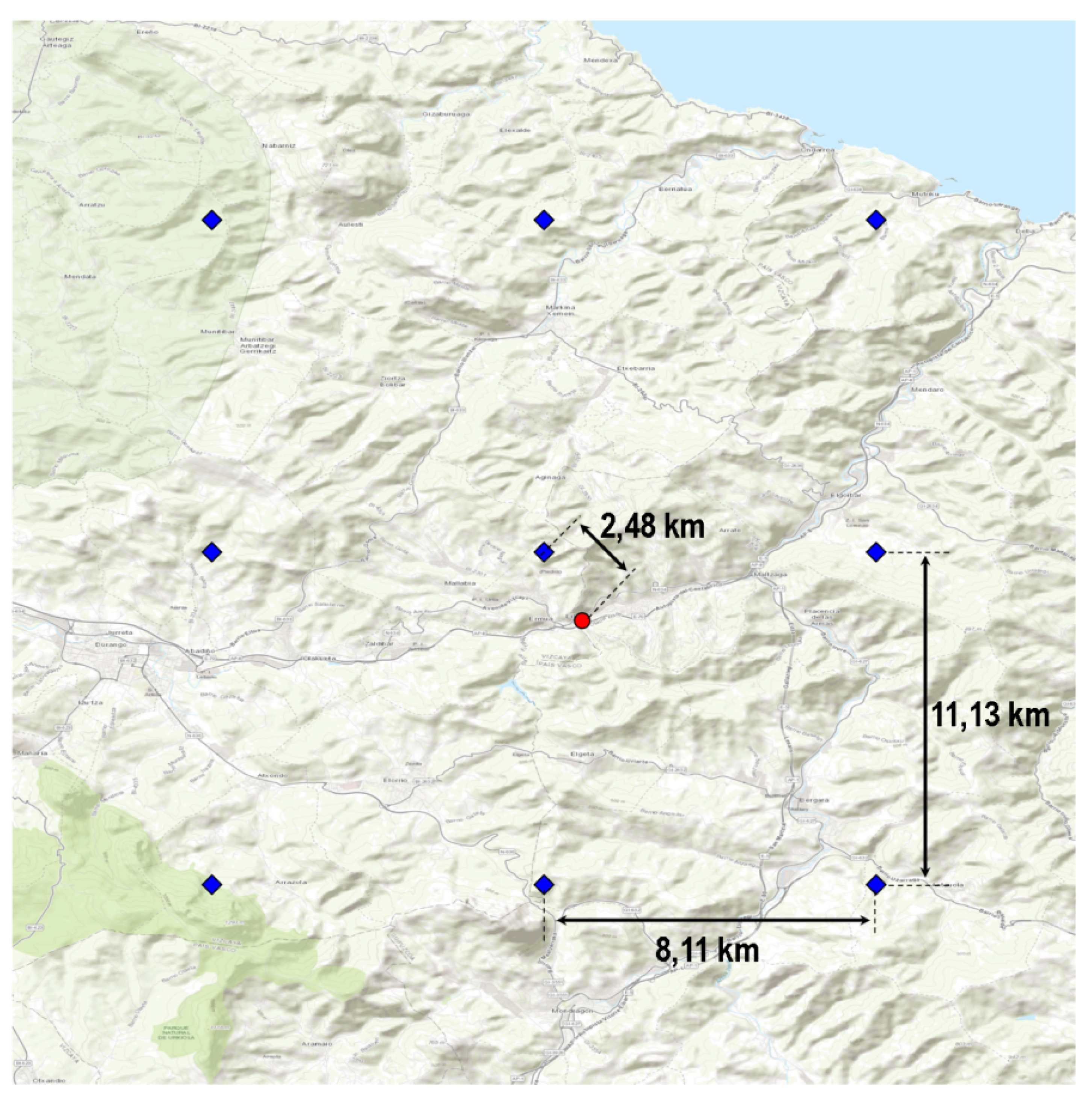
- Taking into account the wind rose in Figure 11, the authors only considered the wind data of ERA5 for the valley direction and for our turbine on the corresponding facade.
- has been corroborated by our small-scale building with PAGVs for different wind speed values in the wind tunnel. Although the optimum vane angle experiment has not yet been developed, the first test results are consistent with values reported in the literature.
- has been corroborated by the real Savonius with the inferior vane.
- The analyses of the wind resource in the open direction of the valley and the corresponding facade yield a wind speed histogram or Weibull distribution that can be applied to the power curve of the turbine with .
- For the first estimation presented here, the working time at rated power due to the increment of wind speed using PAGVs has been computed.
- The turbine’s working hours per year in the interval of rated wind speed (above 17.9 m/s) can be computed if the cumulative density function (Equation (2)) is applied to c, which results in the following working hours:
- Therefore, AEP is kWh at the rated power; it is a very small value since the working hours of a profitable turbine should be around 2000 h per year.
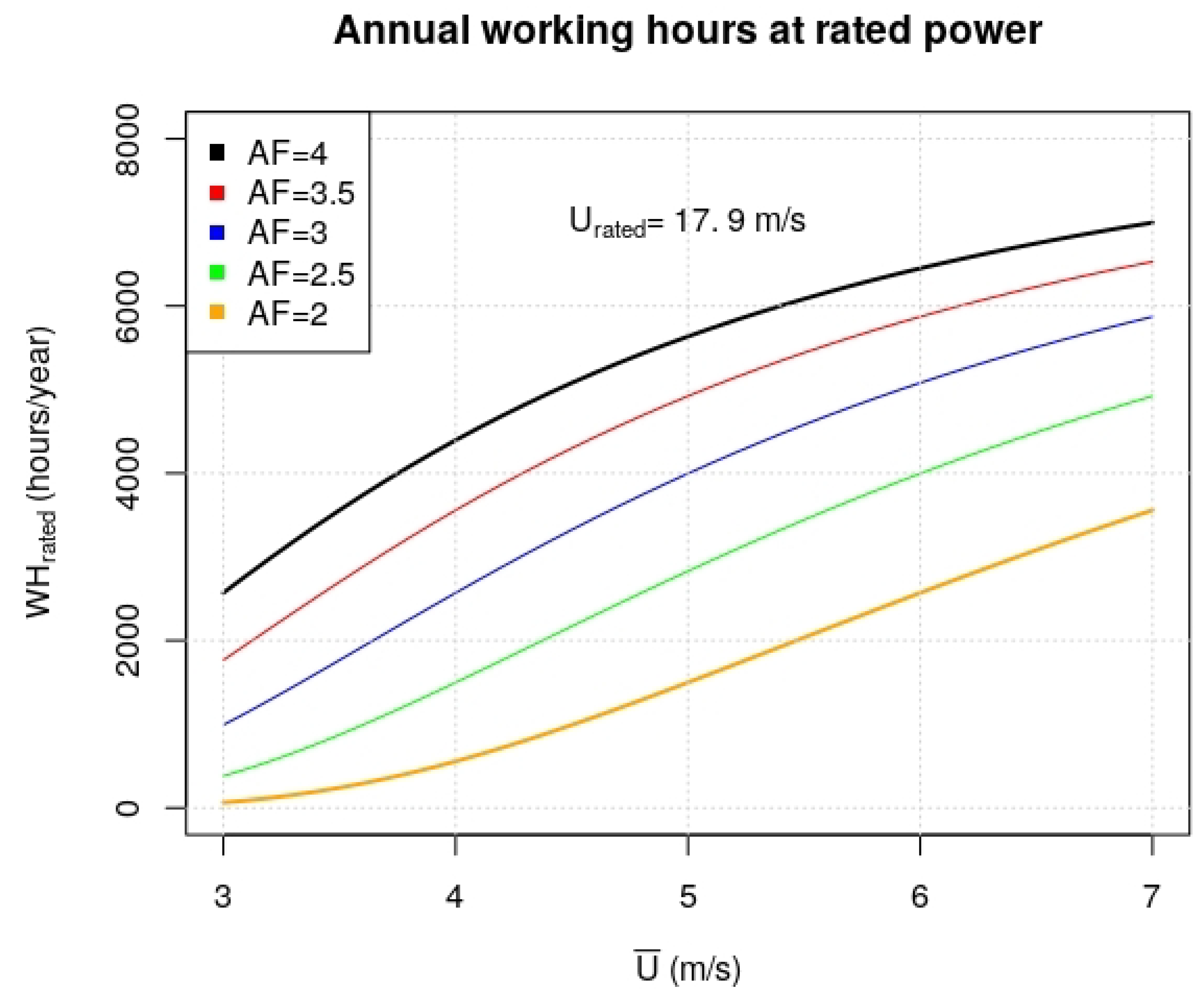
- However, multiplying the scale parameter c by values between 2 and 4 ( is the value obtained in the laboratory using only one inferior vane and 4 the maximum expected value according to the mentioned literature) and keeping the typical value of , the total augmentation factor from the PAGVs and the edge effect increases the AEP and working hours. Figure 13 shows the annual working hours () at rated power in function of the average wind speed of the site for different factors: .At low annual average wind speed of 3 m/s, the maximum can produce 2000 h at rated power. At m/s, between 2.5 and 3 is necessary to ensure the 2000 h. At m/s, the minimum obtained with only the inferior vane (Figure 5) is almost sufficient. At high s, an or 4 implies 75% of the time at rated power.
4. Conclusions and Future Outlook
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| BIWT | Building-Integrated Wind turbine |
| O&M | Operation and maintenance |
| PAGV | Power Augment Guiding Vane |
| Probability Density Function | |
| Annual Energy Production | |
| Augmentation factor | |
| c | Weibull’s scale parameter |
| Power Coefficient | |
| Maximum Power Coefficient | |
| k | Weibull’s shape parameter |
| Tip Speed Ratio | |
| Optimum TSR where is maximum | |
| Optimum TSR with augmentation techniques | |
| Average wind Speed | |
| Wind speed in the prototype | |
| Wind speed in the model | |
| Rated wind speed | |
| Blade tip speed | |
| Annual working hours at rated power | |
| Roughness of the Terrain | |
| Reference height |
References
- WWEA. WWEA Released Latest Global Small Wind Statistics; WWEA: Bonn, Germany, 2018. [Google Scholar]
- Chastas, P.; Theodosiou, T.; Bikas, D.; Kontoleon, K. Embodied energy and nearly zero energy buildings: A review in residential buildings. Procedia Environ. Sci. 2017, 38, 554–561. [Google Scholar] [CrossRef]
- Bogle, I. Integrating wind turbines in tall buildings. CTBUH J. 2011, 4, 30–33. [Google Scholar]
- Smith, R.F.; Killa, S. Bahrain World Trade Center (BWTC): The first large-scale integration of wind turbines in a building. Struct. Des. Tall Spec. Build. 2007, 16, 429–439. [Google Scholar] [CrossRef]
- Balduzzi, F.; Bianchini, A.; Ferrari, L. Microeolic turbines in the built environment: Influence of the installation site on the potential energy yield. Renew. Energy 2012, 45, 163–174. [Google Scholar] [CrossRef]
- Balduzzi, F.; Bianchini, A.; Gentiluomo, D.; Ferrara, G.; Ferrari, L. Rooftop siting of a small wind turbine using a hybrid BEM-CFD model. In Research and Innovation on Wind Energy on Exploitation in Urban Environment Colloquium; Springer: Riva del Garda, Italy, 2017; pp. 91–112. [Google Scholar]
- Oerlemans, S.; Sijtsma, P.; López, B.M. Location and quantification of noise sources on a wind turbine. J. Sound Vib. 2007, 299, 869–883. [Google Scholar] [CrossRef]
- Toja-Silva, F.; Lopez-Garcia, O.; Peralta, C.; Navarro, J.; Cruz, I. An empirical–heuristic optimization of the building-roof geometry for urban wind energy exploitation on high-rise buildings. Appl. Energy 2016, 164, 769–794. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Chichester, UK, 2010. [Google Scholar]
- Dilimulati, A.; Stathopoulos, T.; Paraschivoiu, M. Wind turbine designs for urban applications: A case study of shrouded diffuser casing for turbines. J. Wind Eng. Ind. Aerodyn. 2018, 175, 179–192. [Google Scholar] [CrossRef]
- Hyams, M. 20-Wind energy in the built environment. In Metropolitan Sustainability; Zeman, F., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Cambridge, UK, 2012; pp. 457–499. [Google Scholar]
- Arteaga-López, E.; Ángeles-Camacho, C.; Bañuelos-Ruedas, F. Advanced methodology for feasibility studies on building-mounted wind turbines installation in urban environment: Applying CFD analysis. Energy 2019, 167, 181–188. [Google Scholar] [CrossRef]
- Ulazia, A.; Sáenz, J.; Ibarra-Berastegui, G.; González-Rojí, S.J.; Carreno-Madinabeitia, S. Using 3DVAR data assimilation to measure offshore wind energy potential at different turbine heights in the West Mediterranean. Appl. Energy 2017, 208, 1232–1245. [Google Scholar] [CrossRef]
- Ulazia, A.; Saenz, J.; Ibarra-Berastegui, G. Sensitivity to the use of 3DVAR data assimilation in a mesoscale model for estimating offshore wind energy potential. A case study of the Iberian northern coastline. Appl. Energy 2016, 180, 617–627. [Google Scholar] [CrossRef]
- Edp-Renewable University Challenge Awards. Available online: https://www.edpr.com/en/news/2017/09/28/edpr-celebrates-ninth-edition-university-challenge-awards-spain (accessed on 28 September 2017).
- Chong, W.; Pan, K.; Poh, S.; Fazlizan, A.; Oon, C.; Badarudin, A.; Nik-Ghazali, N. Performance investigation of a power augmented vertical axis wind turbine for urban high-rise application. Renew. Energy 2013, 51, 388–397. [Google Scholar] [CrossRef]
- Chong, W.; Naghavi, M.; Poh, S.; Mahlia, T.; Pan, K. Techno-economic analysis of a wind–solar hybrid renewable energy system with rainwater collection feature for urban high-rise application. Appl. Energy 2011, 88, 4067–4077. [Google Scholar] [CrossRef]
- Tong, C.W.; Zainon, M.; Chew, P.S.; Kui, S.C.; Keong, W.S.; Chen, P.K. Innovative Power-Augmentation-Guide-Vane Design of Wind-Solar Hybrid Renewable Energy Harvester for Urban High Rise Application. In Proceedings of the 2010 Physics Education Research Conference, Portland, OR, USA, 21–22 July 2010; Volume 1225, pp. 507–521. [Google Scholar]
- Park, J.; Jung, H.J.; Lee, S.W.; Park, J. A new building-integrated wind turbine system utilizing the building. Energies 2015, 8, 11846–11870. [Google Scholar] [CrossRef]
- Zemamou, M.; Aggour, M.; Toumi, A. Review of savonius wind turbine design and performance. Energy Procedia 2017, 141, 383–388. [Google Scholar] [CrossRef]
- Kim, S.; Cheong, C. Development of low-noise drag-type vertical wind turbines. Renew. Energy 2015, 79, 199–208. [Google Scholar] [CrossRef]
- Ulazia, A. Multiple roles for analogies in the genesis of fluid mechanics: How analogies can cooperate with other heuristic strategies. Found. Sci. 2016, 21, 543–565. [Google Scholar] [CrossRef]
- Hersbach, H. The ERA5 Atmospheric Reanalysis; AGU Fall Meeting Abstracts: San Francisco, CA, USA, 2016. [Google Scholar]
- Olauson, J. ERA5: The new champion of wind power modelling? Renew. Energy 2018, 126, 322–331. [Google Scholar] [CrossRef]
- Ulazia, A.; Penalba, M.; Ibarra-Berastegui, G.; Ringwood, J.; Saénz, J. Wave energy trends over the Bay of Biscay and the consequences for wave energy converters. Energy 2017, 141, 624–634. [Google Scholar] [CrossRef]
- Penalba, M.; Ulazia, A.; Ibarra-Berastegui, G.; Ringwood, J.; Sáenz, J. Wave energy resource variation off the west coast of Ireland and its impact on realistic wave energy converters’ power absorption. Appl. Energy 2018, 224, 205–219. [Google Scholar] [CrossRef]
- Ulazia, A.; Penalba, M.; Rabanal, A.; Ibarra-Berastegi, G.; Ringwood, J.; Sáenz, J. Historical Evolution of the Wave Resource and Energy Production off the Chilean Coast over the 20th Century. Energies 2018, 11, 2289. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456, 12–29. [Google Scholar] [CrossRef]
- Watanabe, S.; Kanae, S.; Seto, S.; Yeh, P.J.F.; Hirabayashi, Y.; Oki, T. Intercomparison of bias-correction methods for monthly temperature and precipitation simulated by multiple climate models. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef]
- Block, P.; Souza Filho, F.; Sun, L.; Kwon, H.H. A streamflow forecasting framework using multiple climate and hydrological models. J. Am. Water Resour. Assoc. 2009, 45, 828–843. [Google Scholar] [CrossRef]
- Boé, J.; Terray, L.; Habets, F.; Martin, E. Statistical and dynamical downscaling of the Seine basin climate for hydro-meteorological studies. Int. J. Climatol. 2007, 27, 1643–1655. [Google Scholar] [CrossRef]
- Sun, F.; Roderick, M.L.; Lim, W.H.; Farquhar, G.D. Hydroclimatic projections for the Murray-Darling Basin based on an ensemble derived from Intergovernmental Panel on Climate Change AR4 climate models. Water Resour. Res. 2011, 47, W00G02. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Rojas, R.; Feyen, L.; Dosio, A.; Bavera, D. Improving pan-European hydrological simulation of extreme events through statistical bias correction of RCM-driven climate simulations. Hydrol. Earth Syst. Sci. 2011, 15, 2599–2620. [Google Scholar] [CrossRef]
- Bett, P.E.; Thornton, H.E.; Clark, R.T. Using the Twentieth Century Reanalysis to assess climate variability for the European wind industry. Theor. Appl. Climatol. 2015, 127, 1–20. [Google Scholar] [CrossRef]
- Shikha; Bhatti, T.; Kothari, D. Wind energy conversion systems as a distributed source of generation. J. Energy Eng. 2003, 129, 69–80. [Google Scholar] [CrossRef]
- Mertens, S. Wind Energy in the Built Environment: Concentrator Effects of Buildings. Doctoral Thesis, Delf University (TUDelf), Delft, The Netherlands, 2006. [Google Scholar]
- Akwa, J.V.; Vielmo, H.A.; Petry, A.P. A review on the performance of Savonius wind turbines. Renew. Sustain. Energy Rev. 2012, 16, 3054–3064. [Google Scholar] [CrossRef]
- Alom, N.; Saha, U.K. Four decades of research into the augmentation techniques of Savonius wind turbine rotor. J. Energy Resour. Technol. 2018, 140, 050801. [Google Scholar] [CrossRef]
- El-Askary, W.; Nasef, M.; Abdel-Hamid, A.; Gad, H. Harvesting wind energy for improving performance of Savonius rotor. J. Wind Eng. Ind. Aerodyn. 2015, 139, 8–15. [Google Scholar] [CrossRef]
- Mohamed, M.; Janiga, G.; Pap, E.; Thévenin, D. Optimization of Savonius turbines using an obstacle shielding the returning blade. Renew. Energy 2010, 35, 2618–2626. [Google Scholar] [CrossRef]
- Bhatti, T.; Kothari, D. A new vertical axis wind rotor using convergent nozzles. In Proceedings of the Large Engineering Systems Conference on Power Engineering, Montreal, QC, Canada, 7–9 May 2003; pp. 177–181. [Google Scholar]
- Altan, B.D.; Atılgan, M. A study on increasing the performance of Savonius wind rotors. J. Mech. Sci. Technol. 2012, 26, 1493–1499. [Google Scholar] [CrossRef]
- Roy, S.; Saha, U.K. Review on the numerical investigations into the design and development of Savonius wind rotors. Renew. Sustain. Energy Rev. 2013, 24, 73–83. [Google Scholar] [CrossRef]
- Altan, B.D.; Atılgan, M. The use of a curtain design to increase the performance level of a Savonius wind rotors. Renew. Energy 2010, 35, 821–829. [Google Scholar] [CrossRef]
- Wong, K.H.; Chong, W.T.; Sukiman, N.L.; Poh, S.C.; Shiah, Y.C.; Wang, C.T. Performance enhancements on vertical axis wind turbines using flow augmentation systems: A review. Renew. Sustain. Energy Rev. 2017, 73, 904–921. [Google Scholar] [CrossRef]
- Maxon Motor. Available online: https://www.maxonmotor.com (accessed on 15 March 2019).
- Usman, M.; Hanif, A.; Kim, I.H.; Jung, H.J. Experimental validation of a novel piezoelectric energy harvesting system employing wake galloping phenomenon for a broad wind spectrum. Energy 2018, 153, 882–889. [Google Scholar] [CrossRef]
- Choi, C.K.; Kwon, D.K. Wind tunnel blockage effects on aerodynamic behavior of bluff body. Wind Struct. Int. J. 1998, 1, 351–364. [Google Scholar] [CrossRef]
- Emmanuel, B.; Jun, W. Numerical study of a six-bladed Savonius wind turbine. J. Sol. Energy Eng. 2011, 133, 044503. [Google Scholar] [CrossRef]
- Altan, B.D.; Atılgan, M. An experimental and numerical study on the improvement of the performance of Savonius wind rotor. Energy Conv. Manag. 2008, 49, 3425–3432. [Google Scholar] [CrossRef]
- Fiebrich, C.A.; Morgan, C.R.; McCombs, A.G.; Hall, P.K., Jr.; McPherson, R.A. Quality assurance procedures for mesoscale meteorological data. J. Atmos. Ocean. Technol. 2010, 27, 1565–1582. [Google Scholar] [CrossRef]
- Venables, W.N.; Smith, D.M.; Team, R.C. An introduction to R-Notes on R: A programming environment for data analysis and graphics. 2018. Available online: https://cran.r-project.org/doc/manuals/r-release/R-intro.pdf (accessed on 15 March 2019).
- SeaHawk. SeaHawk-Desert Power Savonius Turbine; Desert Power: Palm Desert, CA, USA, 2017. [Google Scholar]
- Rabanal, A.; Ulazia, A.; Ibarra-Berastegi, G.; Sáenz, J.; Elosegui, U. MIDAS: A Benchmarking Multi-Criteria Method for the Identification of Defective Anemometers in Wind Farms. Energies 2018, 12, 28. [Google Scholar] [CrossRef]




| Length; diameter | 2 m; 630 mm |
| Measuring system | Pitot tubes, an ultrasonic anemometer, and air pressure transducers |
| Range of wind speed | 0–13 m/s |
| Materials | Structure of aluminum and dome of polycarbonate |
| Control panel | Potentiometer for the regulation of wind speed, rpm, and torque |
| Generator | maxon RE motor 65 mm, Graphite Brushes, 250 Watt [48] |
| Data acquisition | Variable resistor with measurement of voltage, intensity, and power |
| Experiment | |||
|---|---|---|---|
| PAGV30 | 17.1 | 1.01 | 2.0 |
| PAGV45 | 19.2 | 1.10 | 2.2 |
| PAGV70 | 16.1 | 0.94 | 1.9 |
| NT Wall | 11.6 | 0.68 | 1.4 |
| Pilot test | 6.5 | 0.50 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia, O.; Ulazia, A.; del Rio, M.; Carreno-Madinabeitia, S.; Gonzalez-Arceo, A. An Energy Potential Estimation Methodology and Novel Prototype Design for Building-Integrated Wind Turbines. Energies 2019, 12, 2027. https://doi.org/10.3390/en12102027
Garcia O, Ulazia A, del Rio M, Carreno-Madinabeitia S, Gonzalez-Arceo A. An Energy Potential Estimation Methodology and Novel Prototype Design for Building-Integrated Wind Turbines. Energies. 2019; 12(10):2027. https://doi.org/10.3390/en12102027
Chicago/Turabian StyleGarcia, Oscar, Alain Ulazia, Mario del Rio, Sheila Carreno-Madinabeitia, and Andoni Gonzalez-Arceo. 2019. "An Energy Potential Estimation Methodology and Novel Prototype Design for Building-Integrated Wind Turbines" Energies 12, no. 10: 2027. https://doi.org/10.3390/en12102027
APA StyleGarcia, O., Ulazia, A., del Rio, M., Carreno-Madinabeitia, S., & Gonzalez-Arceo, A. (2019). An Energy Potential Estimation Methodology and Novel Prototype Design for Building-Integrated Wind Turbines. Energies, 12(10), 2027. https://doi.org/10.3390/en12102027





