A Design of PWM Controlled Calibrator of Non-Sinusoidal Voltage Waveforms
Abstract
1. Introduction
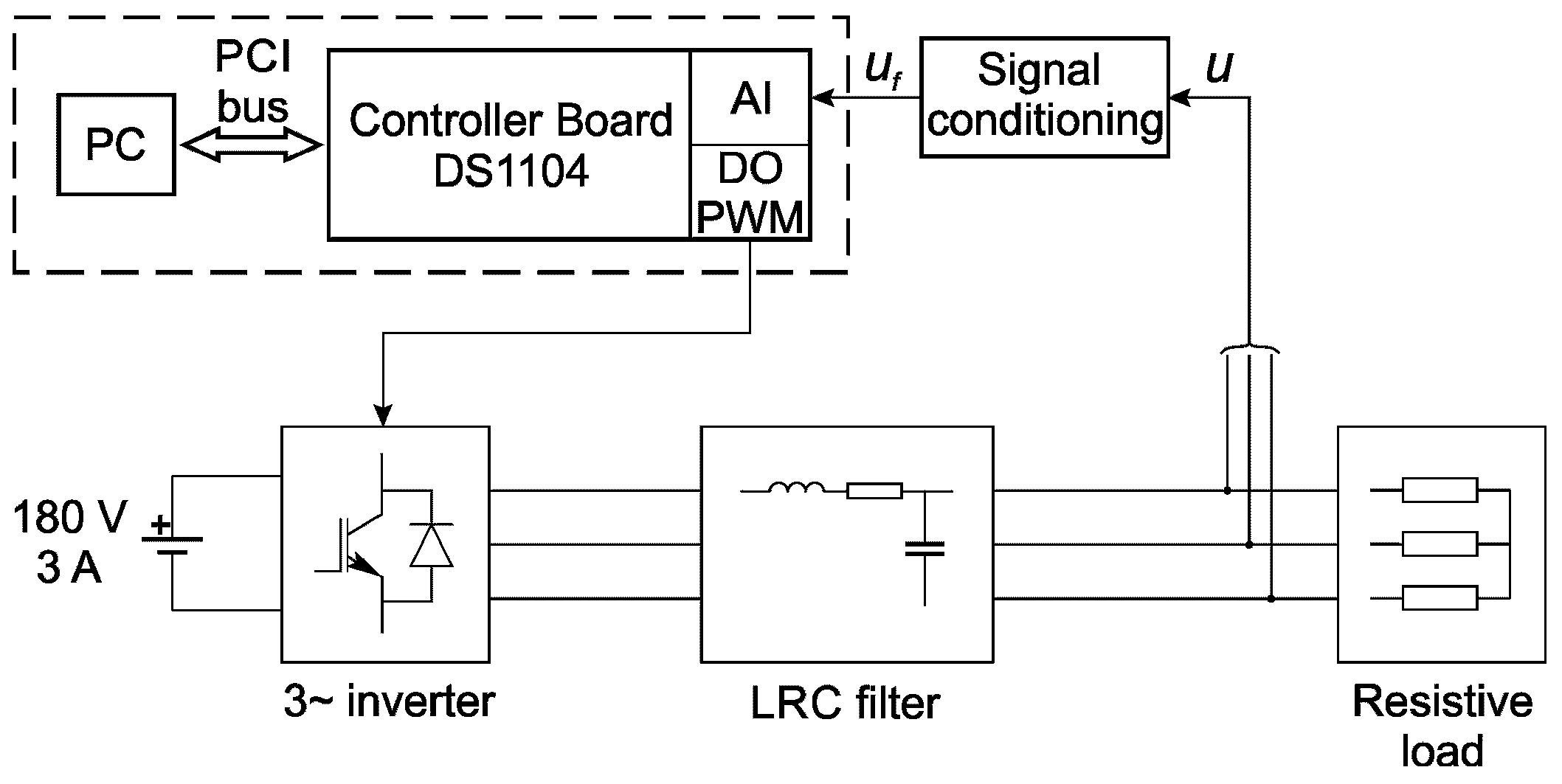
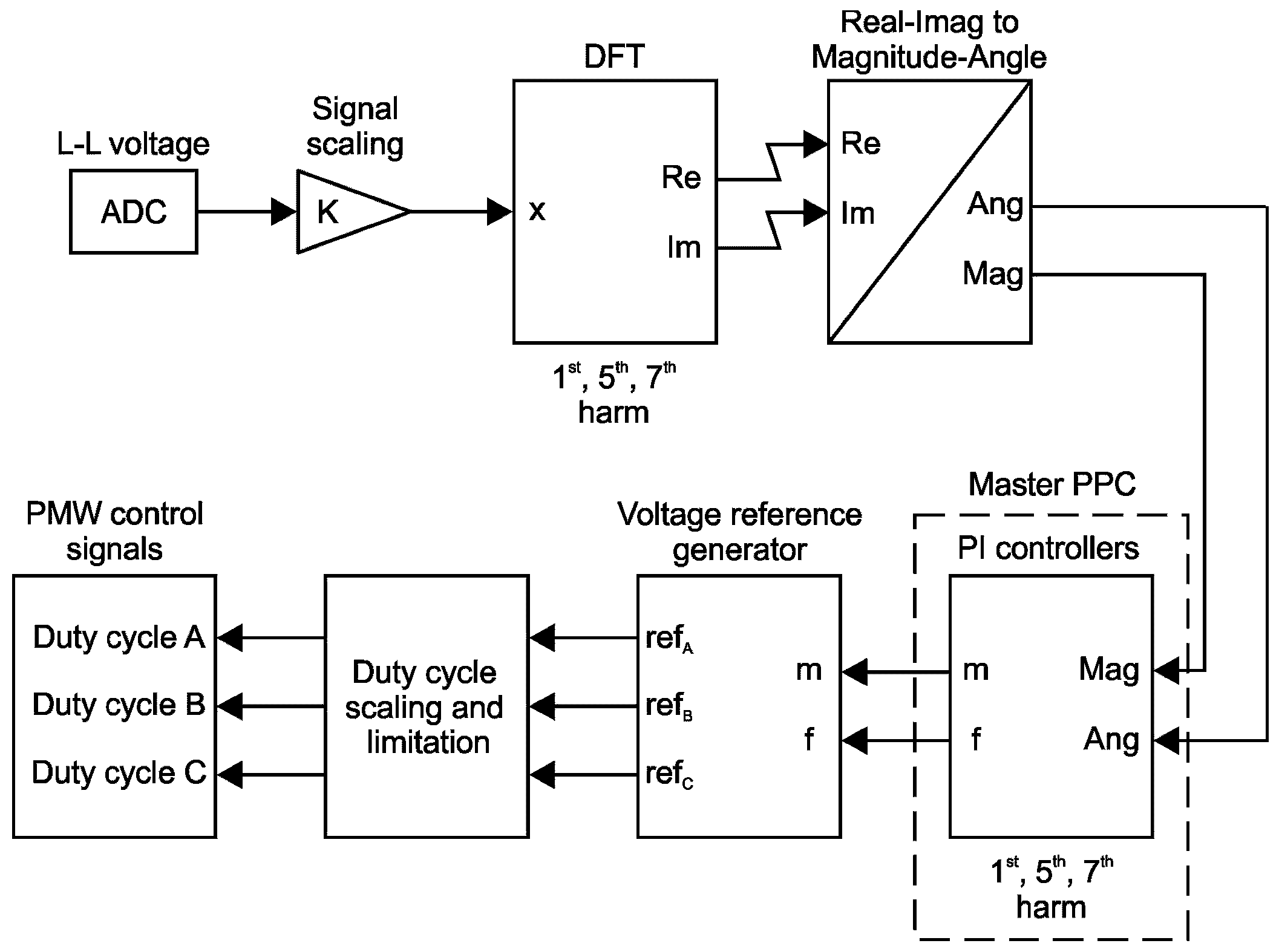
2. System Description
2.1. Discrete Fourier Transform
2.2. Voltage PI Controllers
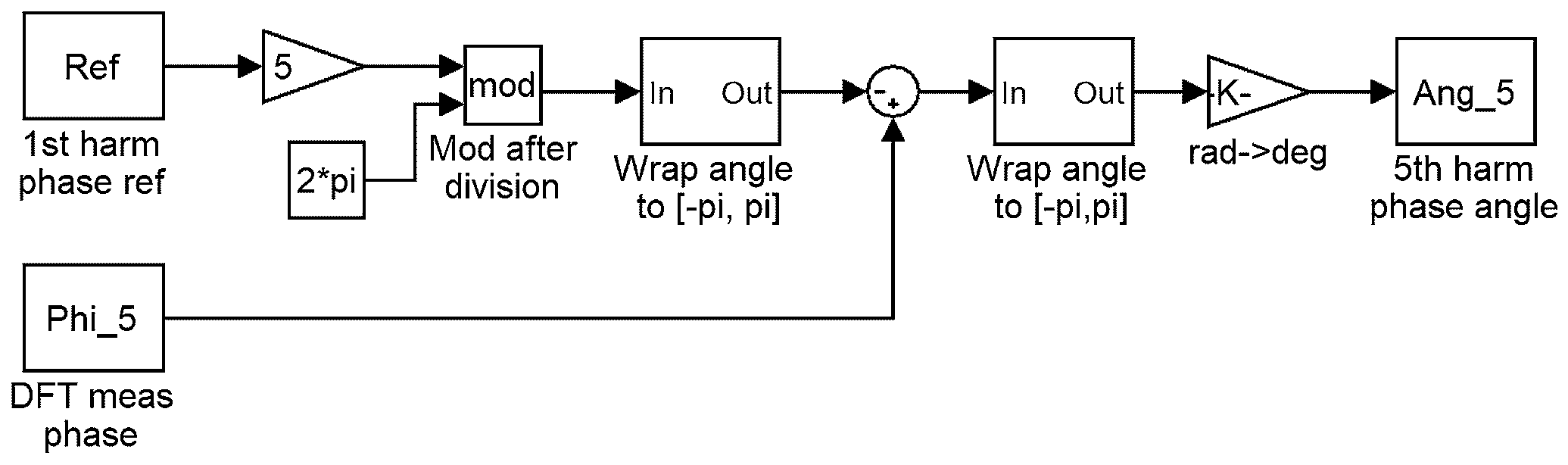
2.3. Voltage Reference Generator
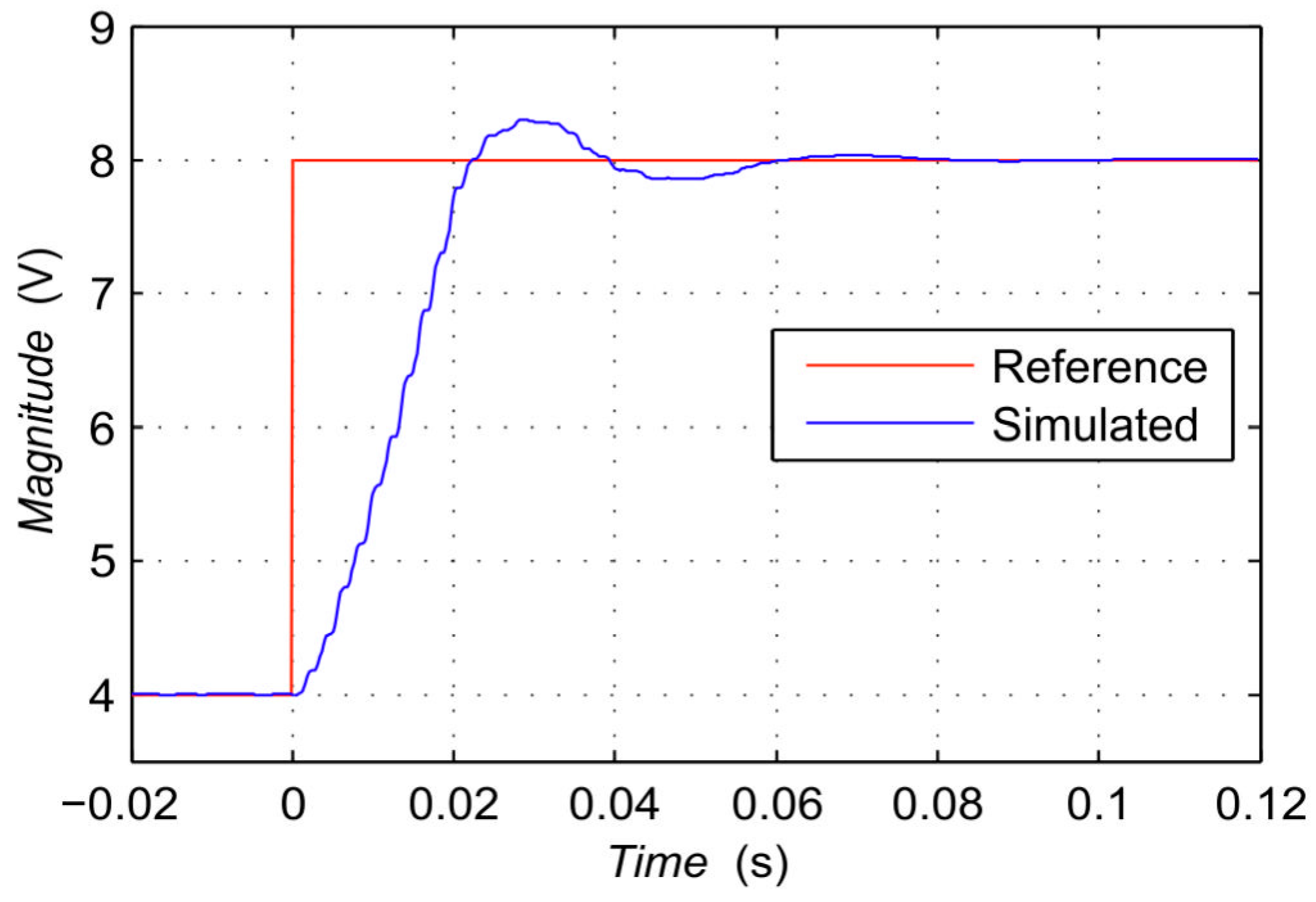
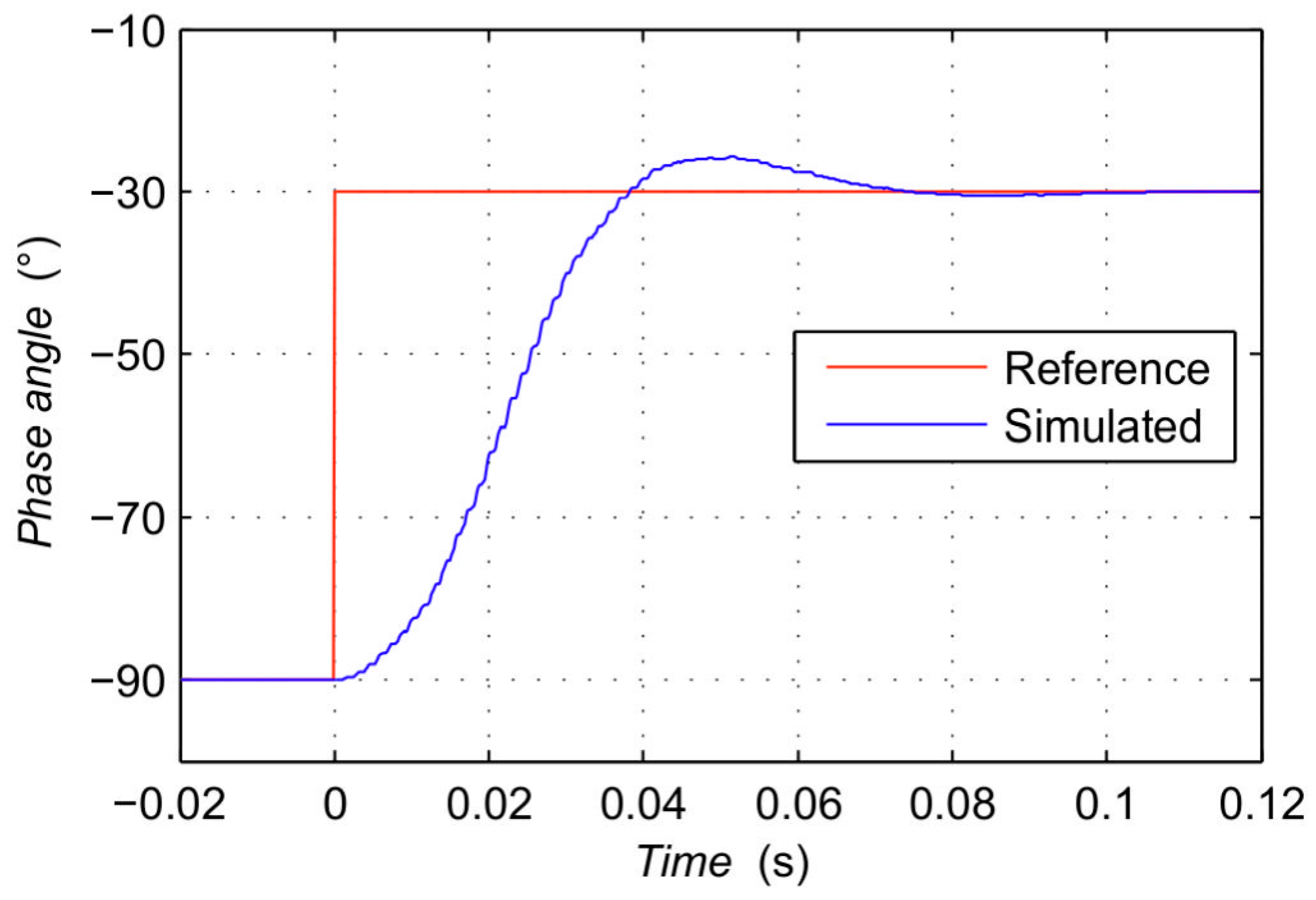
3. Simulation Results
4. Laboratory Setup
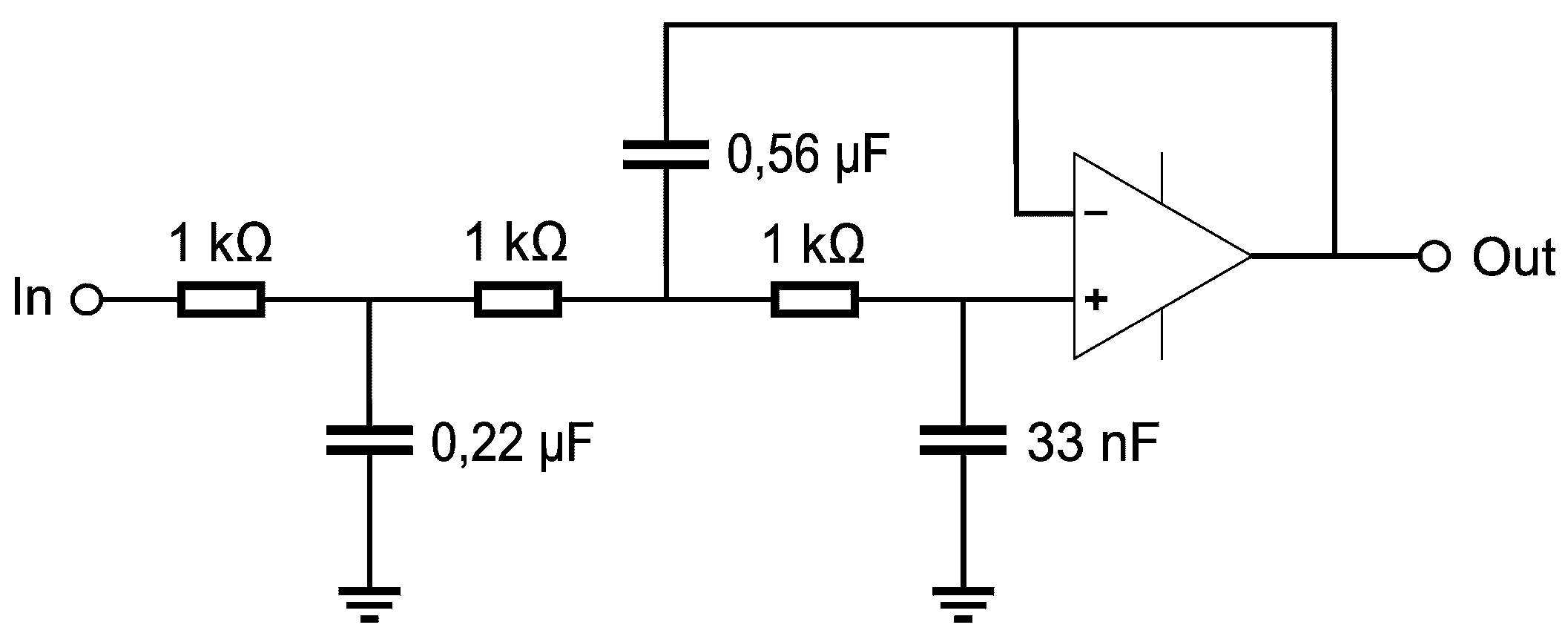
4.1. Anti-Aliasing Filter
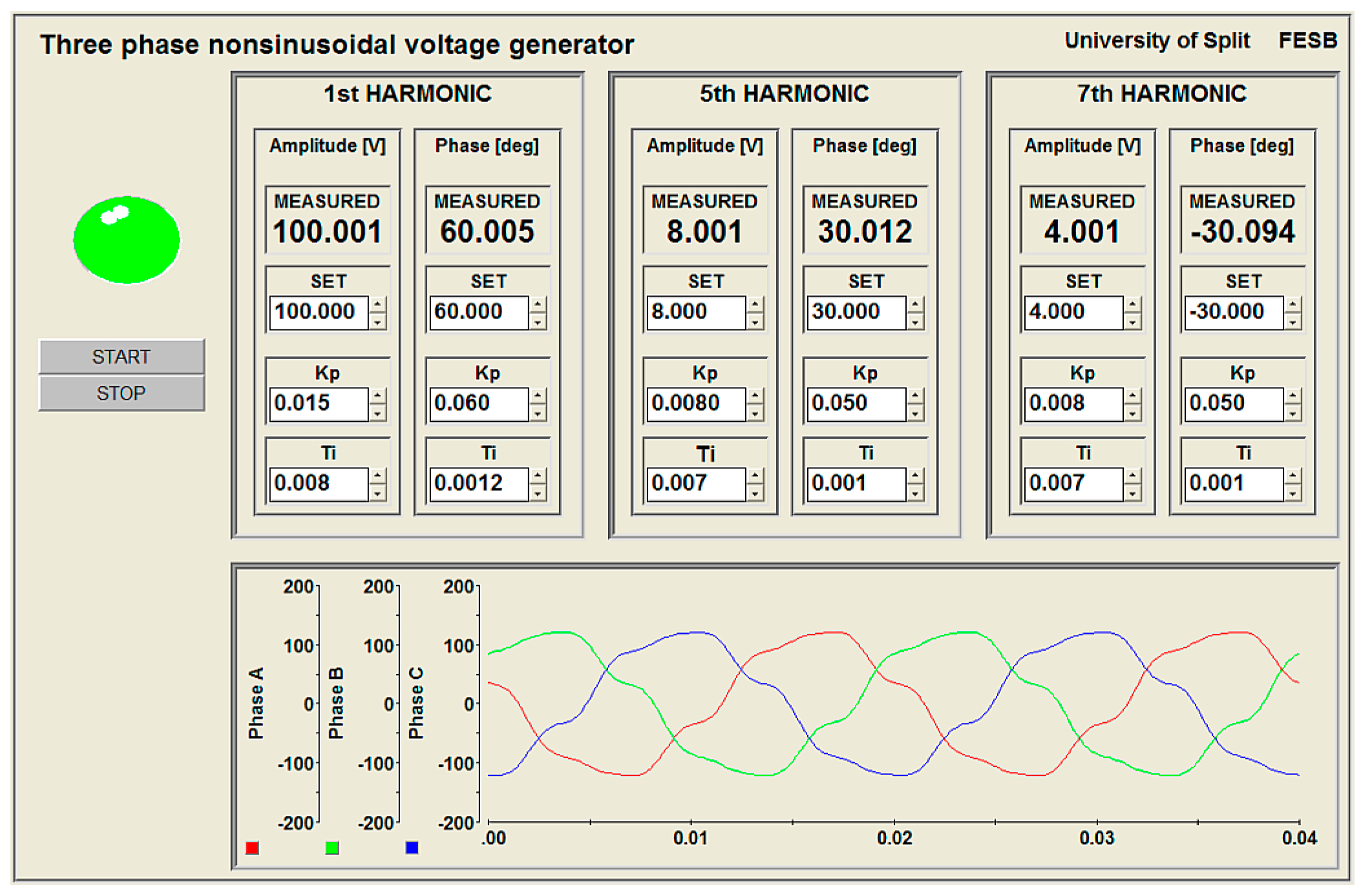
4.2. ControlDesk
5. Algorithm Optimization
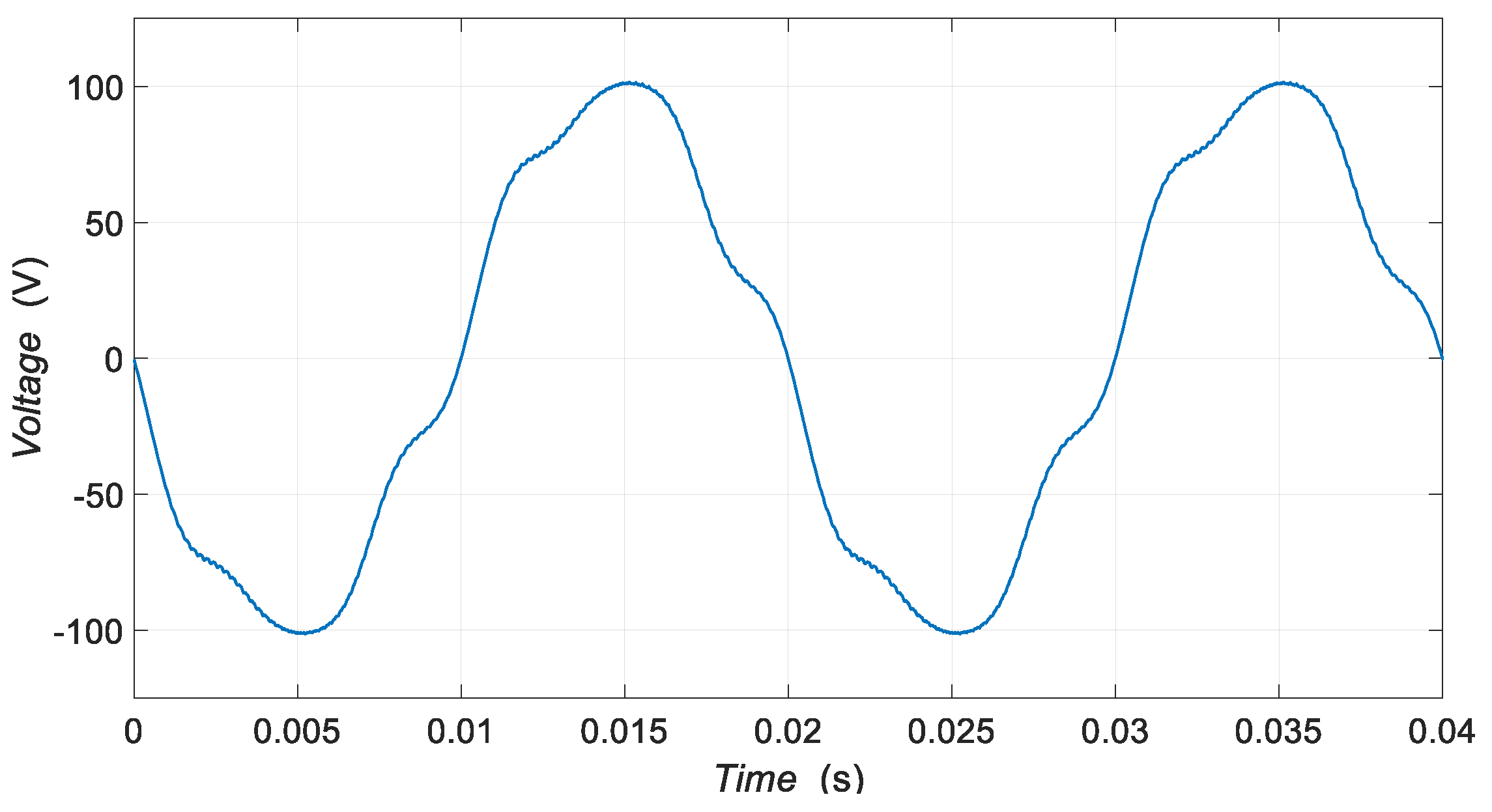
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sharma, K.; Saini, L.M. Performance analysis of smart metering for smart grid: An overview. Renew. Sustain. Energy Rev. 2015, 49, 720–735. [Google Scholar] [CrossRef]
- Arseneau, R.; So, E. Calibration services in support of smart grid applications. In Proceedings of the Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar] [CrossRef]
- Stifter, M.; Cordova, J.; Kazmi, J.; Arghandeh, R. Real-Time Simulation and Hardware-in-the-Loop Testbed for Distribution Synchrophasor Applications. Energies 2018, 11, 876. [Google Scholar] [CrossRef]
- Zhou, N.; Meng, D.; Huang, Z.; Welch, G. Dynamic State Estimation of a Synchronous Machine Using PMU Data—A Comparative Study. IEEE Trans. Smart Grid 2015, 6, 450–460. [Google Scholar] [CrossRef]
- Klaric, M.; Kuzle, I.; Holjevac, N. Wind Power Monitoring and Control Based on Synchrophasor Measurement Data Mining. Energies 2018, 11, 3525. [Google Scholar] [CrossRef]
- Directive 2014/32/EU of the European Parliament and of the Council, Official Journal of the European Union. March 2014. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/HTML/?uri=CELEX: 32014L0032&qid=1484670008365&from=EN (accessed on 22 May 2019).
- Faifer, M.; Ottoboni, R.; Toscani, S.; Cherbaucich, C.; Mazza, P. Metrological characterization of a signal generator for the testing of medium-voltage measurement transducers. IEEE Trans. Instr. Meas. 2015, 64, 1837–1846. [Google Scholar] [CrossRef]
- Aristoy, G.; Trigo, L.; Santos, A.; Brehm, M.; Slomovitz, D. Measuring system for calibrating high voltage instrument transformers at distorted waveforms. In Proceedings of the Conference on Precision Electromagnetic Measurements (CPEM), Ottawa, ON, Canada, 10–15 July 2016. [Google Scholar] [CrossRef]
- Hwang, Y.-S.; Shen, J.-H.; Chen, J.-J.; Fan, M.-R. A THD-reduction high efficiency audio amplifier using inverter-based OTAs with filter-output feedback. Microelectron. J. 2013, 45, 102–109. [Google Scholar] [CrossRef]
- Jasielski, J.; Kuta, S.; Machowski, W.; Kolodziejski, W. Hybrid DPWM implementation using coarse and fine programmable ADLL. Microelectron. J. 2014, 45, 1202–1211. [Google Scholar] [CrossRef]
- Topalis, F.V.; Gonos, I.F.; Vokas, G.A. Arbitrary waveform generator for harmonic distortion tests on compact fluorescent lamps. Measurement 2001, 30, 257–267. [Google Scholar] [CrossRef]
- Manito, A.; Bezerra, U.; Tostes, M.; Matos, E.; Carvalho, C.; Soares, T. Evaluating Harmonic Distortions on Grid Voltages Due to Multiple Nonlinear Loads Using Artificial Neural Networks. Energies 2018, 11, 3303. [Google Scholar] [CrossRef]
- Aurilio, G.; Gallo, D.; Landi, C.; Luiso, M. AC electronic load for on-site calibration of energy meters. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Minneapolis, MN, USA, 6–9 May 2013; pp. 768–773. [Google Scholar] [CrossRef]
- Amicone, D.; Bernieri, A.; Ferrigno, L.; Laracca, M. A smart add-on device for the remote calibration of electrical energy meters. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Singapore, 5–7 May 2009; pp. 1599–1604. [Google Scholar] [CrossRef]
- Georgakopoulos, D.; Wright, P.S. Calibration of energy and power meters under non-sinusoidal conditions. IEE Proc.-Sci. Meas. Technol. 2006, 153, 241–247. [Google Scholar] [CrossRef]
- Montano, J.C.; Leon, C.; Garcia, A.; Lopez, A.; Monedero, I.; Personal, E. Random generation of arbitrary waveforms for emulating three-phase systems. IEEE Trans. Ind. Electr. 2012, 59, 4032–4040. [Google Scholar] [CrossRef]
- Delle Femine, A.; Gallo, D.; Landi, C.; Luiso, M. Advanced instrument for field calibration of electrical energy meters. IEEE Trans. Instr. Meas. 2009, 58, 618–625. [Google Scholar] [CrossRef]
- Slomovitz, D.; Trigo, L. A power standard system for calibration of power analyzers. In Proceedings of the IEEE PES Innovative Smart Grid Technologies (ISGT LATAM), Montevideo, Uruguay, 5–7 October 2015. [Google Scholar] [CrossRef]
- First Work Steps; dSPACE GmbH: Paderborn, Germany, 2007.
- Sundararajan, D. The Discrete Fourier Transform: Theory, Algorithms and Applications; World Scientific Pub Co Inc.: Singapore, 2001; pp. 31–66. [Google Scholar]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters; IEEE Press: Piscataway, NJ, USA, 2003; pp. 95–337. [Google Scholar]
- Bosnic, J.A.; Despalatovic, M.; Petrovic, G.; Majic, G. Three-phase programmable sinusoidal voltage generator. In Proceedings of the 1st International Colloquium Smart Grid Metrology, Split, Croatia, 24–27 April 2018. [Google Scholar]
- TA057. Pico Technology: Cambridgeshire, UK. Available online: https://www.picoauto.com/products/electric-and-hybrid-vehicle/25-mhz-1400-v-differential-oscilloscope-probe-x20-x200 (accessed on 15 April 2019).
- Williams, A.; Taylor, F. Electronic Filter Design Handbook; McGraw-Hill: New York, NY, USA, 2006; pp. 9–441. [Google Scholar]
- Electromagnetic compatibility (EMC)—Part 4-30: Testing and measurement techniques—Power quality measurement methods, IEC 61000-4-30. 2015. Available online: https://webstore.iec.ch/publication/21844 (accessed on 22 May 2019).
- Majic, G.; Despalatovic, M.; Verunica, K. Influence of dead time on voltage harmonic spectrum of grid-connected PWM-VSC with LCL filter. In Proceedings of the 10th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Bydgoszcz, Poland, 29 June–1 July 2016; pp. 228–233. [Google Scholar] [CrossRef]
- Majic, G.; Despalatovic, M.; Terzic, B. LCL Filter Design Method for Grid-Connected PWM-VSC. J. Electr. Eng. Technol. 2017, 12, 1945–1954. [Google Scholar] [CrossRef]


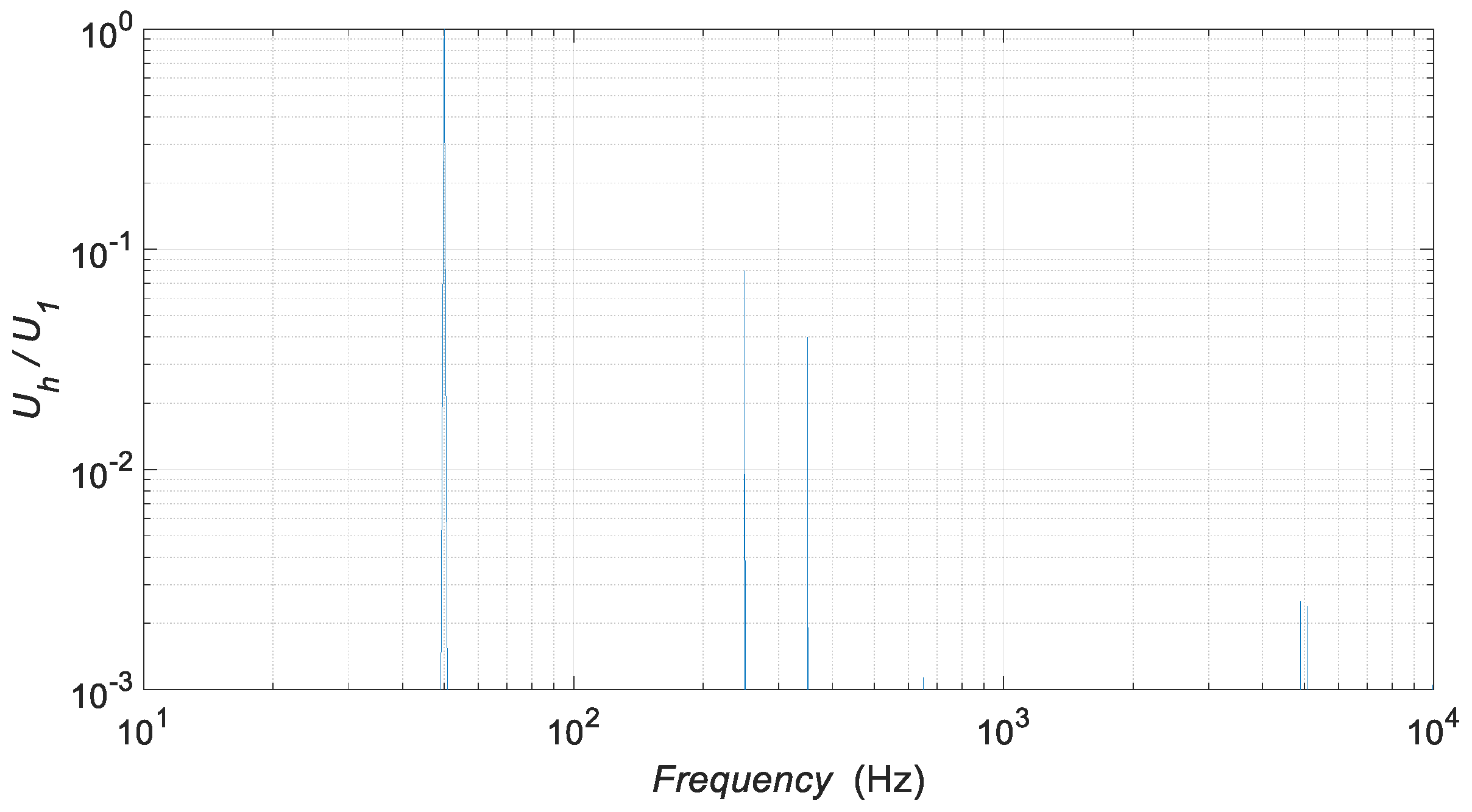
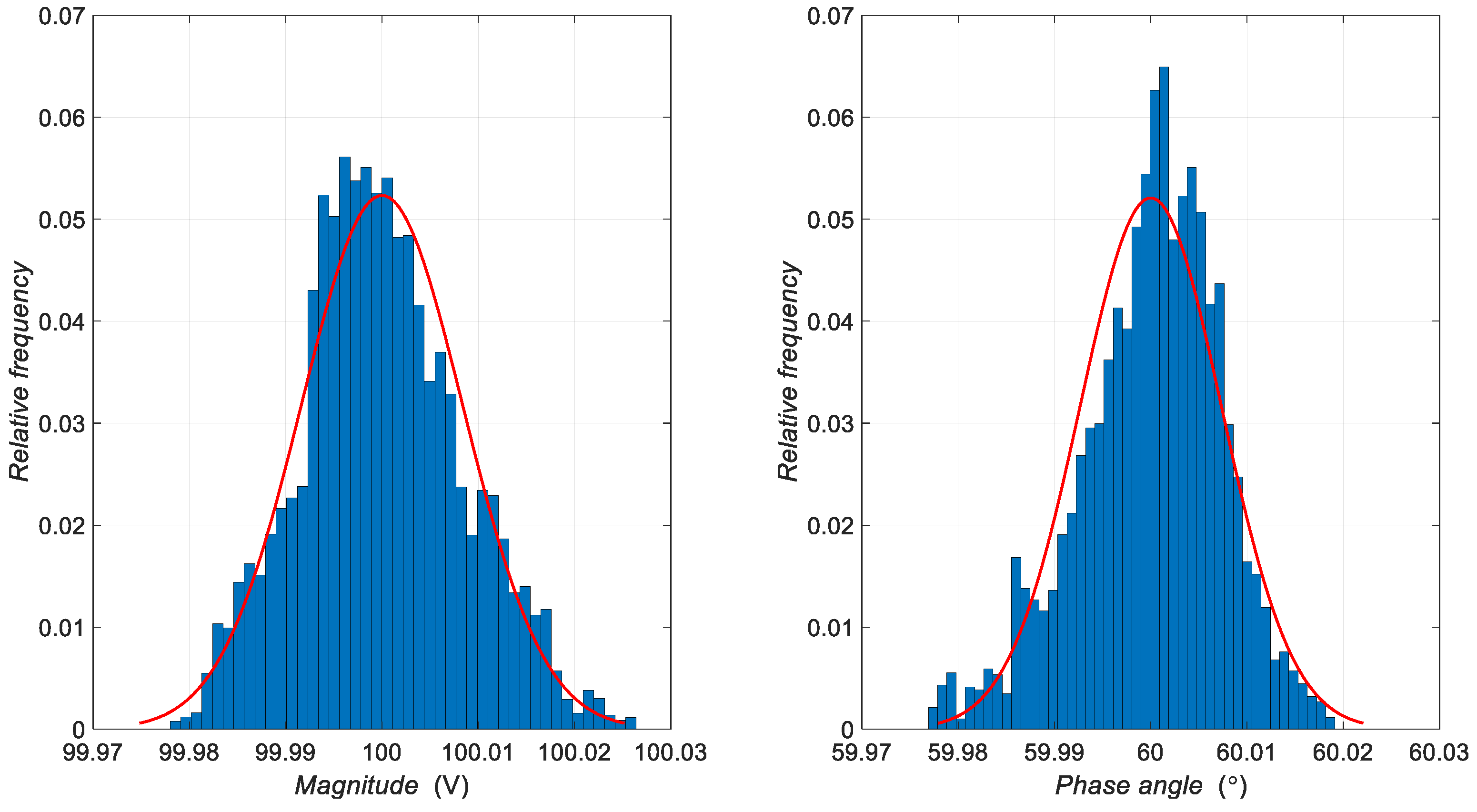
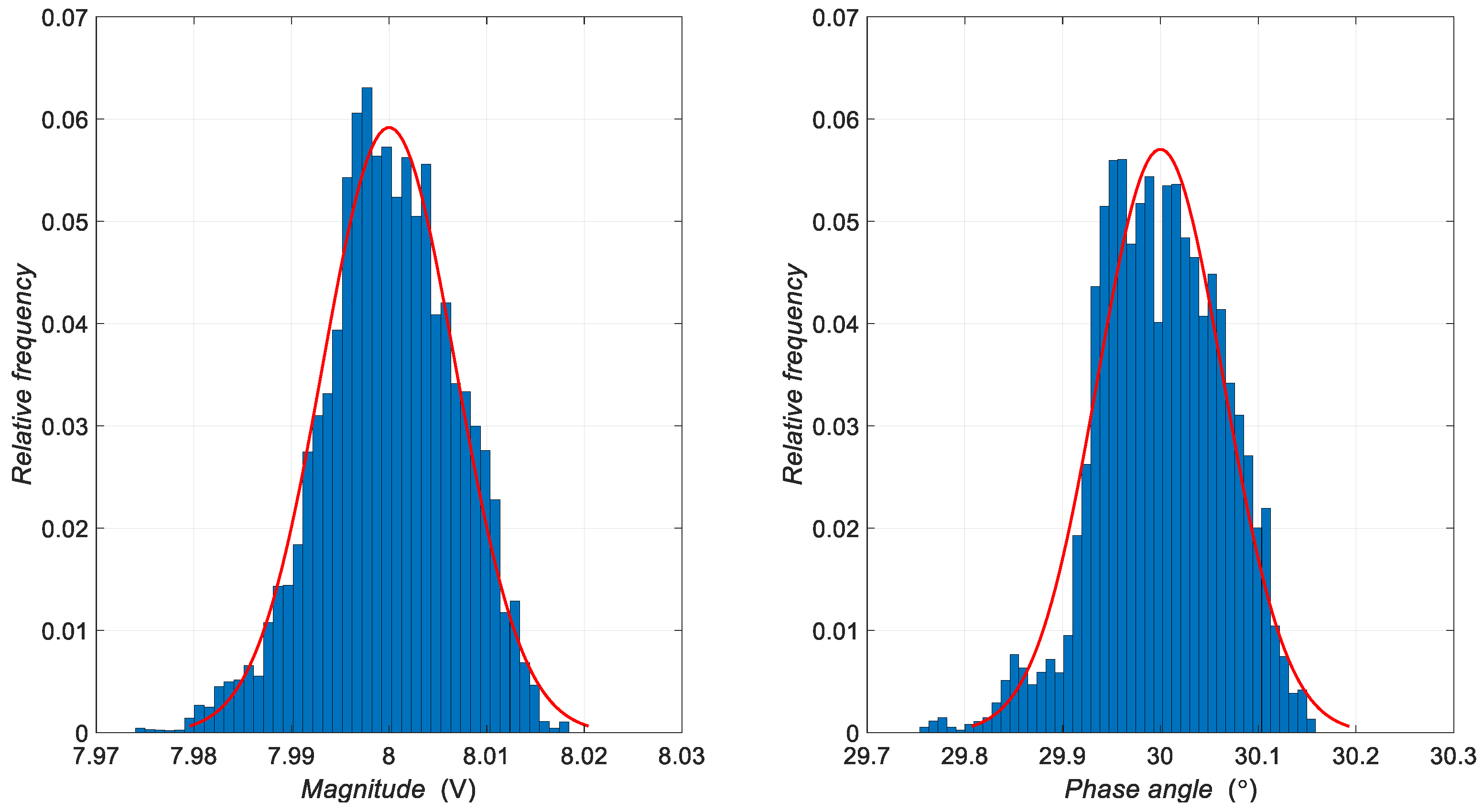
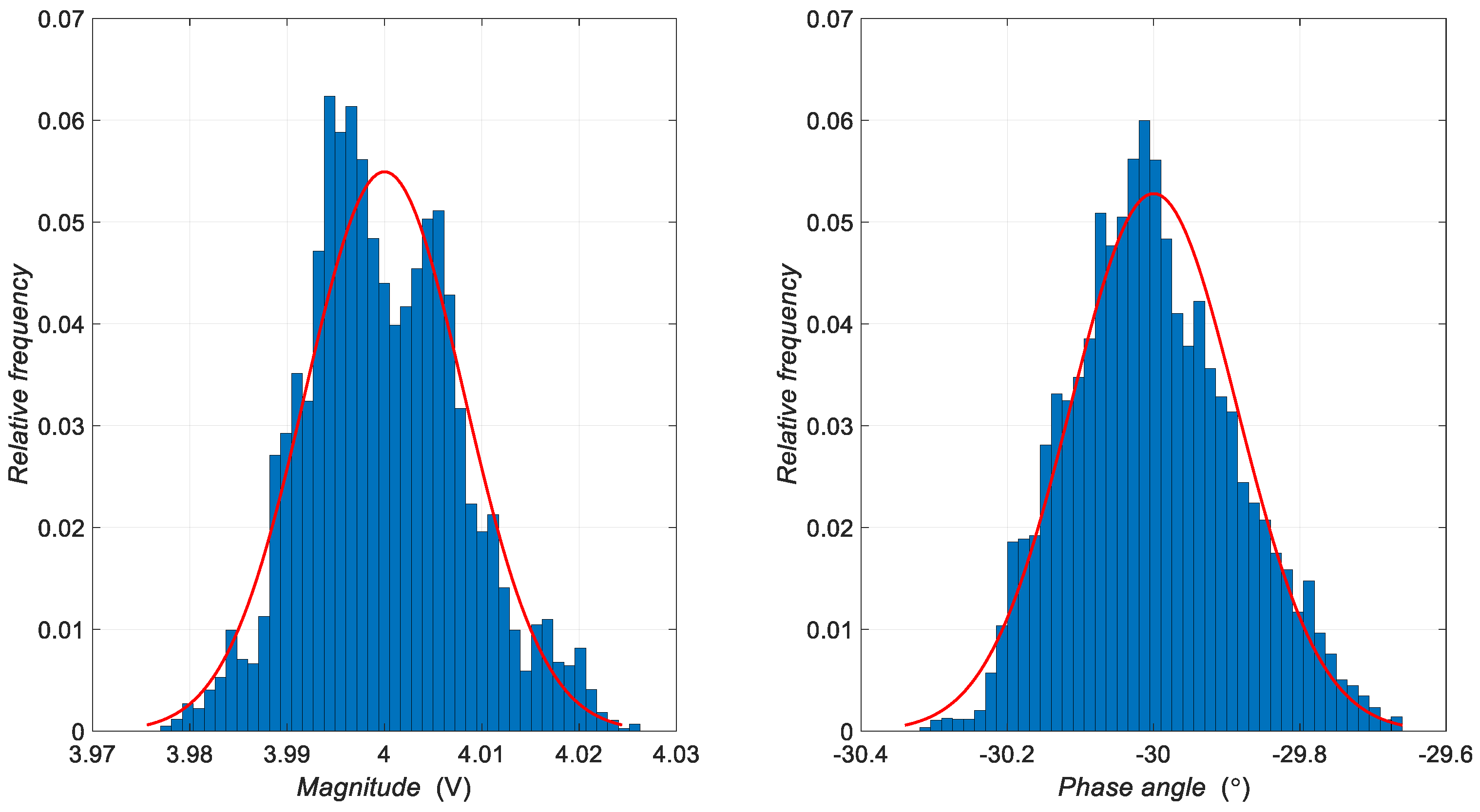
| Harmonic Order | Parameter | Mean | Standard Deviation |
|---|---|---|---|
| 1 | Magnitude Phase angle | 100 V 60 ° | 0.0084 V 0.0074 ° |
| 5 | Magnitude Phase angle | 8 V 30 ° | 0.0068 V 0.0643 ° |
| 7 | Magnitude Phase angle | 4 V –30 ° | 0.0081 V 0.1133 ° |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrovic, G.; Bosnic, J.A.; Majic, G.; Despalatovic, M. A Design of PWM Controlled Calibrator of Non-Sinusoidal Voltage Waveforms. Energies 2019, 12, 1966. https://doi.org/10.3390/en12101966
Petrovic G, Bosnic JA, Majic G, Despalatovic M. A Design of PWM Controlled Calibrator of Non-Sinusoidal Voltage Waveforms. Energies. 2019; 12(10):1966. https://doi.org/10.3390/en12101966
Chicago/Turabian StylePetrovic, Goran, Juraj Alojzije Bosnic, Goran Majic, and Marin Despalatovic. 2019. "A Design of PWM Controlled Calibrator of Non-Sinusoidal Voltage Waveforms" Energies 12, no. 10: 1966. https://doi.org/10.3390/en12101966
APA StylePetrovic, G., Bosnic, J. A., Majic, G., & Despalatovic, M. (2019). A Design of PWM Controlled Calibrator of Non-Sinusoidal Voltage Waveforms. Energies, 12(10), 1966. https://doi.org/10.3390/en12101966





