Evaluation and Optimization of the Oil Jet Lubrication Performance for Orthogonal Face Gear Drive: Modelling, Simulation and Experimental Validation

Abstract

The oil jet lubrication performance of a high-speed and heavy-load gear drive is significantly influenced and determined by the oil jet nozzle layout, as there is extremely limited meshing clearance for the impinging oil stream and an inevitable blocking effect by the rotating gears. A novel mathematical model for calculating the impingement depth of lubrication oil jetting on an orthogonal face gear surface has been developed based on meshing face gear theory and the oil jet lubrication process, and this model contains comprehensive design parameters for the jet nozzle layout and face gear pair. Computational fluid dynamic (CFD) numerical simulations for the oil jet lubrication of an orthogonal face gear pair under different nozzle layout parameters show that a greater mathematically calculated jet impingement depth results in a greater oil volume fraction and oil pressure distribution. The influences of the jet nozzle layout parameters on the lubrication performance have been analyzed and optimized. The relationship between the measured tooth surface temperature from the experiments and the corresponding calculated impingement depth shows that a lower temperature appears in a situation with a greater impingement depth. Good agreement between the mathematical model with the numerical simulation and the experiment validates the effectiveness and accuracy of the method for evaluating the face gear oil jet lubrication performance when using the impingement depth mathematical model.

1. Introduction

Large amounts of energy will be lost in overcoming the internal friction between the meshing gears, and this will seriously reduce the mechanical efficiency and performance of the transmission system, especially for aeronautical gears under high-speed and heavy-load operation conditions. Face gear drives are a new type of transmission in which the involute cylindrical gear meshes with the face gear. Face gear drives have been widely used in aeronautical transmission systems, as they offer the advantages of a large contact ratio, good power splitting effect, compact structure, insensitivity to installation errors, etc. [1,2,3,4]. Due to the high-speed and heavy-load conditions in aeronautical transmission applications, as well as the space limitations for installation and working, face gear drives will inevitably produce a large amount of heat and result in energy loss. An effective way to solve these problems is to lubricate the face gear drivers with an oil jet. If the lubrication is insufficient, gear meshing will occur under starved or even dry operation and ultimately lead to tooth surface scuffing, pitting and failure damage. Therefore, it is of great importance to investigate the lubrication performance of face gear drives and optimize the jet nozzle layout.

Currently, three primary methods have been developed to investigate the oil jet lubrication performance of transmission gears. One method is to use numerical simulations or experiments. For example, hydrodynamic models of spur gears were established to investigate the variation of oil volume and pressure through CFD simulation to optimize the jet parameters [5,6]. High-speed infrared testers and infrared sensors have been adopted to measure the instantaneous tooth temperature to study the influence of the speed, load and jet location on the lubrication performance [7,8]. Ouyang et al. [9] proposed a novel model of a spur gear pair based on friction dynamics theory and studied the lubrication performance in the high-speed condition by CFD simulation. Massini et al. [10] exploited a novel rotating test rig to analyze oil jet lubrication through high-speed visualizations. Zhao et al. [11] proposed a simplified model based on CFD method for investigating the ripple source of gear pumps. Moreover, to analyze the transient temperature behavior of spiral bevel gears, Gan et al. [12] proposed a method combining the mixed elastohydrodynamic lubrication with the finite element method and conducted the thermal analysis using the CFD method. Another method is to calculate the oil film thickness and film pressure based on a theoretical equation. For example, Poulios et al. [13] used a quadratic B-spline basis function to obtain a more accurate oil film thickness and pressure field. Furthermore, Wang et al. [14] established formulas for the contact path of the face gear loaded tooth contact analysis (LTCA) and the dimensionless face gear isothermal elastohydrodynamic lubrication (EHL) to obtain the variation in the lubricating oil film thickness and oil film pressure. Following Wang’s work, Liu et al. [15] established a comprehensive mechanical efficiency model of a helical gear pair and evaluated the tribological performance in terms of the average film thickness, the friction coefficient, the mechanical power loss, etc. A deterministic model combining contact mechanics with pure extrusion lubrication was established by Xu et al. [16], so as to investigate the extrusion effect of the oil film under the transient boundary lubrication condition. Ahmed et al. [17] presented an automatic locally adaptive finite element solver for fully coupled EHL point contact problems to significantly improve the accuracy of the elastic deformation solution. A calculating model for the full tooth surface flash temperature distribution for face gear drives was established to optimize the anti-scuffing tooth modification schedule for face gear drives based on the Blok flash temperature formula [18], and this model improved the anti-scuffing capacity of face gear drives. Thiagarajan et al. [19] proposed a mixed-thermoelastohydrodynamic (TEHD) model for investigating the effects of surface roughness, fluid structure and thermal interaction on the mixed lubrication in the regions of low film thickness. The final method is to analyze the impingement characteristic of lubricating oil on the tooth surface. Previous research on this aspect is as follows, but only spur and helical gears were studied: Akin et al. [20,21] deduced the formulas for the oil jet impingement depth on spur and helical gears and studied the influence of the offset distance, jet angle and jet velocity on the impingement depth. Ambrose et al. [22] used the lattice Boltzmann method (LBM) to study the oil impingement on a spur gear and analyzed the effect of the oil feed delivery rate on the spreading of the oil jet on the tooth and the splashing profiles.

However, as far as the relevant studies are concerned, it could take a long time to analyze and evaluate the oil jet lubrication performance of gears using CFD simulations or experiments. There are still a few assumptions in solving the equations of the oil film thickness and pressure, so the results are not accurate enough. In addition, until now, only the oil jet impingement depth on the tooth surface of the spur or helical gear pair has been studied. Furthermore, there are relatively few studies on the influence of the jet nozzle layout parameters on the lubrication performance and the optimization of the nozzle layout. Therefore, first, a novel mathematical model for the impingement depth calculation for the orthogonal face gear is established based on face gear meshing theory [23], the involute function of the spur gear [24], and the spatial positional relationship of the face gear tooth surface. Subsequently, the oil volume fraction and oil pressure are obtained by CFD simulation to validate the effectiveness and accuracy of the mathematical model. Furthermore, the influence of the nozzle layout parameters on the impingement depth and lubrication performance is analyzed to optimize the nozzle layout. Finally, the steady-state temperature of the gear tooth surface is measured experimentally to analyze the relationship between the impingement depth and the tooth surface temperature. The experiments can also validate the impingement depth mathematical model and provide a method and technique for oil jet lubrication performance evaluation and optimization for various face gears in practical applications.

2. Mathematical Model

The oil jet impingement depth for the face gear is defined as the linear distance from the impingement point on the tooth surface to the gear addendum, as shown in Figure 1.

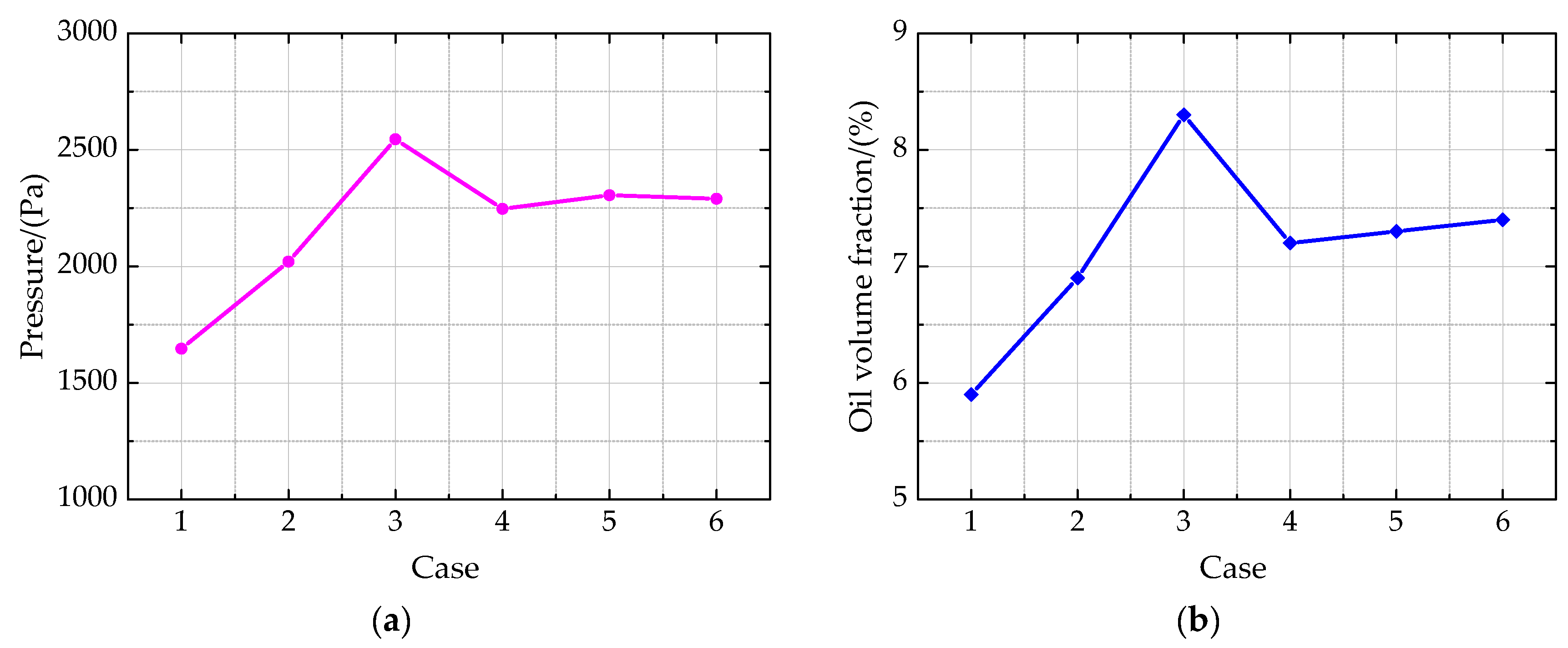
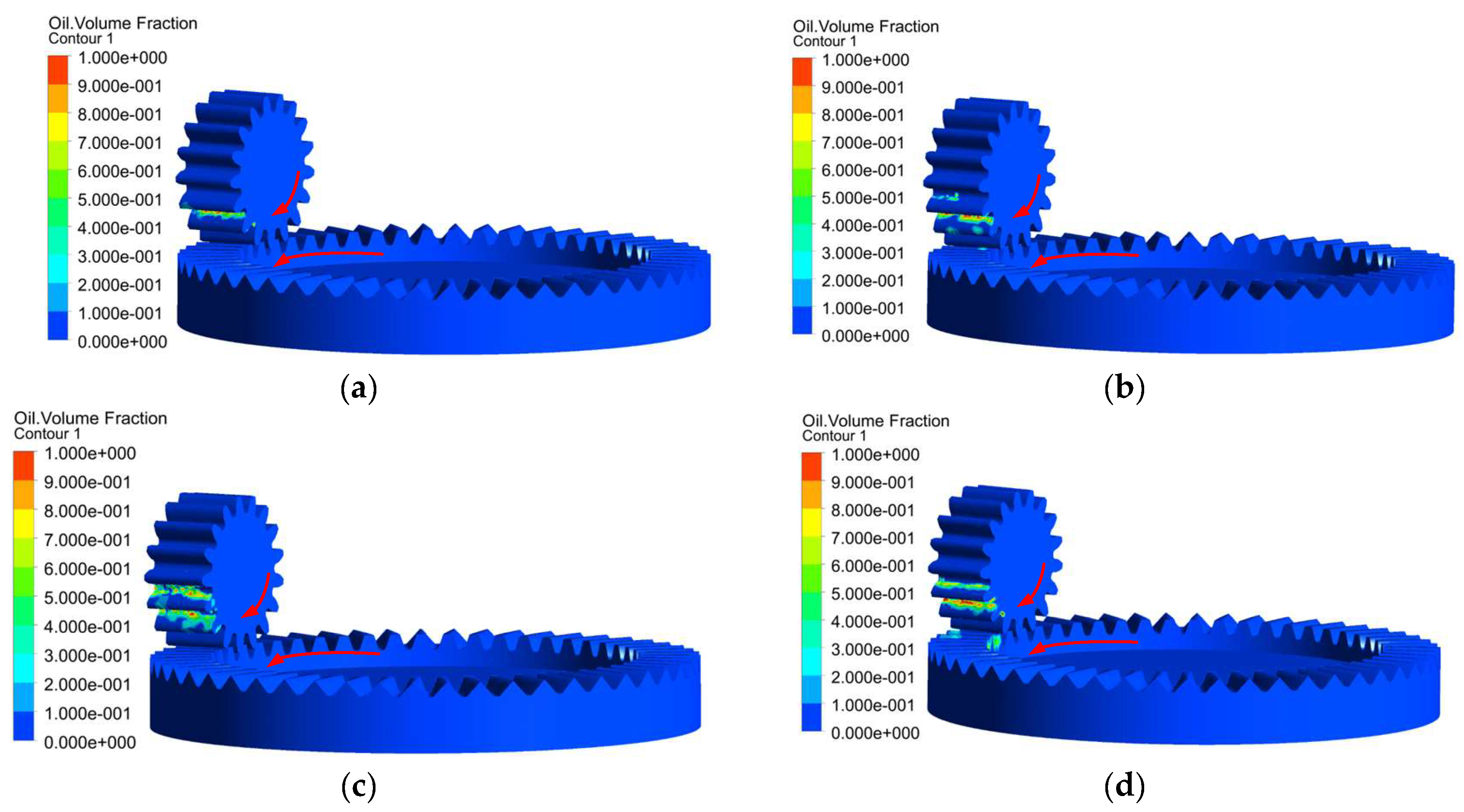
The derivation steps for the mathematical model of the impingement depth are as follows:

• Based on the meshing theory of a face gear, the space coordinate system of the orthogonal face gear is defined.
• The initial position parameters (t₀ = 0) of the pinion and the face gear have been established separately using an involute function of the spur gear and the spatial position of the face gear tooth surface. After a period of time (t₁ = t), the geometrical positions of the face gear pair and jet stream are calculated.
• Since the meshing time of face gear is equal to the time of jet stream reaching the tooth surface, the impingement depth on the pinion and the face gear can be obtained by solving the simultaneous equations.

2.1. Definitions of Nozzle Layout Parameters

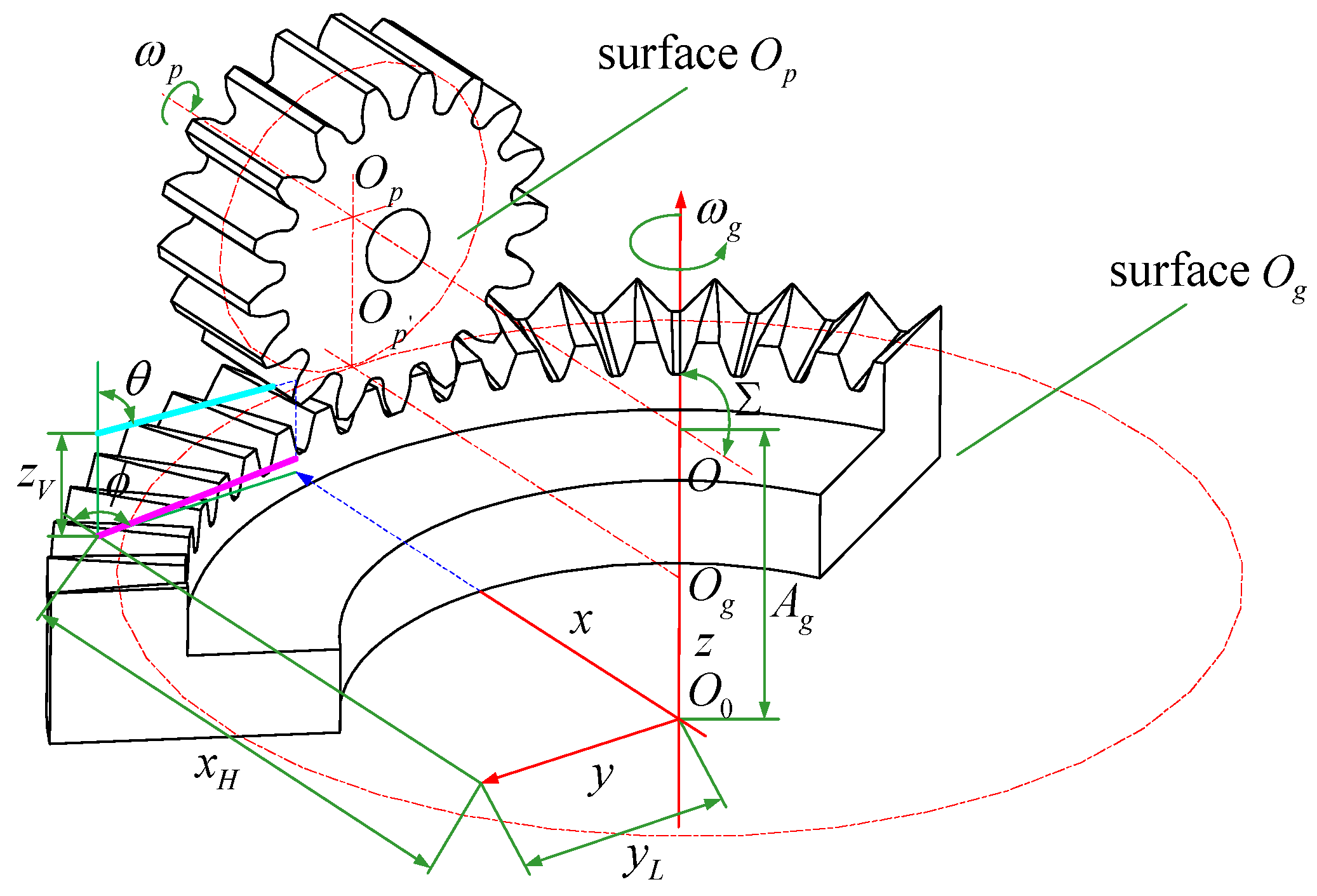
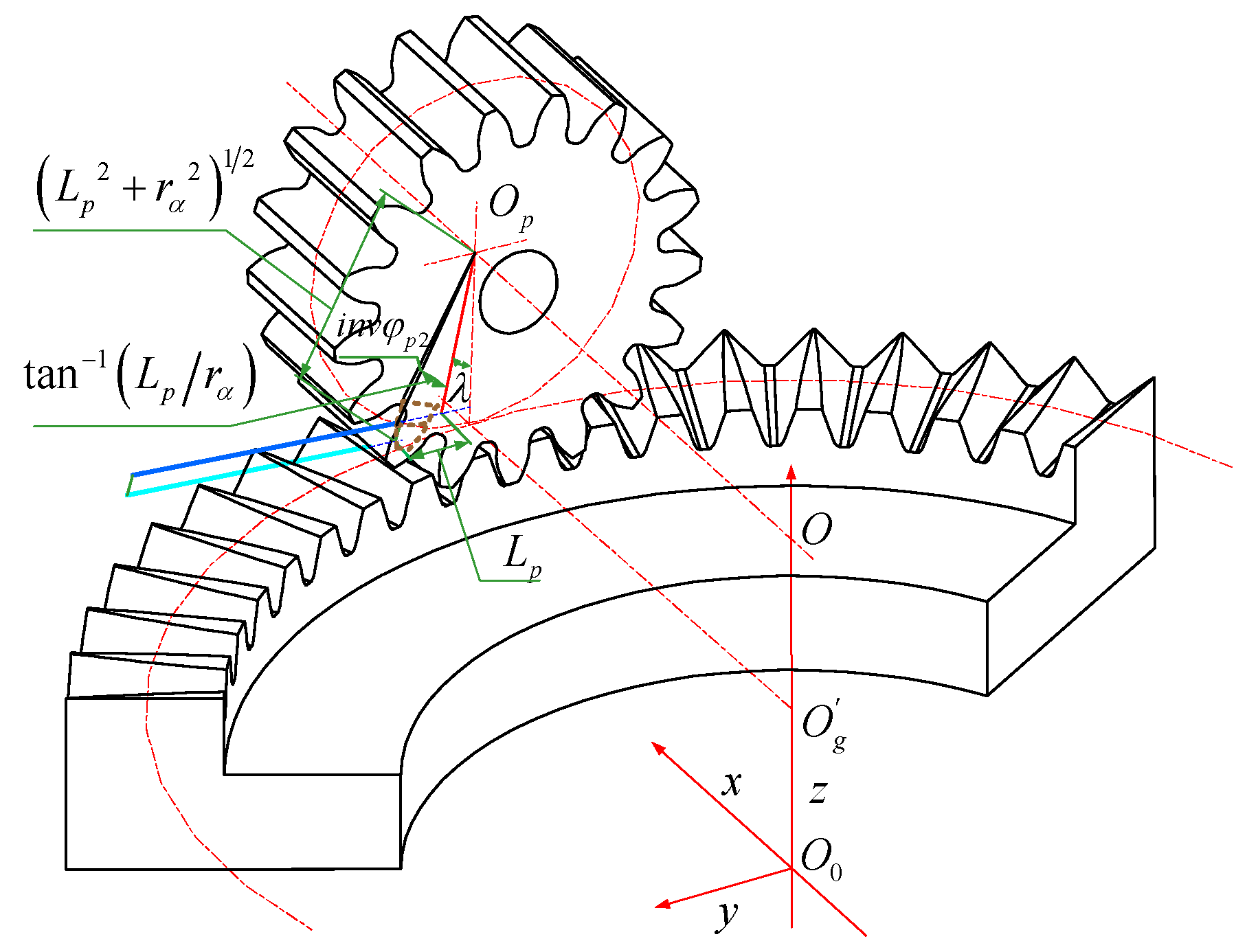
For the orthogonal face gear drive, the tooth contact type is point contact, and the meshing process can be regarded as the involute spur gear meshing with the rack at different shaft cross sections [25]. The space coordinate system is set up as shown in Figure 2. At this time, there is a circle on the pinion pitch cylinder rolling purely with a circle along the direction of the face gear radius. Point $O_0$ is the gear coordinate origin, representing the center of the gear-locating surface. The x-axis represents the intersection line between the symmetry surface and the locating surface of the face gear. The z-axis represents the axis of the face gear. The y-axis can be determined by the right-hand rule. Point $O$ represents the intersection point of the face gear axis and the pinion axis. Furthermore, points $O_p$ and $O_g$ represent the centers of the surfaces through impingement points and perpendicular to the pinion axis and the face gear axis, respectively.

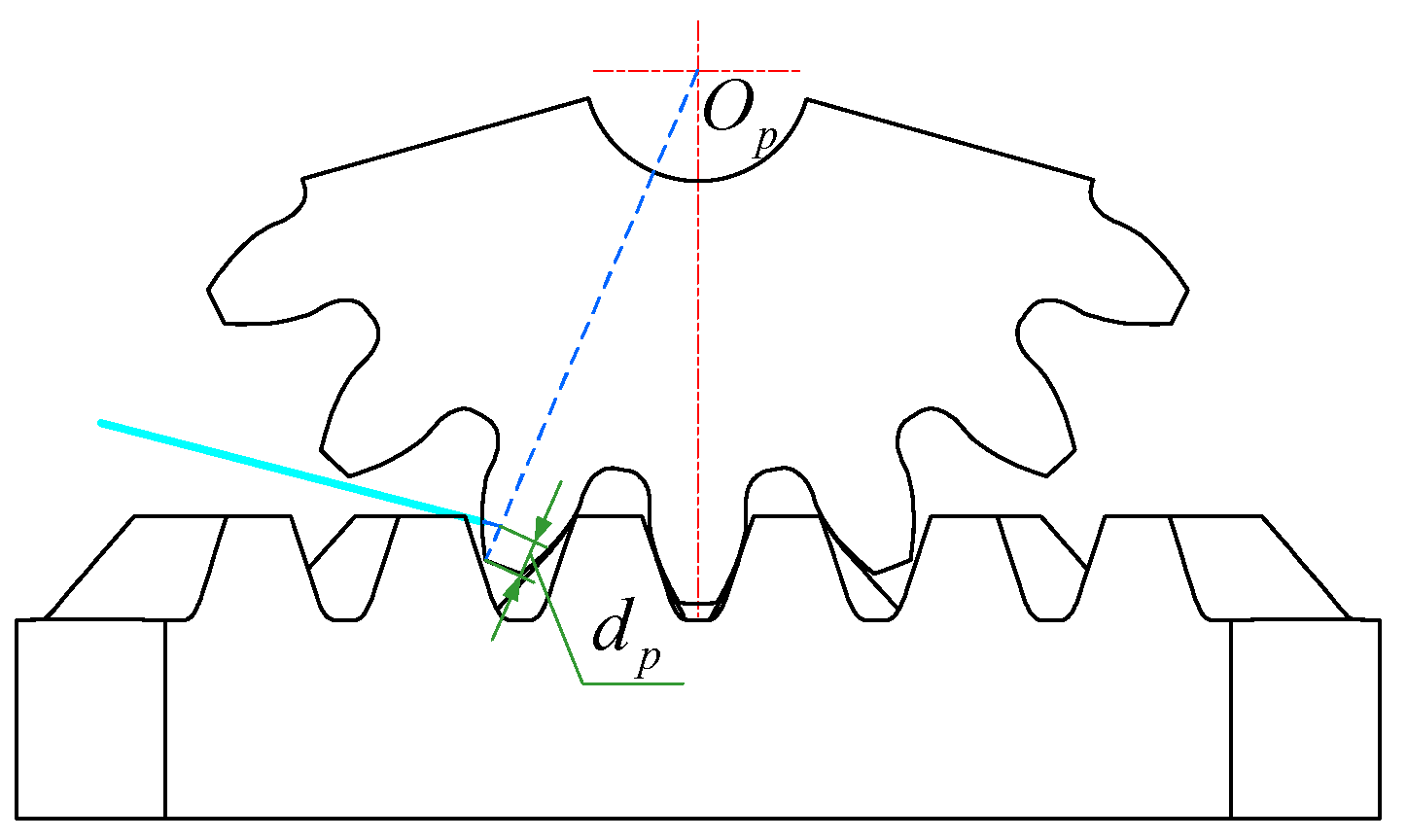
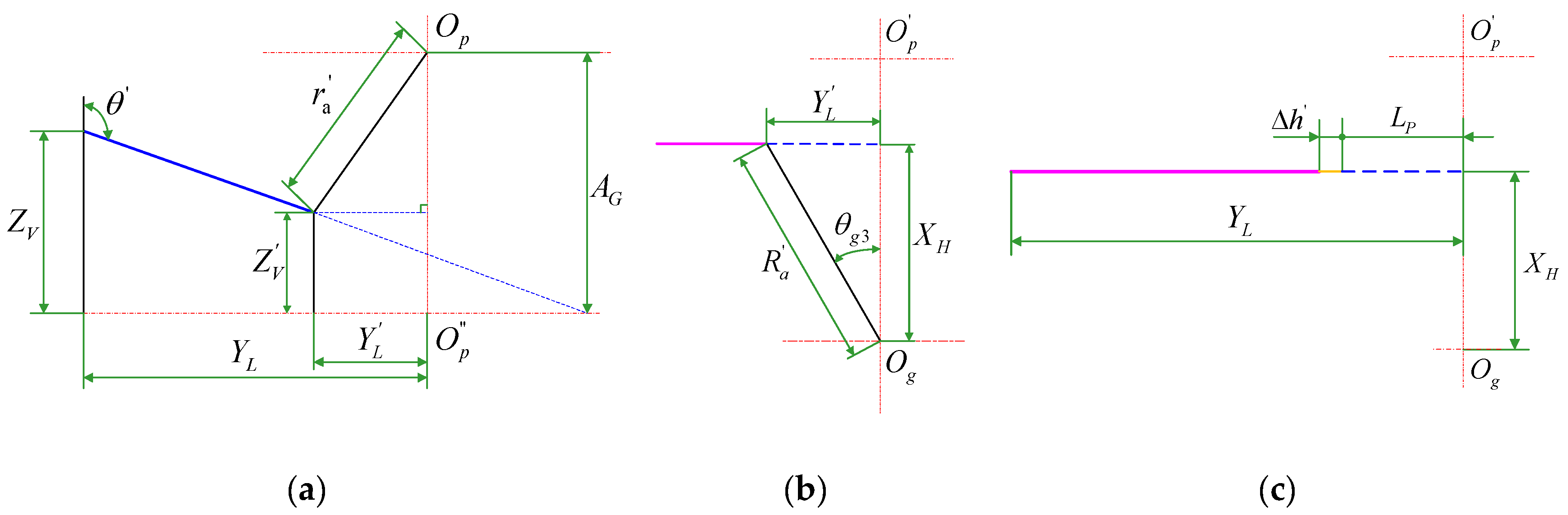
As shown, the impingement depth is directly relevant to the jet orientation parameters $x_H,y_L,z_V,\theta$ and $\varphi$. $x_H,y_L,z_V$ denote the nozzle exit position; the parameter $\theta$ denotes the angle between the jet stream and the z-axis, which is always restricted to $\pi /2\le \theta \le \pi /2$, and the parameter $\varphi$ denotes the angle between the jet stream projection line on the $x{O}_{g}y$ plane and the x-axis. Since the pinion is an involute spur gear with a symmetrical structure, this paper focuses on the case that the jet stream is parallel to the pinion shaft cross section, that is $\varphi =\pi /2$. Additionally, $\Sigma$ denotes the shaft angle of the face gear pair, and $A_g$ is the distance from the pinion axis to the $x{O}_{0}y$ plane.

2.2. Mathematical Model for the Pinion

The oil jet orientation parameters $x_H,y_L,z_V,\theta$ are known initially, and the distance $A_g$ and the oil jet velocity $V_j$ are also given. Thus, the process for calculating the impingement depth of the pinion is as follows.

At the initial moment (t₀ = 0): the position parameters of the face gear pair and the jet stream are as illustrated in Figure 3.

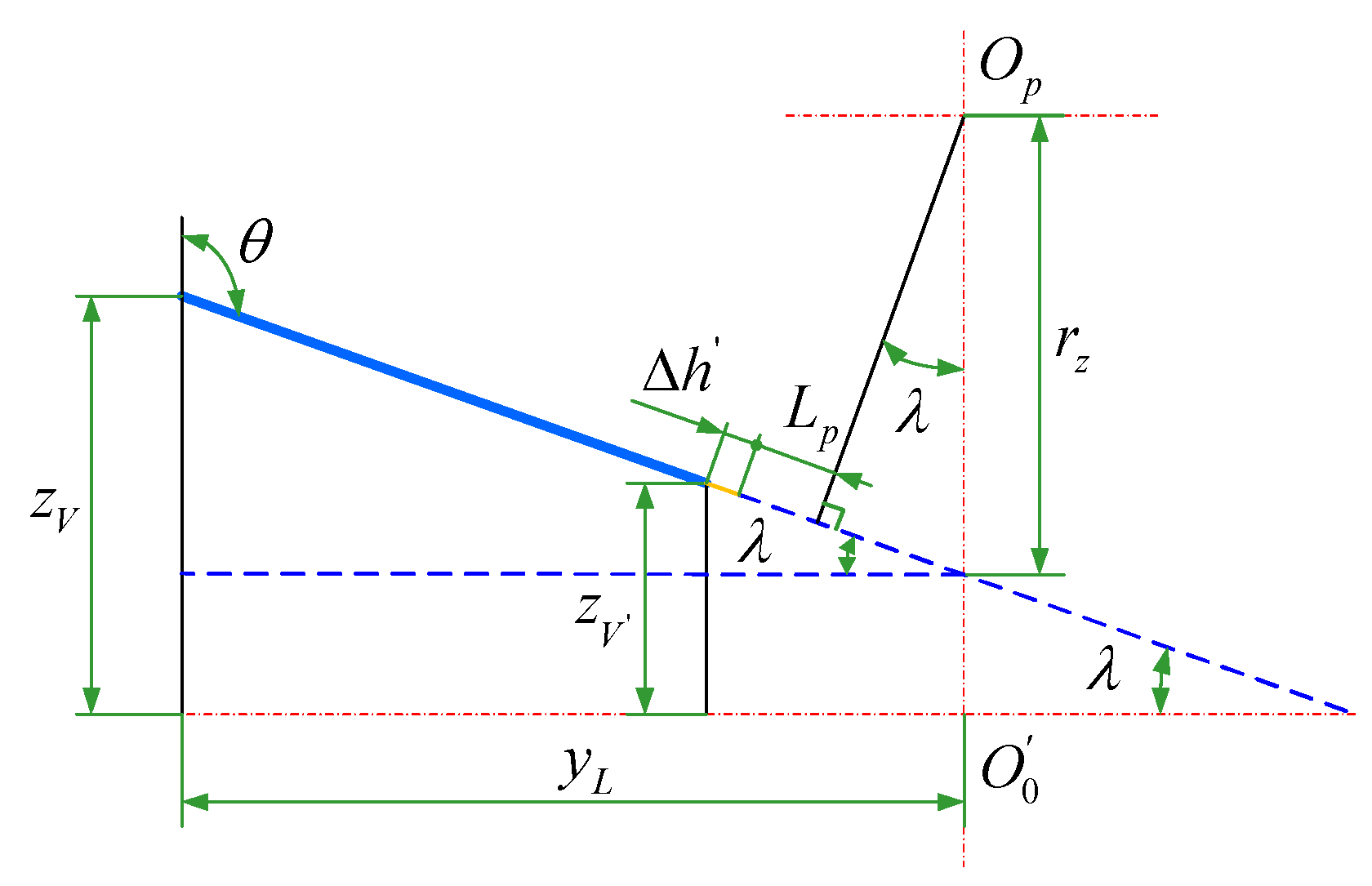
According to Figure 3, the projection length of the line from the point $O_g$ to the face gear addendum on the surface $O_g$ can be expressed as

$$R_a^{\prime }{}^2={\left[x_H-\left(z_V-z_{V^{\prime }}\right)\tan \left(\pi -\theta \right)\sin \left(\frac{\pi }{2}-\varphi \right)\right]}^2+{\left[y_L-\left(z_V-z_{V^{\prime }}\right)\tan \left(\pi -\theta \right)\cos \left(\frac{\pi }{2}-\varphi \right)\right]}^2$$

(1)

Substituting the parameter $\varphi =\pi /2$, Equation (1) can be written as

$$R_a^{\prime }=\sqrt{{\left(x_H\right)}^2+{\left[y_L+\left(z_V-z_{V^{\prime }}\right)\tan \theta \right]}^2}$$

(2)

where $z_{V^{\prime }}$ denotes the z coordinate value of the point where the jet stream passes through the face gear addendum. Let $H$ be the distance from the face gear addendum to the $x{O}_{0}y$ plane; thus,

$$z_{V^{\prime }}=H$$

(3)

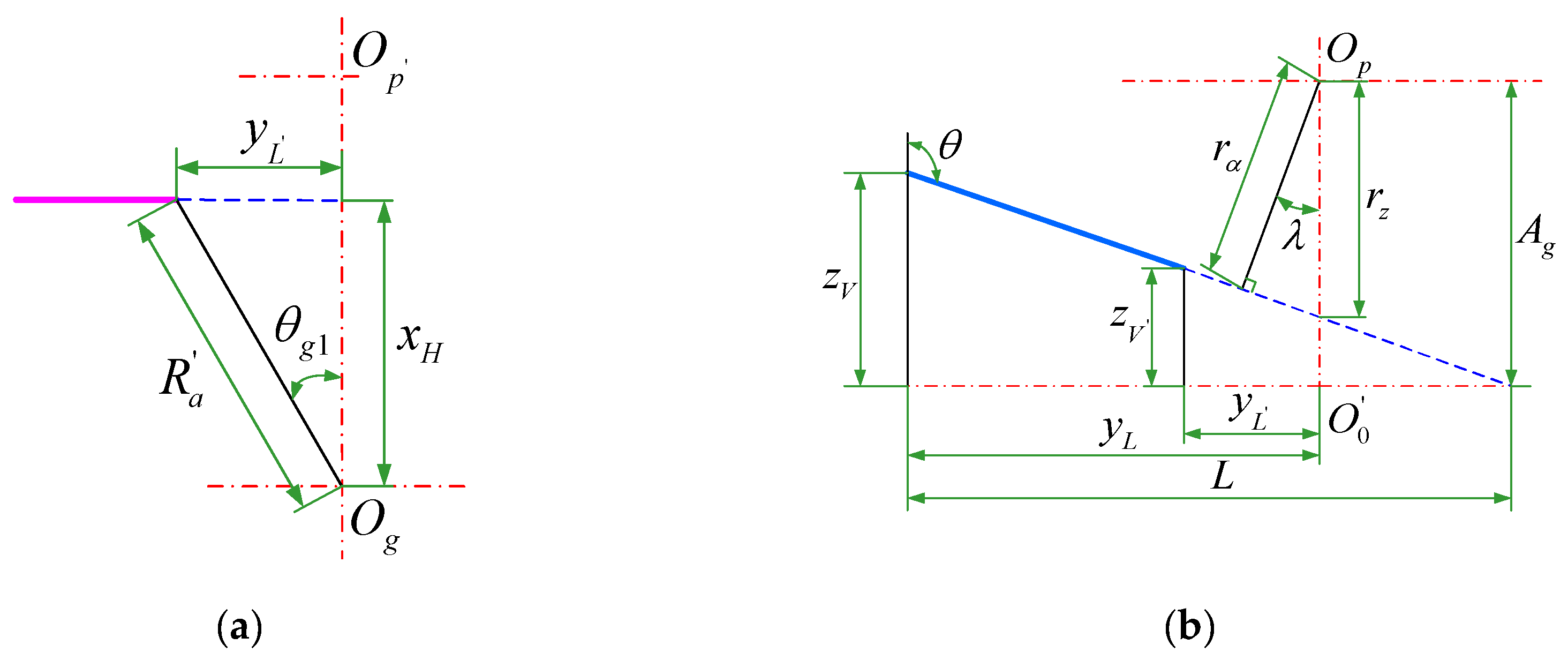
It is known that the jet streamline is parallel to the pinion shaft cross-section; that is, the jet stream is perpendicular to the x-axis. According to Figure 3, the projections of the jet stream on the surface $O_g$ and surface $O_p$ are demonstrated in Figure 4a,b. Furthermore, in Figure 4b, the perpendicular line of the projection line is drawn through the point $O_p$, and the length of the perpendicular line is $r_{\alpha }$.

According to the geometric relationship in Figure 4a, the following equation is obtained:

$$R_a^{\prime }=\sqrt{{\left(x_H\right)}^2+{\left(y_{L^{\prime }}\right)}^2}$$

(4)

Equations (2), (3) and (4) can be rewritten in a combined form:

$$\{\begin{array}{l}{x}_{H^{\prime }}=x_H\\ y_{L^{\prime }}=y_L+\left(z_V-z_{V^{\prime }}\right)\tan \theta \\ z_{V^{\prime }}=H\end{array}$$

(5)

where $x_{H^{\prime }}$ and $y_{L^{\prime }}$ represent the x and y coordinate values of the point where the jet stream passes through the face gear addendum, respectively.

The following equations can be obtained from Figure 4b:

$$r_{\alpha }=r_z\cos \lambda$$

(6)

$$\lambda =\theta -\frac{\pi }{2}$$

(7)

$$L=z_V\tan \left(\pi -\theta \right)$$

(8)

$$A_g=r_z+\left(L-y_L\right)\tan \lambda$$

(9)

By solving Equations (6), (7), (8) and (9), $r_{\alpha }$ and $r_z$ can be expressed as

$$r_z=A_g-z_V-y_L\cot \theta$$

(10)

$$r_{\alpha }=A_g\sin \theta -z_V\sin \theta -y_L\cos \theta$$

(11)

where $r_z$ denotes the distance from the intersection point of the jet stream with line $O_p{O}_0^{\prime }$ to the point $O_p$; $\lambda$ denotes the angle between the line $r_z$ and the line $r_{\alpha }$.

${\theta }_{p1}$ and ${\theta }_{g1}$ represent the position parameters of the pinion and the face gear at the initial time ($t_0=0$), and their relationship can be deduced by the rotation angle relationship between the face gear and the gear shaper cutter during the machining process. The rotation angles ${\phi }_g$ and ${\phi }_s$ of the face gear and the gear shaper cutter satisfy the transmission ratio [26]:

$$\frac{{\phi }_g}{{\phi }_s}=\frac{N_s}{N_g}$$

(12)

where $N_s$ and $N_g$ denote the numbers of teeth on the shaper and the face gear, respectively.

To avoid the interference between the shaper cutter and the edge of the face gear, the face gear drive is changed from an instantaneous line contact to a point contact drive. In this case, the number of teeth on the pinion will be 1–3 teeth less than on the gear shaper cutter [27,28,29].

$$N_s=N_p+\left(1~3\right)$$

(13)

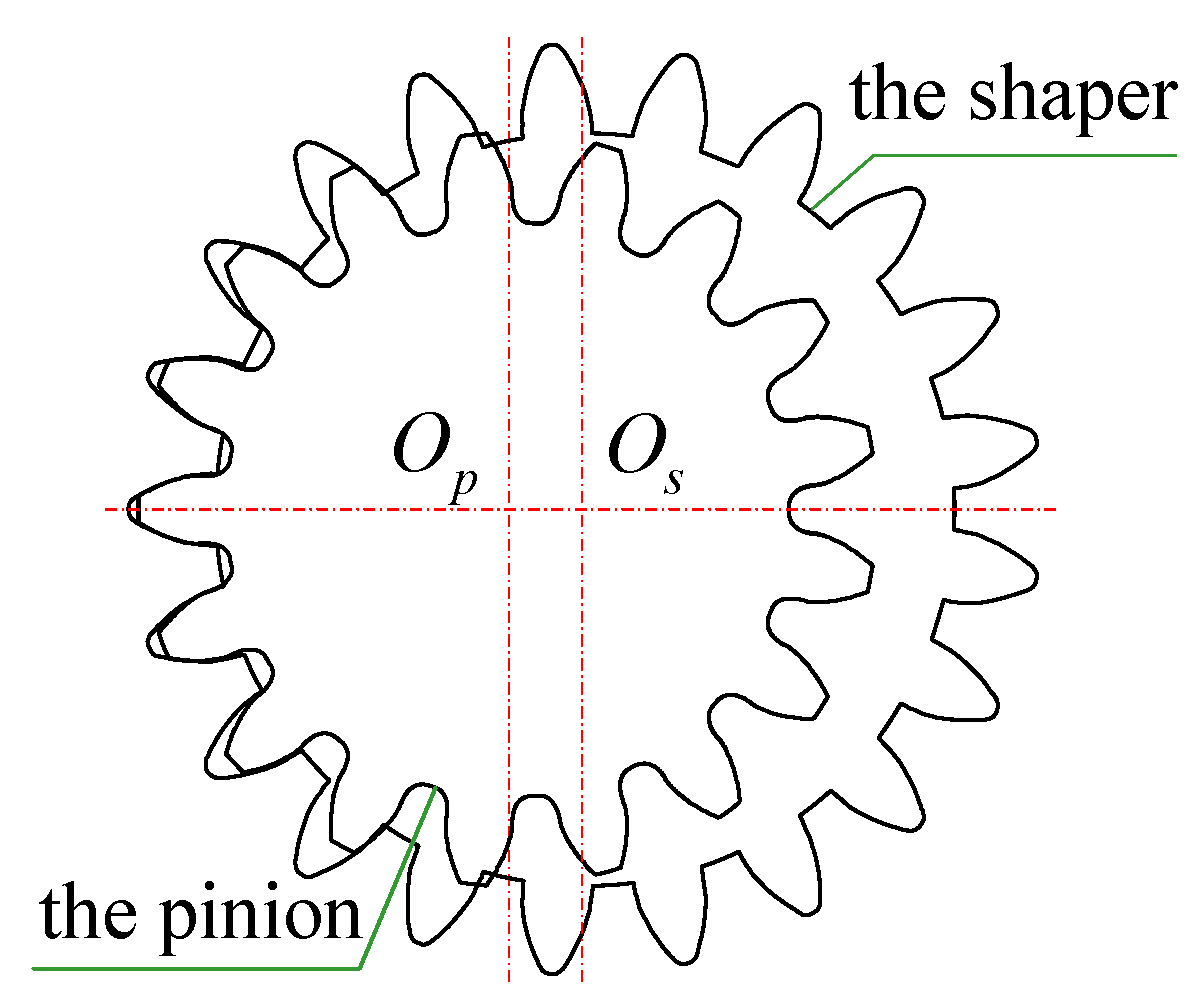
Figure 5 illustrates an imaginary internal tangency of the shaper cutter and the pinion [30,31].

$O_p$ and $O_s$ denote the centers of the pinion and the shaper cutter shaft sections, respectively. Their rotation angles satisfy the following equation:

$$\frac{{\phi }_p}{{\phi }_s}=\frac{N_s}{N_p}$$

(14)

Combining Equation (12) with Equation (14), the relationship between the rotation angle ${\phi }_p$ of the pinion and ${\phi }_g$ of the face gear can be expressed as:

$$\frac{{\phi }_p}{{\phi }_g}=\frac{N_g}{N_p}$$

(15)

According to Figure 3 and Equation (15), the initial position parameter ${\theta }_{p1}$ of the pinion is expressed by

$${\theta }_{p1}=\frac{N_g}{N_s}{\theta }_{g1}+inv{\alpha }_{p1}-\lambda$$

(16)

where $inv{\alpha }_{p1}$ is the involute function of the spur gear, representing the spread angle at the intersection point between the pinion pitch circle and the involute; and the pressure angle ${\alpha }_{p1}$ on pitch circle of the pinion is expressed as

$$inv{\alpha }_{p1}=\tan {\alpha }_{p1}-{\alpha }_{p1}$$

(17)

Obviously, from Figure 4, the initial position parameter ${\theta }_{g1}$ of the face gear is

$${\theta }_{g1}={\tan }^{-1}\frac{y_{L^{\prime }}}{x_H}$$

(18)

At the moment ($t_1=t$), the position parameters of the face gear pair and the jet stream are illustrated in Figure 6.

As the flowing time of the jet steam is equal to the rotation time of the pinion, which is rotating from the angle ${\theta }_{p1}$ at the initial time $t_0$ to the angle ${\theta }_{p2}$ at time $t_1$, the impingement depth $d_p$ can be calculated as

$${(r_a^{\prime }-d_p)}^2=L_p{}^2+r_{\alpha }{}^2$$

(19)

where

$$r_a^{\prime }=\frac{1}{2}{N}_p{m}_p+h_{ap}$$

(20)

where $L_p$ represents the impingement distance, and $r_a^{\prime }$ represents the addendum radius of the pinion.

$$\frac{{\theta }_{p2}-{\theta }_{p1}}{{\omega }_p}=\frac{\Delta h}{V_j}$$

(21)

where ${\omega }_p$ is the angular velocity of the pinion.

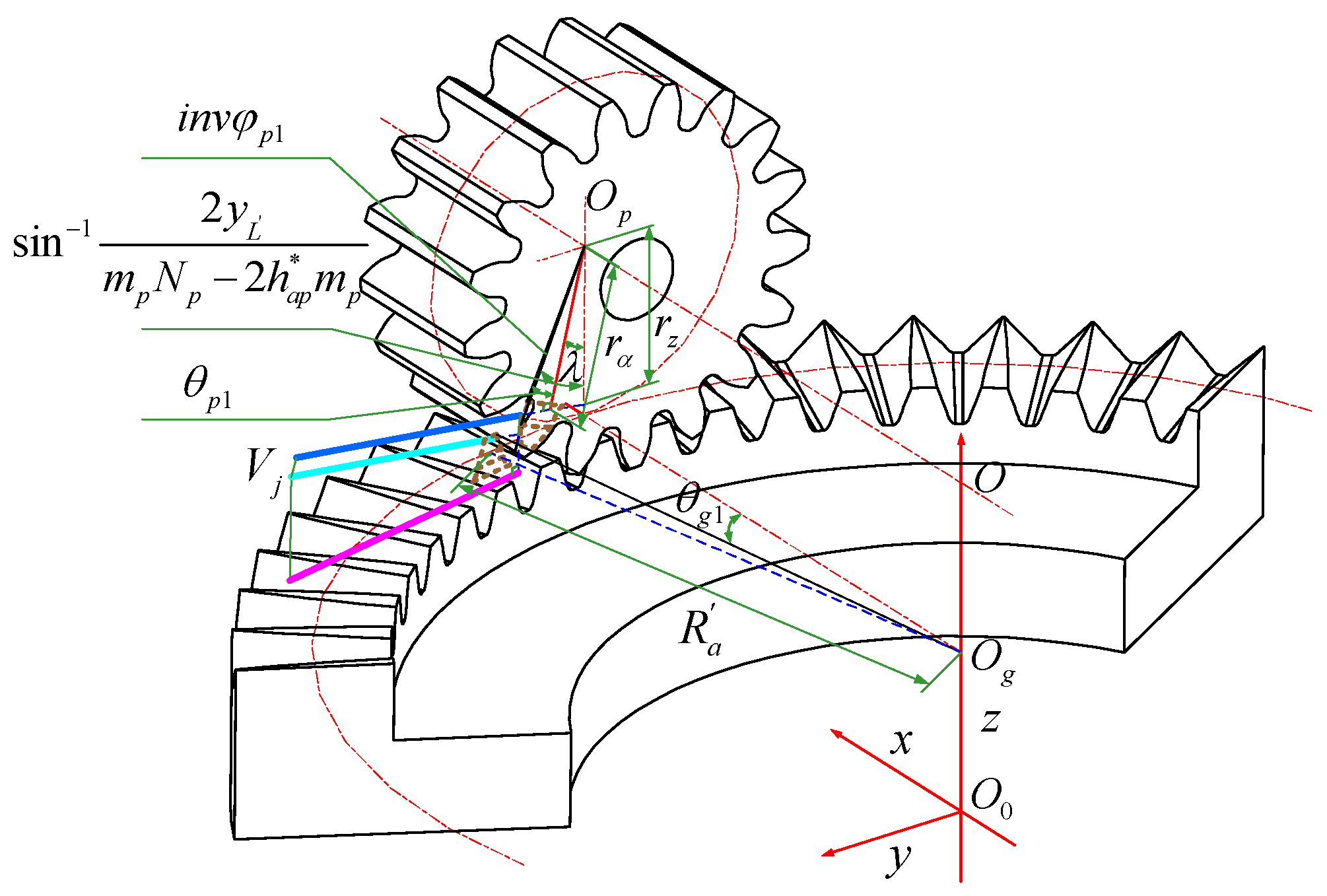
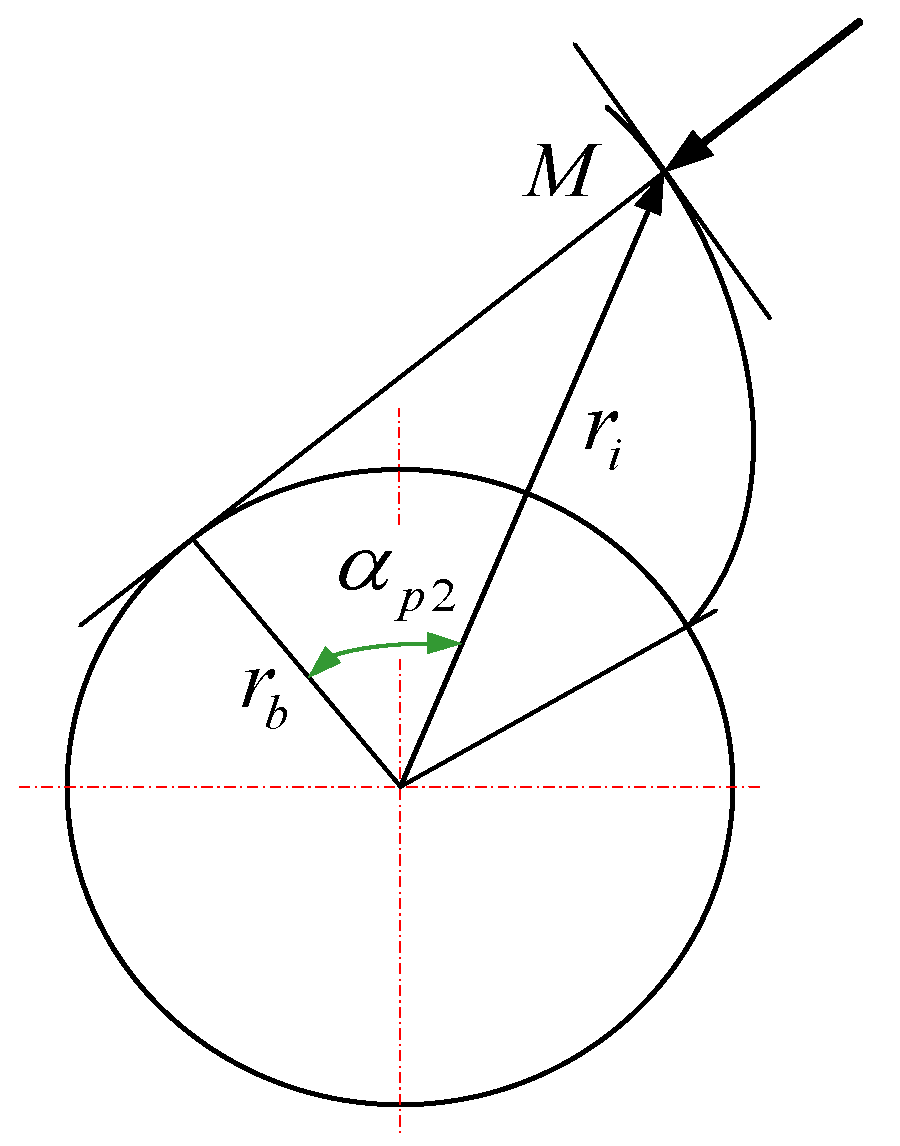
As can be seen in Figure 6, the position parameter of the pinion at $t_1=t$ is

$${\theta }_{p2}={\tan }^{-1}\frac{L_p}{r_a}+inv{\alpha }_{p2}$$

(22)

where $inv{\alpha }_{p2}$ is the involute function of the spur gear, denoting the spread angle at the impingement point M of the involute shown in Figure 7; ${\alpha }_{p2}$ denotes the pressure angle at the impingement point on the volute. Their relationship can be obtained by

$$inv{\alpha }_{p2}=\tan {\alpha }_{p2}-{\alpha }_{p2}$$

(23)

The following equations can be obtained from Figure 6 and Figure 7:

$${\alpha }_{p2}={\cos }^{-1}(r_b/r_i)$$

(24)

$$r_i={(L_p{}^2+r_{\alpha }{}^2)}^{1/2}$$

(25)

where $r_i$ denotes the radius of the pinion at the impingement point, and $r_b$ denotes the base circle radius of the pinion.

Equation (21) can be rewritten as

$$\Delta h=\frac{V_j({\theta }_{p2}-{\theta }_{p2})}{{\omega }_p}$$

(26)

Figure 8 illustrates the projection of the jet stream on the surface $O_p$; according to the geometric relationship, the following equation can be obtained:

$$\frac{y_L}{\cos \lambda }=\frac{z_V-z_{V^{\prime }}}{\sin \lambda }+\Delta h^{\prime }+L_p+r_z\sin \lambda$$

(27)

This can be simplified by substituting Equation (7) into Equation (27):

$$L_p=\frac{y_L}{\sin \theta }+\frac{z_V-z_V^{\prime }}{\cos \theta }-\Delta h^{\prime }+r_z\cos \theta$$

(28)

where $\Delta h^{\prime }$ denotes to the projection of $\Delta h$ on the surface $O_p$. Hence, the relationship between $\Delta h^{\prime }$ and $\Delta h$ is

$$\Delta h^{\prime }=\Delta h$$

(29)

Moreover, Equation (19) can be reformulated as

$$d_p=r_a^{\prime }-{\left(L_p{}^2+r_{\alpha }{}^2\right)}^{1/2}$$

(30)

By substituting Equations (3), (10), (11), (20) and (26) into Equations (28) and (29), the mathematical model of the impingement depth on the pinion can be established as follows:

$$d_p=\frac{1}{2}{N}_p{m}_p+h_{ap}-\sqrt{L_p{}^2+{\left[A_g\sin \theta -z_V\sin \theta -y_L\cos \theta \right]}^2}$$

(31)

where

$$L_p=\frac{y_L}{\sin \theta }+\frac{z_V-H}{\cos \theta }-\frac{V_j\left({\theta }_{p2}-{\theta }_{p1}\right)}{{\omega }_p}+\left[A_g-z_V-y_L\cot \theta \right]\cos \theta$$

(32)

2.3. Mathematical Model for the Face Gear

The deduction process of the mathematical model of impingement depth for the face gear is approximately the same as that for the pinion; therefore, only the main derivation steps are presented in this paper. The position parameters of the face gear pair and the jet stream at the initial moment ($t_0=0$ ) and the moment ($t_1=t$) are as illustrated in Figure 9a,b, respectively.

Additionally, projections of the jet stream on different surfaces at different moments are shown in Figure 10.

Similarly, the position parameters of the pinion and the face gear at the initial time ($t_0=0$) and the face gear at the moment ($t_1=t$) are denoted by ${\theta }_{p4}$, ${\theta }_{g2}$ and ${\theta }_{g3}$, respectively, which can be calculated using the following expressions

$${\theta }_{p4}={\cos }^{-1}\left(\frac{A_G-Z_V^{\prime }}{r_a^{\prime }}\right)-inv{\alpha }_{ak4}+inv{\alpha }_{k4}$$

(33)

$${\theta }_{g2}={\theta }_{p4}\frac{N_p}{N_g}$$

(34)

$${\theta }_{g3}={\tan }^{-1}\frac{L_g}{X_H}$$

(35)

where $A_g$ denotes the distance from the pinion axis to the $x{O}_{0}y$ plane; $Z_V^{\prime }$ denotes the z coordinate value of the point where the jet stream passes through the pinion addendum; ${\alpha }_{ak4}$ and ${\alpha }_{k4}$ denote the pressure angles at the intersection point of the addendum circle and the pitch circle with the involute, respectively; $L_g$ denotes the impingement distance; and $X,Y,Z,{\theta }^{\prime },$ ${\varphi }^{\prime }$ are the jet orientation parameters.

According to the definition of the impingement depth, there is an angle between the line from the impingement point to the face gear addendum and the z-axis. The impingement depth on the face gear is assumed to be equal to its projection on the surface $O_g$. Hence, similar to Equation (19), the impingement depth $d_g$ on the face gear can be calculated as

$${\left[R_i+\left|\frac{X_H}{\cos {\theta }_{g3}}-R_i\right|\right]}^2={\left(L_g-d_g\right)}^2+X_H{}^2$$

(36)

where $R_i$ is the inner radius of the face gear, $L_g$ is the impingement distance, which satisfies the expression $L_g=Y_L-\left(Z_V-Z_V^{\prime }\right)\tan {\theta }^{\prime }-\Delta h^{\prime }$, while $\Delta h^{\prime }$ is defined as $\Delta h^{\prime }=\Delta h\sin (\pi -{\theta }^{\prime })$, which is the projection of $\Delta h$ on the surface $O_g$, as shown in Figure 10a,c.

Therefore, the mathematical model of the impingement depth $d_g$ on the face gear can be established as

$$d_g=L_g-\sqrt{{\left[R_i+\left|\sqrt{L_g{}^2+X_H{}^2}-R_i\right|\right]}^2-X_H{}^2}$$

(37)

where

$$L_g=Y_L+\left(Z_V-Z_V^{\prime }\right)\tan {\theta }^{\prime }-\frac{V_j\left({\theta }_{g3}-{\theta }_{g2}\right)}{{\omega }_g}\sin {\theta }^{\prime }$$

(38)

where $V_j$ denotes the jet velocity; ${\omega }_g$ denotes the angular velocity of the face gear.

3. CFD Numerical Simulations

In the case of the given parameters, such as the gear structures, parameters and working conditions, the oil jet lubrication performance can be judged by the oil volume fraction and oil pressure distribution in the meshing area [32,33,34], and a greater oil volume fraction and pressure is commonly recognized as providing better jet lubrication performance. The Fluent program based on the CFD method was adopted to simulate the distribution of oil-air, two-phase flow in the meshing area.

3.1. CFD Model and Main Settings

For the face gear drive, the generated heat distribution to the pinion is more than the heat distributed to the face gear at the same time; furthermore, the heat transfer coefficient of the pinion is less than that of the face gear, so the pinion is more prone to damage during the meshing process. Hence, this paper focuses on the jet lubrication performance of the pinion. The separation method [35,36] is used to moderately increase the distance between the pinion and the face gear. The parameters of the face gear pair are listed in

Table 1. Main parameters of the face gear pair.

Parameters	Values
Teeth number of the pinion	17
Teeth number of the face gear	51
Module (mm)	2.5
Pressure angle (°)	25
Shaft angle (°)	90
Inner radius of the face gear (mm)	64.0
Outer radius of the face gear (mm)	82.0
Rotation rate of the pinion (r/min)	3000
Rotation rate of the face gear (r/min)	1000

.

To ensure the reliability and accuracy of the transient simulation results, grid independence tests were preferentially performed. The distributions of the oil volume fraction and oil pressure at 0.005 s on a specific plane parallel to the coordinate plane $xOz$ were taken for the grid independence tests.

Table 2. Six cases of the mesh elements.

Case	Mesh Elements of the Gear Body	Mesh Elements of the Fluid Domain	Total Mesh Elements
1	270,556	553,844	824,400
2	406,277	785,481	1,191,758
3	884,096	1,402,760	2,286,856
4	1,190,696	1,909,611	3,100,307
5	1,645,237	2,441,267	4,086,504
6	2,190,696	3,016,876	5,207,572

lists the number of mesh elements in six cases. In the simulations, the number of the mesh elements was ensured as the only independent variable. As seen from simulation results illustrated in Figure 11, the trends of the oil pressure and the oil volume fraction become insignificant with the increasing number of mesh elements. When the mesh elements reach Case 4, the oil pressure and oil volume fraction can be considered to be stable. Therefore, the total mesh elements in all subsequent simulations were controlled at approximately 3.2 million.

According to the grid independence test results, the computation domain was divided into tetrahedral meshes with approximately 3.2 million mesh elements, where the defeature size and curvature size of the engaged teeth were 0.1 mm and 0.4 mm, respectively. Figure 12 presents the final mesh model, where the maximum skewness and the mesh quality are 0.842 and 0.283, respectively. During the progress of oil jet lubrication, the fluid in the gearbox changes from the initially only air into oil-air, two-phase mixture flow. The viscosity and density of the lubrication oil are set as 1.98 mm²/s and 959.4 kg/m³, respectively.

It is known that the two-phase flow distribution is time-varying, so the pressure-solver and transient-state were adopted in the paper. The VOF multiphase flow model was applied to simulate the oil-air flow in the meshing area [37,38]. Considering the swirling effects generated by high-speed rotating gears, the RNG $k-\epsilon$ turbulence model with higher precision was used. The lower circular surface of the nozzle was set as the velocity inlet, and the velocity and hydraulic diameter were set to 50 m/s and 0.0014 m, respectively. Moreover, non-slip boundary conditions were used for all walls. The dynamic mesh was adopted to simulate the real rotation of the face gear drive. Figure 13 demonstrates the distributions of the oil volume fraction at different moments. To obtain more accurate results, the second-order windward methods of the momentum, the turbulent kinetic energy, and the turbulent dissipation rate were adopted for spatial discretization. Furthermore, the standard SIMPLE algorithm was used for pressure-velocity coupling.

For the determination of the time step size, an initial value of $5\times {10}^{-6}\mathrm{s}$ was obtained by the minimum edge length of the nozzle divided by the fluid velocity. With respect to the solving efficiency and accuracy, it was necessary to perform time step independence tests in the six cases of $5\times {10}^{-6}\mathrm{s}$, $2\times {10}^{-5}\mathrm{s}$, $3.5\times {10}^{-5}\mathrm{s}$, $5\times {10}^{-5}\mathrm{s}$, $6.5\times {10}^{-5}\mathrm{s}$ and $8\times {10}^{-5}\mathrm{s}$. Similar to the grid independence tests, the distributions of the oil pressure and oil volume fraction on the specific plane were used for evaluation. As shown in Figure 14, the changes of the oil pressure and oil volume fraction were within an allowable error range before $5\times {10}^{-5}\mathrm{s}$. Subsequently, as the time step increased, the oil pressure and oil volume fraction were significantly affected. Thus, the time step was determined to be $5\times {10}^{-5}\mathrm{s}$.

The simulation results should be obtained in a convergence state. In this paper, whether the calculation reached convergence was mainly judged by the following three aspects: Firstly, all residuals were set to 0.001, including the Continuity Equation, the Momentum Equations, the Turbulent Kinetic Energy Equation and the Turbulent Kinetic Energy Dissipation Rate Equation. Secondly, when the residual values all dropped below 0.001, the residual was adjusted to continue the simulations. Meanwhile, the oil pressure and oil volume fraction in the meshing area were monitored. Finally, when the monitored variables almost exhibited no further change with the increase of the iteration step, the mass and momentum data would be conserved. If the error was within the allowable range, the simulation could be considered to reach the convergence.

According to Equations (31) and (32), the impingement depth on the pinion surface is directly related to the nozzle layout parameters $x_H,y_L,z_V,\theta$. Since the nozzle layout parameters are restricted by the gearbox space, the initial nozzle position is determined as (70, 52, 32, 105°). Each parameter of the initial position is investigated to verify the impingement depth mathematical model and to optimize the nozzle layout.

3.2. Verification and Optimization of Parameter $x_H$

According to the initial position, four groups of the parameter $x_H$ are set preferentially as 65 mm, 70 mm, 75 mm and 80 mm, respectively, while the other three parameters remain the same. Based on the mathematical model established above, the values of the impingement depths corresponding to the four groups are obtained by the implicit function in the program MATLAB, as given in

Table 3. Values of parameter $x_H$ and the corresponding calculated impingement depths.

$\mathbf{Number}$	${\mathit{x}}_{\mathit{H}}(\mathbf{m}\mathbf{m})$	${\mathit{y}}_{\mathit{L}}(\mathbf{m}\mathbf{m})$	${\mathit{z}}_{\mathit{V}}(\mathbf{m}\mathbf{m})$	$\mathit{\theta }(°)$	${\mathit{d}}_{\mathit{p}}(\mathbf{m}\mathbf{m})$
1	65	52	32	105	0.16
2	70	52	32	105	0.60
3	75	52	32	105	0.63
4	80	52	32	105	0.54

. It can be seen that a maximum impingement depth can be obtained with $x_H=75\mathrm{mm}$.

Accordingly, the CFD models using the parameters provided in Table 3 are established. Figure 15 illustrates the distributions of the oil volume fractions in the meshing area in the convergence state of the calculation. Obviously, Figure 15c exhibits superior characteristics on the pinion surface, as the oil distribution is more concentrated and uniform with relatively little oil flowing out.

Figure 16a,b demonstrates the behaviors of the oil volume fractions and oil pressures on the plane parallel to the coordinate plane $xOz$ and near the meshing point within the range of $x\in \left[64\mathrm{mm},82\mathrm{mm}\right]$. In the meshing cycle, the trends of the oil volume fraction and oil pressure generally increase, and both can reach the maximum values in the case of $x_H=75\mathrm{mm}$; consequently, a better lubrication performance can be achieved. Mutual verification was achieved between the mathematical model and the numerical simulation. The oil volume fractions and pressures were observed to fluctuate at different moments; this result was due to the fact that the jet stream was blocked by the rotating gear and could not enter the meshing area smoothly.

Furthermore, the parameter $x_H=75\mathrm{mm}$ may be a point close to the optimal or peak value, and the optimal value could be more accurate, as the solution interval is smaller. Figure 17 illustrates the calculated impingement depth within the range of $x_H\in \left[70\mathrm{mm},80\mathrm{mm}\right]$ with an interval length of only 1 mm. The maximum impingement depth is observed to appear when $x_H=71\mathrm{mm}$, which is regarded as the optimal value for generating a better lubrication performance.

3.3. Verification and Optimization of Parameter $y_L$

Similarly, four groups of the parameter $y_L$ are set preferentially as 37 mm, 42 mm, 47 mm and 52 mm, respectively, while the parameter $x_H$ is set at the optimal value of 71 mm, as determined previously, while the other two parameters remain the same. The corresponding impingement depths are calculated as shown in

Table 4. Values of parameter $y_L$ and corresponding impingement depth.

$\mathbf{Number}$	${\mathit{x}}_{\mathit{H}}(\mathbf{m}\mathbf{m})$	${\mathit{y}}_{\mathit{L}}(\mathbf{m}\mathbf{m})$	${\mathit{z}}_{\mathit{V}}(\mathbf{m}\mathbf{m})$	$\mathit{\theta }(°)$	${\mathit{d}}_{\mathit{p}}(\mathbf{m}\mathbf{m})$
1	71	37	32	105	−2.02
2	71	42	32	105	3.72
3	71	47	32	105	2.57
4	71	52	32	105	0.89

, where negative values indicate that the jet stream could not reach the tooth surface. The maximum impingement depth could be obtained when $y_L=42\mathrm{mm}$.

Accordingly, CFD models were established with the different parameters provided in Table 4. Figure 18 illustrates the distribution of the oil volume fractions in the meshing area; obviously, Figure 18b,c exhibits superior distribution characteristics.

Figure 19 further presents that both the oil volume fraction and the oil pressure can achieve maximum values in the case of $y_L=42\mathrm{mm}$. A good agreement between the mathematical model and the CFD numerical simulation can be achieved. However, moving the nozzle closer to the meshing point does not improve the lubrication performance, as can be seen from the figure; when the $y_L$ decreases to 37 mm, the oil volume fraction and oil pressure both decrease significantly. This condition is due to the noticeable accumulation of oil in the meshing area, leading to more heat accumulation and a poor cooling effect.

Furthermore, Figure 20 illustrates the calculated impingement depth within a range of $y_L\in \left[37\mathrm{mm},47\mathrm{mm}\right]$ with a smaller interval length of 1 mm. The maximum impingement depth occurs when $y_L=40\mathrm{mm}$, which is regarded as an optimal value.

3.4. Verification and Optimization of Parameter $z_V$

When the value of parameter $z_V$ changes, while the jet angle parameter $\theta$ remains unchanged, the jet stream may be prevented by the gear teeth, leading to unexpected lubrication performance. According to the above research, the parameter $z_V$ is set as 27 mm, 32 mm, 37 mm and 42 mm in the case of $x_H=71\mathrm{mm}$ and $x_H=40\mathrm{mm}$, as given in

Table 5. Values of parameter $z_V$ and corresponding impingement depth.

$\mathbf{Number}$	${\mathit{x}}_{\mathit{H}}(\mathbf{m}\mathbf{m})$	${\mathit{y}}_{\mathit{L}}(\mathbf{m}\mathbf{m})$	${\mathit{z}}_{\mathit{V}}(\mathbf{m}\mathbf{m})$	$\mathit{\theta }(°)$	${\mathit{d}}_{\mathit{p}}(\mathbf{m}\mathbf{m})$
1	71	40	27	105	−3.79
2	71	40	32	105	3.92
3	71	40	37	105	−4.07
4	71	40	42	105	−7.20

.

Multiple calculated impingement depths appear to be negative values, indicating that the jet stream could not successfully jet onto the tooth surface. Therefore, there is no need to compare the oil volume fraction and oil pressure distributions, since only the model number 2 has a positive impingement depth. Using a method similar to that employed in Section 3.2 and Section 3.3, an appreciable maximum impingement depth when $z_V=32mm$ could be obtained, as seen in Figure 21.

3.5. Verification and Optimization of Jet Angle $\theta$

Based on the above research, the maximum impingement depth and the best lubrication performance could be obtained in the case of $x_H=71\mathrm{mm}$, $y_L=40\mathrm{mm}$ and $z_V=32\mathrm{mm}$. The jet angles were set preferentially as $100°$, $102.5°$, $105°$, and $107.5°$, respectively, and the corresponding impingement depths are presented in

Table 6. Different jet angles $\theta$ and the corresponding impingement depth.

$\mathbf{Number}$	${\mathit{x}}_{\mathit{H}}(\mathbf{m}\mathbf{m})$	${\mathit{y}}_{\mathit{L}}(\mathbf{m}\mathbf{m})$	${\mathit{z}}_{\mathit{V}}(\mathbf{m}\mathbf{m})$	$\mathit{\theta }(°)$	${\mathit{d}}_{\mathit{p}}(\mathbf{m}\mathbf{m})$
1	71	40	32	100	−2.50
2	71	40	32	102.5	2.74
3	71	40	32	105	3.92
4	71	40	32	107.5	2.87

. The maximum impingement depth could be obtained when the jet angle was $105°$.

Figure 22 and Figure 23 show that both the oil volume fraction and oil pressure can reach maximum values in the case of $\theta =105°$; consequently, a better lubrication performance can be achieved. A good agreement between the mathematical model and the CFD numerical simulation was achieved.

Furthermore, Figure 24 illustrates that the calculated impingement depth within the range of $\theta \in \left[102.5°,107.5°\right]$ with the smaller interval length of only 0.5 degrees. It can be seen that the maximum impingement depth appears when $\theta =105°$, which is regarded as the optimal value.

From the analysis and optimization above, an optimal combination of jet nozzle layout parameters that can generate a greater impingement depth, a greater oil volume fraction and a greater oil pressure for this face gear pair are determined and exhibit a better lubrication performance.

4. Experiments

To validate the feasibility and reliability of the theoretical method for evaluating the lubrication performance using the impingement depth mathematical model, oil jet lubrication experiments were performed under different nozzle layouts, which was an important prerequisite for deriving the novel impingement depth mathematical model for face gears and conducting numerical simulations. Figure 25 shows the whole experimental system, including a gearbox equipped with a nozzle layout adjustment device, a lubrication oil supply system, a driving motor, a loading motor, torque transducers, a thermal infrared imager, and a high-speed camera. The main experimental parameters are shown in

Table 7. Main parameters for the experimental system.

Teeth Number		Rotation Speed (r/min)		Jet Velocity (m/s)	Oil Jet Quantity (mL/min)	Torque (N·m)	Jet Height (mm)	Jet Nozzle Diameter (mm)	Initial Oil Temperature (°C)
Gear	Pinion	Gear	Pinion	5	235.5	200	100	2	30
42	24	856.14	1500

.

Different nozzle layout parameters, including the jet angle and the jet offset distance, as shown in

Table 8. Different nozzle layout parameters with the corresponding calculated impingement depths.

	Jet Angle (degree)	Offset Distance (mm)	Impingement Depth (mm)
1	0	0	0
2	2.5	−4.0	0.93
3	5.0	−8.0	0.95
4	7.5	−11.4	1.02
5	10.0	−14.8	0.98

, were designed and arranged in the experiments. Figure 26 shows the jet oil states photographed by a high-speed camera. Furthermore, a thermal infrared imager was used to capture pictures of the tooth surface temperatures, as listed in

Table 9. Measured tooth surface temperatures for different models.

Model	Jet Angle (Degrees)	Offset Distance (mm)	Impingement Depth (mm)	Pinion Temperature (°C)	Gear Temperature (°C)
1	0	0	0	84.7	80.3
2	2.5	−4.0	0.93	78.8	76.8
3	5.0	−8.0	0.95	77.6	75.9
4	7.5	−11.4	1.02	76.3	75.6
5	10.0	−14.8	0.98	77.3	76.2

. The measured temperatures for one model test are shown in Figure 27.

Figure 28 and Table 9 summarize the measured tooth surface temperatures corresponding to the calculated impingement depths.

As shown, with an increase in the calculated impingement depth, the tooth surface temperature is reduced, and consequently, better lubrication and cooling performance can be achieved, which can validate the effectiveness and accuracy of the method used to evaluate the oil jet lubrication performance using the impingement depth mathematical model.

5. Conclusions

The major conclusions drawn from this work include the following:

• A novel mathematical model for accurately calculating the lubrication oil jet impingement depth on the orthogonal face of a gear pair has been established, and this mode consists of comprehensive and detailed design parameters for the jet nozzle layout and face gear pair.
• CFD numerical simulations of an orthogonal face gear pair under different nozzle layouts reveal that a greater jet impingement depth, as calculated by the mathematical model, results in a greater oil volume fraction and oil pressure in the simulation. In addition, the optimal jet nozzle layout parameters, including the jet nozzle position and jet angle, have been determined and recommended.
• Good agreement was achieved between the mathematical model and the numerical simulation, validating the effectiveness and accuracy of using the impingement depth mathematical model for evaluating the oil jet lubrication performance of face gears. This mathematical model can provide a valuable method for the evaluation and optimization of the oil jet lubrication performance for various face gears in practical applications.
• Through oil jet lubrication experiments, the jet flow trajectories and tooth surface temperatures for different jet nozzle layouts were measured and compared. The relationship between the tooth surface temperature and the jet impingement depth revealed that the method for evaluating the oil jet lubrication performance using the impingement depth mathematical model was feasible and reliable.