Drilling Fluids are considered a key element in the drilling operation. Conventional drilling fluids are water-based, oil-based or synthetic-based fluid systems, which are used in the drilling process to give the best performance under certain temperatures and pressures experienced downhole [
1]. Drilling the section from the sea-bed/land to the top of the reservoir is different, regarding the economic value of the final project, compared to the reservoir section. As in the top sections, the concerns are to seal the permeable formations, and help sustain the wellbore stability.
Special measures will be taken into consideration while drilling the reservoir section to avoid damaging the reservoir and plugging the reservoir pores. For that target, special drilling fluids are used, called reservoir drill-in fluids (RDFs), which are specially formulated to maximize drilling experience and protect the reservoir from being damaged until the completion process is proceeded [
2].
There are many types of RDFs with different chemical compositions, but the concern of this study is about the clear brine-based mud which is often used within completions, as the presence of solids is a major contributor to formation damage [
3]. However, when used as drilling fluid, the solids-free nature of brine operationally improves the rate of penetration (
ROP), stabilization of sensitive formations, density, and abrasion or friction [
4]. Clear brine fluids properties are easier to maintain than conventional solids-laden fluid systems, so that when properly run, clear systems require very little maintenance, because many functional issues are inherently solved by the dissolved salts. Clear brine fluids also allow for drill site cost reductions because of the ability to reuse the fluid [
5].
Brine fluids can be prepared with one salt or a combination of salts. All salts provide unique properties to the base fluid. Saturated brines fluids provide excellent inhibitive properties and lubricity, as compared to conventional aqueous fluids. With optimal heat transference characteristics, they can greatly improve bit life, and increase the rate of penetration in hard rock drilling. Among the different salts used for clear-brine systems, calcium chloride has been selected, as it is considered one of the most economic brine systems, with its broad range of densities (from 9.0 to 11.6
ppg), availability, low cost, and its ability to reduce the water activity of the fluid [
6].
1.1. Drilling Fluid Rheology
Drilling fluid rheology plays a key role in optimizing drilling performance [
7]. These properties significantly affect the efficiency of the hole cleaning and the drilling rate [
8], which are critical factors controlling the performance of drilling operation [
9]. These rheological properties include mud density to provide the control on the formation pressure, while
and
are used for controlling hole cleaning and optimizing the drilling performance [
10]. Plastic viscosity of the drilling fluid is crucial for optimizing the drilling operation [
11]. It is an indication of the solid content in the drilling fluid which may negatively affect the drilling performance when it exceeds critical limits, and can cause many problems like pipe sticking and decreasing the rate of penetration [
12]. Yield point can be simply stated as the attractive forces among colloidal particles in drilling fluid [
11]. The optimization of yield point is central to controlling the efficiency of hole cleaning [
10,
13]. Moreover, apparent viscosity is considered a key factor in the optimization of mud hydraulics while drilling [
8]. In addition, the parameters
k and
n can be used for evaluating hole cleaning during the drilling operation [
14].
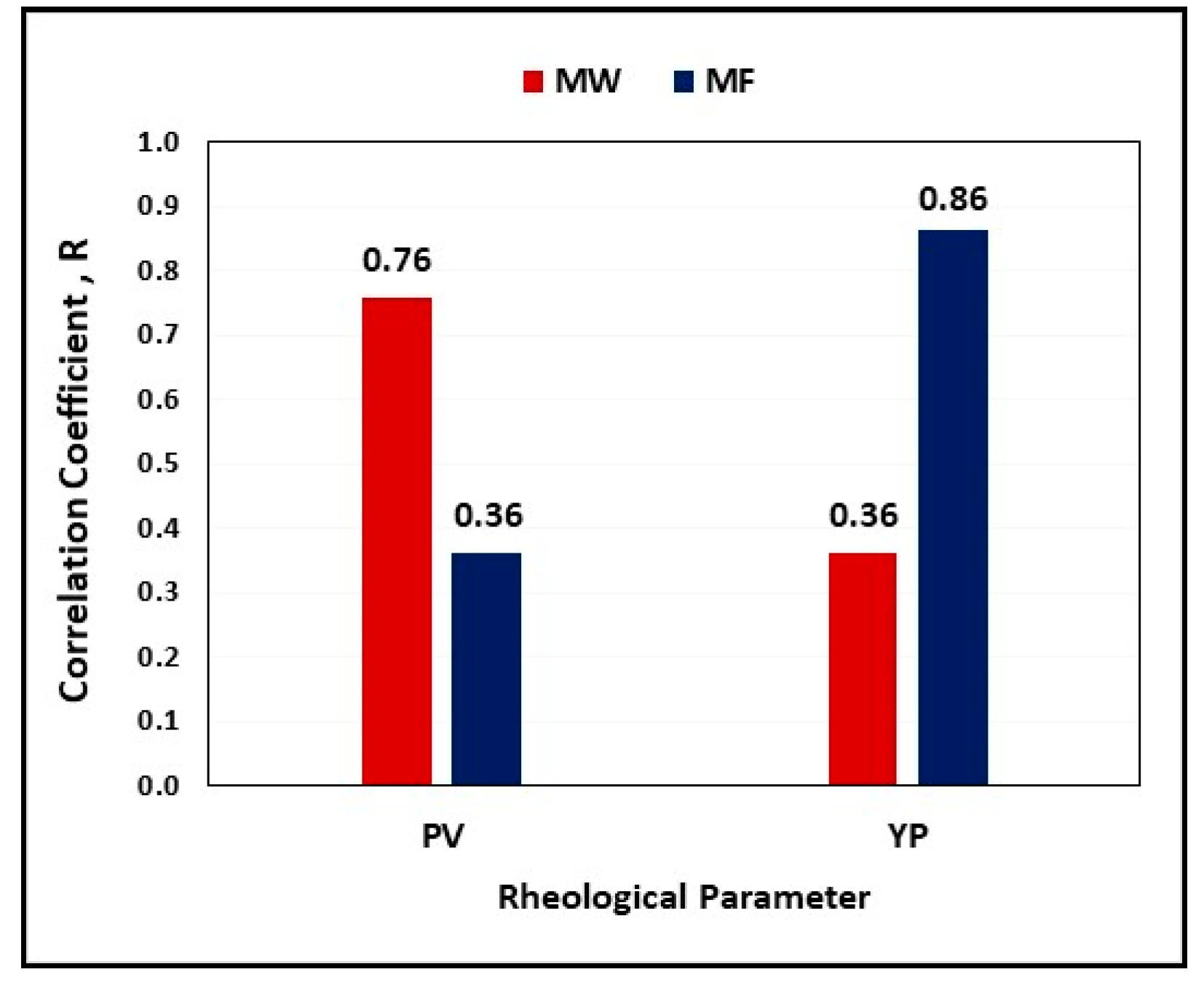
The rheological properties can be measured in the laboratory using mud balance and viscometer. The mud balance is used to measure the mud weight while the rheometer is used to measure (
and
). However, this process takes a relatively long time (2–3 h for taking measurements and cleaning the instruments) which makes it difficult to be performed periodically and practically in the field. Therefore, it is taken as a common procedure that only density and Marsh funnel viscosity are measured periodically every 15–20 min, using mud balance and Marsh funnel devices. On the other hand, a complete mud test (including all the drilling fluid properties), using the mud balance and viscometer, is performed twice a day. Marsh funnel viscosity provides an indication of the changes in the rheology of the drilling fluid. This funnel was first introduced by Marsh [
15]. This tool is cheap and takes a short time, so it can be utilized to give field measurements frequently and estimate some parameters like yield stress [
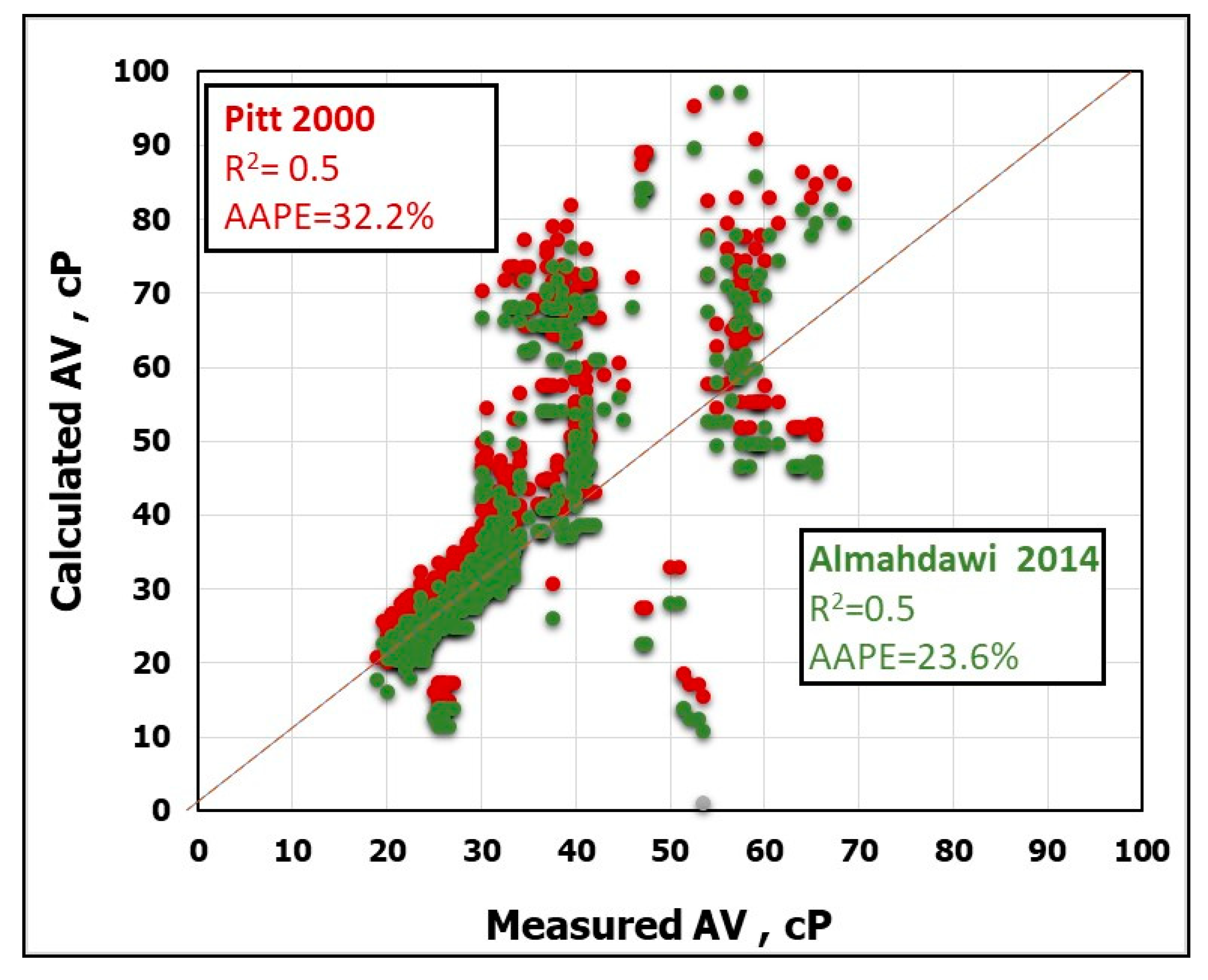
16]. Based on the literature, there are two models developed to predict the drilling fluid viscosity from mud density and Marsh funnel measurements. These two measurements were used as inputs to calculate the effective viscosity of the drilling fluid as stated by Pitt [
17] in Equation (1). Then a modification on the previous model was introduced by Almahdawi et. al. [
18], who figured out that changing the value of the constant to 28 in Equation (2) instead of 25 presented by Pitt [
17], is more effective give more accurate results, as compared to Equation (1).
where
is the apparent viscosity in
cP,
is the fluid density in
,
is the Marsh funnel time in
sec.
Several mathematical models have been mentioned in the literature for estimating the fluid rheological properties using Marsh funnel devices. Some of them suggested using the temporal variations in the fluid height in the funnel to determine different rheological parameters such as
[
19,
20,
21,
22]. They introduced a methodology to determine the shear rate and the shear stress on the walls of the Marsh funnel from the measured discharged fluid volume of the Marsh funnel at different points. Then several rheological parameters have been related to the obtained shear rate and shear stress. Abdulrahman et al. [
23] investigated different water-based drilling fluids using the Marsh funnel and showed that
can be estimated using consistency plots and the methodology described in [
19]. However, these models showed considerable discrepancies between the results obtained from the Marsh funnel and the standard viscometers. Other studies tried to model the fluid volume flow in the Marsh funnel with higher order polynomial functions, rather than the simplified functions used in the previously mentioned studies [
24,
25]. This attempt was to simulate the fluid temporal height in the Marsh funnel more properly, and to get closer results of rheological parameters to those obtained from the standard viscometers.
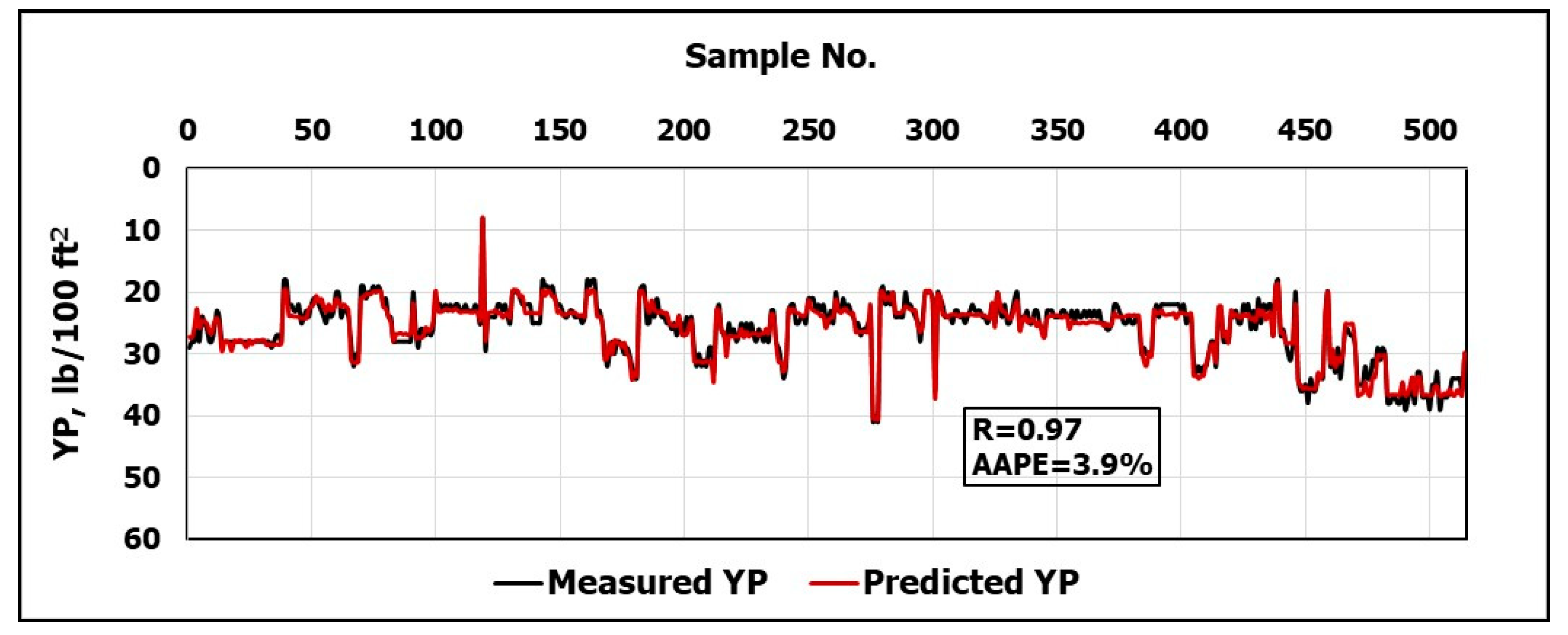
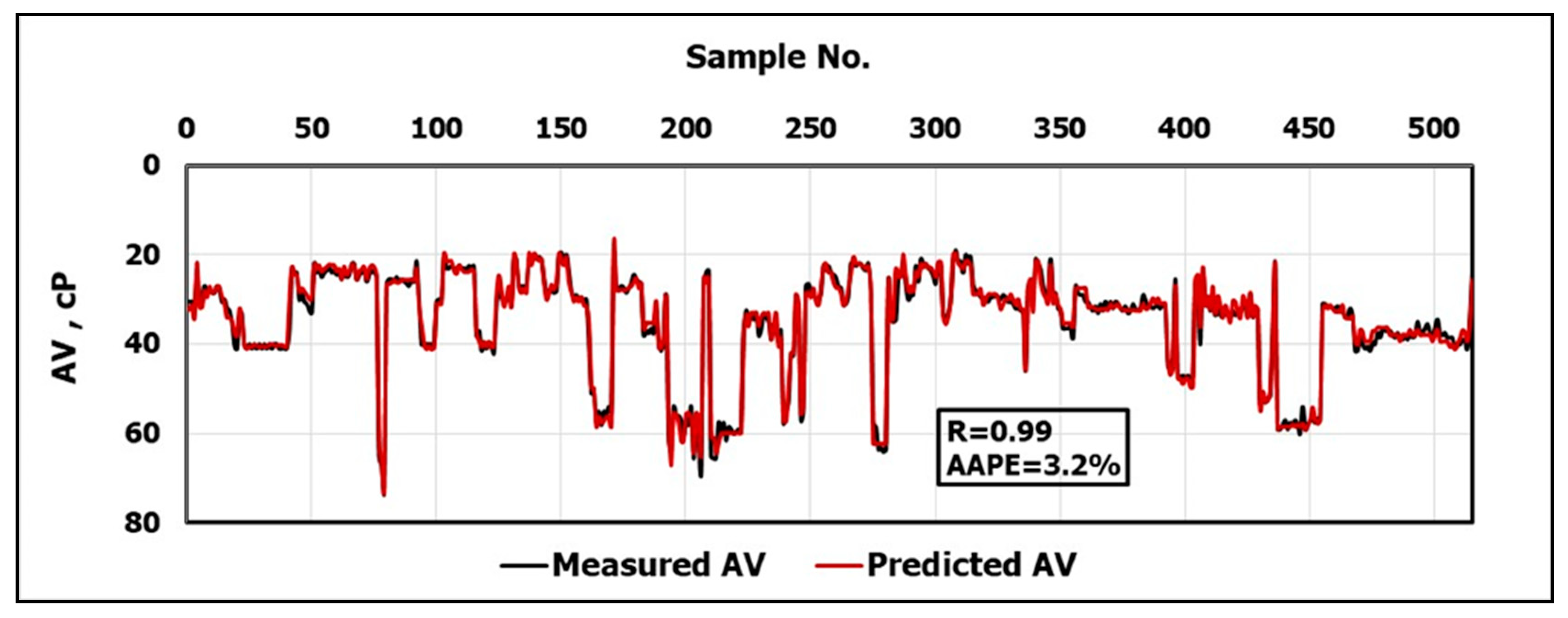
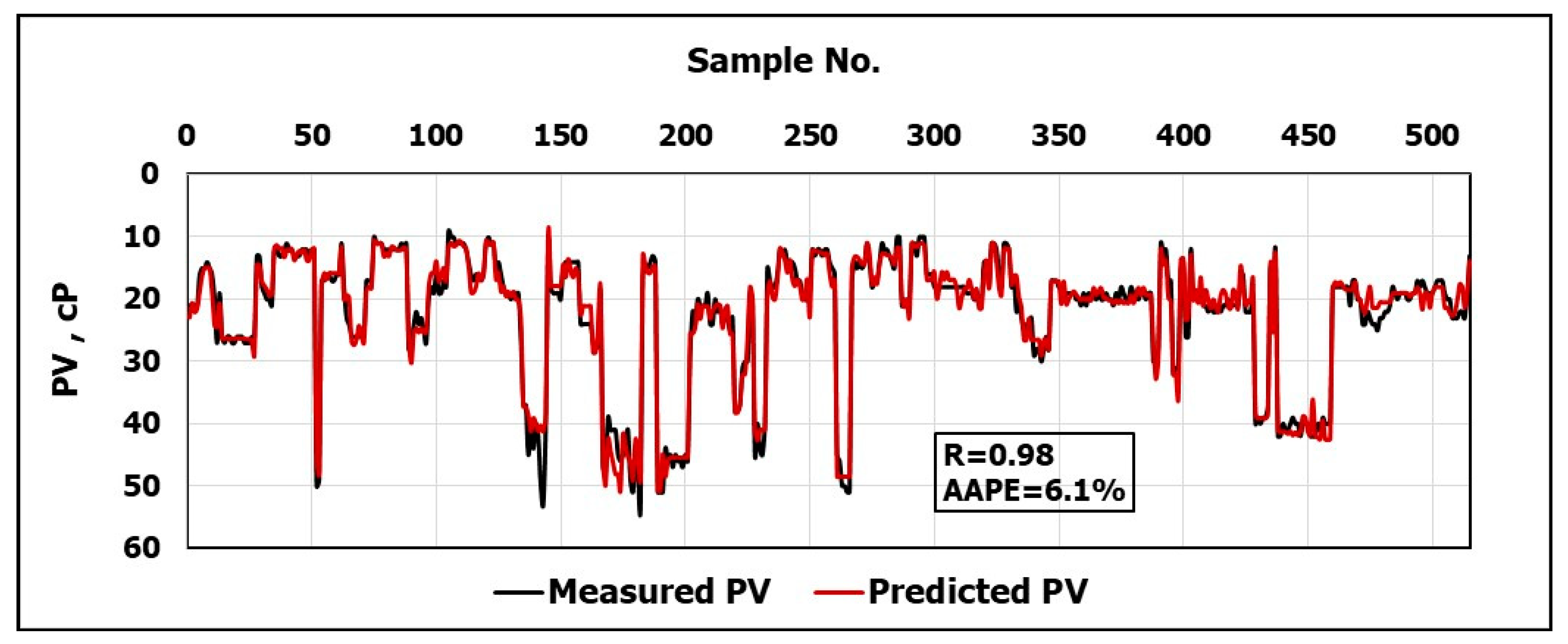
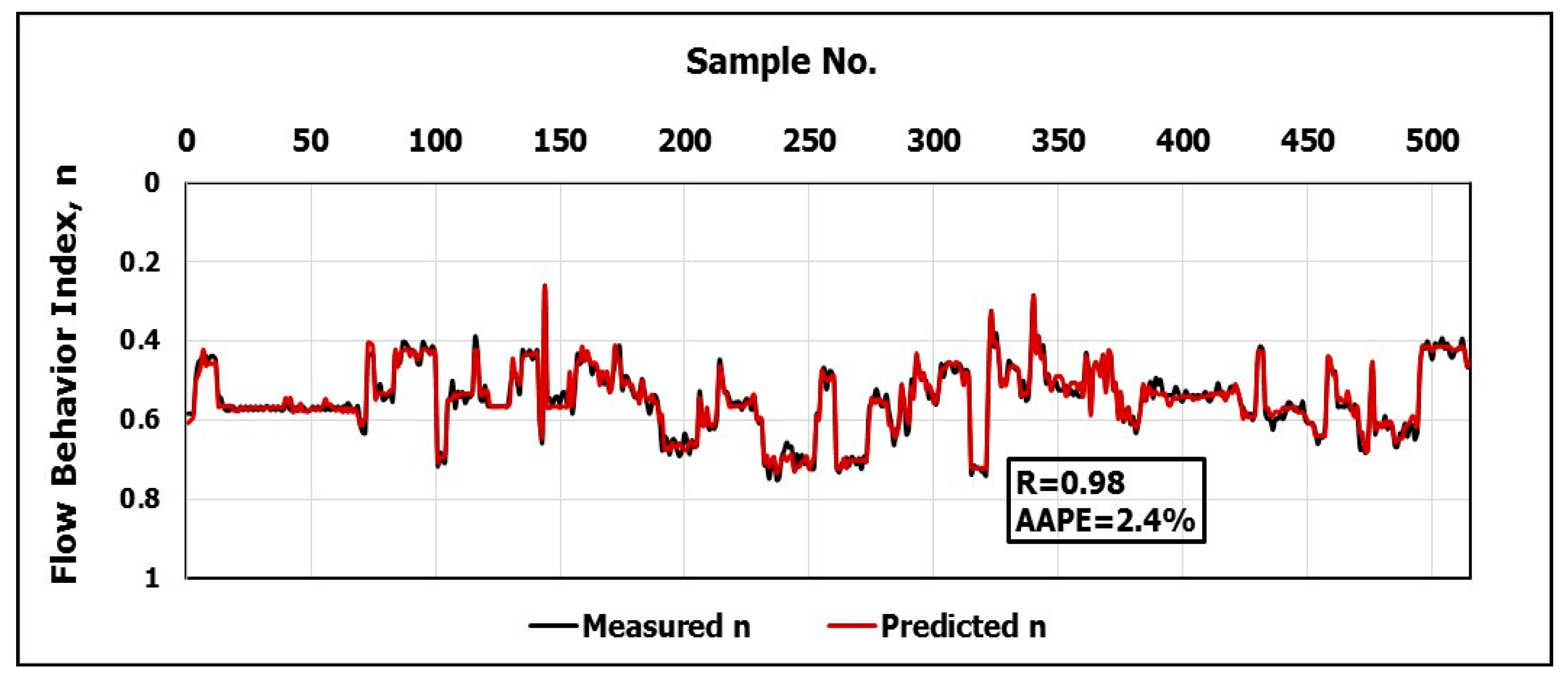
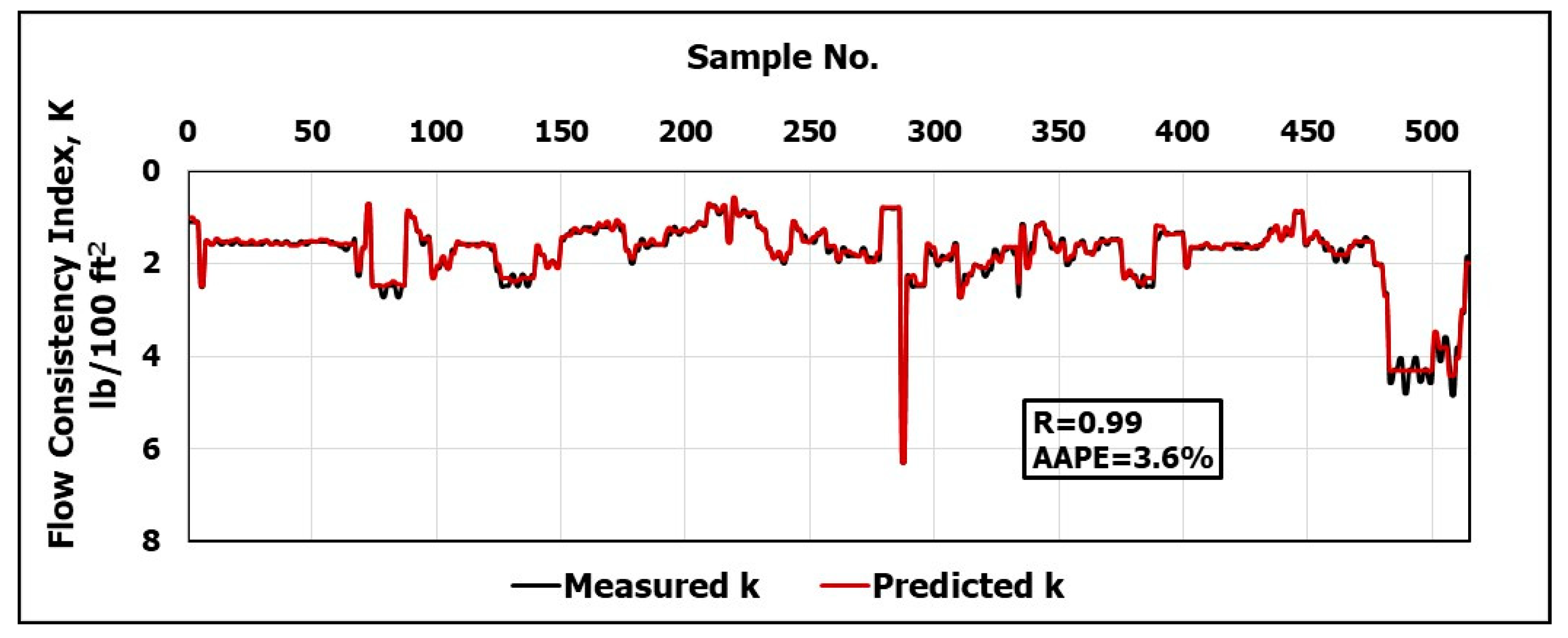
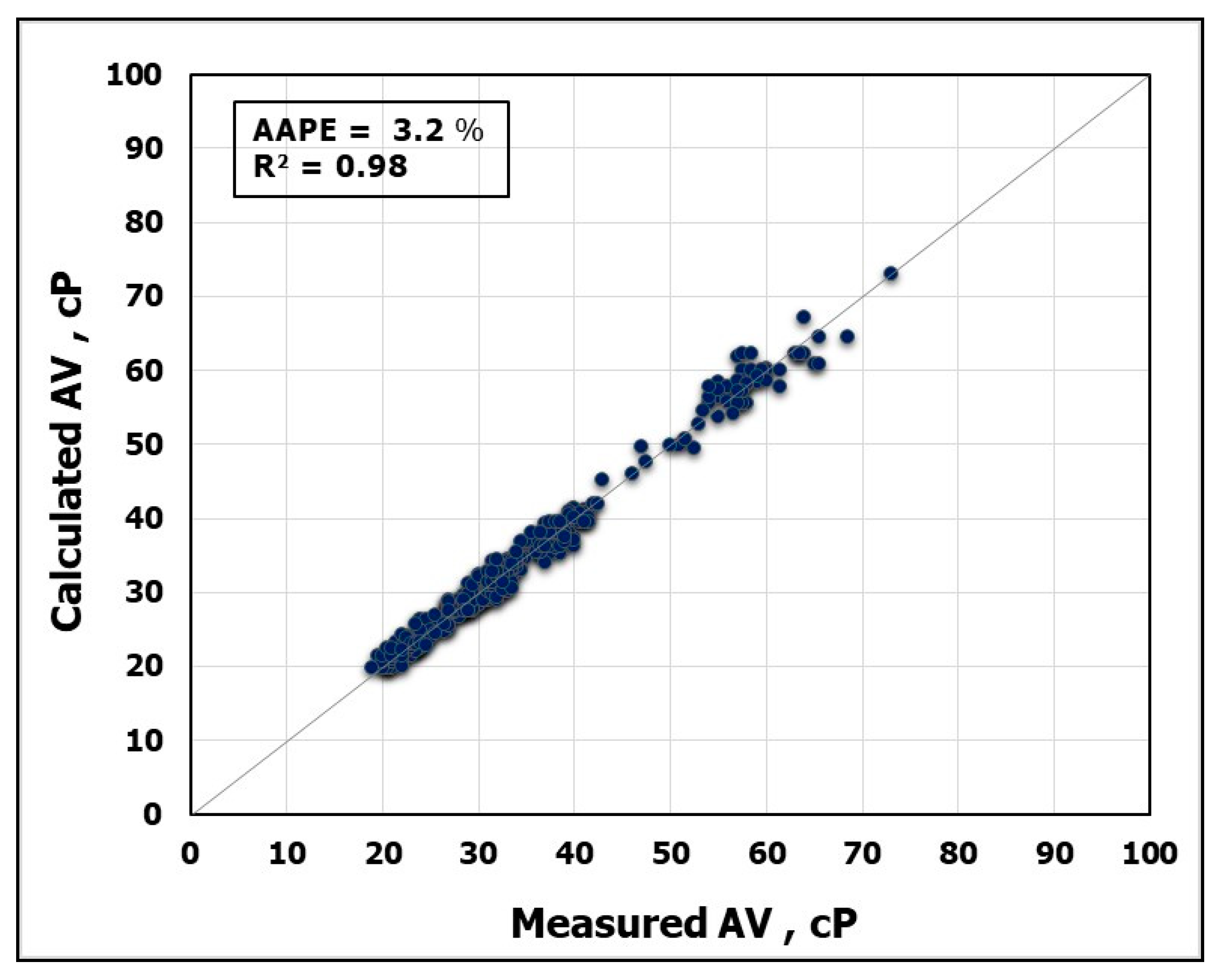
The objective of this work is to develop new models using artificial neural networks, ANN, to predict the rheological properties of the CaCl2 brine-based drilling fluid depending on frequent measurements of and . The real-time measurements of these parameters are very helpful for identifying the efficiency of the hole cleaning, optimizing the drilling fluid hydraulics, equivalent circulating density calculations and swab and surge pressure determination.
1.2. Artificial Neural Network (ANN)
Artificial intelligence, (AI), can be simply defined as the computer science branch for creating intelligent machines [
26] to exhibit human brains to make predictions and help take the right decisions for the future scenarios [
27]. Recently, different AI methods such as fuzzy logic, FL, support vector machine, SVM, genetic algorithm and artificial neural network, ANN, have been applied in petroleum engineering, and specifically in the field of drilling fluid engineering. Some of these applications include fluid flow patterns prediction in wellbore annulus [
28], stuck pipe prediction [
29], drilling hydraulics optimization [
30], frictional pressure loss estimation [
31], hole cleaning and prediction of cutting concentration [
32], estimation of the static Poisson’s ratio from log data [
33].
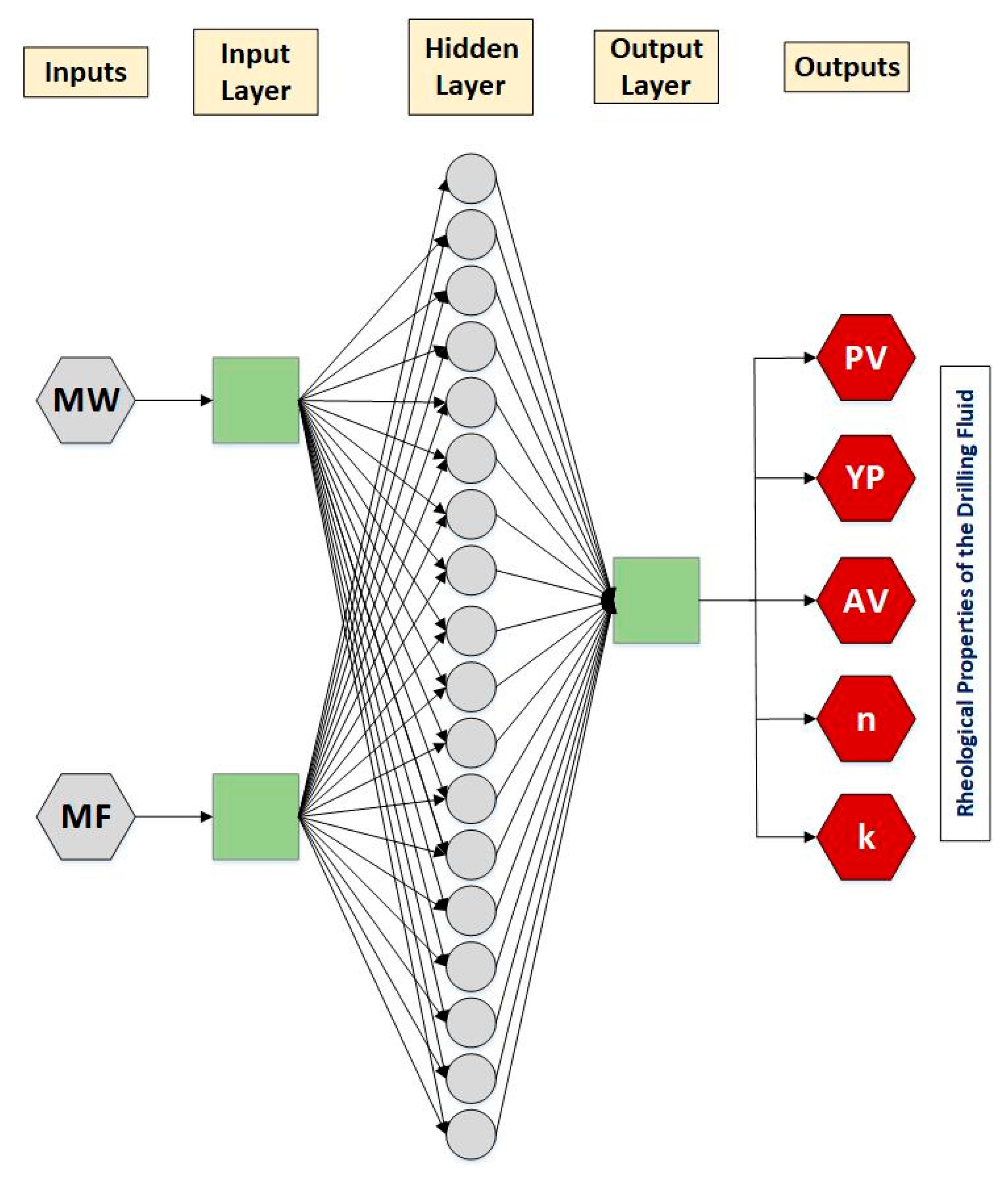
ANN is one of the most common AI techniques which has the ability to deal with different engineering problems with high complexity that exceed the computational capability of classical mathematics and procedures [
34]. It is based on analogy with biological neural networks to simulate the performance of the human biological neural system [
35]. The elementary units for ANN are neurons [
36]. The structure of the ANN consists of three main types of layers. The first one is for the input parameters. The second one is called hidden layers, which include the neurons assigned with the transfer functions between the inputs and the outputs. The third type is for the outputs. These layers, with the suitable training algorithm, describe the nature of the problem [
37]. The performance of the network is controlled by key parameters including the number of neurons, weights and biases [
38]. To optimize the weight and biases, the network is trained using different algorithms to achieve the lowest possible error. Among these algorithms is Levenberg-Marquardt (LM), which is an iterative, curve fitting algorithm. This algorithm proved its outstanding performance in solving non-linear least-squares problems [
39].
There are many ANN applications of ANN in the field of drilling fluid in the last few years. Some of these researches are the prediction of filtration volume and mud cake permeability of water-based mud (WBM) [
40], drill cutting settling velocity prediction [
41], prediction of differential pipe sticking [
42], lost circulation prediction [
43], hole cleaning efficiency of foam fluid [
44], rheological properties of invert emulsion mud [
45], invert emulsion mud rheology [
46] and spud mud rheology prediction [
47], generating geomechanical well logs [
48], prediction of oil PVT properties [
49].
Based on the literature, more than 50 percent of the applications in the drilling fluid area used ANN for the predictions and got high accurate results. Accordingly, ANN has been selected for building the proposed models in this study [
26].