Estimation of Static Young’s Modulus for Sandstone Formation Using Artificial Neural Networks
Abstract
:1. Introduction
2. Uses of Artificial Intelligence in Estimating Rock Mechanical Parameters
3. Methodology
3.1. Data Preparation
3.2. Training the ANN Model
3.3. Evaluation and Validation of the Developed ANN-Based Empirical Correlation
3.4. Evaluation Criterion
4. Results and Discussion
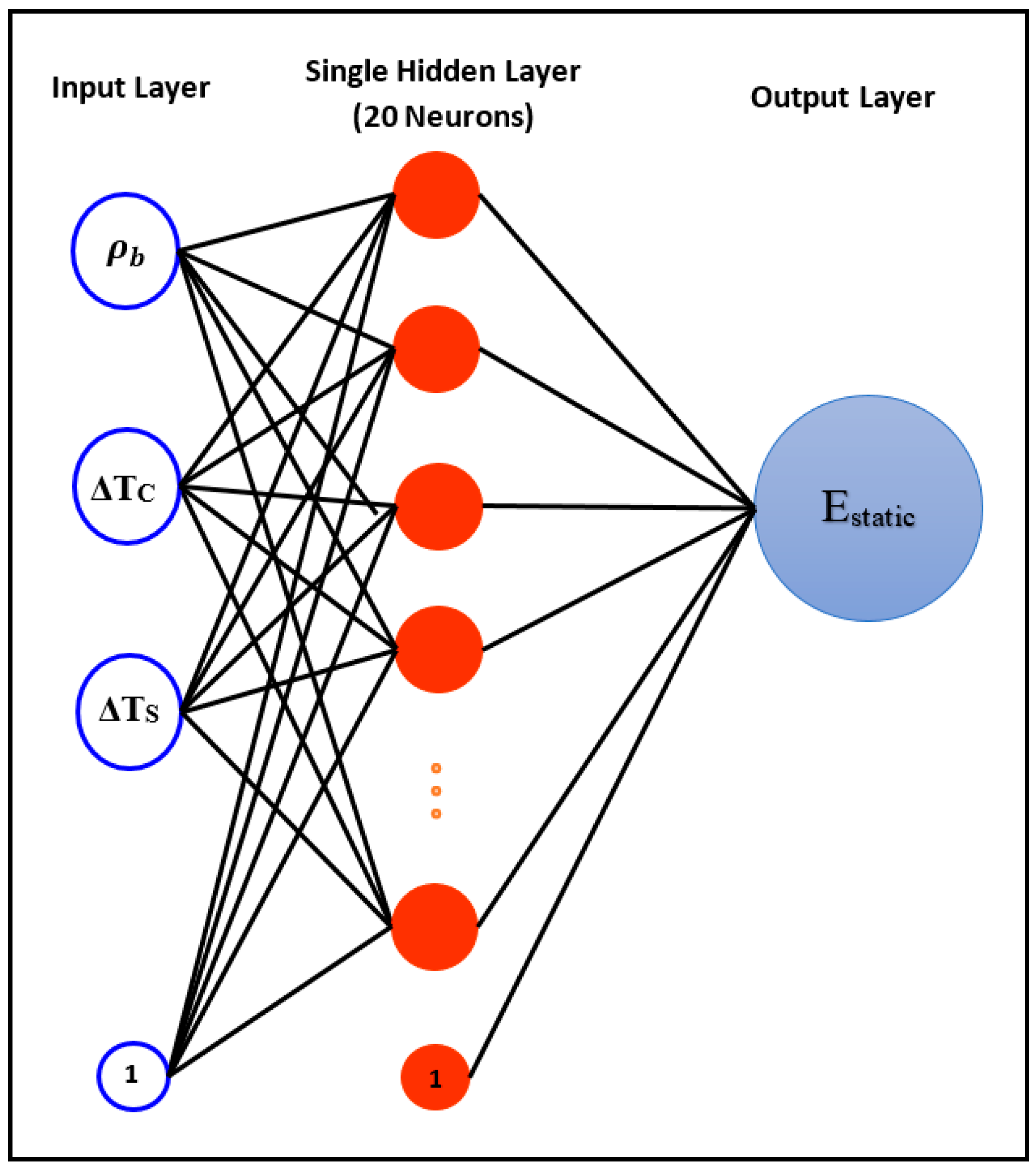
4.1. Training the ANN Model
4.2. Developing the ANN-Based Empirical Correlation
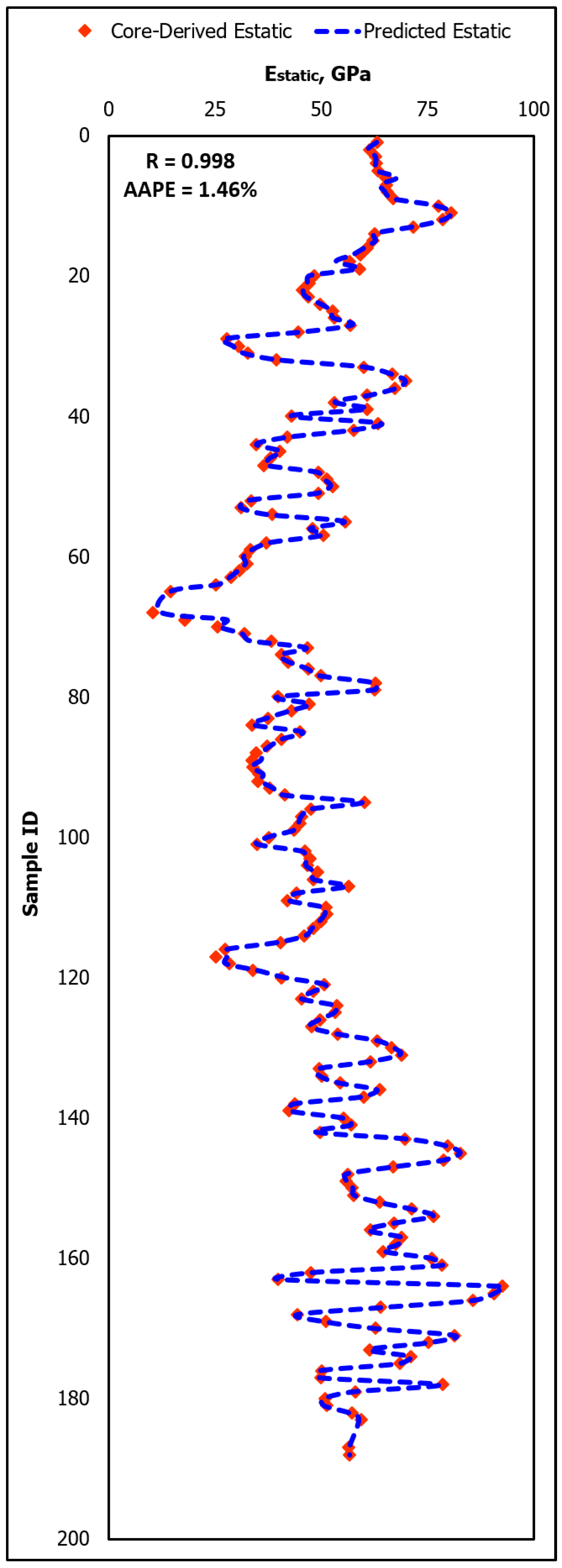
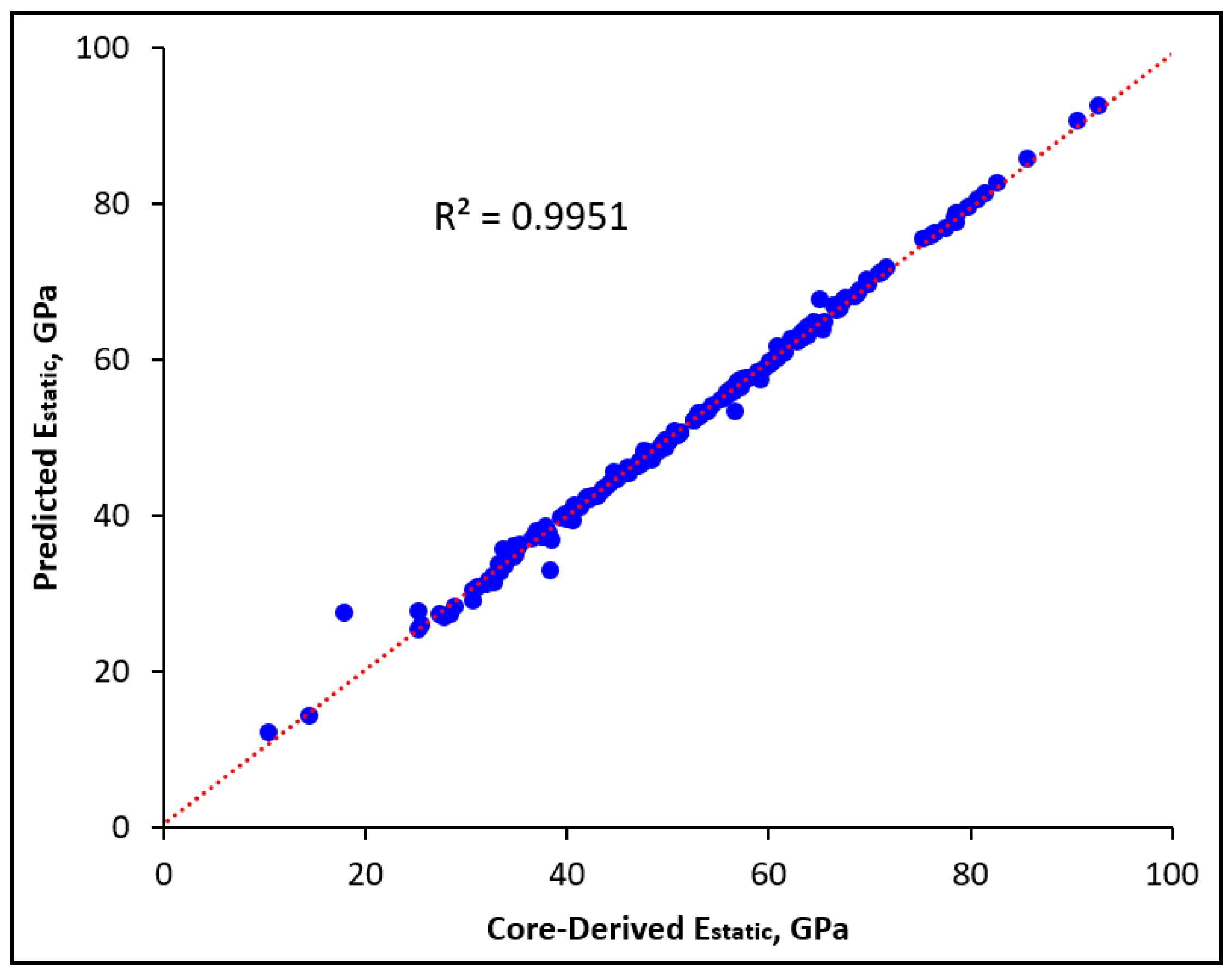
4.3. Testing the Developed ANN-Based Empirical Correlation
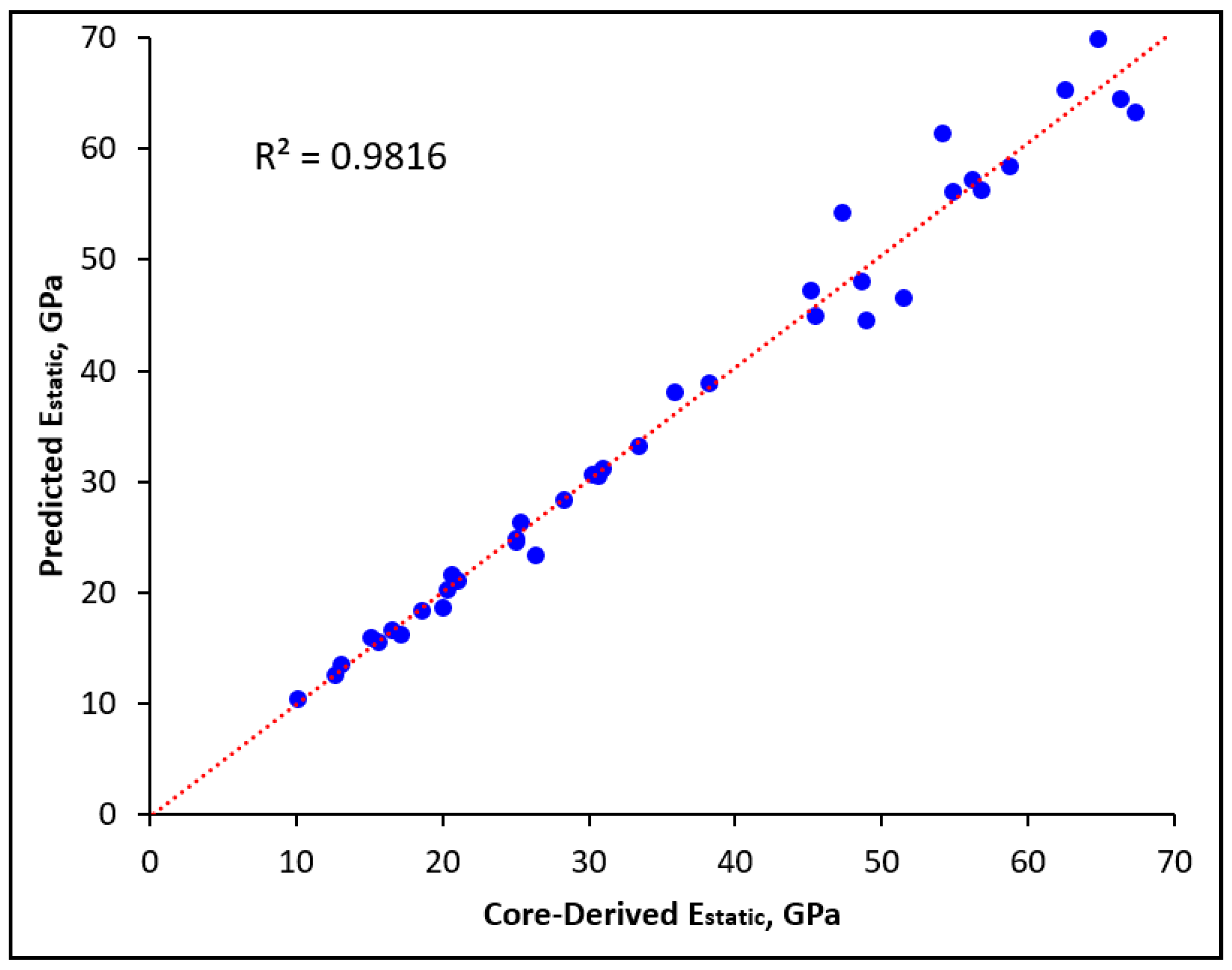
4.4. Validation of the Developed ANN-Based Empirical Correlation
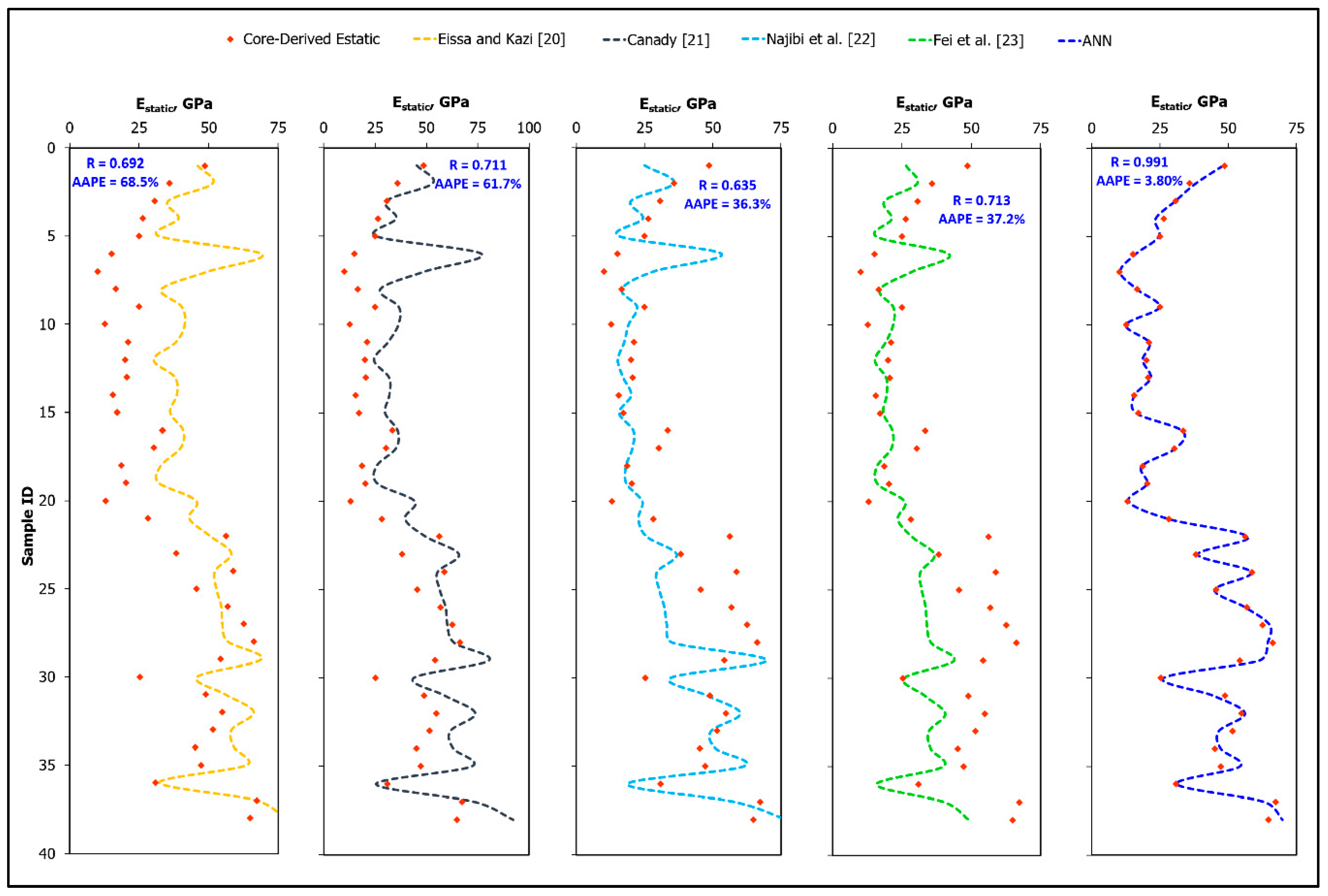
4.5. Comparing the Developed ANN-Based Empirical Correlation to the Available Correlations
5. Conclusions
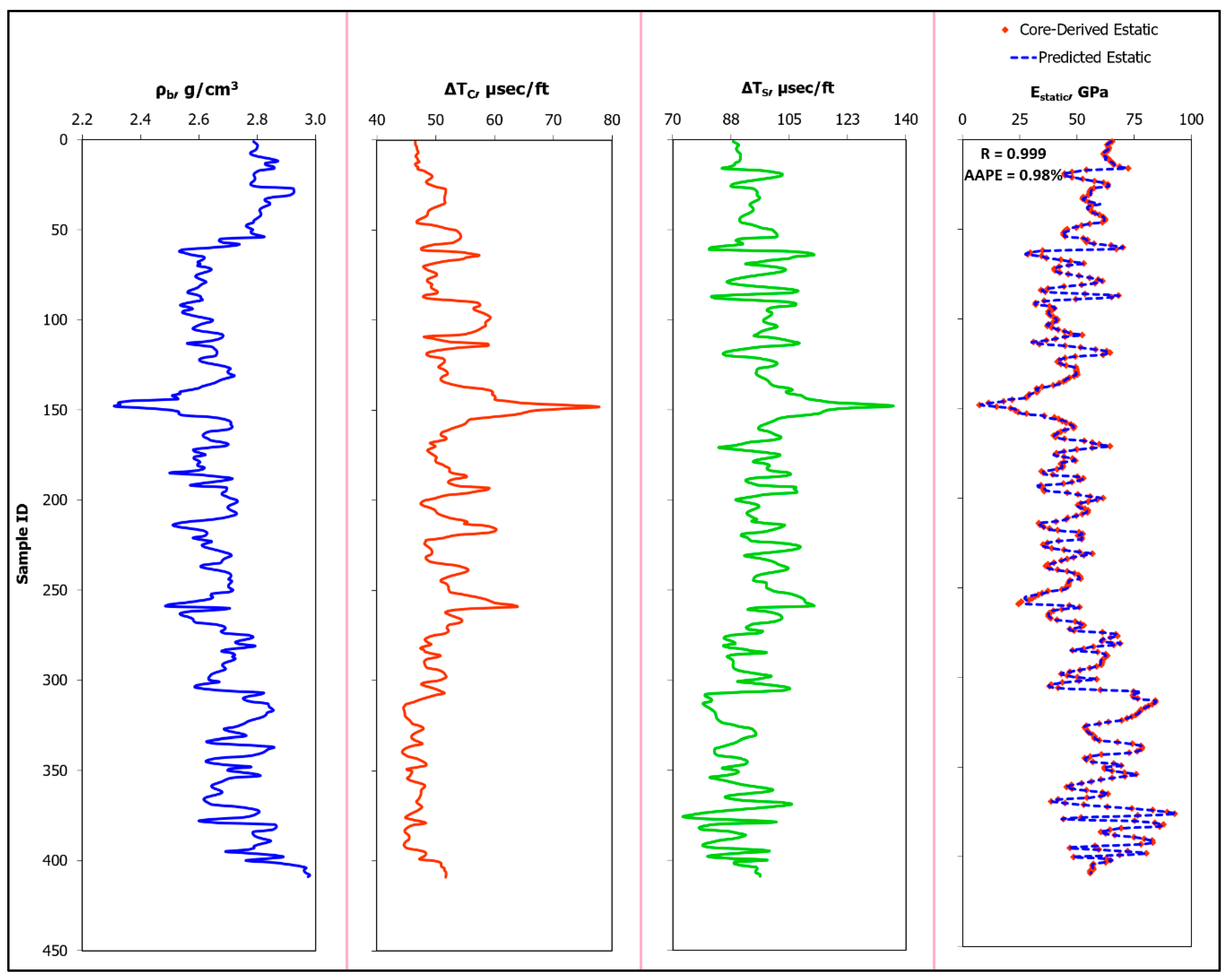
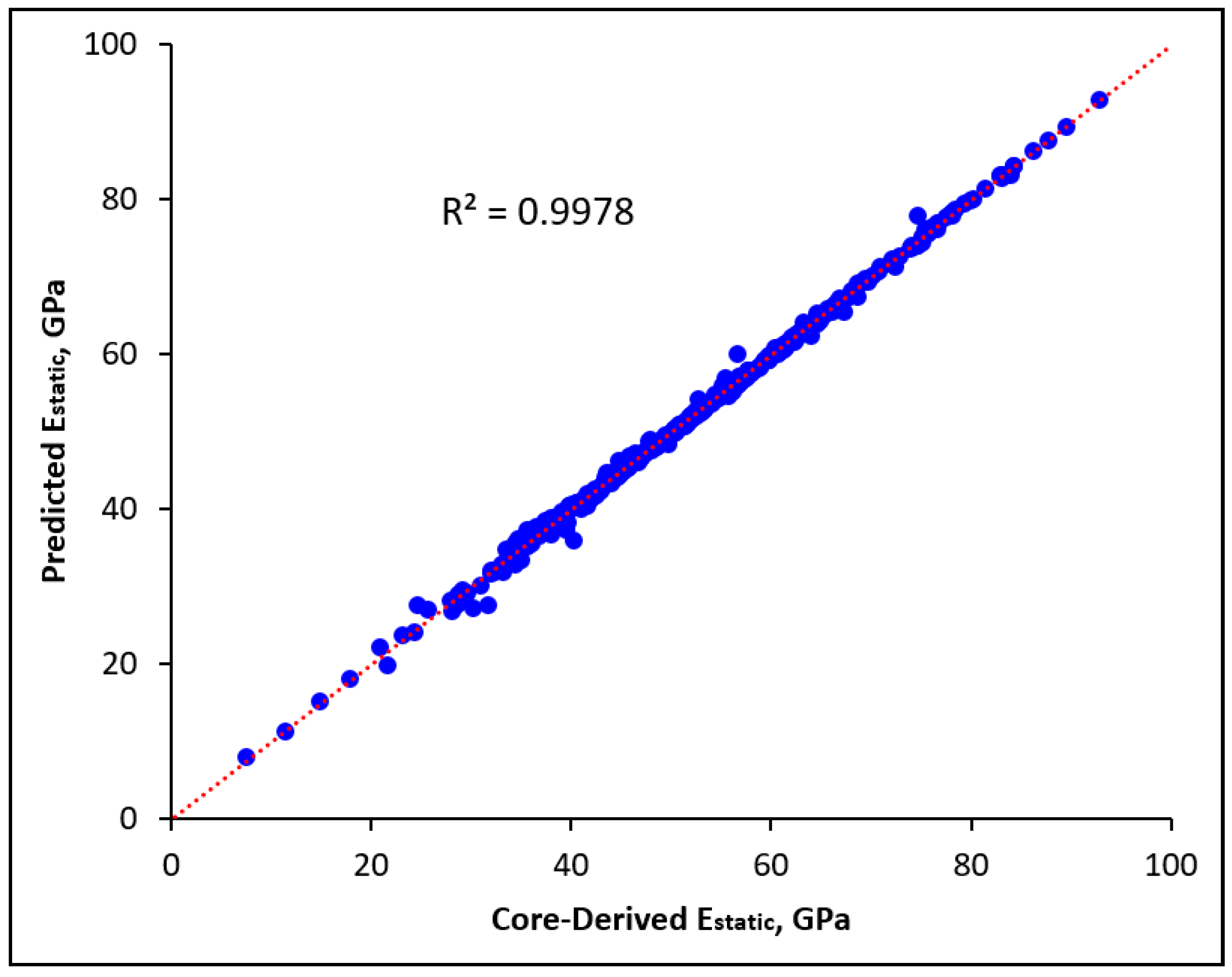
- The developed ANN model was capable of estimating Estatic for the training dataset with very high accuracy, as indicated by the low AAPE of 0.98%, very high R of 0.999, and R2 of 0.9978. The ANN-based empirical correlation was able to predict Estatic for the testing dataset (unseen) accurately; the Estatic values of the testing dataset were estimated with AAPE, R, and R2 values of 1.46%, 0.998, and 0.9951, respectively.
- The developed empirical correlation was validated using a dataset composed of unseen 55 data points of three wells. Validating the developed correlation using the dataset of Well-B (38 points) revealed a highly accurate prediction of the developed correlation where AAPE, R and R2 valueswere 3.8, 0.991 and 0.9816 respectively.
- The ANN-based empirical correlation is useful in predicting continuous profile of static Young’s modulus for sandstone formation using conventional log data, bulk density, shear transit time and compressional transit time when there are no available cores.
- Comparing the predictive accuracy of the ANN-based correlation with four of the available empirical equations confirmed the high accuracy of the ANN-based correlation which was able to estimate the Estatic for the validation data of Well-B with an AAPE of 3.8% compared with an AAPE of more than 36.0% for all available correlations.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| AAPE | Average absolute percentage error |
| ANN | Artificial neural networks |
| ΔTC | Compressional transit time |
| ΔTS | Shear transit time |
| E | Young’s modulus |
| Estatic | Static Young’s modulus |
| Edynamic | Dynamic Young’s modulus |
| logsig | Log-sigmoid |
| R | Correlation coefficient |
| R2 | Coefficient of determination |
| ρb | Bulk density |
| SaDE | Self-adaptive differential evolution |
| trainbr | Bayesian regularization backpropagation |
References
- Fjaer, E.; Horsrud, H.P.; Raaen, A.M.; Risnes, R. Petroleum Related Rock Mechanics; Elsevier B. V.: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Chang, C.; Zoback, M.D.; Khaksar, A. Empirical relations between rock strength and physical properties in sedimentary rocks. J. Pet. Sci. Eng. 2006, 51, 223–237. [Google Scholar] [CrossRef]
- Gatens, J.M.; Harrison, C.W.; Lancaster, D.E.; Guldry, F.K. In-situ stress tests and acoustic logs determine mechanical properties and stress profiles in the devonian shales. SPE Form. Eval. 1990, 5, 248–254. [Google Scholar] [CrossRef]
- Nes, O.M.; Fjaer, E.; Tronvoll, J.; Kristiansen, T.G.; Horsrud, P. Drilling time reduction through an integrated rock mechanics analysis. J. Energy Res. Technol. 2012, 134, 2802:1–2802:7. [Google Scholar] [CrossRef]
- Meyer, B.R.; Jacot, R.H. Impact of stress-dependent Young’s moduli on hydraulic fracture modeling. In Proceedings of the 38th U.S. Symposium on Rock Mechanics, Washington, DC, USA, 7–10 July 2001. ARMA-01-0297. [Google Scholar]
- Howard, G.C.; Fast, C.R. Hydraulic Fracturing. In Doherty Memorial Fund of AIME, Society of Petroleum Engineers of AIME; Henry L.: New York, NY, USA, 1970; Monograph Volume 2 of SPE. [Google Scholar]
- Barree, R.D.; Gilbert, J.V.; Conway, M.W. Stress and rock property profiling for unconventional reservoir stimulation. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 19–21 January 2009. SPE-118703-MS. [Google Scholar]
- Colin, C.; Potter, S.; Darren, F. Formation elastic parameters by deriving S-wave velocity logs. CREWES Res. 1997, 9, 1–10. [Google Scholar]
- King, M.S. Wave Velocities in Rocks as a Function of Changes in Over burden Pressure and Pore Fluid Saturants. Geophysics 1966, 31, 50–73. [Google Scholar] [CrossRef]
- Rinehart, J.S.; Fortin, J.-P.; Baugin, P. Propagation Velocity of Longitudinal Waves in Rock. Effect of State of Stress, Stress Level of the Wave, Water Content, Porosity, Temperature Stratification and Texture. In Proceedings of the 4th Symposium on Rock Mechanics, University Park, PA, USA, 30 March–1 April 1961. ARMA-61-119. [Google Scholar]
- Simmons, G.; Brace, W.I. Comparison of Static and Dynamic Measurements of Compressibility of Rocks. J. Geophys. Res. 1965, 70, 5649–5656. [Google Scholar] [CrossRef]
- Abdulraheem, A.; Ahmed, M.; Vantala, A.; Parvez, T. Prediction of Rock Mechanical Parameters for Hydrocarbon Reservoirs Using Different Artificial Intelligence Techniques. In Proceedings of the Saudi Arabia Section Technical Symposium, Al-Khobar, Saudi Arabia, 9–11 May 2009. SPE-126094-MS. [Google Scholar]
- Larsen, I.; Fjær, E.; Renlie, L. Static and Dynamic Poisson’s Ratio of Weak Sandstones. In Proceedings of the 4th North American Rock Mechanics Symposium, Seattle, WA, USA, 31 July–3 August 2000. ARMA-2000-0077. [Google Scholar]
- Bai, P. Experimental research on rock drillability in the center of junggar basin. Electron. J. Geotech. Eng. 2013, 18, 5065–5074. [Google Scholar]
- Ca, H.; Xi, L.; Guo, L. Rock mechanics study on the safety and efficient extraction for deep moderately inclined medium-thick orebody. Electron. J. Geotech. Eng. 2015, 20, 11073–11082. [Google Scholar]
- Li, P.; Liu, X.; Zhong, Z. Mechanical Property Experiment and Damage Statistical Constitutive Model of Hongze Rock Salt in China. Electron. J. Geotech. Eng. 2015, 20, 81–94. [Google Scholar]
- King, M.S. Static and Dynamic elastic moduli of rocks under pressure. In Proceedings of the 11th U.S. Symposium on Rock Mechanics, Berkeley, CA, USA, 16–19 June 1969. ARMA-69-0329. [Google Scholar]
- Wang, Z.; Nur, A.A. Dynamic versus static elastic properties of reservoir rocks. J. Seism. Acoust. Veloc. Res. Rocks 2000, 19, 531–539. [Google Scholar]
- Khaksar, A.; Taylor, P.G.; Fang, Z.; Kayes, T.; Salazar, A.; Rahman, K. Rock strength from core and logs, where we stand and ways to go. In Proceedings of the EUROPEC/EAGE conference and exhibition, Amsterdam, The Netherlands, 8–11 June 2009. SPE-121972-MS. [Google Scholar]
- Eissa, E.A.; Kazi, A. Relation between static and dynamic Young’s moduli of rocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 479–482. [Google Scholar] [CrossRef]
- Canady, W.J. A Method for Full-Range Young’s Modulus Correction. Presented at the North American Unconventional Gas Conference and Exhibition, The Woodlands, TX, USA, 14–16 June 2011. Paper SPE-143604-MS. [Google Scholar] [CrossRef]
- Najibi, A.R.; Ghafoori, M.; Lashkaripour, G.R.; Asef, M.R. Empirical relations between strength and static and dynamic elastic properties of Asmari and Sarvak limestones, two main oil reservoirs in Iran. J. Pet. Sci. Eng. 2015, 126, 78–82. [Google Scholar] [CrossRef]
- Fei, W.; Huiyuan, B.; Jun, Y.; Yonghao, Z. Correlation of Dynamic and Static Elastic Parameters of Rock. Electron. J. Geotech. Eng. 2016, 21, 1551–1560. [Google Scholar]
- Mahmoud, M.A.; Elkatatny, S.A.; Ramadan, E.; Abdulraheem, A. Development of Lithology-Based Static Young’s Modulus Correlations from Log Data Based on Data Clustering Technique. J. Pet. Sci. Eng. 2016, 146, 10–20. [Google Scholar] [CrossRef]
- Tariq, A.; Elkatatny, S.A.; Mahmoud, M.A.; Zaki, A.; Abdulraheem, A. A New Approach to Predict Failure Parameters of Carbonate Rocks using Artificial Intelligence Tools. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 24–27 April 2017. SPE-187974-MS. [Google Scholar]
- Elkatatny, S.M.; Tariq, Z.; Mahmoud, M.A.; Abdulraheem, A.; Abdelwahab, A.Z.; Woldeamanuel, M. An Artificial Intelligent Approach to Predict Static Poisson’s Ratio. In Proceedings of the 51st US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017. ARMA 17-771. [Google Scholar]
- Tariq, Z.; Elkatatny, S.M.; Mahmoud, M.A.; Abdulazeez, A. A Holistic Approach to Develop New Rigorous Empirical Correlation for Static Young’s Modulus. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, 7–10 November 2016. SPE-183545-MS. [Google Scholar]
- Tariq, Z.; Elkatatny, S.M.; Mahmoud, M.A.; Abdulazeez, A. A New Artificial Intelligence Based Empirical Correlation to Predict Sonic Travel Time. In Proceedings of the International Petroleum Technology Conference, Bangkok, Thailand, 14–16 November 2016. IPTC-19005-MS. [Google Scholar]
- Tariq, Z.; Elkatatny, S.M.; Mahmoud, M.A.; Abdulraheem, A.; Abdelwahab, A.Z.; Woldeamanuel, I.M. Development of New Correlation for Unconfined Compressive Strength for Carbonate Reservoir Using Artificial Intelligence Techniques. In Proceedings of the 51st US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017. ARMA 17-428. [Google Scholar]
- Tariq, Z.; Elkatatny, S.M.; Mahmoud, M.A.; Abdulraheem, A.; Abdelwahab, A.Z.; Woldeamanuel, M. Estimation of Rock Mechanical Parameters using Artificial Intelligence Tools. In Proceedings of the 51st US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017. ARMA 17-301. [Google Scholar]
- Omran, M.G.H.; Salman, A.; Engelbrecht, A.P. Self-adaptive Differential Evolution. In Computational Intelligence and Security; Hao, Y., Liu, J., Wang, Y., Cheung, Y.-m., Yin, H., Jiao, L., Ma, J., Jiao, Y.-C., Eds.; CIS 2005. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3801. [Google Scholar]
- Al-Anazi, A.F.; Gates, I.D. A support vector machine algorithm to classify lithofacies and model permeability in heterogeneous reservoirs. Eng. Geol. 2010, 114, 267–277. [Google Scholar] [CrossRef]
- MathWorks. Available online: https://www.mathworks.com/help/deeplearning/ref/trainbr.html;jsessionid=7cc70c77fdb3f0bb58ed870c69c7 (accessed on 1 April 2019).
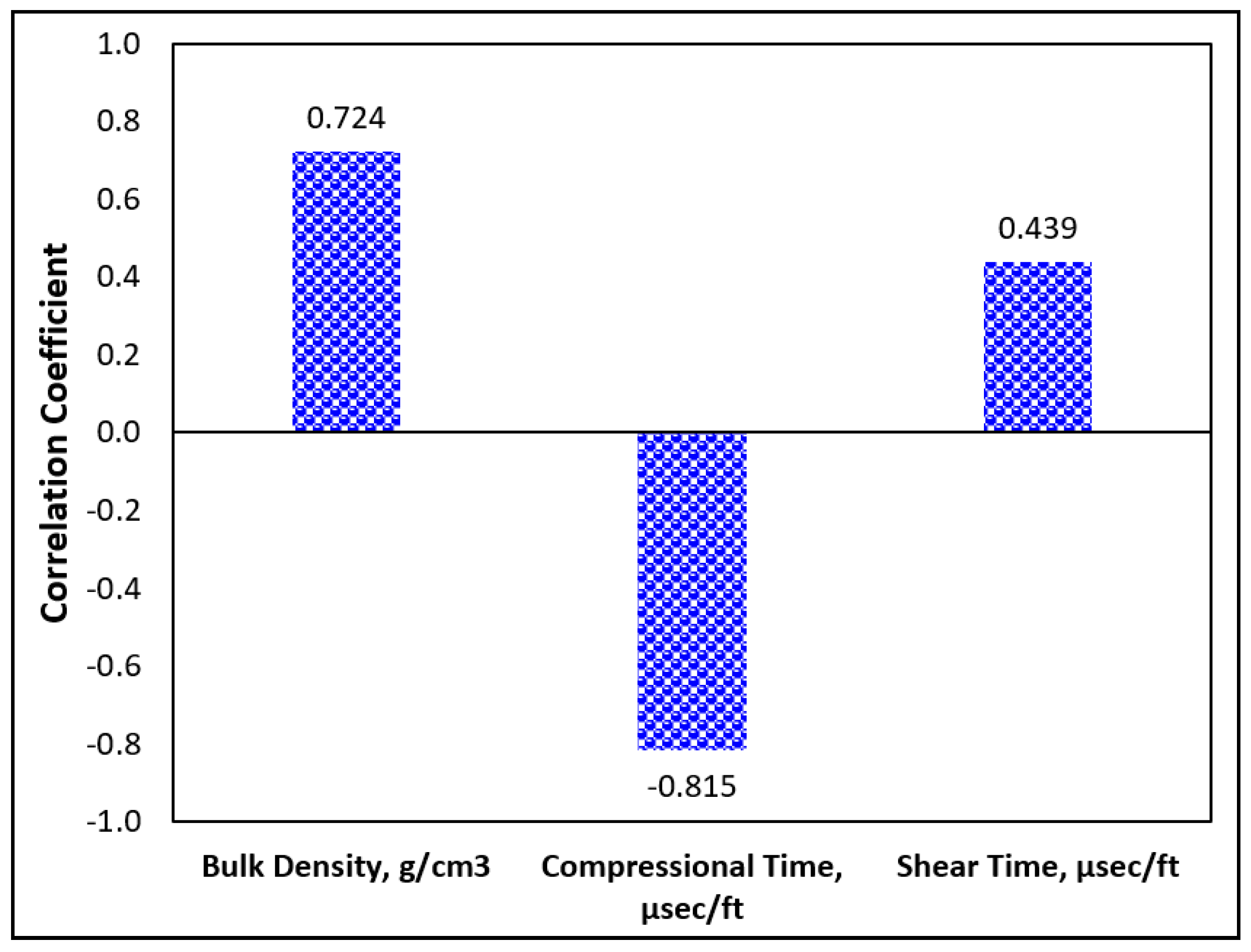

| Statistical Parameter | ρb, g/cm3 | ΔTC, μsec/ft | ΔTS, μsec/ft | Estatic, Gpa |
|---|---|---|---|---|
| Minimum | 2.312 | 44.3 | 73.2 | 7.5 |
| Maximum | 2.968 | 77.8 | 136.1 | 92.8 |
| Range | 0.656 | 33.4 | 62.9 | 85.3 |
| Standard Deviation | 0.106 | 4.69 | 8.39 | 13.93 |
| Sample Variance | 0.011 | 22.0 | 70.3 | 194.0 |
| Kurtosis | 0.569 | 4.262 | 1.673 | 0.167 |
| Skewness | 0.011 | 1.569 | 0.564 | 0.186 |
| Parameter | Value |
|---|---|
| Learning function | trainbr |
| Transfer function | logsig |
| Number of hidden layers | 1 |
| Number of neurons | 20 |
| i | w1i,1 | w1i,2 | w1i,3 | b1i | w2i |
|---|---|---|---|---|---|
| 1 | −4.368 | 20.303 | −14.485 | −3.638 | 5.437 |
| 2 | −0.216 | 1.507 | 2.017 | 4.178 | −2.494 |
| 3 | 1.792 | −2.322 | −21.160 | −3.877 | −4.132 |
| 4 | 0.269 | 0.057 | −0.949 | 1.777 | 6.325 |
| 5 | 1.498 | −19.164 | 3.620 | 6.726 | 9.261 |
| 6 | 13.802 | 12.907 | −0.662 | 2.170 | 0.640 |
| 7 | 3.466 | 8.897 | 1.549 | −3.110 | 4.174 |
| 8 | −4.369 | −0.142 | 17.692 | 1.732 | 5.813 |
| 9 | −1.604 | 21.932 | −1.059 | −9.030 | 5.608 |
| 10 | 10.803 | −12.301 | 24.520 | 16.752 | 9.748 |
| 11 | 14.298 | 13.932 | 0.070 | 0.895 | −5.642 |
| 12 | −49.173 | −25.972 | −1.332 | 15.768 | 9.929 |
| 13 | −3.062 | 15.989 | −11.554 | −3.115 | −4.766 |
| 14 | −18.124 | −17.674 | 0.206 | −1.307 | −3.944 |
| 15 | 40.409 | 23.746 | 0.690 | −14.273 | −11.118 |
| 16 | 6.280 | 3.526 | −8.930 | 2.199 | −0.945 |
| 17 | 7.010 | 3.251 | −11.579 | 1.502 | 1.544 |
| 18 | 19.888 | 7.137 | 0.149 | −8.787 | −1.596 |
| 19 | −32.100 | −16.426 | −1.400 | 11.426 | −23.697 |
| 20 | −3.053 | 1.125 | 19.499 | 2.853 | −9.194 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoud, A.A.; Elkatatny, S.; Ali, A.; Moussa, T. Estimation of Static Young’s Modulus for Sandstone Formation Using Artificial Neural Networks. Energies 2019, 12, 2125. https://doi.org/10.3390/en12112125
Mahmoud AA, Elkatatny S, Ali A, Moussa T. Estimation of Static Young’s Modulus for Sandstone Formation Using Artificial Neural Networks. Energies. 2019; 12(11):2125. https://doi.org/10.3390/en12112125
Chicago/Turabian StyleMahmoud, Ahmed Abdulhamid, Salaheldin Elkatatny, Abdulwahab Ali, and Tamer Moussa. 2019. "Estimation of Static Young’s Modulus for Sandstone Formation Using Artificial Neural Networks" Energies 12, no. 11: 2125. https://doi.org/10.3390/en12112125
APA StyleMahmoud, A. A., Elkatatny, S., Ali, A., & Moussa, T. (2019). Estimation of Static Young’s Modulus for Sandstone Formation Using Artificial Neural Networks. Energies, 12(11), 2125. https://doi.org/10.3390/en12112125






