An Optimal-Control Scheme for Coordinated Surplus-Heat Exchange in Industry Clusters
Abstract
1. Introduction
1.1. Related Work and Main Contribution
1.2. Outline
1.3. Notation
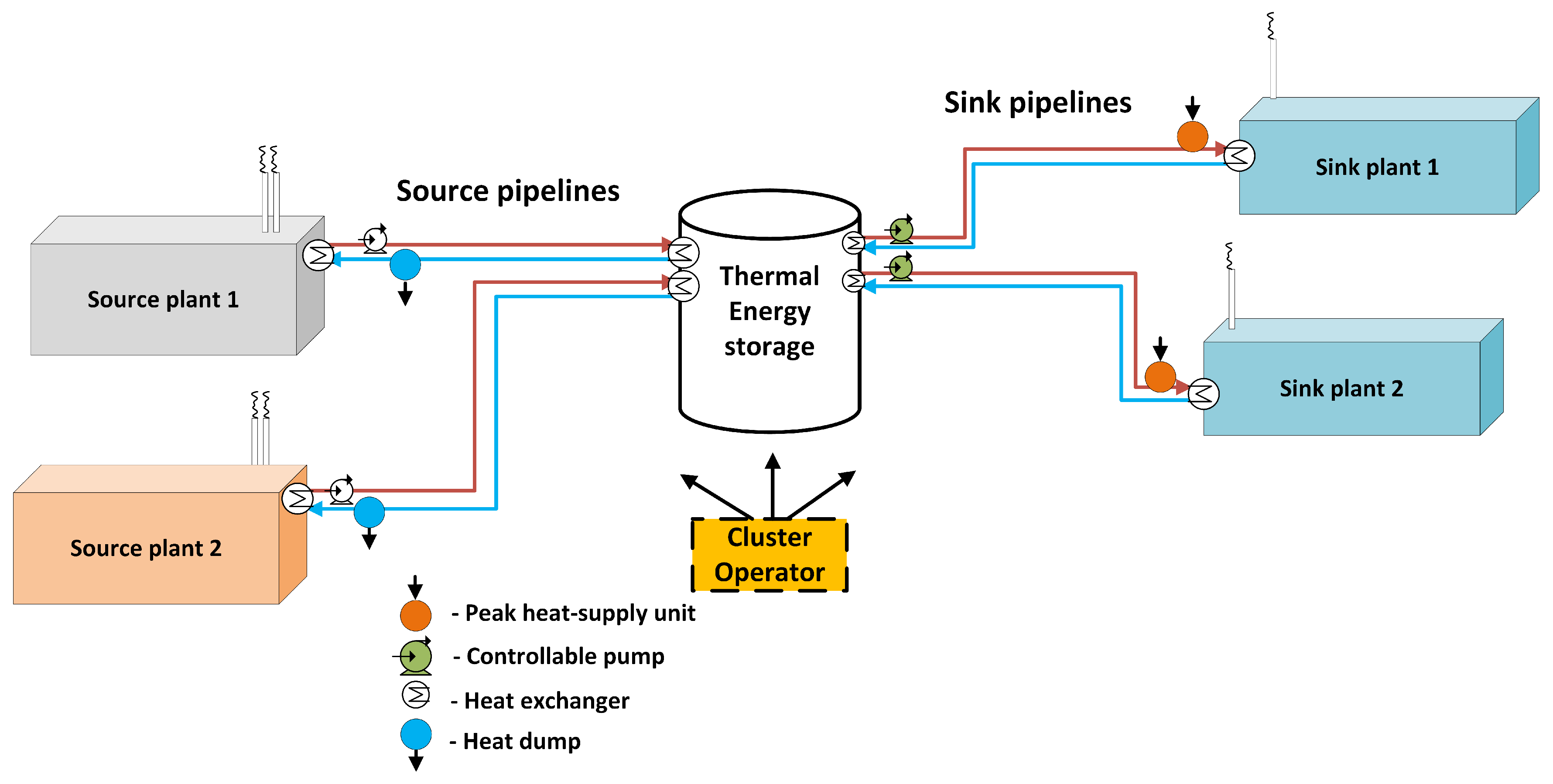
2. Problem Description
3. Methodology
3.1. Systems Modeling of Surplus-Heat Exchange in Industrial Clusters
3.2. Optimal-Control for Coordinated Surplus-Heat Exchange
3.2.1. Control Variables
3.2.2. Constraints
3.2.3. Objective Function
3.2.4. Software Implementation
4. Numerical Case Study
4.1. Comparison Case: Surplus-Hheat Exchange without TES Unit
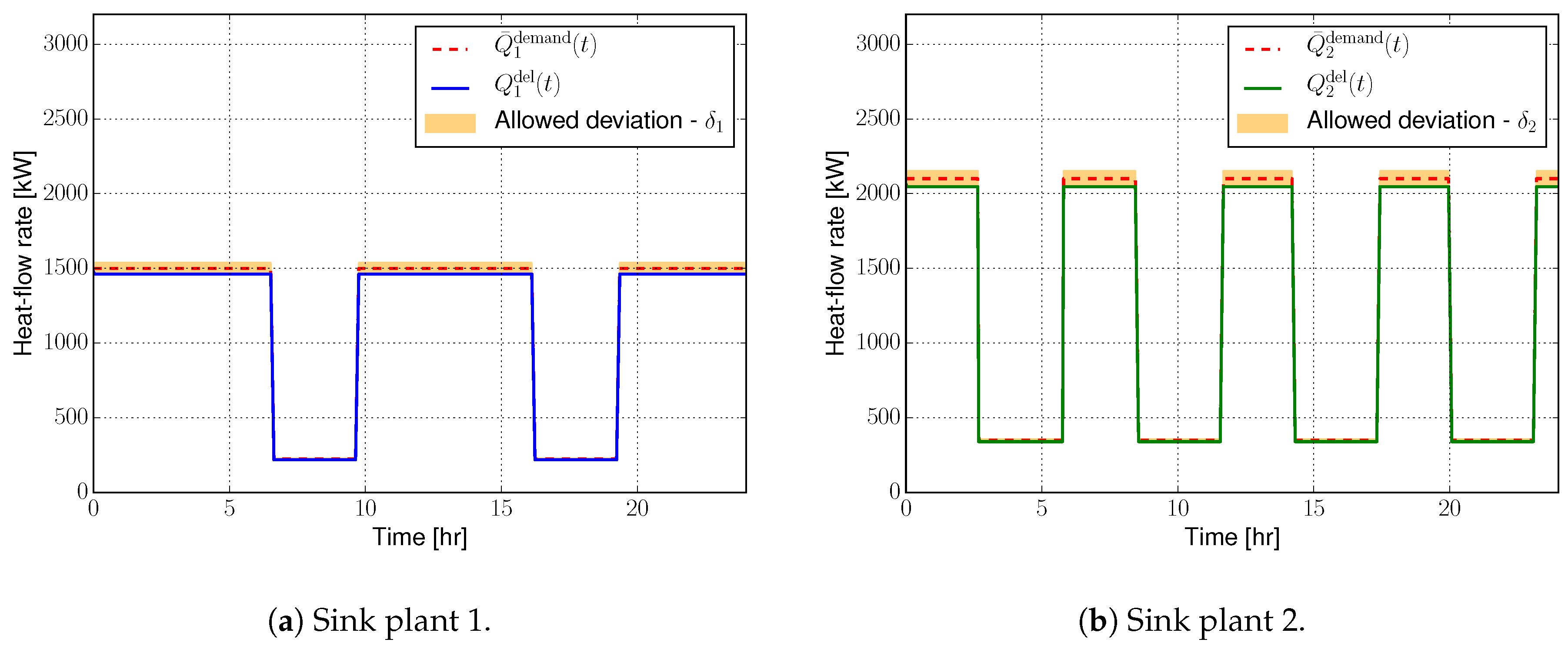
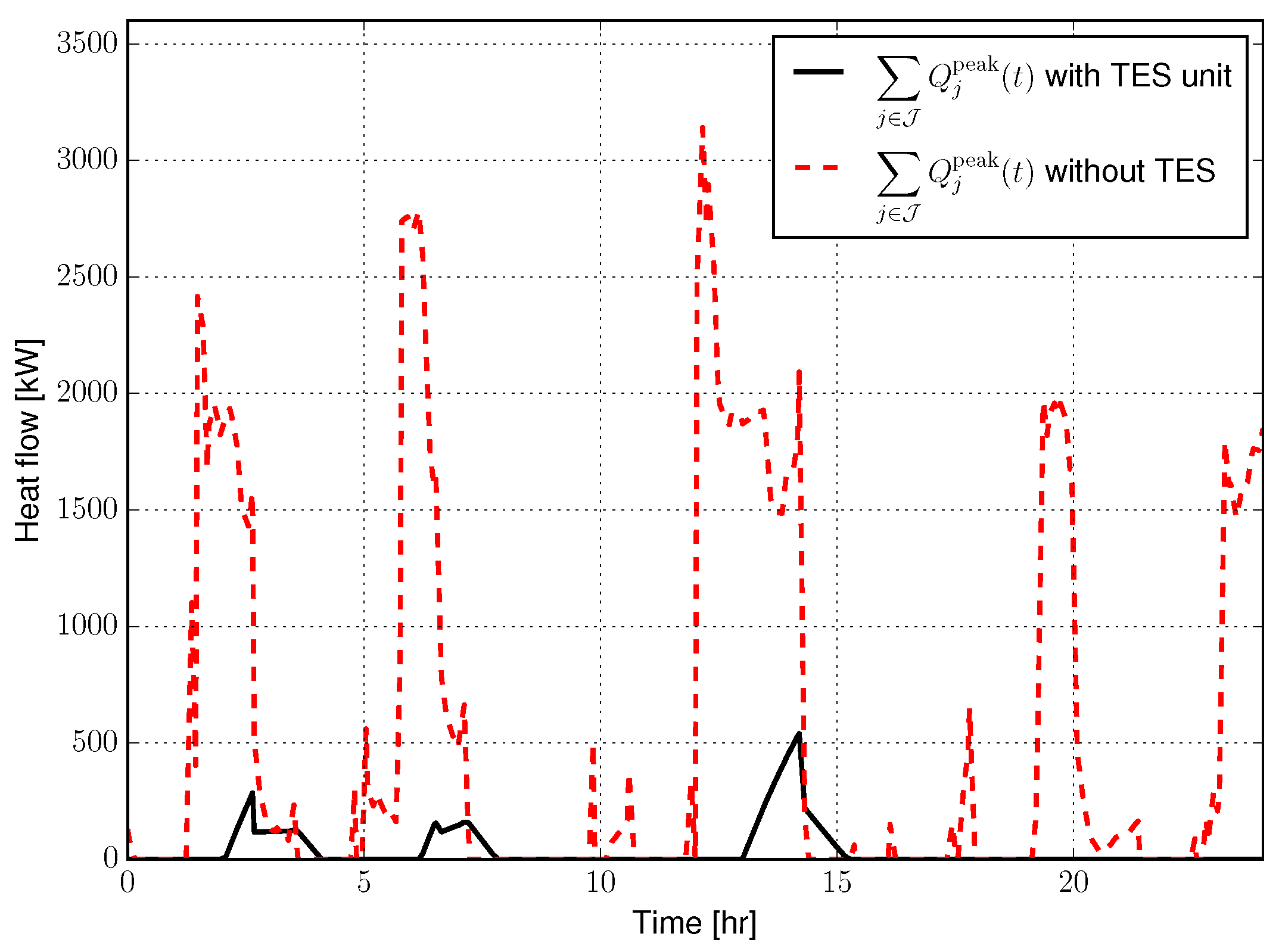
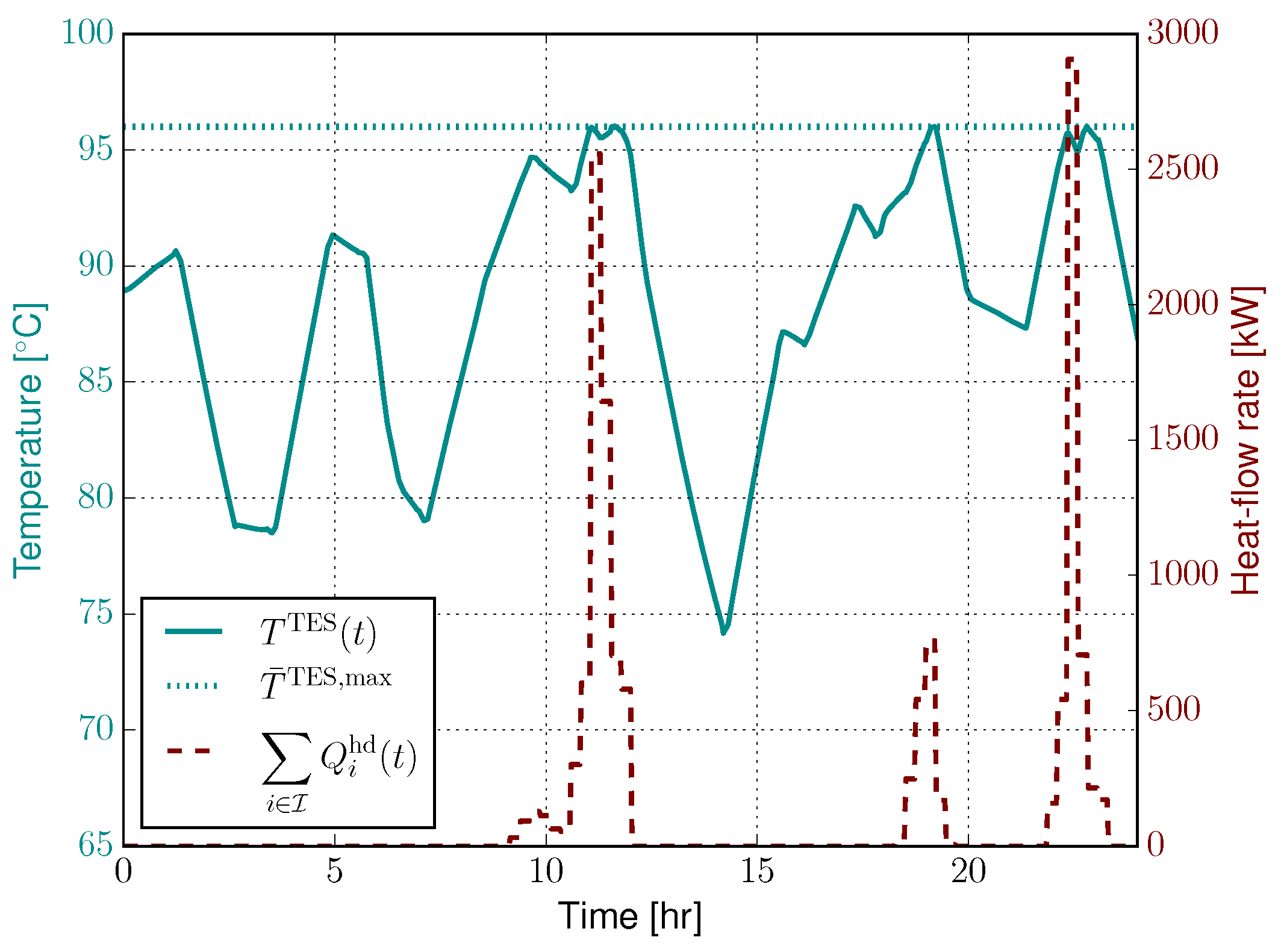
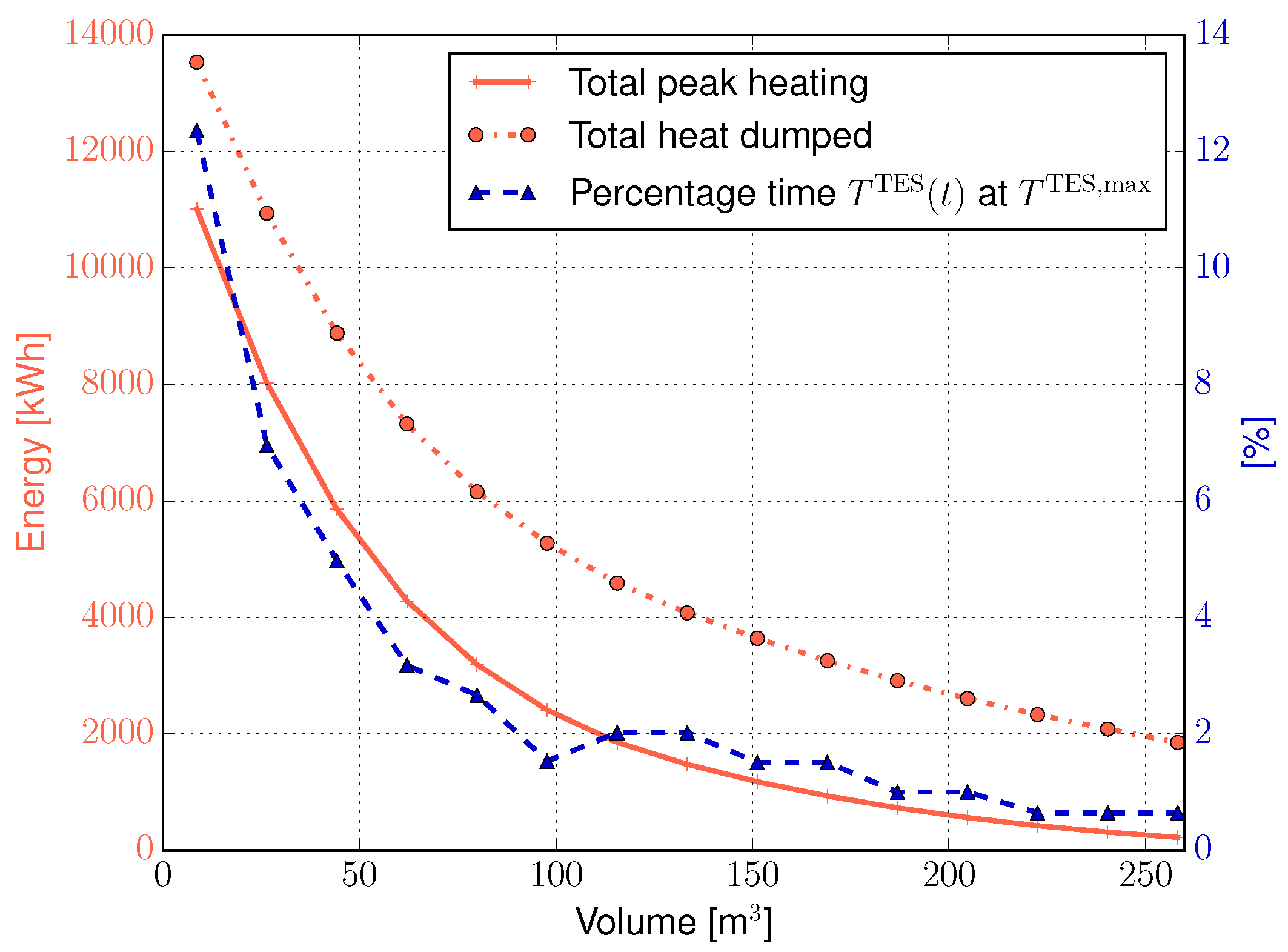
4.2. Results
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations and Nomenclature
| A | Heat transfer cross area [m] |
| amb | Ambient conditions |
| c | Specific heat capacity [kJ/kgK] |
| DAE | Differential algebraic equation |
| DH | District heating |
| del | Delivered |
| HEN | Heat-exchanger network |
| HEX | Heat exchanger |
| hd | Heat dump |
| init | Initial conditions |
| Set of plants with surplus heat | |
| Set of plants with heat demand | |
| LMTD | Log-mean-temperature-difference |
| loss | Loss to surroundings |
| MPC | Model predictive control |
| NLP | Nonlinear programming |
| n | Number of discrete elements |
| peak | Peak-heating unit |
| pipe-source | heat-transfer pipeline from source plant |
| pipe-sink | heat-transfer pipeline to sink plant |
| Q | Heat-flow rate [kW] |
| Available surplus heat-flow rate from source plant [kW] | |
| Heat demand of sink plant [kW] | |
| T | Temperature [K] |
| TES | Thermal energy storage |
| Prediction horizon of optimal control problem [h] | |
| V | Volume [m] |
| Volumetric flow rate [m/s] | |
| u | Control input |
| U | Overall heat-transfer coefficient [kW/mK] |
| z | Algebraic state of pipeline model |
| Allowed deviation between demanded and supplied heat-flow rate [-] | |
| Density [kg/m] | |
| Penalty parameter |
Appendix A. Optimal-Control Problem
References
- Figueres, C.; Schellnhuber, H.J.; Whiteman, G.; Rockstrøm, J.; Hobley, A.; Rahmstorf, S. Three years to safeguard our climate. Nature 2017, 546, 593–595. [Google Scholar] [CrossRef]
- SPIRE. SPIRE Roadmap. In Sustainable Process Industry through Resource and Energy Efficiency; Technical Report; SPIRE: Brussels, Belgium, 2013. [Google Scholar]
- Huang, F.; Zheng, J.; Baleynaud, J.M.; Lu, J. Heat recovery potentials and technologies in industrial zones. J. Energy Inst. 2017, 90, 951–961. [Google Scholar] [CrossRef]
- Chertow, M.R. “Uncovering” Industrial Symbiosis. J. Ind. Ecol. 2007, 11, 11–30. [Google Scholar] [CrossRef]
- Klemeš, J.J.; Kravanja, Z. Forty years of Heat Integration: Pinch analysis (PA) and Mathematical Programming (MP). Curr. Opin. Chem. Eng. 2013, 2, 461–474. [Google Scholar] [CrossRef]
- Yee, T.F.; Grossmann, I.E. Simultaneous optimization models for heat integration II: Heat exchanger network synthesis. Comput. Chem. Eng. 1990, 14, 1165–1184. [Google Scholar] [CrossRef]
- Boix, M.; Montastruc, L.; Azzaro-Pantel, C.; Domenech, S. Optimization methods applied to the design of eco-industrial parks: A literature review. J. Clean. Prod. 2015, 87, 303–317. [Google Scholar] [CrossRef]
- Dal Magro, F.; Meneghetti, A.; Nardin, G.; Savino, S. Enhancing energy recovery in the steel industry: Matching continuous charge with off-gas variability smoothing. Energy Convers. Manag. 2015, 104, 78–89. [Google Scholar] [CrossRef]
- Hiete, M.; Ludwig, J.; Schultmann, F. Intercompany Energy Integration: Adaptation of Thermal Pinch Analysis and Allocation of Savings. J. Ind. Ecol. 2012, 16, 689–698. [Google Scholar] [CrossRef]
- Jiménez-Arreola, M.; Pili, R.; Dal, F.; Wieland, C.; Rajoo, S.; Romagnoli, A. Thermal power fluctuations in waste heat to power systems: An overview on the challenges and current solutions. Appl. Therm. Eng. 2018, 134, 576–584. [Google Scholar] [CrossRef]
- Aguilera, N.; Marchetti, J.L. Optimizing and controlling the operation of heat-exchanger networks. AIChE J. 1998, 44, 1090–1104. [Google Scholar] [CrossRef]
- González, A.H.; Odloak, D.; Marchetti, J.L. Predictive control applied to heat-exchanger networks. Chem. Eng. Process. Process Intensif. 2006, 45, 661–671. [Google Scholar] [CrossRef]
- Bakošová, M.; Oravec, J. Robust model predictive control for heat exchanger network. Appl. Therm. Eng. 2014, 73, 924–930. [Google Scholar] [CrossRef]
- Oravec, J.; Bakošová, M.; Trafczynski, M.; Vasičkaninová, A.; Mészáros, A.; Markowski, M. Robust model predictive control and PID control of shell-and-tube heat exchangers. Energy 2018, 159, 1–10. [Google Scholar] [CrossRef]
- Vasičkaninová, A.; Bakošová, M. Control of a heat exchanger using neural network predictive controller combined with auxiliary fuzzy controller. Appl. Therm. Eng. 2015, 89, 1046–1053. [Google Scholar] [CrossRef]
- Sun, K.; Tseng, C.T.; Wong, D.S.H.; Shieh, S.S.; Jang, S.S.; Kang, J.L.; Hsieh, W.D. Model predictive control for improving waste heat recovery in coke dry quenching processes. Energy 2015, 80, 275–283. [Google Scholar] [CrossRef]
- Wang, X.; Palazoglu, A.; El-farra, N.H. Proactive optimization and control of heat-exchanger super networks. IFAC-PapersOnLine 2015, 48, 593–598. [Google Scholar] [CrossRef]
- Glemmestad, B.; Skogestad, S.; Gundersen, T. Optimal operation of heat exchanger networks. Comput. Chem. Eng. 1999, 23, 509–522. [Google Scholar] [CrossRef]
- Jäschke, J.; Skogestad, S. Optimal operation of heat exchanger networks with stream split: Only temperature measurements are required. Comput. Chem. Eng. 2014, 70, 35–49. [Google Scholar] [CrossRef]
- Scholten, T.; De Persis, C.; Tesi, P. Modeling and Control of Heat Networks with Storage: The Single-Producer Multiple-Consumer Case. IEEE Trans. Control Syst. Technol. 2017, 25, 414–428. [Google Scholar] [CrossRef]
- Sun, L.; Zha, X.; Luo, X. Coordination between bypass control and economic optimization for heat exchanger network. Energy 2018, 160, 318–329. [Google Scholar] [CrossRef]
- Jin, Y.; Gao, N.; Zhu, T. Controlled variable analysis of counter flow heat exchangers based on thermodynamic derivation. Appl. Therm. Eng. 2018, 129, 684–692. [Google Scholar] [CrossRef]
- Bonilla, J.; Roca, L. Model validation and control strategy of a heat recovery system integrated in a renewable hybrid power plant demonstrator. Sol. Energy 2018, 176, 698–708. [Google Scholar] [CrossRef]
- Schumm, G.; Philipp, M.; Schlosser, F.; Hesselbach, J.; Walmsley, T.G.; Atkins, M.J. Hybrid heating system for increased energy efficiency and flexible control of low temperature heat. Energy Effic. 2018, 11, 1117–1133. [Google Scholar] [CrossRef]
- Walmsley, T.G.; Walmsley, M.R.W.; Atkins, M.J.; Neale, J.R. Integration of industrial solar and gaseous waste heat into heat recovery loops using constant and variable temperature storage. Energy 2014, 75, 53–67. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, M.Q.; Dong, E.F.; Wang, Y.F.; Sui, Y.Q. Reliable simultaneous operation strategy in heat exchanger networks under variable heat loads. Appl. Therm. Eng. 2019, 149, 1125–1133. [Google Scholar] [CrossRef]
- Sunil, P.U.; Barve, J.; Nataraj, P.S.V. A robust heat recovery steam generator drum level control for wide range operation flexibility considering renewable energy integration. Energy 2018, 163, 873–893. [Google Scholar] [CrossRef]
- Atkins, M.J.; Walmsley, M.R.W.; Neale, J.R. Process integration between individual plants at a large dairy factory by the application of heat recovery loops and transient stream analysis. J. Clean. Prod. 2012, 34, 21–28. [Google Scholar] [CrossRef]
- Wang, Y.; You, S.; Zheng, W.; Zhang, H.; Zheng, X.; Miao, Q. State space model and robust control of plate heat exchanger for dynamic performance improvement. Appl. Therm. Eng. 2018, 128, 1588–1604. [Google Scholar] [CrossRef]
- Whalley, R.; Ebrahimi, K.M. Heat exchanger dynamic analysis. Appl. Math. Model. 2018, 62, 38–50. [Google Scholar] [CrossRef]
- Chang, H.H.; Chang, C.T.; Li, B.H. Game-theory based optimization strategies for stepwise development of indirect interplant heat integration plans. Energy 2018, 148, 90–111. [Google Scholar] [CrossRef]
- Gu, S.; Liu, L.; Zhang, L.; Bai, Y.; Wang, S.; Du, J. Heat exchanger network synthesis integrated with flexibility and controllability. Chin. J. Chem. Eng. 2018, in press. [Google Scholar] [CrossRef]
- Čuček, L.; Boldyryev, S.; Klemeš, J.J.; Kravanja, Z.; Krajačić, G.; Varbanov, P.S.; Duić, N. Approaches for retrofitting heat exchanger networks within processes and Total Sites. J. Clean. Prod. 2019, 211, 884–894. [Google Scholar] [CrossRef]
- Schlosser, F.; Peesel, R.H.; Meschede, H.; Philipp, M.; Walmsley, T.G.; Walmsley, M.R.W.; Atkins, M.J. Design of Robust Total Site Heat Recovery Loops via Monte Carlo Simulation. Energies 2019, 12, 930. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, L.; Chhabra, P.; Garud, S.S.; Aditya, K.; Romagnoli, A.; Comodi, G.; Dal Magro, F.; Meneghetti, A.; Kraft, M. A novel methodology for the design of waste heat recovery network in eco-industrial park using techno-economic analysis and multi-objective optimization. Appl. Energy 2016, 184, 88–102. [Google Scholar] [CrossRef]
- Hassiba, R.J.; Al-Mohannadi, D.M.; Linke, P. Carbon dioxide and heat integration of industrial parks. J. Clean. Prod. 2017, 155, 47–56. [Google Scholar] [CrossRef]
- Roberts, B.H. The application of industrial ecology principles and planning guidelines for the development of eco-industrial parks: An Australian case study. J. Clean. Prod. 2004, 12, 997–1010. [Google Scholar] [CrossRef]
- Eynard, J.; Grieu, S.; Polit, M. Predictive control and thermal energy storage for optimizing a multi-energy district boiler. J. Process Control 2012, 22, 1246–1255. [Google Scholar] [CrossRef][Green Version]
- Fritzson, P.; Bunus, P. Modelica—A General Object-Oriented Language for Continuous and Discrete-Event System Modeling and Simulation. In Proceedings of the 35th Annual Simulation Symposium, San Deigo, CA, USA, 14–18 April 2002. [Google Scholar]
- Schweiger, G.; Larsson, P.O.; Magnusson, F.; Lauenburg, P.; Velut, S. District heating and cooling systems—Framework for Modelica-based simulation and dynamic optimization. Energy 2017, 137, 566–578. [Google Scholar] [CrossRef]
- Kauko, H.; Kvalsvik, K.H.; Rohde, D.; Nord, N.; Utne, Å. Dynamic modeling of local district heating grids with prosumers: A case study for Norway. Energy 2018, 151, 261–271. [Google Scholar] [CrossRef]
- Rohde, D.; Andresen, T.; Nord, N. Analysis of an integrated heating and cooling system for a building complex with focus on long–term thermal storage. Appl. Therm. Eng. 2018, 145, 791–803. [Google Scholar] [CrossRef]
- Åkesson, J.; Årzén, K.E.; Gäfvert, M.; Bergdahl, T.; Tummescheit, H. Modeling and optimization with Optimica and JModelica.org-Languages and tools for solving large-scale dynamic optimization problems. Comput. Chem. Eng. 2010, 34, 1737–1749. [Google Scholar] [CrossRef]
- Soons, F.; Torrens, J.I.; Hensen, J.; Schrevel, R.D. A Modelica based computational model for evaluating a renewable district heating system. In Proceedings of the 9th International Conference on System Simulation in Buildings, Liege, Belgium, 10–12 December 2014. [Google Scholar]
- Strikwerda, J. Finite Difference Schemes and Partial Differential Equations, 2nd ed.; SIAM: Philadelphia, PA, USA, 2004. [Google Scholar]
- International Energy Agency. Energy Storage Technology Roadmap: Technology Annex; Technical Report; International Energy Agency (IEA): Paris, France, 2014. [Google Scholar]
- Caldwell, J.S.; Bahnfleth, W.P. Identification of mixing effects in stratified chilled-water storage tanks by analysis of time series temperature data. ASHRAE Trans. 1998, 104, 366–376. [Google Scholar]
- Han, Y.M.; Wang, R.Z.; Dai, Y.J. Thermal stratification within the water tank. Renew. Sustain. Energy Rev. 2009, 13, 1014–1026. [Google Scholar] [CrossRef]
- Miró, L.; Gasia, J.; Cabeza, L.F. Thermal energy storage (TES) for industrial waste heat (IWH) recovery: A review. Appl. Energy 2016, 179, 284–301. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Principles of Heat and Mass Transfer; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Wang, H.; Lahdelma, R.; Wang, X.; Jiao, W.; Zhu, C. Analysis of the location for peak heating in CHP based combined district heating systems. Appl. Therm. Eng. 2015, 87, 402–411. [Google Scholar] [CrossRef]
- Timmerman, J.; Hennen, M.; Bardow, A.; Lodewijks, P.; Vandevelde, L.; Eetvelde, G.V. Towards low carbon business park energy systems: A holistic techno-economic optimisation model. Energy 2017, 125, 747–770. [Google Scholar] [CrossRef]
- Jose, P. Stochastic Unit Commitment and Self-scheduling: A Review Considering CO2 Emission Modeling. In Handbook of CO2 in Power Systems Energy Systems; Zheng, Q.P., Rebennack, S., Pardalos, P.M., Pereira, M.V.F., Iliadis, N.A., Eds.; Energy Systems; Springer: Berlin/Heidelberg, Germany, 2012; pp. 311–326. [Google Scholar]
- Biegler, L.T. Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted L1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2005, 106, 25–57. [Google Scholar] [CrossRef]
- HSL. A Collection of Fortran Codes for Large Scale Scientific Computation. 2018. Available online: http://www.hsl.rl.ac.uk/ (accessed on 15 May 2017).
- Andersson, J.; Åkesson, J.; Diehl, M. CasADi: A Symbolic Package for Automatic Differentiation and Optimal Control. In Recent Advances in Algorithmic Differentiation; Forth, S., Hovland, P., Phipps, E., Utke, J., Walther, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 297–307. [Google Scholar] [CrossRef]
- Magnusson, F.; Åkesson, J. Dynamic Optimization in JModelica.org. Processes 2015, 3, 471–496. [Google Scholar] [CrossRef]
- Rawlings, J.; Mayne, D. Model Predictive Control: Theory and Design; Nob Hill Publishing: Madison, WI, USA, 2009. [Google Scholar]
- Magnusson, F.; Åkesson, J. Collocation methods for optimization in a Modelica environment. In Proceedings of the 9th International Modelica Conference, Munich, Germany, 3–5 September 2012; pp. 649–658. [Google Scholar]





| Index | Interpretation | Set | Elements |
|---|---|---|---|
| i | Plants with surplus heat | ||
| j | Plants with heat demands |
| Variable | Description | Unit |
|---|---|---|
| Q | Heat-flow rate | kW |
| T | Temperature | K |
| u | control input | [-] |
| Volumetric flow rate | m/s | |
| z | Algebraic state of pipeline model | - |
| Parameter | Value |
|---|---|
| 24 h | |
| 371 K | |
| 371 K | |
| 100 W/K |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knudsen, B.R.; Kauko, H.; Andresen, T. An Optimal-Control Scheme for Coordinated Surplus-Heat Exchange in Industry Clusters. Energies 2019, 12, 1877. https://doi.org/10.3390/en12101877
Knudsen BR, Kauko H, Andresen T. An Optimal-Control Scheme for Coordinated Surplus-Heat Exchange in Industry Clusters. Energies. 2019; 12(10):1877. https://doi.org/10.3390/en12101877
Chicago/Turabian StyleKnudsen, Brage Rugstad, Hanne Kauko, and Trond Andresen. 2019. "An Optimal-Control Scheme for Coordinated Surplus-Heat Exchange in Industry Clusters" Energies 12, no. 10: 1877. https://doi.org/10.3390/en12101877
APA StyleKnudsen, B. R., Kauko, H., & Andresen, T. (2019). An Optimal-Control Scheme for Coordinated Surplus-Heat Exchange in Industry Clusters. Energies, 12(10), 1877. https://doi.org/10.3390/en12101877






