A Dual-Objective Substation Energy Consumption Optimization Problem in Subway Systems
Abstract
:1. Introduction
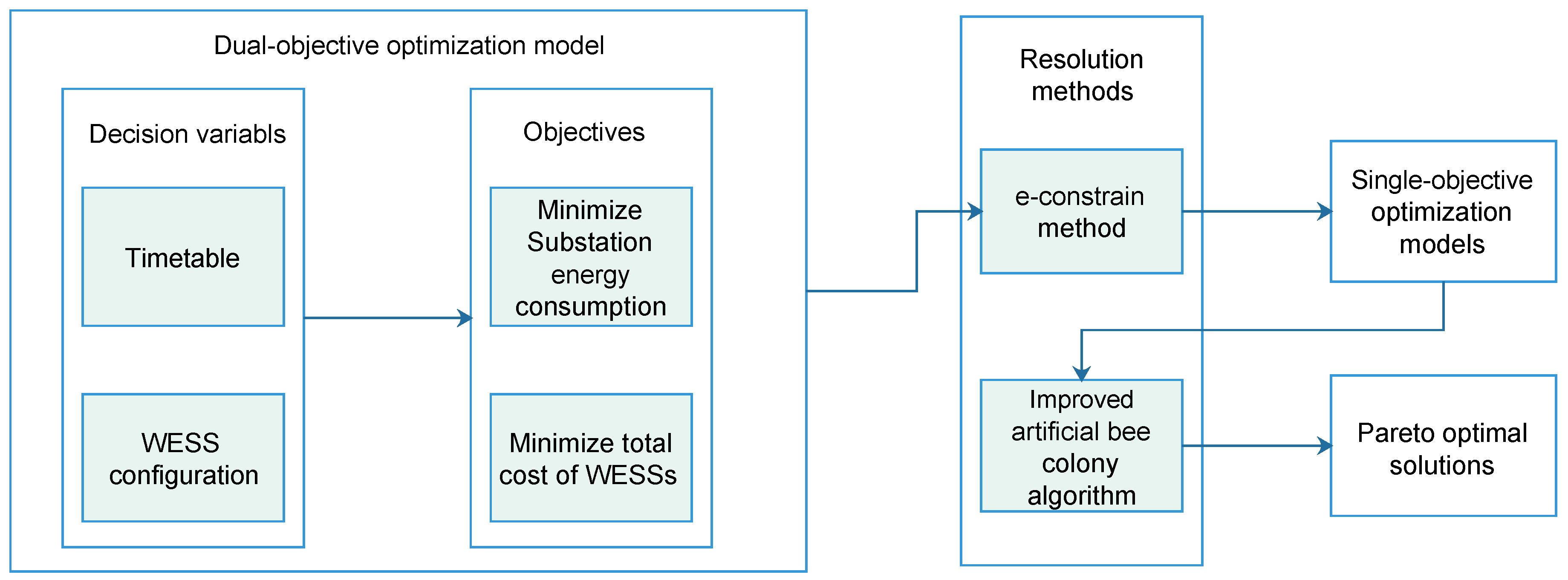
- An integration of timetable optimization and WESS is proposed to maximize regenerative energy utilization, thus to minimize substation energy consumption in a subway system.
- To maximize energy saving with the least cost, a dual-objective optimization model is thereby formulated to simultaneously minimize substation energy consumption and the total investment cost of WESSs. Note that a subway line is divided into several electricity supply intervals. One WESS is installed in each electricity supply interval. the size of each WESS can be different from each other, and both of them are greater than or equal to 0. Their total size determines the total cost of WESSs.
- To solve the proposed dual-objective optimization problem, An -constraint method is first designed to transform it into several single-objective optimization problems. Then, An improved artificial bee colony algorithm is designed to solve these single-objective optimization problems sequentially.
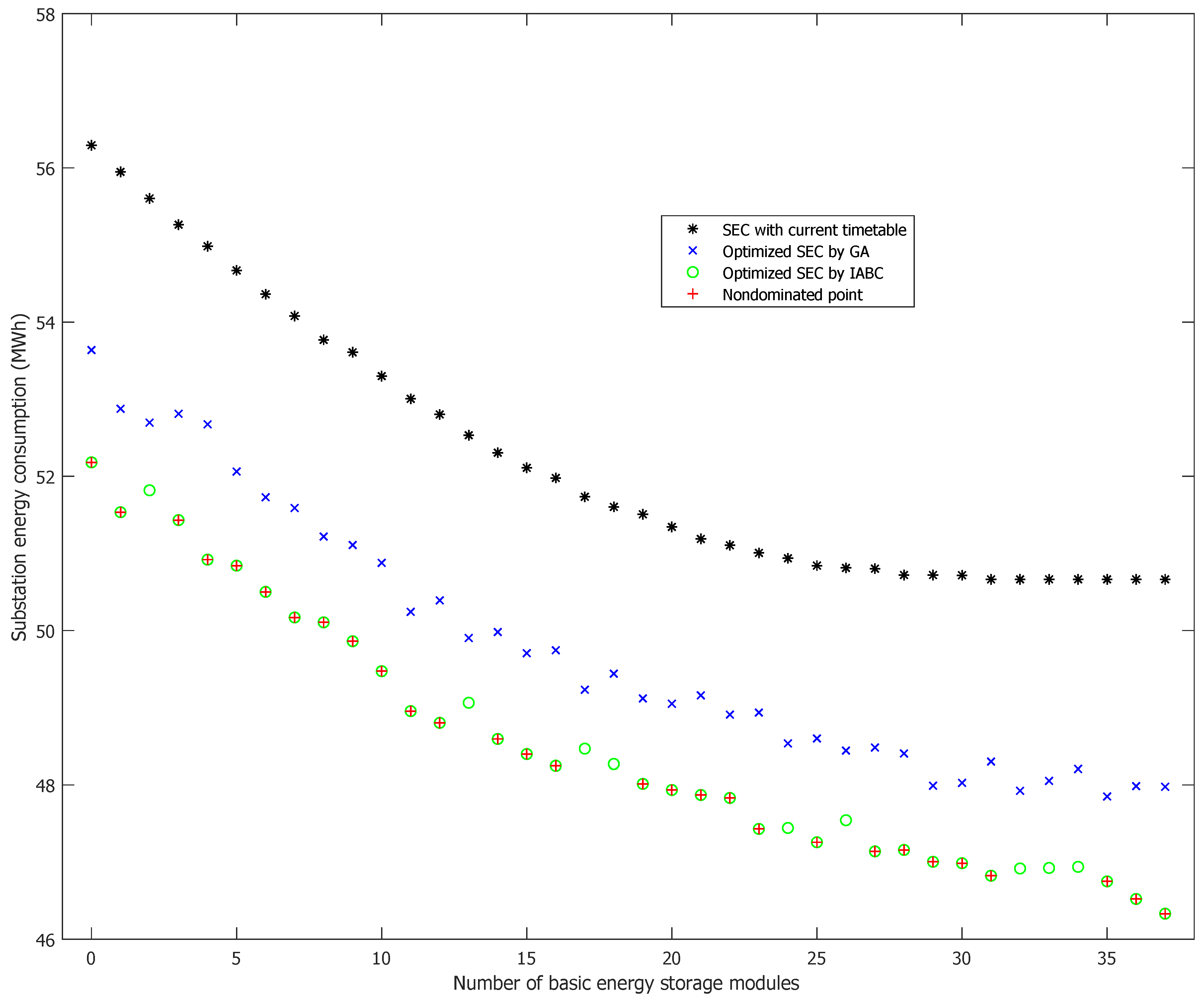
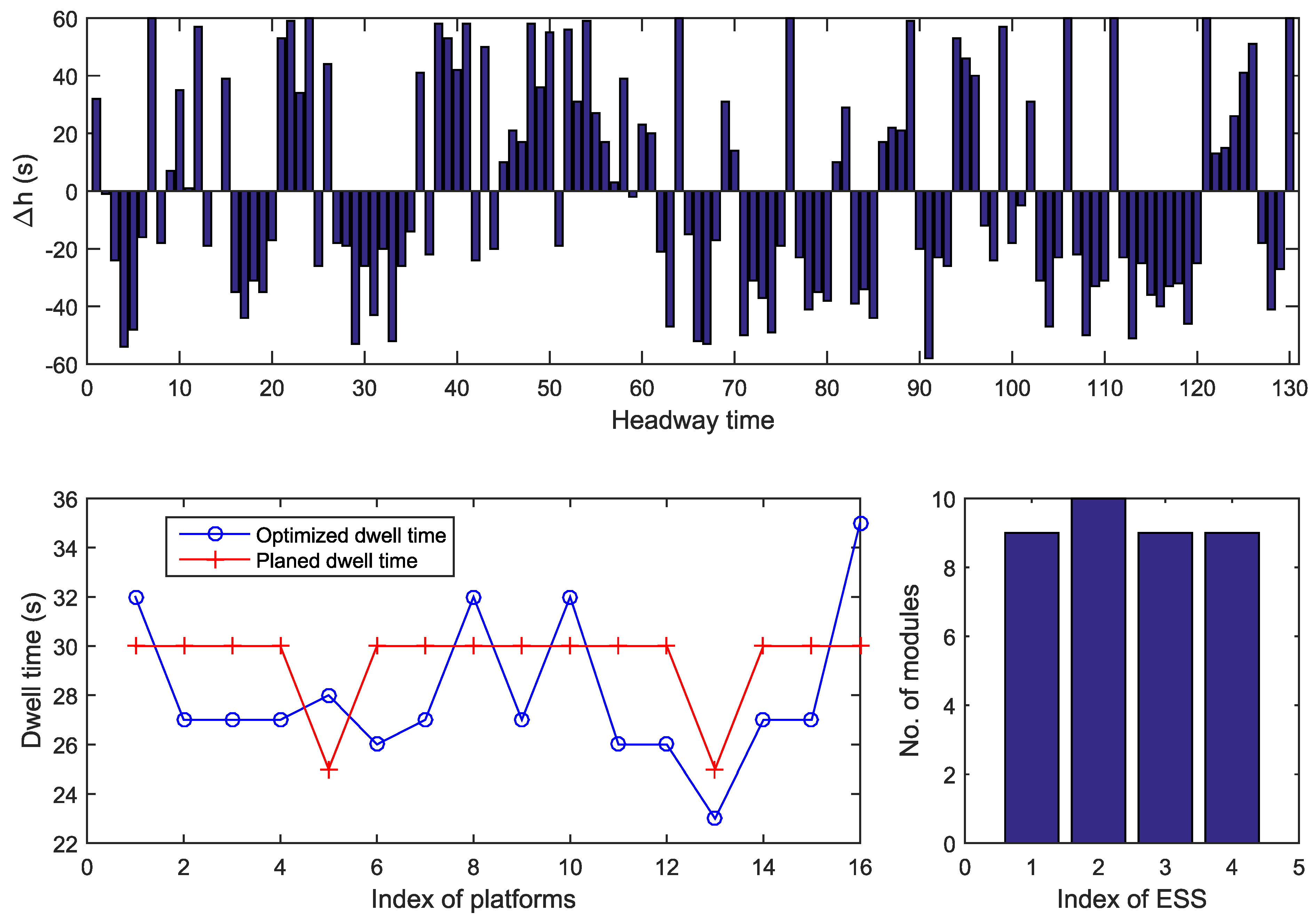
- Numerical examples are constructed based on the actual data obtained from a subway system in China to show the effectiveness of the proposed resolution methods. a set of Pareto optimal solutions is obtained. i.e., for each value of the total size of WESSs, the minimal substation energy consumption is determined, and the optimal configuration of each WESS and the correspondingly optimized timetable are obtained to reach the maximum energy saving.
2. Literature Review
3. Mathematical Model
3.1. Problem Assumptions
- There is reserve time for dwell time at each platform.
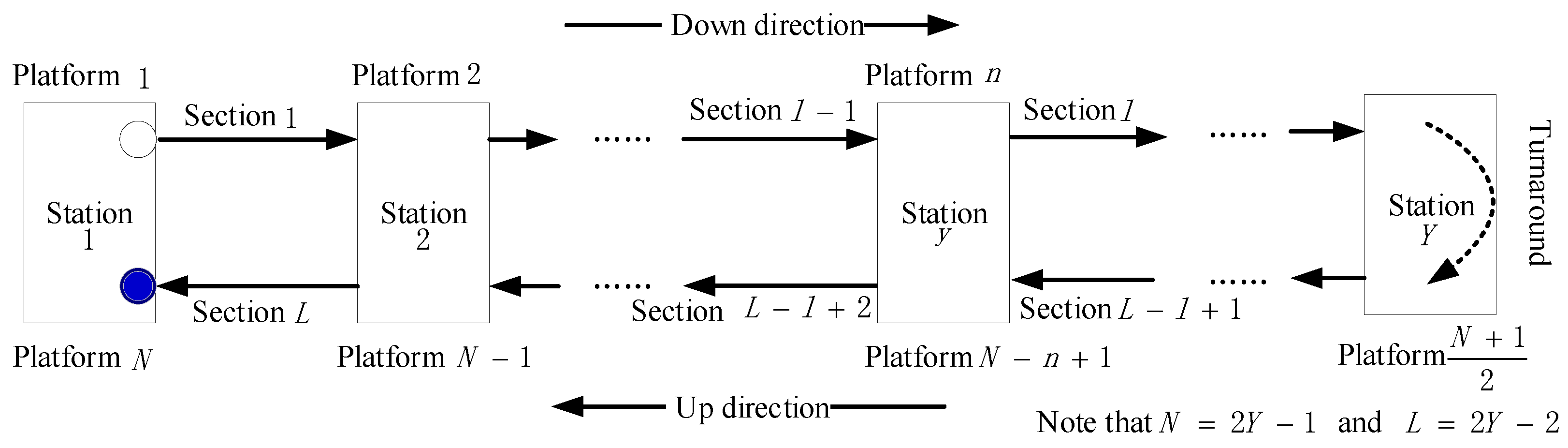
- The subway line is divided into several electricity supply intervals. Each electricity supply interval provides energy for several stations and sections. Electricity can be transmitted within an an electricity supply interval.
- Each electricity supply interval includes one substation, one WESS and a bank of resistors. Each WESS can be installed near the place of a substation. Each WESS consists of several parallel Basic Energy Storage Modules (BESMs). The total cost of all WESSs grows linearly with their total energy capacity (represented by the number of BESMs in this work).
- The transmission loss coefficient of regenerative energy is a constant.
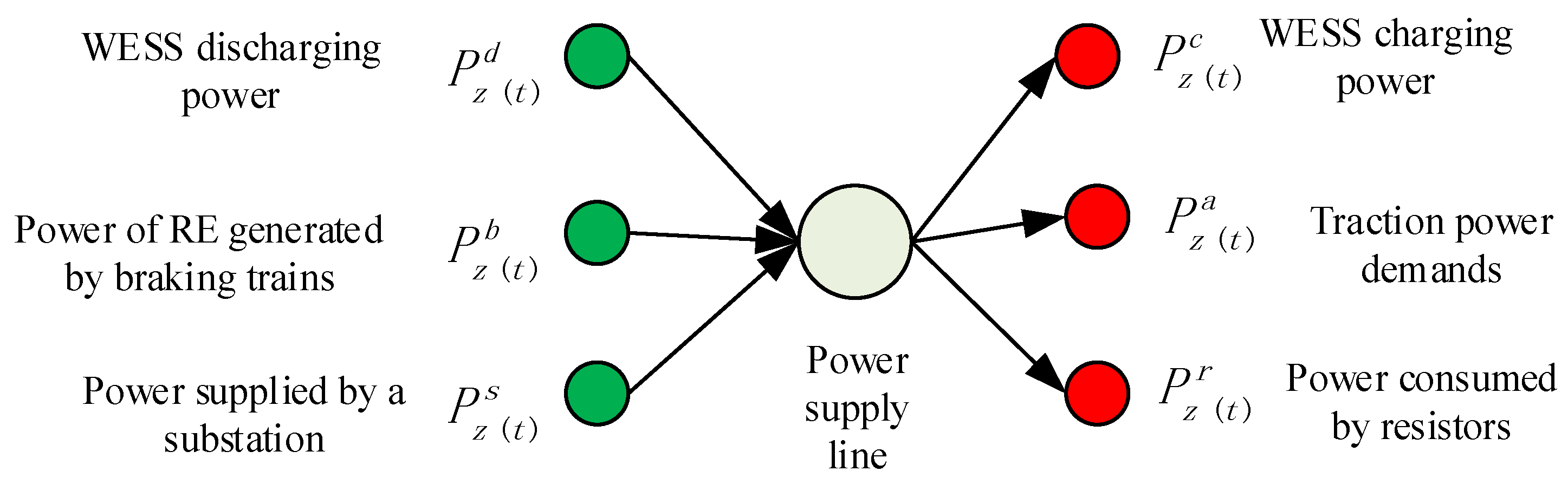
- The other electrical utilities (e.g., lights and air conditioners) are not considered during the simulation, i.e., electrical energy can only be consumed by traction trains, resistors and charged into WESS.
- Regenerative energy is fed back into the power supply line and can be immediately used by traction trains in the same electricity supply interval. If regenerative energy cannot be used fully by traction trains, the surplus is charged into WESS and consumed by resistors if needed.
- The condition of a charge/discharge state transition for a WESS is defined as follows:
- When trains are braking and the power of surplus regenerative energy exceeds a predefined limit, WESS in the same electricity supply interval begins to charge; When the power of surplus regenerative energy gets smaller, the corresponding WESS stops charging.
- When trains are in a traction phase and the power of surplus traction energy exceeds a predefined limit, WESS begins to discharge; when the surplus traction energy gets smaller, WESS stops discharging (the surplus traction energy demand is satisfied by a substation).
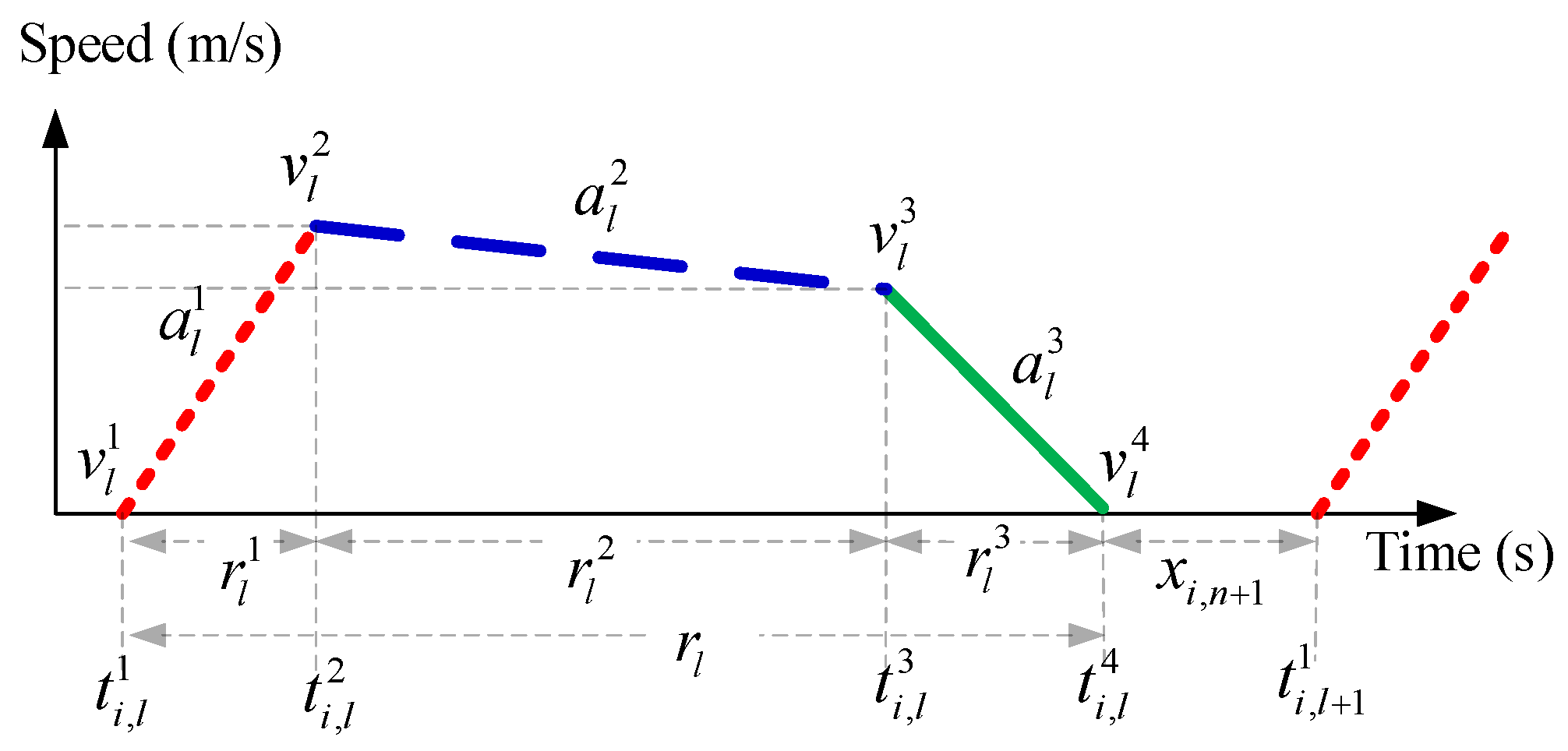
3.2. Train Movement and Timetable Modeling
- Determine the time of the other key points for train i at section l by that train’s start time at that section:
- Determine by the time instant when train i starts its travel:
- Determine by using :where is a given constant which represents the time instant that the first train ends its braking phase at a virtual section 0 (also means arrival time at platform 1); is the headway time between trains i and and it is represented by the time difference of their arrival time at platform 1 in this work, i.e., .
3.3. Energy Consumption Calculation
3.3.1. Total Traction Energy Demand
3.3.2. Available Regenerative Energy from Braking Trains
3.3.3. Energy Dynamics of Wess
3.3.4. Substation Energy Consumption
3.4. Dual-Objective Substation Energy Consumption Optimization Model
4. Resolution Method
4.1. -Constraint Method
| Algorithm 1 Procedure of applying the -constraint method |
| Input: Mathematical model of problem P Output: %Non-dominated points on Pareto front
|
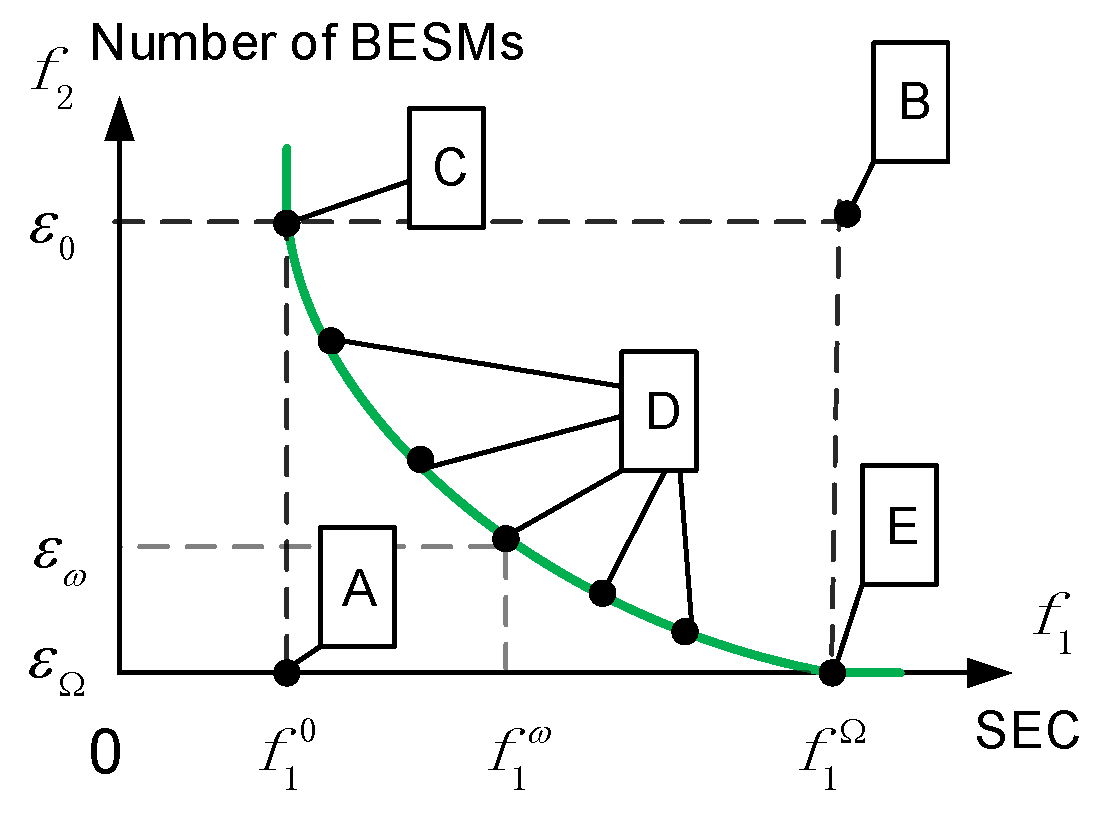
- Obtain problems and respectively, where problem dismisses the second objective in problem P and problem dismisses the other one. The constraints in problem P are kept unchanged in both problems and .
- By solving problem , we obtain the minimal value of the first objective (i.e., substation energy consumption) without consideration of the other objective (WESS cost). The result is illustrated as in Figure 6. Similarly, by solving problem , we obtain the minimal value of the second objective without consideration of the other one. the result is illustrated as .
- Obtain problem by adding constraint (35) into obtaining problem . Note that the constraint is the first objective function in problem P and is the optimized result of problem .
- By solving problem , we obtain the minimal value of WESS size needed (denoted as ) whilst maintaining minimum substation energy consumption. Note that (, ) is a non-dominated point of problem P, shown as point C in Figure 6.
- Obtain problem by adding constraint constraint (36) into obtain problem . Note that the constraint is the second objective function in problem P and is the optimized result of problem .
- By solving problem , we obtain the minimal value of substation energy consumption (denoted as ) whilst the least size of WESS is installed. Note that (, ) is also a non-dominated point of problem P, shown as point E in Figure 6.
- Obtain problem by adding constraint constraint (37) into obtain problem . Note that the constraint is the second objective function in problem P and is a variable which changes from to with a predefined step length. For different values of , it becomes a different problem. Thus, problem represents a series of optimization problems actually.
- By solving problem with each value of , we obtain a set of minimal values of substation energy consumption (denoted as ) whilst certain size of WESS (i.e., totally number of BESMs) is installed. Note that each (, ) is a non-dominated point of problem P, shown as point D in Figure 6. Also note that point D actually represents a set of points in the green curve, as is a changing from to .
4.2. Improved Artificial Bee Colony Algorithm
| Algorithm 2 Procedure of IABC |
| Input:, , , , , , , , , , Output:
|
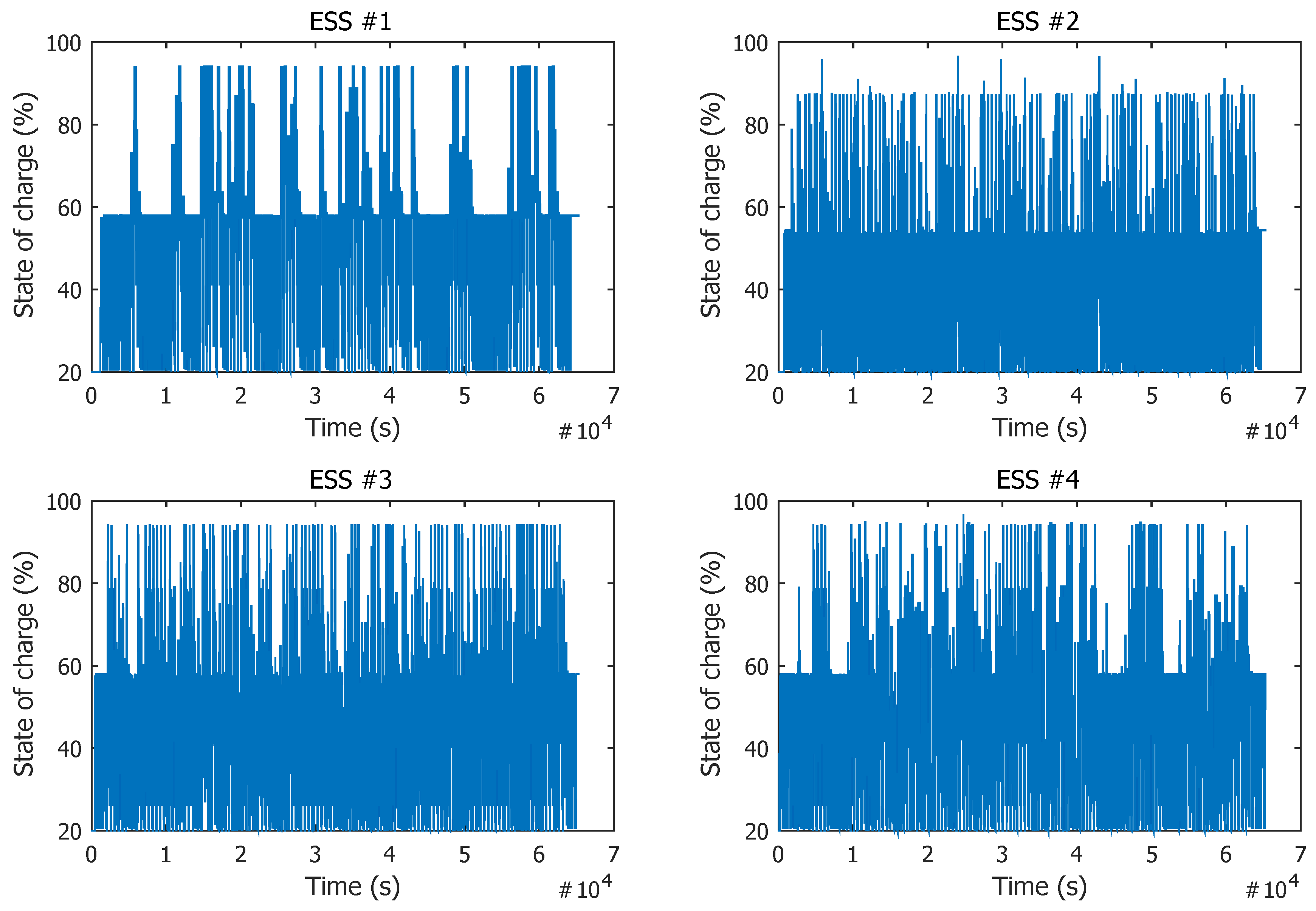
5. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- González-Gil, A.; Palacin, R.; Batty, P.; Powell, J. A systems approach to reduce urban rail energy consumption. Energy Convers. Manag. 2014, 80, 509–524. [Google Scholar] [CrossRef]
- González-Gil, A.; Palacin, R.; Batty, P. Optimal energy management of urban rail systems: Key performance indicators. Energy Convers. Manag. 2015, 90, 282–291. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Ning, B.; Tang, T. A survey on energy-efficient train operation for urban rail transit. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2–13. [Google Scholar] [CrossRef]
- Su, S.; Tang, T.; Wang, Y. Evaluation of strategies to reducing traction energy consumption of metro systems using an optimal train control simulation model. Energies 2016, 9, 105. [Google Scholar] [CrossRef]
- Liu, R.R.; Golovitcher, I.M. Energy-efficient operation of rail vehicles. Transp. Res. Part A Policy Pract. 2003, 37, 917–932. [Google Scholar] [CrossRef]
- Su, S.; Tang, T.; Roberts, C. A cooperative train control model for energy saving. IEEE Trans. Intell. Transp. Syst. 2015, 16, 622–631. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, M.; Guo, X.; Zhang, Z.; Ning, B.; Tang, T. Timetable optimization for regenerative energy utilization in subway systems. IEEE Trans. Intell. Transp. Syst. 2018, 1–11. [Google Scholar] [CrossRef]
- Yang, X.; Ning, B.; Li, X.; Tang, T. A two-objective timetable optimization model in subway systems. IEEE Trans. Intell. Transp. 2014, 15, 1913–1921. [Google Scholar] [CrossRef]
- González-Gil, A.; Palacin, R.; Batty, P. Sustainable urban rail systems: Strategies and technologies for optimal management of regenerative braking energy. Energy Convers. Manag. 2013, 75, 374–388. [Google Scholar] [CrossRef]
- Kampeerawat, W.; Koseki, T. A strategy for utilization of regenerative energy in urban railway system by application of smart train scheduling and wayside energy storage system. Energy Procedia 2017, 138, 795–800. [Google Scholar] [CrossRef]
- Ceraolo, M.; Lutzemberger, G.; Meli, E.; Pugi, L.; Rindi, A.; Pancari, G. Energy storage systems to exploit regenerative braking in dc railway systems: Different approaches to improve efficiency of modern high-speed trains. J. Energy Storage 2018, 16, 269–279. [Google Scholar] [CrossRef]
- Ciccarelli, F.; Iannuzzi, D.; Tricoli, P. Control of metro-trains equipped with onboard supercapacitors for energy saving and reduction of power peak demand. Transp. Res. Part C Emerg. Technol. 2012, 24, 36–49. [Google Scholar] [CrossRef]
- Ramos, A.; Pena, M.T.; Fernandez, A.; Cucala, P. Mathematical programming approach to underground timetabling problem for maximizing time synchronization. In Proceedings of the International Conference on Industrial Engineering and Industrial Management, Madrid, Spain, 5–7 September 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 88–95. [Google Scholar]
- Nasri, A.; Moghadam, M.F.; Mokhtari, H. Timetable optimization for maximum usage of regenerative energy of braking in electrical railway systems. In Proceedings of the International Symposium on Power Electronics Electrical Drives Automation and Motion, Pisa, Italy, 14–16 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1218–1221. [Google Scholar]
- Kim, K.M.; Kim, K.T.; Han, M.S. A model and approaches for synchronized energy saving in timetabling. In Proceedings of the 9th World Congress on Railway Research, Lille, France, 22–26 May 2011. [Google Scholar]
- Pe na-Alcaraz, M.; Fernández, A.; Cucala, A.P.; Ramos, A.; Pecharromán, R.R. Optimal underground timetable design based on power flow for maximizing the use of regenerative-braking energy. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2012, 226, 397–408. [Google Scholar] [CrossRef]
- Fournier, D.; Mulard, D.; Fages, F. Energy optimization of metro timetables: A hybrid approach. In Proceedings of the 18th International Conference on Principles and Practice of Constraint Programming, Quebec City, QC, Canada, 8–12 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 7–12. [Google Scholar]
- Yang, X.; Li, X.; Gao, Z.; Wang, H.; Tang, T. A cooperative scheduling model for timetable optimization in subway systems. IEEE Trans. Intell. Transp. Syst. 2013, 14, 438–447. [Google Scholar] [CrossRef]
- Zhao, L.; Li, K.; Su, S. A multi-objective timetable optimization model for subway systems. In Proceedings of the 2013 International Conference on Electrical and Information Technologies for Rail Transportation (EITRT2013)—Volume I; Springer: Berlin/Heidelberg, Germany, 2014; pp. 557–565. [Google Scholar]
- Le, Z.; Li, K.; Ye, J.; Xu, X. Optimizing the train timetable for a subway system. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2015, 229, 852–862. [Google Scholar] [CrossRef]
- Yang, X.; Chen, A.; Li, X.; Ning, B.; Tang, T. An energy-efficient scheduling approach to improve the utilization of regenerative energy for metro systems. Transp. Res. Part C Emerg. Technol. 2015, 57, 13–29. [Google Scholar] [CrossRef]
- Li, X.; Lo, H.K. Energy minimization in dynamic train scheduling and control for metro rail operations. Transp. Res. Part B Methodol. 2014, 70, 269–284. [Google Scholar] [CrossRef]
- Gong, C.; Zhang, S.; Zhang, F.; Jiang, J.; Wang, X. An integrated energy-efficient operation methodology for metro systems based on a real case of shanghai metro line one. Energies 2014, 7, 7305–7329. [Google Scholar] [CrossRef]
- Xu, X.; Li, K.; Li, X. A multi-objective subway timetable optimization approach with minimum passenger time and energy consumption. J. Adv. Transp. 2016, 50, 69–95. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, M.; Guo, X.; Liu, H.; Tang, T. An abc-based subway timetable optimization model for regenerative energy utilization. In Proceedings of the International Conference on Systems, Man, and Cybernetics, Miyazaki, Japan, 7–10 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1412–1417. [Google Scholar]
- Tian, Z.; Weston, P.; Zhao, N.; Hillmansen, S.; Roberts, C.; Chen, L. System energy optimisation strategies for metros with regeneration. Transp. Res. Part C Emerg. Technol. 2017, 75, 120–135. [Google Scholar] [CrossRef]
- Liu, H.; Tang, T.; Guo, X.; Xia, X. A timetable optimization model and an improved artificial bee colony algorithm for maximizing regenerative energy utilization in a subway system. Adv. Mech. Eng. 2018, 10, 1–13. [Google Scholar] [CrossRef]
- Liu, P.; Yang, L.; Gao, Z.; Huang, Y.; Li, S.; Gao, Y. Energy-efficient train timetable optimization in the subway system with energy storage devices. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1–17. [Google Scholar] [CrossRef]
- Gao, Z.; Fang, J.; Zhang, Y.; Sun, D. Control strategy for wayside supercapacitor energy storage system in railway transit network. J. Mod. Power Syst. Clean Energy 2014, 2, 181–190. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, L.; Tang, T.; Gao, Z.; Cao, F.; Li, K. Train speed profile optimization with on-board energy storage devices: A dynamic programming based approach. Comput. Ind. Eng. 2018, 126, 149–164. [Google Scholar] [CrossRef]
- Ahmadi, S.; Dastfan, A.; Assili, M. Energy saving in metro systems: Simultaneous optimization of stationary energy storage systems and speed profiles. J. Rail Transp. Plan. Manag. 2018, 8, 78–90. [Google Scholar] [CrossRef]
- Wu, P.; Che, A.; Chu, F.; Zhou, M. An improved exact varepsilon-constraint and cut-and-solve combined method for biobjective robust lane reservation. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1479–1492. [Google Scholar] [CrossRef]
- Chankong, V.; Haimes, Y.Y. Multiobjective Decision Making: Theory and Methodology; North-Holland: New York, NY, USA, 1983. [Google Scholar]
- Carli, R.; Dotoli, M. Energy scheduling of a smart home under nonlinear pricing. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 5648–5653. [Google Scholar]
- Carli, R.; Dotoli, M. Cooperative distributed control for the energy scheduling of smart homes with shared energy storage and renewable energy source. IFAC-PapersOnLine 2017, 50, 8867–8872. [Google Scholar] [CrossRef]
- Sperstad, I.B.; Korpås, M. Energy storage scheduling in distribution systems considering wind and photovoltaic generation uncertainties. Energies 2019, 12, 1231. [Google Scholar] [CrossRef]
- T’kindt, V.; Billaut, J.-C. Multicriteria scheduling problems: A survey. RAIRO-Oper. Res. 2001, 35, 143–163. [Google Scholar] [CrossRef]
- Zhou, Z.; Chu, F.; Che, A.; Zhou, M. ε-constraint and fuzzy logic-based optimization of hazardous material transportation via lane reservation. IEEE Trans. Intell. Transp. Syst. 2013, 14, 847–857. [Google Scholar] [CrossRef]
- Guo, X.; Liu, S.; Zhou, M.; Tian, G. Disassembly sequence optimization for large-scale products with multiresource constraints using scatter search and petri nets. IEEE Trans. Cybern. 2016, 46, 2435–2446. [Google Scholar] [CrossRef]
- Guo, X.; Liu, S.; Zhou, M.; Tian, G. Dual-objective program and scatter search for the optimization of disassembly sequences subject to multiresource constraints. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1091–1103. [Google Scholar] [CrossRef]
- Sun, H.; Wu, J.; Ma, H.; Yang, X.; Gao, Z. A bi-objective timetable optimization model for urban rail transit based on the time-dependent passenger volume. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1–12. [Google Scholar] [CrossRef]
- Ehrgott, M. Multicriteria Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; p. 491. [Google Scholar]
- Haimes, Y.Y.; Lasdon, L.; Wismer, D. On a bicriterion formulation of the problems of integrated system identification and system optimization. IEEE Trans. Syst. Man Cybern. 1971, 1, 296–297. [Google Scholar]
- Berube, J.-F.; Gendreau, M.; Potvin, J.-Y. An exact ε-constraint method for bi-objective combinatorial optimization problems: Application to the traveling salesman problem with profits. Eur. J. Oper. Res. 2009, 194, 39–50. [Google Scholar] [CrossRef]
- Feng, J.; Che, A.; Wang, N. Bi-objective cyclic scheduling in a robotic cell with processing time windows and non-euclidean travel times. Int. J. Prod. Res. 2014, 52, 2505–2518. [Google Scholar] [CrossRef]
- Jozefowiez, N.; Semet, F.; Talbi, E.-G. The bi-objective covering tour problem. Comput. Oper. Res. 2007, 34, 1929–1942. [Google Scholar] [CrossRef]
- Leitner, M.; Ljubic, I.; Sinnl, M. Solving the bi-objective prizecollecting steiner tree problem with the varepsilon-constraint method. Electron. Notes Discret. Math. 2013, 41, 181–188. [Google Scholar] [CrossRef]
- Reiter, P.; Gutjahr, W.J. Exact hybrid algorithms for solving a bi-objective vehicle routing problem. Cent. Eur. J. Oper. Res. 2012, 20, 19–43. [Google Scholar] [CrossRef]
- Bouziaren, S.A.; Aghezzaf, B. An improved augmented varepsilon-constraint and branch-and-cut method to solve the tsp with profits. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1–10. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-tr06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Deng, G.; Xu, Z.; Gu, X. A discrete artificial bee colony algorithm for minimizing the total flow time in the blocking flow shop scheduling. Chin. J. Chem. Eng. 2012, 20, 1067–1073. [Google Scholar] [CrossRef]
- Li, J.; Pan, Q.; Gao, K. Pareto-based discrete artificial bee colony algorithm for multi-objective flexible job shop scheduling problems. Int. J. Adv. Manuf. Technol. 2011, 55, 1159–1169. [Google Scholar] [CrossRef]
- Gu, W.; Yu, Y.; Hu, W. Artificial bee colony algorithm-based parameter estimation of fractional-order chaotic system with time delay. IEEE/CAA J. Autom. Sin. 2017, 4, 107–113. [Google Scholar] [CrossRef]
- Singh, A. An artificial bee colony algorithm for the leaf-constrained minimum spanning tree problem. Appl. Soft Comput. 2009, 9, 625–631. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Tasgetiren, M.F.; Suganthan, P.; Chua, T. A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem. Inf. Sci. 2011, 181, 2455–2468. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (abc) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A comparative study of artificial bee colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Tian, G.; Ren, Y.; Zhou, M. Dual-objective scheduling of rescue vehicles to distinguish forest fires via differential evolution and particle swarm optimization combined algorithm. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3009–3021. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S.; Zheng, X. A hybrid estimation of distribution algorithm for unrelated parallel machine scheduling with sequence-dependent setup times. IEEE/CAA J. Autom. Sin. 2016, 3, 235–246. [Google Scholar]
- Mareda, T.; Gaudard, L.; Romerio, F. A parametric genetic algorithm approach to assess complementary options of large scale windsolar coupling. IEEE/CAA J. Autom. Sin. 2017, 4, 260–272. [Google Scholar] [CrossRef]
- Dong, W.; Zhou, M. A supervised learning and control method to improve particle swarm optimization algorithms. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1135–1148. [Google Scholar] [CrossRef]
- Tang, Y.; Luo, C.; Yang, J.; He, H. A chance constrained optimal reserve scheduling approach for economic dispatch considering wind penetration. IEEE/CAA J. Autom. Sin. 2017, 4, 186–194. [Google Scholar] [CrossRef]
- Kang, Q.; Feng, S.; Zhou, M.; Ammari, A.C.; Sedraoui, K. Optimal load scheduling of plug-in hybrid electric vehicles via weight-aggregation multi-objective evolutionary algorithms. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2557–2568. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Carli, R.; Dotoli, M. Model predictive control for real-time residential energy scheduling under uncertainties. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1386–1391. [Google Scholar]
- Touretzky, C.R.; Baldea, M. Integrating scheduling and control for economic mpc of buildings with energy storage. J. Process. 2014, 24, 1292–1300. [Google Scholar] [CrossRef]

| Departure Platform Index n | (s) | (s) | (s) | Arrival Platform Index | (s) |
|---|---|---|---|---|---|
| 1 | 30 | 25 | 35 | 2 | 129 |
| 2 | 30 | 25 | 35 | 3 | 98 |
| 3 | 30 | 25 | 35 | 4 | 117 |
| 4 | 30 | 25 | 35 | 5 | 135 |
| 5 | 25 | 20 | 30 | 6 | 139 |
| 6 | 30 | 25 | 35 | 7 | 84 |
| 7 | 30 | 25 | 35 | 8 | 128 |
| 8 | 30 | 25 | 35 | 9 | 141 |
| 9 | 30 | 25 | 35 | 10 | 136 |
| 10 | 30 | 25 | 35 | 11 | 124 |
| 11 | 30 | 25 | 35 | 12 | 83 |
| 12 | 30 | 25 | 35 | 13 | 140 |
| 13 | 25 | 20 | 30 | 14 | 132 |
| 14 | 30 | 25 | 35 | 15 | 117 |
| 15 | 30 | 25 | 35 | 16 | 96 |
| 16 | 30 | 25 | 35 | 17 | 119 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| I | 131 | N | 9 | m (kg) | 287,080 |
| h (s) | 482 | (s) | 422 | (s) | 542 |
| (s) | 2576 | (s) | 2516 | (s) | 2636 |
| (s) | 188 | (m/s2) | 1 | ||
| (s) | 65236 | (s) | 27 | (s) | 21 |
| Electricity Supply Interval Index | Section Indices | |||||
|---|---|---|---|---|---|---|
| 1 | 8 | 9 | - | - | - | - |
| 2 | 5 | 6 | 7 | 10 | 11 | 12 |
| 3 | 3 | 4 | 13 | 14 | - | - |
| 4 | 1 | 2 | 15 | 16 | - | - |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| (kW) | 2000 | (kWh) | 1 | 1 | |
| (kW) | 300 | (kW) | 300 | ||
| (%) | 90 | (%) | 30 | (%) | 20 |
| 10 | 10 | 20 | 6 | 50 |
| Noise (s) | SEC with Current Timetable (kWh) | SEC with Optimized Timetable (kWh) | Energy Saving Ratio |
|---|---|---|---|
| 0 | 56,293 | 46,331 | 17.70% |
| 1 | 56,302 | 46,418 | 17.55% |
| 2 | 56,313 | 46,592 | 17.26% |
| 3 | 56,233 | 46,925 | 16.55% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Tang, T.; Lv, J.; Chai, M. A Dual-Objective Substation Energy Consumption Optimization Problem in Subway Systems. Energies 2019, 12, 1876. https://doi.org/10.3390/en12101876
Liu H, Tang T, Lv J, Chai M. A Dual-Objective Substation Energy Consumption Optimization Problem in Subway Systems. Energies. 2019; 12(10):1876. https://doi.org/10.3390/en12101876
Chicago/Turabian StyleLiu, Hongjie, Tao Tang, Jidong Lv, and Ming Chai. 2019. "A Dual-Objective Substation Energy Consumption Optimization Problem in Subway Systems" Energies 12, no. 10: 1876. https://doi.org/10.3390/en12101876
APA StyleLiu, H., Tang, T., Lv, J., & Chai, M. (2019). A Dual-Objective Substation Energy Consumption Optimization Problem in Subway Systems. Energies, 12(10), 1876. https://doi.org/10.3390/en12101876





