On the Rising Interdependency between the Power Grid, ICT Network, and E-Mobility: Modeling and Analysis
Abstract
1. Introduction
- A new flow-based network model for the interdependency between the power grid, the ICT network, and e-mobility.
- A common failure propagation index, to identify critical nodes and links within single CIs and between multiple interdependent ones.
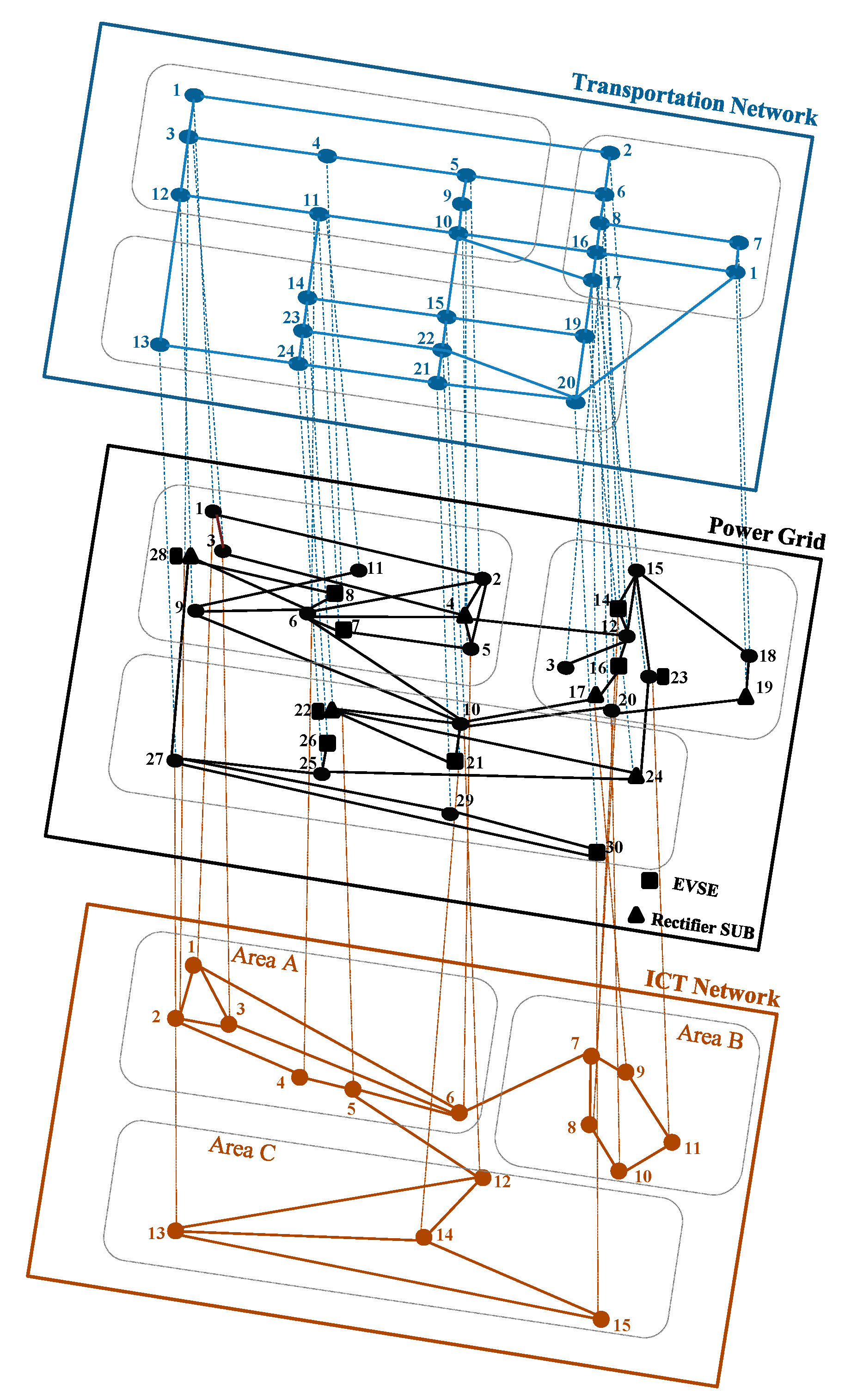
- A new hybrid case study test system that combines a power distribution grid, an ICT network, and a standard transportation test network, which can be used for further analysis and research that integrate these three CIs.
2. Modeling Structural Interdependencies
2.1. Individual Critical Infrastructure (CI) Models
2.2. The Integrated Structural Interdependency Model
3. Modeling Operational Interdependencies
3.1. Interdependency Influence Graphs
3.2. Failure Propagation Index (FPI)
3.3. Microgrids and Energy Storage Systems
3.4. The Integrated Operational Interdependency Model
4. Case Study
5. Results and Discussion
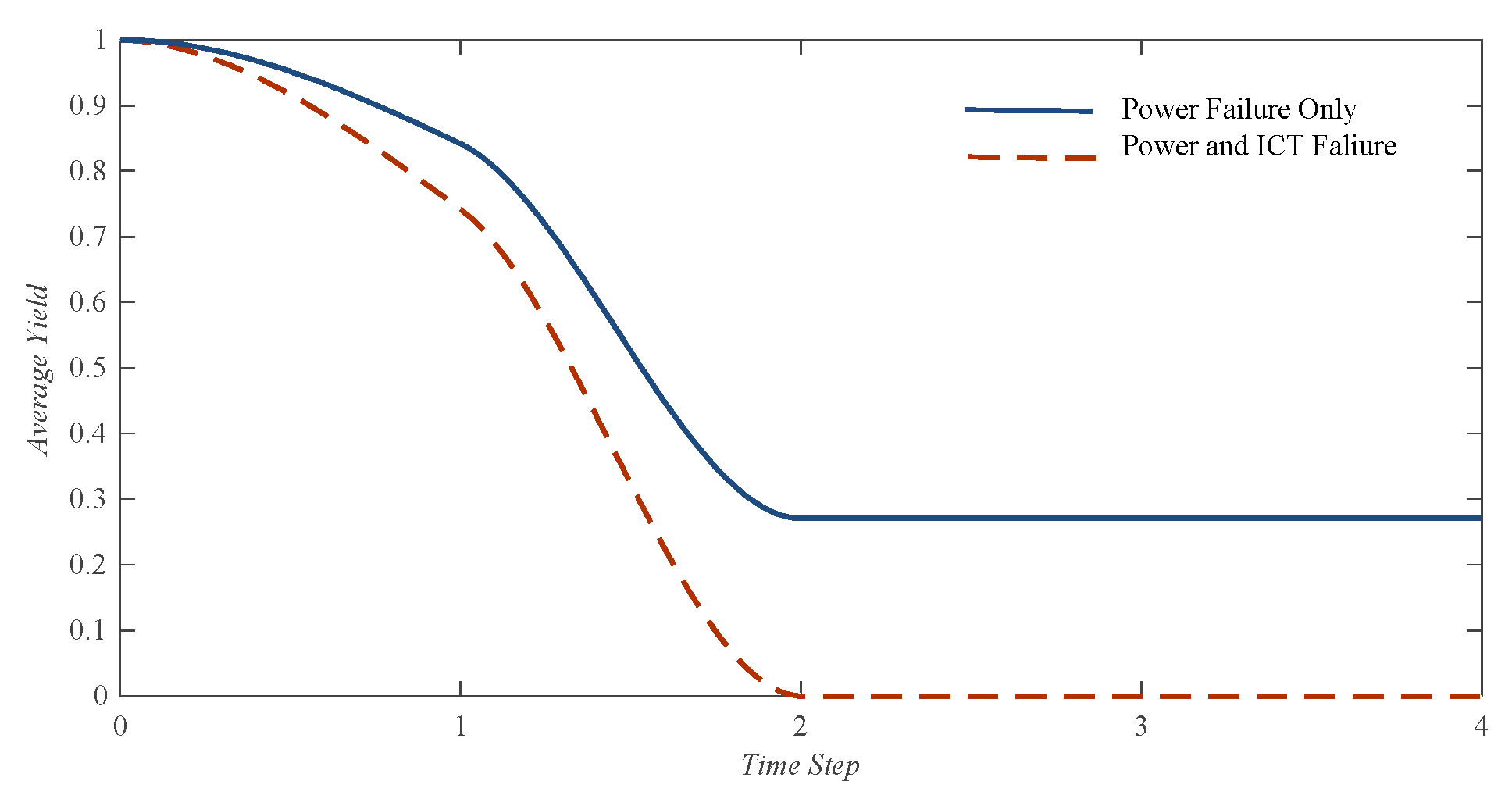
5.1. Scenario I
5.2. Scenario II
6. Conclusions
Funding
Conflicts of Interest
Nomenclature
| , , | Graphs representing the power, ICT, and transportation networks, respectively |
| , , | Sets of power nodes, ICT nodes, and transportation nodes, respectively |
| , , | Sets of power grid links, ICT links, and transportation links, respectively |
| , , | Number of power grid nodes, ICT nodes, and transportation nodes, respectively |
| , , | Number of power grid links, ICT links, and transportation links, respectively |
| , , | Adjacency matrices of the power grid, ICT, and transportation networks, respectively |
| , , | Laplacian matrices for , And , respectively |
| , , | Degrees of the power grid, the ICT network, and the transportation network, respectively |
| Set of generator nodes | |
| Set of non-dispatchable load nodes | |
| Set of dispatchable load nodes | |
| Set of DER nodes | |
| Set of microgrid nodes | |
| Set of EVSE nodes | |
| Set of subway substation nodes | |
| Set of nodes connecting the power grid to infeed from a higher-voltage | |
| Graph representing a community microgrid | |
| Nodes and links of the community microgrid, respectively | |
| Measurement nodes | |
| Router nodes | |
| Control center nodes | |
| Road junctions | |
| Passenger stations | |
| Road sections between adjacent | |
| Train railway sections between adjacent stations | |
| The integrated graph | |
| Nodes and links of , respectively | |
| Links between power nodes and their corresponding ICT nodes | |
| Links between power nodes and their corresponding transportation nodes | |
| Graph to model the operational interdependencies of the power grid | |
| Set of nodes that represent links of | |
| Set of fictitious nodes that are added to To model alternative sources of power, if any | |
| Links that signify the probability of node To fail following a disturbance at node | |
| FPI | Failure propagation index |
| Set of links from Nodes to Nodes | |
| The net power injection at node | |
| The power flow through the link connecting nodes and | |
| The power flow capacity of the link connecting nodes and | |
| Imaginary component of the bus admittance matrix | |
| Set of links from Nodes to Nodes | |
| A vector combining the power variation in the various lines for changes in the power injection vector | |
| Set of edges from nodes to other ones | |
| Line outage distribution factor | |
| Array combining all elements of as a vector | |
| Set of links microgrid nodes and their corresponding fictitious nodes | |
| Maximum power capacity of local microgrid resources | |
| Time-varying availability factor | |
| The operational interdependency influence graph | |
| Nodes and links of | |
| Graph to model the operational interdependencies of the ICT network | |
| Links that determine the influence of ICT nodes on each other | |
| Set of possible shortest paths between node and the control center, excluding those that are be available due to failure of node | |
| State vector of the power grid at a given time | |
| Vector of transformer phase shifts | |
| Voltage magnitude at every bus | |
| Vector of transformer off-nominal voltage ratios | |
| Set of power system measurements | |
| Measurement errors | |
| Square matrix whose off-diagonal elements are zeros, and diagonal elements equal the standard deviation of the measurement errors | |
| Iteration index | |
| Link from a power grid node to an ICT node | |
| Number of ICT nodes connected to power node | |
| Estimated error between the actual measurement of , and its estimated value | |
| Interdependency link from an ICT node to a power grid node | |
| Number of power nodes connected to ICT node | |
| Fictitious power node | |
| Total energy capacity | |
| Total energy capacity | |
| Available energy | |
| Graph representing the transportation network | |
| Set of nodes representing links of | |
| Set of links between a node and a one | |
| Set of links between a Node and another One | |
| , | Road and subway nodes, respectively |
| , | Links between And , and links between And , respectively |
| Change in the flow due to a problem in the link | |
| Remaining capacity of link | |
| , | Probability of travelers changing their mode of travel from road to subway, and subway to road, respectively |
| Links that model dependence of the power grid on the transportation network | |
| Modified demand encountered by node junctions and passenger stations located nearest to node , respectively | |
| , | Sets representing the power demand per unit increase in the traffic and subway demand, respectively |
| Links that model the dependence of the transportation network on the power grid | |
| Dependency related to EVSEs | |
| Dependency related to subway substations | |
| Probability that rectifier substation can support a failed substation |
References
- President′s Commission on Critical Infrastructure Protection (PCCIP). Critical Foundations: Protecting America′s Infrastructures: the Report of the President′S Commission on Critical Infrastructure Protection; Rep. No. 040-000-00699-1; U.S. Government Printing Office: Washington, DC, USA, 1997.
- Adachi, T.; Ellingwood, B. Serviceability of earthquake-damaged water systems: Effects of electrical power availability and power backup systems on system vulnerability. Reliab. Eng. Syst. Saf. 2008, 93, 78–88. [Google Scholar] [CrossRef]
- Anderson, C.W.; Santos, J.R.; Haimes, Y.Y. Risk-based input–output methodology for measuring the effects of the August 2003 Northeast Blackout. Econ. Syst. Res. 2007, 23, 183–204. [Google Scholar] [CrossRef]
- Amin, M. Toward secure and resilient interdependent infrastructures. J. Infrastruct. Syst. 2002, 8, 67–75. [Google Scholar] [CrossRef]
- Nan, C.; Eusgeld, I. Adopting HLA standard for interdependency study. Reliab. Eng. Syst. Saf. 2011, 96, 149–159. [Google Scholar] [CrossRef]
- Mendonca, D.; Wallace, W. Impacts of the 2001 World Trade Center attack on New York City critical infrastructures. J. Infrastruct. Syst. 2006, 12, 260–270. [Google Scholar] [CrossRef]
- Parandehgheibi, M.; Modiano, E. Robustness of Interdependent Networks: The case of communication networks and the power grid. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM 2013), Atlanta, GA, USA, 9–13 December 2013. [Google Scholar]
- Nguyen, D.T.; Shen, Y.; Thai, M.T. Detecting Critical Nodes in Interdependent Power Networks for Vulnerability Assessment. IEEE Trans. Smart Grid 2013, 4, 1–9. [Google Scholar] [CrossRef]
- Mayor’s Office of Long-Term Planning and Sustainability. Exploring Electric Vehicle Adoption In New York City; PlaNYC Progress Report; The City of New York: New York, NY, USA, 2010. [Google Scholar]
- McDaniels, T.; Chang, S.; Peterson, K.; Mikawoz, J.; Reed, D. Empirical framework for characterizing infrastructure failure interdependencies. J. Infrastruct. Syst. 2007, 13, 175–184. [Google Scholar] [CrossRef]
- Barton, D.C.; Eidson, E.D.; Schoenwald, D.A.; Stamber, K.L.; Reinert, R.K. Aspen-EE: An Agent-Based Model of Infrastructure Interdependency; Sandia National Labaratories: Livermore, CA, USA, 2000; pp. 1–69. [Google Scholar]
- Brown, T.; Beyeler, W.; Barton, D. Assessing infrastructure interdependencies: The challenge of risk analysis for complex adaptive systems. Int. J. Crit. Infrastruct. 2004, 1, 108–111. [Google Scholar] [CrossRef]
- Rose, A. Tracing Infrastructure Interdependencies through Economic Interdependencies. 2005. Available online: http://www.usc.edu/dept/ise/assets/002/26423.pdf (accessed on 15 May 2019).
- Patterson, S.A.; Apostolakis, G.E. Identification of critical locations across multiple infrastructures for terrorist actions. Reliab. Eng. Syst. Saf. 2007, 92, 1183–1203. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef]
- Rinaldi, M.S.; Peerenboom, J.P.; Kelly, T.K. Complex Networks, Identifying, Understanding, and Analyzing Critical Infrastructure Interdependencies. IEEE Control Syst. Mag. 2001, 21, 11–25. [Google Scholar]
- Rosato, V.; Issacharoff, L.; Tiriticco, F.; Meloni, S.; Porcellinis, S.; Setola, R. Modelling interdependent infrastructures using interacting dynamical models. Int. J. Crit. Infrastruct. 2008, 4, 63–67. [Google Scholar] [CrossRef]
- Shao, S.; Huang, X.; Stanley, H.E.; Havlin, S. Robustness of a partially interdependent network formed of clustered networks. Phys. Rev. 2014, 89. [Google Scholar] [CrossRef]
- Li, W.; Bashan, A.; Buldyrev, S.V.; Stanley, H.E.; Havlin, S. Cascading Failures in Interdependent Lattice Networks: The Critical Role of the Length of Dependency Links. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef]
- Gao, J.; Buldyrev, S.V.; Stanley, H.E.; Havlin, S. Networks formed from interdependent networks. Nat. Phys. 2012, 8, 40–48. [Google Scholar] [CrossRef]
- Nguyen, T.-D.; Cai, X.; Ouyang, Y.; Housh, M. Modelling infrastructure interdependencies, resiliency and sustainability. Int. J. Crit. Infrastruct. 2016, 12, 4–36. [Google Scholar] [CrossRef]
- Castet, J.; Saleh, J. Interdependent Multi-Layer Networks: Modeling and Survivability Analysis with Applications to Space-Based Networks. PLoS ONE 2013, 8. [Google Scholar] [CrossRef]
- Asavathiratham, C.; Roy, S.; Lesieutre, B.; Verghese, G. The influence model. IEEE Control Syst. 2001, 21, 52–64. [Google Scholar]
- Khodaparastan, M.; Mohamed, A.; Brandauer, W. Recuperation of Regenerative Braking Energy in Electric Rail Transit Systems. IEEE Trans. Intell. Transp. Syst. 2019, 1–17. [Google Scholar] [CrossRef]
- Mohamed, A. A Synthetic Case Study for Analysis of the Rising Interdependency between the Power Grid and E-Mobility. IEEE Access 2019. [Google Scholar] [CrossRef]
- Mohamed, A.; Salehi, V.; Ma, T.; Mohammed, O. Real-Time Energy Management Algorithm for Plug-In Hybrid Electric Vehicle Charging Parks Involving Sustainable Energy. IEEE Trans. Sustain. Energy 2014, 5, 577–586. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, A.A.A. On the Rising Interdependency between the Power Grid, ICT Network, and E-Mobility: Modeling and Analysis. Energies 2019, 12, 1874. https://doi.org/10.3390/en12101874
Mohamed AAA. On the Rising Interdependency between the Power Grid, ICT Network, and E-Mobility: Modeling and Analysis. Energies. 2019; 12(10):1874. https://doi.org/10.3390/en12101874
Chicago/Turabian StyleMohamed, Ahmed Ali A. 2019. "On the Rising Interdependency between the Power Grid, ICT Network, and E-Mobility: Modeling and Analysis" Energies 12, no. 10: 1874. https://doi.org/10.3390/en12101874
APA StyleMohamed, A. A. A. (2019). On the Rising Interdependency between the Power Grid, ICT Network, and E-Mobility: Modeling and Analysis. Energies, 12(10), 1874. https://doi.org/10.3390/en12101874




