Sliding Mode Observer-Based Parameter Identification and Disturbance Compensation for Optimizing the Mode Predictive Control of PMSM
Abstract
:1. Introduction
2. Designof Model Predictive Controller
2.1. Mathematical Model of the PMSM
2.2. Design of DMPC for the PMSM
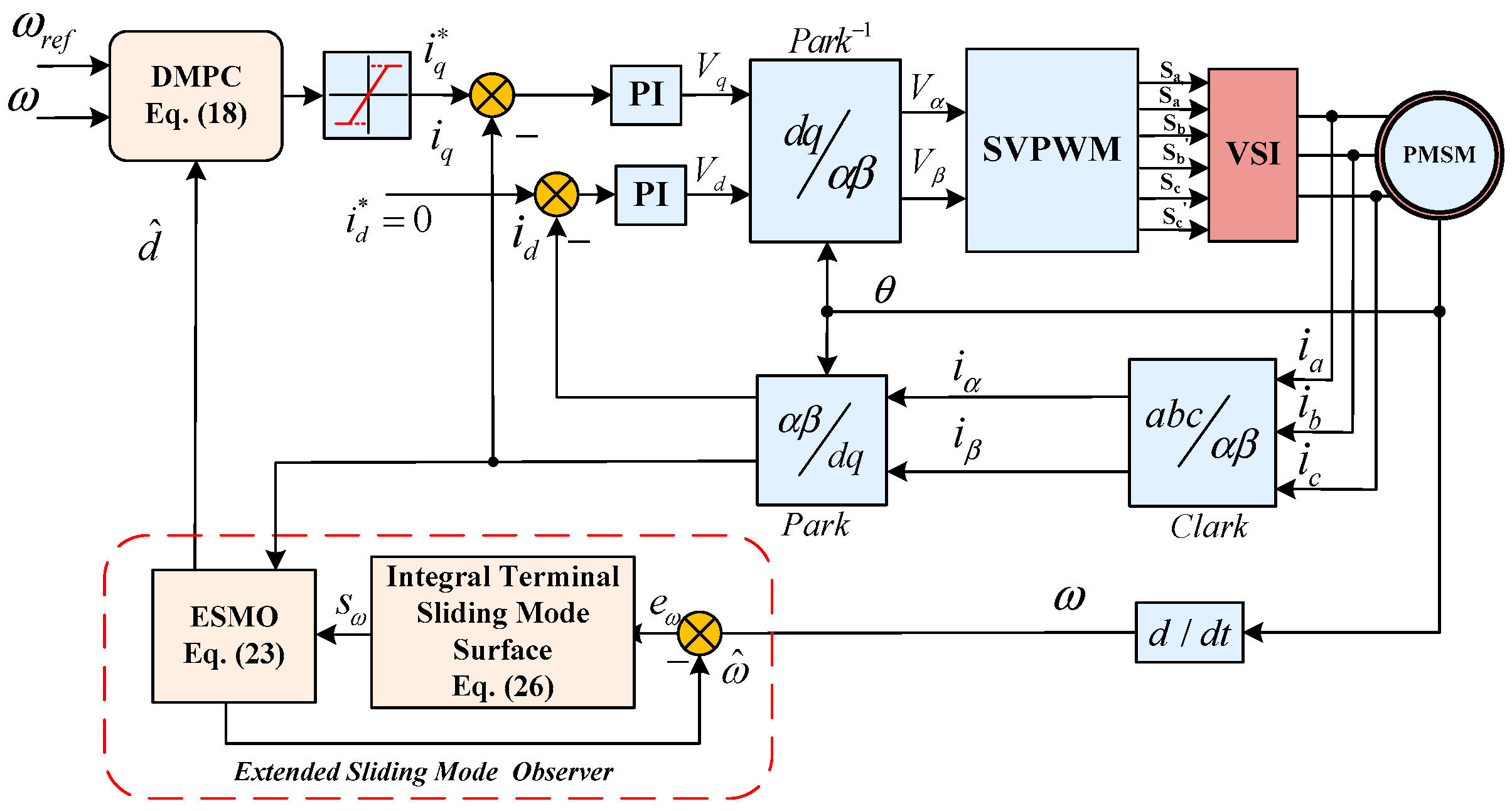
2.3. Closed Loop Implementation of DMPC
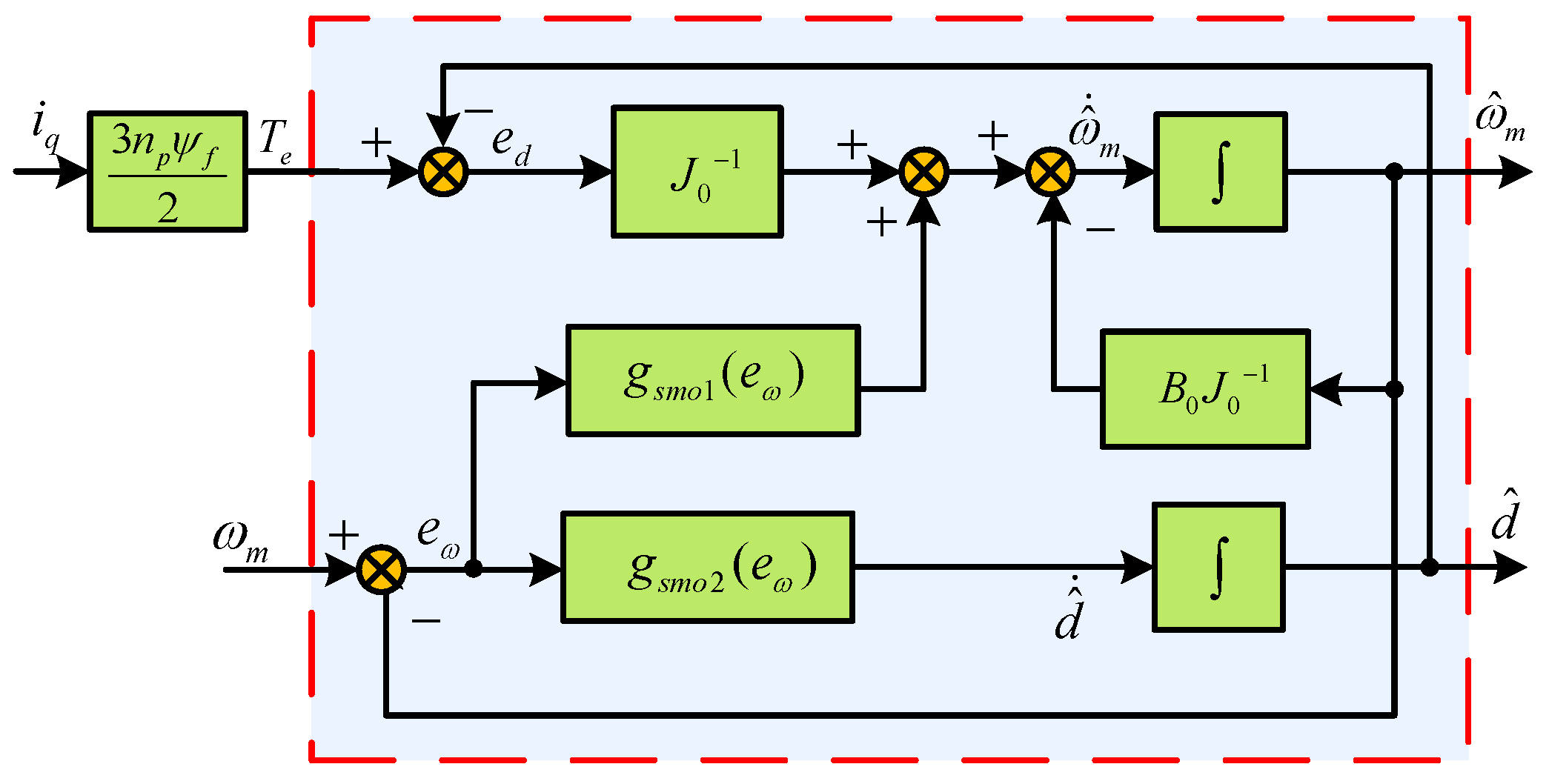
3. Design of Extended Sliding Mode Observer
3.1. DesignofExtended Sliding Mode Observer
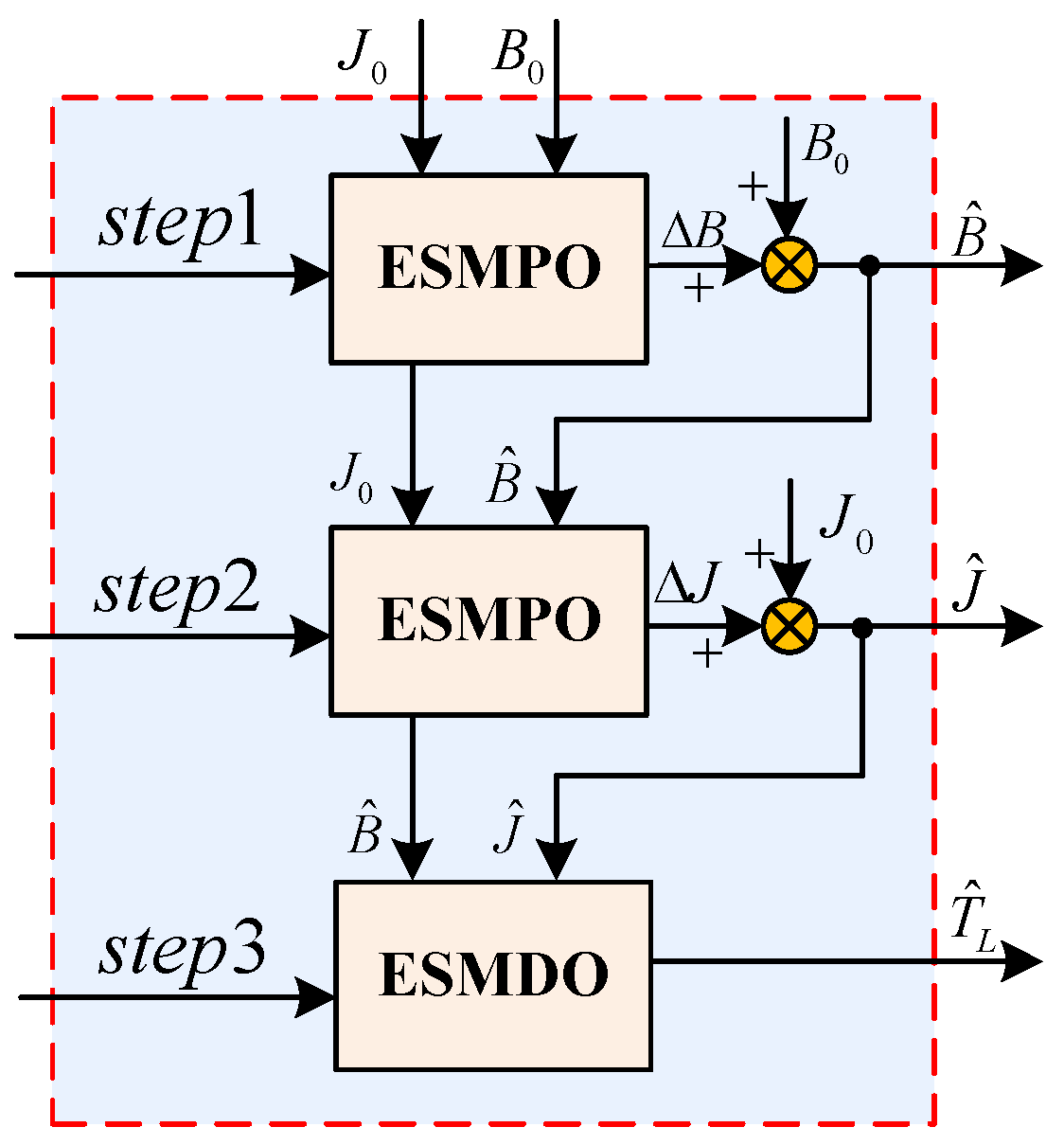
3.2. Parameter Observation Steps
4. Simulation and Experimental Results
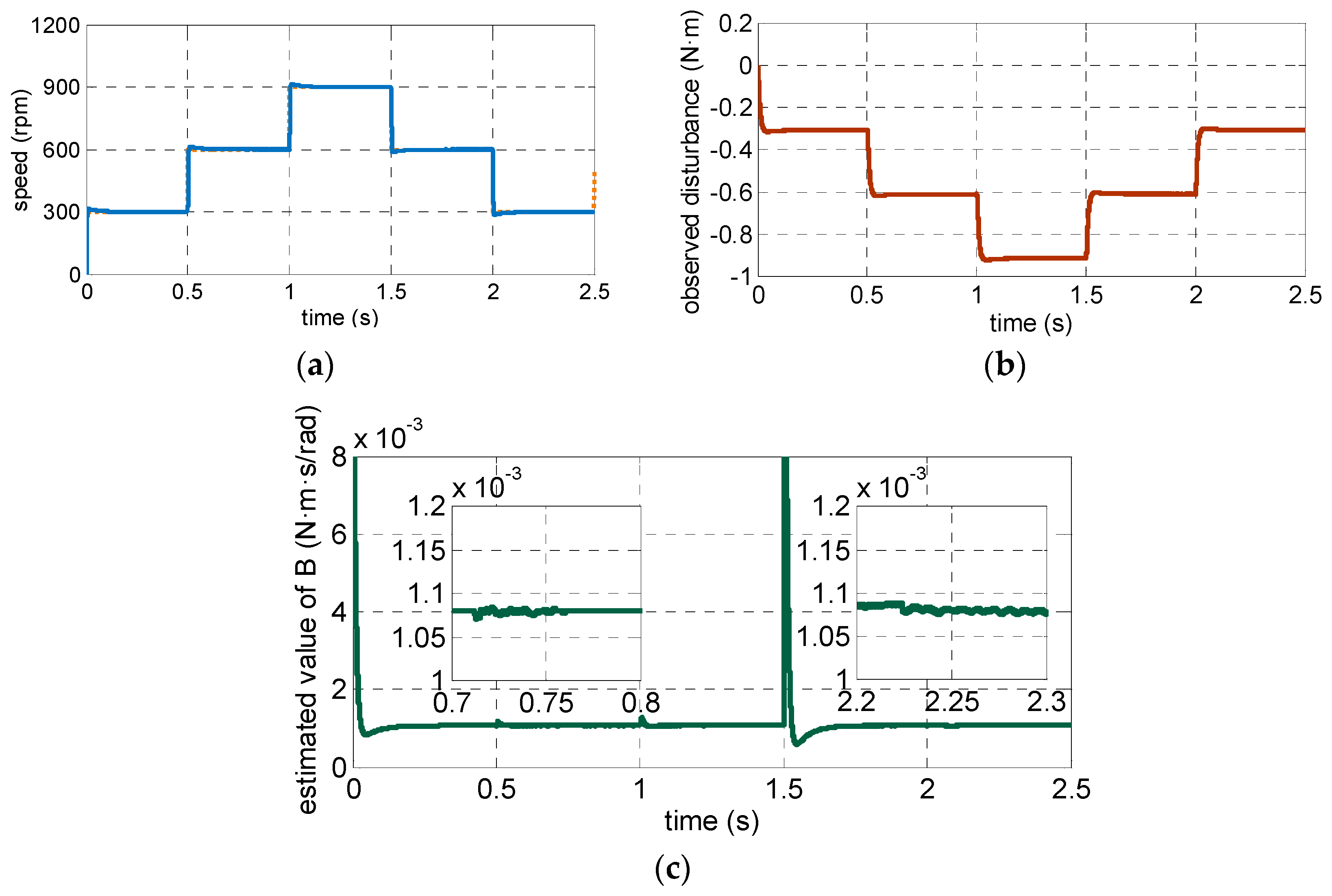
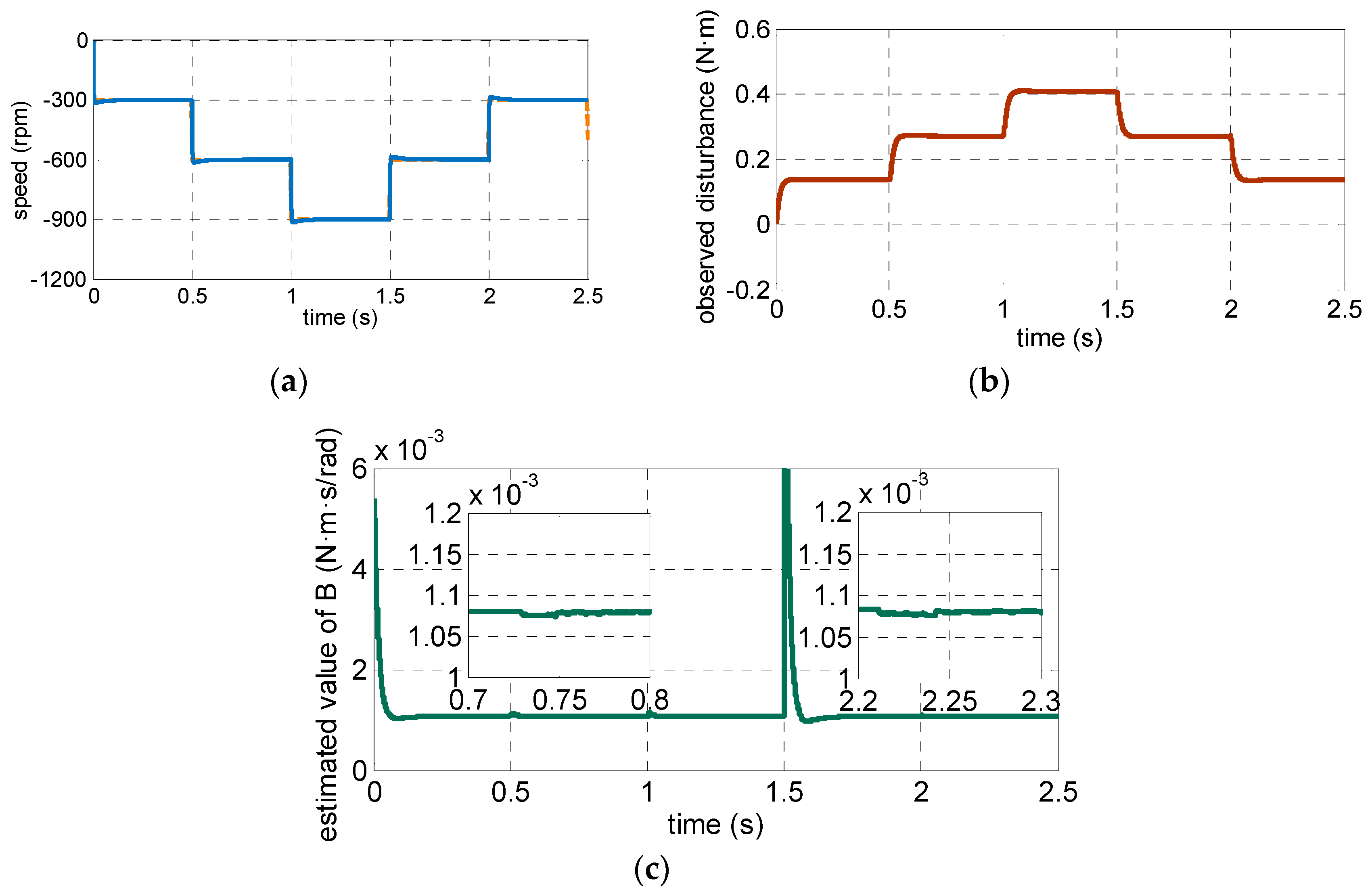
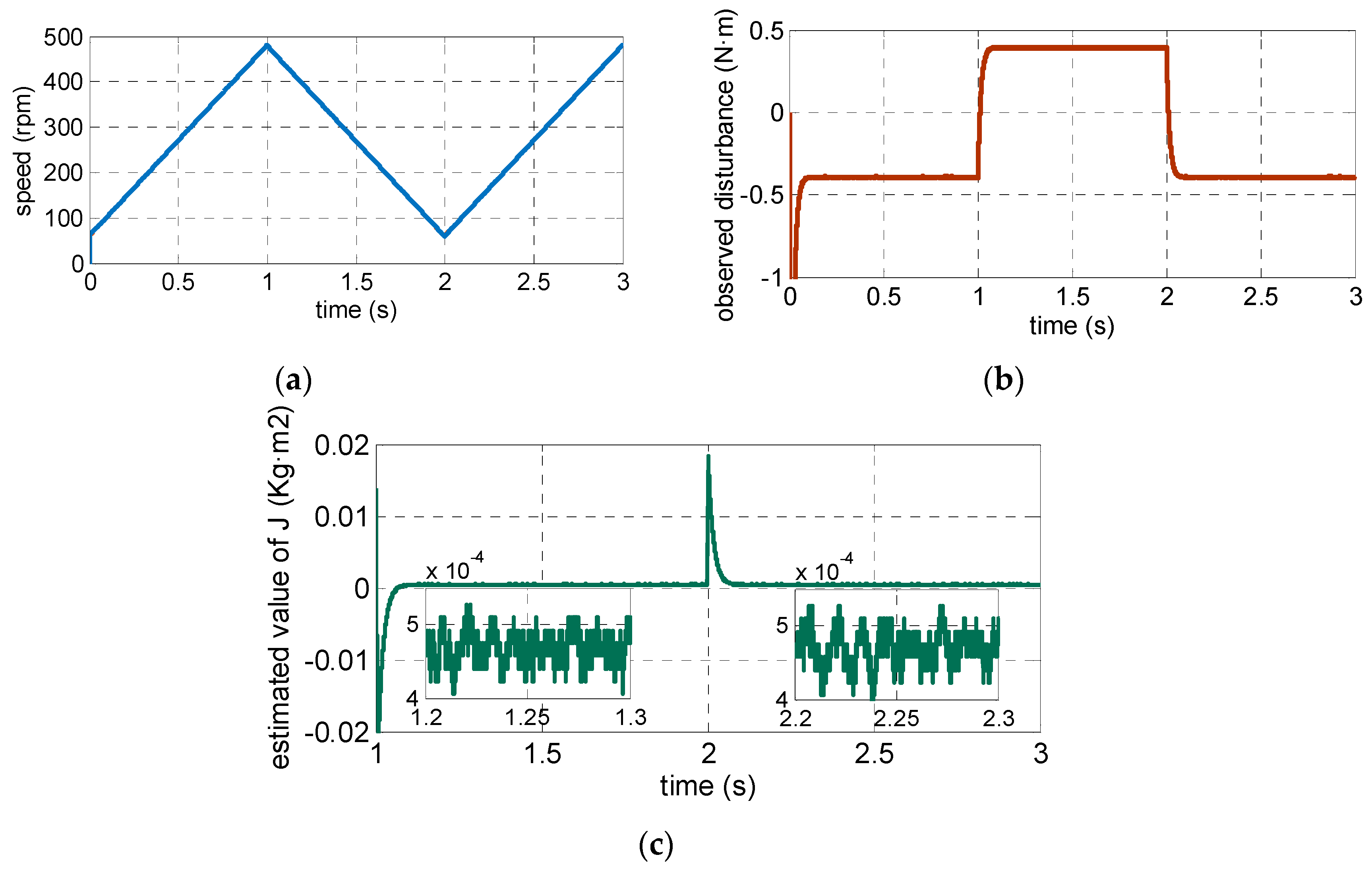
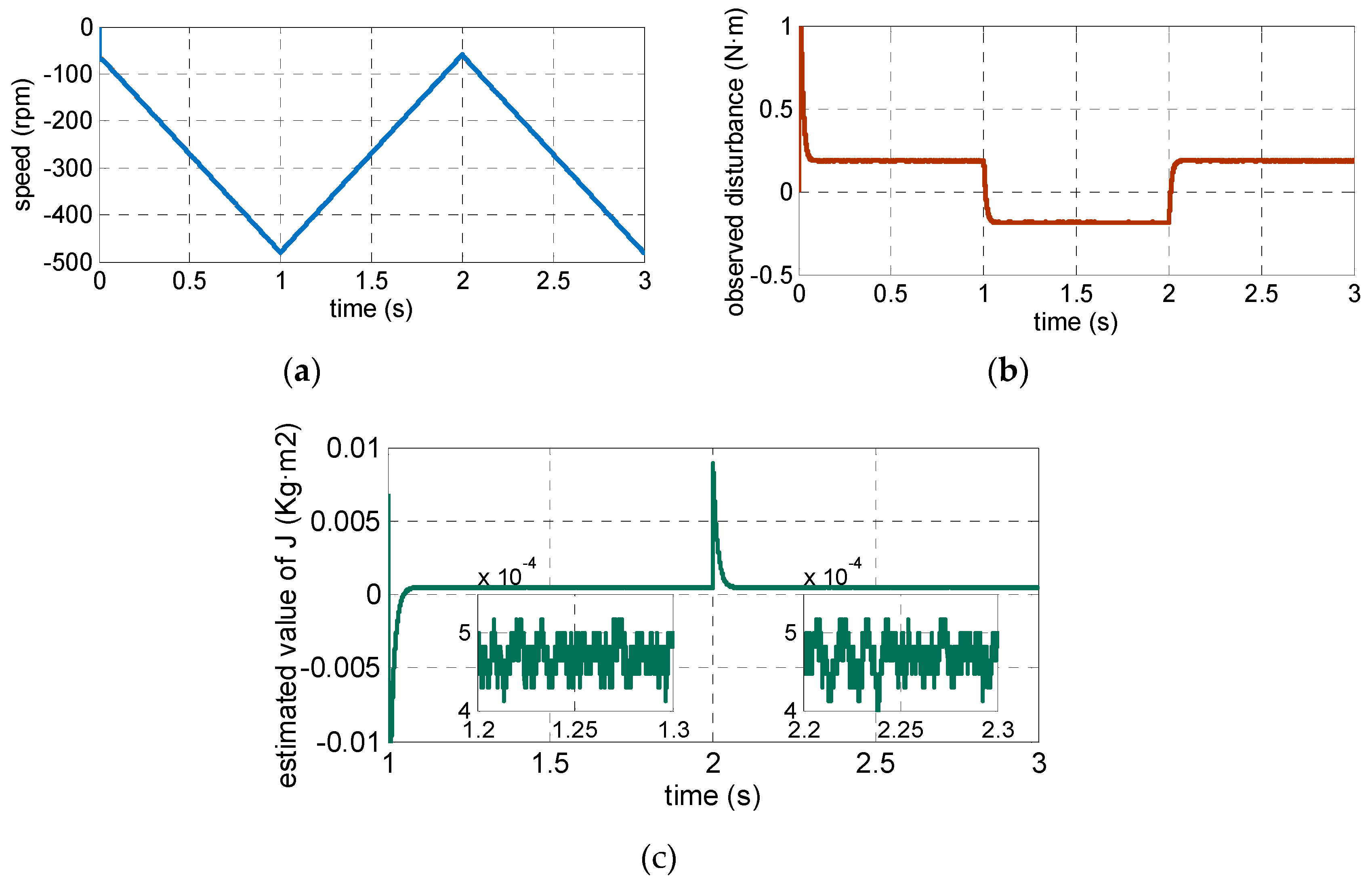
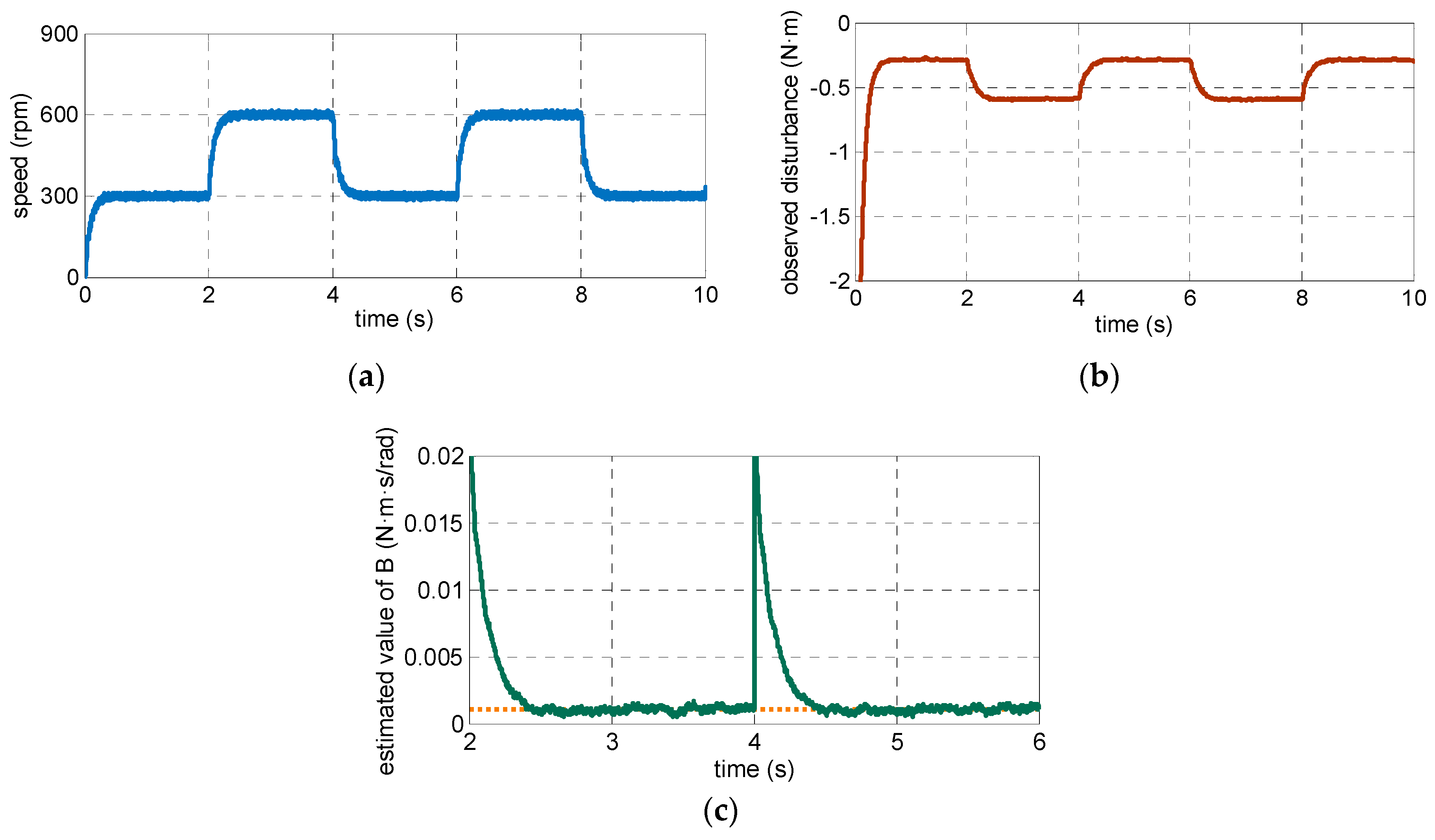
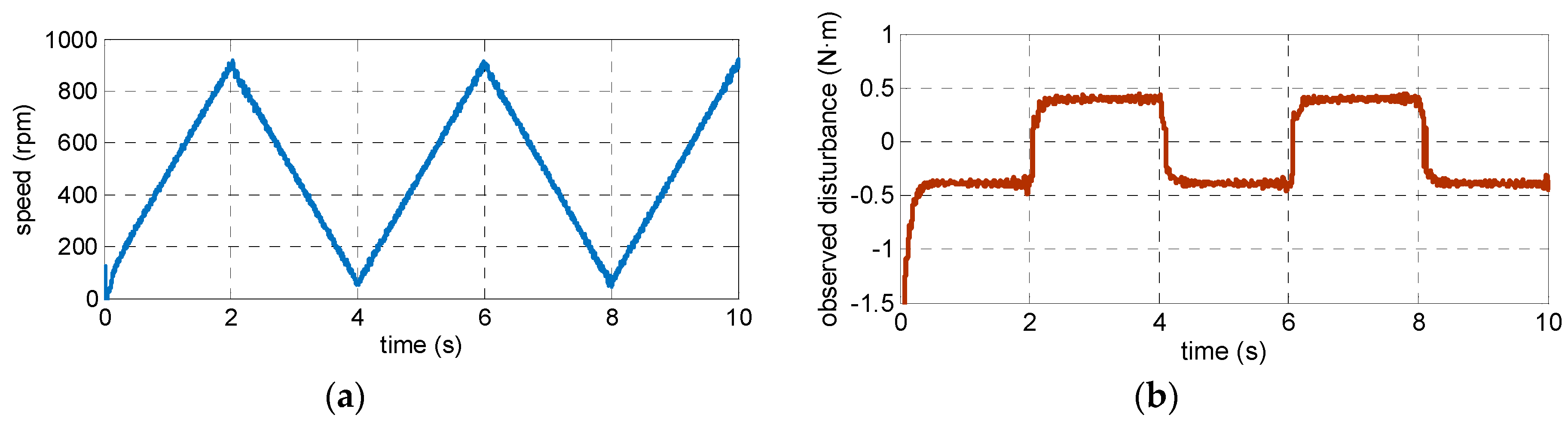
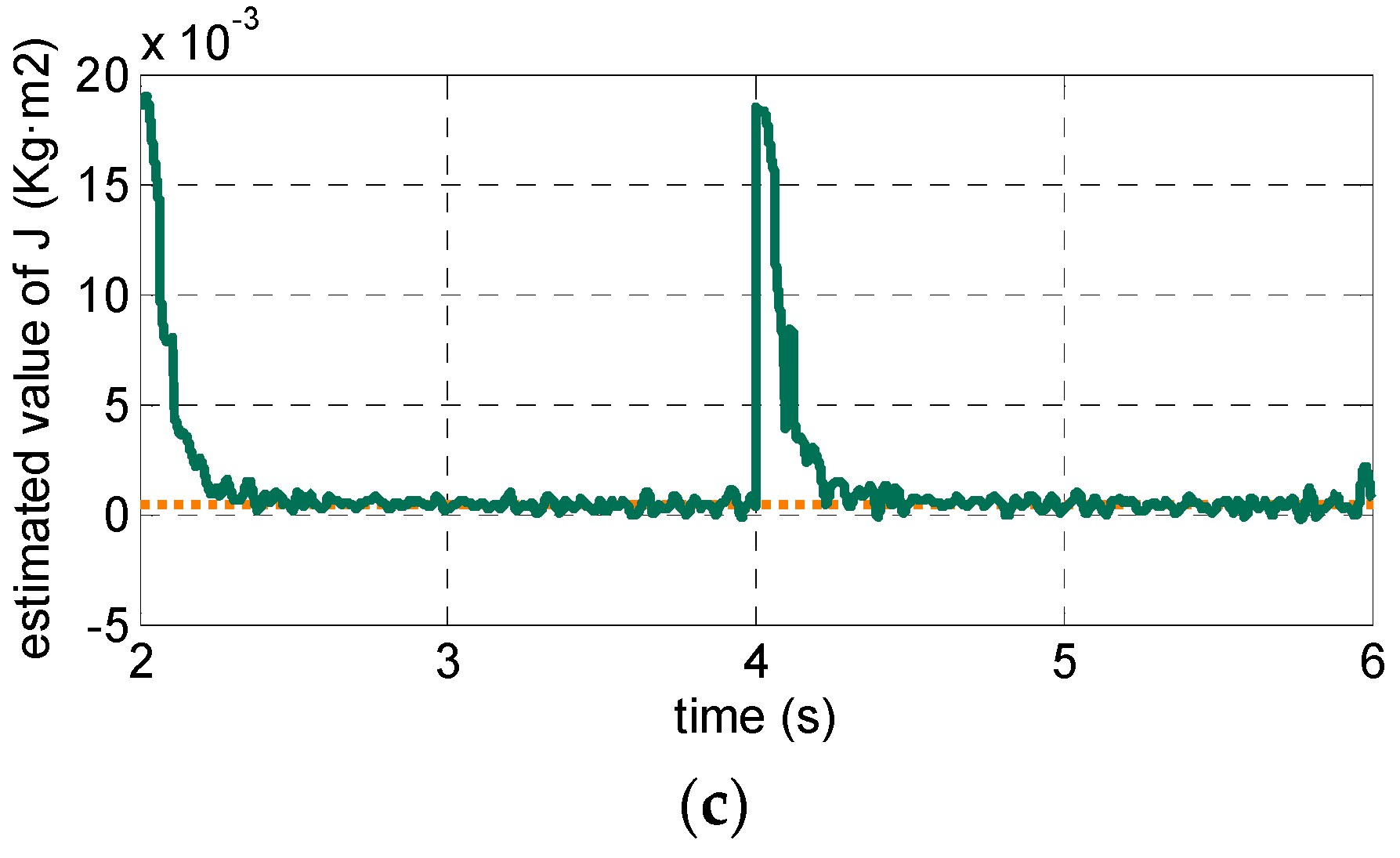
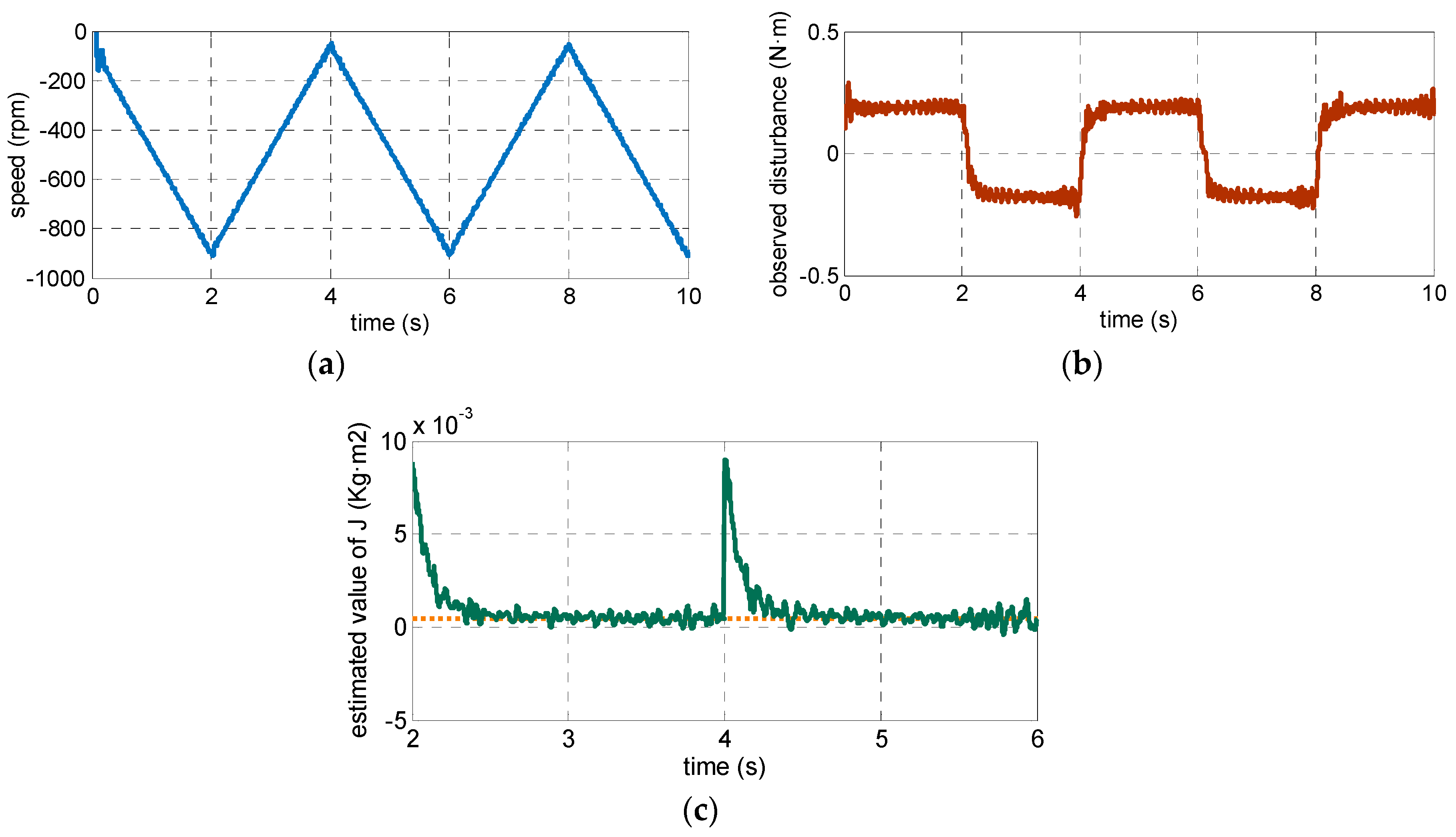
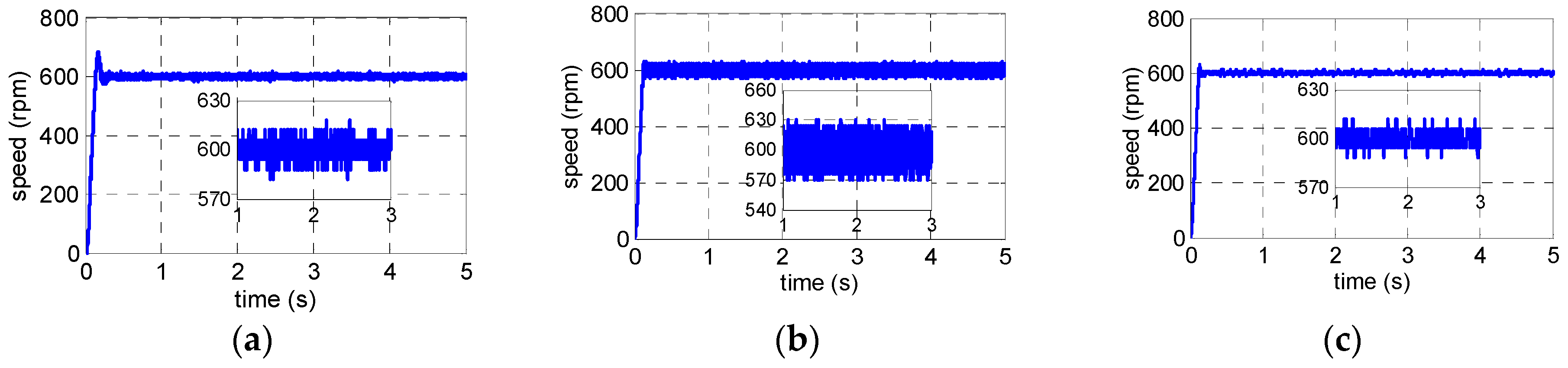
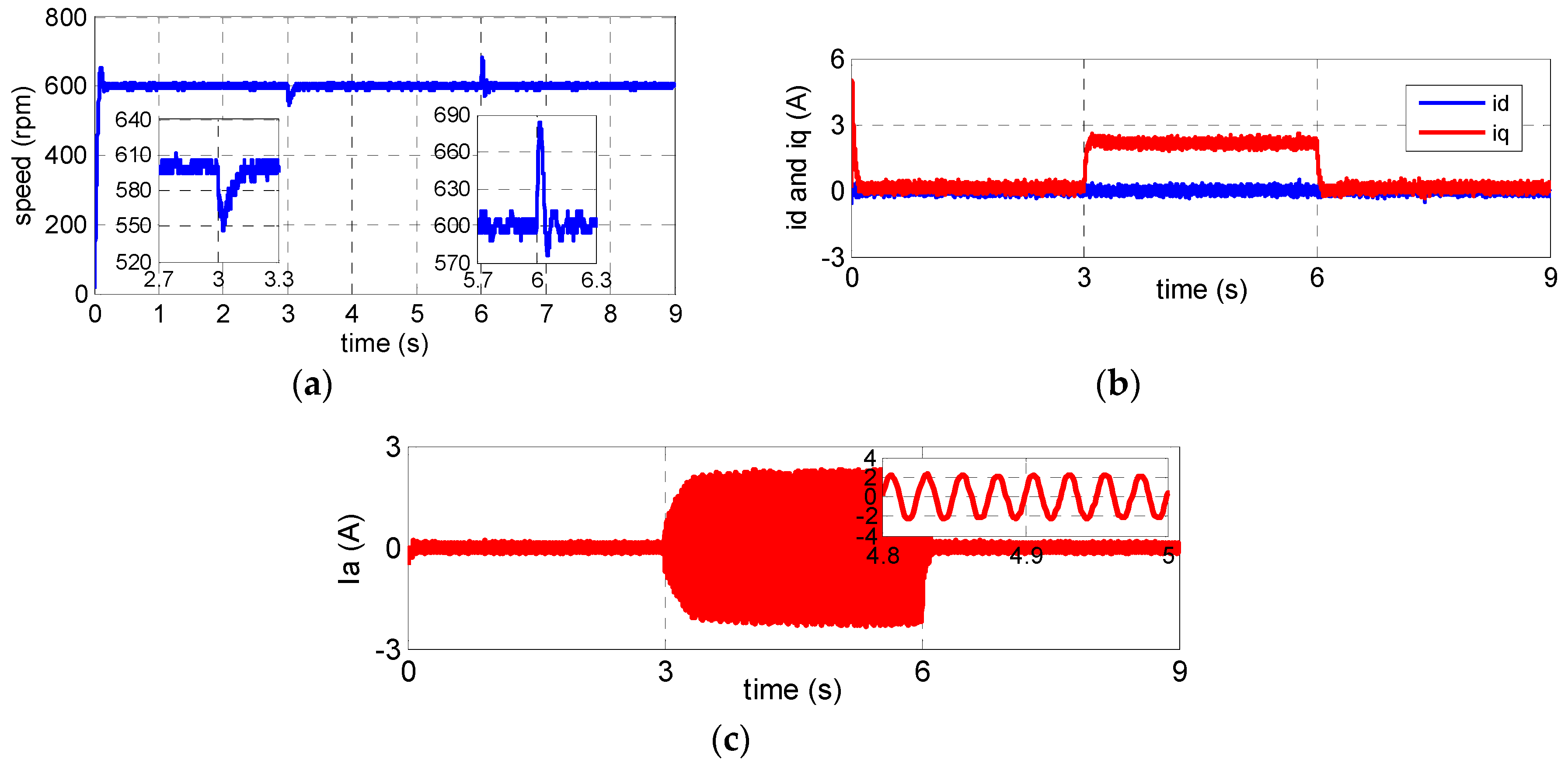
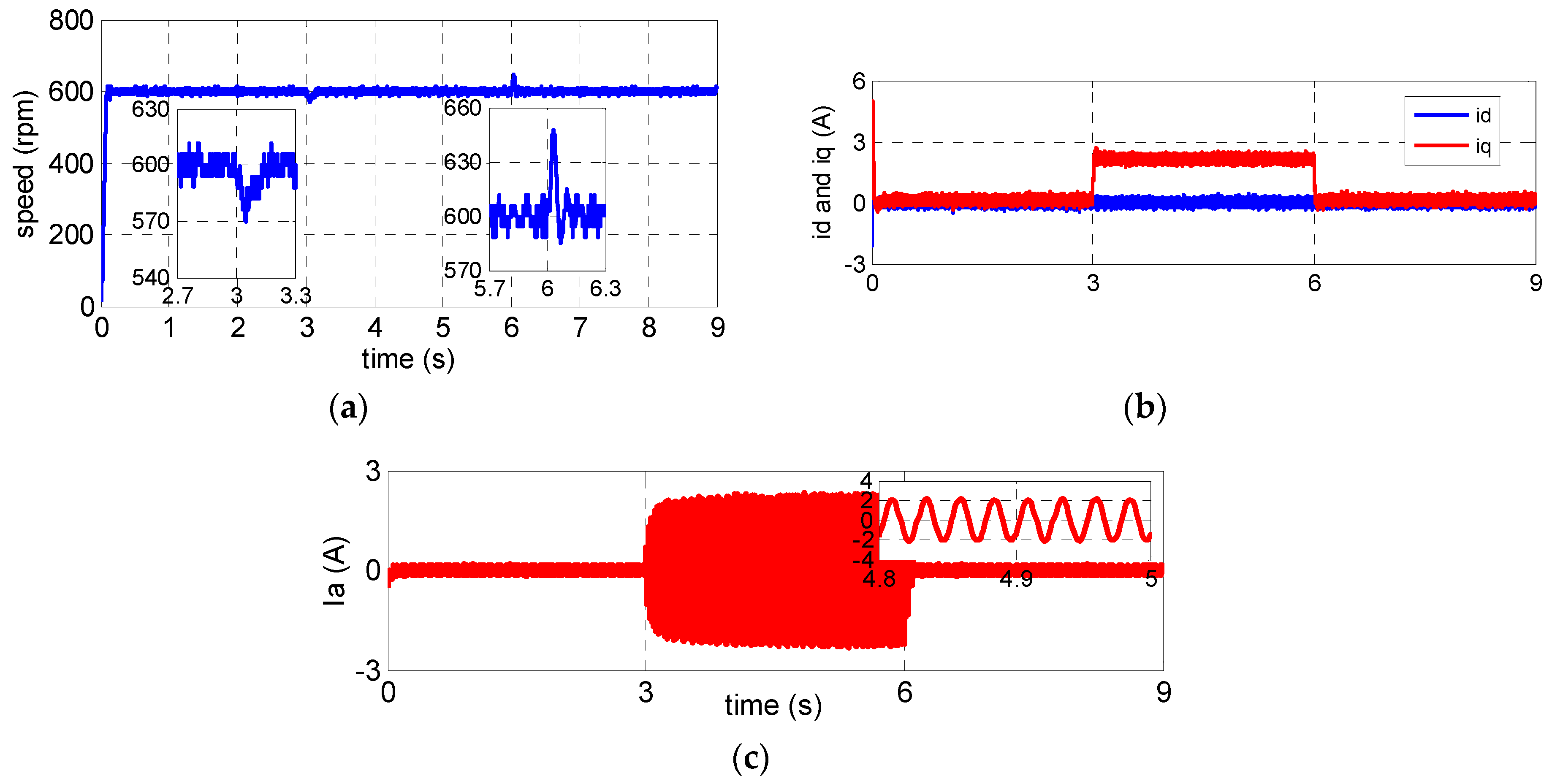
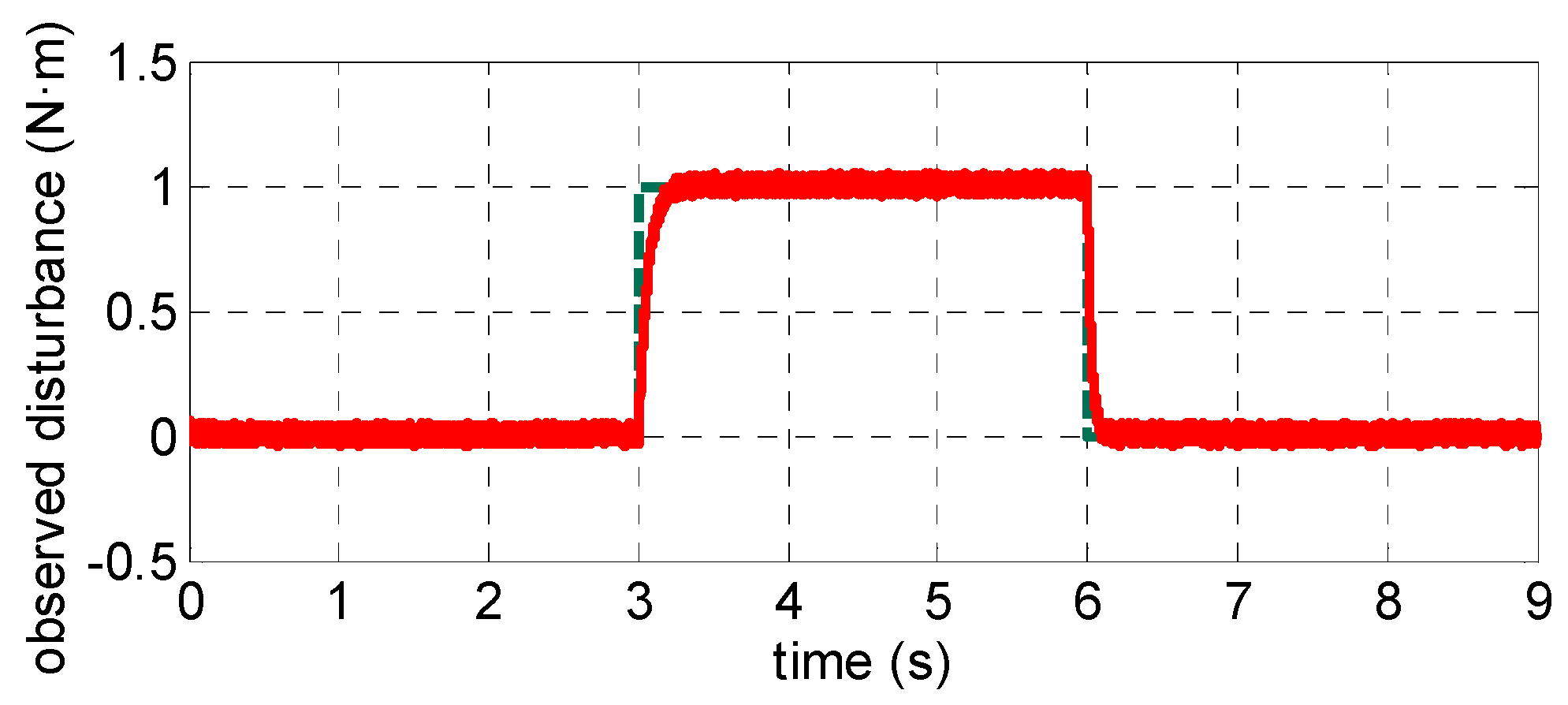
4.1. Simulation Resultsand Analysis
4.2. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Su, D.; Zhang, C.; Dong, Y. An Improved Continuous-Time Model Predictive Control of Permanent Magnetic Synchronous Motors for a Wide-Speed Range. Energies 2017, 10, 2051. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Deng, Y. Torque Ripple Minimization of PMSM Based on Robust ILC Via Adaptive Sliding Mode Control. IEEE Trans. Power Electron. 2018, 33, 3655–3671. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.; Li, K.; Zhang, Q. Robust current control-based generalized predictive control with sliding mode disturbance compensation for PMSM drives. ISA Trans. 2017, 71, 542–552. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Cheng, S.; Ning, B.; Li, Y. Robust model predictive control with simplified repetitive control for electrical machine drives. IEEE Trans. Power Electron. 2019, 34, 4524–4535. [Google Scholar] [CrossRef]
- Qi, L.; Shi, H. Adaptive position tracking control of permanent magnet synchronous motor based on RBF fast terminal sliding mode control. Neurocomputing 2013, 115, 23–30. [Google Scholar] [CrossRef]
- Li, S.; Liu, Z. Adaptive Speed Control for Permanent-Magnet Synchronous Motor System with Variations of Load Inertia. IEEE Trans. Ind. Electron. 2009, 56, 3050–3059. [Google Scholar] [CrossRef]
- Yu, J.; Chen, B.; Yu, H.; Lin, C.; Ji, Z.; Cheng, X. Position tracking control for chaotic permanent magnet synchronous motors via indirect adaptive neural approximation. Neurocomputing 2015, 156, 245–251. [Google Scholar] [CrossRef]
- Kobayashi, H.; Katsura, S.; Ohnishi, K. An Analysis of Parameter Variations of Disturbance Observer for Motion Control. IEEE Trans. Ind. Electron. 2007, 54, 3413–3421. [Google Scholar] [CrossRef]
- Wang, T.; Huang, J.; Ye, M.; Chen, J.; Kong, W.; Kang, M.; Yu, M. An EMF Observer for PMSM Sensorless Drives Adaptive to Stator Resistance and Rotor Flux-linkage. IEEE J. Emerg. Sel. Top. Power Electron. 2019, in press. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.H.; Chen, X. Generalized Extended State Observer Based Control for Systems with Mismatched Uncertainties. IEEE Trans. Ind. Electron. 2012, 59, 4792–4802. [Google Scholar] [CrossRef]
- Lin, F.J.; Sun, I.F.; Yang, K.J.; Chang, J.K. Recurrent Fuzzy Neural Cerebellar Model Articulation Network Fault-Tolerant Control of Six-Phase Permanent Magnet Synchronous Motor Position Servo Drive. IEEE Trans. Fuzzy Syst. 2016, 24, 153–167. [Google Scholar] [CrossRef]
- Liu, H.; Li, S. Speed Control for PMSM Servo System Using Predictive Functional Control and Extended State Observer. IEEE Trans. Ind. Electron. 2012, 59, 1171–1183. [Google Scholar] [CrossRef]
- Kouro, S.; Cortes, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model Predictive Control—A Simple and Powerful Method to Control Power Converters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Chai, S.; Wang, L.; Rogers, E. Model predictive control of a permanent magnet synchronous motor with experimental validation. Control Eng. Pract. 2013, 21, 1584–1593. [Google Scholar] [CrossRef]
- Chai, S.; Wang, L.; Rogers, E. A Cascade MPC Control Structure for a PMSM With Speed Ripple Minimization. IEEE Trans. Ind. Electron. 2013, 60, 2978–2987. [Google Scholar] [CrossRef]
- Belda, K.; Vosmik, D. Explicit Generalized Predictive Control of Speed and Position of PMSM Drives. IEEE Trans. Ind. Electron. 2016, 63, 3889–3896. [Google Scholar] [CrossRef]
- Bolognani, S.; Bolognani, S.; Peretti, L.; Zigliotto, M. Design and Implementation of Model Predictive Control for Electrical Motor Drives. IEEE Trans. Ind. Electron. 2009, 56, 1925–1936. [Google Scholar] [CrossRef]
- Hu, F.; Luo, D.; Luo, C.; Long, Z.; Wu, G. Cascaded Robust Fault-Tolerant Predictive Control for PMSM Drives. Energies 2018, 11, 3087. [Google Scholar] [CrossRef]
- Wang, C.; Yang, M.; Zheng, W.; Long, J.; Xu, D. Vibration Suppression With Shaft Torque Limitation Using Explicit MPC-PI Switching Control in Elastic Drive Systems. IEEE Trans. Ind. Electron. 2015, 62, 6855–6867. [Google Scholar] [CrossRef]
- Shoukry, Y.; El-Kharashi, M.W.; Hammad, S. MPC-On-Chip: An Embedded GPC Coprocessor for Automotive Active Suspension Systems. IEEE Embed. Syst. Lett. 2010, 2, 31–34. [Google Scholar] [CrossRef]
- Song, Z.; Mei, X.; Jiang, G. Inertia identification based on model reference adaptive system with variable gain for AC servo systems. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 188–192. [Google Scholar] [CrossRef]
- Dybkowski, M. Universal Speed and FluxEstimator for Induction Motor. Power Electron. Drives 2018, 38, 157–169. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, M.; Xu, D. A novel algorithm for on-line inertia identification via adaptive recursive least squares. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 2973–2978. [Google Scholar] [CrossRef]
- Wang, K.; Chiasson, J.; Bodson, M.; Tolbert, L.M. A nonlinear least-squares approach for identification of the induction motor parameters. IEEE Trans. Autom. Control 2005, 50, 1622–1628. [Google Scholar] [CrossRef]
- Hong, S.; Lee, C.; Borrelli, F.; Hedrick, J.K. A Novel Approach for Vehicle Inertial Parameter Identification Using a Dual Kalman Filter. IEEE Trans. Intell. Transp. Syst. 2015, 16, 151–161. [Google Scholar] [CrossRef]
- Niu, L.; Xu, D.; Yang, M.; Gui, X.; Liu, Z. On-line Inertia Identification Algorithm for PI Parameters Optimization in Speed Loop. IEEE Trans. Power Electron. 2015, 30, 849–859. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Han, F. High-Order Terminal Sliding-Mode Observer for Parameter Estimation of a Permanent-Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2013, 60, 4272–4280. [Google Scholar] [CrossRef]
- Lian, C.; Xiao, F.; Gao, S.; Liu, J. Load Torque and Moment of Inertia Identification for Permanent Magnet Synchronous Motor Drives Based on Sliding Mode Observer. IEEE Trans. Power Electron. 2019, in press. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z. Sliding-Mode Observer-Based Mechanical Parameter Estimation for Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2016, 31, 5732–5745. [Google Scholar] [CrossRef]
- Xu, W.; Jiang, Y.; Mu, C. Novel Composite Sliding Mode Control for PMSM Drive System Based on Disturbance Observer. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, L.; Zhao, K.; Sun, L. Nonlinear Speed Control for PMSM System Using Sliding-Mode Control and Disturbance Compensation Techniques. IEEE Trans. Power Electron. 2013, 28, 1358–1365. [Google Scholar] [CrossRef]
- Lu, E.; Li, W.; Yang, X.; Xu, S. Composite Sliding Mode Control of a Permanent Magnet Direct-Driven System for a Mining Scraper Conveyor. IEEE Access 2017, 5, 22399–22408. [Google Scholar] [CrossRef]
- Lyu, M.; Wu, G.; Luo, D.; Rong, F.; Huang, S. Robust Nonlinear Predictive Current Control Techniques for PMSM. Energies 2019, 12, 443. [Google Scholar] [CrossRef]
- Chiu, C.S. Derivative and integral terminal sliding mode control for a class of MIMO nonlinear systems. Automatica 2012, 48, 316–326. [Google Scholar] [CrossRef]
- Wang, A.; Jia, X.; Dong, S. A New Exponential Reaching Law of Sliding Mode Control to Improve Performance of Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2013, 49, 2409–2412. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Armature resistance (Rs) | 4.3 (Ω) |
| Armature inductance (Ls) | 20.1 (mH) |
| Torque coefficient (Kt) | 0.498 (N∙m/A) |
| Permanent magnet flux linkage () | 0.083 (Wb) |
| Number of pole pairs (np) | 4 |
| Viscous friction coefficient (B) | 1.08 × 10−3 (N·m·s/rad) |
| Rotational inertia (J) | 4.7 × 10−4 (Kg∙m2) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, M.; Deng, Y.; Li, H.; Liu, J.; Fei, Q. Sliding Mode Observer-Based Parameter Identification and Disturbance Compensation for Optimizing the Mode Predictive Control of PMSM. Energies 2019, 12, 1857. https://doi.org/10.3390/en12101857
Shao M, Deng Y, Li H, Liu J, Fei Q. Sliding Mode Observer-Based Parameter Identification and Disturbance Compensation for Optimizing the Mode Predictive Control of PMSM. Energies. 2019; 12(10):1857. https://doi.org/10.3390/en12101857
Chicago/Turabian StyleShao, Meng, Yongting Deng, Hongwen Li, Jing Liu, and Qiang Fei. 2019. "Sliding Mode Observer-Based Parameter Identification and Disturbance Compensation for Optimizing the Mode Predictive Control of PMSM" Energies 12, no. 10: 1857. https://doi.org/10.3390/en12101857
APA StyleShao, M., Deng, Y., Li, H., Liu, J., & Fei, Q. (2019). Sliding Mode Observer-Based Parameter Identification and Disturbance Compensation for Optimizing the Mode Predictive Control of PMSM. Energies, 12(10), 1857. https://doi.org/10.3390/en12101857





