Mechanism Reduction and Bunsen Burner Flame Verification of Methane
Abstract
1. Introduction
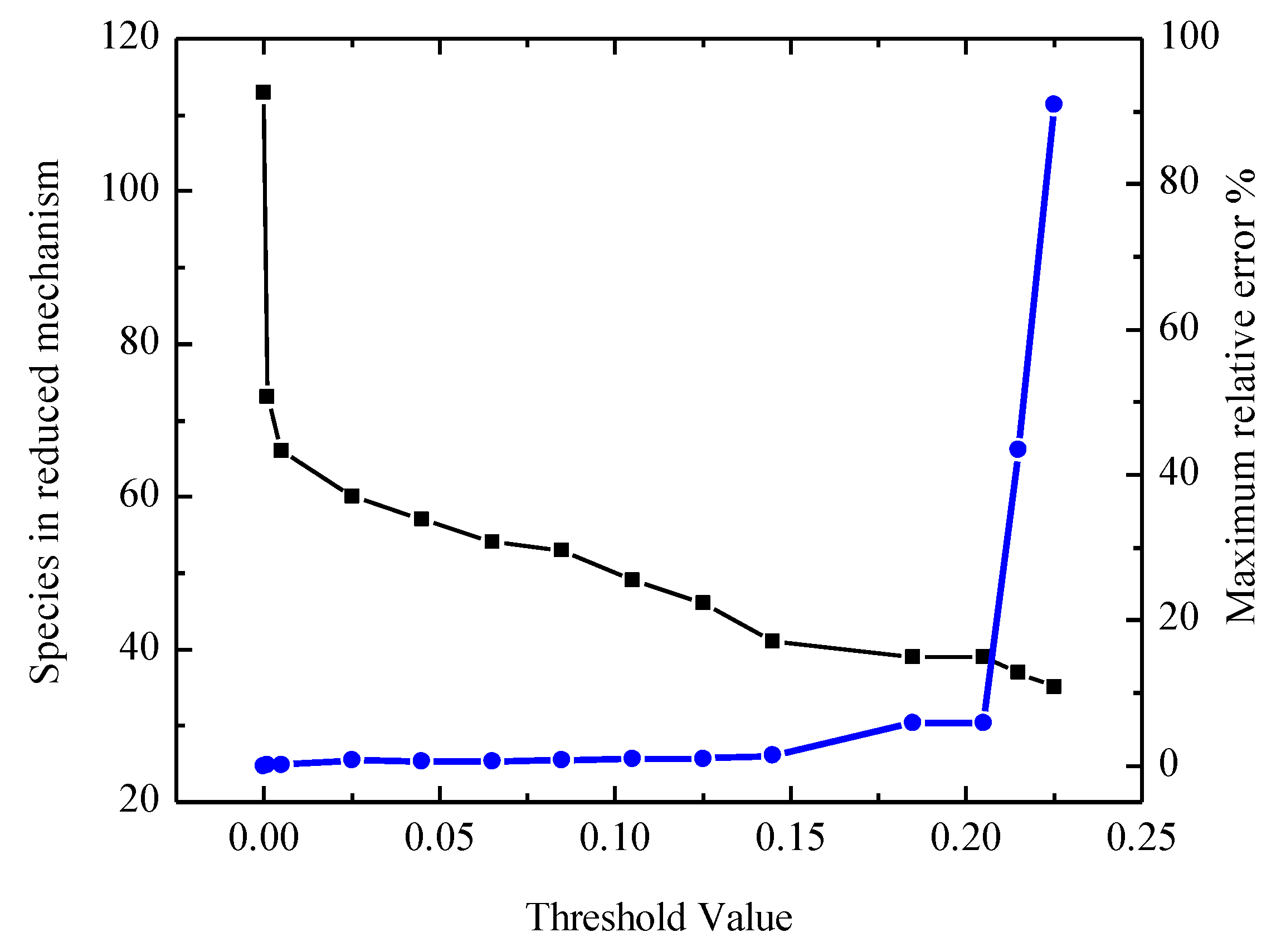
2. Mechanism Reduction
3. Verification of Reduced Mechanism
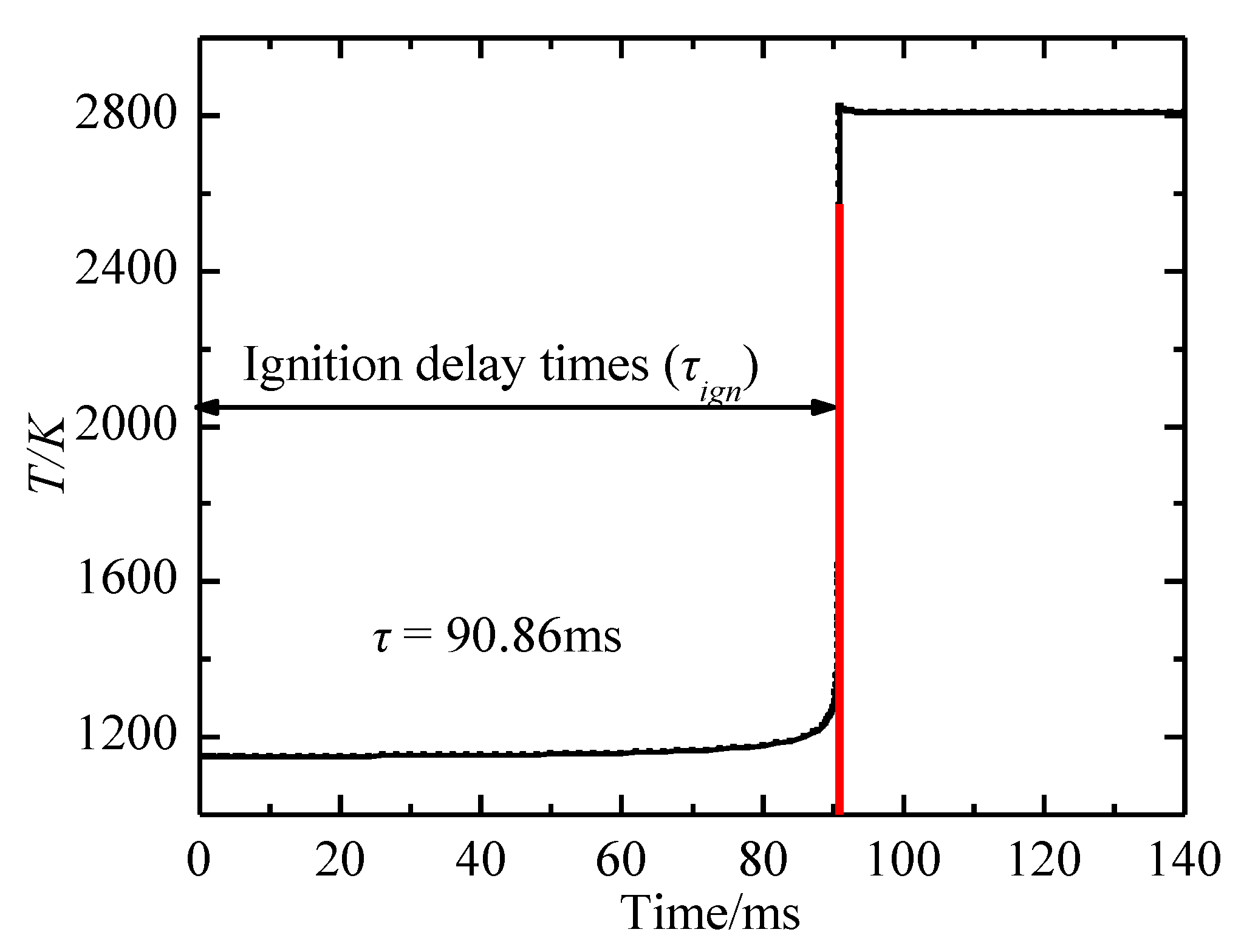
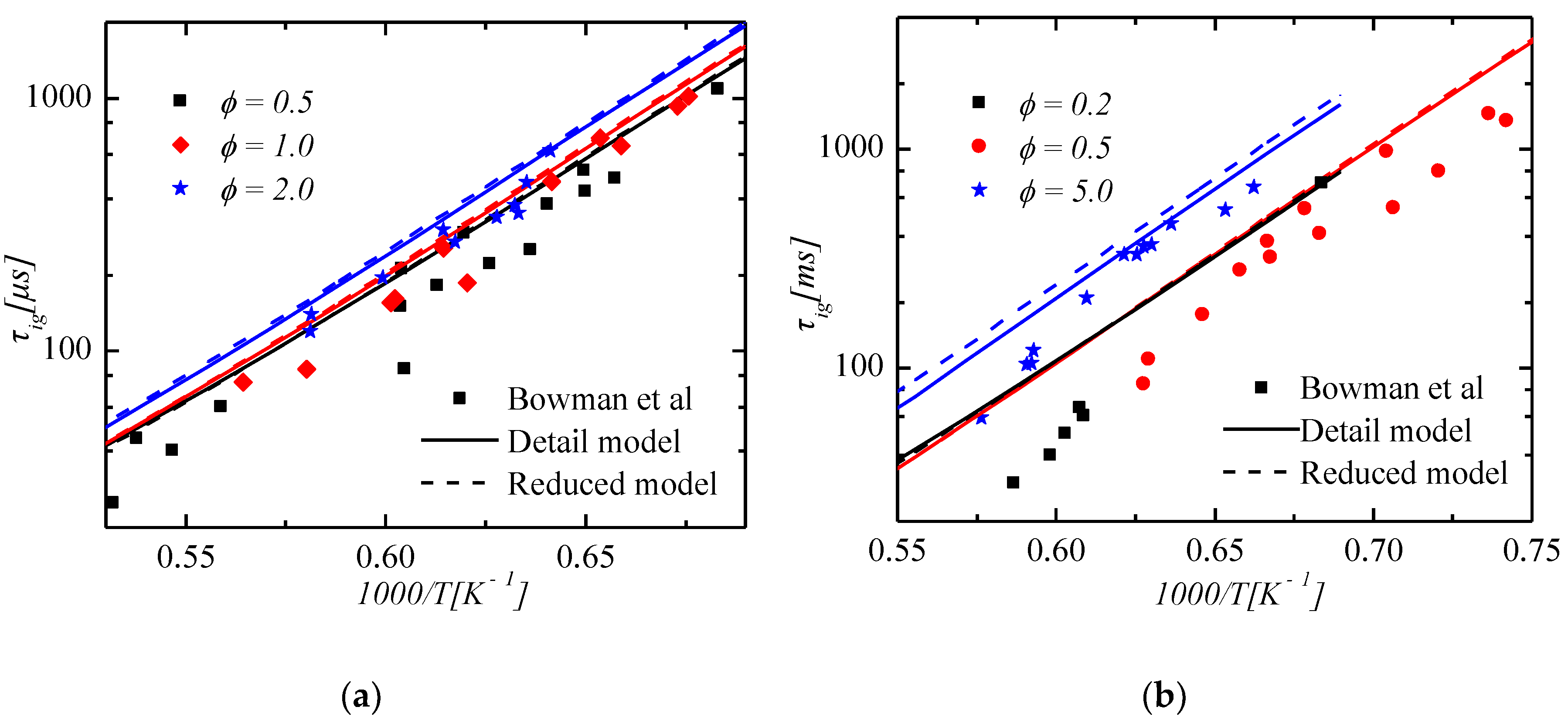
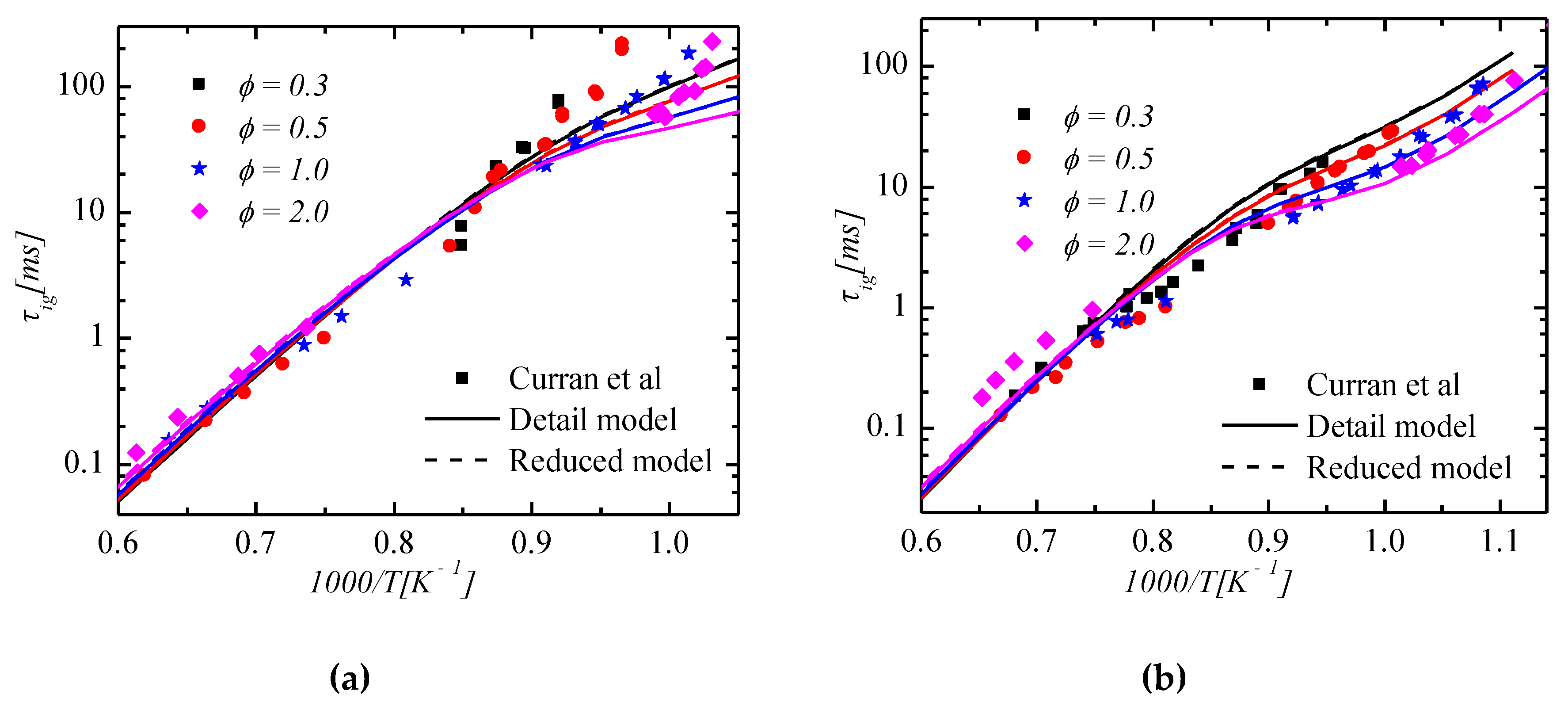
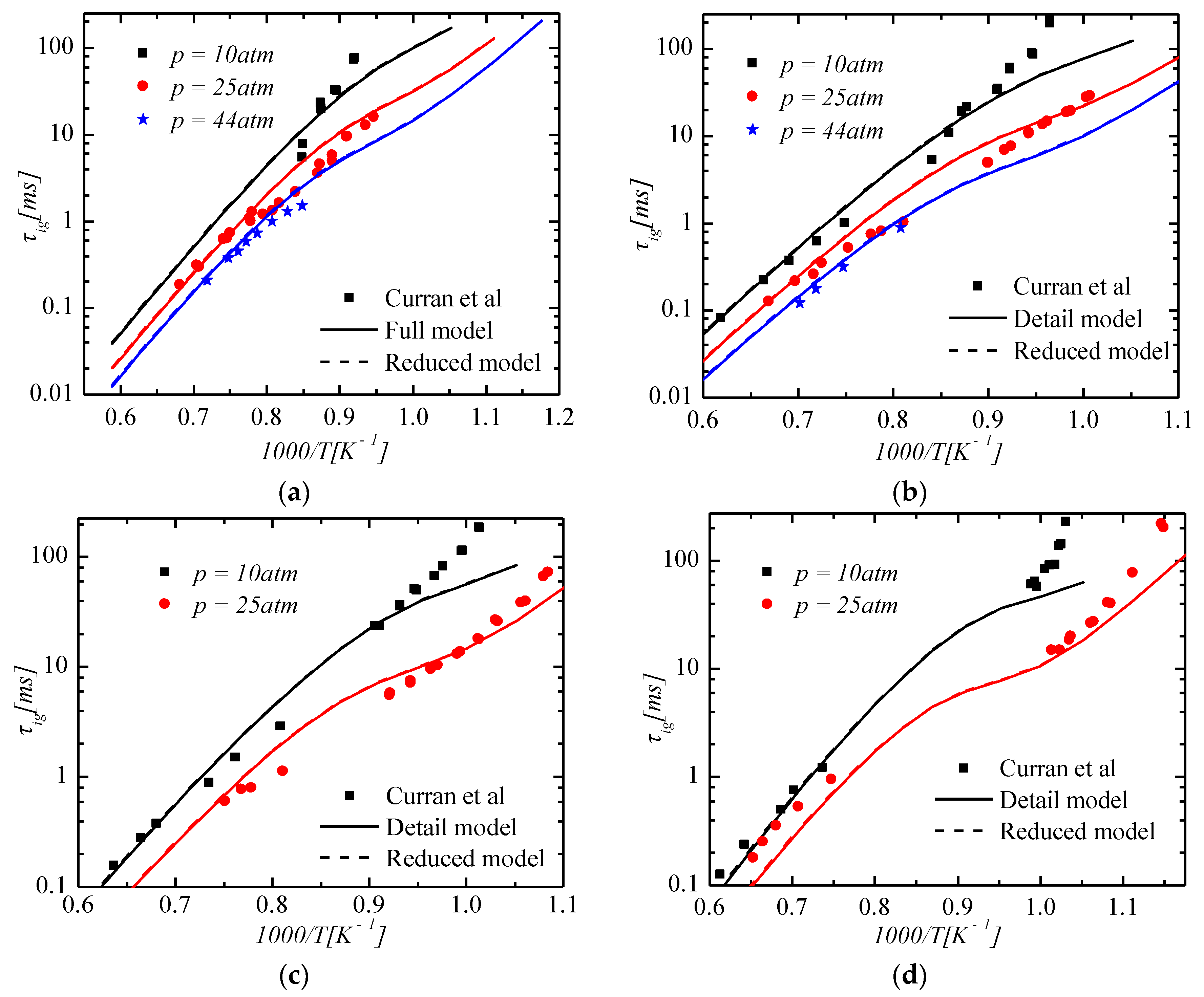
3.1. Verification of Ignition Delay Times
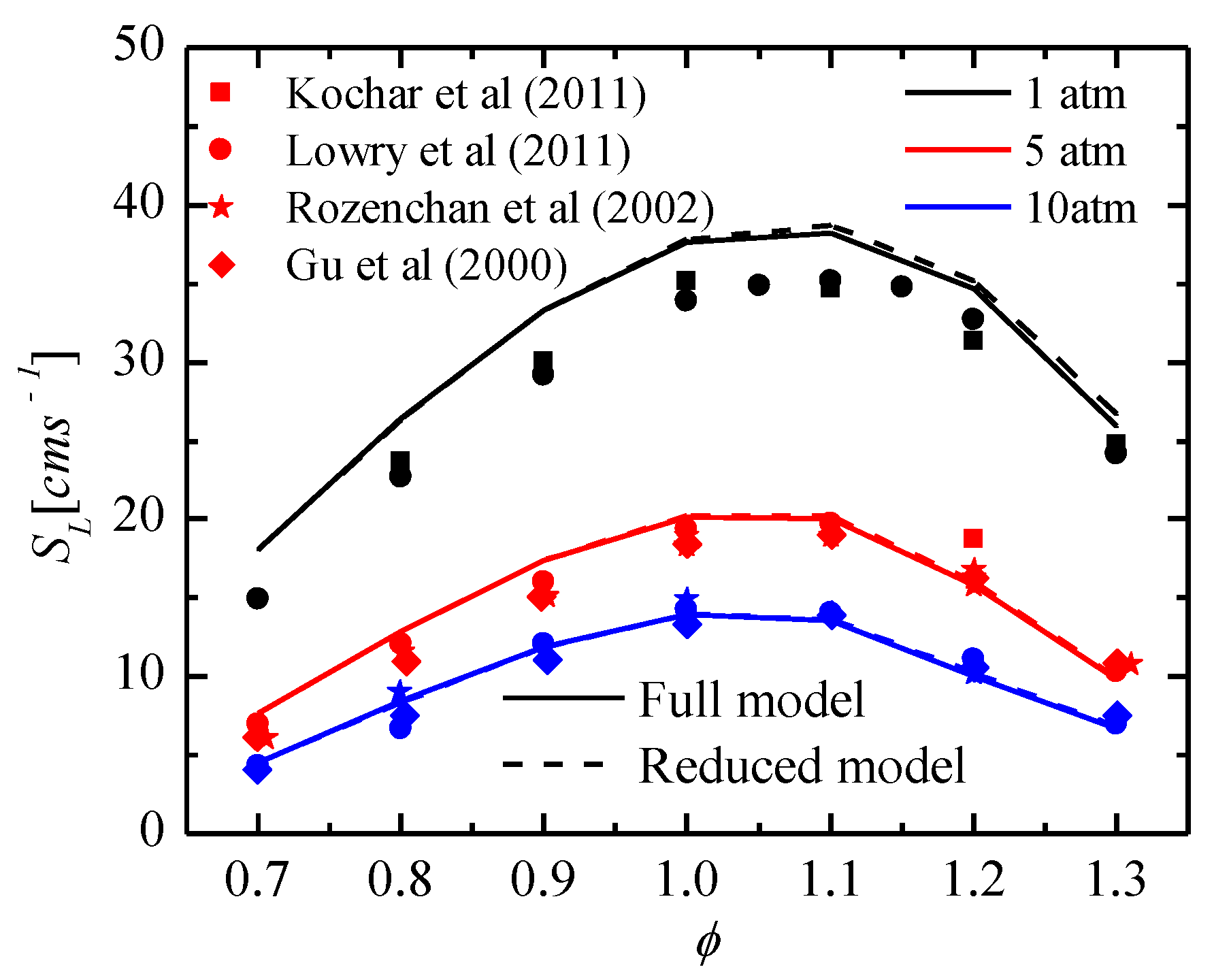
3.2. Verification of Laminar Flame Propagation Speed
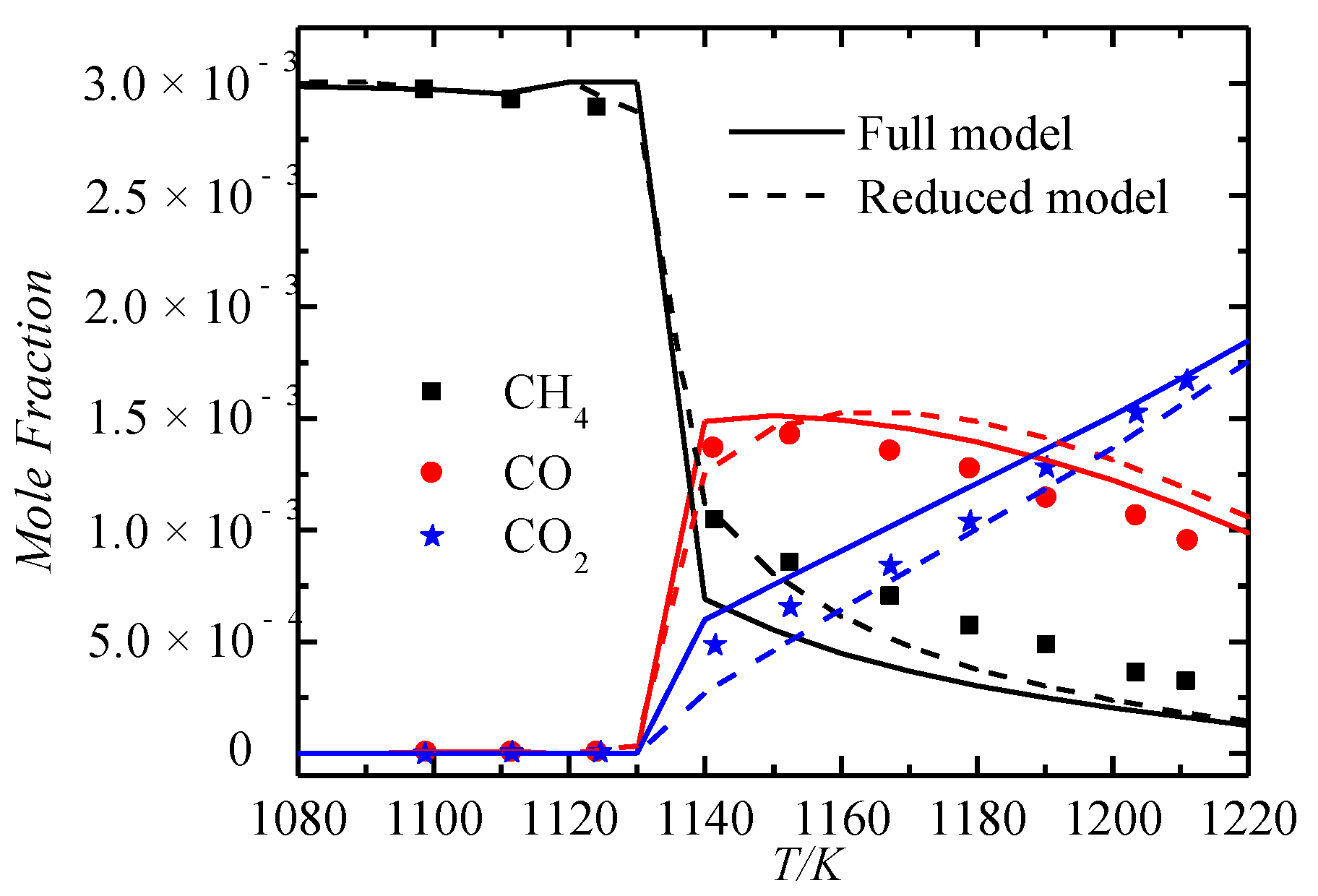
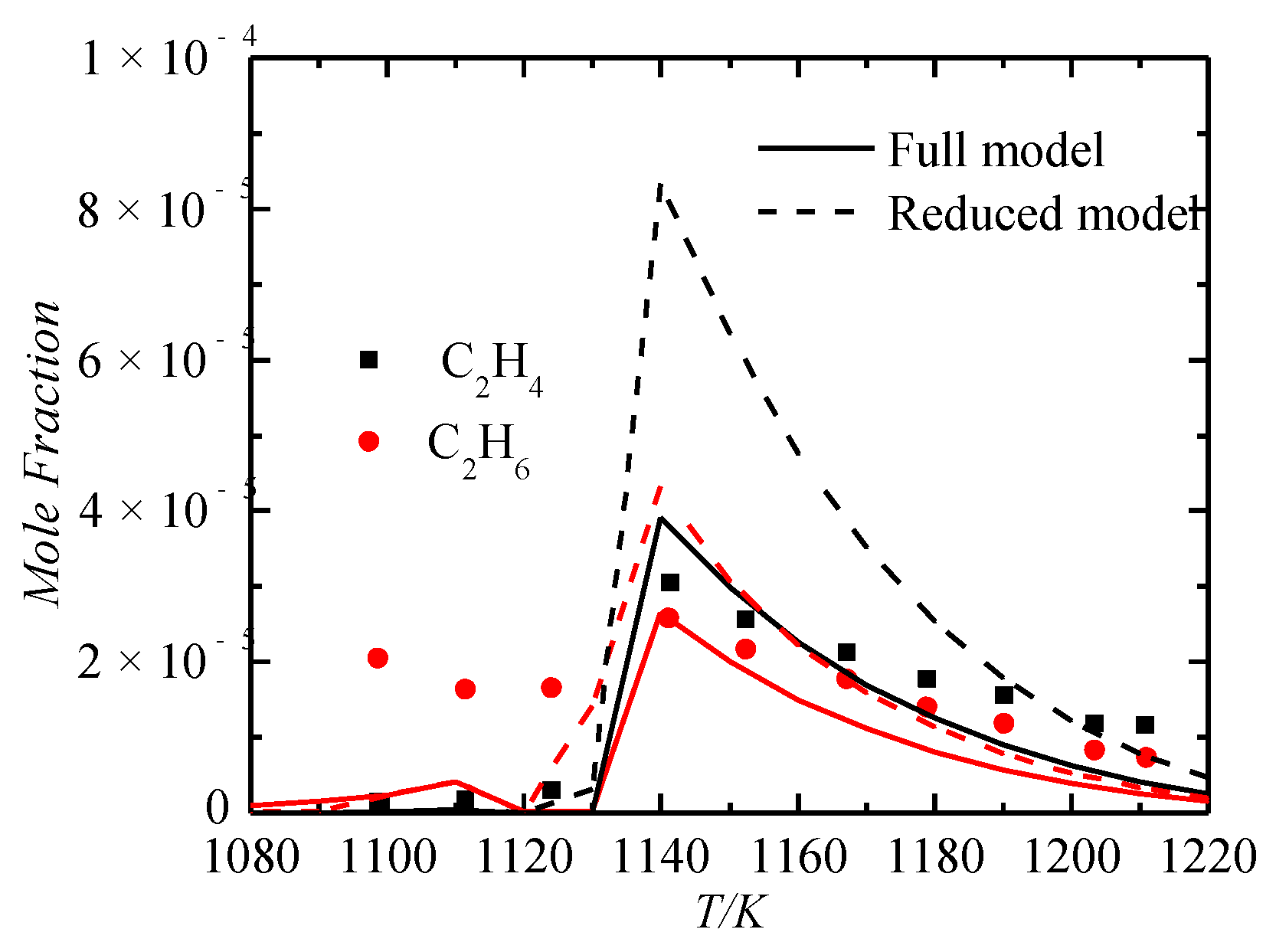
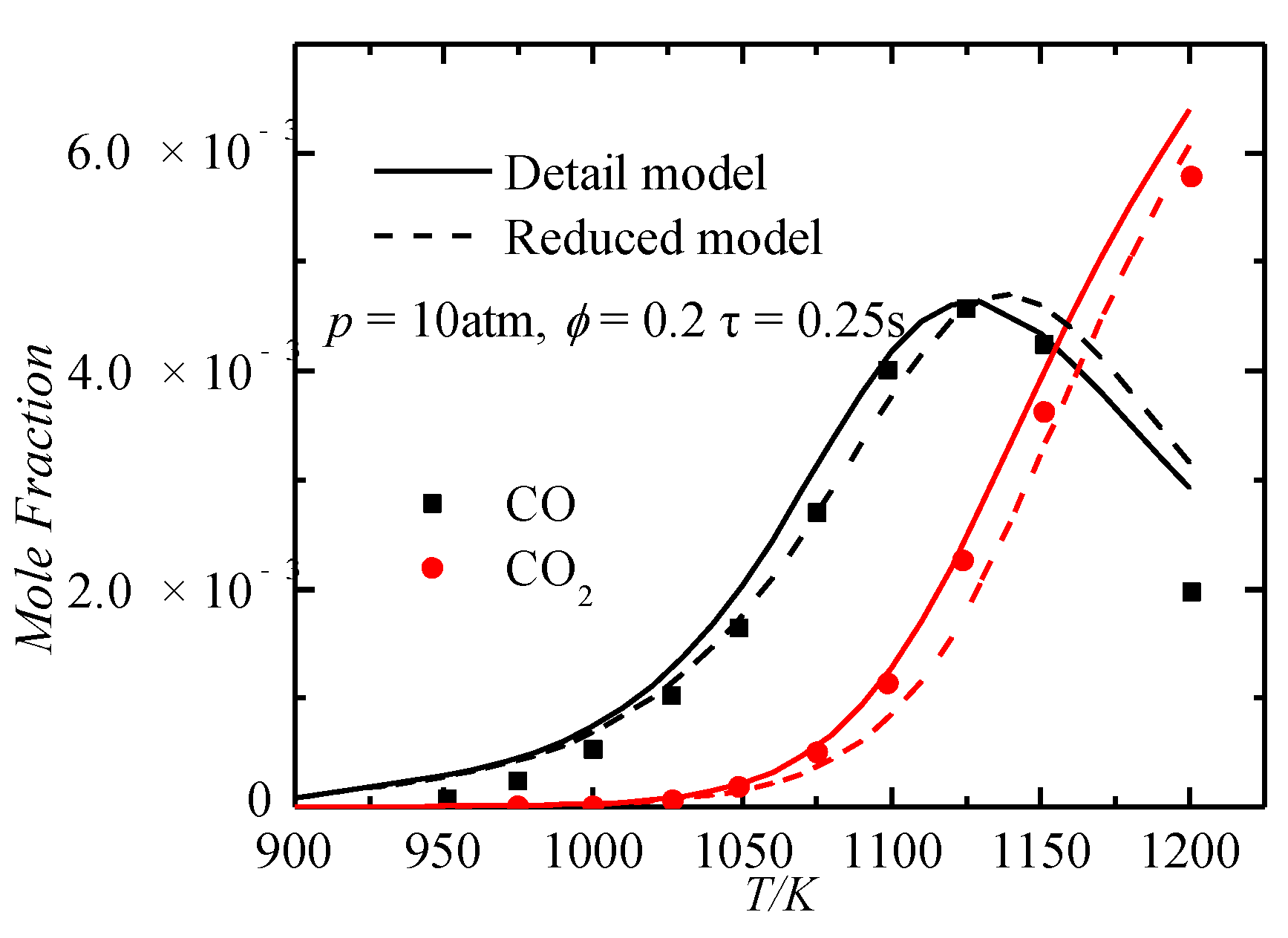
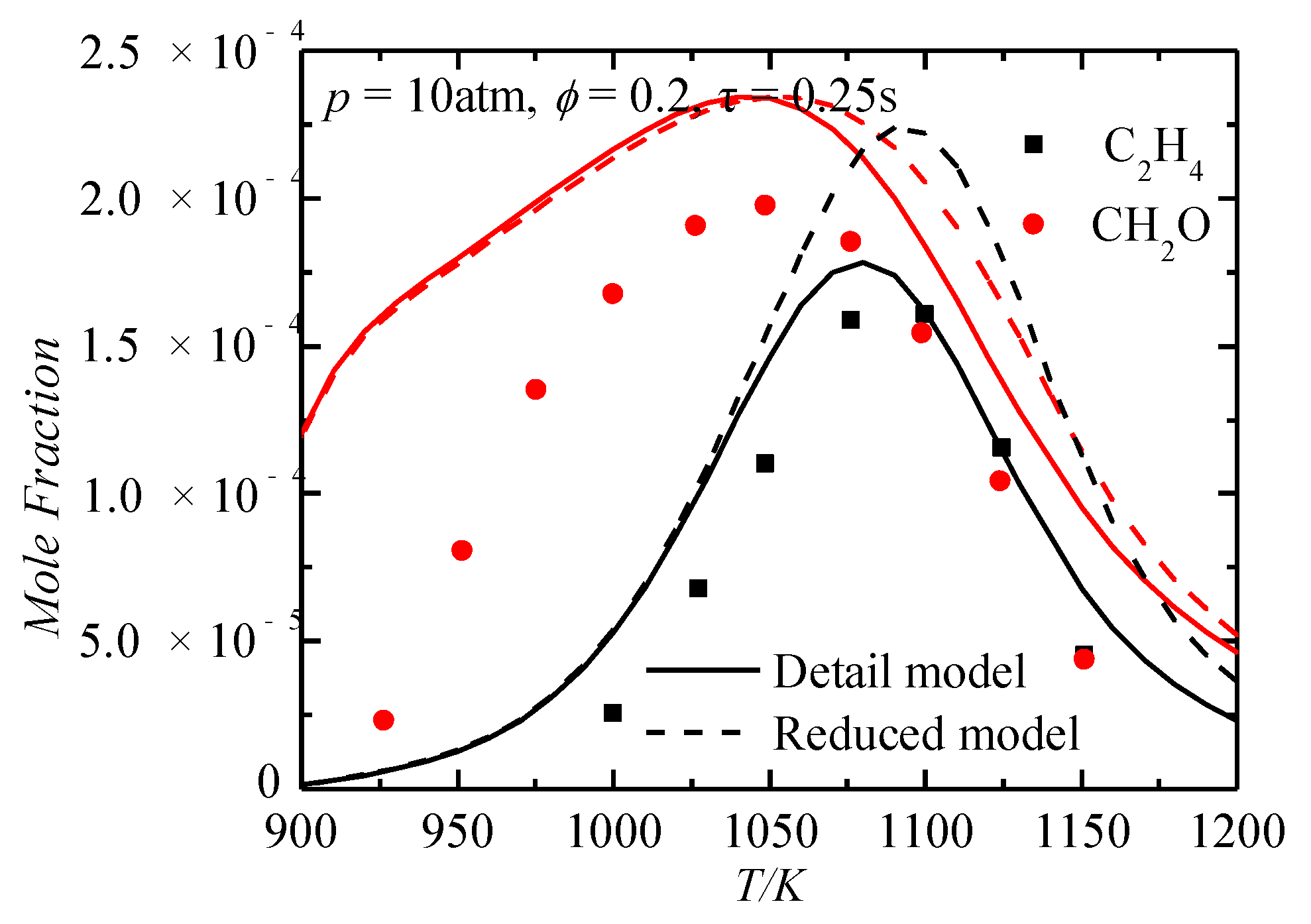
3.3. Verification of Important Species
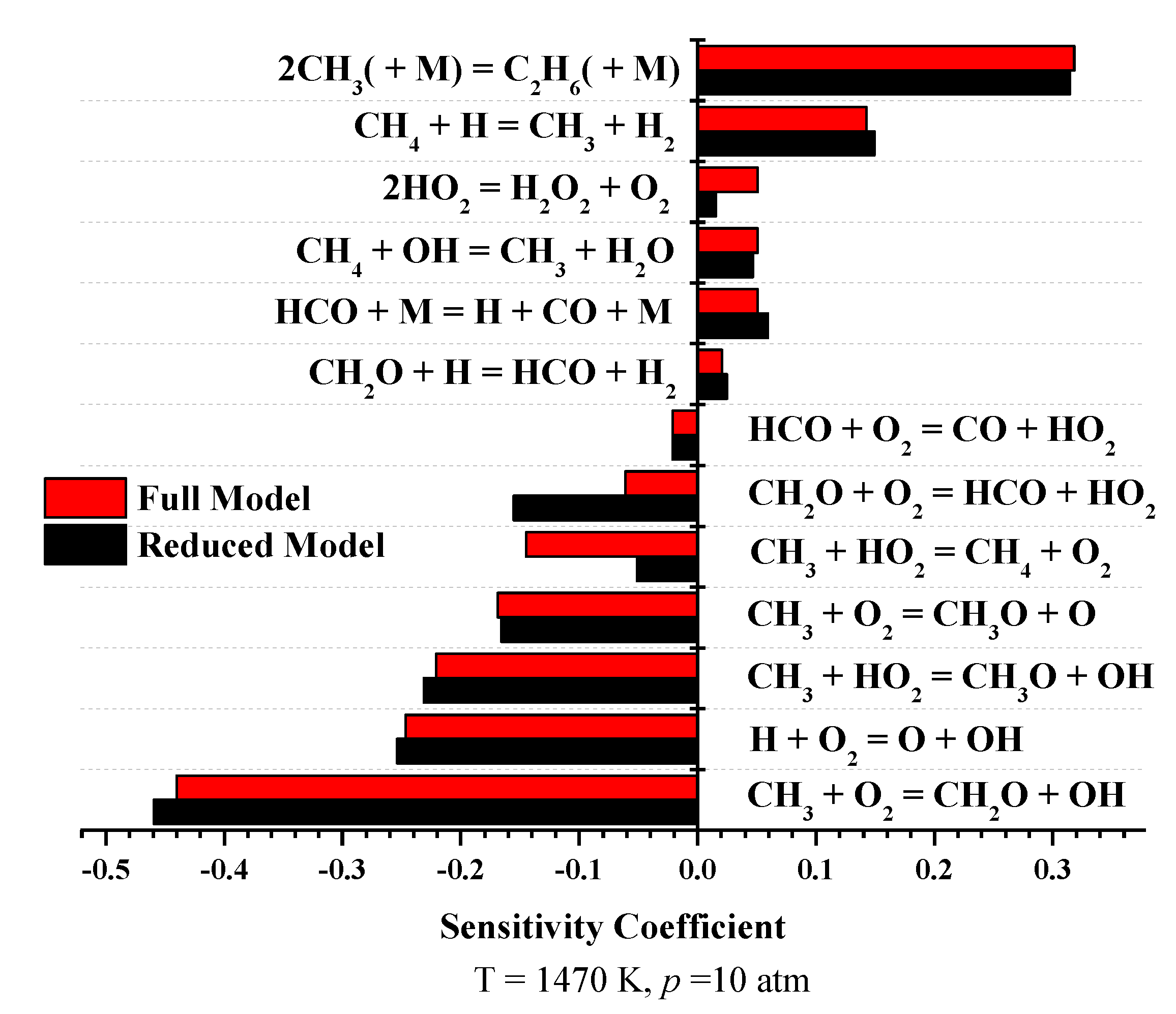
4. Sensitivity Analysis
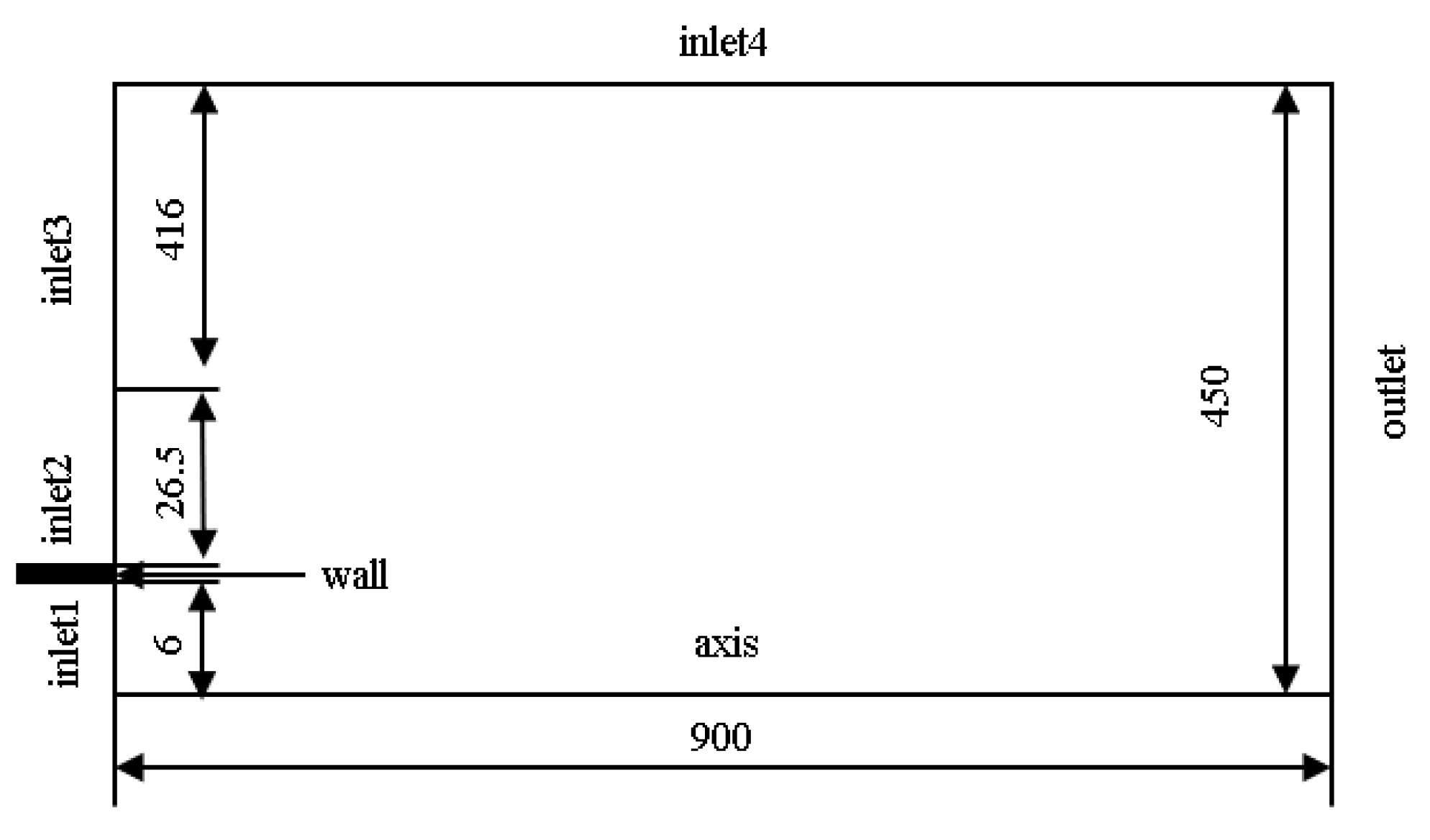
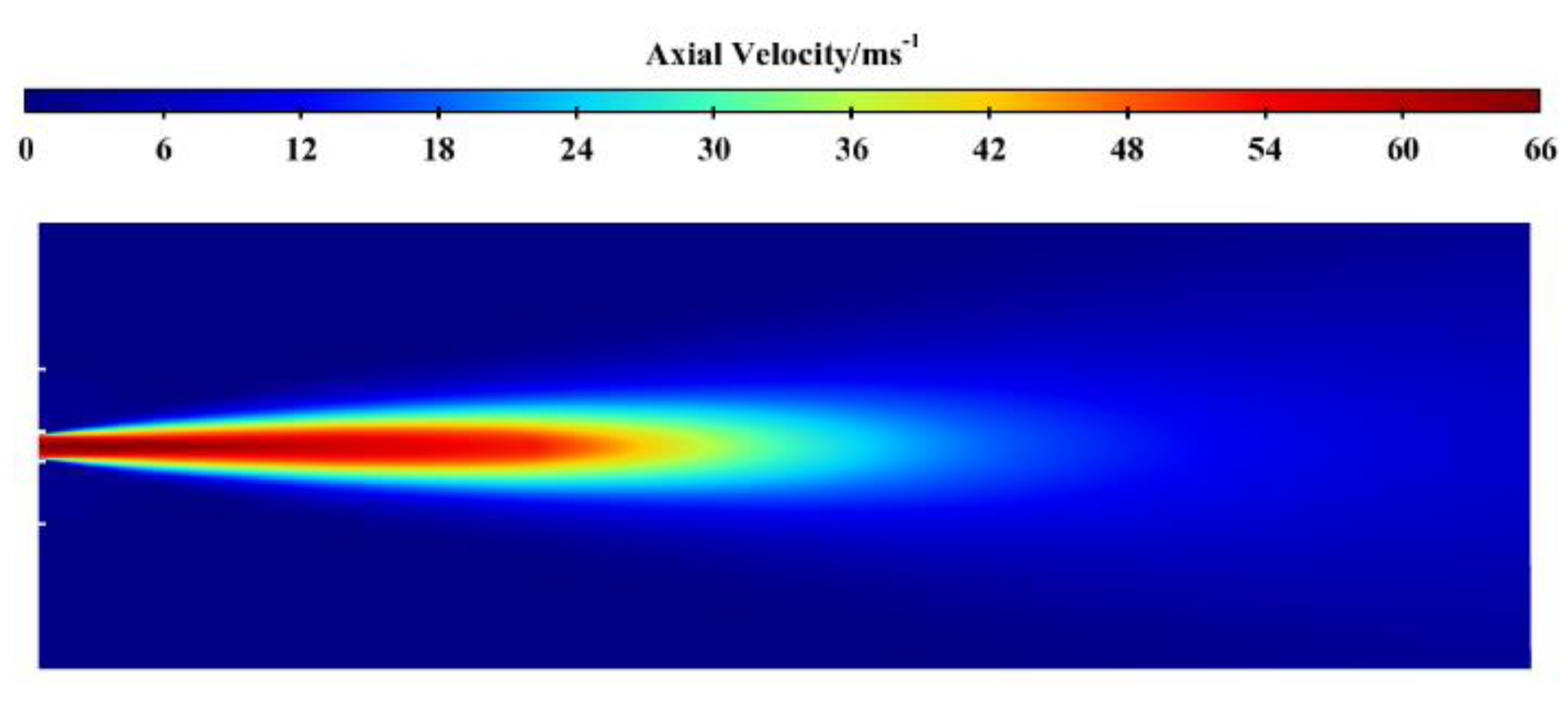
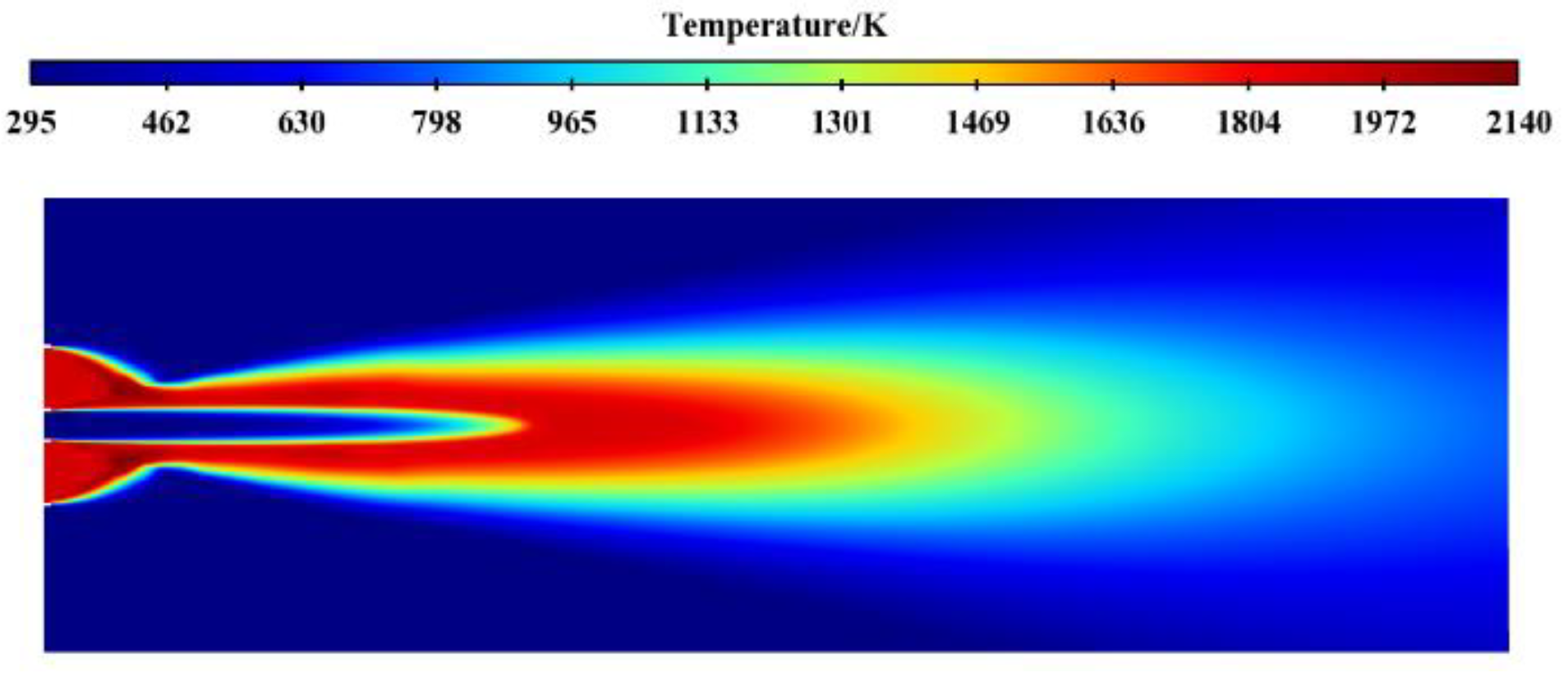
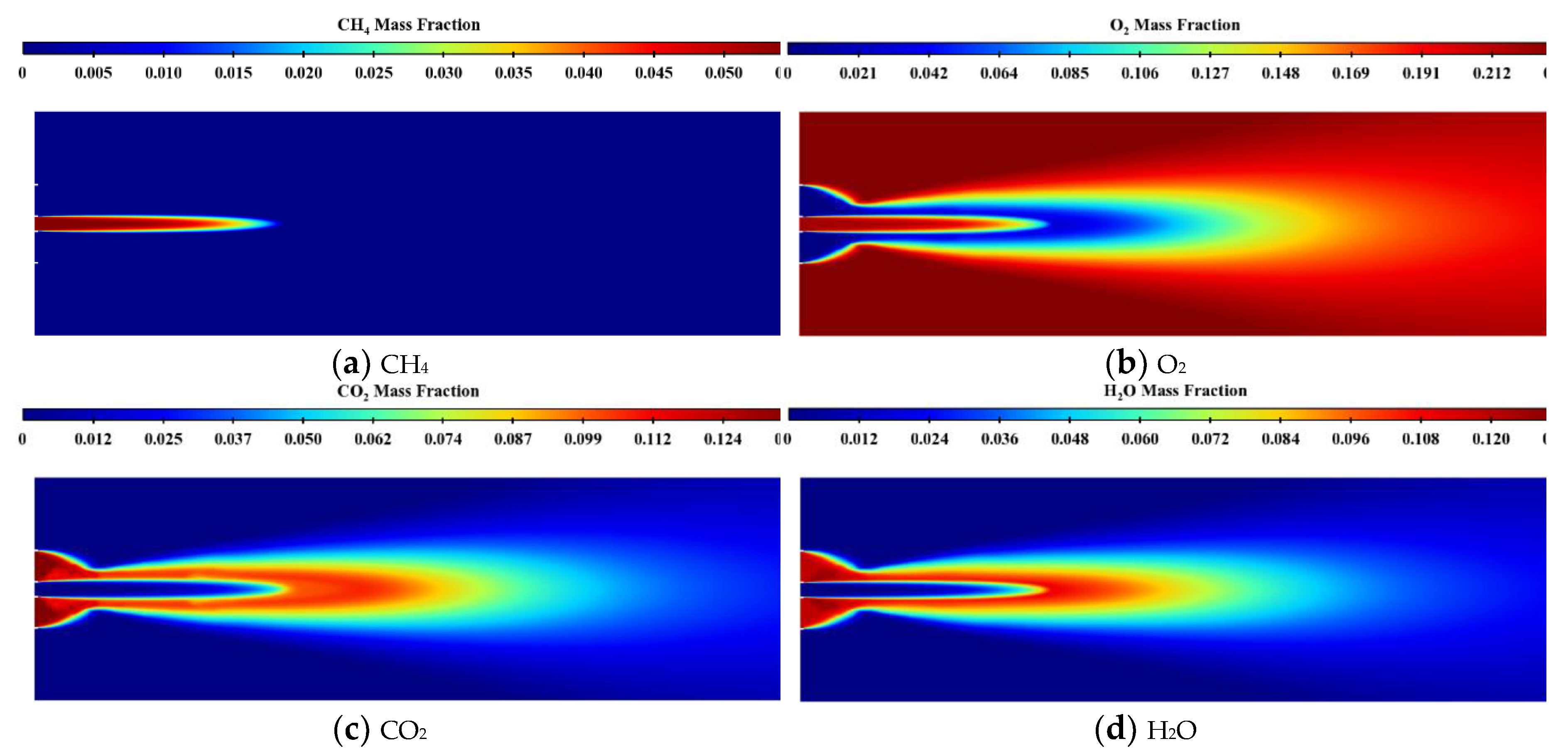
5. Flame Simulation and Verification of Bunsen Burner
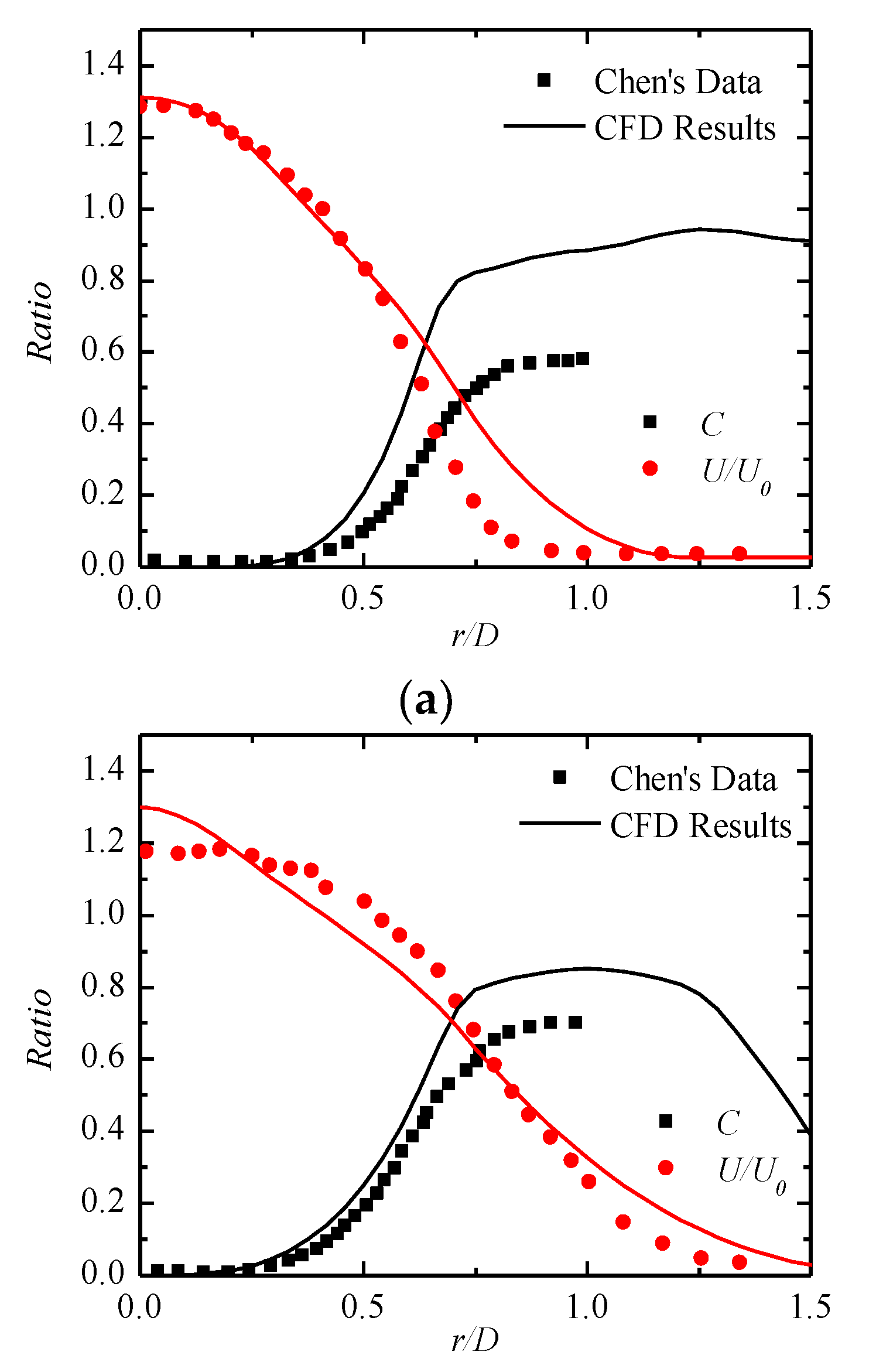
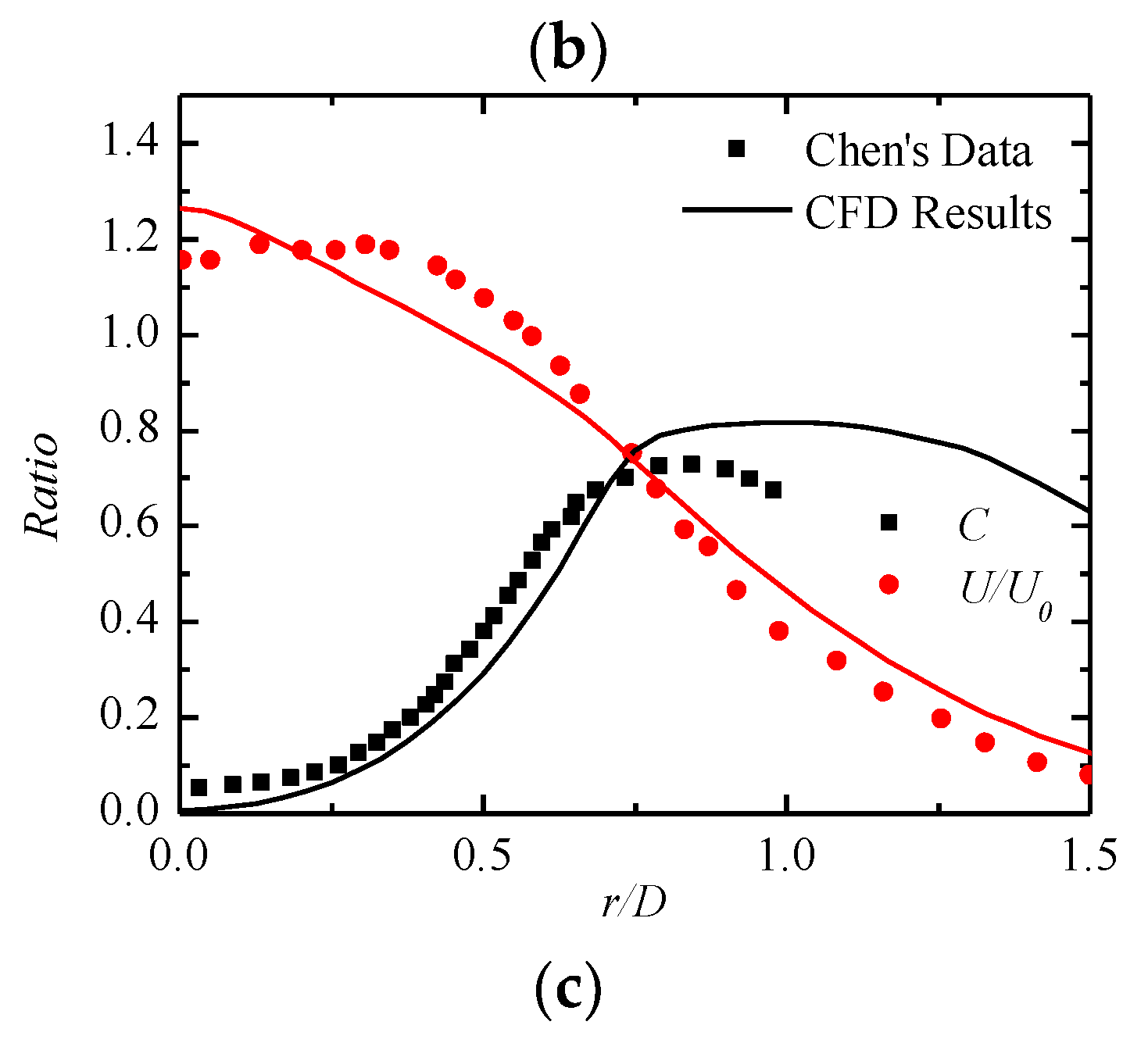
5.1. Comparison of Axis Velocity and Temperature
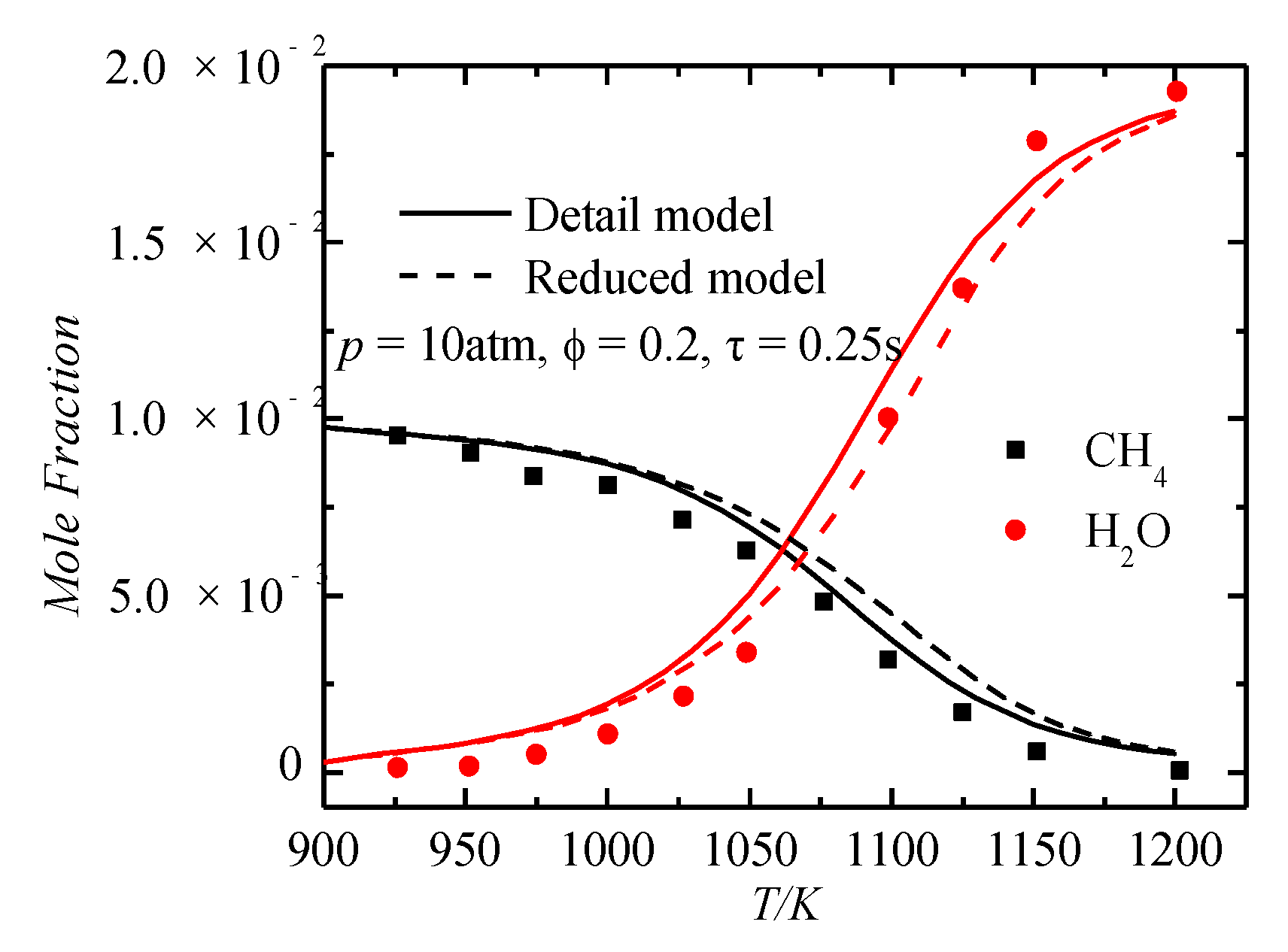
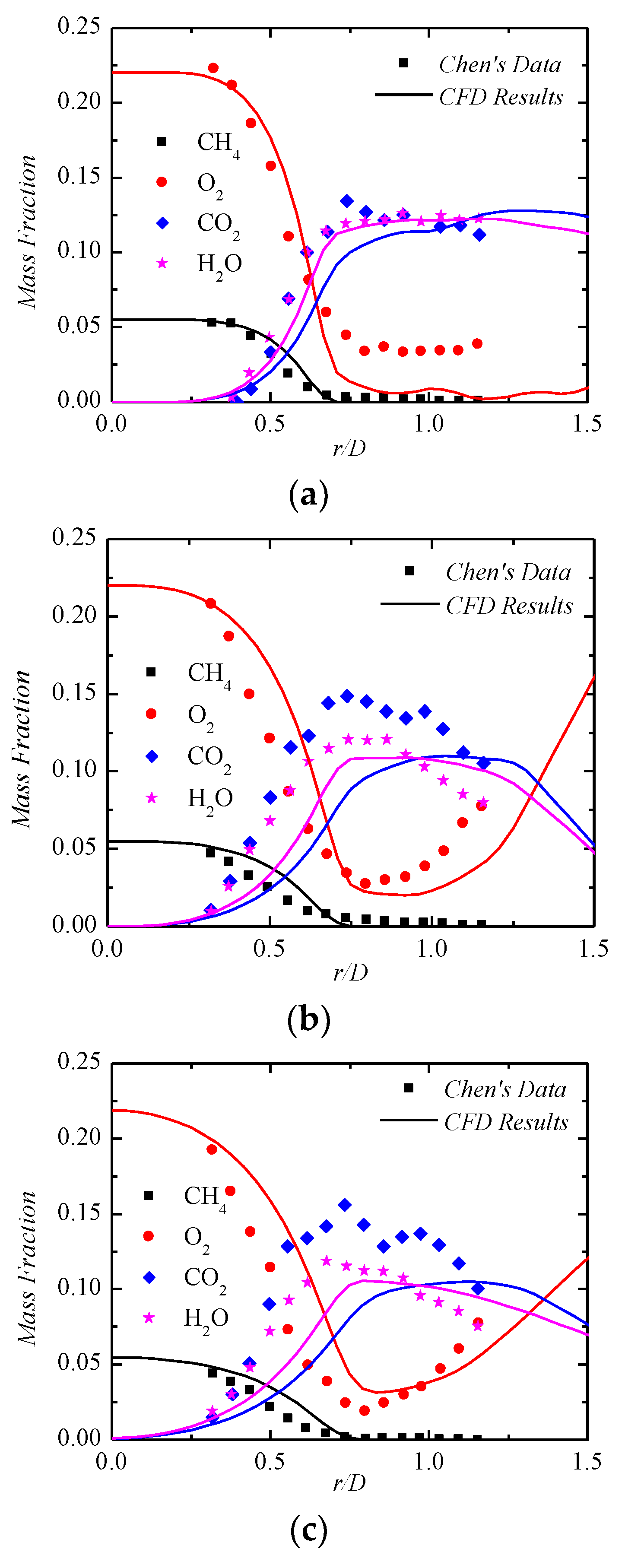
5.2. Comparison of Important Species
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Threshold value (ε) | Species | Different Species |
|---|---|---|
| 0 | 113 | Ar, HOCH2O2H, O2CH2CHO, CH3CO3H, CH3CO3, CH3CO2, C2H5OH, SC2H4OH, O2C2H4OH, CH3COCH3, CH3COCH2O2, C3KET21, C2H5CHO, C2H5CO, CH3OCH2, CH3OCH2O2, CH2OCH2O2H, CH3OCH2O2H, CH3OCH2O, CH3OCHO, CH3OCO, CH2OCHO, He, C3H6OOH1-2, C3H6OOH1-3, CC3H4, CJ*CC*CC*O, C*CC*CCJ*O, CJ*CC*O, C*CC*CCJ, C*CC*CC, C*CC*CCOH, HOC*CC*O, HOC*CCJ*O, HOCO |
| 0.001 | 78 | C2H2OH, HO2CH2CO, PC2H4OH, C2H4O2H, CH3COCH2, C2H3CHO, O2CH2OCH2O2H, HO2CH2OCHO, OCH2OCHO, HOCH2OCO, C3H8, IC3H7, NC3H7, C3H6, C3H5-A, C3H5-S, C3H5-T, C3H5O |
| 0.025 | 60 | HOCH2O2, C, CH3CO, C2H5O2H, C2H5O2, C2H4O1-2, C2H3O1-2, C2H3CO, C3H4-P, C3H4-A, C3H3, H2CC, H2CCC(S), C#CC*CCJ |
| 0.125 | 46 | OCH2O2H, CH*, C2H, CH3CHO, C2H3OH, CH2CHO, C2H5O |
| 0.185 | 39 | H, H2, O, O2, OH, OH*, H2O, N2, HO2, H2O2, CO, CO2, CH2O, HCO, HO2CHO, HCOH, O2CHO, HOCHO, OCHO, HOCH2O, CH3OH, CH2OH, CH3O, CH3O2H, CH3O2, CH4, CH3, CH2, CH2(S), CH, C2H6, C2H5, C2H4, C2H3, C2H2, CH2CO, HCCO, HCCOH, CH3OCH3 |
Appendix B: Comparison of the Reduced Mechanism with Other Simplified Mechanisms
Comparison of Ignition Delay Times
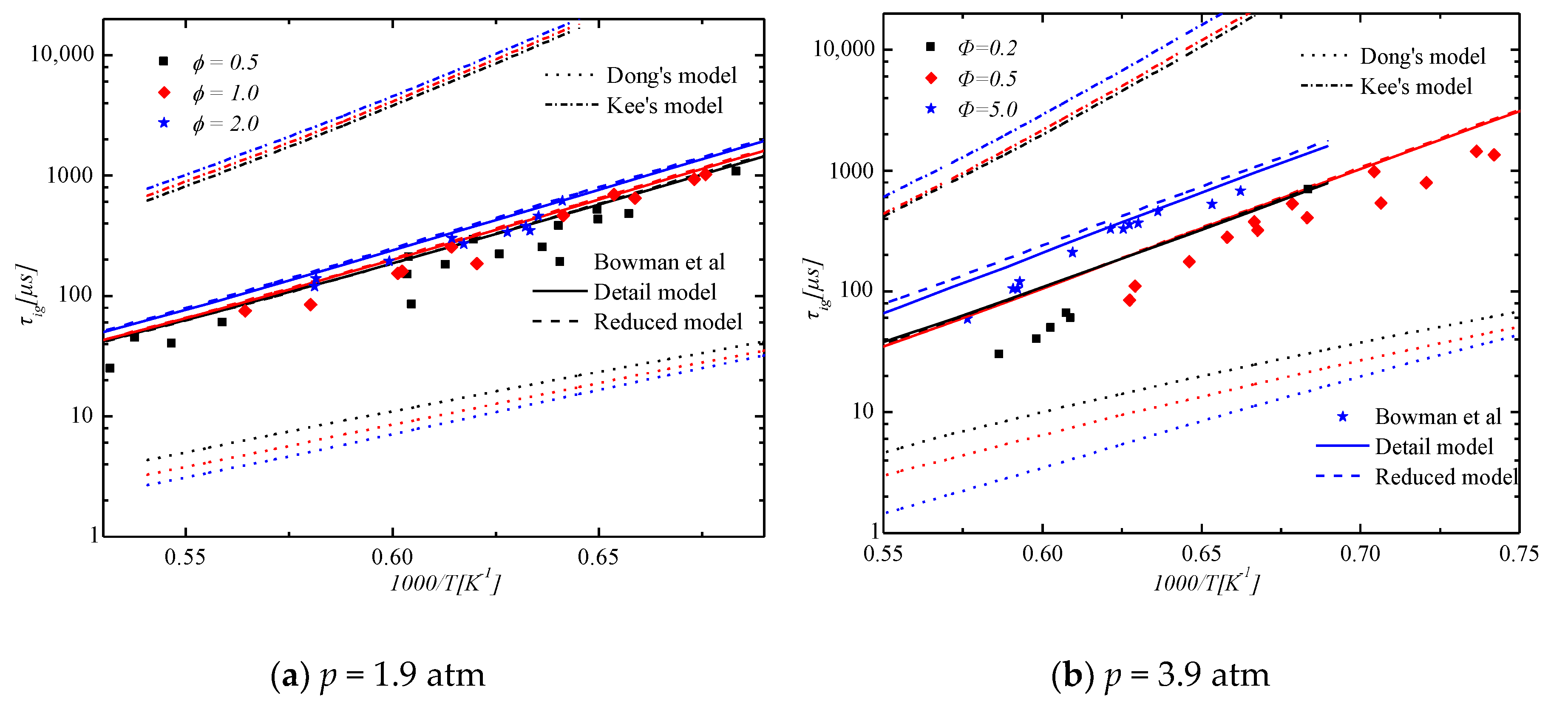
Comparison of the Laminar Flame Propagation Speed
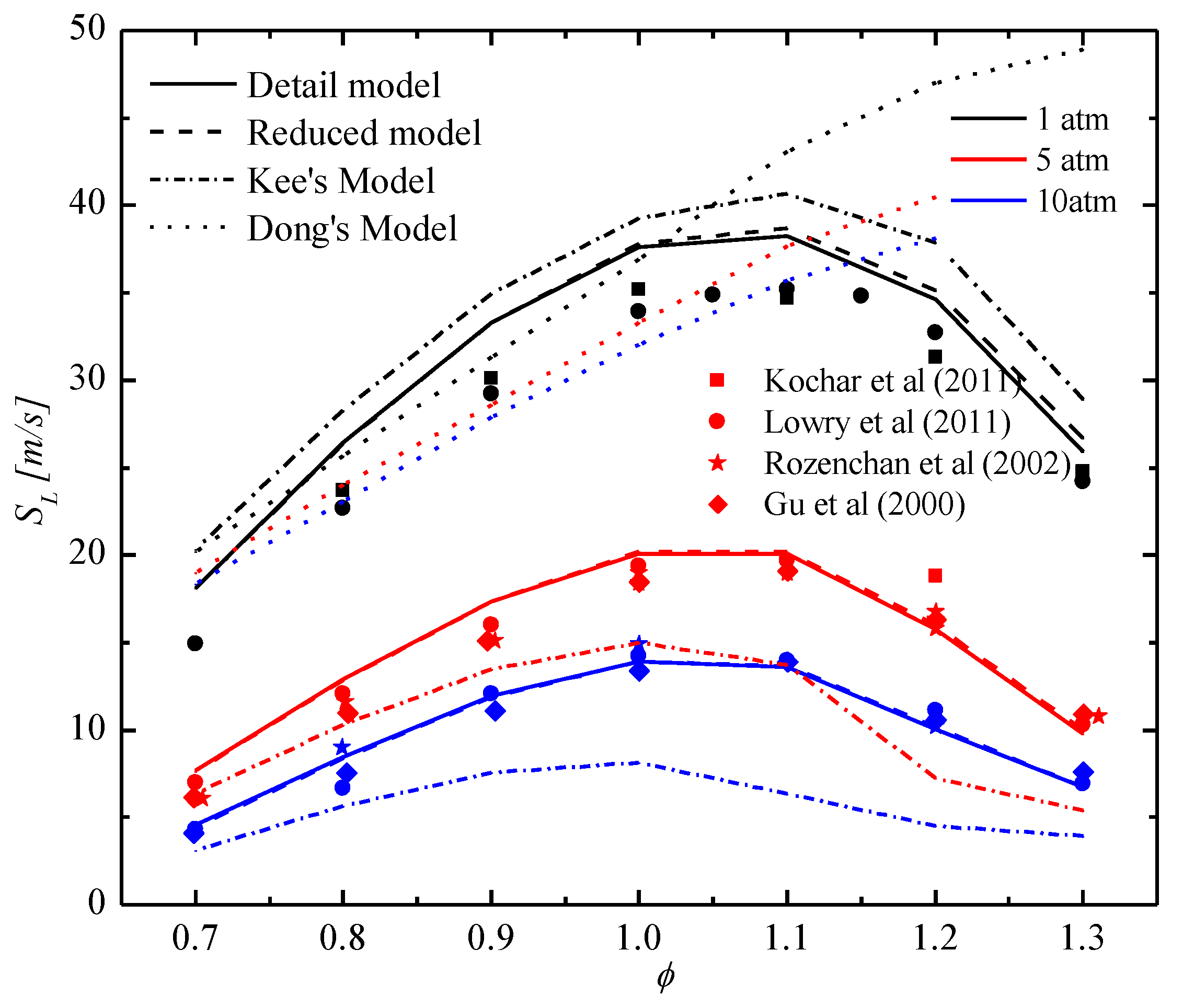
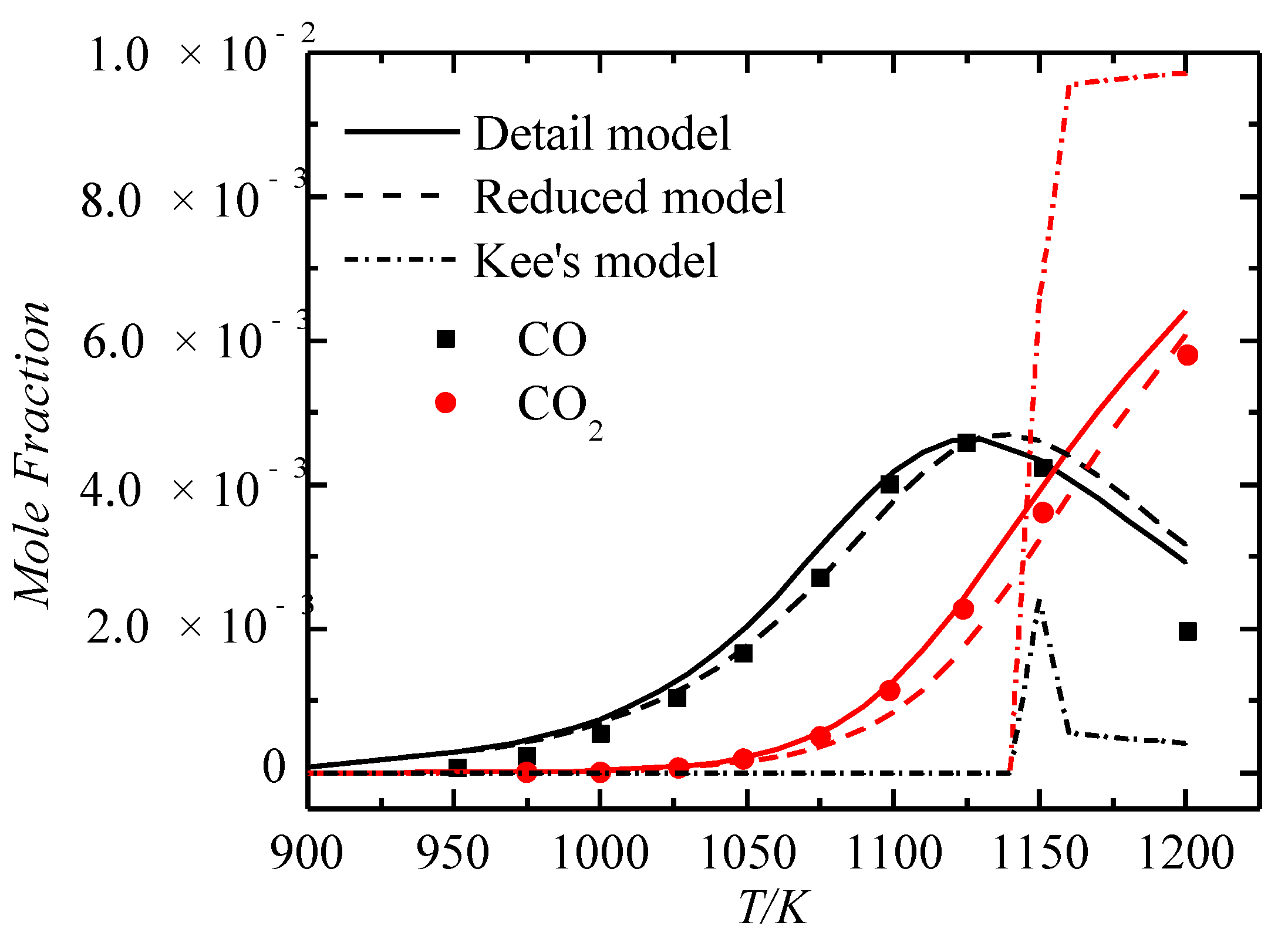
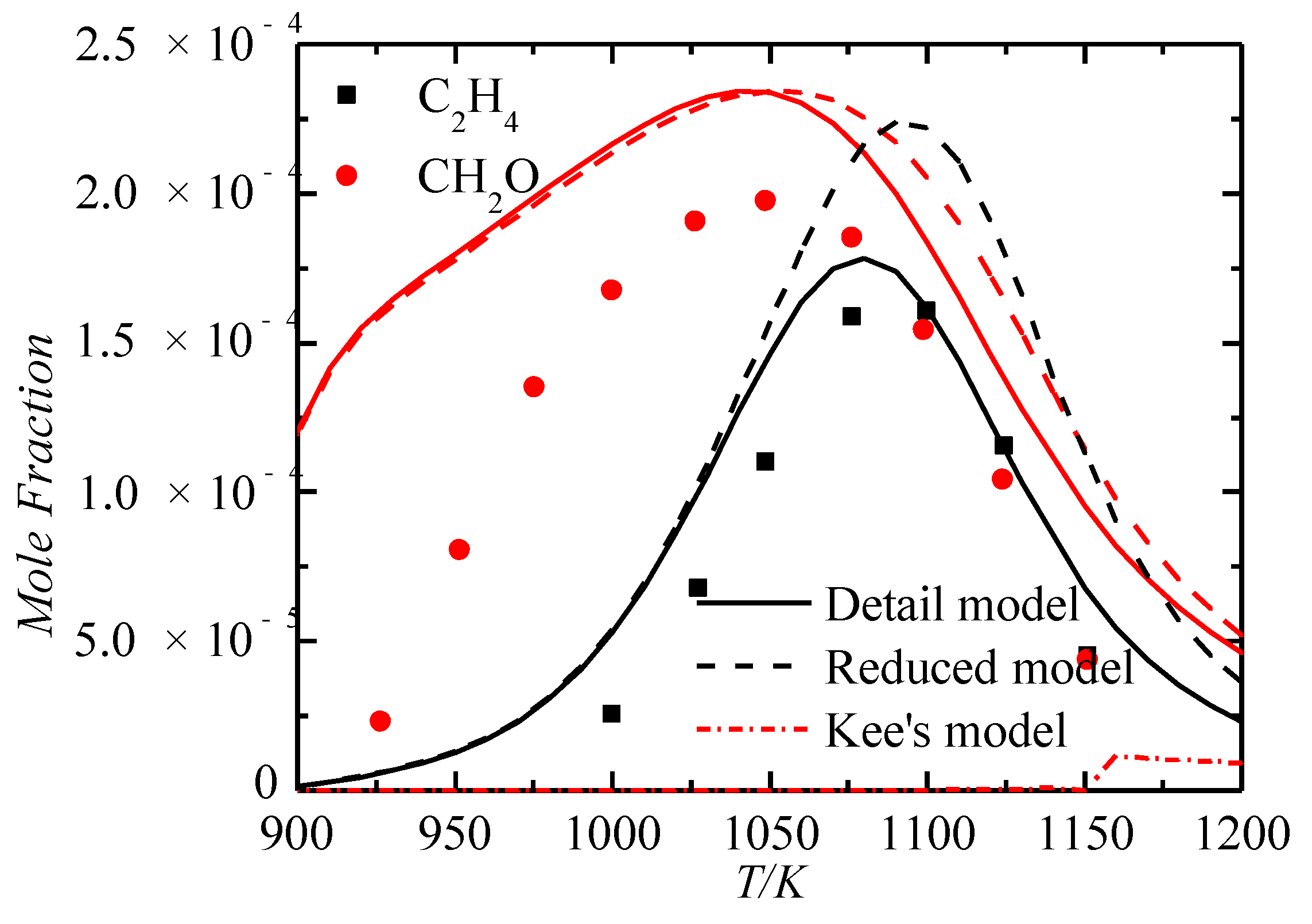
Comparison of Important Species
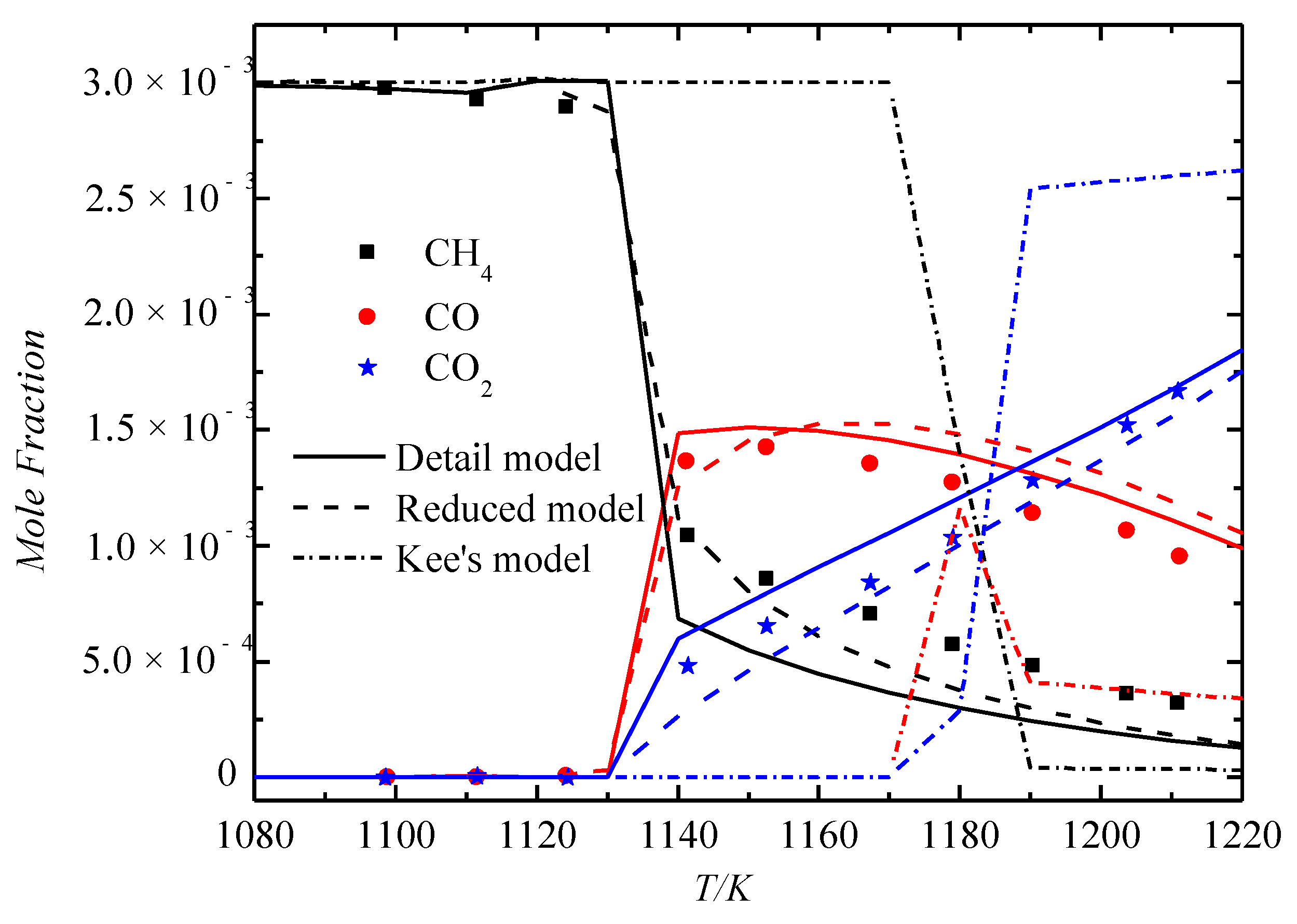
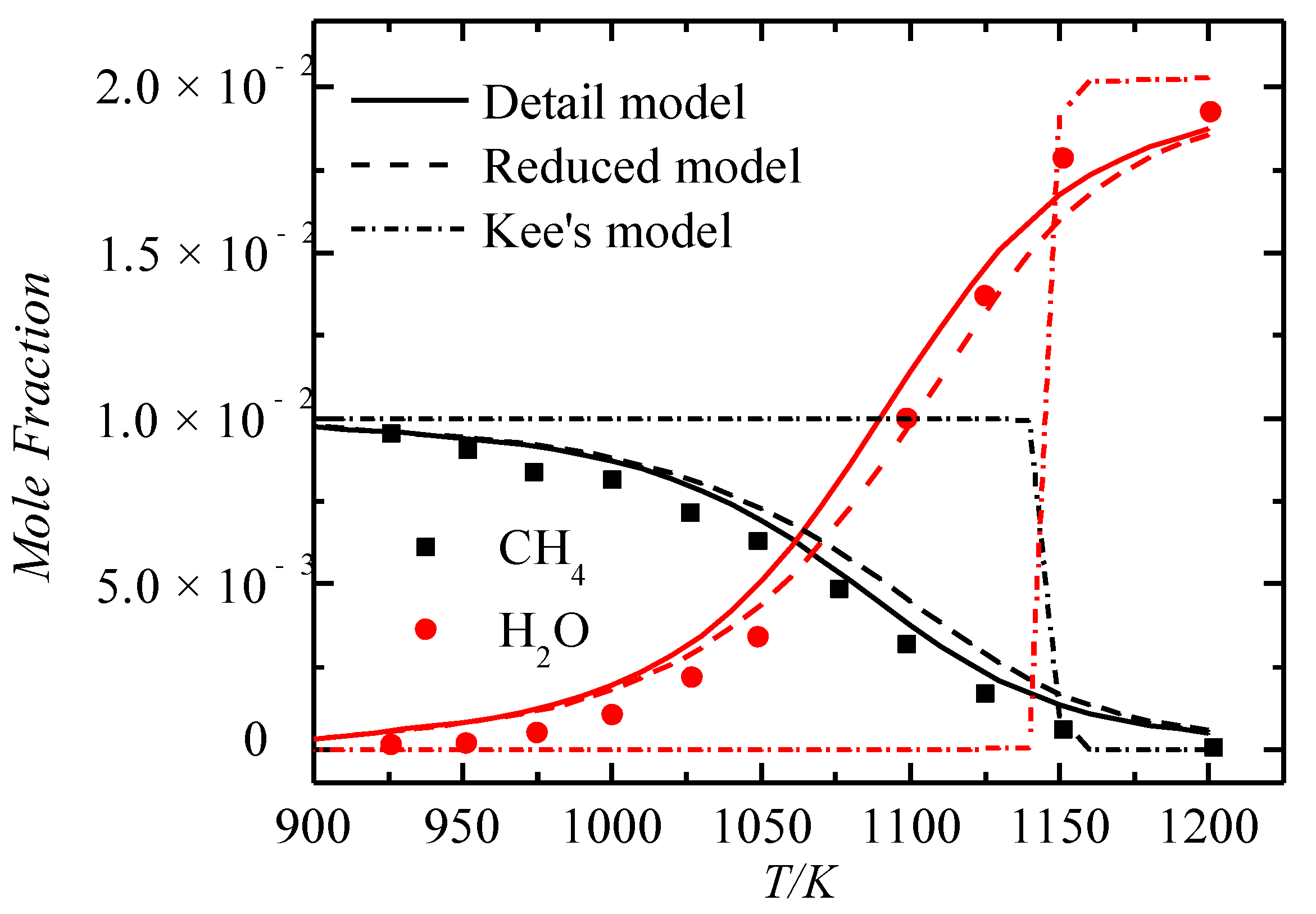
References
- Molino, A.; Nanna, F.; Migliori, M.; Iovane, P.; Ding, Y.; Bikson, B. Experimental and simulation results for biomethane production using peek hollow fiber membrane. Fuel 2013, 112, 489–493. [Google Scholar] [CrossRef]
- Enikolopyan, N.S. Kinetics and mechanism of methane oxidation. Symp. Combust. 1958, 7, 157–164. [Google Scholar] [CrossRef]
- Westbrook, C.K. An Analytical Study of the Shock Tube Ignition of Mixtures of Methane and Ethane. Combust. Sci. Technol. 1979, 20, 5–17. [Google Scholar] [CrossRef]
- Frenklach, M.; Bornside, D.E. Shock-initiated ignition in methane-propane mixtures. Combust. Flame 1984, 56, 1–27. [Google Scholar] [CrossRef]
- Frenklach, M.; Wang, H.; Rabinowitz, M.J. Optimization and analysis of large chemical kinetic mechanisms using the solution mapping method—combustion of methane. Prog. Energy Combust. Sci. 1992, 18, 47–73. [Google Scholar] [CrossRef]
- Ranzi, E.; Sogaro, A.; Gaffuri, P.; Pennati, G.; Faravelli, T. A Wide Range Modeling Study of Methane Oxidation. Combust. Sci. Technol. 1994, 96, 279–325. [Google Scholar] [CrossRef]
- Barbe, P.; Battin-Leclerc, F.; Côme, G.M. Experimental and modelling study of methane and ethane oxidation between 773 and 1573 K. J. Chim. Phys. Physico-Chim. Biol. 1995, 92, 1666–1692. [Google Scholar] [CrossRef]
- Marinov, N.M.; Pitz, W.J.; Westbrook, C.K.; Lutz, A.E.; Vincitore, A.M.; Senkan, S.M. Chemical kinetic modeling of a methane opposed-flow diffusion flame and comparison to experiments. Symp. Combust. 1998, 27, 605–613. [Google Scholar] [CrossRef]
- GRI-Mech, Release 3.0. Available online: http://www.me.berkeley.edu/gri_mech (accessed on 18 July 2018).
- Burke, U.; Somers, K.P.; O’Toole, P.; Zinner, C.M.; Marquet, N.; Bourque, G.; Petersen, E.L.; Metcalfe, W.K.; Serinyel, Z.; Curran, H.J. An ignition delay and kinetic modeling study of methane, dimethyl ether, and their mixtures at high pressures. Combust. Flame 2015, 162, 315–330. [Google Scholar] [CrossRef]
- Tingas, E.A.; Manias, D.M.; Sarathy, S.M.; Goussis, D.A. CH4/Air homogeneous autoignition: A comparison of two chemical kinetics mechanisms. Fuel 2018, 223, 74–85. [Google Scholar] [CrossRef]
- Wang, T.S. Thermophysics characterization of kerosene combustion. J. Thermophys. Heat Transf. 2001, 15, 76–80. [Google Scholar] [CrossRef]
- Xu, J.Q.; Guo, J.J.A.; Liu, K.J.; Wang, L.; Tan, N.X.; Li, X.Y. Construction of Autoignition Mechanisms for the Combustion ofRP-3 Surrogate Fuel and Kinetics Simulation. Acta Phys. Chim. Sin. 2015, 643–652. [Google Scholar] [CrossRef]
- Qiao, Y.; Xu, M.H.; Yao, H. Optimally-reduced kinetic models for GRI-Mech 3. 0 combustion mechanism based on sensitivity analysis. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2007, 35, 85–87. [Google Scholar] [CrossRef]
- Wen, F. The Reduction Method Based on Eigenvalue Analysis for Combustion Mechanisms and Its Applications. Ph.D. Dissertation, Tsinghua University, Beijing, China, 2012. [Google Scholar]
- Wen, F.; Zhong, B.J. Skeletal Mechanism Generation Based on Eigenvalue Analysis Method. Acta Phys. Chim. Sin. 2012, 28, 1306–1312. [Google Scholar] [CrossRef]
- Liu, H.; Chen, F.; Liu, H.; Zheng, Z.H.; Yang, S.H. 18-Step Reduced Mechanism for Methane/Air Premixed Supersonic Combustion. J. Combust. Sci. Technol. 2012, 18, 467–472. [Google Scholar]
- Gou, X.L.; Wang, W.; Gui, Y. Methane reaction using paths flux analysis of three generations method. J. Eng. Thermophys. 2014, 35, 1870–1873. [Google Scholar]
- Wang, W. Studies on the Efficient Reduction Methods for the Combustion Chemical Kinetic Mechanism of Fuel. Ph.D. Dissertation, Chongqing University, Chongqing, China, 2016. [Google Scholar]
- Wu, Z.Z. Study on Mechanism Reduction for Detailed Chemical Kinetics of IC Engine Fuel. Ph.D. Dissertation, Shanghai Jiaotong University, Shanghai, China, 2015. [Google Scholar]
- Hu, X.Z.; Yu, Q.B.; Li, Y.M. Skeletal and Reduced Mechanisms of Methane at O2/CO2 Atmosphere. Chem. J. Chin. Univ. 2018, 39, 95–101. [Google Scholar] [CrossRef]
- Lu, T.; Law, C.K. A directed relation graph method for mechanism reduction. Proc. Combust. Inst. 2005, 30, 1333–1341. [Google Scholar] [CrossRef]
- Lu, T.; Law, C.K. Linear time reduction of large kinetic mechanisms with directed relation graph: N-Heptane and iso-octane. Combust. Flame 2006, 144, 24–36. [Google Scholar] [CrossRef]
- Lu, T.; Law, C.K. On the applicability of directed relation graphs to the reduction of reaction mechanisms. Combust. Flame 2006, 146, 472–483. [Google Scholar] [CrossRef]
- Pepiot-Desjardins, P.; Pitsch, H. An efficient error-propagation-based reduction method for large chemical kinetic mechanisms. Combust. Flame 2008, 154, 67–81. [Google Scholar] [CrossRef]
- Liang, L.; Stevens, J.G.; Farrell, J.T. A dynamic adaptive chemistry scheme for reactive flow computations. Proc. Combust. Inst. 2009, 32, 527–534. [Google Scholar] [CrossRef]
- Wang, Q.D. Skeletal Mechanism Generation for Methyl Butanoate Combustionvia Directed Relation Graph Based Methods. Acta Phys. Chim. Sin. 2016, 32, 595–604. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Chemkin Reaction Workbench 17.0 (15151); ANSYS Reaction Design: San Diego, CA, USA, 2016. [Google Scholar]
- Seery, D.J.; Bowman, C.T. An experimental and analytical study of methane oxidation behind shock waves. Combust. Flame 1970, 14, 37–47. [Google Scholar] [CrossRef]
- Yao, T.; Zhong, B.J. Chemical kinetic model for auto-ignition and combustion of n-decane. Acta Phys. Chim. Sin. 2013, 29, 237–244. [Google Scholar] [CrossRef]
- Zheng, D.; Yu, W.M.; Zhong, B.J. RP-3 Aviation Kerosene Surrogate Fuel and the Chemical Reaction Kinetic Model. Acta Phys. Chim. Sin. 2015, 31, 636–642. [Google Scholar] [CrossRef]
- Kochar, Y.; Seitzman, J.; Lieuwen, T.; Metcalfe, W.; Burke, S.; Curran, H.; Krejci, M.; Lowry, W.; Petersen, E.; Bourque, G. Laminar Flame Speed Measurements and Modeling of Alkane Blends at Elevated Pressures With Various Diluents. ASME Proc. Combust. Fuels Emiss. 2011, 2, 129–140. [Google Scholar] [CrossRef]
- Lowry, W.; Vries, J.D.; Krejci, M.; Petersen, E.; Serinyel, Z.; Metcalfe, W.; Curran, H.; Bourque, G. Laminar Flame Speed Measurements and Modeling of Pure Alkanes and Alkane Blends at Elevated Pressures. In Proceedings of the ASME Turbo Expo 2010, Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; pp. 855–873. [Google Scholar]
- Rozenchan, G.; Zhu, D.L.; Law, C.K.; Tse, S.D. Outward propagation, burning velocities, and chemical effects of methane flames up to 60 ATM. Proc. Combust. Inst. 2002, 29, 1461–1470. [Google Scholar] [CrossRef]
- Gu, X.J.; Haq, M.Z.; Lawes, M.; Woolley, R. Laminar burning velocity and Markstein lengths of methane–air mixtures. Combust. Flame 2000, 121, 41–58. [Google Scholar] [CrossRef]
- Dagaut, P.; Boettner, J.C.; Cathonnet, M. Methane Oxidation: Experimental and Kinetic Modeling Study. Combust. Sci. Technol. 1991, 77, 127–148. [Google Scholar] [CrossRef]
- Cong, T.L.; Dagaut, P.; Dayma, G. Oxidation of Natural Gas, Natural Gas/Syngas Mixtures, and Effect of Burnt Gas Recirculation: Experimental and Detailed Kinetic Modeling. J. Eng. Gas Turbines Power 2008, 130, 635–644. [Google Scholar] [CrossRef]
- Yu, W.M. Research on Flame Propagation Speed and Reaction Dynamic Mechanism of Aviation Kerosene Alternative Fuel. Ph.D. Dissertation, Tsinghua University, Beijing, China, 2014. [Google Scholar]
- Chen, Y.C.; Peters, N.; Schneemann, G.A.; Wruck, N.; Renz, U.; Mansour, M.S. The detailed flame structure of highly stretched turbulent premixed methane-air flames. Combust. Flame 1996, 107, 223–244. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Fluent Theory Guide; ANSYS Inc.: San Diego, CA, USA, 2017. [Google Scholar]
- Duan, Z.Z. Fluid Analysis and Engineering Example of Ansys Fluent; Publishing House of Electronics Industry: Beijing, China, 2015. [Google Scholar]
- Dong, Q.L.; Jiang, Y.; Qiu, R. Reduction and optimization of methane combustion mechanism based on PCAS and genetic algorithm. Fire Saf. Sci. 2014, 23, 43–49. [Google Scholar] [CrossRef]
- Kee, R.J.; Grcar, J.F.; Smooke, M.D.; Miller, J.A. A Fortran Program for Modeling Laminar One-Dimensional Premixed Flames; Sandia Report SAND 85-8240; Sandia N Laboratories: Albuquerque, NM, USA, 1985. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Liu, F.; Wang, Y.; Fan, X.; Yang, J.; Liu, C.; Xu, G. Mechanism Reduction and Bunsen Burner Flame Verification of Methane. Energies 2019, 12, 97. https://doi.org/10.3390/en12010097
Lu H, Liu F, Wang Y, Fan X, Yang J, Liu C, Xu G. Mechanism Reduction and Bunsen Burner Flame Verification of Methane. Energies. 2019; 12(1):97. https://doi.org/10.3390/en12010097
Chicago/Turabian StyleLu, Haitao, Fuqiang Liu, Yulan Wang, Xiongjie Fan, Jinhu Yang, Cunxi Liu, and Gang Xu. 2019. "Mechanism Reduction and Bunsen Burner Flame Verification of Methane" Energies 12, no. 1: 97. https://doi.org/10.3390/en12010097
APA StyleLu, H., Liu, F., Wang, Y., Fan, X., Yang, J., Liu, C., & Xu, G. (2019). Mechanism Reduction and Bunsen Burner Flame Verification of Methane. Energies, 12(1), 97. https://doi.org/10.3390/en12010097





