Wind Speed Modeling by Nested ARIMA Processes
Abstract
1. Introduction
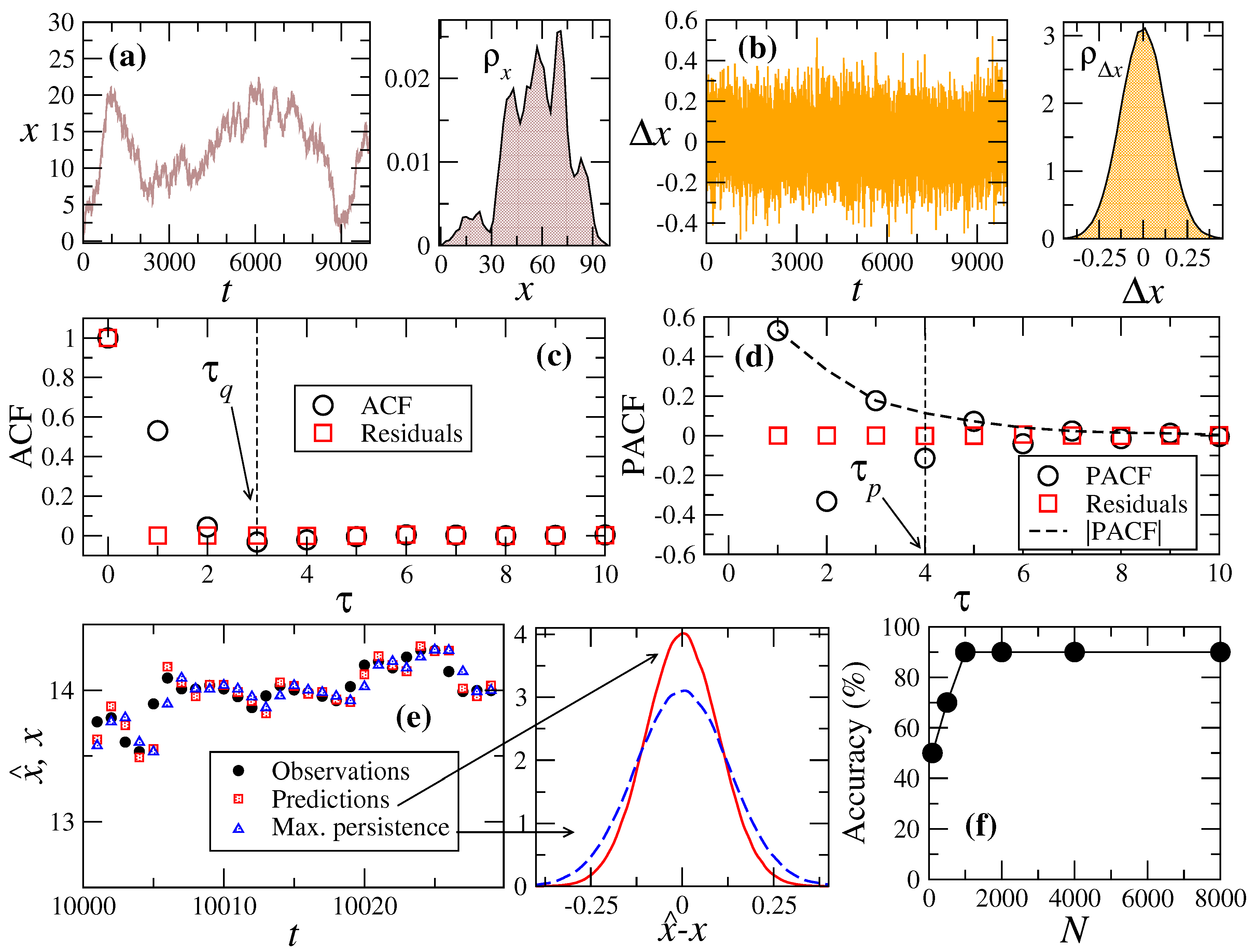
2. ARIMA-Model
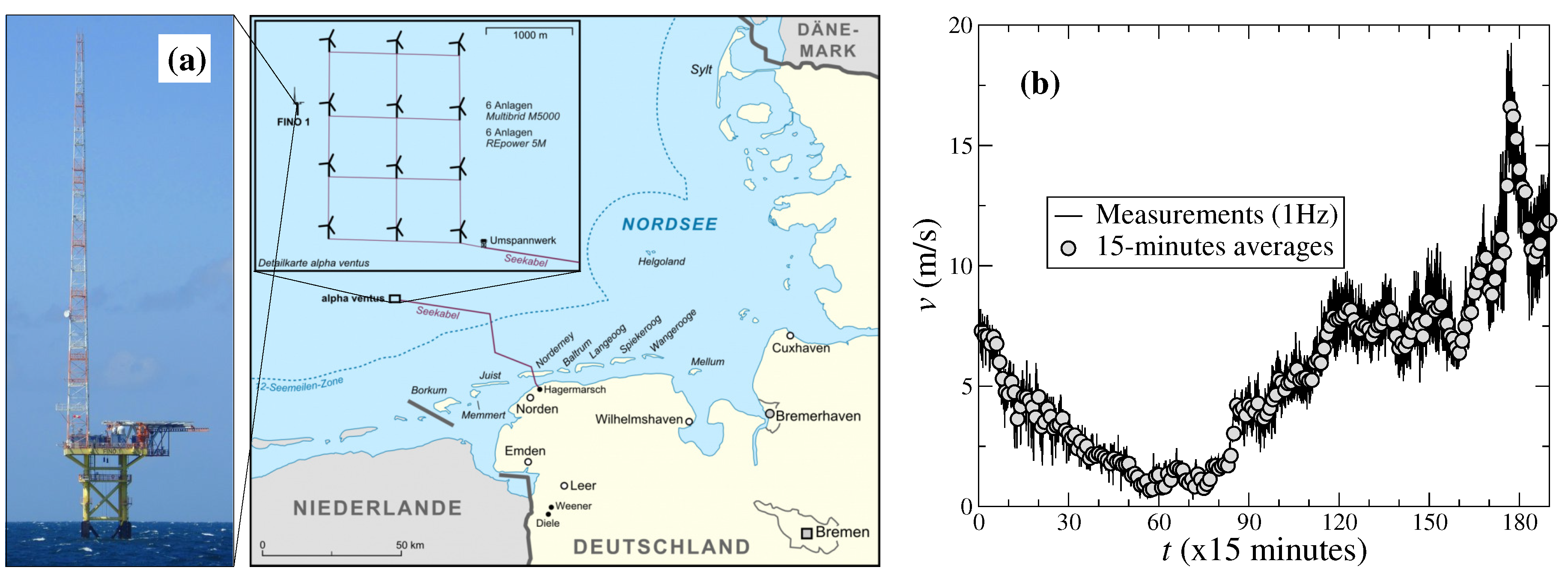
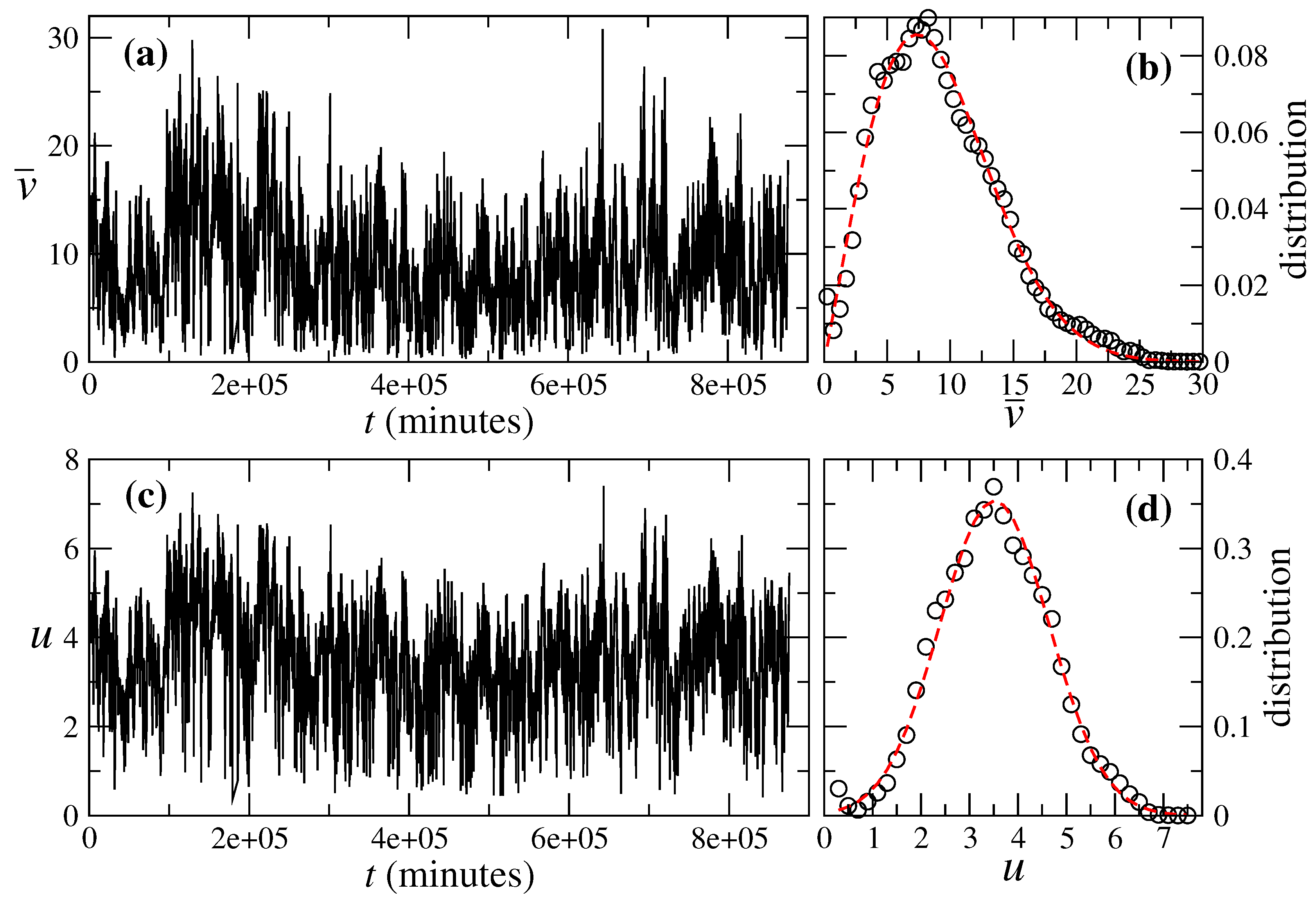
3. ARIMA Model for Wind Speed Measurements
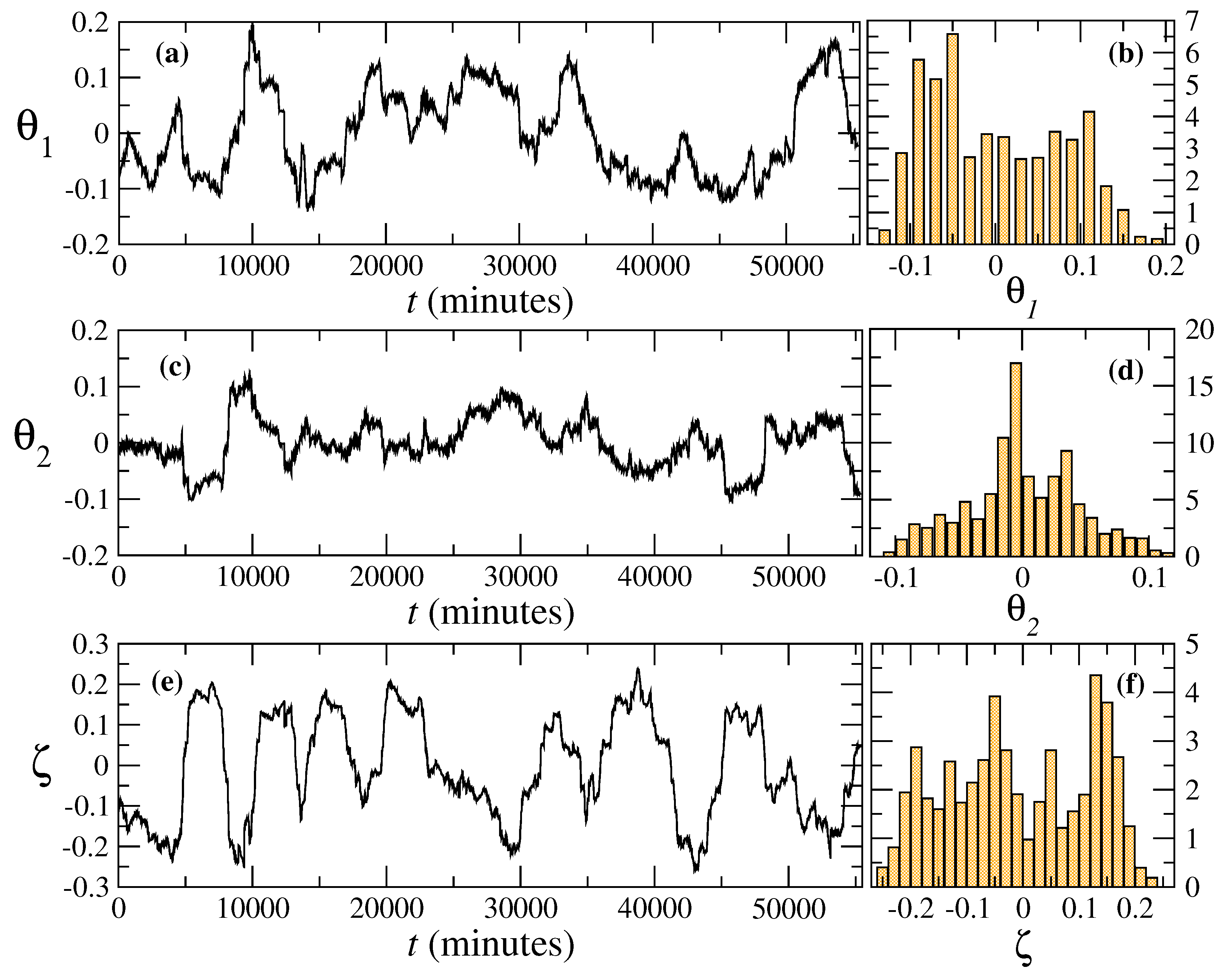
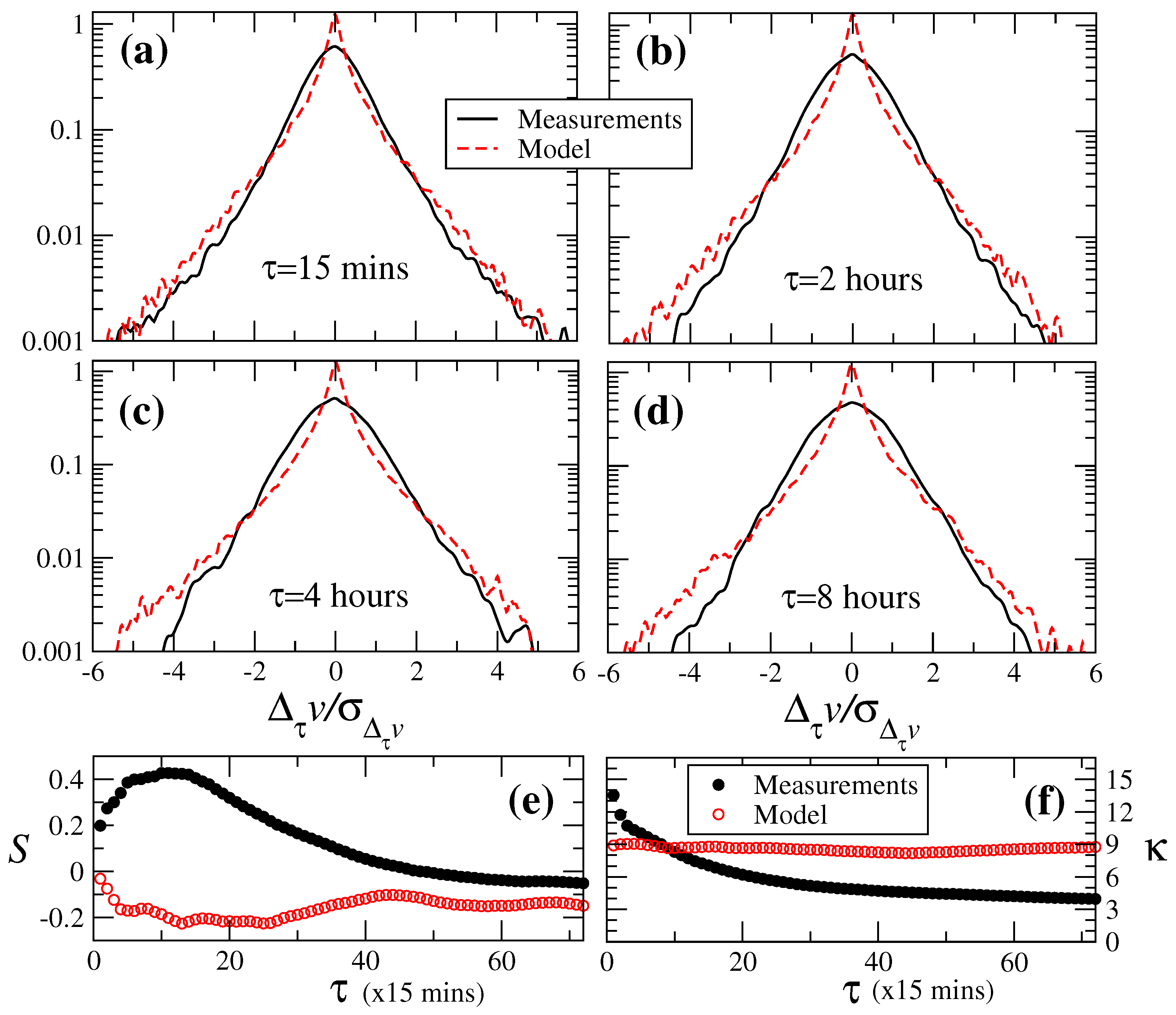
4. Nested ARIMA Model for Wind Speeds
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
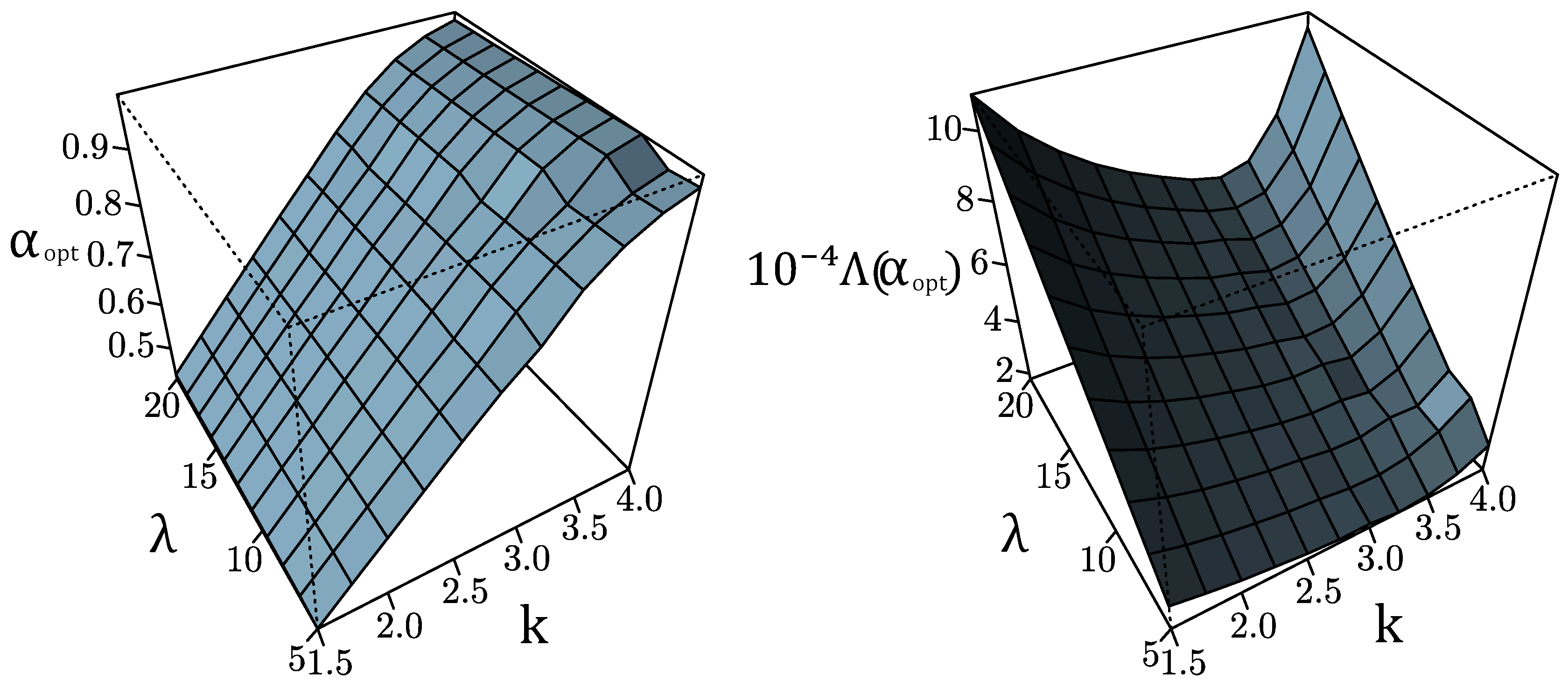
Appendix A. Optimal Non-Linear Variable Transformation of Wind Speeds into a Gaussian Variable
References
- Brown, B.; Katz, R.; Murphy, A. Time series models to simulate and forecast wind speed and wind power. J. Clim. Appl. Meteorol. 1984, 23, 1184–1195. [Google Scholar] [CrossRef]
- Ghadikolaei, H.; Ahmadi, A.; Aghaei, J.; Najafi, M. Risk constrained self-scheduling of hydro/wind units for short term electricity markets considering intermittency and uncertainty. Renew. Sustain. Energy Rev. 2012, 16, 4734–4743. [Google Scholar] [CrossRef]
- Ediger, V.; Akar, S. ARIMA forecasting of primary energy demand by fuel in Turkey. Energy Policy 2007, 25, 667–676. [Google Scholar] [CrossRef]
- Chen, P.; Pedersen, T.; Bak-Jensen, B.; Chen, Z. ARIMA-Based Time Series Model of Stochastic Wind Power Generation. IEEE Trans. Power Syst. 2010, 25, 667–676. [Google Scholar] [CrossRef]
- Yunus, K.; Thiringer, T.; Chen, P. ARIMA-Based Frequency-Decomposed Modeling of Wind Speed Time Series. IEEE Trans. Power Syst. 2016, 31, 2546–2556. [Google Scholar] [CrossRef]
- Lau, A.; Mcsharry, P. Approaches for multi-step density forecasts with application to aggregated wind power. Ann. Appl. Stat. 2010, 4, 1311–1341. [Google Scholar] [CrossRef]
- Kadhem, A.; Wahab, N.; Aris, I.; Jasni, J.; Abdalla, A. Advanced Wind Speed Prediction Model Based on a Combination of Weibull Distribution and an Artificial Neural Network. Energies 2017, 10, 1744. [Google Scholar] [CrossRef]
- Cadenas, E.; Rivera, W.; Campos-Amezcua, R.; Heard, C. Wind Speed Prediction Using a Univariate ARIMA Model and a Multivariate NARX Model. Energies 2016, 9, 109. [Google Scholar] [CrossRef]
- Cao, Q.; Ewing, B.; Thompson, M. Forecasting wind speed with recurrent neural networks. Eur. J. Oper. Res. 2012, 221, 148–154. [Google Scholar] [CrossRef]
- Shumway, R.; Stoffer, D. Time Series Analysis and Its Applications with R Examples; Springer: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Zhao, E.; Zhao, J.; Liu, L.; Su, Z.; An, N. Hybrid Wind Speed Prediction Based on a Self-Adaptive ARIMAX Model with an Exogenous WRF Simulation. Energies 2016, 9, 7. [Google Scholar] [CrossRef]
- Han, Q.; Wu, H.; Hu, T.; Chu, F. Short-Term Wind Speed Forecasting Based on Signal Decomposing Algorithm and Hybrid Linear/Nonlinear Models. Energies 2018, 11, 2976. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Yu, T.H.; Liu, C.Y. Hour-Ahead Wind Speed and Power Forecasting Using Empirical Mode Decomposition. Energies 2013, 6, 6137–6152. [Google Scholar] [CrossRef]
- Alencar, D.; de Mattos Affonso, C.; Oliveira, R.; Moya Rodríguez, J.; Leite, J.; Reston Filho, J.C. Different Models for Forecasting Wind Power Generation: Case Study. Energies 2017, 10, 1976. [Google Scholar] [CrossRef]
- Johnson, G. Wind Energy Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1998. [Google Scholar]
- van Kuik, G.; Peinke, J. Long-term research challenges in wind energy—A research agenda by the European Academy of Wind Energy. Wind Energy Sci. 2016, 1, 1–39. [Google Scholar] [CrossRef]
- FINO I Project and Database. The FINO Project Is Supported by the German Government through BMWi and PTJ. 2016. Available online: http://www.bsh.de (accessed on 24 May 2017).
- Beck, C.; Cohen, E. Superstatistics. Physica A 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Castaing, B.; Gagne, Y.; Hopfinger, E. Velocity Probability Density Functions of High Reynolds Number Turbulence. Physica D 1990, 46, 177–200. [Google Scholar] [CrossRef]
- Rocha, P.; Raischel, F.; Boto, J.; Lind, P. Uncovering the evolution of non-stationary stochastic variables: The example of asset volume-price fluctuations. Phys. Rev. E 2016, 93, 052122. [Google Scholar] [CrossRef] [PubMed]
- Estevens, J.; Rocha, P.; Boto, J.; Lind, P. Stochastic modelling of non-stationary financial assets. Chaos 2017, 27, 113106. [Google Scholar] [CrossRef]
- Milan, P.; Wächter, M.; Peinke, J. Stochastic modeling and performance monitoring of wind farm power production. J. Renew. Sustain. Energy 2014, 6, 033119. [Google Scholar] [CrossRef]
- Lind, P.; Herráez, I.; Wächter, M.; Peinke, J. Fatigue Load Estimation through a Simple Stochastic Model. Energies 2014, 7, 8279–8293. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Brockwell, P.; Davis, R. Time Series: Theory and Methods; Springer: New York, NY, USA, 2009. [Google Scholar]
- Essenwanger, O. Probleme der Windstatistik. Meteorol. Rundsch. 1959, 12, 37–47. [Google Scholar]
- Friedrich, R.; Peinke, J. Description of a Turbulent Cascade by a Fokker-Planck Equation. Phys. Rev. Lett. 1997, 78, 863. [Google Scholar] [CrossRef]
- Ragwitz, M.; Kantz, H. Indispensable Finite Time Corrections for Fokker-Planck Equations from Time Series Data. Phys. Rev. Lett. 2001, 87, 254501. [Google Scholar] [CrossRef] [PubMed]
- Weber, J.; Zachow, C.; Witthaut, D. Modeling long correlation times using additive binary Markov chains: Applications to wind generation time series. Phys. Rev. E 2018, 97, 032138. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, B.; Beck, C.; Aihara, K.; Witthaut, D.; Timme, M. Non-Gaussian power grid frequency fluctuations characterized by Lévy-stable laws and superstatistics. Nat. Energy 2018, 3, 119–126. [Google Scholar] [CrossRef]
- Morales, A.; Peinke, J. Assesment of turbulence by high-order statistics Offshore example. In Proceedings of the EWEA Proceedings, Copenhagen, Denmark, 15–19 April 2012; pp. 1–4. [Google Scholar]
- Mücke, T.; Kleinhans, D.; Peinke, J. Atmospheric turbulence and its influence on the alternating loads on wind turbines. Wind Energy 2010, 14, 301–316. [Google Scholar] [CrossRef]
- Raischel, F.; Russo, A.; Haase, M.; Kleinhans, D.; Lind, P. Optimal variables for describing evolution of NO2 concentration. Phys. Lett. A 2012, 376, 2081–2089. [Google Scholar] [CrossRef]
- Lind, P.; Vera-Tudela, L.; Wächter, M.; Kühn, M.; Peinke, J. Normal Behaviour Models for Wind Turbine Vibrations: Comparison of Neural Networks and a Stochastic Approach. Energies 2017, 10, 1944. [Google Scholar] [CrossRef]
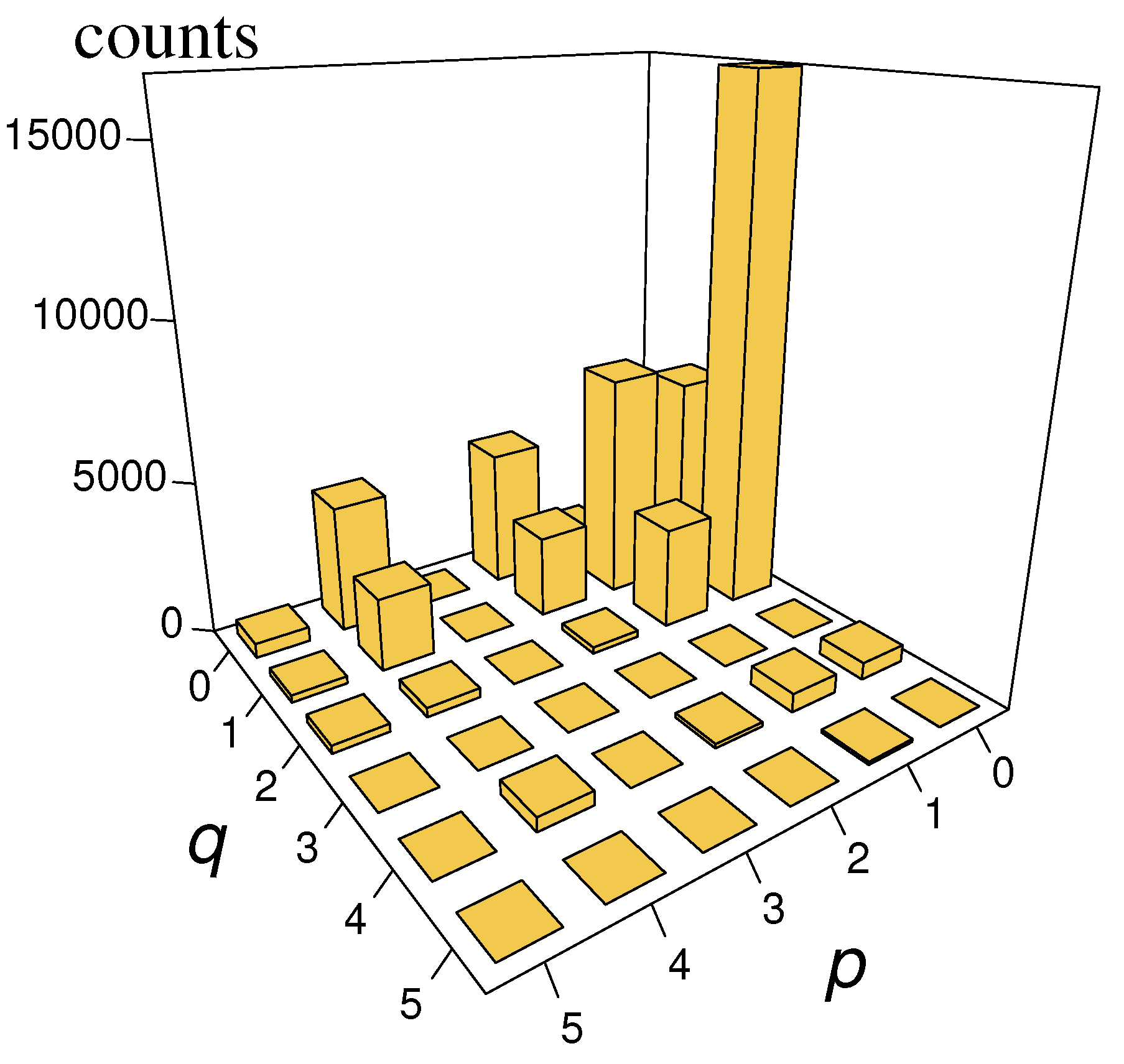

| Model | MAPE |
|---|---|
| ARIMA (Speed, 15 min.) | 5.53% |
| ARIMA (Speed, 10 min.) | 17.61% |
| ARIMA (Speed, 20 min.) | 20.59% |
| Neural Network (Speed, 10 min.) | 5.97% |
| Neural Network (Speed, 20 min.) | 7.03% |
| ARIMA with Neural Net. (Speed, 10 min.) | 4.46% |
| ARIMA with Neural Net. (Speed, 20 min.) | 5.31% |
| Parameter | |||
|---|---|---|---|
| 0.976 | 0.0580 | 1.47 | |
| 0.0255 | – | −0.477 | |
| −0.0191 | – | – | |
| −0.969 | – | −1.29 | |
| – | – | 0.312 | |
| () | 9.91 | 7.19 | 7.46 |
| 2 | |||||||||||||
| 0.425 | 0.451 | 0.478 | 0.504 | 0.529 | 0.556 | 0.583 | 0.609 | 0.633 | 0.657 | 0.687 | 0.712 | 0.737 | |
| 0.426 | 0.452 | 0.479 | 0.505 | 0.530 | 0.557 | 0.584 | 0.609 | 0.634 | 0.658 | 0.688 | 0.713 | 0.738 | |
| 0.426 | 0.453 | 0.479 | 0.506 | 0.531 | 0.558 | 0.585 | 0.610 | 0.635 | 0.663 | 0.689 | 0.714 | 0.738 | |
| 0.427 | 0.453 | 0.480 | 0.506 | 0.532 | 0.559 | 0.585 | 0.611 | 0.636 | 0.664 | 0.689 | 0.715 | 0.739 | |
| 0.428 | 0.454 | 0.481 | 0.507 | 0.533 | 0.560 | 0.586 | 0.612 | 0.636 | 0.665 | 0.690 | 0.715 | 0.740 | |
| 0.428 | 0.455 | 0.481 | 0.508 | 0.533 | 0.560 | 0.587 | 0.612 | 0.637 | 0.665 | 0.691 | 0.716 | 0.740 | |
| 0.429 | 0.455 | 0.482 | 0.508 | 0.534 | 0.561 | 0.587 | 0.613 | 0.637 | 0.666 | 0.691 | 0.716 | 0.741 | |
| 0.429 | 0.456 | 0.482 | 0.509 | 0.534 | 0.561 | 0.588 | 0.613 | 0.638 | 0.666 | 0.692 | 0.717 | 0.741 | |
| 0.430 | 0.456 | 0.483 | 0.509 | 0.535 | 0.562 | 0.588 | 0.614 | 0.638 | 0.667 | 0.692 | 0.717 | 0.741 | |
| 0.430 | 0.456 | 0.483 | 0.510 | 0.535 | 0.562 | 0.589 | 0.614 | 0.639 | 0.667 | 0.693 | 0.718 | 0.742 | |
| 0.431 | 0.457 | 0.484 | 0.510 | 0.536 | 0.562 | 0.589 | 0.615 | 0.639 | 0.668 | 0.693 | 0.718 | 0.742 | |
| 0.431 | 0.457 | 0.484 | 0.510 | 0.536 | 0.563 | 0.590 | 0.615 | 0.642 | 0.668 | 0.694 | 0.718 | 0.742 | |
| 0.431 | 0.457 | 0.484 | 0.511 | 0.537 | 0.563 | 0.590 | 0.615 | 0.642 | 0.668 | 0.694 | 0.719 | 0.742 | |
| 0.432 | 0.458 | 0.485 | 0.511 | 0.537 | 0.563 | 0.590 | 0.616 | 0.643 | 0.669 | 0.694 | 0.719 | 0.742 | |
| 0.432 | 0.458 | 0.485 | 0.511 | 0.537 | 0.564 | 0.591 | 0.616 | 0.643 | 0.669 | 0.695 | 0.719 | 0.742 | |
| 0.432 | 0.458 | 0.485 | 0.512 | 0.538 | 0.564 | 0.591 | 0.616 | 0.643 | 0.669 | 0.695 | 0.719 | 0.743 | |
| 0.432 | 0.459 | 0.486 | 0.512 | 0.538 | 0.564 | 0.591 | 0.616 | 0.644 | 0.670 | 0.695 | 0.719 | 0.743 | |
| 0.433 | 0.459 | 0.486 | 0.512 | 0.538 | 0.564 | 0.591 | 0.617 | 0.644 | 0.670 | 0.695 | 0.720 | 0.748 | |
| 0.433 | 0.460 | 0.486 | 0.512 | 0.538 | 0.564 | 0.592 | 0.617 | 0.644 | 0.670 | 0.696 | 0.720 | 0.749 | |
| 0.433 | 0.460 | 0.486 | 0.513 | 0.539 | 0.565 | 0.592 | 0.617 | 0.645 | 0.670 | 0.696 | 0.720 | 0.749 | |
| 0.433 | 0.460 | 0.487 | 0.513 | 0.539 | 0.565 | 0.592 | 0.617 | 0.645 | 0.671 | 0.696 | 0.720 | 0.749 | |
| 0.434 | 0.460 | 0.487 | 0.513 | 0.539 | 0.565 | 0.592 | 0.617 | 0.645 | 0.671 | 0.696 | 0.720 | 0.749 | |
| 0.434 | 0.460 | 0.487 | 0.513 | 0.539 | 0.565 | 0.592 | 0.618 | 0.645 | 0.671 | 0.696 | 0.720 | 0.749 | |
| 0.433 | 0.461 | 0.487 | 0.513 | 0.540 | 0.566 | 0.593 | 0.618 | 0.645 | 0.671 | 0.696 | 0.720 | 0.750 | |
| 0.434 | 0.461 | 0.487 | 0.514 | 0.540 | 0.567 | 0.593 | 0.618 | 0.646 | 0.671 | 0.696 | 0.721 | 0.750 | |
| 0.434 | 0.461 | 0.487 | 0.514 | 0.540 | 0.567 | 0.593 | 0.618 | 0.646 | 0.672 | 0.697 | 0.721 | 0.750 | |
| 0.434 | 0.461 | 0.488 | 0.514 | 0.540 | 0.567 | 0.593 | 0.618 | 0.646 | 0.672 | 0.697 | 0.721 | 0.750 | |
| 0.435 | 0.461 | 0.488 | 0.514 | 0.540 | 0.567 | 0.593 | 0.620 | 0.646 | 0.672 | 0.697 | 0.725 | 0.750 | |
| 0.435 | 0.461 | 0.488 | 0.514 | 0.540 | 0.567 | 0.593 | 0.620 | 0.646 | 0.672 | 0.697 | 0.725 | 0.751 | |
| 0.435 | 0.461 | 0.488 | 0.514 | 0.541 | 0.567 | 0.594 | 0.620 | 0.646 | 0.672 | 0.697 | 0.725 | 0.751 | |
| 0.435 | 0.462 | 0.488 | 0.514 | 0.541 | 0.568 | 0.594 | 0.620 | 0.646 | 0.672 | 0.697 | 0.725 | 0.751 | |
| 0.435 | 0.462 | 0.488 | 0.514 | 0.541 | 0.568 | 0.594 | 0.620 | 0.647 | 0.672 | 0.697 | 0.725 | 0.751 | |
| 0.435 | 0.462 | 0.488 | 0.515 | 0.541 | 0.568 | 0.594 | 0.621 | 0.647 | 0.673 | 0.697 | 0.725 | 0.751 | |
| 0.435 | 0.462 | 0.488 | 0.515 | 0.541 | 0.568 | 0.594 | 0.621 | 0.647 | 0.673 | 0.698 | 0.725 | 0.751 | |
| 0.435 | 0.462 | 0.489 | 0.515 | 0.541 | 0.568 | 0.594 | 0.621 | 0.647 | 0.673 | 0.698 | 0.726 | 0.751 | |
| 0.435 | 0.462 | 0.489 | 0.515 | 0.541 | 0.568 | 0.594 | 0.621 | 0.647 | 0.673 | 0.698 | 0.726 | 0.751 | |
| 0.436 | 0.462 | 0.489 | 0.515 | 0.541 | 0.568 | 0.594 | 0.621 | 0.647 | 0.673 | 0.698 | 0.726 | 0.752 | |
| 0.436 | 0.462 | 0.489 | 0.515 | 0.542 | 0.568 | 0.594 | 0.621 | 0.647 | 0.673 | 0.698 | 0.726 | 0.752 | |
| 0.436 | 0.462 | 0.489 | 0.515 | 0.542 | 0.568 | 0.595 | 0.621 | 0.647 | 0.673 | 0.699 | 0.726 | 0.752 | |
| 0.436 | 0.462 | 0.489 | 0.515 | 0.542 | 0.569 | 0.595 | 0.621 | 0.648 | 0.673 | 0.699 | 0.726 | 0.752 | |
| 0.436 | 0.463 | 0.489 | 0.515 | 0.542 | 0.569 | 0.595 | 0.621 | 0.648 | 0.673 | 0.698 | 0.726 | 0.752 | |
| 0.436 | 0.463 | 0.489 | 0.515 | 0.542 | 0.569 | 0.595 | 0.622 | 0.648 | 0.673 | 0.698 | 0.726 | 0.752 | |
| 0.436 | 0.463 | 0.489 | 0.516 | 0.542 | 0.569 | 0.599 | 0.622 | 0.648 | 0.673 | 0.698 | 0.726 | 0.752 | |
| 0.436 | 0.463 | 0.489 | 0.516 | 0.542 | 0.569 | 0.595 | 0.622 | 0.648 | 0.674 | 0.698 | 0.727 | 0.752 | |
| 0.436 | 0.463 | 0.489 | 0.516 | 0.542 | 0.569 | 0.595 | 0.622 | 0.648 | 0.674 | 0.701 | 0.727 | 0.752 | |
| 0.436 | 0.463 | 0.489 | 0.516 | 0.542 | 0.569 | 0.595 | 0.622 | 0.648 | 0.674 | 0.701 | 0.727 | 0.752 | |
| 0.436 | 0.463 | 0.489 | 0.516 | 0.542 | 0.569 | 0.595 | 0.622 | 0.648 | 0.674 | 0.701 | 0.727 | 0.752 | |
| 0.436 | 0.463 | 0.490 | 0.516 | 0.542 | 0.569 | 0.595 | 0.622 | 0.648 | 0.674 | 0.701 | 0.727 | 0.753 | |
| 0.436 | 0.463 | 0.490 | 0.516 | 0.543 | 0.569 | 0.595 | 0.622 | 0.648 | 0.674 | 0.701 | 0.727 | 0.753 | |
| 0.436 | 0.463 | 0.490 | 0.516 | 0.543 | 0.569 | 0.595 | 0.622 | 0.648 | 0.674 | 0.701 | 0.727 | 0.753 | |
| 0.436 | 0.463 | 0.490 | 0.516 | 0.543 | 0.570 | 0.595 | 0.622 | 0.648 | 0.674 | 0.701 | 0.727 | 0.753 | |
| 3.3 | |||||||||||||
| 0.761 | 0.783 | 0.803 | 0.840 | 0.863 | 0.884 | 0.903 | 0.920 | 0.934 | 0.945 | 0.955 | 0.963 | 0.970 | |
| 0.761 | 0.783 | 0.804 | 0.841 | 0.864 | 0.884 | 0.903 | 0.920 | 0.933 | 0.945 | 0.954 | 0.962 | 0.968 | |
| 0.762 | 0.784 | 0.817 | 0.841 | 0.864 | 0.885 | 0.903 | 0.919 | 0.933 | 0.944 | 0.954 | 0.961 | 0.968 | |
| 0.762 | 0.784 | 0.818 | 0.842 | 0.864 | 0.885 | 0.903 | 0.919 | 0.933 | 0.943 | 0.953 | 0.960 | 0.967 | |
| 0.763 | 0.784 | 0.819 | 0.842 | 0.865 | 0.885 | 0.903 | 0.919 | 0.932 | 0.943 | 0.952 | 0.960 | 0.966 | |
| 0.763 | 0.784 | 0.819 | 0.843 | 0.865 | 0.885 | 0.903 | 0.918 | 0.931 | 0.942 | 0.951 | 0.959 | 0.965 | |
| 0.763 | 0.795 | 0.820 | 0.843 | 0.865 | 0.885 | 0.903 | 0.917 | 0.931 | 0.941 | 0.950 | 0.958 | 0.964 | |
| 0.764 | 0.795 | 0.820 | 0.844 | 0.865 | 0.885 | 0.902 | 0.918 | 0.930 | 0.941 | 0.949 | 0.957 | 0.963 | |
| 0.764 | 0.796 | 0.820 | 0.844 | 0.865 | 0.885 | 0.902 | 0.917 | 0.930 | 0.940 | 0.949 | 0.956 | 0.962 | |
| 0.764 | 0.796 | 0.821 | 0.844 | 0.865 | 0.885 | 0.902 | 0.917 | 0.929 | 0.969 | 0.978 | 0.984 | 0.989 | |
| 0.772 | 0.797 | 0.821 | 0.844 | 0.866 | 0.885 | 0.902 | 0.916 | 0.956 | 0.969 | 0.978 | 0.984 | 0.989 | |
| 0.772 | 0.797 | 0.821 | 0.844 | 0.865 | 0.884 | 0.901 | 0.915 | 0.956 | 0.968 | 0.977 | 0.984 | 0.988 | |
| 0.772 | 0.797 | 0.822 | 0.844 | 0.865 | 0.884 | 0.901 | 0.940 | 0.956 | 0.968 | 0.977 | 0.983 | 0.988 | |
| 0.773 | 0.798 | 0.822 | 0.845 | 0.865 | 0.884 | 0.901 | 0.940 | 0.956 | 0.968 | 0.977 | 0.983 | 0.988 | |
| 0.773 | 0.798 | 0.822 | 0.845 | 0.865 | 0.884 | 0.900 | 0.940 | 0.955 | 0.967 | 0.976 | 0.983 | 0.987 | |
| 0.773 | 0.798 | 0.822 | 0.845 | 0.865 | 0.884 | 0.921 | 0.940 | 0.955 | 0.967 | 0.976 | 0.982 | 0.987 | |
| 0.774 | 0.798 | 0.822 | 0.845 | 0.865 | 0.883 | 0.921 | 0.940 | 0.955 | 0.967 | 0.975 | 0.982 | 0.986 | |
| 0.774 | 0.799 | 0.822 | 0.845 | 0.865 | 0.883 | 0.921 | 0.939 | 0.955 | 0.966 | 0.975 | 0.982 | 0.986 | |
| 0.774 | 0.799 | 0.823 | 0.845 | 0.865 | 0.883 | 0.921 | 0.939 | 0.954 | 0.966 | 0.975 | 0.981 | 0.986 | |
| 0.774 | 0.799 | 0.823 | 0.845 | 0.865 | 0.900 | 0.921 | 0.939 | 0.954 | 0.965 | 0.974 | 0.981 | 0.985 | |
| 0.774 | 0.799 | 0.823 | 0.845 | 0.865 | 0.900 | 0.921 | 0.939 | 0.953 | 0.965 | 0.974 | 0.980 | 0.985 | |
| 0.775 | 0.799 | 0.823 | 0.845 | 0.865 | 0.900 | 0.921 | 0.939 | 0.953 | 0.965 | 0.974 | 0.980 | 0.985 | |
| 0.775 | 0.800 | 0.823 | 0.845 | 0.864 | 0.900 | 0.921 | 0.939 | 0.953 | 0.964 | 0.973 | 0.979 | 0.984 | |
| 0.775 | 0.800 | 0.823 | 0.845 | 0.864 | 0.900 | 0.921 | 0.938 | 0.953 | 0.964 | 0.973 | 0.979 | 0.984 | |
| 0.775 | 0.800 | 0.823 | 0.845 | 0.864 | 0.900 | 0.921 | 0.938 | 0.953 | 0.964 | 0.972 | 0.979 | 0.984 | |
| 0.775 | 0.800 | 0.823 | 0.845 | 0.878 | 0.900 | 0.921 | 0.938 | 0.952 | 0.963 | 0.972 | 0.978 | 0.983 | |
| 0.776 | 0.800 | 0.823 | 0.844 | 0.878 | 0.900 | 0.921 | 0.938 | 0.952 | 0.963 | 0.972 | 0.978 | 0.983 | |
| 0.776 | 0.800 | 0.823 | 0.844 | 0.878 | 0.900 | 0.921 | 0.938 | 0.952 | 0.963 | 0.971 | 0.978 | 0.983 | |
| 0.776 | 0.800 | 0.823 | 0.844 | 0.878 | 0.900 | 0.921 | 0.938 | 0.951 | 0.963 | 0.971 | 0.977 | 0.982 | |
| 0.776 | 0.800 | 0.823 | 0.844 | 0.878 | 0.901 | 0.920 | 0.937 | 0.951 | 0.962 | 0.971 | 0.977 | 0.982 | |
| 0.776 | 0.800 | 0.823 | 0.844 | 0.878 | 0.900 | 0.920 | 0.937 | 0.951 | 0.962 | 0.970 | 0.977 | 0.982 | |
| 0.776 | 0.800 | 0.823 | 0.844 | 0.878 | 0.900 | 0.920 | 0.937 | 0.951 | 0.961 | 0.970 | 0.976 | 0.981 | |
| 0.776 | 0.800 | 0.823 | 0.854 | 0.878 | 0.900 | 0.920 | 0.937 | 0.950 | 0.961 | 0.970 | 0.976 | 0.981 | |
| 0.776 | 0.800 | 0.823 | 0.854 | 0.878 | 0.900 | 0.920 | 0.936 | 0.950 | 0.961 | 0.969 | 0.976 | 0.981 | |
| 0.776 | 0.800 | 0.823 | 0.854 | 0.878 | 0.900 | 0.920 | 0.936 | 0.950 | 0.961 | 0.969 | 0.975 | 0.980 | |
| 0.777 | 0.801 | 0.823 | 0.855 | 0.878 | 0.900 | 0.920 | 0.936 | 0.950 | 0.960 | 0.969 | 0.975 | 0.980 | |
| 0.777 | 0.801 | 0.823 | 0.855 | 0.878 | 0.900 | 0.920 | 0.936 | 0.949 | 0.960 | 0.968 | 0.975 | 0.980 | |
| 0.777 | 0.801 | 0.823 | 0.855 | 0.878 | 0.900 | 0.919 | 0.936 | 0.949 | 0.960 | 0.968 | 0.974 | 0.979 | |
| 0.777 | 0.801 | 0.823 | 0.855 | 0.878 | 0.900 | 0.919 | 0.936 | 0.949 | 0.959 | 0.968 | 0.974 | 0.979 | |
| 0.777 | 0.801 | 0.823 | 0.855 | 0.878 | 0.900 | 0.919 | 0.935 | 0.949 | 0.959 | 0.967 | 0.974 | 0.979 | |
| 0.777 | 0.801 | 0.823 | 0.855 | 0.878 | 0.900 | 0.919 | 0.935 | 0.948 | 0.959 | 0.967 | 0.973 | 0.978 | |
| 0.777 | 0.801 | 0.823 | 0.855 | 0.878 | 0.900 | 0.919 | 0.935 | 0.948 | 0.958 | 0.967 | 0.973 | 0.978 | |
| 0.777 | 0.801 | 0.823 | 0.855 | 0.879 | 0.900 | 0.919 | 0.935 | 0.948 | 0.958 | 0.966 | 0.973 | 0.978 | |
| 0.777 | 0.801 | 0.830 | 0.855 | 0.879 | 0.900 | 0.919 | 0.935 | 0.948 | 0.958 | 0.966 | 0.973 | 0.978 | |
| 0.777 | 0.801 | 0.830 | 0.855 | 0.879 | 0.900 | 0.919 | 0.934 | 0.947 | 0.958 | 0.966 | 0.972 | 0.977 | |
| 0.777 | 0.801 | 0.831 | 0.855 | 0.879 | 0.900 | 0.918 | 0.934 | 0.947 | 0.958 | 0.966 | 0.972 | 0.977 | |
| 0.777 | 0.801 | 0.831 | 0.855 | 0.879 | 0.900 | 0.918 | 0.934 | 0.947 | 0.957 | 0.965 | 0.972 | 0.977 | |
| 0.777 | 0.801 | 0.831 | 0.855 | 0.879 | 0.900 | 0.918 | 0.934 | 0.947 | 0.957 | 0.965 | 0.971 | 0.976 | |
| 0.777 | 0.801 | 0.831 | 0.855 | 0.879 | 0.899 | 0.918 | 0.933 | 0.946 | 0.957 | 0.965 | 0.971 | 0.976 | |
| 0.777 | 0.801 | 0.831 | 0.855 | 0.879 | 0.900 | 0.918 | 0.933 | 0.946 | 0.956 | 0.964 | 0.971 | 0.976 | |
| 0.777 | 0.801 | 0.831 | 0.855 | 0.879 | 0.900 | 0.918 | 0.933 | 0.946 | 0.956 | 0.964 | 0.970 | 0.975 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sim, S.-K.; Maass, P.; Lind, P.G. Wind Speed Modeling by Nested ARIMA Processes. Energies 2019, 12, 69. https://doi.org/10.3390/en12010069
Sim S-K, Maass P, Lind PG. Wind Speed Modeling by Nested ARIMA Processes. Energies. 2019; 12(1):69. https://doi.org/10.3390/en12010069
Chicago/Turabian StyleSim, So-Kumneth, Philipp Maass, and Pedro G. Lind. 2019. "Wind Speed Modeling by Nested ARIMA Processes" Energies 12, no. 1: 69. https://doi.org/10.3390/en12010069
APA StyleSim, S.-K., Maass, P., & Lind, P. G. (2019). Wind Speed Modeling by Nested ARIMA Processes. Energies, 12(1), 69. https://doi.org/10.3390/en12010069






