On Speed Control of a Permanent Magnet Synchronous Motor with Current Predictive Compensation
Abstract
:1. Introduction
2. Mathematical Model of the PMSM
2.1. PMSM Model
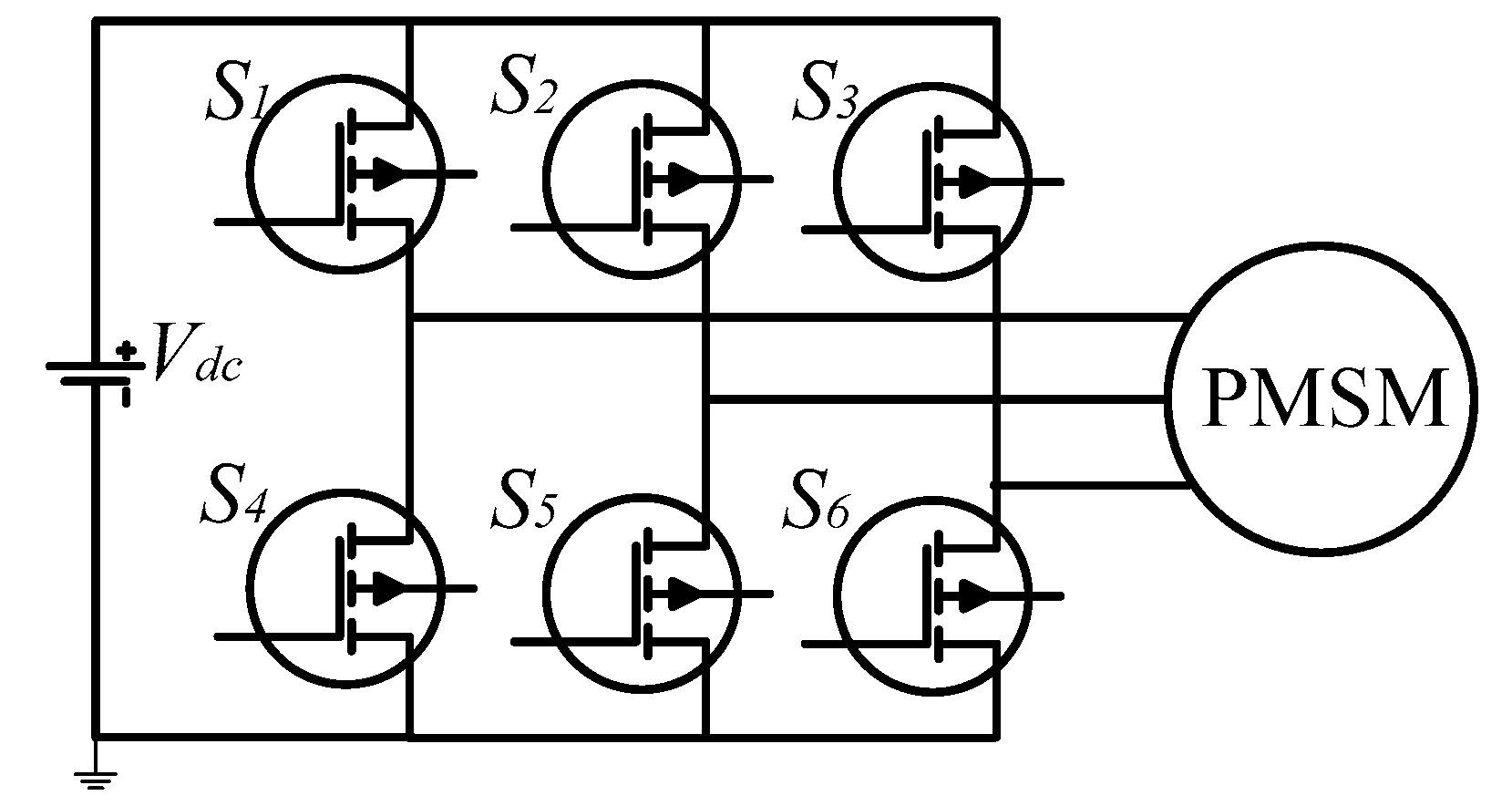
2.2. Drive Topology
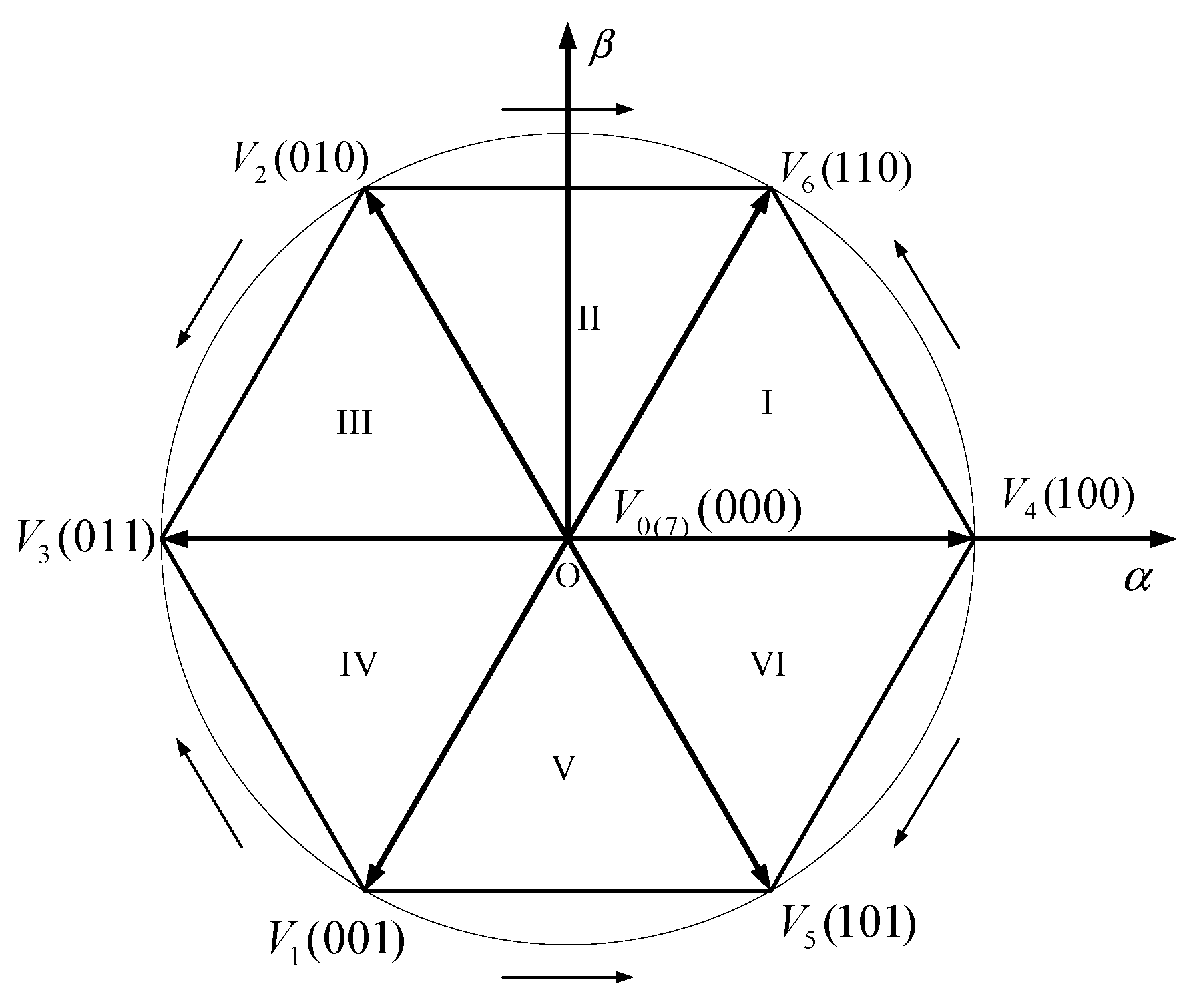
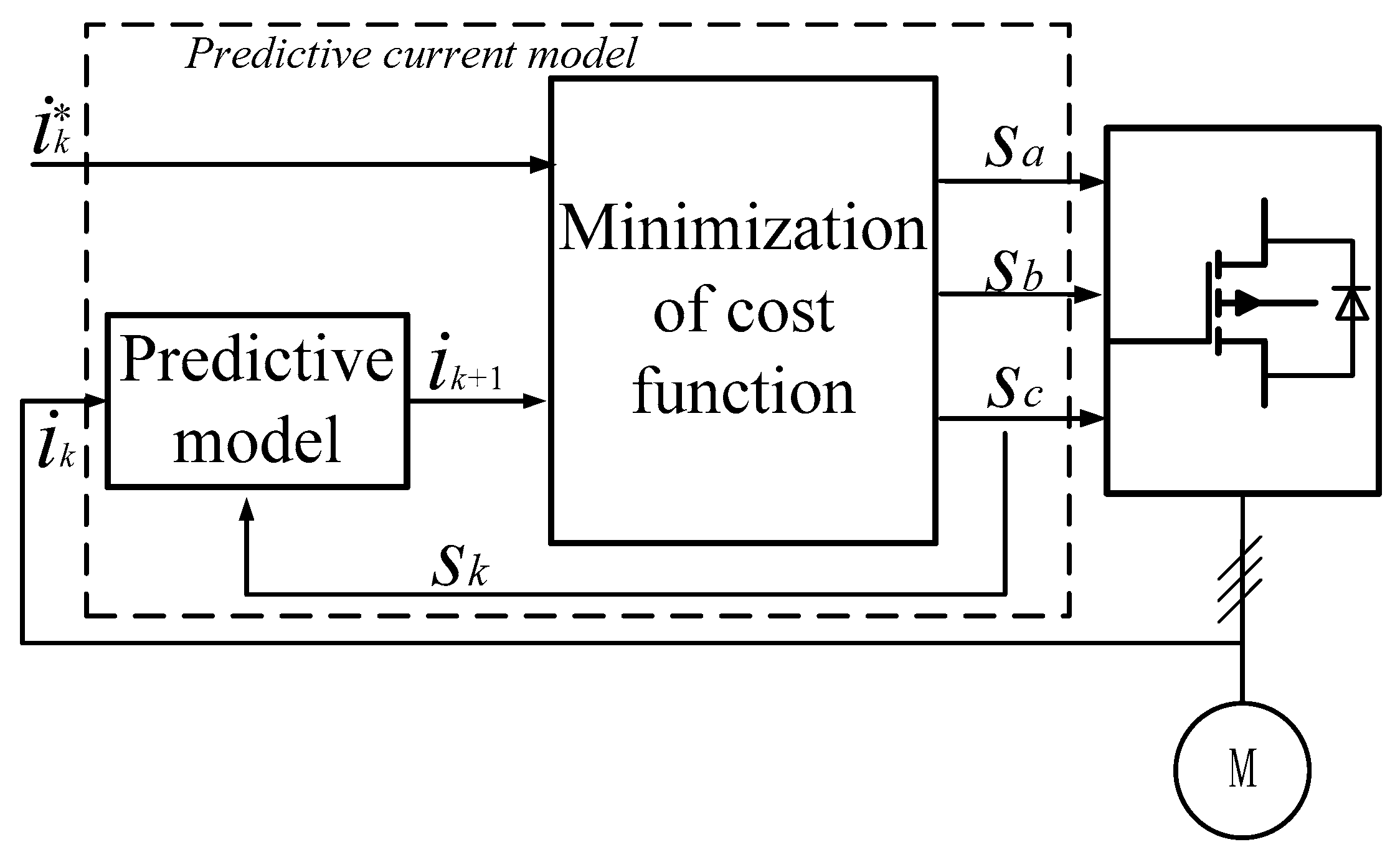
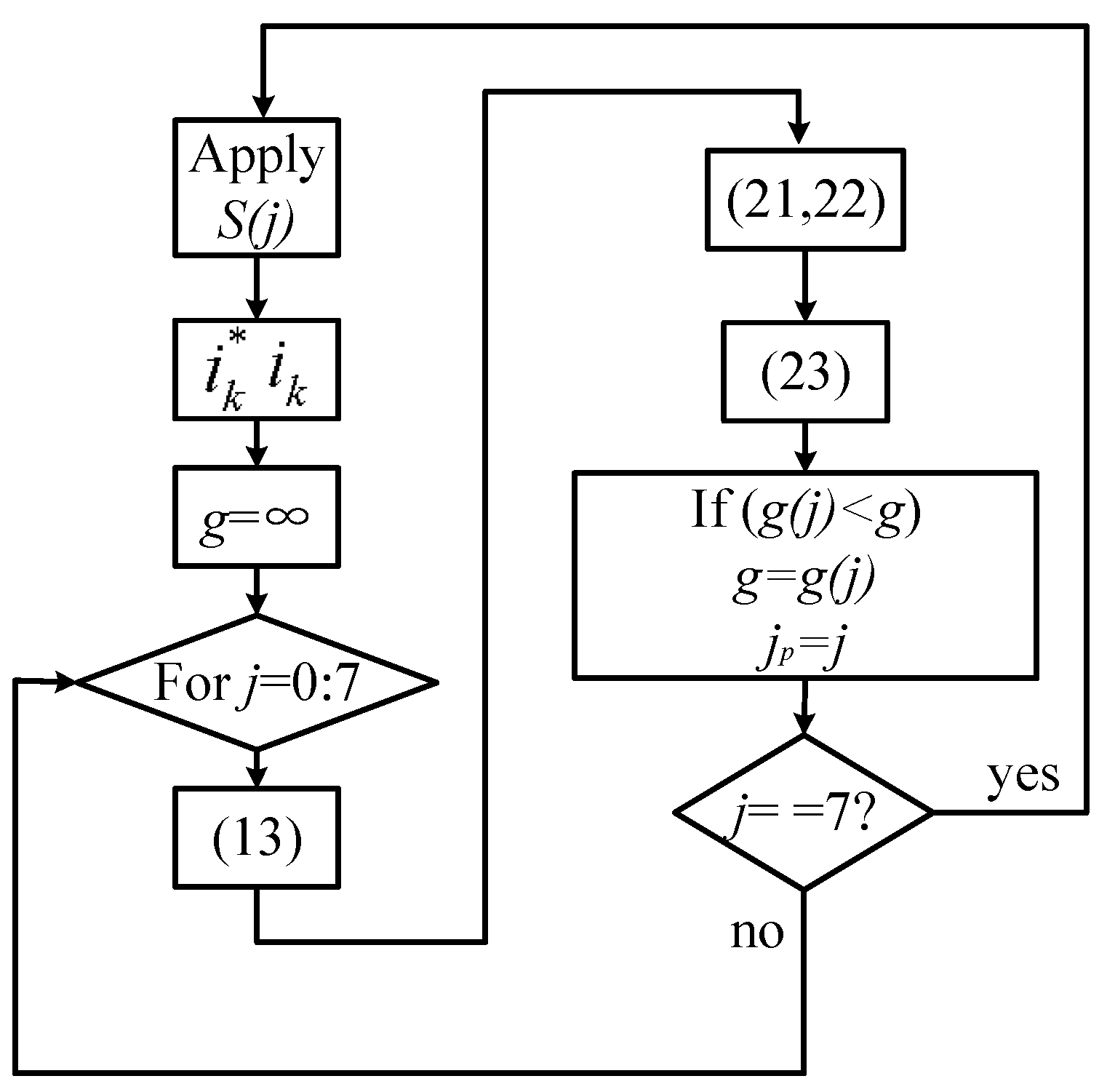
2.3. Model Predictive Control
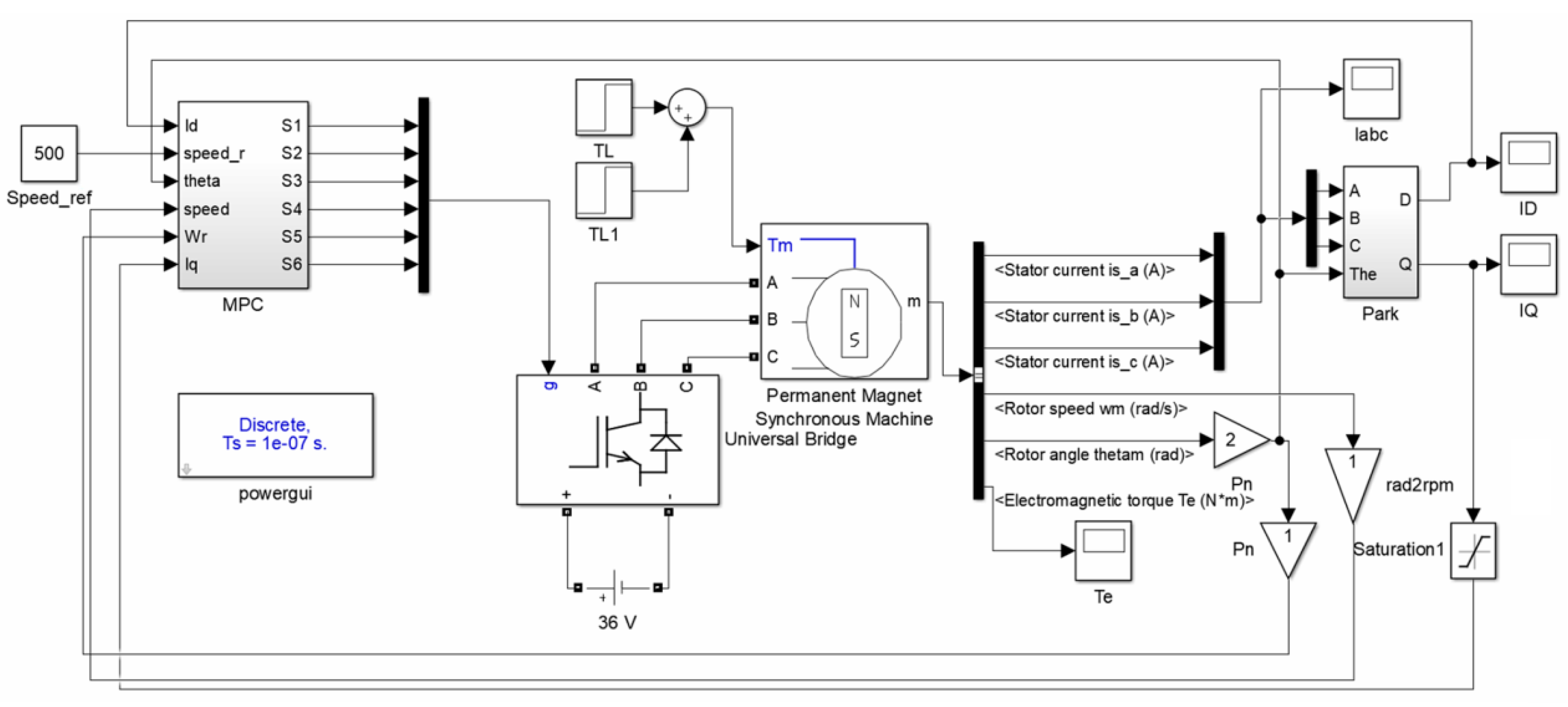
3. Simulink Modeling of the MPC Algorithm
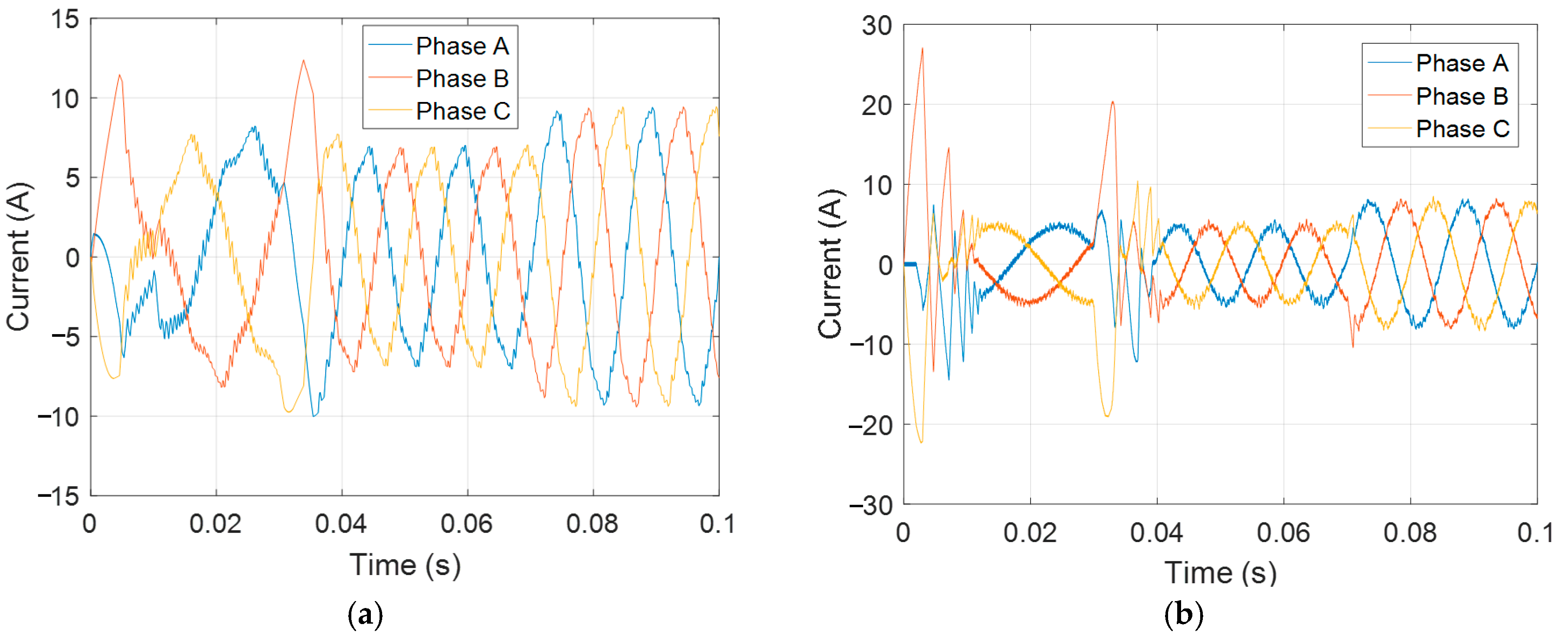
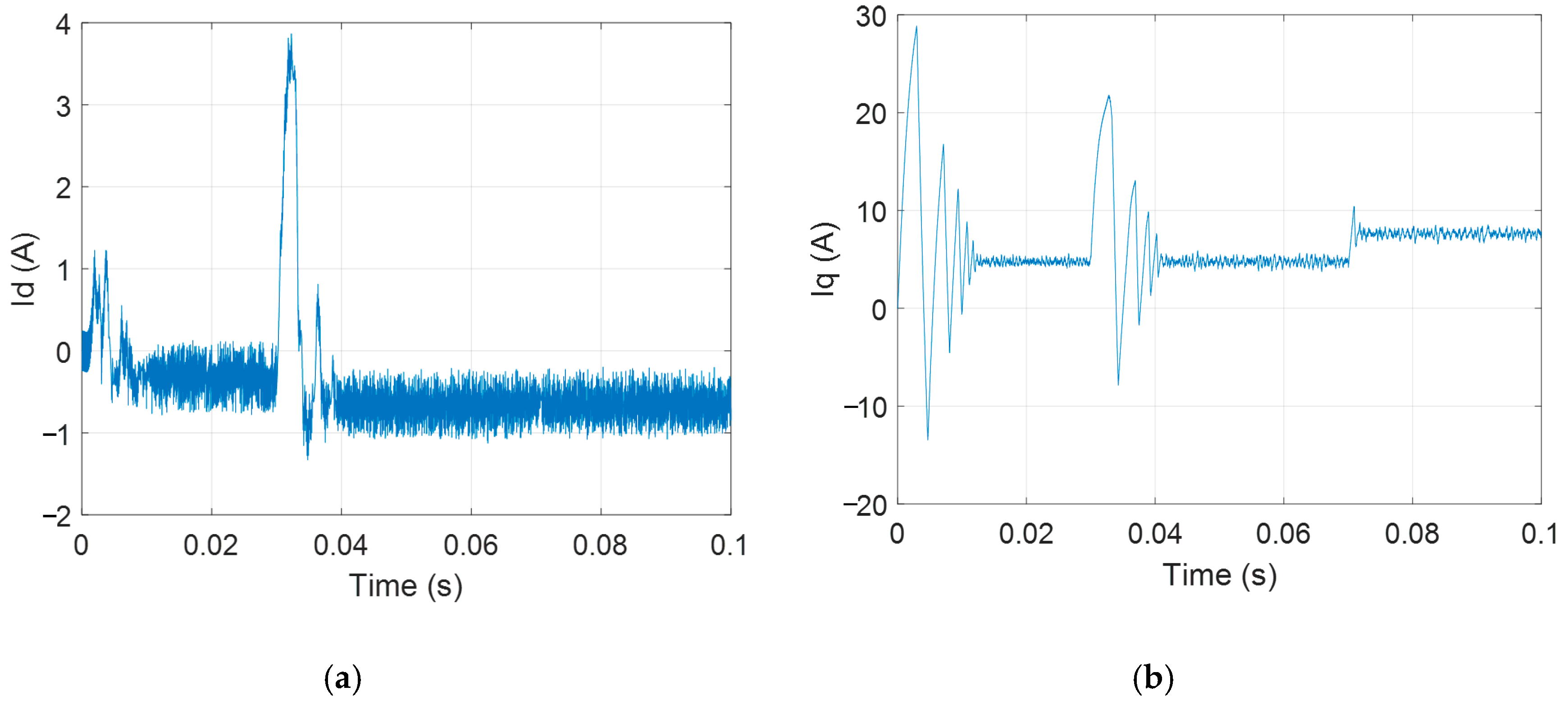
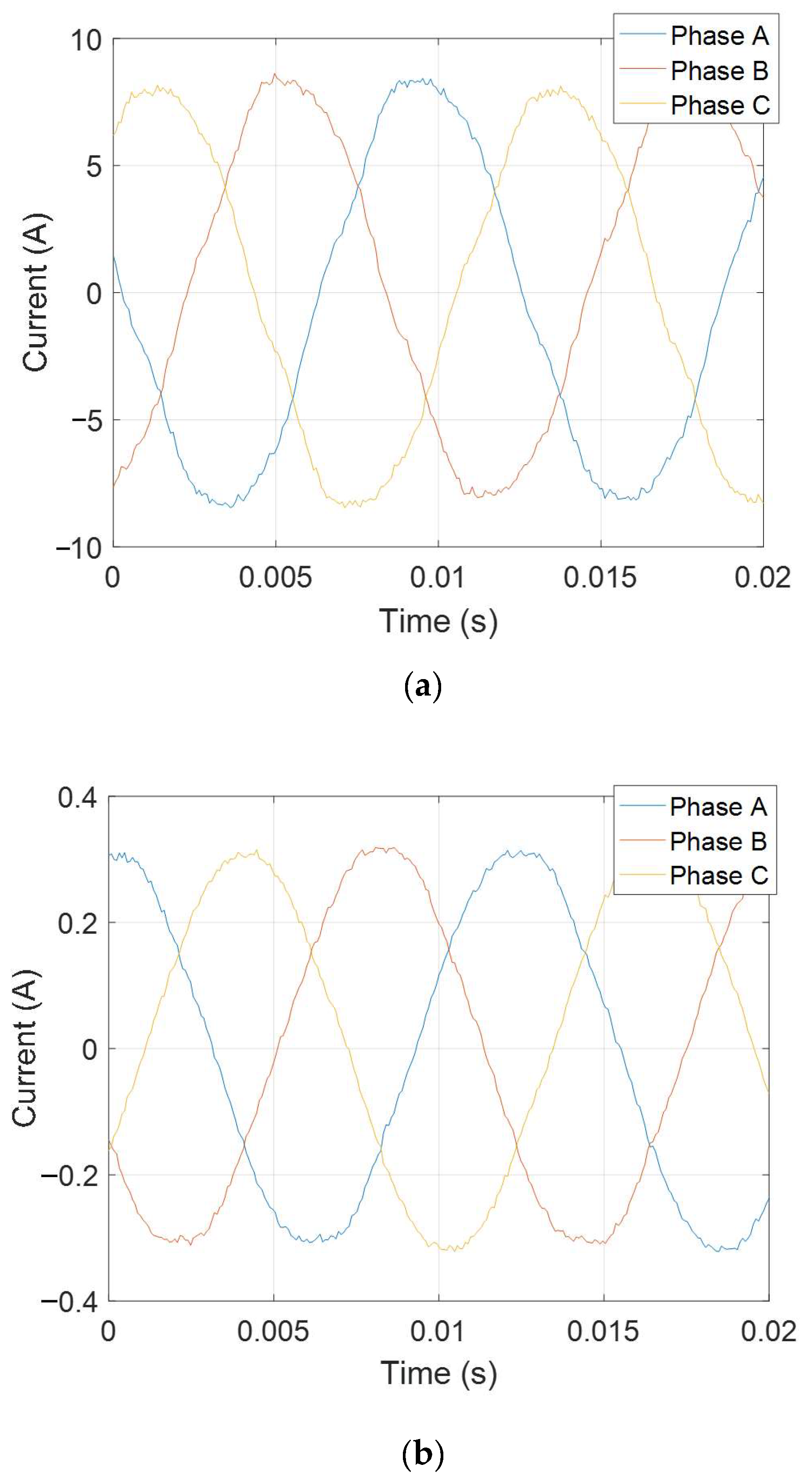
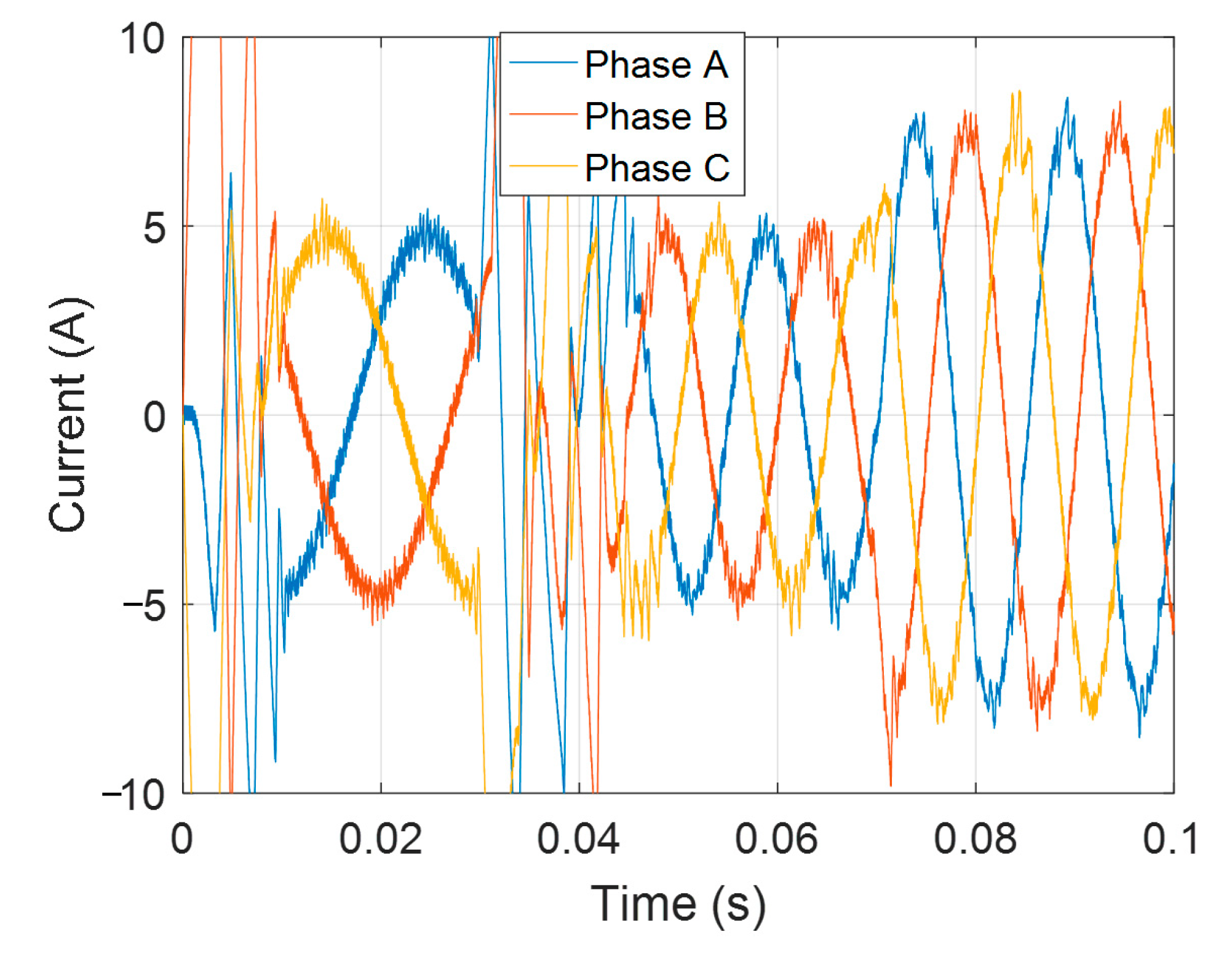
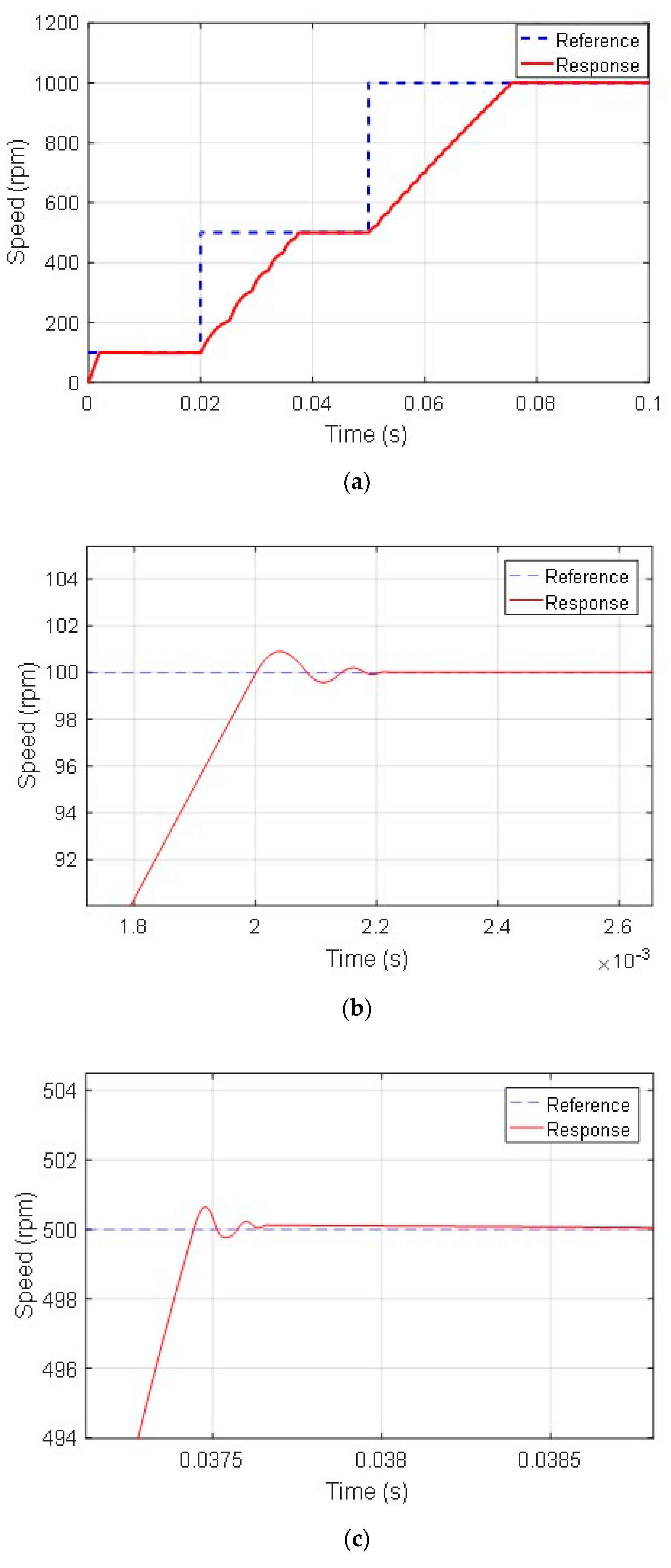
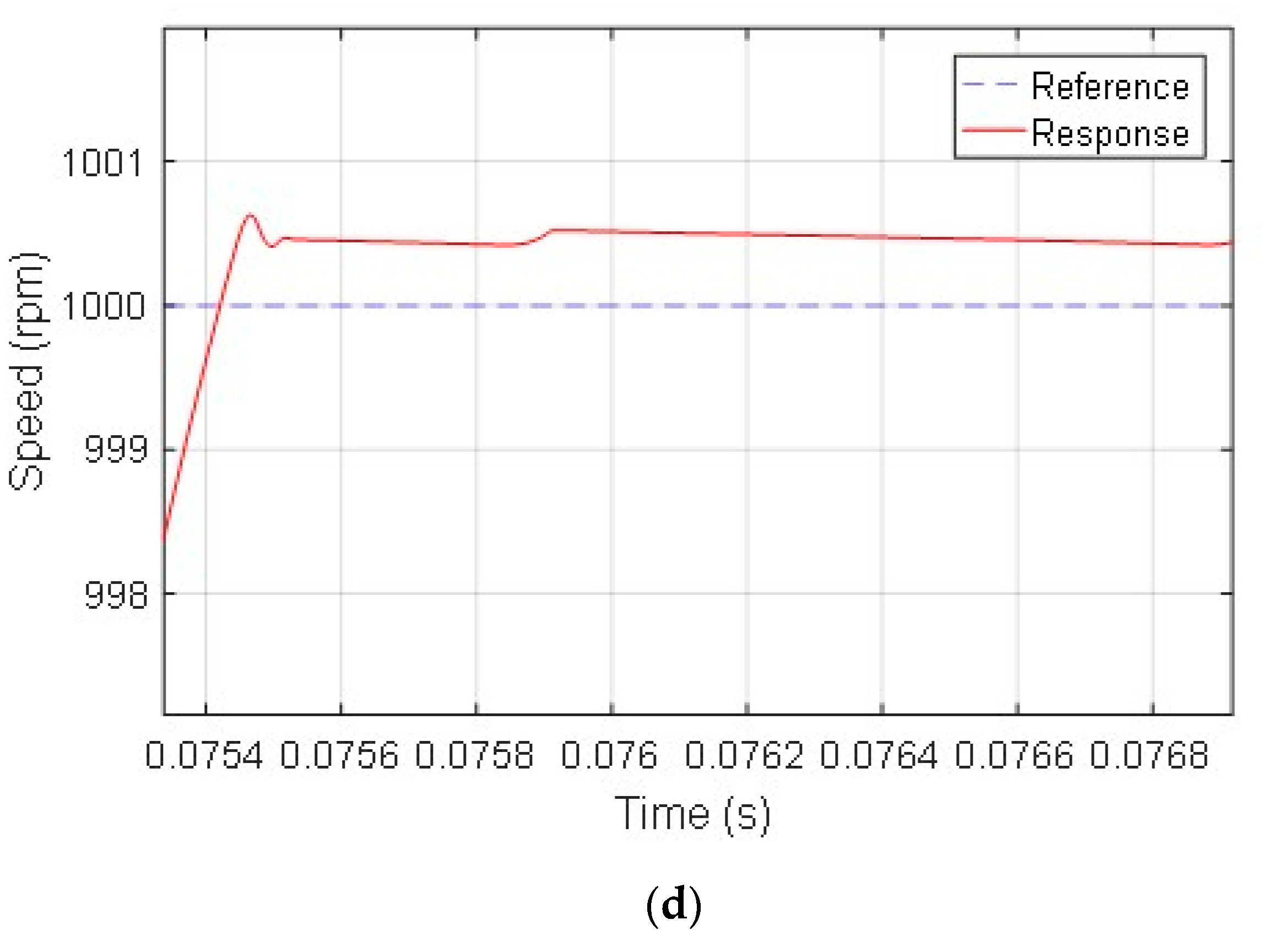
4. Experimental Verification
Experimental Setup
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
function Smin = MPC[wr,id,iq,theta] s = [0 0 0; 0 0 1; 0 1 0; 0 1 1;1 0 0; 1 0 1; 1 1 0; 1 1 1] gm = zeros(8,1); s1 = s2 = s3 = s4 = s5 = s6 = s6 = s7 = 0; for i = 1:8 sa = s(i,1); sb = s(i,2); sc = s(i,3); Vinva = (Vdc*(2*Sa − b − Sc))/3; Vinvb = (Vdc*(2*Sb − Sa − Sc))/3; Vinvc = (Vdc*(2*Sc − Sb − Sa))/3; vsq = (2/3)*((Vinva*cos((Wr*t + theta))) + (Vinvb*cos((Wr*t) + theta + (4*pi/3))) + (Vinvc*cos((Wr*t) + theta + (2*pi/3)))); vsd = (2/3)*((Vinva*sin((Wr*t + teta))) + (Vinvb*sin((Wr*t) + theta + (4*pi/3))) + (Vinvc*sin((Wr*t) + theta + (2*pi/3)))); iq1 = iq + Ts*[vsq − R*iq − L*wr*id − phi*wr]/L; id1 = id + Ts*[vsd − R*id + L*wr*Iq]/L g = abs(idr − id1) + abs(iqr − iq1); if(g < gm) i_min = i; g_min = g; end end v = v(i_min); iq = iq1; id = id1; s = s(:,i_min);
References
- Krishnan, R. Permanent Magnet Synchronous and Brushless DC Motor Drives; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2010. [Google Scholar]
- Hanselman, D.C. Brushless Permanent-Magnet Motor Design; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Abu-Rub, H.; Iqbal, A.; Guzinski, J. High Performance Control of AC Drives with MATLAB/Simulink Models; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Quang, N.P.; Dittrich, J. Vector Control of Three-Phase AC Machines System Development in the Practice; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Rodriguez, J.; Pontt, J.; Silva, C.A.; Correa, P.; Lezana, P.; Cortes, P.; Ammann, U. Predictive Current Control of a Voltage Source Inverter. IEEE Trans. Ind. Electron. 2007, 54, 495–503. [Google Scholar] [CrossRef]
- Bida, V.M.; Samokhvalov, D.V.; Al-Mahturi, F.S. PMSM vector control techniques—A survey. In Proceedings of the IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow, Russia, 29 January–1 February 2018; pp. 577–581. [Google Scholar] [CrossRef]
- Mohan, D.; Zhang, X.; Foo, G.H.B. A Simple Duty Cycle Control Strategy to Reduce Torque Ripples and Improve Low-Speed Performance of a Three-Level Inverter Fed DTC IPMSM Drive. IEEE Trans. Ind. Electron. 2017, 64, 2709–2721. [Google Scholar] [CrossRef]
- Shinohara, A.; Inoue, Y.; Morimoto, S.; Sanada, M. Maximum Torque Per Ampere Control in Stator Flux Linkage Synchronous Frame for DTC-Based PMSM Drives Without Using q-Axis Inductance. IEEE Trans. Ind. Appl. 2017, 53, 3663–3672. [Google Scholar] [CrossRef]
- Xia, C.; Wang, S.; Gu, X.; Yan, Y.; Shi, T. Direct Torque Control for VSI-PMSM Using Vector Evaluation Factor Table. IEEE Trans. Ind. Electron. 2016, 63, 4571–4583. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, G. Predictive DTC Strategy with Fault-Tolerant Function for Six-Phase and Three-Phase PMSM Series-Connected Drive System. IEEE Trans. Ind. Electron. 2018, 65, 9101–9112. [Google Scholar] [CrossRef]
- Wang, S.; Xu, D.D.; Li, C. Dynamic control set-model predictive control for field-oriented control of VSI-PMSM. IEEE Appl. Power Electron. Conf. Expos. 2018, 2630–2636. [Google Scholar] [CrossRef]
- Caseiro, L.M.A.; Mendes, A.M.S.; Cruz, S.M.A. Dynamically Weighted Optimal Switching Vector Model Predictive Control of Power Converters. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Siami, M.; Khaburi, D.A.; Rivera, M.; Rodríguez, J. A Computationally Efficient Lookup Table Based FCS-MPC for PMSM Drives Fed by Matrix Converters. IEEE Trans. Ind. Electron. 2017, 64, 7645–7654. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Koh, B.K.; Lee, Y.I. A Comparison of Finite Control Set and Continuous Control Set Model Predictive Control Schemes for Speed Control of Induction Motors. IEEE Trans. Ind. Inform. 2018, 14, 1334–1346. [Google Scholar] [CrossRef]
- Shoukry, Y.; El-Kharashi, M.W.; Hammad, S. MPC-On-Chip: An Embedded GPC Coprocessor for Automotive Active Suspension Systems. IEEE Embed. Syst. Lett. 2010, 2, 31–34. [Google Scholar] [CrossRef]
- Pejcic, I.; Korda, M.; Jones, C.N. Control of nonlinear systems with explicit-MPC-like controllers. In Proceedings of the IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 4970–4975. [Google Scholar] [CrossRef]
- Vazquez, S.; Aguilera, R.P.; Pablo Acuna, J.P.; Agelidis, V.G. Model Predictive Control for Single-Phase NPC Converters Based on Optimal Switching Sequences. IEEE Trans. Ind. Electron. 2016, 63, 7533–7543. [Google Scholar] [CrossRef]
- Kakosimos, P.; Abu-Rub, H. Predictive Speed Control with Short Prediction Horizon for Permanent Magnet Synchronous Motor Drives. IEEE Trans. Power Electron. 2018, 33, 2740–2750. [Google Scholar] [CrossRef]
- Rubino, S.; Bojoi, R.; Odhano, S.A.; Zanchetta, P. Model predictive direct flux vector control of multi three-phase induction motor drives. IEEE Trans. Ind. Appl. 2018. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, L.; Xu, D.; Liu, J.; Jin, J. Performance evaluation of two-vector-based model predictive current control of PMSM drives. Chin. J. Electr. Eng. 2018, 4, 65–81. [Google Scholar] [CrossRef]
- Zhang, X.; He, Y. Direct Voltage-Selection Based Model Predictive Direct Speed Control for PMSM Drives without Weighting Factor. IEEE Trans. Power Electron. 2018. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. Elimination of Harmonic Currents Using a Reference Voltage Vector Based-Model Predictive Control for a Six-Phase PMSM Motor. IEEE Trans. Power Electron. 2018. [Google Scholar] [CrossRef]
- Zhou, Z.; Xia, C.; Yan, Y.; Wang, Z.; Shi, T. Torque Ripple Minimization of Predictive Torque Control for PMSM With Extended Control Set. IEEE Trans. Ind. Electron. 2017, 24, 6930–6939. [Google Scholar] [CrossRef]

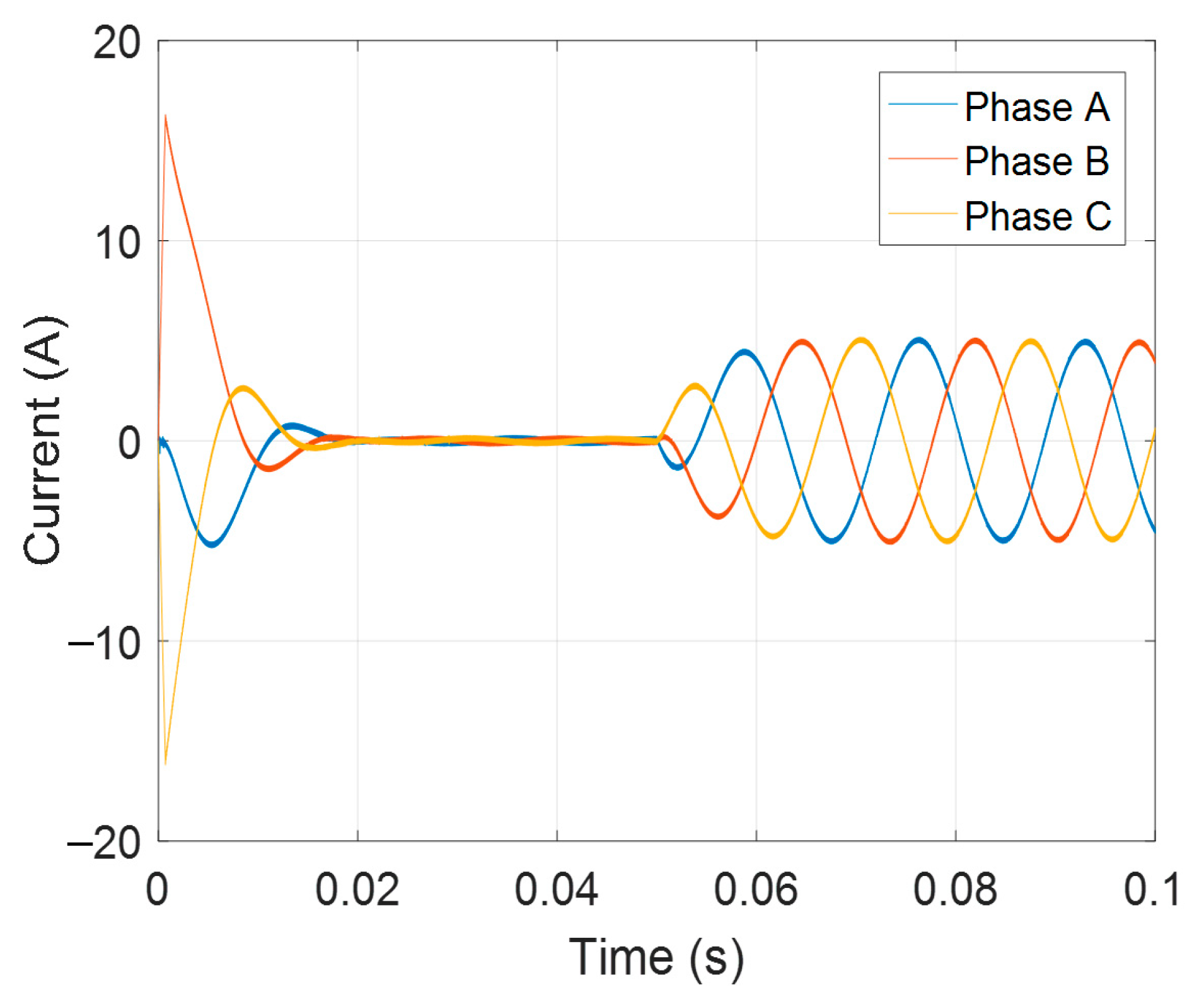
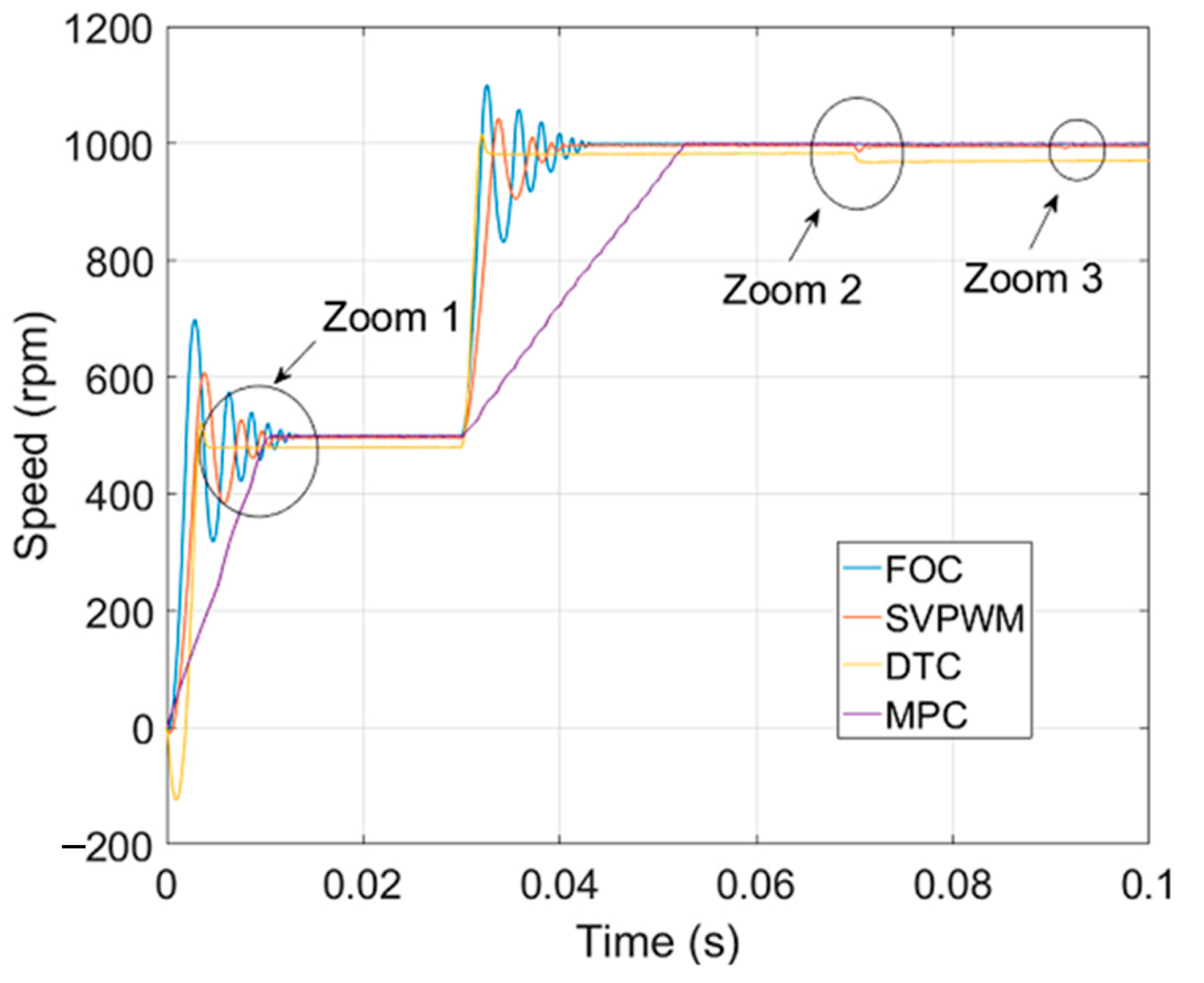
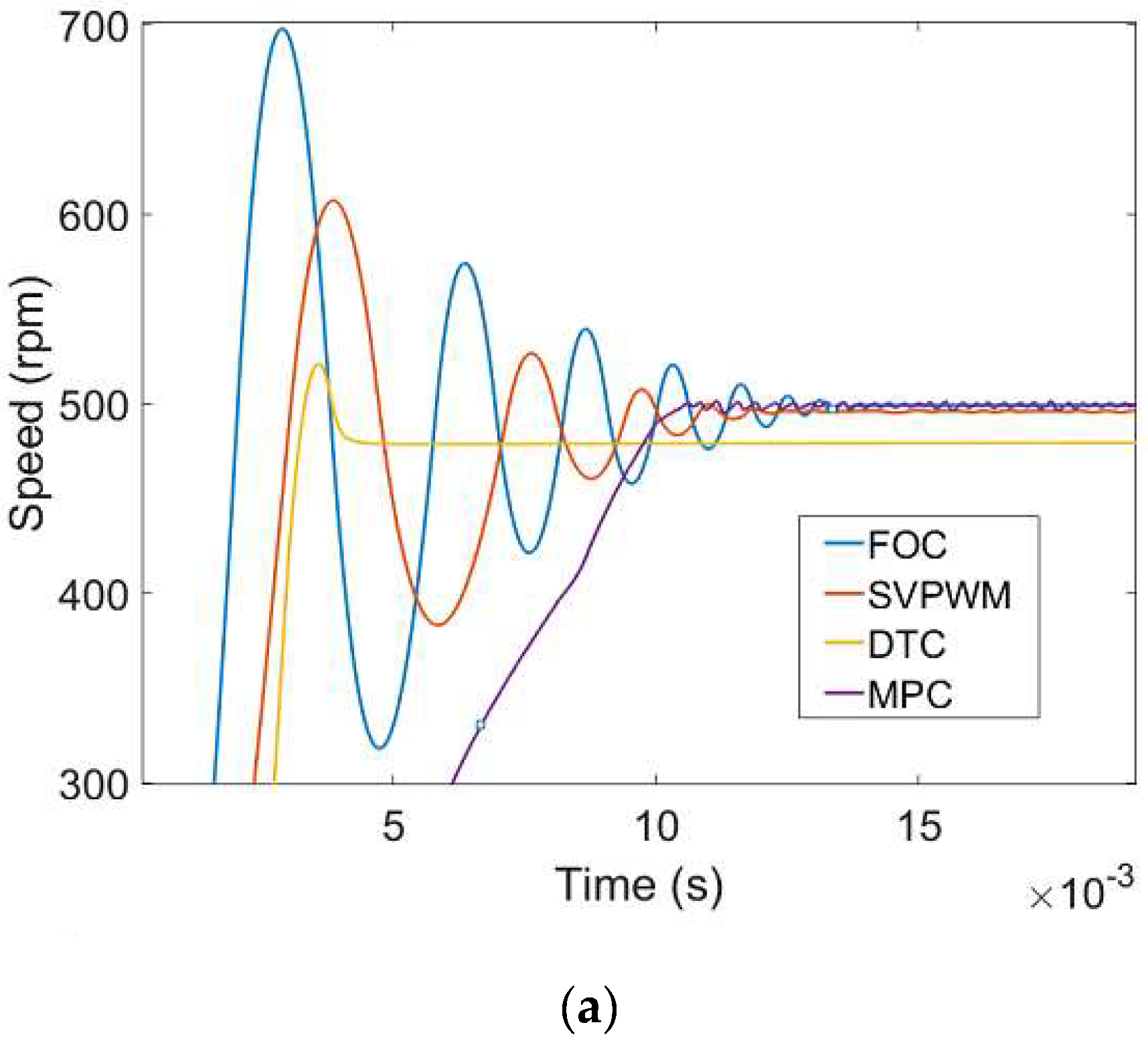
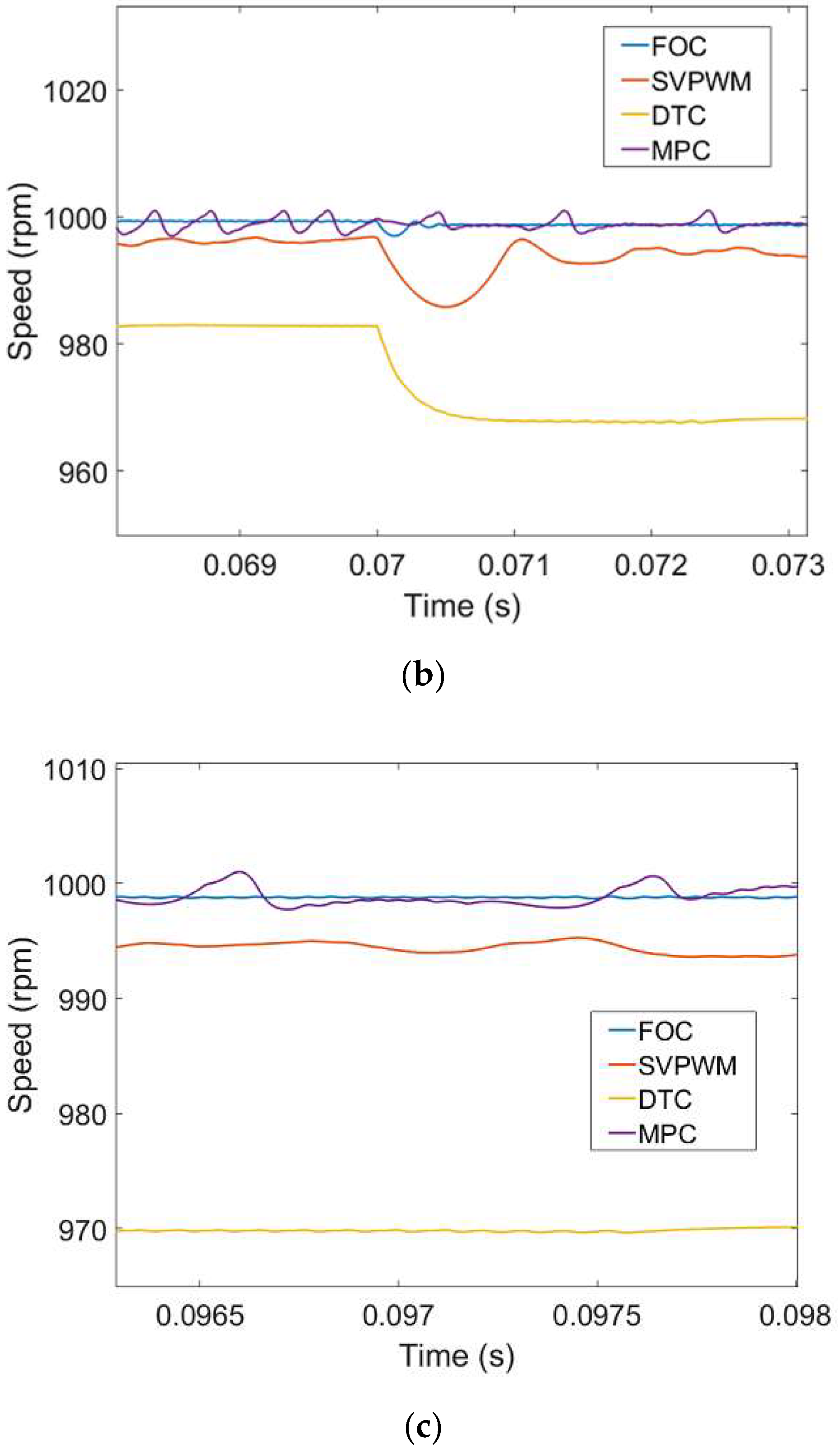
| Specifications | Quantity (SI) |
|---|---|
| Rated power | 500 W |
| Rated current | 8 A |
| Pole number (p) | 8 |
| Length of the stator (l) | 350 mm |
| Number of turns of each coil | 60 |
| Width of the mover plate (w) | 16 mm |
| Height of the mover plate (h) | 16 mm |
| Width of the coil area (c) | 10 mm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, M.; Zhuang, S. On Speed Control of a Permanent Magnet Synchronous Motor with Current Predictive Compensation. Energies 2019, 12, 65. https://doi.org/10.3390/en12010065
Tang M, Zhuang S. On Speed Control of a Permanent Magnet Synchronous Motor with Current Predictive Compensation. Energies. 2019; 12(1):65. https://doi.org/10.3390/en12010065
Chicago/Turabian StyleTang, Meiling, and Shengxian Zhuang. 2019. "On Speed Control of a Permanent Magnet Synchronous Motor with Current Predictive Compensation" Energies 12, no. 1: 65. https://doi.org/10.3390/en12010065
APA StyleTang, M., & Zhuang, S. (2019). On Speed Control of a Permanent Magnet Synchronous Motor with Current Predictive Compensation. Energies, 12(1), 65. https://doi.org/10.3390/en12010065




