1. Introduction
The rapid development of offshore wind farms has been noticed with a trend of continued increasing in turbine size. The favor of larger offshore wind turbines (OWTs) results in decreasing costs of installation and grid connection per unit energy produced [
1]. This comes with new challenges in offshore OWT installation. Single blade installation is a method of OWT blade installation, which allows for a broader range of installation vessels and lower crane capabilities. One blade is lifted in one lifting operation. Passive and active single blade installation methods have been studied [
2,
3,
4,
5,
6,
7].
Typically, the lifting operations are conducted according to pragmatic experiences and short-term weather forecast. The large peak wire rope tension in the initial stages of the lifting and lowering of a payload is risky for safety hazards. Extensive research has been conducted on effective crane and winch control. Various simplified models have been developed to model the crane and payload systems, e.g., Lagrangian models [
8,
9], Newton–Euler equations [
10], and partial differential Equation [
11]. Normally, the axial wire rope elongation is disregarded due to the its high stiffness. The ship-mounted crane systems have more complicated dynamic characteristics, with a higher number of degrees of freedom (DOFs) in the control system. A high-fidelity simulation-verification OWT blade installation model for the control purpose is developed in [
4]. However, the model is unnecessarily complex for design of control laws. The ordinary studied payloads are lumped mass [
12,
13] and distributed mass [
14]. Though wire rope elongation is always neglected in transportation mode, it is an important issue in e.g., heave compensation through a wave zone during moonpool operations [
15,
16,
17,
18,
19].
Model predictive control (MPC) is a widely applied optimal control technology. The MPC controller provides real-time feedback by optimizing the future plant behavior in a finite horizon. Considerable effort has been devoted to improving its robustness and performance [
20,
21,
22,
23,
24,
25]. The performance of the nonlinear model predictive controller (NMPC) depends on the computation interval, initial guess, programming algorithms, etc. The stability can be ensured through a careful selection of designed parameters [
26]. Direct methods transform a continuous system of infinite dimension into a discrete nonlinear programming system of finite dimension. The direct methods can be categorized into sequential and parallel-in-time approaches. Direct single shooting is a sequential approach, with a strong requirement to the initial guess, especially for highly nonlinear systems. However, the shortages of the parallel-in-time approach are the unnecessarily strong nonlinearity of the optimization problem and the poor convergence behaviors to the desired reference trajectory [
27,
28]. Optimization theories have been widely used in marine research [
29,
30,
31]. To effectively solve the programming problem using embedded platforms, automatic code generation is a widely discussed issue. A number of user-friendly codes have been developed, where C++ codes for embedded systems can be generated automatically by several published quadratic programming solvers [
32,
33,
34].
Though efforts have been made to improve the level of automation for blade mating operations [
3,
5,
18,
35,
36], studies are lacking on constrained optimal blade lifting operations from the deck to improve safety and performance. An NMPC framework for lifting a lumped-mass payload was presented by the authors in [
37]. In this paper, we extend the NMPC scheme for a winch servo to reduce the abrupt wire tension load increase and to avoid snap loads resulting from a suspended blade at the initial stages of lift-off (and also lowering) operation. This makes the transfer to the next phase, moving the blade towards the hub safer and more efficient. The main advantages of NMPC are that an optimal control action is achieved, where the performance and efficiency can be targeted by proper tuning of an objective function, while at the same time adhering to constraints that for other methods must be handled through implementation of logics. The lifted blade should reach the desired height in a specified speed abstaining from possible dangers. An optimal control problem is formulated for the lifting process of a blade, with implementation in a well-proven optimization solver. The performance and properties of the method, compared to a standard proportional-derivation (PD) crane lifting control law, are then demonstrated in a simulation study with a high-fidelity numerical model. In [
37], only a simplified lifting system was considered, with a lumped-mass payload and known parameters, whereas wind-induced loads, motor dynamics, hook, and slings were neglected in the simulations. The extensions made in this paper therefore consist of deriving a reduced model for a more realistic blade payload in a lifting control design. Based on this, we design an NMPC controller to solve the formulated constrained optimal lifting problem in a turbulent wind field. Compared to a lumped-mass payload, a blade has more complex dynamics and aerodynamic characteristics. Simulations are finally conducted in turbulent wind fields with different mean wind speeds, as well as varying parametric uncertainties, and the simulation results are discussed.
The paper is structured as follows. In
Section 2, the problem formulation is proposed with a description of the system and an illustrative example. A simplified model of the NMPC controller is introduced in
Section 3. Basic concepts and theories concerning the direct multiple shooting approach are introduced in
Section 4. Simulation results and comparative studies with a proportional-derivative (PD) controller are presented in
Section 5. Finally, conclusions are drawn.
Notation:
and
, respectively, denote the Euclidean vector norm and weighted Euclidean vector norm, i.e.,
and
with
. The vector inequality of
is denoted by
, i.e., component-wise inequalities
hold for
. Overlines and underlines,
,
, stand for vectors containing all the lower and upper limits of the elements in
b, respectively. The saturation operator
is denoted by
2. Problem Formulation
2.1. System Description
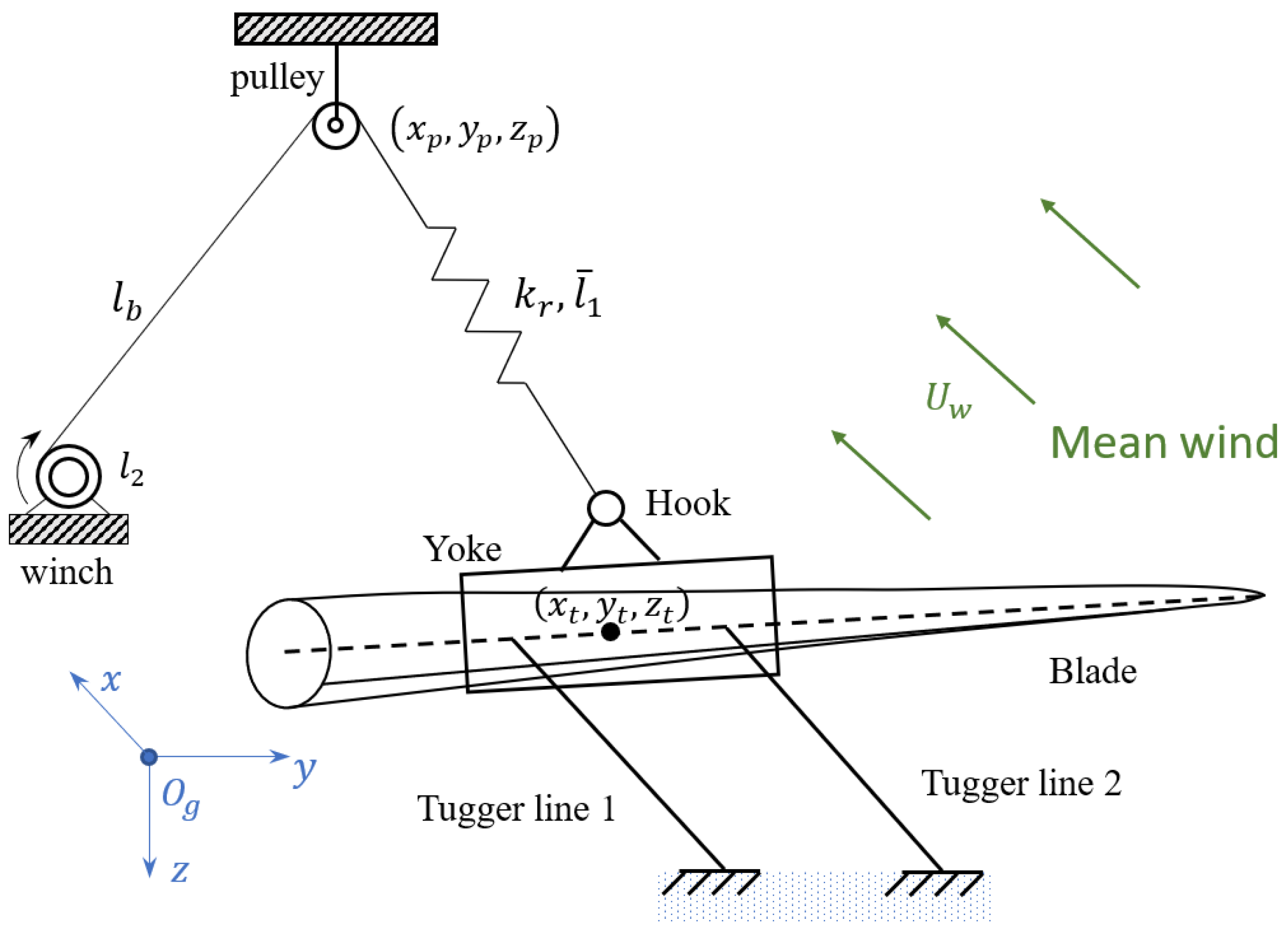
A jackup vessel is considered hereafter for the single blade installation operation. The legs have been lowered into the seafloor and the jack-up vessel has been lifted out of water, which provides a stable platform for lifting operations. The blade lifting operation is conducted by a rigidly fixed boom crane on the vessel. The blade is seized by a yoke through a lift wire and two slings; the configuration is shown in
Figure 1 and
Figure 2. A hook connects the lift wire and two slings. The yoke and crane boom are fastened by two horizontal tugger lines, constraining the blade motion within the horizontal plane due to the wind-induced loads. The lengths of the tugger lines are adjusted with the blade. Active tension force control on the tugger lines, such as [
3], is not considered. The blade is first lifted up from the deck of the jackup or a barge, in which the lift wire gradually takes the gravity of the blade and the wind-induced dynamic loads. The blade is then lifted from a low position up to the hub height. During this phase, the main dynamic loads are the wind loads acting on the blades. If the lifting speed changes, the lift wire experiences the inertial loads on the blade. There are always gravity loads acting on the blade. When the blade is close to the hub height, one may reduce the lifting speed and adjust the position of the blade root for the final connection.
In this paper, we consider a scenario in which the blade starts in the air with a zero lifting speed. The supporting force from the deck is not considered. The lifting speed is increased to the target value and then reduced to zero when it reaches the specific hub height. The payload motion can be estimated by various methods, e.g., GPS and inertial measurement unit (IMU) sensor fusion algorithm and motion capture systems.
2.2. System Modeling
The blade installation simulation framework used is developed in MATLAB and Simulink [
4], in which necessary modules for blade installation are included, e.g., wire rope, suspended blade, hook, winch, and wind turbulence. This approach has been applied to analyze and verify active single blade installation methods [
3].
The hook and blade are modeled in 3DOF and 6DOF, respectively. Lift wires function as single-direction tensile springs that can only provide tension when the axial elongation is greater than zero. A turbulent wind field is generated by the Mann model in HAWC2. Because of the geometric complexity, the wind-induced loads are calculated according to the cross-flow principle. The total wind loads acting on the entire blade are the sum of the lift and drag forces measured at each airfoil segment.
An National Renewable Energy Laboratory (NREL) 5MW wind turbine blade is selected as the payload for a case study [
39]. Due to physical limitations, the winch cannot reach a reference speed infinitely fast, nor exceed the designated safe speed. Hence, we assume the occurrence of saturation for both winch acceleration and winch speed. The main system parameters used are tabulated in
Table 1.
A local Earth-fixed, assumed inertial, reference frame is adopted with the x-, y-, and z-axes pointing in northern, eastern, and downward (NED) directions, respectively. Translational velocities measured along the axes are denoted , , and . The orientations about the fixed axes are given by roll, pitch, and yaw angles, denoted , , and , respectively.
2.3. Case Study
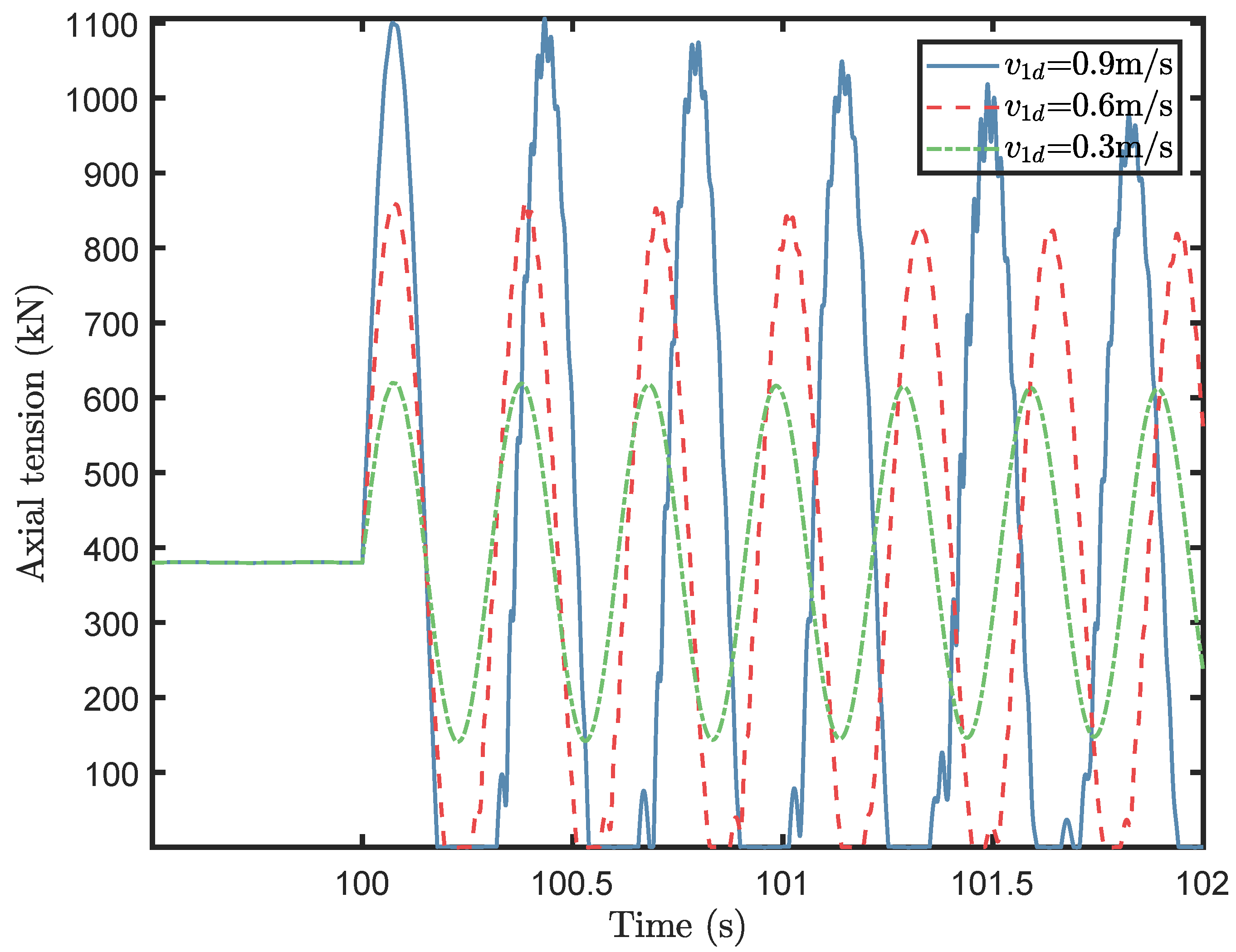
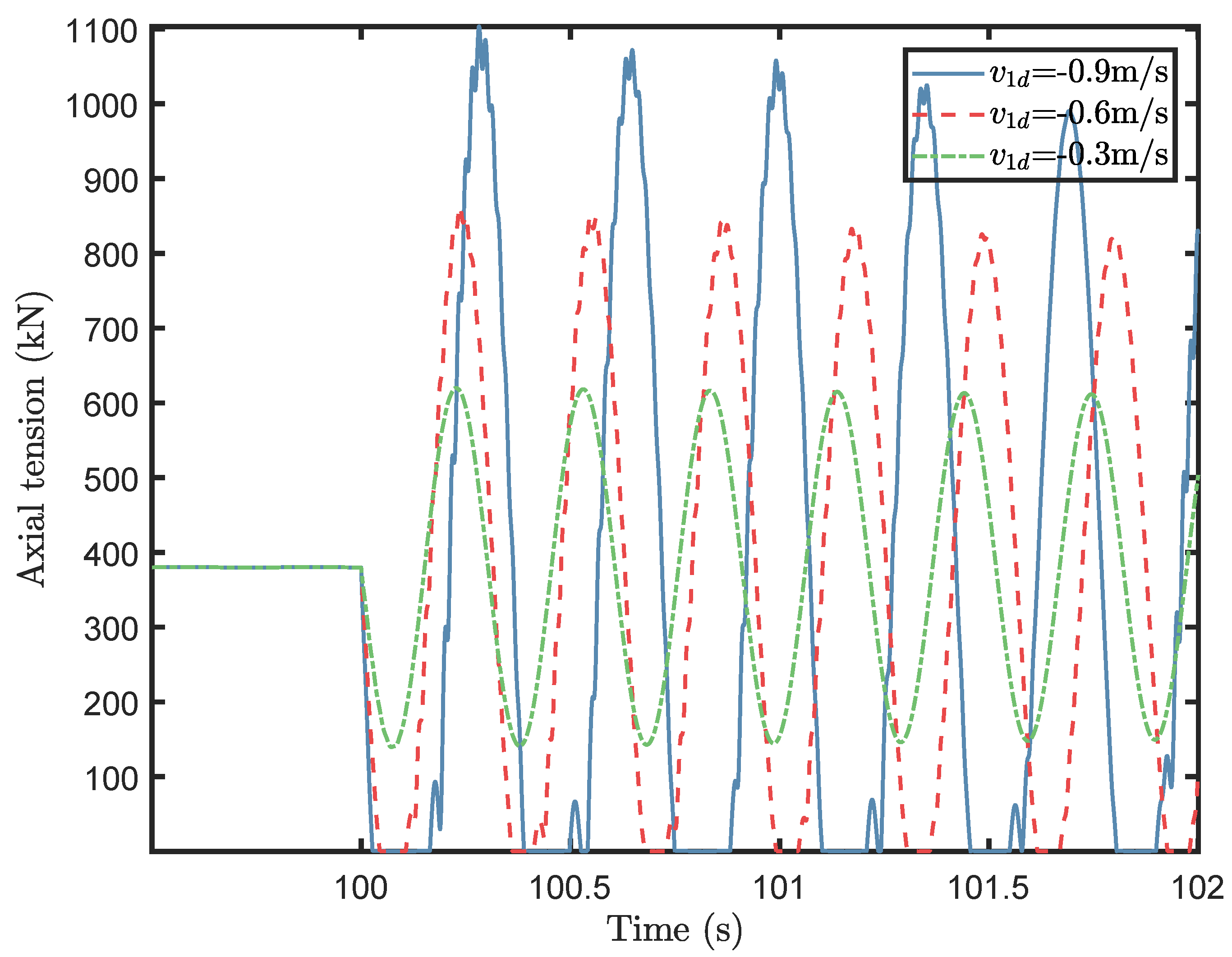
Since the blade is lifted off at a low level where the wind speed is low and the lift-off operation happens in a short duration of a few seconds, we consider a blade lift without aerodynamic loads. At the start of the simulation, the suspended blade is stabilized at an equilibrium point by the lift wire, slings, and tugger lines without oscillation in the lift wire. When a sudden lifting or lowering action is executed at 100 s, the lifting speed is changed to the constant desired speed
in a very short time. The wire tension history is shown in
Figure 3 and
Figure 4 for lifting and lowering, respectively.
In the figures, the only changing parameter is the setpoint lifting speed. It is observed that snap loads or sudden peak tensions are excited in the first 0.5 s, followed by the occurrence of damped oscillations due to the axial damping. The larger sudden tension occurs at the beginning of the lifting operation due to significant winch speed acceleration. The magnitude of the dynamic tension increases with the lifting speed.
In the tension history curves, there are some high-frequency peaks of minor amplitude, which are induced by the slings. The tension deviation caused by the blade’s motion in the horizontal plane is very small compared to the peak values. The amplitude of the oscillation decreases slowly.
Jerking occurs more easily at a higher lifting speed. A sudden tension maximum is dangerous. Snap loads, which occur when the axial tension decreases to below zero, are induced during this lifting operation. The maximum tension, on the other hand, may exceed the lift wire strength. Thus, the minimum value for the axial elongation of the wire should always be non-negative. The restoring force does not act on the payload due to the negative axial elongation when snap occurs. Furthermore, the magnitude of the blade motion is enlarged when snap loads occur, resulting in a potential impact damage between the blade and deck.
In practice, the lifting speed should be changed gradually from 0 to the setpoint speed to prevent the zero tension in the lift wire. In this paper, we show how constrained optimization conveniently can be designed to achieve this while simultaneously satisfying relevant constraints in the control system.
2.4. Problem Statement
The objective is to design a safe and efficient lifting scheme using constrained optimal control to achieve the necessary lifting performance. In more detail, there are seven optimal targets:
- (a)
Reach the desired setpoint lifting speed from zero speed in the shortest time possible within the constraints,
- (b)
Protect overload tension and reduce dynamic tension by controlling the winch speed,
- (c)
Prevent winch servo motor burnout by limiting the winch acceleration,
- (d)
Prevent negative elongation and snap loads,
- (e)
Reduce the wire rope wear,
- (f)
Limit the maximum speed of the servo motor,
- (g)
Reach the desired wire rope length.
The tugger lines are assumed to be released with the lifting operation. Therefore, tugger lines do not provide restoring forces unless wind-induced blade displacement is higher than expected. We assume that the blade orientation variance caused by the lifting operation and the wind-induced load is insignificant, and the lifting or lowering operation is so short that wind-induced motion is not affected.
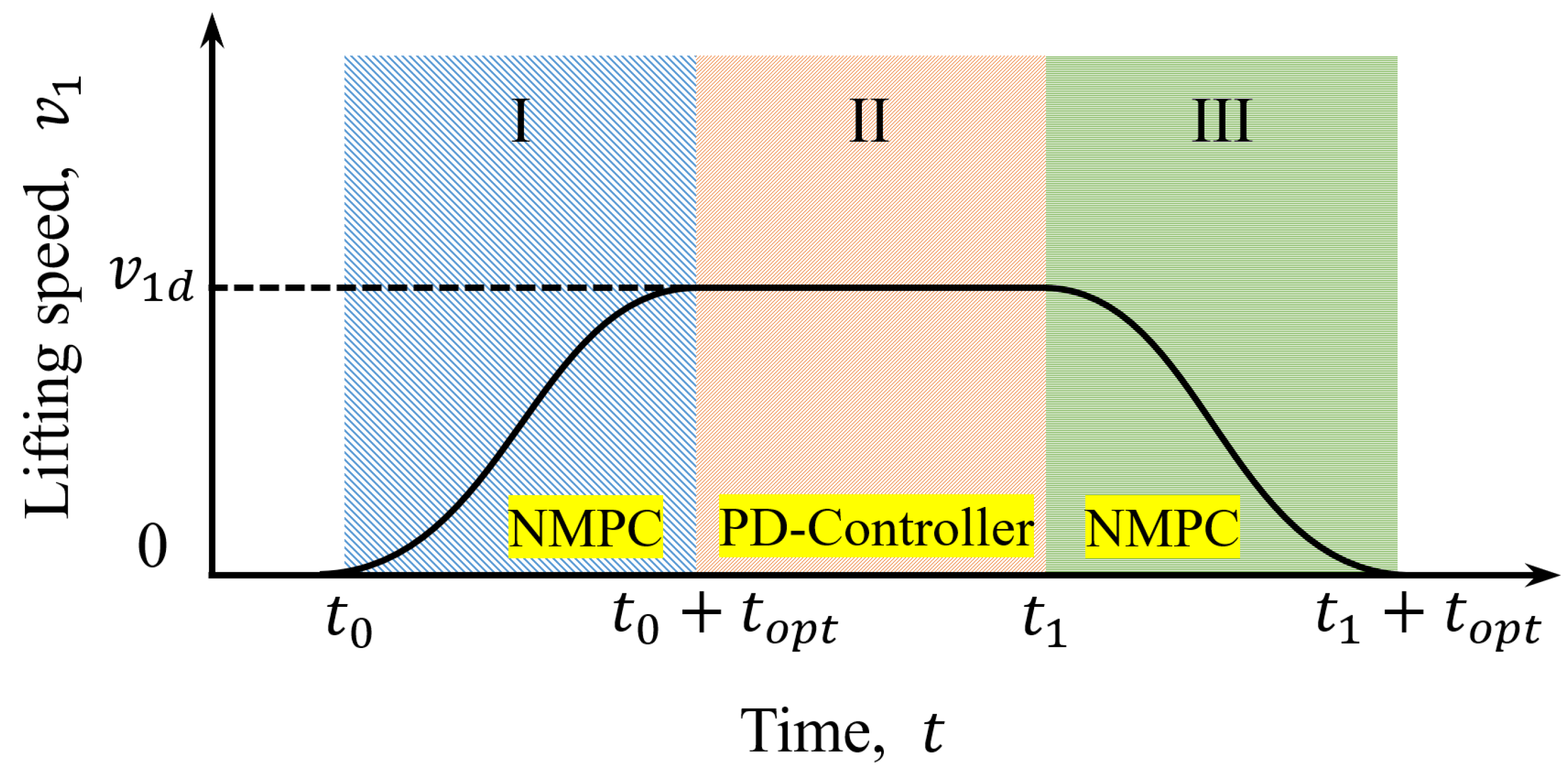
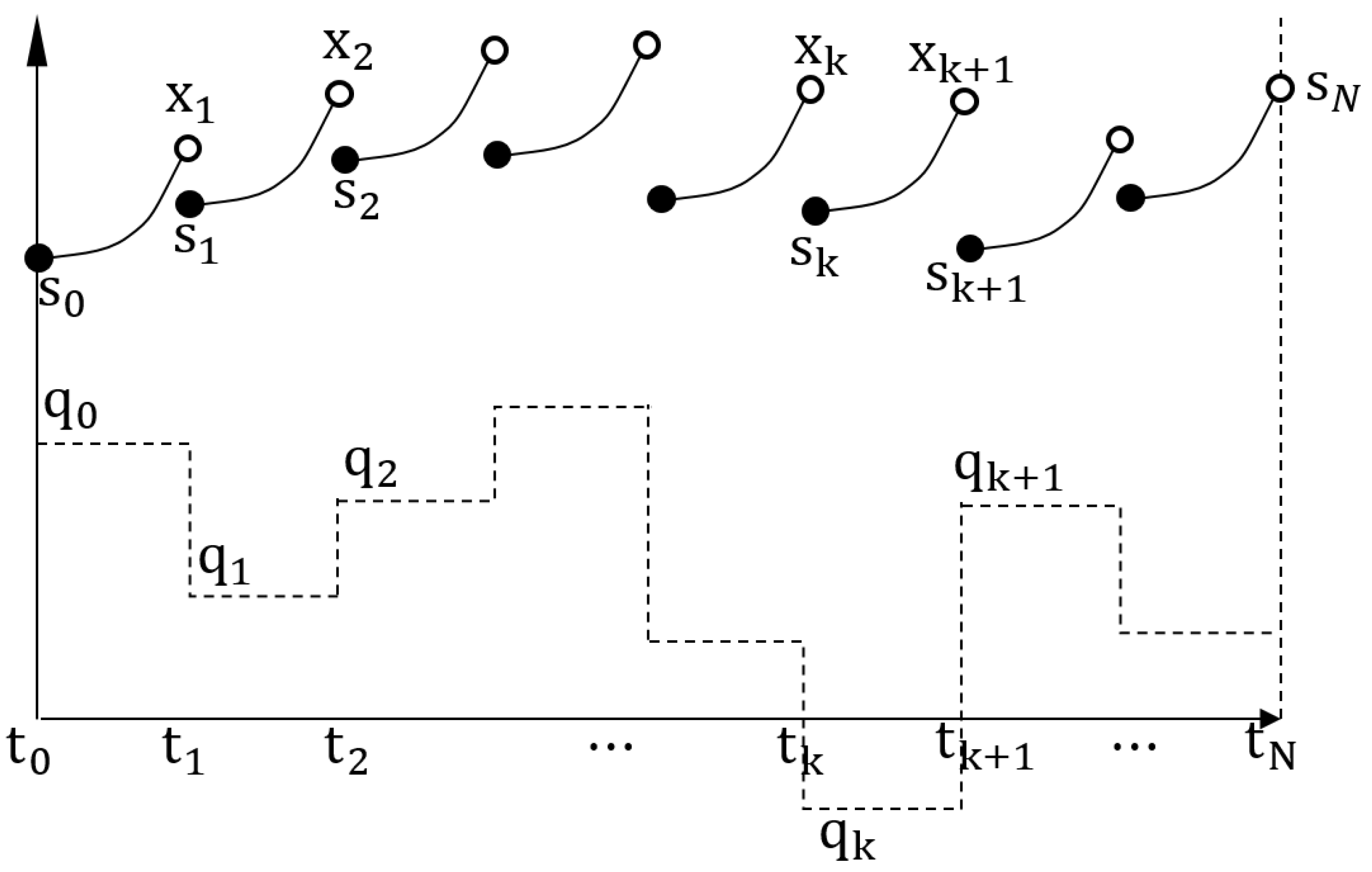
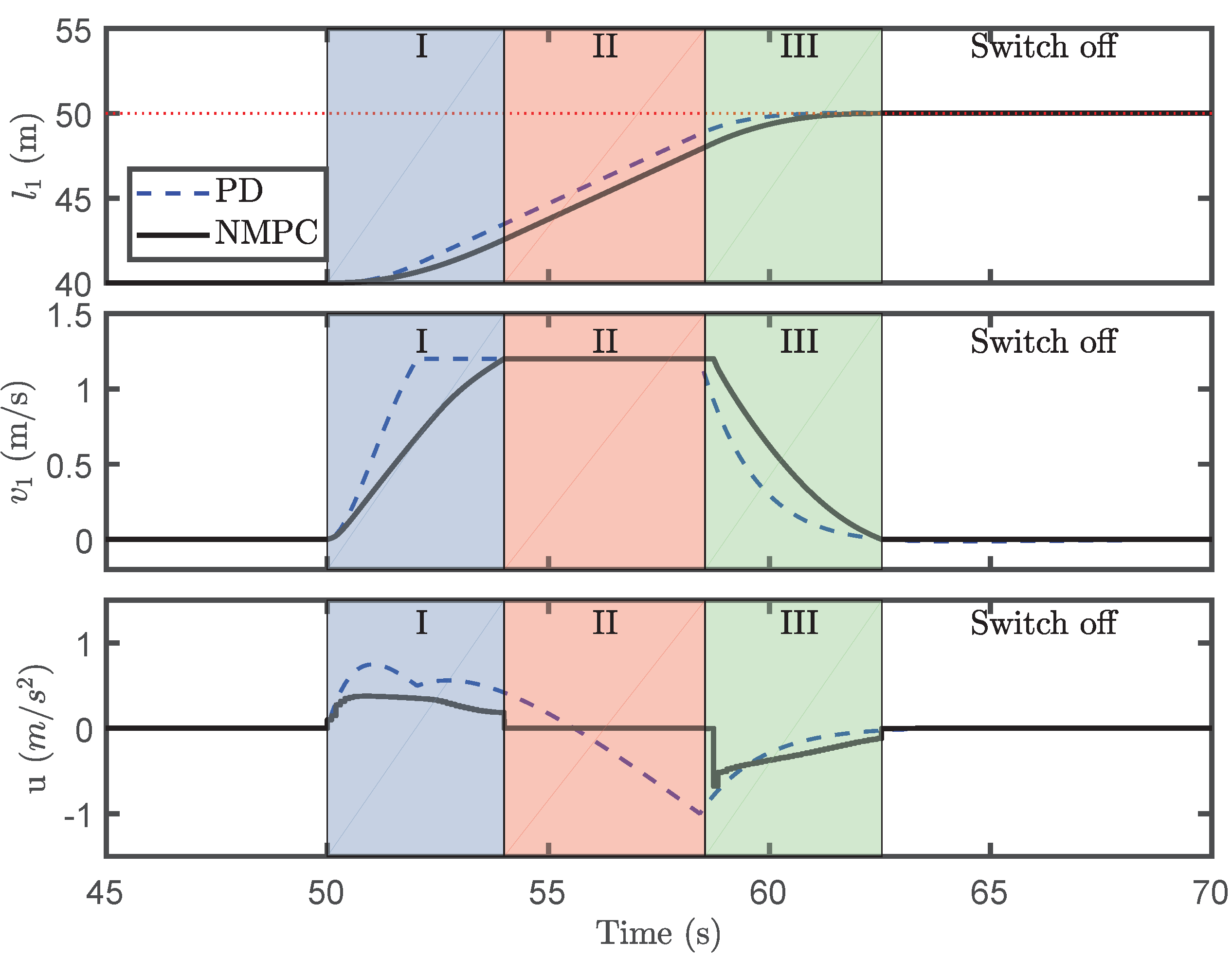
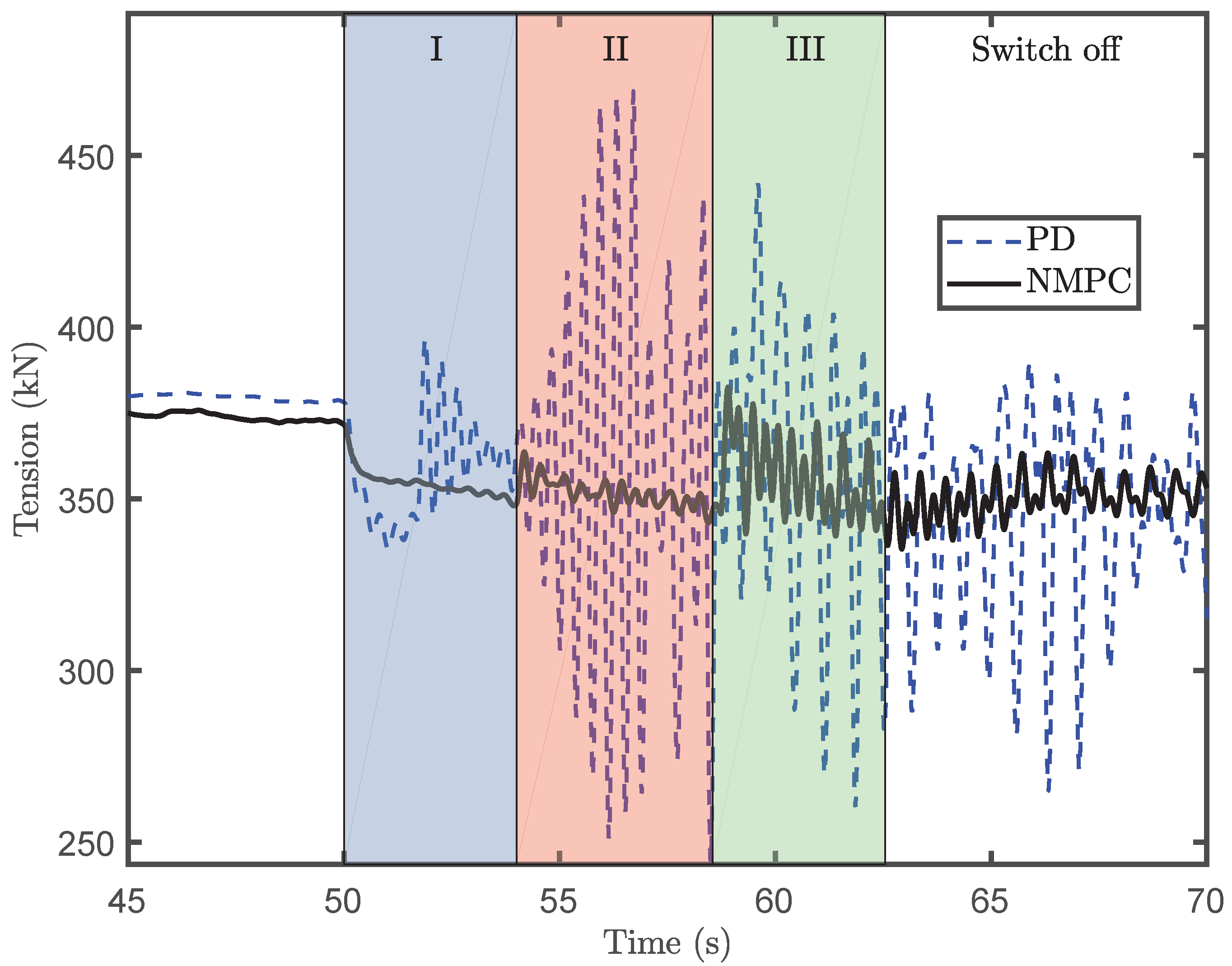
A lifting process is divided into three phases: the startup region, the steady region, and the slowdown region; see
Figure 5. The control objective of each region is tabulated in
Table 2. Region I denotes the startup stage, wherein the payload speeds up to the desired lifting speed
from initial winch speed
. Sudden overloads or snap loads mainly occur at the beginning of Region I. In Region II, spanning from the end of the startup stage to the outset of the slowdown stage, a steady motion is performed. The purpose of this stage is to ensure the desired lifting speed, i.e.,
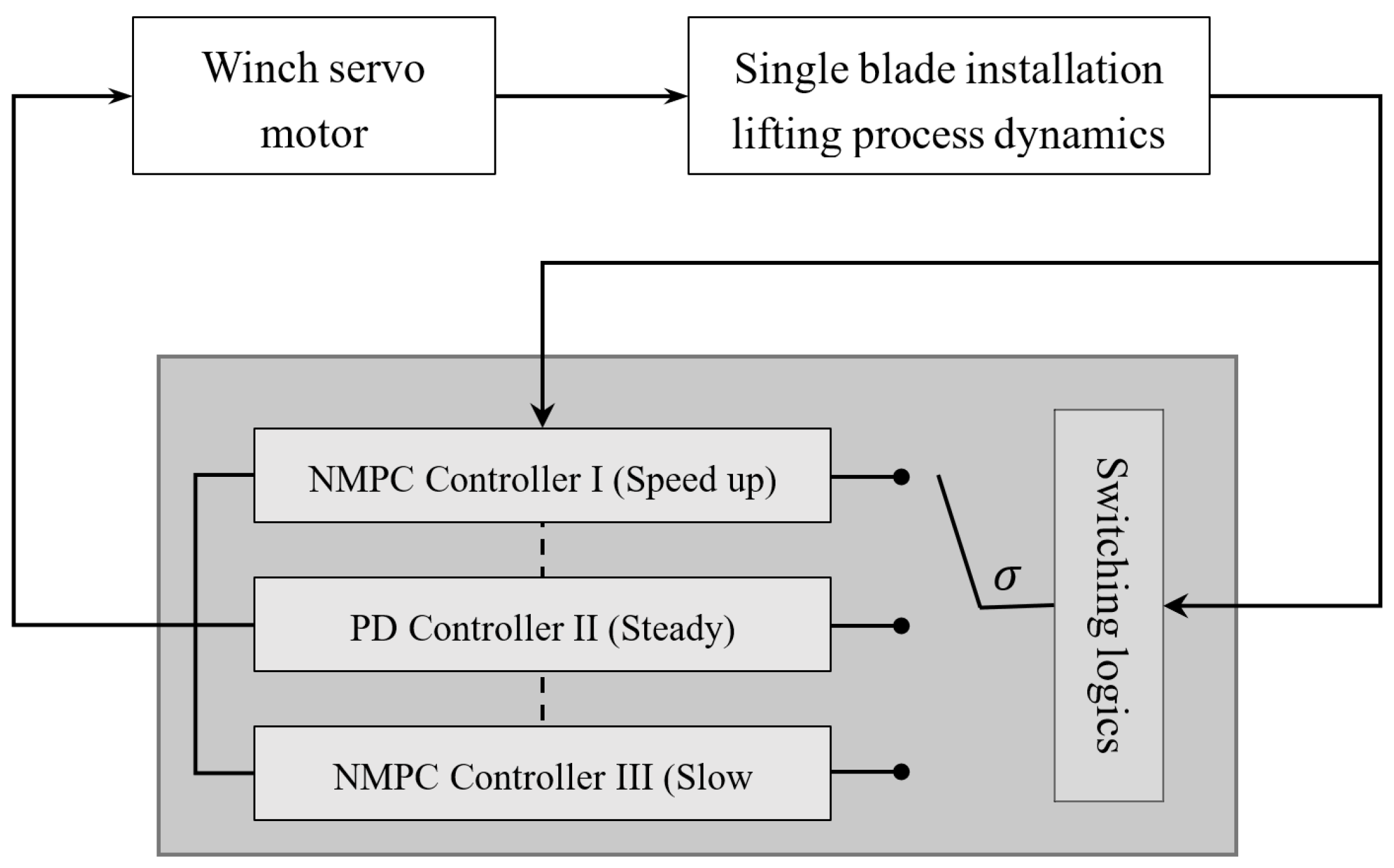
. The controller should be deactivated during this stage due to the low dynamic tension. Instead, a simple proportional controller is used in this phase for its simplicity. Region III is the slowdown stage, where the controller is again activated. The lifting speed should be reduced to zero. Dynamic tension mainly occurs in the initial period. In addition to all requirements for Region I, the desired wire rope length should be achieved. The controller is switched off at the end of Region III.
3. Reduced Model for Control Design
A reduced model is adopted for the optimization problem in a three-dimensional north–east–down (NED) coordinate system [
40]. The crane is assumed to be rigidly fixed on the vessel. The masses of the hook, yoke, and blade are
,
, and
, respectively. We assume that the overall payload mass
is concentrated at the blade center of gravity (COG), where
. Furthermore, the lift wire and slings are considered as one unit without the consideration of the lift wire control; it provides a restoring force on the moving blade. We assume that the ropes are replaced by a lightweight rope, i.e., its mass is assumed to be zero. The blade COG is suspended by the rope, which is connected to the winch through a pulley fixed at the crane tip. Hence, a tensile spring is employed to model the wire rope. The unstretched length of the spring
denotes the distance between the pulley and blade COG. Tugger lines are released at a speed such that only vertical lifting is allowed. Because the lifting operation is executed over a short period, the horizontal wind-induced load is assumed to be restrained by tugger lines and can be disregarded. A 3DOF lifting model, with an elastic wire rope and a controllable winch, is deduced based on the Newton–Euler method in the NED coordinate system. Four vectors are defined correspondingly:
The total force acting on the payload is given by
where the mass matrix is written as
,
G,
,
are the gravity, restoring force, and damping force, respectively. If the lifting speed changes quickly, the main reason for the large dynamic tension is from the lifting wire. Then, the blade wind loads could be considered as quasi-static loads. Hence, the controller is not developed to compensate the dynamic tension due to the disturbance in wind.
3.1. Restoring Force
Additional two vectors are defined to shorten the equations. The relative position vector from the pulley to payload
and its time derivative
are respectively defined as
The restoring force of the lift wire
reacts with positive wire rope axial elongation, i.e.,
where
denotes the restoring action coefficient,
is the elastic elongation, and
is the stiffness. Determined by the material, diameter, and strand construction, the generalized stiffness of the rope is modeled as
where
is the modified coefficient of a stranded wire,
E stands for the Young’s modulus,
denotes the cross-sectional area of the rope, and
, where we assume that the length of rope between the winch and pulley
is constant.
3.2. Damping
The wire rope has a small damping ratio, generally selected as
–
of the critical damping value [
41]. Hence, the damping force
is given by
where
:
denotes the wire length changing rate,
is the damping coefficient, and the elongation changing rate
is given by
3.3. Winch Servo Motor
A variable-speed DC motor with motion feedback control is used as the winch servo motor to follow the specific motion trajectory. The field voltage is employed as an input for the DC motor. The produced magnetic torque
is proportional to the armature current
, given by
where
is the motor constant,
is the load torque, and
is the disturbance torque. The transfer function between
and the field voltage
is given by
where
and
are the armature resistance and inductance. The transfer function between the winch servo motor acceleration,
, and
is given by
where
is the radius of the winch,
is the moment of inertial, and
denotes the viscous friction coefficient. The low-level servo motor speed and torque control is not discussed in this paper. We assume that the field-current-controlled motor can effectively track the signal
u generated from the proposed controller.
3.4. Model Summary
Under the aforementioned assumptions, disregarding wind-induced loads and substituting Equations (
4) and (
6) into Newton’s second law (
2), the simplified control design model for the considered blade lifting operation is produced,
where
, with
, and
is gravity. The nonlinearity of the differential Equation (11) mainly derives from the function
.
5. Simulations and Results
5.1. Simulation Overview
The simulations are conducted in MATLAB. The structural parameters used are tabulated in
Table 1. The limits of the winch loads are considered to be expressed by the maximum acceleration. The wind field with turbulence starts acting on the blade with a ramp over the first five seconds. Class C turbulent winds with corresponding turbulence intensity (
) are adopted in the simulations [
49]. CaSADi and MarIn toolboxes are used to solve the NLP problems. The
ipopt solver is adopted.
The simulation scenario involves lowering a suspended NREL 5 MW wind turbine blade 10 m. The initial wire length is m, the final desired length is m, and the final desired lifting speed is m/s. The control horizon is s with 40 subintervals. The following parameters are used for the different regions:
- (a)
Region I: Start a lifting with an initial wire length and initial speed, and reach a desired speed in :
- (b)
Region II: Stabilize the lifting speed to the desired value:
- (c)
Region III: Stop the lifting operation with the following initial speed, and reach the desired lift wire length in :
Tugger lines are released with a speed of
, i.e.,
where subscript
i is the index of the tugger line,
is the vertical position of the tugger line connection point to the crane boom, and
is the length of the tugger line.
5.2. Basic PD Controller
To compare the NMPC controller performance, PD controllers are used. These open-loop controllers accelerate the winch servo motor to the desired speed. Due to physical limitations of the actuator (winch servo motor), saturation modules are applied to bound the lifting acceleration and velocity. A lowpass filter is used as a reference model. In summary, the combination of the lowpass filter and PD controller is given by
where
and
denote the final reference and desired trajectory for the lift wire length,
is the relative damping ratio, and
is the natural frequency. Select
to ensure critical damping. Different
values are assigned to different regions. In Region II,
can be smaller than
in Regions I and III. In the simulation,
in Region I and III and
in Region II.
5.3. Comparative Simulation Results
By well-tuned weighting matrices, the simulation results are illustrated in
Figure 10,
Figure 11,
Figure 12,
Figure 13 and
Figure 14. In the simulations,
is used in the NMPC controller. Each bar presents the mean value of five simulations with different turbulence seeds.
Note that this is not an accurate value because the overall stiffness is influenced by the slings. The simulations feature a difficult scenario with a short Region II. Typically, the Region II operation can be much longer than five seconds, so that the transient effect in the lifting wire tension may die out. Hence, the maximum dynamic tension in the results simulated here may be higher than those with a longer Region II. The controller is switched off at the end of Region III.
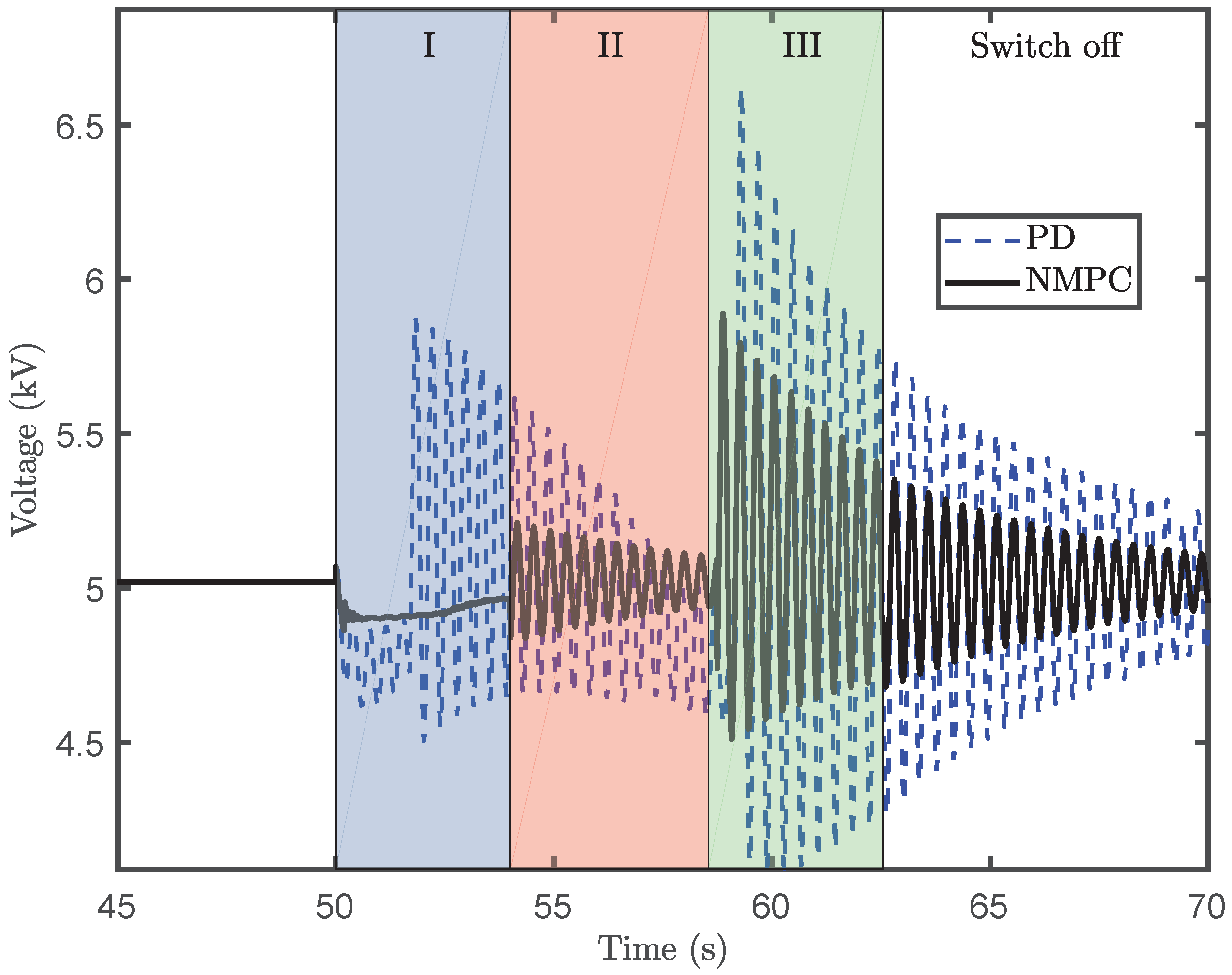
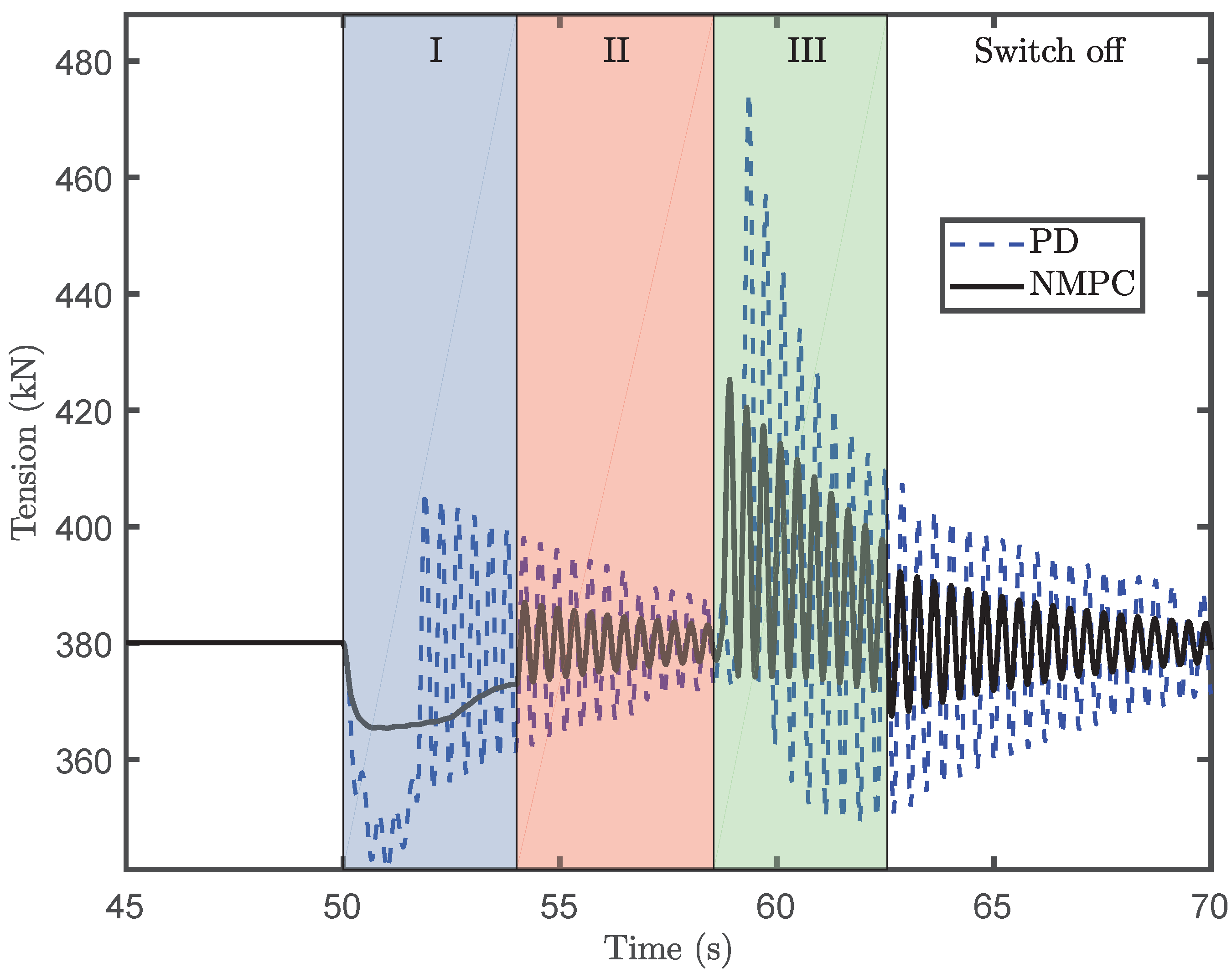
Both the PD controller and NMPC controller are successful at lifting the payload to the desired position at the required speed. However, much less dynamic tension is generated by the NMPC controller than by the PD controller. The PD controller generates a smoother control input profile that is unable to cancel out the axial oscillation. The lift natural frequency of the wire tension is the same for both simulations. Because the NMPC controller significantly reduces the tension on the lift wire, the amplitude oscillation of the servo motor field voltage input is much lower for the NMPC scheme.
Before the start of the lifting operation, the blade is stabilized by the tugger lines, and the tension oscillation is not remarkable. In Region I, the NMPC controller eliminates most of the oscillation. In Region II, the tension oscillation is caused by interactions between the wind-induced load and the tugger lines. However, the tension oscillation is acceptable in this region. Although the axial tension is not perfectly canceled out in Region III, the NMPC controller performs better than the PD controller. Due to the small wire rope damping ratio, the dynamic tension continues to oscillate after reaching the desired lifting speed. Additionally, because of the higher wind loads, the magnitude of the tension oscillation after the end of the lifting operation increases with higher mean wind speed. It is evident that the amplitude of oscillation is effectively reduced by the proposed NMPC scheme.
The NMPC approach exhibits a superior capacity to regulate the dynamic oscillation, compared to the PD controller. Thus, the NMPC algorithm succeeds to limit winch wear. However, its performance can be further improved, as shown in [
37] owing to the simplification of the reduced model.
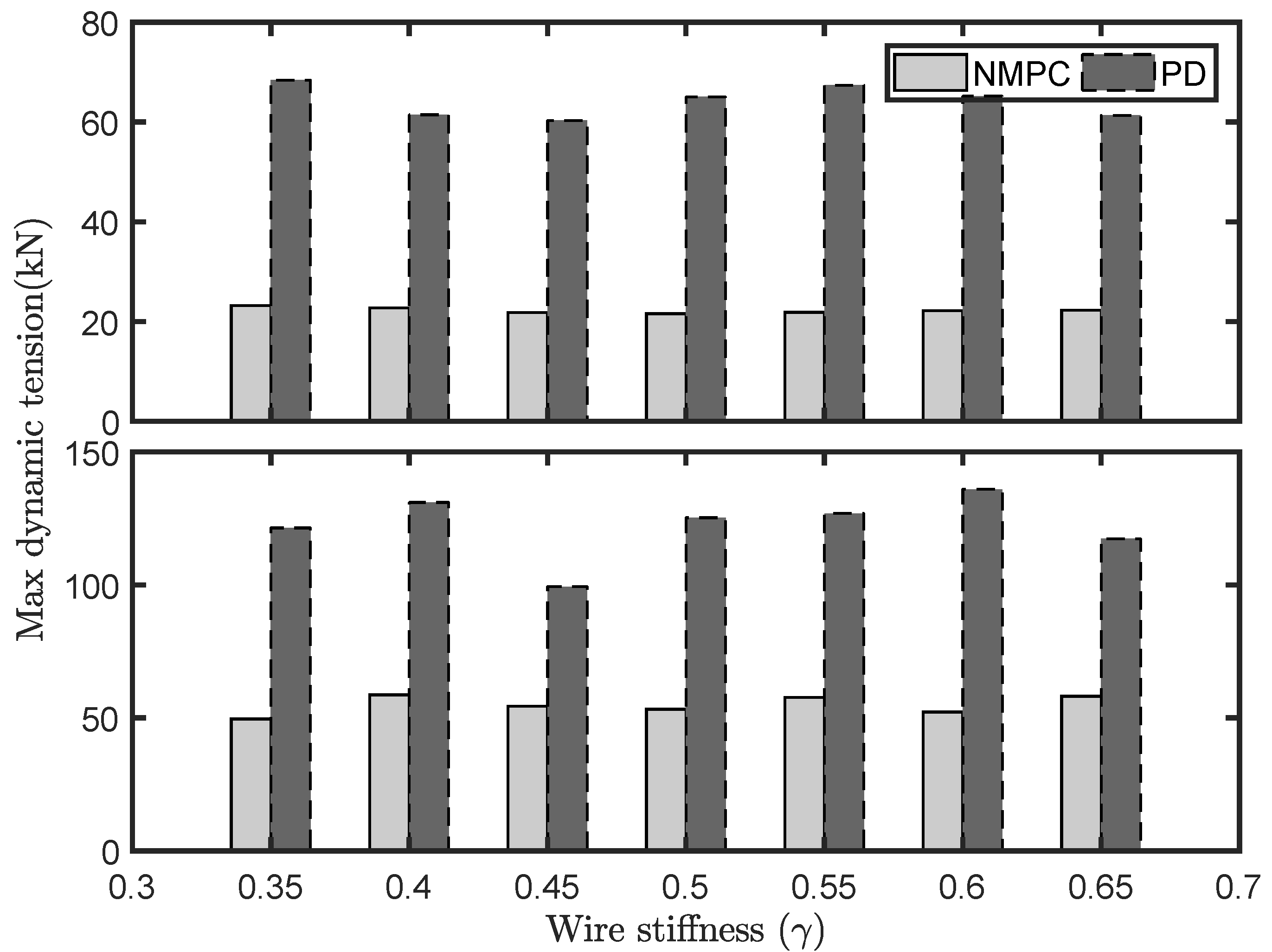
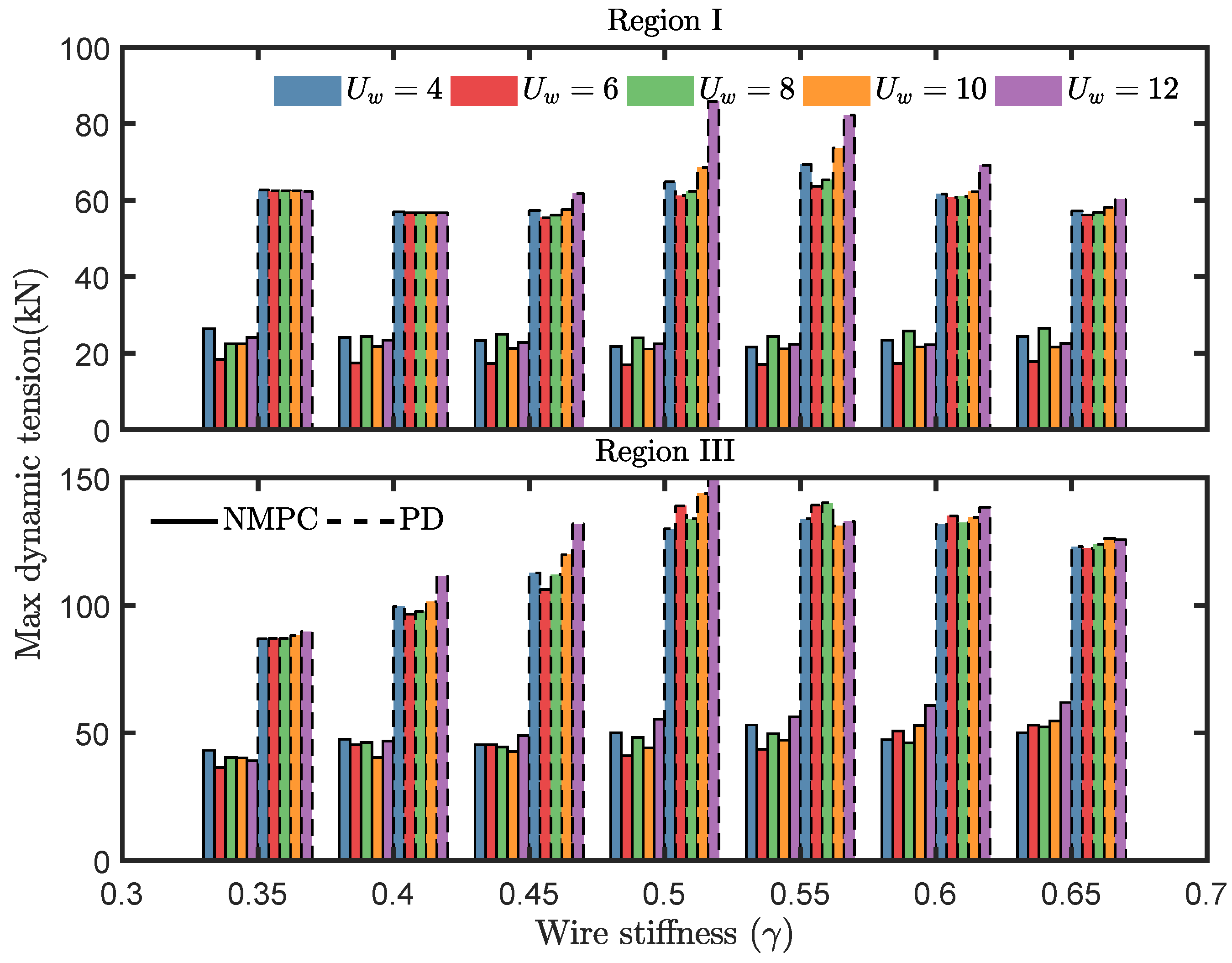
5.4. Robustness Test of the Algorithm
The performance of an NMPC controller is determined by the fidelity of the selected control design model. In our case, the most uncertain parameters are the lift wire stiffness and the neglected wind speed. The effects of model uncertainty matter, as the lift wire stiffness is estimated. Hence, a series of simulations are conducted to test their influence to the controller performance. The wire stiffness is changed by
, while the
of the NMPC controller remains set at
. The mean wind speed is used as a variable in the simulation, ranges from 4–12 m/s. The corresponding results are presented in
Figure 15 and
Figure 16.
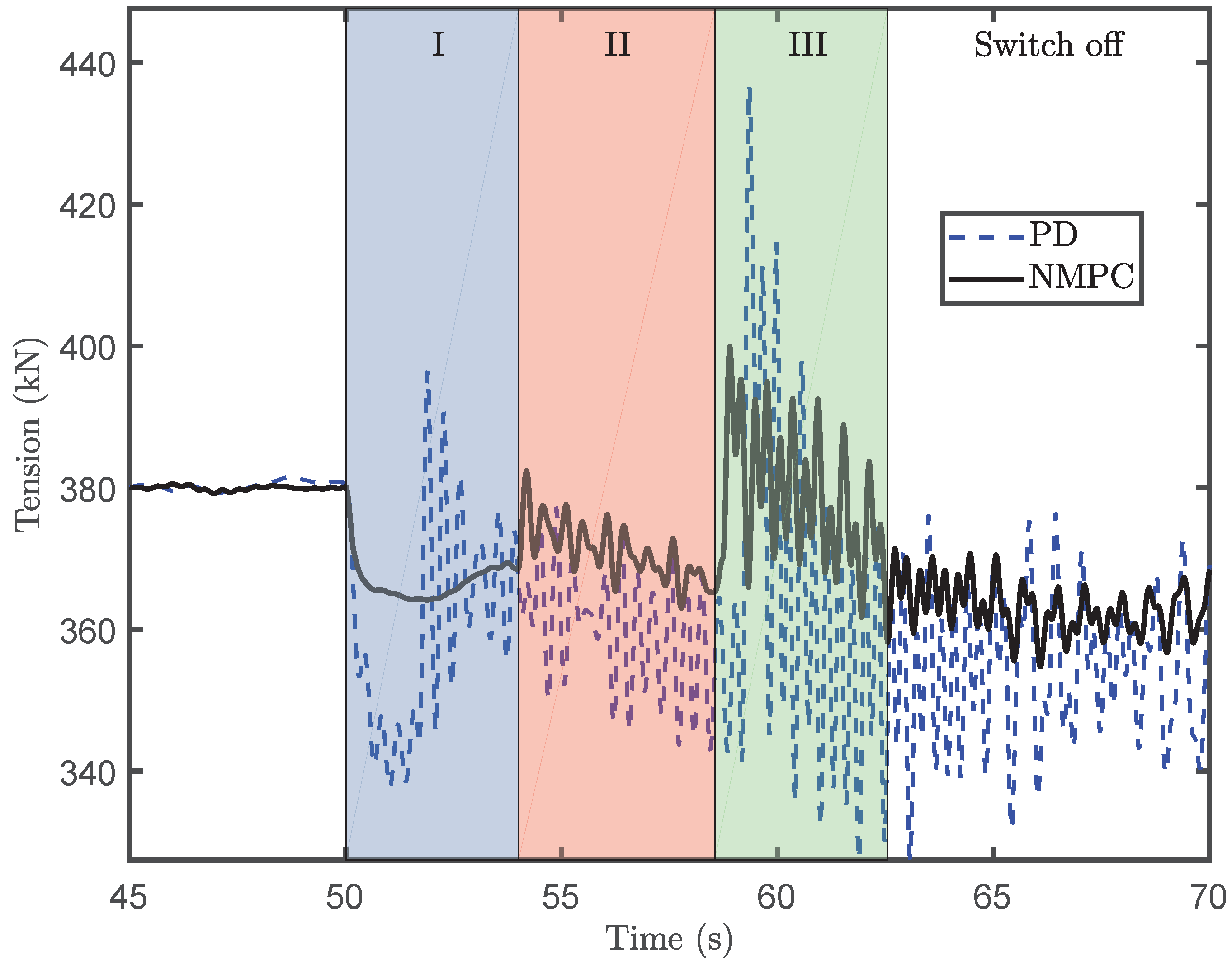
In
Figure 15, we see that the dynamic tension caused by the NMPC controller is almost less than 40% of those resulting from the PD controller. The NMPC controller significantly reduces the dynamic tension at the start and end of a lifting operation, even when the stiffness is not well known. In
Figure 16, the performance variation of the PD controller resulted from the increasing stiffness uncertainty increasing significantly, while the performance variation of the NMPC controller is small under the same uncertainties. The mean wind speed does not weaken the NMPC performance, since the mean wind speed does not seem to influence the wire tension considerably. Wind loads are compensated by the tugger lines. Therefore, the robustness of the proposed NMPC law is satisfactory.
5.5. Discussion
We found that the NMPC performance deteriorates with a large sampling interval. In this case, the sampling rate does not satisfy the Nyquist–Shannon sampling theorem if the interval is greater than twice the natural period of the axial oscillation (approximately 0.4 s), i.e., discrete measurements do not approximate the underlying continuous responses. Using shorter sampling and control intervals, not surprisingly, the performance of the control scheme is significantly improved, resulting in more subtle control. Nonetheless, the computation speed depends on the computational capabilities of the measurement and embedded systems. Hence, a trade-off must be made between hardware capabilities and control performance. In the simulation results, we have chosen the sampling period as 0.1 s for this trade-off. The variance in results observed at various lengths of time horizons is limited, as several axial oscillation periods exist in the selected optimal horizon. Therefore, several tension oscillation periods occur over an optimization horizon.
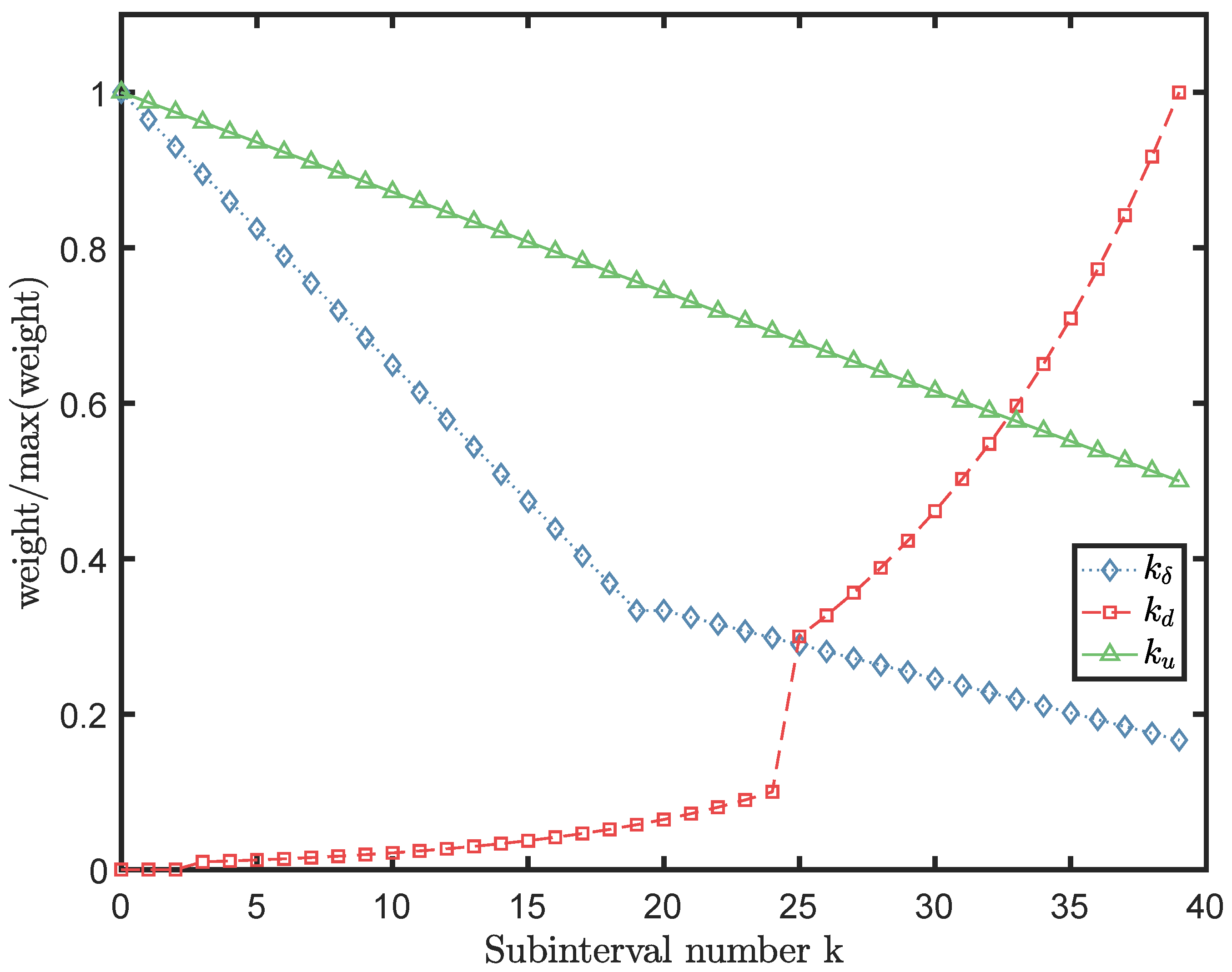
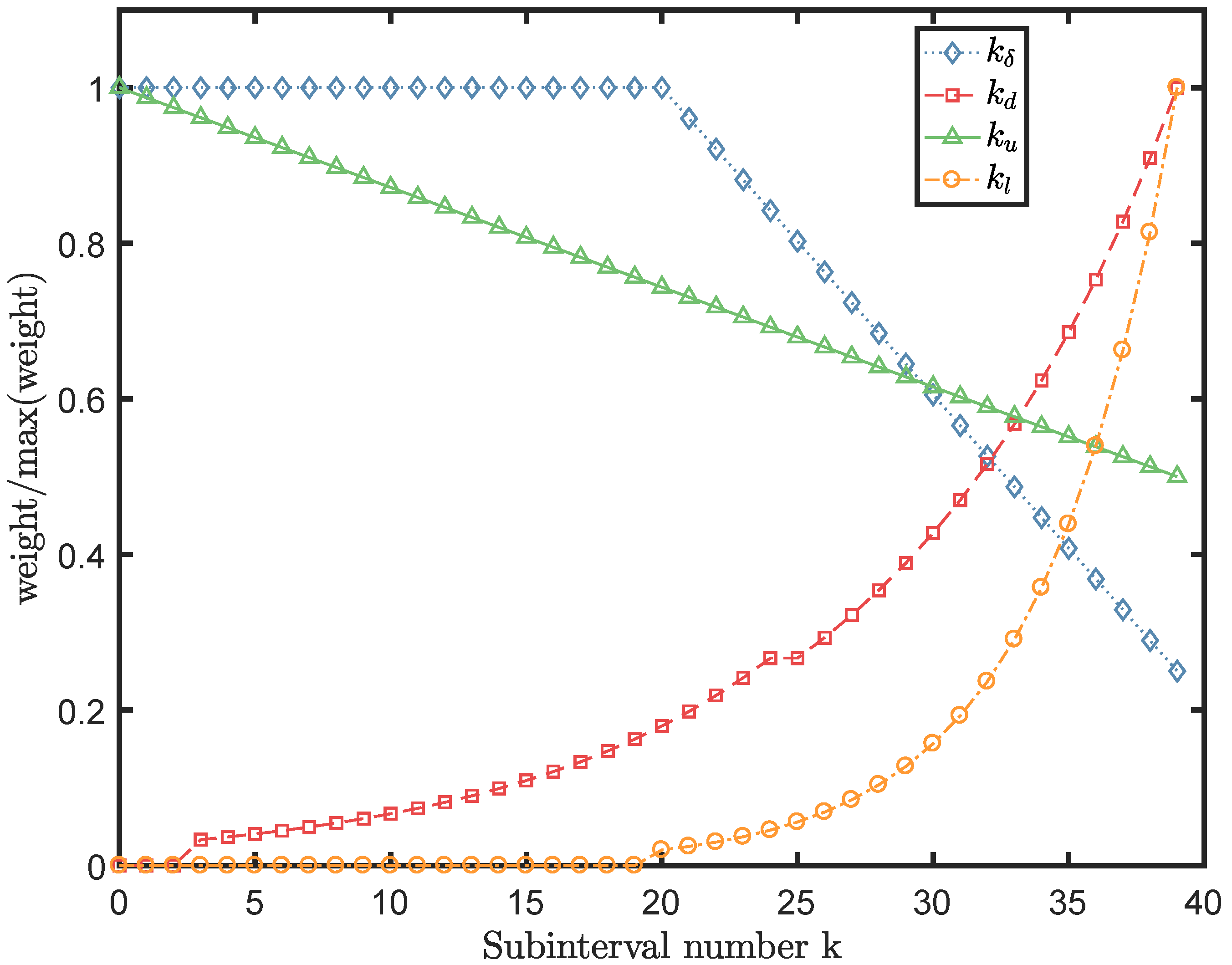
The control effort is determined by the weight matrices in the cost functions. The weights in the Mayer term is more important than the weight values for the end step, since the latter only determines one value among
values of the sum operator. The final performance could be prioritized by enhancing it. The running time for the direct multiple shooting approach is longer than that of the direct single shooting approach due to much fewer Karush–Kuhn–Tucker (KKT) conditions involved in the single shooting approach [
50]. On the other hand, its application is limited by the strong dependence on the initial guess.
6. Conclusions
An NMPC algorithm is proposed as a mean for efficient and safe lifting operations of a wind turbine blade, by limiting sudden overloads and snatch loads. The simplified model for control design is derived using the Newton–Euler approach. The proposed algorithm has a simple structure. According to the comparative study results, the proposed controller successfully prevents the sudden peak tension, tension dynamics, and the axial oscillation. The NMPC controller still performs well when the lift wire stiffness is poorly estimated or the suspended blade is exposed to a turbulent wind field.
To further improve the system performance when exposed to higher wind speed and model uncertainties, the further research emphasis is on adaptive and robust optimal control schemes, e.g., tube-based model predictive control. In addition, NMPC applications to the blade lifting operation using a floating installation vessel for deep water installation will be investigated.