A Two-Step Framework for Energy Local Area Network Scheduling Problem with Electric Vehicles Based on Global–Local Optimization Method
Abstract
1. Introduction
- The application of EVs as VES devices is helpful to reduce the renewable energy volatility in the ELANs and the operating cost. However, the uncertainties of EVs’ charging demand may lead to unavailability of the scheduling plans, which may decrease the utilization efficiency of the renewable energy and the reliability of the ELAN.
- Currently, most scheduling strategies of the ELANs in both industry and academia are designed using forecast data, and the day-ahead dispatch approaches are usually proposed based on global optimization. The goal of global optimization is to find the maximum income of ELAN by formulating a scheduling strategy. If the forecast data utilized is accurate, it is evident that the global optimization method is more efficient than a local optimization one, since it can take all the factors into account from the time dimension, such as the power balance constraints and energy storage state constraints mentioned in this paper. However, the day-ahead forecast data cannot always be exactly the same as the practical data. Therefore, the online local optimization is introduced by some researchers to minimize the income in the current time interval. However, the online local optimization method can only obtain a local optimum solution, which may not consider the effects of the current strategy on the next time intervals. Hence, the total income will not be better than the one by global optimization.
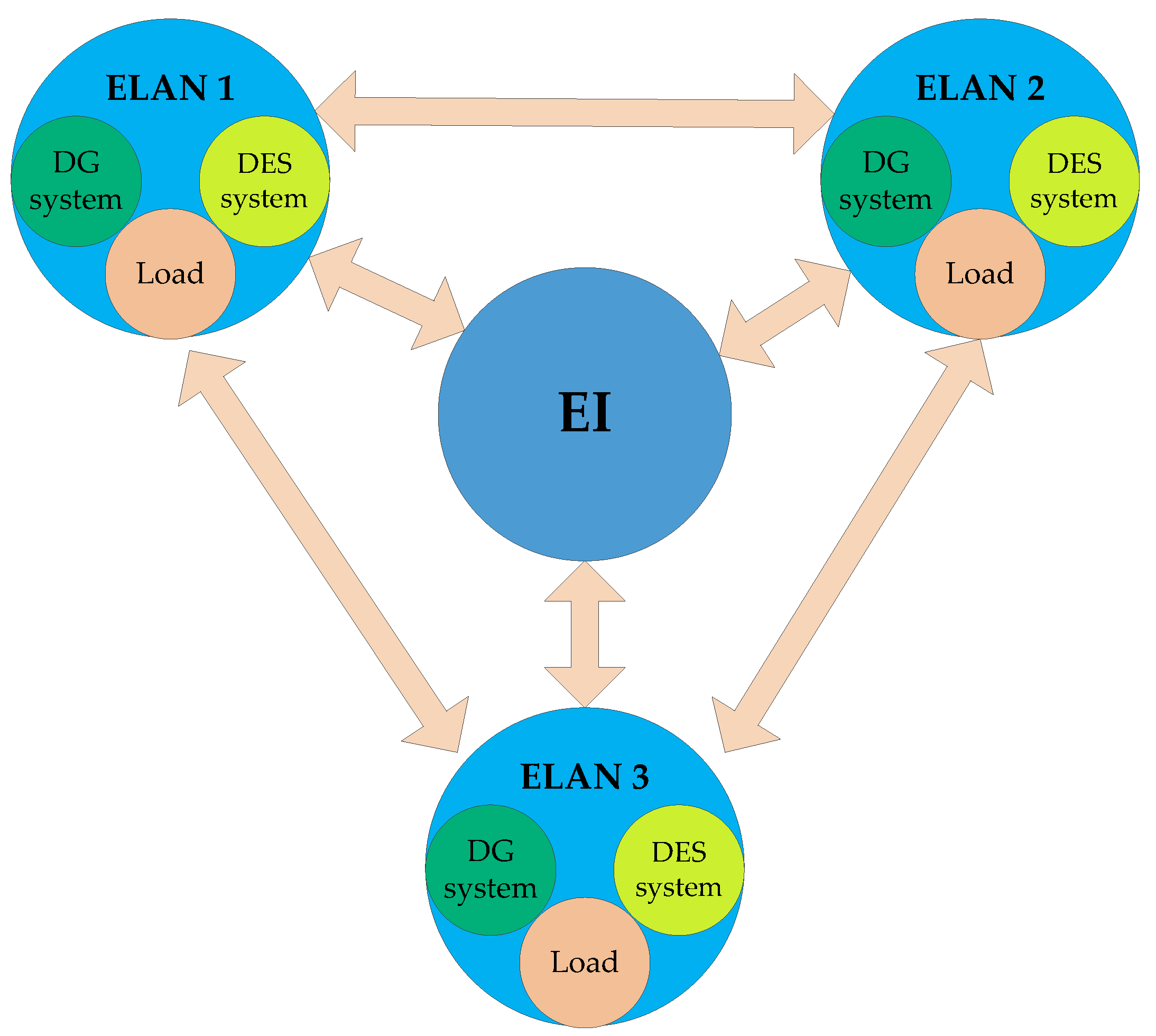
2. ELAN Scheduling Problem
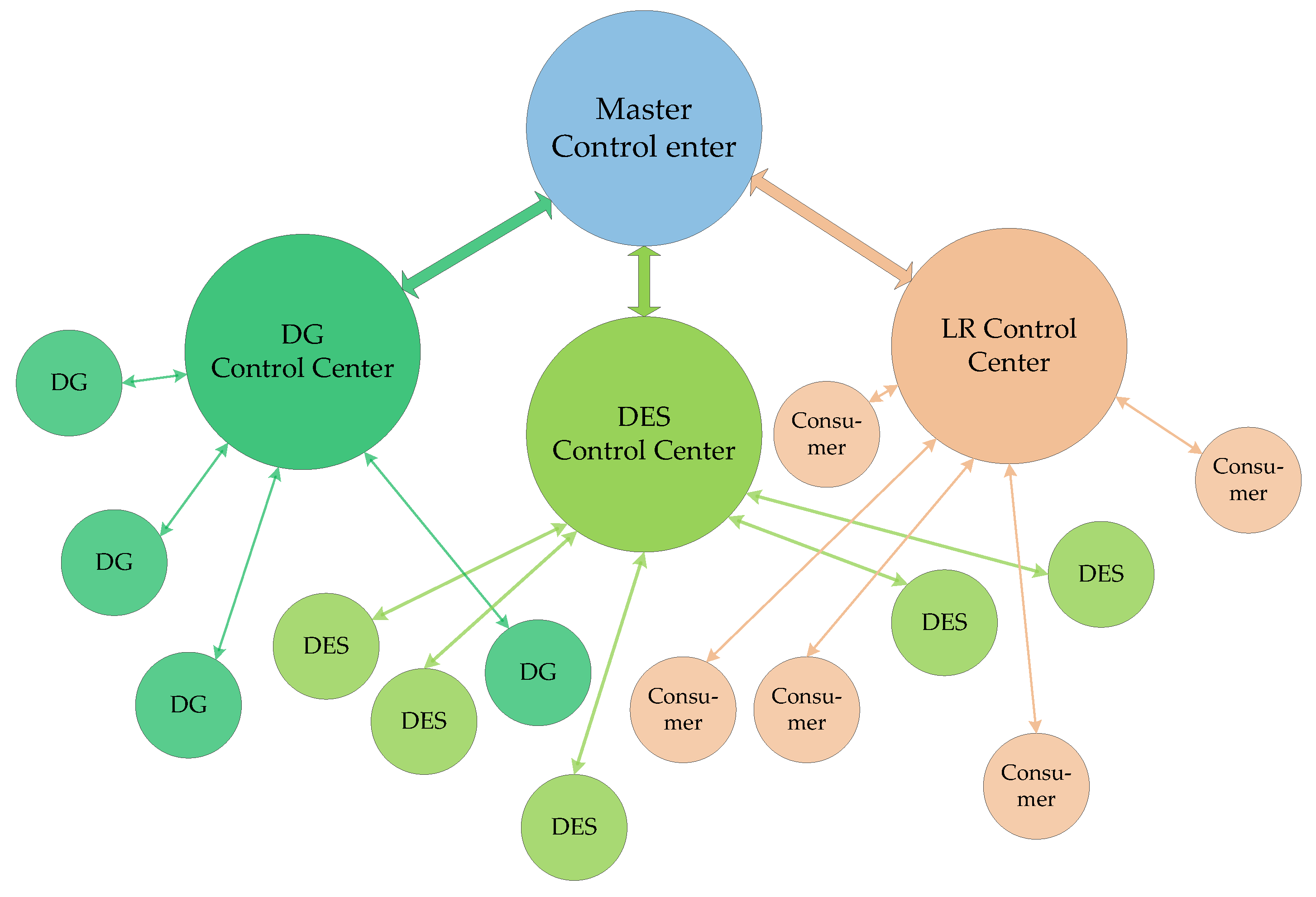
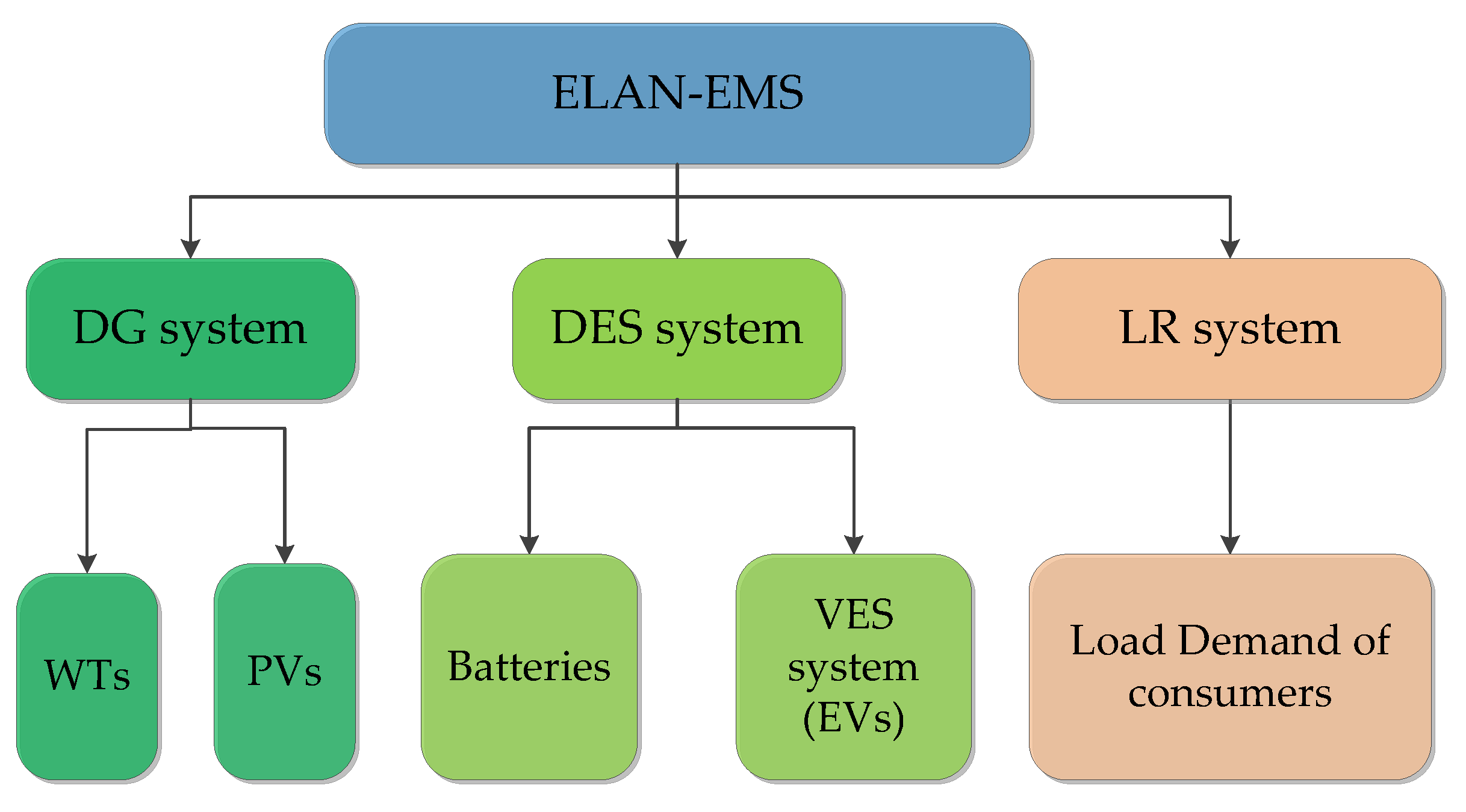
2.1. Description of ELAN-EMS
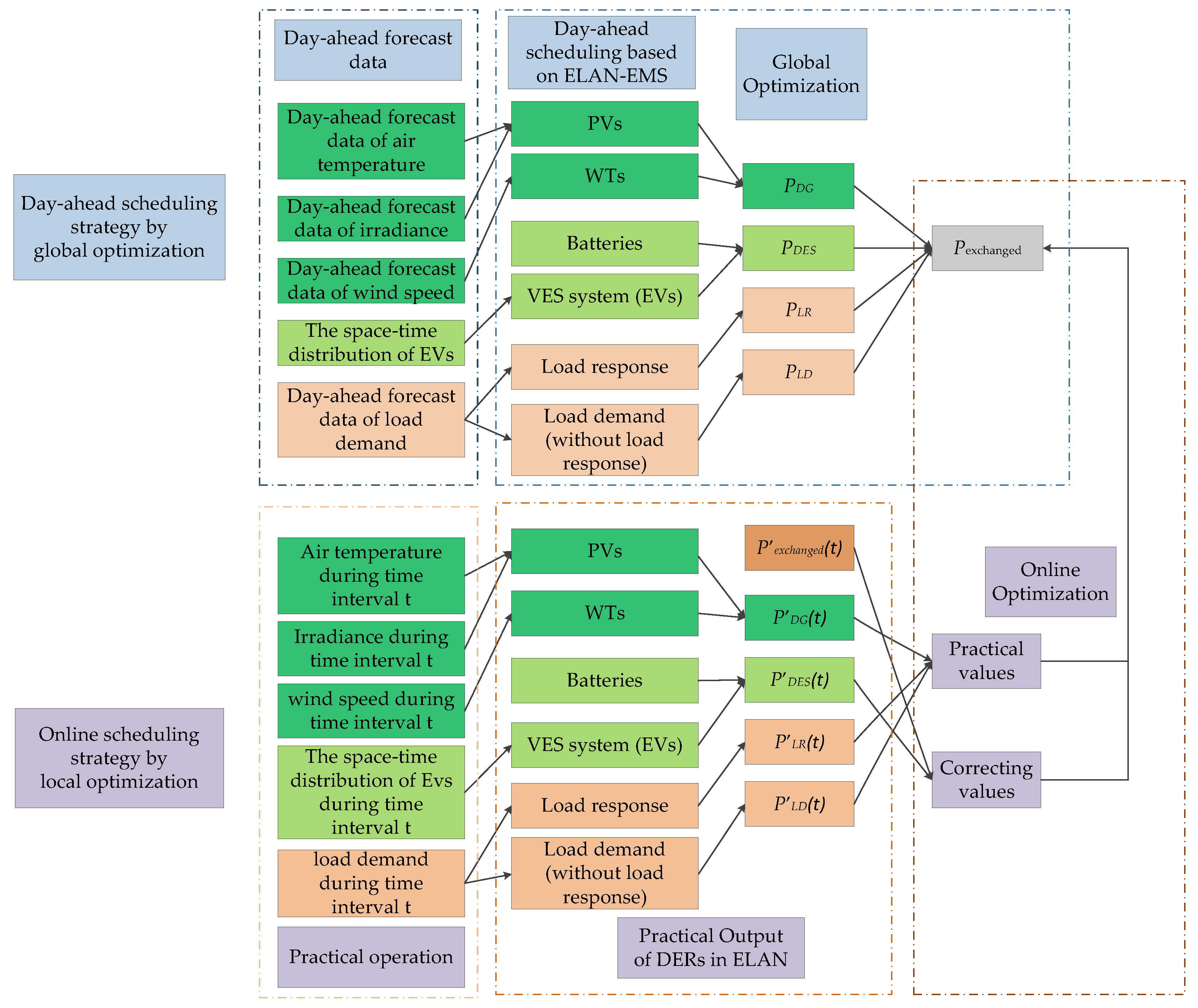
2.2. Two-Step Optimization Framework for ELAN Scheduling Problem
3. Optimization Modeling Based on ELAN-EMS
3.1. Global Optimization Model Based on Forecast Data
3.1.1. Objective Function: Maximization of the ELAN’s Income
3.1.2. Constraints Description
3.2. Online Local Optimization Model during Practical Operation
3.2.1. Objective Function: Minimization of Local Correction Cost
3.2.2. Constraints Description
4. Simulations and Discussion
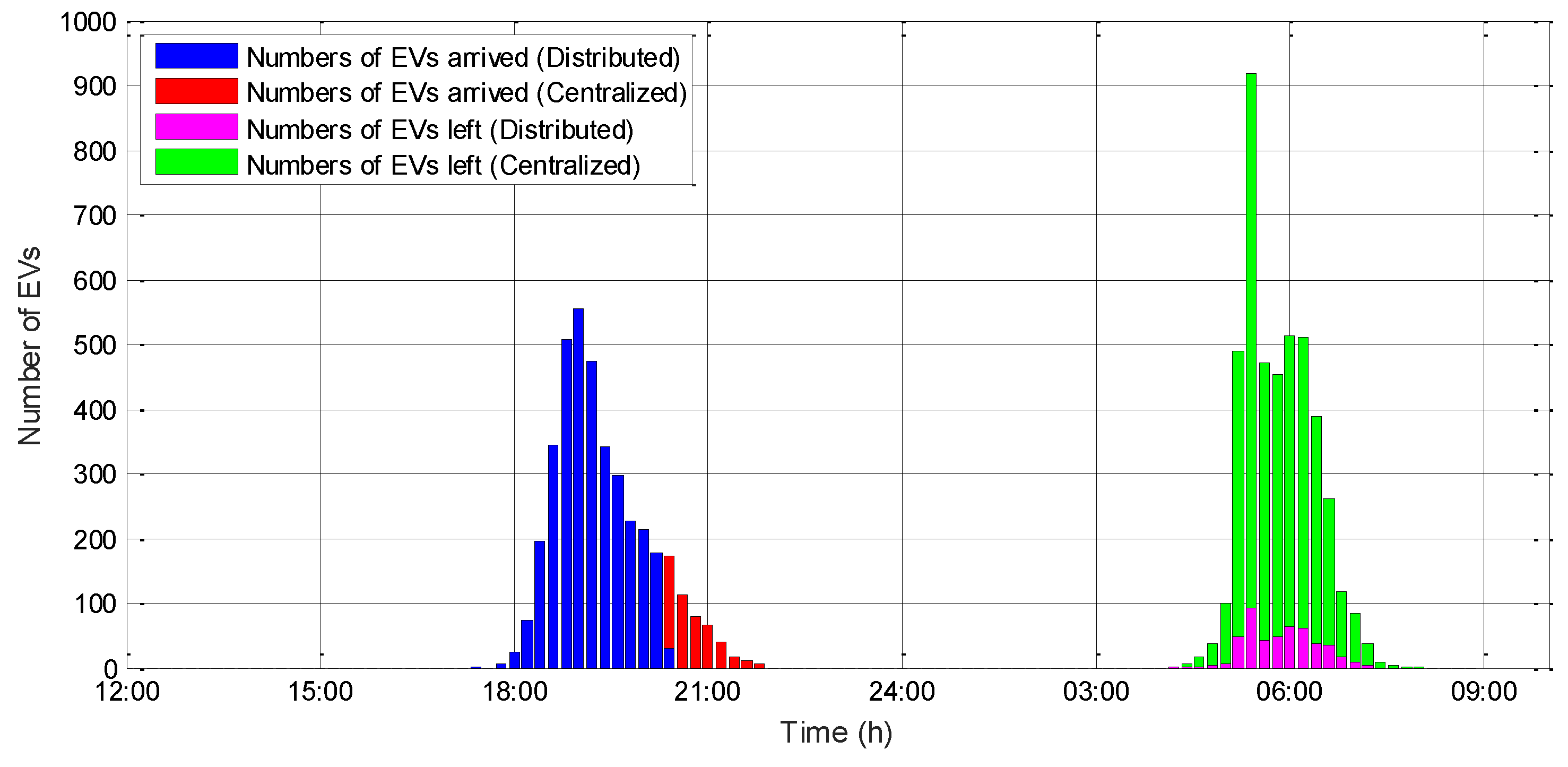
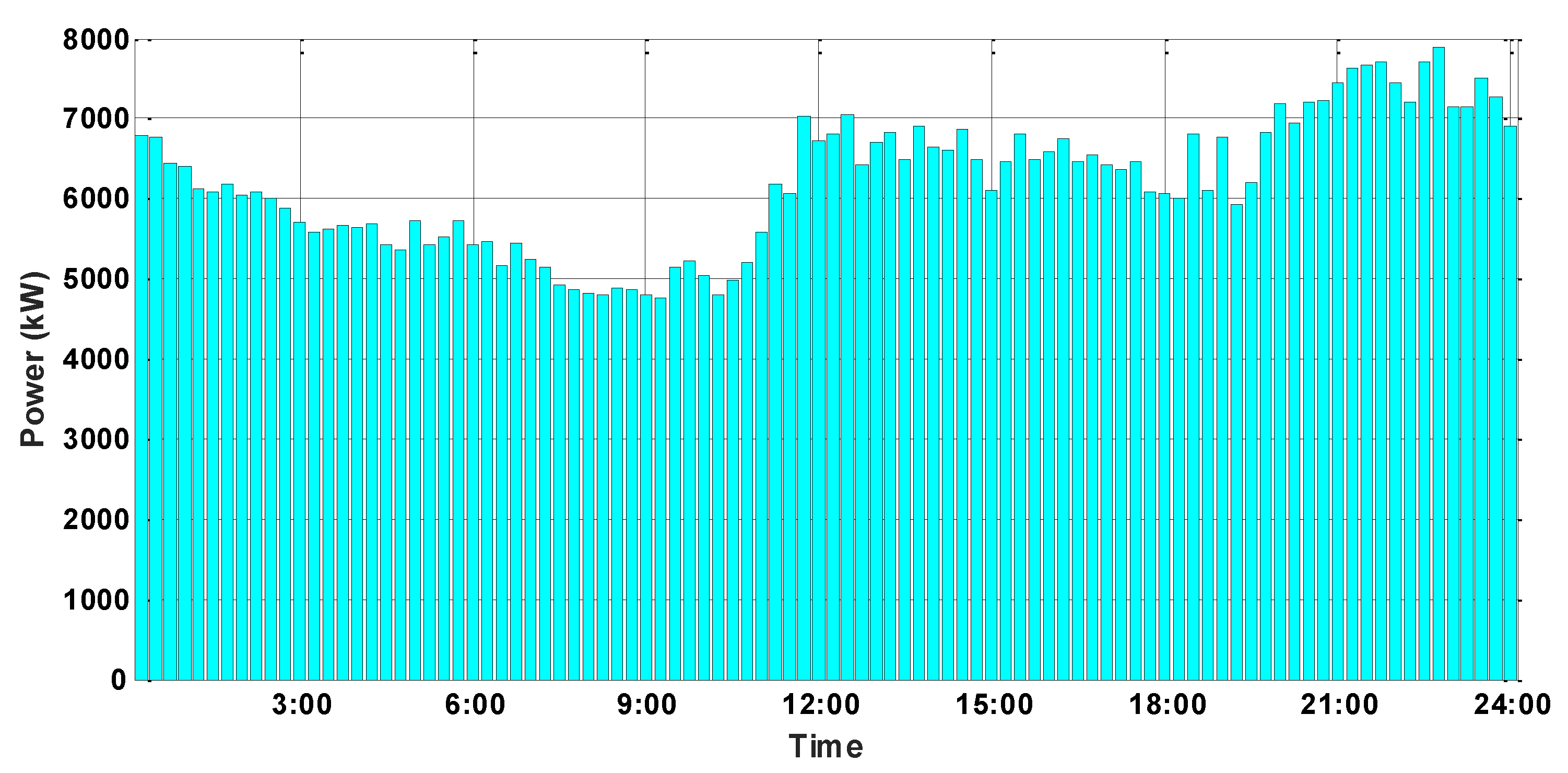
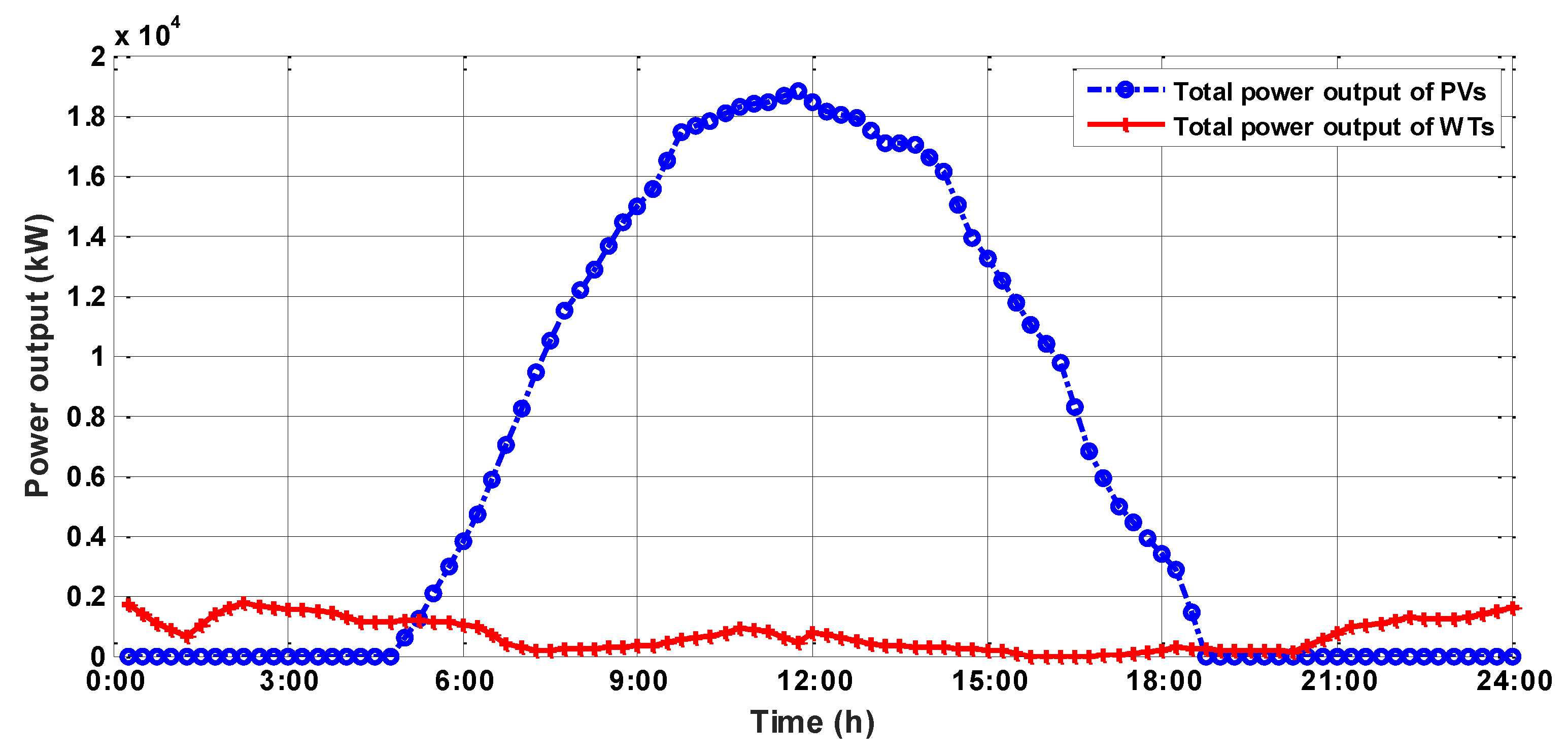
4.1. Data and Parameter Settings
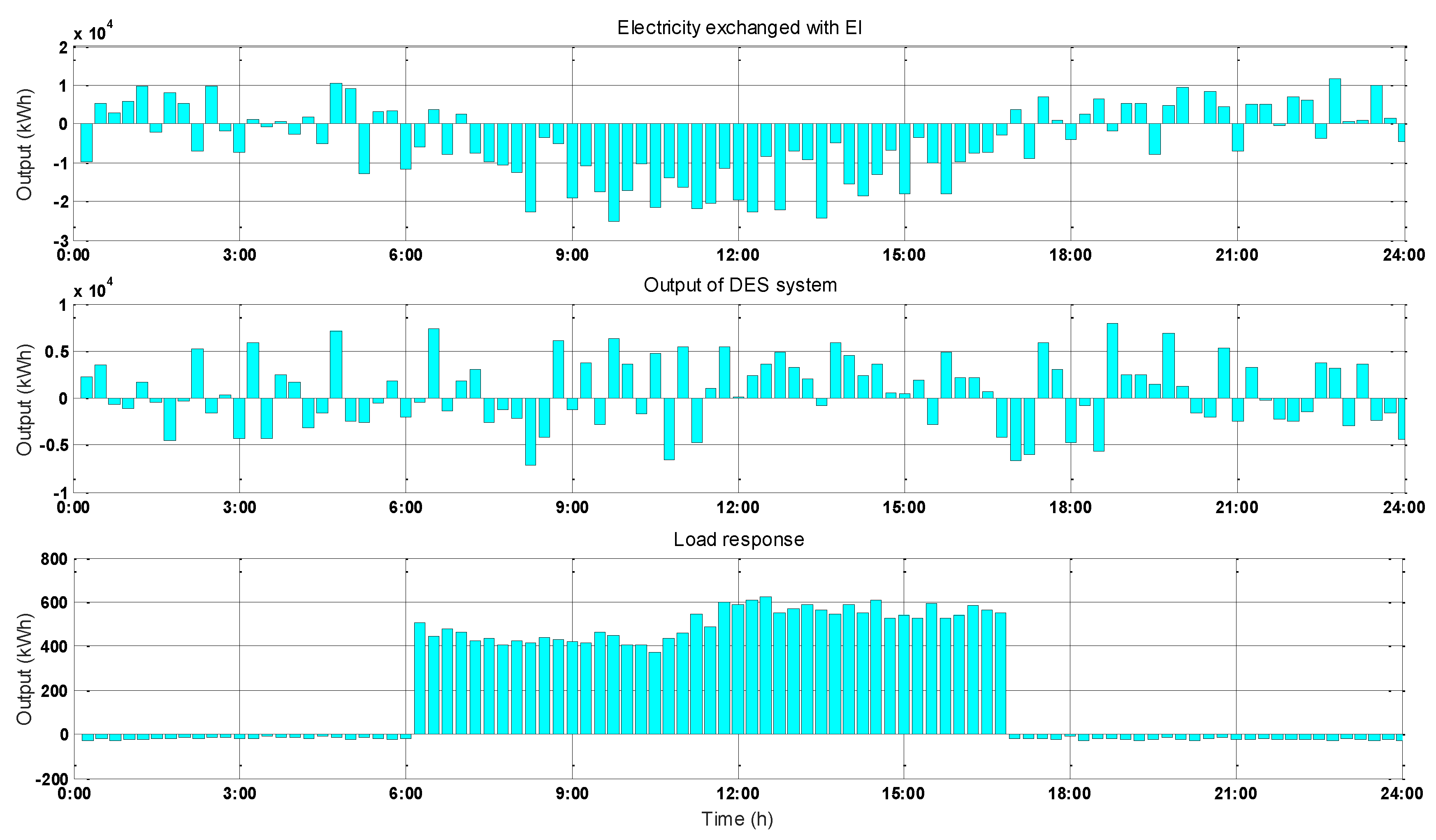
4.2. Global Optimization Results and Analysis
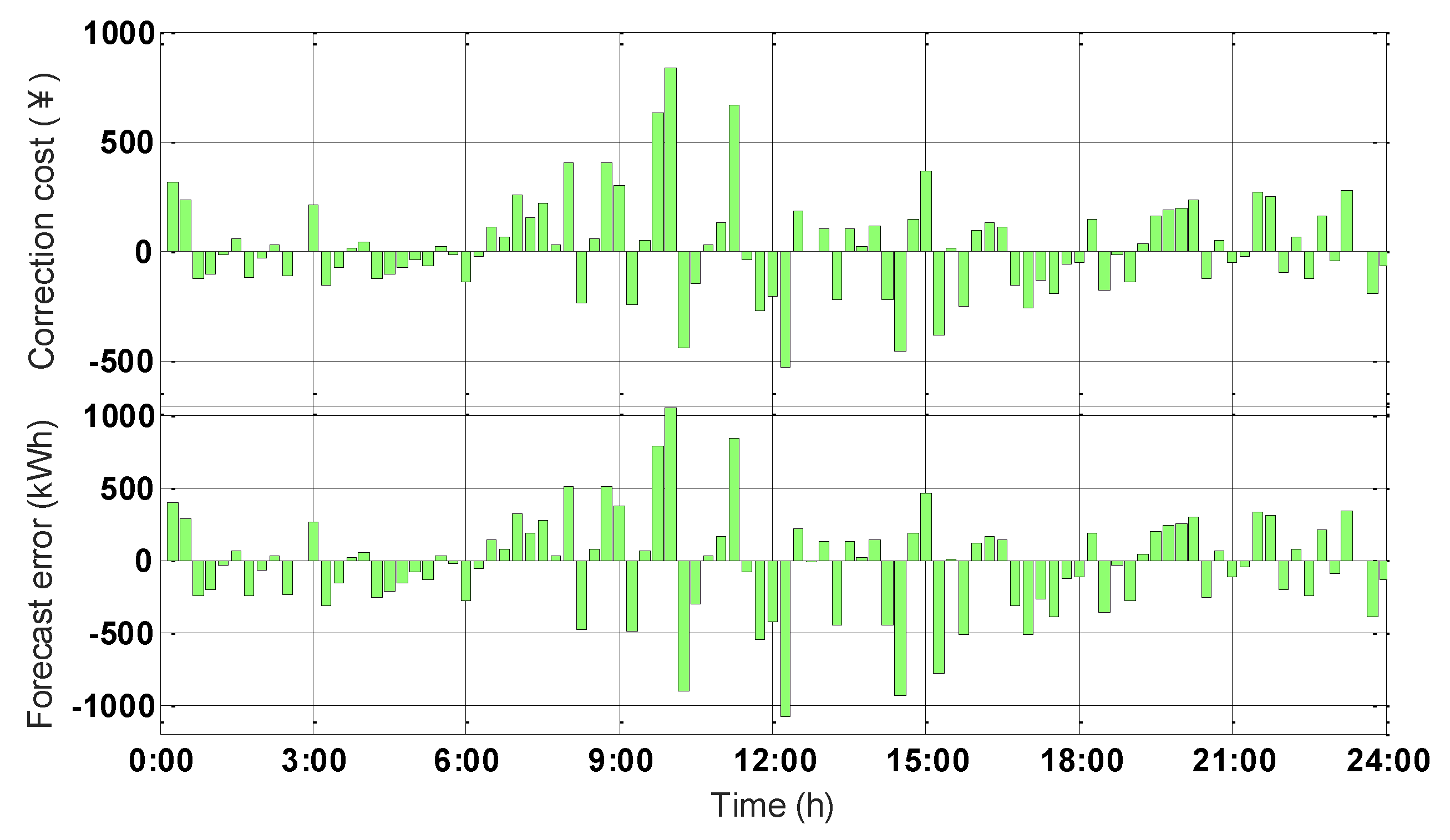
4.3. Online Local Optimization Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Abbreviations | |
| RE | renewable energy |
| EI | energy internet |
| ELAN | energy local area network |
| EMS | energy management system |
| VES | virtual energy storage |
| LR | load response |
| DES | distributed energy storage |
| Mathematical symbols | |
| power generation cost of the DGs by forecast data (¥) | |
| load response cost by day-ahead scheduling (¥) | |
| cost of the DES systems by day-ahead scheduling (¥) | |
| cost of the exchanged electricity with EI by day-ahead scheduling (¥) | |
| / | cost of the i-th WT/j-th PV during time interval t by forecast data (kWh) |
| W/P | number of WTs/PVs |
| / | maintenance cost coefficient of the i-th WT/j-th PV (¥/kWh) |
| / | power output of the i-th WT/j-th PV during time interval t by forecast data (kWh) |
| T | total number of the time intervals |
| M/N | total number of the consumers in LR system/the regions where there are EVs in VES system |
| electricity tariff sold to consumers (¥/kWh) | |
| adjusting value of electricity tariff sold to consumers (¥/kWh) | |
| load of the consumers during time interval t (kWh) | |
| electric quantity of the consumers’ load response during time interval t (kWh) | |
| ε | price elasticity coefficient |
| minimum load of the consumers during time interval t according to statistics (kWh) | |
| βr,m(t) | probability of the consumers’ response to the load during time interval t |
| cost of EVs’ charging/discharging in the n-th region during time interval t (¥) | |
| cost of the batteries by day-ahead scheduling (¥) | |
| charged/discharged power rating of the charging points (kW) | |
| L | total number of the EVs in VES system |
| variation of load response during time interval t (kW) | |
| DG | distributed generator |
| PV | photovoltaic |
| WT | wind turbine |
| EV | electric vehicle |
| DER | distributed energy resource |
| SOC | state of charge |
| PSO | particle swarm optimization |
| power of the consumers’ load response during time interval t (kW) | |
| power exchanged with EI during time interval t (kW) | |
| output power of the DGs during time interval t (kW) | |
| input/output power of the DES systems during time interval t (kW) | |
| / | minimum/maximum power output of the k-th device during time interval t (kW) |
| / | minimum/maximum amount of stored energy inside the DES (Ah) |
| remaining battery capacity of the j-th EV in the i-th region (Ah) | |
| minimum daily electricity consumption of the j-th EV in the i-th region (Ah) | |
| remaining battery capacity of the l-th EV (Ah) | |
| rated battery capacity of the l-th EV (Ah) | |
| τ | total time during which the EV stays in the residential area (h) |
| τ0 | time the EV has spent in the residential area (h) |
| tariff of the electricity purchased from EI (¥/kWh) | |
| tariff of the electricity sold to EI (¥/kWh) | |
| adjusting value of electricity tariff (¥/kWh) | |
| adjusting value of power generation cost of the DGs during time interval t (¥) | |
| adjusting value of load response cost during time interval t (¥) | |
| adjusting value of cost of the exchanged electricity with EI during time interval t (¥) | |
| total power variation during time interval t (kW) | |
| power variation of the DGs during time interval t (kW) | |
| variation of load demand during time interval t (kW) | |
References
- Sun, Q.; Han, R.; Zhang, H.; Zhou, J.; Guerrero, J.M. A multiagent-based consensus algorithm for distributed coordinated control of distributed generators in the energy internet. IEEE Trans. Smart Grid 2015, 6, 3006–3019. [Google Scholar] [CrossRef]
- Bai, H.; Miao, S.H.; Zhang, P.P.; Bai, Z. Reliability evaluation of a distribution network with microgrid based on a combined power generation system. Energies 2015, 8, 1216–1241. [Google Scholar] [CrossRef]
- Destek, M.A.; Aslan, A. Renewable and non-renewable energy consumption and economic growth in emerging economies: Evidence from bootstrap panel causality. Renew. Energy 2017, 111, 757–763. [Google Scholar] [CrossRef]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC microgrids—Part I: A review of control strategies and stabilization techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar]
- Lai, J.; Lu, X.; Yu, X.; Yao, W.; Wen, J.; Cheng, S. Distributed Multi-DER Cooperative Control for Master-Slave-Organized Microgrid Networks with Limited Communication Bandwidth. IEEE Trans. Ind. Inform. 2018. [Google Scholar] [CrossRef]
- Tang, R.; Li, X.; Lai, J. A novel optimal energy-management strategy for a maritime hybrid energy system based on large-scale global optimization. Appl. Energy 2018, 228, 254–264. [Google Scholar] [CrossRef]
- Wang, R.; Wu, J.; Qian, Z.; Lin, Z.; He, X. A graph theory based energy routing algorithm in energy local area network. IEEE Trans. Ind. Inform. 2017, 13, 3275–3285. [Google Scholar] [CrossRef]
- Kouchachvili, L.; Yaïci, W.; Entchev, E. Hybrid battery/supercapacitor energy storage system for the electric vehicles. J. Power Sources 2018, 374, 237–248. [Google Scholar] [CrossRef]
- Erdinc, O. Economic impacts of small-scale own generating and storage units, and electric vehicles under different demand response strategies for smart households. Appl. Energy 2014, 126, 142–150. [Google Scholar] [CrossRef]
- Yi, P.; Zhu, T.; Jiang, B.; Jin, R.; Wang, B. Deploying Energy Routers in an Energy Internet Based on Electric Vehicles. IEEE Trans. Veh. Technol. 2016, 65, 4714–4725. [Google Scholar] [CrossRef]
- Weis, A.; Jaramillo, P.; Michalek, J. Estimating the potential of controlled plug-in hybrid electric vehicle charging to reduce operational and capacity expansion costs for electric power systems with high wind penetration. Appl. Energy 2014, 115, 190–204. [Google Scholar] [CrossRef]
- Jin, X.; Mu, Y.; Jia, H.; Wu, J.; Jiang, T.; Yu, X. Dynamic economic dispatch of a hybrid energy microgrid considering building based virtual energy storage system. Appl. Energy 2017, 194, 386–398. [Google Scholar] [CrossRef]
- Keirstead, J.; Jennings, M.; Sivakumar, A. A review of urban energy system models: Approaches, challenges and opportunities. Renew. Sustain. Energy Rev. 2012, 16, 3847–3866. [Google Scholar] [CrossRef]
- Shao, S.; Pipattanasomporn, M.; Rahman, S. Demand response as a load shaping tool in an intelligent grid with electric vehicles. IEEE Trans. Smart Grid 2011, 2, 624–631. [Google Scholar] [CrossRef]
- Lu, X.; Lai, J.; Yu, X.; Wang, Y.; Guerrero, J.M. Distributed coordination of islanded microgrid clusters using a two-layer intermittent communication network. IEEE Trans. Ind. Inform. 2018, 14, 3956–3969. [Google Scholar] [CrossRef]
- Coelho, V.N.; Coelho, I.M.; Coelho, B.N.; Cohen, M.W.; Reis, A.J.; Silva, S.M.; Guimarães, F.G. Multi-objective energy storage power dispatching using plug-in vehicles in a smart-microgrid. Renew. Energy 2016, 89, 730–742. [Google Scholar] [CrossRef]
- Erdogan, N.; Erden, F.; Kisacikoglu, M. A fast and efficient coordinated vehicle-to-grid discharging control scheme for peak shaving in power distribution system. J. Mod. Power Syst. Clean Energy 2018, 6, 555–566. [Google Scholar] [CrossRef]
- Abedini, M.; Moradi, M.H.; Hosseinian, S.M. Optimal management of microgrids including renewable energy scources using GPSO-GM algorithm. Renew. Energy 2016, 90, 430–439. [Google Scholar]
- Tani, A.; Camara, M.B.; Dakyo, B. Energy management in the decentralized generation systems based on renewable energy—Ultracapacitors and battery to compensate the wind/load power fluctuations. IEEE Trans. Ind. Appl. 2015, 51, 1817–1827. [Google Scholar] [CrossRef]
- Erdinc, O.; Taşcıkaraoğlu, A.; Paterakis, N.G.; Eren, Y.; Catalão, J.P. End-user comfort oriented day-ahead planning for responsive residential HVAC demand aggregation considering weather forecasts. IEEE Trans. Smart Grid 2017, 8, 362–372. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Abunasri, A.; Zare, A.; Hoseinzadeh, R. Impact of plug-in hybrid electric vehicles charging demand on the optimal energy management of renewable micro-grids. Energy 2014, 78, 904–915. [Google Scholar] [CrossRef]
- Bashash, S.; Fathy, H.K. Transport-based load modeling and sliding mode control of plug-in electric vehicles for robust renewable power tracking. IEEE Trans. Smart Grid 2012, 3, 526–534. [Google Scholar] [CrossRef]
- Liu, H.; Ji, Y.; Zhuang, H.; Wu, H. Multi-objective dynamic economic dispatch of microgrid systems including vehicle-to-grid. Energies 2015, 8, 4476–4495. [Google Scholar] [CrossRef]
- Nefedov, E.; Sierla, S.; Vyatkin, V. Internet of energy approach for sustainable use of electric vehicles as energy storage of prosumer buildings. Energies 2018, 11, 2165. [Google Scholar] [CrossRef]
- Peng, C.; Zou, J.; Lian, L.; Li, L. An optimal dispatching strategy for V2G aggregator participating in supplementary frequency regulation considering EV driving demand and aggregator’s benefits. Appl. Energy 2017, 190, 591–599. [Google Scholar] [CrossRef]
- Aghajani, S.; Kalantar, M. Operational scheduling of electric vehicles parking lot integrated with renewable generation based on bilevel programming approach. Energy 2017, 139, 422–432. [Google Scholar] [CrossRef]
- Tang, R.; Wu, Z.; Li, X. Optimal operation of photovoltaic/battery/diesel/cold-ironing hybrid energy system for maritime application. Energy 2018, 162, 697–714. [Google Scholar] [CrossRef]
- Iacobucci, R.; McLellan, B.; Tezuka, T. The Synergies of Shared Autonomous Electric Vehicles with Renewable Energy in a Virtual Power Plant and Microgrid. Energies 2018, 11, 2016. [Google Scholar] [CrossRef]
- Li, L. Study of Economic Operation in Microgrid. Master’s Dissertation, North China Electric Power University, Beijing, China, 2011. [Google Scholar]
- Jin, X.; Mu, Y.; Jia, H. Optimal scheduling method for a combined cooling, heating and power building microgrid considering virtual storage system at demand side. Proc. CSEE 2017, 37, 581–591. [Google Scholar]
- He, Y.; Wang, B. Analysis on response characteristics of residential energy price in Beijing. Mod. Electron. Power 2013, 4, 88–94. [Google Scholar]
- Shi, W. Research on Lifespan Factors and Test Methods of Traction Lithium-Ion Batteries. Doctoral Dissertation, Beijing Jiaotong University, Beijing, China, 2014. [Google Scholar]
- Zhang, X.; Sun, Y.; Yu, J.; Duan, Q. The method of charging piles planning in parking lot. In Proceedings of the 2016 IEEE International Conference on Power System Technology, Wollongong, Australia, 28 September–1 October 2016; pp. 1–5. [Google Scholar]
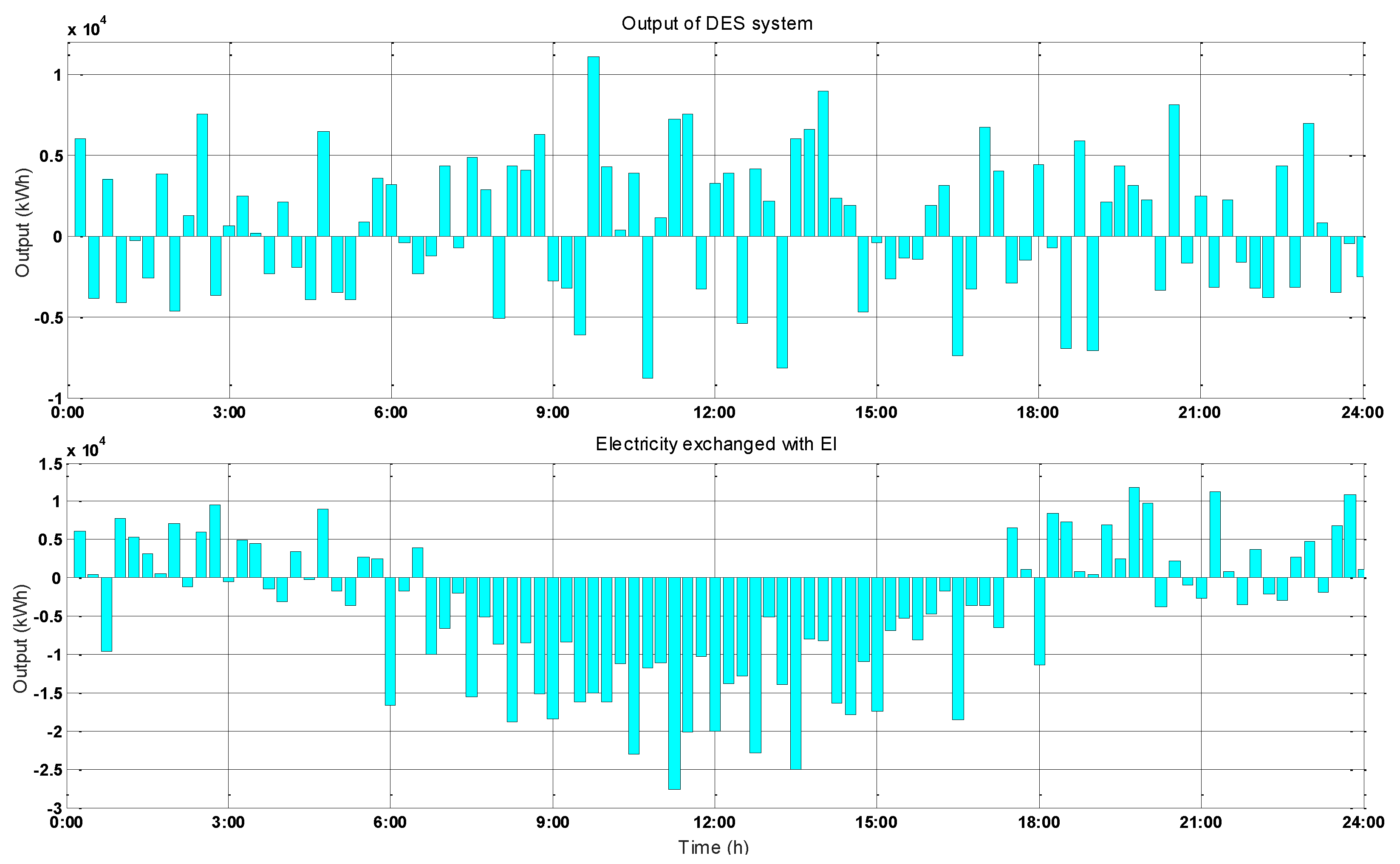
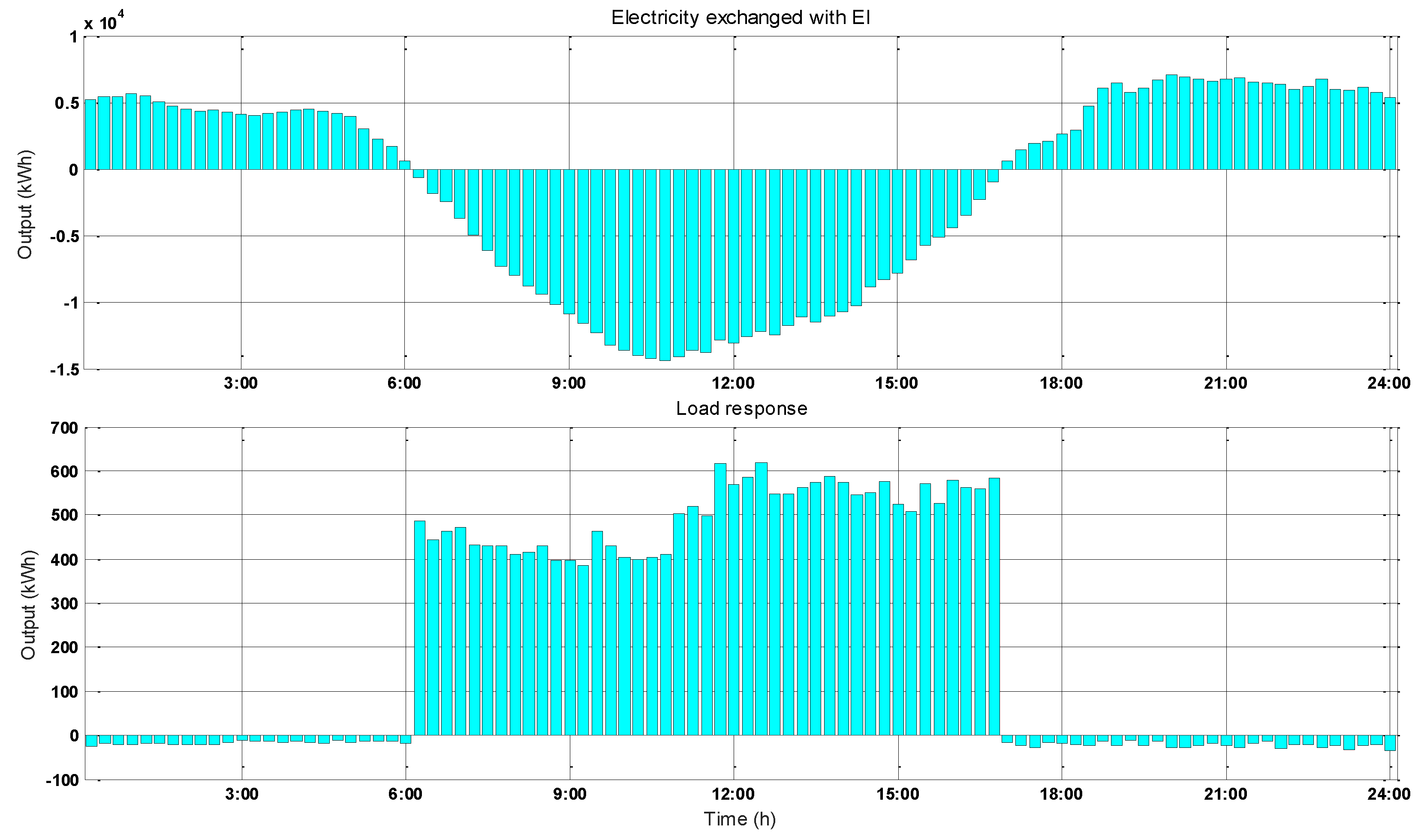
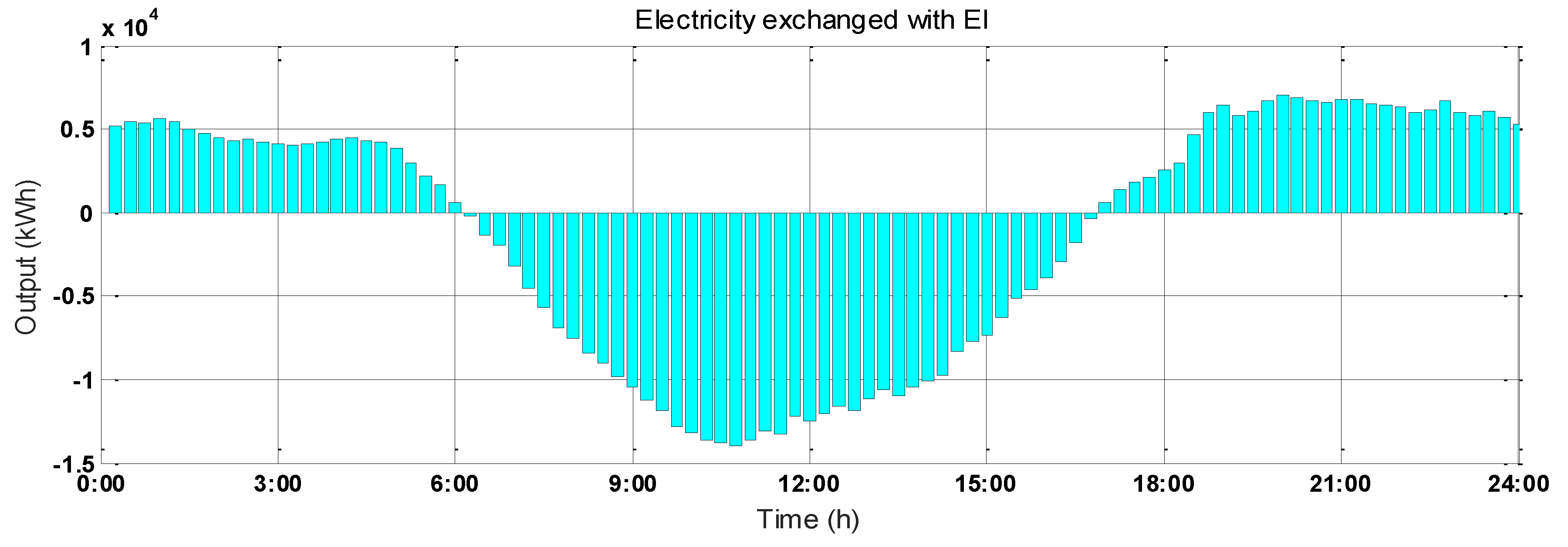
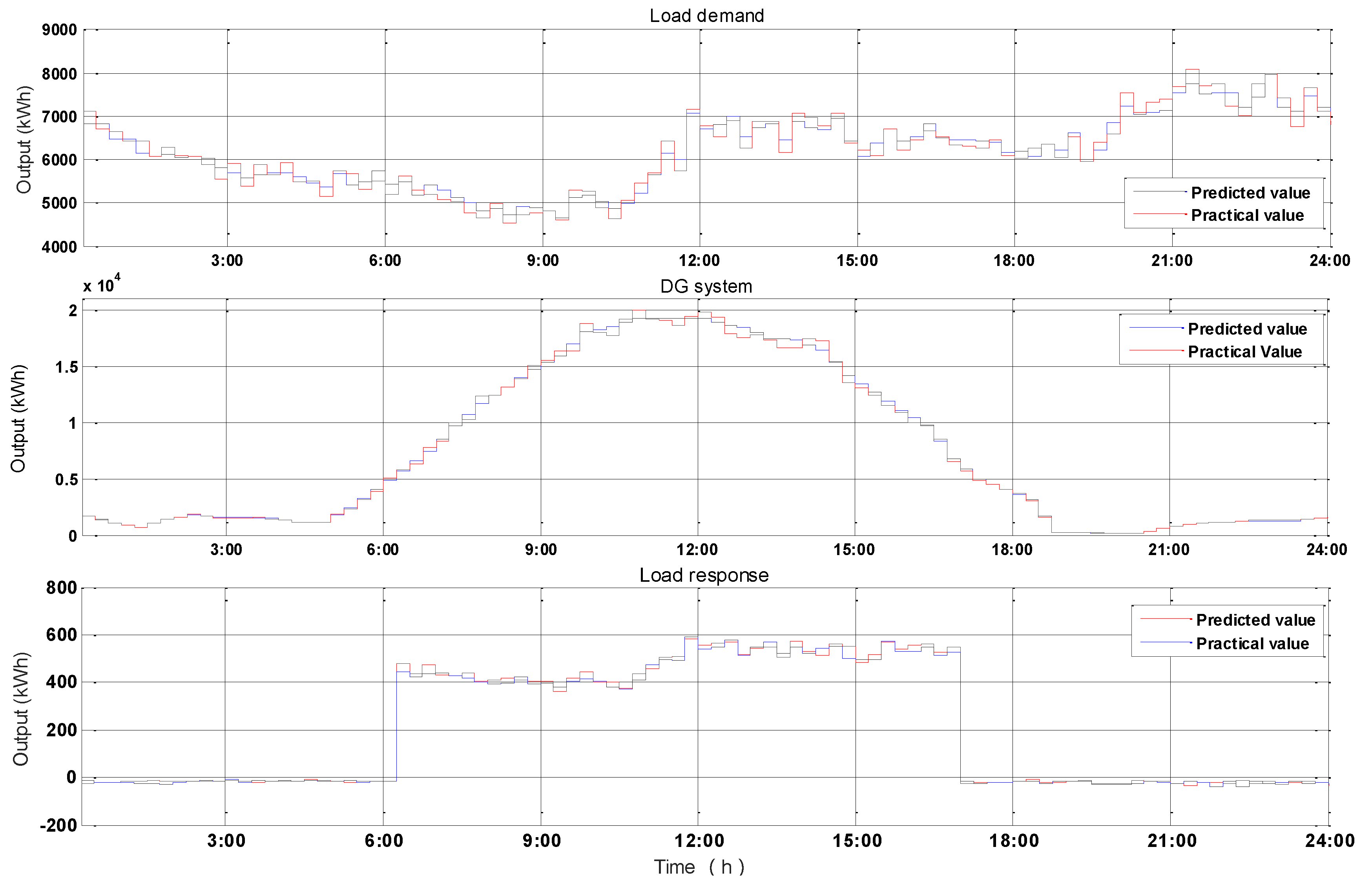
| Scenarios | Income (¥) | Scenarios | Income (¥) |
|---|---|---|---|
| Scenario One | 75,390.3 | Scenario Two | 71,130.8 |
| Scenario Three | 51,636.1 | Scenario Four | 69,102.6 |
| Scenarios | Income by Day-Ahead Global Optimization (¥) | Correction Cost (¥) | Total Income (¥) | ||
|---|---|---|---|---|---|
| Best | Best | Average | Best | Average | |
| Scenario One | 75,390.2 | 1866.2 | 1866.2 | 73,523.8 | 73,523.8 |
| Scenario Four | 69,102.4 | −4421.8 | −3021.1 | 73,523.8 | 72,123.2 |
| Scenario Five | - | - | - | 71,996.1 | 71,942.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, X.; Fan, Y. A Two-Step Framework for Energy Local Area Network Scheduling Problem with Electric Vehicles Based on Global–Local Optimization Method. Energies 2019, 12, 195. https://doi.org/10.3390/en12010195
Li X, Zhang X, Fan Y. A Two-Step Framework for Energy Local Area Network Scheduling Problem with Electric Vehicles Based on Global–Local Optimization Method. Energies. 2019; 12(1):195. https://doi.org/10.3390/en12010195
Chicago/Turabian StyleLi, Xin, Xiaodi Zhang, and Yuling Fan. 2019. "A Two-Step Framework for Energy Local Area Network Scheduling Problem with Electric Vehicles Based on Global–Local Optimization Method" Energies 12, no. 1: 195. https://doi.org/10.3390/en12010195
APA StyleLi, X., Zhang, X., & Fan, Y. (2019). A Two-Step Framework for Energy Local Area Network Scheduling Problem with Electric Vehicles Based on Global–Local Optimization Method. Energies, 12(1), 195. https://doi.org/10.3390/en12010195





