Medium-Term Hydropower Scheduling with Variable Head under Inflow, Energy and Reserve Capacity Price Uncertainty
Abstract
1. Introduction
Contributions
- A procedure to visualize and evaluate the shape of the EFP function to give a better insight into the nonconvexities in dynamic programming problems.
- The application of SDDP with SB cuts on a realistic nonconvex MTHS case study. The SDDP model considers correlated stochastic processes of inflow, energy, and reserve capacity price.
- The representation of nonconcave generation functions that are dependent on discharge and water head by concave regions.
2. The Medium-Term Hydropower Scheduling Problem
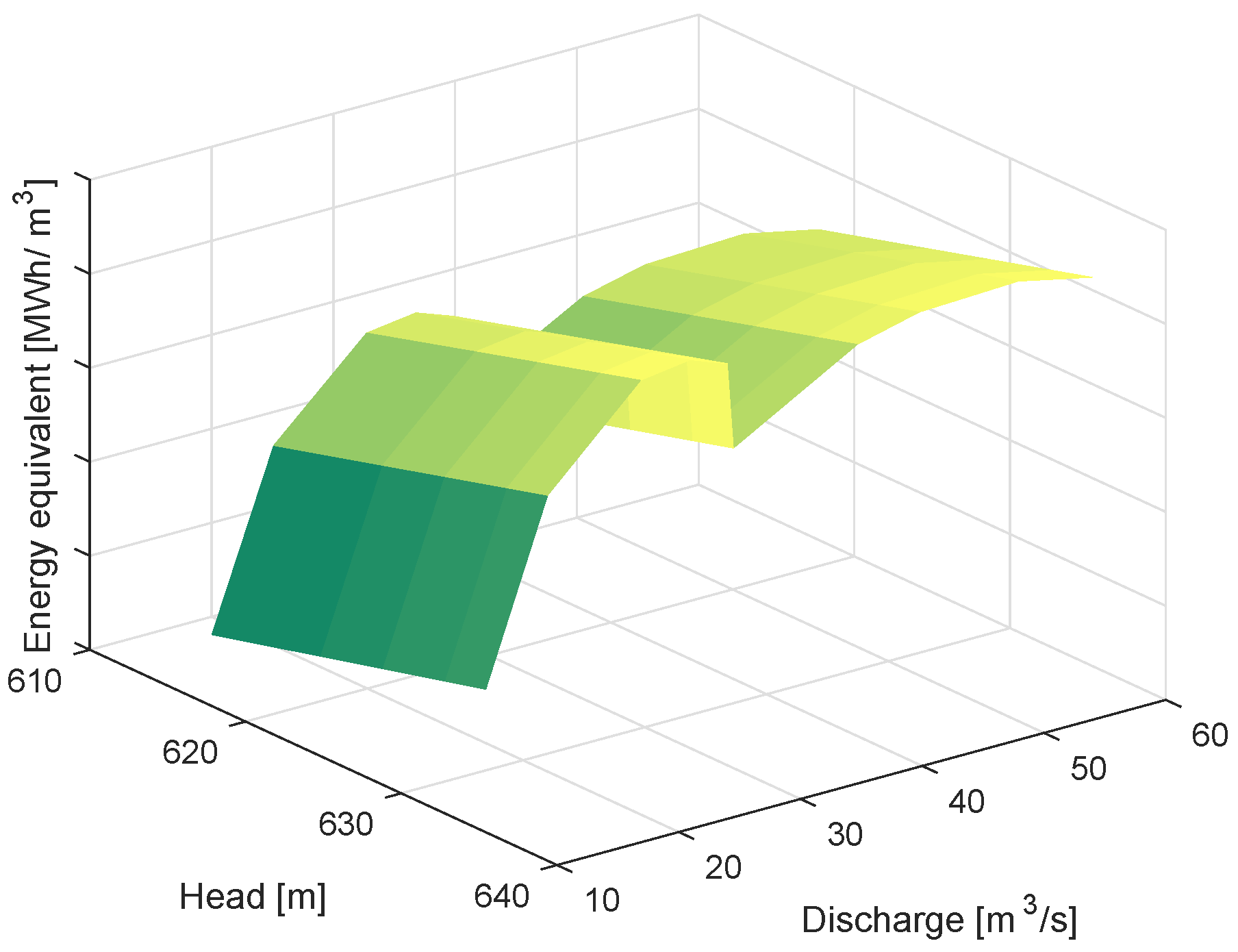
2.1. Generation Function
2.2. Stochastic Processes
3. Methodology
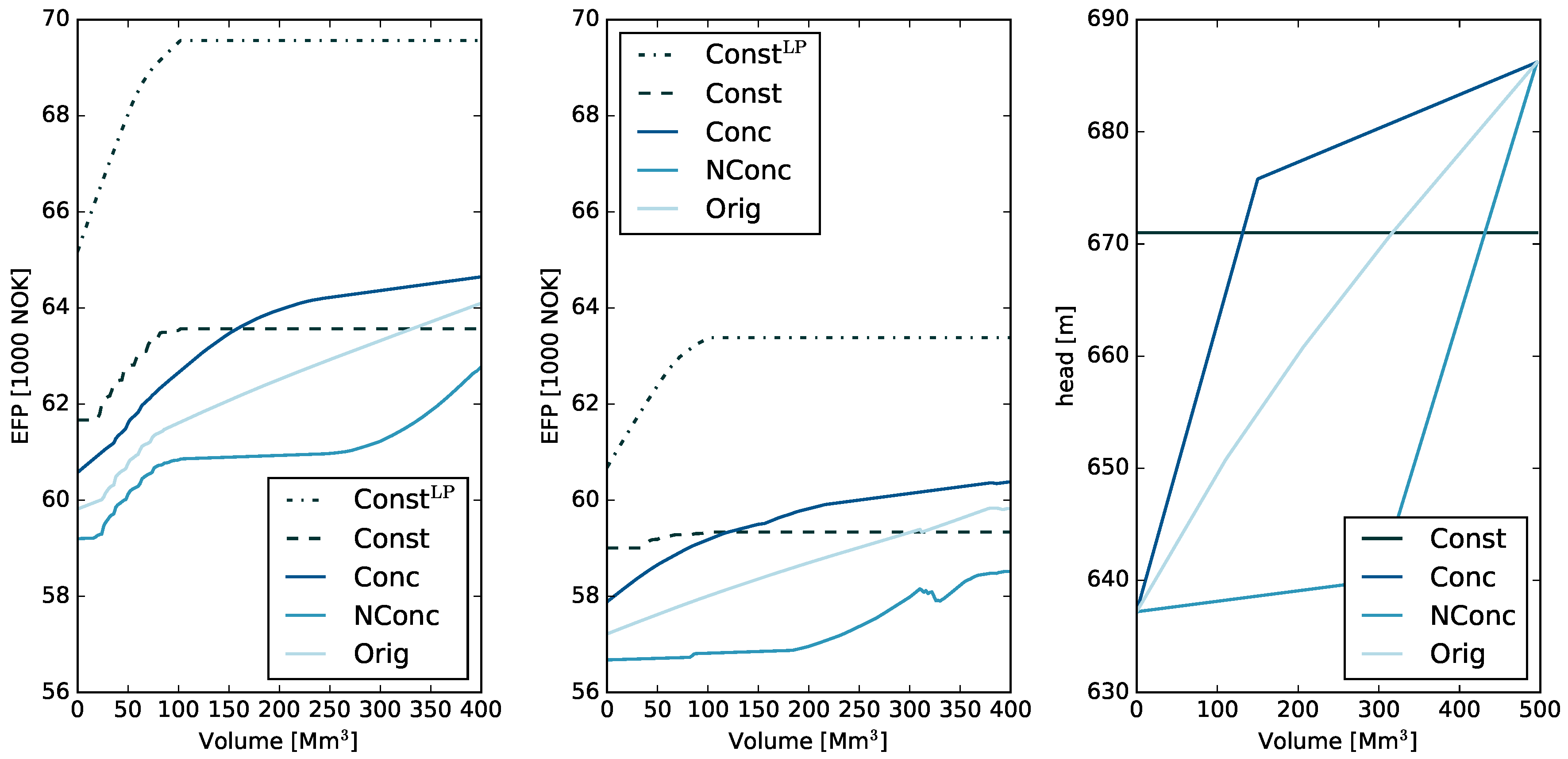
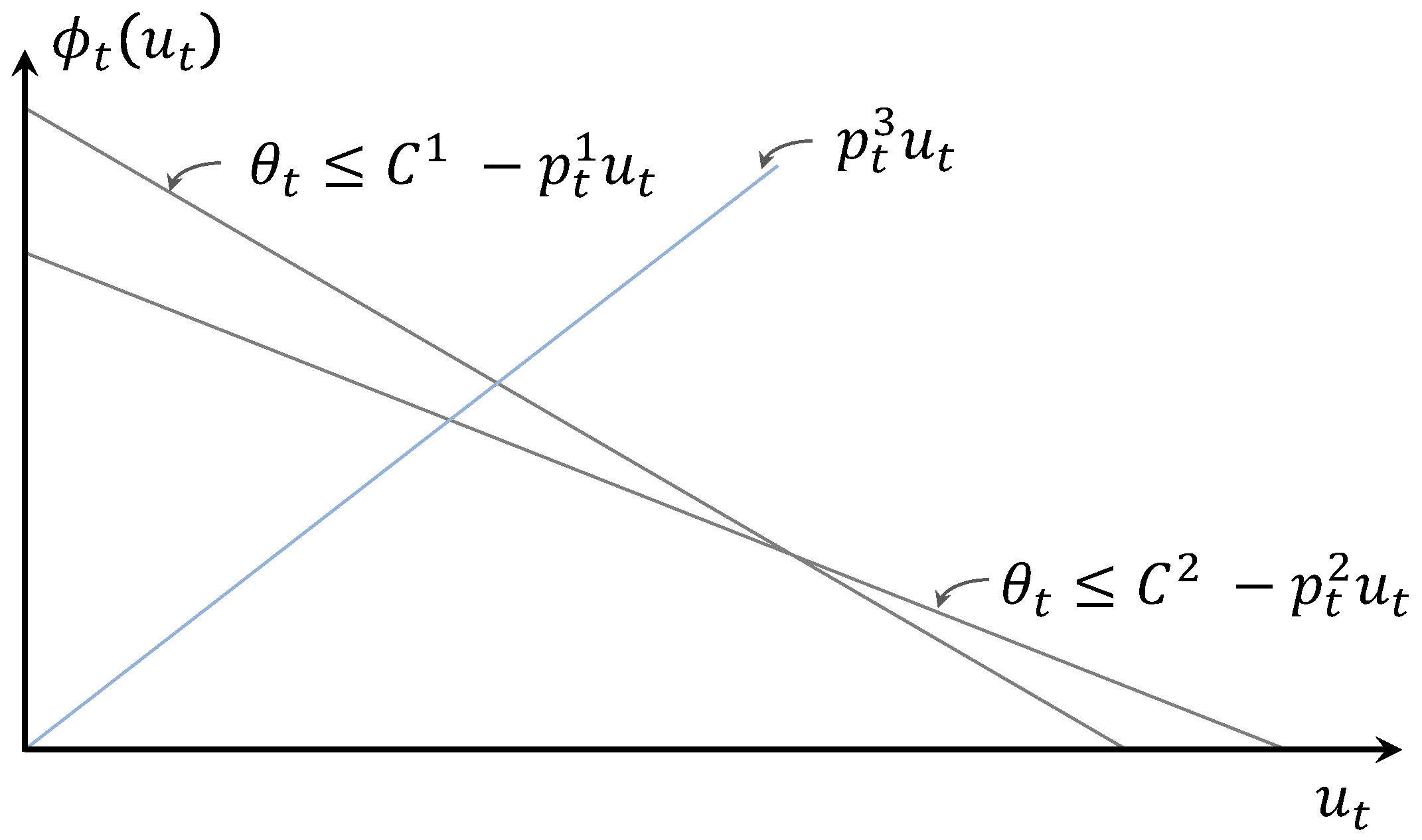
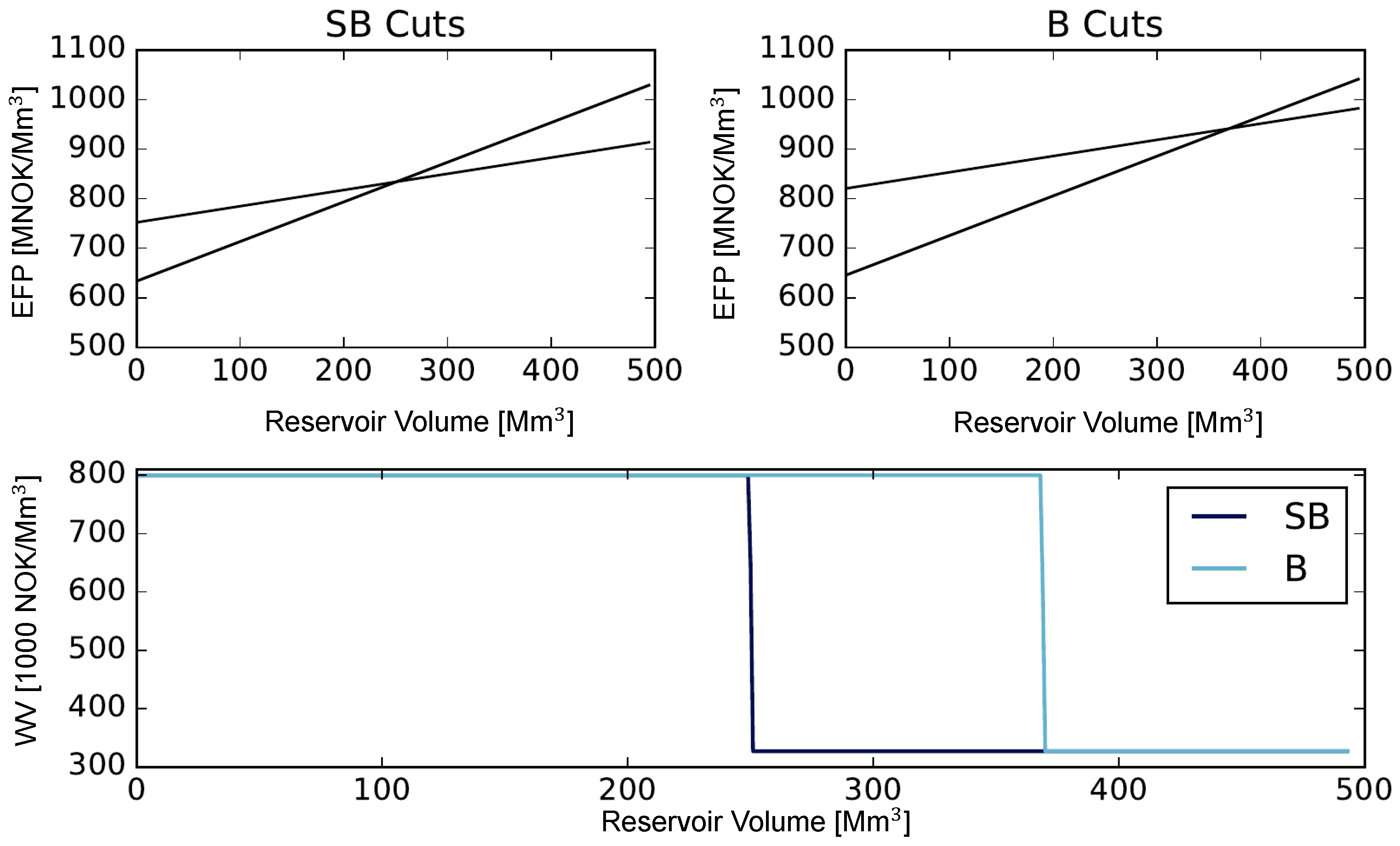
3.1. The EFP Visualization Approach
Inspecting the EFP for the MTHS at Hand
3.2. DP Formulation
3.3. Uncertainty Modeling
3.4. Solution Approach
| Algorithm 1: Solving the MTHS problem. |
| 1 Set , , , and 2 while or some other stopping criteria do 3 Sample N scenarios /* Forward iteration */ 4 for k = 1,…,N do 5 for t = 1,…,T do 6 Solve , and collect solution from Equation (16); 7 /* Compute lower bound */ 8 and 9 /* Backward iteration */ 10 for t = T, …, 2 do 11 for k = 1,…, N do 12 for m do 13 Solve , and collect from Equation (22) 14 if B cuts then 15 Collect from Equation (20); 16 else if SB cuts then 17 Solve , and collect from Equation (24) 18 Collect from Equation (15) 19 Add desired cut to /* Compute upper bound */ 20 21 /* Final simulation */ 22 Sample M scenarios 23 for k = 1,…,M do 24 for t = 1,…,T do 25 Solve , and collect solution from Equation (16)–(19) 26 /* Compute lower bound */ 27 and 28 |
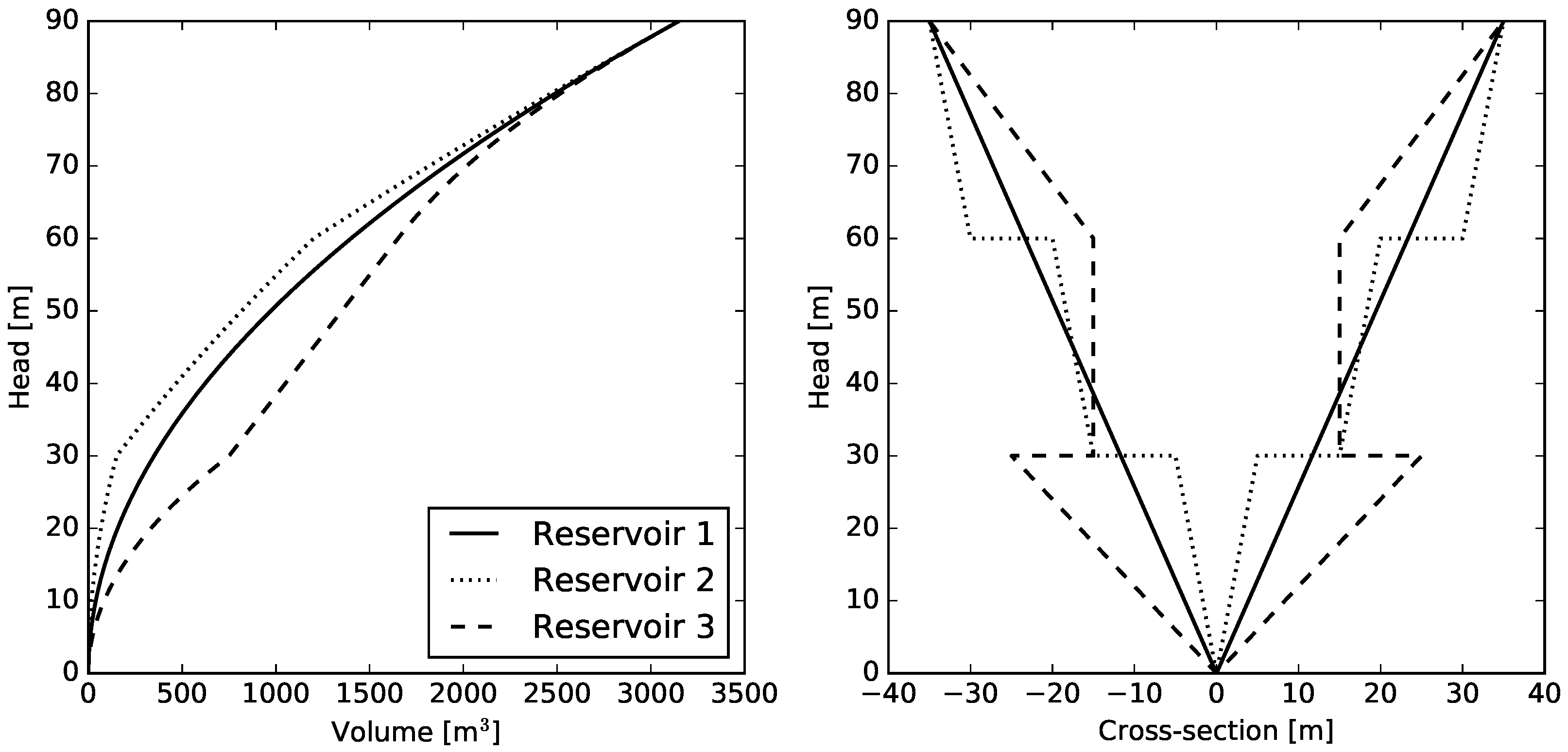
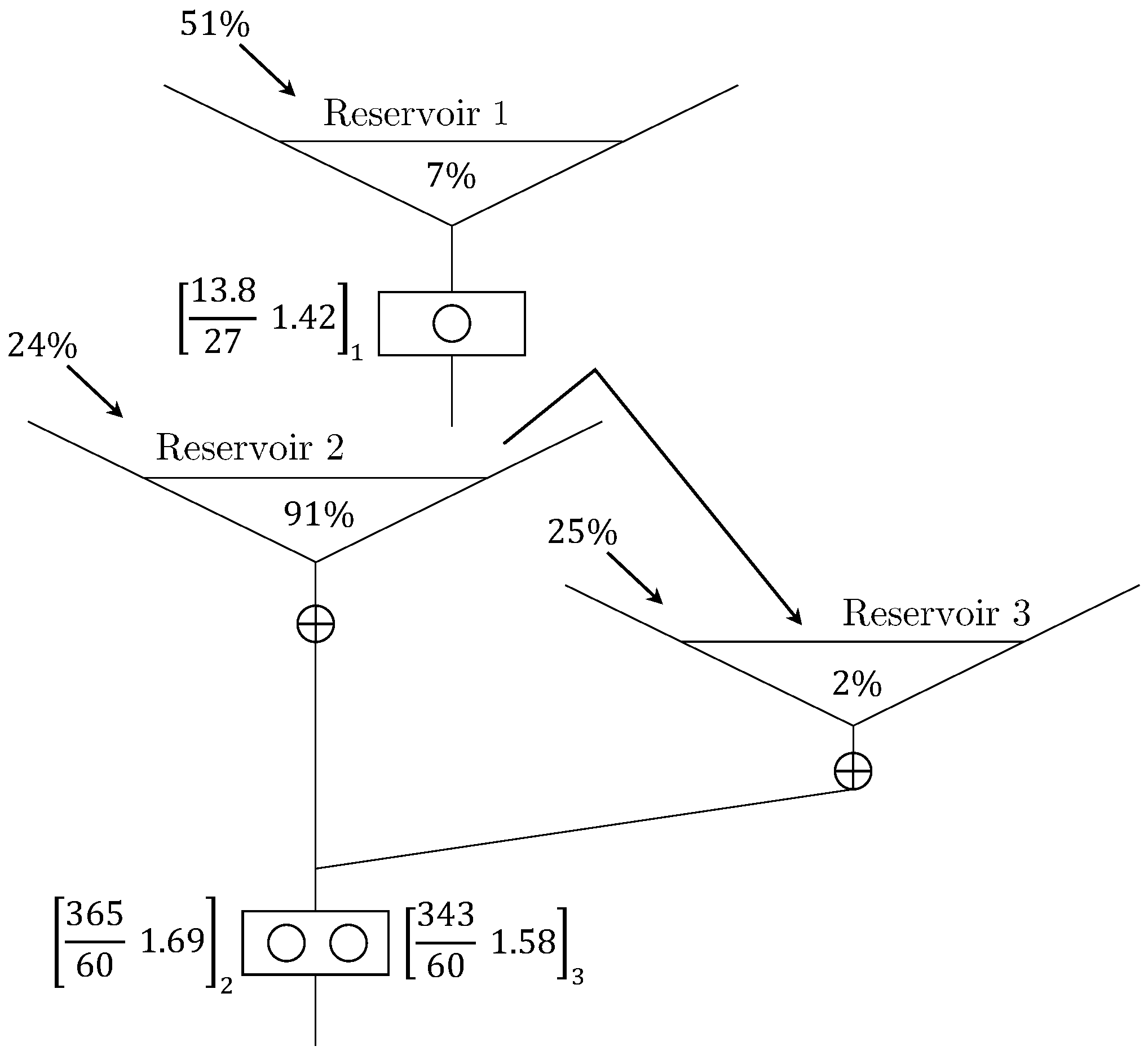
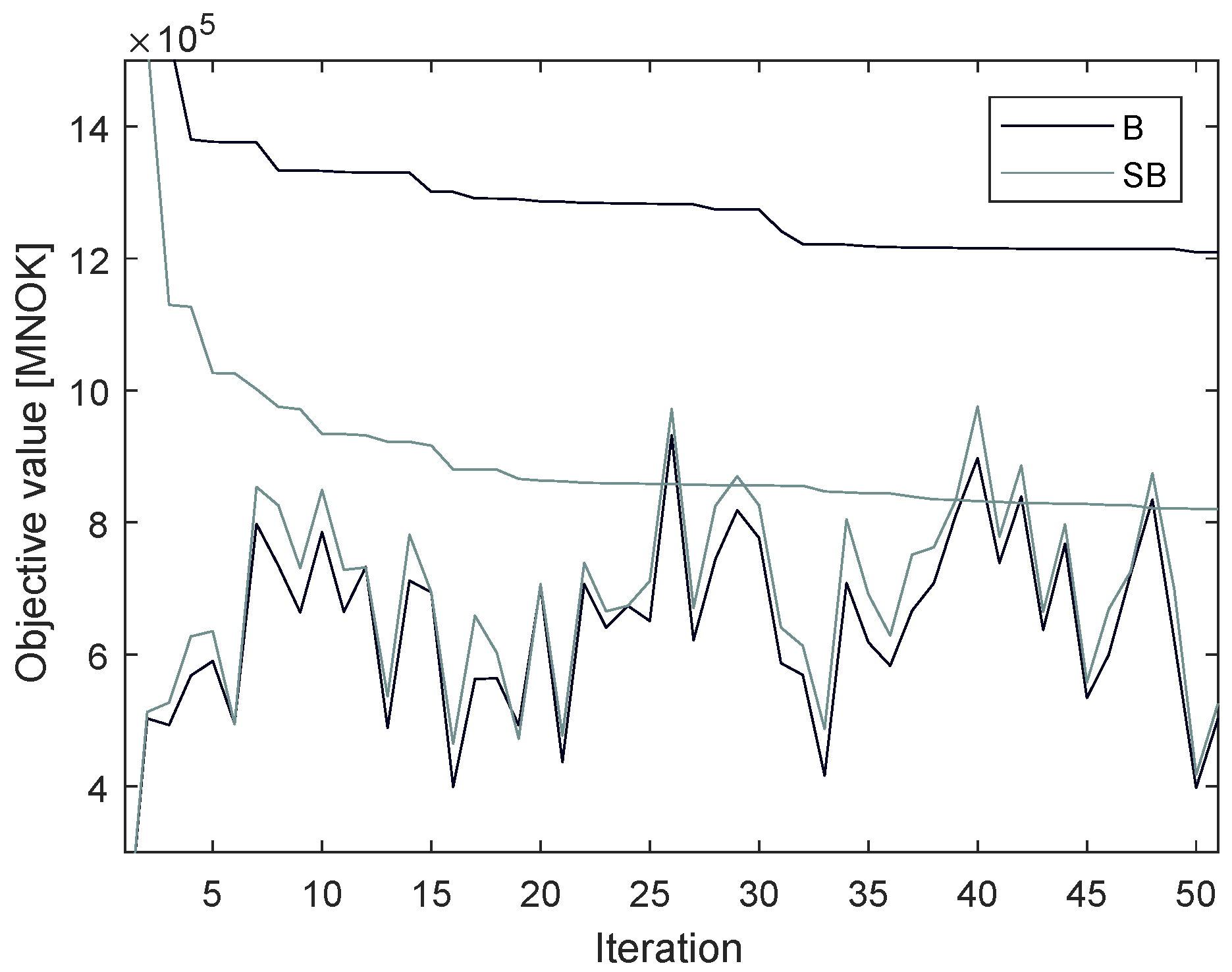
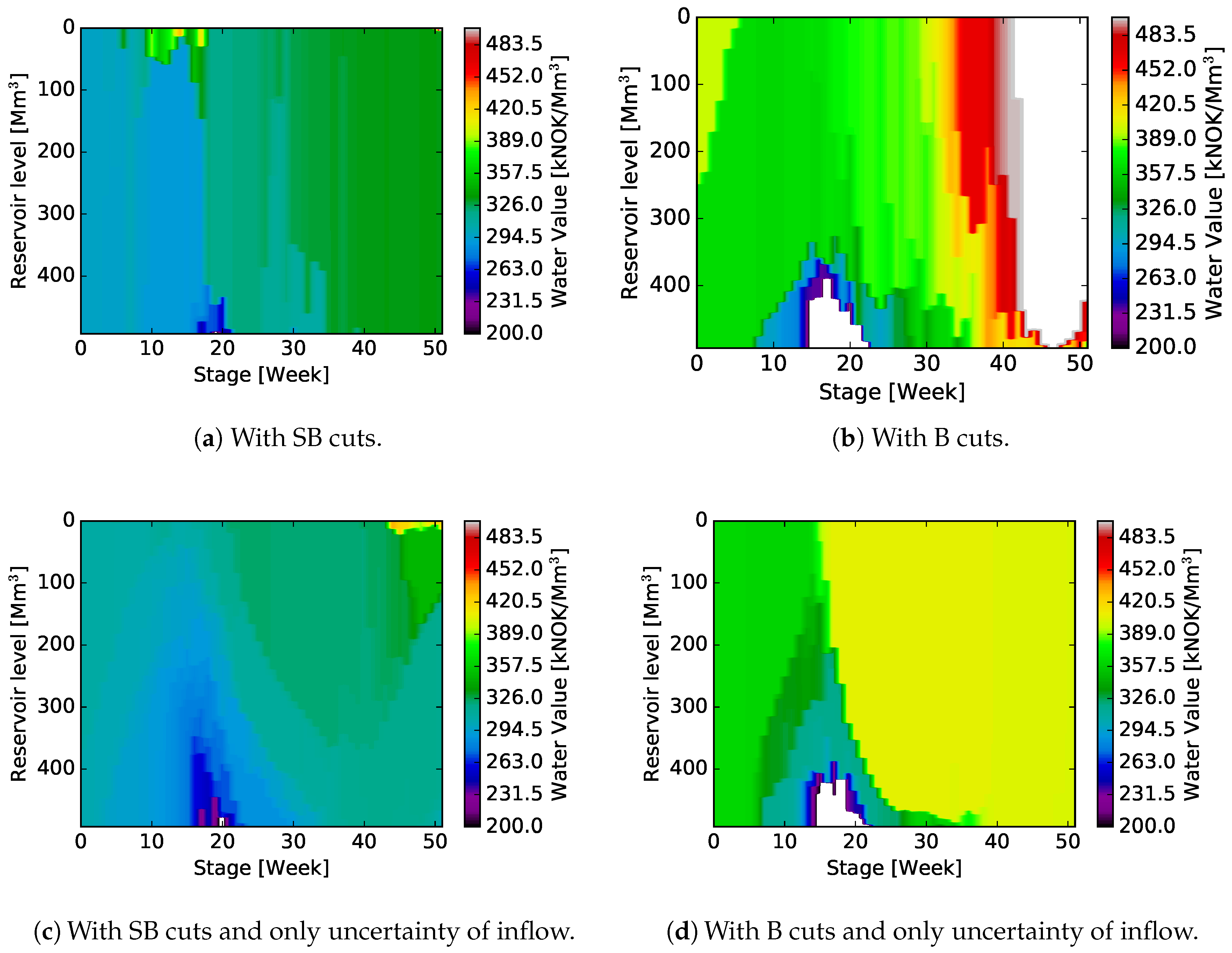
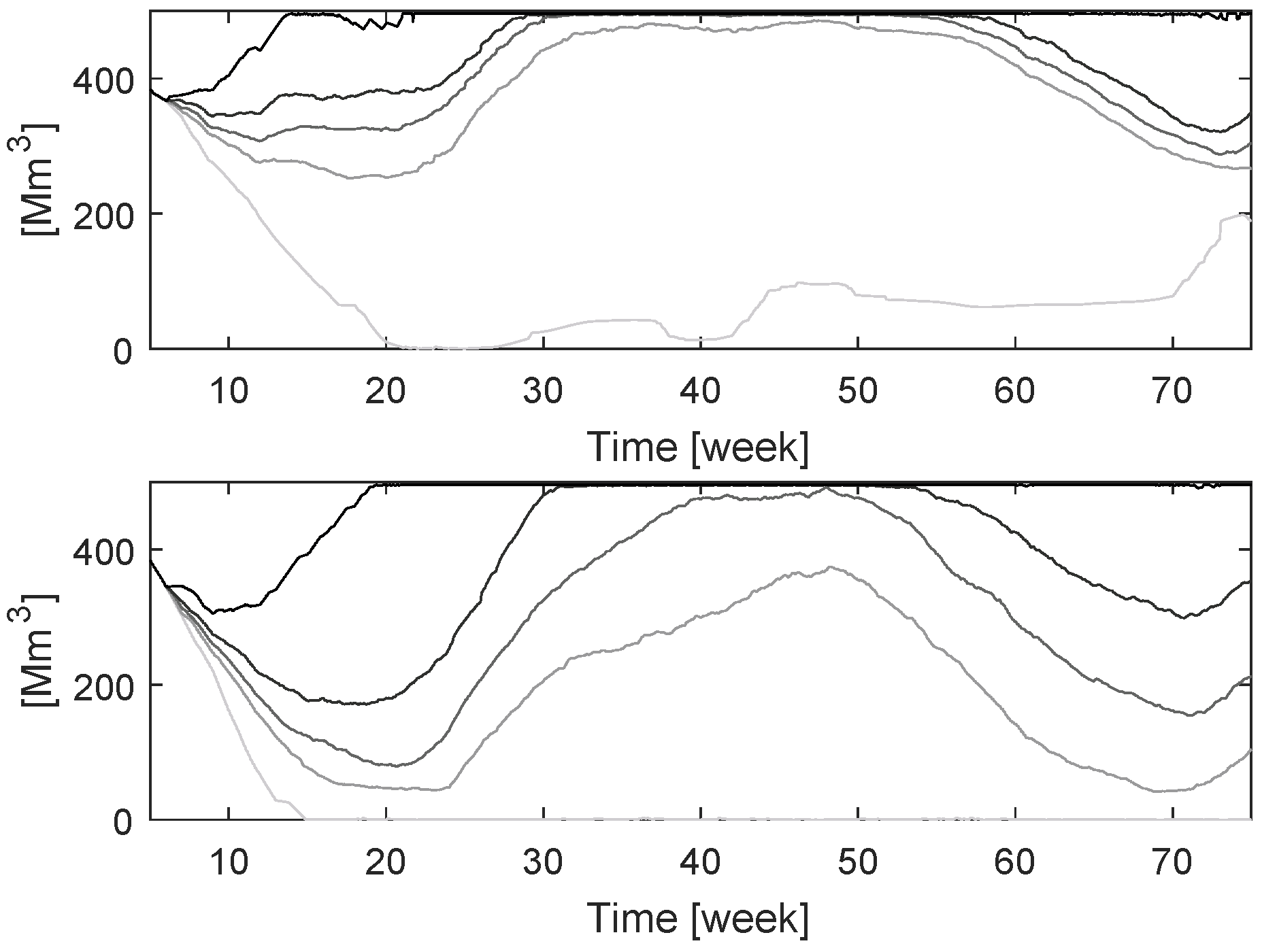
4. Case Study
Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| B | Benders |
| DP | Dynamic programming |
| EFP | Expected future profit |
| LP | Linear programming |
| MIP | Mixed integer programming |
| MTHS | Medium-term hydropower scheduling |
| SB | Strengthened Benders |
| SDDiP | Stochastic dual dynamic integer programming |
| SDDP | Stochastic dual dynamic programming |
| SDP | Stochastic dynamic programming |
| WV | Water values |
References
- Pereira, M.V.F. Optimal Stochastic Operations Scheduling of Large Hydroelectric Systems. Int. J. Electr. Power Energy Syst. 1989, 11, 161–169. [Google Scholar] [CrossRef]
- Birge, J.R. Decomposition and partitioning methods for multistage stochastic linear programs. Oper. Res. 1985, 33, 989–1007. [Google Scholar] [CrossRef]
- Pereira, M.V.F.; Campodónico, N.; Kelman, R. Application of Stochstic Dual Dp and Extensions to Hydrothermal Scheduling; Technical Report 2; PSRI: Rio De Janeiro, Brazil, 1999. [Google Scholar]
- Shapiro, A.; Tekaya, W.; da Costa, J.P.; Soares, M.P. Risk neutral and risk averse stochastic dual dynamic programming method. Eur. J. Oper. Res. 2013, 224, 375–391. [Google Scholar] [CrossRef]
- Gjelsvik, A.; Belsnes, M.; Haugstad, A. An algorithm for stochastic medium-term hydrothermal scheduling under spot price uncertainty. In Proceedings of the Power Systems Computation Conference (PSCC), Trondheim, Norway, 28 June–2 July 1999. [Google Scholar]
- Zou, J.; Ahmed, S.; Sun, X.A. Stochastic dual dynamic integer programming. Math. Program. 2018. [Google Scholar] [CrossRef]
- Hjelmeland, M.N.; Zou, J.; Helseth, A.; Ahmed, S. Nonconvex Medium-Term Hydropower Scheduling by Stochastic Dual Dynamic Integer Programming. IEEE Trans. Sustain. Energy 2018. [Google Scholar] [CrossRef]
- Thome, F.; Pereira, M.V.F.; Granville, S.; Fampa, M. Non-Convexities Representation on Hydrothermal Operation Planning Using SDDP. 2013. Available online: https://www.researchgate.net/publication/283091434_Non-Convexities_Representation_on_Hydrothermal_Operation_Planning_using_SDDP (accessed on 20 September 2018).
- Abgottspon, H.; Andersson, G. Medium-term optimization of pumped hydro storage with stochastic intrastage subproblems. In Proceedings of the Power Systems Computation Conference (PSCC), Wroclaw, Poland, 18–22 August 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Philpott, A.B.; Wahid, F.; Bonnans, F. MIDAS: A Mixed Integer Dynamic Approximation Scheme; Electric Power Optimization Centre, University of Auckland: Auckland, New Zealand, 2016. [Google Scholar]
- Steeger, G.; Rebennack, S. Dynamic Convexification within Nested Benders Decomposition using Lagrangian Relaxation: An Application to the Strategic Bidding Problem. Eur. J. Oper. Res. 2017, 257, 669–686. [Google Scholar] [CrossRef]
- Gjelsvik, A.; Mo, B.; Haugstad, A. Long- and Medium-term Operations Planning and Stochastic Modelling in Hydro-dominated Power Systems Based on Stochastic Dual Dynamic Programming. In Handbook of Power Systems I; Energy Systems; Section 2; Springer: Berlin/Heidelberg, Germany, 2010; pp. 33–55. [Google Scholar]
- Helseth, A.; Fodstad, M.; Mo, B. Optimal Medium-Term Hydropower Scheduling Considering Energy and Reserve Capacity Markets. IEEE Trans. Sustain. Energy 2016, 7, 934–942. [Google Scholar] [CrossRef]
- Baucke, R.; Downward, A.; Zakeri, G. A Deterministic Algorithm for Solving Stochastic Minimax Dynamic Programmes. 2018. Available online: http://www.optimization-online.org/DB_HTML/2018/02/6449.html (accessed on 5 September 2018).
- Downward, A.; Dowson, O.; Baucke, R. Stochastic Dual Dynamic Programming with Stagewise Dependent Objective Uncertainty. 2018. Available online: www.optimization-online.org/DB_HTML/2018/02/6454.html (accessed on 5 September 2018).
- Hjelmeland, M.N.; Helseth, A.; Korpås, M. Impact of Modelling Details on the Generation Function for a Norwegian Hydropower Producer. J. Phys. Conf. Ser. 2018, 1042, 012010. [Google Scholar] [CrossRef]
- Fosso, O.B.; Belsnes, M.M. Short-term hydro scheduling in a liberalized power system. In Proceedings of the 2004 International Conference on Power System Technology (PowerCon 2004), Singapore, 21–24 November 2004; Volume 2, pp. 1321–1326. [Google Scholar] [CrossRef]
- Guedes, L.S.M.; de Mendonça Maia, P.; Lisboa, A.C.; Vieira, D.A.G.; Saldanha, R.R. A Unit Commitment Algorithm and a Compact MILP Model for Short-Term Hydro-Power Generation Scheduling. IEEE Trans. Power Syst. 2017, 32, 3381–3390. [Google Scholar] [CrossRef]
- Borghetti, A.; D’Ambrosio, C.; Lodi, A.; Martello, S. An MILP Approach for Short-Term Hydro Scheduling and Unit Commitment With Head-Dependent Reservoir. IEEE Trans. Power Syst. 2008, 23, 1115–1124. [Google Scholar] [CrossRef]
- Diniz, A.L.; Maceira, M.E.P. A Four-Dimensional Model of Hydro Generation for the Short-Term Hydrothermal Dispatch Problem Considering Head and Spillage Effects. IEEE Trans. Power Syst. 2008, 23, 1298–1308. [Google Scholar] [CrossRef]
- Cerisola, S.; Latorre, J.M.; Ramos, A. Stochastic dual dynamic programming applied to nonconvex hydrothermal models. Eur. J. Oper. Res. EJOR 2012, 218, 687–697. [Google Scholar] [CrossRef]
- McCormick, G. Computability of global solutions to factorable nonconvex programs: Part I—Convex underestimating problems. Math. Program. 1976, 10, 147–175. [Google Scholar] [CrossRef]
- Abgottspon, H. Hydro Power Planning: Multi-Horizon Modeling and Its Applications. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2015. [Google Scholar]
- Hjelmeland, M.N.; Korpås, M.; Helseth, A. Combined SDDP and simulator model for hydropower scheduling with sales of capacity. In Proceedings of the 2016 13th International Conference on the European Energy Market (EEM), Porto, Portugal, 6–9 June 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Wolfgang, O.; Haugstad, A.; Mo, B.; Gjelsvik, A.; Wangensteen, I.; Doorman, G. Hydro reservoir handling in Norway before and after deregulation. Energy 2009, 34, 1642–1651. [Google Scholar] [CrossRef]
- Helseth, A.; Braaten, H. Efficient Parallelization of the Stochastic Dual Dynamic Programming Algorithm Applied to Hydropower Scheduling. Energies 2015, 8, 12431. [Google Scholar] [CrossRef]
| UB | stat. LB | Gap | Time | |
|---|---|---|---|---|
| (kNOK) | (kNOK) | (%) | (h min) | |
| B | 1,209,510 | 502,838 | 58.4 | 5 17 |
| SB | 820,466 | 525,493 | 36.0 | 23 59 |
| B | 1,017,580 | 537,808 | 47.1 | 5 52 |
| SB | 614,616 | 563,280 | 8.4 | 34 31 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hjelmeland, M.N.; Helseth, A.; Korpås, M. Medium-Term Hydropower Scheduling with Variable Head under Inflow, Energy and Reserve Capacity Price Uncertainty. Energies 2019, 12, 189. https://doi.org/10.3390/en12010189
Hjelmeland MN, Helseth A, Korpås M. Medium-Term Hydropower Scheduling with Variable Head under Inflow, Energy and Reserve Capacity Price Uncertainty. Energies. 2019; 12(1):189. https://doi.org/10.3390/en12010189
Chicago/Turabian StyleHjelmeland, Martin N., Arild Helseth, and Magnus Korpås. 2019. "Medium-Term Hydropower Scheduling with Variable Head under Inflow, Energy and Reserve Capacity Price Uncertainty" Energies 12, no. 1: 189. https://doi.org/10.3390/en12010189
APA StyleHjelmeland, M. N., Helseth, A., & Korpås, M. (2019). Medium-Term Hydropower Scheduling with Variable Head under Inflow, Energy and Reserve Capacity Price Uncertainty. Energies, 12(1), 189. https://doi.org/10.3390/en12010189





