Demand-Side Management with a State Space Consideration
Abstract
:1. Introduction
2. Modeling of Willingness-to-Pay Curves
2.1. Modeling Willingness-to-Pay Curves
2.2. Direct Current (DC) Optimal Power Flow
2.3. State Space
2.4. Improving the Objective Function with Demand-Side Management
- If , a scalar value of λ* is easily identified by a divide-and-conquer approach to satisfy , where . The solution x is:where ej is the jth column vector in an identity matrix.
- Otherwise,If is a rank-deficient matrix, a minimization problem is formulated:(16) is a quadratic programming.
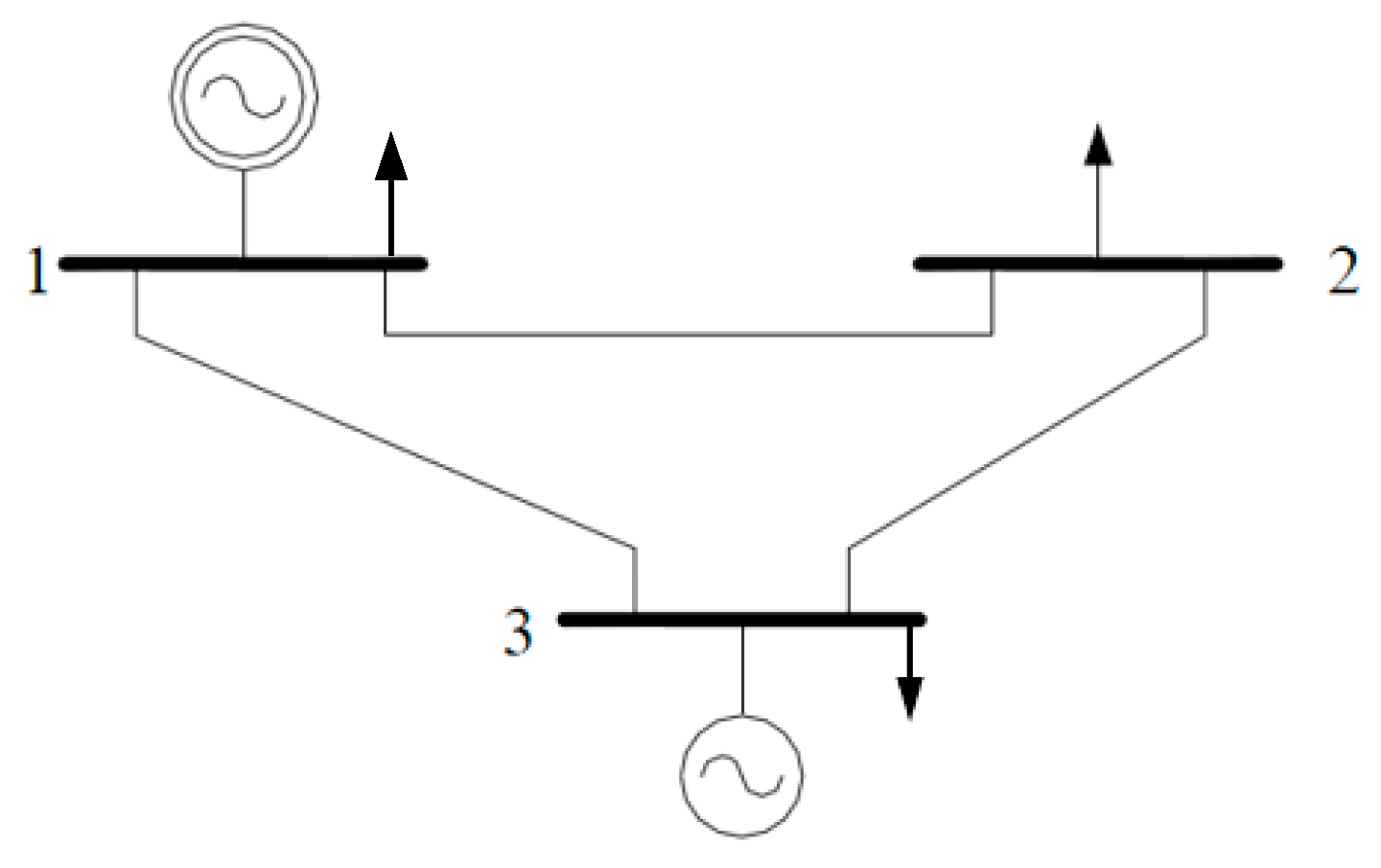
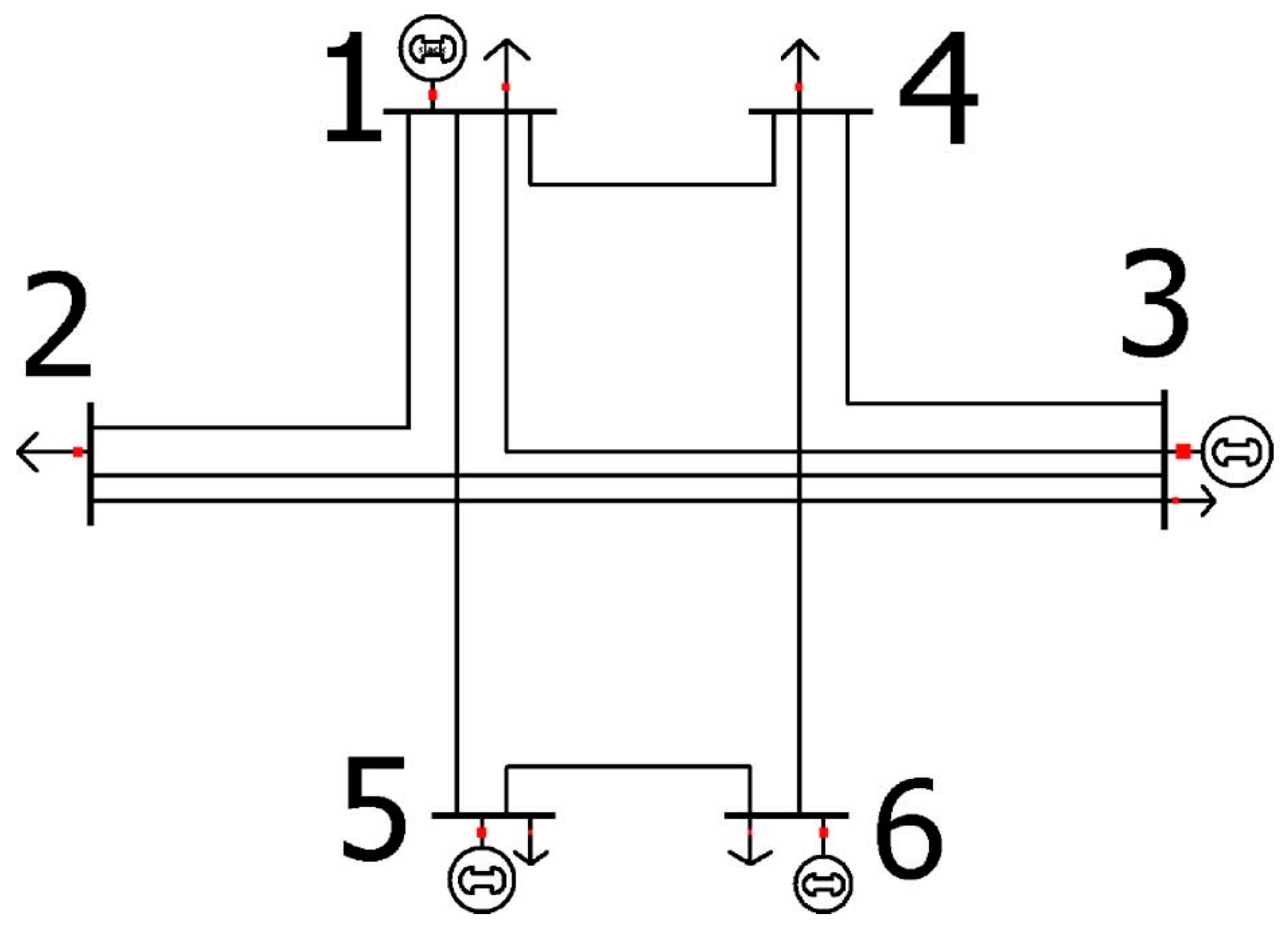
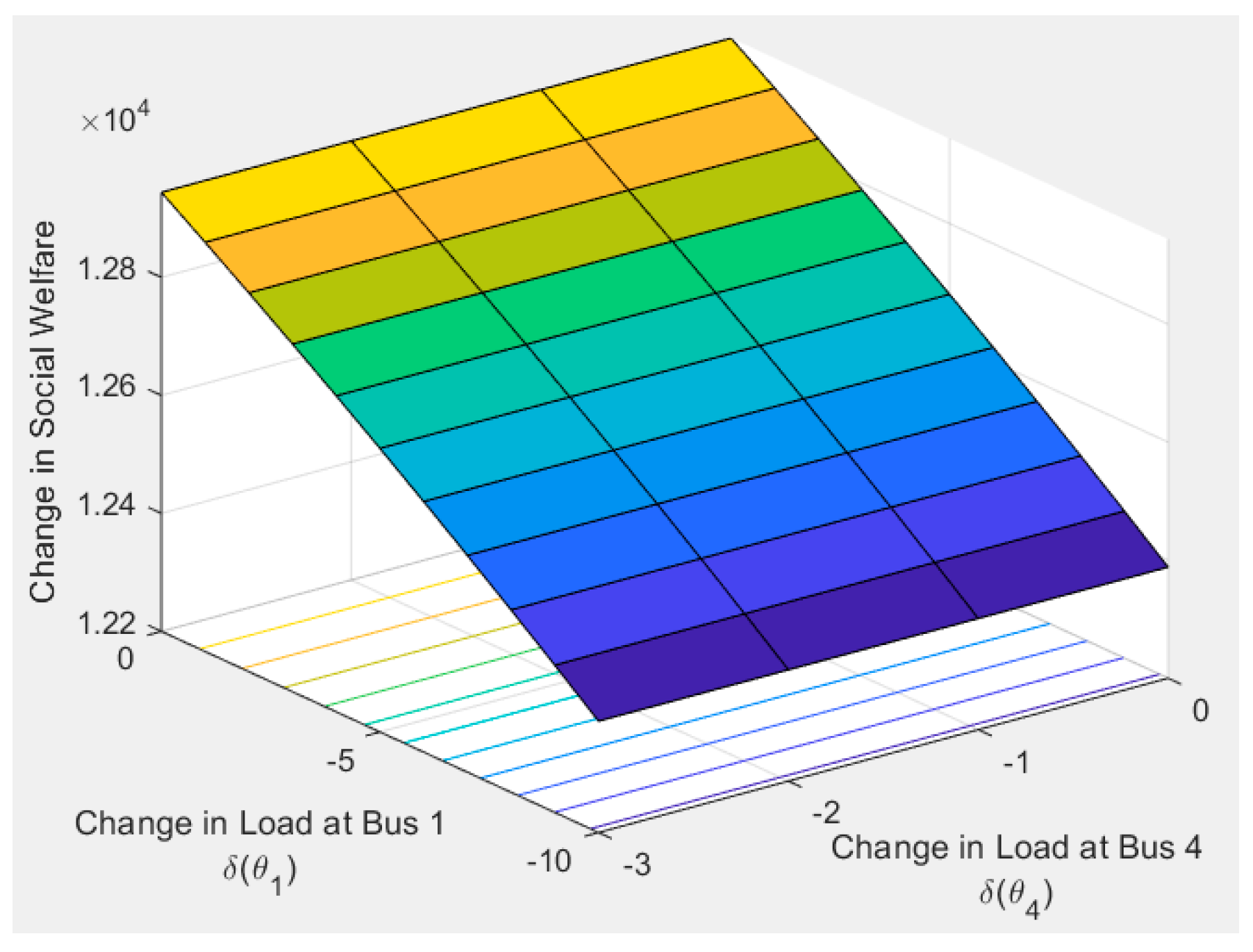
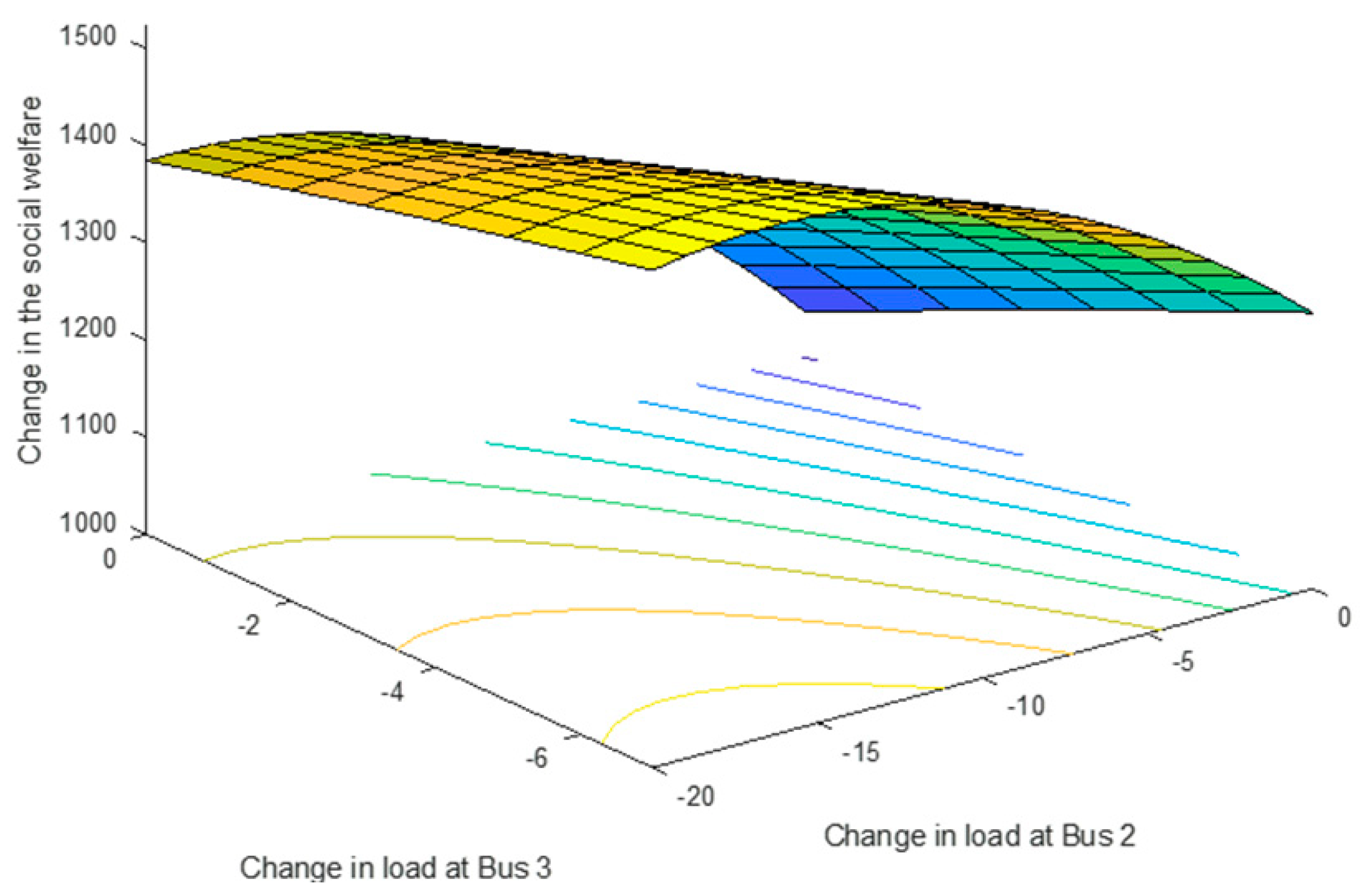
3. Simulation Results
State-Space Representation
4. Discussion and Future Works
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Energy Vortex. Available online: https://www.energyvortex.com/energydictionary/transmission_congestion.html (accessed on 13 August 2018).
- Schweppe, F.; Caramanis, M.; Tabors, R.; Bohn, R. Spot Pricing of Electricity; Springer: New York, NY, USA, 1988. [Google Scholar]
- Murthy Balijepalli, V.S.K.; Pradhan, V.; Khaparde, S.A.; Shereef, R.M. Review of demand response under smart grid paradigm. ISGT2011-India 2011, 236–243. [Google Scholar] [CrossRef]
- Energy Information Administration. U.S. Electric Utility Demand-Side Management; U.S. Department of Energy: Washington, DC, USA, 2002.
- Farhar, B.; Houston, A. Willingness to Pay for Electricity from Renewable Energy. Available online: https://www.nrel.gov/docs/legosti/old/21216.pdf (accessed on 13 August 2018).
- Ntanos, S.; Kyriakopoulos, G.; Chalikias, M.; Arabatzis, G.; Skordoulis, M. Public perceptions and willingness to pay for renewable energy: A case study from Greece. Sustainability 2018, 10, 687. [Google Scholar] [CrossRef]
- Oh, H.; Thomas, R.J. Demand side agents: modeling and simulation. IEEE Trans. Power Syst. 2008, 23, 3. [Google Scholar]
- City-Data, Advameg, Inc. Available online: http://www.city-data.com/ (accessed on 13 August 2018).
- U.S. Census Bureau. U.S. Census Bureau Announces 2010 Census Population Counts—Apportionment Counts Delivered to President; United States Census Bureau: Suitland, MD, USA, 12 December 2010.
- Kittel, C. Introduction to Solid State Physics, 4th ed.; John Wiley & Sons: New York, NY, USA, 1971. [Google Scholar]
- New York Independent System Operator, Price Data. Available online: http://www.nyiso.com/public/markets_operations/market_data/pricing_data/index.jsp (accessed on 13 August 2018).
- Zimmerman, R.D.; Murillo-Sánchez, C. MATPOWER 6.0 User’s Manual. 2016. Available online: http://www.pserc.cornell.edu/matpower/manual.pdf (accessed on 13 August 2018).
- Guo, Y.; Tong, L.; Wu, W.; Zhang, B.; Sun, H. Multi-Area Economic Dispatch via State Space Decomposition. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016. [Google Scholar]
- Ji, Y.; Kim, J.; Thomas, R.J.; Tong, L. Forecasting Real-Time Locational Marginal Price: A State Space Approach. In Proceedings of the Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 2013. [Google Scholar]
- Tondel, P.; Johansen, T.; Bemporad, A. An Algorithm for Multi-Parametric Quadratic Programming and Explicit MPC Solutions. In Proceedings of the IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001. [Google Scholar]
- Faísca, N.P.; Dua, V.; Pistikopoulos, E.N. Multiparametric linear and quadratic programming. Multi-Parametr. Model-Based Control 2007, 3–23. [Google Scholar] [CrossRef]
- McCalley, J. Costs of Generating Electrical Energy Overview. Available online: http://home.engineering.iastate.edu/~jdm/ee553/CostCurves.pdf (accessed on 13 August 2018).
- Golub, G.; Van Loan, C. Matrix Computations; Johns Hopkins University Press: Baltimore, MD, USA, 2012. [Google Scholar]
- Oberdieck, R.; Diangelakis, N.A.; Papathanasiou, M.M.; Nascu, I.; Pistikopoulos, E.N. POP—Parametric Optimization Toolbox. Ind. Eng. Chem. Res. 2016, 55, 8979–8991. [Google Scholar]
- NYISO, New York Independent System Operator, Power Trends 2018. Available online: https://home.nyiso.com/wp-content/uploads/2018/05/2018-Power-Trends_050318.pdf (accessed on 13 August 2018).
- Oh, H. A New Network Reduction Methodology for Power System Planning Studies. IEEE Trans. Power Syst. 2010, 25, 677–684. [Google Scholar] [CrossRef]
- Oh, H. Aggregation of Buses for a Network Reduction. IEEE Trans. Power Syst. 2012, 27, 705–712. [Google Scholar]
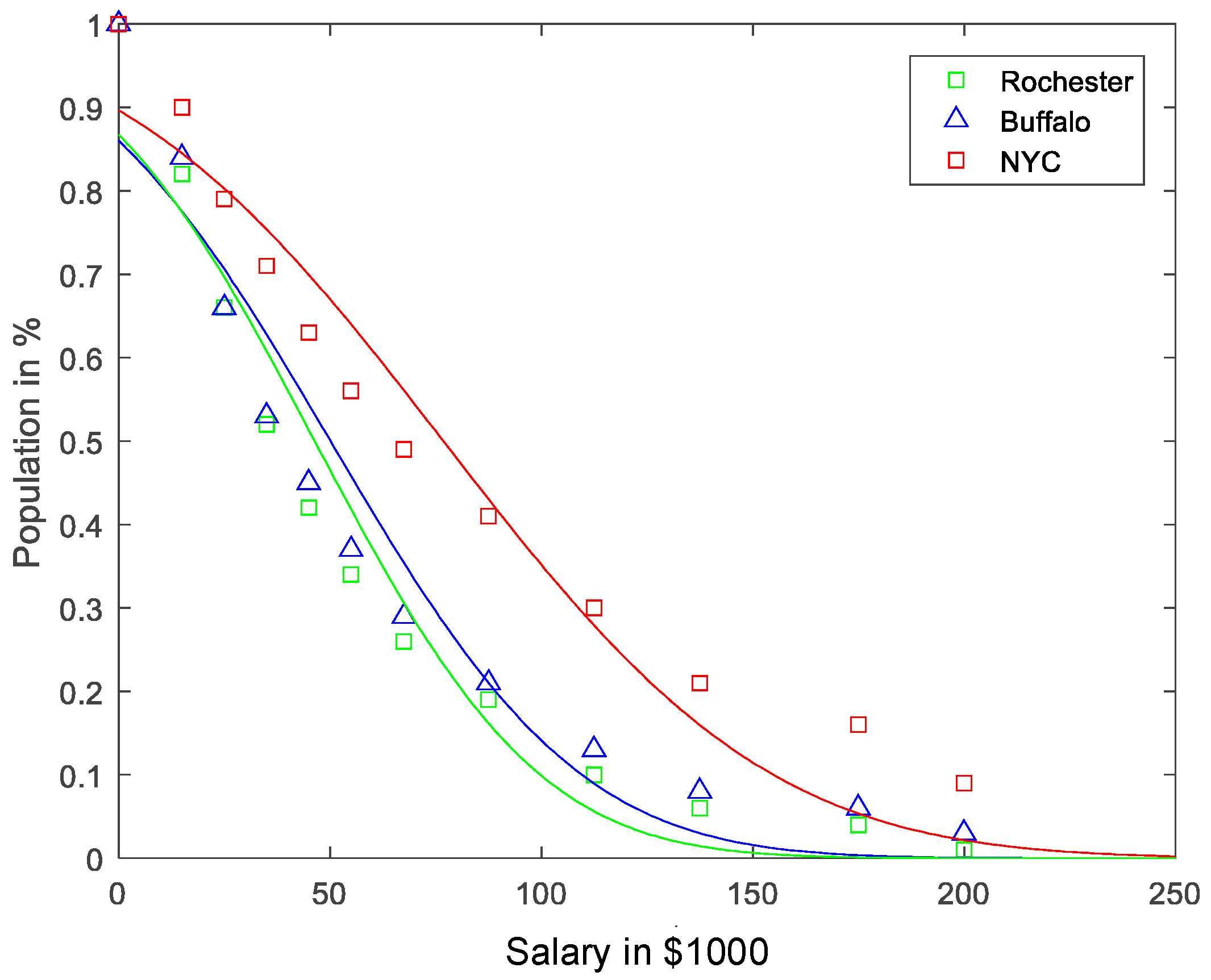




| Population [9] | Area in Mile 2 | Average Salary, μ | Standard Deviation, σ | |
|---|---|---|---|---|
| Rochester | 208,880 | 37.1 | $46,410 | $41,630 |
| New York City | 8,175,133 | 468.4 | $76,820 | $60,900 |
| Buffalo | 256,902 | 52.5 | $50,120 | $46,420 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, H. Demand-Side Management with a State Space Consideration. Energies 2018, 11, 2444. https://doi.org/10.3390/en11092444
Oh H. Demand-Side Management with a State Space Consideration. Energies. 2018; 11(9):2444. https://doi.org/10.3390/en11092444
Chicago/Turabian StyleOh, HyungSeon. 2018. "Demand-Side Management with a State Space Consideration" Energies 11, no. 9: 2444. https://doi.org/10.3390/en11092444





