Investigation of the Effect of Winding Clamping Structure on Frequency Response Signature of 11 kV Distribution Transformer
Abstract
:1. Introduction
2. Methodology
2.1. Experiment Setup
2.2. Statistical Analysis
2.2.1. Pearson’s Correlation Coefficient (PCC)
2.2.2. Spearman’s Correlation Coefficient (SCC)
2.2.3. Kendall’s Tau Correlation Coefficient (KCC)
2.2.4. Cross-Correlation Coefficient (CCF)
2.2.5. Root Mean Square Error (RMSE)
2.2.6. Absolute Sum of Logarithmic Error (ASLE)
2.2.7. F-Test
2.2.8. Relative Factor (RF)
3. Frequency Response Plot
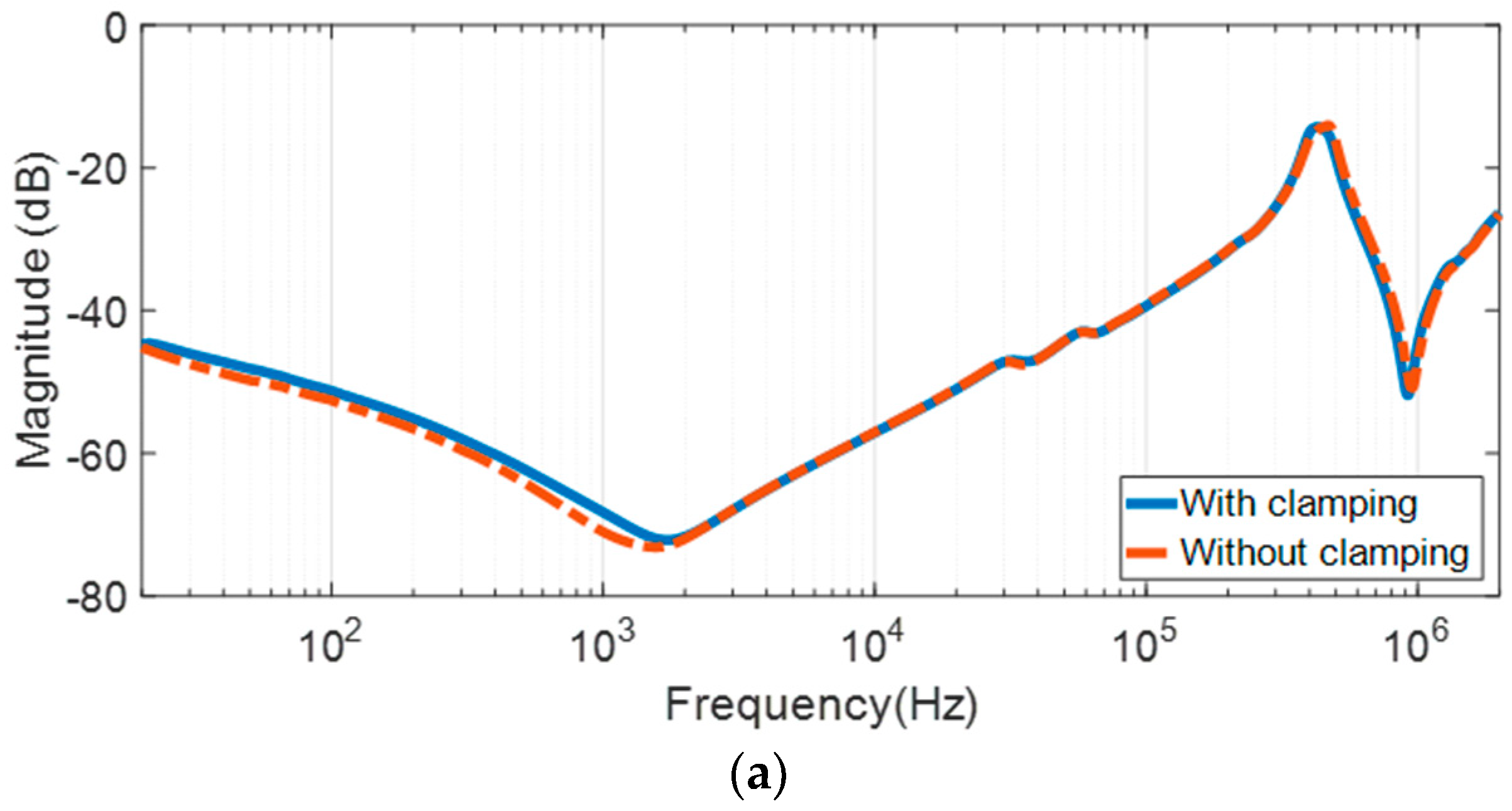
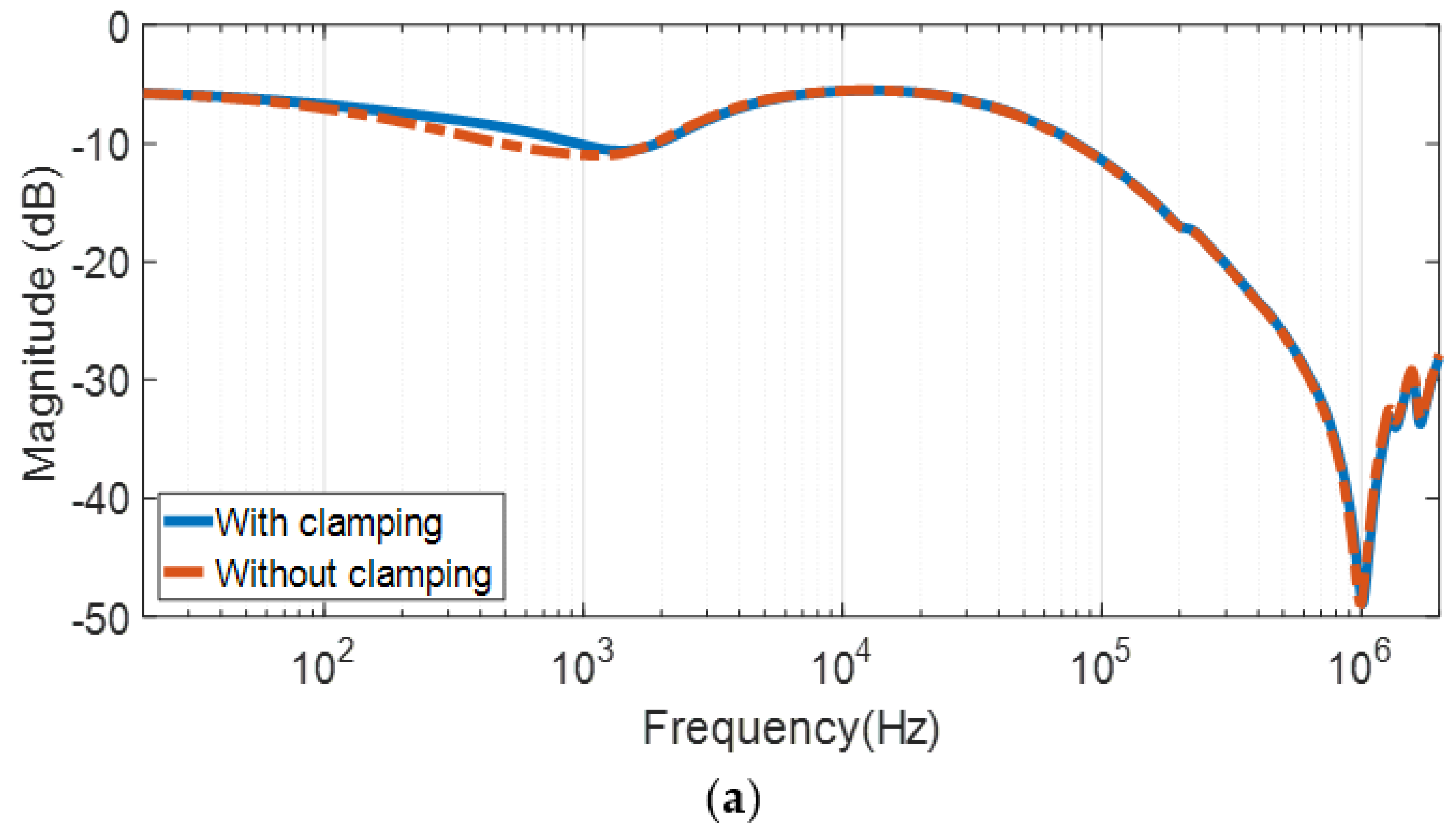
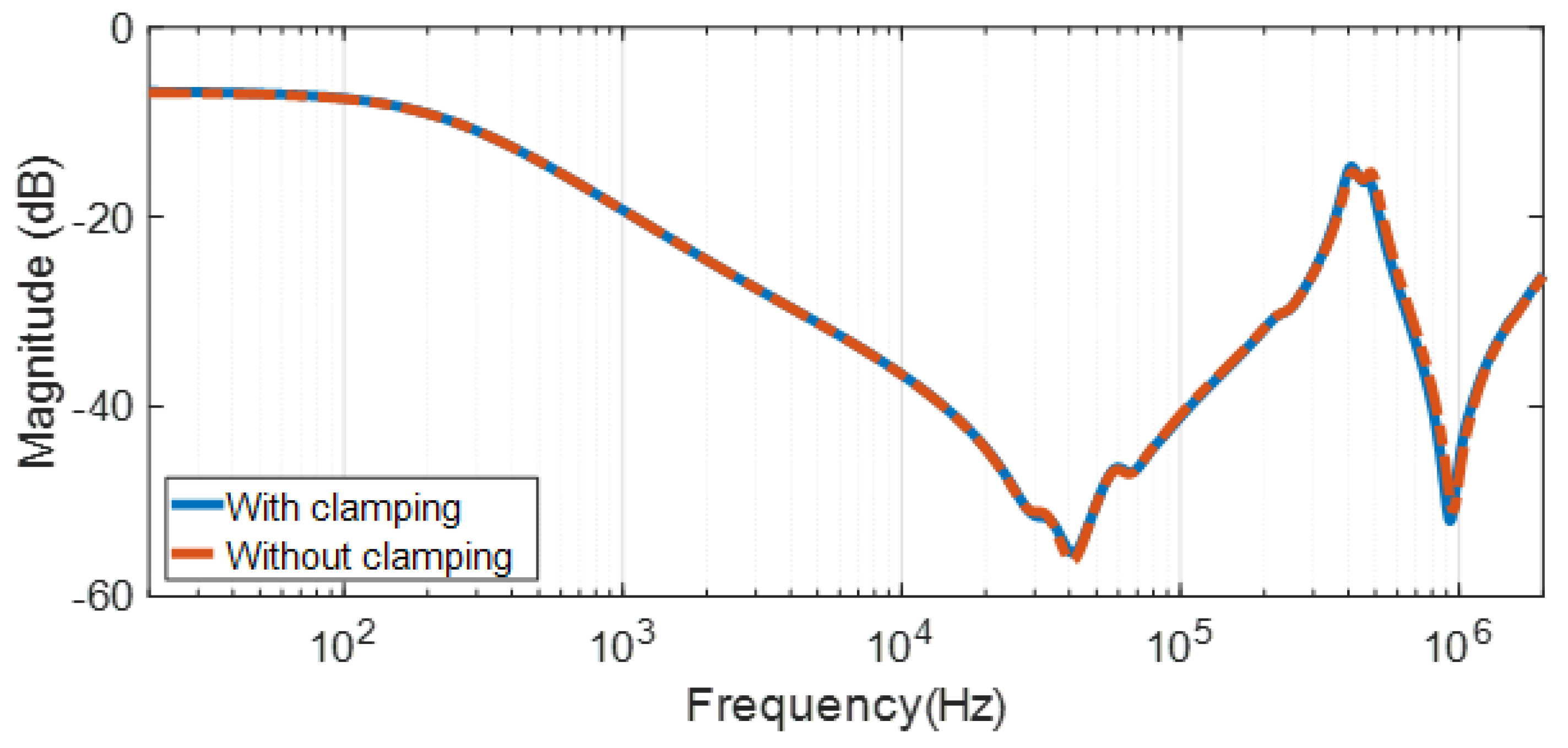
3.1. End-to-End Open Circuit Test
3.2. End-to-End Short Circuit Test
4. Statistical Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Amini, A.; Das, N.; Islam, S. Impact of buckling deformation on the FRA signature of power transformer. In Proceedings of the 2013 Australasian Universities Power Engineering Conference (AUPEC), Hobart, TAS, Australia, 29 September–3 October 2013; pp. 1–4. [Google Scholar]
- Bagheri, M.; Naderi, M.S.; Blackburn, T. Advanced transformer winding deformation diagnosis: Moving from off-line to on-line. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1860–1870. [Google Scholar] [CrossRef]
- Reykherdt, A.A.; Davydov, V. Case studies of factors influencing frequency response analysis measurements and power transformer diagnostics. IEEE Electr. Insul. Mag. 2011, 27, 22–30. [Google Scholar] [CrossRef]
- Bagheri, M.; Phung, B.; Blackburn, T.; Naderian, A. Influence of temperature on frequency response analysis of transformer winding. In Proceedings of the 2013 IEEE Electrical Insulation Conference (EIC), Ottawa, ON, Canada, 2–5 June 2013; pp. 1393–1404. [Google Scholar]
- Behjat, V.; Mahvi, M. Statistical approach for interpretation of power transformers frequency response analysis results. IET Sci. Meas. Technol. 2015, 9, 367–375. [Google Scholar] [CrossRef]
- Nirgude, P.M.; Ashokraju, D.; Rajkumar, A.D.; Singh, B.P. Application of numerical evaluation techniques for interpreting frequency response measurements in power transformers. IET Sci. Meas. Technol. 2008, 2, 275–285. [Google Scholar] [CrossRef]
- Tang, W.H.; Shintemirov, A.; Wu, Q.H. Detection of minor winding deformation fault in high frequency range for power transformer. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–6. [Google Scholar]
- Ryder, S.A. Diagnosing Transformer Faults Using Frequency Response Analysis. IEEE Electr. Insul. Mag. 2003, 19, 16–22. [Google Scholar] [CrossRef]
- Wimmer, R.; Tenbohlen, S.; Feser, K.; Kraetge, A.; Krüger, M.; Christian, J. Development of algorithms to assess the FRA. In Proceedings of the 15th International Symposium on High Voltage Engineering, Ljubljana, Slovenia, 27–31 August 2007; pp. 1–6. [Google Scholar]
- Bolboaca, S.D.; Jäntschi, L. Pearson versus Spearman and Kendall’s tau correlation analysis on structure-activity relationships of biologic active compounds. Leonardo J. Sci. 2006, 5, 179–200. [Google Scholar]
- Hauke, J.; Kossowski, T. Comparison of values of Pearson’s and Spearman’s correlation coefficients on the same sets of data. Quaest. Geogr. 2011, 30, 87–93. [Google Scholar] [CrossRef]
- Shong, N. Pearson’s Versus Spearman’s and Kendall’s Correlation Coefficients for Continuous Data. Master’s Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2010. [Google Scholar]
- Vaca Vargas, P.; Mombello, E. Time-Frequency Analysis for the Interpretation of FRA Measurements. In Proceedings of the VDE High Voltage Technology 2016, ETG-Symposium, Berlin, Germany, 14–16 November 2016; pp. 390–394. [Google Scholar]
- Shintemirov, A.; Tang, W.H.; Wu, Q.H. Transformer winding condition assessment using frequency response analysis and evidential reasoning. IET Electr. Power Appl. 2010, 4, 198–212. [Google Scholar] [CrossRef]
- Abu-Siada, A.; Islam, S. A novel online technique to detect power transformer winding faults. IEEE Trans. Power Deliv. 2012, 27, 849–857. [Google Scholar] [CrossRef]
- Yousof, M.F.M.; Ekanayake, C.; Saha, T.K. Study of transformer winding deformation by frequency response analysis. In Proceedings of the IEEE Power and Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Abu-Siada, A.; Hashemnia, N.; Islam, S.; Masoum, M. Understanding power transformer frequency response analysis signatures. IEEE Electr. Insul. Mag. 2013, 29, 48–56. [Google Scholar] [CrossRef]
- Kraetge, A.; Krüger, M.; Fong, P. Frequency response analysis—Status of the worldwide standardization activities. In Proceedings of the International Conference on Condition Monitoring and Diagnosis CMD, G-05, Beijing, China, 21–24 April 2008; pp. 651–654. [Google Scholar]
- Picher, P.; Lapworth, J.; Noonan, T.; Christian, J. Mechanical Condition Assessment of Transformer Windings Using Frequency Response Analysis (FRA); CIGRE: Paris, France, 2008. [Google Scholar]
- Islam, S.M. Detection of shorted turns and winding movements in large power transformers using frequency response analysis. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting, Singapore, 23–27 January 2000; pp. 2233–2238. [Google Scholar]
- Institute of Electrical and Electronics Engineers. IEEE Std. C57.149-2012—IEEE Guide for the Application and Interpretation of Frequency Response Analysis for Oil-Immersed Transformers; IEEE Power and Energy Society: Park Avenue, NY, USA, 2013; pp. 1–72. [Google Scholar]
- Mohammad, M.S.; Samimi, H.; Tenbohlen, P.S. The Numerical Indices Proposed for the Interpretation of the FRA Results: A Review. In Proceedings of the VDE High Voltage Technology 2016, ETG-Symposium, Berlin, Deutschland, 14–16 November 2016; pp. 377–383. [Google Scholar]
- Sardar, S.; Kumar, A.; Chatterjee, B.; Dalai, S. Application of Statistical Interpretation Technique for Frequency Response Analysis and Detection of Axial Displacement in Transformer Winding. In Proceedings of the 2017 IEEE Calcutta Conference (CALCON), Kolkata, India, 2–3 December 2017; pp. 461–464. [Google Scholar]
- Patel, M.R. Dynamic Response of Power Transformers Under Axial Short Circuit Forces Part II—Windings and Clamps as a Combined System. IEEE Trans. Power Appar. Syst. 1973, PAS-92, 1567–1576. [Google Scholar] [CrossRef]
- Patel, M.R. Dynamic Response of Power Transformers Under Axial Short Circuit Forces Part I—Winding and Clamp as Individual Components. IEEE Trans. Power Appar. Syst. 1973, PAS-92, 1558–1566. [Google Scholar] [CrossRef]
- Hashemnia, N.; Abu-Siada, A.; Masoum, M.A.S.; Islam, S.M. Characterization of transformer FRA signature under various winding faults. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis (CMD), Bali, Indonesia, 23–27 September 2012; pp. 446–449. [Google Scholar]
- International Electrotechnical Commission. IEC 60076-18, Power Transformers—Part 18: Measurement of Frequency Response; International Electrotechnical Commission: Geneva, Switzerland, 2012. [Google Scholar]
- Mukherjee, P.; Satish, L. Estimating the Equivalent Air-cored Inductance of Transformer Winding from Measured FRA. IEEE Trans. Power Deliv. 2018, 33, 1620–1627. [Google Scholar] [CrossRef]
- Yousof, M.F.M. Frequency Response Analysis for Transformer Winding Condition Monitoring. Ph.D. Thesis, The University of Queensland, St Lucia, QLD, Australia, 2015. [Google Scholar]
- Myers, J.L.; Well, A.; Lorch, R.F. Research Design and Statistical Analysis; Routledge: Abingdon, UK, 2012. [Google Scholar]
- Saleh, S.M.; EL-Hoshy, S.H.; Gouda, O.E. Proposed diagnostic methodology using the cross-correlation coefficient factor technique for power transformer fault identification. IET Electr. Power Appl. 2017, 11, 412–422. [Google Scholar] [CrossRef]
- Mahvi, M.; Behjat, V.; Rahimpour, E. New statistical approach to interpret power transformer frequency response analysis: Non-parametric statistical methods. IET Sci. Meas. Technol. 2016, 10, 364–369. [Google Scholar]
- Yousof, M.F.M.; Riang, S.; Uyup, M.K.A. The influence of data size in statistical analysis of power transformer frequency response. In Proceedings of the 2016 IEEE International Conference on Power and Energy (PECon), Melaka, Malaysia, 28–29 November 2016; pp. 595–599. [Google Scholar]
- Tarimoradi, H.; Gharehpetian, G.B. Novel calculation method of indices to improve classification of transformer winding fault type, location, and extent. IEEE Trans. Ind. Inform 2017, 13, 1531–1540. [Google Scholar] [CrossRef]
- Kennedy, G.M.; Mcgrail, A.J.; Lapworth, J.A. Using Cross-Correlation Coefficients to Analyze Transformer Sweep Frequency Response Analysis. In Proceedings of the IEEE Power Engineering Society Conference and Exposition in Africa—PowerAfrica, Johannesburg, South Africa, 16–20 July 2007; pp. 1–6. [Google Scholar]
- Yousof, M.F.M.; Ekanayake, C.; Saha, T.K. Frequency response analysis to investigate deformation of transformer winding. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2359–2367. [Google Scholar] [CrossRef]
- Yousof, M.F.M.; Ekanayake, C.; Saha, T.K. Locating inter-disc faults in transformer winding using frequency response analysis. In Proceedings of the 2013 Australasian Universities Power Engineering Conference (AUPEC), Hobart, TAS, Australia, 29 September–3 October 2013; pp. 1–6. [Google Scholar]
- Badgujar, K.P.; Kulkarni, S.V. Fuzzy Logic Based Identification of Deviations in Frequency Response of Transformer Windings. pp. 1–6. Available online: http://www.iitk.ac.in/npsc/Papers/NPSC2012/papers/12145.pdf (accessed on 5 April 2018).
- Kim, J.W.; Park, B.; Jeong, S.C.; Kim, S.W.; Park, P. Fault diagnosis of a power transformer using an improved frequency-response analysis. IEEE Trans. Power Deliv. 2005, 20, 169–178. [Google Scholar] [CrossRef]




| Degree of Winding Deformation | Relative Factors, Rxy |
|---|---|
| Severe Deformation | RLF < 0.6 |
| Obvious Deformation | 1.0 > RLF ≥ 0.6 or RMF < 0.6 |
| Slight Deformation | 2.0 > RLF ≥ 1.0 or 0.6 ≤ RMF < 1.0 |
| Normal Winding | RLF ≥ 2.0, RMF ≥ 1.0 and RHF ≥ 0.6 |
| Test Configuration | Frequency Range | PCC | SCC | KCC | CCF | RMSE | ASLE | F-Test |
|---|---|---|---|---|---|---|---|---|
| HV R-Y | 20 Hz–2 kHz | 0.9981 | 0.9977 | 0.9841 | 0.9982 | 0.4816 | 1.6715 | 0.6742 |
| 2 kHz–400 kHz | 0.9999 | 0.9998 | 0.9965 | 0.9994 | 0.1722 | 0.7407 | 0.9397 | |
| 400 kHz–2 MHz | 0.9872 | 0.9905 | 0.9312 | 0.9766 | 1.4203 | 0.8155 | 0.7324 | |
| HV Y-B | 20 Hz–1.5 kHz | 0.9971 | 0.9990 | 0.9907 | 0.997 | 0.5308 | 2.2633 | 0.0072 |
| 1.5 kHz–450 kHz | 0.9986 | 0.9999 | 0.9971 | 0.9985 | 0.7856 | 1.1532 | 0.5466 | |
| 450 kHz–2 MHz | 0.9766 | 0.9841 | 0.9158 | 0.9766 | 1.7513 | 1.213 | 0.3021 | |
| HV B-R | 20 Hz–2 kHz | 0.9982 | 0.9982 | 0.9865 | 0.9982 | 0.4599 | 1.3665 | 0.3748 |
| 2 kHz–450 kHz | 0.9998 | 0.9998 | 0.9971 | 0.9998 | 0.2735 | 0.6346 | 0.9014 | |
| 450 kHz–2 MHz | 0.9345 | 0.9591 | 0.8666 | 0.9344 | 2.7098 | 0.9446 | 0.4024 |
| Test Configuration | Frequency Range | PCC | SCC | KCC | CCF | RMSE | ASLE | F-Test |
|---|---|---|---|---|---|---|---|---|
| LV r-n | 20 Hz–1.5 kHz | 0.9701 | 0.9931 | 0.9679 | 0.9707 | 0.3377 | 0.7739 | 0.0000 |
| 1.5 kHz–1 MHz | 0.9999 | 0.9997 | 0.9897 | 0.9999 | 0.1470 | 0.3384 | 0.6274 | |
| 1 MHz–2 MHz | 0.9986 | 0.9968 | 0.9656 | 0.9986 | 0.2971 | 0.3791 | 0.5096 | |
| LV y-n | 20 Hz–1.5 kHz | 0.9858 | 0.9573 | 0.8848 | 0.9863 | 0.1954 | 1.3230 | 0.0002 |
| 1.5 kHz–1 MHz | 0.9995 | 0.9987 | 0.9783 | 0.9995 | 0.2945 | 0.5848 | 0.5205 | |
| 1 MHz–2 MHz | 0.9976 | 0.9954 | 0.9613 | 0.9976 | 0.3419 | 0.6492 | 0.1454 | |
| LV b-n | 20 Hz–1.5 kHz | 0.9827 | 0.9919 | 0.9656 | 0.9829 | 0.2533 | 0.6625 | 0.0029 |
| 1.5 kHz–1 MHz | 0.9992 | 0.9998 | 0.9915 | 0.9992 | 0.3747 | 0.3748 | 0.2105 | |
| 1 MHz–2 MHz | 0.9865 | 0.9906 | 0.9358 | 0.9865 | 0.9179 | 0.5742 | 0.0426 |
| Test Configuration | Relative Factor, Rxy | Suggested Winding Condition | ||
|---|---|---|---|---|
| LF | MF | HF | ||
| HV R-Y | 10 | 10 | 10 | Normal |
| HV Y-B | 10 | 10 | 10 | |
| HV B-R | 10 | 10 | 10 | |
| LV r-n | 10 | 10 | 10 | |
| LV y-n | 10 | 10 | 10 | |
| LV b-n | 10 | 10 | 10 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srikanta Murthy, A.; Azis, N.; Al-Ameri, S.; Mohd Yousof, M.F.; Jasni, J.; Talib, M.A. Investigation of the Effect of Winding Clamping Structure on Frequency Response Signature of 11 kV Distribution Transformer. Energies 2018, 11, 2307. https://doi.org/10.3390/en11092307
Srikanta Murthy A, Azis N, Al-Ameri S, Mohd Yousof MF, Jasni J, Talib MA. Investigation of the Effect of Winding Clamping Structure on Frequency Response Signature of 11 kV Distribution Transformer. Energies. 2018; 11(9):2307. https://doi.org/10.3390/en11092307
Chicago/Turabian StyleSrikanta Murthy, Avinash, Norhafiz Azis, Salem Al-Ameri, Mohd Fairouz Mohd Yousof, Jasronita Jasni, and Mohd Aizam Talib. 2018. "Investigation of the Effect of Winding Clamping Structure on Frequency Response Signature of 11 kV Distribution Transformer" Energies 11, no. 9: 2307. https://doi.org/10.3390/en11092307
APA StyleSrikanta Murthy, A., Azis, N., Al-Ameri, S., Mohd Yousof, M. F., Jasni, J., & Talib, M. A. (2018). Investigation of the Effect of Winding Clamping Structure on Frequency Response Signature of 11 kV Distribution Transformer. Energies, 11(9), 2307. https://doi.org/10.3390/en11092307






