Transient Faults in Wind Energy Conversion Systems: Analysis, Modelling Methodologies and Remedies
Abstract
1. Introduction
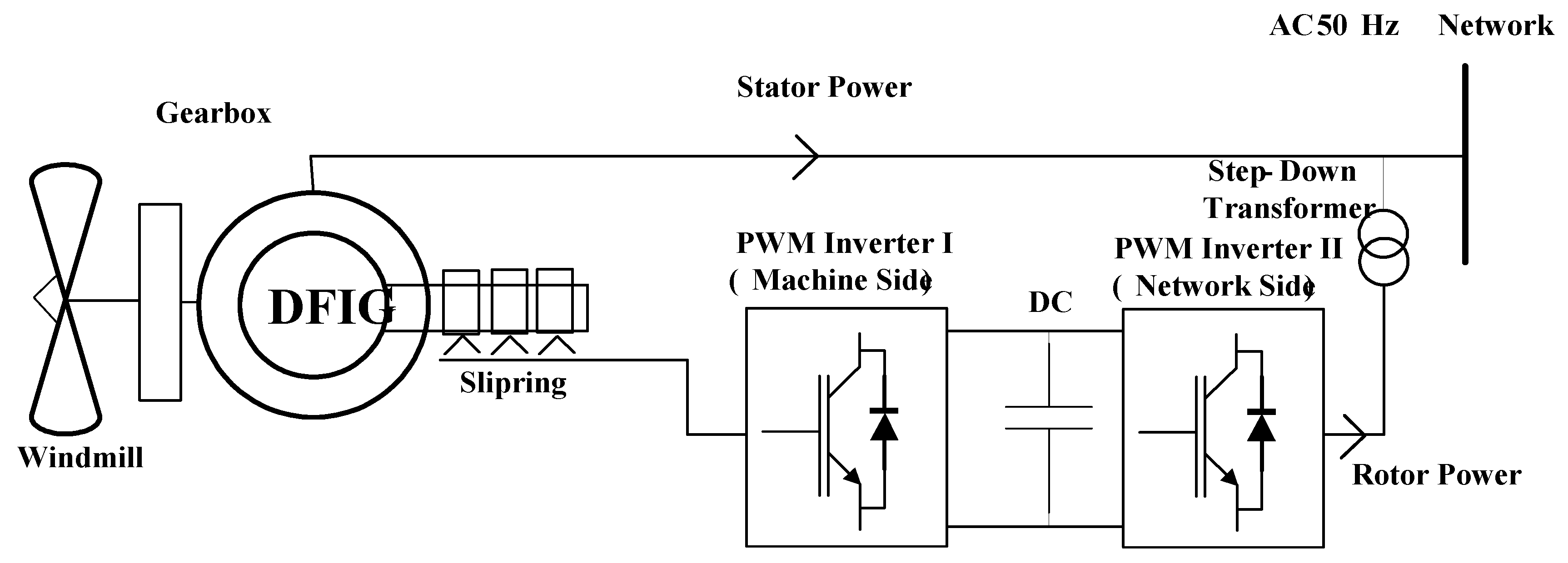
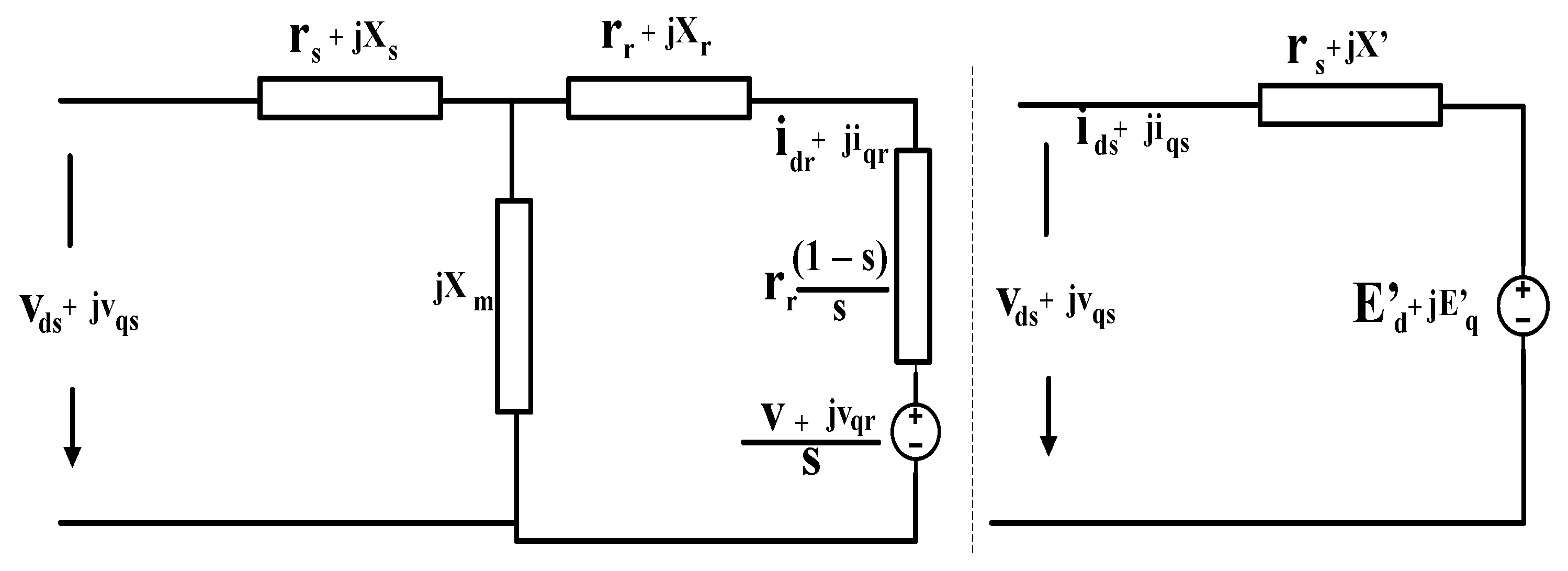
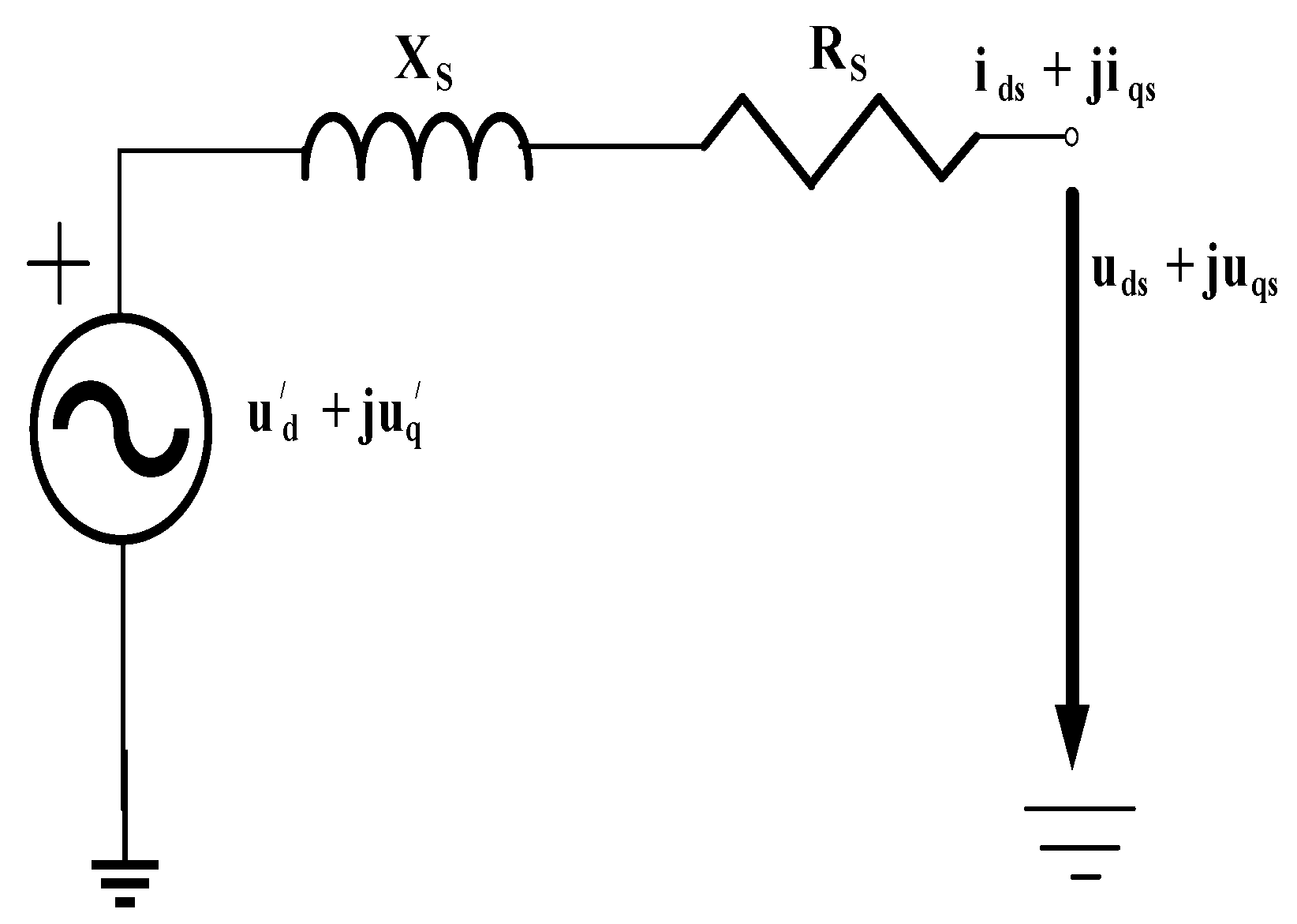
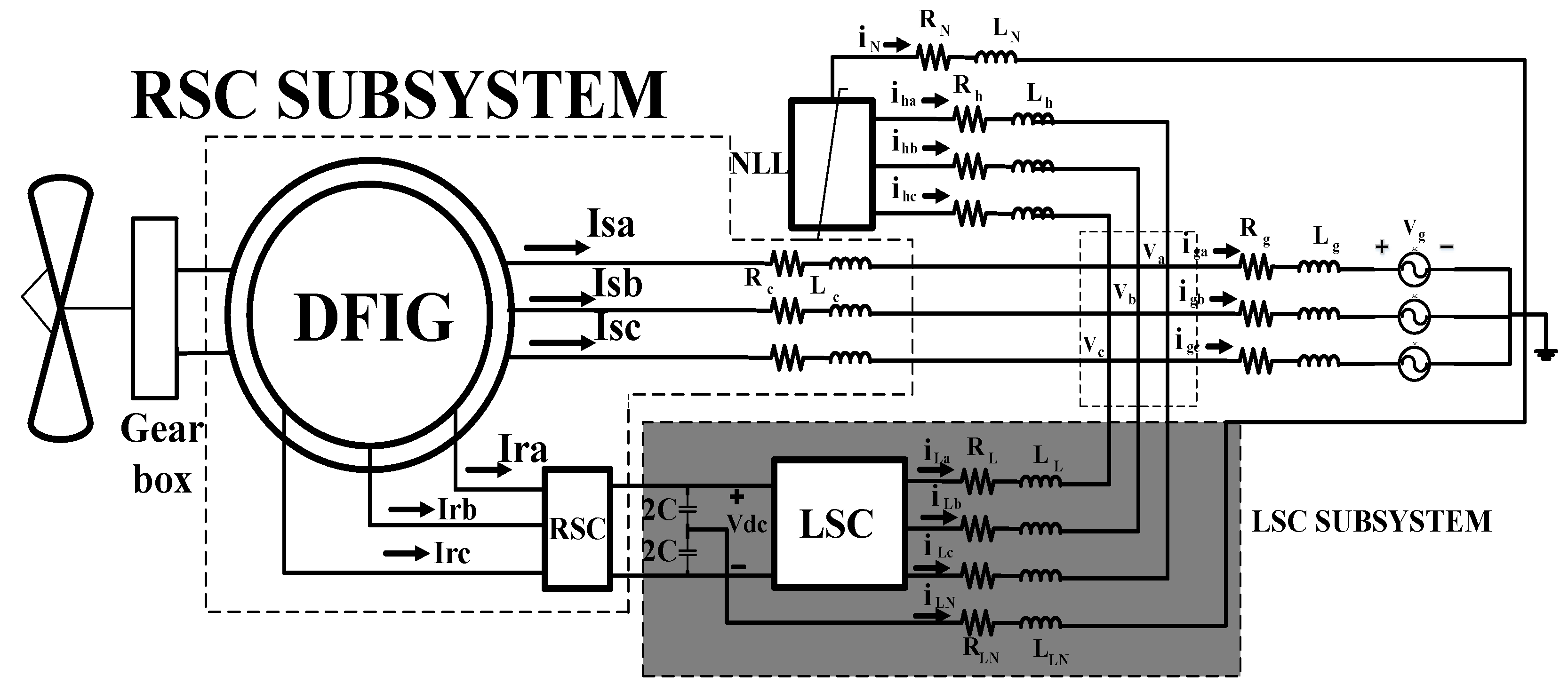
2. Transient Models of Associate Components in WECS
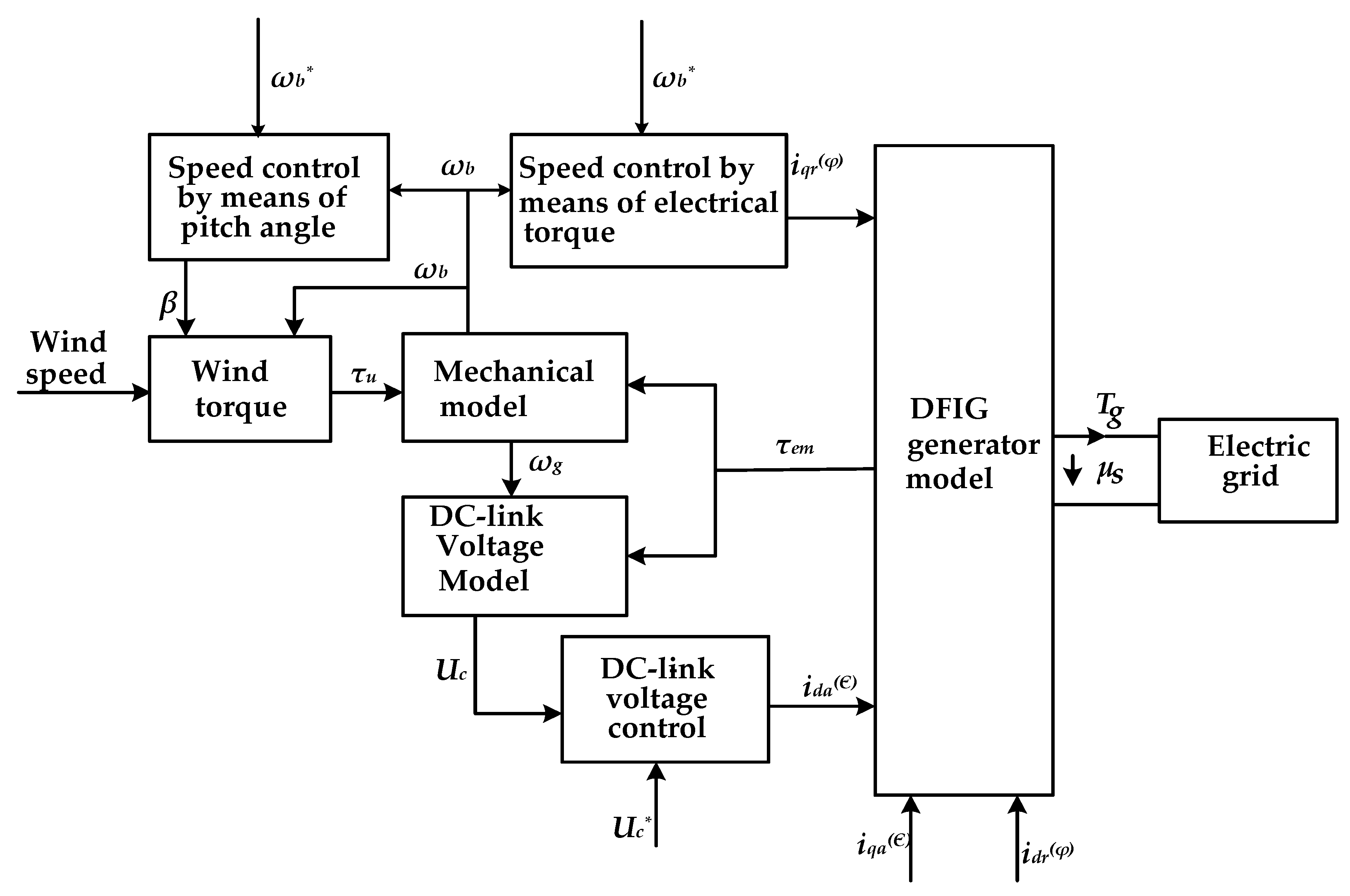
2.1. Wind Turbine Generator Transient Model
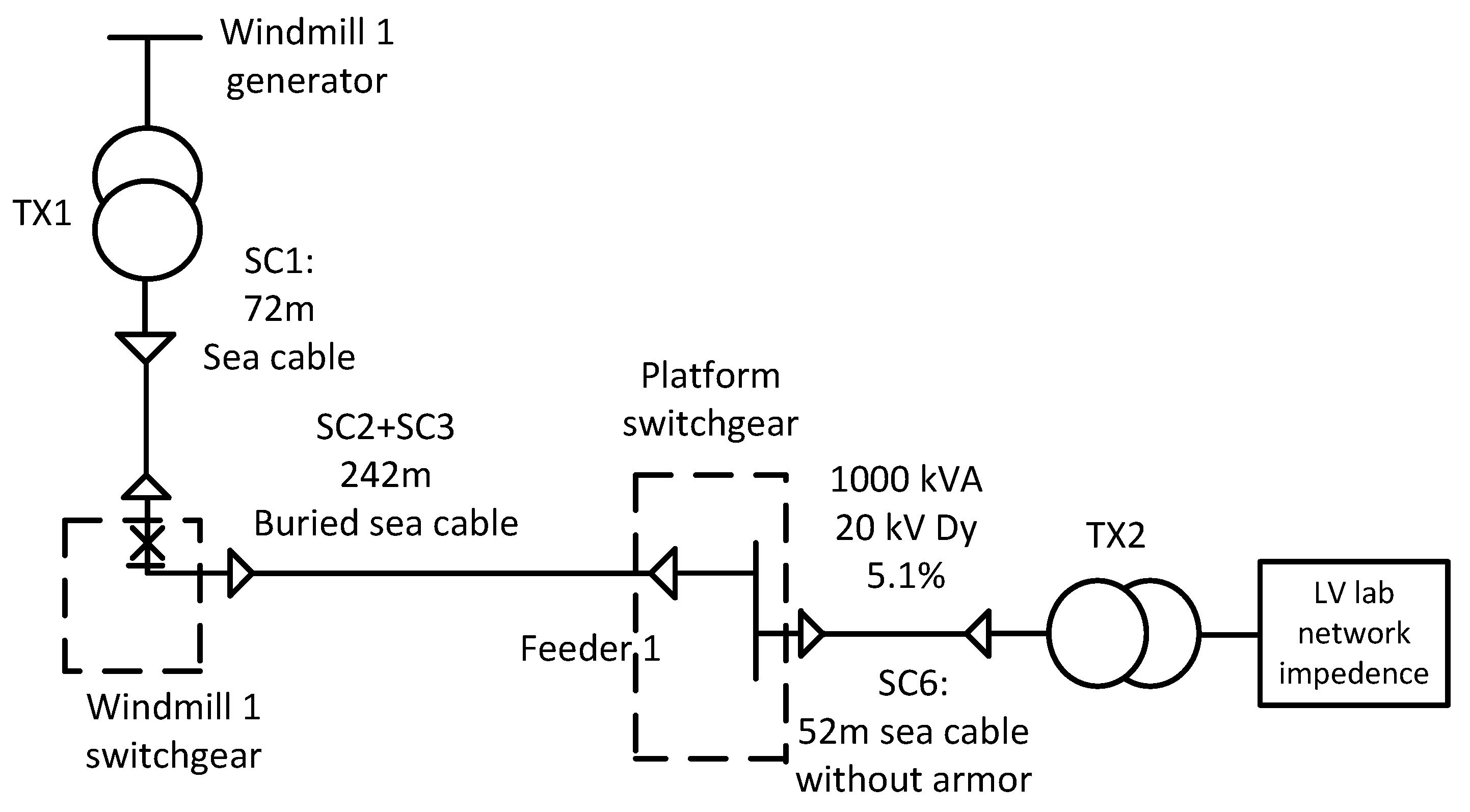
2.1.1. Windmill Transient Model
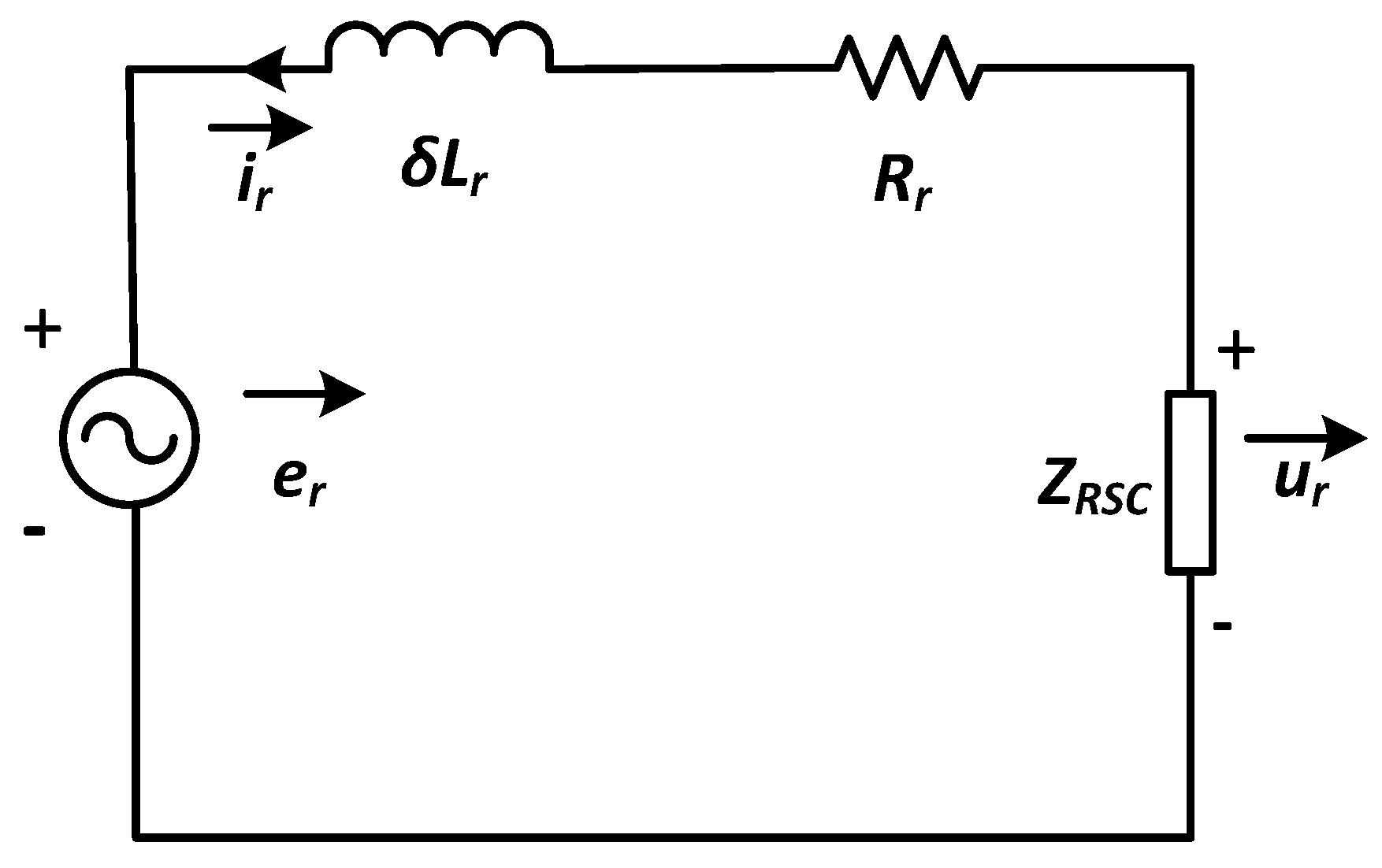
2.1.2. Circuit Breaker Transient Models
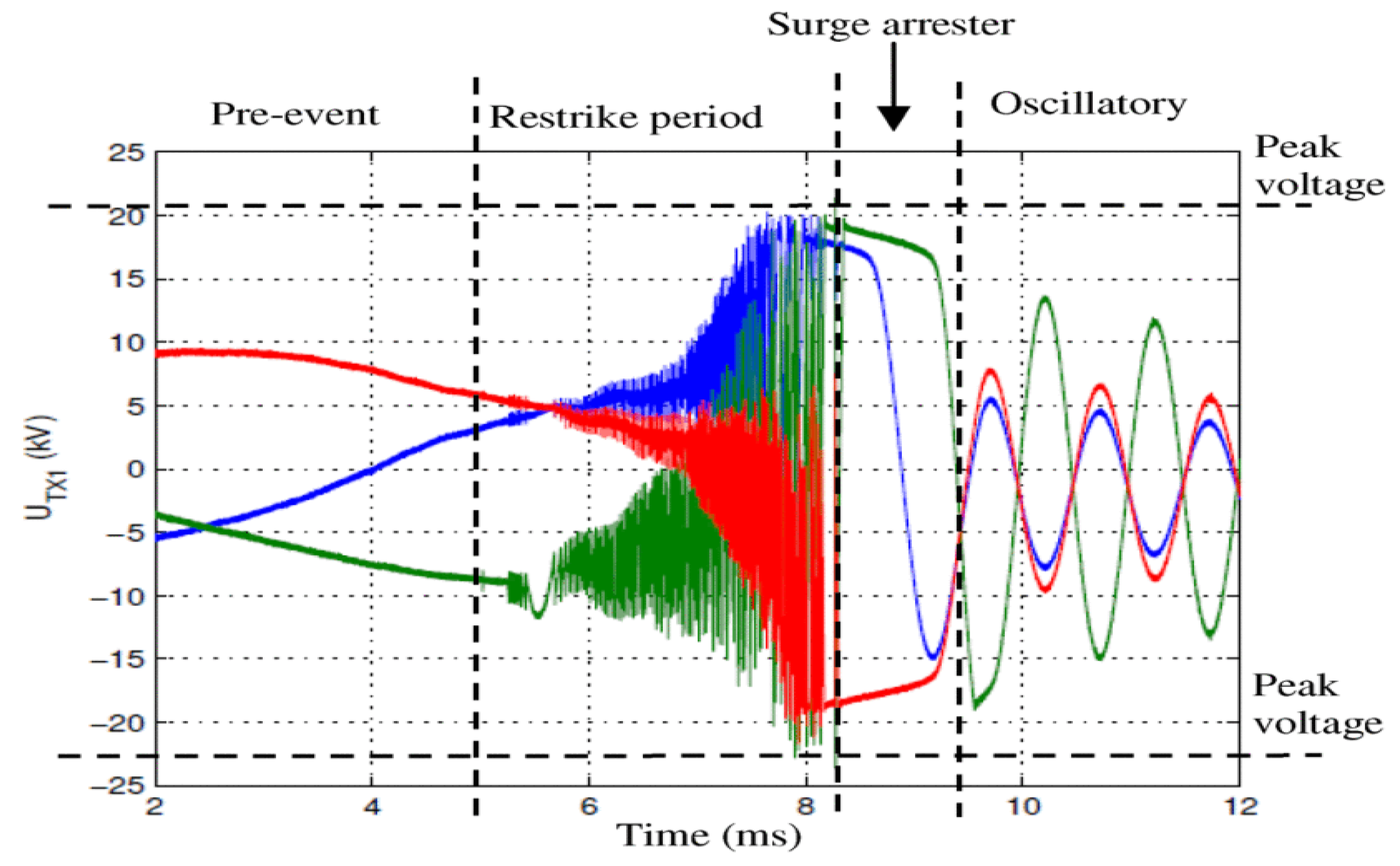
3. Transient Analysis in WECS
- (1)
- maximum voltage,
- (2)
- rate at which the voltage rises,
- (3)
- oscillation frequencies at each closing of the restrike or prestrike period,
- (4)
- breaker maximum current,
- (5)
- traveling time of the cables and
- (6)
- the relationship of the voltage to the current.
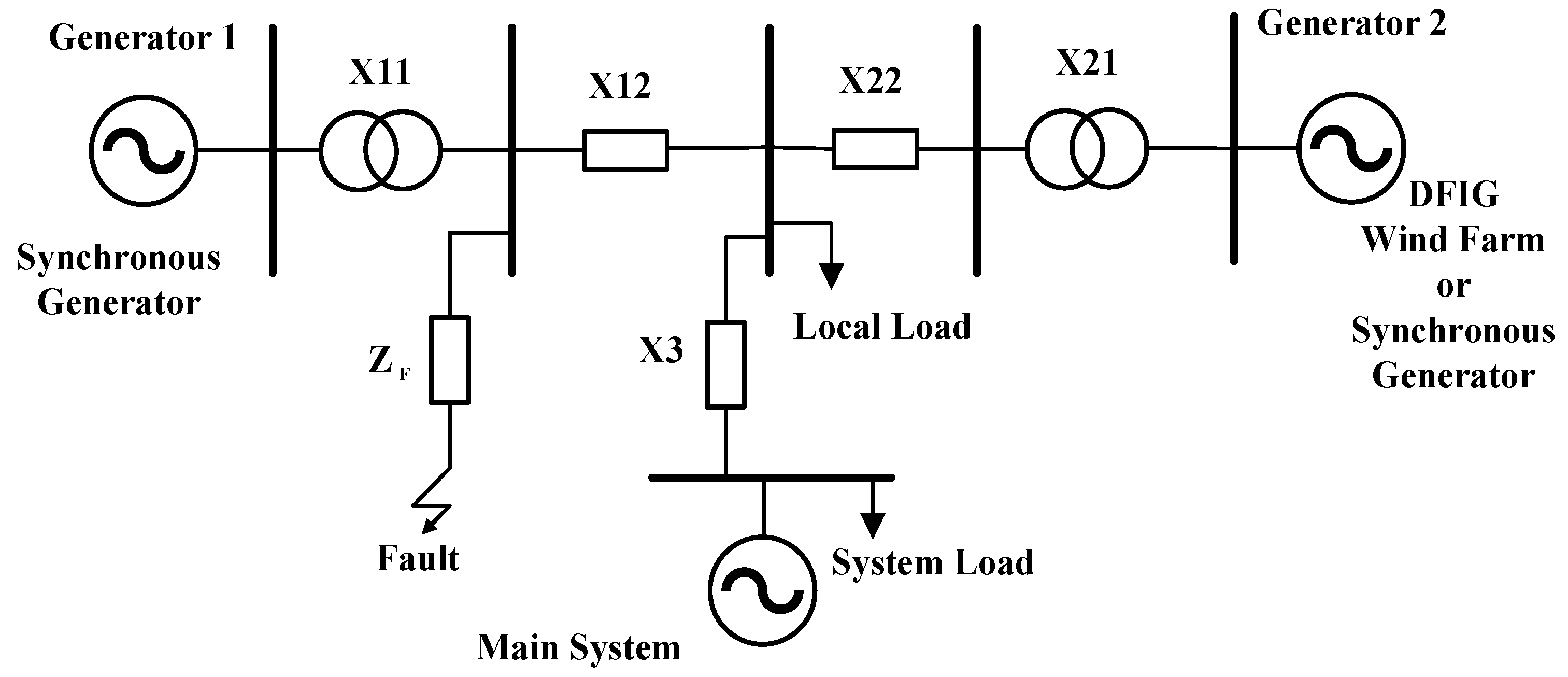
Transient Stability Analysis in WECS
4. Transient Phenomena in HVDC and Offshore Wind Farms
HVDC Transient Protection and Improvement Scheme
5. Methods for Mitigation and Control of Transients in Wind Turbine Generators
5.1. Transient Control Techniques in WECS
- fast recovery
- speed variation of the transient for a limited period that enables a special type of generator to inject the required amount of active power to remedy the transient frequency deviations.
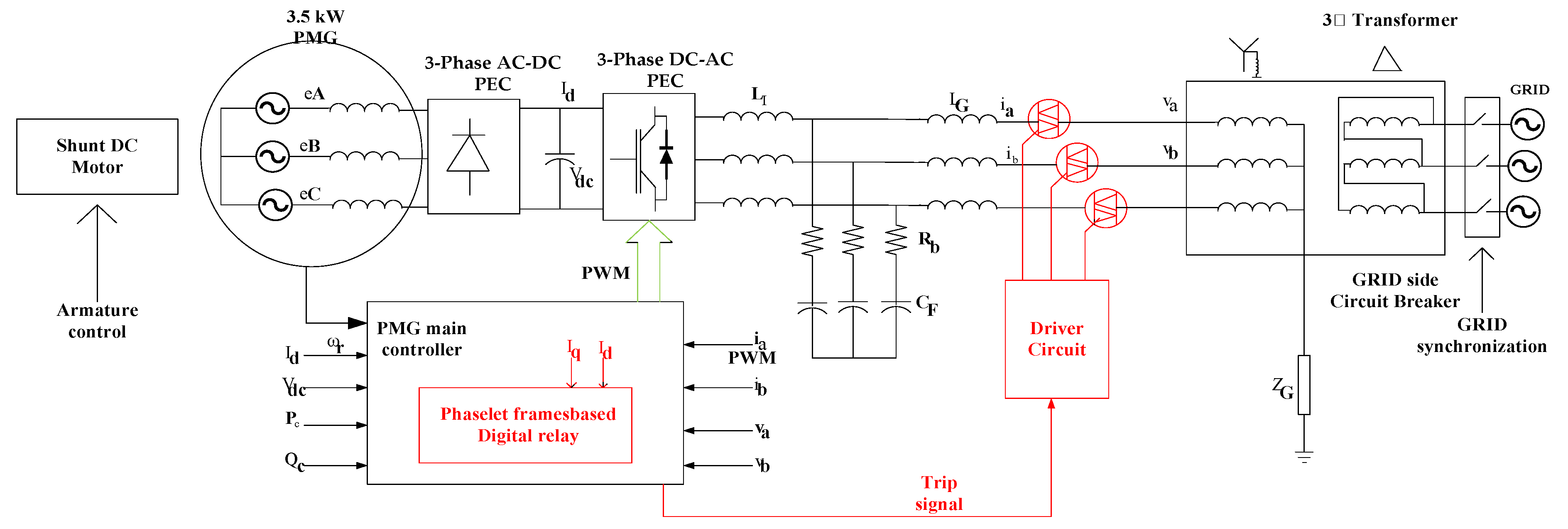
5.2. Transient Protection Techniques on WECS
5.3. Transient Protection of Wind Turbine Blade from Lightning
6. Discussion
7. Conclusions and Predictive Validity of Research
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Simulation Parameters of the DFIG | |
| Rated Power | 4 kW |
| Stator resistance | |
| Rotor resistance | |
| Stator inductance | |
| Rotor inductance | |
| Mutual inductance | |
| Rated voltage | |
| Number of pole pairs | |
| Rated speed | |
| Friction coefficient | |
| Moment of inertia | |
| Slip | |
| Parameters of the emulated wind turbines | |
| Rated Power | 10 kW |
| Number of pole pairs | |
| Blade diameter | |
| Gain | |
| Moment of inertia | |
| Friction coefficient | |
| Air density | |
References
- Chen, Z.; Guerrero, J.M.; Blaabjerg, F. A review of the state of the art of power electronics for wind turbines. IEEE Trans. Power Electron. 2009, 24, 1859–1875. [Google Scholar] [CrossRef]
- Kramer, W.; Chakraborty, S.; Kroposki, B.; Thomas, H. Advanced Power Electronic Interfaces for Distributed Energy Systems; Report NREL/Tp-581-42672; National Renewable Energy Laboratory: Cambridge, MA, USA, 2008; Volume 1.
- Simoes, M.G.; Farret, F.A. Alternative Energy Systems: Design and Analysis with Induction Generators; CRC Press: Boca Raton, FL, USA, 2011; Volume 13. [Google Scholar]
- Nunes, M.V.; Lopes, J.P.; Zurn, H.H.; Bezerra, U.H.; Almeida, R.G. Influence of the variable-speed wind generators in transient stability margin of the conventional generators integrated in electrical grids. IEEE Trans. Energy Convers. 2004, 19, 692–701. [Google Scholar] [CrossRef]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar]
- Gautam, D.; Vittal, V.; Harbour, T. Impact of increased penetration of DFIG-based wind turbine generators on transient and small signal stability of power systems. IEEE Trans. Power Syst. 2009, 24, 1426–1434. [Google Scholar] [CrossRef]
- Tajdinian, M.; Seifi, A.R.; Allahbakhshi, M. Transient Stability of Power Grids Comprising Wind Turbines: New Formulation, Implementation, and Application in Real-Time Assessment. IEEE Syst. J. 2018, 1–12. [Google Scholar] [CrossRef]
- Datta, R.; Ranganathan, V. Variable-speed wind power generation using doubly fed wound rotor induction machine-a comparison with alternative schemes. IEEE Trans. Energy Convers. 2002, 17, 414–421. [Google Scholar] [CrossRef]
- Mauricio, J.M.; Marano, A.; Gómez-Expósito, A.; Ramos, J.L.M. Frequency regulation contribution through variable-speed wind energy conversion systems. IEEE Trans. Power Syst. 2009, 24, 173–180. [Google Scholar] [CrossRef]
- Badrzadeh, B.; Hogdahl, M.; Isabegovic, E. Transients in wind power plants—Part I: Modeling methodology and validation. IEEE Trans. Ind. Appl. 2012, 48, 794–807. [Google Scholar] [CrossRef]
- Geebeln, B.; Leterme, W.; Van Hertem, D. Analysis of DC breaker requirements for different HVDC grid protection schemes. In Proceedings of the 11th IET International Conference on AC and DC Power Transmission, Edgbaston, Birmingham, 10–12 February 2015. [Google Scholar]
- Kunjumuhammed, L.P.; Pal, B.C.; Oates, C.; Dyke, K.J. The Adequacy of the Present Practice in Dynamic Aggregated Modeling of Wind Farm Systems. IEEE Trans. Sustain. Energy 2017, 8, 23–32. [Google Scholar] [CrossRef]
- Wu, Y.-K.; Wang, L.; Huang, Y.-Q.; Liu, S.-W. Overview of Imprtant State-of-the-Art Technologies in Offshore Wind Energy Systems. Int. J. Smart Grid Clean Energy 2013, 2, 215–222. [Google Scholar] [CrossRef]
- Nehrir, M.; Wang, C.; Strunz, K.; Aki, H.; Ramakumar, R.; Bing, J.; Miao, Z.; Salameh, Z. A review of hybrid renewable/alternative energy systems for electric power generation: Configurations, control, and applications. IEEE Trans. Sustain. Energy 2011, 2, 392–403. [Google Scholar] [CrossRef]
- Nehrir, M.H.; Wang, C.; Strunz, K.; Aki, H.; Ramakumar, R.; Bing, J.; Miao, Z.; Salameh, Z. A review of hybrid renewable/alternative energy systems for electric power generation: Configurations, control, and applications. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; Volume 2, pp. 392–403. [Google Scholar]
- Lei, Y.; Mullane, A.; Lightbody, G.; Yacamini, R. Modeling of the wind turbine with a doubly fed induction generator for grid integration studies. IEEE Trans. Energy Convers. 2006, 21, 257–264. [Google Scholar] [CrossRef]
- Feijóo, A.; Cidrás, J.; Carrillo, C. A third order model for the doubly-fed induction machine. Electr. Power Syst. Res. 2000, 56, 121–127. [Google Scholar] [CrossRef]
- Qiao, W.; Zhou, W.; Aller, J.M.; Harley, R.G. Wind speed estimation based sensorless output maximization control for a wind turbine driving a DFIG. IEEE Trans. Power Electron. 2008, 23, 1156–1169. [Google Scholar] [CrossRef]
- Simon, L.; Swarup, K.S. Wide area oscillation damping control with DFIG based wind turbines using WAMS. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Hansen, A.D.; Jauch, C.; Sørensen, P.E.; Iov, F.; Blaabjerg, F. Dynamic Wind Turbine Models in Power System Simulation Tool; Danmarks Tekniske Universitet, Risø Nationallaboratoriet for Bæredygtig Energi: Roskilde, Denmark, 2004. [Google Scholar]
- Li, W.; Chao, P.; Liang, X.; Sun, Y.; Qi, J.; Chang, X. Modeling of complete fault ride-through processes for DFIG-Based wind turbines. Renew. Energy 2018, 118, 1001–1014. [Google Scholar] [CrossRef]
- Junyent-Ferré, A.; Gomis-Bellmunt, O.; Sumper, A.; Sala, M.; Mata, M. Modeling and control of the doubly fed induction generator wind turbine. Simul. Model. Pract. Theory 2010, 18, 1365–1381. [Google Scholar] [CrossRef]
- Tsirekis, C.; Tsekouras, G.; Hatziargyriou, N.; Papadias, B. Investigation of switching transient effects on power systems including wind farms. In Proceedings of the 2001 IEEE Porto Power Tech Proceedings, Porto, Portugal, 10–13 September 2001; Volume 4, p. 6. [Google Scholar]
- Ledesma, P.; Usaola, J.; Rodriguez, J. Transient stability of a fixed speed wind farm. Renew. Energy 2003, 28, 1341–1355. [Google Scholar] [CrossRef]
- Fernandez, L.M.; Saenz, J.R.; Jurado, F. Dynamic models of wind farms with fixed speed wind turbines. Renew. Energy 2006, 31, 1203–1230. [Google Scholar] [CrossRef]
- Baroudi, J.A.; Dinavahi, V.; Knight, A.M. A review of power converter topologies for wind generators. Renew. Energy 2007, 32, 2369–2385. [Google Scholar] [CrossRef]
- Torkaman, H.; Keyhani, A. A review of design consideration for Doubly Fed Induction Generator based wind energy system. Electr. Power Syst. Res. 2018, 160, 128–141. [Google Scholar] [CrossRef]
- Yuan, H.; Yuan, X.; Hu, J. Modeling and large-signal stability of DFIG wind turbine in dc-voltage control time scale. In Proceedings of the Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Hu, J.; Yuan, H.; Yuan, X. Modeling of DFIG-based WTs for small-signal stability analysis in DVC timescale in power electronized power systems. IEEE Trans. Energy Convers. 2017, 32, 1151–1165. [Google Scholar] [CrossRef]
- Hughes, F.M.; Anaya-Lara, O.; Jenkins, N.; Strbac, G. Control of DFIG-based wind generation for power network support. IEEE Trans. Power Syst. 2005, 20, 1958–1966. [Google Scholar] [CrossRef]
- Ledesma, P.; Usaola, J. Doubly fed induction generator model for transient stability analysis. IEEE Trans. Energy Convers. 2005, 20, 388–397. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Muyeen, S.; Ali, M.H.; Takahashi, R.; Murata, T.; Tamura, J.; Tomaki, Y.; Sakahara, A.; Sasano, E. Transient stability analysis of grid connected wind turbine generator system considering multi-mass shaft modeling. Electr. Power Compon. Syst. 2006, 34, 1121–1138. [Google Scholar] [CrossRef]
- CIGRE. Guidelines for Representation of Network Elements When Calculating Transients; CIGRE Technical Brochures; CIGRÉ: Paris, France, 1990; Brochure 39. [Google Scholar]
- Bizjak, G.; Zunko, P.; Povh, D. Circuit breaker model for digital simulation based on Mayr’s and Cassie’s differential arc equations. IEEE Trans. Power Deliv. 1995, 10, 1310–1315. [Google Scholar] [CrossRef]
- Lopes, J.P.; Hatziargyriou, N.; Mutale, J.; Djapic, P.; Jenkins, N. Integrating distributed generation into electric power systems: A review of drivers, challenges and opportunities. Electr. Power Syst. Res. 2007, 77, 1189–1203. [Google Scholar] [CrossRef]
- El-Moursi, M.S.; Bak-Jensen, B.; Abdel-Rahman, M.H. Novel STATCOM controller for mitigating SSR and damping power system oscillations in a series compensated wind park. IEEE Trans. Power Electron. 2010, 25, 429–441. [Google Scholar] [CrossRef]
- Kayikci, M.; Milanovic, J. Assessing transient response of DFIG-based wind plants—The influence of model simplifications and parameters. IEEE Trans. Power Syst. 2008, 23, 545–554. [Google Scholar] [CrossRef]
- Datta, U.; Kalam, A.; Shi, J. Power system transient stability with aggregated and dispersed penetration of hybrid distributed generation. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018. [Google Scholar]
- Zhu, D.; Zou, X.; Deng, L.; Huang, Q.; Zhou, S.; Kang, Y. Inductance-emulating Control for DFIG-Based Wind Turbine to Ride-through Grid Faults. IEEE Trans. Power Electron. 2016, 32, 8514–8525. [Google Scholar] [CrossRef]
- Flannery, P.; Venkataramanan, G. Unbalanced voltage sag ride-through of a doubly fed induction generator wind turbine with series grid side converter. In Proceedings of the 2008 IEEE Industry Applications Society Annual Meeting (IAS’08), Edmonton, AB, Canada, 5–9 October 2008; pp. 1–8. [Google Scholar]
- Wang, L.; Xie, X.; Jiang, Q.; Liu, H.; Li, Y.; Liu, H. Investigation of SSR in practical DFIG-based wind farms connected to a series-compensated power system. IEEE Trans. Power Syst. 2015, 30, 2772–2779. [Google Scholar] [CrossRef]
- García, H.; Segundo, J.; Rodríguez-Hernández, O.; Campos-Amezcua, R.; Jaramillo, O. Harmonic Modelling of the Wind Turbine Induction Generator for Dynamic Analysis of Power Quality. Energies 2018, 11, 104. [Google Scholar] [CrossRef]
- Stojčić, G.; Pašanbegović, K.; Wolbank, T.M. Detecting faults in doubly fed induction generator by rotor side transient current measurement. IEEE Trans. Ind. Appl. 2014, 50, 3494–3502. [Google Scholar] [CrossRef]
- Hashemi, S.; Sanaye-Pasand, M. Study of out-of-step phenomena in grid-connected inverter-interfaced synchronous generators. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Doha, Qatar, 10–12 April 2018; pp. 1–6. [Google Scholar]
- Liu, Z.; Liu, C.; Li, G.; Liu, Y.; Liu, Y. Impact study of PMSG-based wind power penetration on power system transient stability using EEAC theory. Energies 2015, 8, 13419–13441. [Google Scholar] [CrossRef]
- Alsmadi, Y.M.; Xu, L.; Blaabjerg, F.; Ortega, A.P.; Abdelaziz, A.Y.; Wang, A.; Albataineh, Z. Detailed Investigation and Performance Improvement of the Dynamic Behavior of Grid-Connected DFIG-Based Wind Turbines under LVRT Conditions. IEEE Trans. Ind. Appl. 2018. [Google Scholar] [CrossRef]
- Badrzadeh, B.; Zamastil, M.H.; Singh, N.K.; Breder, H.; Srivastava, K.; Reza, M. Transients in wind power plants—Part II: Case studies. IEEE Trans. Ind. Appl. 2012, 48, 1628–1638. [Google Scholar] [CrossRef]
- Breder, H.; Muhamad, R. V-110 Ccable System Transient Study; Vindforsk: Stockholm, Sweden, 2009. [Google Scholar]
- Lamabadu, D.; Rajakaruna, S. Dynamic Analysis of a Novel Single-Phase Induction Generator Using an Improved Machine Model. IEEE Trans. Energy Convers. 2017, 32, 1–11. [Google Scholar] [CrossRef]
- Li, D.-Y.; Li, P.; Cai, W.-C.; Song, Y.-D.; Chen, H.-J. Adaptive fault-tolerant control of wind turbines with guaranteed transient performance considering active power control of wind farms. IEEE Trans. Ind. Electron. 2018, 65, 3275–3285. [Google Scholar] [CrossRef]
- Muyeen, S.; Ali, M.H.; Takahashi, R.; Murata, T.; Tamura, J.; Tomaki, Y.; Sakahara, A.; Sasano, E. Comparative study on transient stability analysis of wind turbine generator system using different drive train models. IET Renew. Power Gener. 2007, 1, 131–141. [Google Scholar] [CrossRef]
- Zubia, I.; Ostolaza, X.; Tapia, G.; Tapia, A.; Saenz, J. Electrical fault simulation and dynamic response of a wind farm. In Proceedings of the IASTED International Conference on Power and Energy Systems, Clearwater, FL, USA, 19–22 November 2001; pp. 595–600. [Google Scholar]
- Arulampalam, A.; Barnes, M.; Jenkins, N.; Ekanayake, J.B. Power quality and stability improvement of a wind farm using STATCOM supported with hybrid battery energy storage. IEE Proc. Gener. Transm. Distrib. 2006, 153, 701–710. [Google Scholar] [CrossRef]
- Ekanayake, J.; Holdsworth, L.; Jenkins, N. Comparison of 5th order and 3rd order machine models for doubly fed induction generator (DFIG) wind turbines. Electr. Power Syst. Res. 2003, 67, 207–215. [Google Scholar] [CrossRef]
- Rahimi, M.; Parniani, M. Dynamic behavior and transient stability analysis of fixed speed wind turbines. Renew. Energy 2009, 34, 2613–2624. [Google Scholar] [CrossRef]
- Lorenzo-Bonache, A.; Honrubia-Escribano, A.; Jiménez-Buendía, F.; Molina-García, Á.; Gómez-Lázaro, E. Generic Type 3 Wind Turbine Model Based on IEC 61400-27-1: Parameter Analysis and Transient Response under Voltage Dips. Energies 2017, 10, 1441. [Google Scholar] [CrossRef]
- Potamianakis, E.G.; Vournas, C.D. Short-term voltage instability: effects on synchronous and induction machines. IEEE Trans. Power Syst. 2006, 21, 791–798. [Google Scholar] [CrossRef]
- Sahni, M.; Badrzadeh, B.; Muthumuni, D.; Cheng, Y.; Yin, H.; Huang, S.-H.; Zhou, Y. Sub-synchronous interaction in wind power plants—Part II: An ERCOT case study. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–9. [Google Scholar]
- Hansen, A.D.; Michalke, G. Fault ride-through capability of DFIG wind turbines. Renew. Energy 2007, 32, 1594–1610. [Google Scholar] [CrossRef]
- Tang, W.; Hu, J.; Chang, Y.; Yuan, X.; Liu, F. Modeling of DFIG-based WT for System Transient Response Analysis in Rotor Speed Control Timescale. IEEE Trans. Power Syst. 2018. [Google Scholar] [CrossRef]
- Sharifabadi, K.; Harnefors, L.; Nee, H.-P.; Norrga, S.; Teodorescu, R. Design, Control, and Application of Modular Multilevel Converters for HVDC Transmission Systems; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Zhu, J.; Booth, C.D.; Adam, G.P.; Roscoe, A.J.; Bright, C.G. Inertia emulation control strategy for VSC-HVDC transmission systems. IEEE Trans. Power Syst. 2013, 28, 1277–1287. [Google Scholar] [CrossRef]
- Saad, H.; Peralta, J.; Dennetiere, S.; Mahseredjian, J.; Jatskevich, J.; Martinez, J.; Davoudi, A.; Saeedifard, M.; Sood, V.; Wang, X. Dynamic averaged and simplified models for MMC-based HVDC transmission systems. IEEE Trans. Power Deliv. 2013, 28, 1723–1730. [Google Scholar] [CrossRef]
- Rebello, E.; Vanfretti, L.; Almas, M.S. PMU-based real-time damping control system software and hardware architecture synthesis and evaluation. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Ghafourian, S.; Arana, I.; Holbøll, J.; Sørensen, T.; Popov, M.; Terzija, V. General analysis of vacuum circuit breaker switching overvoltages in offshore wind farms. IEEE Trans. Power Deliv. 2016, 31, 2351–2359. [Google Scholar] [CrossRef]
- Ladenburg, J. Visual impact assessment of offshore wind farms and prior experience. Appl. Energy 2009, 86, 380–387. [Google Scholar] [CrossRef]
- Bishop, I.D. Determination of thresholds of visual impact: the case of wind turbines. Environ. Plan. B Plan. Des. 2002, 29, 707–718. [Google Scholar] [CrossRef]
- Szechtman, M.; Wess, T.; Thio, C. A benchmark model for HVDC system studies. In Proceedings of the International Conference on AC and DC Power Transmission, London, UK, 17–20 September 1991; pp. 374–378. [Google Scholar]
- Faruque, M.; Zhang, Y.; Dinavahi, V. Detailed modeling of CIGRE HVDC benchmark system using PSCAD/EMTDC and PSB/SIMULINK. IEEE Trans. Power Deliv. 2006, 21, 378–387. [Google Scholar] [CrossRef]
- Yang, L.; Xiao, X.; Pang, C. Oscillation analysis of a DFIG-based wind farm interfaced with LCC-HVDC. Sci. China Technol. Sci. 2014, 57, 2453–2465. [Google Scholar] [CrossRef]
- Gao, B.; Zhang, R.; Li, R.; Yu, H.; Zhao, G. Subsynchronous Torsional Interaction of Wind Farms with FSIG Wind Turbines Connected to LCC-HVDC Lines. Energies 2017, 10, 1435. [Google Scholar] [CrossRef]
- Taj, T.A.; Hasanien, H.M.; Alolah, A.I.; Muyeen, S.M. Transient stability enhancement of a grid-connected wind farm using an adaptive neuro-fuzzy controlled-flywheel energy storage system. IET Renew. Power Gener. 2015, 9, 792–800. [Google Scholar] [CrossRef]
- Soeth, A.B.; de Souza, P.R.F.; Custódio, D.T.; Voloh, I. Traveling wave fault location on HVDC lines. In Proceedings of the 2018 71st Annual Conference for Protective Relay Engineers (CPRE), College Station, TX, USA, 26–29 March 2018; pp. 1–16. [Google Scholar]
- Amirat, Y.; Benbouzid, M.E.H.; Al-Ahmar, E.; Bensaker, B.; Turri, S. A brief status on condition monitoring and fault diagnosis in wind energy conversion systems. Renew. Sustain. Energy Rev. 2009, 13, 2629–2636. [Google Scholar] [CrossRef]
- Georgilakis, P.S. Technical challenges associated with the integration of wind power into power systems. Renew. Sustain. Energy Rev. 2008, 12, 852–863. [Google Scholar] [CrossRef]
- Roy, C.; Sengupta, A. Implementation of STATCOM to overcome disturbances in grid connected wind farm. In Proceedings of the 2015 International Conference on Energy, Power and Environment: Towards Sustainable Growth (ICEPE), Shillong, India, 12–13 June 2015; pp. 1–4. [Google Scholar]
- Chen, Z.; Blaabjerg, F.; Hu, Y. Voltage recovery of dynamic slip control wind turbines with a STATCOM. In Proceedings of the IPEC’05, Niigata, Japan, 4–8 April 2005. [Google Scholar]
- Naik, K.A.; Gupta, C.P. Output Power Smoothing and Voltage Regulation of a Fixed Speed Wind Generator in the Partial Load Region Using STATCOM and a Pitch Angle Controller. Energies 2017, 11, 58. [Google Scholar] [CrossRef]
- Mosaad, M.I. Model reference adaptive control of STATCOM for grid integration of wind energy systems. IET Electr. Power Appl. 2018, 12, 605–613. [Google Scholar] [CrossRef]
- Liang, J.; Howard, D.F.; Restrepo, J.A.; Harley, R.G. Feedforward transient compensation control for DFIG wind turbines during both balanced and unbalanced grid disturbances. IEEE Trans. Ind. Appl. 2013, 49, 1452–1463. [Google Scholar] [CrossRef]
- Godoy Simões, M.; Farret, F.A. Renewable Energy Systems: Design and Analysis with Induction Generators; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Chen, J.; Chen, J.; Gong, C. On optimizing the transient load of variable-speed wind energy conversion system during the MPP tracking process. IEEE Trans. Ind. Electron. 2014, 61, 4698–4706. [Google Scholar] [CrossRef]
- Bayhan, S.; Kakosimos, P.; Rivera, M. Predictive torque control of brushless doubly fed induction generator fed by a matrix converter. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Doha, Qatar, 10–12 April 2018; pp. 1–6. [Google Scholar]
- Alam, M.S.; Abido, M.A.Y. Fault ride through capability enhancement of a large-scale PMSG wind system with bridge type fault current limiters. Adv. Electr. Comput. Eng. 2018, 18, 43–50. [Google Scholar] [CrossRef]
- Gururaj, M.; Padhy, N.P. PHIL experimentation on fault ride through behavior of doubly fed induction generator based wind system in the presence of fault current limiter. In Proceedings of the 2018 IEEMA Engineer Infinite Conference (eTechNxT), New Delhi, India, 13–14 March 2018; pp. 1–6. [Google Scholar]
- Chang, Y.; Hu, J.; Tang, W.; Song, G. Fault Current Analysis of Type-3 WTs Considering Sequential Switching of Internal Control and Protection Circuits in Multi Time Scales during LVRT. IEEE Trans. Power Syst. 2018. [Google Scholar] [CrossRef]
- Abdelsalam, I.; Adam, G.P.; Williams, B.W. Current source back-to-back converter for wind energy conversion systems. IET Renew. Power Gener. 2016, 10, 1552–1561. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Qiu, D.; Zhang, Y.; Cao, P.; Jiang, L. Passivity-based Linear Feedback Control of Permanent Magnetic Synchronous Generator based Wind Energy Conversion System: Design and Analysis. IET Renew. Power Gener. 2018, 12, 981–991. [Google Scholar] [CrossRef]
- Geng, H.; Liu, L.; Li, R. Synchronization and Reactive Current Support of PMSG based Wind Farm during Severe Grid Fault. IEEE Trans. Sustain. Energy 2018. [Google Scholar] [CrossRef]
- Meng, W.; Yang, Q.; Ying, Y.; Sun, Y.; Yang, Z.; Sun, Y. Adaptive power capture control of variable-speed wind energy conversion systems with guaranteed transient and steady-state performance. IEEE Trans. Energy Convers. 2013, 28, 716–725. [Google Scholar] [CrossRef]
- Wang, X.; Shen, Y. Fault-Tolerant Control Strategy of a Wind Energy Conversion System Considering Multiple Fault Reconstruction. Appl. Sci. 2018, 8, 794. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Rajaei Salmasi, F. Analysis and detection of a wind system failure in a micro-grid. J. Renew. Sustain. Energy 2016, 8, 043302. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Fault-tolerant supervisory controller for a hybrid AC/DC micro-grid. IEEE Trans. Smart Grid 2016, 99, 2809–2823. [Google Scholar] [CrossRef]
- Jauch, C.; Sørensen, P.; Norheim, I.; Rasmussen, C. Simulation of the impact of wind power on the transient fault behavior of the Nordic power system. Electr. Power Syst. Res. 2007, 77, 135–144. [Google Scholar] [CrossRef]
- Mohseni, M.; Islam, S.M. Transient control of DFIG-based wind power plants in compliance with the Australian grid code. IEEE Trans. Power Electron. 2012, 27, 2813–2824. [Google Scholar] [CrossRef]
- Mohseni, M.; Islam, S.M.; Masoum, M.A. Enhanced hysteresis-based current regulators in vector control of DFIG wind turbines. IEEE Trans. Power Electron. 2011, 26, 223–234. [Google Scholar] [CrossRef]
- Kazmierkowski, M.P.; Malesani, L. Current control techniques for three-phase voltage-source PWM converters: A survey. IEEE Trans. Ind. Electron. 1998, 45, 691–703. [Google Scholar] [CrossRef]
- Zheng, D.; Ouyang, J.; Xiong, X.; Xiao, C.; Li, M. A System Transient Stability Enhancement Control Method Using Doubly Fed Induction Generator Wind Turbine with Considering Its Power Constraints. Energies 2018, 11, 945. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, J.; Hung, W.; Wang, C.; Zhang, X.; Bu, S.; Li, Q.; Urdal, H.; Booth, C.D. Synthetic Inertia Control Strategy for Doubly Fed Induction Generator Wind Turbine Generators Using Lithium-Ion Supercapacitors. IEEE Trans. Energy Convers. 2018, 33, 773–783. [Google Scholar] [CrossRef]
- Jin, M.; Weiming, M. Power converter EMI analysis including IGBT nonlinear switching transient model. IEEE Trans. Ind. Electron. 2006, 53, 1577–1583. [Google Scholar] [CrossRef]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics; Wiley: Hoboken, NJ, USA, 1995. [Google Scholar]
- Chang, E.-C. Improving Performance for Full-Bridge Inverter of Wind Energy Conversion System Using a Fast and Efficient Control Technique. Energies 2018, 11, 262. [Google Scholar] [CrossRef]
- Duong, M.Q.; Grimaccia, F.; Leva, S.; Mussetta, M.; Le, K.H. A hybrid Fuzzy-PI cascade controller for transient stability improvement in DFIG wind generators. In Proceedings of the 2016 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Vancouver, BC, Canada, 24–29 July 2016; pp. 1733–1739. [Google Scholar]
- May, S.; Sergey, E.; Ilya, I. Universal and Energy Efficient Transistor Autonomous Inverter on Semiconductor Switches. In Proceedings of the 2018 17th International Ural Conference on AC Electric Drives (ACED), Ekaterinburg, Russia, 26–30 March 2018. [Google Scholar]
- Sheng, Y.-W.; Ke, D.-P.; Sun, Y.-Z.; Daniel, K.; Wang, Y.-S.; Hu, Y.-C. A novel transient rotor current control scheme of a doubly-fed induction generator equipped with superconducting magnetic energy storage for voltage and frequency support. Chin. Phys. B 2015, 24, 070201. [Google Scholar] [CrossRef]
- Tang, Y.; Dai, J.; Ning, J.; Dang, J.; Li, Y.; Tian, X. An Extended System Frequency Response Model Considering Wind Power Participation in Frequency Regulation. Energies 2017, 10, 1797. [Google Scholar] [CrossRef]
- Duong, M.Q.; Leva, S.; Mussetta, M.; Le, K.H. A Comparative Study on Controllers for Improving Transient Stability of DFIG Wind Turbines During Large Disturbances. Energies 2018, 11, 480. [Google Scholar] [CrossRef]
- Duong, M.Q.; Grimaccia, F.; Leva, S.; Mussetta, M.; Le, K.H. Improving transient stability in a grid-connected squirrel-cage induction generator wind turbine system using a fuzzy logic controller. Energies 2015, 8, 6328–6349. [Google Scholar] [CrossRef]
- Todeschini, G.; Emanuel, A.E. Transient response of a wind energy conversion system used as active filter. IEEE Trans. Energy Convers. 2011, 26, 522–531. [Google Scholar] [CrossRef]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Jabr, H.M.; Kar, N.C. Effects of main and leakage flux saturation on the transient performances of doubly-fed wind driven induction generator. Electr. Power Syst. Res. 2007, 77, 1019–1027. [Google Scholar] [CrossRef]
- Shuai, Z.; He, D.; Xiong, Z.; Lei, Z.; Shen, Z.J. Comparative Study of Short-Circuit Fault Characteristics for VSC-based DC Distribution Networks with Different Distributed Generators. IEEE J. Emerg. Sel. Top. Power Electron. 2018. [Google Scholar] [CrossRef]
- Jia, K.; Li, Y.; Fang, Y.; Zheng, L.; Bi, T.; Yang, Q. Transient current similarity based protection for wind farm transmission lines. Appl. Energy 2018, 225, 42–51. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, W.; Han, J.; Wang, G. A new wind turbine fault diagnosis method based on the local mean decomposition. Renew. Energy 2012, 48, 411–415. [Google Scholar] [CrossRef]
- Tang, B.; Liu, W.; Song, T. Wind turbine fault diagnosis based on Morlet wavelet transformation and Wigner-Ville distribution. Renew. Energy 2010, 35, 2862–2866. [Google Scholar] [CrossRef]
- Huang, S.-J.; Hsieh, C.-T. High-impedance fault detection utilizing a Morlet wavelet transform approach. IEEE Trans. Power Deliv. 1999, 14, 1401–1410. [Google Scholar] [CrossRef]
- Silva, K.; Souza, B.A.; Brito, N.S. Fault detection and classification in transmission lines based on wavelet transform and ANN. IEEE Trans. Power Deliv. 2006, 21, 2058–2063. [Google Scholar] [CrossRef]
- De Souza, J.S.; Meza, E.M.; Schilling, M.T.; Do Coutto Filho, M.B. Alarm processing in electrical power systems through a neuro-fuzzy approach. IEEE Trans. Power Deliv. 2004, 19, 537–544. [Google Scholar] [CrossRef]
- Samantaray, S.; Dash, P. Wavelet packet-based digital relaying for advanced series compensated line. IET Gener. Transm. Distrib. 2007, 1, 784–792. [Google Scholar] [CrossRef]
- Saleh, S.A.; Ozkop, E.; Aljankawey, A.S. Performance of the Phaselet Frames-Based Digital Protection for Distributed Generation Units. IEEE Trans. Ind. Appl. 2016, 52, 2095–2109. [Google Scholar] [CrossRef]
- Saleh, S.A.; Ahshan, R.; Abu-Khaizaran, M.S.; Alsayid, B.; Rahman, M. Implementing and Testing d − q WPT-Based Digital Protection for Microgrid Systems. IEEE Trans. Ind. Appl. 2014, 50, 2173–2185. [Google Scholar] [CrossRef]
- Li, M.; Yu, D.; Chen, Z.; Xiahou, K.; Ji, T.; Wu, Q. A Data-Driven Residual-Based Method for Fault Diagnosis and Isolation in Wind Turbines. IEEE Trans. Sustain. Energy 2018. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, F.; Fu, W. Fault Detection and Isolation for Redundant Inertial Measurement Unit under Quantization. Appl. Sci. 2018, 8, 865. [Google Scholar] [CrossRef]
- Saleh, S.; Ahshan, R.; Rahman, M. Performance Evaluation of an Embedded d − q WPT-Based Digital Protection for IPMSM Drives. IEEE Trans. Ind. Appl. 2014, 50, 2277–2291. [Google Scholar] [CrossRef]
- Kramer, S.G.; Leon, F.P.; Appert, B. Fiber optic sensor network for lightning impact localization and classification in wind turbines. In Proceedings of the 2006 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Berlin/Heidelberg, Germany, 3–6 September 2006; pp. 173–178. [Google Scholar]
- Rodrigues, R.B.; Mendes, V.M.; Catalão, J.P. Analysis of transient phenomena due to a direct lightning strike on a wind energy system. Energies 2012, 5, 2545–2558. [Google Scholar] [CrossRef]
- Chowdhuri, P.; Anderson, J.; Chisholm, W.; Field, T.; Ishii, M.; Martinez, J.; Marz, M.; McDaniel, J.; McDermott, T.; Mousa, A. Parameters of lightning strokes: A review. IEEE Trans. Power Deliv. 2005, 20, 346–358. [Google Scholar] [CrossRef]
- Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galván, E.; PortilloGuisado, R.C.; Prats, M.M.; León, J.I.; Moreno-Alfonso, N. Power-electronic systems for the grid integration of renewable energy sources: A survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]

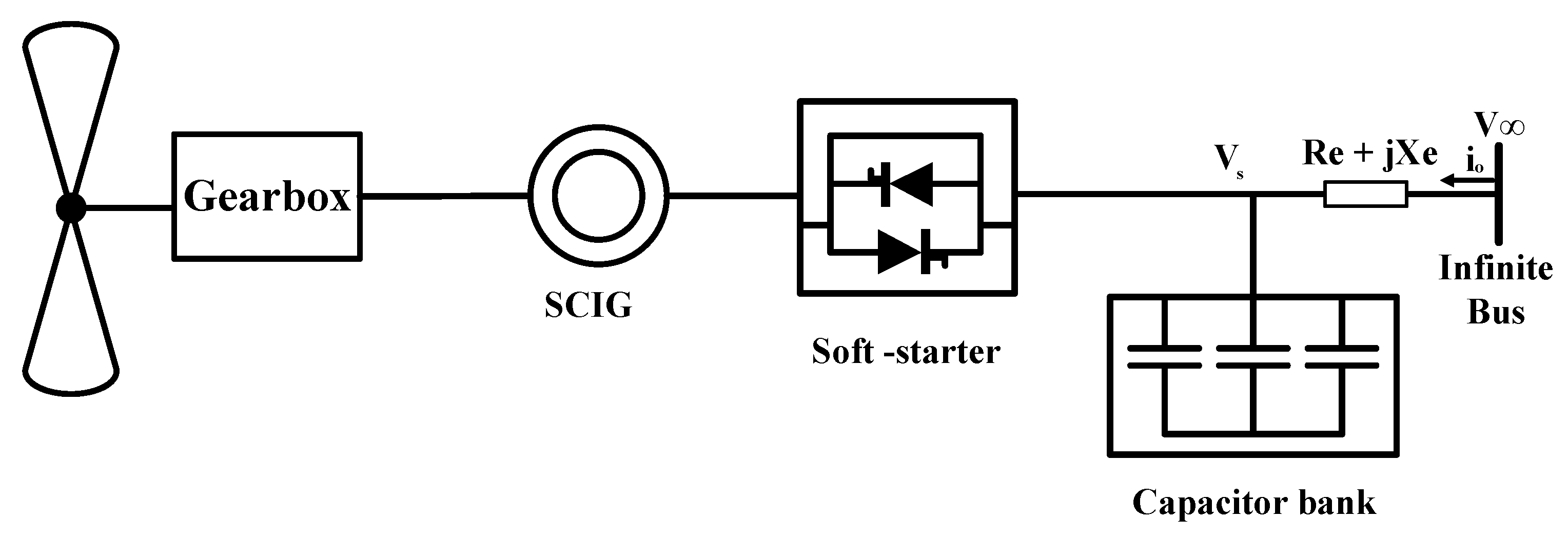
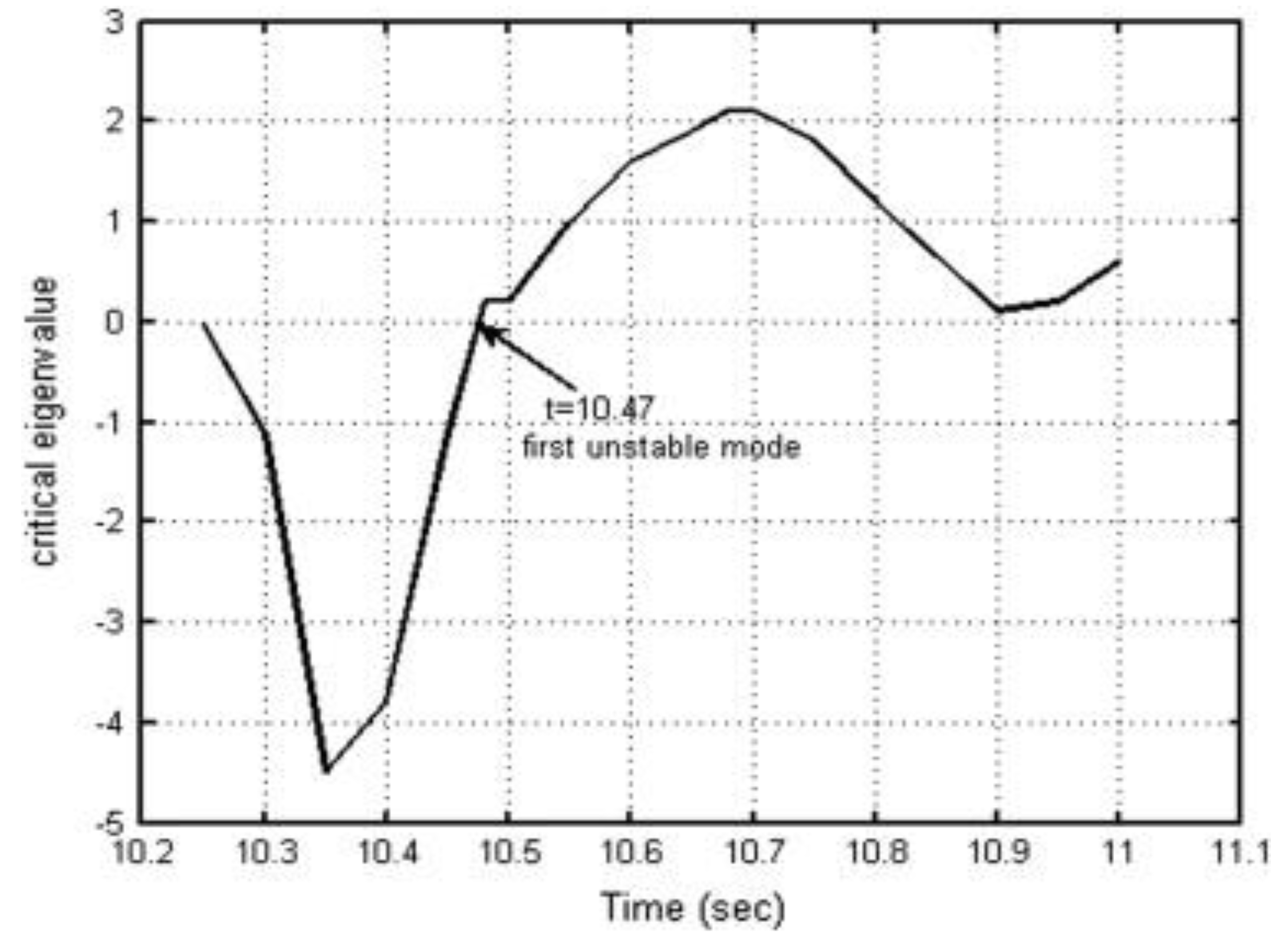
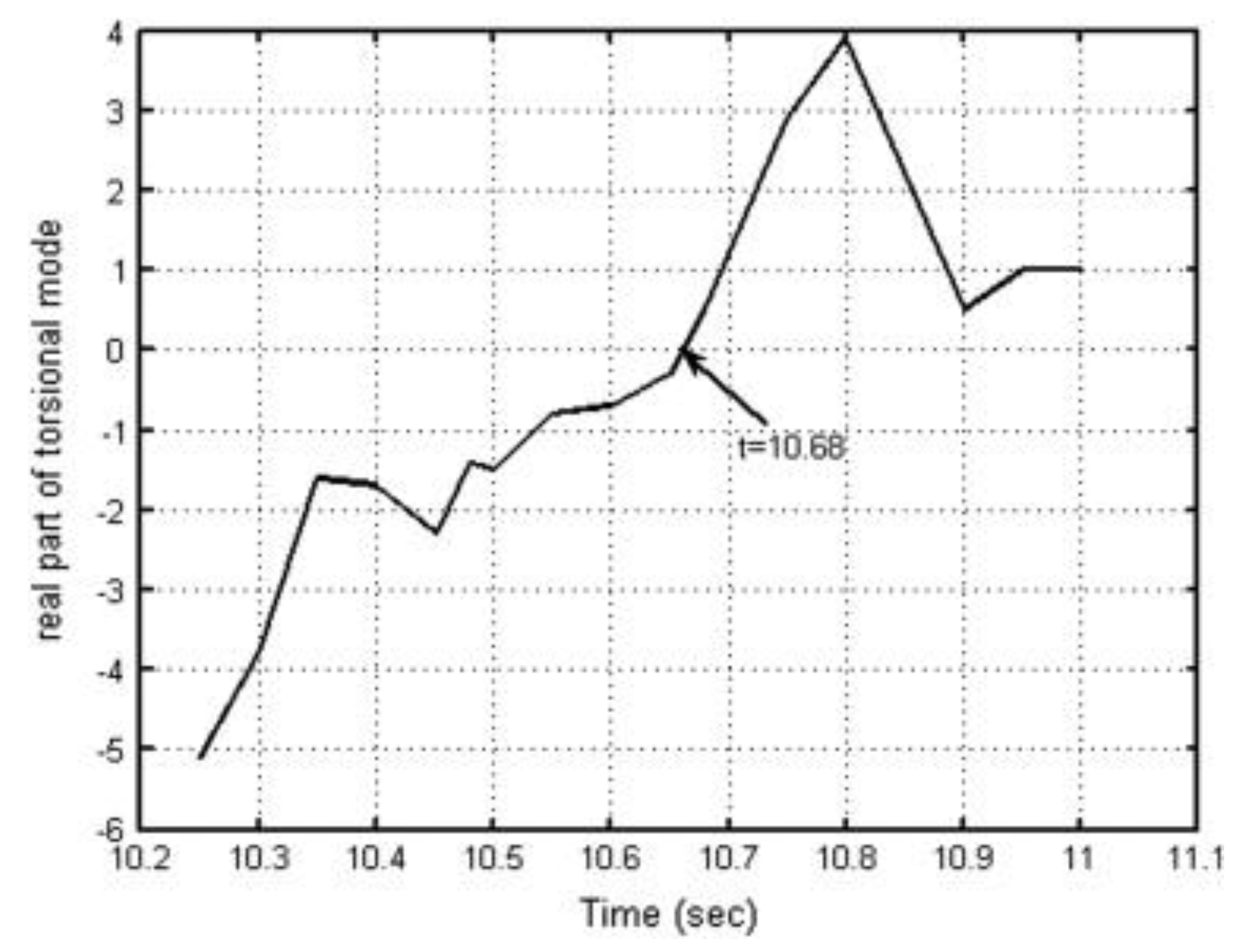
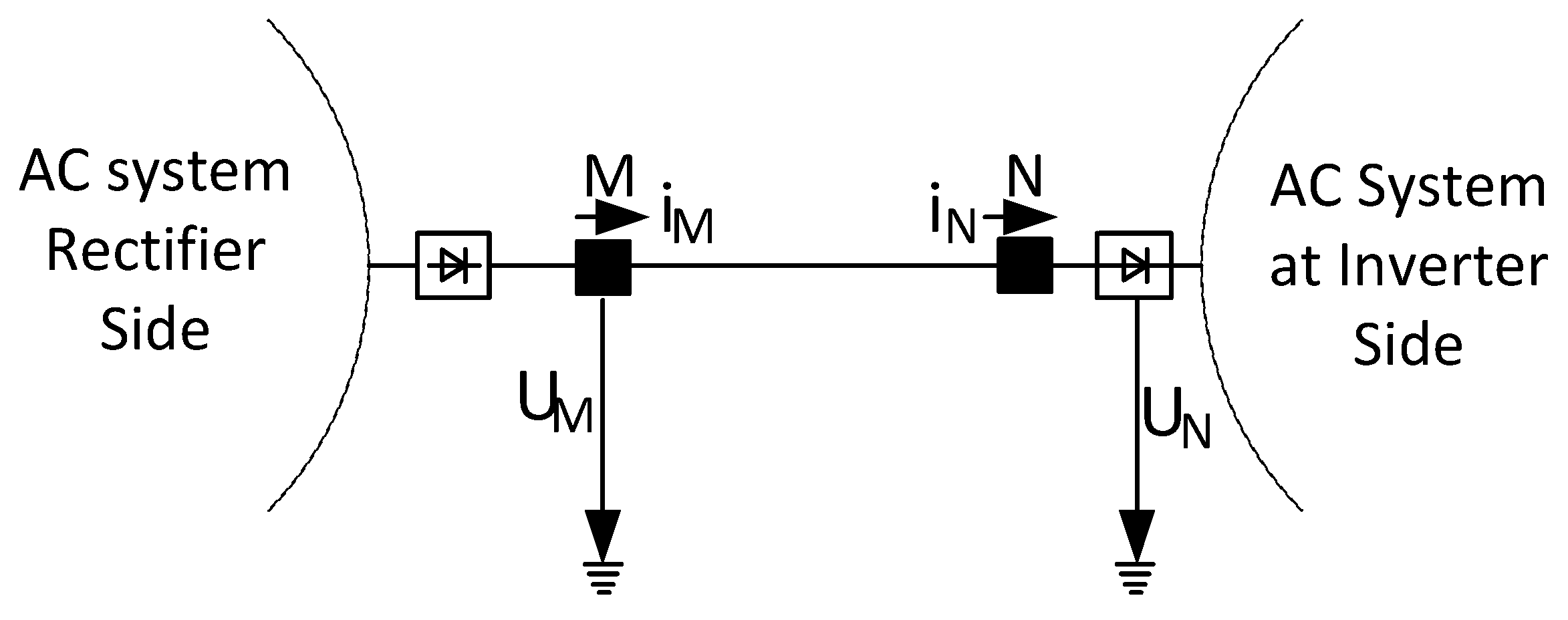
| Induction Generator Power (MW) | 1LG Fault | 2LS Fault | 2LG Fault | 3LG Fault | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2M | 3M | 6M | 2M | 3M | 6M | 2M | 3M | 6M | 2M | 3M | 6M | |
| 50 | S | S | S | S | S | S | U | U | U | U | U | U |
| 44 | S | S | S | S | S | S | U | U | U | U | U | U |
| 43 | S | S | S | S | S | S | S | S | S | U | U | U |
| 40 | S | S | S | S | S | S | S | S | S | U | U | U |
| 39 | S | S | S | S | S | S | S | S | S | S | S | S |
| Induction Generator Power (MW) | 1LG Fault | 2LS Fault | 2LG Fault | 3LG Fault | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2M | 3M | 6M | 2M | 3M | 6M | 2M | 3M | 6M | 2M | 3M | 6M | |
| 50 | S | S | S | S | S | S | S | S | S | S | S | S |
| No | Subject | Technique/Concept | WECS Part | Ref. |
|---|---|---|---|---|
| 1 | Transient Analysis | Single Machine Infinite Bus (SMIB) | DFIG | [61] |
| 2 | Transient Stability Index (TSI) | DFIG | [6] | |
| 3 | Transient Security Assessment Tool (TSAT) | DFIG | [51] | |
| 4 | Critical Clearing Time (CCT) | DFIG | [7] | |
| 5 | Eigen Value Tracking | FSWT | [58] | |
| 6 | Runge–Kutta Method | Induction Generator (IG) | [50] | |
| 7 | Equal Area Criterion (EAC) Theory | IISG | [45] | |
| 8 | Extended Equal Area Criterion Theory (EEAC) | PMSG | [46] | |
| 9 | Space Phasor and Asymmetry Phasor Approximation | DFIG | [44] | |
| Modelling Methodologies | ||||
| 10 | Two-Masses or Three Mass | Windmill | [52] | |
| 11 | Six-Mass Drive Train Model | Windmill | [33] | |
| 12 | Wound Rotor Asynchronous Machine | DFIG | [22] | |
| 13 | Controlled Current Source | PMSG | [26] | |
| 14 | or T Network Models | Transmission lines | [22] | |
| 15 | IGBT Switches with Parasitic Capacitance | Converter | [101] | |
| 16 | Cassie’s/Mayr’s Model | Circuit breaker | [35] |
| Subject | Remedy Approach | Concept | Generator | Ref. No. |
|---|---|---|---|---|
| Control Scheme | Conventional Vector a-b-c-d-q Control | DSP/Field-Programmable Gate Array (FPGA) | DFIG/PMSG | [2] |
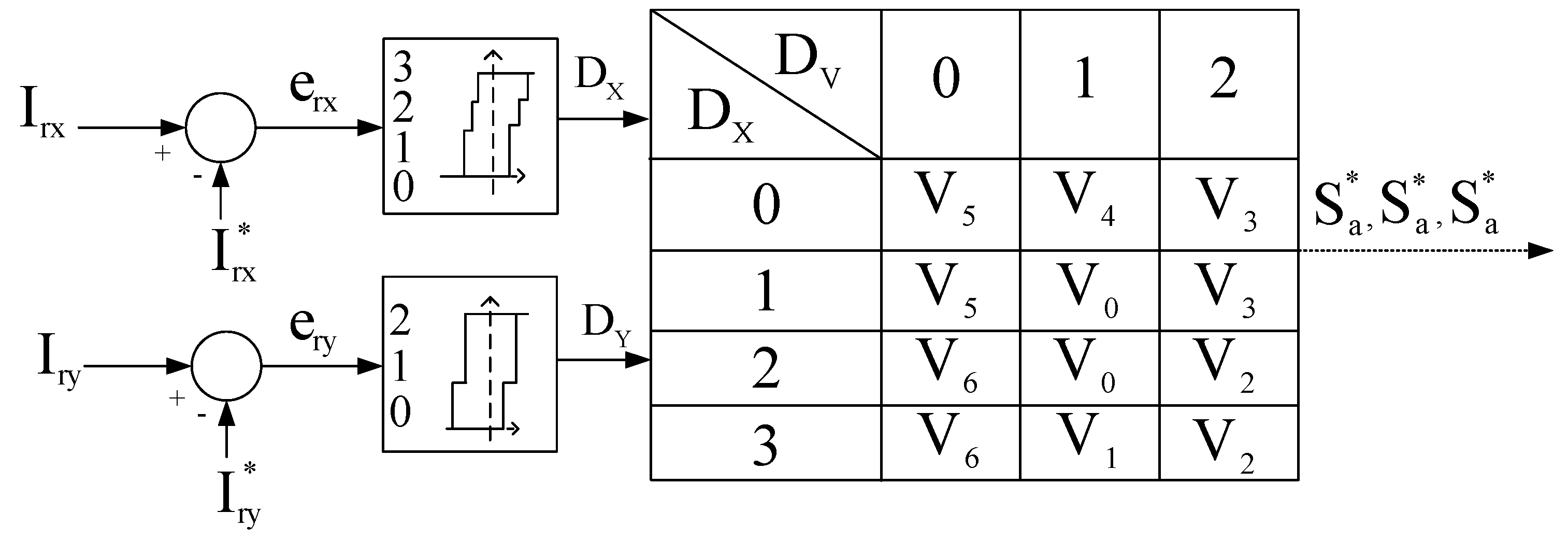
| Variable Band Vector-based Hysteresis Control | Tracking of Errors | DFIG | [96] | |
| Novel RSC Vector Control | Stator Flux (d-q) | DFIG | [47] | |
| Neural Network Adaptive Controller | Novel Error Transformation | WT | [91] | |
| Adaptive Neuro-Fuzzy Fly-wheel Controller | Fly-wheel Storage | DFIG | [73] | |
| Modal Reference Adaptive Controller (MRAC) | SPWM | Self-Excited Induction Generator (SEIG) | [80] | |
| Adaptive Fault-tolerant Controller | Barrier Lyapunov Function | WT | [51] | |
| Fault-tolerant Controller | Sliding Mode Observer (SMO) | DFIG | [92] | |
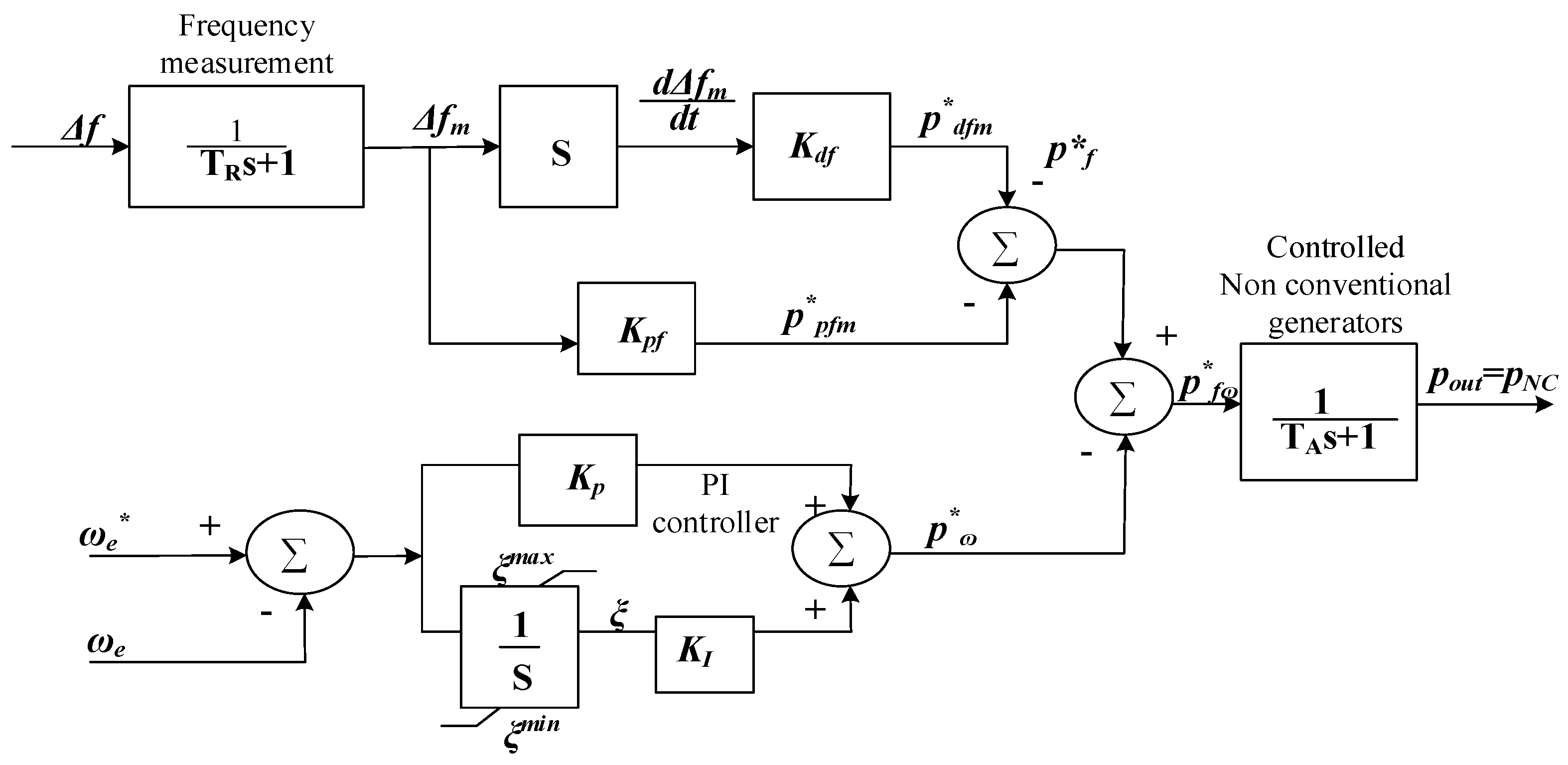
| Proportional and Inertial Control | Extended Frequency Response | DFIG | [107] | |
| Hybrid (PI/Fuzzy) Controllers | Fuzzy Logic Technique | SCIG | [109] | |
| Sliding Mode Guidance Law Controller | Fourier Nonlinear Grey Bernoulli Method | PMSG | [103] | |
| Speed Controller | Basic speed control loop with current source converter | PMSG | [88] | |
| Passivity-Based Linear Feedback Control (PBLFC) | Passivity Theory/FLC | PMSG | [89] | |
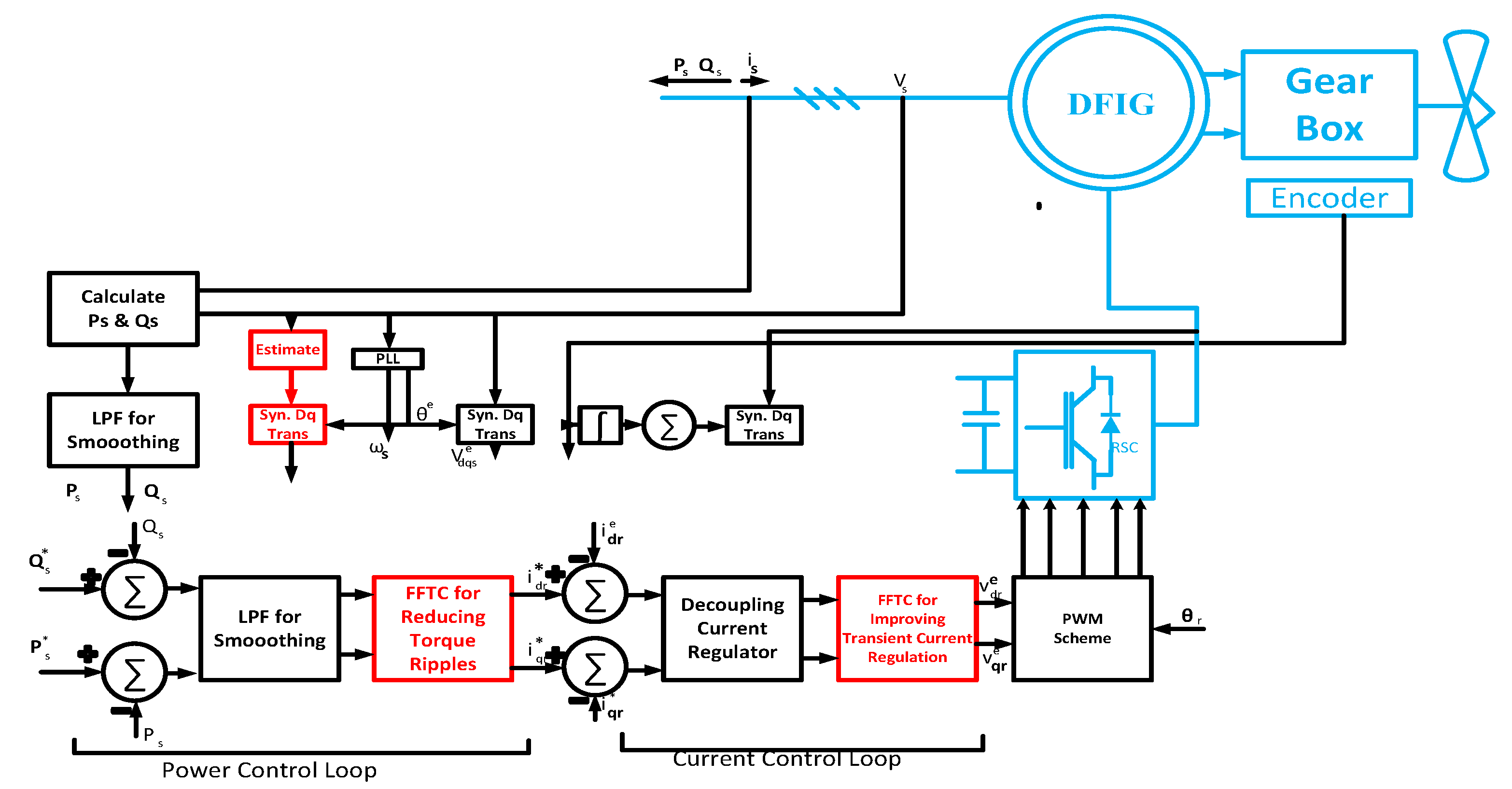
| Feed-Forward Transient Compensation | Back EMF and Resonant Regulator | DFIG | [81] | |
| Secondary Damping Controller | Wide Area Measurement System (WAM) | DFIG | [19] | |
| Predictive Torque Control (PTC) | Matrix Converter | BDFIG | [84] | |
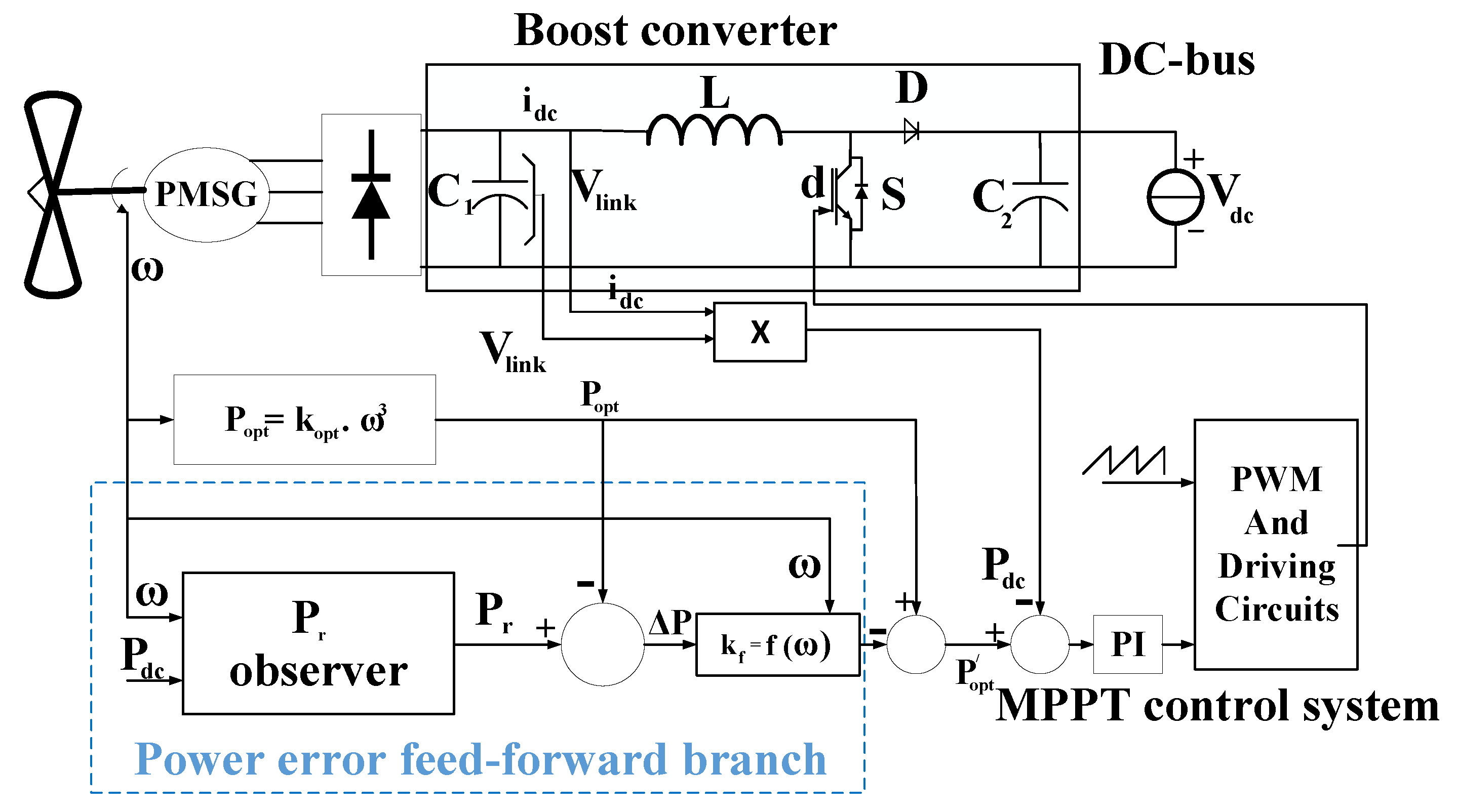
| MPPT Control | Transient Load and Bandwidth | PMSG | [83] | |
| Bridge-type Fault Current Limiter | Real-Time Hardware in the Loop (RTHIL) | DFIG | [85] | |
| Supervisory Controller | Gearbox Elements | All Except SG | [94] | |
| Protection Measures | Mechanical Switch Capacitors | Bank of Shunt Capacitors | DFIG | [1] |
| Active Power Filtering | RLC | DFIG | [110] | |
| Three-Channel Filters | Quantization | Aerodynamics of WTs | [124] | |
| Digital Signal Processing (DSP) Relays | Phaselet Packet Transform (PPT), WPT, Travelling Wave Fault Locators (TWFL), | DGU Interconnections and HVDC | [121,122] | |
| Artificial Intelligent-based relays | ANN and Fuzzy Logic Relays | DGU Interconnections | [39,118] | |
| Deep Long Short-Term Memory (DLSTM) | Residual Data-driven Method | Wind Turbines Generally | [123] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abubakar, U.; Mekhilef, S.; Mokhlis, H.; Seyedmahmoudian, M.; Horan, B.; Stojcevski, A.; Bassi, H.; Hosin Rawa, M.J. Transient Faults in Wind Energy Conversion Systems: Analysis, Modelling Methodologies and Remedies. Energies 2018, 11, 2249. https://doi.org/10.3390/en11092249
Abubakar U, Mekhilef S, Mokhlis H, Seyedmahmoudian M, Horan B, Stojcevski A, Bassi H, Hosin Rawa MJ. Transient Faults in Wind Energy Conversion Systems: Analysis, Modelling Methodologies and Remedies. Energies. 2018; 11(9):2249. https://doi.org/10.3390/en11092249
Chicago/Turabian StyleAbubakar, Ukashatu, Saad Mekhilef, Hazlie Mokhlis, Mehdi Seyedmahmoudian, Ben Horan, Alex Stojcevski, Hussain Bassi, and Muhyaddin Jamal Hosin Rawa. 2018. "Transient Faults in Wind Energy Conversion Systems: Analysis, Modelling Methodologies and Remedies" Energies 11, no. 9: 2249. https://doi.org/10.3390/en11092249
APA StyleAbubakar, U., Mekhilef, S., Mokhlis, H., Seyedmahmoudian, M., Horan, B., Stojcevski, A., Bassi, H., & Hosin Rawa, M. J. (2018). Transient Faults in Wind Energy Conversion Systems: Analysis, Modelling Methodologies and Remedies. Energies, 11(9), 2249. https://doi.org/10.3390/en11092249










