1. Introduction
Permanent magnet (PM) machines are widely used in applications on multi-axis machine tools due to their high dynamic response and high torque density [
1,
2,
3,
4]. Considering manufacturing using machine tools, the machining allowance should be limited within a 6~320-mm diameter. In order to overcome this demanded error allowance, closed-loop motion control is preferred by installing high-resolution position sensors in PM machines.
High-resolution position sensors can be categorized into encoders with the output of digital pulse signals and resolvers with analog position signals. For these sensors, a rotating mechanism must be attached to the machine’s rotor in order to measure the instantaneous rotor position. It is noteworthy that the installation of the position sensor increases the overall machine size, leading to the reduction of torque density under the same machine size [
5]. Considering motion systems with a size limitation, position sensing using separated position sensors might not be well-suited to maximize the drive power density [
6,
7].
Elimination of a separated position sensor by using the spatial information in the machine itself (self-sensing) has become a promising solution for next-generation machine drives [
5,
8]. Different from sensor-based drives, the rotor position has to be estimated from the position-dependent signal in the electromotive force (EMF) voltage or the saliency of a machine [
9,
10,
11]. For EMF-based sensorless drives, the EMF voltage is obtained based on a machine model through current measurements. However, EMF voltage is a speed-dependent function; the signal-to-noise (SNR) ratio of EMF voltage decreases as the speed decreases [
12]. For motion applications requiring low-speed operation, an EMF-based drive might not be stable enough for closed-loop control due to the low EMF SNR [
13,
14]. Currently, EMF-based drives are still limited for speeds beyond ~5% of the rated speed under load [
15,
16,
17].
Unlike EMF voltage, the spatial signal inside the machine’s saliency is speed-independent, which is suited for sensorless drives at low speed [
18]. However, this type of spatial signal is typically lower than the signal in EMF at normal speed. Under this effect, several implementation issues on the position estimation error might appear. In [
19,
20], a rotating sine-wave voltage injection in a stator frame and a pulsating sine-wave voltage injection in a rotor frame are evaluated in an interior PM (IPM) machine. It is reported that the pulsating injection results in lower estimation error at steady state. Besides this, an additional voltage sensor is used to directly measure the saliency from the machine’s neutral point voltage [
21,
22,
23]. Due to an additional voltage sensor dedicated to saliency signal measurement, a better SNR of the spatial signal is achieved compared to measurement through the phase current sensors. However, the galvanic isolation between the voltage sensor and inverter power switches is still a challenge in inverters [
22]. Considering the saliency-based drive at low speed, the low SNR of saliency in PM machines is still a problem which needs to be solved.
In addition to the low SNR of saliency, secondary saliency harmonics also affect the position estimation accuracy. As reported in [
24,
25], the PWM dead-time causes error in the high-frequency (HF) voltage signal. To mitigate the dead-time effect, the injection voltage must be higher than a certain voltage to remove the capacitor clamping effect [
26,
27]. However, injection-reflected acoustic noises might be a potential problem for a voltage injection with high magnitude [
28]. In [
29,
30,
31], a third-order harmonic in the estimated position is observed when the square-wave injection voltage frequency is equal to the PWM switching frequency. The inverter dead-time distortion on the injected voltage is the primary issue. However, if the voltage frequency is lower than the PWM frequency, the third-order harmonic changes to a sixth-order harmonic where the magnitudes are reduced.
Similar to dead-time, the flux saturation also results in saliency harmonics and position estimation errors [
31]. For a rotating sine-wave voltage injection, these saliency harmonics can be decoupled with knowledge of harmonic magnitudes and phases [
32]. However, dead-time harmonics in the saliency greatly increase when a rotating voltage is superimposed [
33]. More importantly, these dead-time harmonics are usually higher than the harmonics caused by flux saturation [
34]. Recently in [
35], position estimation using the pulsating voltage with a square-wave and a sine-wave has been compared. The sine-wave injection demonstrates lower dead-time harmonics. The compensation for the saturation saliency harmonic further improves the sine-wave pulsating injection technique.
This paper improves a PM machine’s saliency-based drive by determining a suited HF voltage signal. Both saliency harmonics and position estimation errors under different load conditions are evaluated with two different injection signals. In general, PM machines are widely used for motion control because of their high torque density and efficiency. However, considering sensorless PM machine drives, position estimation errors from inverter dead-time and flux saturation must be improved. Considering the influence of inverter dead-time, saliency-based position estimation contains a second-order and a sixth-order spatial harmonic. This saliency harmonic can be decreased by injecting a sine-wave voltage signal. At full load, saliency harmonics are decreased because the dead-time voltage error can easily compensate for high currents in the inverter. Besides this, considering the flux saturation, the second-order saliency harmonic due to the reduction of q-axis inductance is the primary issue. This harmonic results in the same estimation error between two injection signals. Analytical equations are developed to investigate the position error caused by the dead-time and flux saturation. An IPM machine with a 1.41 saliency ratio (Lq/Ld) is built to evaluate the estimation performance using different voltage injection signals.
2. HF Sine-Wave Voltage Injection
This section analyzes a saliency-based drive using sine-wave voltage injection. The pulsating sine-wave injection technique originally reported in [
10] is firstly explained. Key position estimation errors caused by the flux saturation and inverter dead-time are investigated by extending the analytical models in [
10].
In order to obtain a high-bandwidth spatial saliency signal, a sine-wave voltage of around a few kilohertz can be injected along the direction of the estimated d-axis in a rotor frame.
where v
c is the carrier voltage magnitude and ω
c is the injection frequency. Considering the small signal due to HF injection, the inductive voltage drop is dominant. Under this effect, the HF machine model is simplified by [
10]
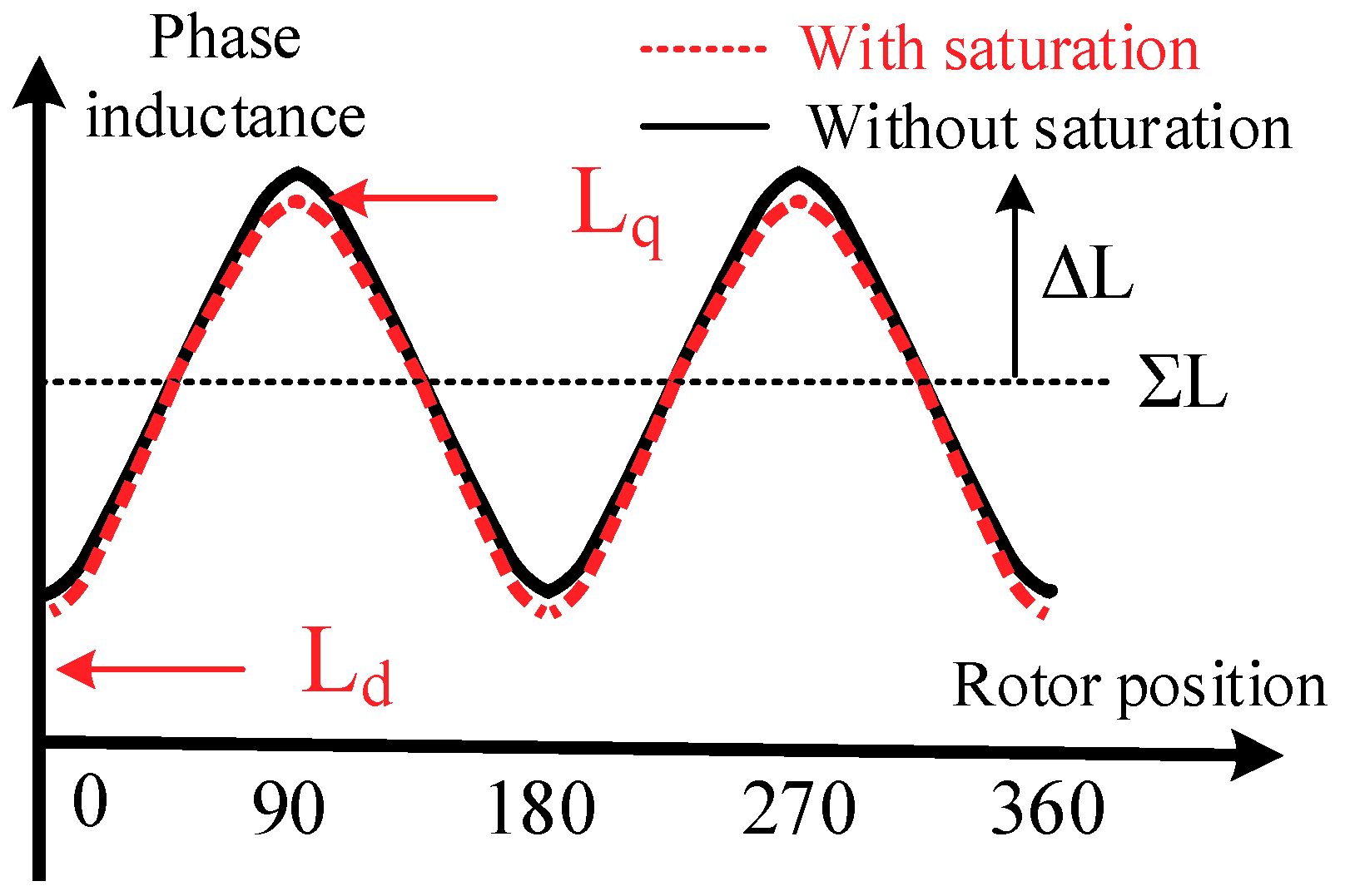
In (2), ΣL and ΔL are the average and differential inductance, respectively.
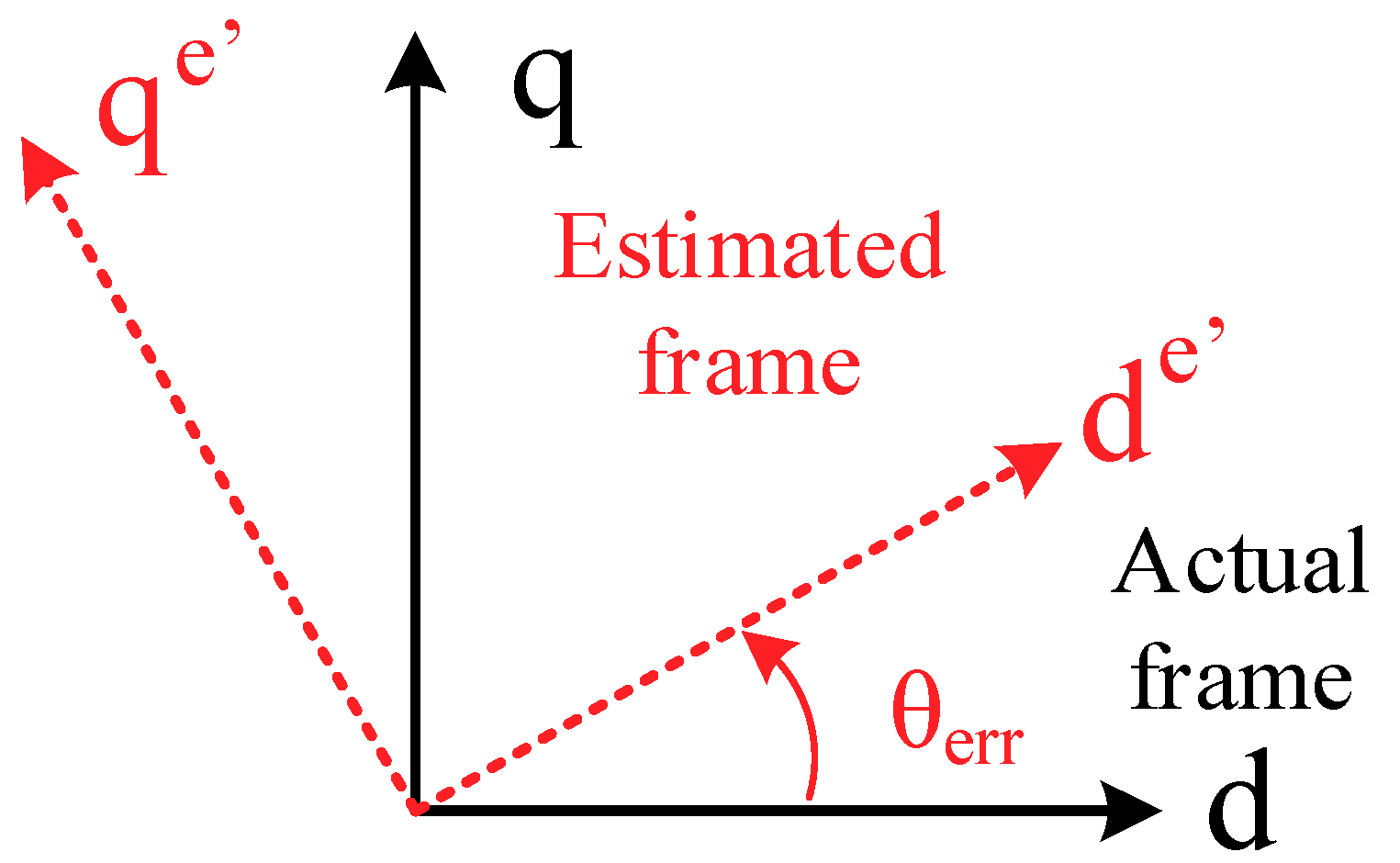
Figure 1 illustrates ΣL and ΔL with respect to the inductance waveform versus position. The superscript e’ in (2) represents the estimated synchronous rotor frame while θ
err is the position error between the estimated rotor frame and the actual frame. The relative location between these two rotor frames is shown in
Figure 2. The differential operator p in (2) is equal to jω
c assuming a steady state with the sine-wave injection. Substituting (1) into (2), the voltage injection induced current is given by
Assuming the estimated frame in
Figure 2 is not aligned with the actual frame at the initial estimation state, a saliency current
in (3) appears where the magnitude is dependent on ΔL. The rotor position can be obtained by regulating θ
err to be zero in
. However,
is modulated by cos(ω
ct) due to the HF sine-wave injection. In [
19,
20], a signal process by multiplying the same per unit sine voltage and adding a low-pass filter (LPF) is proposed to obtain the spatial saliency signal, i
sal_sine.
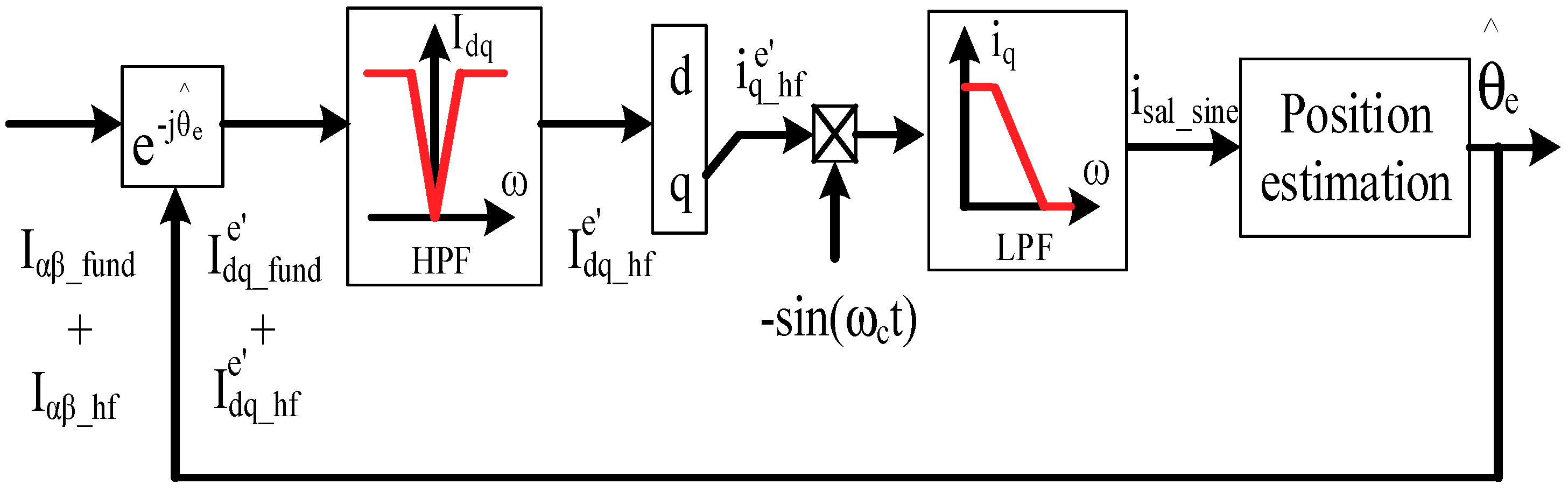
Figure 3 illustrates the signal process of saliency-based position estimation using a sine-wave voltage injection. In addition to the LPF, a high-pass filter (HPF) is applied to isolate the injection-induced current from the fundamental current. The corresponding analytical equation of i
sal_sine is given by
In (4), only a single saliency harmonic with respect to 2θ
e is considered [
10]. It is assumed that the phase inductance waveform in
Figure 1 is purely sinusoidal where the frequency is 2 times with respect to the rotor position. However, for actual machines, flux saturation must occur due to the nonlinear relationship between flux density and magnetic field strength. Considering the flux saturation, the phase inductance waveform might be changed by the red signal in
Figure 1. Under this effect, secondary saliency harmonics instead of a 2θ
e harmonic occur, leading to saliency-based position estimation error. In this paper, the ideal saliency signal in (4) is extended to consider saturation saliency harmonics as depicted in (5).
where i
sal_sine_sat is the saliency signal considering saturation harmonics, and ΔL
4 and ΔL
6 are the magnitudes of fourth-order and sixth-order saturation harmonics. These secondary harmonics are dependent on the condition of flux saturation. In (5), high-order secondary harmonics (larger than sixth-order) are negligible. Due to the influence of saturation harmonics, periodic position estimation errors might occur on the position estimation using the sine-wave voltage injection.
In addition to the flux saturation, inverter dead-time also causes secondary harmonics in the saliency signal i
sal_sine.
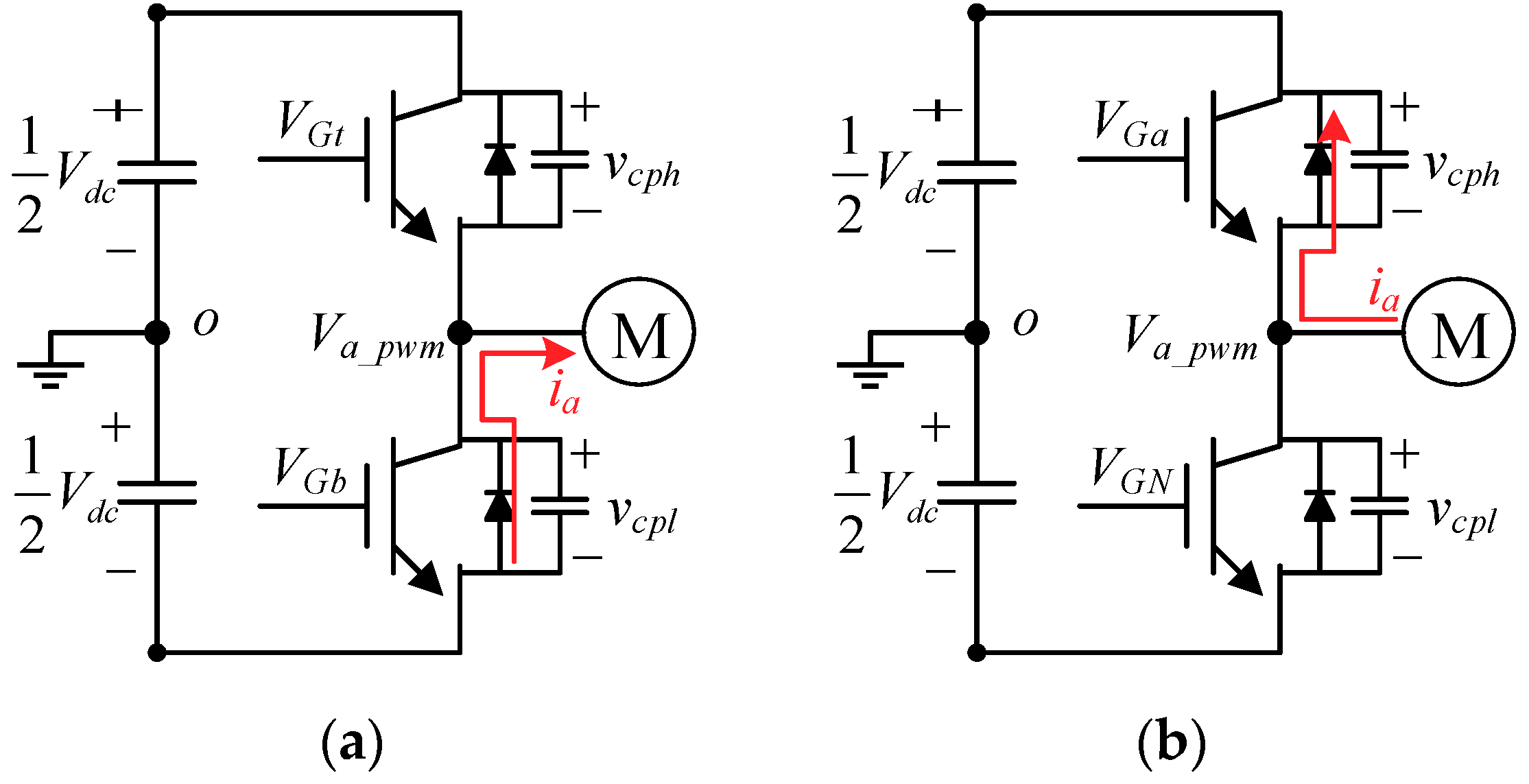
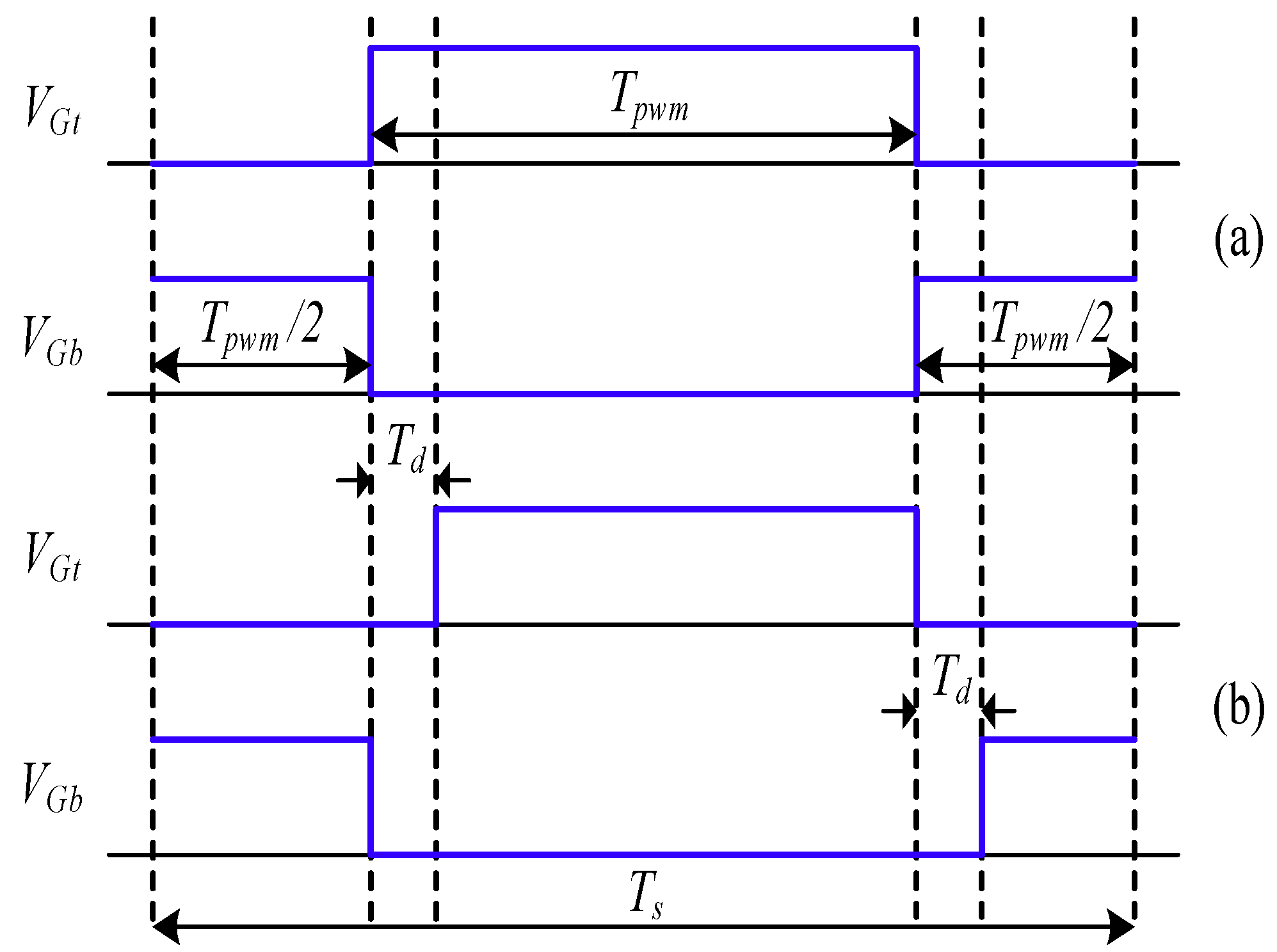
Figure 4 illustrates the dead-time effect on the inverter’s A-phase leg. In (a), when both gate signals V
Gt and V
Gb suddenly turn off, the phase current flows from the low-side diode D
b to the windings when the current polarity is positive. At this instant, a negative voltage error results on the A-phase PWM voltage V
a_pwm. By contrast, in (b), once the current is negative, a positive voltage error occurs during the dead-time period. Considering the influence of dead-time, the injection voltage in (1) needs to be corrected by
where V
err_dt_d and V
err_dt_q are the d- and q-axis dead-time voltage error, respectively, which is shown by (7).
In (7),
and
represent the period of PWM and dead-time, respectively. In addition,
and
are respectively the switch turn-on and off time period. In this paper,
and
are assumed to be sufficiently smaller than
for simplicity. In addition, sign(i) is the polarity of three phase currents during internal switching, as given by
Figure 5 illustrates the actual A-phase high-side and low-side PWM signal considering the dead-time effect. Substituting (6) into (2), the injection-reflected HF current,
and
in (3), is
By using the same signal process in (4) with a dead-time effect, the saliency signal is changed by i
sal_sine_dt in (10).
As shown in (10), dead-time leads to additional harmonics modulated by sin(ω
ct) in i
sal_sine_dt. These harmonics are proportional to the dead-time voltage error V
err_dt. However, it is noted that these harmonics can be filtered based on the LPF for the signal process in
Figure 3. Thus, the selection of LPF bandwidth is the trade-off between the position estimation bandwidth and the estimation error.
In (10), only the dead-time error is considered. For actual inverter circuits, device parasitic capacities also cause a HF voltage error for the instant when the phase current flows across zero. According to the analysis in [
5,
6], this error causes a second-order saliency harmonic with respect to the rotor position.
3. HF Square-Wave Voltage Injection
The flux saturation and inverter dead-time on a square-wave voltage saliency-based drive are investigated in this section. As reported in [
29,
30,
31], a square-wave voltage in (11) can be superimposed in the estimated d-axis.
where v
squ is the magnitude of square-wave voltage. By injecting a square-wave voltage, the HF model is given by
In (12), ΔT is the time period of the square-wave voltage. Besides this,
and
represent the d-axis and q-axis current difference, respectively, based on the current state T
1 and the last state T
0. They are expressed by
Substituting (11) into (12),
and
are given by
By injecting a square-wave voltage, a position signal dependent on ΔL appears in
once the estimated frame in
Figure 2 is not the same as the actual frame as shown in
Figure 2. Different to sine-wave injection in (4),
is modulated by a ± sign due to the square-wave property. A signal process by multiplying the
sign was proposed to obtain the saliency signal, i
sal_squ [
30], as seen in (15).
Similar to i
sal_sine in (4), the rotor position is estimated by regulating θ
err in i
sal_squ to be zero.
Figure 6 illustrates the signal processing for the position estimation with square-wave injection. Compared to
Figure 3 using sine-wave injection, ± sign correction in (15) instead of an LPF in (4) is applied. By removing the LPF in
Figure 6, a higher estimation bandwidth can be of benefit to a sensorless drive.
It is noted that secondary saliency harmonics caused by the flux saturation also occur on the saliency signal with square-wave injection. Considering saturation-reflected saliency harmonics, the saliency signal, i
sal_squ_scnd, should be modified from (15).
By comparing isal_squ_scnd in (16) and isal_sine_sat in (5), the flux saturation effect is the same on both isal_squ_scnd and isal_sine_sat using either the sine-wave or the square-wave voltage.
The influence of dead-time on the square-wave voltage is also analyzed in this paper. Similar to the sine-wave voltage in (6), the HF square-wave voltage in (11) should be modified by
In (17), the dead-time causes the same voltage error,
, mentioned in (7). By replacing (17) into (12), the current differences,
and
, are shown by
For the position estimation in
Figure 6 the saliency signal is obtained based on the demodulation of
, which can be derived by
where i
sal_squ_dt is the saliency current considering the dead-time. By comparing the square-wave saliency signal i
sal_square_dt in (19) and the sine-wave saliency signal i
sal_sine_dt in (10), i
sal_square_dt contains dead-time harmonics where the magnitudes are directly proportional to v
err_dt_q. By contrast, i
sal_sine_dt might achieve negligible dead-time error because of the LPF used in
Figure 3. As a result, the position estimation using the sine-wave voltage injection reduces the dead-time error, which can be of benefit to a saliency-based sensorless drive.
4. Experimental Results
An IPM machine with a 1.41 saliency ratio (L
q/L
d) is built to verify the saliency-based position estimation analyzed in
Section 2 and
Section 3.
Table 1 lists the specifications of this test machine. A two-level inverter with 150-V DC bus voltage is used to generate PWM voltages. The PWM frequency is designed at 10-kHz to balance the dynamic response and switching losses.
Figure 7 illustrates the test setup of the saliency-based drive for the test machine. A hysteresis brake is back-to-back connected to the test machine for operation under load. All the control and position-sensing algorithms are implemented in a fixed-point 32-bit microcontroller TI-TMS320F28069. For the following experiments, the magnitudes and frequencies of the two injection voltages are the same at 30 V and 1 kHz to easily evaluate the performance difference.
A. Dead-Time Harmonics:
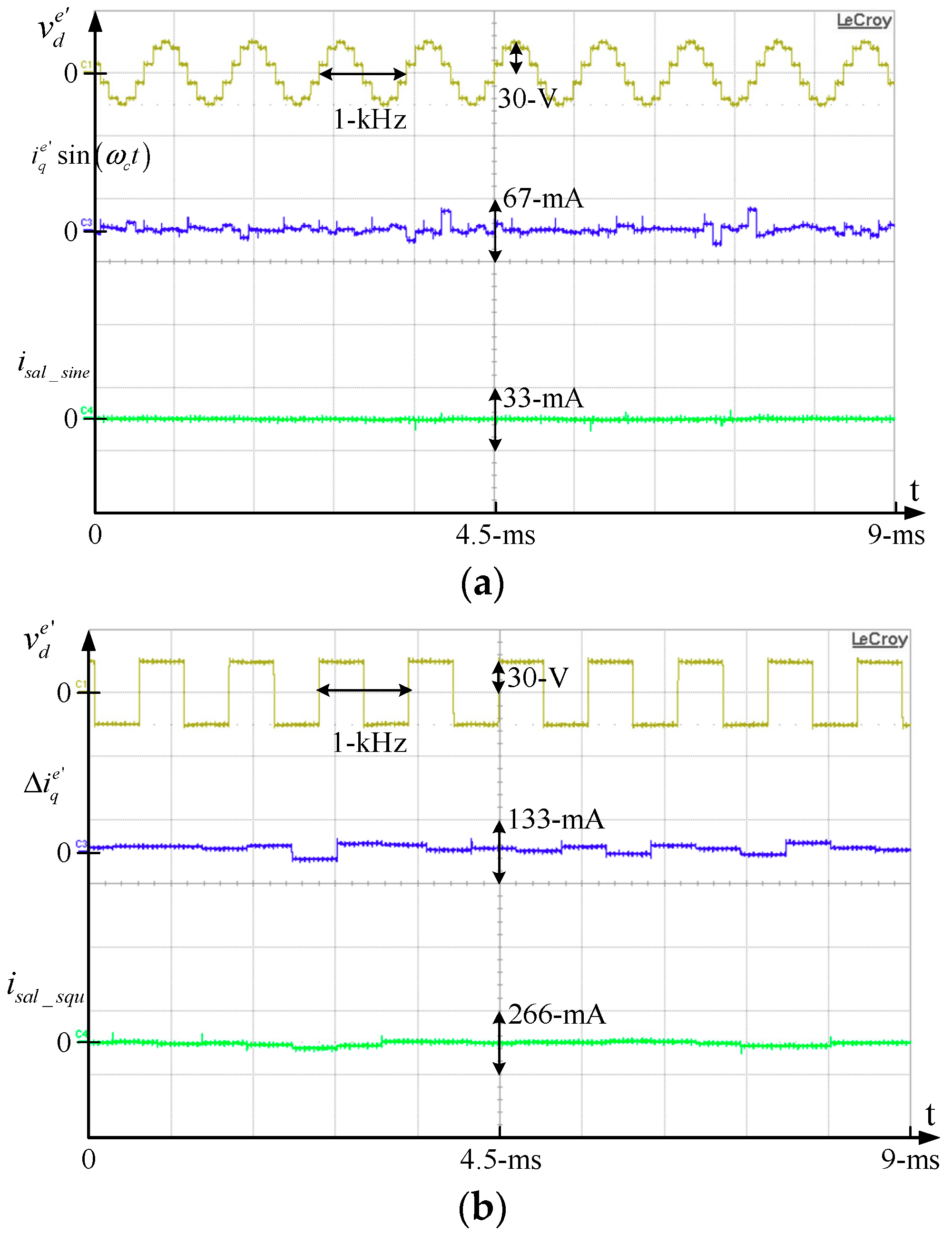
This part evaluates the dead-time effect on both the sine-wave saliency signal, isal_sine_dt, in (9) and the square-wave signal, isal_squ_dt, in (18). The dead-time is set at 2 μs during a 100-μs PWM period.
The rotor position is locked at 0 degrees by applying an external load. Because the rotor is locked, i
sal_sine_dt and i
sal_squ_dt should both be maintained at zero considering an ideal inverter without dead-time.
Figure 8a illustrates waveforms of
in (6) and
sin(ω
ct) and i
sal_sine_dt in (10). In this figure,
sin(ω
ct) instead of
is shown to clearly demonstrate the dead-time distortion on the HF current. By contrast,
Figure 8b compares
in (16) and
and i
sal_squ_dt in (18). Considering the sine-wave injection signal process in
Figure 3, the bandwidths of the LPF and the HPF are respectively designed at 100 Hz and 20 Hz for the experimental tests. In addition, for the square-wave signal process, the HPF in
Figure 6 is the same at 20 Hz. It is observed that i
sal_sine_dt in (a) achieves lower harmonic errors than i
sal_squ_dt in (b) due to the LPF in
Figure 3. This result verifies the analytical model explained in
Section 2 It is concluded that the dead-time effect is reduced for the position estimation using the sine-wave voltage injection.
B. Saliency-Based Position Estimation:
This part compares the saliency-based position estimation using two different voltage injection signals. Both position estimation at no load and full load are evaluated to verify secondary saliency harmonics under different operating conditions.
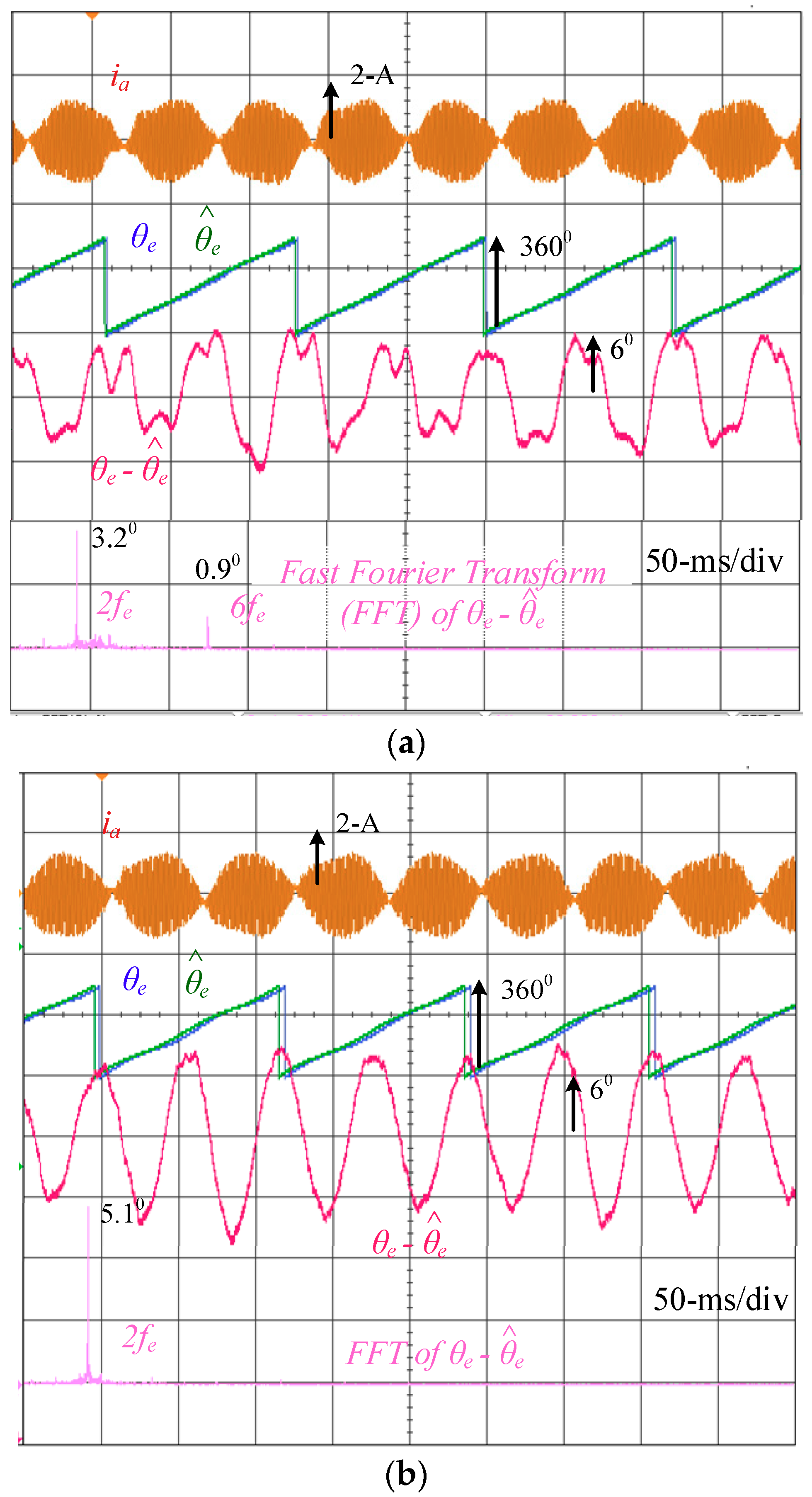
Figure 9 shows the saliency-based position estimation at no load using (a) sine-wave and (b) square-wave voltage injection. The injection frequency is set at 1 kHz to clearly evaluate the position error on the two injection signals. The speed is maintained at 100 rpm (ωe = 2π × 5 rad/s). As seen in (a) using sine-wave voltage, the position error is around 6 degrees consisting of a second- and a sixth-order harmonic. By contrast, in (b) using square-wave voltage injection, the error increases to 8.5 degrees where the second-order harmonic dominates. It is shown that the second-order harmonic using the square-wave injection is higher than that using the sine-wave injection. The dead-time distortion on HF voltages is the primary issue especially when phase currents cross zero.
Figure 10 shows the same position estimation comparison at full load. Due to additional fundamental currents for load operation, the dead-time-reflected voltage distortion can be easily compensated for. Under this effect, the position estimation error decreases as the fundamental current increases. For the sine-wave injection in (a), the position error is approximately the same as the error at no load because the dead-time harmonic has been filtered under the demodulation process with an LPF. However, for the square-wave in
Figure 10b, the second-order harmonic decreases as the fundamental current increases. This result is consistent with the analysis in
Section 4 part B. The dead-time harmonic cannot be filtered for the square-wave injection if the current difference demodulation in
Figure 6 is applied. Considering the saliency-based drive using square-wave injection, this visible second-order harmonic at no load can be compensated for if the harmonic magnitude and phase are known based on off-line measurement. In addition, high-voltage magnitude injection is also useful to reduce dead-time harmonics for square-wave injection. By contrast, at full load, the second-order harmonic magnitudes are almost the same between the two different injection signals. This harmonic component is primary caused by the machine’s secondary saliency harmonic which cannot be compensated for by selecting different injection signals.
C. Sensorless Position Control:
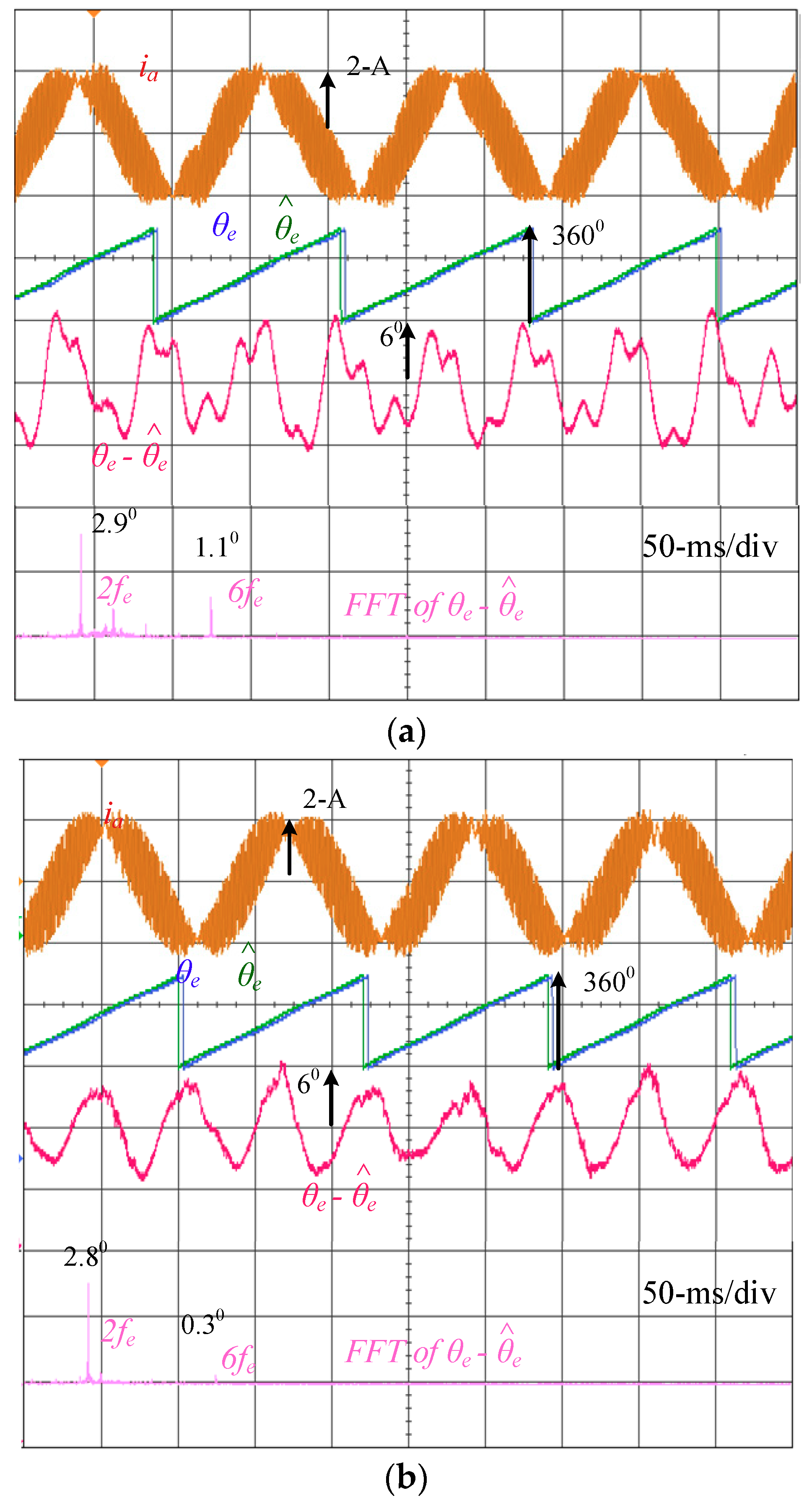
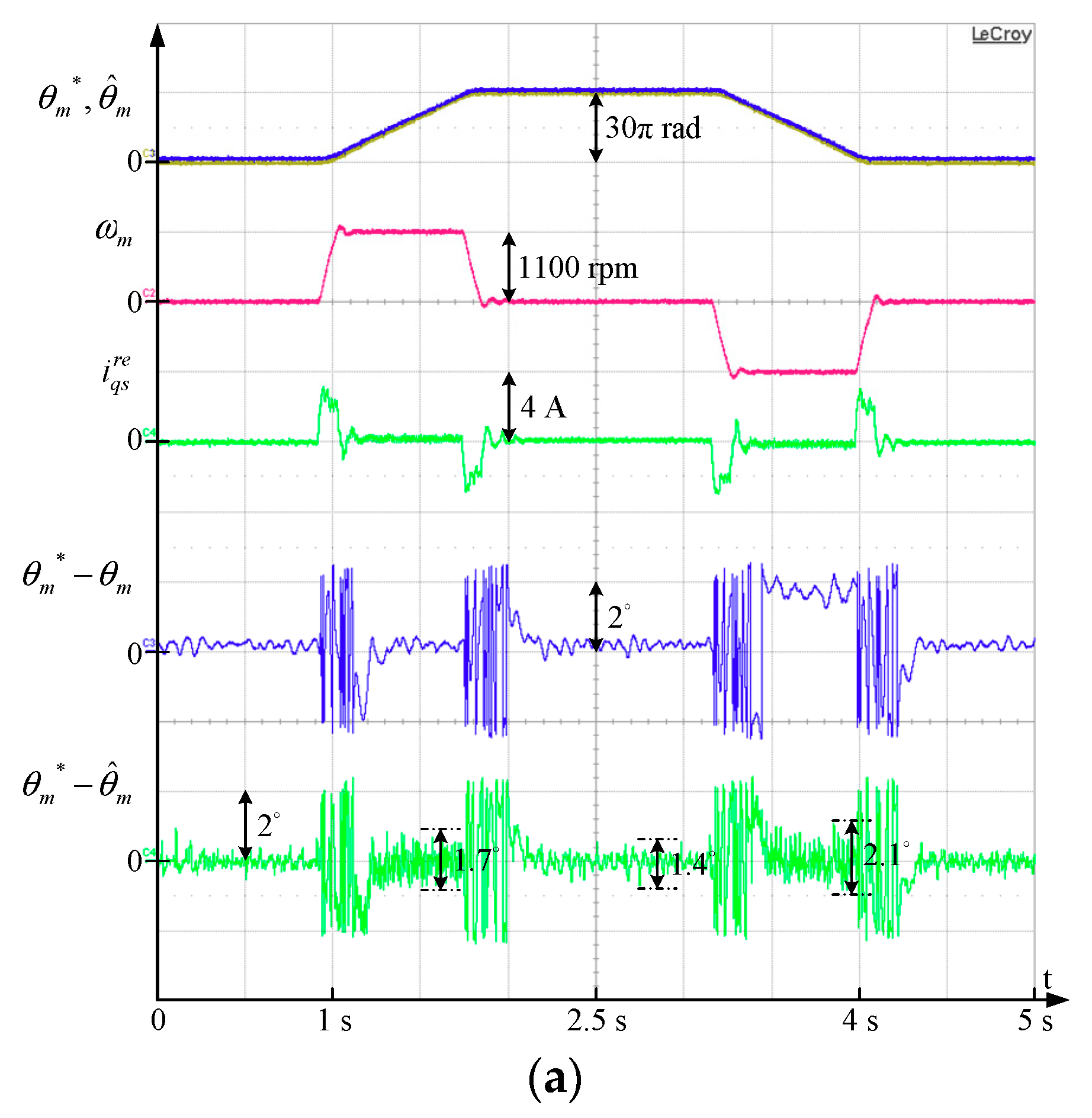
Position control based on saliency-based position estimation using different injection signals is compared in
Figure 11. As seen in (a), the saliency-based drive with sine-wave voltage injection is applied. The machine’s position is manipulated from the mechanical position
= 0 rad to 30π rad. During the speed transition, the peak-to-peak mechanical position estimation error θ
m–
is around 4.2 degrees. However, this error can be negligible once the drive arrives at steady state. By contrast, the position control error
–
is around 1.4 degrees at steady state.
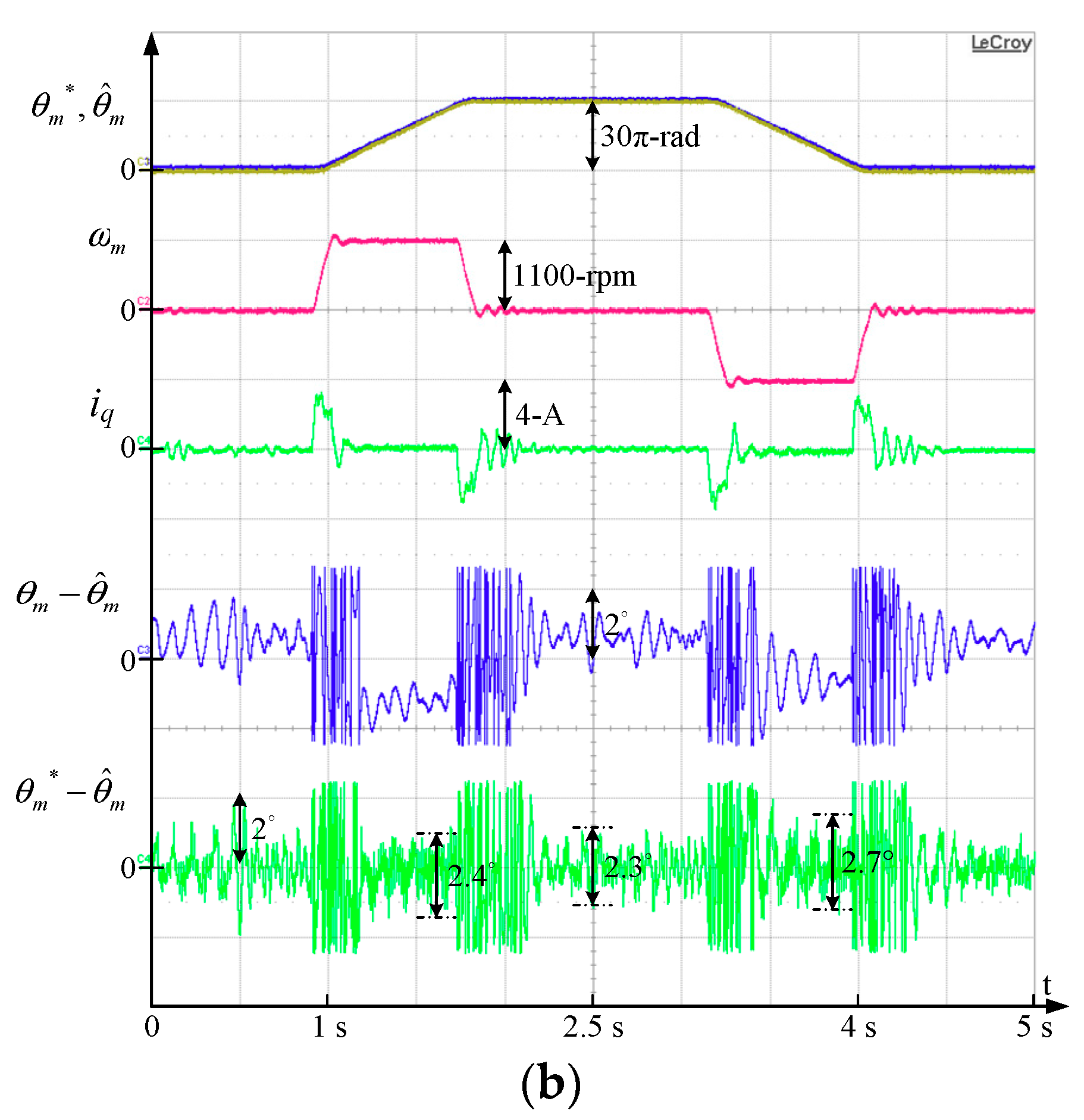
Figure 11b compares the similar position control with the saliency-based drive while the square-wave voltage is used. At steady state, the estimation error θ
m–
increases to 2 degrees. The control error
–
also increases to 2.3 degrees, resulting in degraded position control accuracy. Similar to prior experimental results, the influence of dead-time on the square-wave voltage signal is the primary issue to cause this higher estimation error.
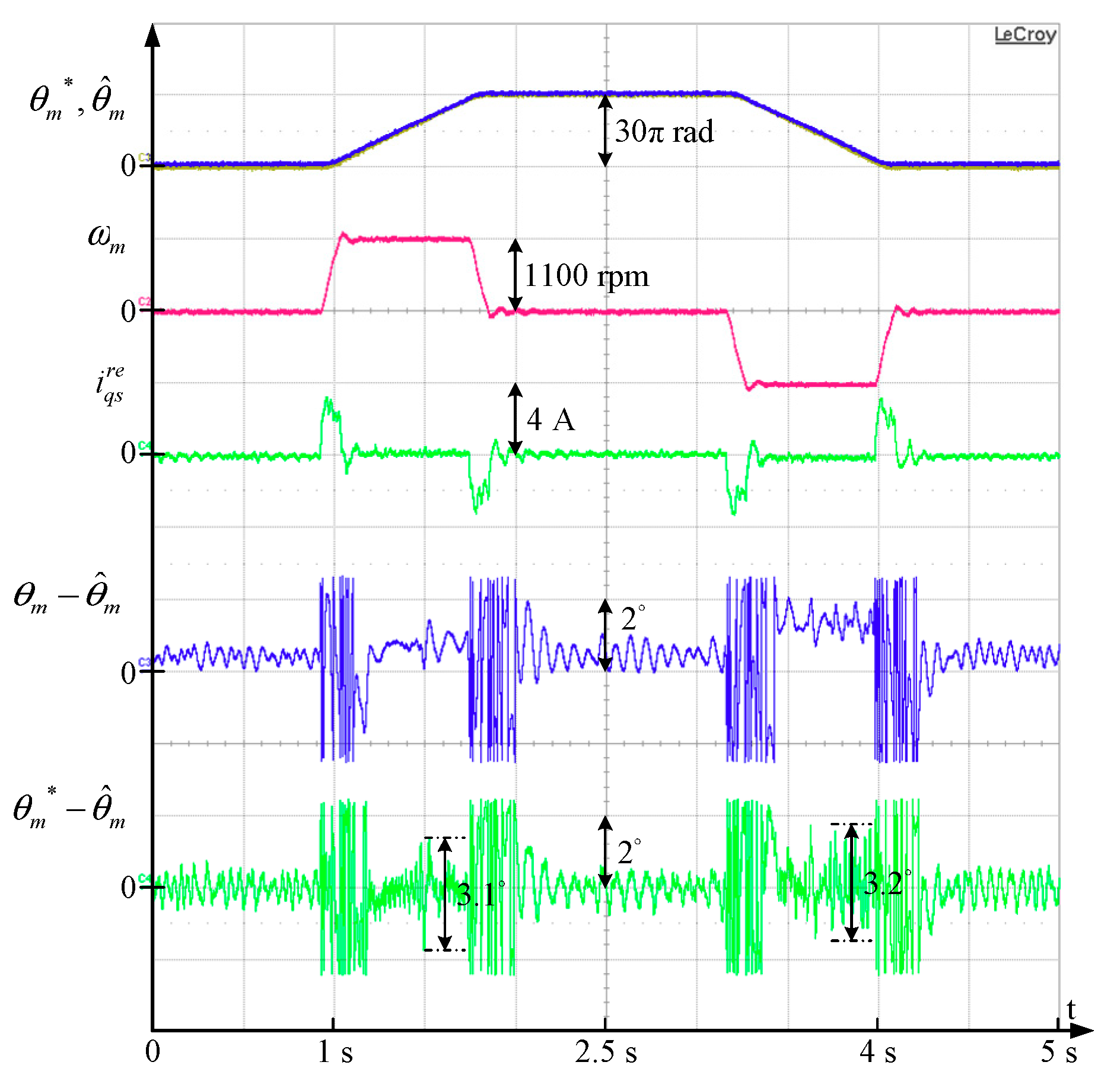
It is noted that the injection frequency of both the sine-wave and the square-wave is selected at 1 kHz to compare the position estimation performance. For the sine-wave voltage, the injection frequency is limited by the PWM frequency. High injection frequency might lead to considerable discretized harmonics which is not recommended for position estimation. By contrast, for square-wave voltage, the injection frequency can be increased near the PWM frequency without a discretized effect.
Figure 12 shows the same sensorless position control with 5 kHz square-wave voltage injection. In this experiment, the injection flux is maintained the same as in
Figure 11b for the comparison of square-wave injection estimation performance using 1 kHz and 5 kHz frequencies. It is observed that the position estimation error decreases as the injection frequency increases. Under the same flux injection, the voltage magnitude is higher for the 5 kHz voltage signal. In general, a high voltage magnitude is useful to reduce the dead-time voltage effect, leading to a reduction of position estimation errors.