Research on a Plug-In Hybrid Electric Bus Energy Management Strategy Considering Drivability
Abstract
1. Introduction
2. Configuration of the Power Drive System and the PHEB Control Method
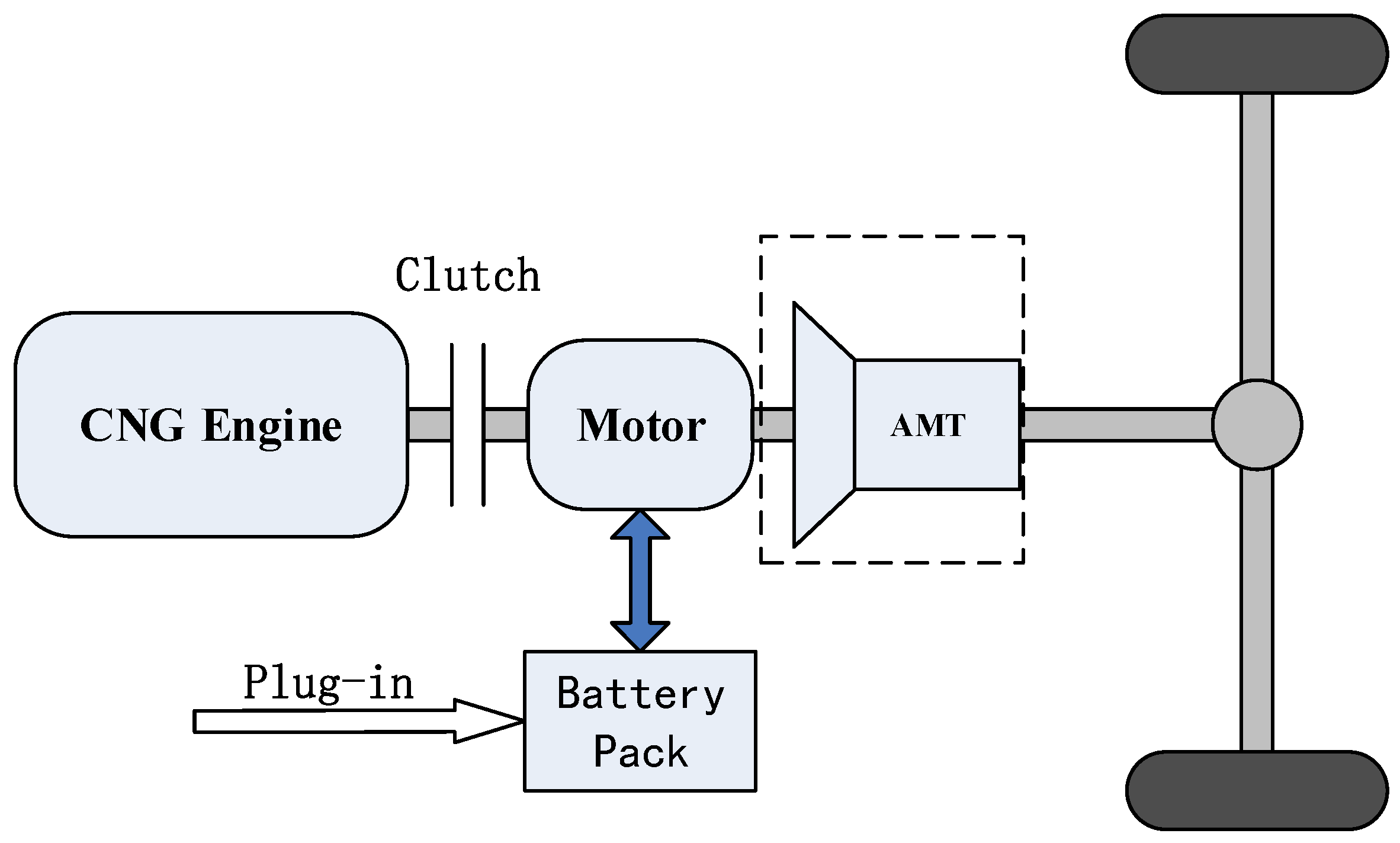
2.1. Configuration of the Power System and Work Mode
2.2. System Models
2.2.1. Vehicle Longitudinal Dynamics
2.2.2. Transmission System Model
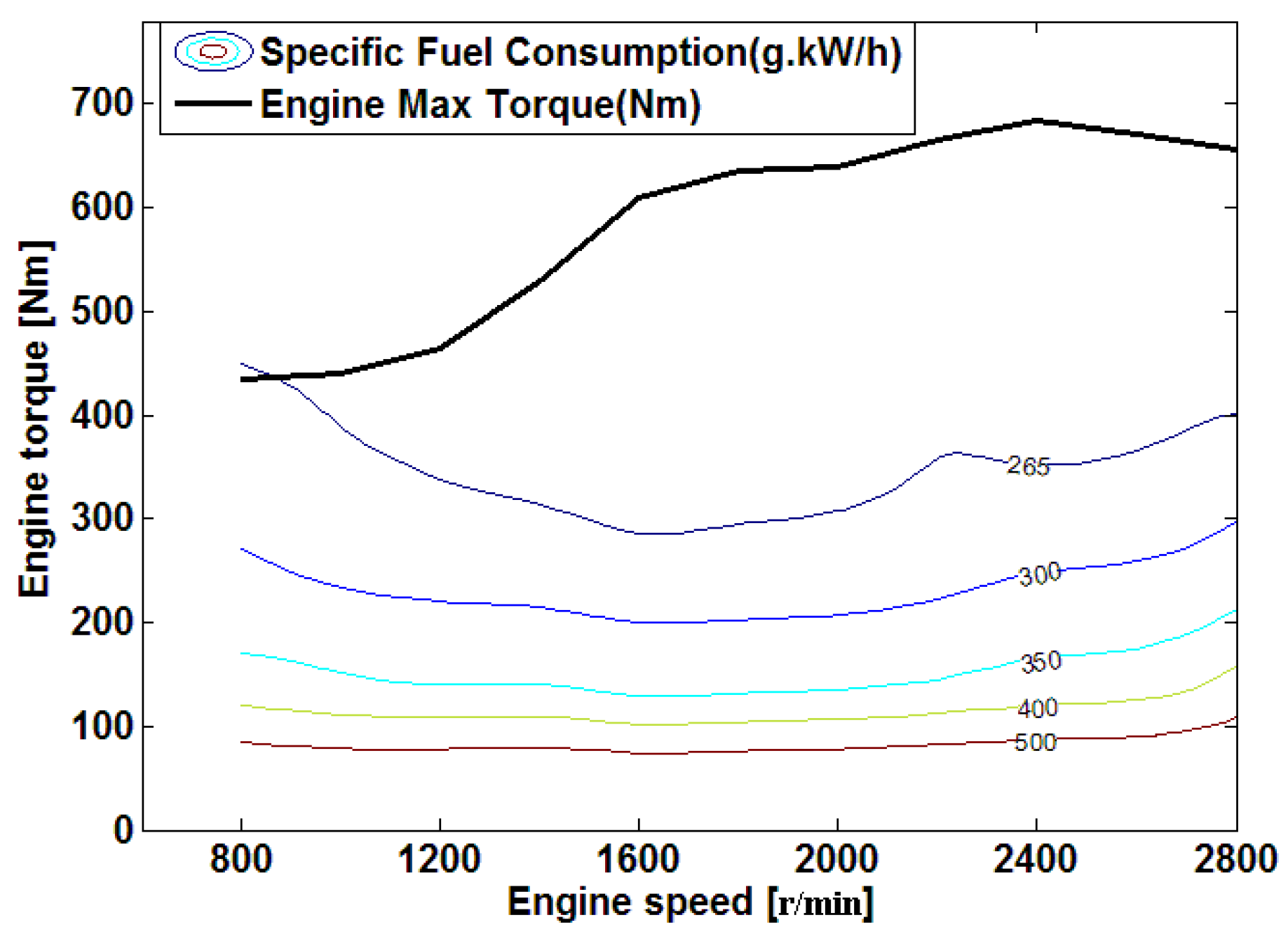
2.2.3. Engine Model
2.2.4. EM Model
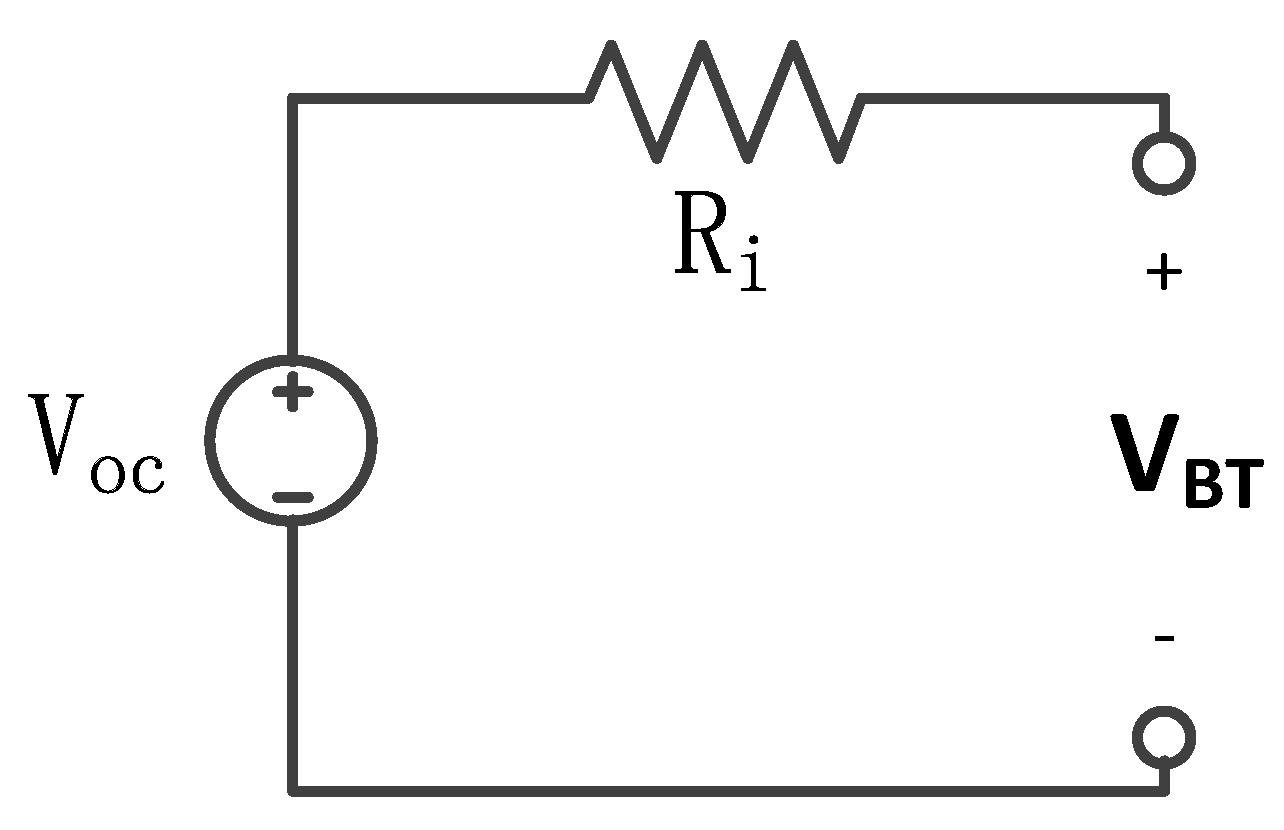
2.2.5. Battery Model
3. The Energy Management Optimization for REEBs
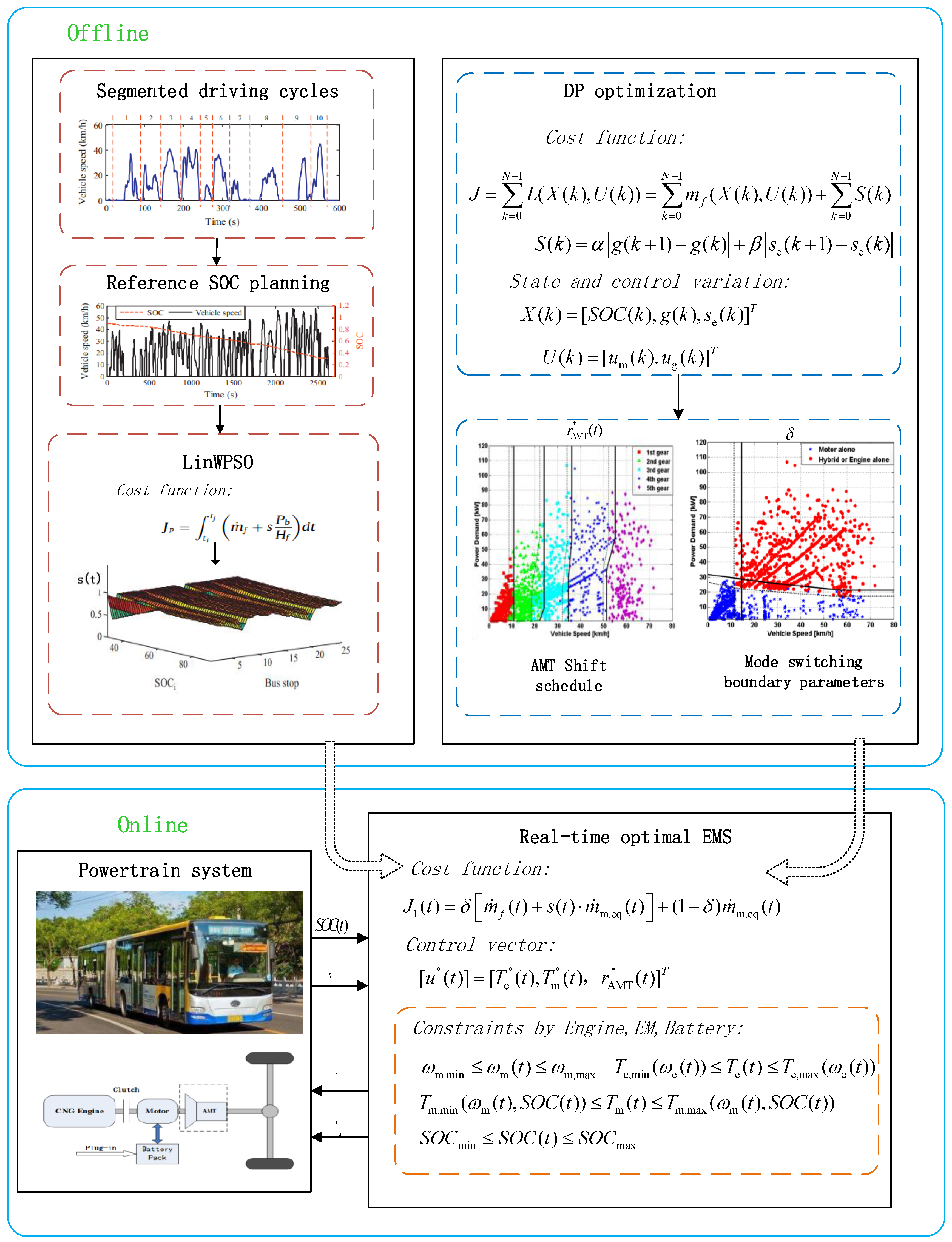
3.1. Real-Time Optimal Energy Management Strategy
3.2. s(t) Optimization
4. Dynamic Programming
4.1. Problem Formulation
4.2. Parameter Extraction
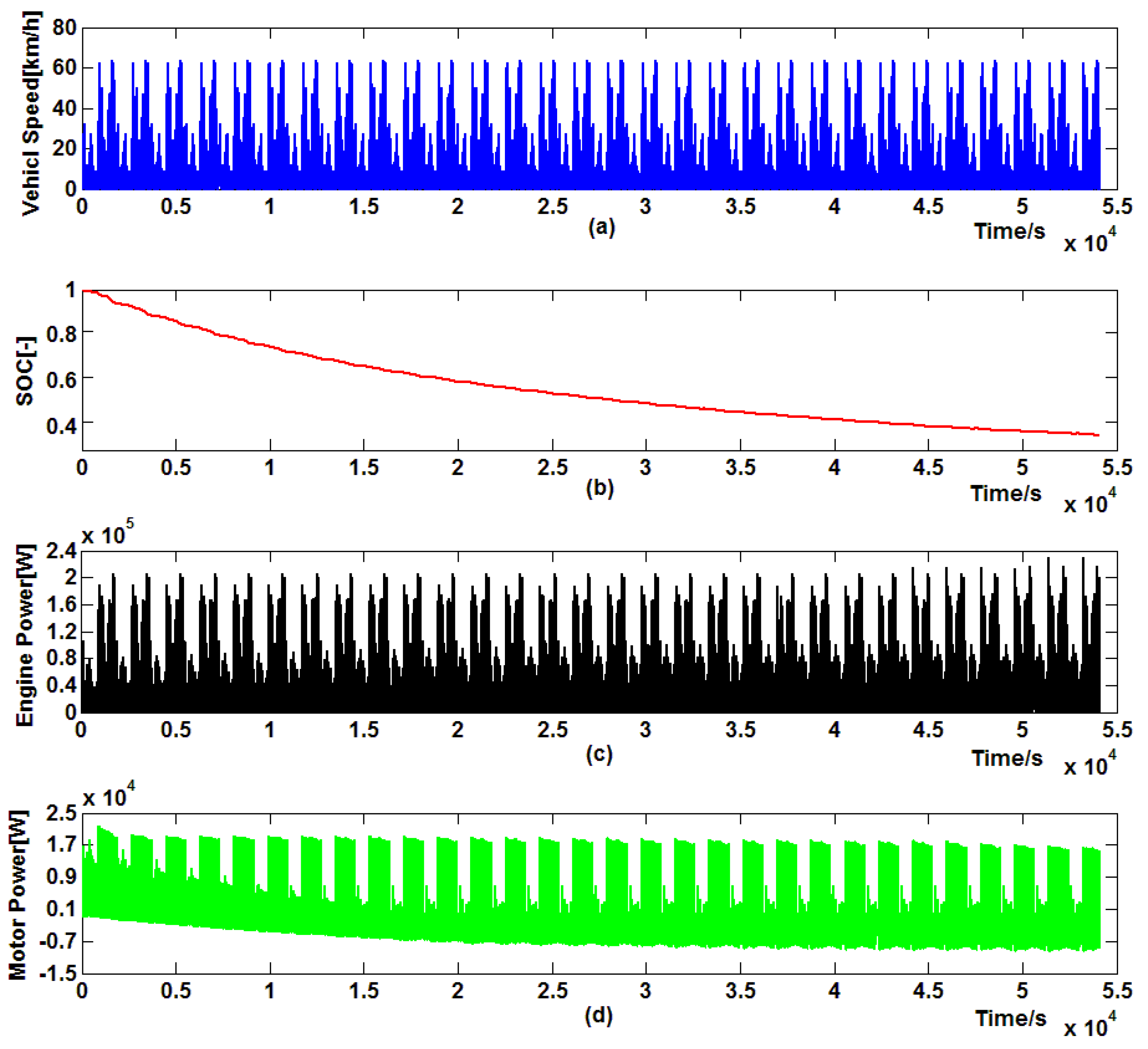
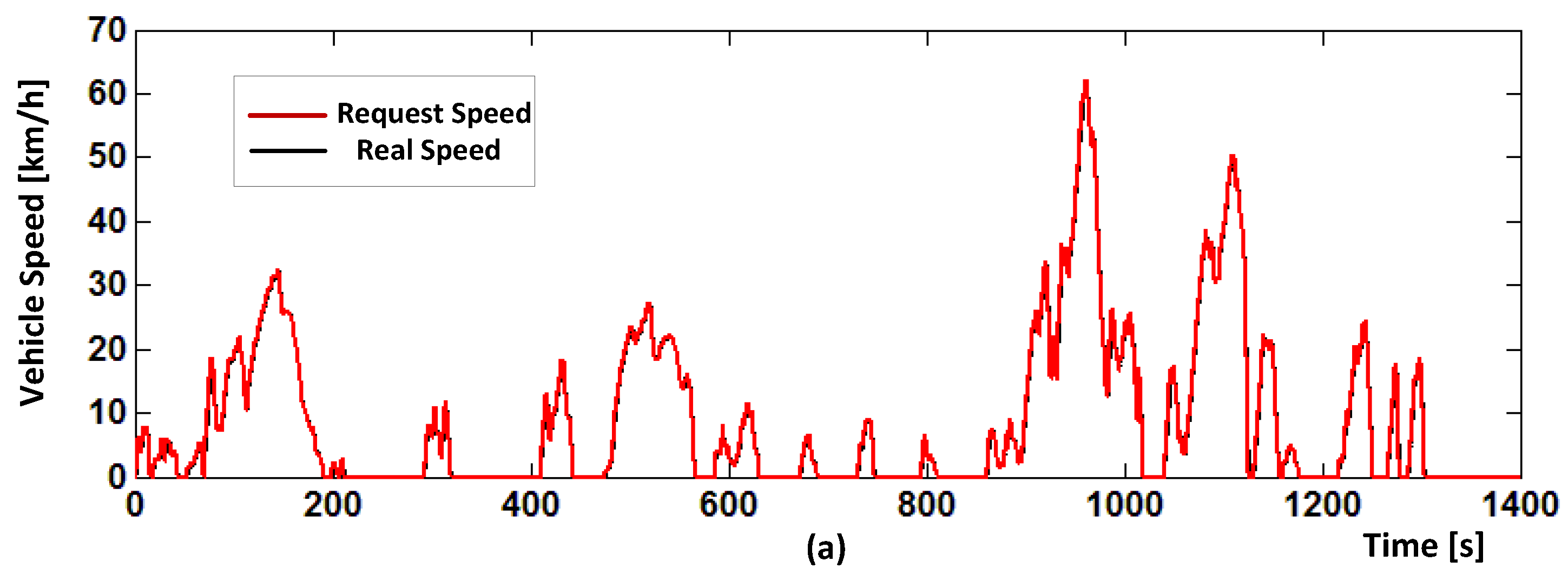
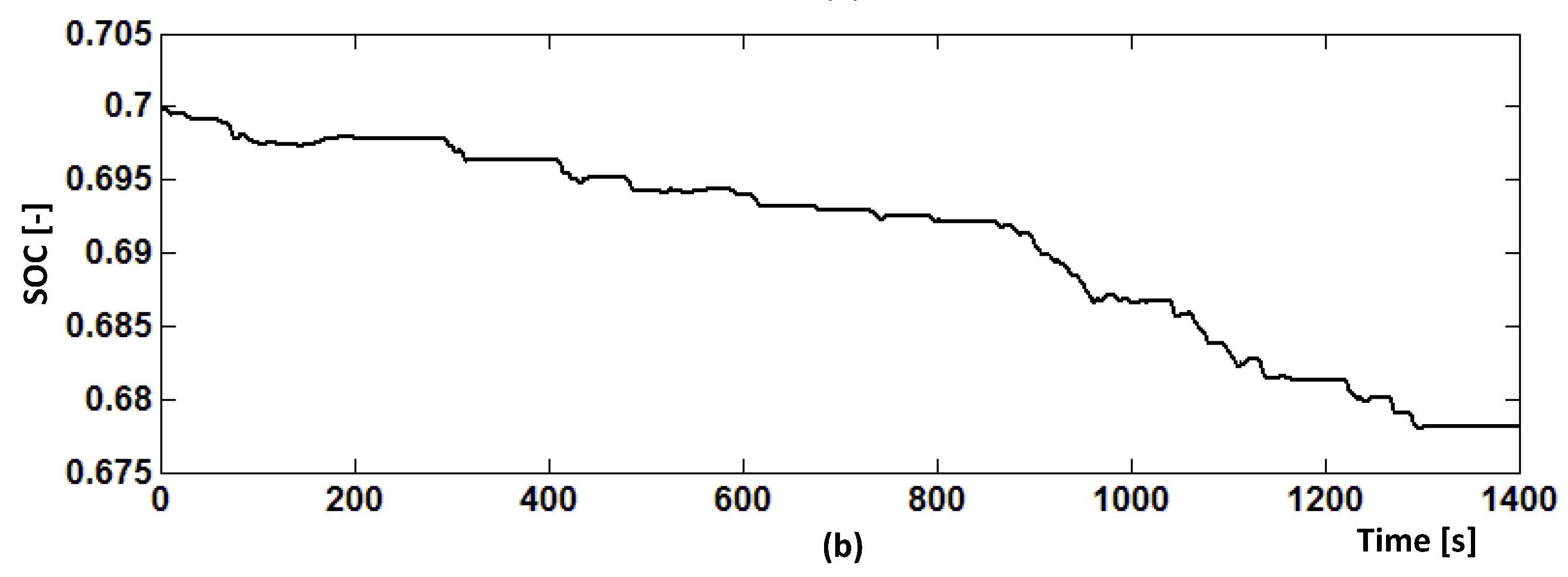
5. Verification and Discussion
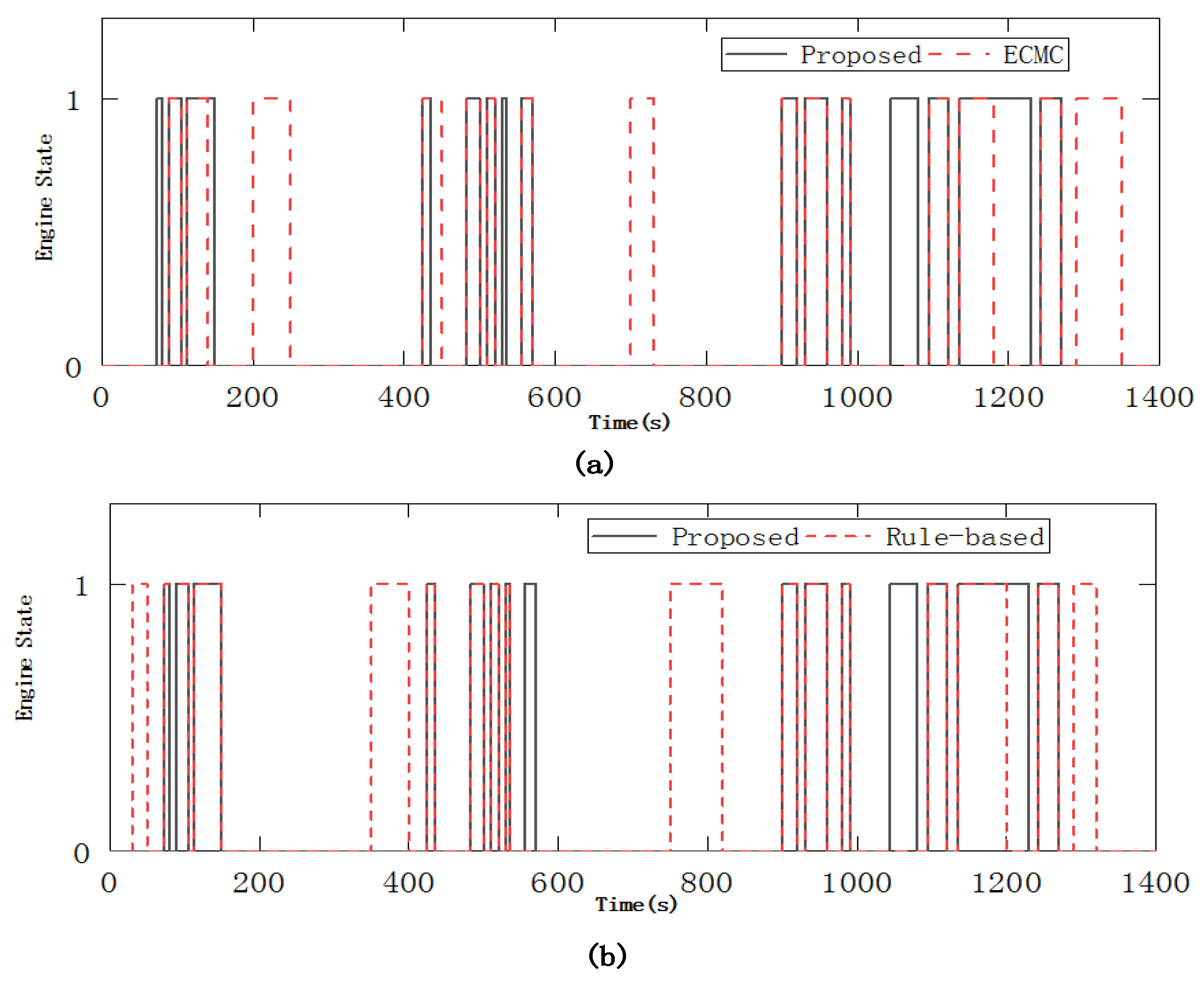
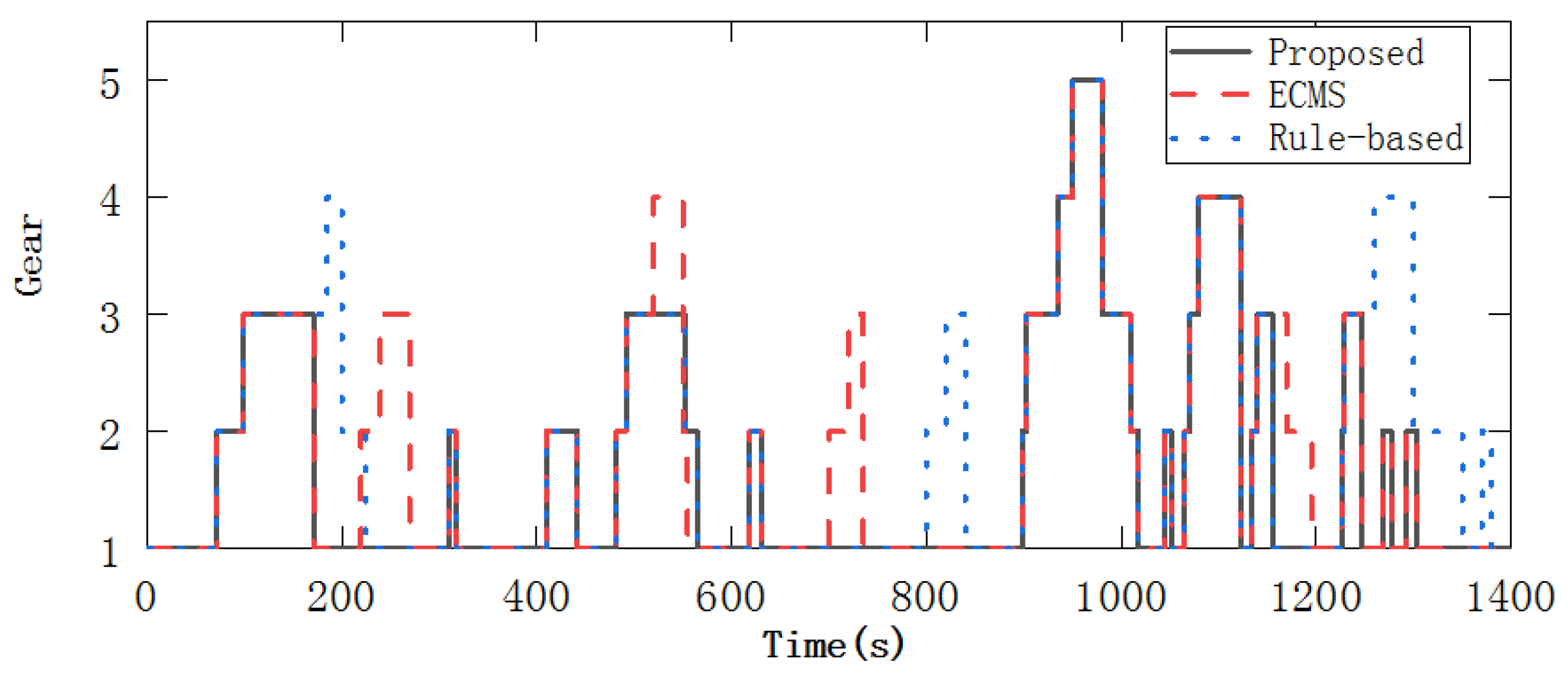
5.1. Control Performance of Proposed Control Strategy
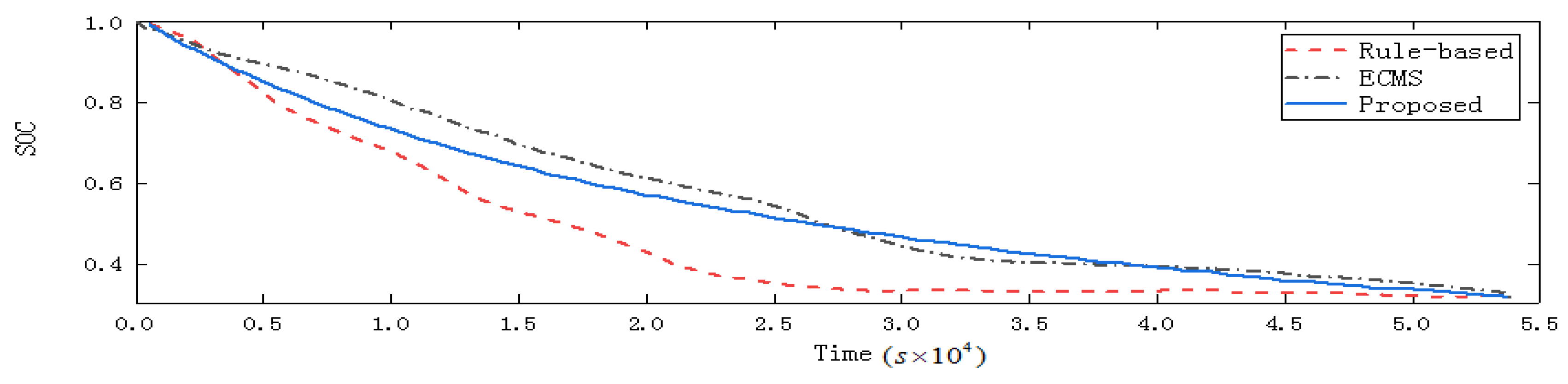
5.2. Energy Consumption
5.3. Drivability
6. Conclusions
- (1)
- In response to the fuel economy problem, combined with the complex but regular characteristics of the bus routine, a linear weight particle swarm optimization algorithm was used to obtain the optimal array of s(t) by minimizing the fuel consumption. Considering the drivability of the PHEB, the DP algorithm was used to extract the parameters of the mode switching boundary and the AMT gear-shifting correction. Then, the novel algorithm is brought forward to improve the fuel economy and the drivability of the PHEB, combined with the s(t), gear-shifting correction and mode switching boundary parameters.
- (2)
- The proposed strategy was verified in a real-world driving cycle simulation. Results show that the proposed energy management strategy is effective in improving the fuel economy of the PHEB by moving the working points of the two power sources into the high-efficiency area. In addition, the results also verify that the proposed strategy ensures the drivability by their reduction of AMT gear-shifting frequency and the engine start-stop times. The overall performance is 18.54% improvement compared with the rule-based control strategy.
Author Contributions
Funding
Conflicts of Interest
References
- Martinez, C.M.; Hu, X.; Cao, D.; Velenis, E.; Gao, B.; Wellers, M. Energy Management in Plug-in Hybrid Electric Vehicles: Recent Progress and a Connected Vehicles Perspective. IEEE Trans. Veh. Technol. 2017, 66, 4534–4549. [Google Scholar] [CrossRef]
- Sun, F.; Xiong, R.; He, H. A systematic state-of-charge estimation framework for multi-cell battery pack in electric vehicles using bias correction technique. Appl. Energy 2016, 162, 1399–1409. [Google Scholar] [CrossRef]
- Amini, M.H.; Islam, A. Allocation of electric vehicle’s parking lots in distribution network. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 19–22 February 2014; pp. 1–5. [Google Scholar]
- Hu, X.; Moura, S.J.; Murgovski, N.; Egardt, B.; Cao, D. Integrated optimization of battery sizing, charging, and power management in plug-in hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2016, 24, 1036–1043. [Google Scholar] [CrossRef]
- Li, G.; Zhang, J.; He, H. Battery SOC constraint comparison for predictive energy management of plug-in hybrid electric bus. Appl. Energy 2017, 194, 578–587. [Google Scholar] [CrossRef]
- Wirasingha, S.G.; Emadi, A. Classification and Review of Control Strategies for Plug-In Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2011, 60, 111–122. [Google Scholar] [CrossRef]
- Pisu, P.; Rizzoni, G. A comparative study of supervisory control strategies for hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2007, 15, 506–518. [Google Scholar] [CrossRef]
- Gao, Y.M.; Ehsani, M. Design and control methodology of plug-in hybrid electric vehicles. IEEE Trans. Ind. Electron. 2010, 57, 633–640. [Google Scholar]
- Banvait, H.; Anwar, S.; Chen, Y. A rule-based energy management strategy for plug-in hybrid electric vehicle (PHEV). In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3938–3943. [Google Scholar]
- Peng, J.K.; Fan, H.; He, H.W.; Pan, D. A rule-based energy management strategy for a plug-in hybrid school bus based on a controller area network bus. Energies 2015, 8, 5122–5142. [Google Scholar] [CrossRef]
- Martínez, J.S.; John, R.I.; Hissel, D. A survey-based type-2 fuzzy logic system for energy management in hybrid electrical vehicles. Inf. Sci. 2012, 190, 192–207. [Google Scholar] [CrossRef]
- Li, S.G.; Sharkh, S.M.; Walsh, F.C.; Zhang, C.N. Energy and battery management of a plug-in series hybrid electric vehicle using fuzzy logic. IEEE Trans. Veh. Technol. 2011, 60, 3571–3585. [Google Scholar] [CrossRef]
- Denis, N.; Dubois, M.R.; Desrochers, A. Fuzzy-based blended control for the energy management of a parallel plug-in hybrid electric vehicle. Intell. Trans. Syst. IET 2015, 9, 30–37. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Xiong, R.; Xu, J.; You, C. Energy management of a power-split plug-in hybrid electric vehicle based on genetic algorithm and quadratic programming. J. Power Sources 2014, 248, 416–426. [Google Scholar] [CrossRef]
- Arabali, A.; Ghofrani, M.; Etezadi-Amoli, M.; Fadali, M.S.; Baghzouz, Y. Genetic-algorithm-based optimization approach for energy management. IEEE Trans. Power Deliv. 2013, 28, 162–170. [Google Scholar] [CrossRef]
- Kum, D.; Peng, H.; Bucknor, N.K. Optimal energy and catalyst temperature management of plug-in hybrid electric vehicles for minimum fuel consumption and tail-pipe emissions. IEEE Trans. Control Syst. Technol. 2013, 21, 14–26. [Google Scholar] [CrossRef]
- Pu, J.; Yin, C. Optimal control of fuel economy in parallel hybrid electric vehicles. J. Autom. Eng. 2007, 221, 1097–1106. [Google Scholar] [CrossRef]
- Peng, J.; He, H.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2017, 185, 1633–1643. [Google Scholar] [CrossRef]
- Chen, B.; Wu, Y.; Tsai, H. Design and analysis of power management strategy for range extended electric vehicle using dynamic programming. Appl. Energy 2014, 113, 1764–1774. [Google Scholar] [CrossRef]
- Zhang, S.; Xiong, R. Adaptive energy management of a plug-in hybrid electric vehicle based on driving pattern recognition and dynamic programming. Appl. Energy 2015, 155, 68–78. [Google Scholar] [CrossRef]
- Chen, Z.; Li, L.; Yan, B.; Yang, C.; Marina, M.C.; Cao, D. Multimode Energy Management for Plug-In Hybrid Electric Buses Based on Driving Cycles Prediction. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2811–2821. [Google Scholar] [CrossRef]
- Chen, Z.; Xia, B.; You, C.; Mi, C.C. A novel energy management method for series plug-in hybrid electric vehicles. Appl. Energy 2015, 145, 172–179. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Chen, J.; Zhang, X. Study on energy management strategy and dynamic modeling for auxiliary power units in range-extended electric vehicles. Appl. Energy 2017, 194, 363–375. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, C.; Li, J.; Fathy, H.K. A Pseudospectral Strategy for Optimal Power Management in Series Hybrid Electric Powertrains. IEEE Trans. Veh. Technol. 2016, 65, 4813–4825. [Google Scholar] [CrossRef]
- Zou, C.F.; Manzie, C.; Nesic, D. Model Predictive Control for Lithium-Ion Battery Optimal Charging. IEEE-ASME Trans. Mechatron. 2018, 23, 947–957. [Google Scholar] [CrossRef]
- Zou, C.; Hu, X.; Wei, Z.; Tang, X. Electrothermal dynamics-conscious lithium-ion battery cell-level charging management via state-monitored predictive control. Energy 2017, 141, 250–259. [Google Scholar] [CrossRef]
- Kermani, S.; Delprat, S.; Guerra, T.M.; Trigui, R.; Jeanneret, B. Predictive energy management for hybrid vehicle. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–9 September 2012; pp. 408–420. [Google Scholar]
- Sun, C.; Hu, X.S.; Moura, S.J.; Sun, F.C. Velocity predictors for predictive energy management in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2015, 23, 1197–1204. [Google Scholar]
- Cairano, S.D.; Bernardini, D.; Bemporad, A.; Kolmanovsky, I.V. Stochastic MPC with learning for driver-predictive vehicle control and its application to HEV energy management. IEEE Trans. Veh. Technol. 2014, 22, 1018–1031. [Google Scholar] [CrossRef]
- Musardo, C.; Rizzoni, G.; Staccia, B. A-ECMS: An adaptive algorithm for hybrid electric vehicle energy management. Eur. J. Control 2005, 11, 1816–1823. [Google Scholar] [CrossRef]
- Feng, T.; Lin, Y.; Gu, Q.; Hu, Y. A supervisory control strategy for plug-in hybrid electric vehicles based on energy demand prediction and route preview. IEEE Trans. Veh. Technol. 2015, 64, 1691–1700. [Google Scholar]
- Kessels, J.T.B.A.; Koot, M.W.T.; Bosch, P.P.J.; Kok, D.B. Online energy management for hybrid electric vehicles. IEEE Trans. Veh. Technol. 2008, 57, 3428–3440. [Google Scholar] [CrossRef]
- Zhao, D.; Stobart, R.; Dong, G.; Winward, E. Real-time energy management for diesel heavy duty hybrid electric vehicles. IEEE Trans. Veh. Technol. 2015, 23, 829–841. [Google Scholar]
- Du, Y.; Zhao, Y.; Wang, Q.; Zhang, Y.; Xia, H. Trip-oriented stochastic optimal energy management strategy for Plug-in Hybrid Electric Bus. Energy 2016, 115, 1259–1271. [Google Scholar] [CrossRef]
- Johri, R.; Baseley, S.; Filipill, Z. Simultaneous optimization of supervisory control and gear shift logic for a parallel hydraulic hybrid refuse truck using stochastic dynamic programming. In Proceedings of the ASME Dynamic Systemsand Control Conference, Arlington, TX, USA, 31 October–2 November 2011; pp. 99–106. [Google Scholar]
- Li, L.; Yang, C.; Zhang, Y.; Zhang, L.; Song, J. Correctional DP-Based Energy Management Strategy of Plug-In Hybrid Electric Bus for City-Bus Route. IEEE Trans. Veh. Technol. 2015, 64, 2792–2803. [Google Scholar] [CrossRef]
- Li, L.; Yan, B.; Yang, C.; Zhang, Y.; Chen, Z.; Jiang, G. Application-Oriented Stochastic Energy Management for Plug-in Hybrid Electric Bus with AMT. IEEE Trans. Veh. Technol. 2016, 65, 4459–4470. [Google Scholar] [CrossRef]
- Yang, C.; Du, S.; Li, L.; You, S.; Yang, Y.; Zhao, Y. Adaptive real-time optimal energy management strategy based on equivalent factors optimization for plug-in hybrid electric vehicle. Appl. Energy 2017, 203, 883–896. [Google Scholar] [CrossRef]



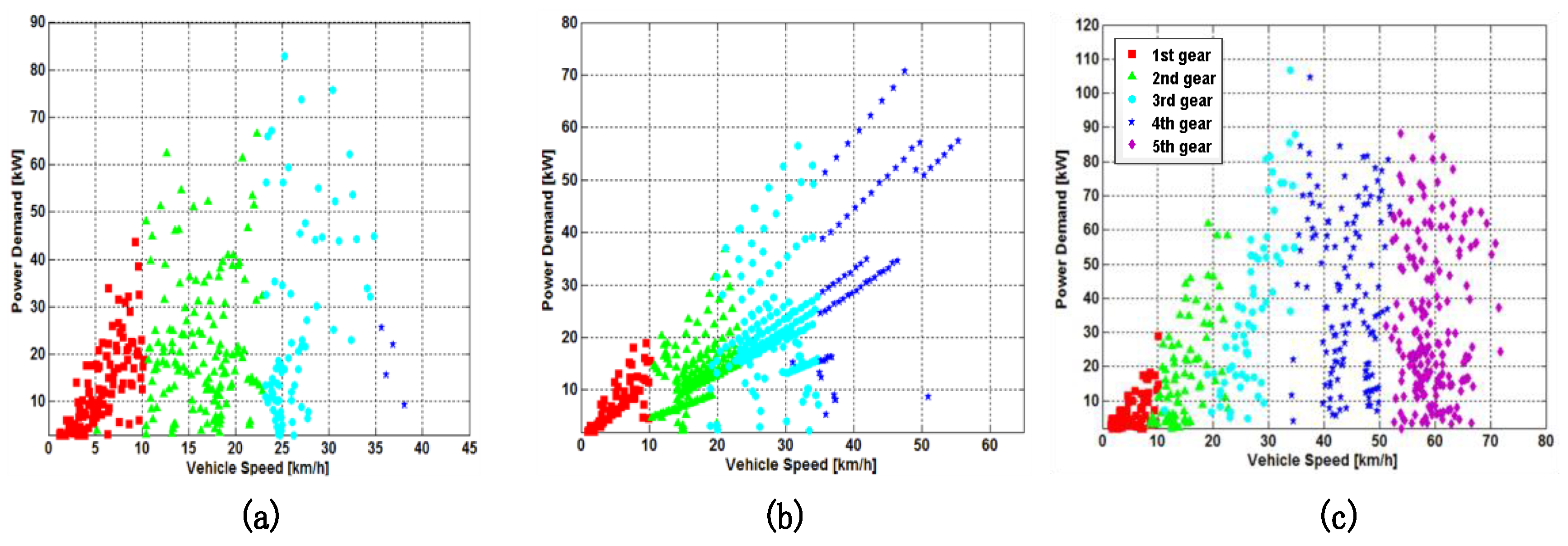
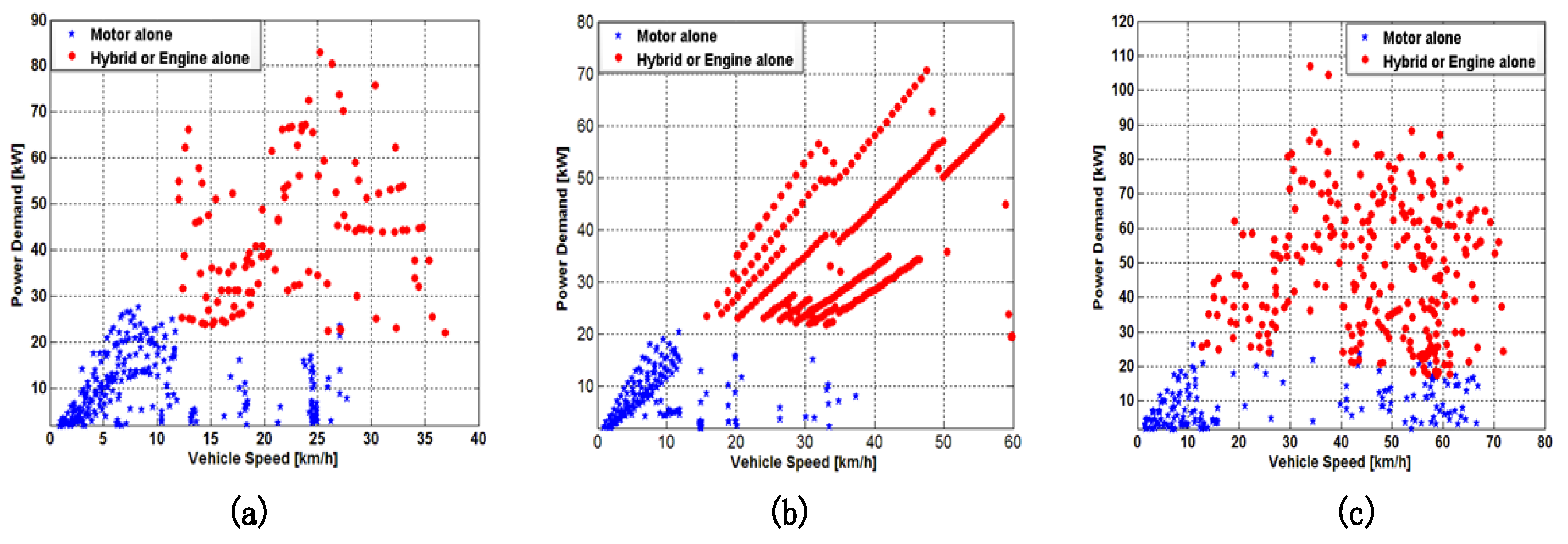
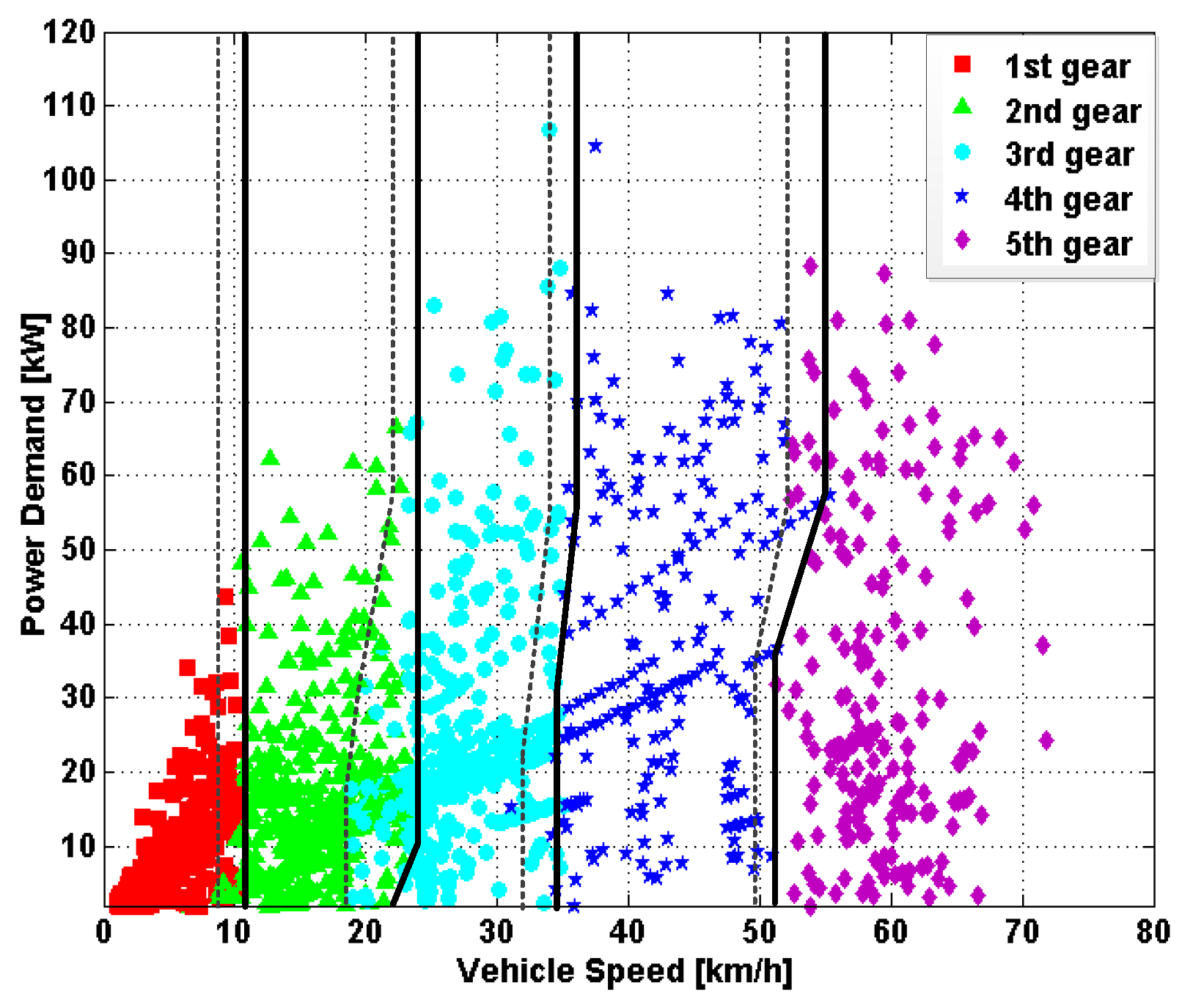

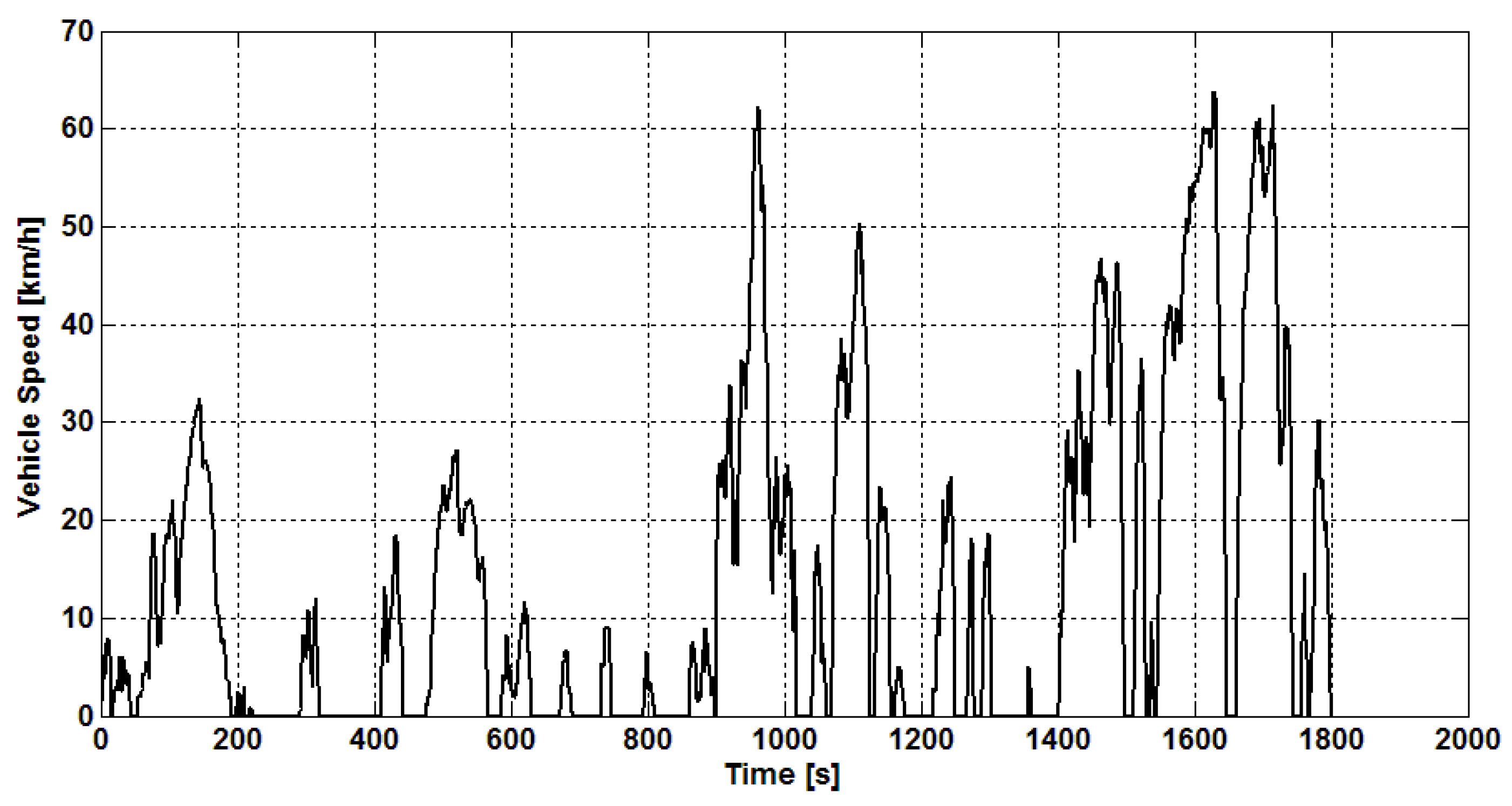


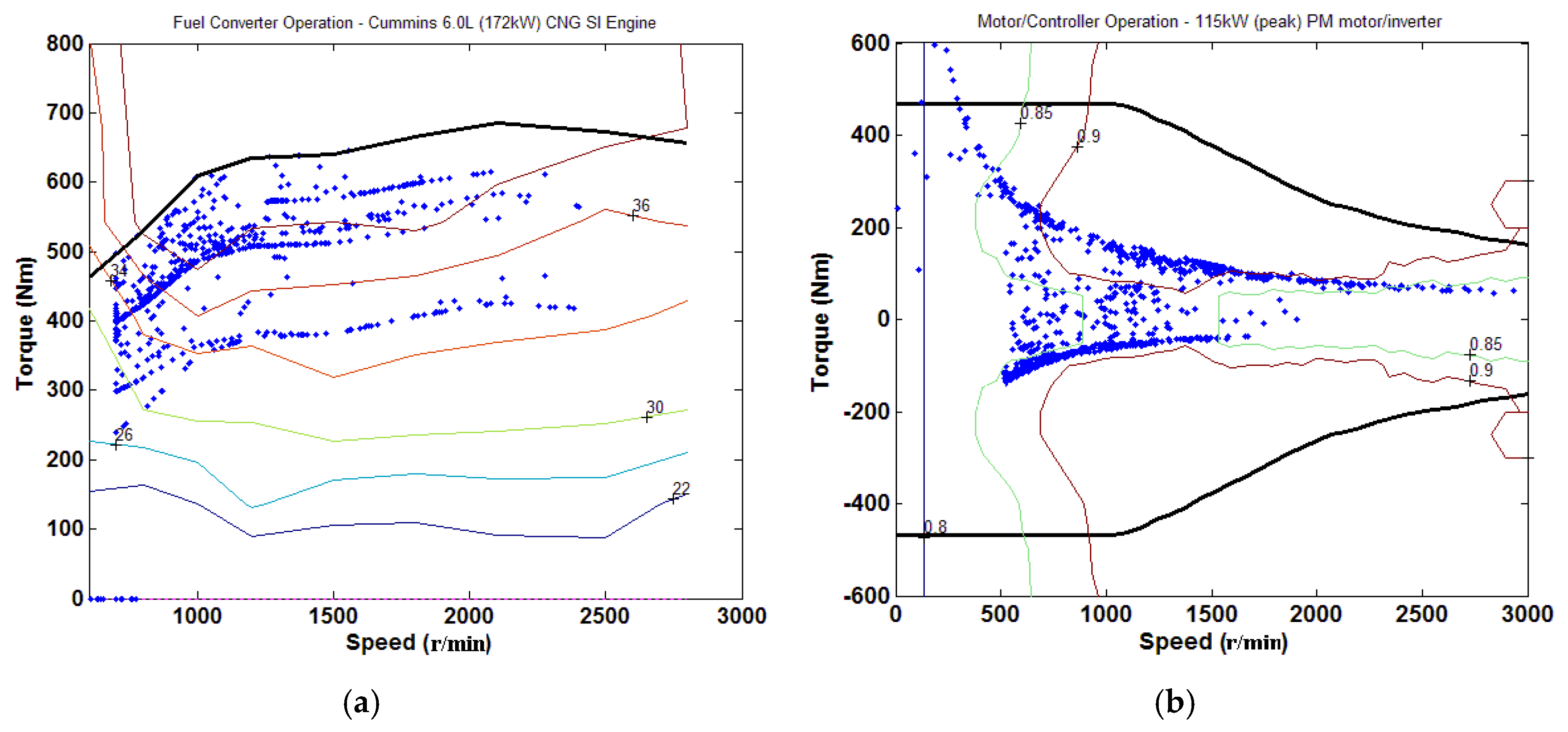
| Items | Detailed Information |
|---|---|
| Total vehicle mass | 18,000 kg |
| Engine | CNG, 5.9 L, nominal power: 172 kw, Max torque: 678 Nm |
| EM | Permanent magnet, max torque: 750 Nm, Nominal/peak power: 70 kw/115 kw |
| Battery | Capacity: 120 Ah, voltage: 336 V |
| AMT | 5-speed, gear ratio: (6.11, 3.66, 2.17, 1.42, 1) |
| Final drive | 6.14 |
| Cycles | Driving Time | Travel Distance | Average Speed | Maximum Speed | Maximum Acceleration | Maximum Deceleration |
|---|---|---|---|---|---|---|
| 1 | 1804 s | 6.81 km | 13.6 km/h | 63.8 km/h | 2.33 m/s2 | −3.44 m/s2 |
| Strategy | CNG Consumption (m3/100 km) | Final SOC (%) | Improvement (%) |
|---|---|---|---|
| Rule-based | 36.45 | 30.25 | — |
| ECMS | 31.67 | 30.12 | 13.11 |
| Proposed | 32.24 | 30.15 | 11.55 |
| EMC | Mf (m3/100 km) | Shift | State | Comprehensive Evaluation | |
|---|---|---|---|---|---|
| Jmulti | Improvement | ||||
| Rule-based | 36.45 | 7.58 | 7.46 | 62.86 | — |
| ECMS | 31.67 | 7.65 | 7.90 | 58.70 | 6.61% |
| Proposed | 32.24 | 5.29 | 5.73 | 51.20 | 18.54% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zhang, Y.; Tian, J.; Zhang, S. Research on a Plug-In Hybrid Electric Bus Energy Management Strategy Considering Drivability. Energies 2018, 11, 2177. https://doi.org/10.3390/en11082177
Yang Y, Zhang Y, Tian J, Zhang S. Research on a Plug-In Hybrid Electric Bus Energy Management Strategy Considering Drivability. Energies. 2018; 11(8):2177. https://doi.org/10.3390/en11082177
Chicago/Turabian StyleYang, Ye, Youtong Zhang, Jingyi Tian, and Si Zhang. 2018. "Research on a Plug-In Hybrid Electric Bus Energy Management Strategy Considering Drivability" Energies 11, no. 8: 2177. https://doi.org/10.3390/en11082177
APA StyleYang, Y., Zhang, Y., Tian, J., & Zhang, S. (2018). Research on a Plug-In Hybrid Electric Bus Energy Management Strategy Considering Drivability. Energies, 11(8), 2177. https://doi.org/10.3390/en11082177





