Online Speed Estimation Using Artificial Neural Network for Speed Sensorless Direct Torque Control of Induction Motor based on Constant V/F Control Technique
Abstract
:1. Introduction
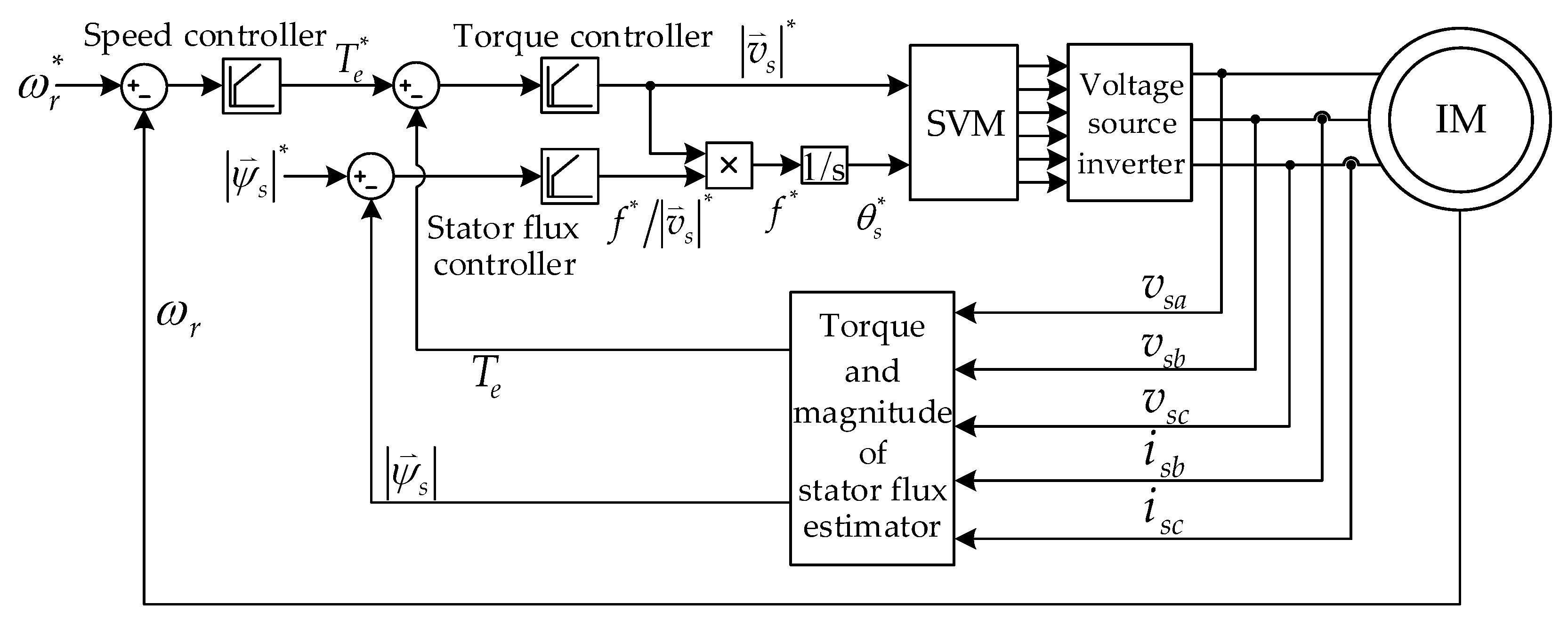
2. Direct Torque Control Based on Constant Voltage per Frequency (V/F) Control Technique
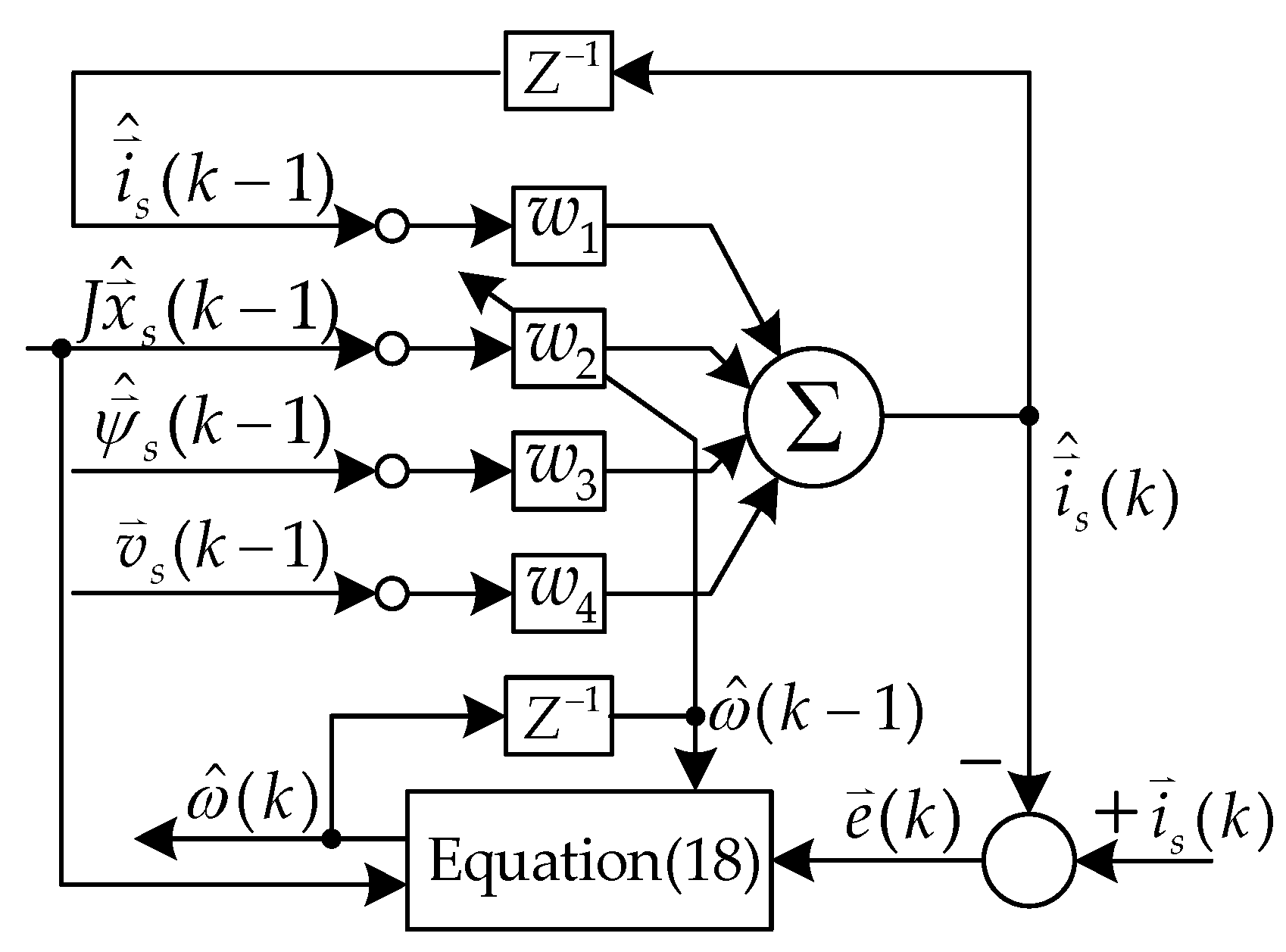
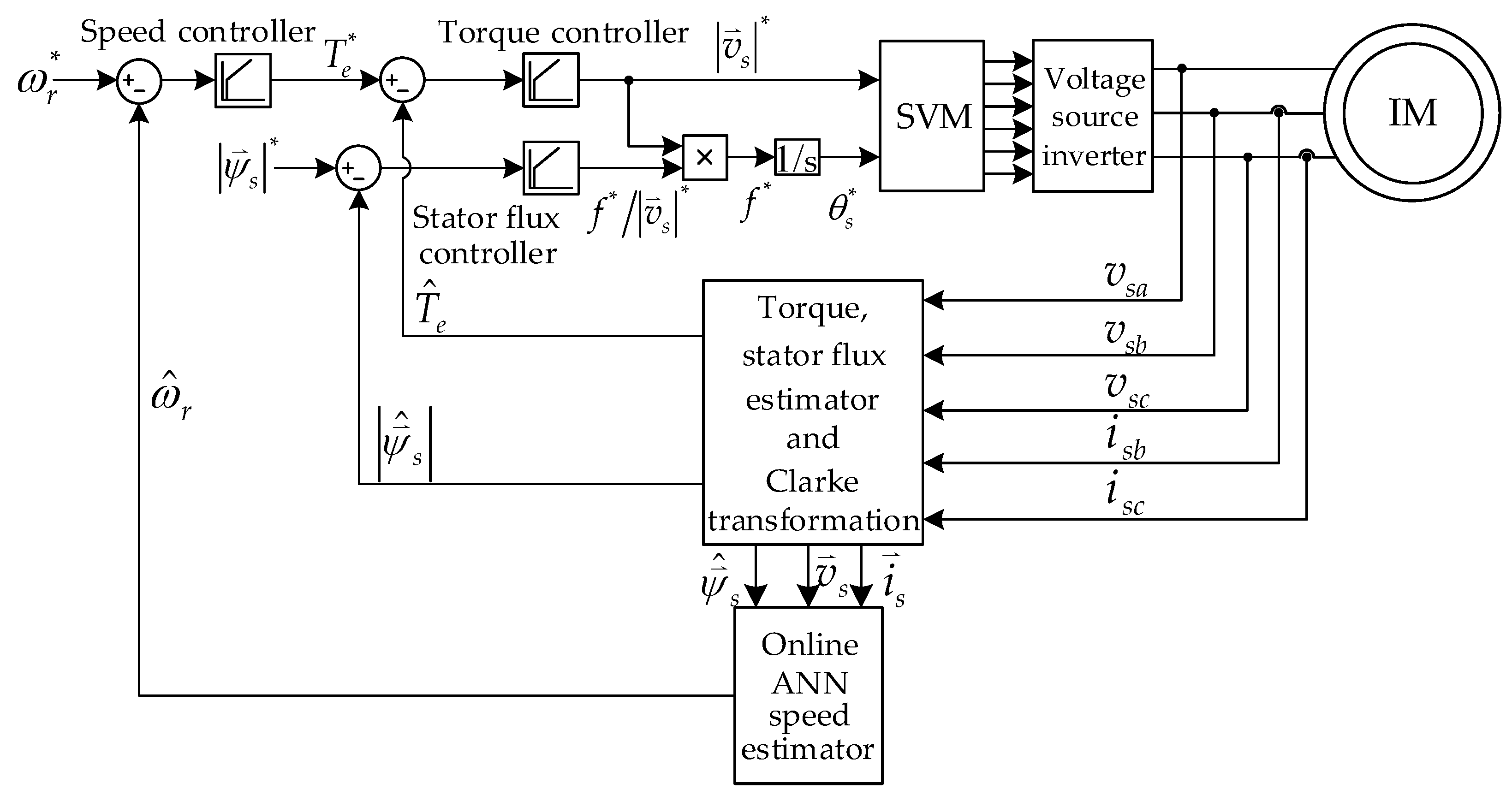
3. Online Artificial Neural Network Speed Estimator
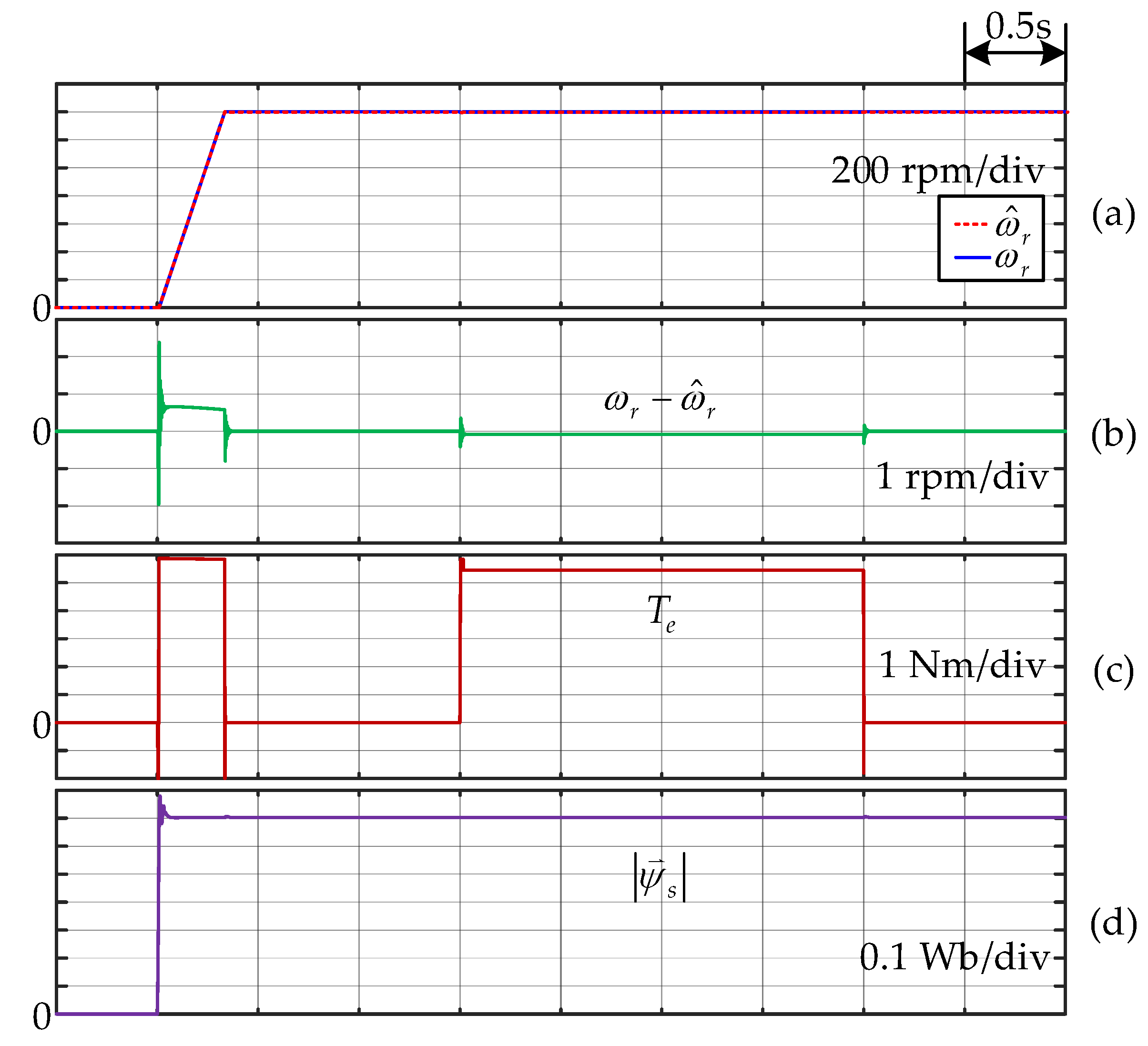
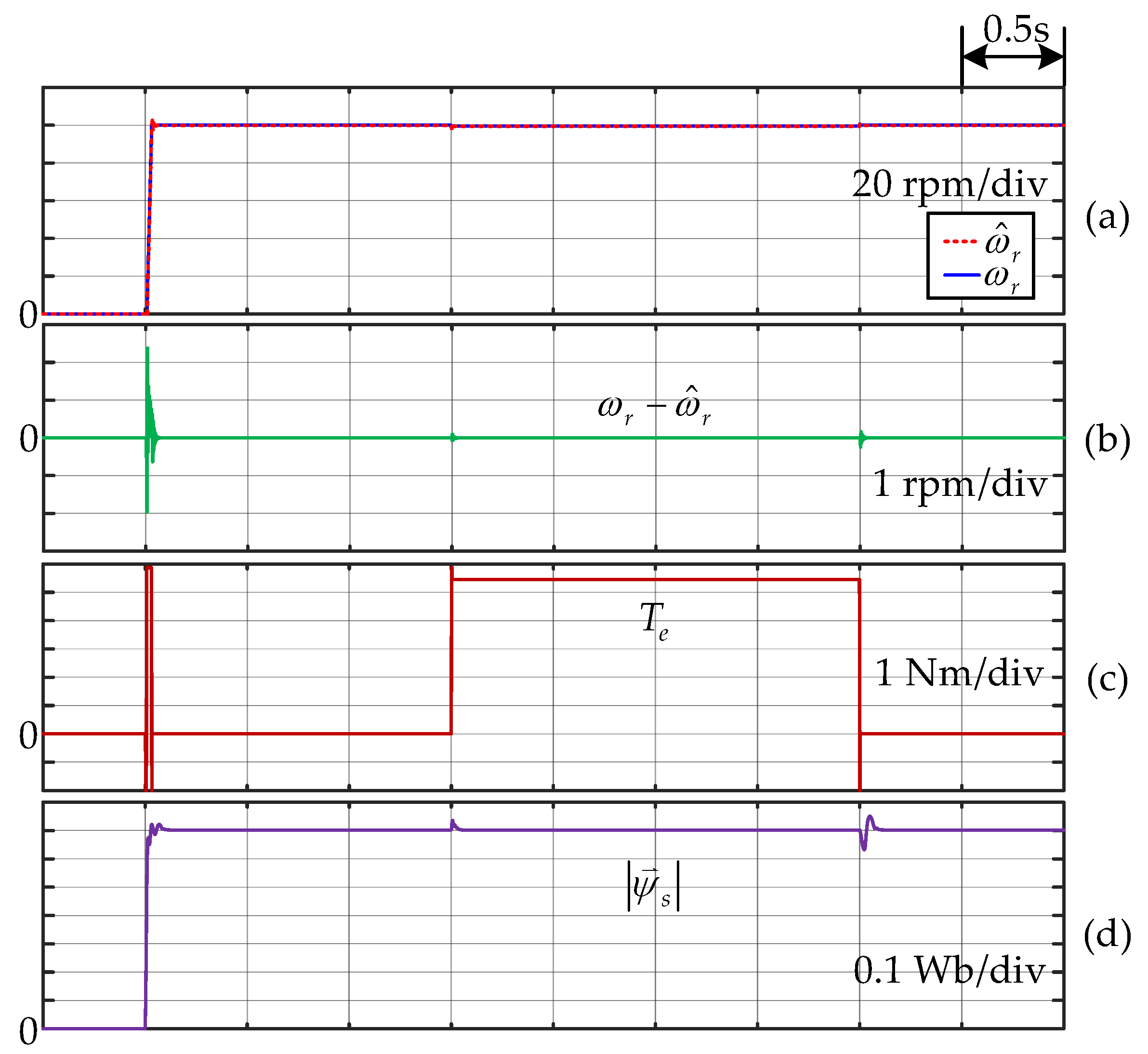
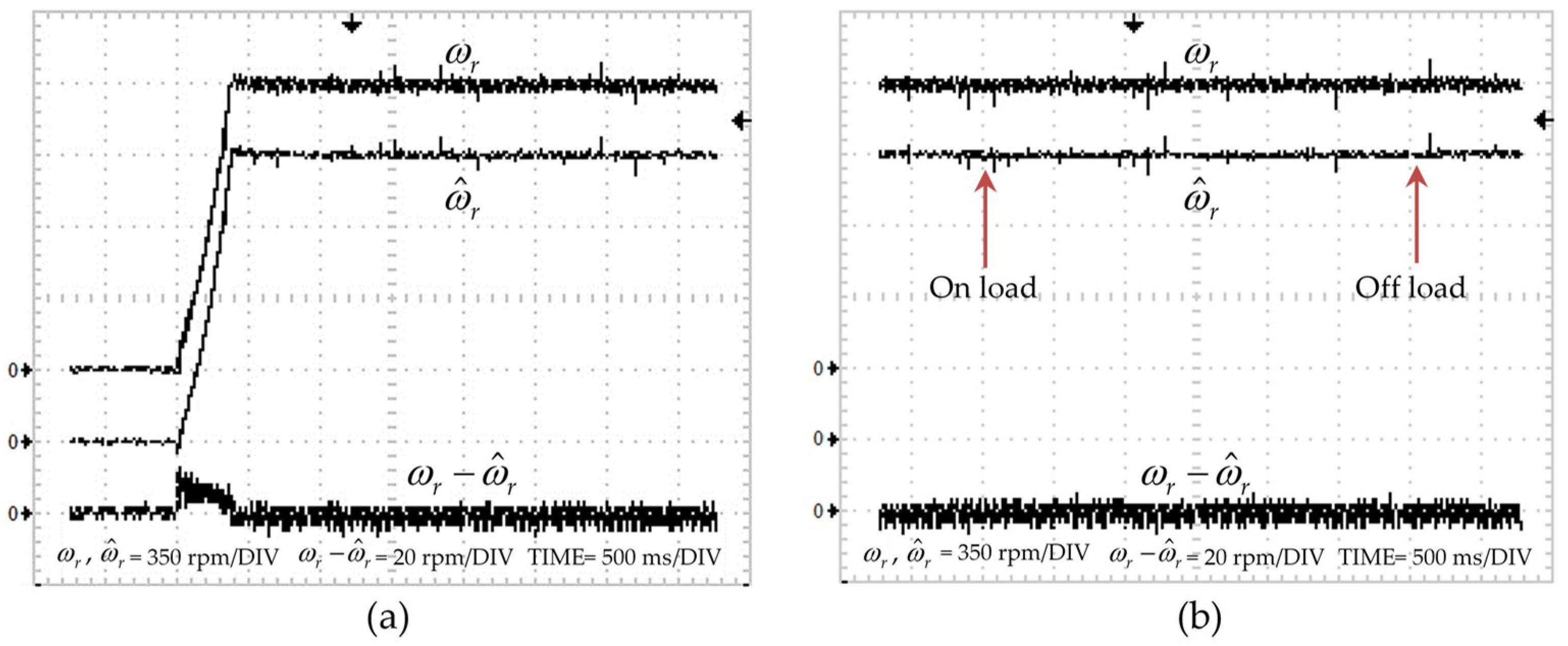
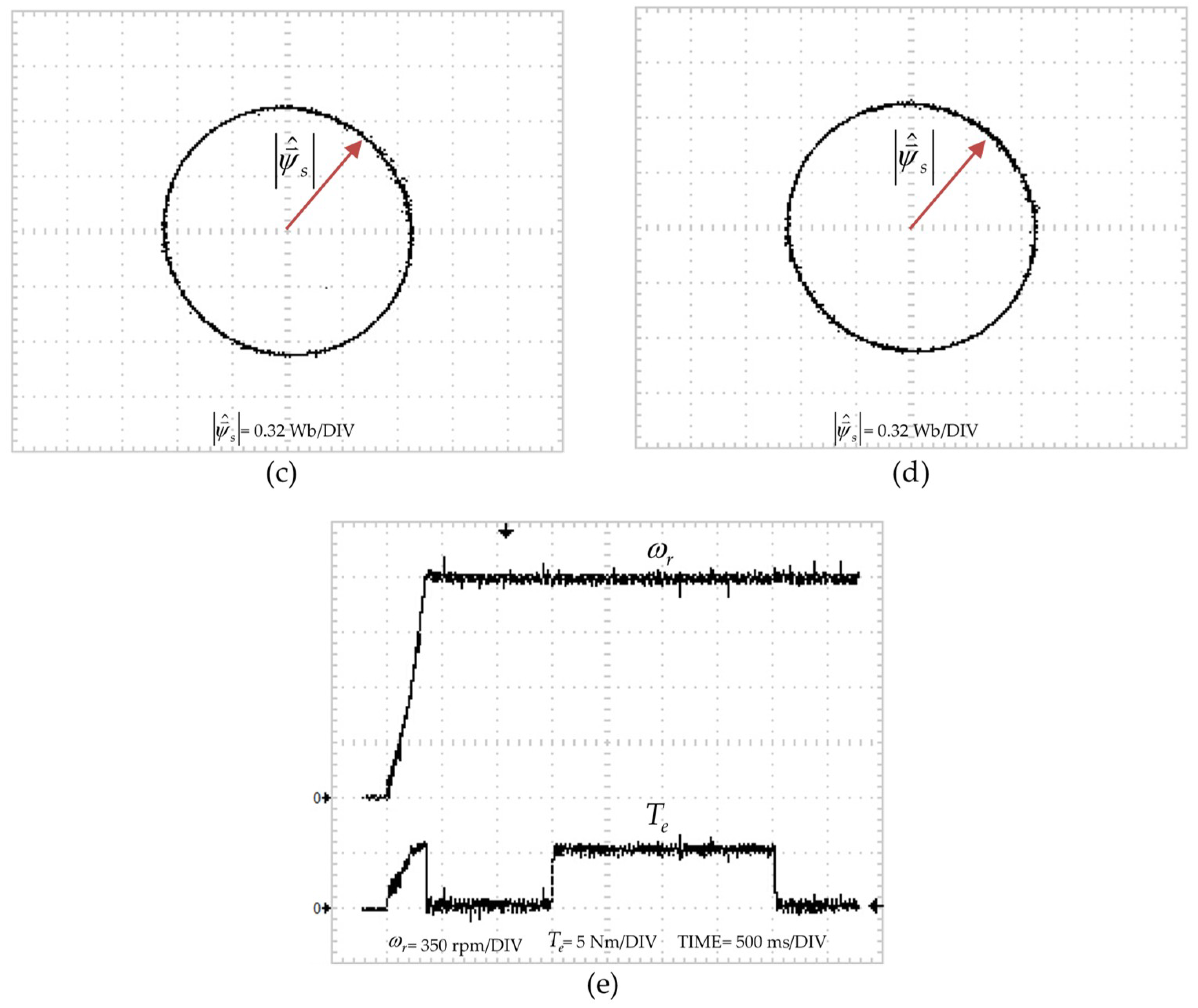
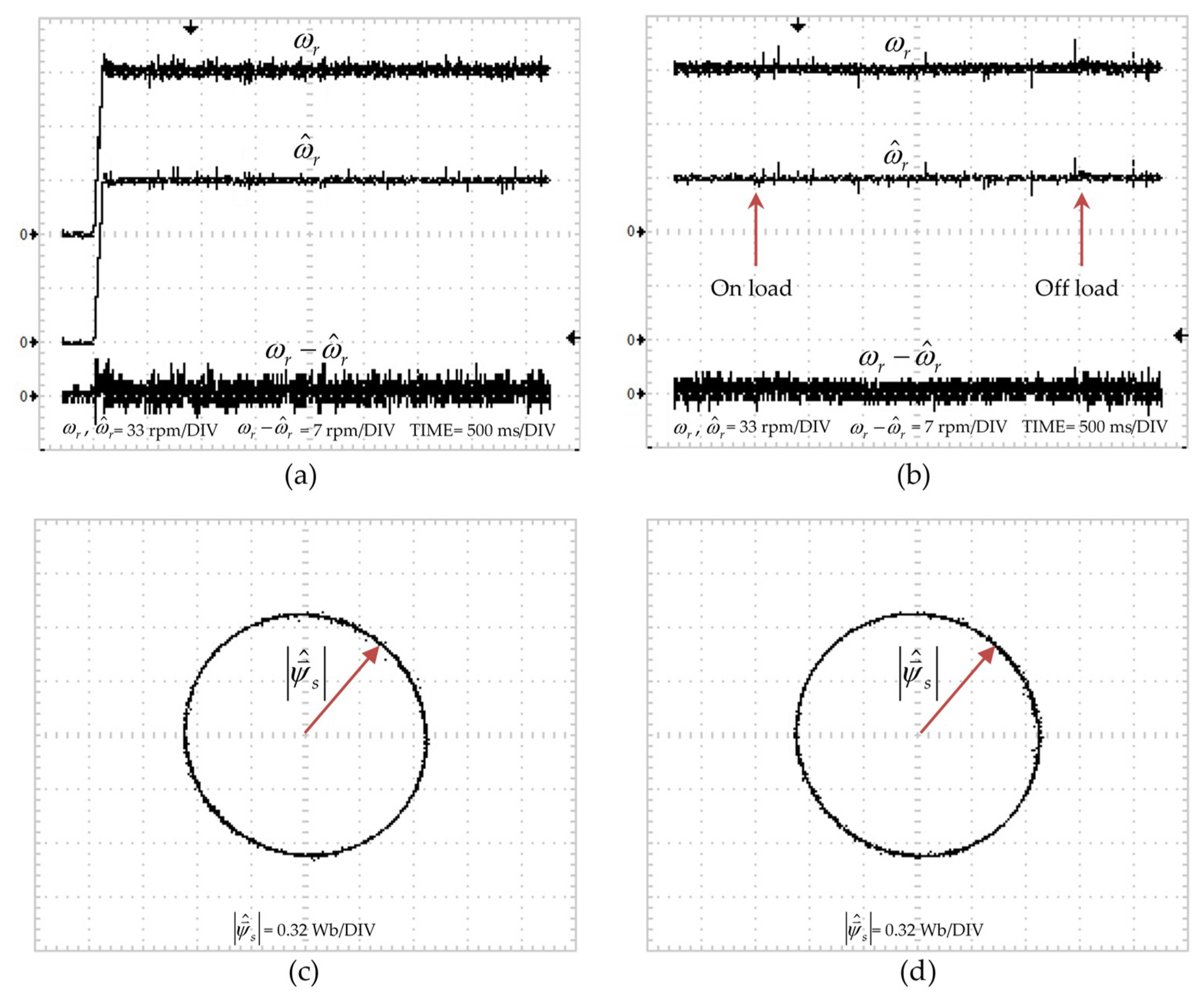
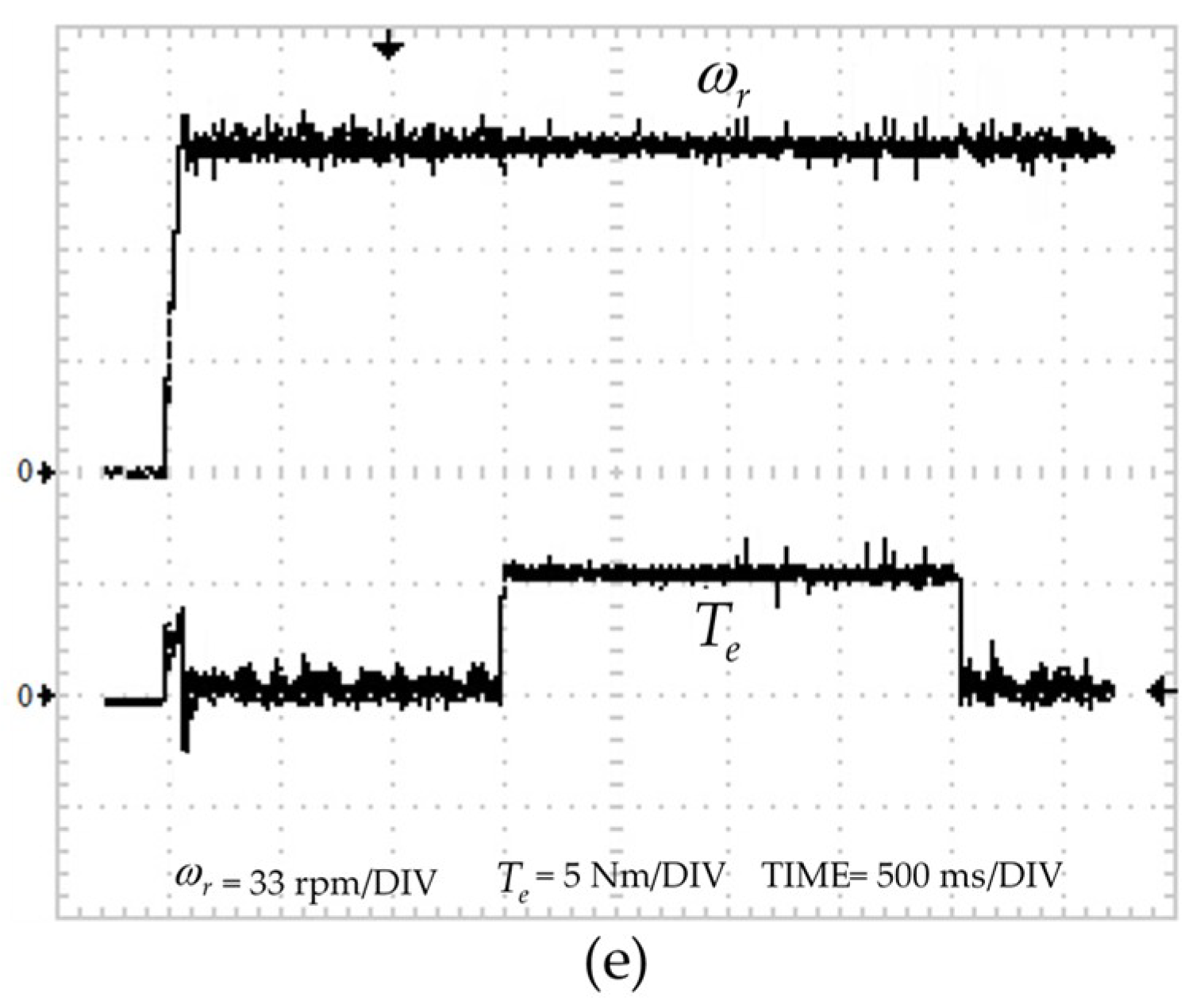
4. Simulation and Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kruselj, D. Methods for Direct Torque Control of Induction Machines. In Proceedings of the 2017 19th International Conference on Electrical Drives and Power Electronics (EDPE), Dubrovnik, Croatia, 4–6 October 2017; pp. 218–225. [Google Scholar]
- Garg, R.; Mahajan, P.; Gupta, P.; Saroa, H. A Comparative Study between Field Oriented Control and Direct Torque Control of AC Traction Motor. In Proceedings of the International Conference on Recent Advances and Innovations in Engineering (ICRAIE-2014), Jaipur, India, 9–11 May 2014; pp. 1–6. [Google Scholar]
- Parthan, A.; Suresh, L.P.; Raj, J.R.A. A Brief Review on Torque Control of Induction Motor. In Proceedings of the 2017 International Conference on Circuit, Power and Computing Technologies (ICCPCT), Kollam, India, 20–21 April 2017; pp. 1–5. [Google Scholar]
- Kumar, T.V.; Rao, S.S. Direct Torque Control Method for Induction Motor Drives based on Modified Amplitude and Angle Decoupled Control of Stator Flux. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems & 2010 Power India, New Delhi, India, 20–23 December 2010; pp. 1–6. [Google Scholar]
- Zhang, Y.; Zhu, J.; Xu, W.; Guo, Y. A Simple Method to Reduce Torque Ripple in Direct Torque-Controlled Permanent-Magnet Synchronous Motor by Using Vectors with Variable Amplitude and Angle. IEEE Trans. Ind. Electron. 2010, 58, 2848–2859. [Google Scholar] [CrossRef]
- Pimkumwong, N.; Onkrong, A.; Sapaklom, T. Modeling and Simulation of Direct Torque Control Induction Motor Drives via Constant Volt/Hertz Technique. Procedia Eng. 2012, 31, 1211–1216. [Google Scholar] [CrossRef]
- Pimkumwong, N.; Wang, M.S. Full-Order Observer for Direct Torque Control of Induction Motor based on Constant V/F Control Technique. ISA Trans. 2018, 73, 189–200. [Google Scholar] [CrossRef] [PubMed]
- Suwankawin, S.; Srivorakul, A. A Syncho-Perspective-Based High-Frequency Voltage Injection Method for Position-Sensorless Vector Control of Doubly Fed Induction Machines. IEEE Trans. Ind. Appl. 2018, 54, 3326–3337. [Google Scholar]
- Pacas, M. Sensorless Drives in Industrial Applications. IEEE Ind. Electron. Mag. 2011, 5, 16–23. [Google Scholar] [CrossRef]
- Xu, L.; Inoa, E.; Liu, Y.; Guan, B. A New High-Frequency Injection Method for Sensorless Control of Doubly Fed Induction Machines. IEEE Trans. Ind. Appl. 2012, 48, 1556–1564. [Google Scholar] [CrossRef]
- Jung, S.H.; Doki, S.; Okuma, S.; Fujitsuna, M. Sensorless Control Method with Relatively Low Frequency Signal Injection for Low Acoustic Noise. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–7. [Google Scholar]
- Zaky, M.S.; Metwaly, M.K.; Azazi, H.Z.; Deraz, S.A. A New Adaptive SMO for Speed Estimation of Sensorless Induction Motor Drives at Zero and Very Low Frequencies. IEEE Trans. Ind. Electron. 2018, 65, 6901–6911. [Google Scholar] [CrossRef]
- Yin, Z.; Li, G.; Zhang, Y.; Liu, J. Symmetric-Strong-Tracking-Extended-Kalman-Filter-Based Sensorless Control of Induction Motor Drives for Modeling Error Reduction. IEEE Trans. Ind. Inform. 2018. [Google Scholar] [CrossRef]
- Xu, D.; Wang, B.; Zhang, G.; Wang, G.; Yu, Y. A Review of Sensorless Control Methods for AC Motor Drives. CES Trans. Electr. Mach. Syst. 2018, 2, 104–115. [Google Scholar]
- Finch, J.W.; Giaouris, D. Controlled AC Electrical Drives. IEEE Trans. Ind. Electron. 2008, 55, 481–491. [Google Scholar] [CrossRef]
- Lascu, C.; Boldea, I.; Blaabjerg, F. A Class of Speed-Sensorless Sliding-Mode Observer for High-Performance Induction Motor Drives. IEEE Trans. Ind. Electron. 2009, 56, 3394–3403. [Google Scholar] [CrossRef]
- Vieira, R.P.; Gastaldini, C.C.; Azzolin, R.Z.; Grundling, H.A. Sensorless Sliding-Mode Rotor Speed Observer of Induction Machines Based on Magnetizing Current Estimation. IEEE Trans. Ind. Electron. 2014, 61, 4573–4582. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, J.; Liu, H.; Li, B.; Kong, W. Second-Order Sliding-Mode Observer with Online Parameter Identification for Sensorless Induction Motor Drives. IEEE Trans. Ind. Electron. 2014, 61, 5280–5289. [Google Scholar] [CrossRef]
- Gennaro, S.D.; Dominguez, J.R.; Meza, M.A. Sensorless High Order Sliding Mode Control of Induction Motors with Core Loss. IEEE Trans. Ind. Electron. 2014, 61, 2678–2689. [Google Scholar] [CrossRef]
- Rattanaudompisut, A.; Po-ngam, S. The Practical and Simple Feedback Gains Design of an Adaptive Full-Order Observer for Speed-Sensorless Induction Motor Drives. In Proceedings of the 2015 12th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Hua Hin, Thailand, 24–27 June 2015; pp. 1–6. [Google Scholar]
- Chen, B.; Yao, W.; Chen, F.; Lu, Z. Parameter Sensitivity in Sensorless Induction Motor Drives with the Adaptive Full-Order Observer. IEEE Trans. Ind. Electron. 2015, 62, 4307–4318. [Google Scholar] [CrossRef]
- Sun, W.; Yu, Y.; Wang, G.; Li, B.; Xu, D. Design Method of Adaptive Full Order Observer with or without Estimated Flux Error in Speed Estimation Algorithm. IEEE Trans. Power Electron. 2016, 31, 2609–2626. [Google Scholar] [CrossRef]
- Po-ngam, S.; Sangwongwanich, S. Stability and Dynamic Performance Improvement of Adaptive Full-Order Observer for Sensorless PMSM Drive. IEEE Trans. Power Electron. 2012, 27, 588–600. [Google Scholar] [CrossRef]
- Sun, W.; Gao, J.; Yu, Y.; Wang, G.; Xu, D. Robustness Improvement of Speed Estimation in Speed-Sensorless Induction Motor Drives. IEEE Trans. Ind. Electron. 2016, 52, 2525–2536. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Lascu, C.; Fadali, M.S. State Estimation of Induction Motor Drives Using the Unscented Kalman Filters. IEEE Trans. Ind. Electron. 2012, 59, 4207–4216. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Idris, N.R.N. Simple Flux Regulation for Improving State Estimation at Very Low and Zero Speed of a Speed Sensorless Direct Torque Control of an Induction Motor. IEEE Trans. Power Electron. 2016, 31, 3027–3035. [Google Scholar] [CrossRef]
- Hilairet, M.; Auger, F.; Berthelot, E. Speed and Rotor Flux Estimation of Induction Machines Using a Two-Stage Extended Kalman Filter. Autometica 2009, 45, 1819–1827. [Google Scholar] [CrossRef]
- Kumar, R.; Das, S.; Syam, P.; Chattopadhyay, A.K. Review on Model Reference Adaptive System for Sensorless Vector Control of Induction Motor Drives. IET Electr. Power Appl. 2015, 9, 496–511. [Google Scholar] [CrossRef]
- Verma, V.; Chakraborty, C. New Series of MRAS for Speed Estimation of Vector Controlled Induction Motor Drive. In Proceedings of the IECON 2014–40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 755–761. [Google Scholar]
- Teja, A.V.R.; Verma, V.; Chakraborty, C. A New Formulation of Reactive-Power-Based Model Reference Adaptive System for Sensorless Induction Motor Drive. IEEE Trans. Ind. Electron. 2015, 62, 6797–6808. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Dybkowski, M. Stator-Current-Based MRAS Estimator for a Wide Range Speed-Sensorless Induction-Motor Drive. IEEE Trans. Ind. Electron. 2010, 57, 1296–1308. [Google Scholar] [CrossRef]
- Yang, Y. A Neural Network Model Reference Adaptive System for Speed Estimation of Sensorless Induction Motor. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 6864–6868. [Google Scholar]
- Nguyen, S.T.; Pham, P.H.; Pham, T.V.; Ha, H.X.; Nguyen, C.T.; Do, P.C. A Sensorless Three-Phase Induction Motor Drive Using Indirect Field Oriented Control and Artificial Neural Network. In Proceedings of the 2017 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Combodia, 18–20 June 2017; pp. 1454–1459. [Google Scholar]
- Nentwig, M.; Mercorelli, P. Throttle Valve Control Using an Inverse Local Linear Model Tree Based on a Fuzzy Neural Network. In Proceedings of the 2008 7th IEEE International Conference on Cybernetic Intelligent Systems, London, UK, 9–10 September 2008; pp. 1–6. [Google Scholar]
- Sedhuraman, K.; Himavathi, S.; Muthuramalingam, A. Comparison of Learning Algorithms for Neural Network Based Speed Estimation in Sensorless Induction Motor Drives. In Proceedings of the IEEE—International Conference on Advances in Engineering, Science and Management (ICAESM-2012), Nagapattinam, Tamil Nadu, India, 30–31 March 2012; pp. 196–202. [Google Scholar]
- Kartalopoulos, S.V. Understanding Neural Networks and Fuzzy Logic: Basic Concepts and Applications, 1st ed.; IEEE Press: Piscataway, NJ, USA, 1995; pp. 46–73. [Google Scholar]
- Trzynadlowski, A.M. Control of Induction Motors, 1st ed.; Academic Press: San Diego, CA, USA, 2001; pp. 29–98. [Google Scholar]
- Vas, P. Sensorless Vector and Direct Torque Control, 1st ed.; Oxford University Press: New York, NY, USA, 1998; pp. 39–422. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Workman, M. Digital Control of Dynamic System, 3rd ed.; Addison Wesley Longman, Inc.: Redwood City, CA, USA, 1997; pp. 189–195. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall International, Inc.: Upper Saddle River, NJ, USA, 1999; pp. 128–133. [Google Scholar]
- Ellis, G. Control System Design Guide, 2nd ed.; Academic Press: San Diego, CA, USA, 2000; pp. 105–106. [Google Scholar]
- Hu, J.; Wu, B. New Integration Algorithms for Estimating Motor Flux over a Wide Speed Range. IEEE Trans. Power Electron. 1998, 13, 969–977. [Google Scholar]

| Voltage | 220 V Delta Connected | 8.2 | |
| Current | 3.5 A Delta Connected | 8.62 | |
| Power | 0.8 kW | 700.79 mH | |
| Poles | 4 | 700.79 mH | |
| Frequency | 50 Hz | 644.87 mH | |
| Speed | 1400 rpm | 0.013 kgm2 | |
| Torque | 5.45 Nm | Flux | 0.7 Wb |
| KP | KI | |
|---|---|---|
| Speed | 500 | 20 |
| Torque | 200 | 5 |
| Stator flux magnitude | 800 | 20 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pimkumwong, N.; Wang, M.-S. Online Speed Estimation Using Artificial Neural Network for Speed Sensorless Direct Torque Control of Induction Motor based on Constant V/F Control Technique. Energies 2018, 11, 2176. https://doi.org/10.3390/en11082176
Pimkumwong N, Wang M-S. Online Speed Estimation Using Artificial Neural Network for Speed Sensorless Direct Torque Control of Induction Motor based on Constant V/F Control Technique. Energies. 2018; 11(8):2176. https://doi.org/10.3390/en11082176
Chicago/Turabian StylePimkumwong, Narongrit, and Ming-Shyan Wang. 2018. "Online Speed Estimation Using Artificial Neural Network for Speed Sensorless Direct Torque Control of Induction Motor based on Constant V/F Control Technique" Energies 11, no. 8: 2176. https://doi.org/10.3390/en11082176
APA StylePimkumwong, N., & Wang, M.-S. (2018). Online Speed Estimation Using Artificial Neural Network for Speed Sensorless Direct Torque Control of Induction Motor based on Constant V/F Control Technique. Energies, 11(8), 2176. https://doi.org/10.3390/en11082176





