Modeling and Parameter Design of Voltage-Controlled Inverters Based on Discrete Control
Abstract
:1. Introduction
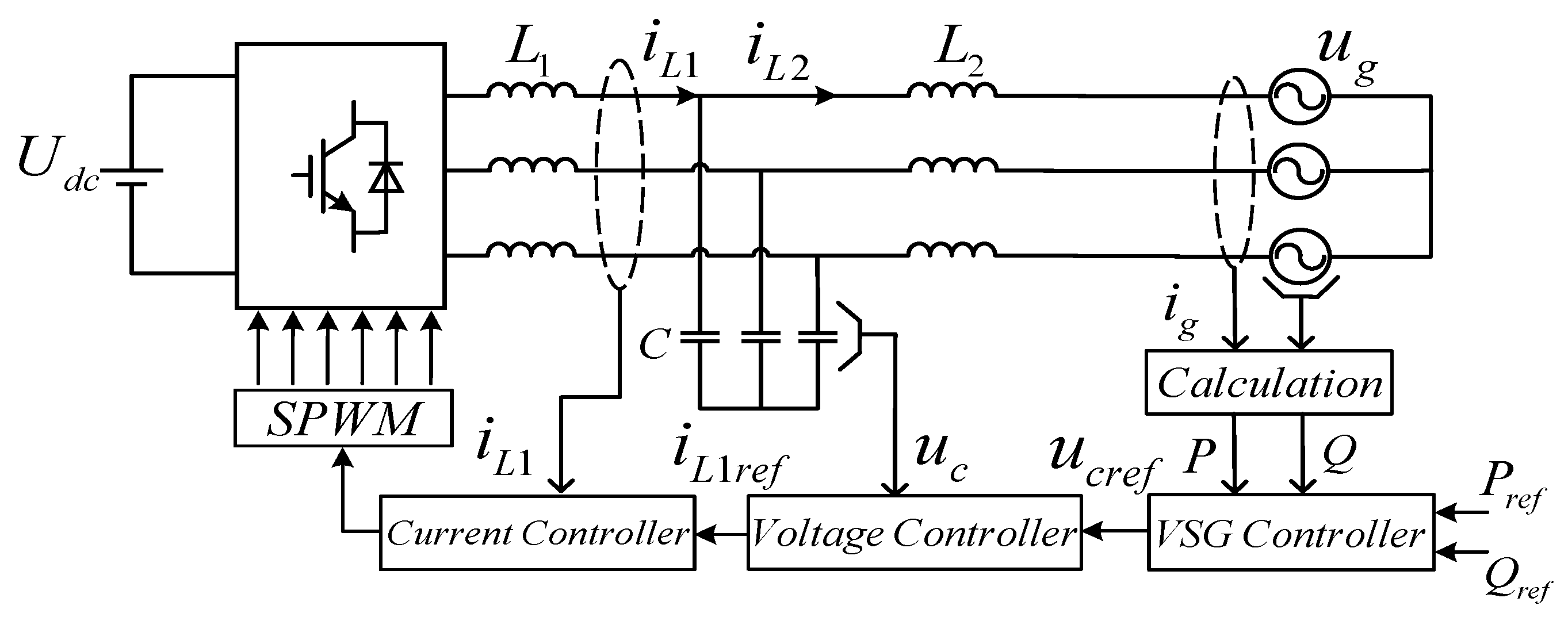
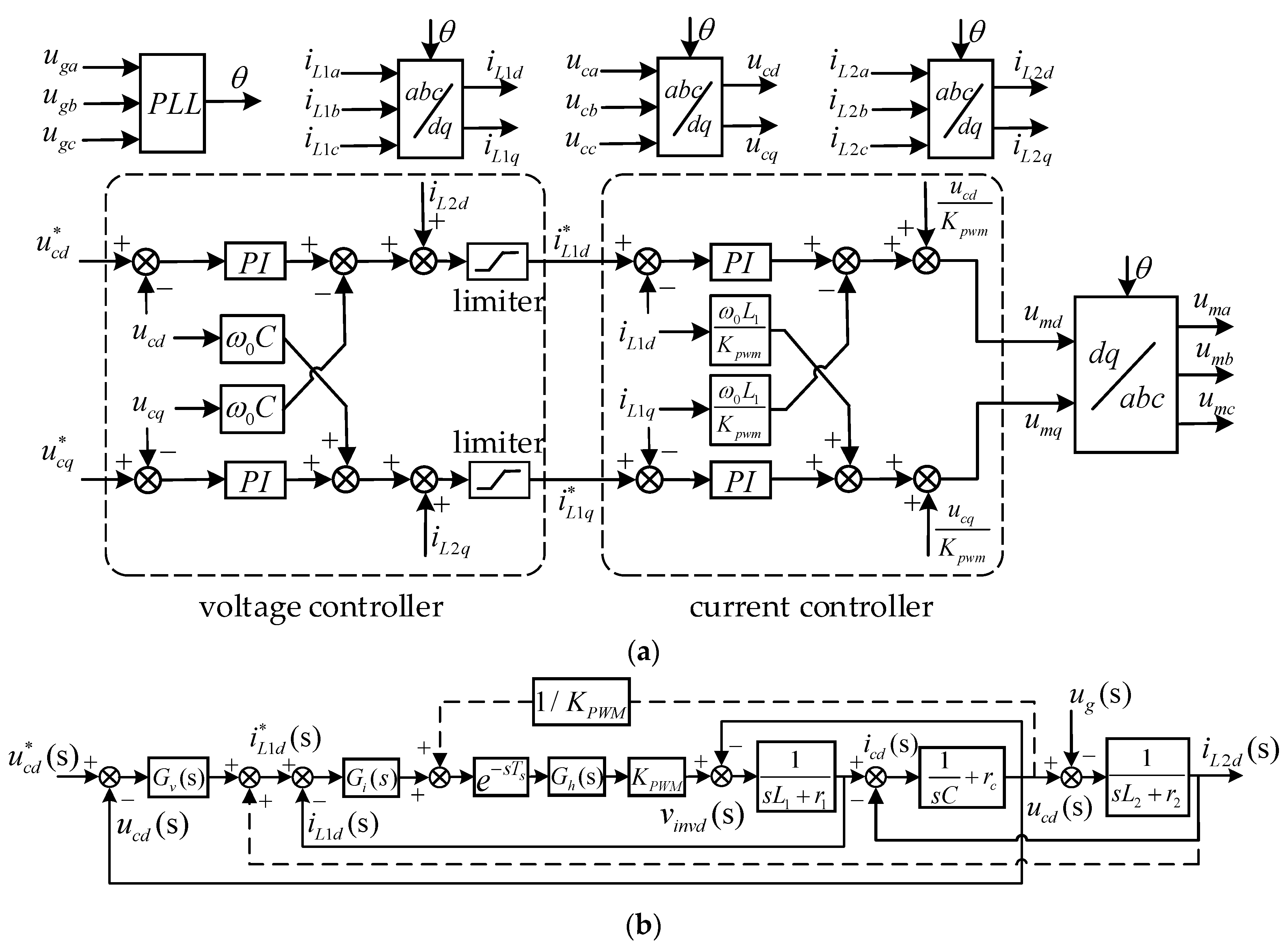
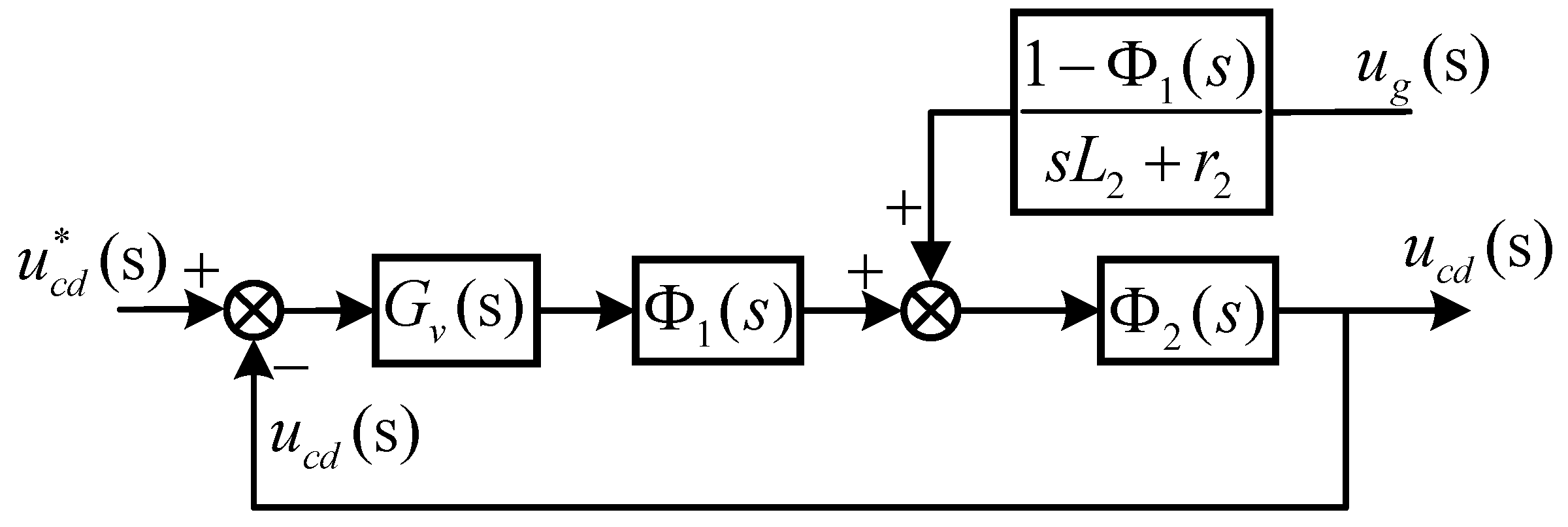
2. Modeling of the Voltage and Current Loops in VSG
3. Parameter Design of Current Controller
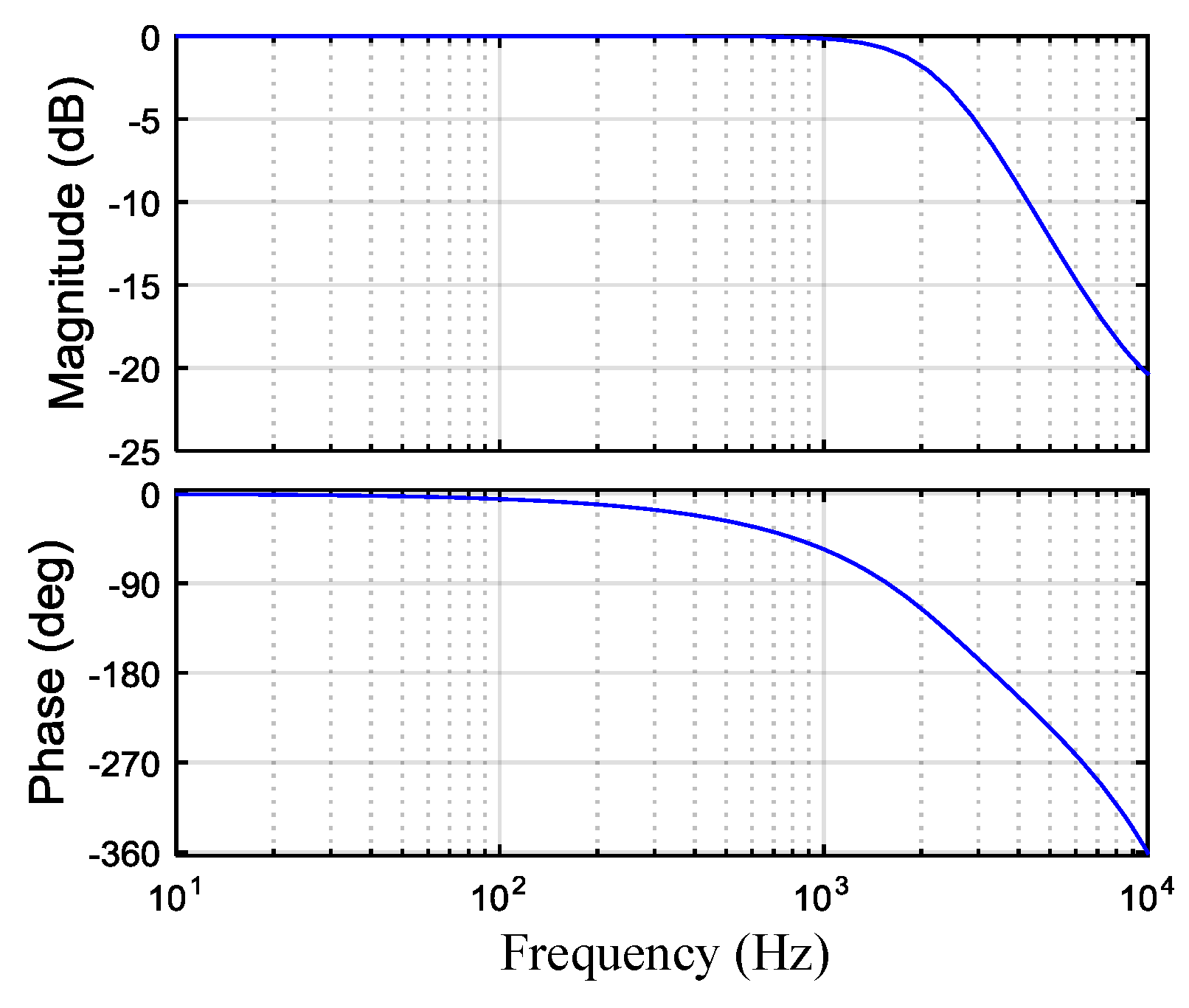
3.1. Model of the Current Loop
3.2. Parameter Design of the Current Loop
3.3. Summary
4. Parameter Design of Voltage Controller
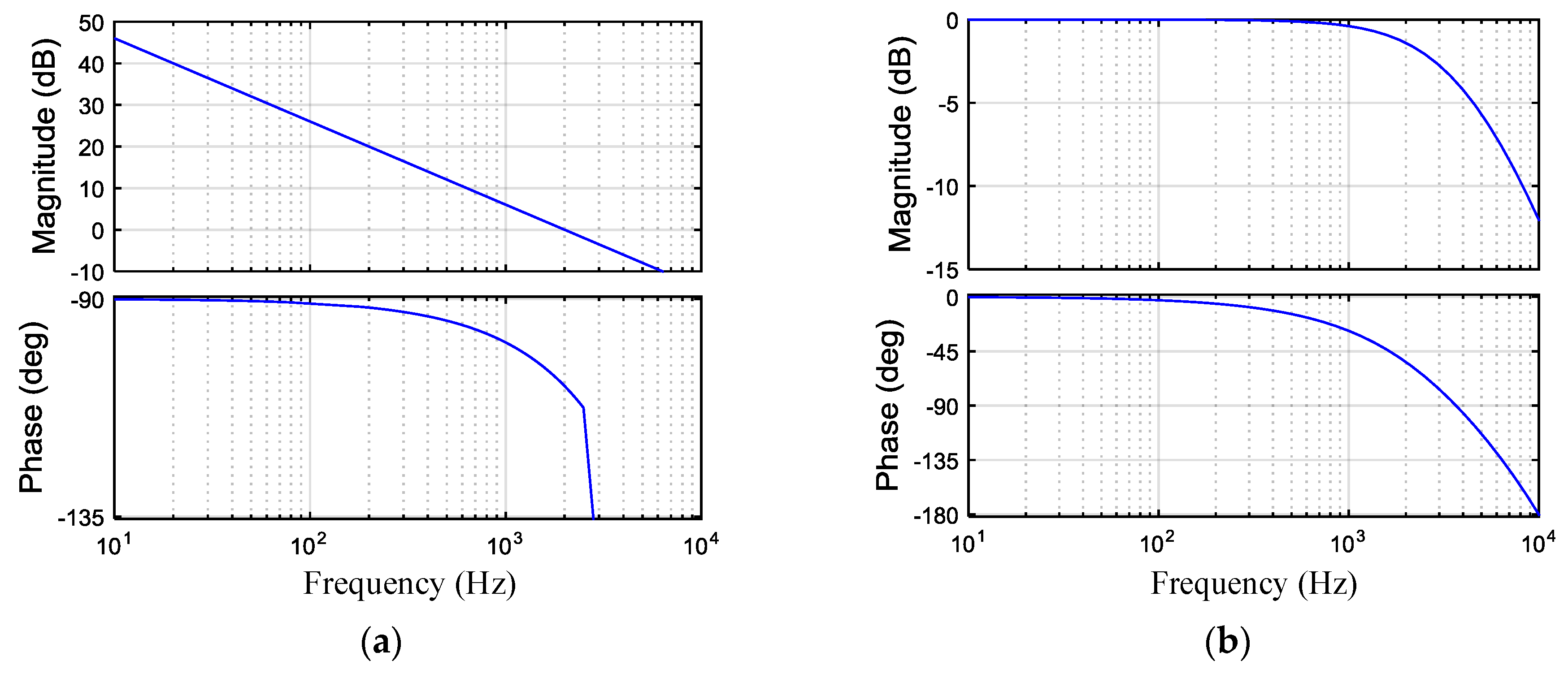
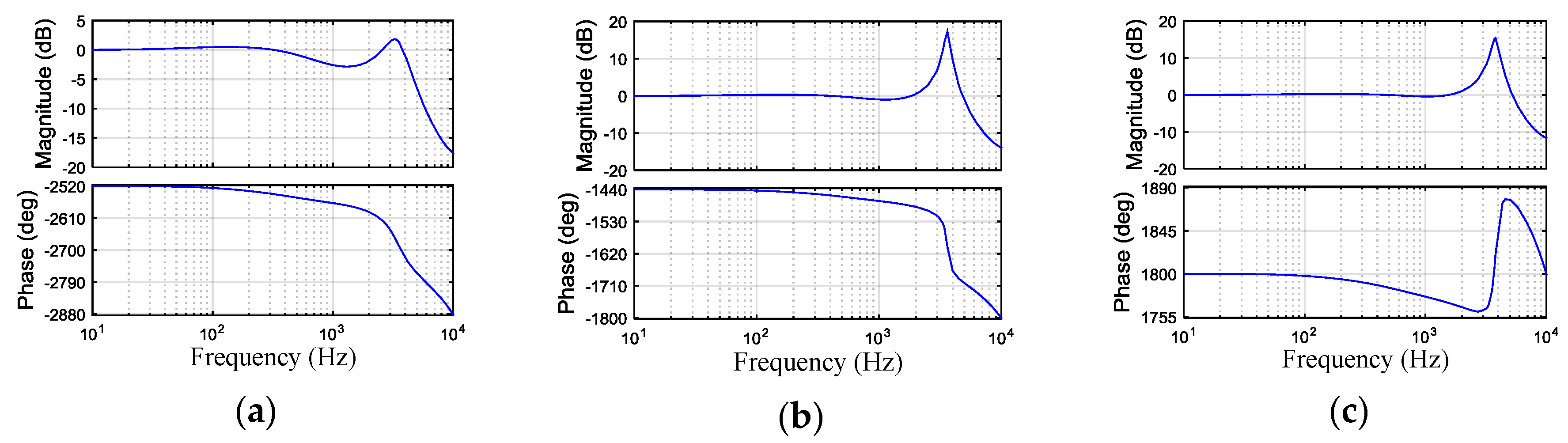
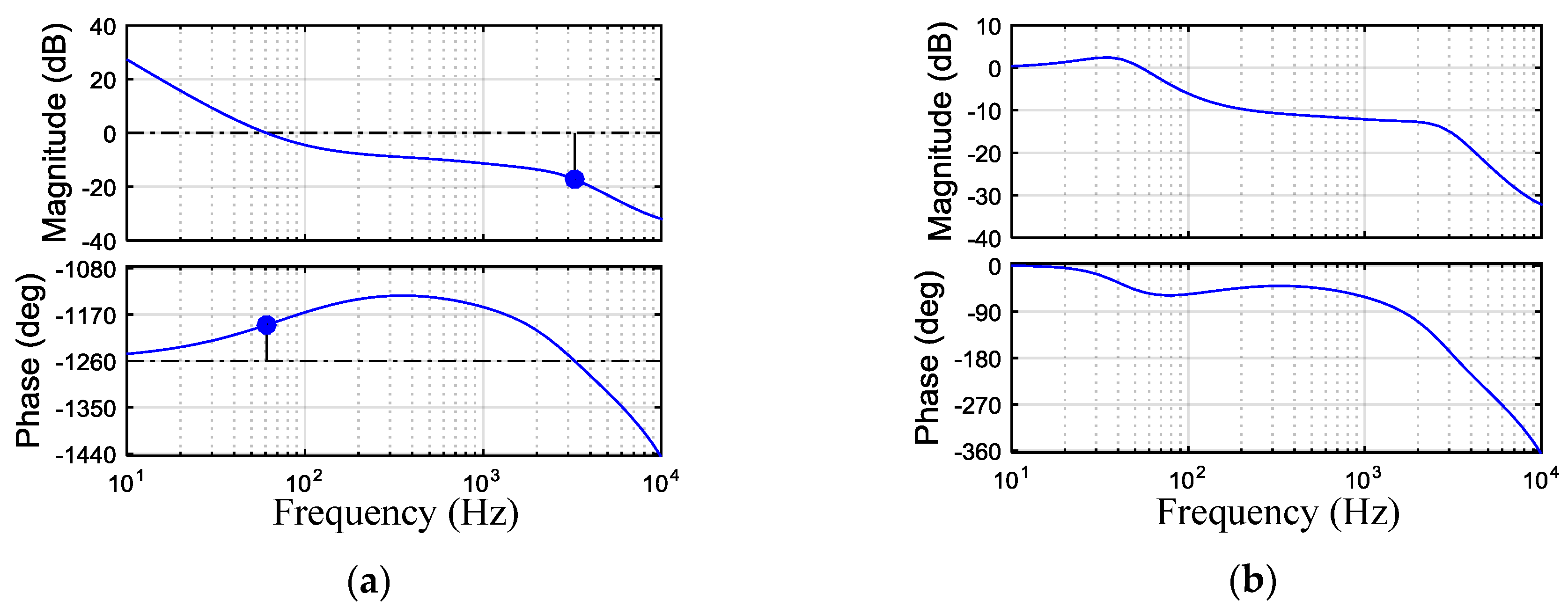
4.1. The Effects of These Parameters on the Voltage Loop
4.1.1. The Effects of τ on the Voltage Loop
4.1.2. The Effects of rc on the Voltage Loop
4.1.3. The Effects of Kvp on the Voltage Loop
4.1.4. The Effects of fz on the Voltage Loop
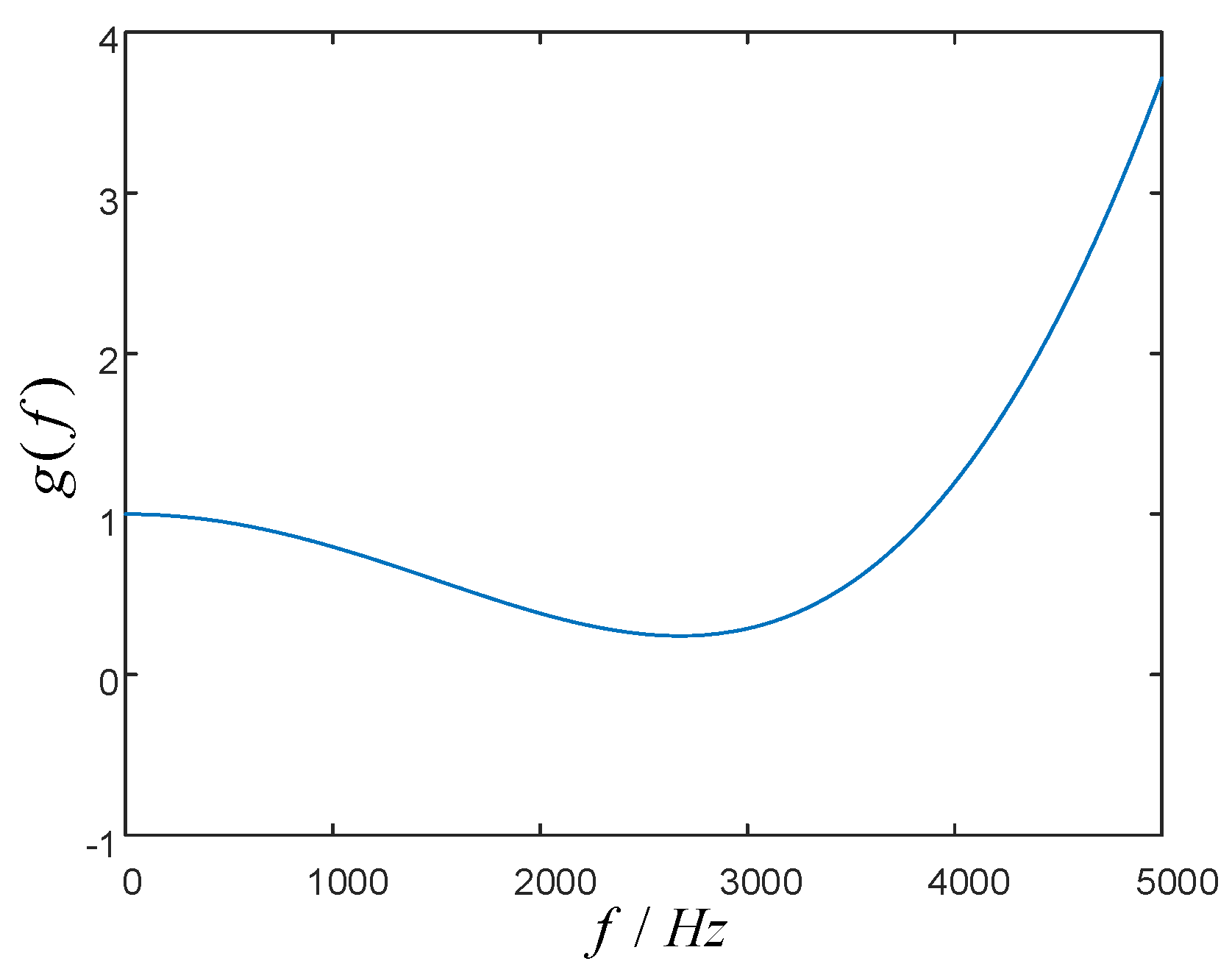
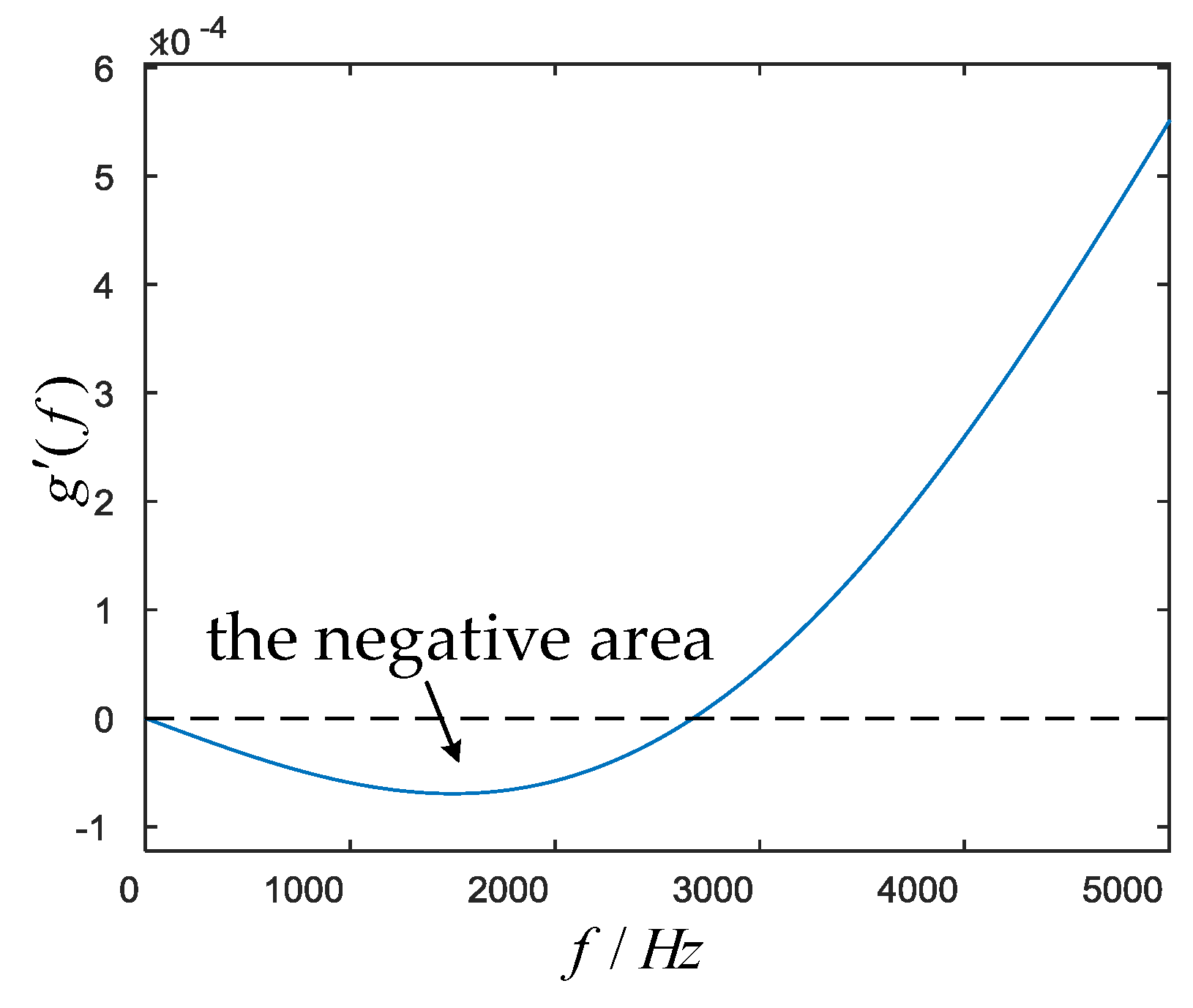
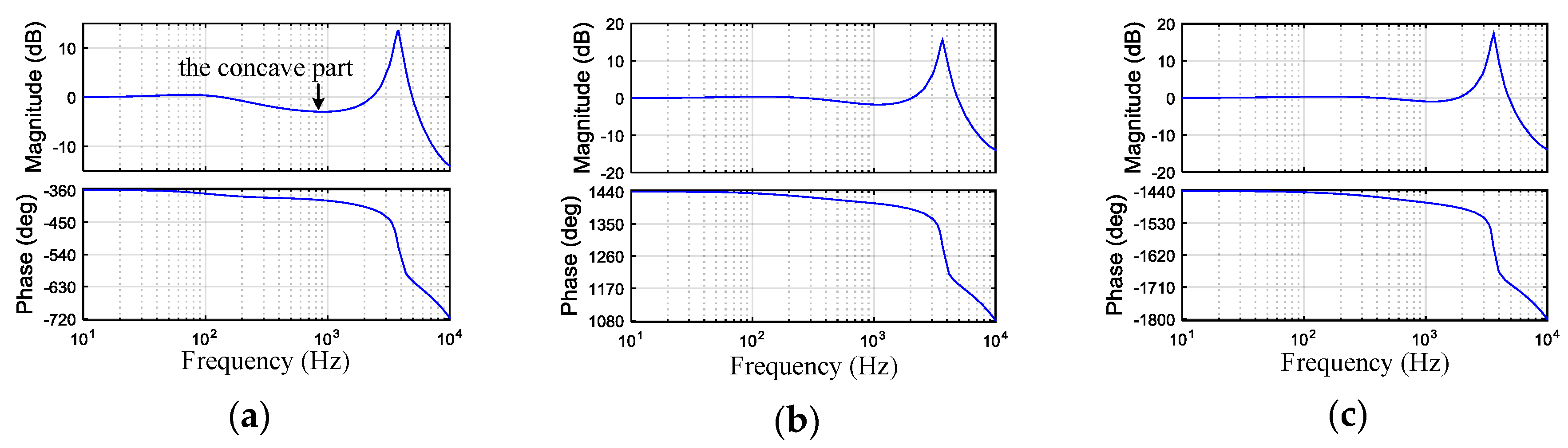
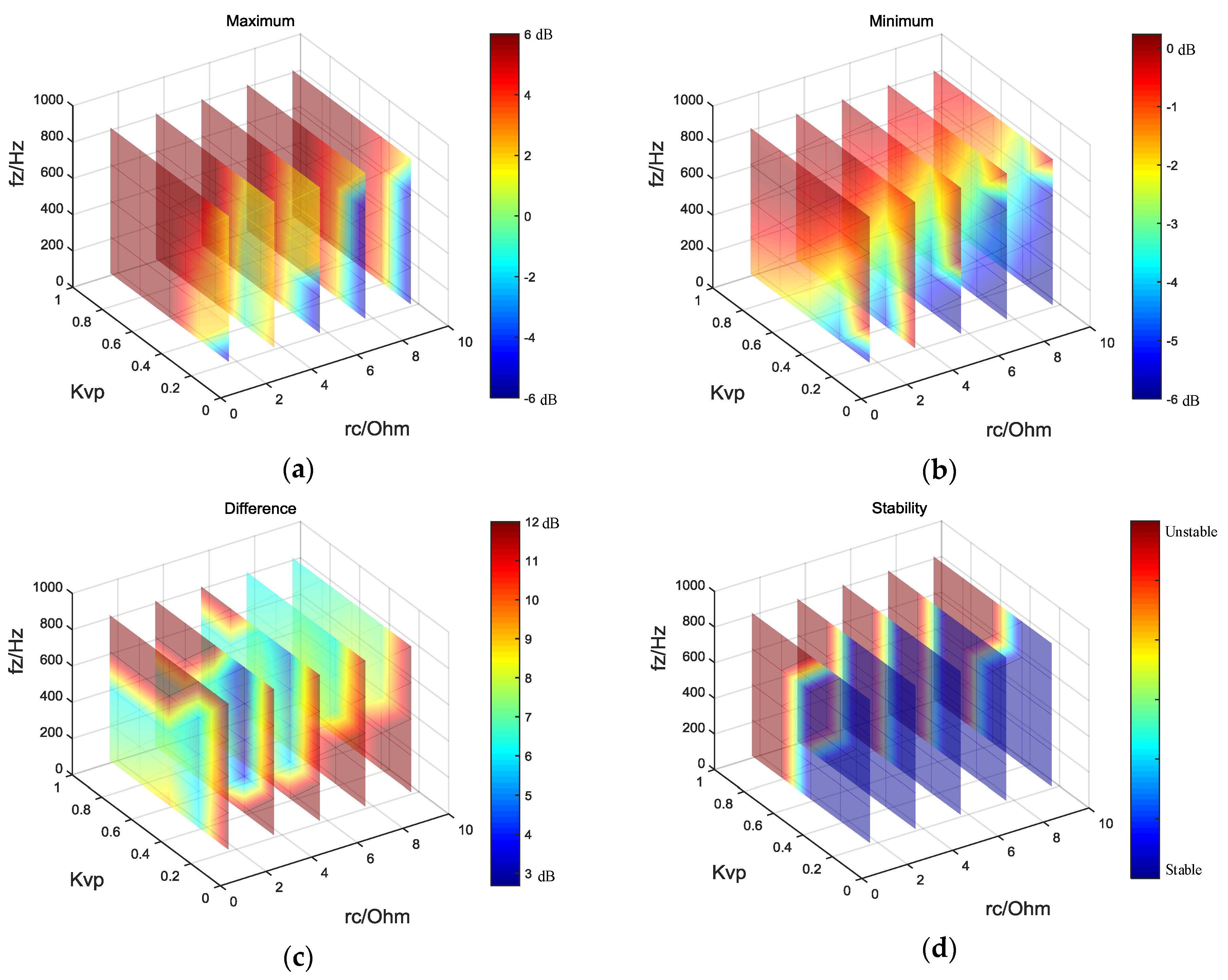
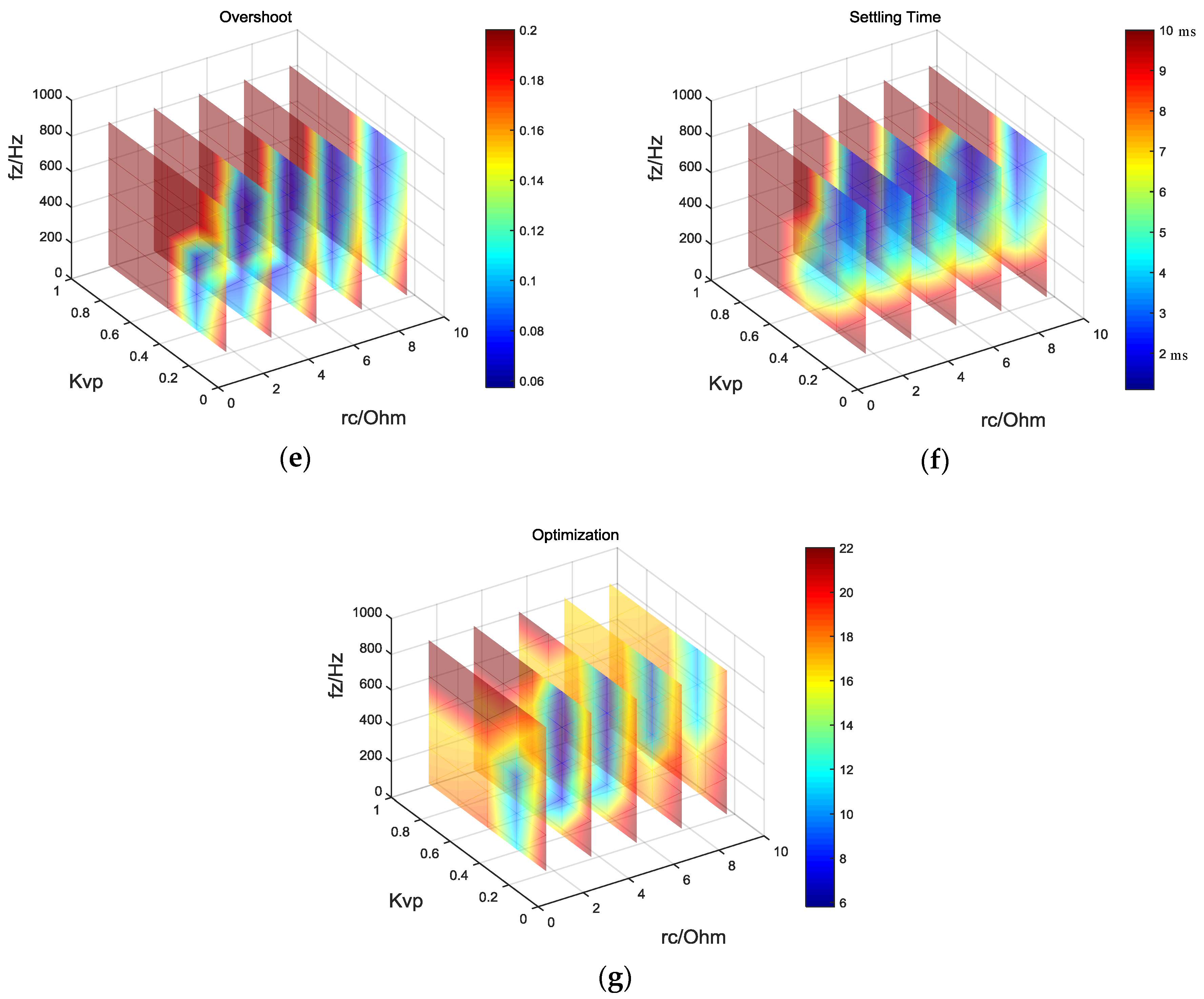
4.2. The Optimum Parameter Design
- (1)
- Considering the resonance peak suppression, make the gain of the resonance peak equal to the minimum of the concave part as possible.
- (2)
- Considering the bandwidth of the voltage loop, make the gain of the resonance peak and the minimum of the concave part larger than –5 dB to ensure the bandwidth of the voltage loop wide enough.
- (3)
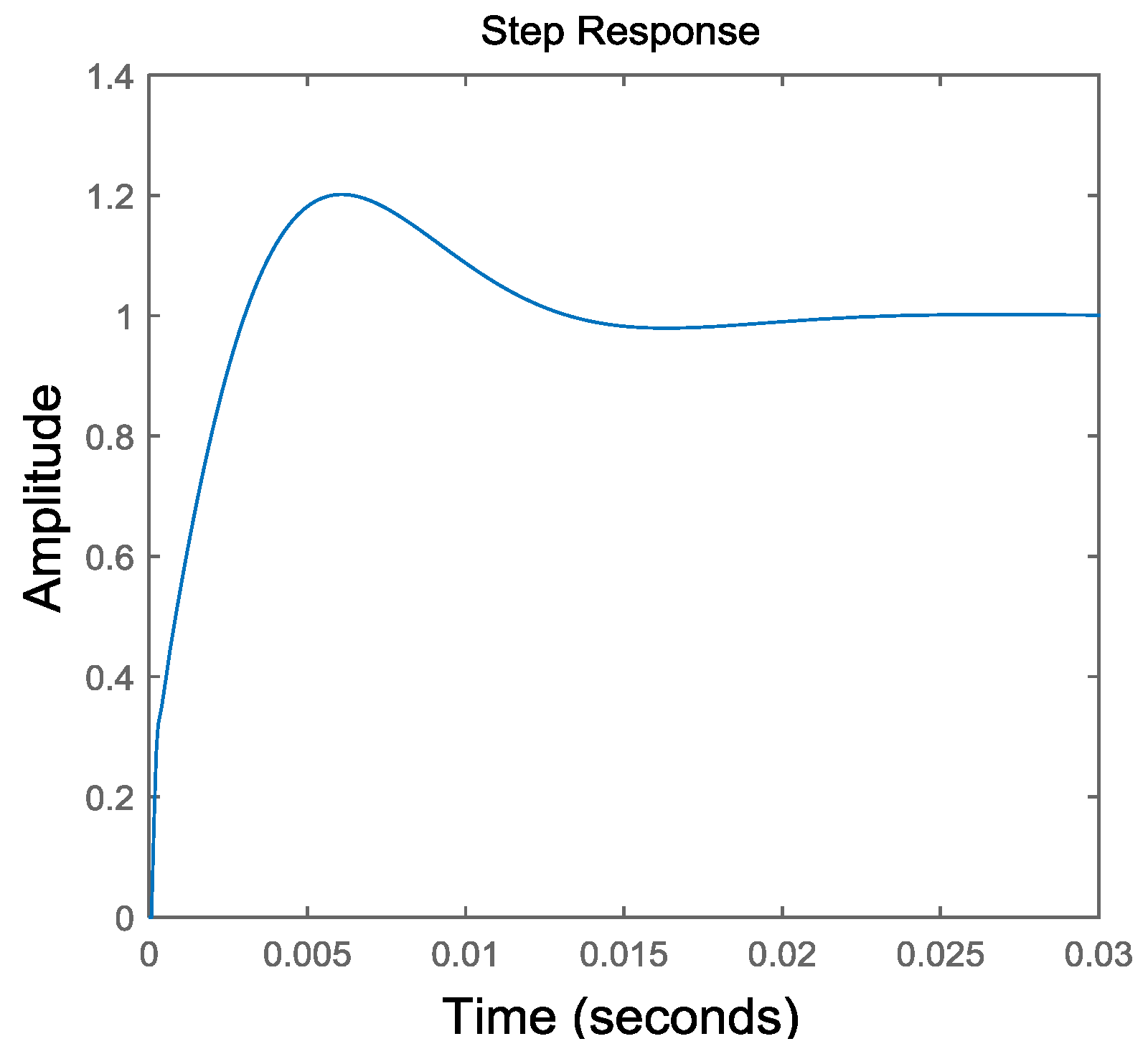
- Considering the dynamic properties, make both the overshoot and the settling time of step response as small as possible.
4.3. Stability and Dynamic Property
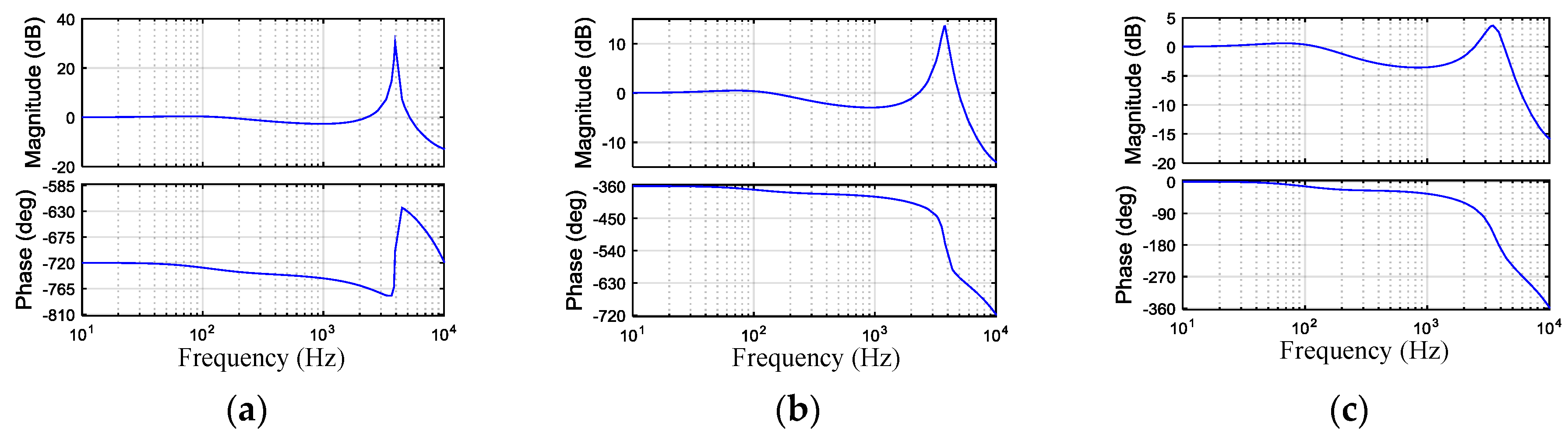
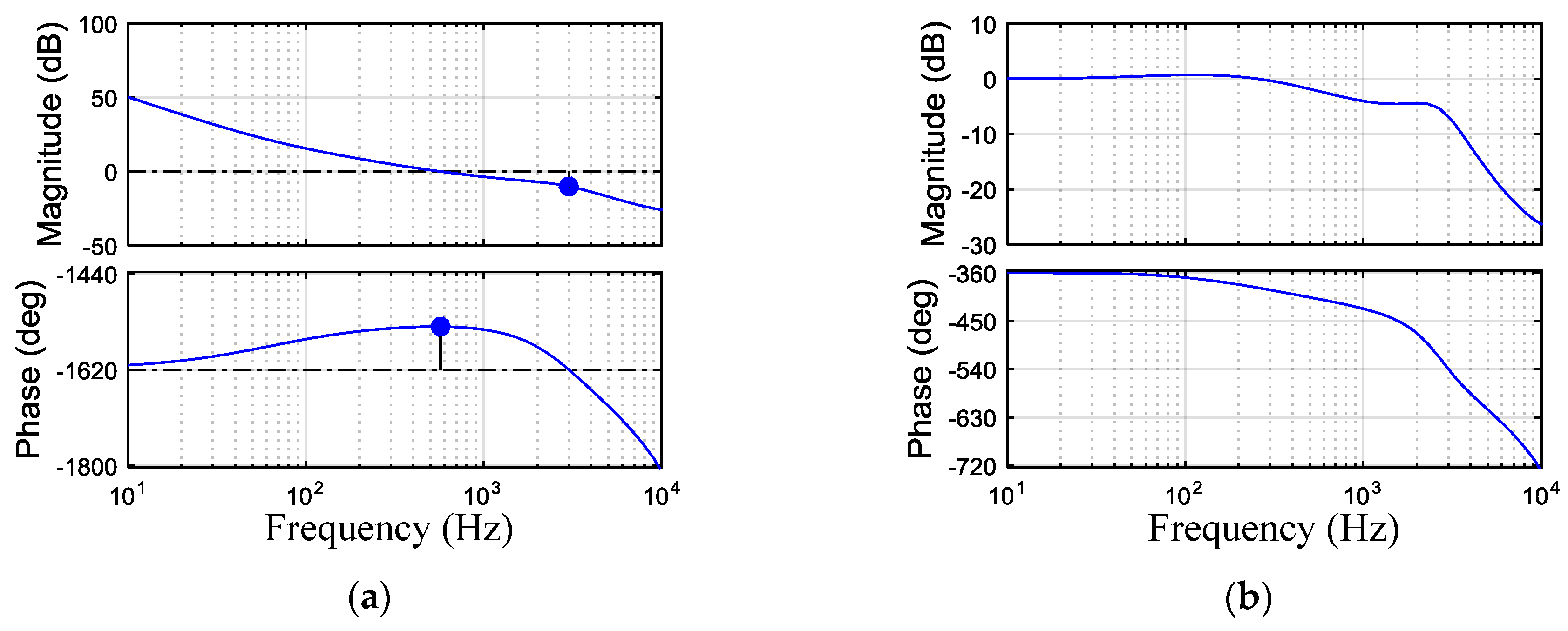
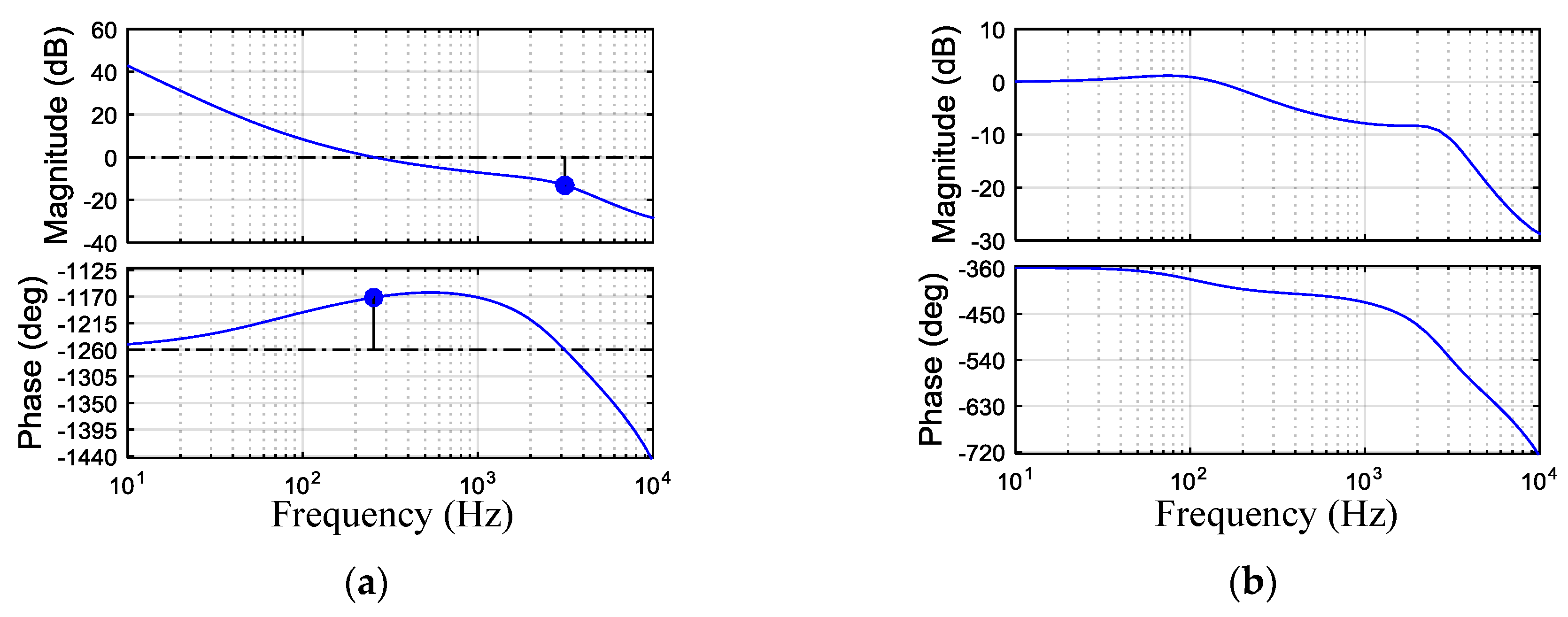
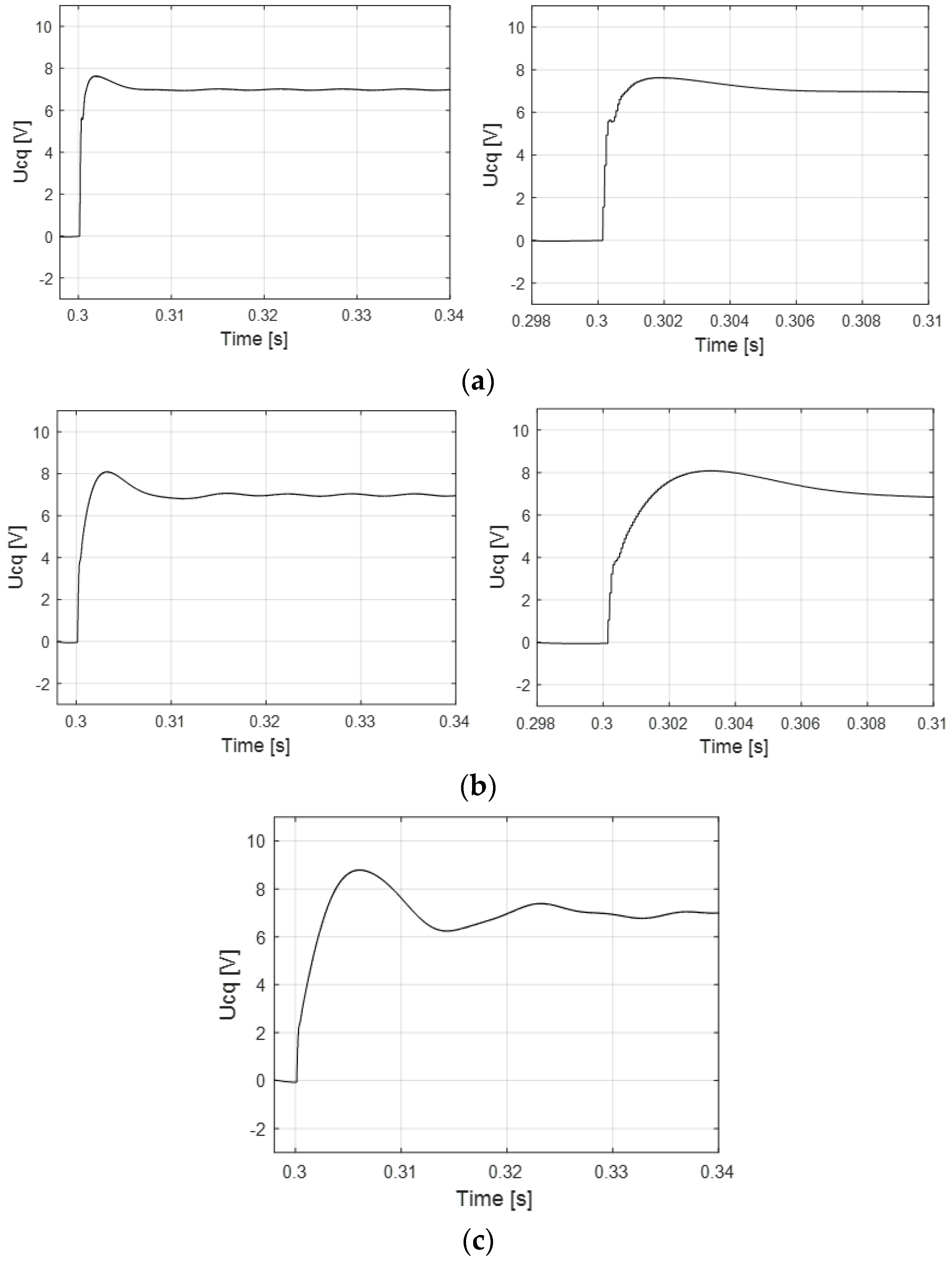
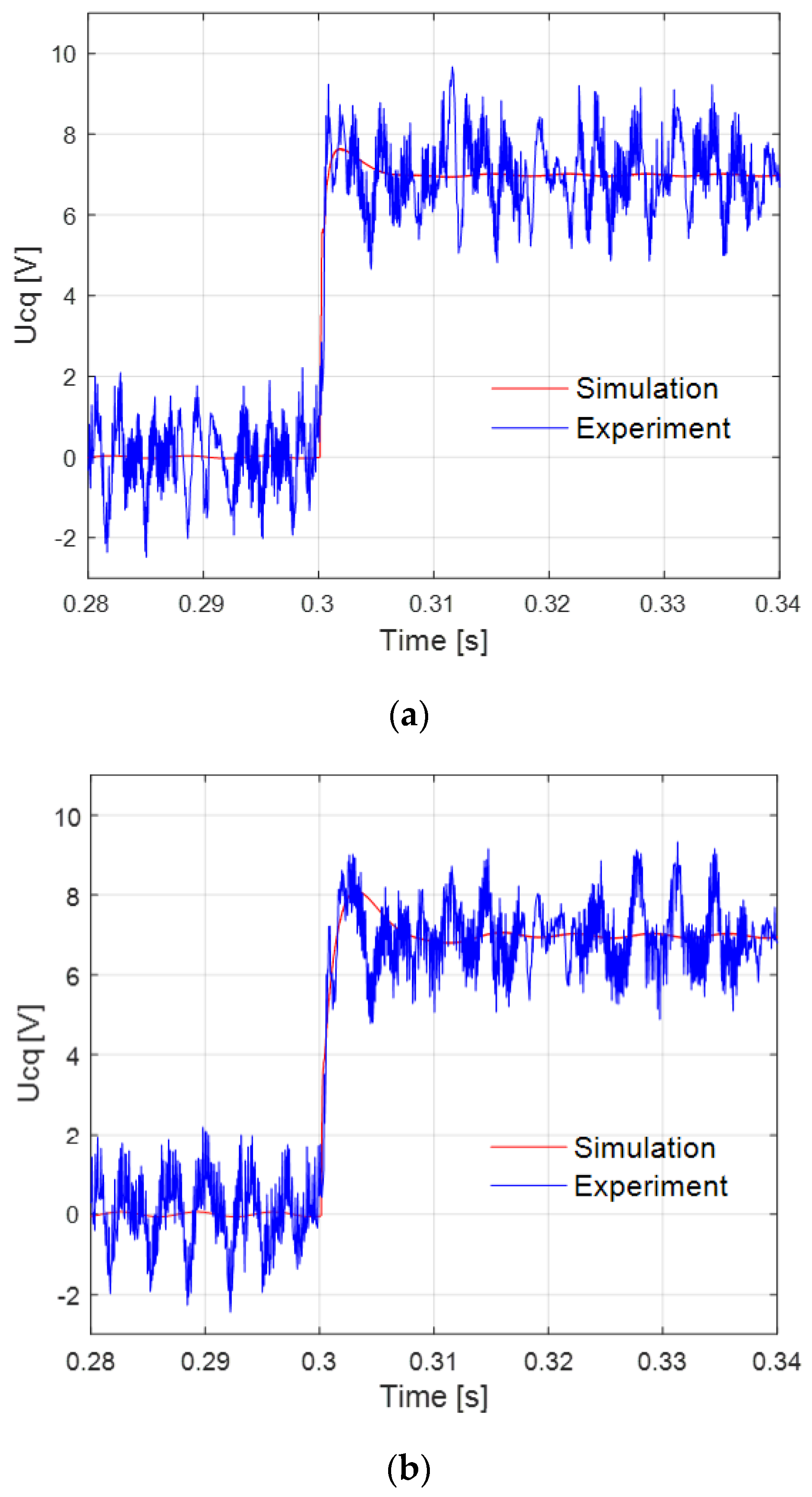
4.3.1. Set 1: rc = 2.5 Ω, Kvp = 0.2, fz = 700 Hz, in the Blue Area
4.3.2. Set 2: rc = 2.5 Ω, Kvp = 0.15, fz = 400 Hz, in the Blue Area
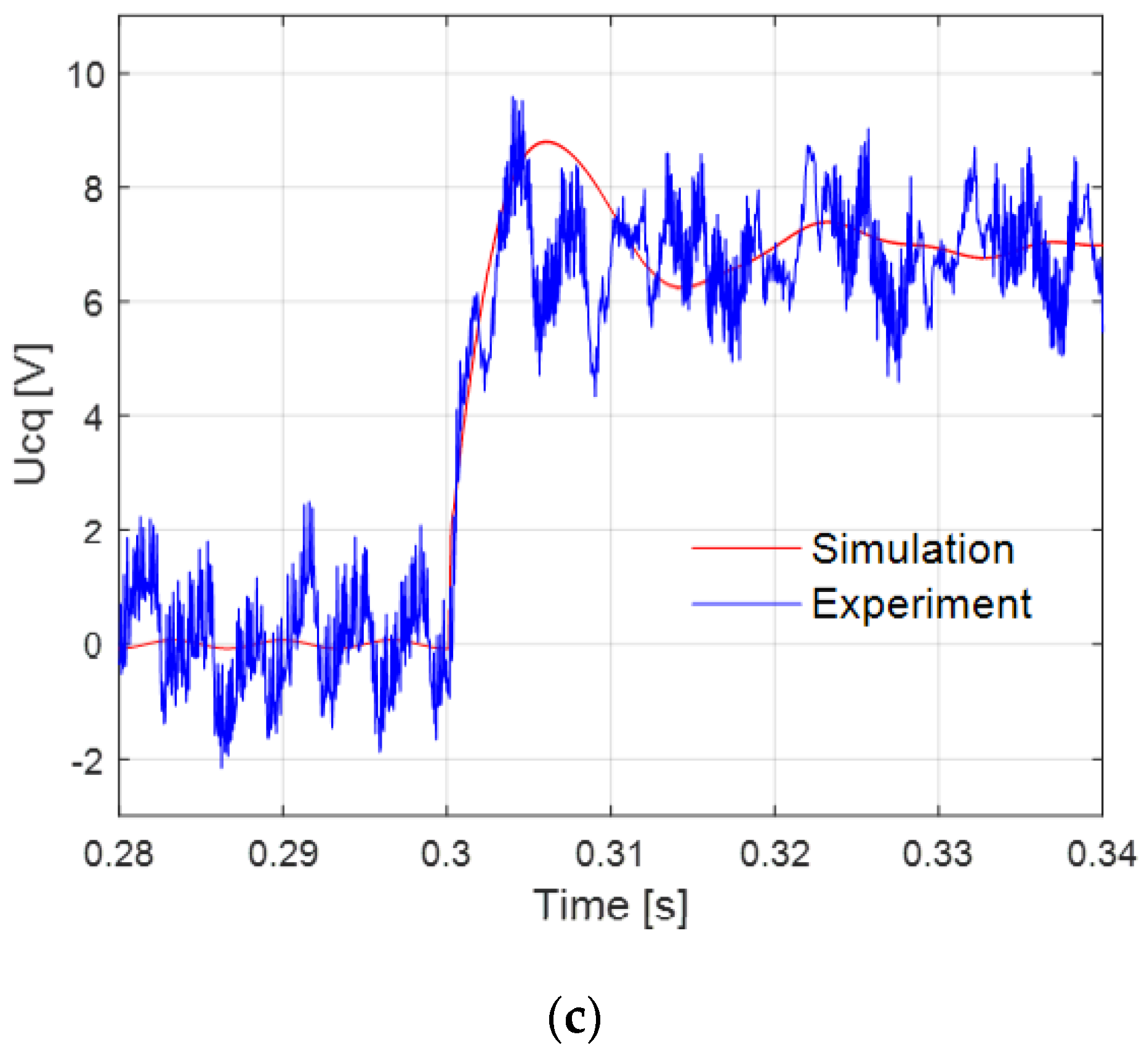
4.3.3. Set 3: rc = 2.5 Ω, Kvp = 0.1, fz = 200 Hz, outside the Blue Area
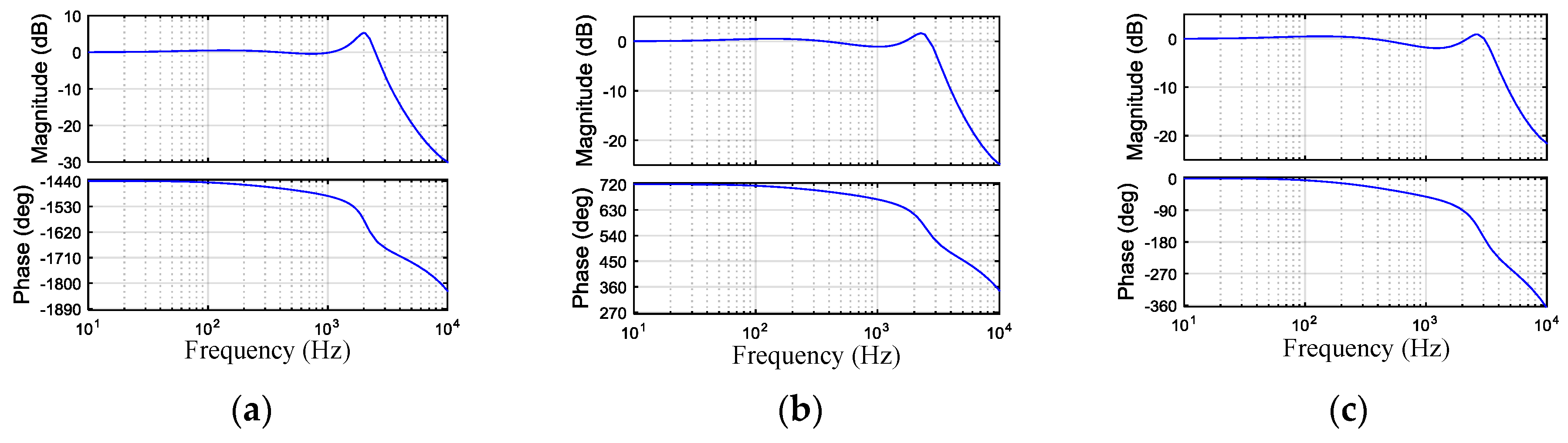
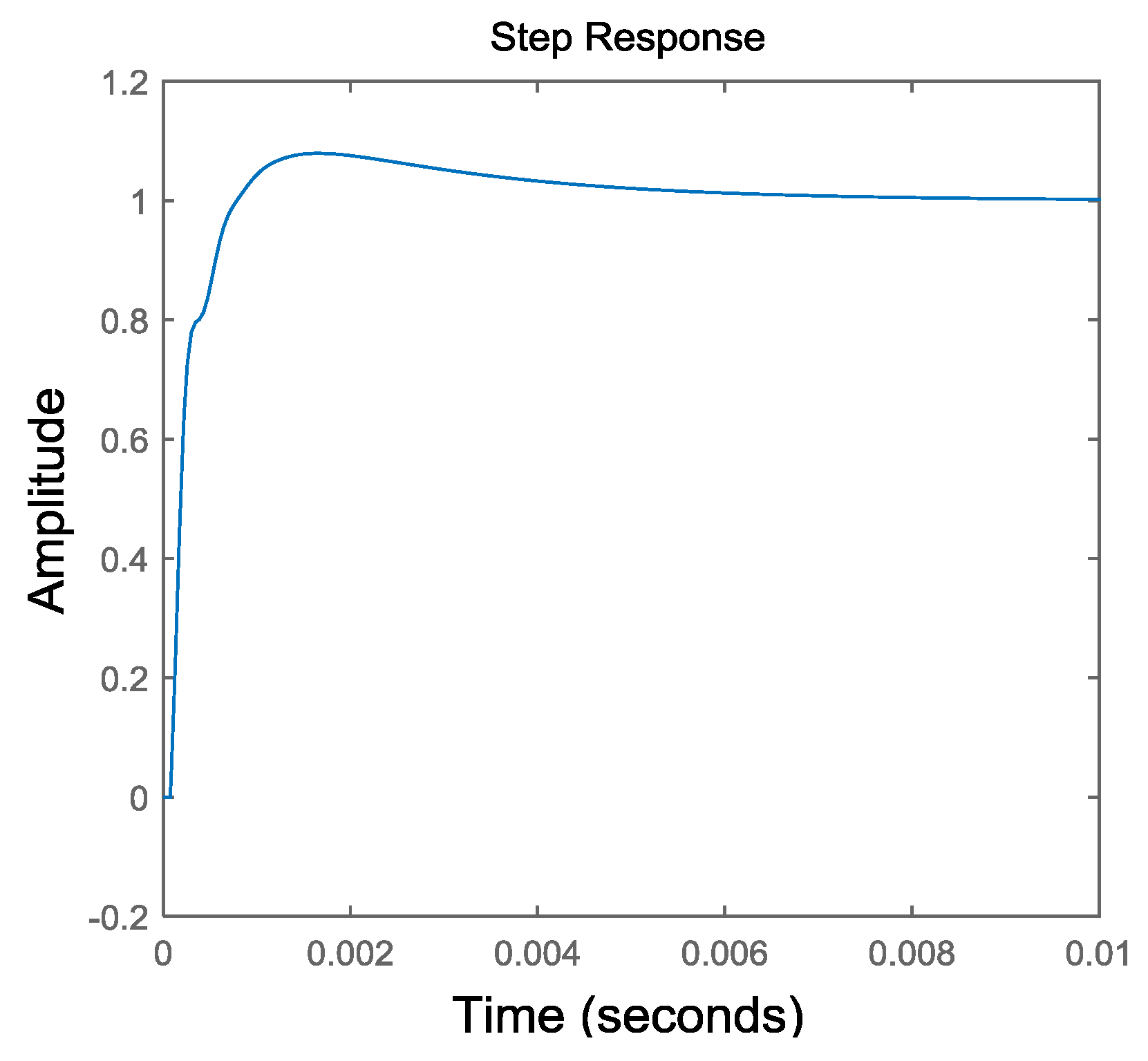
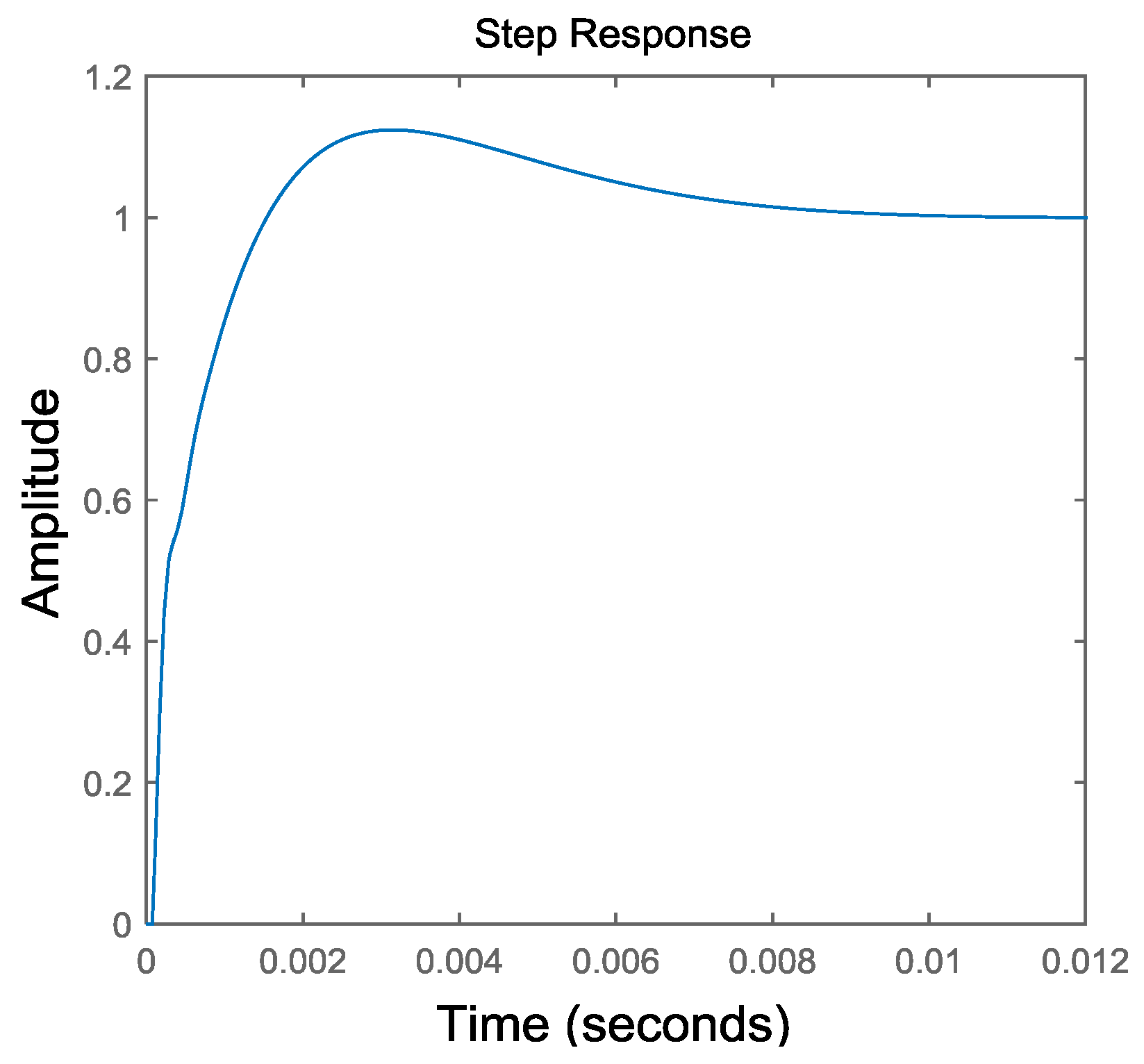
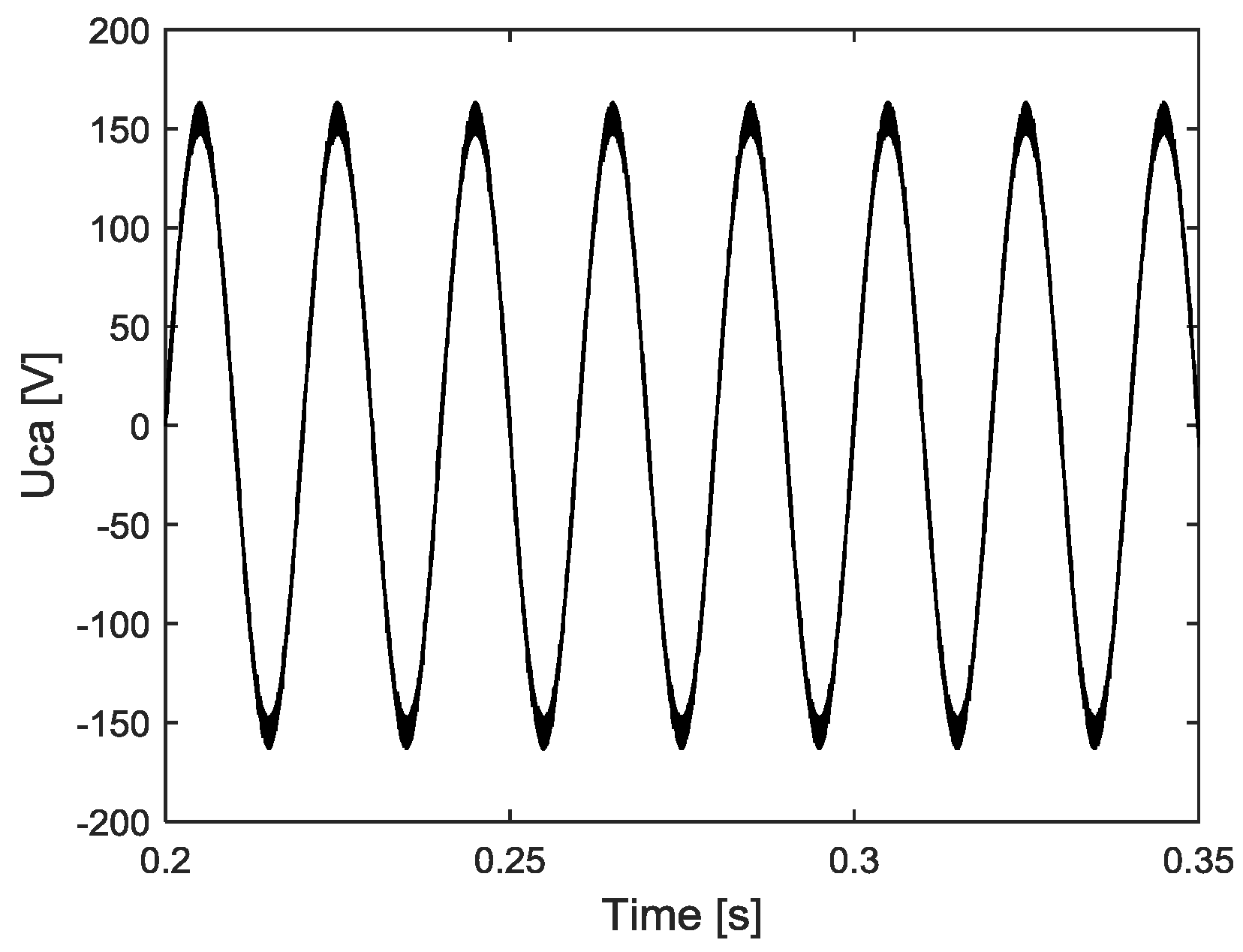
5. Simulation Results and Analysis
6. Experimental Validation
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
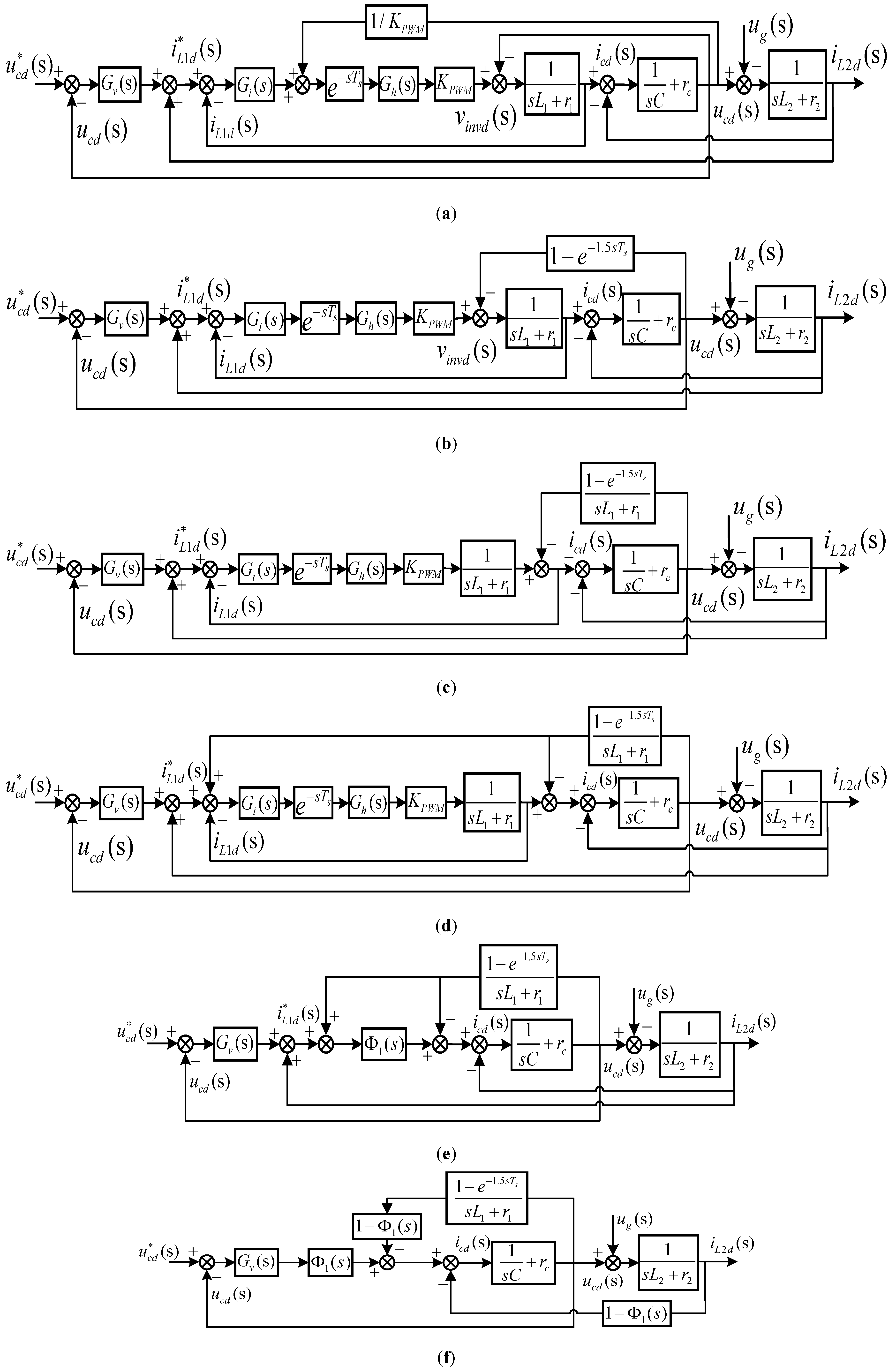
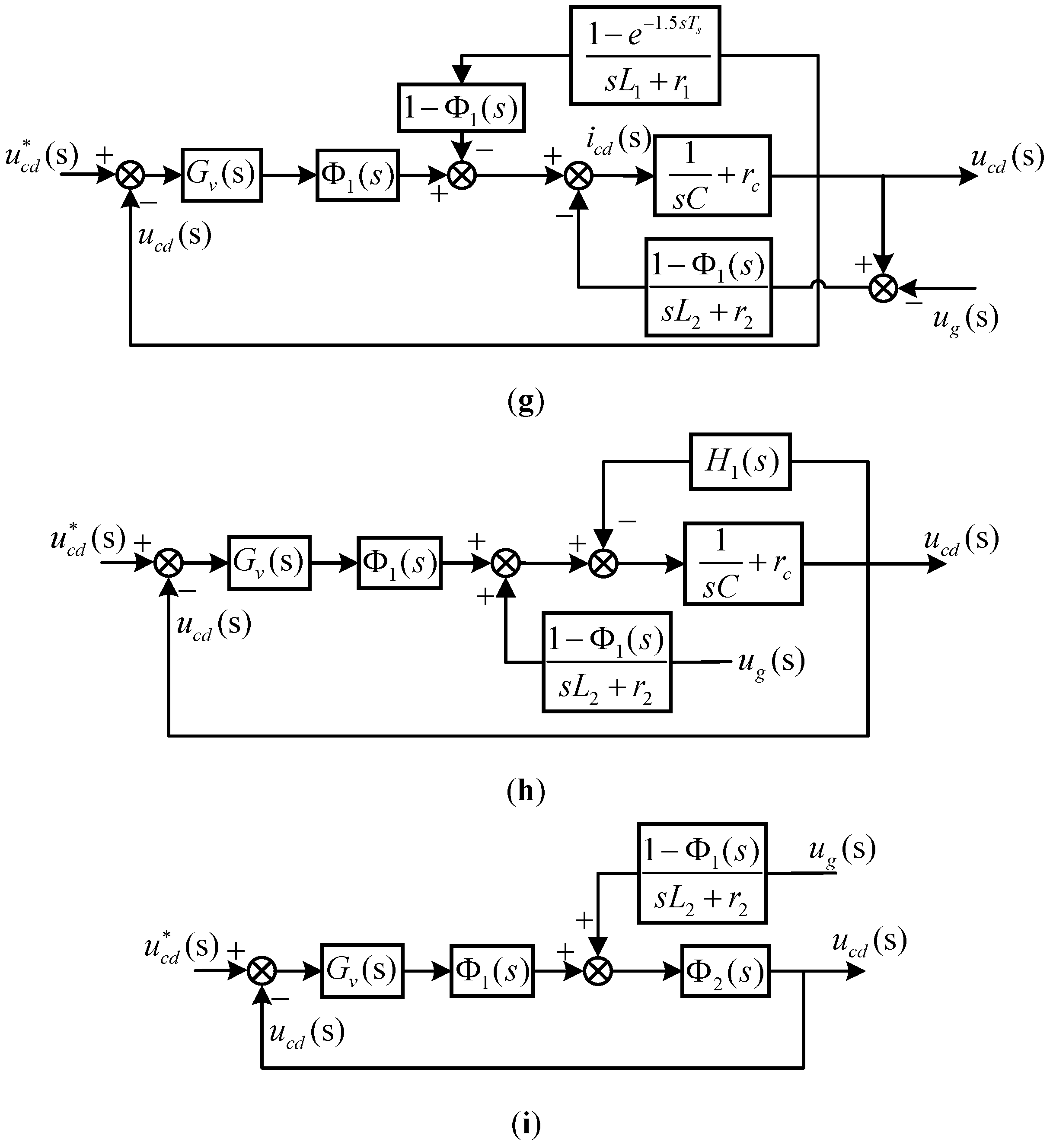
Appendix B
References
- Malinowski, M.; Leon, J.I.; Abu-Rub, H. Solar photovoltaic and thermal energy systems: Current technology and future trends. Proc. IEEE 2017, 105, 2132–2146. [Google Scholar]
- Guo, X. Three-phase CH7 inverter with a new space vector modulation to reduce leakage current for transformerless photovoltaic systems. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 708–712. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Ma, K. Wind Energy Systems. Proc. IEEE 2017, 105, 2116–2131. [Google Scholar]
- Li, P.; Song, Y.; Li, D.; Cai, W.; Zhang, K. Control and monitoring for grid-friendly wind turbines: Research overview and suggested approach. IEEE Trans. Power Electron. 2015, 30, 1979–1986. [Google Scholar] [CrossRef]
- Wu, F.; Li, X.; Feng, F.; Gooi, H.B. Multi-topology-Mode grid-connected inverter to improve comprehensive performance of renewable energy source generation system. IEEE Trans. Power Electron. 2017, 32, 3623–3633. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, H.; Ran, L. Comparison on control strategies of inverters in AC microgrids. Autom. Electr. Power Syst. 2016, 40, 142–151. [Google Scholar]
- Fantino, R.A.; Busada, C.A.; Solsona, J.A. Optimum PR control applied to LCL filters with low resonance frequency. IEEE Trans. Power Electron. 2018, 33, 793–801. [Google Scholar] [CrossRef]
- Wu, F.; Li, X.; Duan, J. Improved elimination scheme of current zero-crossing distortion in unipolar hysteresis current controlled grid-connected inverter. IEEE Trans. Ind. Inform. 2015, 11, 1111–1118. [Google Scholar] [CrossRef]
- Marati, N.; Prasad, D. A modified feedback scheme suitable for repetitive control of inverter with nonlinear load. IEEE Trans. Power Electron. 2018, 33, 2588–2600. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Peng, K. Overview of typical control methods for grid-connected inverters of distributed generation. Proc. Chin. Soc. Univ. –Electr. Power Syst. Autom. 2012, 24, 12–20. [Google Scholar]
- Wang, S.; Hu, J.; Yuan, X. Virtual synchronous control for grid-connected DFIG-based wind turbines. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 932–944. [Google Scholar] [CrossRef]
- Adhikari, S.; Li, F. Coordinated V-f and P-Q control of solar photovoltaic generators with MPPT and battery storage in microgrids. IEEE Trans. Smart Grid 2014, 5, 1270–1281. [Google Scholar] [CrossRef]
- Sang, S.; Gao, N.; Cai, X.; Li, R. A power-voltage controlled grid-connected inverter and its adaptability research under weak grid conditions. Proc. CSEE 2017, 37, 2339–2351. [Google Scholar]
- Wang, Y.; Luo, A.; Jin, G. Improved robust droop multiple loop control for parallel inverters in microgrid. Trans. Chin. Electrotech. Soc. 2015, 30, 116–123. [Google Scholar]
- Zhang, Q.; Peng, C.; Chen, Y.; Jin, G.; Luo, A. A control strategy for parallel operation of multi-inverters in microgrid. Proc. CSEE 2012, 32, 126–132. [Google Scholar]
- Zhong, Q.; Weiss, G. Synchronverters: inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Wang, Z.; Wu, K.; Wang, H.; Hu, J.; Lu, C. A virtual synchronous control for voltage-source converters utilizing dynamics of DC-link capacitor to realize self-synchronization. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1565–1577. [Google Scholar] [CrossRef]
- Zhang, X.; Spencer, J.W.; Guerrero, J.M. Small-signal modeling of digitally controlled grid-connected inverters with LCL filters. IEEE Trans. Ind. Electron. 2013, 60, 3752–3765. [Google Scholar] [CrossRef]
- Yin, J.; Duan, S.; Liu, B. Stability analysis of grid-connected inverter with lcl filter adopting a digital single-loop controller with inherent damping characteristic. IEEE Trans. Ind. Electron. 2013, 9, 1104–1112. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. A real-time computation method with dual sampling mode to improve the current control performance of the LCL-type grid-connected inverter. IEEE Trans. Ind. Electron. 2015, 62, 4563–4572. [Google Scholar] [CrossRef]


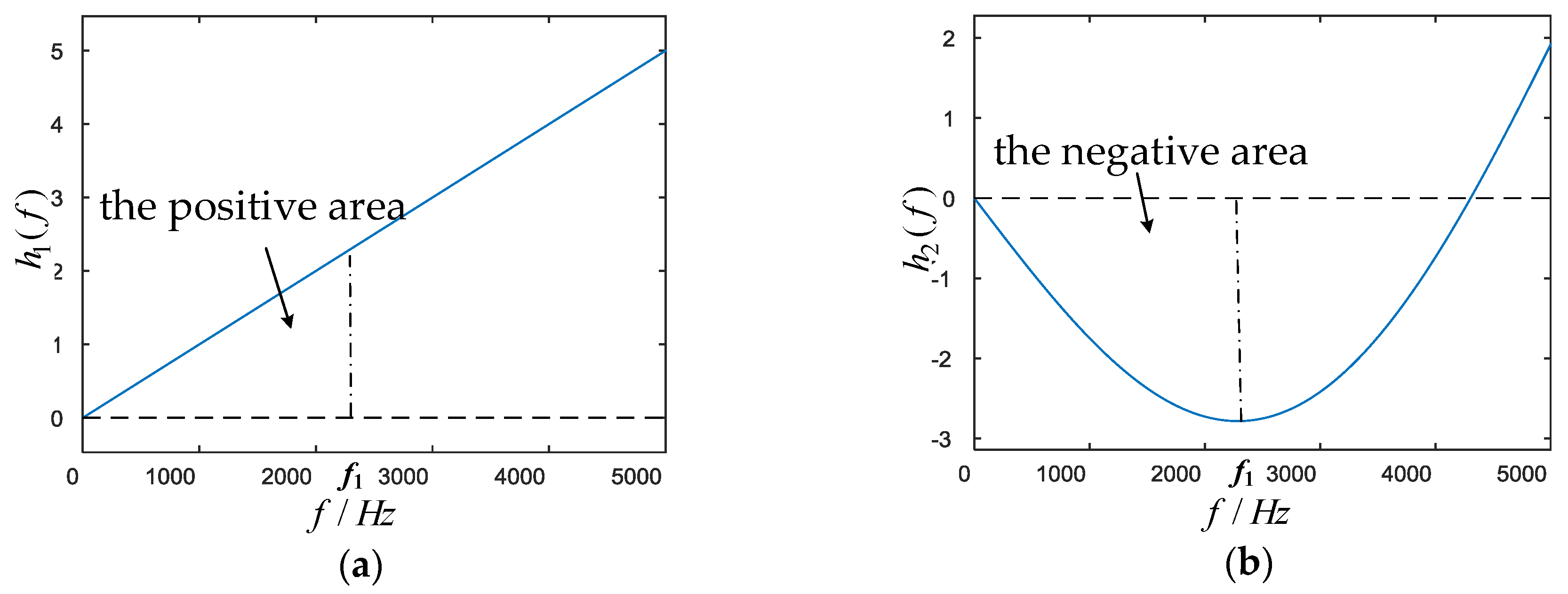
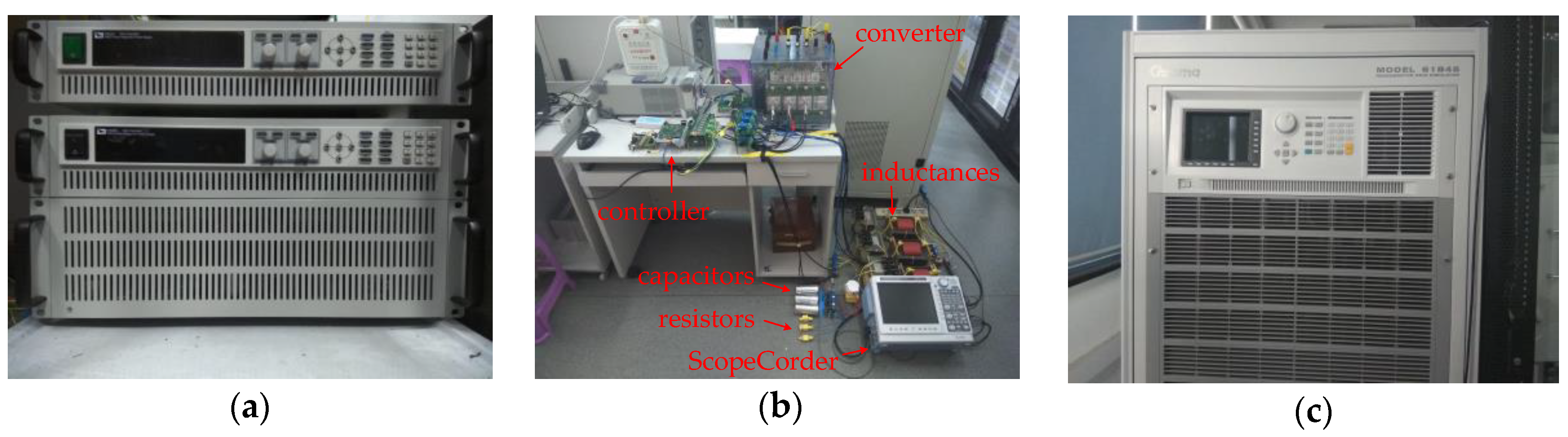
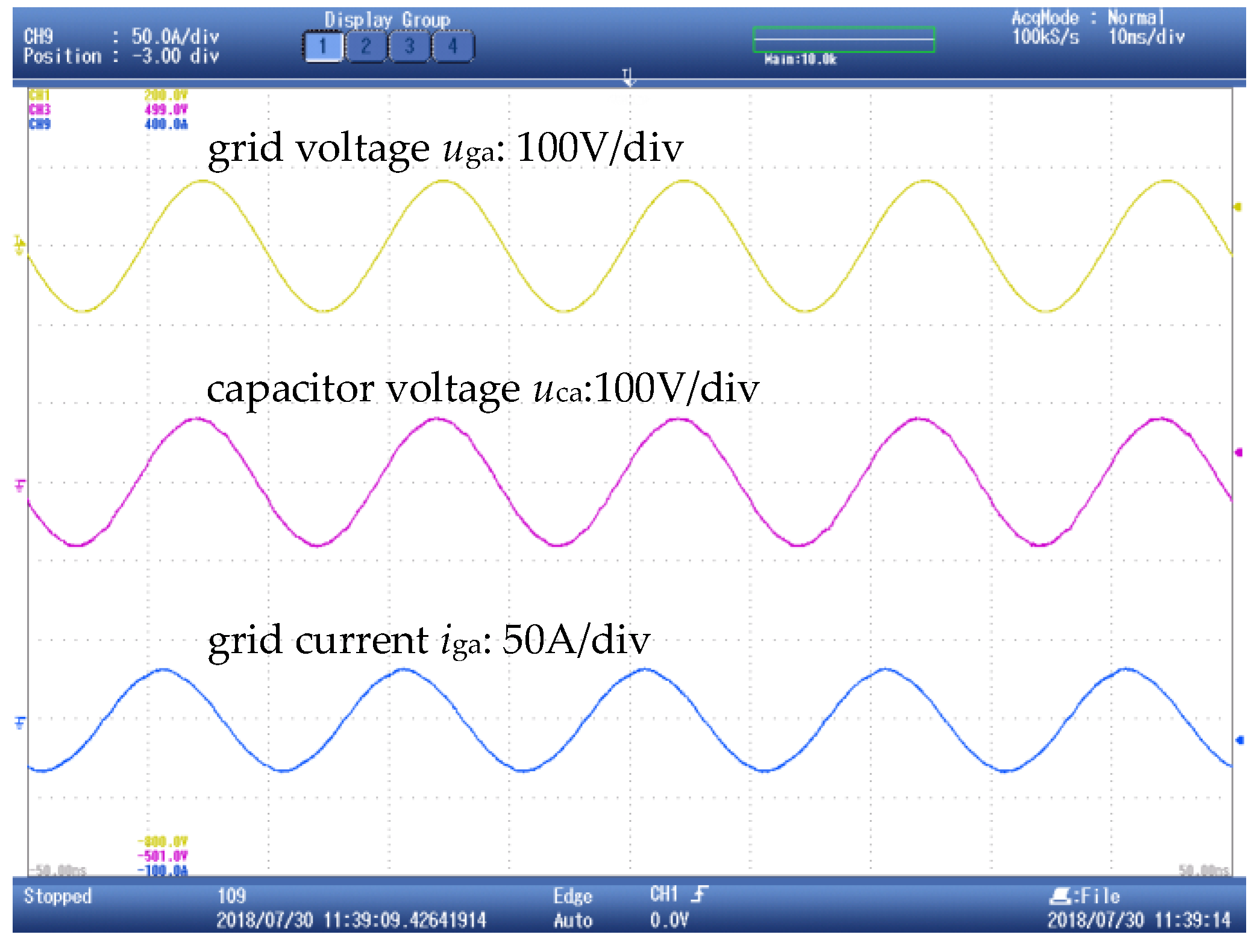
| Elements | Parameters and Values |
|---|---|
| DC source | Udc = 380 V |
| Switching circuit | Kpwm = 12 |
| LCL filter | L1 = 1.85 mH, r1 = 0.018 Ω C = 35 μF L2 = 570 μH, r2 = 0.23 Ω |
| Utility grid | phase RMS voltage Ug = 110 V |
| PWM modulation | asymmetric regular sampling switching frequency: 10 kHz sampling frequency: 20 kHz |
| Elements | Parameters and Values |
|---|---|
| DC source | Udc = 190 V |
| Switching circuit | Kpwm = 12 |
| LCL filter | L1 = 1.85 mH, r1 = 0.018 Ω C = 35 μF L2 = 570 μH, r2 = 0.23Ω |
| Utility grid | phase RMS voltage Ug = 55 V |
| PWM modulation | asymmetric regular sampling switching frequency: 10 kHz sampling frequency: 20 kHz |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, N.; Yang, H.; Han, J.; Zhao, R. Modeling and Parameter Design of Voltage-Controlled Inverters Based on Discrete Control. Energies 2018, 11, 2154. https://doi.org/10.3390/en11082154
Dong N, Yang H, Han J, Zhao R. Modeling and Parameter Design of Voltage-Controlled Inverters Based on Discrete Control. Energies. 2018; 11(8):2154. https://doi.org/10.3390/en11082154
Chicago/Turabian StyleDong, Ningbo, Huan Yang, Junfei Han, and Rongxiang Zhao. 2018. "Modeling and Parameter Design of Voltage-Controlled Inverters Based on Discrete Control" Energies 11, no. 8: 2154. https://doi.org/10.3390/en11082154
APA StyleDong, N., Yang, H., Han, J., & Zhao, R. (2018). Modeling and Parameter Design of Voltage-Controlled Inverters Based on Discrete Control. Energies, 11(8), 2154. https://doi.org/10.3390/en11082154




