Regional Energy, CO₂, and Economic and Air Quality Index Performances in China: A Meta-Frontier Approach

Abstract

Rapid economic development has resulted in a significant increase in energy consumption and pollution such as carbon dioxide (CO₂), particulate matter (PM_2.5), particulate matter 10 (PM₁₀), SO₂, and NO₂ emissions, which can cause cardiovascular and respiratory diseases. Therefore, to ensure a sustainable future, it is essential to improve economic efficiency and reduce emissions. Using a Meta-frontier Non-radial Directional Distance Function model, this study took energy consumption, the labor force, and fixed asset investments as the inputs, Gross domestic product (GDP) as the desirable output, and CO₂ and the Air Quality Index (AQI) scores as the undesirable outputs to assess energy efficiency and air pollutant index efficiency scores in China from 2013–2016 and to identify the areas in which improvements was necessary. It was found that there was a large gap between the western and eastern cities in China. A comparison of the CO₂ and AQI in 31 Chinese cities showed a significant difference in the CO₂ emissions and AQI efficiency scores, with the lower scoring cities being mainly concentrated in China’s western region. It was therefore concluded that China needs to pay greater attention to the differences in the economic levels, stages of social development, and energy structures in the western cities when developing appropriately focused improvement plans.

1. Introduction

The increase in the use of fossil fuels since the Industrial Revolution has led to a rapid increase in the atmospheric concentrations of greenhouse gases such as CO₂, and air pollution from fine particles such as PM_2.5, sulphur dioxide (SO₂), and nitrogen dioxide (NO₂), all of which have had a negative impact on water resources, crops, natural ecosystems, and human health, and a consequent negative effect on medium- and long-term sustainable social and economic development [1].

Over the past 30 years, China’s reforms and opening up policies have been primarily aimed at economic development, which has resulted in an over-exploitation of the natural resources and a significant increase in environmental pollution and ecological damage. The associated increase in coal-fired energy consumption has caused increased and worsening air pollution and higher concentrations of greenhouse gases such as CO₂. The International Energy Agency [2] estimated that China’s share of global CO₂ emissions from 2002 to 2030 was going to increase from 14% to 19%, and the United States Energy Agency [3] estimated that China’s CO₂ emissions would comprise 24.5% of the world’s total by 2030. The World Bank [4] claimed that by 2020, China’s air pollution would annually cause 600,000 early deaths and 20 million respiratory disease sufferers, and its water pollution would affect 190 million people and the deaths of 30,000 children from diarrhea.

China’s focus on industrialization and economic growth in the past two decades has also resulted in a significant increase in air pollutant emissions such as sulfur dioxide (SO₂), nitrogen oxides (NO_X), carbon monoxide (CO), non-methane volatile organic compounds (NMVOC), and black carbon (BC) [5,6]. The impact of these atmospheric pollutants on health and the environment has caused significant concern [7,8] as air pollution resulted in 1.2 million premature deaths in China in 2010, with a further 25 million people contracting severe respiratory illnesses [8].

Because of China’s severe city air pollution, high energy consumption, and environmental problems need to be urgently addressed to ensure the all-round development of China’s economy, improving energy efficiency and reducing air pollution and CO₂ emissions have become critical issues.

In recent years, Chinese governments at all levels have begun focusing on air pollution and CO₂ emissions reductions with some positive results [9]; however, severe air pollution and CO₂ emissions levels remain a serious issue in many cities. Further, because of the global impact of climate change, it has become increasingly difficult to domestically control air pollution and CO₂ levels.

Because of its size, China’s eastern and western regions have wide variations in their economic and social development in terms of resource endowments, industrial structures and geographical conditions, which means there are also significant regional disparities in air pollution controls. In general, the impact of existing policy measures has been effective in the short term, but in some cities, the medium to long-term results are not satisfactory. Further, most measures have failed to solve the fundamental causes of air pollution.

Energy efficiency analyses have tended to be based on conventional total factor analysis frameworks and have only considered ideal output such as economic output while ignoring unfavorable output such as environmental pollutants, meaning that the economic performance assessments and efficiency and productivity estimates were biased. More current productivity analysis frameworks [10,11,12], however, have included all energy, environmental, and ecological efficiency elements.

To analyze energy, the environment, and eco-efficiency or productivity, recent studies from both China and Europe have included GDP as the desirable output and CO₂ emissions as the undesirable output and have used static analyses, dynamic analyses, or Meta-frontier DEA (Data Envelopment Analysis) methods to assess energy efficiency. Three main static analyses have been used to assess energy efficiency, including; Charnes, Cooper, Rhodes (CCR), Banker, Charnes, Cooper (BCC), and radial methods [13]; Slack-Based Measures method [14,15,16]; and direction distance function methods [17,18,19]. There are also three main dynamic energy efficiency analysis methods; Window analysis [20]; the Malmquist Productivity Index [21,22,23], and Dynamic SBM models [24]. In some cases, both dynamic and static methods have been used to compare energy [25]. For the Meta-Frontier Method, dynamic meta-frontiers [26], Meta-Frontier non-radial directional distance functions [12,27,28], and Bootstrapped DEA Methods [29,30] have been used to measure energy efficiency and obtain accurate energy efficiency estimates.

To assess environmental efficiency, non-radial DEA methods [31,32,33], and Directional Distance Functions [34,35] have been used; however, only a few studies [13,28] have examined ecological efficiency.

Sulfur dioxide (SO₂) has been used as an environmental pollution measure in energy efficiency environmental evaluations in non-radial DEA models [36,37,38] and two stage methods [9,39,40]. In other studies, both SO₂ and NO₂ have been used as environmental pollution indicators [35,40,41]. However, only considering CO₂ as the undesirable output and ignoring other air pollutants such as PM_2.5, SO₂, and NO₂ can bias the energy, environmental, ecological efficiency and productivity analyses. Therefore, to analyze environmental energy efficiency, both CO₂ and SO₂ (or NO₂) need to be considered as undesirable outputs. Maximum Entropy methods [42], non-radial DEA models with both CO₂ and SO₂ as undesirable outputs [20,43,44] and dynamic DEA methods [45] have all been used to explore environmental efficiency.

Air pollutants can have a significant impact on economic costs; for example, in 2010, the health impact of PM₁₀ in Chinese cities was estimated at US 74 billion [46], which was equivalent to 1.3% of the GDP in that year. In 2013, the Chinese government developed an Air Pollution Control Action Plan, which highlighted air governance and economic development as an official government performance measure. As stated, only including CO₂ as the undesirable output and ignoring other undesirable air pollutants such as PM_2.5, SO₂, and NO₂ can lead to biased reports and poor policy advice. Another problem is that most DEA studies on urban efficiency have only been only at a national level, with few analyses on the efficiency in cities in different regions. Because China has large regional differences, different levels of economic development, and varying resource endowments, the same production technology standard cannot be used for all analyses, especially in the eastern and western regions. Therefore, it is necessary to compare and investigate urban efficiencies between regions to ensure more accurate policy recommendations.

The difference between this study and previous similar studies is that urban energy consumption, CO₂ emissions, and atmospheric environmental efficiencies are investigated and the economic development level endowment differences between cities in the eastern and western regions of China considered. To do this, this study employed a meta-frontier non-radial directional distance function to analyze regional energy, CO₂, the economy, and air quality index (AQI) efficiencies.

This study divided 31 Chinese cities into eastern and western regions and using data from 2013–2016 examined each city’s energy consumption, labor force, and fixed asset size as the input indicators, GDP as the desirable output, and CO₂ and AQI as the undesirable outputs.

The remainder of this paper is organized as follows: Section 2 presents the research method; Section 3 lists the empirical results and provides relevant discussions; and Section 4 gives the conclusions.

2. Materials and Methods

Data envelopment analysis (DEA), which is based on the Pareto Optimal solution concept, uses a linear programming method to evaluate the relative utility of Decision Making Units (DMUs), and is able to simultaneously measure the efficiency between multiple inputs and multiple outputs to determine a production efficiency frontier, calculate the DMU production position and the distance to the efficiency frontier, and assess the DMU efficiency value.

DEA was first proposed by Charnes et al. [47] as the CCR model, which was based on a constant return to scale hypothesis. Banker et al. [48] then relaxed the constant returns to scale hypothesis and developed a BCC model based on a variable return to scale assumption. The DEA method has been widely used for industrial efficiency analyses in the financial industry [49], the transportation industry [50], the service industry [51], and the manufacturing industry [52]. As environmental issues have become a greater public concern, applications have been developed [10,11] to measure energy and environmental efficiencies. However, many of these conventional research efficiency analyses have failed to include the undesirable outputs. To resolve the problems associated with the application of undesirable outputs in the DEA model, a radial directional output distance function was proposed [53,54] based on an extension of the output distance function concept in Shephard [55]. The advantage of the radial directional output distance function is that it allows the DMU to simultaneously adjust the factor inputs and output and therefore can be adjusted to increase the desired output and reduce the undesirable output.

However, these radial efficiency models have tended to ignore the variances in the variables, which can lead to estimation errors. To overcome these defects, Fare et al. [56] developed a non-radial directional distance function, which proved superior to other methods as it had more reasonable, more accurate estimation results. Consequently, non-radial directional distance functions have been applied to energy and environmental efficiency analyses [17,57,58,59].

2.1. Environmental Production Technology

Assume that N cities use three inputs; capital (K), labor (L), and energy consumption (E); to produce one desirable output; gross domestic production (Y); and two undesirable outputs; CO₂ emissions (C), and the AQI (A) (please refer to the AQI calculations in Section 2.5 for detail). The production technology set (T) is defined below [60,61,62,63].

T = {(K, L, E, Y, C, A): (K, L, E) can produce (Y, C, A)}

(1)

The production technology follows standard production theory axioms [60]. Here, T is assumed to be a closed, bounded set with finite inputs that produces finite outputs. To model the joint-production technology, T is assumed to have weak disposability and null-jointness properties.

2.2. Non-Radial Directional Distance Functions

Suppose that there is an N-dimensional DMU set denoted r_i where DMU_o represents the DMU under evaluation and DMU_o ∈ N. The inputs and outputs are defined as $x\in R_{+}^m$, with the inputs producing the desirable output Y $\in R_{+}^s$ and the undesirable output Z $\in R_{+}^j$. Following [17,59,60], the non-radial directional distance function can be expressed as:

$$\begin{gathered} D\left(X^m,Y^s,Z^j;g\right)=\max w_m^x{\theta }_m^x+w_s^y{\theta }_s^y+w_j^z{\theta }_j^z \\ s.t.\hspace{1em}{\displaystyle \sum _{n=1}^N{\lambda }_n{x}_{mn}}\le x_m-{\theta }_m^x{g}_{xm}, m=1,\dots ,M, \\ {\displaystyle \sum _{n=1}^N{\lambda }_n{y}_{sn}}\le y_s-{\theta }_s^y{g}_{ys}, s=1,\dots ,S, \\ {\displaystyle \sum _{n=1}^N{\lambda }_n{Z}_{jn}}\le Z_j-{\theta }_j^z{g}_{zj}, j=1,\dots ,J, \\ {\theta }_m^x,{\theta }_s^y,{\theta }_j^z\ge 0 \end{gathered}$$

(2)

where, λ_n is an intensity variable, w = $\left(w_m^x,w_s^y,w_j^z\right)$ denotes a weight vector, g = $\left(-g_x,g_y,-g_z\right)$ denotes an explicit directional vector, and θ = $\left({\theta }_m^x,{\theta }_s^y,{\theta }_j^z\right)$ denotes a scale vector.

2.3. Meta-Frontier Non-Radial Directional Distance Function

To investigate the technological gap between the eastern and western regions, this paper considers these different groups to be different regions. Two types of frontier technologies are also defined; a meta-frontier non-radial directional distance function and a group-frontier non-radial directional distance function. As proposed in [60,61,62,63] the technical efficiency (TEE) for the different groups can be compared using a meta-frontier model. Suppose there are technological heterogeneities between H groups. The N DMUs can be separated into H subgroups based on their production technologies; therefore, the number of DMUs in the $h$-th group is $N^h$, and ${\displaystyle \sum _{h=1}^H{N}^h}=N$. Each subgroup has own specific production technology, with the DMUs belonging to the same subgroups having a homogeneous technology level under the group frontier.

$T^h$ and $T^m$ are assumed to be the production technology set for the $h$-th group under the group and meta-frontiers, with $T^m=\left\{T^1\cup T^2\cdots T^H\right\}$ satisfying the over-arching requirement.

Following [63], the group-frontier non-radial directional distance function for group h is defined based on Equation (2) and the group-frontier (GFE) technical efficiency is determined by solving Equation (2).

Unlike the group-frontier technology, meta-frontier technologies are based on all observations between the groups. As in [17,56,57], the value for $D\left(X^m,Y^s,Z^j;g\right)$ is determined after solving the following DEA model (Equation (3)). The technical efficiency of the meta-frontier (MFE) is also determined by solving Equation (3).

$$\begin{gathered} D\left(X^m,Y^s,Z^j;g\right)=\max w_m^x{\theta }_m^x+w_s^y{\theta }_s^y+w_j^z{\theta }_j^z \\ s.t. {\displaystyle \sum _{h=1}^H{\displaystyle \sum _{n=1}^N{\lambda }_n{x}_{mn}}\le x_m-{\theta }_m^x{g}_{xm}, m=1,\dots ,M,} \\ {\displaystyle \sum _{h=1}^H{\displaystyle \sum _{n=1}^N{\lambda }_n{y}_{sn}}\le y_s-{\theta }_s^y{g}_{ys}, s=1,\dots ,S,} \\ {\displaystyle \sum _{h=1}^H{\displaystyle \sum _{n=1}^N{\lambda }_n{Z}_{jn}}\le Z_j-{\theta }_j^z{g}_{zj}, j=1,\dots ,J,} \\ h=1\dots H {\theta }_m^x, {\theta }_s^y,{\theta }_j^z\ge 0 \end{gathered}$$

(3)

Technology Gap Ratio (TGR):

As the meta-frontier is an envelope curve for the group frontiers [62,63], $T^h$ is a sub-set of $T^m$ ($T^h\subseteq T^m$); therefore, the technical efficiency of the meta-frontier (MFE) is less than the technical efficiency of the group frontier (GFE). This so-called technical gap ratio (TGR) is:

TGR = MFE/GFE

(4)

If TGR is equal to unity, the region is considered efficient for the group technology set production process (the meta-technology set); if the TGR is less than unity, the region is considered inefficient.

2.4. Urban Energy Environmental, CO₂, AQI, and GDP Efficiencies

As in the total-factor energy efficiency index used in [64], there are four key features included in this present study: energy environmental efficiency, CO₂ efficiency, AQI efficiency, and GDP efficiency. In this study, “i” represents the area and “t” represents time. The four efficiency models are defined in the following:

$$\mathrm{Energy} \mathrm{environmental} \mathrm{efficiency} = \frac{\mathrm{Target} \mathrm{energy} \mathrm{input} \left(\mathrm{i}, \mathrm{t}\right)}{\mathrm{Actual} \mathrm{energy} \mathrm{input} \left(\mathrm{i}, \mathrm{t}\right)}$$

$${\mathrm{CO}}_2 \mathrm{efficiency} = \frac{\mathrm{Target} c{o}_2 \mathrm{Undesirable} \mathrm{output} \left(\mathrm{i}, \mathrm{t}\right)}{\mathrm{Actual} c{o}_2 \mathrm{Undesirable} \mathrm{output} \left(\mathrm{i}, \mathrm{t}\right)}$$

$$\mathrm{AQI} \mathrm{efficiency} = \frac{\mathrm{Target} \mathrm{AQI} \mathrm{Undesirable} \mathrm{output} \left(\mathrm{i}, \mathrm{t}\right)}{\mathrm{Actual} \mathrm{AQI} \mathrm{Undesirable} \mathrm{output} \left(\mathrm{i}, \mathrm{t}\right)}$$

$$\mathrm{GDP} \mathrm{efficiency} = \frac{\mathrm{Actual} \mathrm{GDP} \mathrm{desirable} \mathrm{output} \left(\mathrm{i}, \mathrm{t}\right)}{\mathrm{Target} \mathrm{GDP} \mathrm{desirable} \mathrm{output} \left(\mathrm{i}, \mathrm{t}\right)}$$

If the target energy input equals the actual input and the CO₂ and AQI undesirable outputs equal the actual undesirable outputs, then the environmental energy, CO₂, and AQI efficiencies equal 1, indicating overall efficiency. If the target energy input is less than the actual input and the CO₂ and AQI undesirable outputs are less than the actual undesirable outputs, then the environmental energy, CO₂, and AQI efficiencies are less than 1, indicating overall inefficiency.

If the target GDP desirable output is equal to the actual GDP desirable output, then the GDP efficiency equals 1, indicating overall efficiency. If the actual GDP desirable output is less than the target GDP desirable output, then the GDP efficiency is less than 1, indicating overall inefficiency.

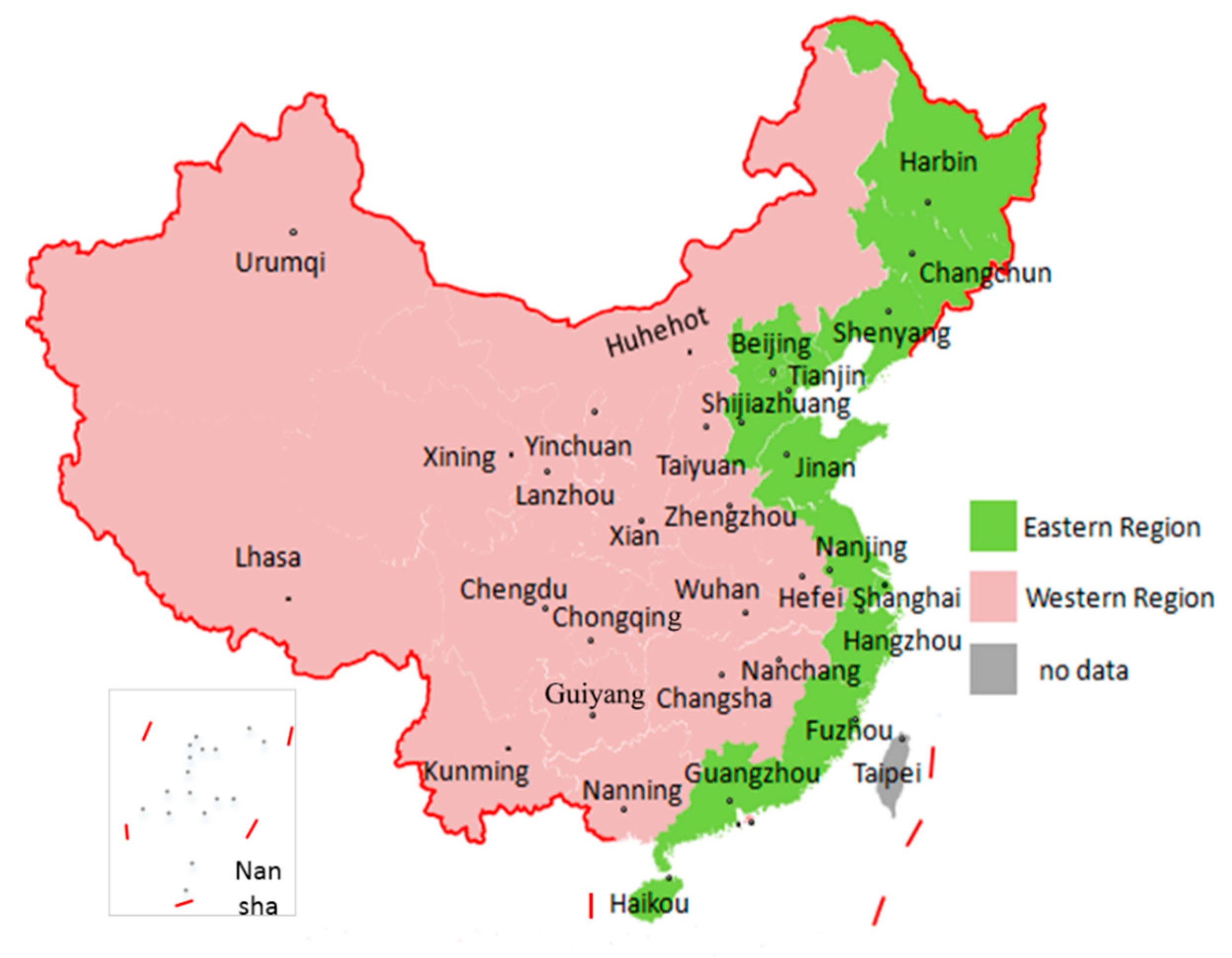
2.5. Data and Variables

This study used 2013 to 2016 panel data for 31 of the most developed cities in eastern and western China. Data were collected from the Statistical Yearbook of China [65] and the Demographics and Employment Statistical Yearbooks of China [66] from all cities. Air pollutant data were collected from China’s Environmental and Protection Bureau reports [67]. The variables used in the analysis are listed in the following.

2.5.1. Input Variables

Labor input: Number of employees in each city at the end of each year: unit = 1000 persons.

Capital input: Capital stock in each city calculated from the fixed assets in each city: unit = 100 million CNY (Chinese Yuan).

Energy consumed: Calculated according to each city’s total energy consumption: unit = 100 million tonnes. The energy consumption data were taken from China’s Environmental and Protection Bureau reports from 2014 to 2017 [67]. The total energy consumption unit was 10,000 tonnes of standard coal. From the statistical yearbook [65] data from each city, the energy consumption per unit of GDP by region and the unit GDP in each city were used to calculate the total energy consumption in each city, and included coal, oil, natural gas, and the total consumption of primary electricity and other energy.

2.5.2. Output Variable

Desired output: The GDP in each city was the output: 100 million CNY. The GDP data in each provincial capital were derived from the GDP stated in each province’s statistical yearbook for the given period [65], which consisted of the gross output for the primary, secondary, and tertiary industries calculated at current prices: unit: 100 million CNY.

2.5.3. Undesirable Output Variables

(A) Air quality index (AQI) data were based on the impact of the ambient air quality standards and various pollutants on human health, the ecology, and the environment, with the concentration of several routinely monitored air pollutants being simplified into a single conceptual index. In accordance with China’s environmental protection standards [67], the AQI represents the short-term air quality conditions and trends in each city. The main pollutants involved in the air quality assessment were fine particles, inhalable particles, sulfur dioxide, nitrogen dioxide, ozone, and carbon monoxide.

Based on China’s environmental protection standards [67], the AQI calculation and evaluation processes were as follows:

Step 1:

To compare the concentration limits of the various pollutants; the fine particulate matter (PM_2.5), inhalable particulate matter (PM₁₀), sulfur dioxide (SO₂), nitrogen dioxide (NO₂), ozone (O₃), carbon monoxide (CO₂) and other measured concentration values (including PM_2.5, PM₁₀ by 24 h average concentration) were calculated separately for the Air Quality Index (Individual Air Quality Index, referred to as IAQI).

Step 2:

To select the maximum value from the IAQI for each pollutant and determine its AQI; if the AQI was greater than 50, the largest IAQI pollutant was identified as the primary pollutant.

Step 3:

To establish the AQI grading standard air quality level, type, color, health impact and recommended actions were determined.

In short, the AQI was considered the maximum value for the Individual air quality index (IAQI) for each pollutant. When the AQI was greater than 50, the corresponding pollutant was the primary pollutant, with pollutants with an IAQI greater than 100 being considered excessive.

(B) The CO₂ emissions data for each city were estimated from the energy consumption. CO₂ emissions have been recognized as the primary cause of changing global temperatures and rising sea levels. In the past 100 years, global temperatures have risen by 0.6 °C, and it is estimated that by the middle of the 21st century, global temperatures will have increased by 1.5–4.5 °C and sea levels will have risen by 14 cm. As sea levels rise, the Amazon rainforest is expected to disappear, and the Antarctic and Arctic Ocean ice caps are expected to melt. Air generally contains about 0.03% of CO₂; however, due to human activities (such as the burning of fossil fuels), the CO₂ content has risen dramatically since the beginning of the industrial revolution, which has resulted in global warming, melting glaciers, and rising sea levels. Due to the above characteristics, CO₂, unlike other air pollutants, is used as the sole carbon emissions measure and the main measurement for global solutions to climate change.

This study divided the 31 sample cities into two regions: western region cities (18 in total); Chengdu, Changsha, Chongqing, Guiyang, Hefei, Huhehot, Kunming, Lanzhou, Lhasa, Nanchang, Nanning, Taiyuan, Wuhan, Urumqi, Xian, Xining, Yinchuan, and Zhengzhou; and eastern region cities (13 in total); Beijing, Changchun, Fuzhou, Guangzhou, Harbin, Haikou, Hangzhou, Jinan, Nanjing, Shanghai, Shenyang, Shijiazhuang, and Tianjin (see Figure 1).

3. Results and Discussion

3.1. Input-Output Index Statistical Analyses

Figure 2 compares the input and output indicators for the western and eastern Chinese cities. The employment, fixed asset, energy consumption, GDP, AQI and CO₂ indicators clearly show that the average value for employment, fixed asset investment, and energy consumption in the eastern cities was greater than the average value in the western cities, and that the GDP, CO₂ and AQI values were lower.

The employment growth rate in the eastern cities in 2013 was slightly higher than in the western cities, but from 2014, while the rate in the eastern cities began to slowly decline, the rate in the western cities began to grow, reflecting the continued development.

Both the eastern and western cities had a downward trend in energy consumption, with the eastern cities’ energy consumption declining faster than in the western cities. While fixed assets investment in both the western and eastern cities had declining growth rates, the decline was greater in the eastern than the western cities. The average GDP growth rate however, was similar in both the eastern and western regions; overall, however, the average GDP growth rate in the eastern cities was lower, reflecting their more developed status.

The average CO₂ emissions in the eastern cities dropped by about 0.3% from 2013 to 2014, and from 2014 to 2015, the average CO₂ emissions in the eastern cities declined more rapidly than those in the western cities. The average CO₂ emissions in the western cities were rising slowly from 2013 to 2014, but began to decline from 2014 to 2016, and from 2015 to 2016, the average CO₂ emissions in the western cities had a greater decline than in the eastern cities.

While in the eastern cities and western cities the average AQI was similar, it was initially slightly higher in the eastern cities; however, in 2016, the average AQI was higher in the western cities. The average AQI began to decline in the eastern cities from 2013 to 2014 and from 2014 to 2015, the average AQI decline in the western cities was slightly higher than in the eastern cities, but from 2015 to 2016, the decline in the eastern cities was greater than in the western cities, indicating that there was a greater average AQI improvement in the eastern cities than in the western cities.

3.2. Overall Efficiency Score Ranking from 2013–2016

Table 1. Overall efficiency score rankings between 2013 and 2016.

No.	DMU	2013		2014		2015		2016
		Score	Rank	Score	Rank	Score	Rank	Score	Rank
1	Chengdu	0.7777	24	0.788	24	0.7996	21	0.762	26
2	Changsha	0.9183	10	0.9233	9	0.934	9	0.945	10
3	Chongqing	0.7496	26	0.8102	21	0.7915	23	0.803	22
4	Guiyang	0.676	30	0.7556	27	0.7909	24	0.789	24
5	Hefei	0.8554	19	0.8607	18	0.8601	18	0.821	21
6	Huhehot	0.9113	12	0.9039	12	0.9123	11	0.904	12
7	Kunming	0.9999	6	0.8432	19	0.8583	19	0.842	20
8	Lanzhou	0.7302	28	0.6511	29	0.6705	30	0.667	30
9	Lhasa	1	1	1	1	1	1	1	1
10	Nanchang	0.9191	9	0.917	10	0.9001	13	0.874	16
11	Nanning	1	1	1	1	1	1	1	1
12	Taiyuan	0.6855	29	0.7027	28	0.7009	28	0.729	28
13	Wuhan	0.8564	18	0.8708	16	0.874	17	0.89	14
14	Urumqi	0.8185	21	0.7761	25	0.7855	25	0.784	25
15	Xian	0.7769	25	0.7886	23	0.7699	27	0.734	27
16	Xining	0.737	27	0.6407	30	0.686	29	0.709	29
17	Yinchuan	0.7817	23	0.7641	26	0.7754	26	0.791	23
18	Zhengzhou	0.9435	8	0.9407	8	0.9678	7	0.852	18
19	Beijing	1	1	1	1	1	1	1	1
20	Changchun	0.9016	14	0.8941	14	0.9117	12	0.882	15
21	Fuzhou	0.9882	7	0.864	17	0.8799	16	0.861	17
22	Guangzhou	1	1	1	1	1	1	1	1
23	Harbin	0.8983	15	0.8838	15	0.8887	15	0.848	19
24	Haikou	0.8933	16	1	1	0.9999	6	1	8
25	Hangzhou	0.8929	17	0.9031	13	0.9163	10	0.934	11
26	Jinan	0.7864	22	0.7959	22	0.7967	22	1	1
27	Nanjing	0.9133	11	0.9666	7	0.9462	8	0.963	9
28	Shanghai	1	1	1	1	1	1	1	1
29	Shenyang	0.8245	20	0.8353	20	0.8042	20	1	1
30	Shijiazhuang	0.5708	31	0.5588	31	0.5825	31	0.574	31
31	Tianjin	0.9091	13	0.9096	11	0.893	14	0.902	13

shows the efficiency scores and rankings for each city from 2013 to 2016. The total efficiency score for five cities was 1 for four consecutive years, indicating that these cities were efficient. The cities with poor efficiency scores and declining rankings were; Kunming, which ranked 6th in efficiency in 2013, but dropped to 19th between 2014 to 2016; Nanchang ranked 9th in 2013 with a score of 0.92 but dropped to 16th with a score of 0.87 in 2016; Zhengzhou, which was ranked 8th from 2013 to 2015, was ranked 18th in 2016 as the efficiency declined sharply to 0.85. The other cities with declining scores and rankings were Harbin, Hefei, Nanjing, Wuhan, Urumqi, Xian, and Xining. The cities that improved their efficiency scores and rankings were; Jinan, which had the highest efficiency score increase from 0.78 in 2013 to 1 in 2016; Shenyang, where the efficiency score rose from 0.82 in 2013 to 1 in 2016; Hangzhou, which had an efficiency score of 0.89 in 2013 and was ranked 17th, raised its score to 0.93 and a rank of 11th; and Guiyang, which had an efficiency score of 0.67 in 2013 and was ranked 30th, improved to 0.79 in 2016 and was ranked 24th.

A Wilcoxon signed rank was applied to further test the differences between the eastern and western region efficiencies. The p-values were compared with the confidence levels α, which were set at 0.01 and 0.05 to assess the distinctions between the average efficiency in the two regional groups.

Table 2. Wilcoxon signed rank Test of average Technical efficiency.

Years	Average of Eastern	Average of Western	Wilcoxon Scorer Test
2013	0.8907	0.8409	0.1011
2014	0.8932	0.8298	0.0454 *
2015	0.8938	0.8376	0.0422 *
2016	0.9203	0.8275	0.007 **

Notes: * For the two-tailed test, the confidence interval 0.05was significant, ** For the two-tailed test, the confidence interval 0.01 was significant.

shows the detailed test results.

At a significance level of 5%, the eastern region efficiencies were significantly different from the western region efficiencies from 2014–2016; however, there were less differences in 2013.

3.3. Efficiency Scores and Rankings for Energy Consumption, GDP, CO₂, and AQI from 2013 to 2016.

Table 3. Efficiency scores and rankings for energy consumption, GDP, CO₂, and AQI in the cities from 2013 to 2016.

DMU	2013				2014				2015				2016
	com	GDP	CO2	AQI	com	GDP	CO2	AQI	com	GDP	CO2	AQI	com	GDP	CO2	AQI
Chengdu	0.778	0.818	0.715	0.786	0.714	0.825	0.788	0.692	0.8	0.8331	0.8	0.603	0.762	0.808	0.762	0.762
Changsha	0.657	0.924	0.198	0.116	0.664	0.929	0.203	0.121	0.665	0.938	0.195	0.192	0.656	0.948	0.177	0.022
Chongqing	0.75	0.8	0.757	0.75	0.742	0.84	0.618	0.81	0.791	0.8275	0.791	0.791	0.803	0.835	0.803	0.803
Guiyang	0.446	0.755	0.274	0.676	0.547	0.804	0.202	0.756	0.599	0.8271	0.513	0.791	0.63	0.826	0.324	0.789
Hefei	0.855	0.874	0.761	0.124	0.858	0.878	0.861	0.148	0.86	0.8773	0.86	0.235	0.821	0.848	0.808	0.821
Huhehot	0.384	0.919	0.32	0.302	0.748	0.912	0.101	0.158	0.725	0.9194	0.281	0.224	0.692	0.913	0.242	0.052
Kunming	1	1	0.929	1	0.489	0.864	0.148	0.843	0.664	0.8759	0.271	0.858	0.727	0.863	0.451	0.842
Lanzhou	0.32	0.788	0.125	0.73	0.358	0.741	0.183	0.768	0.302	0.7522	0.143	0.612	0.319	0.75	0.147	0.284
Lhasa	1	1	0.993	0.997	1	1	1	0.994	1	1	1	0.992	1	1	1	0.991
Nanchang	0.919	0.925	0.778	0.386	0.897	0.923	0.917	0.735	0.9	0.9092	0.9	0.553	0.874	0.888	0.842	0.874
Nanning	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
Taiyuan	0.164	0.761	0.101	0.739	0.185	0.771	0.1	0.344	0.176	0.7698	0.1	0.532	0.23	0.787	0.103	0.035
Wuhan	0.736	0.874	0.359	0.104	0.725	0.886	0.435	0.128	0.76	0.8881	0.464	0.167	0.747	0.901	0.359	0.011
Urumqi	0.653	0.846	0.383	0.212	0.652	0.817	0.332	0.135	0.699	0.8234	0.486	0.2	0.784	0.822	0.784	0.019
Xian	0.777	0.818	0.792	0.145	0.765	0.826	0.789	0.182	0.77	0.813	0.77	0.342	0.734	0.79	0.734	0.067
Xining	0.217	0.792	0.1	0.737	0.25	0.736	0.133	0.734	0.261	0.761	0.124	0.686	0.62	0.774	0.578	0.709
Yinchuan	0.37	0.821	0.116	0.716	0.34	0.809	0.134	0.722	0.275	0.8166	0.105	0.442	0.277	0.827	0.1	0.04
Zhengzhou	0.942	0.947	0.943	0.194	0.939	0.944	0.941	0.1	0.968	0.9688	0.968	0.1	0.852	0.871	0.852	0.079
Beijing	1	1	1	1	1	1	0.999	1	1	1	1	1	1	1	1	1
Changchun	0.872	0.91	0.902	0.427	0.894	0.904	0.716	0.181	0.912	0.9188	0.912	0.171	0.882	0.894	0.86	0.882
Fuzhou	0.988	0.988	0.717	0.988	0.696	0.88	0.391	0.864	0.716	0.8927	0.321	0.88	0.746	0.878	0.45	0.861
Guangzhou	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
Harbin	0.892	0.908	0.898	0.215	0.884	0.896	0.718	0.367	0.889	0.8999	0.889	0.205	0.848	0.868	0.844	0.848
Haikou	0.811	0.904	0.541	0.893	1	1	1	1	1	0.9999	1	1	1	1	1	1
Hangzhou	0.739	0.903	0.372	0.127	0.759	0.912	0.332	0.227	0.798	0.9227	0.447	0.201	0.804	0.938	0.397	0.03
Jinan	0.518	0.824	0.192	0.129	0.525	0.83	0.195	0.109	0.555	0.8311	0.218	0.136	1	1	1	1
Nanjing	0.643	0.92	0.171	0.1	0.601	0.968	0.157	0.967	0.885	0.9489	0.869	0.178	0.862	0.964	0.511	0.02
Shanghai	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
Shenyang	0.64	0.851	0.316	0.216	0.644	0.859	0.249	0.835	0.64	0.8363	0.321	0.198	1	1	1	1
Shijiazhuang	0.39	0.7	0.339	0.168	0.41	0.694	0.299	0.197	0.368	0.7055	0.582	0.465	0.388	0.701	0.276	0.029
Tianjin	0.708	0.917	0.25	0.227	0.719	0.917	0.288	0.111	0.709	0.9033	0.286	0.149	0.713	0.91	0.273	0.01

lists the energy consumption and GDP efficiency scores for each city, from which it can be seen that there were large CO₂ and AQI efficiency score differences between 2013 and 2016. While some cities had obviously lower CO₂ efficiency scores and higher AQI efficiency scores, the AQI efficiency scores in most cities rose over time. For example, the cities with an AQI efficiency of 1 were Beijing, Guangzhou, Haikou, Nanning, and Shanghai, with Lhasa being close to 1. The cities with AQI efficiency scores below 0.4 were Changsha, Hangzhou, Tianjin, Wuhan, Urumqi, and Zhengzhou, indicating that air pollution improvements were necessary.

As can be seen from Table 3, the CO₂ efficiency scores in the different cities differed considerably. Beijing, Guangzhou, Haikou, Nanning, and Shanghai had CO₂ emissions efficiencies of 1 and Lhasa at 0.993 was very close to 1 in 2013 and 1 in 2016. The CO₂ emissions efficiency scores in the other cities varied greatly, clearly showing that different efficiency improvements were needed. Changsha, Lanzhou, Taiyuan, Xining, and Yinchuan had CO₂ emissions efficiency scores below 0.2, and in Taiyuan in particular, the CO₂ efficiency score was under 0.2 in the whole examined period. The CO₂ efficiency scores in Changsha and Yinchuan declined over time, indicating that greater improvement efforts were needed. Fuzhou, Guiyang, Hangzhou, Huhehot, Kunming, Nanjing, Shenyang, Tianjin, Wuhan, and Xining had CO₂ efficiency scores between 0.2 and 0.4, and Chengdu, Changchun, Chongqing, Harbin, Nanchang, and Xian had efficiency scores of around 0.8. The AQI efficiency score and the CO₂ efficiency scores also varied widely. Except for Beijing, Guangzhou, Nanning, and Shenyang, which had AQI efficiency scores of 1 (Figure 2), in the other cities the differences between these two efficiency indicators were relatively large. Haikou’s AQI efficiency score was 0.89 in 2013 and 1 from 2014 to 2016. Changchun, Changsha, Hangzhou, Hefei, Jinan, Nanjing, Tianjin, Wuhan, Urumqi, and Zhengzhou Cities had AQI efficiency scores below 0.2 from 2013 to 2016, and Changsha, Wuhan, Zhengzhou, Tianjin, and Urumqi had efficiency scores at or below 0.2. Therefore, large AQI efficiency improvements are needed in these cities as the effect of the governance measures was not obvious.

The efficiencies in Changchun, Hefei, Huhehot, Jinan, Shijiazhuang, and Xian changed significantly over time. By 2016, the AQI efficiency scores had risen above 0.6 to around 0.8, indicating that in 2016, AQI governance in these cities was achieving positive results. Chengdu, Chongqing, Guiyang, Lanzhou, and Xining had efficiency scores between 0.6–0.8.

There were wide variations in the CO₂ and AQI efficiency scores between and within the different cities. For example, there was a large difference between the CO₂ and AQI efficiency scores in Zhengzhou because of poor AQI governance and control and while there were small CO₂ emissions efficiency improvements up to 2016, after this time, the CO₂ efficiency began to decline. In Yinchuan, the AQI scores were mostly between 0.6 and 0.8, but there was also poor control of the CO₂ emissions. Lanzhou’s AQI efficiency score was also noticeably higher than its CO₂ efficiency score, indicating that governance should be focused on CO₂ emissions. A similar situation was observed in Kunming, Guiyang, Fuzhou, and Taiyuan. However, even though Taiyuan’s AQI efficiency score was higher than its CO₂ efficiency score, it was still low and therefore focused improvements are needed in both areas. This was also true for Changsha, Hangzhou, Huhehot, Jinan, Nanjing, Shenyang, Shijiazhuang, Wuhan, Tianjin, and Urumqi.

As can be seen from Table 3, there were large differences in the energy consumption and GDP efficiency scores between the cities. Overall, effective energy consumption and economic growth were observed in Beijing, Guangzhou, Lhasa, Nanning, and Shanghai, all of which had efficiency scores of 1. Overall, the GDP in most other cities had an upward trend; however, the GDP efficiency scores dropped in 2016 in Chengdu, Changchun, Fuzhou, Guiyang, Harbin, Hefei, Nanchang, Shijiazhuang, Zhengzhou, and Xian.

Compared to the GDP efficiency scores, the energy consumption scores were lower and the gap between the cities greater. Changchun, Harbin, Hefei, Nanchang, and Zhengzhou had energy consumption efficiencies between 0.8 and 1, but Lanzhou, Taiyuan, Shijiazhuang, Xining, and Yinchuan had energy consumption efficiencies below 0.4. Guiyang, Lanzhou, Shijiazhuang, Taiyuan, Xining, and Yinchuan all needed to improve their energy consumption, GDP, and CO₂ emissions efficiencies.

3.4. Comparison of Meta-Frontier and Group Frontiers

Table 4. Comparison of the meta frontier and group frontier city rankings (2013–2016).

DMU	2013 Rank by Meta-Frontier	2013 Rank by Group-Frontier	2014 Rank by Meta-Frontier	2014 Rank by Group-Frontier	2015 Rank by Meta-Frontier	2015 Rank by Group-Frontier	2016 Rank by Meta-Frontier	2016 Rank by Group-Frontier
Chengdu	29	1	28	1	30	1	31	1
Changsha	18	1	12	1	15	1	15	1
Chongqing	31	1	26	1	31	1	28	1
Guiyang	28	17	25	14	28	11	26	11
Hefei	19	12	17	12	21	12	23	13
Huhehot	20	1	19	1	18	1	18	1
Kunming	7	1	23	1	9	1	24	1
Lanzhou	27	13	30	16	29	17	25	17
Lhasa	1	1	1	1	1	1	1	1
Nanchang	14	11	16	1	20	1	21	1
Nanning	1	1	1	1	1	1	1	1
Taiyuan	30	14	31	1	27	15	29	15
Wuhan	25	1	22	1	23	1	19	1
Urumqi	26	1	29	1	24	13	27	12
Xian	23	15	21	15	26	14	30	14
Xining	24	18	27	18	25	18	20	18
Yinchuan	17	16	18	17	17	16	16	16
Zhengzhou	12	1	11	1	10	1	22	1
Beijing	1	1	1	1	1	1	1	1
Changchun	13	7	14	5	19	1	11	10
Fuzhou	8	6	1	8	1	10	1	12
Guangzhou	1	1	1	1	1	1	1	1
Harbin	21	1	20	1	22	1	14	11
Haikou	22	1	1	1	8	1	10	1
Hangzhou	9	9	10	6	11	8	12	8
Jinan	16	12	13	9	16	11	1	1
Nanjing	10	8	9	1	12	7	13	7
Shanghai	1	1	1	1	1	1	1	1
Shenyang	11	11	24	1	14	12	1	1
Shijiazhuang	15	13	15	10	13	13	17	13
Tianjin	1	10	8	7	1	9	1	9

illustrates the gaps in the meta-frontier and group frontier rankings from 2013 to 2016. No gap between the meta-frontier rankings and the group frontier rankings were found for Beijing, Guangzhou, Lhasa, Nanning, Shanghai, and some other cities. Chengdu, Chongqing, Guiyang, Lanzhou, Taiyuan, Urumqi, Xian, and Xining, all of which are in the western region, were nine of the ten cities with the largest group frontier and meta-frontier rankings.

Table 4 shows that in their own regions, cities were efficient. For example, Chongqing, Chengdu, Urumqi, and Wuhan were all ranked 1st in group efficiency; however, compared with the other cities in the country, there was a large gap. Other western cities also had large differences between the group frontier rankings and the meta-frontier rankings. For example, Huhehot and Zhengzhou rank 1st regionally, but 20th and 12th in comparison with the eastern cities, clearly indicating the gap that exists between western and eastern Chinese cities and the greater need for efficiency improvements in the west.

The gap between each city’s efficiency group frontier ranking and meta frontier ranking changed significantly each year. The difference between Chengdu’s efficiency ranking and the national ranking in 2013 was 29, in 2014 was 28, in 2015 was 30 and in 2016 was 31, which indicated that the gap between Chengdu’s efficiency ranking and the meta frontier ranking was widening in 2015 and 2016. Therefore, even though the improvements in the city’s efficiency were relatively good in comparison with other cities in the western region, there were still significant improvements needed to be in line with the eastern cities.

In most cities the improvement gap narrowed over time. For example, Fuzhou, moved from 8th in 2013 to 1st, Harbin increased 7 ranks, Haikou rose 12 ranks from 22nd to 10th, Jinan jumped from 16th to 1st, Shenyang went from 11th to 1st, and Wuhan rose from 25th to 19th.

However, Kunming, Zhengzhou, Xian, Nanchang, Hefei and some other cities. most of which were in the western region, saw a rise in their efficiency gap. For example, Kunming’s gap widened the most from 7th in 2013 to 24th in 2016 and Zhengzhou widened from 12th in 2013 to 22nd in 2016. The regional rankings also indicated that some cities such as Fuzhou had a greater rank gap than their efficiency ranking.

In Figure 3, it can be seen that the efficiency gap in some cities in the eastern region and especially in the economically developed capital cities in the coastal areas was 0, while there were still relatively large gaps in the few underdeveloped cities in the east. The efficiency of the provincial capital cities in the western region was generally lower than in the eastern cities, and there was a relatively continuous gap in the overall efficiency.

From Figure 4, an obvious efficiency gap between the eastern and western regions can be seen. The average gap for the eastern cities was less than in the western cities, and over time, this gap continued to widen. In 2016, while the efficiency in the eastern cities was increasing, the efficiency in the western cities was declining, further widening the gap between the two regions.

A Wilcoxon signed rank Test was applied to further test the differences between the technological gap in the eastern and western regions.

Table 5. Wilcoxon signed rank Test of technology gap.

Years	Eastern	Western	Wilcoxon Scorer Test
2013	0.9561	0.8827	0.01 **
2014	0.9547	0.8669	0.005 **
2015	0.9655	0.8887	0.006 **
2016	0.9855	0.8641	0.0005 **

Notes: * For the two-tailed test, the confidence interval 0.05 was significant, ** For the two-tailed test, the confidence interval 0.01 was significant.

gives the detailed test results. At a 5% significance level, from 2013–2016, the technological gap in the eastern region was significantly better than the technological gap in the western region.

3.5. Comparative Gaps between the CO₂ and AQI Efficiencies

Table 6. CO₂ and AQI gap analysis.

DMU	2013 Gap Rank (Not Including CO2)	2013 Gap Rank (Not Including AQI)	2014 Gap Rank (Not Including CO2)	2014 Gap Rank (Not Including AQI)	2015 Gap Rank (Not Including CO2)	2015 Gap Rank (Not Including AQI)	2016 Gap Rank (Not Including CO2)	2016 Gap Rank (Not Including AQI)
Chengdu	29	28	31	25	30	30	31	29
Changsha	18	17	12	11	14	12	15	10
Chongqing	31	31	26	29	31	31	28	31
Guiyang	28	27	25	26	27	25	26	17
Hefei	19	18	18	17	21	17	23	19
Huhehot	20	19	19	18	18	18	18	14
Kunming	7	30	23	31	9	28	24	25
Lanzhou	27	26	29	28	29	26	25	23
Lhasa	1	1	1	1	1	1	1	1
Nanchang	14	12	17	10	20	14	21	18
Nanning	1	1	1	1	1	1	1	30
Taiyuan	30	29	30	30	28	27	29	26
Wuhan	25	22	22	21	23	22	19	15
Urumqi	26	25	28	27	24	23	27	24
Xian	23	21	21	19	26	24	30	27
Xining	24	24	27	24	25	21	20	21
Yinchuan	17	16	16	16	16	16	16	11
Zhengzhou	12	11	11	9	10	7	22	20
Beijing	1	1	1	1	1	1	1	1
Changchun	13	13	14	14	19	19	11	13
Fuzhou	8	9	1	8	1	13	1	16
Guangzhou	1	1	1	1	1	1	1	1
Harbin	21	20	20	20	22	20	14	22
Haikou	22	23	7	22	8	29	10	28
Hangzhou	9	7	10	7	11	8	12	8
Jinan	16	15	13	12	15	15	1	1
Nanjing	10	8	9	13	12	9	13	9
Shanghai	1	1	1	1	1	1	1	1
Shenyang	11	10	24	23	13	11	1	1
Shijiazhuang	15	14	15	15	17	10	17	12
Tianjin	1	1	8	6	1	1	1	1

shows the differences in the gap rankings between the CO₂ and AQI efficiencies compared to the total efficiency in China. In most cities, there was a distinct gap found between the individual CO₂-only efficiency and the AQI-only efficiency; however, there was only a narrow efficiency gap between them. While in some cities, the efficiency gaps were expanding over time, in others, they were narrowing.

In 2013, there was little difference between the CO₂-only and AQI-only efficiency gaps in Haikou, which ranked 22nd and 23rd. In 2014, the CO₂-only efficiency ranking rose to 7th and in 2016 rose to 10th; however, the AQI-only efficiency gap ranking dropped to 29th in 2015 and then to 28th in 2016, which indicated that while Haikou was better than the other cities in terms of air pollution, its CO₂ emissions were more serious. Therefore, as one of the few cities with good air quality in China, Haikou should pay more attention to their CO₂ emissions.

While the large differences in the efficiency gaps in 2013 between the cities were affected by the CO₂ emissions and the AQI, the differences in influence expanded over time. In Nanchang, in 2014, the efficiency gap that excluded CO₂ ranked 17th and the efficiency gap that excluded AQI ranked 10th, in 2015, the efficiency gap that excluded CO₂ ranked 20th and the efficiency gap that excluded AQI ranked 14th, and in 2016, the performance worsened, with the efficiency gap that excluded CO₂ ranking 21st and the efficiency gap that excluded AQI ranking 18th. This indicated that compared with the other cities, Nanchang’s CO₂ emissions and air pollution were continuing to deteriorate.

Most efficiency gap rankings rose over time such as in Shenyang, Wuhan, Chongqing, and Changsha; however, in other cities such as Zhengzhou and Xian, the efficiency gap rankings dropped, indicating that the air pollution and CO₂ emissions were more serious than in the other cities, indicating that serious attention needs to be paid to strengthening governance. In Zhengzhou in 2013 the efficiency gap for both CO₂ and AQI ranked 12th and 13th, but in 2016, dropped to 20th. Overall, the total efficiency gap rankings in Nanchang, Nanjing, Haikou, Xian, Hefei, and Chengdu all dropped and there were large differences in the efficiency gaps between air pollution and CO₂.

4. Conclusions and Policy Recommendations

4.1. Conclusions

This study divided 31 cities in China into eastern and western regions to analyze and assess the 2013–2016 energy consumption, GDP, CO₂ and AQI efficiency scores, and determine the needed efficiency improvements. The empirical results were as follows.

The cities with low efficiency scores for both AQI and CO₂ were Changsha, Hangzhou, Huhehot, Jinan, Nanjing, Shenyang, Shijiazhuang, Tianjin, Wuhan, Urumqi, and Xian. The cities with AQI efficiency scores of 1 were Beijing, Guangzhou, Haikou, Nanning, and Shanghai. The cities with CO₂ efficiency scores of 1 were Beijing, Guangzhou, Haikou, Nanning, and Shanghai.

The calculation results for the meta-frontier method indicated that there was remained a large gap between the western and eastern cities. There were only small efficiency differences between the western cities, with many having efficiency scores of 1, which indicated that policies were being effective. However, nine of the ten cities with the largest gaps were located in the west and all had relatively high efficiency values. Compared with the other cities, the greatest gaps were in urban efficiency, where additional improvements are needed.

The efficiency scores between the different cities were not only different but also exhibited varying trends over time. The inter-regional comparison found that the differences between the western cities and the eastern cities were relatively small; however, when comparing the cities with the whole country, the differences between the eastern cities and the western cities were found to be relatively large. In some cities with large efficiency gaps, the gap had expanded over time, which tended to indicate that the efficiency gap was continuing to widen between the western and eastern cities.

4.2. Policy Recommendations

Based on the above results, the central government needs to delegate additional authority to local governments so that individual cities are able to formulate strategic approaches and targets in line with their specific efficiency indicators. Due to the large economic growth and social development differences between the eastern and western cities, the above findings also confirmed that there was a large and widening energy consumption and AQI and CO₂ efficiency score gap between the eastern and western cities, with the lower CO₂ and AQI efficiency scores mainly concentrated in the western region. Therefore, China needs to pay more attention to the differing economic levels, social development stages, industrial structures, energy structures, and technological development in the western cities and adopt systematic solutions based on local meteorological and climatic conditions, economic and social development, and population quality.

Cities that need to significantly alleviate their CO₂ emissions could refer to international green low-carbon development trends. As the Chinese government has highlighted low-carbon development as a major strategy for economic and social development and a sustainable ecology, effective measures must be implemented to control greenhouse gas emissions.

China also needs to speed up its domestic science and technological innovation by offering research and development incentives, giving full play to the market allocation of resources, having both central and local governments take leading roles, strengthening the synergetic control of CO₂ and air pollutant emissions, encouraging low carbon leadership, promoting energy structural reform and industrial upgrading, and initiating supply-side structural reforms and consumption-side transformations. China can also assist the coordinated development of the regions by participating in global climate governance, making additional contributions to sustainable economic and social development, and safeguarding global ecological security.

The 13th Five-Year Plan set a higher goal for CO₂ emissions reductions in China. By 2020, the target for CO₂ emissions per unit of GDP is planned to be 18% lower than in 2015, and total CO₂ emissions are expected to be effectively controlled. Efforts to control hydro-fluorocarbons, methane, nitrous oxide, per-fluorocarbon, sulfur hexafluoride, and other non-CO₂ greenhouse gas are to be further enhanced and carbon sink capacities expanded.

China is striving to hit a first peak in CO₂ emissions efficiency for some heavy and chemical industries by around 2020. The transformation to low-carbon energy systems, industrial systems, and consumer sectors is expected to yield positive results. A national carbon trading market has already started operations, and laws, regulations and a standards system for climate change issues have been established. Systems for statistical accounting, evaluation, and accountability are now complete, low-carbon pilot project demonstrations are increasing, the synergy between carbon and carbon reductions has been further strengthened, and the public’s low-carbon awareness has significantly improved. To achieve these goals, China needs to make positive energy and industrial restructuring, urbanization, and technological innovation moves.

For pollution prevention and control, some cities with low AQI efficiencies managed to achieve significant efficiency improvements in 2016, which is the result of the government’s determination in recent years to fight and control air pollution and to continuously improve the quality of the ecological environment. While the various governance measures taken are related, the air pollution sources are different from the CO₂ emissions sources. Therefore, the measures that need to be taken and the air pollution treatments are also different from those applied to CO₂ emissions.

We recommend that China pay more attention to governance in the following areas:

First, as the sources of atmospheric pollution are more complex and have regional differences, diagnoses of the atmospheric pollution causes would assist in its governance. Therefore, China should increase research investment in to the causes of the air pollution in different cities and regions and implement solutions through appropriate and focused governance measures.

Second, different geographical locations, meteorological conditions, industrial systems, economic development levels, population levels, and education levels in Chinese cities all influence atmospheric pollution governance. Therefore, power should be decentralized so that individual cities can determine their own city-specific or regional-specific governance measures to target air pollution prevention and control.

Third, as energy structure not only affects carbon emissions but also air pollution prevention, to help control CO₂ emissions and pollution, China must proactively adopt measures that assist in new energy development and application.

Fourth, in the short term, a better scientific use of traditional fossil energy is also an effective measure. As new energy cannot immediately replace traditional fossil energy, new and more effective technologies need to be implemented to increase the efficient, clean use of fossil energy. The re-use of fossil energy emissions could also raise the usage efficiency of traditional fossil energy and positively affect the AQI efficiency. Further, China can also continue to build effective public transport services to reduce the use of private cars and could produce motor vehicle emissions purification equipment to further reduce motor vehicle emissions.

Finally, China can strengthen the monitoring and supervision of illegal air pollution emissions, adhere to present legislation and law enforcement, and control unregulated emissions through the promulgation of new laws and regulations.