Optimal P-Q Control of Grid-Connected Inverters in a Microgrid Based on Adaptive Population Extremal Optimization
Abstract
1. Introduction
- (1)
- To the best of the authors’ knowledge, the adaptive population-based extremal optimization is applied firstly to the optimal P-Q control issue of three-phase grid-connected inverters in a microgrid.
- (2)
- The superiority of the proposed method is demonstrated by both the simulation and experimental results for a three-phase grid-connected inverter in a microgrid. In fact, the previous reported PSO-based P-Q control method [16] was tested only using its simulation results.
- (3)
- In cases of both nominal and variable reference active power values, the proposed APEO-based P-Q control method can improve the performance of a three-phase grid-connected inverter in a microgrid compared to the traditional Z-N empirical method, the adaptive GA-based, and the PSO-based P-Q control methods.
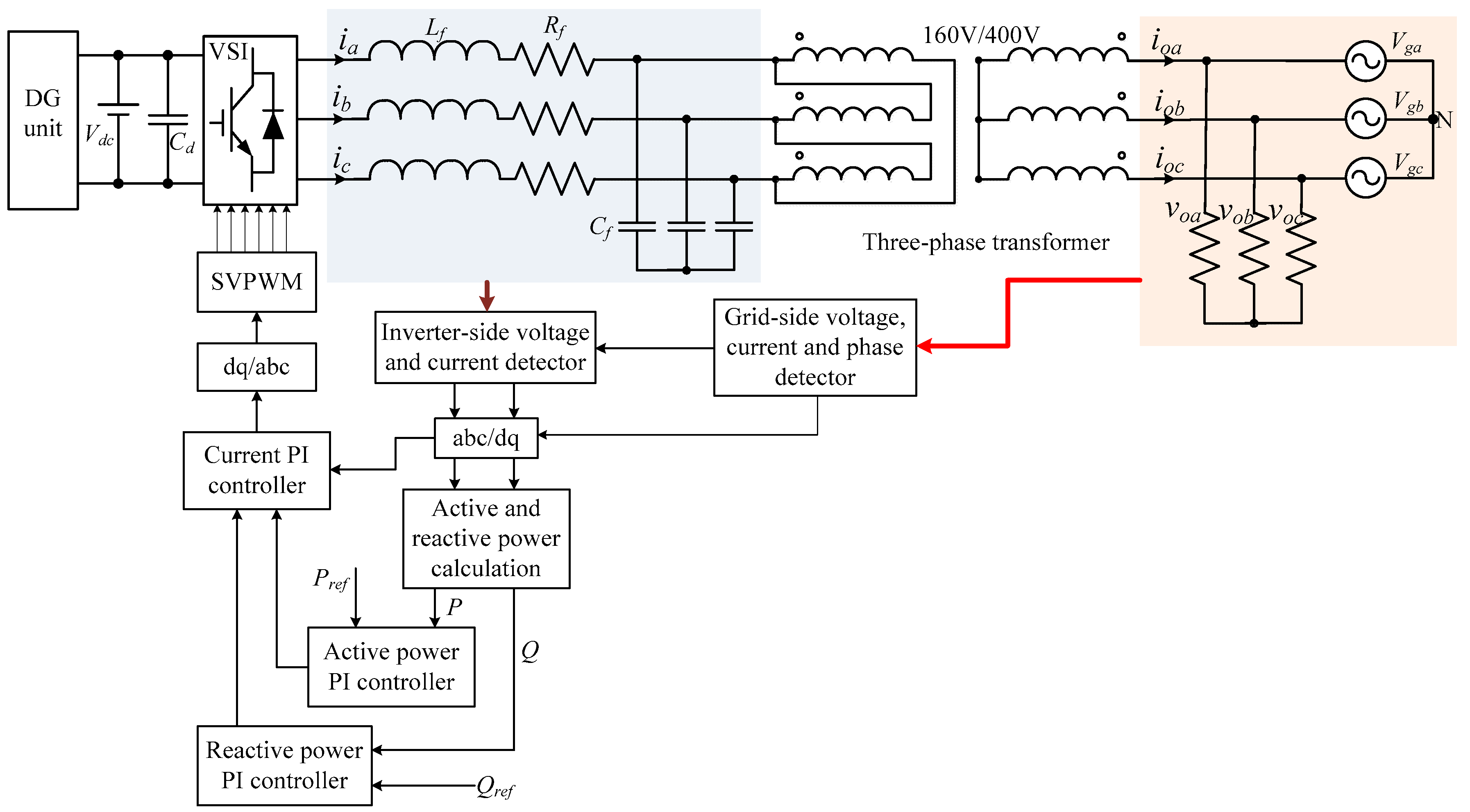
2. Problem Formulation
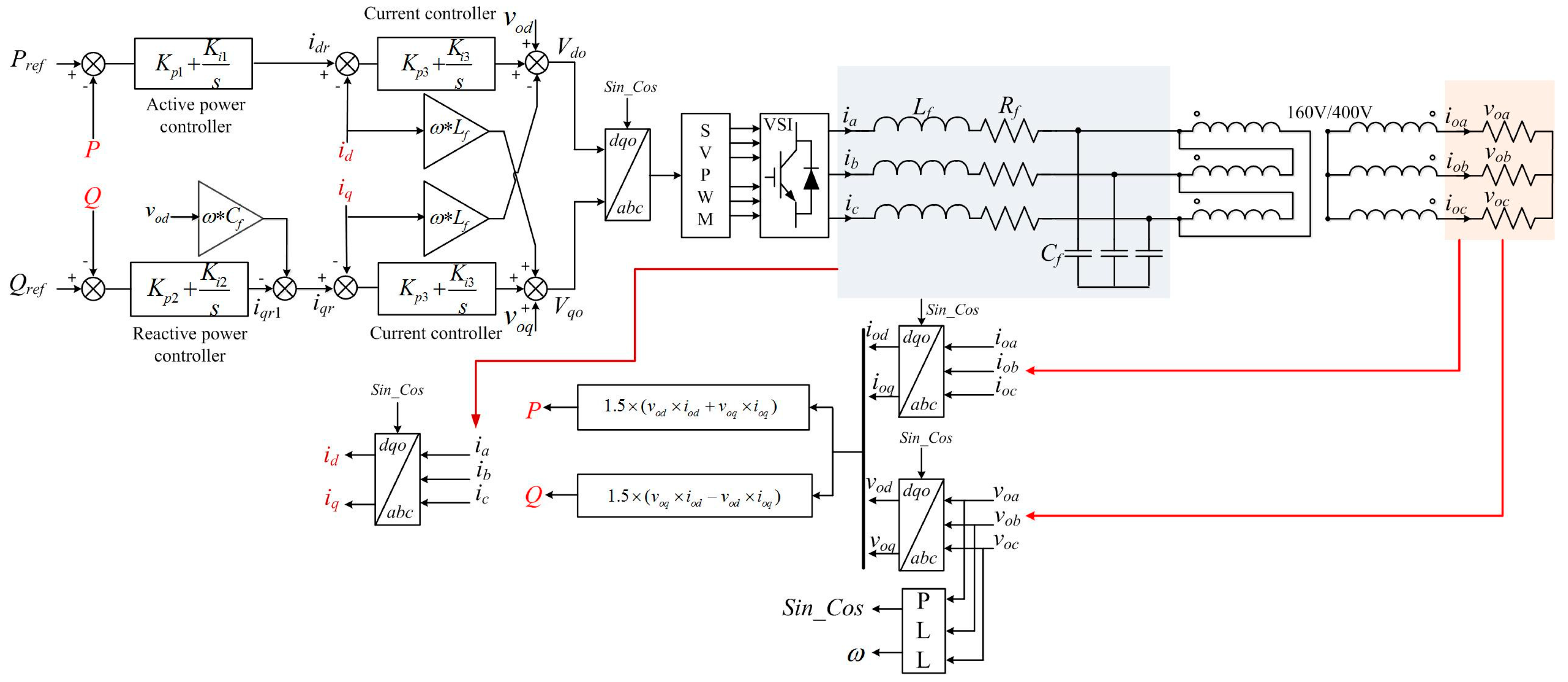
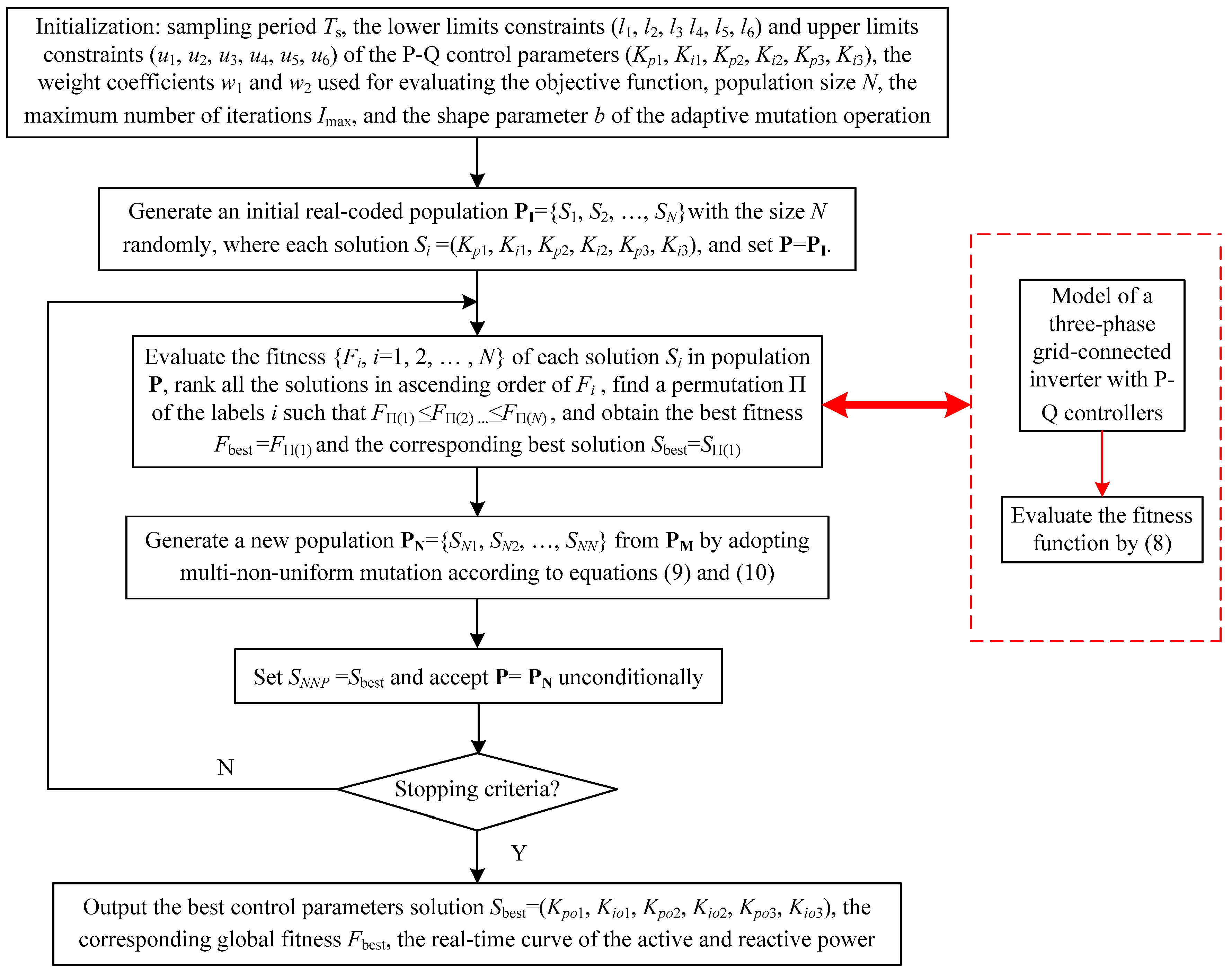
3. The Proposed Method
4. Simulation Results
4.1. Test for Benchmark Functions
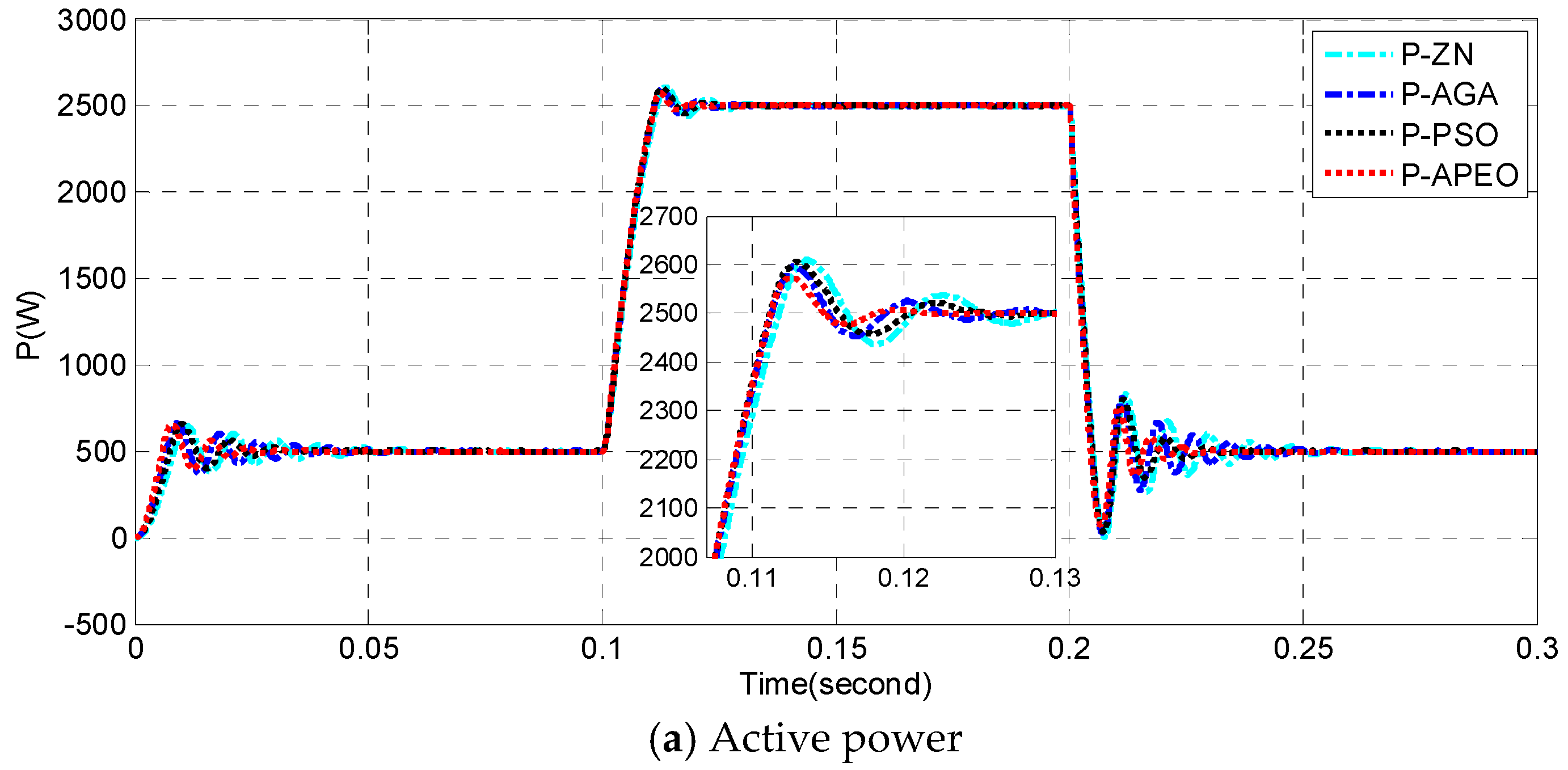
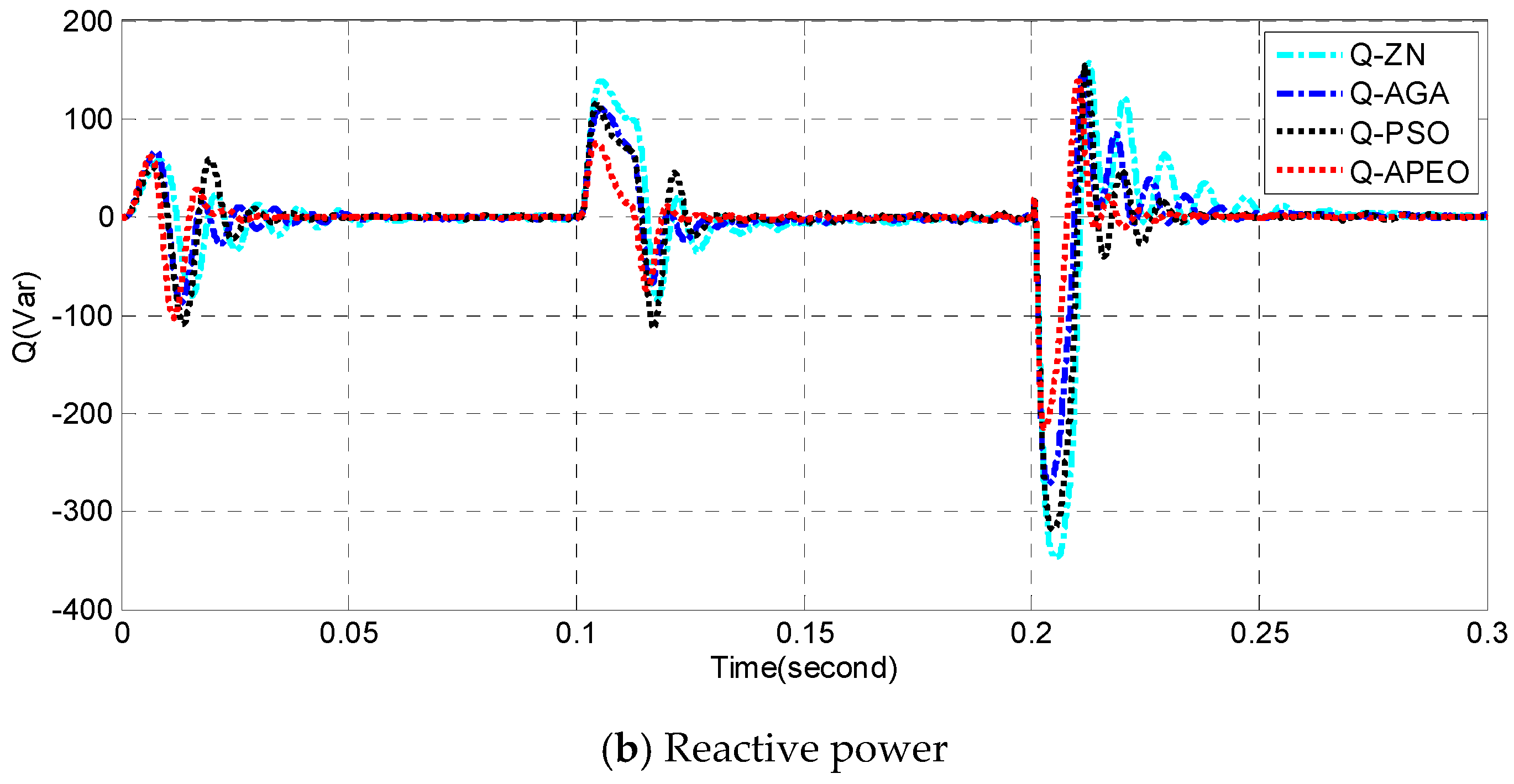
4.2. Simulation Study for P-Q Control of Three-Phase Grid-Connected Inverter
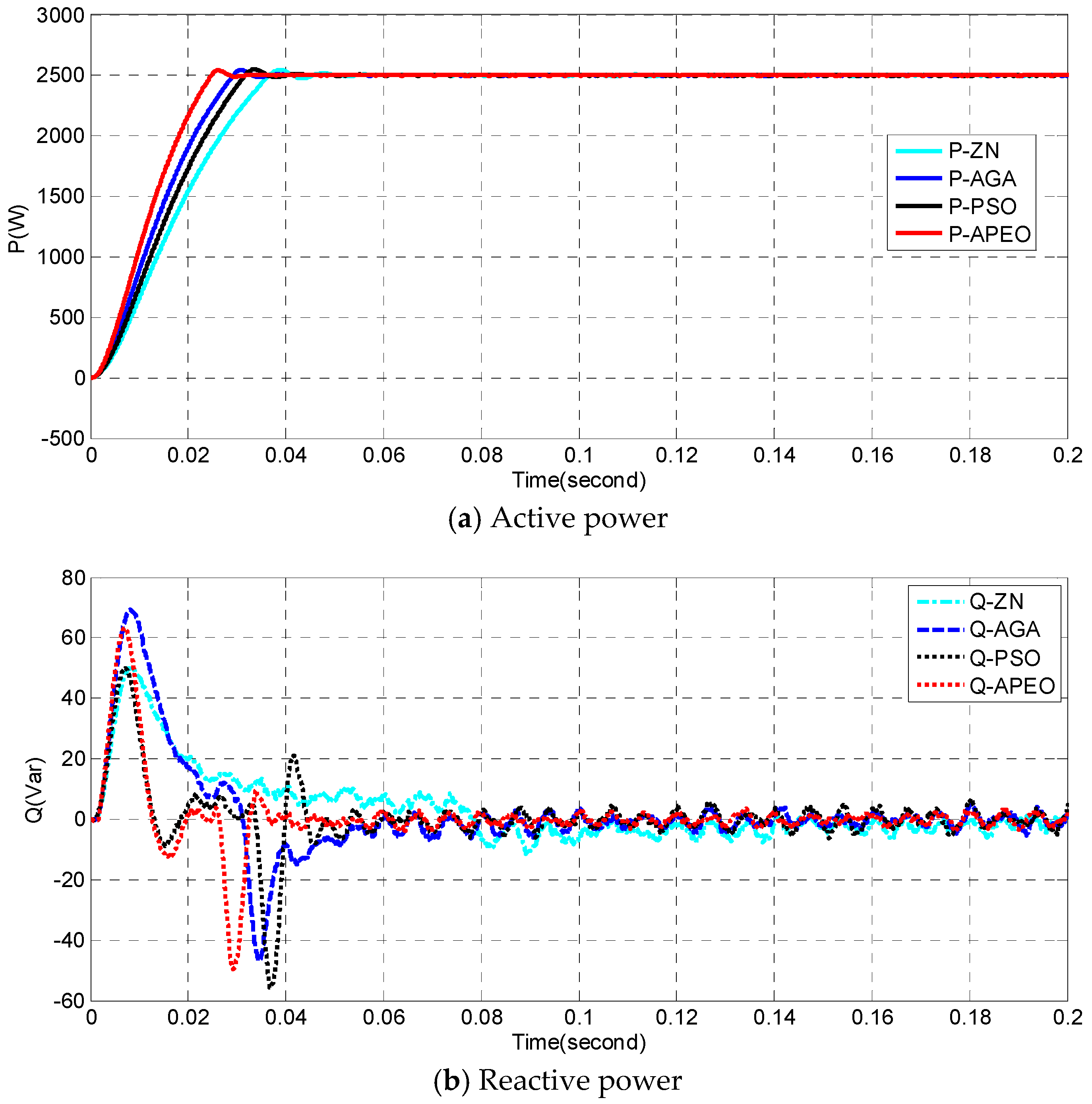
4.2.1. Case 1: Under Nominal Condition
4.2.2. Case 2: Robustness Test
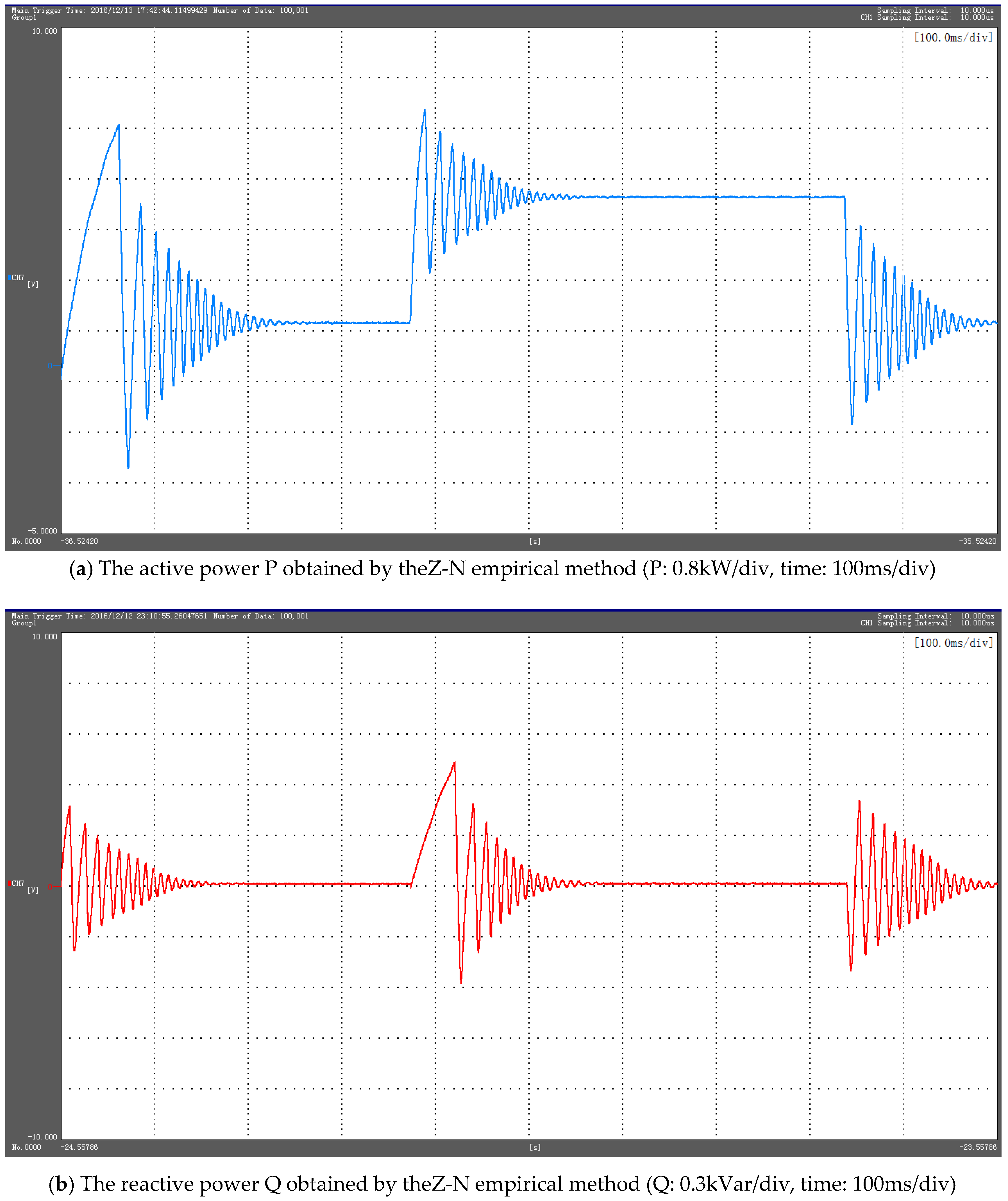
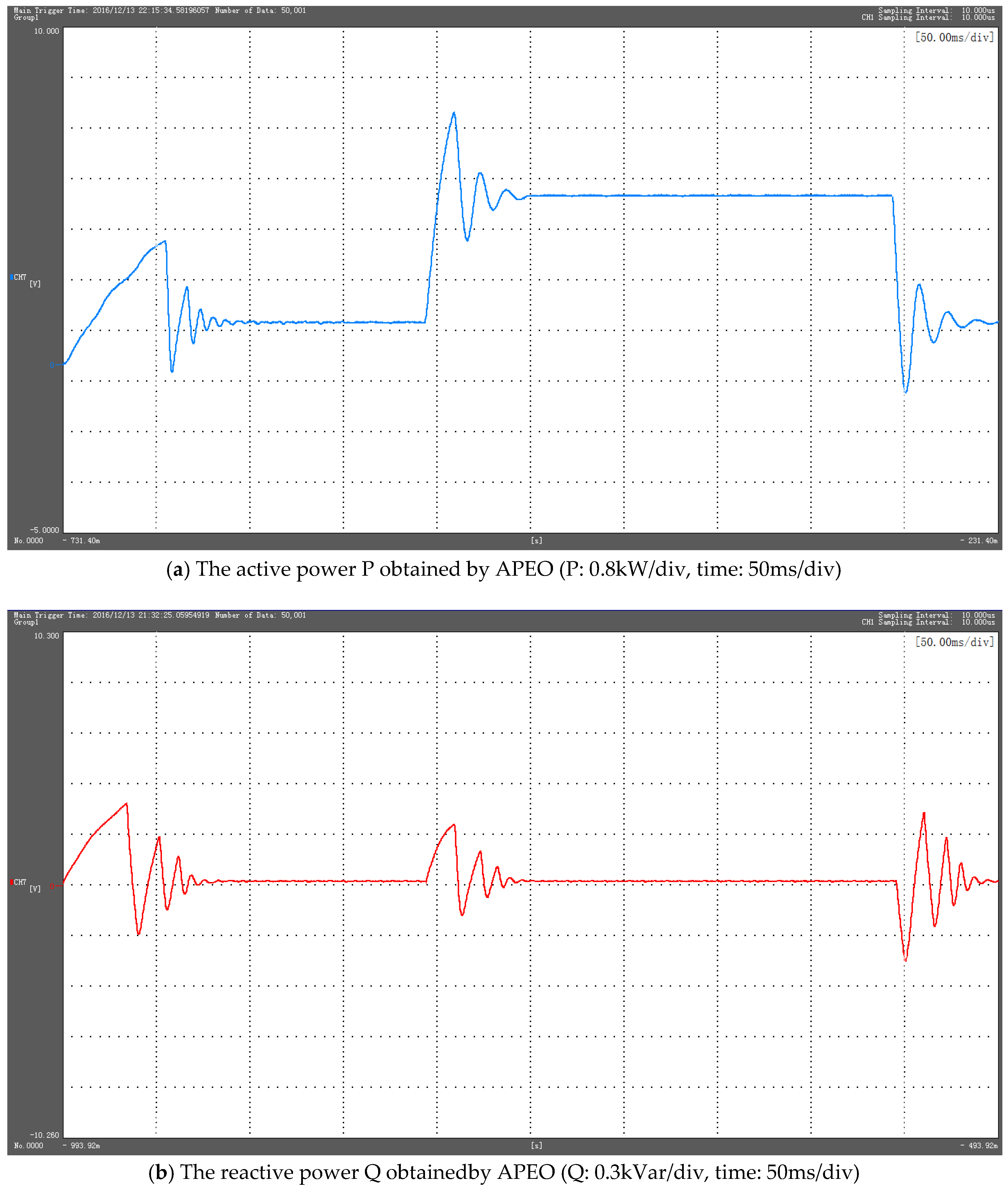
5. Experimental Results
6. Conclusions and Open Problems
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the art in research on microgrids: A review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Arul, P.G.; Ramachandaramurthy, K.V.; Rajkumar, R.K. Control strategies for a hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2015, 42, 597–608. [Google Scholar] [CrossRef]
- Fathima, A.H.; Palanisamy, K. Optimization in microgrids with hybrid energy systems-A review. Renew. Sustain. Energy Rev. 2015, 45, 431–446. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Chandorkar, M.; Lee, T.L.; Loh, P.C. Advanced control architectures for intelligent microgrids, part I: Decentralized and hierarchical control. IEEE Trans. Ind. Electron. 2013, 60, 1254–1262. [Google Scholar] [CrossRef]
- Colak, I.; Kabalci, E.; Fulli, G.; Lazarou, S. A survey on the contributions of power electronics to smart grid systems. Renew. Sustain. Energy Rev. 2015, 47, 562–579. [Google Scholar] [CrossRef]
- Hassan, M.A.; Abido, M.A. Optimal design of microgrids in autonomous and grid-connected modes using particle swarm optimization. IEEE Trans. Power Electron. 2011, 26, 755–769. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Russo, M.; Valeri, S.; De Santis, M. Sensitivity-based model of low voltage distribution systems with distributed energy resources. Energies 2016, 9, 801. [Google Scholar] [CrossRef]
- Casolino, G.M.; Di Fazio, A.R.; Losi, A.; Russo, M.; De Santis, M. A voltage optimization tool for smart distribution grids with distributed energy resources. In Proceedings of the 2017 AEIT International Annual Conference, Cagliari, Italy, 20–22 September 2017. [Google Scholar]
- Dai, M.; Marwali, M.N.; Keyhani, A. Power flow control of a single distributed generation unit. IEEE Trans. Power Electron. 2008, 23, 343–352. [Google Scholar] [CrossRef]
- Li, Y.W.; Kao, C.N. An accurate power control strategy for power-electronics-interfaced distributed generation units operating in a low-voltage multibus microgrid. IEEE Trans. Power Electron. 2009, 24, 2977–2988. [Google Scholar]
- Jang, M.; Mihai, C.; Agelidis, V.G. A single-phase grid-connected fuel cell system based on a boost-inverter. IEEE Trans. Power Electron. 2013, 28, 279–288. [Google Scholar] [CrossRef]
- Fazeli, S.M.; Ping, H.W.; Rahim, N.B.A.; Ooi, B.T. Individual-phase decoupled PQ control of three-phase voltage source converter. IET Gener. Transm. Distrib. 2013, 7, 219–1228. [Google Scholar] [CrossRef]
- Adhikari, S.; Li, F.X. Coordinated V-f and P-Q control of solar photovoltaic generators with MPPT and battery storage in microgrids. IEEE Trans. Smart Grid 2014, 5, 1270–1281. [Google Scholar] [CrossRef]
- Adhikari, S.; Li, F.X.; Li, H.J. PQ and PV Control of Photovoltaic Generators in Distribution Systems. IEEE Trans. Smart 2015, 6, 2929–2941. [Google Scholar] [CrossRef]
- Liu, W.; Gu, W.; Xu, Y.; Wang, Y.; Zhang, K. General distributed secondary control for multi-microgrids with both PQ-controlled and droop-controlled distributed generators. IET Gener. Transm. Distrib. 2017, 11, 707–718. [Google Scholar] [CrossRef]
- Al-Saedi, W.; Lachowicz, S.W.; Habibi, D.; Bass, O. Power flow control in grid-connected microgrid operation using particle swarm optimization under variable load conditions. Int. J. Electr. Power Energy Syst. 2013, 49, 76–85. [Google Scholar] [CrossRef]
- Liu, C.H.; Hsu, Y.Y. Design of a self-tuning PI controller for a STATCOM using particle swarm optimization. IEEE Trans. Ind. Electr. 2010, 57, 702–715. [Google Scholar]
- Al-Saedi, W.; Lachowicz, S.W.; Habibi, D.; Bass, O. Voltage and frequency regulation based DG unit in an autonomous microgrid operation using particle swarm optimization. Int. J. Electr. Power Energy Syst. 2013, 53, 742–751. [Google Scholar] [CrossRef]
- Ambia, M.N.; Hasanien, H.M.; Al-Durra, A.; Muyeen, S.M. Harmony search algorithm-based controller parameters optimization for a distributed-generation system. IEEE Trans. Power Deliv. 2015, 30, 246–255. [Google Scholar] [CrossRef]
- Bak, P.; Sneppen, K. Punctuated equilibrium and criticality in a simple model of evolution. Phys. Rev. Lett. 1993, 71, 4083–4086. [Google Scholar] [CrossRef] [PubMed]
- Boettcher, S.; Percus, A. Nature’s way of optimizing. Artif. Intell. 2000, 119, 275–286. [Google Scholar] [CrossRef]
- Boettcher, S.; Percus, A. Optimization with extremal dynamics. Phys. Rev. Lett. 2001, 86, 5211–5214. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.W.; Zhu, Y.J.; Yang, G.K.; Lu, Y.Z. Improved extremal optimization for the asymmetric traveling salesman problem. Phys. A Stat. Mech. Appl. 2011, 390, 4459–4465. [Google Scholar] [CrossRef]
- Liu, J.M.; Chen, Y.W.; Yang, G.K.; Lu, Y.Z. Self-organized combinatorial optimization. Expert Syst. Appl. 2011, 38, 10532–10540. [Google Scholar] [CrossRef]
- Dai, Y.X.; Wang, H.; Zeng, G.Q. Double closed-loop PI control of three-phase inverters by binary-coded extremal optimization. IEEE Access 2016, 4, 7621–7632. [Google Scholar] [CrossRef]
- Lu, Y.Z.; Chen, Y.W.; Chen, M.R.; Chen, P.; Zeng, G.Q. Extremal Optimization: Fundamentals, Algorithms, and Applications; CRC Press & Chemical Industry Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Huo, H.B.; Zhu, X.J.; Cao, G.Y. Design for two-degree-of-freedom PID regulator based on improved generalized extremal optimization algorithm. J. Shanghai Jiaotong Univ. Sci. 2007, E-12, 148–153. [Google Scholar]
- Zeng, G.Q.; Chen, J.; Dai, Y.X.; Li, L.M.; Zheng, C.W.; Chen, M.R. Design of fractional order PID controller for automatic regulator voltage system based on multi-objective extremal optimization. Neurocomputing 2015, 160, 173–184. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Chen, J.; Chen, M.R.; Dai, Y.X.; Li, L.M.; Lu, K.D.; Zheng, C.W. Design of multivariable PID controllers using real-coded population-based extremal optimization. Neurocomputing 2015, 151, 1343–1353. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Lu, K.D.; Dai, Y.X.; Zhang, Z.J.; Chen, M.R.; Zheng, C.W.; Wu, D.; Peng, W.W. Binary-coded extremal optimization for the design of PID controllers. Neurocomputing 2014, 138, 180–188. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Xie, X.Q.; Chen, M.R.; Weng, J. Adaptive population extremal optimization based PID neural network for multivariable nonlinear control systems. Swarm Evol. Comput. 2018, in press. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Liu, H.Y.; Wu, D.; Li, L.M.; Wu, L.; Dai, Y.X.; Lu, K.D. A real-coded extremal optimization method with multi-non-uniform mutation for the design of fractional order PID controllers. Inform. Technol. Control 2016, 45, 358–375. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, G.Q.; Dai, Y.X.; Bi, D.Q.; Sun, J.L.; Xie, X.Q. Design of fractional order frequency PID controller for an islanded microgrid: A multi-objective extremal optimization method. Energies 2017, 10, 1502. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Tang, P.H.; Tseng, M.H. Adaptive directed mutation for real-coded genetic algorithms. Appl. Soft Comput. 2013, 13, 600–614. [Google Scholar] [CrossRef]
- Chen, M.R.; Li, X.; Zhang, X.; Lu, Y.Z. A novel particle swarm optimizer hybridized with extremal optimization. Appl. Soft Comput. 2010, 10, 367–373. [Google Scholar] [CrossRef]
- Chen, M.R.; Lu, Y.Z.; Yang, G.K. Population-based extremal optimization with adaptive Lévy mutation for constrained optimization. Comput. Intell. Secur. Lect. Notes Comput. Sci. 2007, 4456, 144–155. [Google Scholar]
- Li, L.M.; Lu, K.D.; Zeng, G.Q.; Wu, L.; Chen, M.R. A novel real-coded population-based extremal optimization algorithm with polynomial mutation: A non-parametric statistical study on continuous optimization problems. Neurocomputing 2016, 174, 577–587. [Google Scholar] [CrossRef]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Liang, M.; Zheng, T.Q. Synchronous PI control for three-phase grid-connected photovoltaic inverter. In Proceedings of the 2010 Chinese Control and Decision Conference, Xuzhou, China, 26–28 May 2010. [Google Scholar]





| Function | Function Expression | Search Space | n | Global Optimum |
|---|---|---|---|---|
| Michalewicz | (0, π)n | 10 | −9.66 min | |
| Schwefel | (−500, 500)n | 30 | −12,569.487 min | |
| Rastrigin | (−5.12, 5.12)n | 30 | 0 min | |
| Ackley | (−32.768, 32.768)n | 30 | 0 min | |
| Rosenbrock | (−30, 30)n | 30 | 0 min |
| Test Function | Algorithm | Best | Average | Worst | Standard Deviation | Rank |
|---|---|---|---|---|---|---|
| F1 | APEO | −9.66 | −9.66 | −9.66 | 1.45 × 10−15 | 1 |
| RPEO-PLM [38] | −9.66 | −9.66 | −9.66 | 5.767 × 10−5 | 2 | |
| PSO-EO [36] | −9.66 | −9.66 | −9.66 | 2.15 × 10−3 | 3 | |
| PSO [36] | −9.66 | −9.52 | −9.06 | 0.17 | 6 | |
| GA [36] | −9.66 | −9.62 | −9.50 | 0.06 | 4 | |
| PEO [37] | −9.61 | −9.55 | −9.50 | 0.03 | 5 | |
| F2 | APEO | −12,569.5 | −12,569.5 | −12,569.5 | 1.82 × 10−5 | 1 |
| RPEO-PLM [38] | −12,569.5 | −12,569.5 | −12,569.5 | 1.052 × 10−5 | 2 | |
| PSO-EO [36] | −12,569.5 | −12,568.0 | −12,562.6 | 2.01 | 3 | |
| PSO [36] | −9577.7 | −10,139.3 | −11,026.2 | 625.7 | 5 | |
| GA [36] | −9549.3 | −8846.0 | −8404.5 | 481.0 | 6 | |
| PEO [37] | −12,214.2 | −12,083.3 | −11,977.3 | 90.3 | 4 | |
| F3 | APEO | 0 | 0 | 0 | 0 | 1 |
| RPEO-PLM [38] | 0 | 0 | 0 | 0 | 1 | |
| PSO-EO [36] | 0 | 0 | 0 | 0 | 1 | |
| PSO [36] | 0 | 0 | 0 | 0 | 1 | |
| GA [36] | 0.046 | 0.014 | 9.93 × 10−4 | 0.014 | 5 | |
| PEO [37] | 2.47 | 2.14 | 1.85 | 0.25 | 6 | |
| F4 | APEO | −8.88 × 10−16 | −8.88 × 10−16 | −8.88 × 10−16 | 0 | 1 |
| RPEO-PLM [38] | −8.88 × 10−16 | −8.88 × 10−16 | −8.88 × 10−16 | 0 | 1 | |
| PSO-EO [36] | −8.88 × 10−16 | −8.88 × 10−16 | −8.88 × 10−16 | 0 | 1 | |
| PSO [36] | −8.88 × 10−16 | −8.88 × 10−16 | −8.88 × 10−16 | 0 | 1 | |
| GA [36] | 0.094 | 0.054 | 0.03 | 0.02 | 5 | |
| PEO [37] | 0.12 | 0.11 | 0.09 | 8.4 × 10−3 | 6 | |
| F5 | APEO | 1.21 × 10−19 | 4.47 × 10−17 | 4.67 × 10−16 | 1.15 × 10−16 | 1 |
| RPEO-PLM [38] | 3.050 × 10−10 | 8.360 × 10−7 | 1.050 × 10−5 | 2.283 × 10−6 | 2 | |
| PSO-EO [36] | 9.99 × 10−4 | 9.88 × 10−4 | 9.54 × 10−4 | 2.39 × 10−5 | 3 | |
| PSO [36] | 26.8 | 26.0 | 25.4 | 0.59 | 5 | |
| GA [36] | 39.7 | 33.1 | 30.1 | 3.95 | 6 | |
| PEO [37] | 9.63 | 9.42 | 9.30 | 0.13 | 4 |
| Algorithm | Parameters Setting |
|---|---|
| AGA [35] | Population size N = 30, Imax = 30, the crossover probability pc = 0.9, the mutation probability pm = 0.1 − 0.01 × n/N, where n = 1, 2,..., N. |
| PSO [16] | Population size = 30, Imax = 30, inertia weight w = 0.6, the upper limit of velocity Vmax = 0.05, the lower limit of velocity Vmin = −0.05, acceleration factors c1 = 2.0, c2 = 2.0. |
| APEO | N = 30, Imax = 30, b = 0.1. |
| Algorithm | fmax | fmedian | fmean | fmin | fsd |
|---|---|---|---|---|---|
| AGA [35] | 0.2646 | 0.2589 | 0.2586 | 0.2531 | 0.0038 |
| PSO [16] | 0.2532 | 0.2495 | 0.2494 | 0.2462 | 0.0023 |
| APEO | 0.2434 | 0.2430 | 0.2431 | 0.2427 | 0.0002 |
| Algorithm | Kpo1 | Kio1 | Kpo2 | Kio2 | Kpo3 | Kio3 | Fmin | TsP(s) | TsQ(s) |
|---|---|---|---|---|---|---|---|---|---|
| Z-N method | 0.0219 | 31.4093 | 0.0292 | 2.8040 | 10.7959 | 303.2478 | 0.6870 | 0.0501 | 0.0783 |
| AGA | 0.0242 | 41.4078 | 0.0267 | 7.1365 | 24.7489 | 429.25268 | 0.2531 | 0.0406 | 0.0582 |
| PSO | 0.0299 | 30 | 0.03 | 10 | 25 | 500 | 0.2462 | 0.0450 | 0.0461 |
| APEO | 0.0285 | 49.9947 | 0.0299 | 9.9600 | 24.9999 | 499.9615 | 0.2427 | 0.0324 | 0.0375 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.-R.; Wang, H.; Zeng, G.-Q.; Dai, Y.-X.; Bi, D.-Q. Optimal P-Q Control of Grid-Connected Inverters in a Microgrid Based on Adaptive Population Extremal Optimization. Energies 2018, 11, 2107. https://doi.org/10.3390/en11082107
Chen M-R, Wang H, Zeng G-Q, Dai Y-X, Bi D-Q. Optimal P-Q Control of Grid-Connected Inverters in a Microgrid Based on Adaptive Population Extremal Optimization. Energies. 2018; 11(8):2107. https://doi.org/10.3390/en11082107
Chicago/Turabian StyleChen, Min-Rong, Huan Wang, Guo-Qiang Zeng, Yu-Xing Dai, and Da-Qiang Bi. 2018. "Optimal P-Q Control of Grid-Connected Inverters in a Microgrid Based on Adaptive Population Extremal Optimization" Energies 11, no. 8: 2107. https://doi.org/10.3390/en11082107
APA StyleChen, M.-R., Wang, H., Zeng, G.-Q., Dai, Y.-X., & Bi, D.-Q. (2018). Optimal P-Q Control of Grid-Connected Inverters in a Microgrid Based on Adaptive Population Extremal Optimization. Energies, 11(8), 2107. https://doi.org/10.3390/en11082107




