Prediction Error Analysis of Finite-Control-Set Model Predictive Current Control for IPMSMs
Abstract
:1. Introduction
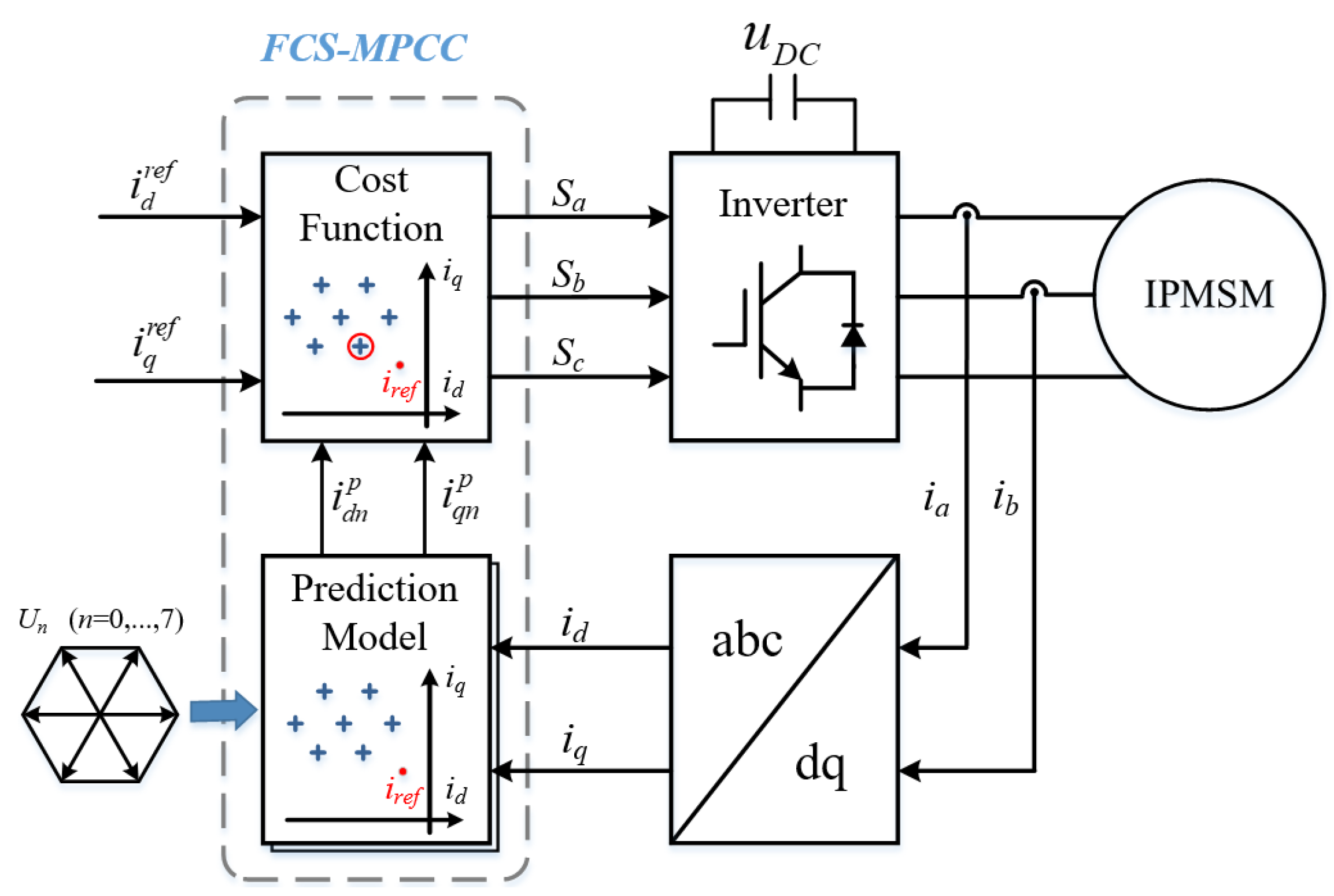
2. Basic FCS-MPCC Algorithm
2.1. IPMSM Model
| ud, uq | d- and q-axis voltage components |
| id, iq | d- and q-axis current components |
| Rs | stator resistance |
| Ld, Lq | d- and q-axis inductance components |
| ψf | flux linkage of permanent magnet |
| ωe | electrical angular speed |
| p | differential operator |
2.2. Control Delay Compensation
2.3. Cost Function
3. Prediction Error Analysis
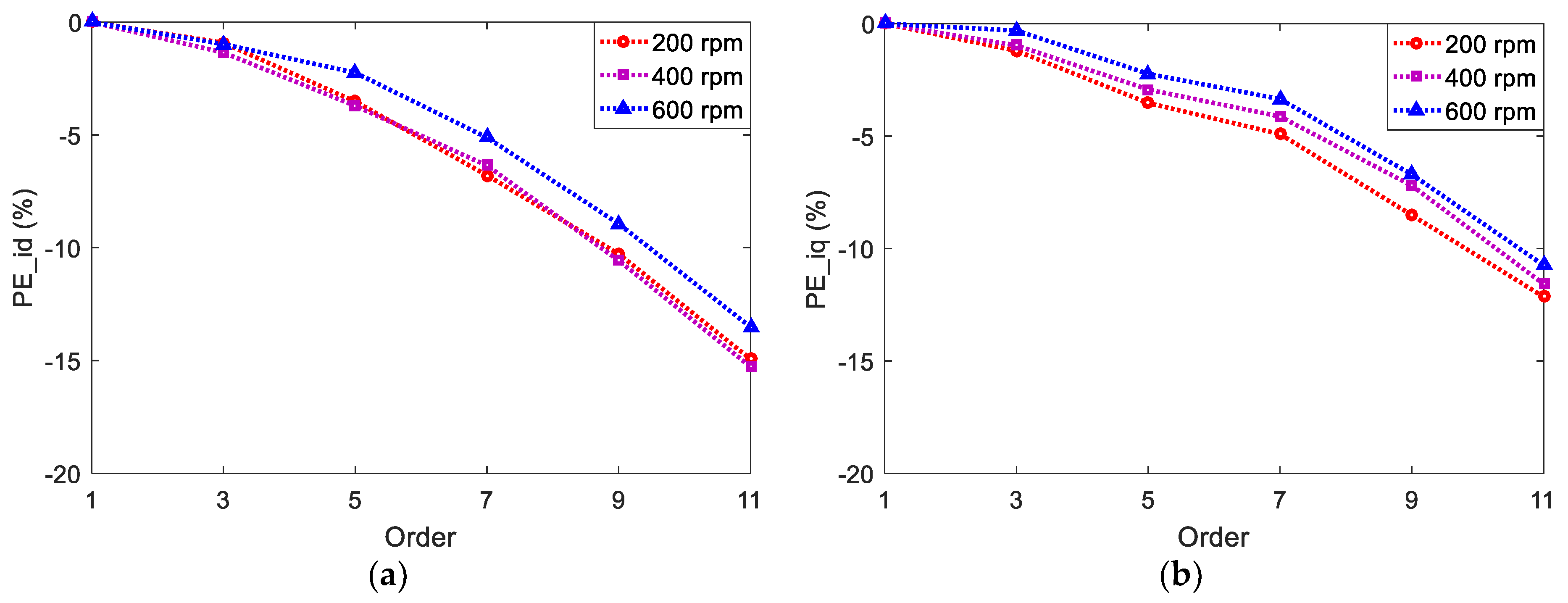
3.1. Discretization Method
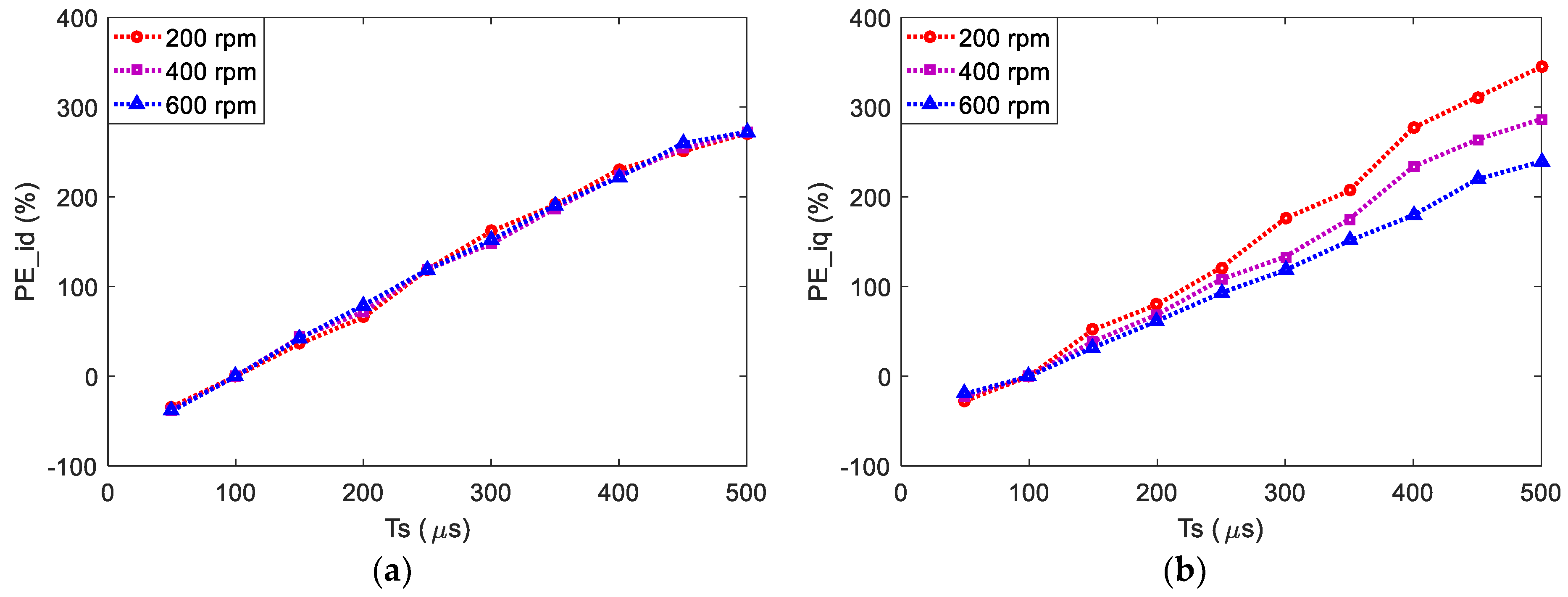
3.2. Prediction Stepsize
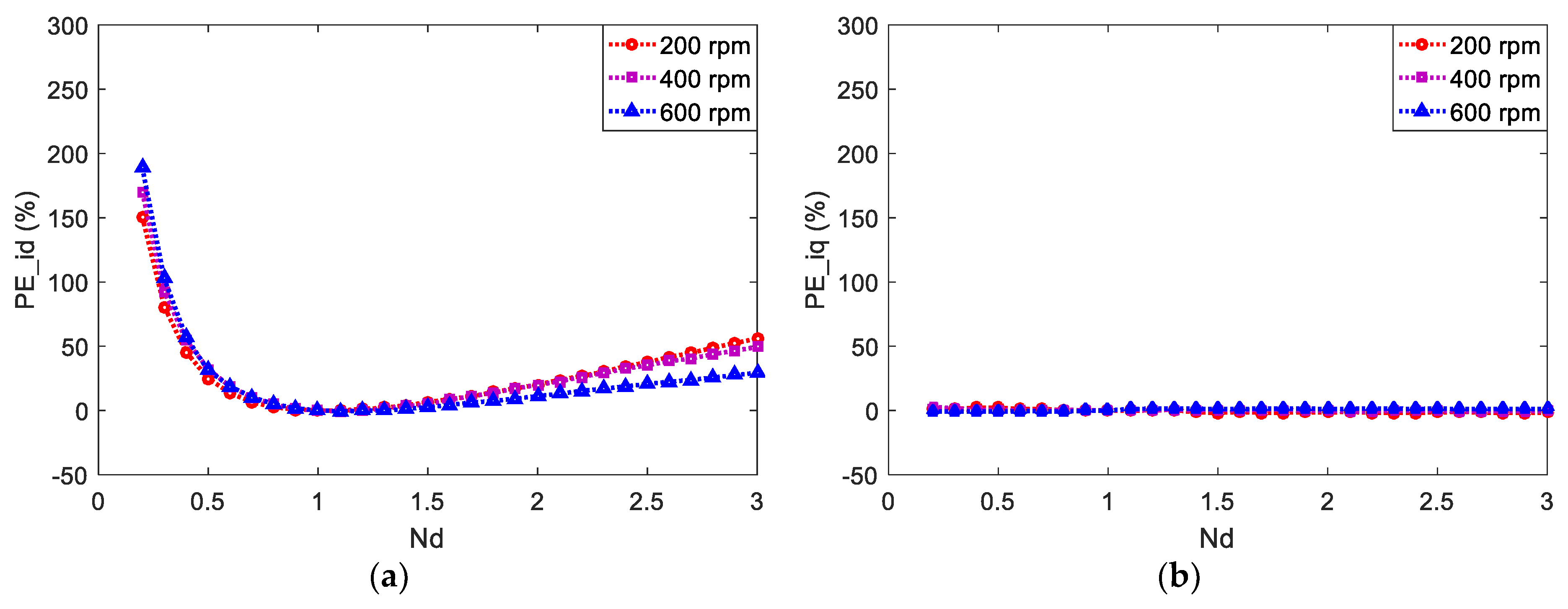
3.3. Parameter Mismatch
4. Experimental Results
4.1. Discretization Order
4.2. Prediction Stepsize
4.3. Stator Inductances Mismatch
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Abbreviations | |
| CCS-MPC | Continuous-control-set model predictive control |
| FCS-MPC | Finite-control-set model predictive control |
| FCS-MPCC | Finite-control-set model predictive current control |
| MPC | Model predictive control |
| IM | Induction motor |
| IPMSM | Interior permanent magnet synchronous motor |
| PE | Prediction error |
| PI | Proportional integral |
| PWM | Pulse width modulation |
| RMS | Root mean square |
| SPMSM | Surface permanent magnet synchronous motor |
| VC | Vector control |
| VSI | Voltage-source inverter |
| Variables and parameters | |
| ud, uq | d- and q-axis voltage components |
| id, iq | d- and q-axis current components |
| Rs | Stator resistance |
| Ld, Lq | d- and q-axis inductance components |
| ψf | Flux linkage of permanent magnet |
| ωe | Electrical angular speed |
| p | Differential operator |
| Ts | Prediction stepsize/control period/sampling time |
| N | Discretization order |
| Ldn, Lqn | Stator inductances of practical motor |
| Ldp, Lqp | Stator inductances in prediction model |
| Nd, Nq | Coefficients between stator inductances in prediction model and of practical motor |
| PE_id, PE_iq | Prediction errors of d- and q-axis currents |
| PERMS | RMS value of prediction error |
| PEbase | RMS prediction error under basic reference setting of three influencing factors |
| ΔPE | Relative prediction error |
| Superscripts | |
| P | Prediction quantity |
| ref | Reference quantity |
References
- Li, H.; Gao, J.; Huang, S.; Fan, P. A Novel Optimal Current Trajectory Control Strategy of IPMSM Considering the Cross Saturation Effects. Energies 2017, 10, 1460. [Google Scholar] [CrossRef]
- Sul, S.K. Control of Electric Machine Drive Systems; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Vazquez, S.; Rodríguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Preindl, M.; Bolognani, S. Comparison of Direct and PWM Model Predictive Control for Power Electronic and Drive Systems. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition, Long Beach, CA, USA, 17–21 March 2013. [Google Scholar]
- Singh, V.K.; Tripathi, R.N.; Hanamoto, T. HIL Co-Simulation of Finite Set-Model Predictive Control Using FPGA for a Three-Phase VSI System. Energies 2018, 11, 909. [Google Scholar] [CrossRef]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers, 6th ed.; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Niu, F.; Wang, B.; Babel, A.S.; Li, K.; Strangas, E.G. Comparative Evaluation of Direct Torque Control Strategies for Permanent Magnet Synchronous Machines. IEEE Trans. Power. Electron. 2016, 31, 1408–1424. [Google Scholar] [CrossRef]
- Preindl, M.; Bolognani, S. Model Predictive Direct Torque Control with Finite Control Set for PMSM Drive Systems, Part 1: Maximum Torque Per Ampere Operation. IEEE Trans. Ind. Informat. 2013, 9, 1912–1921. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, J.; Jin, M. Adaptive finite-control-set model predictive current control for IPMSM drives with inductance variation. IET Electr. Power Appl. 2017, 11, 874–884. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, D.; Liu, J.; Gao, S.; Xu, W. Performance Improvement of Model-Predictive Current Control of Permanent Magnet Synchronous Motor Drives. IEEE Trans. Ind. Appl. 2017, 53, 3683–3695. [Google Scholar] [CrossRef]
- Vaclavek, P.; Blaha, P. PMSM Model Discretization for Model Predictive Control Algorithms. In Proceedings of the 2013 IEEE/SICE International Symposium on System Integration, Kobe, Japan, 15–17 December 2013. [Google Scholar]
- Silva, C.A.; Yuz, J.I. On Sampled-data Models for Model Predictive Control. In Proceedings of the 36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010. [Google Scholar]
- Kawamura, A.; Chuarayapratip, R.; Haneyoshi, T. Deadbeat Control of PWM Inverter with Modified Pulse Patterns for Uninterruptible Power Supply. IEEE Trans. Ind. Electron. 1988, 35, 295–300. [Google Scholar] [CrossRef]
- Damiano, A.; Gatto, G.; Marongiu, I.; Perfetto, A.; Serpi, A. Operating Constraints Management of a Surface-Mounted PM Synchronous Machine by Means of an FPGA-Based Model Predictive Control Algorithm. IEEE Trans. Ind. Informat. 2014, 10, 243–255. [Google Scholar] [CrossRef]
- Rodríguez, J.; Pontt, J.; Silva, C.A.; Correa, P.; Lezana, P.; Cortés, P.; Ammann, U. Predictive Current Control of a Voltage Source Inverter. IEEE Trans. Ind. Electron. 2007, 54, 495–503. [Google Scholar] [CrossRef]
- Joshi, B.M.; Chandorkar, M.C. Time Discretization Issues in Induction Machine Model Solving for Real-time Applications. In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference, Niagara Falls, ON, Canada, 15–18 May 2011. [Google Scholar]
- Diao, L.; Sun, D.; Dong, K.; Zhao, L.; Liu, Z. Optimized Design of Discrete Traction Induction Motor Model at Low-Switching Frequency. IEEE Trans. Power Electron. 2013, 28, 4803–4810. [Google Scholar] [CrossRef]
- Nalakath, S.; Preindl, M.; Emadi, A. Online Multi-parameter Estimation of Interior Permanent Magnet Motor Drives with Finite Control Set Model Predictive Control. IET Electr. Power Appl. 2017, 11, 944–951. [Google Scholar] [CrossRef]
- Lin, C.; Liu, T.; Yu, J.; Fu, L.; Hsiao, C. Model-Free Predictive Current Control for Interior Permanent-Magnet Synchronous Motor Drives Based on Current Difference Detection Technique. IEEE Trans. Ind. Electron. 2014, 61, 667–681. [Google Scholar] [CrossRef]
- Lin, C.; Yu, J.; Lai, Y.; Yu, H. Improved Model-Free Predictive Current Control for Synchronous Reluctance Motor Drives. IEEE Trans. Ind. Electron. 2016, 63, 3942–3953. [Google Scholar] [CrossRef]
- Sawma, J.; Khatounian, F.; Monmasson, E.; Idkhajine, L.; Ghosn, R. Analysis of the Impact of Online Identification on Model Predictive Current Control Applied to Permanent Magnet Synchronous Motors. IET Electr. Power Appl. 2017, 11, 864–873. [Google Scholar] [CrossRef]
- Wang, W.; Xiao, X. Research on Predictive Control for PMSM Based on Online Parameter Identification. In Proceedings of the 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada 25–28 October 2012. [Google Scholar]
- Xia, C.; Wang, M.; Song, Z.; Liu, T. Robust Model Predictive Current Control of Three-Phase Voltage Source PWM Rectifier with Online Disturbance Observation. IEEE Trans. Ind. Informat. 2012, 8, 459–471. [Google Scholar] [CrossRef]
- Preindl, M.; Bolognani, S. Model Predictive Direct Speed Control with Finite Control Set of PMSM Drive Systems. IEEE Trans. Power Electron. 2013, 28, 1007–1015. [Google Scholar] [CrossRef]
- Yang, M.; Lang, X.; Long, J.; Xu, D. Flux Immunity Robust Predictive Current Control with Incremental Model and Extended State Observer for PMSM Drive. IEEE Trans. Power Electron. 2017, 32, 9267–9279. [Google Scholar] [CrossRef]
- Young, H.A.; Perez, M.A.; Rodríguez, J. Analysis of Finite-Control-Set Model Predictive Current Control with Model Parameter Mismatch in a Three-Phase Inverter. IEEE Trans. Ind. Electron. 2016, 63, 3100–3107. [Google Scholar] [CrossRef]
- Siami, M.D.; Khaburi, A.; Abbaszadeh, A.; Rodríguez, J. Robustness Improvement of Predictive Current Control Using Prediction Error Correction for Permanent-Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2016, 63, 3458–3466. [Google Scholar] [CrossRef]
- Cortés, P.; Rodríguez, J.; Silva, C.; Flores, A. Delay Compensation in Model Predictive Current Control of a Three-Phase Inverter. IEEE Trans. Ind. Electron. 2012, 59, 1323–1325. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, W. Low Complexity Model Predictive Control—Single Vector-Based Approach. IEEE Trans. Power Electron. 2014, 29, 5532–5541. [Google Scholar] [CrossRef]
- Rodríguez, J.; Cortés, P. Predictive Control of Power Converters and Electrical Drives, 1st ed.; Wiley: New York, NY, USA, 2012. [Google Scholar]
- Bogado, B.; Barrero, F.; Arahal, M.R.; Toral, S.; Levi, E. Sensitivity to Electrical Parameter Variations of Predictive Current Control in Multiphase Drives. In Proceedings of the 39th Annual Conference on IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013. [Google Scholar]
- Niu, F.; Li, K.; Wang, Y. Direct Torque Control for Permanent-Magnet Synchronous Machines Based on Duty Ratio Modulation. IEEE Trans. Ind. Electron. 2015, 62, 6160–6170. [Google Scholar] [CrossRef]
- Hu, D.; Alsmadi, Y.M.; Xu, L. High-fidelity Nonlinear IPM Modeling Based on Measured Stator Winding Flux Linkage. IEEE Trans. Ind. Appl. 2015, 51, 3012–3019. [Google Scholar] [CrossRef]

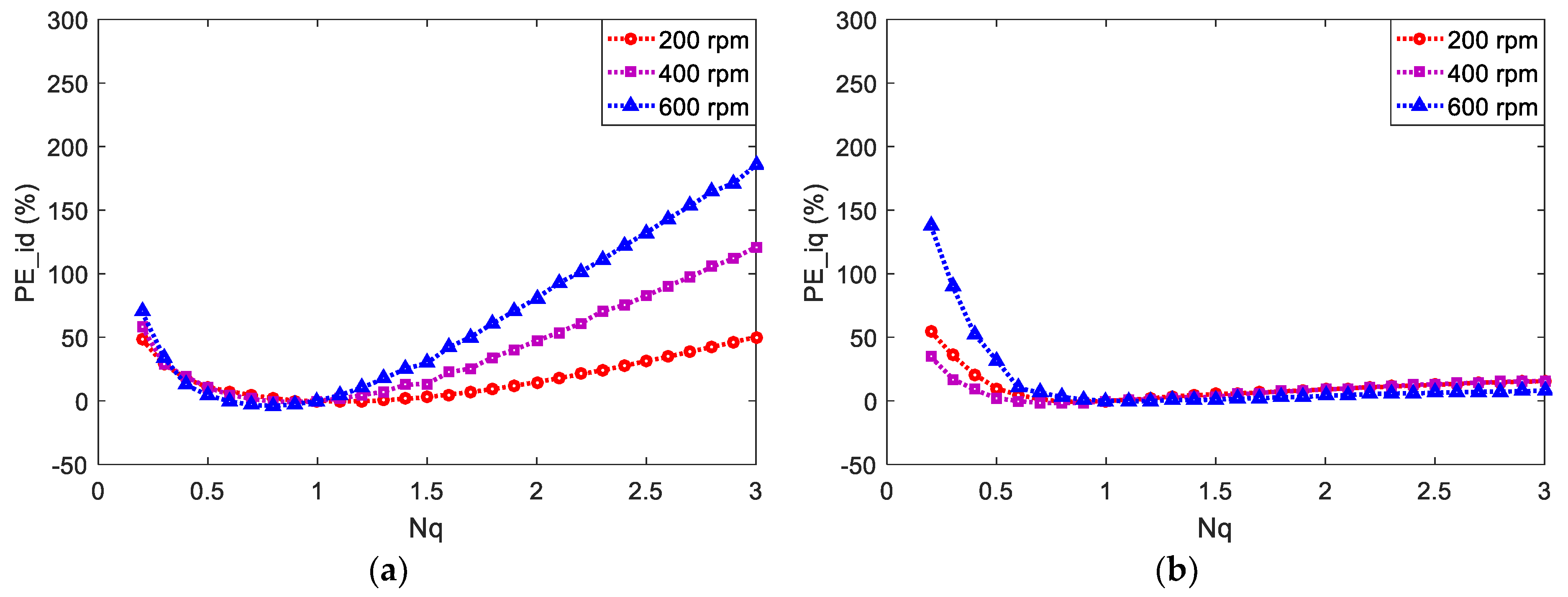
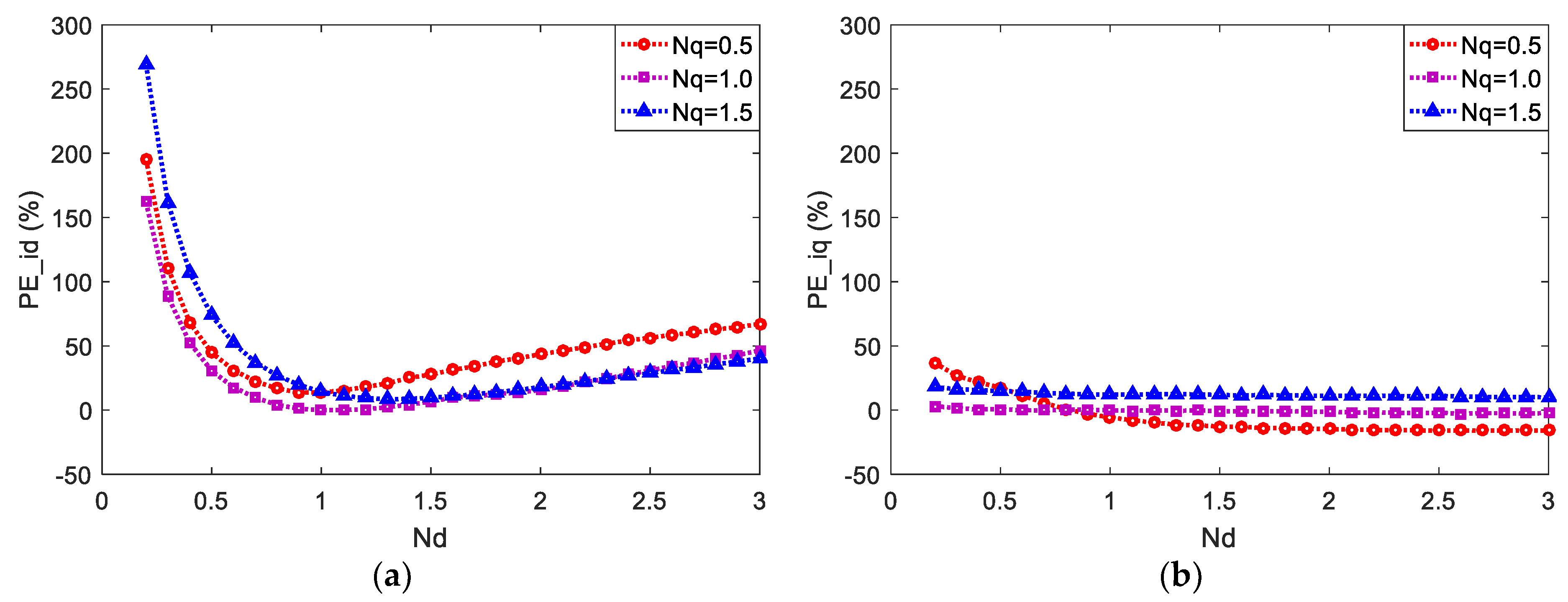
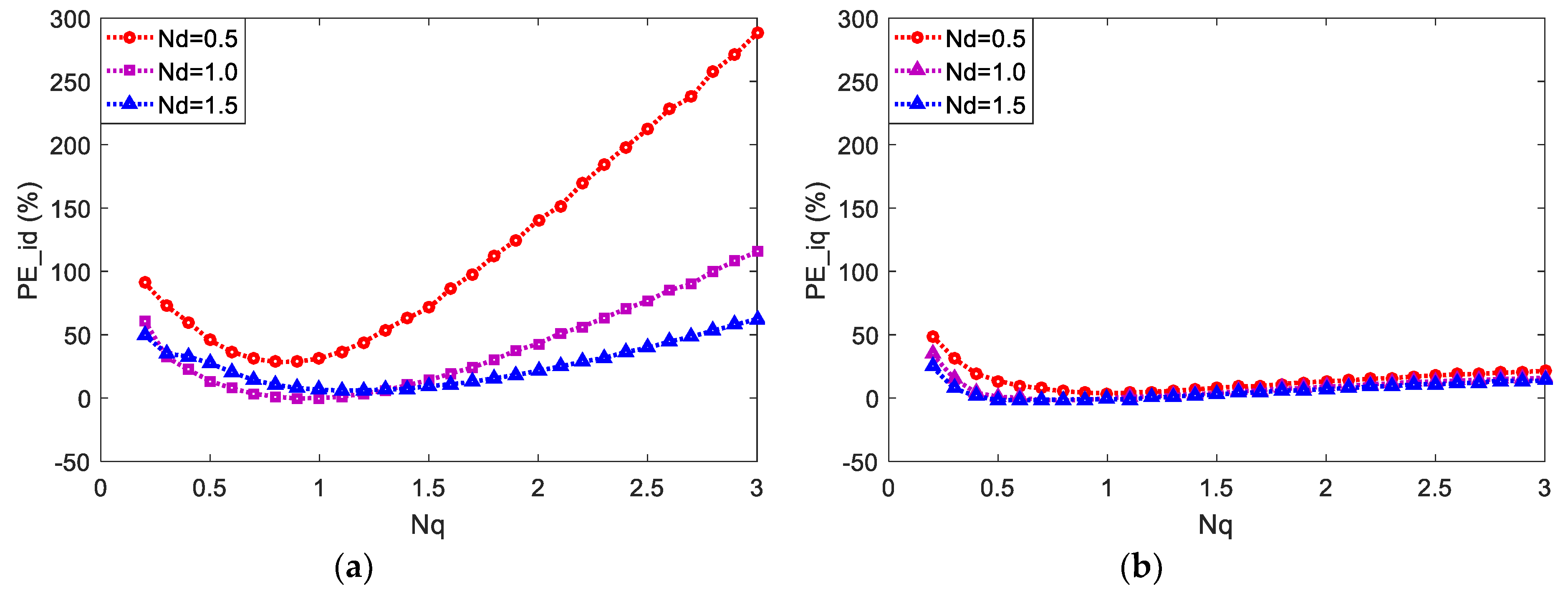
| Parameters | Value |
|---|---|
| Rated power | 2 kW |
| Rated phase voltage (peak) | 170 V |
| Rated phase current (peak) | 10 A |
| Rated speed | 800 rpm |
| Stator resistance | 4.1 Ω |
| d-axis inductance | 0.056 H |
| q-axis inductance | 0.119 H |
| Permanent magnet flux linkage | 0.936 Wb |
| Pole pairs | 2 |
| Speed (rpm) | PEbase of id (A) | PEbase of iq (A) |
|---|---|---|
| 200 | 0.136 | 0.139 |
| 400 | 0.149 | 0.127 |
| 600 | 0.161 | 0.119 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Huang, X.; Niu, F.; You, C.; Wu, L.; Fang, Y. Prediction Error Analysis of Finite-Control-Set Model Predictive Current Control for IPMSMs. Energies 2018, 11, 2051. https://doi.org/10.3390/en11082051
Li J, Huang X, Niu F, You C, Wu L, Fang Y. Prediction Error Analysis of Finite-Control-Set Model Predictive Current Control for IPMSMs. Energies. 2018; 11(8):2051. https://doi.org/10.3390/en11082051
Chicago/Turabian StyleLi, Jian, Xiaoyan Huang, Feng Niu, Chaojie You, Lijian Wu, and Youtong Fang. 2018. "Prediction Error Analysis of Finite-Control-Set Model Predictive Current Control for IPMSMs" Energies 11, no. 8: 2051. https://doi.org/10.3390/en11082051
APA StyleLi, J., Huang, X., Niu, F., You, C., Wu, L., & Fang, Y. (2018). Prediction Error Analysis of Finite-Control-Set Model Predictive Current Control for IPMSMs. Energies, 11(8), 2051. https://doi.org/10.3390/en11082051






