A Torque Impulse Balance Control for Multi-Tooth Fault Tolerant Switched-Flux Machines under Open-Circuit Fault
Abstract
1. Introduction
- (1)
- Excellent torque capability and high power density.
- (2)
- High reliability and strong fault tolerant capability.
- (3)
- Superior steady-state and dynamic performance for the system under both healthy condition and open-circuit faults.
- (1)
- The PMs are mounted on the stator, being free from centrifugal force.
- (2)
- Simple and robust rotor.
- (3)
- The PM field and the armature field distribute in parallel, leading to very low risk of demagnetization.
- (4)
- The FSPM machine can suppress the short-circuit current by increasing self-inductance, whereas the rotor-PM machine needs to increase the leakage inductance to suppress the short-circuit current. Therefore, the SFPM machine can guarantee relatively high torque density while enhancing the ability to suppress the short-circuit [12].
- (1)
- The mutual inductance of the SRM is basically zero, whereas the FTFSPM needs the alternate pole-wound structure to reduce the mutual inductance.
- (2)
- The short-circuit current of the SRM is basically zero due to the absence of PMs, whereas the FTFSPM needs a special design to suppress the short-circuit current.
- (3)
- The SRM operates in half-cycle mode, whereas the FTFSPM operates in whole-cycle mode owing to the PMs, making a relatively high torque density and efficiency. In addition, although with doubly salient structure and concentrated winding, the SFPM machine can provide high sinusoidal PM back-electromotive force (back-EMF) due to the complementary winding structure; thus, this kind of machine is suitable for operation in BLAC mode [11,12].
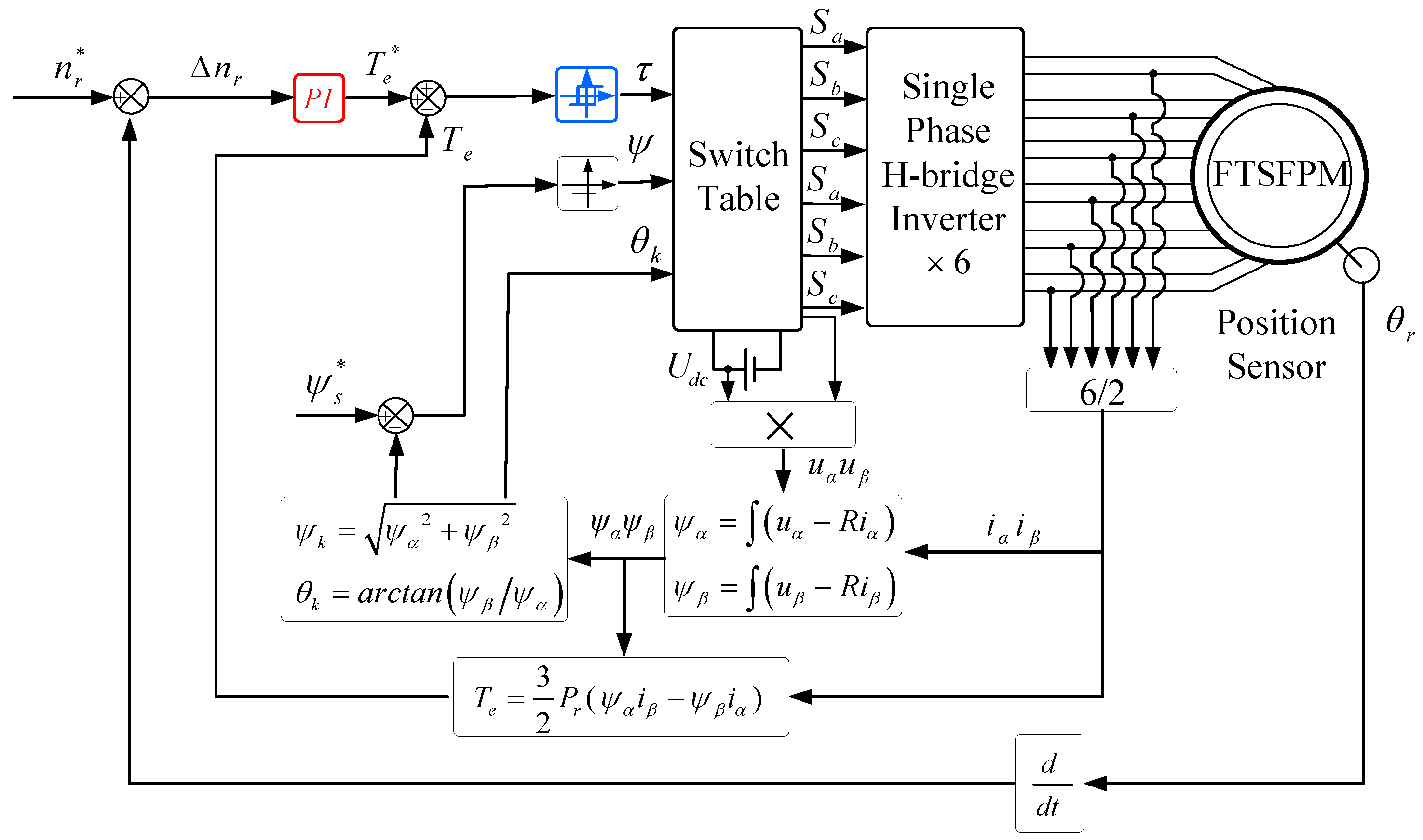
2. System Structure and Operation Principle
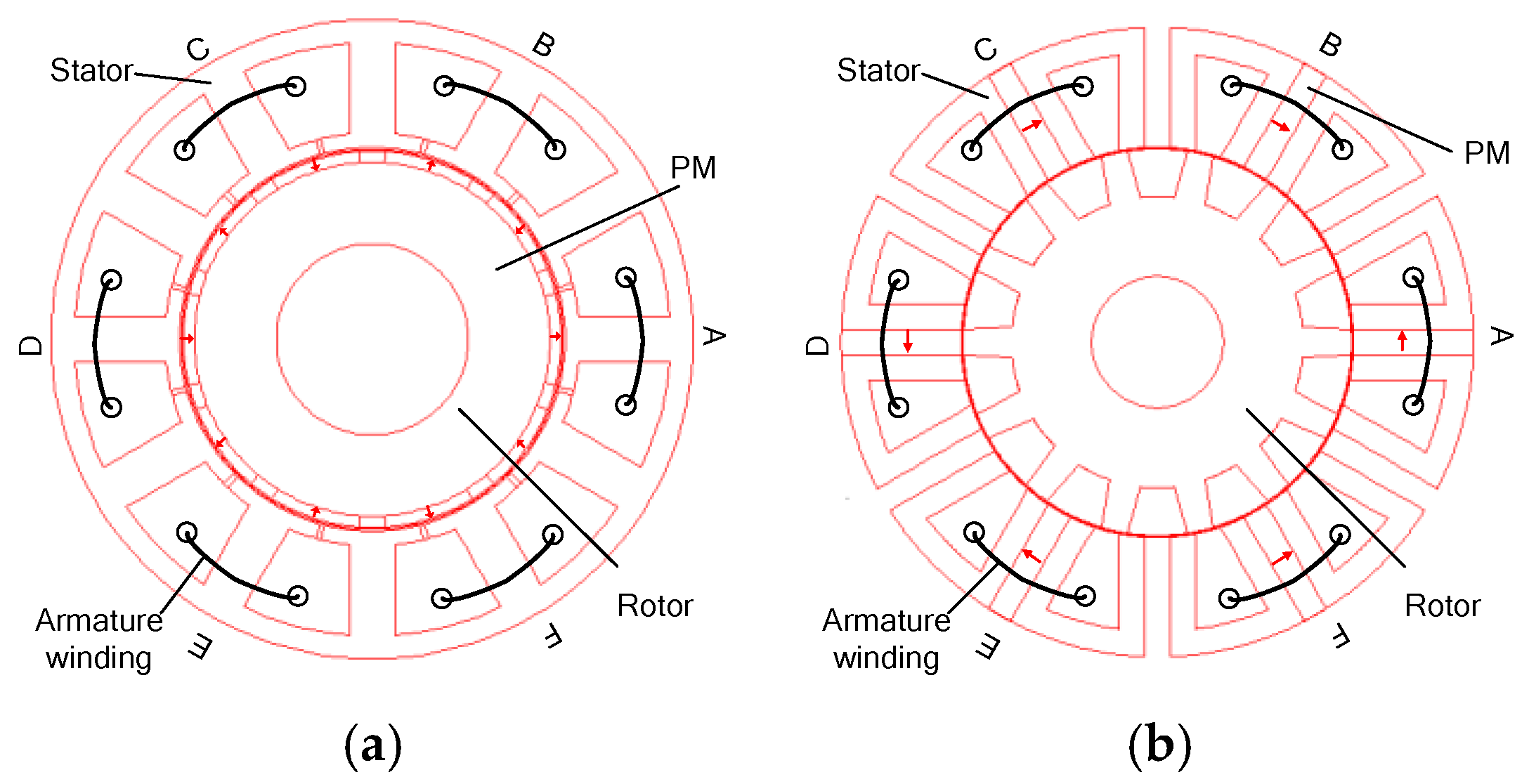
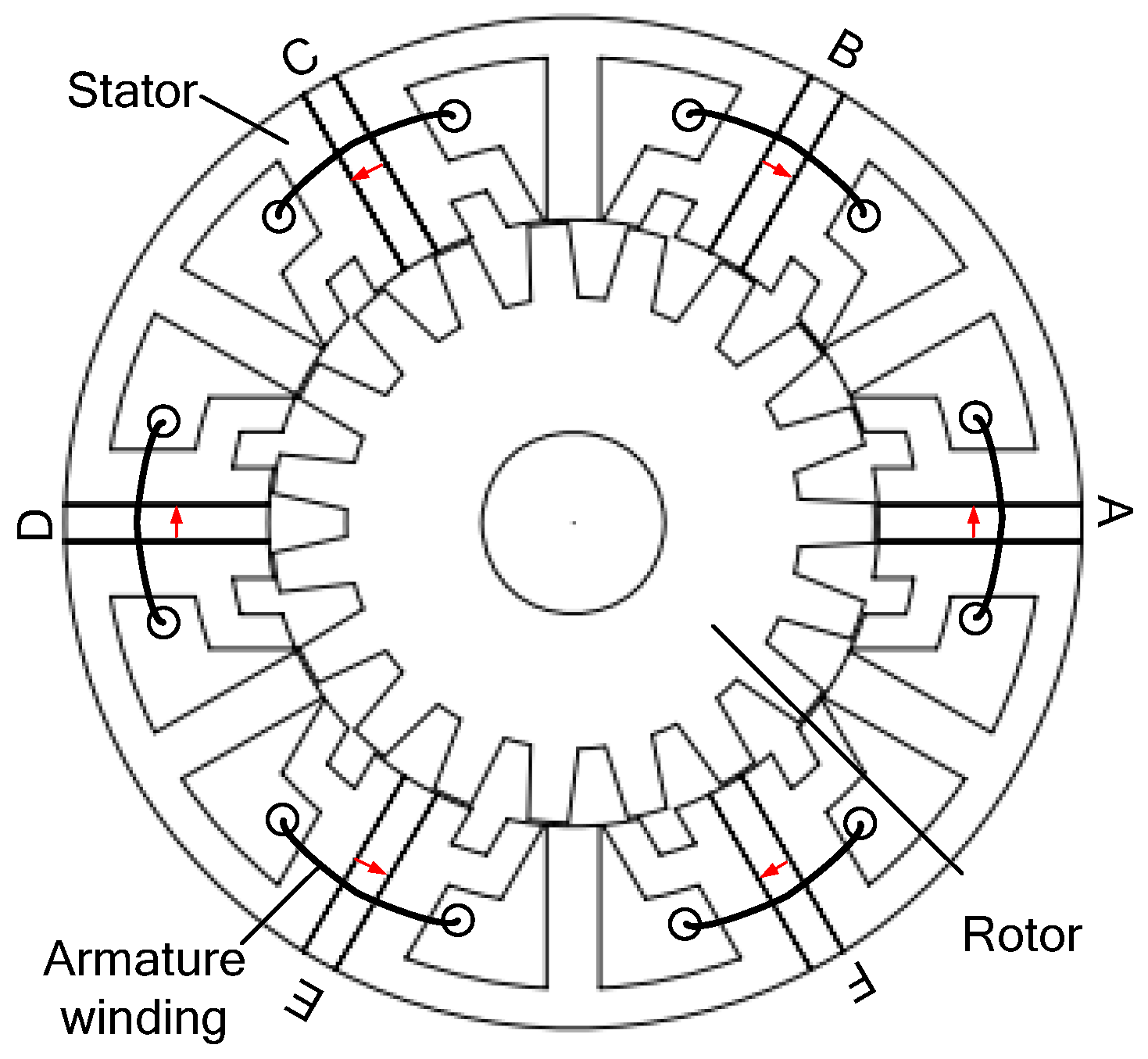
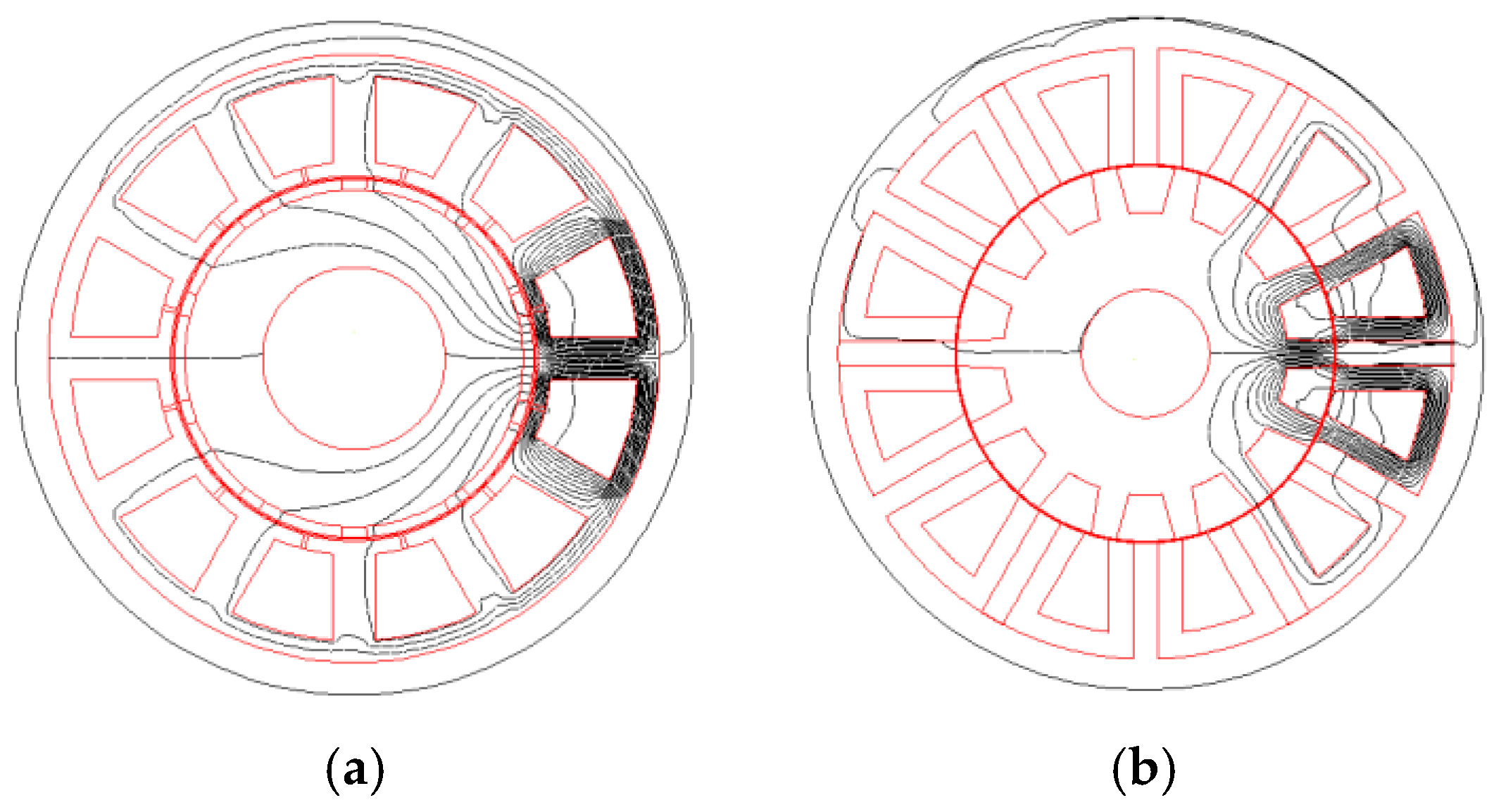
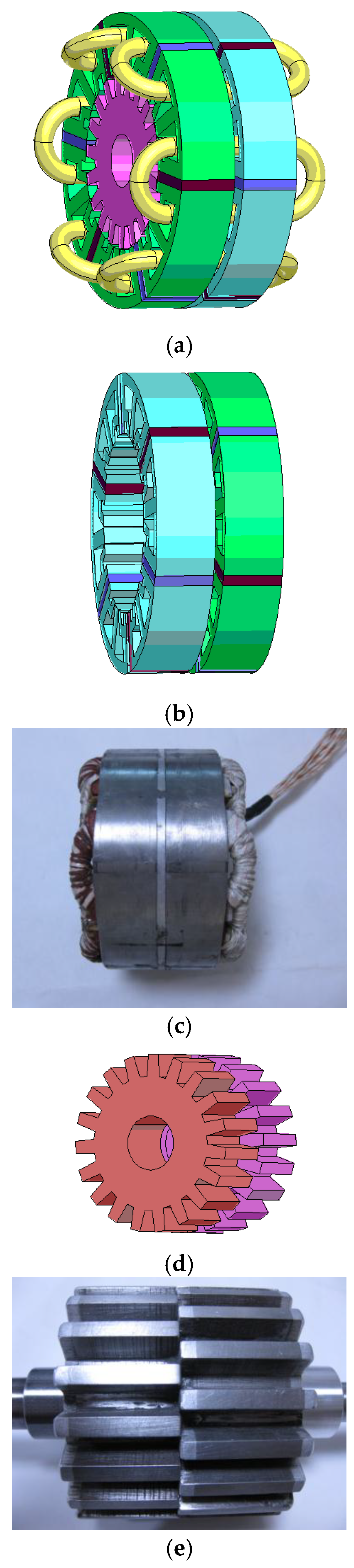
2.1. Machine Topology
- (1)
- The stagger degree between the two parts of the rotor is 180° (electrical degree).
- (2)
- The two-part PMs in a stator tooth have opposite magnetization direction.
- (1)
- The multi-tooth structure can effectively improve the ability to restrain short-circuit currents and maintain a relatively high torque density.
- (2)
- Based on the twisted-rotor, the phase back-EMF of high sinusoidal and symmetric can be obtained without amplitude decrease.
2.2. Influence of PI Controller on Rotor Speed Dynamic Performance
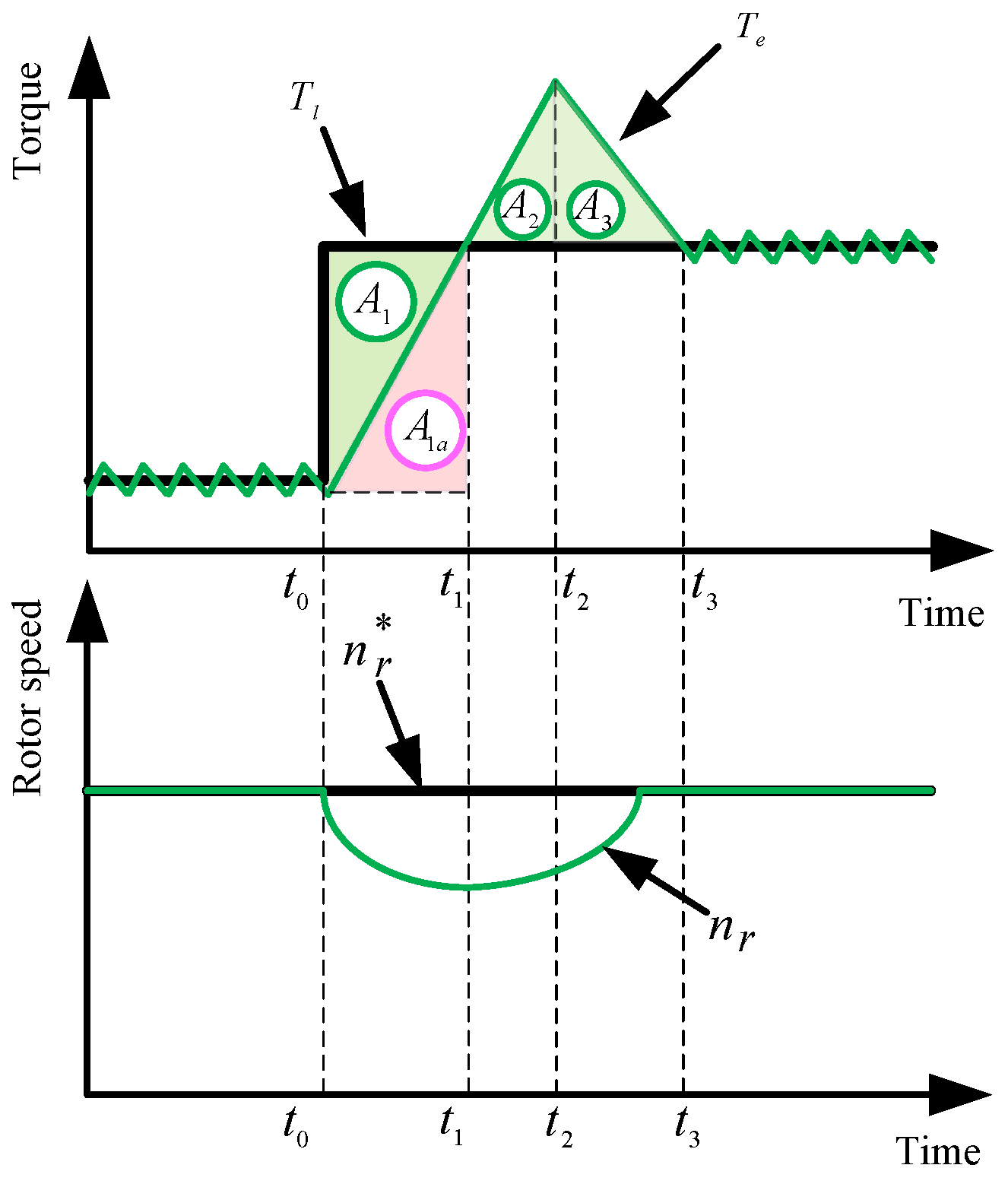
- (1)
- For the control system, the electromagnetic torque and the rotor speed converge at the same time are sufficient conditions for restoring to the steady-state.
- (2)
- The PI parameters of the speed loop in the RDTC always affect the dynamic response of both electromagnetic torque and rotor speed. The PI controller cannot possibly guarantee the optimal dynamic performance.
- (3)
- A group of switching vector sequences can be found to simultaneously restore the electromagnetic torque and the rotor speed at t1. Thus, the speed can be restored to the reference after a decrease and increase only once without overshooting, that is, the possible optimal dynamic response of nr can be obtained.
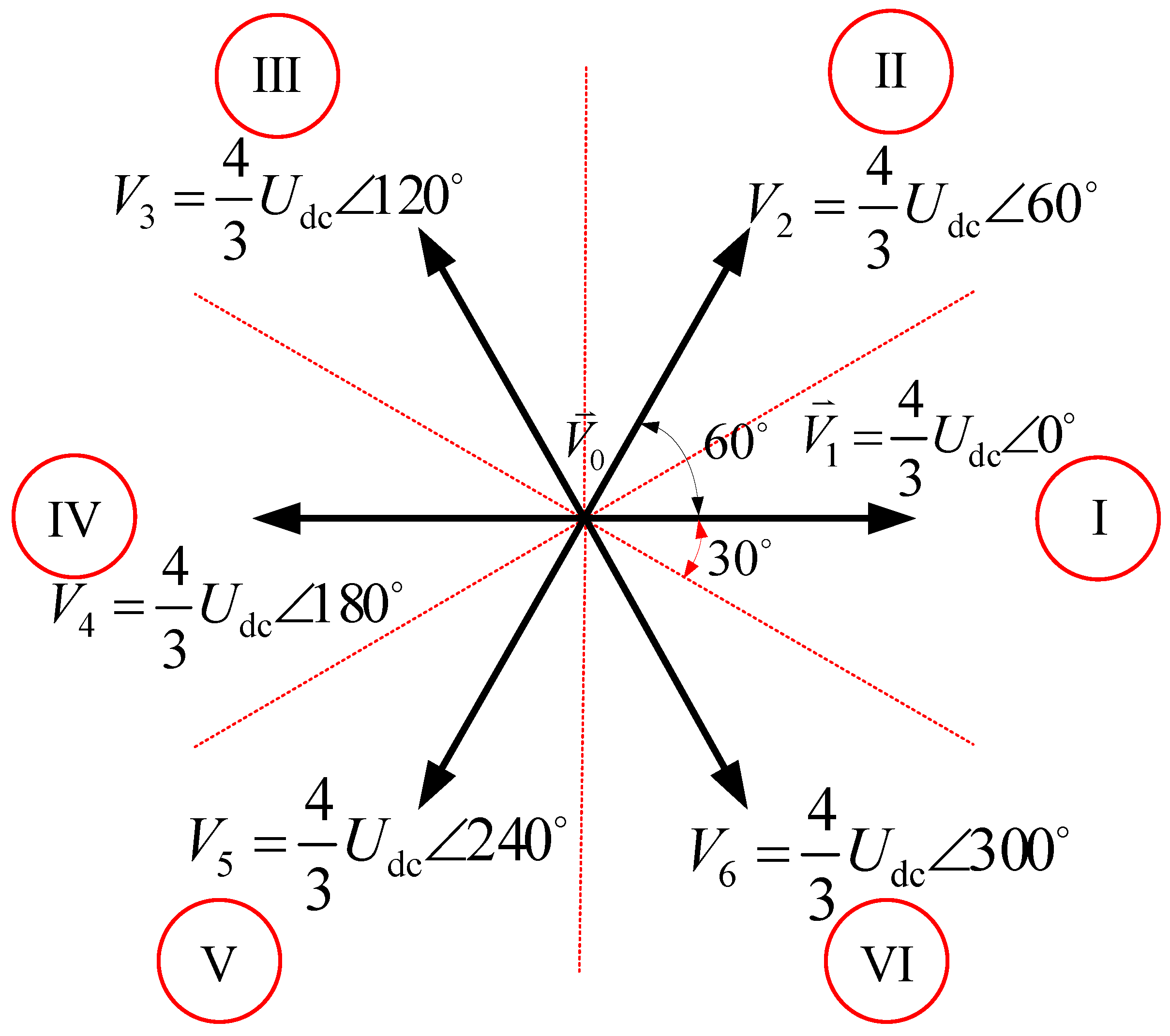
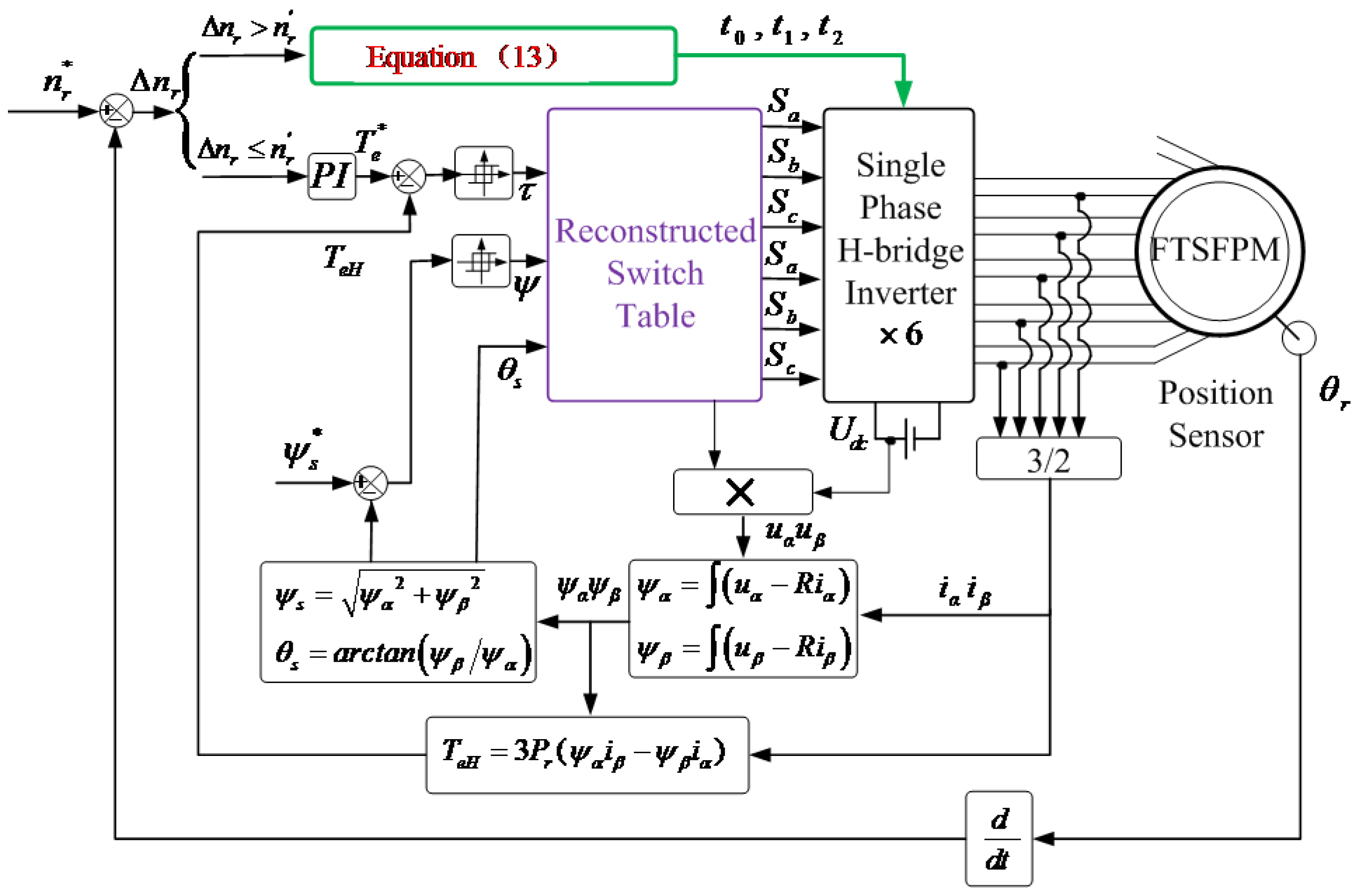
2.3. Torque Impulse Balance Control
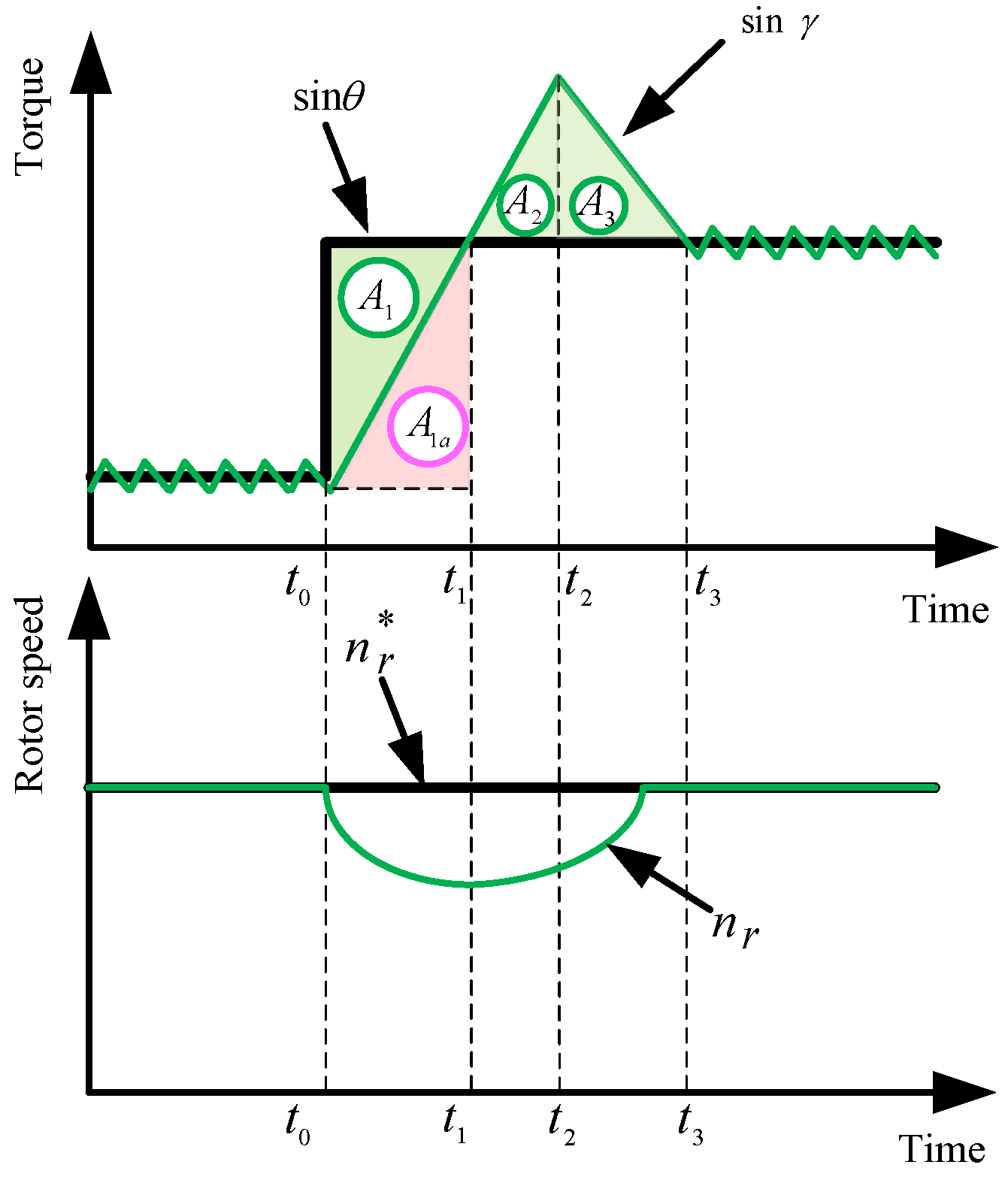
- In sector II and V of the stator flux linkage, see (8).
- In sector I, III, IV and VI of the stator flux linkage, see (9).
- In sector II and V of the stator flux linkage, see (10).
- In sector I, III, IV and VI of the stator flux linkage, see (11).where θ2 is the torque angle at t2.
- (1)
- First, achieve the double integral value of k1 from t0 to t1, where t1 is the moment when .
- (2)
- Then, calculate the double integral value of using t1, the moment when this integral value is equal to is t2.
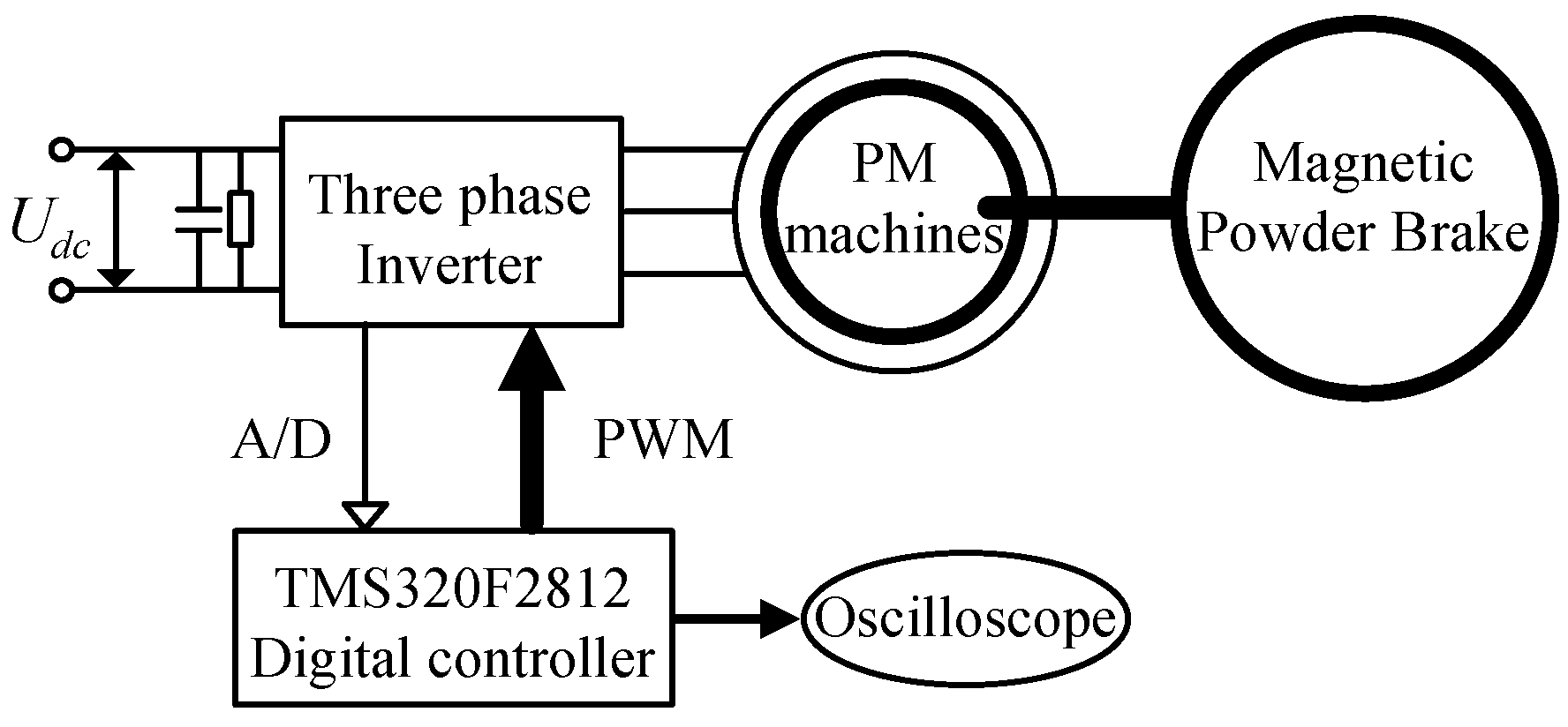
3. Experimental Results
3.1. Experimental Results under Open-Circuit Fault
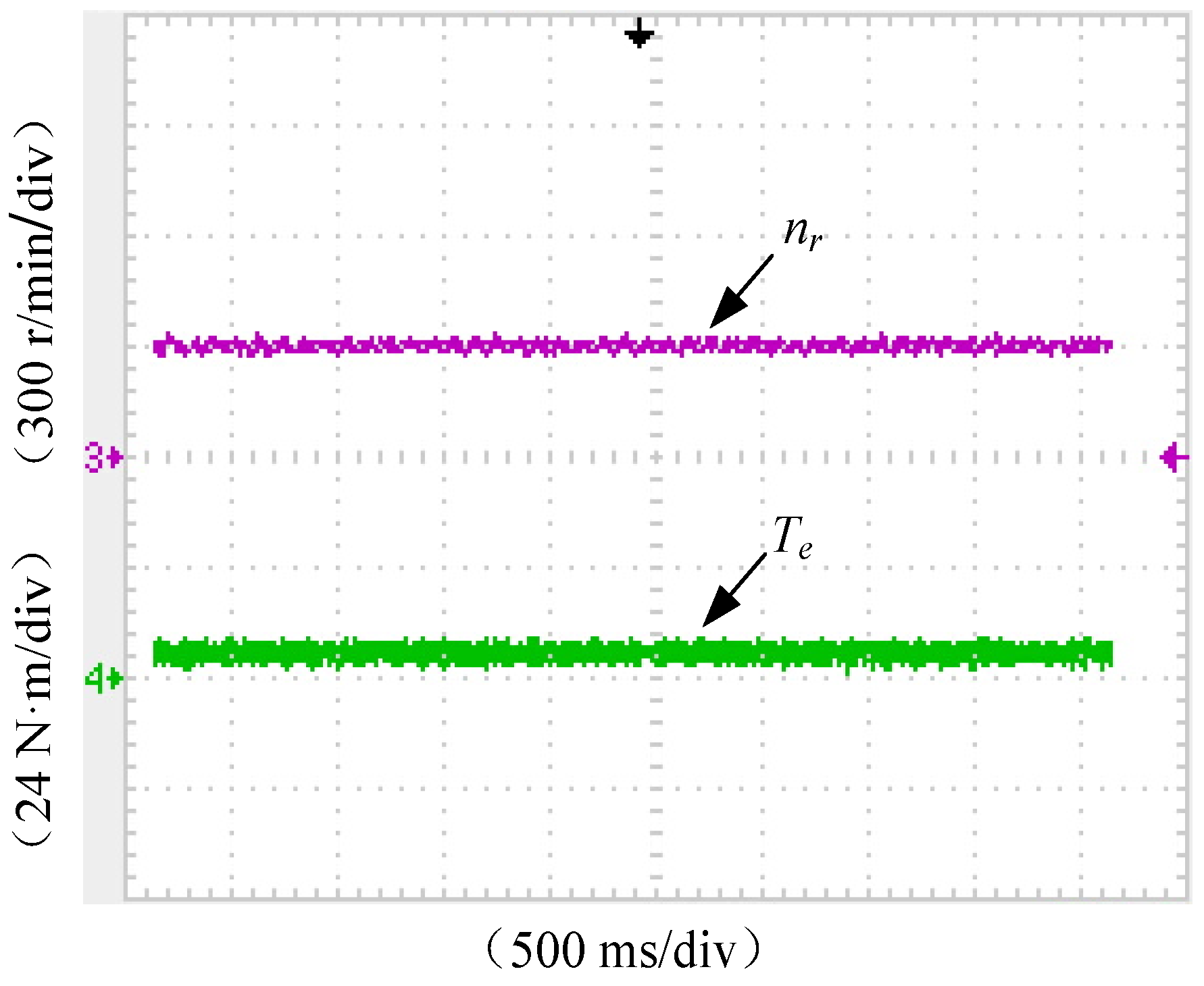
3.1.1. Steady-State Performance
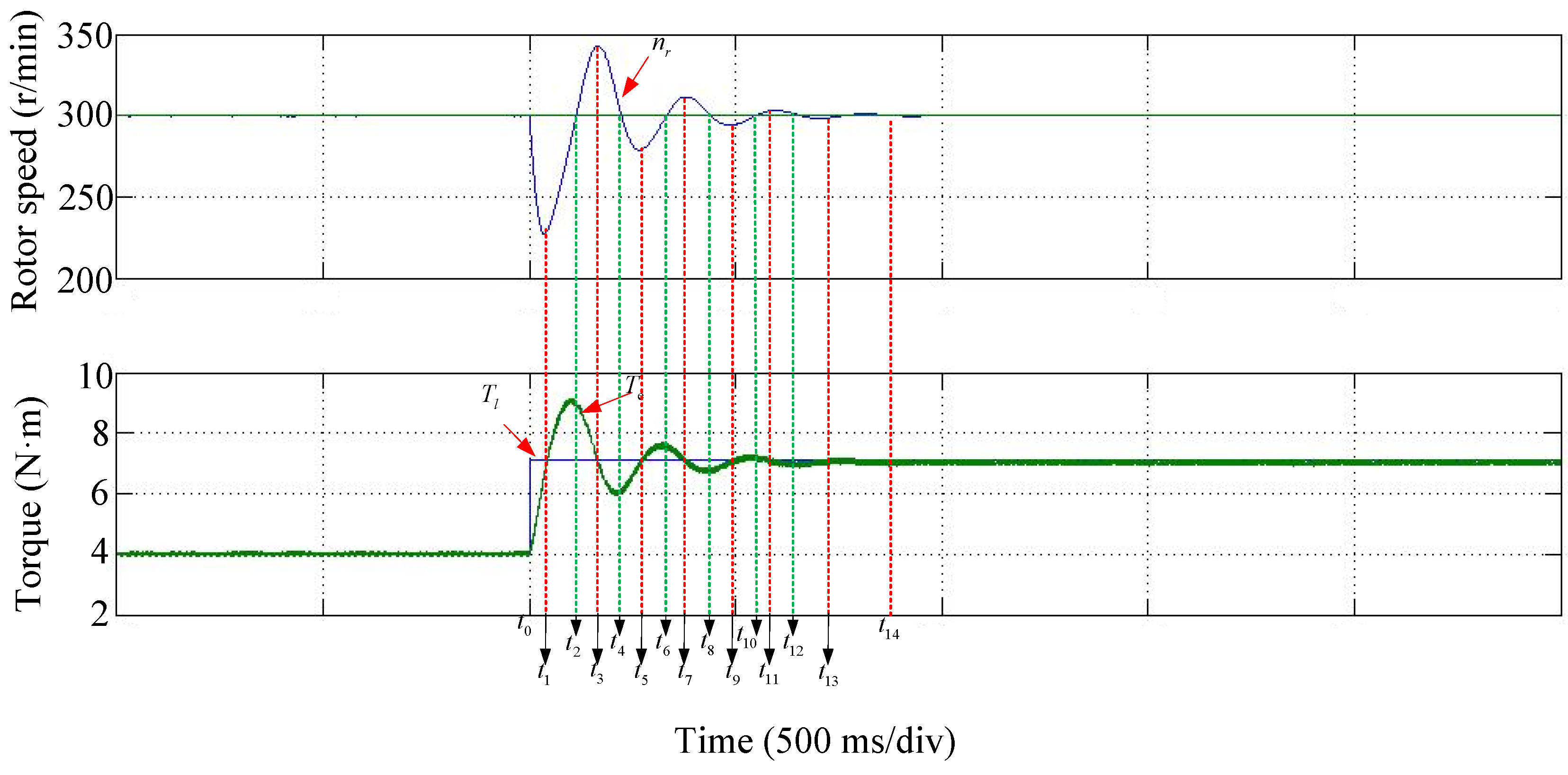
3.1.2. Dynamic Performance
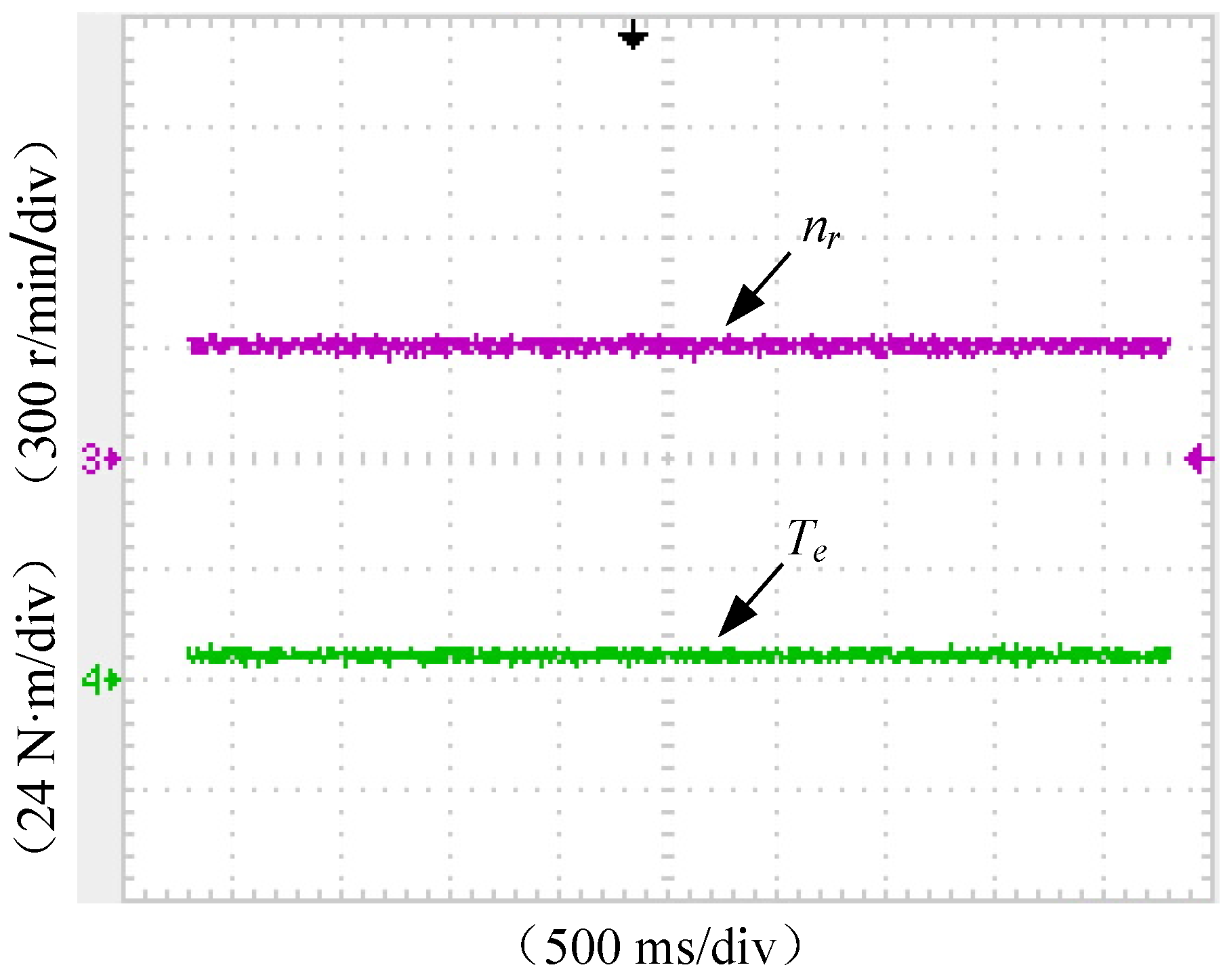
3.2. Experimental Results under Healthy Condition
4. Conclusions
- Compared with the vector control with current vector compensation technology, the direct torque control with voltage vector reconstruction technique (RDTC) can achieve the electromagnetic torque with good dynamic performance, but for the rotor speed, its dynamic performance is always influenced by the PI parameters of the speed loop.
- In the dynamic process, the torque impulse balance control (TIBC) can obtain an optimal voltage vector sequence which has only one switch between forward vectors and zero vectors.
- The optimal voltage vector can achieve excellent dynamic performance of the rotor speed: (1) No overshoot in the speed; (2) Only one adjustment; (3) The shortest settling time.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chau, K.T.; Chan, C.C.; Liu, C.H. Overview of permanent-magnet brushless drives for electric and hybrid electric vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2246–2257. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Zigliotto, M. High-performance PM synchronous motor drive for an electrical scooter. IEEE Trans. Ind. Appl. 2001, 37, 1348–1355. [Google Scholar] [CrossRef]
- Dúbravka, P.; Rafajdus, P.; Makyš, P.; Szabó, L. Control of Switched Reluctance Motor by Current Profiling under Normal and Open Phase Operating Condition. IET Electr. Power Appl. 2017, 11, 548–556. [Google Scholar] [CrossRef]
- Miller, T.J.E. Electronic Control of Switched Reluctance Machines, 1st ed.; Newnes: Oxford, UK, 2001. [Google Scholar]
- Pyrhönen, J.; Jokinen, T.; Hrabovcová, V. Design of Rotating Electrical Machines, 1st ed.; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Jack, A.G.; Mecrow, B.C.; Haylock, J.A. A comparative study of permanent magnet and switched reluctance motors for high-performance fault-tolerant applications. IEEE Trans. Ind. Appl. 1996, 32, 889–895. [Google Scholar] [CrossRef]
- Ishak, D.; Zhu, Z.Q.; Howe, D. Comparison of PM brushless motors, with either all teeth or alternate teeth wound. IEEE Trans. Energy Convers. 2006, 21, 95–103. [Google Scholar] [CrossRef]
- Ishak, D.; Zhu, Z.Q.; Howe, D. Permanent magnet brushless machines with unequal tooth widths and similar slot and pole numbers. IEEE Trans. Ind. Appl. 2005, 41, 584–590. [Google Scholar] [CrossRef]
- Owen, R.L.; Zhu, Z.Q.; Thomas, A.S.; Jewell, G.W.; Howe, D. Fault-tolerant flux-switching permanent magnet brushless ac machines. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 5–9 October 2008; pp. 1–8. [Google Scholar]
- Mecrow, B.C.; Jack, A.G.; Haylock, J.A.; Coles, J. Fault-tolerant permanent magnet machine drives. IEE Proc. Inst. Electr. Power Appl. 1996, 143, 437–442. [Google Scholar] [CrossRef]
- Hua, H.; Zhu, Z.Q. Novel partitioned stator hybrid excited switched flux machines. IEEE Trans. Energy Convers. 2017, 32, 495–504. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, Z. A multi-tooth fault-tolerant flux-switching permanent-magnet machine with twisted-rotor. IEEE Trans. Magn. 2012, 48, 2674–2684. [Google Scholar] [CrossRef]
- Owen, R.L.; Zhu, Z.Q.; Thomas, A.S.; Jewell, G.W.; Howe, D. Alternate poles wound flux-switching permanent-magnet brushless AC machines. IEEE Trans. Ind. Appl. 2010, 46, 790–797. [Google Scholar] [CrossRef]
- Chen, J.T.; Zhu, Z.Q.; Howe, D. Stator and Rotor Pole Combinations for multi-tooth flux-switching PM brushless AC machines. IEEE Trans. Magn. 2008, 44, 4659–4667. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Chen, J.T.; Pang, Y.; Howe, D.; Iwasaki, S.; Deodhar, R. Analysis of a novel multi-tooth flux-switching PM brushless AC machine for high torque direct-drive applications. IEEE Trans. Magn. 2008, 44, 4313–4316. [Google Scholar] [CrossRef]
- Aboelhassan, M.O.; Raminosoa, T.; Goodman, A.; De Lillo, L.; Gerada, C. Performance evaluation of a vector-control fault-tolerant flux-switching motor drive. IEEE Trans. Ind. Electron. 2013, 60, 2997–3006. [Google Scholar] [CrossRef]
- Hoang, K.D.; Zhu, Z.Q.; Foster, M. Direct torque control of permanent magnet brushless AC drive with single-phase open-circuit fault accounting for influence of inverter voltage drop. IET Electr. Power Appl. 2013, 7, 369–380. [Google Scholar] [CrossRef]
- Gobbi, R.; Ramar, K. Optimisation techniques for a hysteresis current controller to minimise torque ripple in switch ed reluctance motors. IET Electr. Power Appl. 2009, 3, 453–460. [Google Scholar] [CrossRef]
- Dubravka, P.; Rafajdus, P.; Makys, P.; Peniak, A.; Hrabovcova, V.; Szabo, L.; Ruba, M. Design of fault tolerant control technique for SRM drive. In Proceedings of the 2014 16th European Conference on Power Electronics and Applications (EPE’4-ECCE Europe), Lappeenranta, Finland, 26–28 August 2014; pp. 1–8. [Google Scholar]
- Gameiro, N.S.; Cardoso, A.J.M. Fault tolerant cont rol strategy of SRM drives. In Proceedings of the International Symposiun on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 11–13 June 2008; pp. 301–306. [Google Scholar]
- Mir, S.; Islam, M.S.; Sebastian, T.; Husain, I. Fault-tolerant switched reluctance motor drive using adaptive fuzzy logic controller. IEEE Trans. Power Electron. 2004, 19, 289–295. [Google Scholar] [CrossRef]
- Zeng, H.; Chen, H.; Shi, J. Direct instantaneous torque control with wide operating range for switched reluctance motors. IET Electr. Power Appl. 2015, 9, 578–585. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, H.; Yang, Z. Average torque control of switched reluctance machine drives for electric vehicles. IET Electr. Power Appl. 2015, 9, 459–468. [Google Scholar] [CrossRef]
- Sahin, C.; Amac, A.E.; Karacor, M.; Emadi, A. Reducing torque ripple of switched reluctance machines by relocation of rotor moulding clinches. IET Electr. Power Appl. 2012, 6, 753–760. [Google Scholar] [CrossRef]
- Inderka, R.B.; De Doncker, R.W.A.A. DITC-direct instantaneous torque control of switched reluctance drives. IEEE Trans. Ind. Appl. 2003, 39, 1046–1051. [Google Scholar] [CrossRef]
- Wong, K.F.; Cheng, K.W.E.; Ho, S.L. Four-quadrant instantaneous torque control of switched reluctance machine at low speed based on co-energy control. IET Electr. Power Appl. 2009, 3, 431–444. [Google Scholar] [CrossRef]
- Vujicic, V.P. Mini mization of torq ue ripple and copper losses in switched reluctance drive. IEEE Trans. Power Electron. 2012, 27, 388–399. [Google Scholar] [CrossRef]
- Schramm, D.S.; Williams, B.W.; Green, T.C. Torque ripple reduction of switched reluctance motors by phase current optimal profiling. In Proceedings of the Power Electronics Specialists Conference, Toledo, Spain, 29 June–3 July 1992; pp. 857–860. [Google Scholar]
- Venkatesha, L.; Ramanarayanan, V. Torque ripple minimisation in switched reluctance motor with optimal control of phase currents. In Proceedings of the International Conference on Power Electronics, Drives and Energy Systems for Industrial Growth, Perth, Australia, 1–3 December 1998; pp. 529–534. [Google Scholar]
- Shaked, N.T.; Rabinovici, R. New procedures for minimizing the torque ripple in switched reluctance motors by optimizing the phase- current profile. IEEE Trans. Magn. 2005, 41, 1184–1192. [Google Scholar] [CrossRef]
- Mikail, R.; Sozer, Y.; Husain, I.; Islam, M.S.; Sebastian, T. Torque ripple minimization of switched reluctance machines through current pro filing. IEEE Trans. Ind. Appl. 2013, 49, 1258–1267. [Google Scholar] [CrossRef]
- Zhao, W.; Cheng, M.; Chau, K.T.; Hua, W.; Jia, H.; Ji, J.; Li, W. Stator-flux-oriented fault-tolerant control of flux-switching permanent-magnet motors. IEEE Trans. Magn. 2011, 47, 4191–4194. [Google Scholar] [CrossRef]
- Zhao, W.; Cheng, M.; Hua, W.; Jia, H.; Cao, R. Back-EMF Harmonic Analysis and Fault-Tolerant Control of Flux-Switching Permanent-Magnet Machine with Redundancy. IEEE Trans. Ind. Electron. 2011, 58, 1926–1935. [Google Scholar] [CrossRef]
- Zhao, W.; Cheng, M.; Chau, K.T.; Cao, R.; Ji, J. Remedial Injected-Harmonic-Current Operation of Redundant Flux-Switching Permanent-Magnet Motor Drives. IEEE Trans. Ind. Electron. 2013, 60, 151–159. [Google Scholar] [CrossRef]
- Buja, G.S.; Kazmierkowski, M.P. Direct torque control of PWM inverter-fed AC motors—A survey. IEEE Trans. Ind. Electron. 2004, 51, 744–757. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, Z.Q. Enhancement of steady-state performance in direct-torque-controlled dual three-phase permanent-magnet synchronous machine drives with modified switching table. IEEE Trans. Ind. Electron. 2015, 62, 3338–3350. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, L.; Huang, W.; Bu, F. A fault-tolerant induction generator system based on instantaneous torque control (ITC). IEEE Trans. Energy Convers. 2010, 25, 412–421. [Google Scholar] [CrossRef]
- Jia, L.; Liu, Y.F. Voltage-Based Charge Balance Controller Suitable for Both Digital and Analog Implementations. IEEE Trans. Power Electron. 2013, 28, 930–944. [Google Scholar] [CrossRef]



| Torque and Flux-Linkage | I | II | III | IV | V | VI |
|---|---|---|---|---|---|---|
| Torque and Flux-Linkage | I | II | III | IV | V | VI |
|---|---|---|---|---|---|---|
| Terms for Comparison | Mechanical System | Electrical System |
|---|---|---|
| Coordinate | Angular displacement θ | Flux-linkage ψ |
| Velocity | Angular velocity ω | Voltage u |
| Force | Torque T | Current i |
| Inertial element | Moment of inertia J | Capacitor C |
| Elastic element | Torsional stiffness coefficient Kθ | Inductance reciprocal 1/L |
| Resistance element | Rotation resistance coefficient Rω | Conductance G |
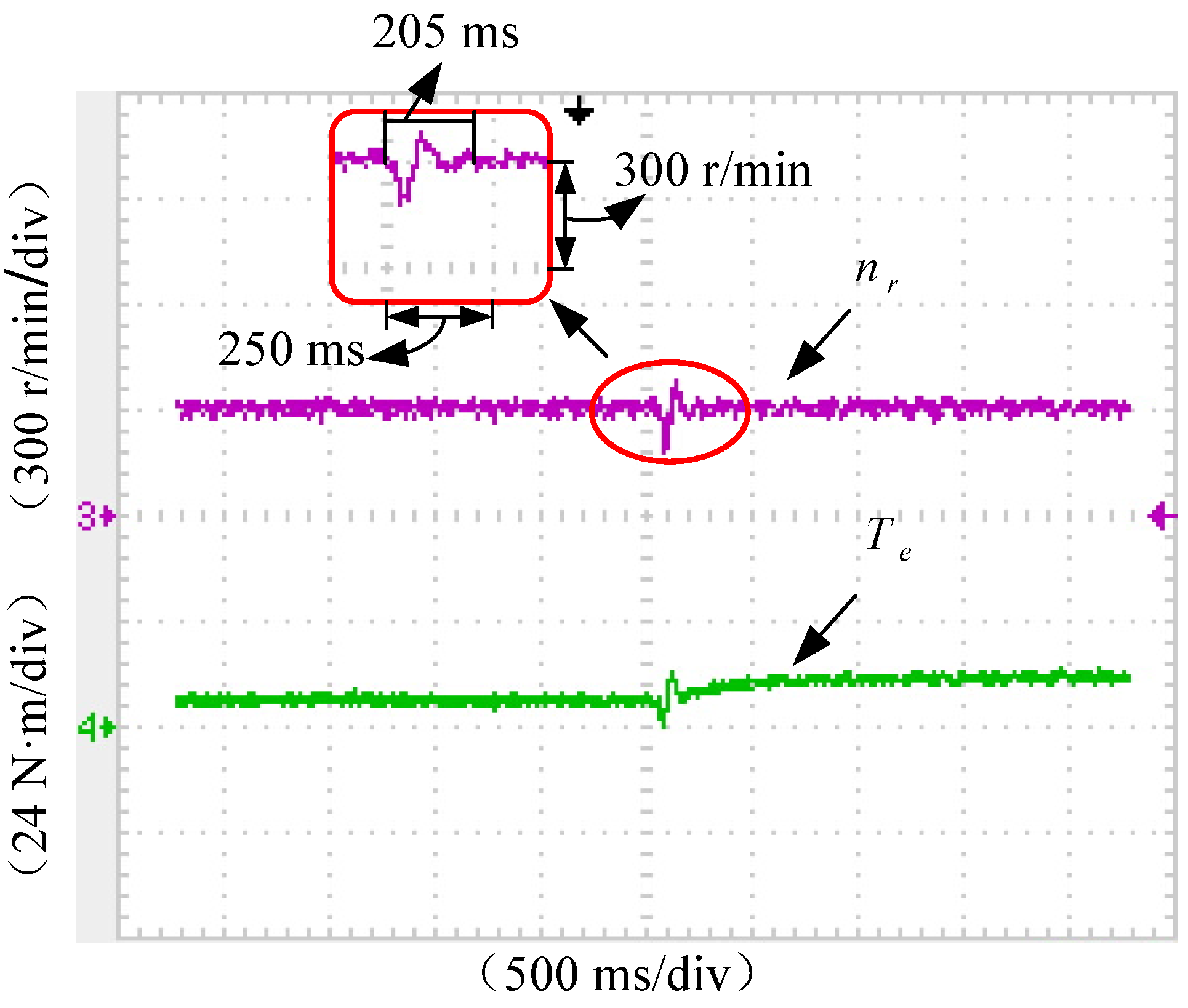
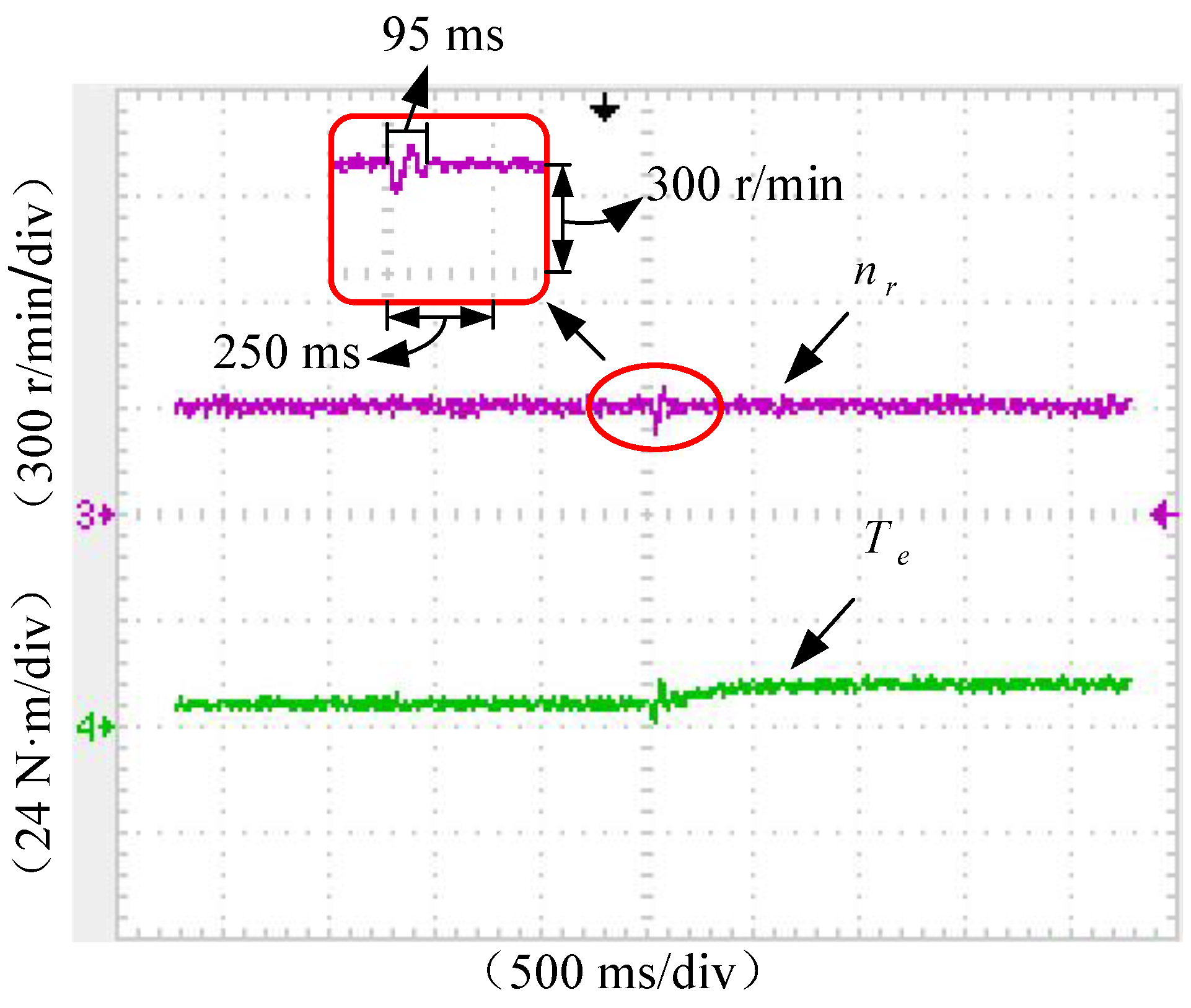
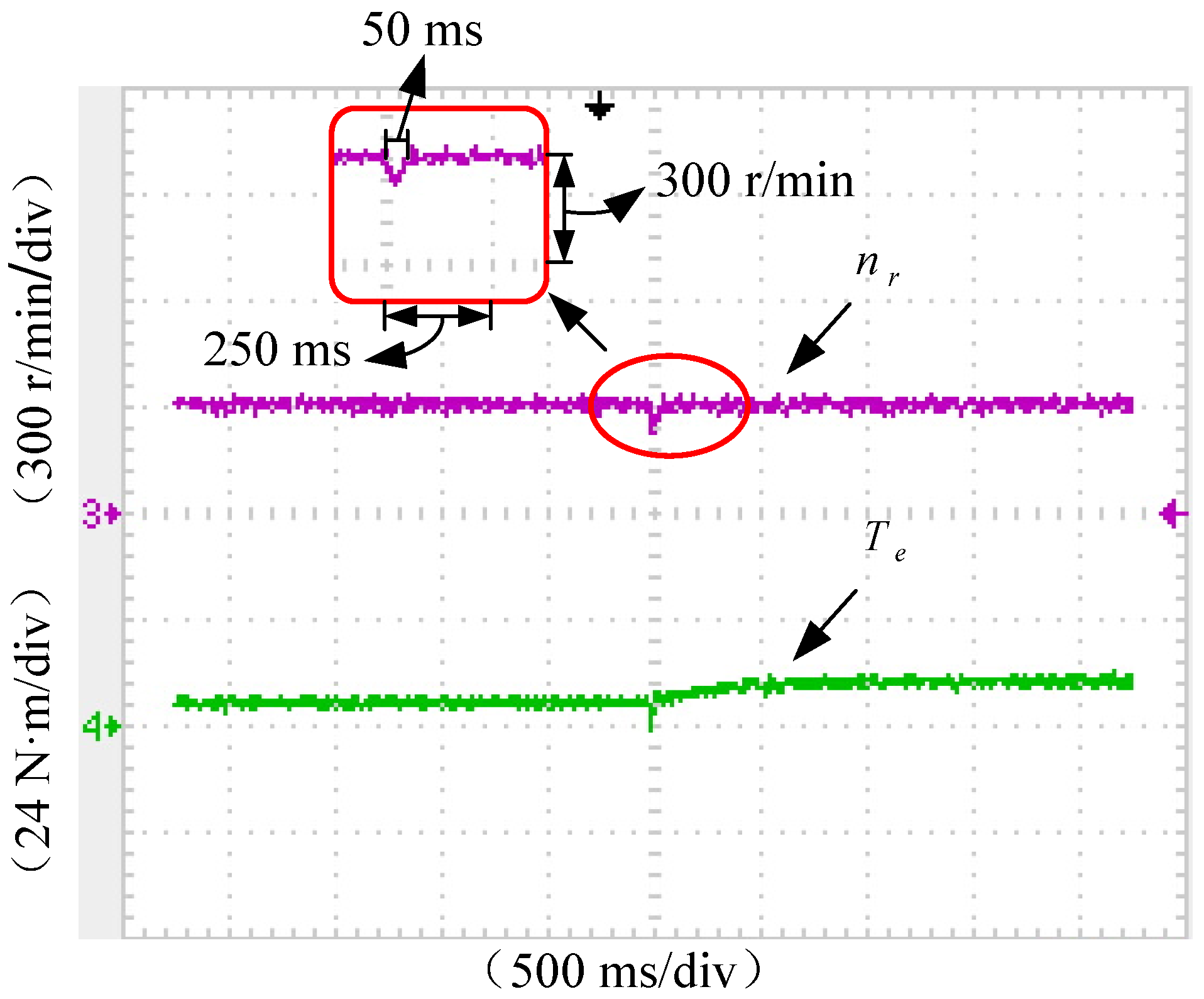
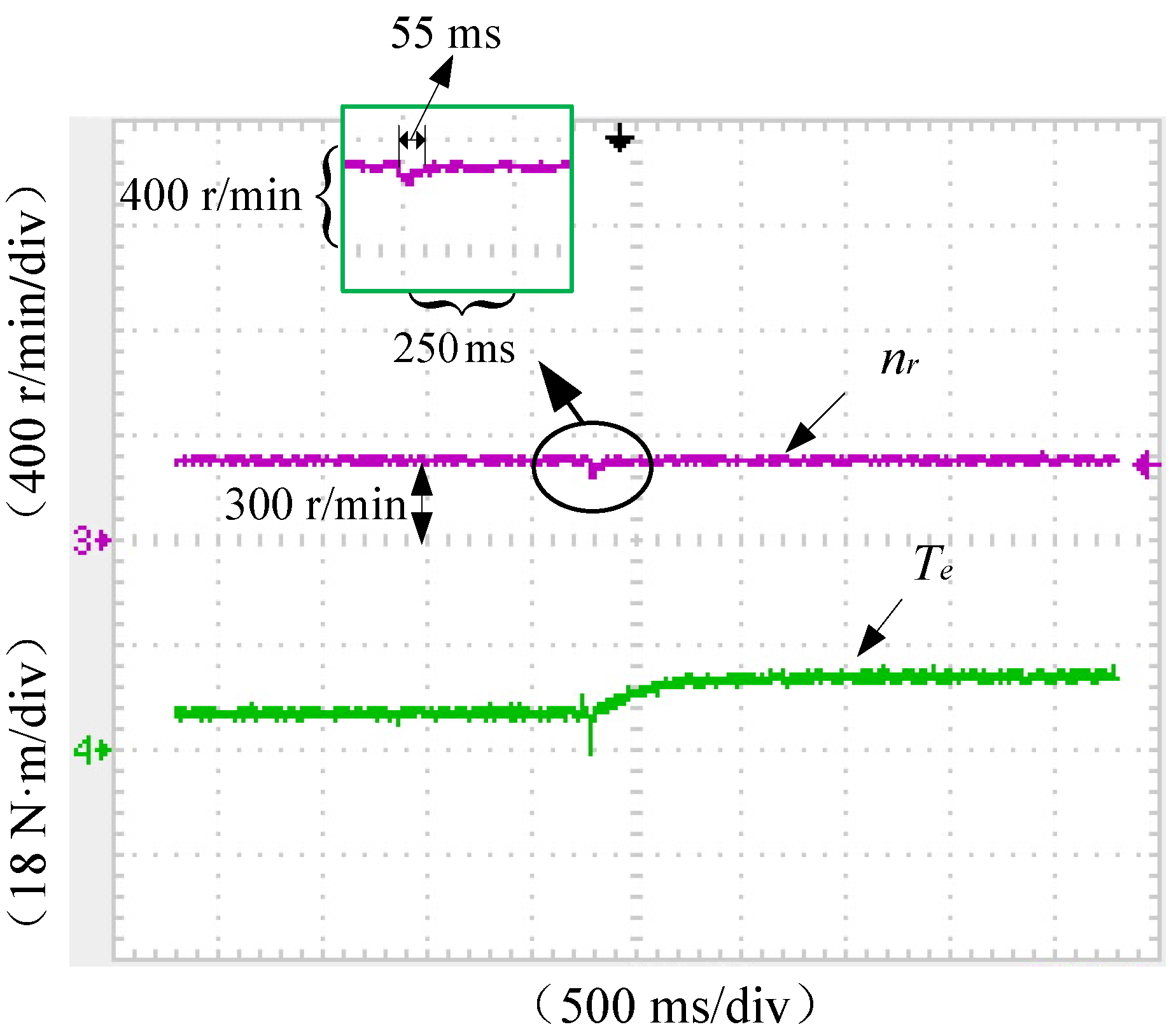
| Methods | Settling Time | Peak Value Time | Speed Dip Δn-down | Over Shoot Amount | Adjustment Times |
|---|---|---|---|---|---|
| RDTC without TIBC (P = 7.2, I = 0.96) | 205 ms | 75 ms | 120 r/min | 16.67% | 3 |
| RDTC without TIBC (P = 9.5, I = 1.1) | 95 ms | 60 ms | 70 r/min | 13.33% | 4 |
| RDTC with TIBC (TIBC-RDTC) | 50 ms | 50 ms | 60 r/min | 0.00% | 1 |
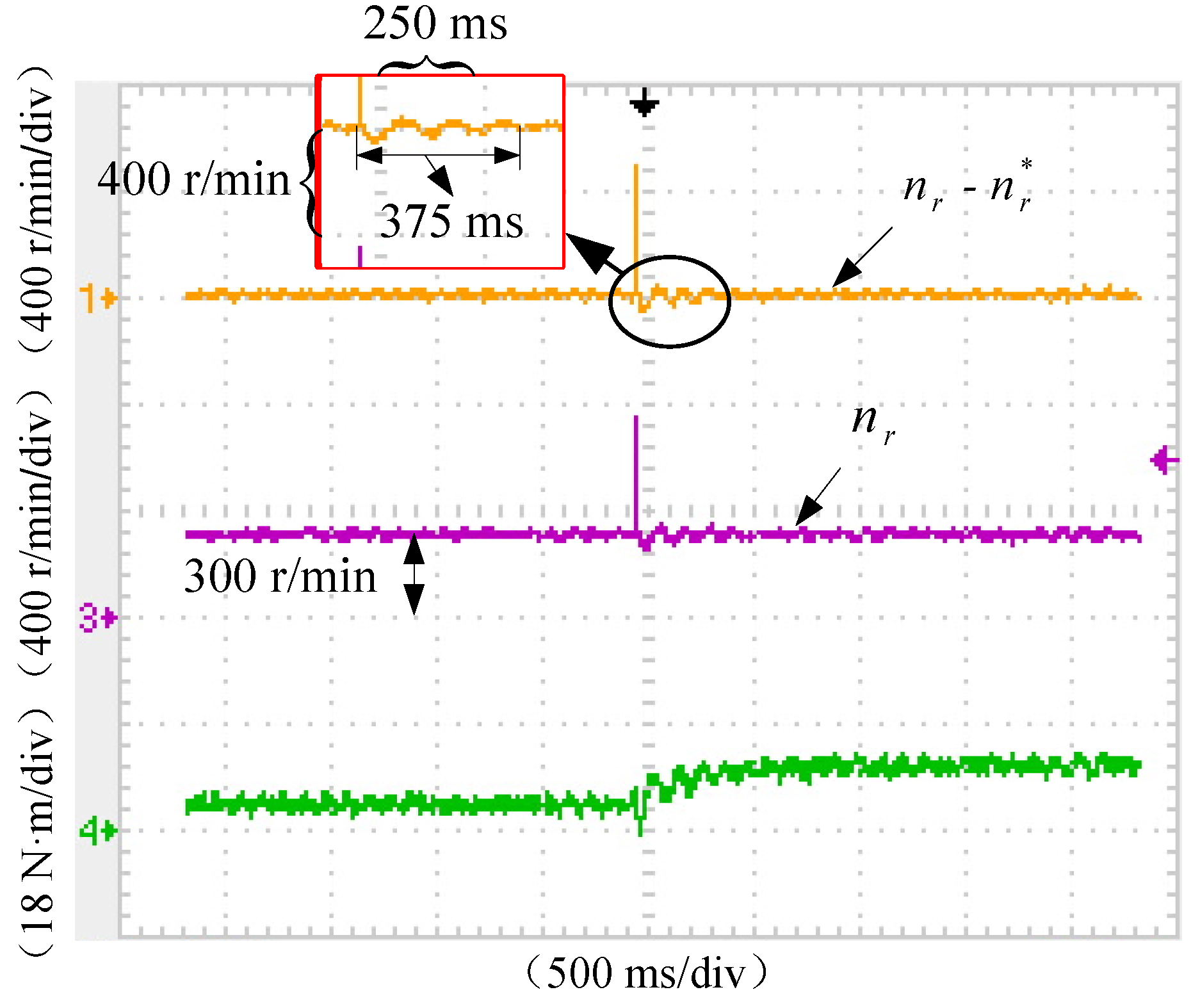
| Methods | -down | ||||
|---|---|---|---|---|---|
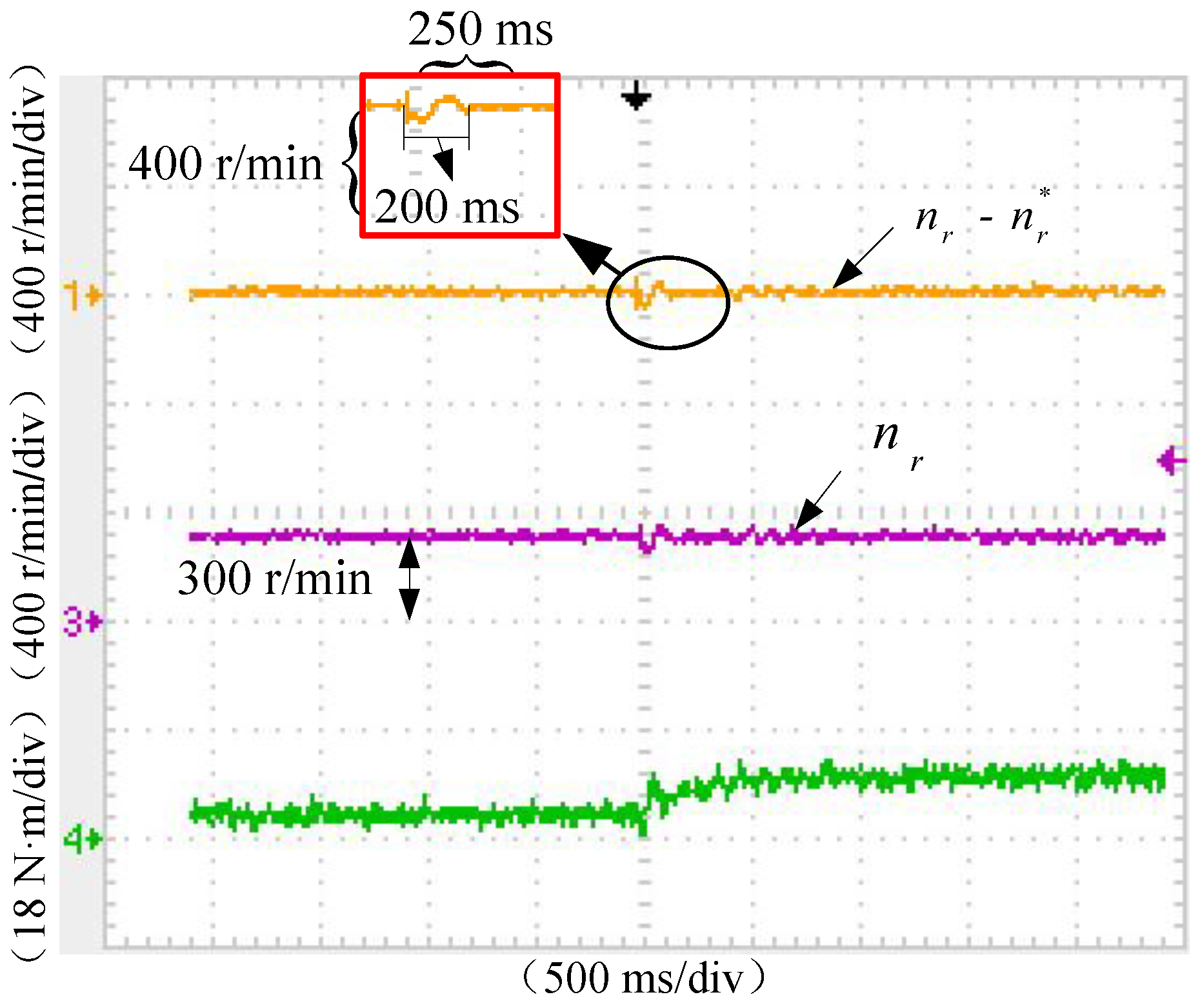
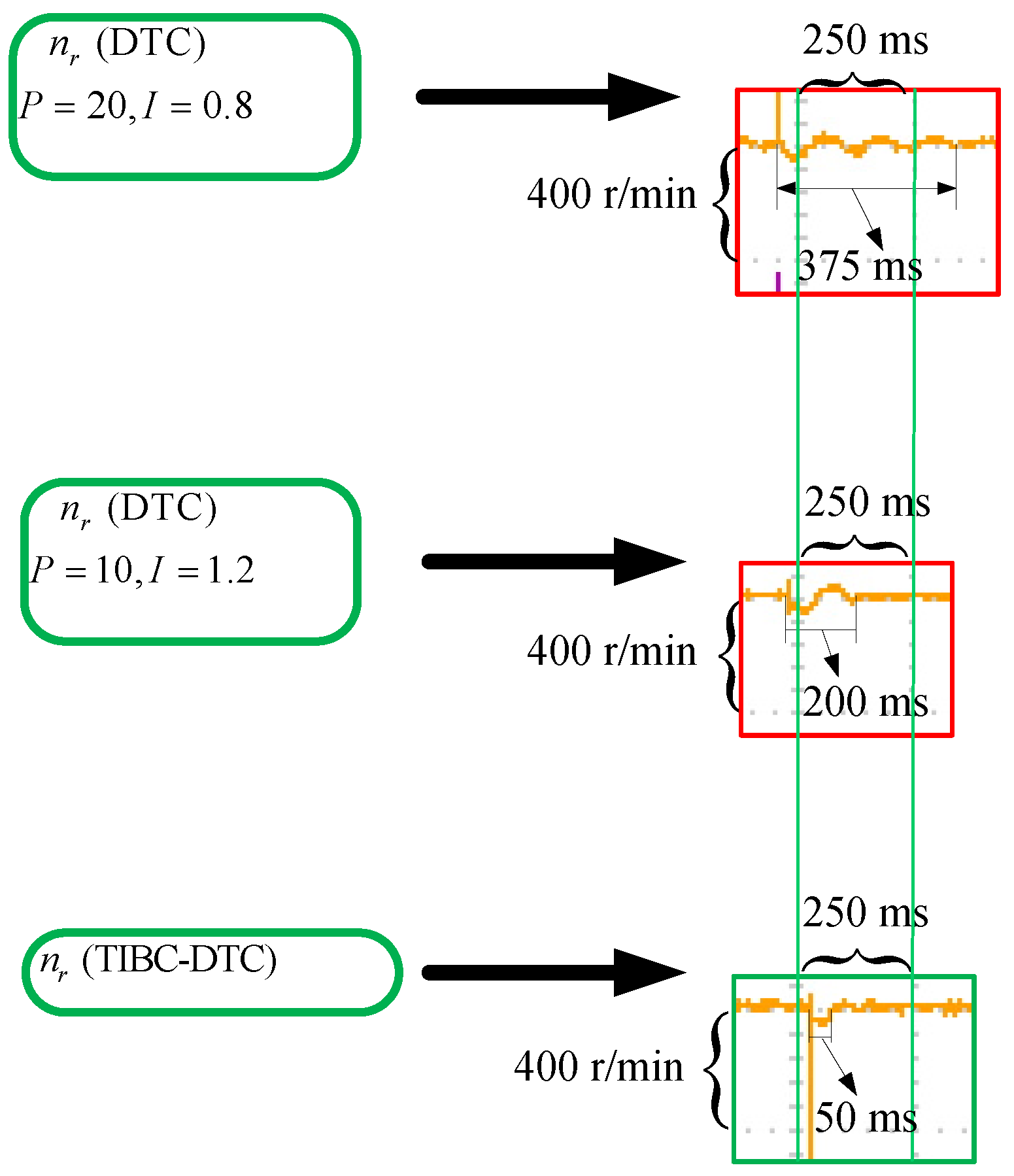
| DTC (P = 20, I = 0.8) | 375 ms | 175 ms | 65 r/min | 21.67% | 6 |
| DTC (P = 10, I = 1.2) | 200 ms | 160 ms | 48 r/min | 16.00% | 2 |
| TIBC-DTC | 50 ms | 50 ms | 40 r/min | 13.33% | 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Hao, W. A Torque Impulse Balance Control for Multi-Tooth Fault Tolerant Switched-Flux Machines under Open-Circuit Fault. Energies 2018, 11, 1919. https://doi.org/10.3390/en11071919
Wang Y, Hao W. A Torque Impulse Balance Control for Multi-Tooth Fault Tolerant Switched-Flux Machines under Open-Circuit Fault. Energies. 2018; 11(7):1919. https://doi.org/10.3390/en11071919
Chicago/Turabian StyleWang, Yu, and Wenjuan Hao. 2018. "A Torque Impulse Balance Control for Multi-Tooth Fault Tolerant Switched-Flux Machines under Open-Circuit Fault" Energies 11, no. 7: 1919. https://doi.org/10.3390/en11071919
APA StyleWang, Y., & Hao, W. (2018). A Torque Impulse Balance Control for Multi-Tooth Fault Tolerant Switched-Flux Machines under Open-Circuit Fault. Energies, 11(7), 1919. https://doi.org/10.3390/en11071919





