Abstract
Micro-phasor measurement unit (μPMU) is under fast development and becoming more and more important for application in future distribution networks. It is unrealistic and unaffordable to place all buses with μPMUs because of the high costs, leading to the necessity of determining optimal placement with minimal numbers of μPMUs in the distribution system. An optimal μPMU placement (OPP) based on the information entropy evaluation and node selection strategy (IENS) using greedy algorithm is presented in this paper. The uncertainties of distributed generations (DGs) and pseudo measurements are taken into consideration, and the two-point estimation method (2PEM) is utilized for solving stochastic state estimation problems. The set of buses selected by improved IENS, which can minimize the uncertainties of network and obtain system observability is considered as the optimal deployment of μPMUs. The proposed method utilizes the measurements of smart meters and pseudo measurements of load powers in the distribution systems to reduce the number of μPMUs and enhance the observability of the network. The results of the simulations prove the effectiveness of the proposed algorithm with the comparison of traditional topological methods for the OPP problem. The improved IENS method can obtain the optimal complete and incomplete μPMU placement in the distribution systems.
1. Introduction
Nowadays, more and more distributed generations (DGs) are integrated in distribution systems. One of the advantages of DG is that it can provide clean energy and diminish the emissions of CO2. The integrations of DGs would also cause bidirectional power flow and great uncertainties, which makes the supervision and operation of distribution more complicated. It is necessary to use different strategies to improve the reliability, efficiency, and safety in planning and operation of distribution, such as fault analysis [1,2], dynamic operation and control strategies [3], and the improvement of transient stability [4]. Therefore, the distribution system needs powerful and accurate monitoring meting devices. Phasor measurement unit (PMU) is the current most advanced metering device of synchronized measurement technology which plays an important role in wide-area measurement system [5]. Phasor measurement unit can provide real-time and high-accurate magnitude and phase angle measurements of both voltage and current. Based on PMU measurements, many applications, such as state estimation, fault location, outage management, and event detection can be exploited [6,7]. For example, a hierarchical architecture for monitoring the distribution grid based on PMU data is proposed [8]. A linear model which considers PMU location for the observability assessment in different contingencies is presented [9]. Currently, PMU has been widely applied in the transmission network, but not in the distribution network. With the development of PMU technology and the integration of DGs, it is promising to deploy PMUs in distribution level. The number of nodes in the distribution network is far larger than that of the transmission network. So, it is important to study the optimal PMU placement (OPP) problem considering the characteristics of distribution network.
Though great merits PMU has, it is quite difficult for PMUs to replace the supervisory control and data acquisition (SCADA) system due to expensive cost of PMUs. Thus, the PMUs and SCADA are expected to coexist in the power system for a long time in future [10]. The PMU measurements and traditional measurements from SCADA can be collectively used for improvement of state estimation [11,12,13,14] and the accurate power system model parameter estimation [15,16]. An algorithm to use synchrophasor data conditioning in the prefix part of the existing linear state estimation formulation is presented [17]. Phasor measurement unit measurements can be integrated to refine the estimations according to the measurements from SCADA [18,19]. Traditional measurements such as power flow measurements (PFMs) and injection measurements (IMs) can be considered in the optimal PMU placement model with PMU measurements in [20,21].
Typically, there are two main categories in the problem of OPP models. The first one aims to calculate the minimal number and locations of PMUs to ensure the full observability of power system. Topological [22] and numerical [23] algorithms are two common methods for solving the OPP problem. The concept of spanning tree of full rank is constructed when the network is considered to be fully observable in the topological methodology. Based on such graph theory, great numbers of algorithms have been proposed to do observability analysis by considering different constraints. A methodology based on graph theoretical observability analysis for complete system observability is proposed [24]. An integer linear programming method is utilized for optimal PMU placement considering various arrangements of lines connections at complex buses [25]. Great numbers of heuristic algorithms, such as Tabu search [26] and immunity genetic [27], have been widely used to solve the OPP problem, which are classified and compared with different points of views [28]. A binary semi-definite programing (BSDP) model is utilized to make power system numerically observable in the presence of conventional measurements [29]. The channel limits of PMUs are taken into consideration in the formulation of OPP model in Reference [30]. The iterated local search (ILS) metaheuristic method is used to minimize the size of PMU configuration which makes the network observable [31]. An upgraded binary harmony search algorithm is presented to attain the minimum number of PMUs and their relevant locations considering the different installation cost of PMUs at different buses [32]. A modified greedy algorithm is proposed to solve the OPP problem under both normal operating and contingency conditions [33]. The second category is to realize some specific applications instead of full observability. For instance, a mixed-integer linear programming (MILP) framework is proposed for placing minimal PMUs to locate any fault in transmission system [34]. Different contingency conditions in power systems including measurement losses, line outages, and communication constraints are considered in the optimal PMU placement model [35]. An iterative linear program algorithm is applied to meet the prescribed synchrophasor availability profile in a smart grid in [36]. A fast greedy algorithm is used to strategically place secure PMUs at important buses to enhance the security of network and defend against data injection attacks [37]. The bad data detection and identification capability of the power system can be highly improved according to the optimal PMU placement [38]. An optimal placement for power system dynamic state estimation is presented by using empirical observability Gramian in [39]. A systematic framework is proposed for enhancing the situational awareness of the system operator using PMU placement [40]. A two-stage methodology for online identification of power system dynamic signature using PMU measurements and data mining is discussed in [41]. The multinomial logistic regression is utilized to place PMU optimally for identifying a single line outage in a power grid [42].
Besides the above methods, another PMU placement method using information-theoretic criterion called mutual information is presented in [43]. It is stated that typical methods are very likely to result in suboptimal placement and significant performance loss when only topological observability criterion is centered around. The information gain achieved by the PMU measurements is modeled as Shannon mutual information (MI) to obtain the full observability and incomplete observability. The PMU placement results based on information-theoretic criterion have been proved the effectiveness of the integration of mutual information to OPP model. In [25], the information-theoretic criterion could only be applied in the DC power flow model which cannot work in the AC power flow mode.
Phasor measurement units have not been widely applied at the distribution level due to great challenges in both technical and economic aspects [44]. To overcome these problems, several laboratories such as Power Standards Lab and Lawrence Berkeley National Lab have devoted to developing a novel powerful micro-phasor measurement unit (μPMU) and studied its practical and potential distribution system applications [45,46]. An advanced predictive analytics application for monitoring, protection, and control of distribution system assets using μPMU technology is presented in [47]. The diagnostic applications promising for future work are discussed for the presence of high penetrations of DGs. Despite the powerful functions μPMU has, it still requires a great number of μPMUs to obtain full observability which makes the cost of placement unaffordable. Therefore, the conventional measurements from smart meters such as feeder terminal units (FTUs) need to be considered in the placement model. Also, the data from historical database is necessarily utilized to generate pseudo measurements of load power as injection measurements by using load forecasting methods.
With the increasing DGs and the use of pseudo measurements in distribution level, the measurements errors need to be considered which results in stochastic state estimation. Few studies have been carried out about the stochastic state estimation in the literature. However, two-point estimate method (2PEM) which has been used to handle the uncertain variables based on the deterministic problem in mathematics field has been applicable for solving uncertainty problems in the field of electric system [48,49]. For instance, it has been used to account for uncertainties in the optimal power flow problem in electricity markets in [48] and to quantify the power transfer capability uncertainty in [49]. Thus, 2PEM is utilized to solve stochastic state estimation problem in this paper.
This paper proposes a novel optimal μPMU placement methodology by using the information entropy evaluation and node selection strategy (IENS) based on the mutual information theory. The results of stochastic state estimation which solved by 2PEM are used for the calculation of mutual information gain. The improved IENS method is also presented with two important rules. With the integration of pseudo measurements and FTU measurements, the proposed improved IENS can obtain the optimal μPMU placement for both complete and incomplete observability.
The contribution of this paper can be summarized as follows:
- (1)
- The 2PEM is proposed to solve the stochastic state estimation considering the measurement errors of distribution network caused by DGs and pseudo injection measurements.
- (2)
- The differential entropy of mutual information is proposed to evaluate the uncertainty of network which can be used in the AC power flow mode in distribution level.
- (3)
- The improved IENS is proposed to obtain the optimal μPMU placement for both complete and incomplete observability under the improvement of initial IENS.
The rest of the paper is organized as follows. In Section 2, the formulation of mathematical model and IENS and improved IENS are illustrated. In Section 3, different case studies of revised IEEE 123-bus test system for complete and incomplete observability are presented. The conclusions are noted in Section 4.
2. Mathematical Formulation of Optimal μPMU Placement
In this section, the mathematical model of proposed method is elaborated in detail. The measurement errors of the distribution system are taken into consideration when using DGs and pseudo injection measurements obtained by load forecasting methods. The differential entropy of mutual information theory is firstly illustrated to assess the uncertainty of network under specific measurement configurations. Then 2PEM is proposed to solve the stochastic state estimation problem and standard deviation and mean of state variables can be calculated. Finally, IENS and improved INES are presented to obtain the optimal μPMU set.
2.1. Differential Entropy for Assessing Uncertainty of Network
As shown in [43], maximizing the mutual information is equivalent to minimizing the state estimation error covariance matrix. The concept of information gain is also used to assess the uncertainty of the distribution network.
Different from the mutual information only used in DC power flow model in [43], the differential entropy in this paper can be utilized to model the uncertainties of network using system states in AC power flow model:
where I(x) is differential entropy for the continuous variable x, and x represents magnitude and phasor of voltage in this paper, and is the standard deviation and mean of. The uncertainty of the network under specific measurement configurations can be assessed by the above equation according to the standard deviation of state variables.
The standard deviation used in Equation (1) can be calculated through 2PEM for stochastic state estimation, which will be introduced in the following part.
2.2. Stochastic State Estimation Using Two-Point Estimation Method
The deterministic state estimation model is firstly introduced, and the formulation of stochastic state estimation model and two-point estimation method comes next.
The formulation for deterministic state estimation including both μPMU and SCADA measurements is adopted here, just as the estimator with phasor measurements mixed with traditional measurements in Reference [11], given by:
where is the state variables of network, is the vector of traditional measurements from SCADA, and is the vector of measurements obtained from μPMUs, ) is the nonlinear function of state vector, and is the measurement error vector of SCADA measurements and μPMU measurements, with the covariance matrix and .
where is the variance of ith measurements, and is the number of SCADA measurements and μPMU measurements, respectively.
The Jacobian matrix is usually obtained by following derivation:
It is considered to be a nonlinear problem and Newton iterative method is usually used to solve this kind of problem. Deterministic weighted least square (WLS) state estimation is solved by following iterative equation:
where q is the number of iteration, is the gain matrix calculated by
is the block diagonal matrix given by
where is the general rotation matrix [25]. According to the WLS iterative method, state variables of the network can be calculated when it reaches the required accuracy.
Various methods and techniques such as linear regression models, autoregressive and moving average models, and artificial neural networks have been applied in the field of load forecasting. The pseudo injection measurements of load power can be obtained according to the database of distribution management system by using certain load forecasting method which is not the key part in this paper. It is inevitable to have prediction errors in pseudo measurements which results in uncertainty in the state estimation of power system.
Taking the forecasting errors of loads and DGs into consideration, the deterministic state estimation then turns to be the stochastic one. As described in [50,51], two-point estimate method is a variation of point estimation estimate method, and it can be used to decompose Equation (2) into sub-problems by using two deterministic values of every uncertain variable on both sides of corresponding mean. The results of stochastic state estimation can be obtained by 2 runs of the deterministic state estimation for each uncertain variables in the measurement model, once for the value above the mean, once for the value below the mean, and other variables are set to be corresponding means. For example, if there are m uncertain measurements, then only 2m runs of deterministic state estimation are needed. Then the statistical results like mean, variance, and probability density function of state variables could be acquired after the calculation of stochastic state estimation. The uncertainty of the network could be assessed by calculation of mutual information gain using Equation (1).
In the state estimation, let Y denote the random variable with probability density function (PDF) where Y is the measurements vector in state estimation model. For nonlinear function where X is the state variables vector of distribution network. The procedure for calculating stochastic state estimation using two-point estimation method can be summarized as follows:
- (1)
- Determine the number of uncertain variables of pseudo measurements as n, and the number of certain measurements obtained from PMU and SCADA as .
- (2)
- Set and .
- (3)
- Set , and carry out the following steps until .
- (4)
- Calculate concentrations , locations of concentrations and its probabilitieswhere and is the mean and the standard deviation of according to the measurement information.
- (1)
- Run the deterministic state estimation for by using .
- (2)
- Update and
Calculate the mean and the standard deviation of state variables and then .
According to the calculation of mean and the standard deviation of state variables for stochastic state estimation by 2PEM, the uncertainties of network can be evaluated by Equation (1) under certain configuration of μPMU placement.
2.3. Information Entropy Evaluation and Node Selection Strategy for μPMU Sets
After the illustration of differential entropy and two-point estimate method, the following part aims to illustrate the IENS and improved IENS for calculating the optimal μPMU placement to maximize the information gain of the distribution system and obtain the observability of the network.
2.3.1. Information Entropy Evaluation and Node Selection Strategy
It is assumed that pseudo measurements of injections powers of all buses can be acquired according to the historical database in the distribution energy management using load forecasting method. FTU measurements are also integrated with pseudo measurements to enhance the observability of distribution network.
In general, the greedy algorithm is used to obtain the set of optimal μPMU placement sequentially following an incremental expansion strategy in IENS.
The steps of IENS are introduced as follows:
Step One:
- (1)
- Define the set of candidate buses from which to choose for the installation of new μPMU: . The location of new μPMU is selected from the buses in. It is assumed to contain all the buses in the network if there is no mandatory μPMU allocated beforehand. The bus to be installed with new μPMU will be discarded from after the selection of new μPMU.
- (2)
- Define the set of buses for the installation of μPMU as . The buses in would be installed with μPMUs. is null if there is no μPMU allocated beforehand. The bus to be installed with new μPMU will be added into after the selection of new μPMU.
- (3)
- Set the number of μPMUs to be installed in the network as.
Step Two:
Run stochastic state estimation using 2PEM and obtain the statistical results under initial measurement configuration which consists of pseudo measurements and FTU measurements. The initial differential entropy of network can be calculated by Equation (17):
where is the number of all buses, is the standard deviation of the voltage amplitude and phase angle at bus .
Step Three:
- (1)
- Run the following part:
For : (a) Build a new set: where first columns are buses already installed with μPMUs and last column means the lth bus candidate for the location of μPMU. (b) Add μPMU measurements of into initial measurement configuration as new measurement configuration. Then run stochastic state estimation by using 2PEM under lth measurement configuration and calculate its differential entropy using Equation (17). End - (2)
- Find bus k which maximizes the improvement in information gain of differential entropy.Then , excludes bus k from , adds bus k into ,
Step Four:
If the current number of installed μPMU satisfies the desired number, then output the set as the installation set of μPMUs; otherwise turn to Step Three.
The optimal μPMU set can be obtained according to IENS. Usually, the number of μPMUs to be allocated in the network is decided by the project budget which is expected to be as much as possible. However, the upper limit of μPMU should not exceed , the number of optimal placement calculated by topological method for network full observability. An integrated model based on topological method is presented considering the effects of the zero injections buses (ZIBs) and conventional measurements (CMs) such as power flow measurements and injection measurements in [22]. The model of injection measurements is considered the same as that of ZIBs. This method is applied in this paper to determine the maximum number of μPMUs to be stalled in the network.
2.3.2. Selection Rules to Be Noticed
The IENS and topological method in Reference [22] is applied on a 11-bus test system where a FTU placed on line as shown in Figure 1. The FTU can measure the voltage magnitude of the tail bus of installed line and the power flow of the line.
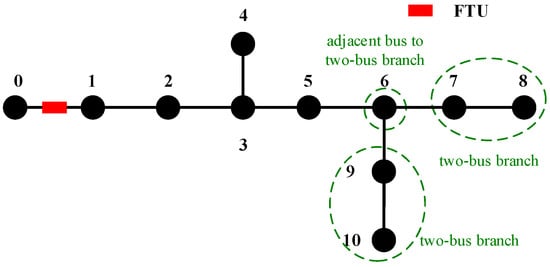
Figure 1.
11-bus test system.
According to the power flow measurements, the optimal μPMU placement obtained by topological method is shown in Figure 2. It needs only 4 μPMUs to make the network full observable.
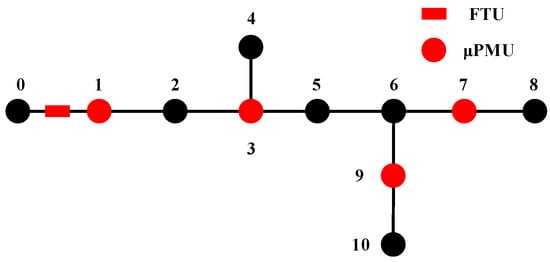
Figure 2.
Optimal placement by topological method.
Take the number of results by topological method as the required number of μPMUs to be installed in IENS: 4, the placement by IENS is shown in Figure 3.
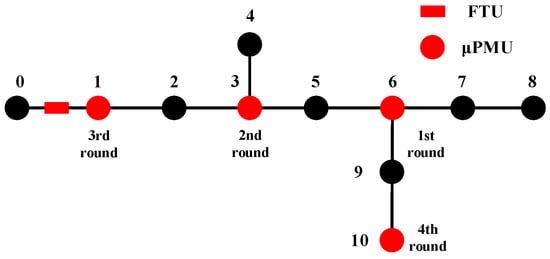
Figure 3.
Optimal placement by information entropy evaluation and node selection strategy (IENS).
The sequence of the selected candidate bus in order is . It is reasonable to install μPMU at since it can obtain the maximum information gain at the first round. Then it comes to and . After the selection of , the fourth bus to be installed with μPMU is . However, the results calculated by IENS obviously cannot obtain the full observability for the 11-bus test system since is unobservable.
Compare the results of IENS with the results of topological method, the major reason for the unobservability of placement of IENS is the selection of . Although the selection of can maximize the information gain of the network in the first round, it results in additional 2 μPMUs to make observable, which means it needs 5 μPMUs to make 11-bus test system by IENS. When 2 μPMUs are located at and instead of and , the placement can obtain the full observability just as shown in Figure 2. Considering the full observability of 11-bus network, may not be the ideal location for μPMU. To sum up, the bus which has one or more two-bus branches cannot be the selection of new μPMU. For instance, branch 7–8 and 9–10 is the two-bus branch of the bus as shown in Figure 1, and would not be the selection of μPMU considering the full observability of the network.
Thus the node selection part needs to be improved with the combination of characteristics of the placement of topological method for full observability. After the application of IENS on different networks for many times, two rules are summarized to be observed to improve the observability of IENS. The rules of the selection of candidate bus for μPMU should be proposed as follows:
Rule 1:
Find the bus k which maximizes the improvement in information gain of differential entropy by using Equation (9), if bus k has one or more two-bus branches, then add the buses adjacent to bus k on two-bus branches into new set , sort the buses in by information gain and find the bus q which maximizes the improvement of information gain, then ; if there is no two-bus branch collected to bus k, then . (Bus represents the selected bus to be installed with new μPMU in current round).
For example, is the bus which maximizes the improvement in information gain in the 11-bus test system, result of IENS proves that is not the ideal location for μPMU. Then according to Rule 1, has two-bus braches 7–8 and 9–10, adds and into set , sort and by the information gain, and find the bus which maximizes the improvement of information gain as the selection bus for installation of μPMU.
The simulation test on 11-bus test system shows that the location of new μPMU cannot simply be the bus which maximizes the information gain of network. This kind of bus is not the optimal location for new μPMU when it has one or more two-bus branches. Taking the full observability into consideration, after finding the bus k which can maximize the information gain of differential entropy of network, the selection bus to be installed for μPMU should be determined by Rule 1.
Rule 2:
The terminal bus cannot be installed with μPMU in the distribution network.
Considering the radial structure of distribution system, since a μPMU can measure both the voltage magnitude and phasor angle of associated bus and current magnitude and phasor along all lines collected to this bus, the μPMU should not be placed at terminal bus.
2.3.3. Improved Information Entropy Evaluation and Node Selection Strategy
According to the rules above, the improved IENS can be modified based on the IENS with Rules 1 and 2 in node selection part.
In the simulation of 11-bus test system, the result of improved IENS is same as the result of topological method in Figure 2, which also needs four μPMUs to make network full observable. The order of the locations of four μPMUs is 7, 3, 9, and 1. should be the installation of new μPMU in the first selection since it obtains the maximal information gain. However, turns to be the location for μPMU according to Rule 1 since has larger improvement of information gain than. Then and is selected to be installed with μPMU in the following round due to their maximization of improvement of information gain.
The process of improved IENS combined with Rules 1 and 2 for optimal μPMU set is shown in Figure 4.
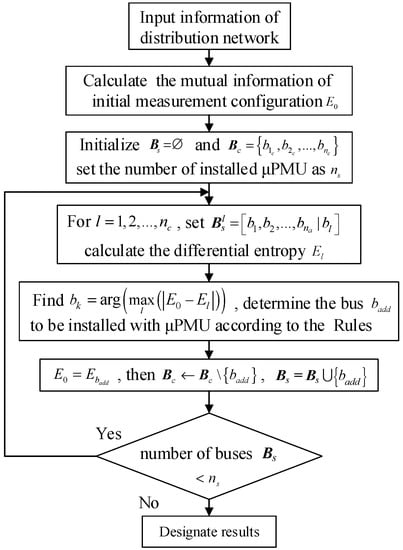
Figure 4.
Block diagram of improved IENS.
3. Case Studies
The modified IEEE 123 test system is used to verify the effectiveness of proposed method. The layout of the test system is shown in Figure 5. The test system contains five distribution generations denoted by gray rectangles. Details of the test system can be referred to in Reference [52].
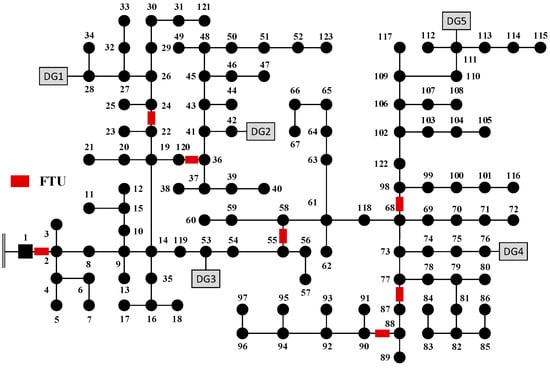
Figure 5.
The modified Institute of Electrical and Electronics Engineers (IEEE) 123 test system.
It is assumed that seven FTUs have been installed in the test distribution system. The locations of FTUs are on lines 1–2, 55–58, 36–120, 22–24, 68–98, 77–87, 88–90 which are denoted by red rectangles in Figure 5.
Three types of measurements with different accuracy values are considered in this paper. The settings of their maximum percentage errors are as follows:
Pseudo measurements: 50%. These measurements are obtained by load forecasting methods according to the historical data.
FTU measurements: 2%.
PMU measurements: it is assumed to be 1% total vector error in the worst case.
The simulation is performed using MATLAB 2017a, on Xeon E3-1230 3.30-GHz personal computer with 8 G memory.
3.1. Optimal Placement for Full Observability by Improved IENS
Considering the measurements of seven FTUs depicted in Figure 5, the minimal number of μPMUs to make modified 123-bus system full observable is calculated to be 45 by topological method. However, it needs 46 μPMUs to make system observable using genetic algorithm. The drawback of heuristic algorithms such as genetic algorithm is that it is difficult to get the global optimal solution while the topological one can. The optimal μPMUs placements for full observability with and without FTU measurements in modified 123-bus system are shown in Table 1, the results show that the integration of FTUs helps reduce the number of μPMUs.

Table 1.
Minimal micro-phasor measurement unit (μPMU) numbers for full observability with and without feeder terminal unit (FTU) measurements.
According to the results by topological method, the required number of μPMUs is set to be 45 in improved IENS. In this case, the pseudo measurements of injection power of all buses in the network are assumed to be acquired in improved IENS for the selection of μPMU set. Under the initial measurement configuration, the mutual information gain is calculated with the pseudo injection measurements and FTU measurements. Based on the incremental expansion strategy of improved IENS, the locations of 45 μPMUs can be obtained in order as: 2, 9, 20, 61, 22, 68, 56, 79, 107, 109, 41, 88, 32, 24, 28, 59, 71, 92, 48, 75, 15, 101, 111, 43, 54, 106, 83, 85, 46, 94, 37, 64, 66, 4, 104, 31, 90, 52, 114, 16, 6, 96, 39, 99, 29, the optimal deployment of μPMUs is shown in Figure 6.
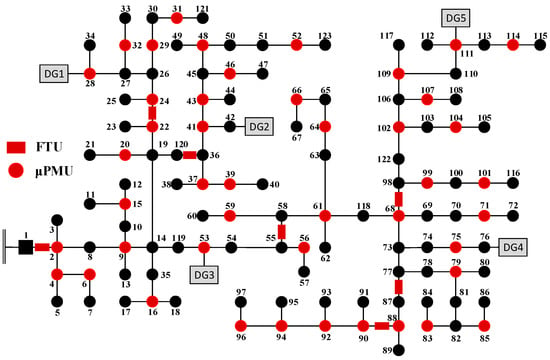
Figure 6.
Optimal μPMU placement by improved IENS.
According to the mutual information theory, the first several buses are expected to be selected with the maximal information gain for the installations of μPMUs. For example, in the first six selection of μPMUs: 2, 9, 20, 61, 22, 68, , and are the buses adjacent to four buses which means more μPMUs measurements can be acquired. Thus, maximal information gain would be obtained when μPMUs are deployed at these buses.
Take the determination of second selection bus for μPMU as illustration, should be the installation of new μPMU in the second selection since it obtains the maximal information gain after the first selection. However, has a two-bus branch 9–13 and it could not be the selection bus for μPMU according to Rule 1. It is easily to be understood that another μPMU needs to be allocated at to make observable if the second μPMU is located at. Therefore, is determined to be second bus for the location of new μPMU according to Rule 1. So as the selection of and . According to Rule 2, there is no μPMU to be installed at the terminal bus in the network. The results calculated by improved IENS can obtain the full observability of the network which has the same effect of the placement of topological method with the identical number of μPMUs.
The pseudo measurements of DGs are usually considered to have more measurement errors than the pseudo measurements of loads. According to the proposed mutual information theory, the bus installed with DG has the priority to be placed with μPMU since that bus has more uncertainties. For example, when DG3 is located at b54, the μPMU would also be located at b54 instead of b53.
3.2. Incomplete Observability Analysis
The full observability of the distribution system can be obtained when enough μPMUs are deployed in the network. However, such μPMUs cannot be installed in one time due to the huge cost of placement, and only part of them can be placed. With the consideration of partial placement, the μPMU placement for maximal observability with limited number are studied in both the topological method and improved IENS method.
It is assumed that all pseudo measurements of injection power can be obtain in the ideal situation which rarely happens in reality. Only part of the pseudo injection measurements of the buses can be acquired for the state estimation according to the distribution management system. The different ratios of acquired pseudo injection measurements should be taken into account for the incomplete observability, the observable capability is used to assess the μPMU placements of different required numbers using numerical method. The observable capability is evaluated by the number of configurations which can make network observable with the μPMU placement divided by the number of all configurations in the set.
The case is still tested on the modified IEEE 123 test system. To evaluate the observable capability of the μPMU placement under different ratios of pseudo measurements, numerical simulation needs to be conducted. Two sets of pseudo measurements configurations with different ratios are considered, one is 90% and the other is 80%, which means only 80% or 90% pseudo injection measurements of buses can be obtained in a pseudo measurement configuration. Each set has 10,000 different configurations in which the pseudo injection measurements of different ratios are randomly generated first. For example, in the configuration of set with 90% pseudo measurement in modified IEEE 123 test system, about the pseudo injection powers of 111 buses can be used for observability analysis. Then the μPMU placement will be tested to be observable or not by numerical method under 10,000 different configurations. The percentage of observable placements under 10,000 configurations is considered to be the observable capability of the μPMU placement.
In improved IENS, the optimal μPMU set for full observability is calculated in the order of information gain. When it comes to the circumstance that the required μPMU number is smaller than the number for full observability, the buses can be easily selected from the optimal μPMU set which can make system full observable. However, it is hard for topological method to choose μPMUs for incomplete observability since the topological method can only obtain the optimal placement for full observability. For simplicity, buses are selected randomly from the results of topological method for full observability as 500 different placements. These placements are tested by numerical method with the integration of pseudo measurements configurations and the mean observability capability is compared with the one of improved IENS.
The observability capability of results of improved IENS and topological method under different circumstances are shown in Table 2.

Table 2.
Observability capability of improved IENS and topological method under different circumstances.
As shown in Table 2, the mean observable capability of results of topological method in 500 configurations is selected to be compared with the observable capability of results of Improved IENS. The observable capability of both topological method and improved IENS seem to be better when the numbers of μPMUs increased. Under both of 80% and 90% pseudo measurement configurations, the observable capabilities of improved IENS are better than the topological method. Due to the methodology of improved IENS, the incremental expansion strategy helps the mutual information of network nearly maximal at the incremental placement of μPMUs which obtains better observable capability than the topological method.
Take 40 μPMUs to be installed under 90% pseudo measurements configurations as an example; the observable capability of improved IENS is 97%, which is larger than the mean value of 500 placements of topological method. The observable capability of improved IENS is still larger than the mean value of topological method when the number of required μPMUs is 30 or 35. The observable capability of improved IENS outbalances the average level of the placements according to the results of topological method. The placement of both improved IENS and topological method seems to have better observable capability when the pseudo measurement configurations increased from 80 to 90%.
3.3. Effects of Two Rules
According to the results by topological method, the required number of μPMUs is set to be 45 in IENS and improved IENS. Also, the pseudo measurements of injection power of all buses in the network are used in improved IENS and IENS. Under 45, the results of both IENS and improved IENS are shown in Table 3 in the order of node selection. The results of three methods are tested for observability through numerical method. The observability of corresponding methods are shown in Table 3.

Table 3.
Optimal μPMU placements of three methods.
The result of topological method and improved IENS is tested to be observable by using a numerical method, while the result calculated by IENS is unobservable. As depicted in Figure 7 and Figure 8, the buses in the green ellipses are the main differences between results of IENS and topological method. Note the area surrounded by green ellipses, μPMUs are mostly located at the buses adjacent to the terminal buses in Figure 7 while μPMUs are not in Figure 8. In the area 1, 3, 5, and 6 the buses in areas are all observable in Figure 7, while are not observable in Figure 8. These areas need more μPMUs for observable due to the suboptimal placement of μPMUs. The number of μPMUs will decrease effectively when μPMU is installed at the bus which is adjacent to the terminal bus in the green areas in Figure 8. Especially in the area 7, which contains , the information gain would be larger when the μPMU is placed at, but and would be out of observability if there is no other μPMU in this area. It needs three μPMUs to make area 7 observable in Figure 8, while only two μPMUs are needed in Figure 7.
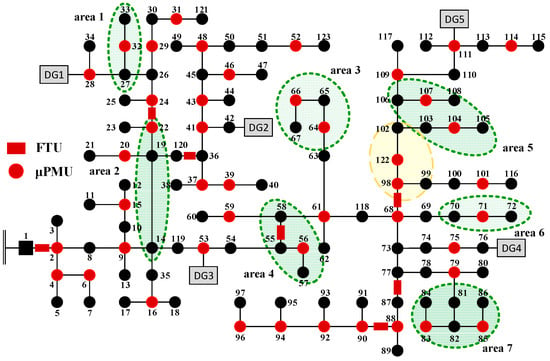
Figure 7.
Optimal μPMU placement by topological method.
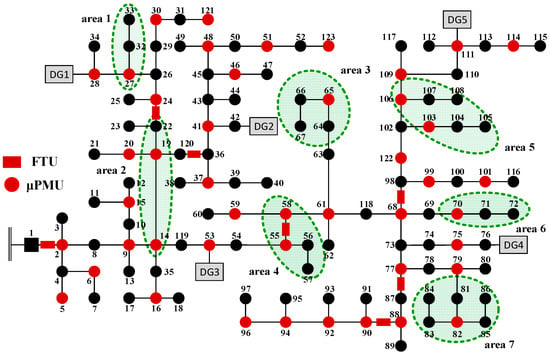
Figure 8.
Optimal μPMU placement by IENS.
With the compliance of rules, the placement of μPMUs calculated by improved IENS is shown in Table 3 and Figure 9, the results are proved to be full observable under the test of numerical method with the same μPMU number of topological method. The placement of improved IENS is quite similar to the results in Figure 7 except the yellow area.
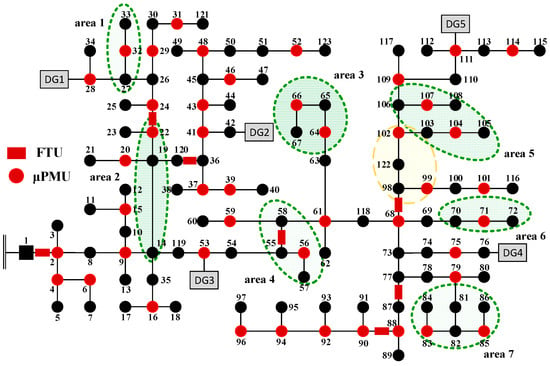
Figure 9.
Optimal μPMU placement by improved IENS.
According to the Rules 1 and 2, the buses in the green areas in Figure 9 can be full observable under the optimal locations of μPMUs. The μPMUs are deployed at the buses adjacent to the terminal bus which cooperates with other μPMUs, making the network full observable. The results prove the effectiveness of improved IENS for full observability compared with the results of topological method with the same number of μPMUs.
3.4. Limitations of the Improved IENS
Although the improved IENS has good performance in both complete and incomplete observability, it still has some limitations. The proposed method requires the integration of pseudo measurements in the stochastic state estimation, and the pseudo measurements are assumed to be obtained from historical data using load forecasting method. However, such historical data information is hard to be acquired in the actual distribution. Also, the proposed method only focuses on the observability of the network. The accuracy of state estimation, stability in fault and limitations in μPMU channels have not been taken into consideration.
4. Conclusions
This paper presents an optimal μPMU placement based on IENS using greedy algorithm. The differential entropy of mutual information theory is introduced and utilized to evaluate the uncertainty of distribution network in AC power flow mode using the results of 2PEM. By using mutual information theory, the IENS method is proposed first. However, the effectiveness of IENS is not satisfied enough and could not obtain full observability under the same number of placement of topological method. With the consideration of characteristic of the placement of topological method, improved IENS is presented with two rules based on the IENS strategy. The improved IENS proves to have the same effect as topological method in complete observability, using 45 μPMUs to make modified IEEE 123 test system full observable. As shown in Table 2, the improved IENS has better observable capability when the required μPMUs cannot make system full observable compared with topological method. The placement seems to have better observable capability when the pseudo measurement configurations increase. The results on the simulations prove the effectiveness of improved IENS both in full observability and incomplete observability. The proposed method only focuses on optimal placement under normal operation, and the reliability such as N-1 PMU loss will be considered in future work.
Author Contributions
The contribution of Z.W. is review and editing, the contribution of X.D. is writing he original draft, review and editing, the contribution of W.G. is review and editing, the contribution of P.L. is data curation and investigation, the contribution of J.L. is conducting formal analysis and supervision, the contribution of C.F. is providing methodology and resources.
Funding
This work was supported by National Key Research and Development Program of China (Grant No. 2017YFB0902800) and the State Grid Corporation of China.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Sets and Indices | |
| The set of candidate buses where the installation of new micro-phasor measurement unit (μPMU) is selected from. | |
| The set of buses for the installation of μPMU, the location of new μPMU will be added in this set. | |
| The set of buses at th iteration. | |
| The set of buses which contains the buses adjacent to bus k on two-bus branches. | |
| The line connected between bus i and bus j. | |
| The ith bus. | |
| The bus k which maximizes the improvement in information gain of differential entropy. | |
| The selected bus to be installed with new μPMU in current round. | |
| Parameters | |
| The standard deviation of variable x. | |
| The mean of variable x. | |
| Vector of measurements. | |
| Error vector of measurements. | |
| Variance of ith measurements. | |
| The Jacobian matrix. | |
| The number of measurements. | |
| The covariance matrix of measurements. | |
| The block diagonal matrix. | |
| The number of iteration in weighted least square (WLS) state estimation. | |
| The general rotation matrix. | |
| The measurements vector in state estimation. | |
| The ith measurement in state estimation. | |
| The number of uncertain variables of pseudo measurements. | |
| The number of certain measurements obtained from phasor measurement unit (PMU) and supervisory control and data acquisition (SCADA) system. | |
| The expectation of state variables vector. | |
| The expectation of square of state variables vector. | |
| The concentration of measurement at step t. | |
| The location of concentration of measurement at step t. | |
| The probability of concentration of measurement at step t. | |
| The concentration of measurement at step t. | |
| The measurements vector at step t. | |
| The mean value of , obtained from measurement information. | |
| The standard deviation of , obtained from measurement information. | |
| The mean value of state variables . | |
| The standard deviation of state variables | |
| The initial differential entropy of the network. | |
| The differential entropy of the network. | |
| The number of all buses in the network. | |
| The standard deviation of voltage amplitude at bus i. | |
| The standard deviation of voltage phase angle at bus i. | |
| The number of candidate buses which can be the location for new μPMU. | |
| The number of round in the information entropy evaluation and node selection strategy (IENS). | |
| The differential entropy of the network at th iteration. | |
| The number of μPMUs decided to be installed in the network according to the budget. | |
| The number of optimal placement calculated by topological method for network full observability. | |
| Variables | |
| State variables of network, including magnitude and phasor angle of voltage. | |
| The state variables vector in state estimation. | |
| Nonlinear function of state variables. | |
| I(x) | Differential entropy for the continuous variable x. |
References
- Ou, T.C. A novel unsymmetrical faults analysis for microgrid distribution systems. Int. J. Electr. Power Energy Syst. 2012, 43, 1017–1024. [Google Scholar] [CrossRef]
- Ou, T.C. Ground fault current analysis with a direct building algorithm for microgrid distribution. Int. J. Electr. Power Energy Syst. 2013, 53, 867–875. [Google Scholar] [CrossRef]
- Ou, T.C.; Hong, C.M. Dynamic operation and control of microgrid hybrid power systems. Energy 2014, 66, 314–323. [Google Scholar] [CrossRef]
- Ou, T.C.; Lu, K.H.; Huang, C.J. Improvement of Transient Stability in a Hybrid Power Multi-System Using a Designed NIDC (Novel Intelligent Damping Controller). Energies 2017, 10, 488. [Google Scholar] [CrossRef]
- Ree, J.D.L.; Centeno, V.; Thorp, J.S.; Phadke, A.G. Synchronized Phasor Measurement Applications in Power Systems. IEEE Trans. Smart Grid 2010, 1, 20–27. [Google Scholar]
- Bertsch, J.; Carnal, C.; Karlson, D.; Mcdaniel, J.; Vu, K. Wide-Area Protection and Power System Utilization. Proc. IEEE 2005, 93, 997–1003. [Google Scholar] [CrossRef]
- Dong, Z.Y.; Xu, Y.; Zhang, P.; Wong, K.P. Using IS to Assess an Electric Power System’s Real-Time Stability. IEEE Intell. Syst. 2013, 28, 60–66. [Google Scholar] [CrossRef]
- Jamei, M.; Scaglione, A.; Roberts, C.; Stewart, E.; Peisert, S.; Mcparland, C.; Mceachern, A. Anomaly Detection Using Optimally-Placed μPMU Sensors in Distribution Grids. IEEE Trans. Power Syst. 2017, 33. [Google Scholar] [CrossRef]
- Teimourzadeh, S.; Aminifar, F.; Shahidehpour, M. Contingency-Constrained Optimal Placement of Micro-PMUs and Smart Meters in Microgrids. IEEE Trans. Smart Grid 2017, 1. [Google Scholar] [CrossRef]
- Askounis, D.T.; Kalfaoglou, E. The Greek EMS-SCADA: From the contractor to the user. IEEE Trans. Power Syst. 2000, 15, 1423–1427. [Google Scholar] [CrossRef]
- Zhou, M.; Centeno, V.A.; Thorp, J.S.; Phadke, A.G. An Alternative for Including Phasor Measurements in State Estimators. IEEE Trans. Power Syst. 2006, 21, 1930–1937. [Google Scholar] [CrossRef]
- Costa, A.S.E.; Albuquerque, A.; Bez, D. An estimation fusion method for including phasor measurements into power system real-time modeling. IEEE Trans. Power Syst. 2013, 28, 1910–1920. [Google Scholar] [CrossRef]
- Glavic, M.; Cutsem, T.V. Reconstructing and tracking network state from a limited number of synchrophasor measurements. IEEE Trans. Power Syst. 2013, 28, 1921–1929. [Google Scholar] [CrossRef]
- Manousakis, N.M.; Korres, G.N.; Aliprantis, J.N.; Vavourakis, G.P.; Makrinas, G.C.J. A two-stage state estimator for power systems with PMU and SCADA measurements. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
- Ritzmann, D.; Wright, P.S.; Holderbaum, W.; Potter, B. A Method for Accurate Transmission Line Impedance Parameter Estimation. IEEE Trans. Instrum. Meas. 2016, 65, 2204–2213. [Google Scholar] [CrossRef]
- Wydra, M. Performance and Accuracy Investigation of the Two-Step Algorithm for Power System State and Line Temperature Estimation. Energies 2018, 11, 1005. [Google Scholar] [CrossRef]
- Jones, K.D.; Pal, A.; Thorp, J.S. Methodology for Performing Synchrophasor Data Conditioning and Validation. IEEE Trans. Power Syst. 2015, 30, 1121–1130. [Google Scholar] [CrossRef]
- Avila-Rosales, R.; Rice, M.J.; Giri, J.; Beard, L.; Galvan, F. Recent experience with a hybrid SCADA/PMU on-line state estimator. In Proceedings of the 2009 Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar]
- Chakrabarti, S.; Kyriakides, E.; Ledwich, G.; Ghosh, A. A comparative study of the methods of inclusion of PMU current phasor measurements in a hybrid state estimator. In Proceedings of the Power and Energy Society General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–7. [Google Scholar]
- Gou, B. Optimal Placement of PMUs by Integer Linear Programming. IEEE Trans. Power Syst. 2008, 23, 1525–1526. [Google Scholar] [CrossRef]
- Kavasseri, R.; Srinivasan, S.K. Joint Placement of Phasor and Power Flow Measurements for Observability of Power Systems. IEEE Trans. Power Syst. 2011, 26, 1929–1936. [Google Scholar] [CrossRef]
- Khajeh, K.G.; Bashar, E.; Rad, A.M.; Gharehpetian, G.B. Integrated Model Considering Effects of Zero Injection Buses and Conventional Measurements on Optimal PMU Placement. IEEE Trans. Smart Grid 2017, 8, 1006–1013. [Google Scholar]
- Wu, F.F.; Monticelli, A. Network Observability: Theory. IEEE Trans. Power Appar. Syst. 1985, PAS 104, 1042–1048. [Google Scholar] [CrossRef]
- Xie, N.; Torelli, F.; Bompard, E.; Vaccaro, A. A graph theory based methodology for optimal PMUs placement and multiarea power system state estimation. Electr. Power Syst. Res. 2015, 119, 25–33. [Google Scholar] [CrossRef]
- Khorram, E.; Jelodar, M.T. PMU placement considering various arrangements of lines connections at complex buses. Int. J. Electr. Power Energy Syst. 2018, 94, 97–103. [Google Scholar] [CrossRef]
- Peng, J.; Sun, Y.; Wang, H.F. Optimal PMU placement for full network observability using Tabu search algorithm. Int. J. Electr. Power Energy Syst. 2006, 28, 223–231. [Google Scholar] [CrossRef]
- Aminifar, F.; Lucas, C.; Khodaei, A.; Fotuhi-Firuzabad, M. Optimal Placement of Phasor Measurement Units Using Immunity Genetic Algorithm. IEEE Trans. Power Deliv. 2009, 24, 1014–1020. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B. Application of heuristic algorithms to optimal PMU placement in electric power systems: An updated review. Renew. Sustain. Energy Rev. 2015, 50, 214–228. [Google Scholar] [CrossRef]
- Korres, G.N.; Manousakis, N.M.; Xygkis, T.C.; Löfberg, J. Optimal phasor measurement unit placement for numerical observability in the presence of conventional measurements using semi-definite programming. IET Gener. Transm. Distrib. 2015, 9, 2427–2436. [Google Scholar] [CrossRef]
- Manousakis, N.M.; Korres, G.N. Optimal PMU Placement for Numerical Observability Considering Fixed Channel Capacity—A Semidefinite Programming Approach. IEEE Trans. Power Syst. 2016, 31, 3328–3329. [Google Scholar] [CrossRef]
- Hurtgen, M.; Maun, J.C. Optimal PMU placement using Iterated Local Search. Int. J. Electr. Power Energy Syst. 2010, 32, 857–860. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B. Optimal placement of phasor measurement units to attain power system observability utilizing an upgraded binary harmony search algorithm. Energy Syst. 2015, 6, 201–220. [Google Scholar] [CrossRef]
- Tran, V.-K.; Zhang, H.-S. Optimal PMU Placement Using Modified Greedy Algorithm. J. Control Autom. Electr. Syst. 2018, 29, 99–109. [Google Scholar] [CrossRef]
- Pokharel, S.P.; Brahma, S. Optimal PMU placement for fault location in a power system. In Proceedings of the North American Power Symposium, Starkville, MS, USA, 4–6 October 2009; pp. 1–5. [Google Scholar]
- Aminifar, F.; Khodaei, A.; Fotuhi-Firuzabad, M.; Shahidehpour, M. Contingency-Constrained PMU Placement in Power Networks. IEEE Trans. Power Syst. 2010, 25, 516–523. [Google Scholar] [CrossRef]
- Sarailoo, M.; Wu, N.E. A new PMU placement algorithm to meet a specified synchrophasor availability. In Proceedings of the Innovative Smart Grid Technologies Conference, Minneapolis, MN, USA, 6–9 September 2016; pp. 1–5. [Google Scholar]
- Kim, T.T.; Poor, H.V. Strategic Protection Against Data Injection Attacks on Power Grids. IEEE Trans. Smart Grid 2011, 2, 326–333. [Google Scholar] [CrossRef]
- Chen, J.; Abur, A. Placement of PMUs to Enable Bad Data Detection in State Estimation. IEEE Trans. Power Syst. 2006, 21, 1608–1615. [Google Scholar] [CrossRef]
- Qi, J.; Sun, K.; Kang, W. Optimal PMU Placement for Power System Dynamic State Estimation by Using Empirical Observability Gramian. IEEE Trans. Power Syst. 2015, 30, 2041–2054. [Google Scholar] [CrossRef]
- Sodhi, R.; Sharieff, M.I. Phasor measurement unit placement framework for enhanced wide-area situational awareness. IET Gener. Transm. Distrib. 2015, 9, 172–182. [Google Scholar] [CrossRef]
- Guo, T.Y.; Milanovic, J.V. Online Identification of Power System Dynamic Signature Using PMU Measurements and Data Mining. IEEE Trans. Power Syst. 2016, 31, 1760–1768. [Google Scholar] [CrossRef]
- Kim, T.; Wright, S.J. PMU Placement for Line Outage Identification via Multinomial Logistic Regression. IEEE Trans. Smart Grid 2018, 9, 122–131. [Google Scholar] [CrossRef]
- Li, Q.; Cui, T.; Weng, Y.; Negi, R.; Franchetti, F.; Ilic, M.D. An Information-Theoretic Approach to PMU Placement in Electric Power Systems. IEEE Trans. Smart Grid 2013, 4, 446–456. [Google Scholar] [CrossRef]
- Abdelsalam, H.A.; Abdelaziz, A.Y.; Mukherjee, V. Optimal PMU placement in a distribution network considering network reconfiguration. In Proceedings of the International Conference on Circuit, Power and Computing Technologies, Nagercoil, India, 20–21 March 2014; pp. 191–196. [Google Scholar]
- Meier, A.V.; Culler, D.; Mceachern, A.; Arghandeh, R. Micro-synchrophasors for distribution systems. In Proceedings of the Innovative Smart Grid Technologies Conference, Washington, DC, USA, 19–22 February 2014; pp. 1–5. [Google Scholar]
- Meier, A.V.; Stewart, E.; Mceachern, A.; Andersen, M.; Mehrmanesh, L. Precision Micro-Synchrophasors for Distribution Systems: A Summary of Applications. IEEE Trans. Smart Grid 2017, 8, 2926–2936. [Google Scholar] [CrossRef]
- Stewart, E.; Stadler, M.; Roberts, C.; Reilly, J.; Dan, A.; Joo, J.Y. Data-driven approach for monitoring, protection, and control of distribution system assets using micro-PMU technology. CIRED Open Access Proc. J. 2017, 2017, 1011–1014. [Google Scholar] [CrossRef]
- Verbic, G.; Canizares, C.A. Probabilistic Optimal Power Flow in Electricity Markets Based on a Two-Point Estimate Method. IEEE Trans. Power Syst. 2006, 21, 1883–1893. [Google Scholar] [CrossRef]
- Su, C.L.; Lu, C.N. Two-point estimate method for quantifying transfer capability uncertainty. IEEE Trans. Power Syst. 2005, 20, 573–579. [Google Scholar] [CrossRef]
- Rosenblueth, E. Two-point estimates in probabilities. Appl. Math. Model. 1981, 5, 329–335. [Google Scholar] [CrossRef]
- Hong, H.P. An efficient point estimate method for probabilistic analysis. Reliab. Eng. Syst. Saf. 1998, 59, 261–267. [Google Scholar] [CrossRef]
- Chen, X.; Wu, W.; Zhang, B. Robust Restoration Method for Active Distribution Networks. IEEE Trans. Power Syst. 2016, 31, 4005–4015. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).